El SSIM se introdujo por primera vez en el documento de IEEE de 2004, Evaluación de la calidad de imagen: De la visibilidad de errores a la Similitud Estructural. El resumen proporciona una buena intuición sobre la idea detrás del sistema propuesto,
Los métodos objetivos para evaluar la calidad de la imagen perceptiva tradicionalmente intentaban cuantificar la visibilidad de los errores (diferencias) entre una imagen distorsionada y una imagen de referencia utilizando una variedad de propiedades conocidas del sistema visual humano. Bajo el supuesto de que la percepción visual humana está altamente adaptada para extraer información estructural de una escena, introducimos un marco complementario alternativo para la evaluación de la calidad basado en la degradación de la información estructural.
Resumen: Los autores hacen 2 puntos esenciales,
- La mayoría de las técnicas de evaluación de la calidad de imagen se basan en la cuantificación de errores entre una imagen de referencia y una de muestra. Una métrica común es cuantificar la diferencia en los valores de cada uno de los píxeles correspondientes entre la muestra y las imágenes de referencia (utilizando, por ejemplo, el Error Cuadrado Medio).
- El sistema de percepción visual humana es altamente capaz de identificar información estructural de una escena y, por lo tanto, identificar las diferencias entre la información extraída de una escena de referencia y una escena de muestra. Por lo tanto, una métrica que replica este comportamiento funcionará mejor en las tareas que implican diferenciar entre una muestra y una imagen de referencia.
La métrica Índice de Similitud Estructural (SSIM) extrae 3 características clave de una imagen:
- Luminancia
- Contraste
- Estructura
La comparación entre las dos imágenes se realiza sobre la base de estas 3 características.
La figura 1 que figura a continuación muestra la disposición y el flujo del sistema de Medición de Similitud Estructural. La señal X y la Señal Y se refieren a las Imágenes de Referencia y de Muestra.

Pero, ¿qué calcula esta métrica?
Este sistema calcula el Índice de Similitud Estructural entre 2 imágenes dadas, que es un valor entre -1 y +1. Un valor de +1 indica que las 2 imágenes dadas son muy similares o iguales, mientras que un valor de -1 indica que las 2 imágenes dadas son muy diferentes. A menudo, estos valores se ajustan para estar en el rango , donde los extremos tienen el mismo significado.
Ahora, exploremos brevemente cómo se representan matemáticamente estas características y cómo contribuyen a la puntuación final de SSIM.Luminancia
- : La luminancia se mide promediando todos los valores de píxeles. Su denotado por μ (Mu) y la fórmula se da a continuación,
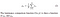
- Contraste: Se mide tomando la desviación estándar (raíz cuadrada de varianza) de todos los valores de píxeles. Se denota por σ (sigma) y se representa mediante la fórmula siguiente,
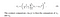
- Estructura: La comparación estructural se realiza utilizando una fórmula consolidada (más sobre eso más adelante), pero en esencia, dividimos la señal de entrada con su desviación estándar para que el resultado tenga una desviación estándar unitaria que permita una comparación más robusta.
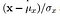
Así que ahora que hemos establecido la intuición matemática detrás de los tres parámetros. Pero espera! Aún no hemos terminado con los cálculos, un poco más. Lo que nos falta ahora son funciones de comparación que puedan comparar las dos imágenes dadas en estos parámetros, y finalmente, una función de combinación que las combine todas. Aquí, definimos las funciones de comparación y finalmente la función de combinación que produce el valor del índice de similitud
- Función de comparación de luminancia: Está definida por una función, l(x, y) que se muestra a continuación. μ (mu) representa la media de una imagen dada. x e y son las dos imágenes que se comparan.
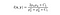
donde C1 es una constante para garantizar la estabilidad cuando el denominador se hace 0. C1 está dado por,
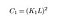
Actualización: A lo largo del artículo, no habíamos explorado cuáles son las constantes K y L en esta ecuación. Afortunadamente, un lector señaló eso en los comentarios, y por lo tanto, en el interés de hacer que este artículo sea un poco más útil, simplemente los definiré aquí.
L es el rango dinámico para los valores de píxeles (lo configuramos como 255 ya que estamos tratando con imágenes estándar de 8 bits). Puedes leer más sobre los diferentes tipos de imágenes y lo que significan, aquí.
K1, K2 son constantes normales, ¡no hay mucho!
- Función de comparación de contraste: Está definida por una función c (x, y) que se muestra a continuación. σ denota la desviación estándar de una imagen dada. x e y son las dos imágenes que se comparan.
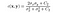
donde C2 es dada por,
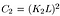
- la Estructura de la función de comparación: Es definido por la función s(x, y) que se muestra a continuación. σ denota la desviación estándar de una imagen dada. x e y son las dos imágenes que se comparan.
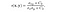
donde σ(xy) se define como,
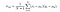
Y por último, el SSIM puntuación está dada por,

donde α > 0, β > 0, γ > 0 denota la importancia relativa de cada una de las métricas. Para simplificar la expresión, si asumimos, α = β = γ = 1 y C3 = C2/2, podemos obtener,
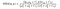
Pero hay un giro de la trama!
Si bien podría implementar SSIM utilizando las fórmulas anteriores, es probable que no sea tan bueno como las implementaciones listas para usar disponibles, ya que los autores explican que,
Para la evaluación de la calidad de imagen, es útil aplicar el índice SSIM localmente en lugar de globalmente. En primer lugar, las características estadísticas de las imágenes suelen ser altamente espaciales no estacionarias. En segundo lugar, las distorsiones de la imagen, que pueden o no depender de las estadísticas de la imagen local, también pueden ser variantes espaciales. En tercer lugar, a distancias de visión típicas, solo un área local de la imagen puede ser percibida con alta resolución por el observador humano en una sola instancia (debido a la función de foveación del HVS ). Y, por último, la medición de calidad localizada puede proporcionar un mapa de calidad de la imagen que varía espacialmente, lo que proporciona más información sobre la degradación de la calidad de la imagen y puede ser útil en algunas aplicaciones.
Resumen: En lugar de aplicar las métricas anteriores globalmente (es decir, en toda la imagen a la vez), es mejor aplicar las métricas regionalmente (es decir, en secciones pequeñas de la imagen y tomando la media general).
Este método se conoce a menudo como el Índice de Similitud Estructural Media.
Debido a este cambio de enfoque, nuestras fórmulas también merecen modificaciones para reflejar el mismo (debe tenerse en cuenta que este enfoque es más común y se utilizará para explicar el código).
(Nota: Si el contenido a continuación parece un poco abrumador, ¡no te preocupes! Si entiendes lo esencial, entonces revisar el código te dará una idea mucho más clara.)
Los autores utilizan una función de pesaje gaussiana circular simétrica de 11×11 (básicamente, una matriz de 11×11 cuyos valores se derivan de una distribución gaussiana) que se mueve píxel por píxel sobre toda la imagen. En cada paso, las estadísticas locales y el índice SSIM se calculan dentro de la ventana local. Dado que ahora estamos calculando las métricas localmente, nuestras fórmulas se revisan como,
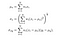
Donde wi es la función de ponderación gaussiana.
Si te pareció un poco poco intuitivo, ¡no te preocupes! Basta con imaginar wi como un multiplicando que se utiliza para calcular los valores requeridos con la ayuda de algunos trucos matemáticos.
Una vez que se realizan los cálculos en toda la imagen, simplemente tomamos la media de todos los valores locales de SSIM y llegamos al valor global de SSIM.
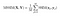
Finalmente hacerse con la teoría! ¡Ahora al código!