Si ha leído el post anterior sobre qué es un inductor, pasemos al siguiente nivel, qué es los circuitos de fórmula de inductancia.
Ahora que el inductor se ha añadido a nuestra lista de elementos pasivos, es necesario ampliar la poderosa herramienta de combinación serie-paralelo. Necesitamos saber cómo encontrar la inductancia equivalente de un conjunto de inductores conectados en serie o conectados en paralelo que se encuentra en circuitos prácticos.
Inductores en serie
Considere una conexión en serie de inductores N, como se muestra en la Figura.(1 bis), con el circuito equivalente que se muestra en la figura.(1 ter).

Los inductores tienen la misma corriente a través de ellos. Aplicando KVL al bucle,

La sustitución de vk = Lk di / dt da como resultado Circuitos de Fórmula de Inductancia
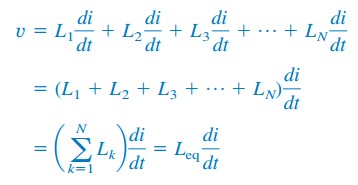
donde

Así,
La inductancia equivalente de los inductores conectados en serie es la suma de las inductancias individuales.
Los inductores en serie se combinan exactamente de la misma manera que las resistencias en serie.
Inductores paralelos
Ahora consideramos una conexión paralela de inductores N, como se muestra en la Figura.(2 bis), con el circuito equivalente en la figura.(2 ter). Los inductores tienen el mismo voltaje a través de ellos. Usando KCL,

Pero


por lo tanto,

donde
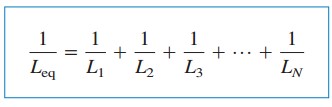
KCL espera que la corriente inicial i(t0) a través de Leq en t= t0 sea la suma de las corrientes inductoras en t0. Por lo tanto, de acuerdo con la Ecuación.(5),
![]()
De acuerdo con la Ecuación.(6),
La inductancia equivalente de los inductores paralelos es el recíproco de la suma de los recíprocos de las inductancias individuales.
Tenga en cuenta que los inductores en paralelo se combinan de la misma manera que las resistencias en paralelo.
Para dos inductores en paralelo (N = 2), Ecuación.(6) se convierte en
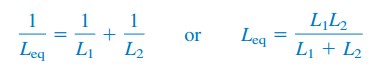
Ejemplos de Circuitos de Fórmula de Inductancia
1. Encuentre la inductancia equivalente del circuito que se muestra en la Figura.(3).
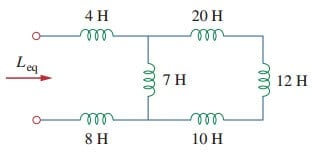
Solución:
Los inductores de 10 H, 12 H y 20 H están en serie; por lo tanto, combinarlos da una inductancia de 42 H. Este inductor de 42 horas está en paralelo con el inductor de 7 horas para que se combinen,para dar


Este inductor de 6 horas está en serie con los inductores de 4 horas y 8 horas. Por lo tanto,
![]()
2. Para el circuito en Figura.(4),
i(t) = 4(2 − e−10t) mA. Si i2(0) = -1 mA, encontrarás:
(a) i1(0);
(b) v(t) v1(t) y v2(t);
(c) i1(t) e i2(t).

Solución:
(a) A partir de i(t) = 4 (2 − e−10t) mA, i(0) = 4(2 − 1) = 4 mA.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) La corriente i1 se obtiene como


Del mismo modo,


Tenga en cuenta que i1(t) + i2(t) = i(t).