Použití a Interpretaci Saint-Venant Princip

Všechny strukturální inženýři použití Saint-Venant principu, ať už aktivně, nebo podvědomě. Různé formulace tohoto principu najdete ve většině učebnic strukturální mechaniky, ale jeho přesný význam není zřejmý. Saint-Venant princip nám říká, že přesné rozložení zatížení není důležité, daleko od naloženo regionu, tak dlouho, jako výslednice zatížení jsou správné. V tomto blogu budeme zkoumat princip Saint-Venant, zejména v kontextu analýzy konečných prvků (FE).

Historie Saint-Venant Princip

francouzský vědec Barré de Saint-Venant vytvořil jeho slavný princip v roce 1855, ale to bylo spíš konstatování, než přísné matematické prohlášení:

„Jestliže síly působící na malou část povrchu pružné tělo jsou nahrazena jinou staticky ekvivalentní soustavy sil působících na stejné části povrchu, toto přerozdělení zatížení vytváří velké změny v napětí lokálně, ale má zanedbatelný vliv na napětí na vzdálenosti, které jsou velké ve srovnání s lineární rozměry povrchu, na kterém jsou síly změnit.“

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Portrét Saint-Venant. Obrázek ve veřejné doméně, přes Wikimedia Commons.

Mnoho velké mozky v oboru aplikované mechaniky — Boussinesq, Láska, von Mises, Domalována, a jiní — byli zapojeni v tom, Saint-Venant princip v přesnější podobě a poskytuje matematické důkazy pro to. Jak se ukazuje, je to pro obecnější případy poměrně obtížné a výzkum na toto téma stále probíhá. (Argumentace byla občas docela živá.)

jednoduchý příklad: analýza napětí ve vzdálenosti

začněme něčím docela jednoduchým: tenká obdélníková deska s kruhovým otvorem v určité vzdálenosti od zatížené hrany, která je tažena axiálně. Pokud nás zajímá koncentrace napětí v díře, jak důležité je skutečné rozložení zatížení?

na pravé hranici jsou aplikovány tři různé typy zatížení:

1. konstantní axiální napětí 100 MPa
2. symetrické parabolické rozložení napětí s maximální amplitudou 150 MPa
3. Na střed bod zatížení se stejným výsledným jako dva předchozí případy zatížení

Jak je vidět v obrázcích níže, rozložení napětí v otvoru není ovlivněna tím, jak působí zatížení. Klíčem je samozřejmě to, že díra je dostatečně daleko od zátěže.

Von Mises napěťové kontury pro tři zatěžovací případy.

dalším způsobem vizualizace tohoto scénáře je použití hlavních stresových šipek. Takový spiknutí zdůrazňuje stresové pole jako tok a dává dobrý pocit pro přerozdělení.

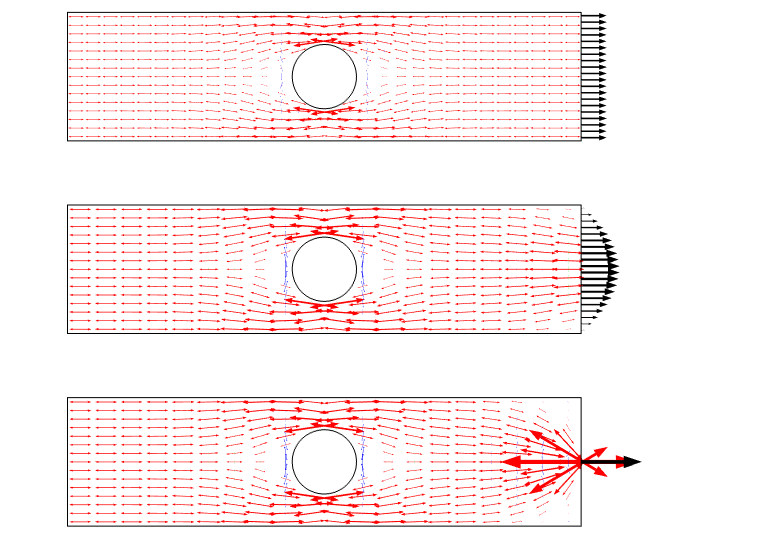
hlavní zátěžový graf pro tři zatěžovací případy. Všimněte si, že při použití bodového zatížení existuje singularita.

grafováním napětí podél čáry vidíme, že všechny tři případy se navzájem sbíhají ve vzdálenosti od okraje, což je přibližně rovno šířce desky.

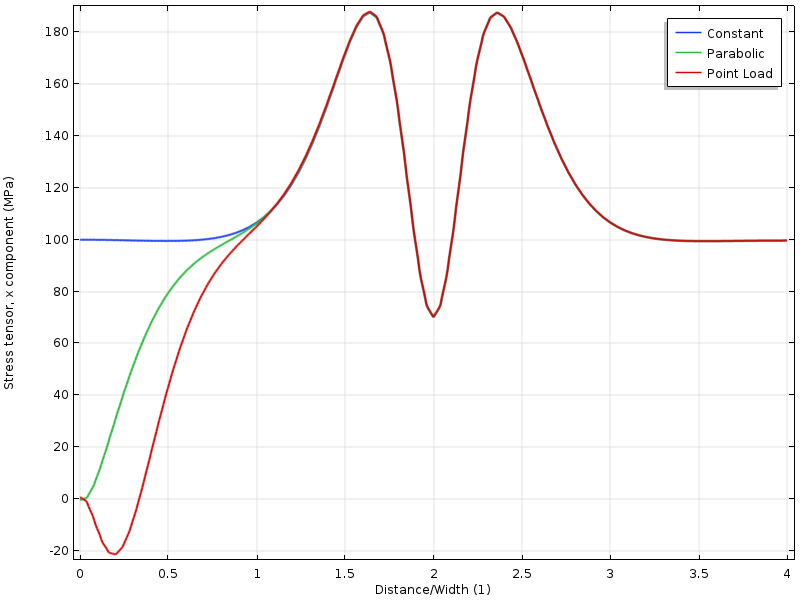
napětí podél horního okraje jako funkce vzdálenosti od zatížené hranice. Vzdálenost je normalizována šířkou desky.

pokud je díra posunuta blíže k načtené hranici, dostaneme další situaci. Stav napětí kolem otvoru nyní závisí na rozložení zatížení. Ale ještě zajímavější je, že vzdálenost k místu, kde se nyní shodují tři pole napětí, je dvakrát tak daleko od zatížené hranice. Použití principu Saint-Venant vyžaduje, aby napětí bylo volně přerozdělováno. V tomto případě je toto přerozdělení částečně blokováno dírou.

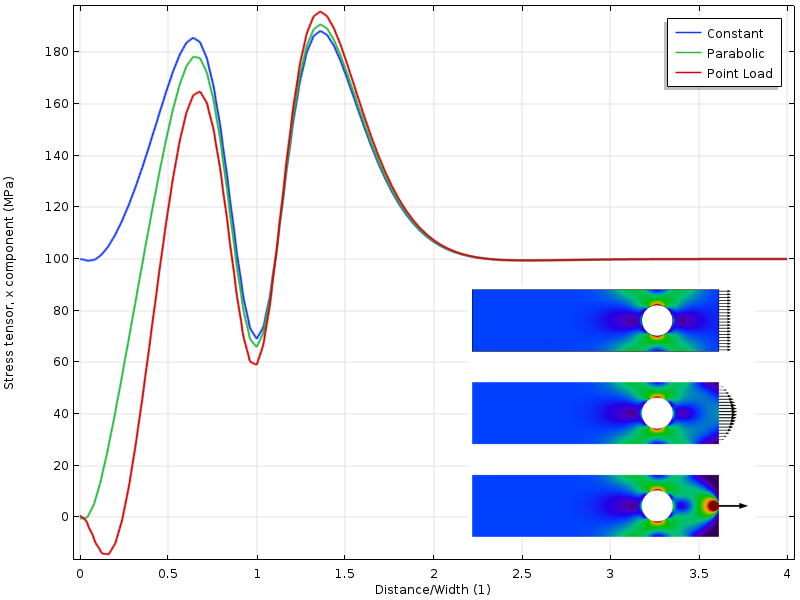
napněte podél horního okraje s otvorem blíže k zatížené hranici.

Všimněte si, že princip Saint-Venant nám říká, že neexistuje žádný rozdíl ve stavu napětí ve vzdálenosti, která je řádově lineární dimenze zatížené oblasti. Zatížená oblast, která má být vzata v úvahu, však nemusí být oblast, která je skutečně načtena! Toto tvrzení může znít divně, ale přemýšlejte o tom takto: Když je díra daleko, můžeme vypočítat faktor koncentrace stresu pomocí příručky (Moje říká 4.32) spíše než řešením FE. Příručka obsahuje implicitní předpoklad, že zatížení je rovnoměrně rozloženo jako v prvním případě zatížení. Takže i když skutečné zatížení bylo aplikováno pouze na malou část hranice, kritická Vzdálenost v tomto případě souvisí s velikostí celé hranice.

při řešení problému pomocí metody konečných prvků (FEM) může být otvor libovolně blízko zátěže. Limit stanovuje to, že z fyzického hlediska je rozložení zátěže dobře definováno. Jakmile však učiníme předpoklady o redistribuci, existuje implicitní předpoklad o rozložení zátěže, které se může lišit od skutečného.

nulové výsledné systémy a hustota energie deformace

doposud jsme říkali, že napětí jsou stejná nezávislá na detailech zatížení v určité vhodné vzdálenosti. Protože se zde zabýváme lineární elasticitou, je vždy možné překrýt zatěžovací případy. Při práci s doklady Saint-Venant principu, je jednodušší formulovat princip podél těchto linek: zdůrazňuje, že v důsledku zatížení systému není výsledná síla nebo moment bude malý ve vzdálenosti, která je stejného řádu jako velikost vloženého hranice.

studujeme tedy napětí způsobené rozdílem mezi dvěma zatěžovacími systémy se stejnými výsledky. Většina moderních důkazů je založena na odhadech rozpadu hustoty energie deformace pro takový nulový výsledný systém.

Vrátíme-li se k výše uvedenému problému, můžeme vypočítat rozdíl mezi zatěžovacími případy. To nám umožňuje studovat skutečný rozpad napětí nebo hustoty energie deformace pro rozdíl stresových polí.

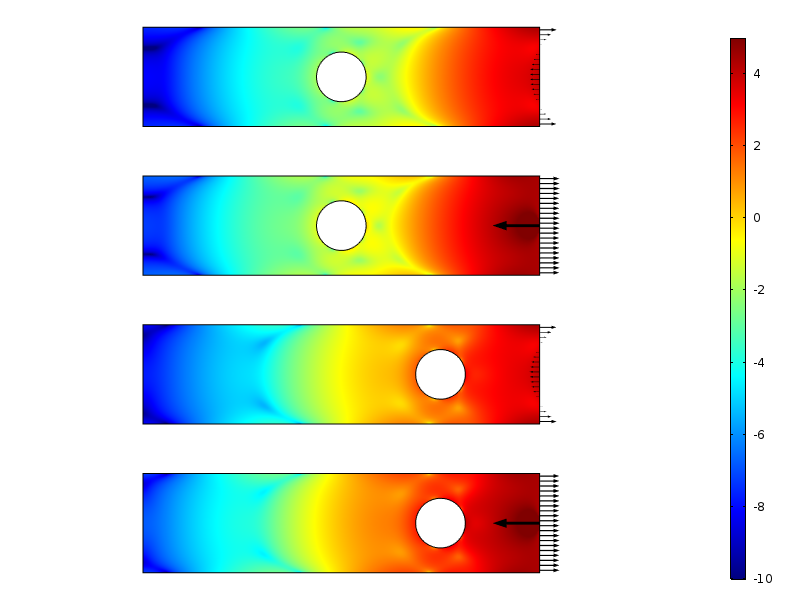
logaritmus hustoty deformační energie pro případy nulového zatížení.

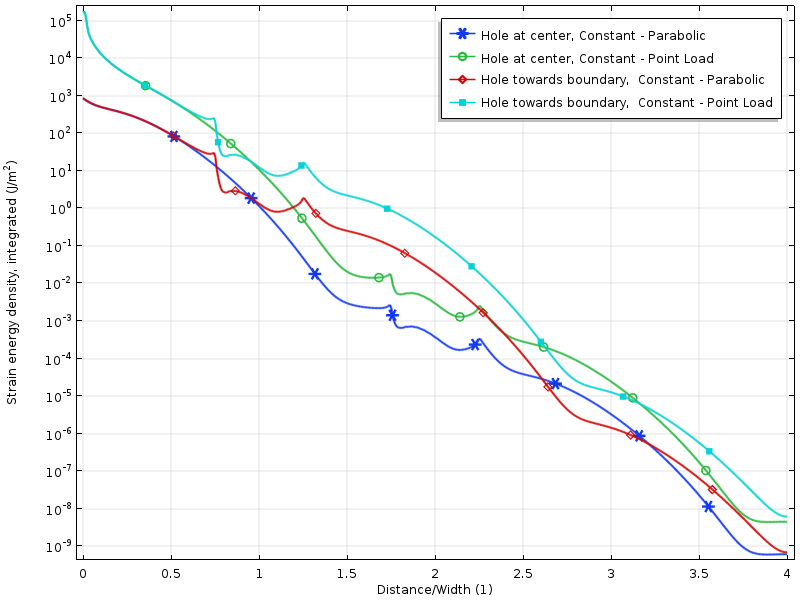
hustota energie deformace podél desky pro nulové výsledné zatěžovací případy. Energie je integrována ve svislém směru, aby se vytvořilo množství, které je pouze funkcí vzdálenosti od zátěže.

rozpad v logaritmu hustoty kmenové energie je víceméně lineární se vzdáleností od zatížené hranice. To je ve skutečnosti v souladu s tím, co předpovídají moderní důkazy: exponenciální rozpad hustoty energie kmene. Můžeme také jasně vidět, jak díra dočasně snižuje rychlost rozpadu.

Použití Saint-Venant Principu Tenké Struktury

Pro tenčí konstrukcí, jako jsou mušle, trámy a krovy, je dobře známo, že Saint-Venant principu nemůže být použita stejným způsobem jako pro „pevný“ objekt. Poruchy cestují na delší vzdálenosti, než očekáváme, protože cesty zatížení v tenké struktuře jsou mnohem omezenější. To je stejný jev, jaký vidíme s dírou ve výše uvedeném příkladu, ale výrazněji.

zde studujeme paprsek se standardním průřezem IPE100. Konec nosníku je vystaven axiálnímu namáhání s amplitudou, která má lineární rozložení v obou směrech průřezu.

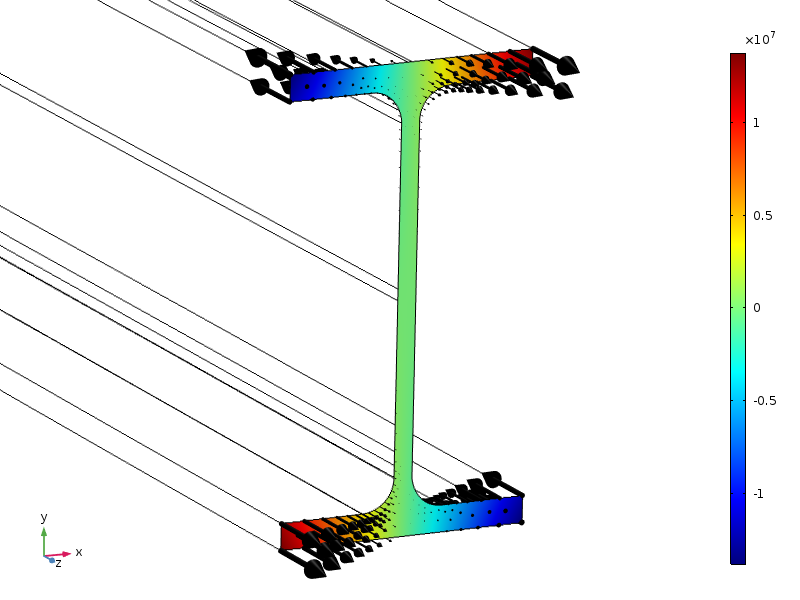
rozložení zatížení, zobrazeno jako obrysy a šipky.

díky symetrii má toto zatížení nulovou výslednou sílu a nulový moment kolem všech OS. Výška průřezu je 100 mm, takže pokud je použitelná standardní forma principu Saint-Venant, měla by být napětí malá ve vzdálenosti přibližně 100 mm od koncové části.

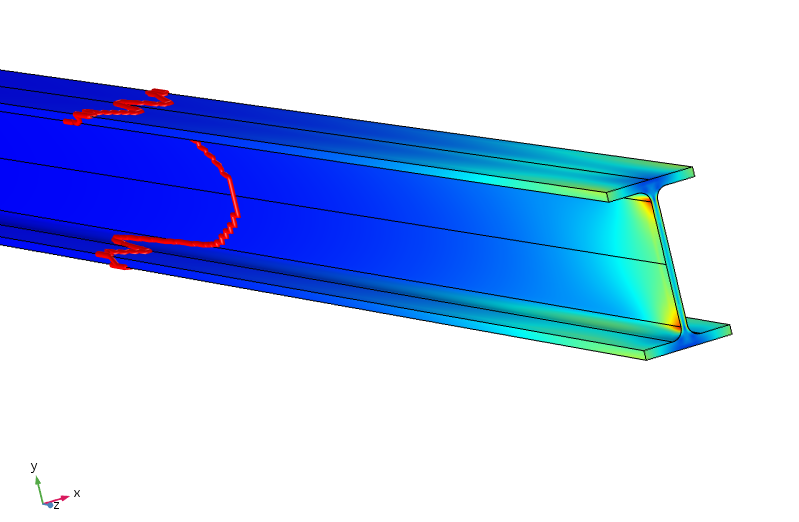
ekvivalentní napětí v paprsku. Červený obrys označuje, kde je napětí menší než 5% maximálního aplikovaného napětí.

ukazuje se, že k tomu, aby napětí bylo pod 5% maximálního aplikovaného napětí, musíme cestovat téměř metr podél paprsku. Redistribuce zatížení je zde tedy mnohem méně účinná, protože rovnováha mezi horní a spodní přírubou vyžaduje přenos momentu přes tenký pás.

Pokud jste obeznámeni s teorií pro nerovnoměrný krut nosníků (tj. deformace teorie nebo Vlasov teorie), poznáte, že použité zatížení má významný bimoment. Bimoment je průřezová veličina s fyzickým rozměrem síla X délka2.

možná (to je jen moje osobní spekulace), účinný princip Saint-Venant pro tento případ by měl vyžadovat nejen sílu a okamžik, ale také bimoment nuly. Toho lze dosáhnout přidáním čtyřbodových zatížení, které poskytují protiváhu bimomentu. Výsledek takové analýzy je uveden níže.

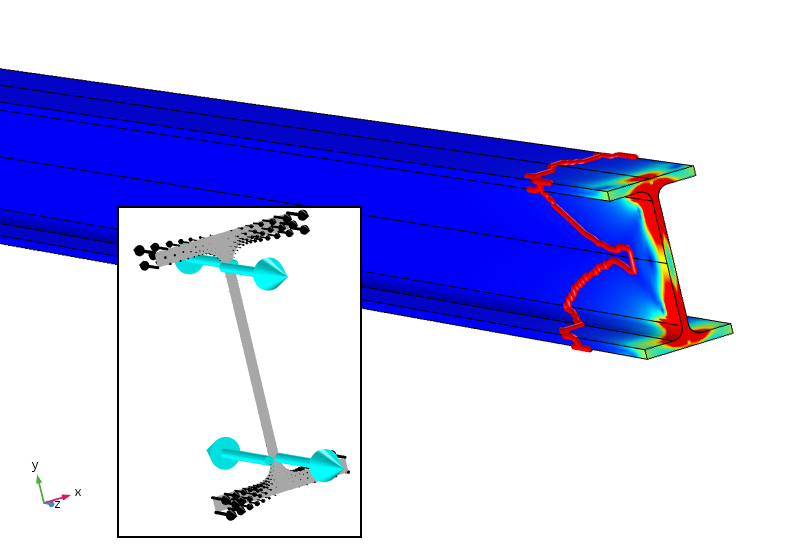
ekvivalentní napětí se čtyřmi bodovými zatíženími, které také poskytují nulový bimoment. Obrys napětí 5% je nyní mnohem blíže k zatížené hranici.

aplikovaná bodová zatížení, která nejsou záměrně optimálně umístěna, způsobují extrémně vysoká (ve skutečnosti singulární) lokální napětí. Nicméně, stres má klesat mnohem rychleji a je nižší než 5% po cca 100 mm. 5% hranice je ještě z hlediska aplikované rozložené zatížení, takže to není upraveno pro nové místní napětí. Logaritmická rychlost rozpadu hustoty energie deformace je třikrát rychlejší po přidání bodového zatížení.

Saint-Venant Princip v Analýze Konečných elementů

V některých případech, můžete intuitivně zvážit Saint-Venant je v zásadě použitelná pro FE discretized problém. Zde se podíváme na distribuované zatížení a nekonformní sítě.

distribuované zatížení

v modelu FE jsou zatížení vždy aplikována na uzly sítě, i když je zadáte jako spojité hraniční zatížení. Zatížení je interně distribuováno do uzlů prvku pomocí principu virtuální práce, jak je ukázáno v následujícím příkladu.

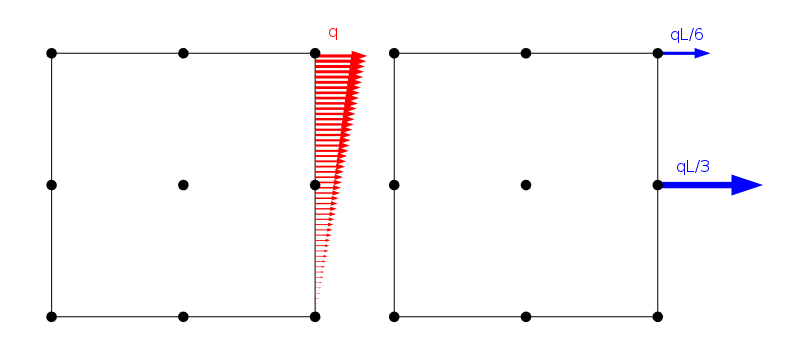
lineárně rozložené zatížení a jak je aplikovat na uzly druhého řádu Lagrange prvek s boční délka L

Tam je, nicméně, nekonečný počet zatížení distribucí, které dávají stejné uzlové zatížení tak dlouho, jak oni sdílejí stejnou výslednou sílu a moment. Je zřejmé, že řešení problému konečných prvků je pro všechny tyto případy stejné. Ze Saint-Venantova principu však můžeme usoudit, že všechna taková zatížení by měla poskytnout v podstatě stejné pole napětí, jakmile jsme v určité vzdálenosti.

Od velikosti plochy, přes který budeme distribuovat zatížení je prvek, obličej, lineární rozměr, po kterém není žádný rozdíl je v podstatě jeden prvek vrstva uvnitř struktury. Řešení v nejvzdálenější vrstvě prvků tedy nemusí odpovídat skutečnému zatížení, ale dále to dělá.

jako příklad můžeme načíst obdélníkovou desku s hraničním zatížením, které má exponenciální rozložení napětí. Napětí vypočtené jemnou sítí je uvedeno níže.

obrysový graf rozložení axiálního napětí.

Protože Saint-Venant je princip, pole napětí se rozloží na čistý ohýbání stát v určité vzdálenosti od načtené hrany, stejně jako očekáváme. To však není cílem současné diskuse. Spíše zkoumáme rozdíl mezi výše uvedeným rozložením napětí a tím, co získáme s řadou hrubých OK.

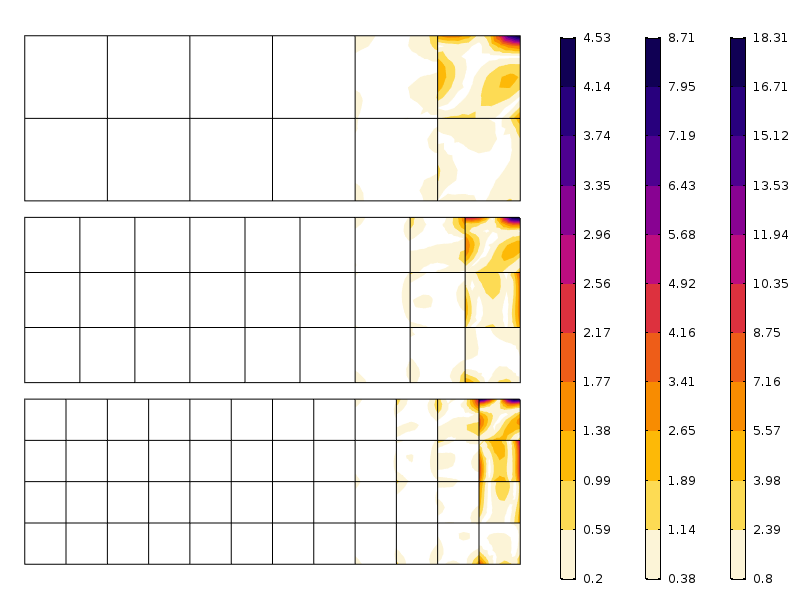
chyba v axiálním namáhání pro tři různá oka. Všimněte si různých měřítek. Jak se dalo očekávat, chyba je menší, když je síť jemnější.

jak je vidět na obrázku, chyba rychle klesá po první vrstvě prvku. To, co zde vidíme, je ve skutečnosti kombinace konvergence sítě a přerozdělování napětí implikovaných principem Saint-Venant.

Nevyhovujících Ok

nevyhovujícího pletiva dochází, když se tvar funkce ve dvou propojených prvků se neshodují. Nejběžnějším případem je připojení sestavy pomocí párů identit a podmínek kontinuity. Abychom to ilustrovali, můžeme studovat rovnou tyč s úmyslně neodpovídající sítí. S jednoduchým zatížením, jako je jednoosé napětí, je možné studovat stresové poruchy způsobené přechodem.

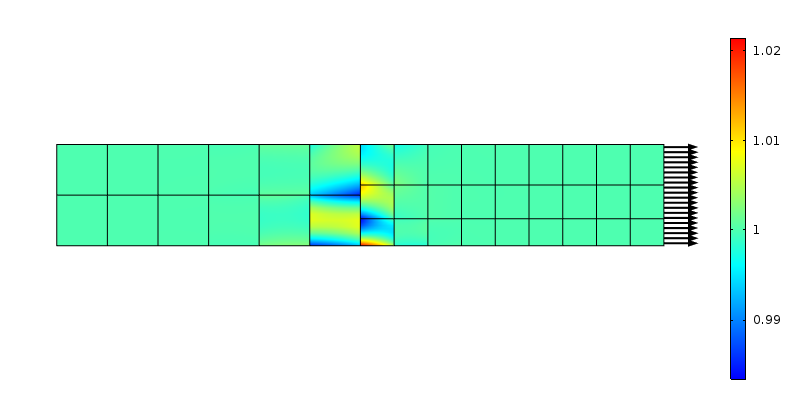
axiální napětí při nekonformním síťovém přechodu. Používají se prvky druhého řádu.

síly přenášené uzly na obou stranách neodpovídají předpokladu konstantního napětí. Opět to lze považovat za místní přerozdělení zátěže v oblasti, která je velikostí prvku. Použití uvažování Saint-Venant, porucha by měla zmizet ve vzdálenosti „velikosti prvku“ od přechodu. Podívejme se, co se stane, když je síť rafinována v axiálním směru.

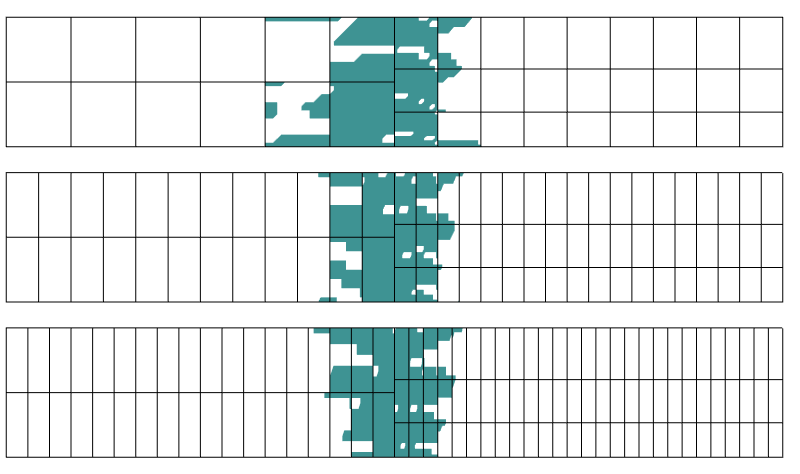
Region s více než 0,1% chybou ve stresu. V axiálním směru se používají tři různé diskretizace.

ukázalo se, že oblast poruchy není ovlivněna moc diskretizaci ve směru kolmém k přechodu hranice. To je přesně to, co nám říká princip Saint-Venant.

Závěrečné Poznámky

Bez použití Saint-Venant principu, mnoho strukturálních analýz, které jsou obtížné provést, jednoduše proto, že detailní rozložení zatížení, není známo.

princip je formálně platný pouze pro lineární elastické materiály. V praxi ji také intuitivně používáme denně pro jiné situace. Pokud, například, materiál, v „deska s dírou“ příklad byly elastoplastic, očekáváme, že by dva rozložené zatížení dávat rovnocenné výsledky, tak dlouho, jak výnos je stres nad stresem aplikována na hranici tak, že tam je pouze plastické deformace v okolí otvoru. Bodové zatížení však vždy dává jiné řešení, protože materiál se pohybuje kolem zatíženého bodu. Pro delší diskusi, přečtěte si tento blogový příspěvek o singularitách při bodovém zatížení.

další kroky

další informace o používání softwaru COMSOL Multiphysics® pro FEA.

Další Čtení

• Y. C. Fung a P. Tong, Klasické a Počítačové Mechaniky těles, World Scientific Publishing Co. PTE. Ltd., 2001.