Saint-Venant elvének alkalmazása és értelmezése

minden szerkezeti mérnök használja Saint-Venant elvét, akár aktívan, akár tudat alatt. Ennek az elvnek a különféle megfogalmazásait megtalálhatja a legtöbb szerkezeti mechanika tankönyvben, de pontos jelentése nem nyilvánvaló. Saint-Venant elve azt mondja nekünk, hogy a terhelés pontos eloszlása nem fontos a betöltött régiótól távol, mindaddig, amíg a terhelés eredményei helyesek. Ebben a blogbejegyzésben megvizsgáljuk Saint-Venant elvét, különösen a végeselem (Fe) elemzés összefüggésében.

a Saint-Venant-elv története

a francia tudós Barrot de Saint-Venant 1855-ben fogalmazta meg híres elvét, de ez inkább megfigyelés volt, mint szigorú matematikai állítás:

“ha a rugalmas test felületének egy kis részére ható erőket egy másik, statikailag ekvivalens erőrendszer váltja fel, amely a felület ugyanazon részére hat, akkor a terhelés ezen újraelosztása lokálisan jelentős változásokat eredményez a feszültségekben, de elhanyagolható hatást gyakorol a feszültségekre olyan távolságokon, amelyek nagyok annak a felületnek a lineáris méreteihez képest, amelyen az erők megváltoznak.”

B. Saint-Venant, M … M. savants alterntrangers, vol. 14, 1855.

Saint-Venant portréja. Kép a nyilvánosság számára, a Wikimedia Commons-on keresztül.

az alkalmazott mechanika területén számos nagy elme — Boussinesq, Love, von Mises, Toupin és mások — részt vettek a Saint-Venant-elv pontosabb megfogalmazásában és matematikai bizonyítékokkal. Mint kiderült, ez általánosabb esetekben meglehetősen nehéz, a témával kapcsolatos kutatások még folyamatban vannak. (Az érvelés időnként meglehetősen élénk volt.)

egyszerű példa: a feszültségek elemzése távolról

kezdjük valami nagyon egyszerűvel: vékony téglalap alakú lemez, kör alakú lyukkal, a betöltött éltől bizonyos távolságra, amelyet tengelyirányban húznak. Ha érdekel a lyuk feszültségkoncentrációja, akkor mennyire fontos a tényleges terheléseloszlás?

három különböző terhelési típust alkalmaznak a jobb szélső határon:

1. 100 MPa állandó axiális feszültség
2. szimmetrikus parabolikus feszültségeloszlás csúcs amplitúdóval 150 MPa
3. egy központosított pontterhelés, amelynek ugyanaz az eredménye, mint a két előző terhelési esetnek

amint az alábbi ábrákon látható, a furat feszültségeloszlását nem befolyásolja a terhelés alkalmazásának módja. A kulcs itt természetesen az, hogy a lyuk elég messze van a terheléstől.

von Mises feszültség kontúrok a három terhelési esetben.

a forgatókönyv megjelenítésének másik módja a fő feszültség nyilak használata. Egy ilyen cselekmény hangsúlyozza a stresszmezőt, mint fluxust, és jó érzést ad az újraelosztáshoz.

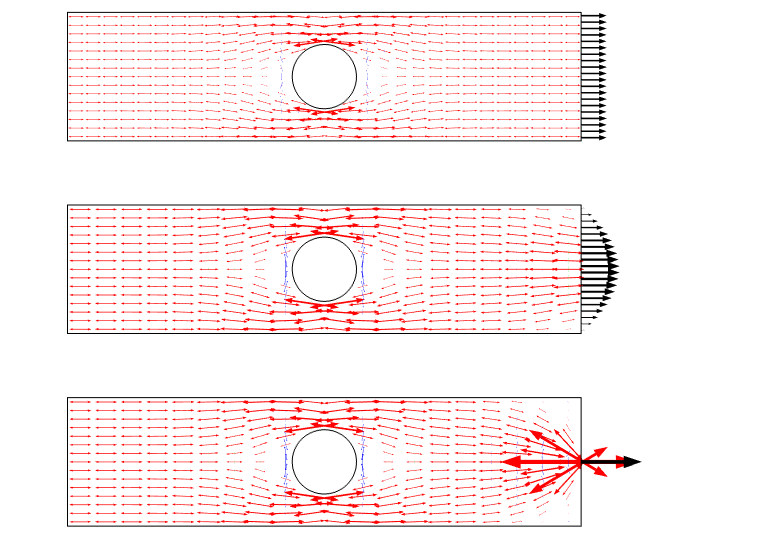
a három terhelési eset fő feszültségdiagramja. Vegye figyelembe, hogy pontterhelés esetén szingularitás van.

a feszültség egy vonal mentén történő ábrázolásával láthatjuk, hogy mindhárom eset egymáshoz közelít a széltől, ami megközelítőleg megegyezik a lemez szélességével.

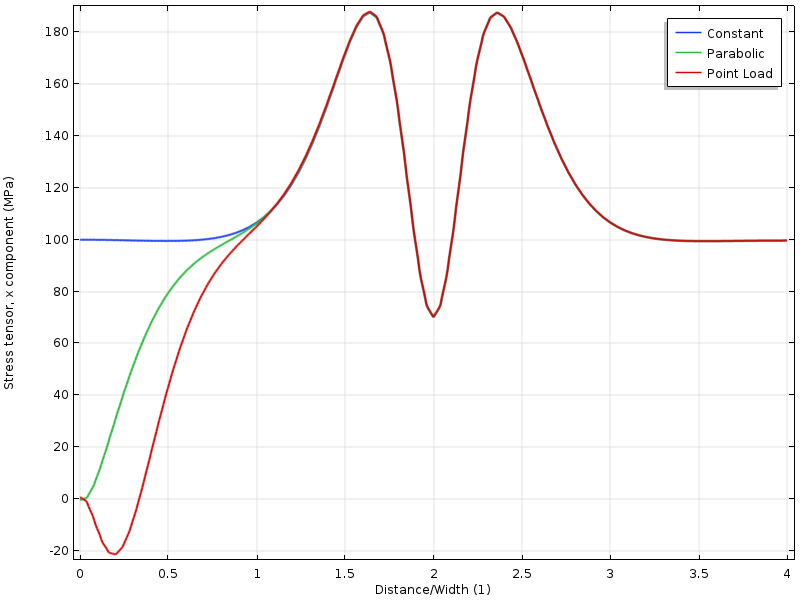
feszültség a felső él mentén a betöltött határtól való távolság függvényében. A távolságot a lemez szélessége normalizálja.

ha a lyuk közelebb kerül a betöltött határhoz, akkor egy másik helyzetet kapunk. A lyuk körüli feszültségállapot most a terhelés eloszlásától függ. De még érdekesebb, hogy a távolság, ahol a három stresszmező egyetért, kétszer olyan messze van a betöltött határtól. Saint-Venant elvének alkalmazása megköveteli, hogy a feszültségek szabadon újraeloszthatók legyenek. Ebben az esetben az újraelosztást részben blokkolja a lyuk.

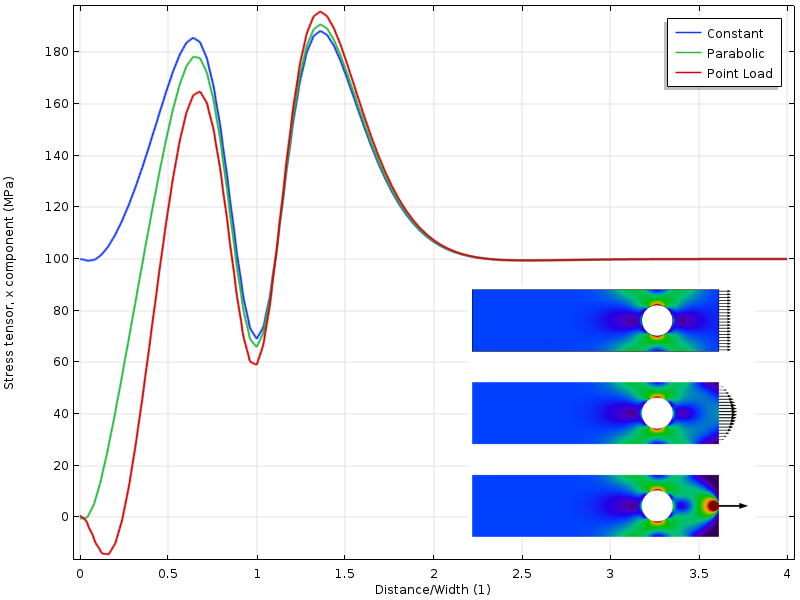
feszítse a felső él mentén úgy, hogy a lyuk közelebb legyen a betöltött határhoz.

vegye figyelembe, hogy Saint-Venant elve azt mondja nekünk, hogy nincs különbség a stresszállapotban a betöltött terület lineáris dimenziójának sorrendjében. A figyelembe veendő betöltött terület azonban nem feltétlenül a ténylegesen betöltött terület! Ez az állítás furcsán hangozhat, de gondoljon rá így: amikor a lyuk messze van, a stresszkoncentrációs tényezőt egy kézikönyv segítségével (az enyém szerint 4.32) számíthatjuk ki, nem pedig FE-megoldással. A kézikönyv megközelítése implicit feltételezést tartalmaz, miszerint a terhelés egyenletesen oszlik el, mint az első terhelési esetben. Tehát még akkor is, ha a tényleges terhelést a határnak csak egy kis részére alkalmazták, a kritikus távolság ebben az esetben a teljes határ nagyságához kapcsolódik.

a probléma végeselemes módszerrel (FEM) történő megoldásakor a lyuk önkényesen közel lehet a terheléshez. A határértéket az határozza meg, hogy fizikai szempontból a terheléseloszlás jól meghatározott. Amint feltételezéseket teszünk az újraelosztásról, van egy implicit feltételezés a terheléseloszlásról, amely eltérhet a ténylegestől.

nulla eredő rendszerek és a törzs energia sűrűsége

eddig azt mondtuk, hogy a feszültségek azonosak a terhelés részleteitől függetlenül, megfelelő távolságban. Mivel itt lineáris rugalmassággal foglalkozunk, mindig lehetséges a terhelési esetek egymásra helyezése. Ha Saint-Venant elvének bizonyítékaival dolgozunk, könnyebb megfogalmazni egy elvet ezen a vonalon: a terhelési rendszer által okozott feszültségek, amelyek nem eredményeznek erőt vagy nyomatékot, kicsiek lesznek olyan távolságban, amely ugyanolyan nagyságrendű, mint a betöltött határ nagysága.

így tanulmányozzuk a két terhelési rendszer közötti különbség által okozott stresszt egyenlő eredményekkel. A legtöbb modern bizonyíték a törzs energia sűrűségének bomlására vonatkozó becsléseken alapul egy ilyen nulla eredményű rendszer esetében.

visszatérve a fenti problémára, kiszámolhatjuk a terhelési esetek közötti különbséget. Ez lehetővé teszi számunkra, hogy tanulmányozzuk a stressz vagy a törzs energia sűrűségének tényleges bomlását a stresszmezők különbségéhez.

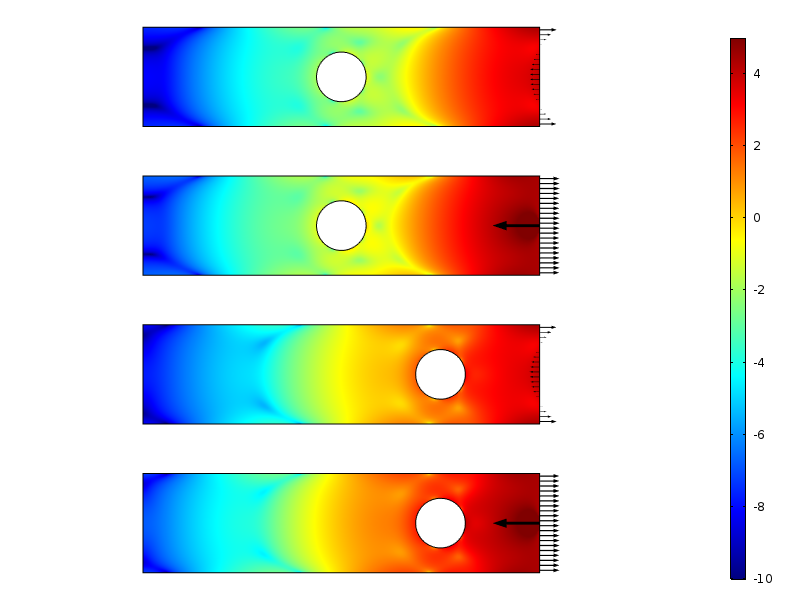
a törzs energia sűrűségének logaritmusa a nulla eredő terhelési esetekre.

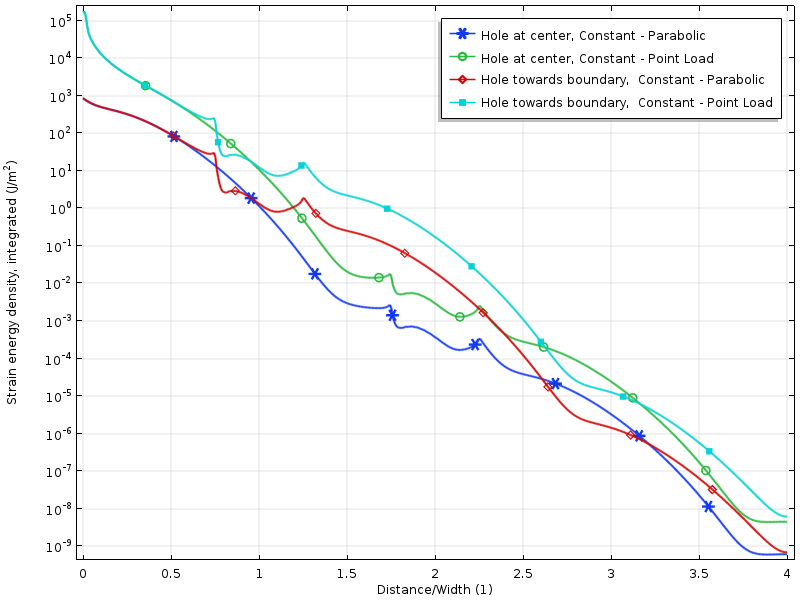
a törzs energia sűrűsége mentén a lemez a nulla eredő terhelés esetekben. Az energiát a függőleges irány mentén integrálják annak érdekében, hogy olyan mennyiséget hozzanak létre, amely csak a terheléstől való távolság függvénye.

a törzs energia sűrűségének logaritmusában a bomlás többé-kevésbé lineáris a betöltött határtól való távolsággal. Ez valójában összhangban van azzal, amit a modern bizonyítékok megjósolnak: a törzs energia sűrűségének exponenciális bomlása. Világosan láthatjuk azt is, hogy a lyuk ideiglenesen csökkenti a bomlási sebességet.

a Saint-Venant-elv alkalmazása vékony szerkezetekre

vékonyabb szerkezetekre, mint a héjak, gerendák és rácsok, jól ismert, hogy a Saint-Venant-elv nem alkalmazható ugyanúgy, mint egy “szilárdabb” tárgyra. A zavarok nagyobb távolságokat tesznek meg, mint amire számítunk, mert a vékony szerkezetben a terhelési utak sokkal korlátozottabbak. Ez ugyanaz a jelenség, amelyet a fenti példa lyukával látunk, de hangsúlyosabban.

itt egy szabványos IPE100 keresztmetszetű gerendát tanulmányozunk. A gerenda vége axiális feszültségnek van kitéve, amelynek amplitúdója lineáris eloszlású mindkét keresztmetszeti irányban.

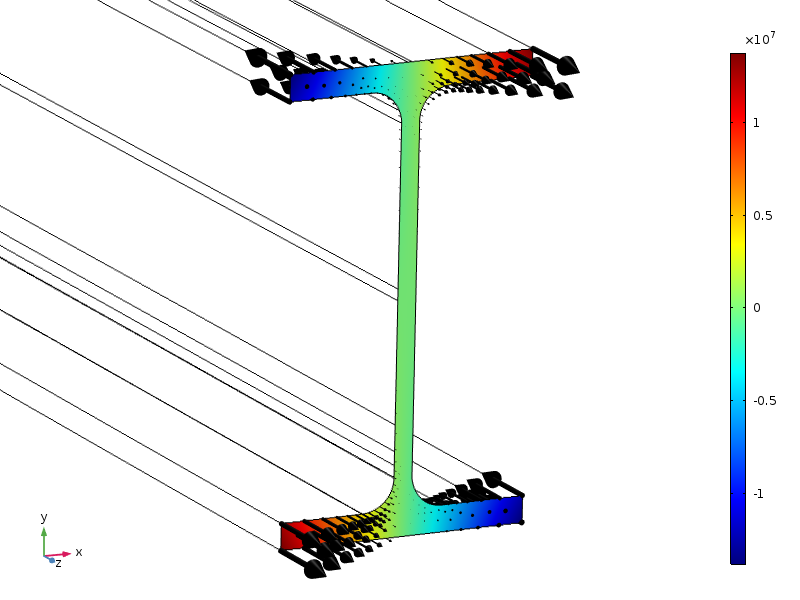
terheléselosztás, kontúrként és nyilakként jelenik meg.

a szimmetriák miatt ennek a terhelésnek nulla eredő ereje van, valamint nulla momentuma van az összes tengely körül. A keresztmetszet magassága 100 mm, tehát ha a Saint-Venant elvének szabványos formája alkalmazható, akkor a feszültségeknek kicsinek kell lenniük a végszakasztól körülbelül 100 mm távolságra.

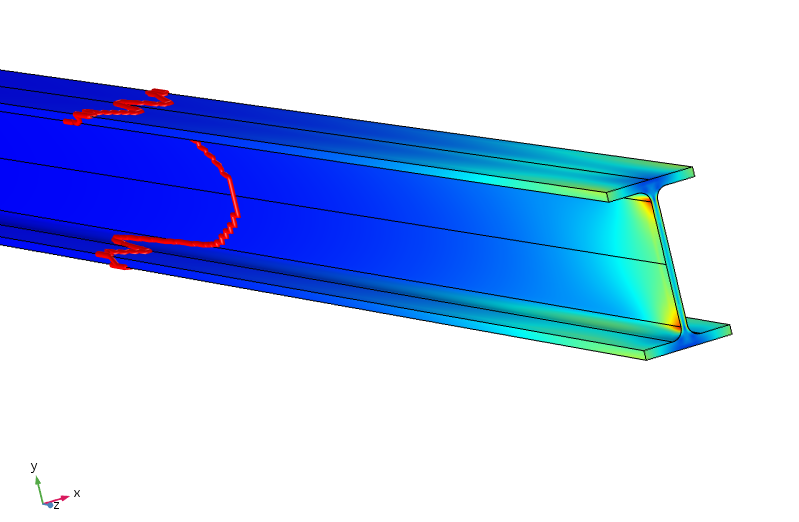
egyenértékű feszültség a sugárban. A piros kontúr azt jelzi, hogy a feszültség kevesebb, mint az alkalmazott csúcsfeszültség 5% – a.

kiderült, hogy ahhoz, hogy a feszültség az alkalmazott csúcsfeszültség 5% – a alatt legyen, majdnem egy métert kell haladnunk a gerenda mentén. Így a terhelés újraelosztása itt sokkal kevésbé hatékony, mivel a felső és az alsó karimák közötti egyensúlyhoz pillanatátvitel szükséges a vékony szövedéken keresztül.

ha ismeri a gerendák nem egyenletes torziójának elméletét (azaz a vetemedéselméletet vagy a Vlasov-elméletet), akkor felismeri, hogy az alkalmazott terhelésnek jelentős bimomentuma van. A bimoment egy keresztmetszeti mennyiség, amelynek fizikai dimenziós ereje X hosszúság2.

talán (ez csak az én személyes spekulációm), a hatékony Saint-Venant-elvnek ebben az esetben nemcsak erőt és pillanatot kell megkövetelnie, hanem a nulla bimomentumát is. Ezt négy pontterhelés hozzáadásával lehet elérni, amelyek ellensúlyozó bimomentumot biztosítanak. Az ilyen elemzés eredményét az alábbiakban mutatjuk be.

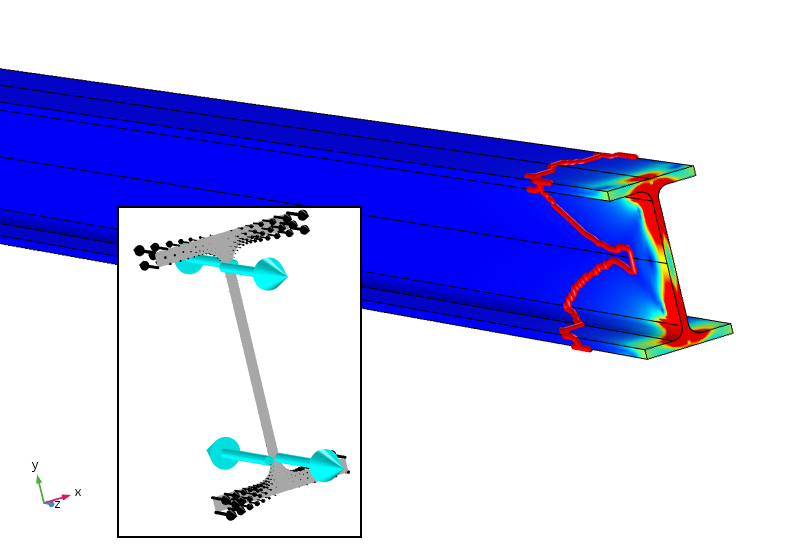
egyenértékű feszültség négy pontterheléssel, amelyek szintén nulla bimomentumot biztosítanak. Az 5% – os feszültség kontúr most sokkal közelebb van a betöltött határhoz.

az alkalmazott pontterhelések, amelyek nem optimálisan vannak elhelyezve a célra, rendkívül magas (valójában egyedülálló) helyi feszültségeket adnak. A feszültség azonban sokkal gyorsabban csökken, és 5% alatt van körülbelül 100 mm után. az 5% – os határ továbbra is az alkalmazott elosztott terhelés szempontjából van, tehát nem igazodik az új helyi feszültségekhez. A törzs energia sűrűségének logaritmikus bomlási sebessége háromszor gyorsabb a pontterhelések hozzáadása után.

Saint-Venant elve a végeselem-elemzésben

bizonyos esetekben intuitív módon úgy tekintheti, hogy Saint-Venant elve alkalmazható az FE diszkretizált problémájára. Itt az elosztott terheléseket és a nem megfelelő hálókat vizsgáljuk.

elosztott terhelések

az FE modellben a terhelések mindig a hálócsomópontokon kerülnek alkalmazásra, annak ellenére, hogy folyamatos határterhelésként adja meg őket. A terhelés belsőleg eloszlik az elem csomópontjaira a virtuális munka elvével, amint az az alábbi példában látható.

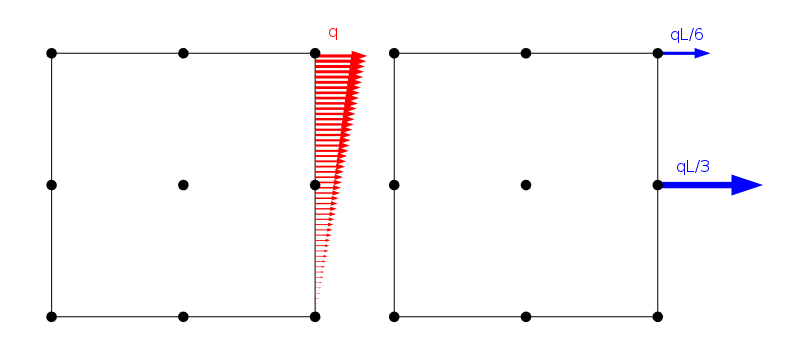
lineárisan elosztott terhelés és annak alkalmazása egy másodrendű Lagrange elem csomópontjain, amelynek oldalhossza L.

van azonban végtelen számú terheléseloszlás, amelyek ugyanazokat a csomóponti terheléseket adják, mindaddig, amíg ugyanazt az eredő erőt és nyomatékot osztják meg. Nyilvánvaló, hogy a végeselem-probléma megoldása mindezen esetekben azonos. Saint-Venant elvéből azonban arra a következtetésre juthatunk, hogy minden ilyen terhelésnek lényegében ugyanazt a stresszmezőt kell adnia, amint bizonyos távolságra vagyunk.

mivel a terhelések újraelosztásának területe egy elemfelület, a lineáris dimenzió, amely után nincs különbség, lényegében egy elemréteg a szerkezeten belül. Így az elemek legkülső rétegében lévő megoldás nem feltétlenül felel meg a tényleges terhelésnek, de tovább, igen.

példaként egy téglalap alakú lemezt tölthetünk be olyan határterheléssel, amelynek exponenciális feszültségeloszlása van. A finom hálóval kiszámított feszültséget az alábbiakban mutatjuk be.

az axiális feszültségeloszlás Kontúrdiagramja.

Saint-Venant elve miatt a feszültségmezőt tiszta hajlítási állapotba osztják el a betöltött éltől bizonyos távolságra, ahogy azt elvárjuk. Ez azonban nem a jelenlegi vita tárgya. Inkább megvizsgáljuk a fenti stresszeloszlás különbségét, és azt, amit számos durva hálóval kapunk.

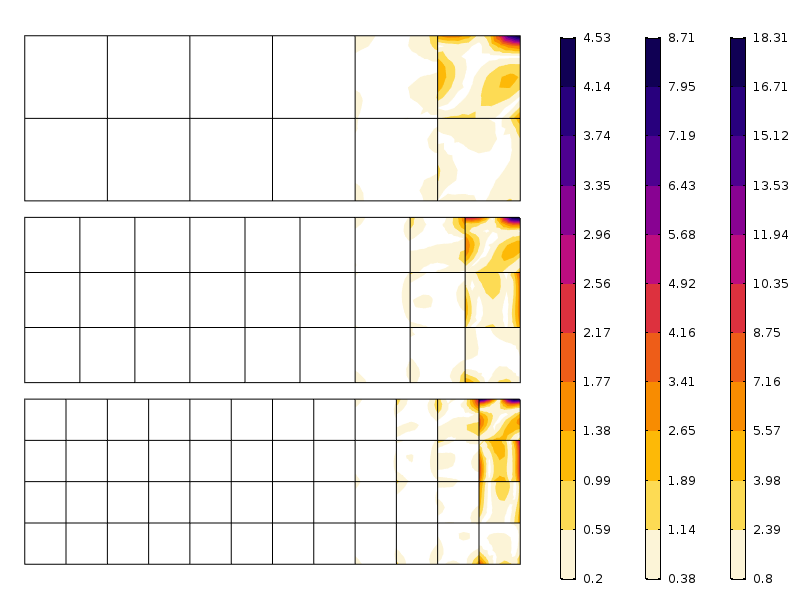
hiba az axiális feszültségben három különböző hálószemnél. Vegye figyelembe a különböző skálákat. Ahogy az várható volt, a hiba kisebb, ha a háló finomabb.

mint az ábrán látható, a hiba gyorsan csökken az első elemréteg után. Amit itt látunk, az valójában a háló konvergenciájának és a stressz újraelosztásának kombinációja, amelyet a Saint-Venant-elv magában foglal.

nem megfelelő háló

nem megfelelő háló akkor fordul elő, ha két összekapcsolt elem alakfüggvényei nem egyeznek. A leggyakoribb eset az, amikor egy összeállítást identitáspárokkal és folytonossági feltételekkel kötnek össze. Ennek példázására, tanulmányozhatunk egy egyenes sávot szándékosan nem illő hálóval. Egy egyszerű terhelési tokkal, például egytengelyes feszültséggel meg lehet vizsgálni az átmenet által okozott stressz zavarokat.

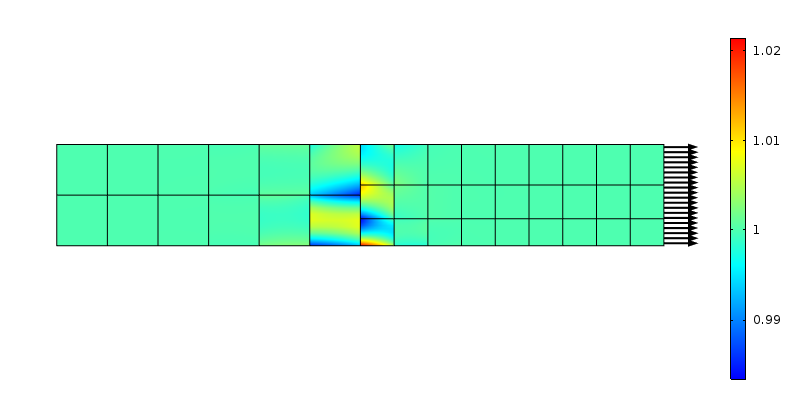
axiális feszültség nem megfelelő hálóátmenetnél. Másodrendű elemeket használnak.

a csomópontok által a két oldalon továbbított erők nem felelnek meg az állandó stressz feltételezésének. Ez ismét helyi terhelés-újraelosztásnak tekinthető egy olyan területen, amely az elem mérete. Saint-Venant érvelésének felhasználásával a zavarnak az átmenettől “elemméretű” távolságra kell elhalványulnia. Vizsgáljuk meg, mi történik, ha a hálót tengelyirányban finomítják.

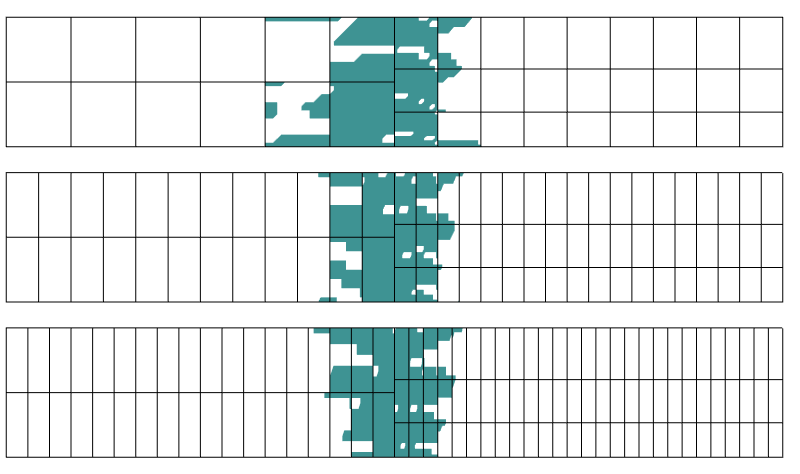
régió, ahol több mint 0,1% hiba van a stresszben. Három különböző diszkretizációt alkalmaznak tengelyirányban.

kiderült, hogy a zavar régióját nem befolyásolja nagymértékben az átmeneti határra merőleges irányú diszkretizáció. Pontosan ezt mondja nekünk Saint-Venant elve.

Záró megjegyzések

a Saint-Venant-elv alkalmazása nélkül sok szerkezeti elemzést nehéz elvégezni, egyszerűen azért, mert a terhelés részletes eloszlása nem ismert.

az elv formálisan csak lineáris rugalmas anyagokra érvényes. A gyakorlatban intuitív módon napi rendszerességgel használjuk más helyzetekre is. Ha például a “lyukas lemez” példában szereplő anyag elasztoplasztikus lenne, akkor azt várnánk, hogy a két elosztott terhelés egyenértékű eredményt ad, mindaddig, amíg a hozamfeszültség meghaladja a határon alkalmazott feszültséget, így a lyuk körül csak képlékeny deformáció van. A pontterhelés azonban mindig más megoldást ad,mivel az anyag a terhelt pont körül hoz létre. Hosszabb beszélgetéshez, olvassa el ezt a blogbejegyzést a szingularitásokról a pontterheléseknél.

következő lépések

Tudjon meg többet a COMSOL Multiphysics szoftver fea.

további olvasmányok

• Y. C. Fung és P. Tong, klasszikus és számítási szilárd mechanika, World Scientific Publishing Co. Pte. Kft., 2001.