zastosowanie i interpretacja Zasady Saint-venanta

wszyscy inżynierowie konstrukcyjni stosują zasadę Saint-venanta, aktywnie lub podświadomie. Można znaleźć różne sformułowania tej zasady w większości podręczników mechaniki konstrukcji, ale jej dokładne znaczenie nie jest oczywiste. Zasada Saint-venanta mówi nam, że dokładny rozkład obciążenia nie jest ważny daleko od załadowanego obszaru, o ile wypadkowe obciążenia są prawidłowe. W tym wpisie na blogu przyjrzymy się zasadzie Saint-venanta, szczególnie w kontekście analizy elementów skończonych (Fe).

Historia Zasady Saint-venanta

francuski naukowiec Barré de Saint-Venant sformułował swoją słynną zasadę w 1855 roku, ale była to bardziej obserwacja niż ścisłe twierdzenie matematyczne:

„jeżeli siły działające na niewielką część powierzchni ciała sprężystego są zastępowane przez inny statycznie równoważny system sił działających na tę samą część powierzchni, to redystrybucja obciążenia powoduje znaczne zmiany naprężeń lokalnie, ale ma znikomy wpływ na naprężenia w odległościach, które są duże w porównaniu z wymiarami liniowymi powierzchni, na której siły są zmieniane.”

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Portret Saint-Venant. Obraz w domenie publicznej, za pośrednictwem Wikimedia Commons.

wiele wielkich umysłów w dziedzinie mechaniki stosowanej — Boussinesq, Love, von Mises, Toupin i inni — było zaangażowanych w określenie Zasady Saint-venanta w bardziej dokładnej formie i dostarczenie matematycznych dowodów na to. Jak się okazuje, jest to dość trudne w przypadku bardziej ogólnych przypadków, a badania na ten temat nadal trwają. (Argumentacja była czasami dość żywa.)

prosty przykład: analiza naprężeń na odległość

Zacznijmy od czegoś dość prostego: cienka prostokątna płytka z okrągłym otworem w pewnej odległości od obciążonej krawędzi, która jest ciągnięta osiowo. Jeśli interesuje nas koncentracja naprężeń w otworze, to jak ważny jest rzeczywisty rozkład obciążenia?

trzy różne typy obciążeń są stosowane na prawej granicy:

1. stałe naprężenie osiowe 100 MPa
2. symetryczny rozkład naprężeń parabolicznych z amplitudą szczytową 150 MPa
3. wyśrodkowane obciążenie punktowe z tym samym wynikiem co dwa poprzednie przypadki obciążenia

jak widać na wykresach poniżej, rozkład naprężeń w otworze nie ma wpływu na sposób przyłożenia obciążenia. Kluczem jest oczywiście to, że otwór jest wystarczająco daleko od ładunku.

Von Mises kontury naprężeń dla trzech przypadków obciążenia.

innym sposobem wizualizacji tego scenariusza jest użycie strzałek naprężeń głównych. Taki wykres podkreśla pole stresu jako strumień i daje dobre wyczucie redystrybucji.

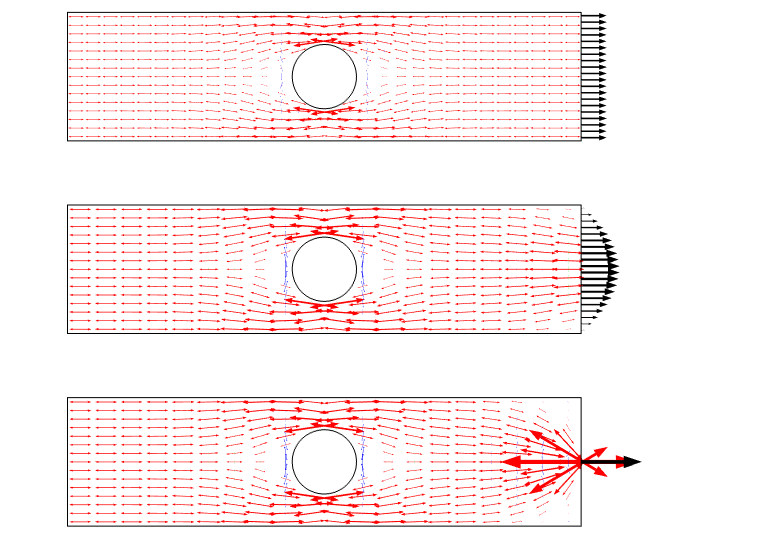
główny Wykres naprężeń dla trzech przypadków obciążenia. Zauważ, że istnieje osobliwość, gdy używane jest obciążenie punktowe.

na wykresie naprężenia wzdłuż linii, możemy zobaczyć, że wszystkie trzy przypadki zbiegają się do siebie w odległości od krawędzi, która jest w przybliżeniu równa szerokości płytki.

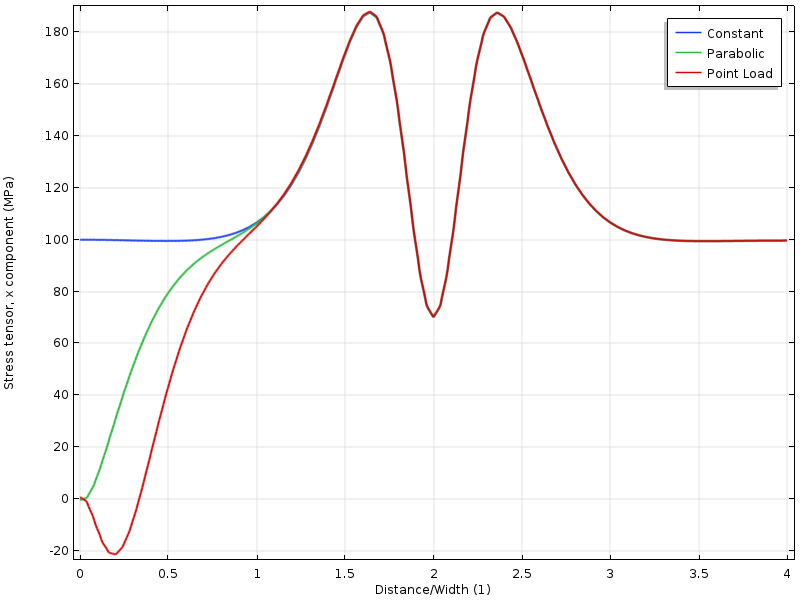
naprężenie wzdłuż górnej krawędzi jako funkcja odległości od obciążonej granicy. Odległość jest znormalizowana przez szerokość płyty.

jeśli otwór jest przesunięty bliżej załadowanej granicy, otrzymujemy inną sytuację. Stan naprężenia wokół otworu zależy teraz od rozkładu obciążenia. Ale jeszcze bardziej interesujące jest to, że odległość do miejsca, w którym trzy pola naprężeń zgadzają się teraz, jest dwa razy większa od załadowanej granicy. Zastosowanie zasady Saint-venanta wymaga, aby naprężenia mogły swobodnie się redystrybuować. W tym przypadku redystrybucja jest częściowo zablokowana przez otwór.

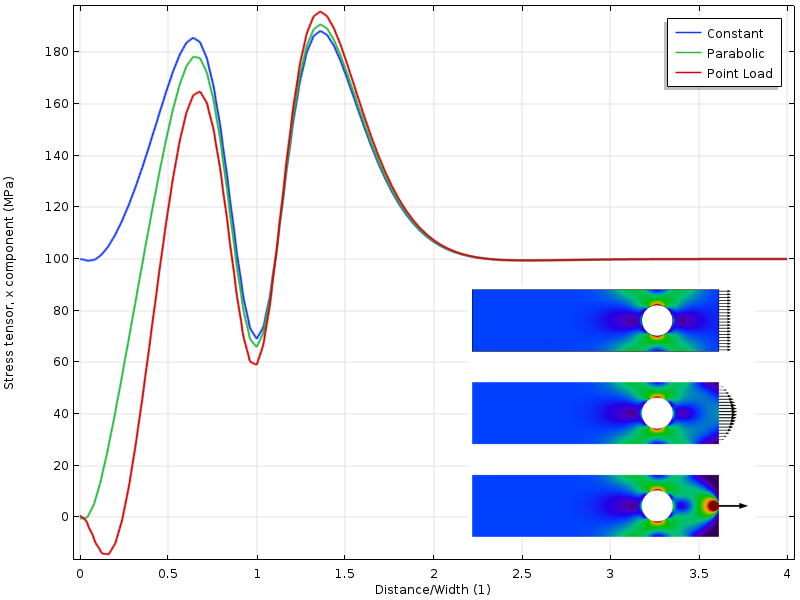
naprężenie wzdłuż górnej krawędzi z otworem bliżej obciążonej granicy.

zauważ, że zasada Saint-venanta mówi nam, że nie ma różnicy w stanie naprężenia w odległości, która jest rzędu wymiaru liniowego obszaru obciążonego. Załadowany obszar, który należy wziąć pod uwagę, może jednak nie być obszarem, który jest faktycznie załadowany! To stwierdzenie może wydawać się dziwne, ale pomyśl o tym w ten sposób: kiedy dziura jest daleko, możemy obliczyć współczynnik koncentracji stresu za pomocą podręcznika (mój mówi 4.32), a nie za pomocą rozwiązania FE. Podejście oparte na podręczniku zawiera domniemane założenie, że obciążenie jest równomiernie rozłożone, jak w pierwszym przypadku obciążenia. Tak więc nawet jeśli rzeczywiste obciążenie zostało przyłożone tylko do niewielkiej części granicy, odległość krytyczna w tym przypadku jest związana z wielkością całej granicy.

podczas rozwiązywania problemu za pomocą metody elementów skończonych (fem), otwór może być arbitralnie blisko obciążenia. To, co wyznacza granicę, to to, że z fizycznego punktu widzenia rozkład obciążenia jest dobrze zdefiniowany. Gdy tylko podejmiemy założenia dotyczące redystrybucji, pojawia się jednak domniemane założenie dotyczące rozkładu obciążenia, które może różnić się od rzeczywistego.

zerowe Układy wynikowe i gęstość energii odkształcenia

do tej pory powiedzieliśmy, że naprężenia są takie same niezależnie od szczegółów obciążenia w odpowiedniej odległości. Ponieważ mamy tu do czynienia z elastycznością liniową, zawsze można nakładać przypadki obciążeń. Podczas pracy z dowodami Zasady Saint-venanta łatwiej jest sformułować zasadę opartą na tych liniach: naprężenia spowodowane przez układ obciążenia bez wynikowej siły lub momentu będą małe w odległości takiej samej wielkości jak wielkość obciążonej granicy.

w ten sposób badamy naprężenia spowodowane różnicą między dwoma układami obciążeń o równych wynikach. Większość współczesnych dowodów opiera się na szacunkach rozkładu gęstości energii odkształcenia dla takiego układu zerowego.

Wracając do powyższego problemu, możemy obliczyć różnicę między przypadkami obciążenia. Dzięki temu możemy zbadać rzeczywisty rozkład naprężeń lub gęstość energii odkształcenia dla różnicy pól naprężeń.

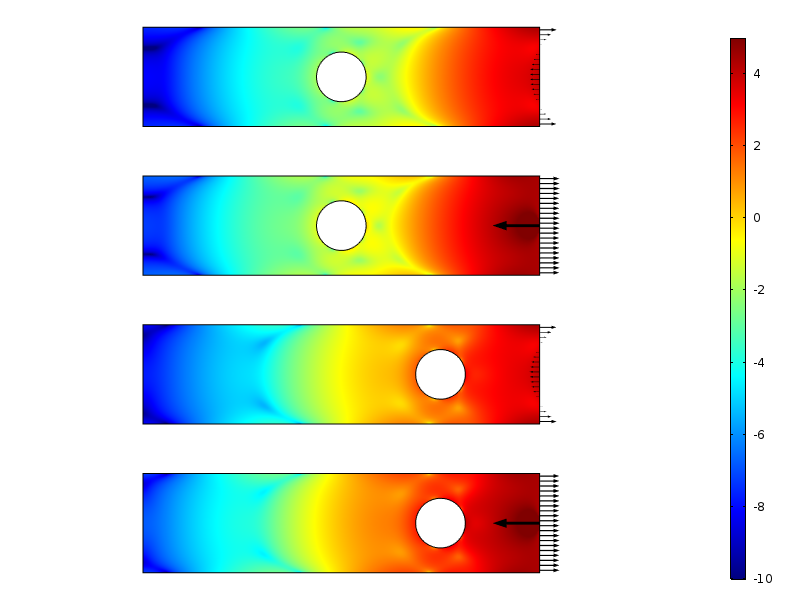
Logarytm gęstości energii odkształcenia dla przypadków zerowego obciążenia wynikowego.

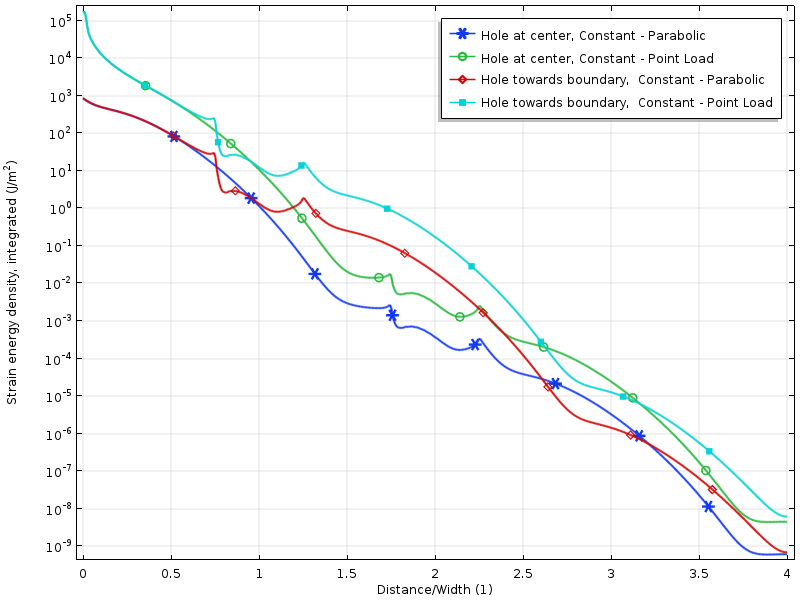
gęstość energii naprężenia wzdłuż płytki dla zerowych przypadków obciążenia wynikowego. Energia jest zintegrowana wzdłuż kierunku pionowego w celu wytworzenia ilości, która jest tylko funkcją odległości od obciążenia.

rozpad w logarytmie gęstości energii odkształcenia jest mniej lub bardziej liniowy z odległością od obciążonej granicy. Jest to zgodne z tym, co przewidują współczesne dowody: wykładniczym zanikiem gęstości energii szczepu. Możemy również wyraźnie zobaczyć, jak otwór tymczasowo zmniejsza szybkość rozpadu.

zastosowanie zasady Saint-venanta do cienkich konstrukcji

w przypadku cieńszych konstrukcji, takich jak łuski, belki i kratownice, powszechnie wiadomo, że zasada Saint-venanta nie może być stosowana w taki sam sposób, jak w przypadku bardziej „solidnych” obiektów. Zakłócenia przemieszczają się na większe odległości niż się spodziewamy, ponieważ ścieżki obciążenia w cienkiej konstrukcji są znacznie bardziej ograniczone. Jest to to samo zjawisko, które widzimy z dziurą w powyższym przykładzie, ale bardziej wyeksponowane.

tutaj badamy belkę o standardowym przekroju IPE100. Koniec wiązki poddawany jest naprężeniu osiowemu, o amplitudzie, która ma rozkład liniowy w obu kierunkach przekroju.

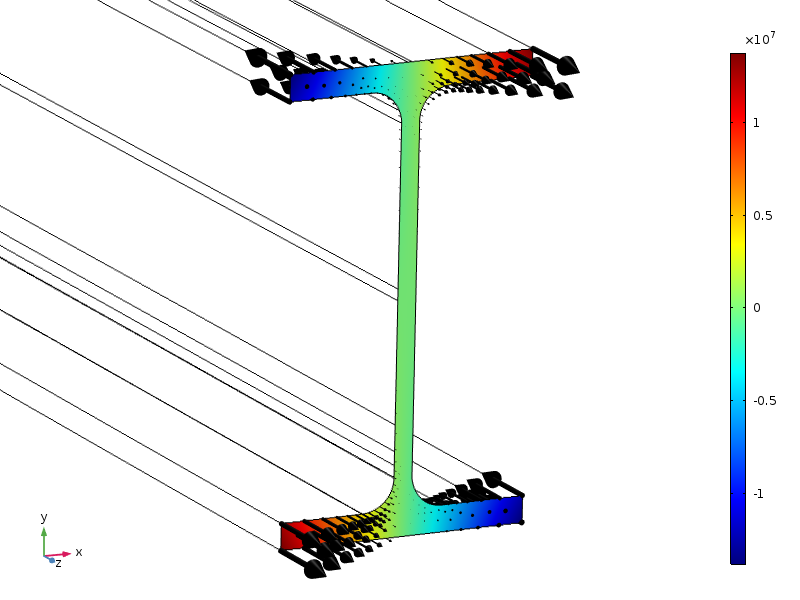
rozkład obciążenia, wyświetlany jako kontury i strzałki.

ze względu na symetrie obciążenie to ma zerową siłę wynikową, a także moment zerowy wokół wszystkich osi. Wysokość przekroju wynosi 100 mm, więc jeśli ma zastosowanie standardowa forma Zasady Saint-venanta, to naprężenia powinny być małe w odległości około 100 mm od przekroju końcowego.

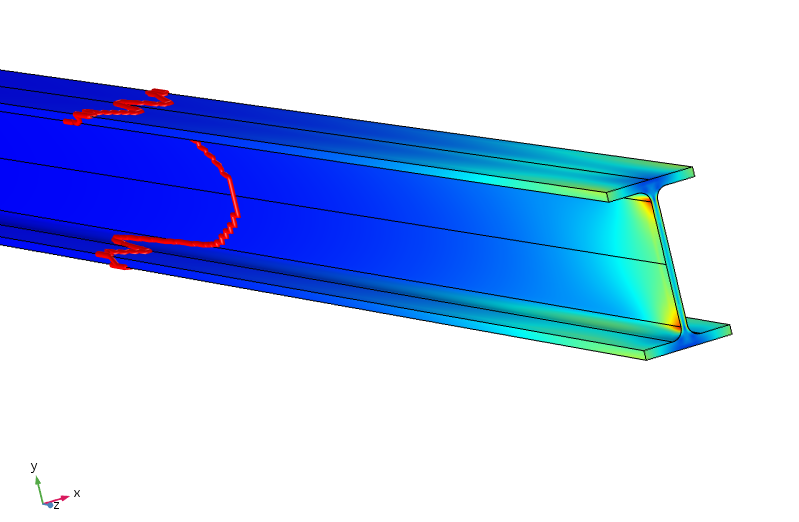
równoważne naprężenia w wiązce. Czerwony kontur wskazuje, gdzie naprężenie jest mniejsze niż 5% szczytowego przyłożonego naprężenia.

okazuje się, że aby naprężenie było poniżej 5% szczytowego przyłożonego naprężenia, musimy przemieścić się prawie metr wzdłuż belki. Tak więc redystrybucja obciążenia jest tutaj znacznie mniej wydajna, ponieważ równowaga między górnym i dolnym kołnierzem wymaga przeniesienia momentu przez cienką wstęgę.

jeśli znasz teorię nieuniform skrętu belek (tj. teorię wypaczenia lub teorię Własowa), zauważysz, że przyłożone obciążenie ma znaczący biment. Bimoment jest wielkością przekrojową o wymiarze fizycznym x długość2.

może (to tylko moje osobiste spekulacje), skuteczna zasada Saint-venanta w tym przypadku powinna wymagać nie tylko siły i chwili, ale także bimomentu zera. Można to osiągnąć poprzez dodanie czteropunktowych obciążeń, które zapewniają bimoment przeciwdziałający. Wynik takiej analizy przedstawiono poniżej.

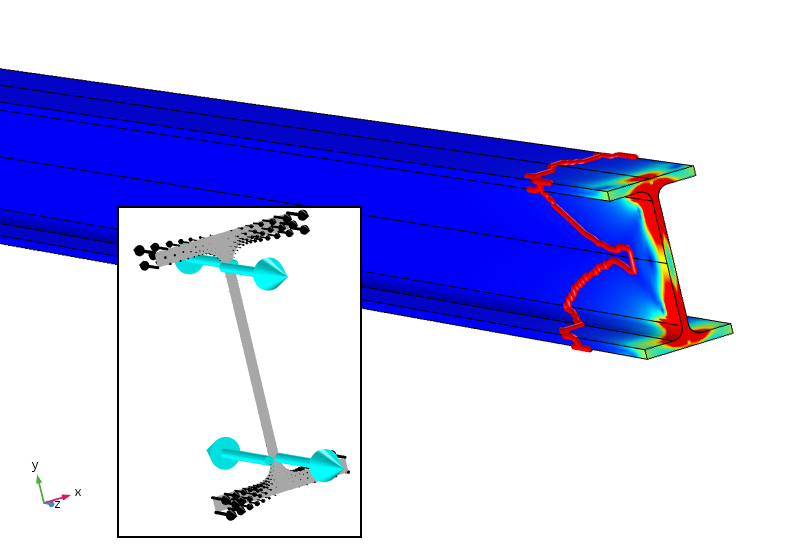
równoważne naprężenie z czteropunktowymi obciążeniami, które również zapewniają zerowy bimoment. Kontur naprężenia 5% jest teraz znacznie bliżej obciążonej granicy.

przyłożone obciążenia punktowe, które nie są celowo optymalnie rozmieszczone, dają bardzo wysokie (właściwie pojedyncze) naprężenia lokalne. Jednak naprężenie spada znacznie szybciej i wynosi poniżej 5% po około 100 mm. granica 5% jest nadal pod względem zastosowanego obciążenia rozproszonego, więc nie jest dostosowana do nowych naprężeń lokalnych. Logarytmiczna szybkość rozpadu gęstości energii odkształcenia jest trzykrotnie szybsza po dodaniu ładunków punktowych.

zasada Saint-venanta w analizie Elementów Skończonych

w niektórych przypadkach można intuicyjnie uznać zasadę Saint-venanta za mającą zastosowanie do problemu FE. Tutaj patrzymy na obciążenia rozproszone i siatki niezgodne.

obciążenia rozproszone

w modelu FE obciążenia są zawsze stosowane w węzłach siatki, nawet jeśli określa się je jako ciągłe obciążenie graniczne. Obciążenie jest wewnętrznie rozłożone na węzły elementu przy użyciu zasady pracy wirtualnej, jak pokazano w poniższym przykładzie.

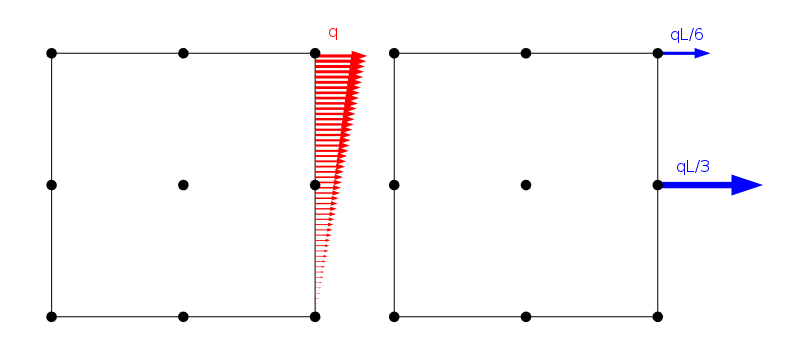
liniowo rozłożone obciążenie i sposób jego zastosowania na węzłach elementu Lagrange ’ a drugiego rzędu o długości boku L.

istnieje jednak nieskończona liczba rozkładów obciążenia, które dają te same obciążenia węzłowe, o ile mają tę samą siłę wynikową i moment. Oczywiście rozwiązanie problemu elementów skończonych jest takie samo dla wszystkich tych przypadków. Z zasady Saint-venanta możemy jednak wnioskować, że wszystkie takie ładunki powinny dawać zasadniczo to samo pole naprężeń, gdy tylko będziemy w pewnej odległości.

ponieważ wielkość obszaru, na którym rozkładamy obciążenia, jest powierzchnią elementu, wymiar liniowy, po którym nie ma różnicy, jest zasadniczo jedną warstwą elementu wewnątrz struktury. Tak więc rozwiązanie w zewnętrznej warstwie elementów może nie odpowiadać rzeczywistemu obciążeniu, ale dalej tak.

jako przykład możemy załadować prostokątną płytę z obciążeniem granicznym o wykładniczym rozkładzie naprężeń. Naprężenie obliczone za pomocą drobnej siatki przedstawiono poniżej.

Wykres konturowy rozkładu naprężeń osiowych.

ze względu na zasadę Saint-venanta, pole naprężeń jest redystrybuowane do czystego stanu zginania w pewnej odległości od obciążonej krawędzi, tak jak tego oczekujemy. Nie jest to jednak cel obecnej dyskusji. Raczej badamy różnicę między rozkładem naprężeń powyżej, a tym, co otrzymujemy z wieloma grubymi siatkami.

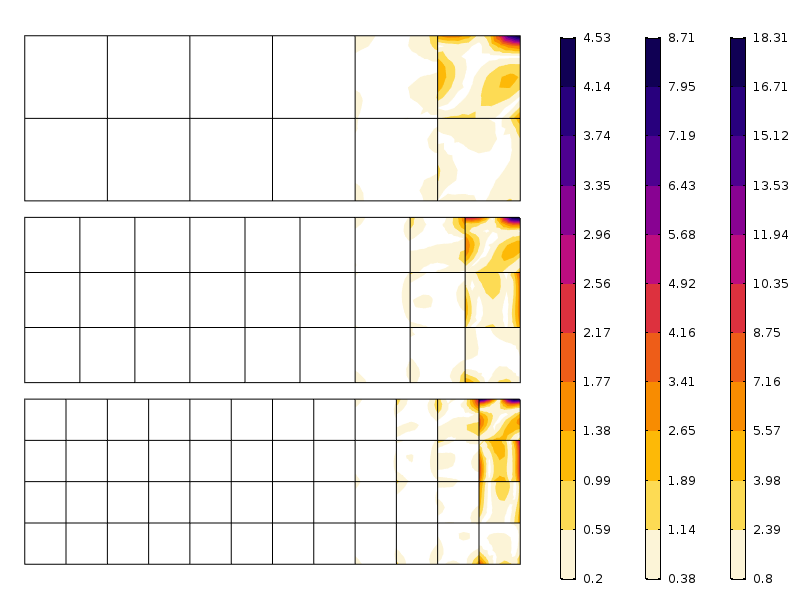
błąd naprężenia osiowego dla trzech różnych oczek. Zwróć uwagę na różne skale. Zgodnie z oczekiwaniami, błąd jest mniejszy, gdy siatka jest drobniejsza.

jak widać na rysunku, błąd szybko zmniejsza się po pierwszej warstwie elementu. To, co tu widzimy, to połączenie zbieżności siatki i redystrybucji naprężeń implikowanych przez zasadę Saint-venanta.

Siatka niezgodna

siatka niezgodna występuje, gdy funkcje kształtu w dwóch połączonych elementach nie pasują. Najczęstszym przypadkiem jest, gdy zespół jest połączony za pomocą par tożsamości i warunków ciągłości. Aby to zilustrować, możemy zbadać prosty pręt z celowo niepasującą siatką. Przy prostym przypadku obciążenia, takim jak napięcie jednoosiowe, możliwe jest zbadanie zaburzeń naprężeń spowodowanych przejściem.

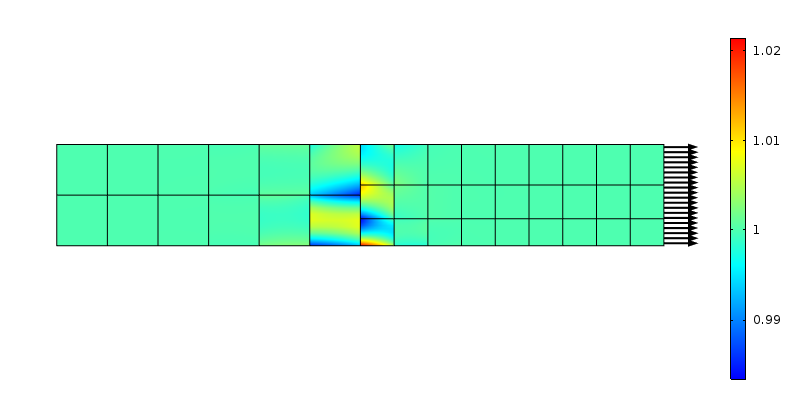
naprężenie osiowe przy niezgodnym przejściu siatki. Stosowane są elementy drugiego rzędu.

siły przenoszone przez węzły po obu stronach nie pasują do założenia stałego naprężenia. Ponownie, może to być postrzegane jako lokalna redystrybucja obciążenia na obszarze, który jest rozmiarem elementu. Korzystając z rozumowania Saint-venanta, zaburzenie powinno zanikać w odległości „wielkości elementu” od przejścia. Zbadajmy, co się stanie, jeśli siatka zostanie udoskonalona w kierunku osiowym.

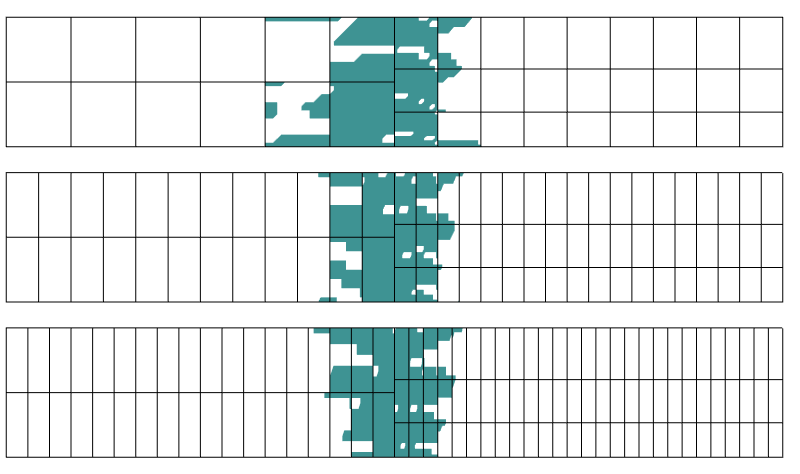
Region z ponad 0,1% błędem w stresie. W kierunku osiowym stosuje się trzy różne dyskrecje.

okazuje się, że obszar zakłóceń nie ma większego wpływu na dyskrecję w kierunku prostopadłym do granicy przejściowej. Dokładnie to mówi nam zasada Saint-venanta.

Uwagi końcowe

bez zastosowania zasady Saint-venanta wiele analiz strukturalnych jest trudnych do wykonania, po prostu dlatego, że szczegółowy rozkład obciążenia nie jest znany.

zasada jest formalnie ważna tylko dla liniowych materiałów elastycznych. W praktyce intuicyjnie wykorzystujemy go również na co dzień w innych sytuacjach. Jeśli na przykład materiał w przykładzie „płyta z otworem” był elastoplastyczny, spodziewalibyśmy się, że dwa rozłożone obciążenia dadzą równoważne wyniki, o ile naprężenie plonu jest powyżej naprężenia zastosowanego na granicy, tak że wokół otworu występuje tylko odkształcenie plastyczne. Jednak obciążenie punktowe zawsze daje inne rozwiązanie, ponieważ materiał uzyskuje się wokół załadowanego punktu. Aby uzyskać dłuższą dyskusję, przeczytaj ten post na blogu na temat osobliwości w ładunkach punktowych.

kolejne kroki

dowiedz się więcej o korzystaniu z oprogramowania COMSOL Multiphysics® dla Mes.

Czytaj dalej

• Y. C. Fung and p. Tong, Classical and Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.