すべての構造技術者は、積極的にも無意識的にも、Saint-Venantの原則を使用しています。 ほとんどの構造力学の教科書では、この原則のさまざまな公式を見つけることができますが、その正確な意味は明らかではありません。 Saint-Venantの原理は、荷重の結果が正しい限り、荷重の正確な分布は荷重領域から遠く離れて重要ではないことを示しています。 このブログ記事では、特に有限要素(FE)解析の文脈で、Saint-Venantの原理を探求します。
サン・ヴェナンの原理の歴史
フランスの科学者Barré de Saint-Venantは1855年に彼の有名な原理を定式化しましたが、それは厳密な数学的声明よりも観察の方:
“弾性体の表面の小さな部分に作用する力が表面の同じ部分に作用する別の静的に等価な力系に置き換えられると,この荷重の再分布は局所的に応力に大きな変化をもたらすが,力が変化する表面の線形寸法と比較して大きい距離での応力には無視できる影響を与える。”
B.Saint-Venant,Mém. サヴァンツ・エトランジェス(savants étrangers)、vol. 14, 1855.

サン=ヴェナンの肖像画。 ウィキメディア-コモンズを介して、パブリックドメインの画像。
Boussinesq、Love、von Mises、Toupinなどの応用力学の分野の多くの偉大な心は、Saint—Venantの原理をより正確な形で述べ、それに対する数学的証明を提供することに関与していました。 結局のところ、これはより一般的なケースでは非常に困難であり、トピックに関する研究はまだ進行中です。 (議論は時々非常に鮮やかでした。)
簡単な例:距離での応力の分析
非常に簡単なものから始めましょう: 軸方向に引っ張られている荷を積まれた端からの間隔の円の穴が付いている薄い長方形の版。 穴の応力集中に興味があるのであれば、実際の荷重分布はどれくらい重要ですか?
右端の境界に三つの異なる荷重タイプが適用されます:
- 100MPaの一定軸応力
- ピーク振幅150MPaの対称放物線応力分布
- 前の二つの荷重ケースと同じ結果を持つ中心点荷重
下のプロットに見られるように、穴の応力分布は荷重の適用方法に影響されません。 ここで重要なのは、もちろん、穴が負荷から十分に遠いことです。

Von Mises応力輪郭は、三つの負荷ケースのために。
このシナリオを視覚化する別の方法は、主応力矢印を使用することです。 このようなプロットは応力場をフラックスとして強調し,再分布に対して良い感じを与える。
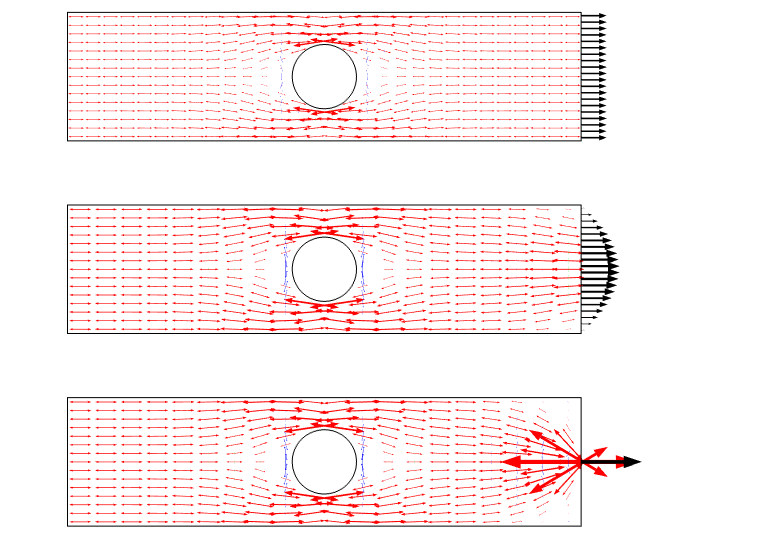
3つの荷重ケースの主応力プロット。 点荷重が使用される場合、特異点があることに注意してください。
線に沿って応力をグラフ化することにより、三つのケースはすべて、プレートの幅にほぼ等しいエッジからの距離で互いに収束することがわかります。
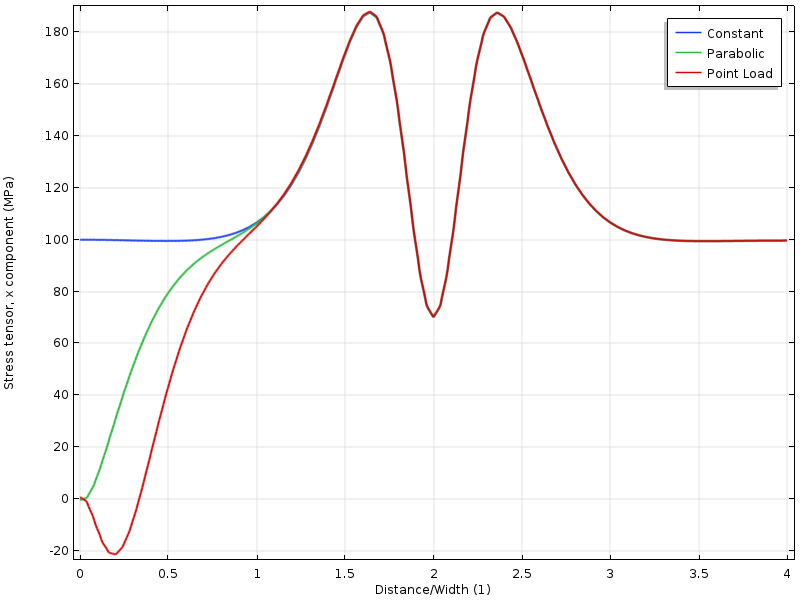
負荷された境界からの距離の関数としての上端に沿った応力。 距離はプレートの幅によって正規化されます。
穴がロードされた境界に近づくと、別の状況が発生します。 穴の周りの応力状態は荷重分布に依存します。 しかし、さらに興味深いのは、3つの応力場が現在一致する場所までの距離が、負荷境界から2倍離れていることです。 Saint-Venantの原則を適用するには、ストレスが自由に再分配される必要があります。 この場合、その再分配は穴によって部分的にブロックされる。
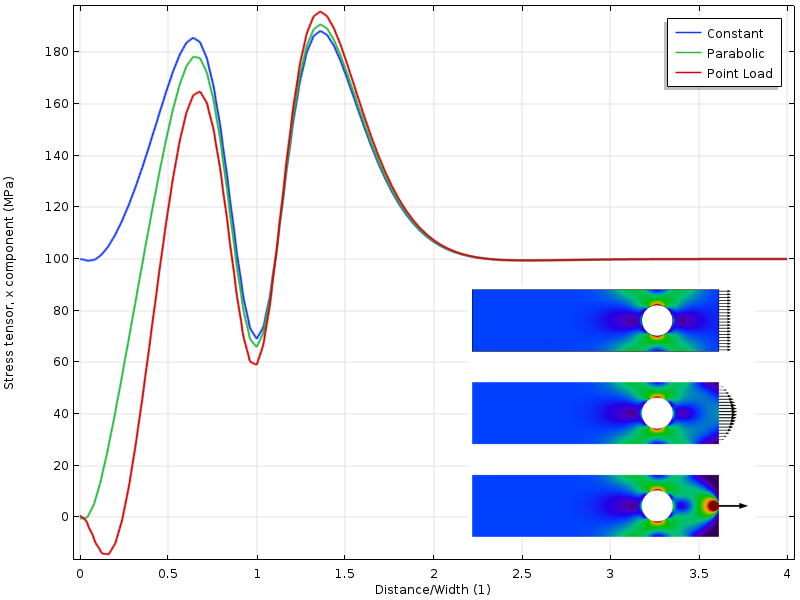
負荷境界に近い穴を持つ上端に沿った応力。
Saint-Venantの原理は、荷重領域の線形次元のオーダーである距離での応力状態に差がないことを示していることに注意してください。 しかし、考慮すべきロードされた領域は、実際にロードされた領域ではないかもしれません! この声明は奇妙に聞こえるかもしれませんが、このように考えてください:穴が遠くにあるとき、FE溶液ではなくハンドブック(鉱山は4.32と言います)を ハンドブックのアプローチには、負荷が最初の負荷の場合と同様に均等に分散されるという暗黙の仮定が含まれています。 したがって、実際の荷重が境界のほんの一部にしか適用されなかったとしても、その場合の臨界距離は境界全体の大きさに関連しています。
有限要素法(FEM)を使用して問題を解決する場合、穴は荷重に任意に近づけることができます。 制限を設定するのは、物理的な観点からは、負荷分散が明確に定義されていることです。 しかし、再分配について仮定するとすぐに、負荷分布について暗黙の仮定があり、実際のものとは異なる可能性があります。
ゼロ結果システムとひずみエネルギー密度
これまで、応力はある適切な距離での負荷の詳細に依存しない同じであると述べてきました。 ここでは線形弾性を扱っているので、荷重ケースを重ね合わせることは常に可能です。 Saint-Venantの原理の証明を使用する場合、これらの線に沿って原理を定式化する方が簡単です:結果として生じる力やモーメントのない荷重システムによっ
したがって、我々は等しい結果を持つ二つの負荷システムの違いによって引き起こされる応力を研究します。 現代のほとんどの証明は、そのようなゼロ結果システムのひずみエネルギー密度の減衰の推定値に基づいています。
上記の問題に戻ると、負荷ケース間の差を計算することができます。 そうすることで、応力場の差に対する応力またはひずみエネルギー密度の実際の減衰を研究することができます。
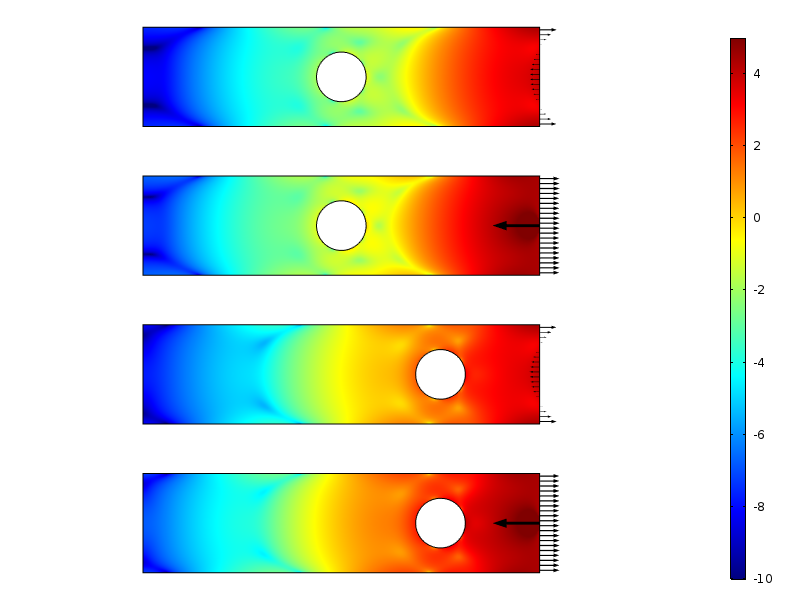
ゼロ結果荷重の場合のひずみエネルギー密度の対数。
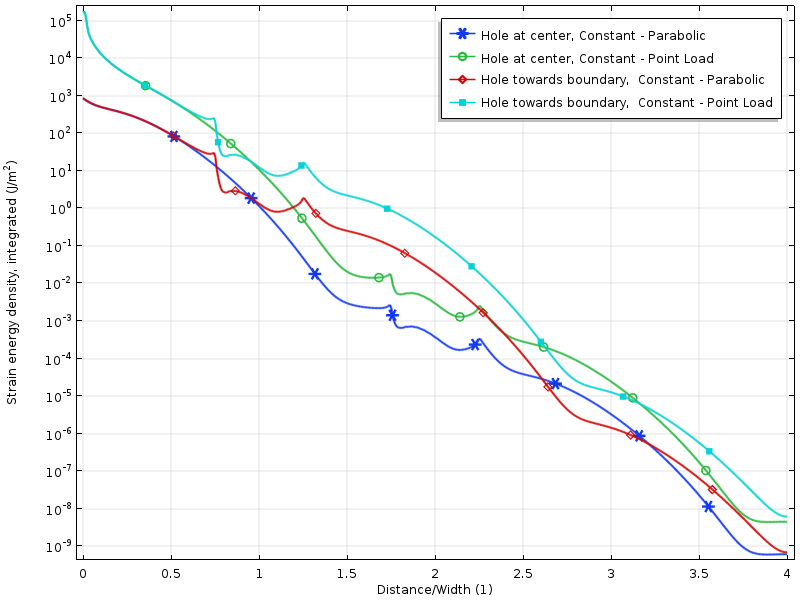
結果として生じる荷重ゼロの場合のプレートに沿ったひずみエネルギー密度。 エネルギーは、負荷からの距離の関数に過ぎない量を生成するために、垂直方向に沿って積分される。
ひずみエネルギー密度の対数の減衰は、負荷境界からの距離に対して多かれ少なかれ線形です。 これは実際には、現代の証明が予測するものと一致しています:ひずみエネルギー密度の指数関数的減衰。 また、穴が一時的に減衰率をどのように減少させるかを明確に見ることができます。
サンヴェナンの原理を薄い構造に適用する
シェル、梁、トラスのような薄い構造の場合、サンヴェナンの原理は、より”固体”の物体と同じように適用できないことはよく知られている。 外乱は、薄い構造の負荷経路がはるかに限られているため、予想よりも長い距離を移動します。 これは、上記の例の穴で見られるのと同じ現象ですが、より顕著です。
ここでは、標準的なIPE100断面を持つ梁を研究します。 ビームの端は両方の横断面の方向で線形配分がある広さの軸圧力に、服従します。
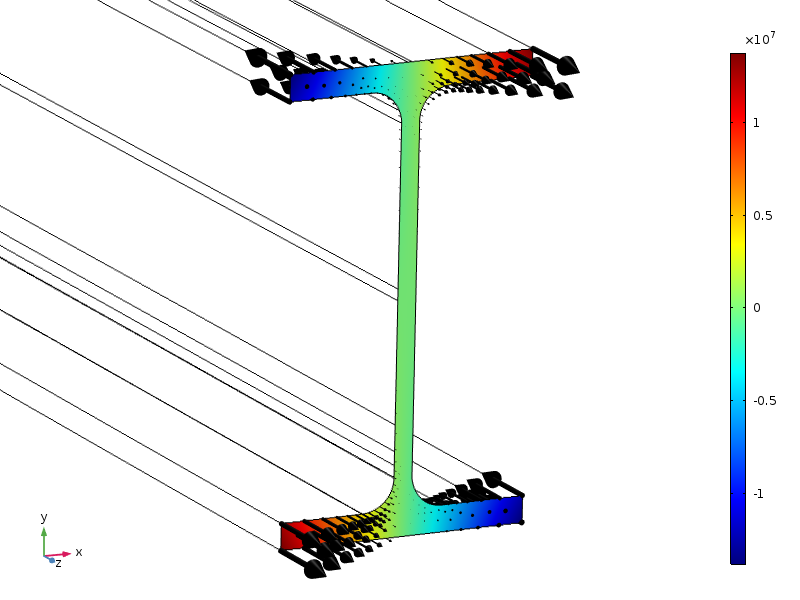
等高線と矢印で表示される荷重分布。
対称性のために、この荷重はすべての軸の周りにゼロ合力とゼロモーメントを持っています。 横断面の高さは100つのmmである、従ってSaint-Venantの主義の標準的な形態が適当なら、圧力は端セクションからのおよそ100つのmmの間隔で小さいべきである。
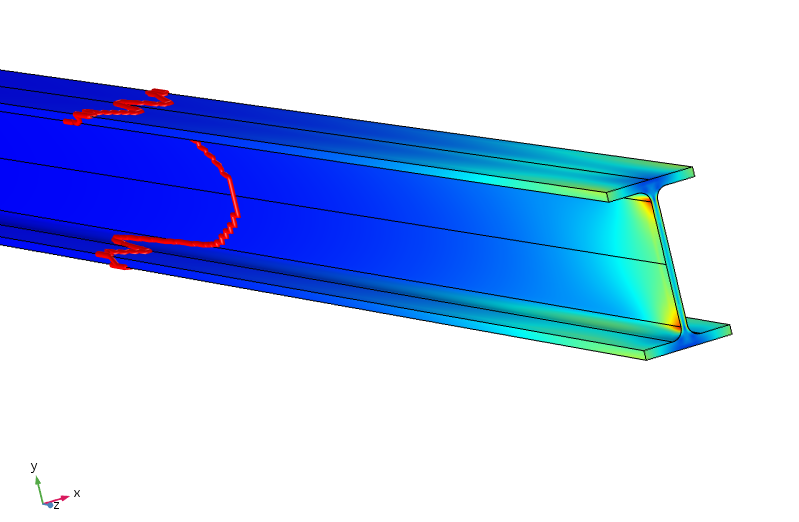
ビーム内の等価応力。 赤い輪郭は、応力がピーク印加応力の5%未満であることを示しています。
応力がピーク印加応力の5%以下になるためには、ビームに沿ってほぼ1メートル移動する必要があることが判明しました。 したがって、上部フランジと下部フランジの間の平衡化は、薄いウェブを介したモーメント移動を必要とするため、負荷再分配はここでははるかに効率的ではありません。
梁の不均一なねじりの理論(つまり、反り理論またはVlasov理論)に精通している場合は、適用される荷重が有意なバイモーメントを有することがわかります。 二量体は、物理的な寸法力X長さ2を有する断面量である。
たぶん(これは私の個人的な推測です)、この場合の効率的なSaint-Venantの原則は、力と瞬間だけでなく、ゼロのバイモーメントも必要とするはずです。 これは妨害のbimomentを提供する4つのポイント負荷を加えることによって達成することができる。 このような分析の結果を以下に示す。
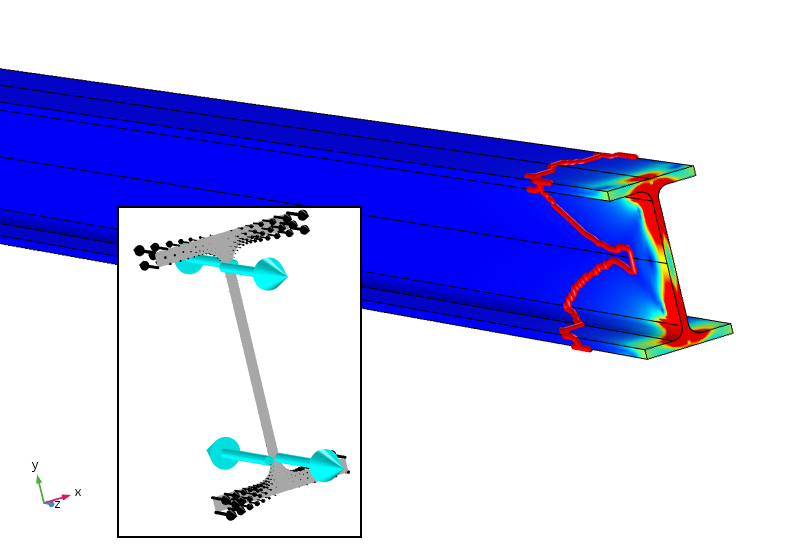
四点荷重と同等の応力で、ゼロバイモメントも提供します。 5%の応力輪郭は、ロードされた境界にはるかに近いものになりました。
適用された点荷重は、意図的に最適に配置されていないため、非常に高い(実際には特異な)局所応力を与えます。 しかし、応力ははるかに速く低下し、約100mm後に5%以下になります。5%の制限は適用される分散荷重の点ではまだあるため、新しい局所応力に対して調整されません。 ひずみエネルギー密度の対数減衰率は、点荷重が加算された後、三倍高速です。
有限要素解析におけるSaint-Venantの原理
場合によっては、SAINT-Venantの原理がFE離散化された問題に適用できると直感的に考えることができます。 ここでは、分散負荷と不適合メッシュを見ていきます。
分散荷重
FEモデルでは、連続境界荷重として指定しても、常にメッシュノードに荷重が適用されます。 負荷は、以下の例に示すように、仮想作業の原則を使用して要素のノードに内部的に分散されます。
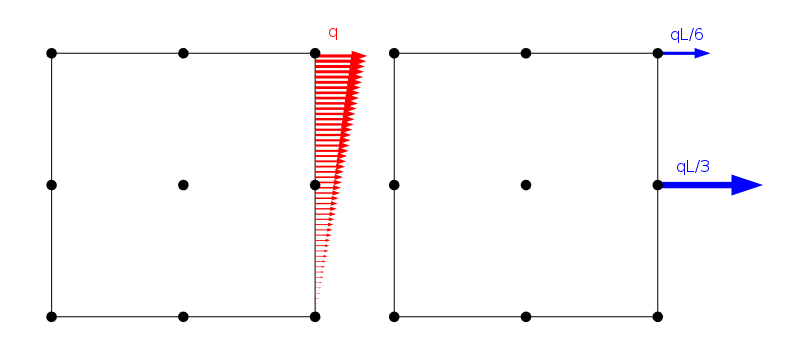
直線的に分布する荷重であり、辺の長さがLの二次ラグランジュ要素のノードにどのように適用されるか
しかし、同じ合力とモーメントを共有する限り、同じ節点荷重を与える荷重分布は無限大である。 明らかに、有限要素問題の解は、これらのすべての場合で同じです。 しかし、Saint-Venantの原理から、そのような荷重はすべて、ある程度離れているとすぐに本質的に同じ応力場を与えるべきであると結論付けることができま
荷重を再分配する領域のサイズは要素面であるため、その後に差がない線形寸法は本質的に構造内の要素層です。 したがって、要素の最も外側の層の溶液は、実際の負荷に対応しない場合がありますが、さらに、それはありません。
一例として、指数応力分布を持つ境界荷重を持つ長方形の板を荷重することができます。 細かいメッシュで計算された応力を以下に示します。

軸方向応力分布の等高線グラフ。
Saint-Venantの原理により、応力場は期待どおりに荷重されたエッジからある距離で純粋な曲げ状態に再分配されます。 しかし、これは現在の議論の対象ではありません。 むしろ、上記の応力分布と、多数の粗いメッシュで得られるものとの違いを調べます。
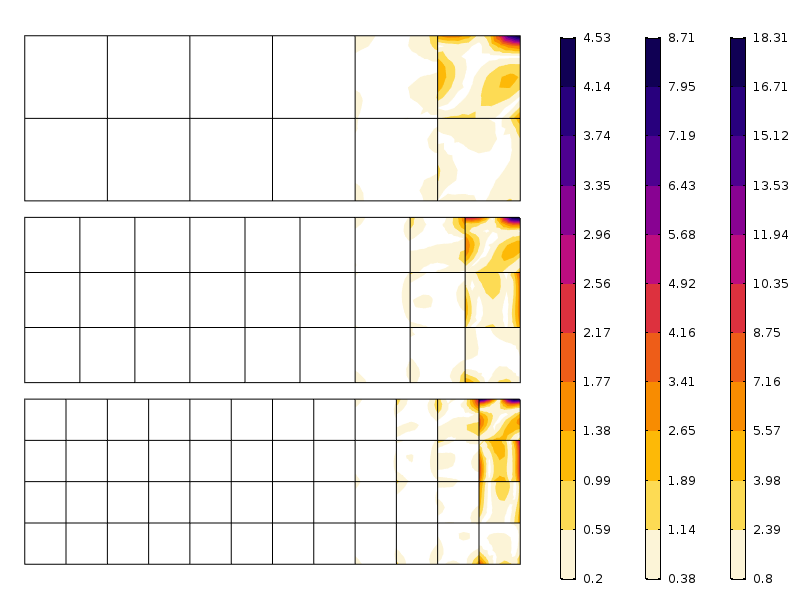
三つの異なるメッシュの軸方向応力の誤差。 異なるスケールに注意してください。 予想通り、メッシュが細かい場合、誤差は小さくなります。
図に見られるように、最初の要素層の後に誤差が急速に減少します。 ここで見られるのは、実際にはメッシュ収束とSaint-Venantの原理によって暗示される応力の再分布の組み合わせです。
不適合メッシュ
不適合メッシュは、二つの接続された要素の形状関数が一致しない場合に発生します。 最も一般的なケースは、アセンブリがidペアと連続性条件を使用して接続されている場合です。 これを例証するために,意図的に一致しないメッシュを持つ直線バーを研究することができる。 一軸張力のような単純な荷重ケースでは、遷移によって引き起こされる応力外乱を研究することが可能である。
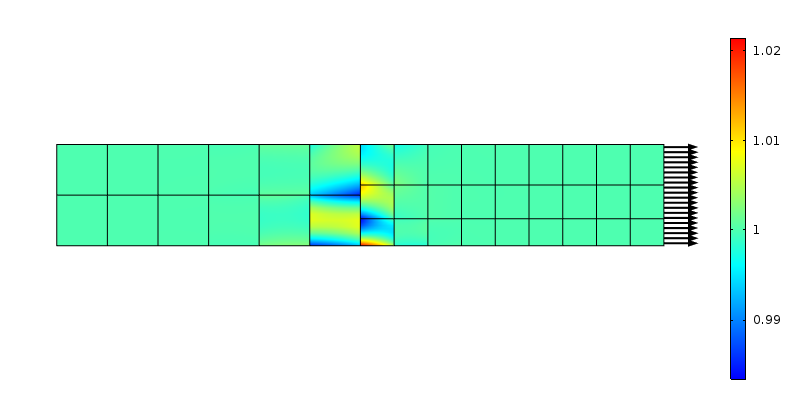
不適合メッシュ遷移における軸方向応力。 二次要素が使用されます。
両側のノードによって伝達される力は、一定の応力の仮定と一致しません。 繰り返しになりますが、これは要素サイズである領域に対する局所的な負荷の再分配と見なすことができます。 Saint-Venantの推論を使用すると、外乱は遷移から”要素サイズ”の距離で消えてしまうはずです。 メッシュが軸方向に洗練された場合に何が起こるかを調べてみましょう。
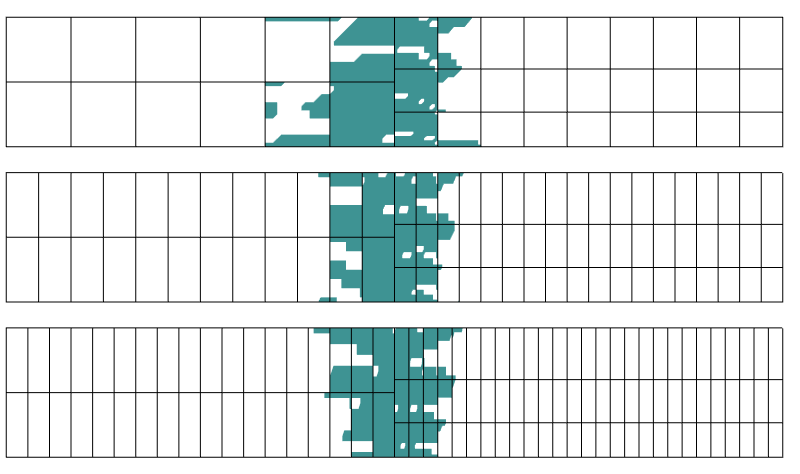
応力に0.1%以上の誤差がある領域。 軸方向に三つの異なる離散化を用いた。
遷移境界に垂直な方向の離散化によって外乱領域はあまり影響されないことが判明しました。 これはまさにSaint-Venantの原則が私たちに伝えていることです。
最終的な発言
Saint-Venantの原理を利用しないと、詳細な荷重分布がわからないため、多くの構造解析を実行することは困難です。
この原理は形式的には線形弾性材料に対してのみ有効である。 実際には、我々はまた、直感的に他の状況のために日常的にそれを使用しています。 たとえば、”穴のある板”の例の材料が弾塑性であった場合、降伏応力が境界に加えられる応力を超えて穴の周りに塑性変形のみがある限り、二つの分布荷重が同等の結果を与えることが期待されます。 しかし、負荷された点の周りに材料が生成されるため、点荷重は常に異なる解を与えます。 より長い議論のために、点負荷での特異点に関するこのブログ記事を読んでください。
次の手順
COMSOL Multiphysics®ソフトウェアをFEAに使用する方法の詳細については、こちらをご覧ください。
さらに読む
- Y.C.Fung and P.Tong,Classical and Computational Solid Mechanics,World Scientific Publishing Co. Pte. (株), 2001.