anvendelse og fortolkning af Saint-Venants princip

alle bygningsingeniører bruger Saint-Venants princip, hvad enten det er aktivt eller ubevidst. Du kan finde forskellige formuleringer af dette princip i de fleste strukturelle mekanikbøger, men dens nøjagtige betydning er ikke indlysende. Saint-Venants princip fortæller os, at den nøjagtige fordeling af en belastning ikke er vigtig langt væk fra det belastede område, så længe resultaterne af belastningen er korrekte. I dette blogindlæg vil vi undersøge Saint-Venants princip, især i forbindelse med finite element (FE) analyse.

historien om Saint-Venant ‘ s princip

den franske videnskabsmand Barr Kristian de Saint-Venant formulerede sit berømte princip i 1855, men det var mere en observation end en streng matematisk erklæring:

“hvis de kræfter, der virker på en lille del af overfladen af et elastisk legeme, erstattes af et andet statisk ækvivalent system af kræfter, der virker på den samme del af overfladen, frembringer denne omfordeling af belastning væsentlige ændringer i spændingerne lokalt, men har en ubetydelig virkning på spændingerne i afstande, der er store i sammenligning med de lineære dimensioner af overfladen, på hvilken kræfterne ændres.”

B. Saint-Venant, M. Kristiansand, vol. 14, 1855.

portræt af Saint-Venant. Billede i det offentlige domæne, via Commons.

mange store sind inden for anvendt mekanik — Boussinesks, kærlighed, von Mises, Toupin og andre — var involveret i at angive Saint-Venants princip i en mere præcis form og give matematiske beviser for det. Som det viser sig, er dette ret vanskeligt for mere generelle sager, og forskning om emnet er stadig i gang. (Argumentationen har til tider været ret levende .)

simpelt eksempel: analyse af spændinger på afstand

lad os starte med noget ret simpelt: en tynd rektangulær plade med et cirkulært hul i en vis afstand fra den belastede kant, som trækkes aksialt. Hvis vi er interesseret i stresskoncentrationen ved hullet, hvor vigtig er den faktiske belastningsfordeling?

tre forskellige belastningstyper anvendes længst til højre:

1. en konstant aksial spænding på 100 MPa
2. en symmetrisk parabolsk spændingsfordeling med spidsamplitude 150 MPa
3. en centreret punktbelastning med samme resulterende som de to foregående belastningstilfælde

som det ses i nedenstående plot, påvirkes spændingsfordelingen ved hullet ikke af, hvordan belastningen påføres. Nøglen her er selvfølgelig, at hullet er langt nok fra belastningen.

Von Mises stresskonturer for de tre belastningssager.

en anden måde at visualisere dette scenario på er ved at bruge hovedspændingspile. Et sådant plot understreger stressfeltet som en strøm og giver en god følelse for omfordelingen.

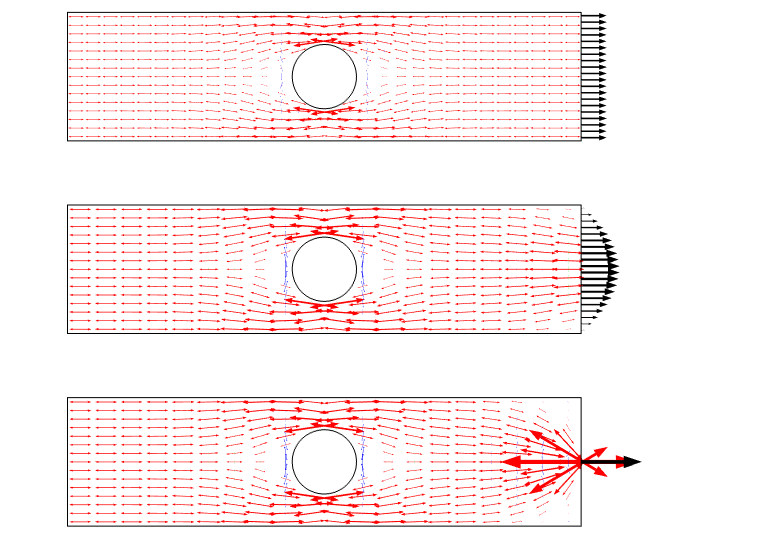
Hovedspændingsplot for de tre belastningssager. Bemærk, at der er en singularitet, når der anvendes en punktbelastning.

ved at tegne spændingen langs en linje kan vi se, at alle tre tilfælde konvergerer til hinanden i en afstand fra kanten, som er omtrent lig med pladens bredde.

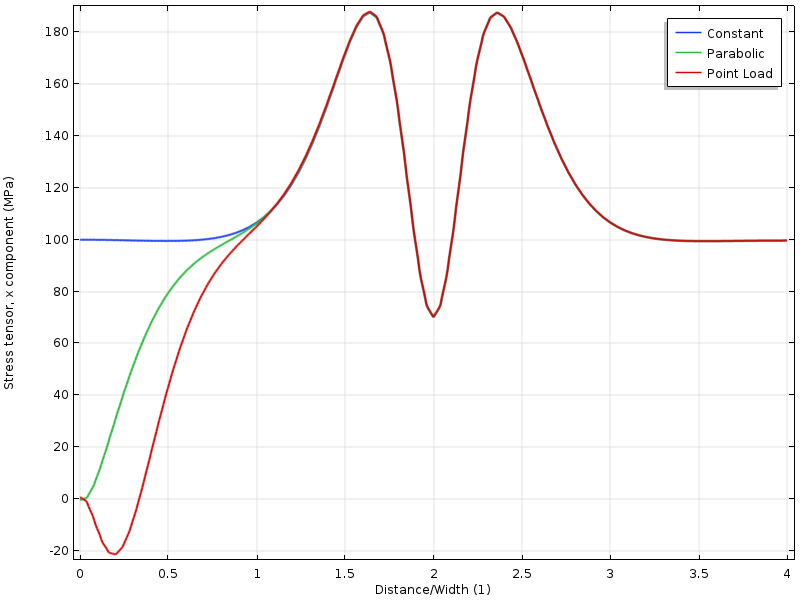
Stress langs den øvre kant som en funktion af afstanden fra den belastede grænse. Afstanden normaliseres af pladens bredde.

hvis hullet flyttes tættere på den belastede grænse, får vi en anden situation. Spændingstilstanden omkring hullet afhænger nu af belastningsfordelingen. Men endnu mere interessant er, at afstanden til hvor de tre stressfelter er enige nu, er dobbelt så langt fra den belastede grænse. Anvendelsen af Saint-Venants princip kræver, at stressene frit kan omfordeles. I dette tilfælde er denne omfordeling delvist blokeret af hullet.

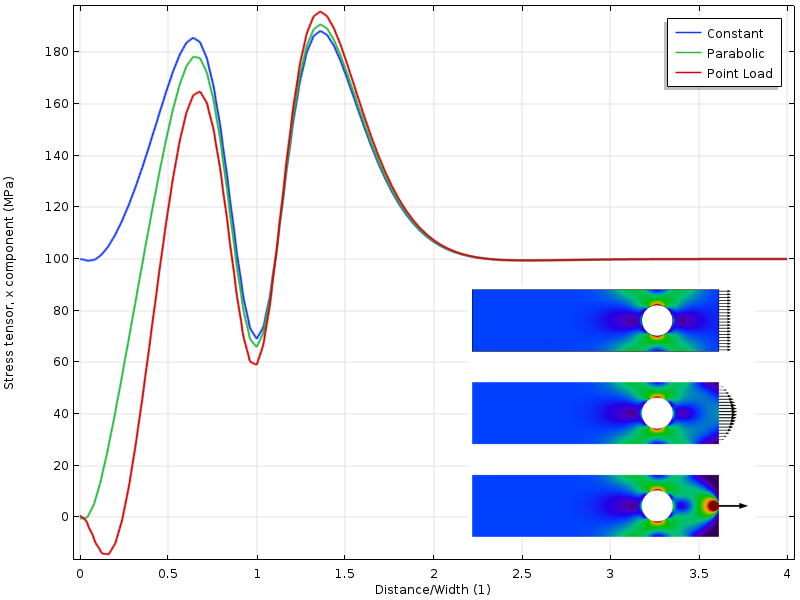
spænd langs den øvre kant med hullet tættere på den belastede grænse.

Bemærk, at Saint-Venants princip fortæller os, at der ikke er nogen forskel i stresstilstanden i en afstand, der er af rækkefølgen af den lineære dimension af det belastede område. Det belastede område, der skal tages i betragtning, er dog muligvis ikke det område, der faktisk er indlæst! Denne erklæring lyder måske mærkeligt, men tænk på det på denne måde: når hullet er langt væk, kan vi beregne stresskoncentrationsfaktoren ved hjælp af en håndbog (min siger 4.32) snarere end ved en FE-løsning. Håndbogens tilgang indeholder en implicit antagelse om, at belastningen er jævnt fordelt som i den første belastningssag. Så selvom den faktiske belastning kun blev anvendt på en lille del af grænsen, er den kritiske Afstand i så fald relateret til størrelsen af hele grænsen.

når problemet løses ved hjælp af den endelige elementmetode (FEM), kan hullet være vilkårligt tæt på belastningen. Det, der sætter grænsen, er, at belastningsfordelingen fra det fysiske synspunkt er veldefineret. Så snart vi antager antagelser om omfordeling, er der imidlertid en implicit antagelse om belastningsfordelingen, som kan afvige fra den faktiske.

nul resulterende systemer og Belastningsenergitæthed

indtil videre har vi sagt, at spændingerne er de samme uafhængige af belastningsdetaljerne i en passende afstand. Da vi har at gøre med lineær elasticitet her, er det altid muligt at overlejre belastningssager. Når man arbejder med bevis for Saint-Venants princip, er det lettere at formulere et princip i denne retning: spændingerne forårsaget af et belastningssystem uden resulterende kraft eller øjeblik vil være små i en afstand, der er af samme størrelsesorden som størrelsen på den belastede grænse.

således studerer vi stress forårsaget af forskellen mellem de to belastningssystemer med lige resultater. De fleste moderne beviser er baseret på skøn over forfaldet af belastningsenergitætheden for et sådant nul-resulterende system.

når vi vender tilbage til problemet ovenfor, kan vi beregne forskellen mellem belastningssagerne. Dette giver os mulighed for at studere det faktiske forfald af stress eller belastningsenergitæthed for forskellen i stressfelterne.

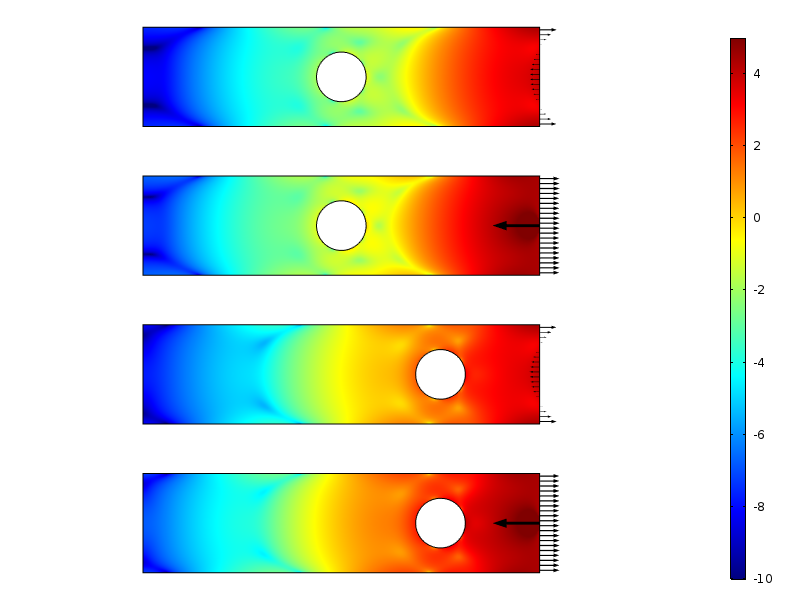
logaritme af belastningsenergitæthed for de nul-resulterende belastningstilfælde.

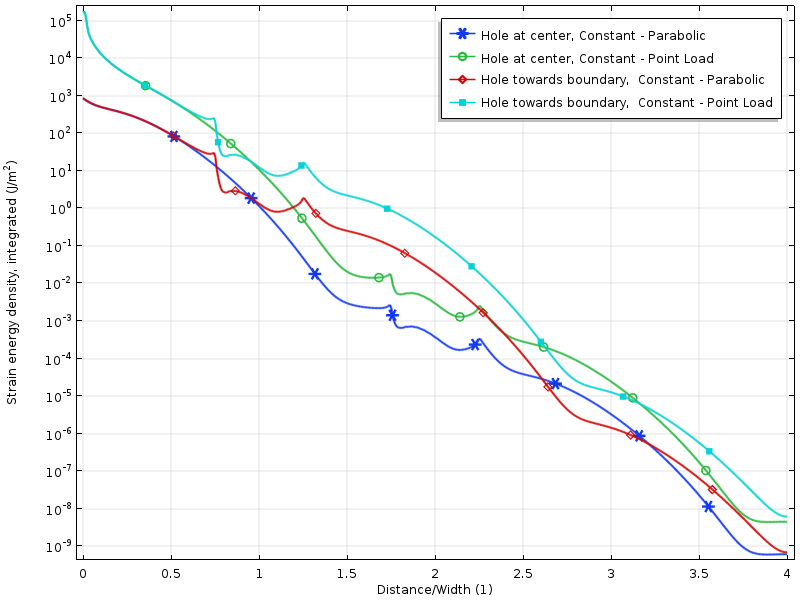
belastningsenergitætheden langs pladen for de nul resulterende belastningstilfælde. Energien er integreret i lodret retning for at producere en mængde, der kun er en funktion af afstanden fra belastningen.

henfaldet i logaritmen af belastningsenergitætheden er mere eller mindre lineær med afstanden fra den belastede grænse. Dette er faktisk i tråd med, hvad moderne beviser forudsiger: et eksponentielt henfald af belastningsenergitætheden. Vi kan også tydeligt se, hvordan hullet midlertidigt reducerer forfaldshastigheden.

anvendelse af Saint-Venants princip på tynde strukturer

for tyndere strukturer som skaller, bjælker og bindingsværk er det velkendt, at Saint-Venants princip ikke kan anvendes på samme måde som for et mere “solidt” objekt. Forstyrrelser rejser længere afstande end hvad vi forventer, fordi belastningsstierne i en tynd struktur er meget mere begrænsede. Dette er det samme fænomen, vi ser med hullet i eksemplet ovenfor, men mere fremtrædende.

her studerer vi en stråle med et standard IPE100 tværsnit. Enden af strålen udsættes for en aksial spænding med en amplitude, der har en lineær fordeling i begge tværsnitsretninger.

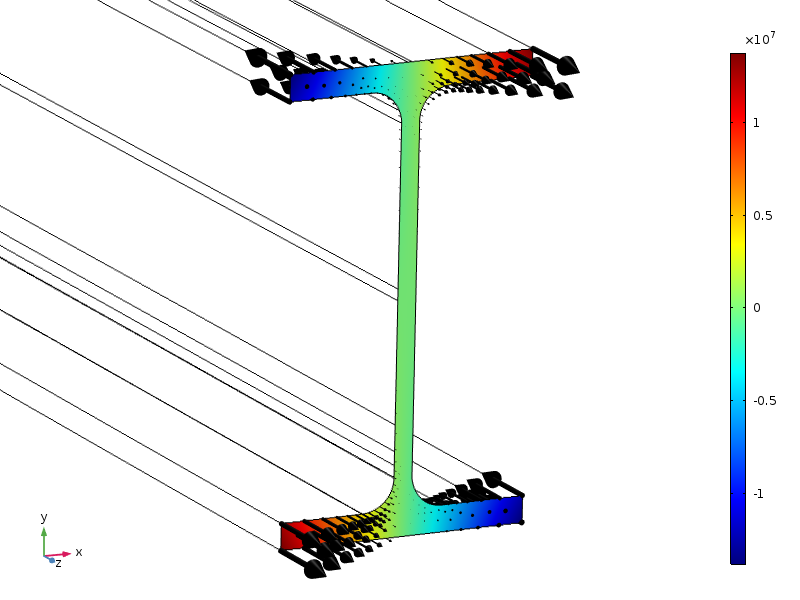
belastningsfordeling, vist som konturer og pile.

på grund af symmetrierne har denne belastning en nul-resulterende kraft såvel som nulmoment omkring alle akser. Tværsnitets højde er 100 mm, så hvis standardformen for Saint-Venants princip er anvendelig, skal spændingerne være små i en afstand på cirka 100 mm fra endeafsnittet.

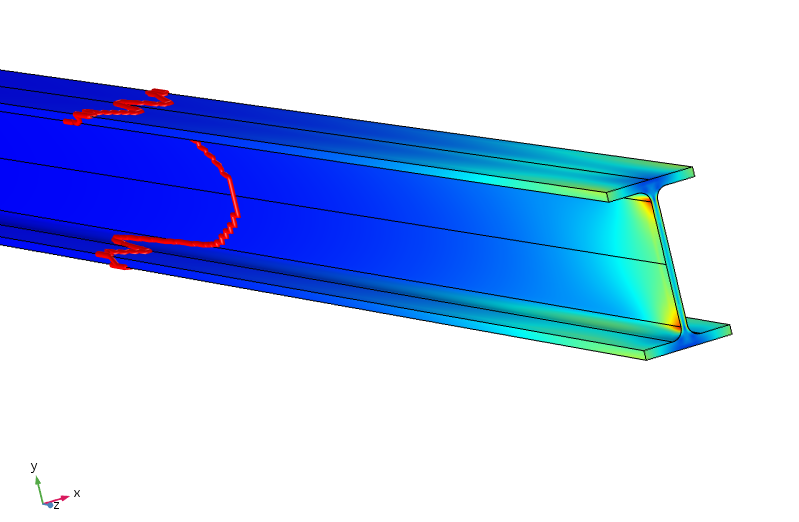
ækvivalent stress i strålen. Den røde kontur angiver, hvor spændingen er mindre end 5% af den maksimale anvendte stress.

det viser sig, at for at stressen skal være under 5% af den maksimale anvendte stress, er vi nødt til at rejse næsten en meter langs bjælken. Således er belastningsfordelingen meget mindre effektiv her, da ækvilibreringen mellem de øverste og nederste flanger kræver øjeblikkelig overførsel gennem den tynde bane.

hvis du er bekendt med teorien om ikke-ensartet torsion af bjælker (dvs.vridningsteori eller Vlasov-teori), vil du erkende, at den anvendte belastning har et signifikant bimoment. Bimomentet er en tværsnitsmængde med den fysiske dimensionskraft * længde2.

måske (dette er bare min personlige spekulation), et effektivt Saint-Venants princip for denne sag skal kræve ikke kun kraft og øjeblik, men også et bimoment på nul. Dette kan opnås ved at tilføje fire punktbelastninger, der giver et modvirkende bimoment. Resultatet af en sådan analyse er vist nedenfor.

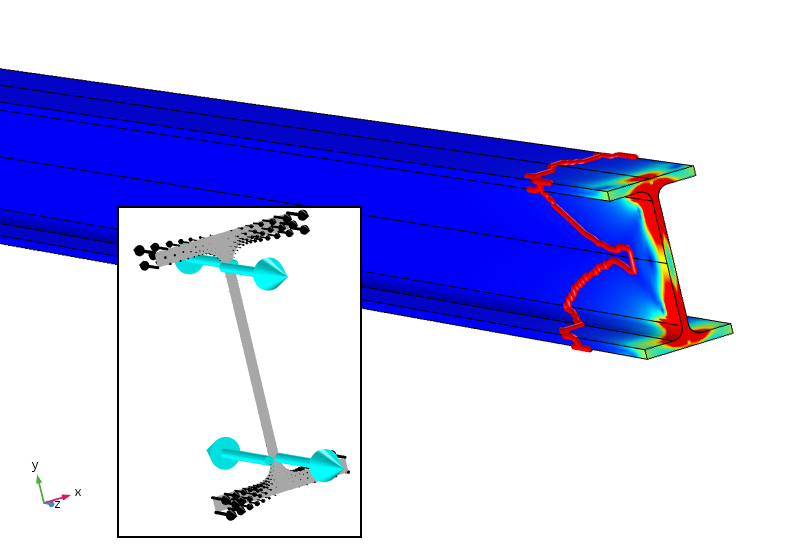
ækvivalent stress med firepunktsbelastninger, der også giver et nul bimoment. Spændingskonturen på 5% er nu meget tættere på den belastede grænse.

de anvendte punktbelastninger, som ikke er optimalt placeret med vilje, giver ekstremt høje (faktisk ental) lokale belastninger. Spændingen falder dog meget hurtigere og er under 5% Efter ca. 100 mm.grænsen på 5% er stadig med hensyn til den påførte distribuerede belastning, så den justeres ikke for de nye lokale belastninger. Den logaritmiske henfaldshastighed for belastningsenergitætheden er tre gange hurtigere, efter at punktbelastningerne er tilføjet.

Saint-Venants princip I endelig elementanalyse

i nogle tilfælde kan du intuitivt betragte Saint-Venants princip som anvendeligt på FE-diskretiseret problem. Her ser vi på distribuerede belastninger og ikke-konforme masker.

distribuerede belastninger

i FE-modellen anvendes belastninger altid på maskenoderne, selvom du angiver dem som en kontinuerlig grænsebelastning. Belastningen fordeles internt til elementets noder ved hjælp af princippet om virtuelt arbejde, som vist i eksemplet nedenfor.

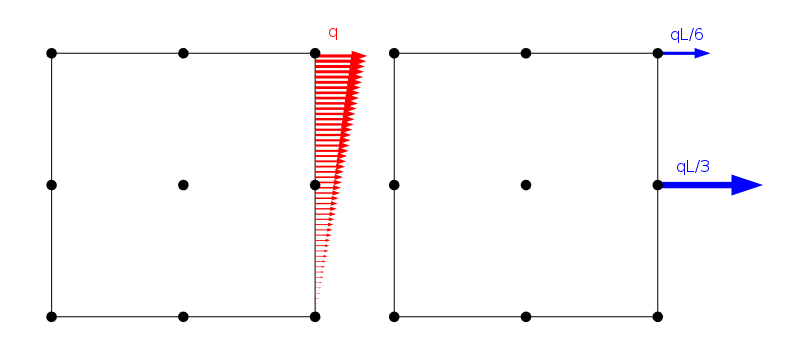
en lineært fordelt belastning, og hvordan den påføres ved knudepunkterne i et andet ordens Lagrange-element med sidelængde L.

der er dog et uendeligt antal belastningsfordelinger, der giver de samme knudebelastninger, så længe de deler den samme resulterende kraft og øjeblik. Naturligvis er løsningen på det endelige elementproblem det samme for alle disse tilfælde. Fra Saint-Venants princip kan vi imidlertid konkludere, at alle sådanne belastninger i det væsentlige skal give det samme stressfelt, så snart vi er et stykke væk.

da størrelsen på det område, over hvilket vi omfordeler belastninger, er et elementflade, er den lineære dimension, hvorefter der ikke er nogen forskel, i det væsentlige et elementlag inde i strukturen. Således kan opløsningen i det yderste lag af elementer ikke svare til den faktiske belastning, men længere ind gør den det.

som et eksempel kan vi indlæse en rektangulær plade med en grænsebelastning, der har en eksponentiel spændingsfordeling. Spændingen beregnet med et fint net er vist nedenfor.

Konturplot af den aksiale spændingsfordeling.

på grund af Saint-Venants princip omfordeles stressfeltet til en ren bøjningstilstand i en vis afstand fra den belastede kant, ligesom vi forventer. Dette er dog ikke målet for den aktuelle diskussion. Snarere undersøger vi forskellen mellem stressfordelingen ovenfor, og hvad vi får med et antal grove masker.

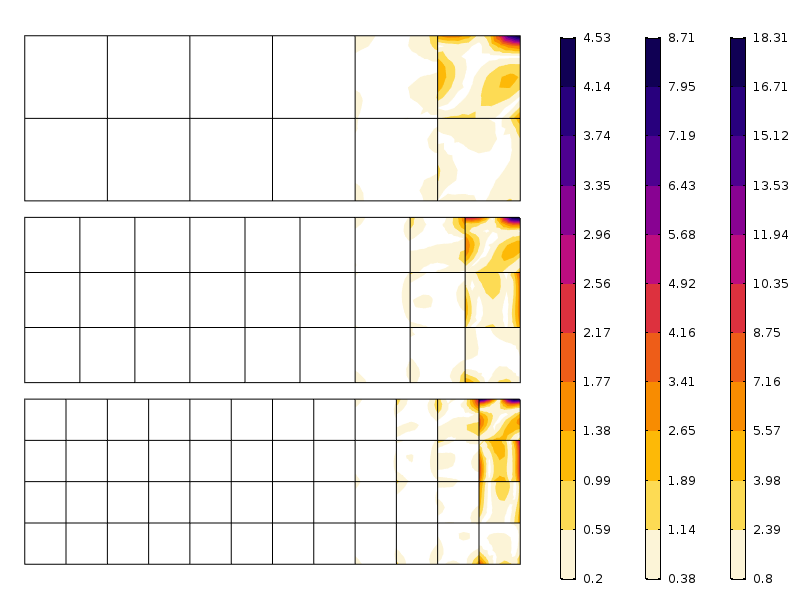
fejl i aksial spænding for tre forskellige masker. Bemærk de forskellige skalaer. Som forventet er fejlen mindre, når masken er finere.

som det fremgår af figuren, falder fejlen hurtigt efter det første elementlag. Det, vi ser her, er faktisk en kombination af mesh-konvergens og omfordeling af stress underforstået af Saint-Venants princip.

ikke-overensstemmende Mesh

et ikke-overensstemmende mesh opstår, når formfunktionerne i to tilsluttede elementer ikke stemmer overens. Det mest almindelige tilfælde er, når en samling er forbundet ved hjælp af identitetspar og kontinuitetsforhold. For at eksemplificere dette kan vi studere en lige stang med et bevidst ikke-matchende net. Med en simpel belastningskasse, såsom enaksial spænding, er det muligt at studere stressforstyrrelser forårsaget af overgangen.

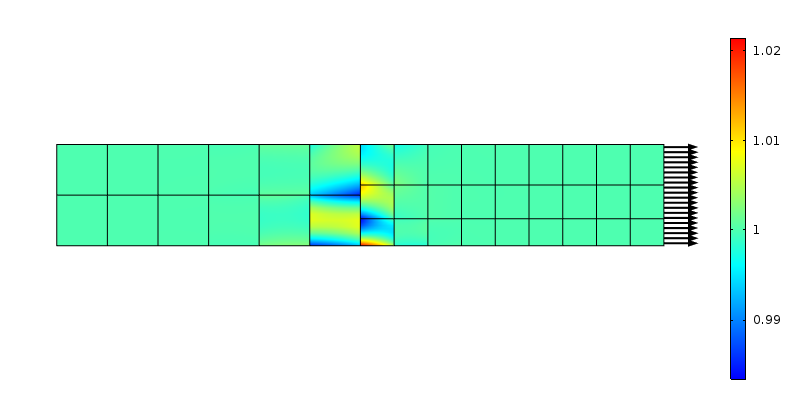
aksial spænding ved en ikke-konform maskeovergang. Andenordens elementer anvendes.

de kræfter, der transmitteres af knuderne på de to sider, svarer ikke til antagelsen om konstant stress. Igen kan dette ses som en lokal belastningsfordeling over et område, der er elementstørrelsen. Ved hjælp af Saint-Venants ræsonnement skal forstyrrelsen forsvinde i en” Elementstørrelse ” afstand fra overgangen. Lad os undersøge, hvad der sker, hvis masken er raffineret i aksial retning.

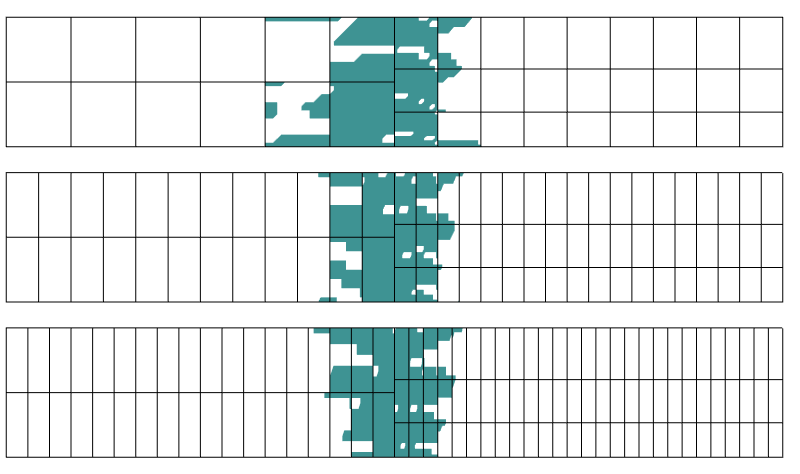
Region med mere end 0,1% fejl i stress. Tre forskellige diskretiseringer anvendes i aksial retning.

det viser sig, at forstyrrelsesområdet ikke påvirkes meget af diskretiseringen i retningen vinkelret på overgangsgrænsen. Dette er præcis, hvad Saint-Venants princip fortæller os.

afsluttende bemærkninger

uden at gøre brug af Saint-Venants princip er mange strukturelle analyser vanskelige at udføre, simpelthen fordi den detaljerede belastningsfordeling ikke er kendt.

princippet gælder formelt kun for lineære elastiske materialer. I praksis bruger vi det også intuitivt dagligt til andre situationer. Hvis for eksempel materialet i “pladen med et hul” – eksempel var elastoplastisk, ville vi forvente, at de to distribuerede belastninger ville give tilsvarende resultater, så længe udbyttespændingen er over den spænding, der påføres ved grænsen, så der kun er plastisk deformation omkring hullet. Punktbelastningen giver dog altid en anden løsning, da materialet giver omkring det belastede punkt. For en længere diskussion, Læs dette blogindlæg om singulariteter ved punktbelastninger.

næste trin

Lær mere om brug af COMSOL Multiphysics-programmet til fea.

yderligere læsning

• Y. C. Fung og P. Tong, klassisk og Computational Solid Mechanics, verdens videnskabelige udgivelse Co. Pte. Ltd., 2001.