tillämpa och tolka Saint-Venants princip

alla konstruktörer använder Saint-Venants princip, vare sig aktivt eller undermedvetet. Du kan hitta olika formuleringar av denna princip i de flesta strukturmekaniska läroböcker, men dess exakta betydelse är inte uppenbar. Saint-Venants princip säger att den exakta fördelningen av en last inte är viktig långt ifrån den laddade regionen, så länge lastens resultat är korrekta. I det här blogginlägget kommer vi att undersöka Saint-Venants princip, särskilt i samband med finita element (FE) analys.

historien om Saint-Venants princip

den franska forskaren Barr Bisexual de Saint-Venant formulerade sin berömda princip 1855, men det var mer en observation än ett strikt matematiskt uttalande:

”om krafterna som verkar på en liten del av ytan på en elastisk kropp ersätts av ett annat statiskt ekvivalent system av krafter som verkar på samma del av ytan, ger denna omfördelning av belastningen väsentliga förändringar i spänningarna lokalt, men har en försumbar effekt på spänningarna på avstånd som är stora i jämförelse med de linjära dimensionerna på ytan på vilken krafterna ändras.”

B. Saint-Venant, M. savants taiwantrangers, vol. 14, 1855.

porträtt av Saint-Venant. Bild i det offentliga rummet, via Wikimedia Commons.

många stora sinnen inom tillämpad mekanik — Boussinesq, Love, von Mises, Toupin och andra — var inblandade i att ange Saint-Venants princip i en mer exakt form och tillhandahålla matematiska bevis för det. Som det visar sig är detta ganska svårt för mer allmänna fall, och forskning om ämnet pågår fortfarande. (Argumentationen har ibland varit ganska levande.)

enkelt exempel: analysera spänningar på avstånd

låt oss börja med något ganska enkelt: en tunn rektangulär platta med ett cirkulärt hål på något avstånd från den laddade kanten, som dras axiellt. Om vi är intresserade av spänningskoncentrationen vid hålet, Hur viktig är den faktiska lastfördelningen?

tre olika belastningstyper appliceras längst till höger:

1. en konstant axiell spänning på 100 MPa
2. en symmetrisk parabolisk spänningsfördelning med toppamplitud 150 MPa
3. en centrerad punktbelastning med samma resultat som de två tidigare belastningsfallen

som framgår av nedanstående diagram påverkas inte spänningsfördelningen vid hålet av hur belastningen appliceras. Nyckeln här är naturligtvis att hålet är tillräckligt långt från lasten.

Von Mises spänningskonturer för de tre belastningsfallen.

ett annat sätt att visualisera detta scenario är att använda huvudspänningspilar. En sådan tomt betonar stressfältet som ett flöde och ger en bra känsla för omfördelningen.

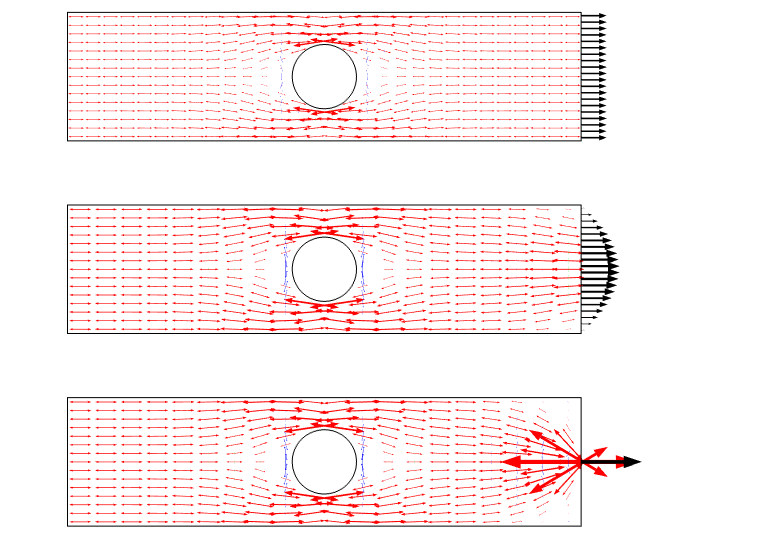
Huvudspänningsplot för de tre belastningsfallen. Observera att det finns en singularitet när en punktbelastning används.

genom att rita spänningen längs en linje kan vi se att alla tre fallen konvergerar till varandra på avstånd från kanten, vilket är ungefär lika med plattans bredd.

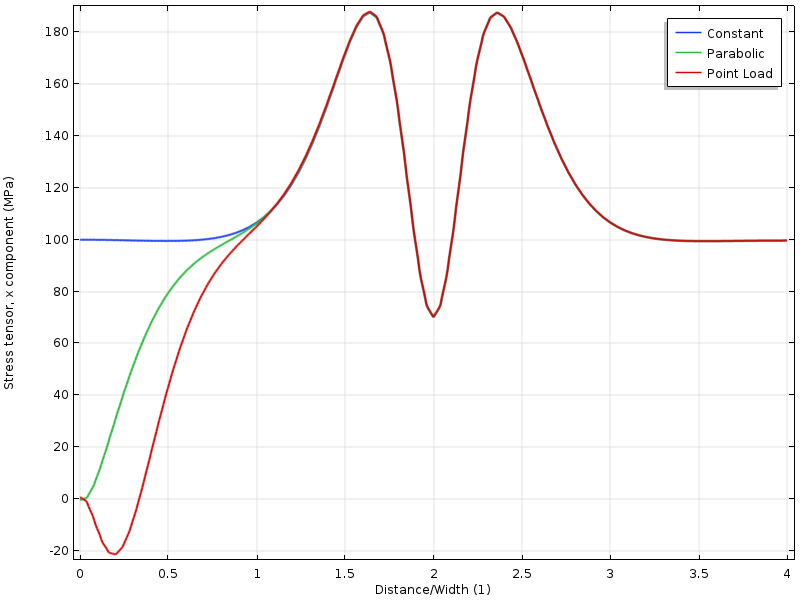
spänning längs den övre kanten som en funktion av avståndet från den laddade gränsen. Avståndet normaliseras av plattans bredd.

om hålet flyttas närmare den laddade gränsen får vi en annan situation. Spänningstillståndet runt hålet beror nu på belastningsfördelningen. Men ännu mer intressant är att avståndet till där de tre stressfälten är överens nu är dubbelt så långt från den laddade gränsen. Tillämpningen av Saint-Venants princip kräver att spänningarna är fria att omfördela. I detta fall blockeras omfördelningen delvis av hålet.

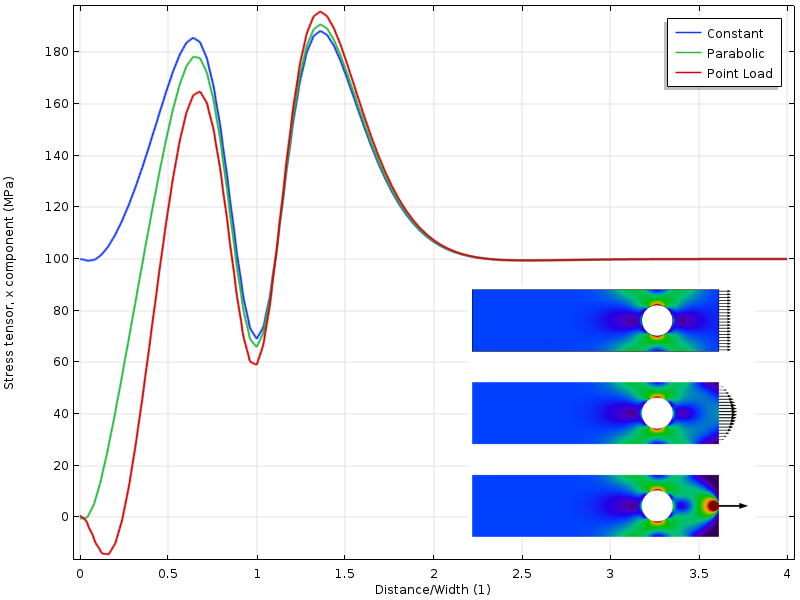
spänn längs den övre kanten med hålet närmare den laddade gränsen.

Observera att Saint-Venants princip säger att det inte finns någon skillnad i spänningstillståndet på ett avstånd som är i storleksordningen den linjära dimensionen av det laddade området. Det laddade området som ska beaktas kan dock inte vara det område som faktiskt är laddat! Detta uttalande kan låta konstigt, men tänk på det så här: när hålet är långt borta kan vi beräkna spänningskoncentrationsfaktorn med hjälp av en handbok (min säger 4.32) snarare än med en FE-lösning. Handboksmetoden innehåller ett implicit antagande att lasten är jämnt fördelad som i det första belastningsfallet. Så även om den faktiska belastningen applicerades på endast en liten del av gränsen, är det kritiska avståndet i så fall relaterat till storleken på hela gränsen.

när du löser problemet med finita elementmetoden (FEM), kan hålet vara godtyckligt nära lasten. Det som sätter gränsen är att ur fysisk synvinkel är lastfördelningen väl definierad. Så snart vi gör antaganden om omfördelning finns det emellertid ett implicit antagande om lastfördelningen, som kan skilja sig från den faktiska.

noll resulterande system och Belastningsenergidensitet

hittills har vi sagt att spänningarna är desamma oberoende av belastningsdetaljerna på något lämpligt avstånd. Eftersom vi har att göra med linjär elasticitet här är det alltid möjligt att överlappa lastfall. När man arbetar med bevis på Saint-Venants princip är det lättare att formulera en princip enligt dessa linjer: spänningarna som orsakas av ett lastsystem utan resulterande kraft eller ögonblick kommer att vara små på ett avstånd som är av samma storleksordning som storleken på den laddade gränsen.

således studerar vi spänningen som orsakas av skillnaden mellan de två belastningssystemen med lika resultat. De flesta moderna bevis är baserade på uppskattningar av sönderfallet av belastningsenergidensiteten för ett sådant nollresultat system.

återgå till problemet ovan kan vi beräkna skillnaden mellan lastfallen. Genom att göra det kan vi studera det faktiska förfallet av stress eller belastningsenergidensitet för skillnaden mellan stressfälten.

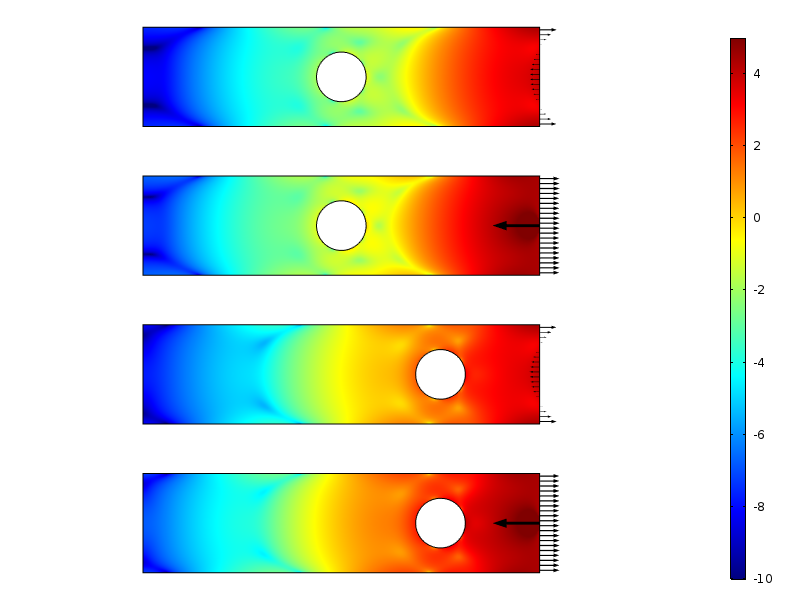
logaritmen för belastningsenergitätheten för de noll resulterande belastningsfallen.

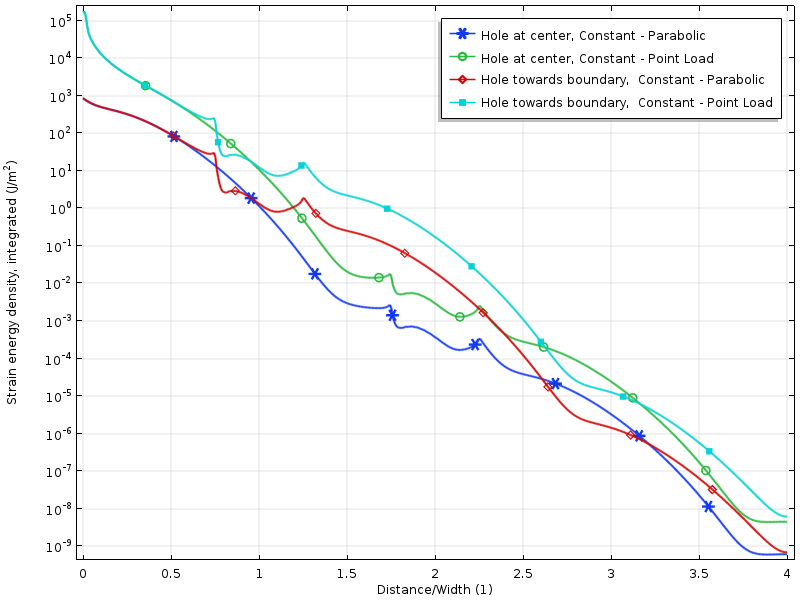
stammen energitäthet längs plattan för noll resulterande belastningsfall. Energin integreras i vertikal riktning för att producera en mängd som bara är en funktion av avståndet från lasten.

sönderfallet i logaritmen för belastningsenergidensiteten är mer eller mindre linjärt med avståndet från den laddade gränsen. Detta är faktiskt i linje med vad moderna bevis förutsäger: ett exponentiellt förfall av belastningsenergitätheten. Vi kan också tydligt se hur hålet tillfälligt minskar sönderfallshastigheten.

tillämpa Saint-Venants princip på tunna strukturer

för tunnare strukturer som skal, balkar och fackverk är det välkänt att Saint-Venants princip inte kan tillämpas på samma sätt som för ett mer ”solidt” objekt. Störningar färdas längre sträckor än vad vi förväntar oss, eftersom lastvägarna i en tunn struktur är mycket mer begränsade. Detta är samma fenomen som vi ser med hålet i exemplet ovan, men mer framträdande.

här studerar vi en stråle med ett standard ipe100-tvärsnitt. Strålens ände utsätts för en axiell spänning, med en amplitud som har en linjär fördelning i båda tvärsnittsriktningarna.

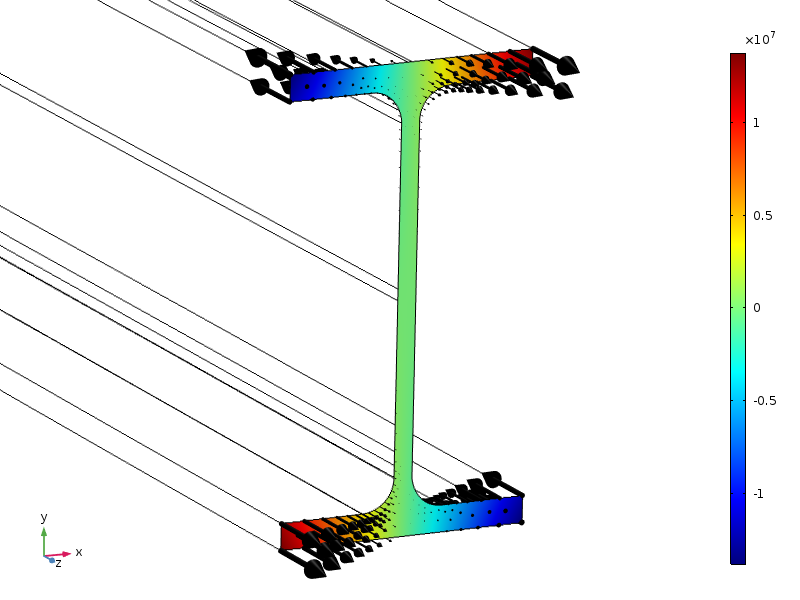
lastfördelning, visas som konturer och pilar.

på grund av symmetrierna har denna belastning en noll-resulterande kraft, liksom nollmoment runt alla axlar. Tvärsnittets höjd är 100 mm, så om standardformen för Saint-Venants princip är tillämplig, bör spänningarna vara små på ett avstånd av ca 100 mm från ändsektionen.

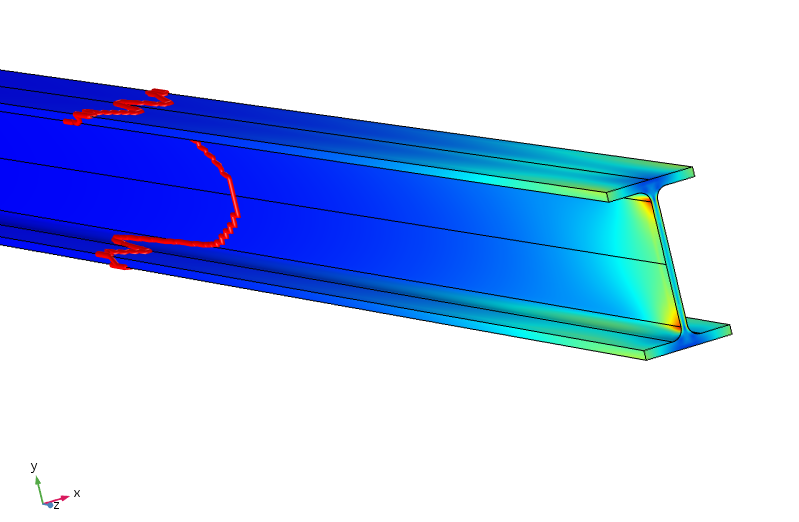
ekvivalent spänning i strålen. Den röda konturen indikerar var spänningen är mindre än 5% av den maximala applicerade spänningen.

det visar sig att för att spänningen ska vara under 5% av den maximala applicerade spänningen måste vi resa nästan en meter längs strålen. Således är lastfördelningen mycket mindre effektiv här, eftersom jämvikten mellan de övre och nedre flänsarna kräver momentöverföring genom den tunna banan.

om du är bekant med teorin för icke-enhetlig vridning av balkar (dvs vridningsteori eller Vlasov-teori) kommer du att inse att den applicerade belastningen har en signifikant bimoment. Bimomentet är en tvärsnittsmängd med den fysiska dimensionen kraft X längd2.

kanske (det här är bara min personliga spekulation), en effektiv Saint-Venants princip för detta fall bör kräva inte bara kraft och ögonblick utan också en bimoment av noll. Detta kan åstadkommas genom att lägga till fyra punktbelastningar som ger en motverkande bimoment. Resultatet av en sådan analys visas nedan.

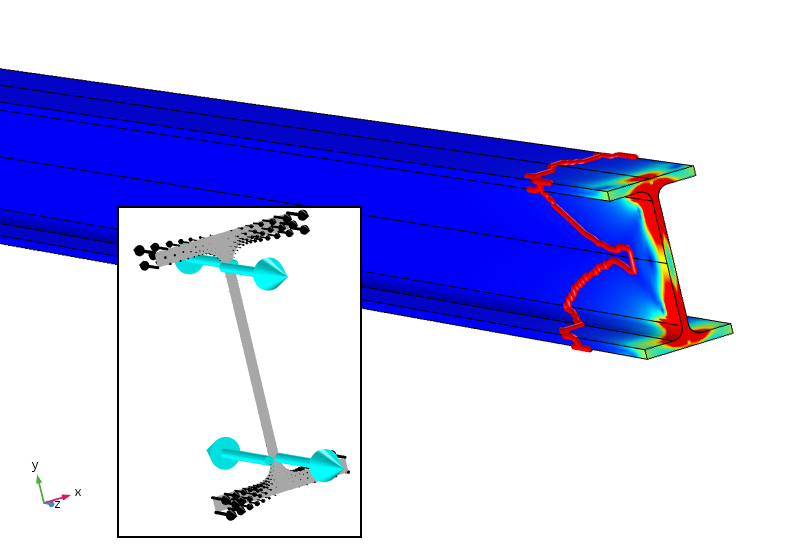
ekvivalent stress med fyra punktbelastningar som också ger en noll bimoment. Spänningskonturen på 5% är nu mycket närmare den laddade gränsen.

de applicerade punktbelastningarna, som inte är optimalt placerade med syfte, ger extremt höga (faktiskt singulära) lokala spänningar. Spänningen sjunker dock mycket snabbare och ligger under 5% Efter cirka 100 mm. gränsen på 5% är fortfarande i termer av den applicerade distribuerade belastningen, så den justeras inte för de nya lokala spänningarna. Den logaritmiska sönderfallshastigheten för belastningsenergitätheten är tre gånger snabbare efter att punktbelastningarna har lagts till.

Saint-Venants princip i finita elementanalys

i vissa fall kan du intuitivt betrakta Saint-Venants princip som tillämplig på det Fe-diskretiserade problemet. Här tittar vi på distribuerade laster och avvikande maskor.

distribuerade laster

i FE-modellen appliceras laster alltid vid masknoderna, även om du anger dem som en kontinuerlig gränsbelastning. Lasten distribueras internt till elementets noder med principen om virtuellt arbete, som visas i exemplet nedan.

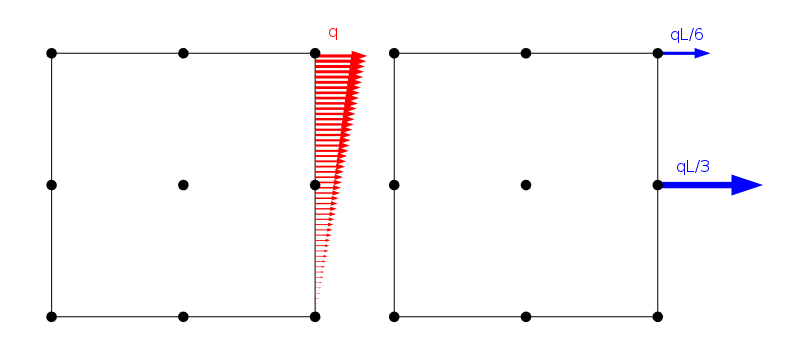
en linjärt fördelad belastning och hur den appliceras vid noderna i ett andra ordningens Lagrange-element med sidolängd L.

det finns dock ett oändligt antal belastningsfördelningar som ger samma nodbelastningar så länge de delar samma resulterande kraft och ögonblick. Självklart är lösningen på det finita elementproblemet detsamma för alla dessa fall. Från Saint-Venants princip kan vi dock dra slutsatsen att alla sådana belastningar borde ge i stort sett samma stressfält så snart vi är på avstånd.

eftersom storleken på det område över vilket vi omfördelar laster är ett element ansikte, är den linjära dimensionen efter vilken det inte finns någon skillnad i huvudsak ett elementskikt inuti strukturen. Således kan lösningen i det yttersta skiktet av element inte motsvara den faktiska belastningen, men längre in gör den det.

som ett exempel kan vi ladda en rektangulär platta med en gränsbelastning som har en exponentiell spänningsfördelning. Spänningen beräknad med ett fint nät visas nedan.

Konturplott för axiell spänningsfördelning.

på grund av Saint-Venants princip omfördelas stressfältet till ett rent böjningstillstånd på något avstånd från den laddade kanten, precis som vi förväntar oss. Detta är dock inte målet för den aktuella diskussionen. Snarare undersöker vi skillnaden mellan stressfördelningen ovan och vad vi får med ett antal grova maskor.

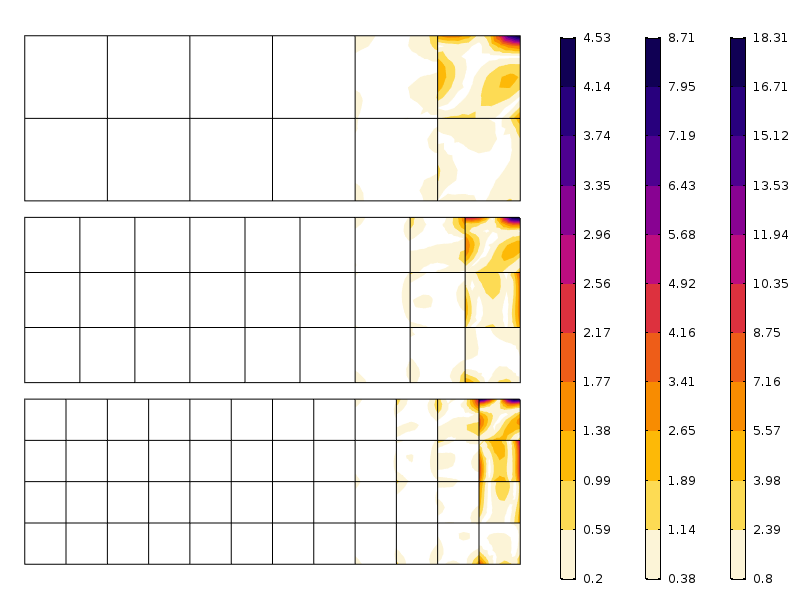
fel i axiell spänning för tre olika maskor. Notera de olika skalorna. Som förväntat är felet mindre när nätet är finare.

som framgår av figuren minskar felet snabbt efter det första elementskiktet. Det vi ser här är faktiskt en kombination av nätkonvergens och omfördelningen av spänningar som antyds av Saint-Venants princip.

avvikande nät

ett avvikande nät uppstår när formfunktionerna i två anslutna element inte matchar. Det vanligaste fallet är när en montering är ansluten med identitetspar och kontinuitetsförhållanden. För att exemplifiera detta kan vi studera en rak stång med ett avsiktligt icke-matchande nät. Med ett enkelt lastfall, såsom enaxlig spänning, är det möjligt att studera stressstörningar orsakade av övergången.

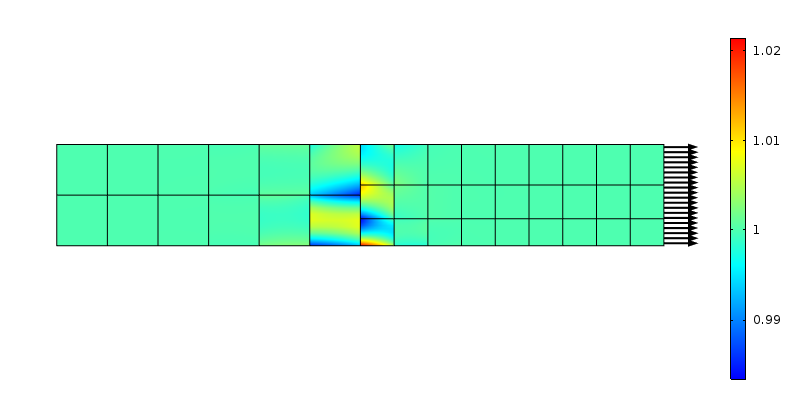
axiell spänning vid en avvikande nätövergång. Andra ordningens element används.

de krafter som överförs av noderna på de två sidorna matchar inte antagandet om konstant stress. Återigen kan detta ses som en lokal belastningsfördelning över ett område som är elementstorleken. Med hjälp av resonemanget från Saint-Venant bör störningen blekna bort på ett ”elementstorlek” avstånd från övergången. Låt oss undersöka vad som händer om nätet förfinas i axiell riktning.

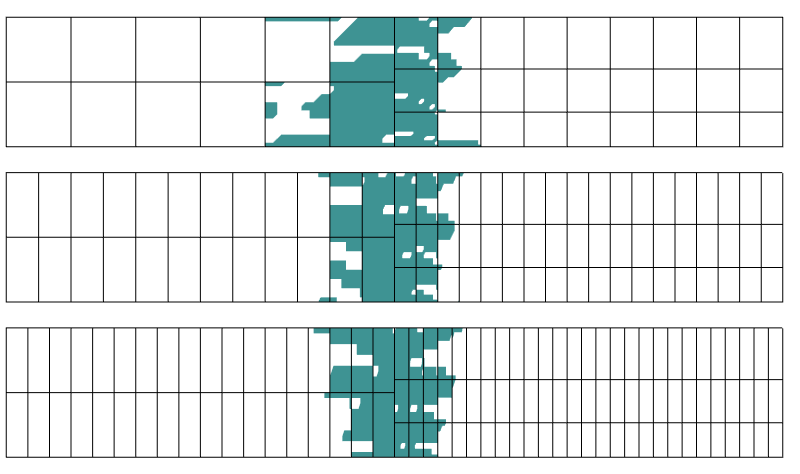
Region med mer än 0,1% fel i stress. Tre olika diskretiseringar används i axiell riktning.

det visar sig att störningsområdet inte påverkas mycket av diskretiseringen i riktningen vinkelrätt mot övergångsgränsen. Det är precis vad Saint-Venants princip berättar för oss.

slutliga anmärkningar

utan att använda Saint-Venants princip är många strukturella analyser svåra att utföra, helt enkelt för att den detaljerade belastningsfördelningen inte är känd.

principen gäller formellt endast för linjära elastiska material. I praktiken använder vi det också intuitivt dagligen för andra situationer. Om exempelvis materialet i” plattan med ett hål ” – exempel var elastoplastisk, skulle vi förvänta oss att de två fördelade belastningarna ger likvärdiga resultat, så länge avkastningsspänningen ligger över spänningen som appliceras vid gränsen så att det bara finns plastisk deformation runt hålet. Punktbelastningen ger emellertid alltid en annan lösning, eftersom materialet ger runt den laddade punkten. För en längre diskussion, Läs detta blogginlägg om singulariteter vid punktbelastningar.

nästa steg

lär dig mer om hur du använder COMSOL Multiphysics-programvaran för FEA.

Vidare läsning

• YC Fung och P. Tong, klassisk och beräknings Hållfasthetslära, World Scientific Publishing Co. Pte. Ltd., 2001.