Anvende Og Tolke Saint-Venants Prinsipp

Alle bygningsingeniører bruker Saint-Venants prinsipp, enten aktivt eller ubevisst. Du kan finne ulike formuleringer av dette prinsippet i de fleste strukturelle mekanikk lærebøker, men den nøyaktige betydningen er ikke åpenbar. Saint-Venants prinsipp forteller oss at den nøyaktige fordeling av en last ikke er viktig langt borte fra den belastede regionen, så lenge resultatene av lasten er riktige. I dette blogginnlegget vil Vi utforske Saint-Venants prinsipp, spesielt i sammenheng med fe-analyse.

Historien Om Saint-Venants Prinsipp

den franske vitenskapsmannen Barré De Saint-Venant formulerte sitt berømte prinsipp i 1855, men det var mer en observasjon enn en streng matematisk uttalelse:

«hvis kreftene som virker på en liten del av overflaten av en elastisk kropp, erstattes av et annet statisk ekvivalent system av krefter som virker på samme del av overflaten, gir denne omfordeling av lasting betydelige endringer i spenningene lokalt, men har en ubetydelig effekt på spenningene på avstander som er store i forhold til de lineære dimensjonene på overflaten som kreftene endres på.»

B. Saint-Venant, Mé. savants hryvners, vol. 14, 1855.

Portrett Av Saint-Venant. Bilde i public domain, Via Wikimedia Commons.

Mange store hjerner innen anvendt mekanikk-Boussinesq, Love, von Mises, Toupin og andre-var involvert i å si Saint-Venants prinsipp i en mer nøyaktig form og gi matematiske bevis for Det. Som det viser seg, er dette ganske vanskelig for mer generelle saker, og forskning på emnet pågår fortsatt. (Argumentasjonen har til tider vært ganske levende.)

Enkelt Eksempel: Analysere Spenninger På Avstand

la oss starte med noe ganske enkelt: en tynn rektangulær plate med et sirkulært hull i noen avstand fra den lastede kanten, som trekkes aksialt. Hvis vi er interessert i spenningskonsentrasjonen ved hullet, så hvor viktig er den faktiske lastfordelingen?

Tre forskjellige lasttyper brukes ved grensen lengst til høyre:

1. en konstant aksial spenning på 100 MPa
2. en symmetrisk parabolisk spenningsfordeling med toppamplitude 150 mpa
3. en sentrert punktbelastning med samme resultat som de to foregående lastkassene

som vist i tomtene nedenfor, påvirkes ikke spenningsfordelingen ved hullet av hvordan lasten påføres. Nøkkelen her er selvfølgelig at hullet er langt nok fra lasten.

Von Mises stress konturer for de tre last tilfeller.

en annen måte å visualisere dette scenariet på er å bruke hovedspenningspiler. Et slikt plott legger vekt på stressfeltet som en flux og gir en god følelse for omfordeling.

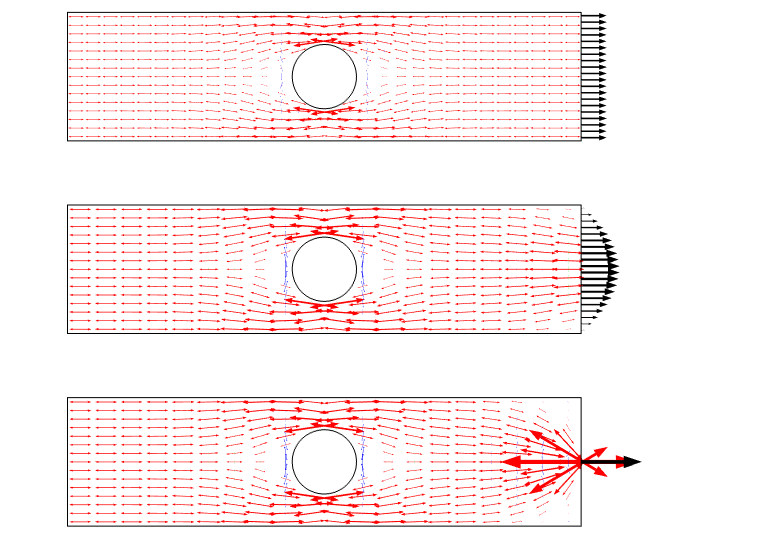
Principal stress plot for de tre last tilfeller. Merk at det er en singularitet når en punktbelastning brukes.

ved å tegne spenningen langs en linje, kan vi se at alle tre tilfellene konvergerer til hverandre i en avstand fra kanten, som er omtrent lik bredden på platen.

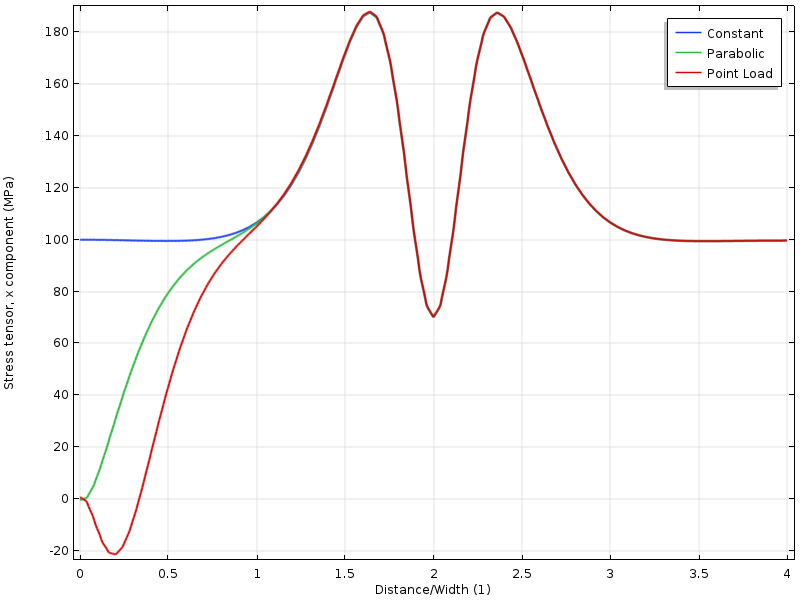
Stress langs øvre kant som en funksjon av avstanden fra den lastede grensen. Avstanden er normalisert av platenes bredde.

hvis hullet flyttes nærmere den lastede grensen, får vi en annen situasjon. Spenningstilstanden rundt hullet avhenger nå av lastfordelingen. Men enda mer interessant er at avstanden til hvor de tre stressfeltene er enige nå, er dobbelt så langt fra den lastede grensen. Anvendelsen Av Saint-Venants prinsipp krever at stressene er frie til å omfordele. I dette tilfellet er den omfordeling delvis blokkert av hullet.

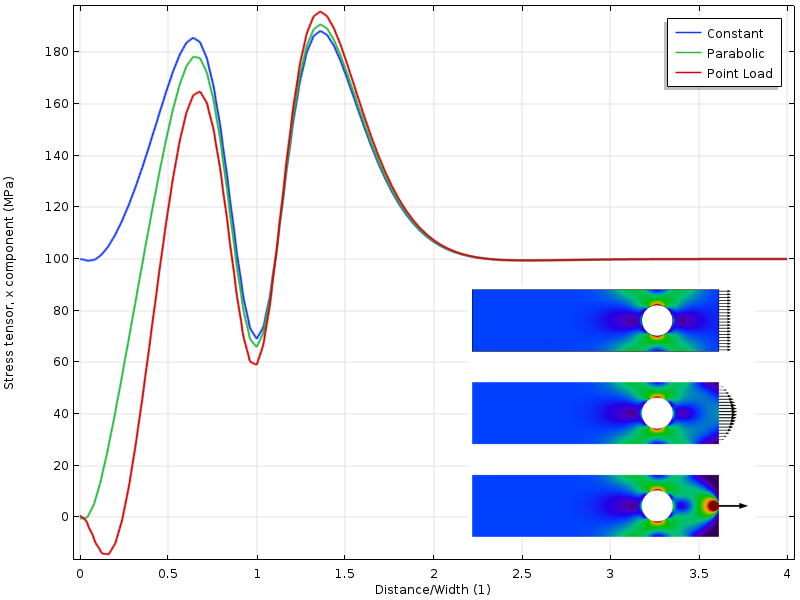
Stress langs øvre kant med hullet nærmere den lastede grensen.

Merk At Saint-Venants prinsipp forteller oss at det ikke er noen forskjell i spenningstilstanden i en avstand som er av rekkefølgen av den lineære dimensjonen av det lastede området. Det lastede området som skal tas i betraktning, kan imidlertid ikke være det området som faktisk er lastet! Denne uttalelsen kan høres rart ut, men tenk på det på denne måten: Når hullet er langt unna, kan vi beregne stresskonsentrasjonsfaktoren ved hjelp av en håndbok (min sier 4.32) i stedet for MED EN FE-løsning. Håndbokens tilnærming inneholder en implisitt antagelse om at lasten er jevnt fordelt som i første lasttilfelle. Så selv om den faktiske belastningen ble brukt på bare en liten del av grensen, er den kritiske avstanden i så fall relatert til størrelsen på hele grensen.

når du løser problemet ved hjelp av den endelige elementmetoden (FEM), kan hullet være vilkårlig nær lasten. Det som setter grensen er at lastfordelingen fra det fysiske synspunktet er veldefinert. Så snart vi gjør antagelser om omfordeling, er det imidlertid en implisitt antagelse om lastfordelingen, som kan avvike fra den faktiske.

Null Resulterende Systemer Og Belastningsenergitetthet

Så langt har Vi sagt at stressene er de samme uavhengig av lastdetaljer på en passende avstand. Siden vi har å gjøre med lineær elastisitet her, er det alltid mulig å overlegge lastsaker. Når Man arbeider med Bevis På Saint-Venants prinsipp, er det lettere å formulere et prinsipp langs disse linjene: spenningene forårsaket av et lastsystem uten resulterende kraft eller øyeblikk vil være små i en avstand som er av samme størrelsesorden som størrelsen på den lastede grensen.

dermed studerer vi stresset som skyldes forskjellen mellom de to lastsystemene med like resultater. De fleste moderne bevis er basert på estimater av forfallet av belastningsenergitettheten for et slikt null-resulterende system.

Tilbake til problemet ovenfor, kan vi beregne forskjellen mellom lastesakene. Gjør du det tillater oss å studere den faktiske forfall av stress eller belastning energitetthet for forskjellen på stress felt.

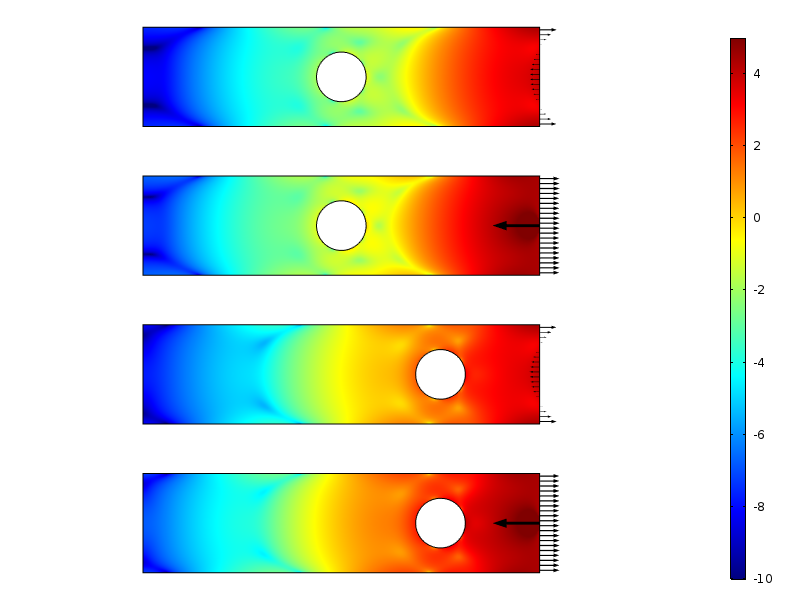
Logaritme av belastningsenergitetthet for null-resulterende last tilfeller.

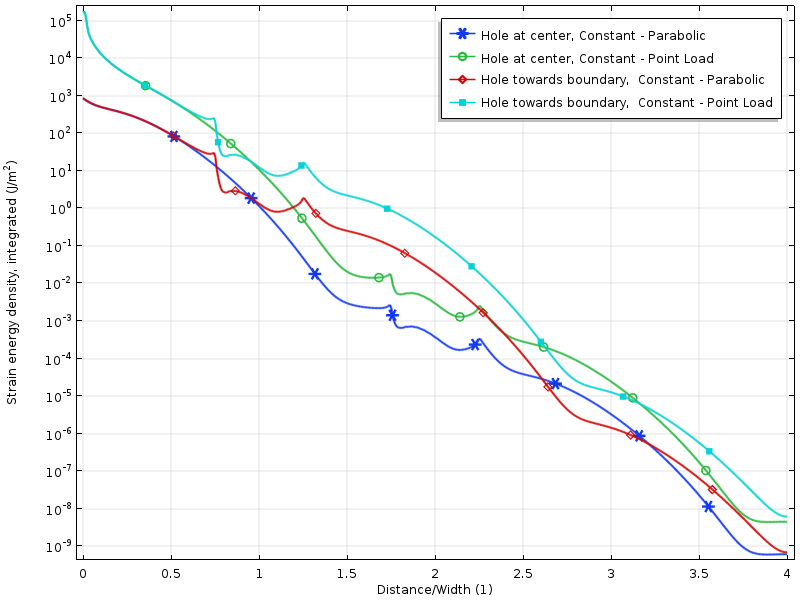
belastningsenergitettheten langs platen for null resulterende last tilfeller. Energien er integrert langs vertikal retning for å produsere en mengde som bare er en funksjon av avstanden fra lasten.

forfallet i logaritmen av belastningsenergitettheten er mer eller mindre lineær med avstanden fra den lastede grensen. Dette er faktisk i tråd med hva moderne bevis forutsier: et eksponentielt forfall av belastningsenergitettheten. Vi kan også tydelig se hvordan hullet midlertidig reduserer forfallshastigheten.

Anvendelse Av Saint-Venants Prinsipp På Tynne Strukturer

for tynnere strukturer som skall, bjelker og takstoler, er Det velkjent At Saint-Venants prinsipp ikke kan brukes på samme måte som for et mer «solid» objekt. Forstyrrelser reiser lengre avstander enn hva vi forventer, fordi lastbanene i en tynn struktur er mye mer begrenset. Dette er det samme fenomenet vi ser med hullet i eksemplet ovenfor, men mer fremtredende.

her studerer vi en stråle med et standard IPE100 tverrsnitt. Enden av strålen blir utsatt for en aksial spenning, med en amplitude som har en lineær fordeling i begge tverrsnittsretninger.

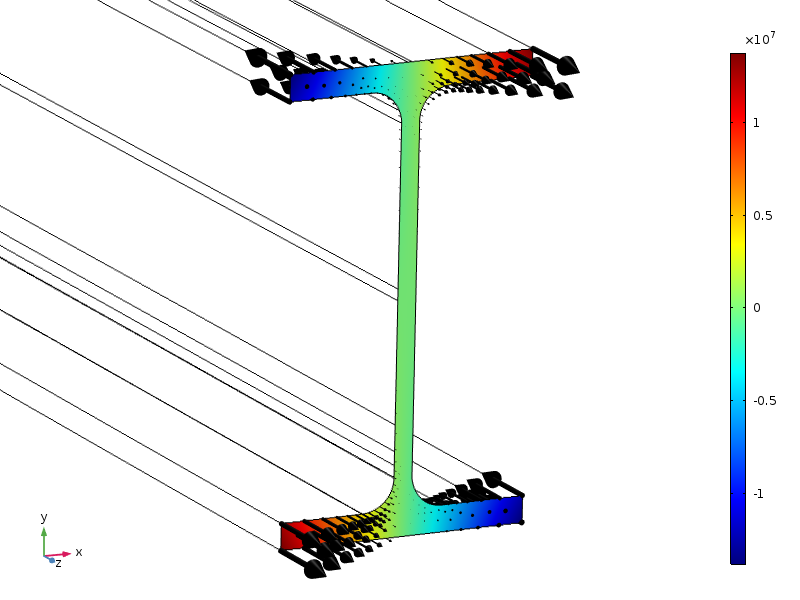
Lastfordeling, vises som konturer og piler.

på grunn av symmetrier har denne belastningen en null-resulterende kraft, samt nullmoment rundt alle akser. Høyden på tverrsnittet er 100 mm, så hvis standardformen Av Saint-Venants prinsipp gjelder, bør spenningene være små i en avstand på ca 100 mm fra endeseksjonen.

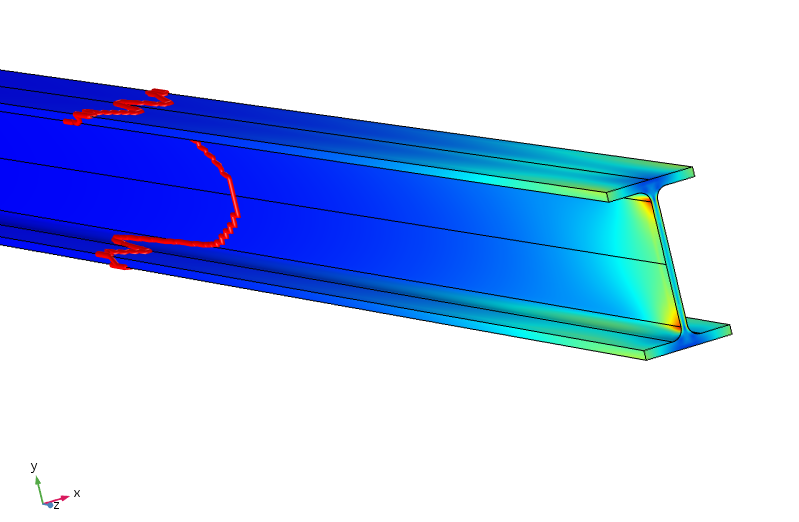
Ekvivalent spenning i strålen. Den røde konturen indikerer hvor stresset er mindre enn 5% av topppåført stress.

det viser seg at for at stresset skal være under 5% av toppspenningen, må vi reise nesten en meter langs strålen. Dermed er lastfordelingen mye mindre effektiv her, siden balansen mellom topp-og bunnflensene krever øyeblikksoverføring gjennom tynnbanen.

hvis du er kjent med teorien for nonuniform torsjon av bjelker (dvs.vridningsteori eller Vlasovteori), vil du gjenkjenne at den påførte belastningen har en betydelig bimoment. Bimomentet er en tverrsnittsmengde Med den fysiske dimensjonskraften X lengde2.

Kanskje (dette er bare min personlige spekulasjon), bør Et effektivt Saint-Venants prinsipp for denne saken kreve ikke bare kraft og øyeblikk, men også en bimoment på null. Dette kan oppnas ved a legge til fire punktbelastninger som gir en motvirkende bimoment. Resultatet av en slik analyse er vist nedenfor.

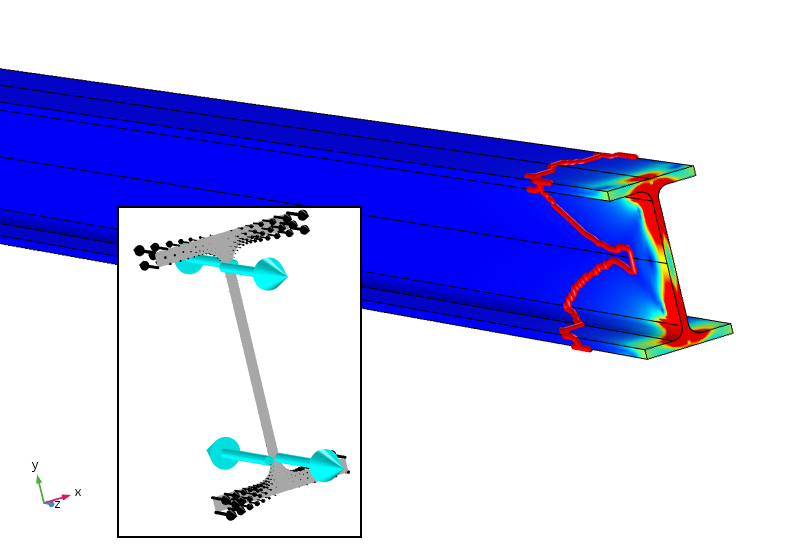
Ekvivalentspenning med firepunktsbelastninger som også gir null bimoment. 5% spenningskonturen er nå mye nærmere den lastede grensen.

de anvendte punktbelastningene, som ikke er optimalt plassert med vilje, gir ekstremt høye (faktisk entall) lokale påkjenninger. Spenningen faller imidlertid mye raskere og er under 5% etter ca. 100 mm. grensen på 5% er fortsatt når det gjelder den påførte fordelte belastningen, så den er ikke justert for de nye lokale belastningene. Den logaritmiske forfallshastigheten til belastningsenergitettheten er tre ganger raskere etter at punktbelastningene er lagt til.

Saint-Venants Prinsipp I Finite Element Analysis

i noen tilfeller kan Du intuitivt vurdere Saint-Venants prinsipp å være aktuelt FOR FE diskretisert problem. Her ser vi på distribuerte laster og ikke-konformerende masker.

Distribuerte Laster

i FE-modellen brukes alltid laster på nettnodene, selv om du angir dem som en kontinuerlig grensebelastning. Lasten distribueres internt til elementets noder ved hjelp av prinsippet om virtuelt arbeid, som vist i eksemplet nedenfor.

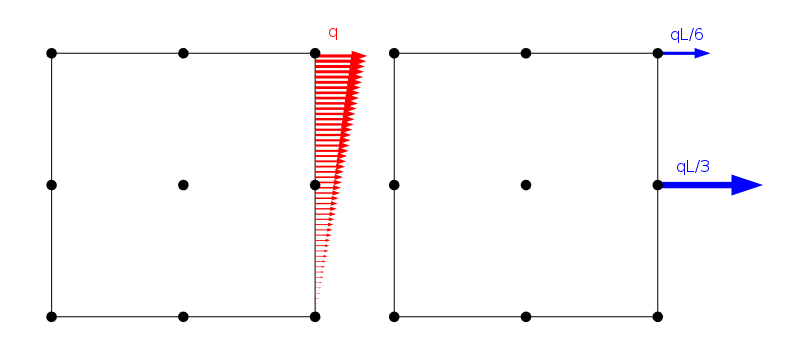
en lineært fordelt last og hvordan den påføres ved nodene til et Andreordens Lagrange-element Med sidelengde L.

Det er imidlertid et uendelig antall lastfordelinger som gir de samme nodale belastningene så lenge de deler samme resulterende kraft og øyeblikk. Åpenbart er løsningen på det endelige elementproblemet det samme for alle disse tilfellene. Fra Saint-Venants prinsipp kan vi imidlertid konkludere med at alle slike belastninger bør gi det samme stressfeltet så snart vi er litt avstand unna.

siden størrelsen på området over hvilket vi omfordeler belastninger er et elementflate, er den lineære dimensjonen etter hvilken det ikke er noen forskjell i hovedsak ett elementlag inne i strukturen. Dermed kan løsningen i det ytre lag av elementer ikke svare til den faktiske belastningen, men videre inn gjør den det.

som et eksempel kan vi laste en rektangulær plate med en grensebelastning som har en eksponentiell spenningsfordeling. Spenningen beregnet med et fint nett er vist nedenfor.

Konturplott av den aksiale spenningsfordelingen.

på Grunn Av Saint-Venants prinsipp blir stressfeltet omfordelt til en ren bøyestatus i noen avstand fra den lastede kanten, akkurat som vi forventer. Dette er imidlertid ikke målet for den nåværende diskusjonen. Snarere undersøker vi forskjellen mellom stressfordelingen ovenfor, og hva vi får med en rekke grove masker.

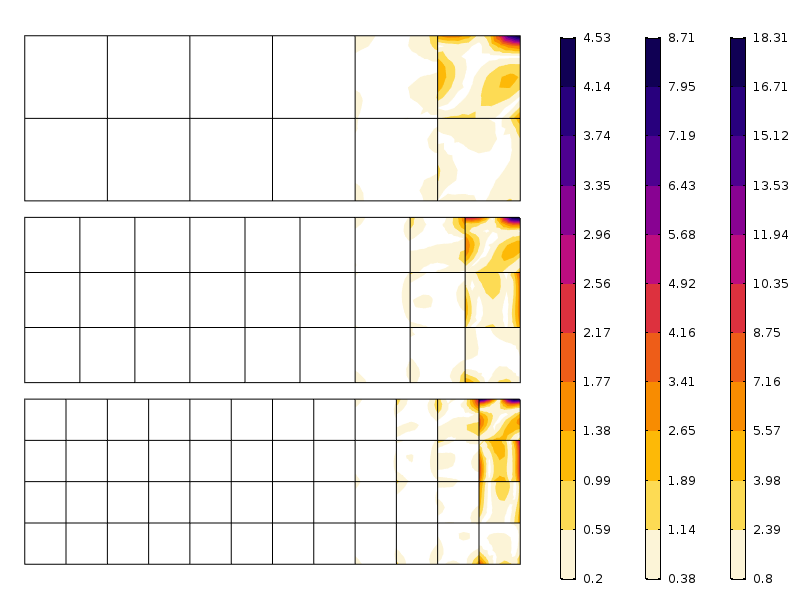
feil i aksial spenning for tre forskjellige masker. Legg merke til de forskjellige skalaene. Som forventet er feilen mindre når nettverket er finere.

som det fremgår av figuren, reduseres feilen raskt etter det første elementlaget. Det vi ser her er faktisk en kombinasjon av maskekonvergens og omfordeling av stress underforstått Av Saint-Venants prinsipp.

Nonconforming Mesh

et nonconforming mesh oppstår Når formen fungerer i to tilkoblede elementer ikke samsvarer. Det vanligste tilfellet er når en samling er koblet ved hjelp av identitetspar og kontinuitetsforhold. For å eksemplifisere dette kan vi studere en rett bar med et forsettlig nonmatching mesh. Med et enkelt lasthus, som uniaxial spenning, er det mulig å studere stressforstyrrelser forårsaket av overgangen.

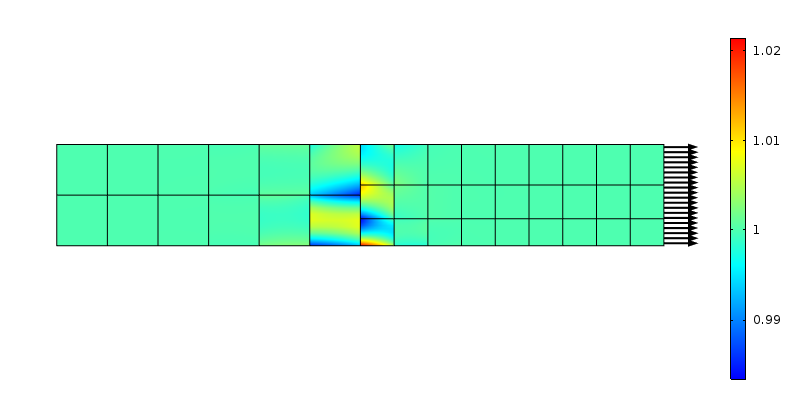
Aksial spenning ved en nonconforming mesh overgang. Andre ordens elementer brukes.

kreftene som overføres av nodene på de to sidene, samsvarer ikke med antagelsen om konstant stress. Igjen kan dette ses som en lokal lastfordeling over et område som er elementstørrelsen. Ved å bruke Begrunnelsen Til Saint-Venant, bør forstyrrelsen falme bort i en» elementstørrelse » avstand fra overgangen. La oss undersøke hva som skjer hvis nettverket er raffinert i aksial retning.

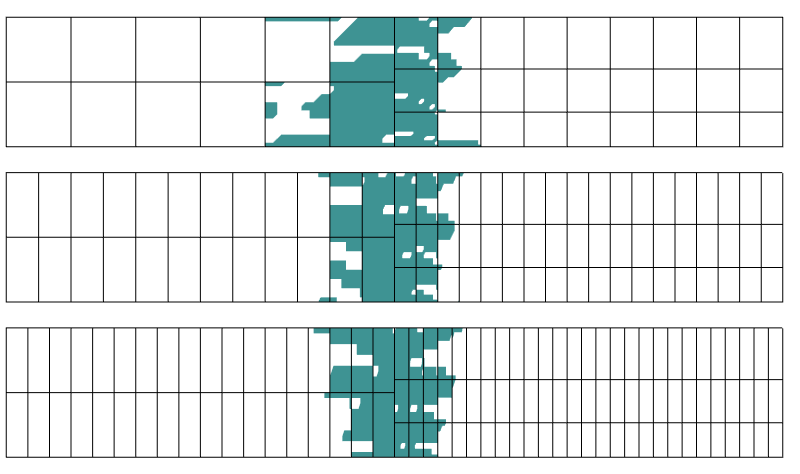
Region med mer enn 0,1% feil i stress. Tre forskjellige diskretiseringer brukes i aksial retning.

det viser seg at forstyrrelsesområdet ikke påvirkes mye av diskretiseringen i retningen vinkelrett på overgangsgrensen. Dette er Akkurat Hva Saint-Venants prinsipp forteller oss.

Avsluttende Bemerkninger

uten Å gjøre Bruk Av Saint-Venants prinsipp er mange strukturelle analyser vanskelige å utføre, rett og slett fordi den detaljerte lastfordelingen ikke er kjent.

prinsippet er formelt bare gyldig for lineære elastiske materialer. I praksis bruker vi det også intuitivt på daglig basis for andre situasjoner. Hvis for eksempel materialet i» plate with a hole » – eksemplet var elastoplastisk, forventer vi at de to fordelte belastningene gir tilsvarende resultater, så lenge avkastningsspenningen er over spenningen som påføres ved grensen, slik at det bare er plastisk deformasjon rundt hullet. Punktbelastningen gir imidlertid alltid en annen løsning, siden materialet gir rundt det lastede punktet. For en lengre diskusjon, les dette blogginnlegget om singulariteter på point loads.

Neste Trinn

Lær mer om BRUK AV COMSOL Multiphysics® programvare FOR FEA.

Videre Lesing

• Y. C. Fung Og P. Tong, Klassisk Og Beregnings Solid Mekanikk, World Scientific Publishing Co. Pte. Ltd., 2001.