Luku 12
12.1 peruskäsitteet
momenttijakaumamenetelmä rakenteiden analysoimiseksi
Hardy Cross kehitti momenttijakaumamenetelmän palkkien ja kehysten analysoimiseksi ja esitti sen virallisesti vuonna 1930. Vaikka tämä menetelmä on kaltevuus-taipuma-menetelmän kaltainen muodonmuutosmenetelmä, se on likimääräinen menetelmä eikä siten vaadi samanaikaisten yhtälöiden ratkaisemista, kuten viimeksi mainitussa menetelmässä. Momenttijakauman menetelmällä saatujen tulosten tarkkuusaste riippuu peräkkäisten likiarvojen määrästä tai iteraatioprosessista.
momenttijakauman käsitteen havainnollistamiseksi tarkastellaan Kuvassa 12.1 esitettyä kehystä. Rungon jäsenet ovat prismaattisia, eikä niiden oleteta muuttavan aksiaalisesti eikä kääntävän toisiinsa nähden. Liitokset ACD runko on kiinteä, kun taas yhteinen B voi pyöriä hieman, koska sovellettu kuormitus. Ensinnäkin, ennen kuin suoritetaan momenttijakauma jäsenten kesken, kaikkien nivelten oletetaan olevan väliaikaisesti lukittuina puristimella.
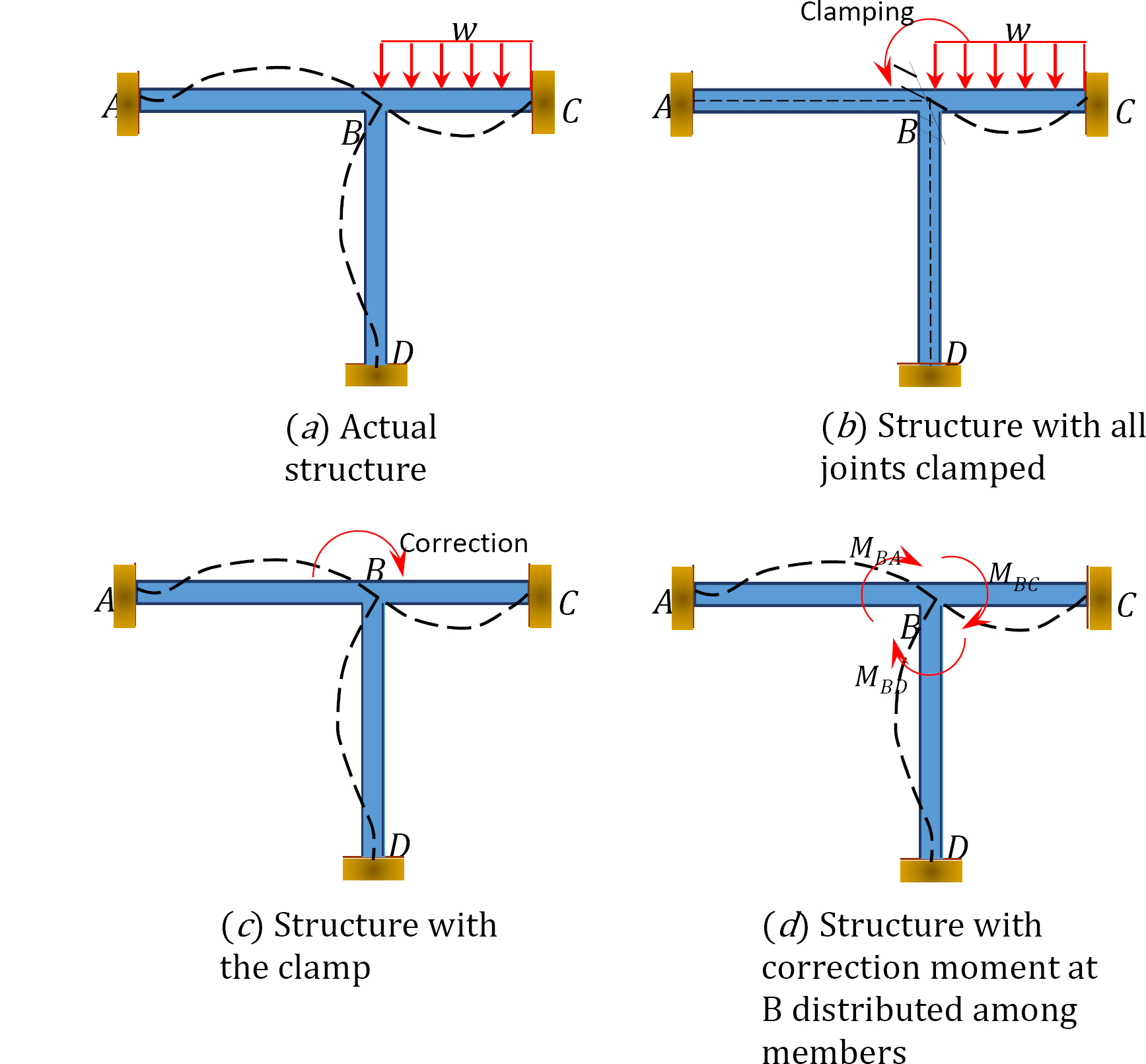
Kuva. 12.1. Kehys.
12.2 Merkkikäytäntö
merkkikäytäntö momentin jakautumismenetelmälle on samanlainen kuin kulmakertoimen menetelmälle vahvistettu; toisin sanoen momenttia jäsenen lopussa pidetään positiivisena, jos sillä on taipumus kääntää jäsenen päätä myötäpäivään ja negatiivisena, jos sillä on taipumus kääntää sitä vastapäivään.
12.3 määritelmät
epätasapainoiset momentit: tämä analyysimenetelmä olettaa, että rakenteen liitokset ovat aluksi kiinni tai lukittuneet ja sitten vapautuvat peräkkäin. Kun liitos on julkaistu, tapahtuu rotaatio, koska kyseisessä liitoksessa kokoontuvien jäsenten kiinteiden loppuhetkien summa ei ole nolla. Saadun loppumomenttien summan arvo on epätasapainoinen momentti kyseisessä liitoksessa.
Siirtohetket: yhteisessä kokouksessa kokoontuneiden jäsenten päissä olevat jakautuneet momentit muissa päissä, joiden oletetaan olevan kiinteitä. Näitä muissa päissä olevia indusoituja hetkiä kutsutaan siirtohetkiksi.
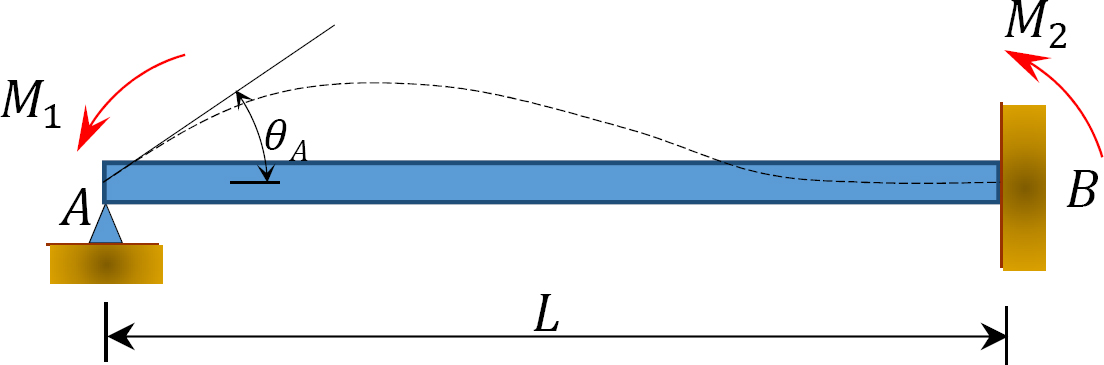
Kuva. 12.2. Lataamaton prismasäde.
tarkastellaan lataamatonta prismapalkkia, joka on kiinnitetty päähän B, kuten kuvassa 12.2 esitetään. Jos säteen vasempaan päähän kohdistetaan momentti M1, voidaan säteen molemmille päille kirjoittaa kaltevuus-taipumisyhtälöt seuraavasti:


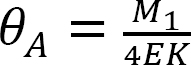 korvaaminen yhtälöstä 12.1 yhtälöön 12.2 viittaa seuraaviin:
korvaaminen yhtälöstä 12.1 yhtälöön 12.2 viittaa seuraaviin:

yhtälö 12.3 viittaa siihen, että toiseen päähän kohdistetusta momentista johtuva säteen kiinteään päähän siirretty momentti on yhtä suuri kuin puolet käytetystä momentista.
siirtokerroin: indusoidun momentin ja käytetyn momentin suhdetta kutsutaan siirtokertoimeksi. Kuvassa 12.2 esitetyn säteen siirtokerroin on seuraava:

hajautettu tekijä (DF): Hajautettu tekijä on tekijä, jota käytetään määrittämään kunkin jäsenen yhteisen kokouksen epätasapainoisen hetken osuus. Kuvassa 12.3 esitetyn kehyksen yhteisessä O-kokouksessa kokoontuneiden jäsenten jakaumakertoimet lasketaan seuraavasti:
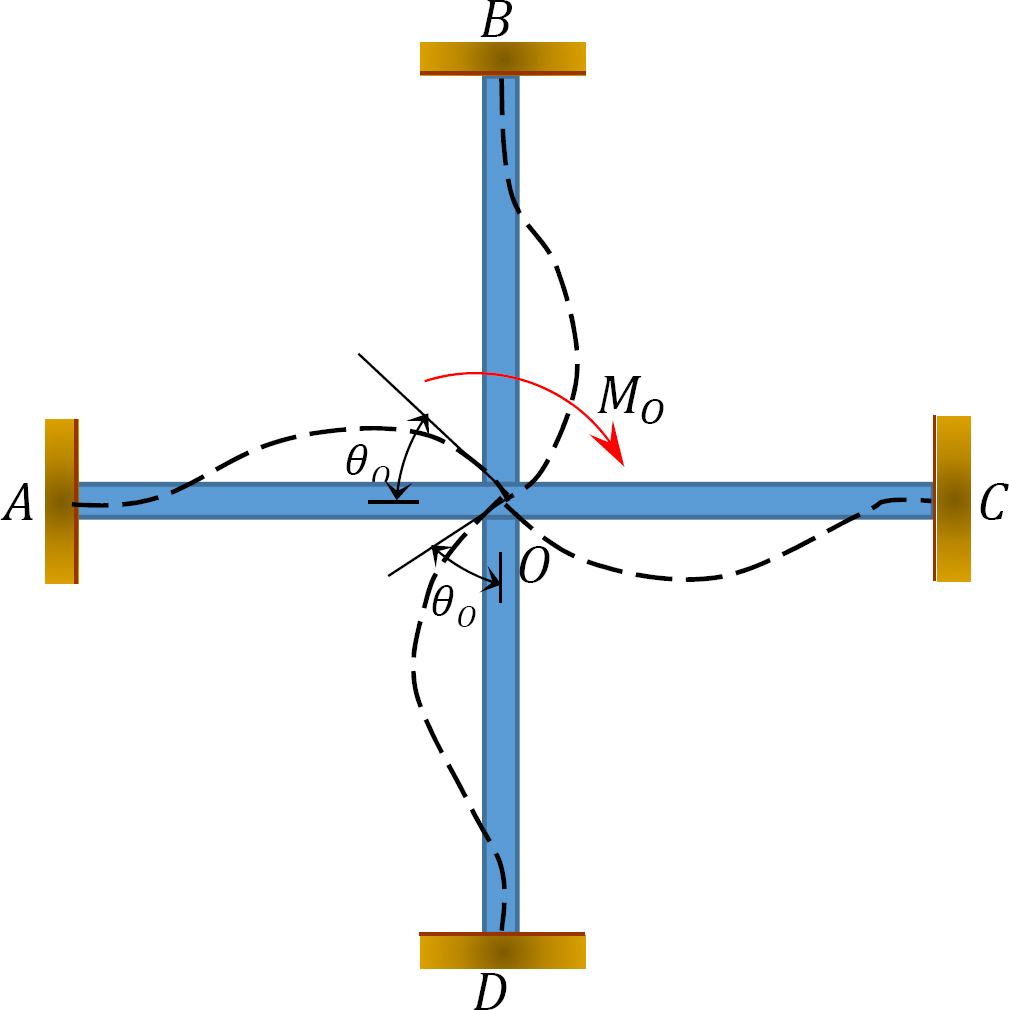
Kuva. 12.3. Kehys.

hajautetut hetket: kun kuvitteellinen puristin vapautuu liitoksessa, epätasapainoinen hetki kyseisessä liitoksessa saa sen pyörimään. Rotaatio pyörittää jäsenten kokouksen loppua liitoksessa, mikä johtaa vastustavien hetkien kehittymiseen. Näitä vastustavia hetkiä kutsutaan hajautetuiksi hetkiksi. Kuvassa 12.3 esitetyn kehyksen jäsenille jaetut momentit lasketaan seuraavasti:
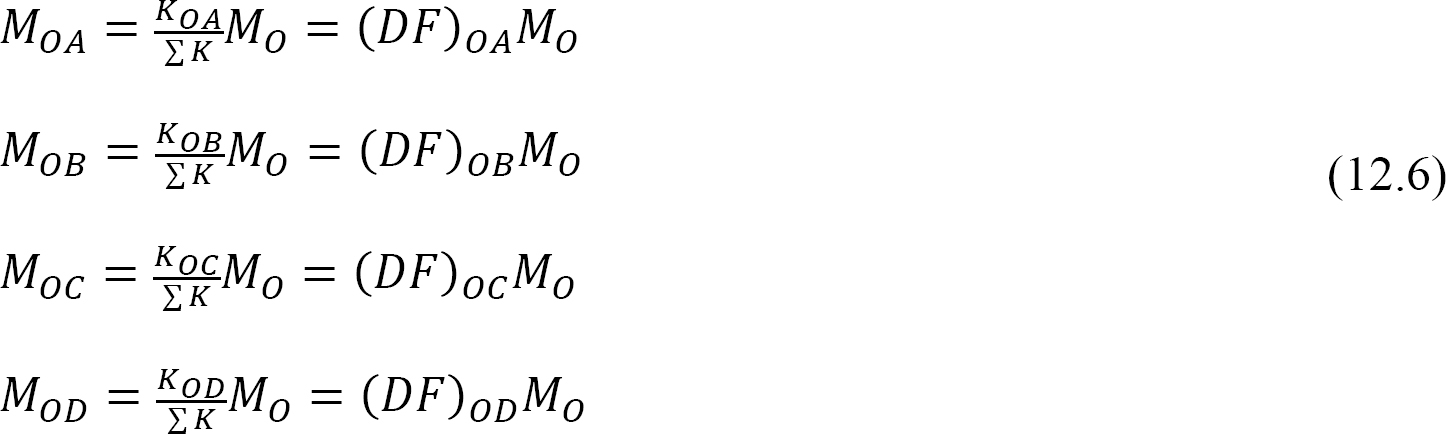
12.4 Jäsenjäykkyyden muutos
joskus momenttijakauman iterointiprosessia voidaan merkittävästi vähentää säätämällä joidenkin epämääräisen rakenteen jäsenten joustojäykkyyttä. Tässä jaksossa tarkastellaan vaikutusta kiinteän – ja pin-end tukea taivutusjäykkyys epämääräinen palkki.
tapaus 1: Toisesta päästä saranoitu palkki, joka on kiinnitetty toiseen
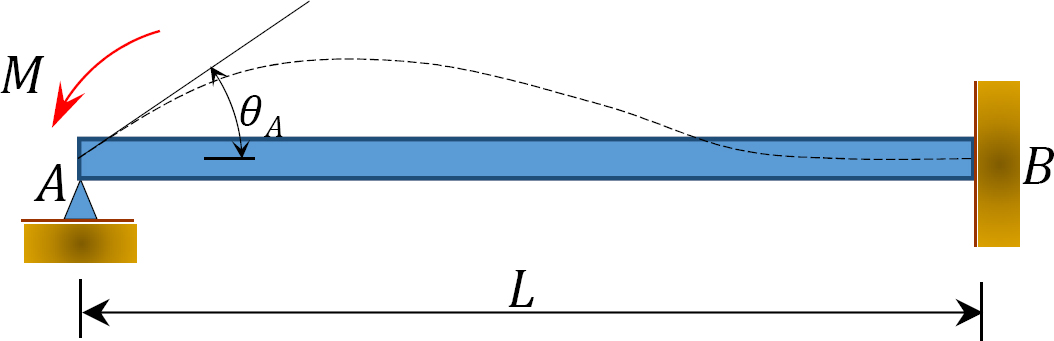
Kuva. 12.4. Valokeilan
katsotaan olevan A-päässä saranoitu ja B-päässä kiinteä valo, kuten kuvassa 12.4 esitetään. Soveltamalla momenttia M pyörittää saranan päätä määrällä θ. Kirjoitetaan kulmakertoimen yhtälö jäsenen loppuun A ja todetaan, että 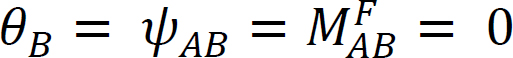 ehdottaa seuraavaa:
ehdottaa seuraavaa:
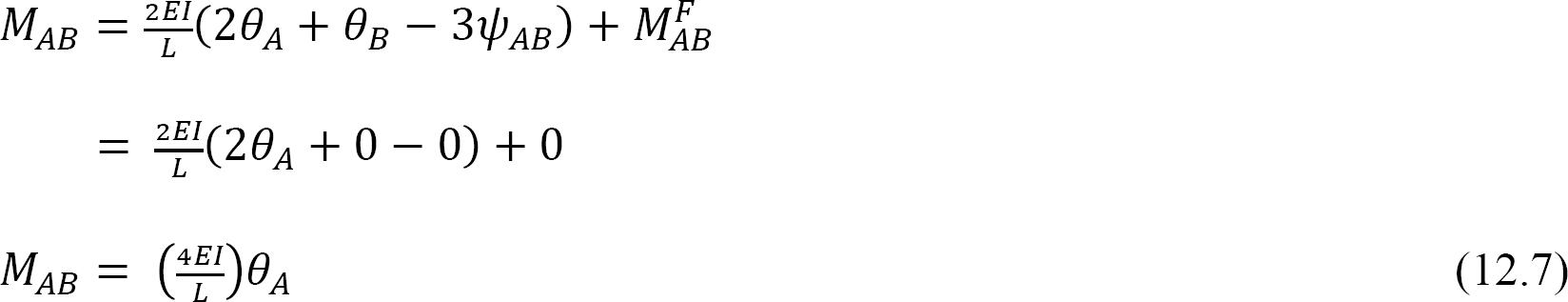
rakenteellisen jäsenen taivutusjäykkyys on määritelmän mukaan momentti, joka on kohdistettava jäsenen päähän, jotta tämän pään yksikkökierto saadaan aikaan. Taivutusjäykkyys jäsenelle, jolla on kiinteä kaukopää, ilmaistaan seuraavasti korvattaessa θA = 1 yhtälöllä 12.7:

määritelmän mukaan jäsenen suhteellinen taivutusjäykkyys määritetään jakamalla jäsenen taivutusjäykkyys 4E: llä. jakamalla yhtälö 12,8 4E: llä voidaan suhteelliselle jäykkyydelle esittää seuraavaa lauseketta tarkasteltavassa tapauksessa:

Tapaus 2: palkki saranoitu molemmissa päissä
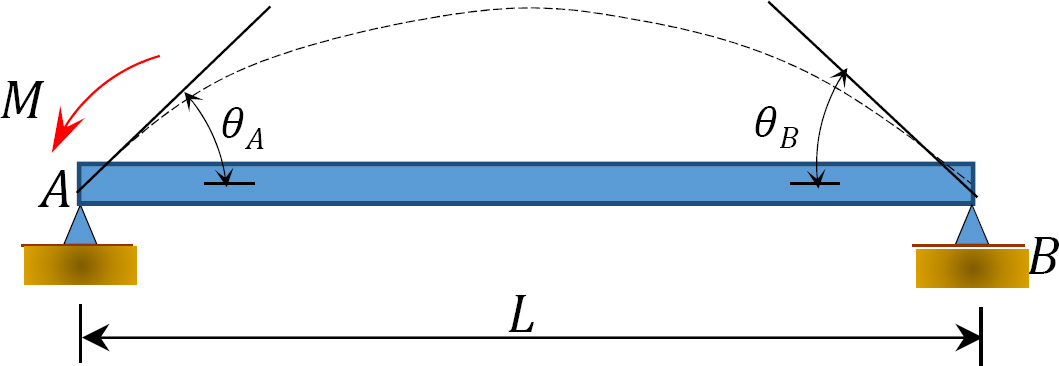
Kuva. 12.5. Yksinkertaisesti tuettu palkki.
soveltamalla momenttia M kuvassa 12.5 esitetyn yksinkertaisesti tuetun säteen päähän a pyörittää sädettä kulmalla θA saranoidussa päässä. Käyttäen 11 luvun 11.4 jaksosta johdettua muunnettua kaltevuuspainumayhtälöä ja todeten, että 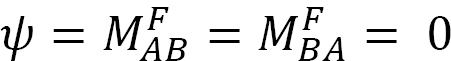 viittaa seuraavaan lausekkeeseen siitä hetkestä, joka on saranoidussa päässä, johon kuormitus kohdistuu:
viittaa seuraavaan lausekkeeseen siitä hetkestä, joka on saranoidussa päässä, johon kuormitus kohdistuu:
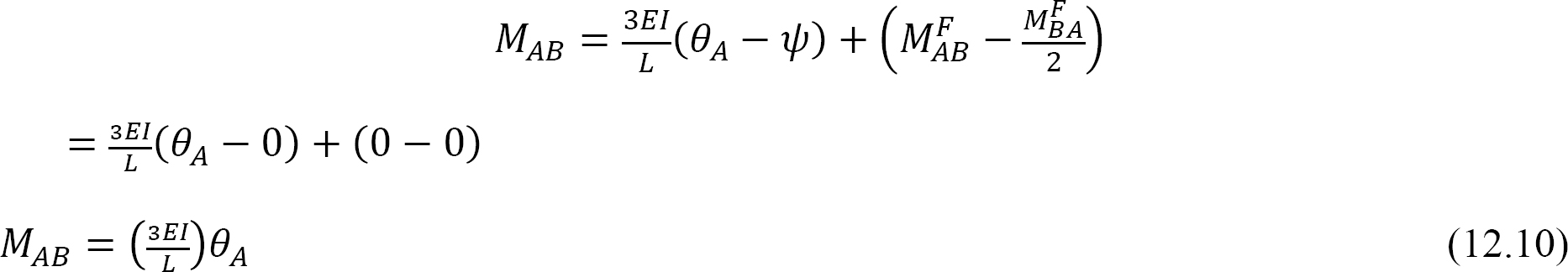
θA = 1: n korvaaminen yhtälöllä 12.10 ehdottaa seuraavaa lauseketta taivutusjäykkyydelle jäsenelle, jolla on saranoitu etäpää:

suhteellinen jäykkyys jäsenelle, jolla on saranoitu kaukopää saadaan jakamalla yhtälö 12.11 luvulla 4E seuraavasti:

vertaamalla yhtälöt 12.12 ja 12.9 viittaa siihen, että jäsen, jolla on saranoitu kaukana pää on kolme neljäsosaa niin jäykkä kuin jäsen, jolla on sama geometria, mutta kiinteä kaukana lopussa. Tämä vakiintunut tosiasia voi merkittävästi vähentää iteraation määrää analysoitaessa säteitä tai kehyksiä, joissa on saranoitu kauko-pää käyttäen momenttijakauman menetelmää. Tällöin lähipään säteen suhteellinen jäykkyys säädetään ensin yhtälön 12.12 mukaisesti ja sen jakaumakerroin lasketaan mukautetulla jäykkyydellä. Tasapainotusoperaation aikana loppupää tasapainotetaan vain kerran niin, ettei hetkiä enää siirretä sen päästä tai sen päähän.
12.5 määrittelemättömien palkkien analyysi
määrittämättömien palkkien analysointimenettely momenttijakauman menetelmällä on lyhyesti esitetty seuraavasti::
menettely määrittämättömien säteiden analysoimiseksi Momenttijakaumamenetelmällä
•lasketaan jäsenten kiinteät loppumomentit olettaen, että liitokset ovat kiinni pyörimisliikkeessä.
* laske jakaumakerroin kullekin liitoksessa kytketylle jäsenelle
•laske epätasapainoinen momentti kussakin liitoksessa ja Jaa sama niiden jäsenten päihin, jotka ovat kytkettyinä kyseiseen liitokseen.
•Siirrä yli puolet jaetusta hetkestä jäsenten muihin päihin.
* Lisää tai vähennä nämä loppumomentit (vaiheilla kolme ja neljä saadut momentit) alkuperäisiin kiintomomentteihin tai niistä.
* sovelletaan määritettyjä loppumomentteja annetun rakenteen niveliin.
* piirretään vapaan rungon kaavio kunkin säteen jännevälistä, josta ilmenevät momenttijakaumalla saadut kuormitukset ja momentit liitoksissa.
* määritä kunkin span tukireaktiot.
* Laske ja muodosta leikkausvoima-ja taivutusmomenttikaaviot jokaiselle jännevälille.
* Piirrä annetulle säteelle yksi taivutusmomentti ja yksi leikkausvoimakaavio yhdistämällä vaiheen 9 kaaviot.
esimerkki 12.1
momenttijakaumamenetelmän avulla määritetään loppumomentit ja reaktiot kuvassa 12.6 a esitetyn säteen tukiin. Piirrä leikkausvoima ja taivutusmomenttikaaviot. EI = vakio.
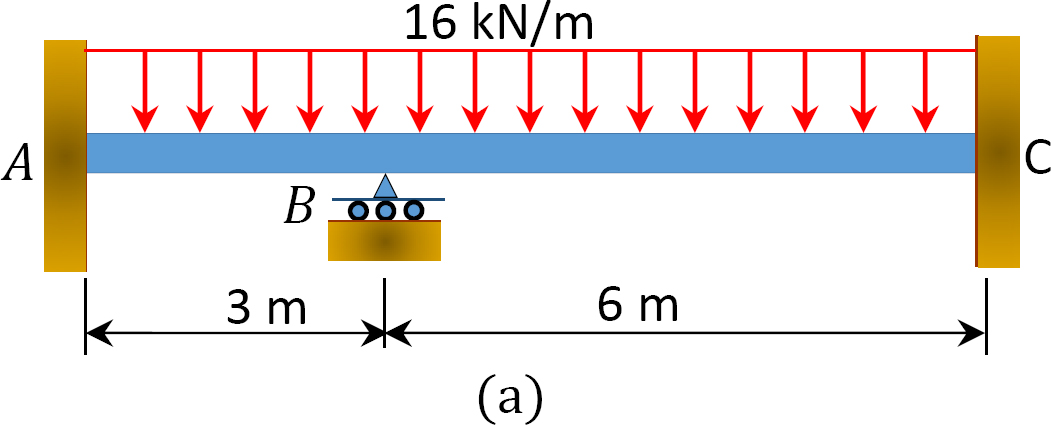
Kuva. 12.6. Lasersäde.
ratkaisu
kiinteä loppumomentti.
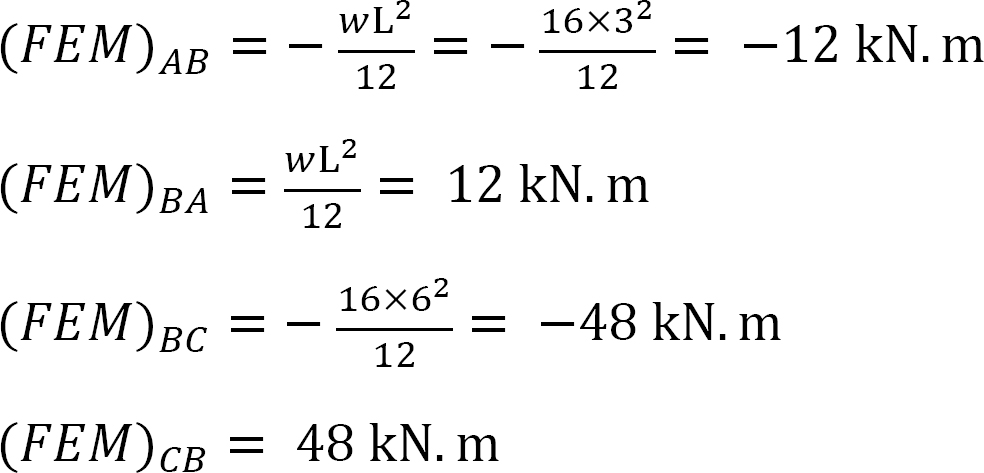
Jäykkyystekijä.
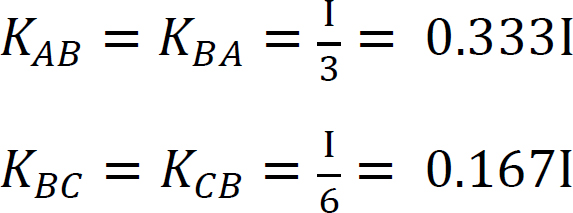
Jakelukerroin.
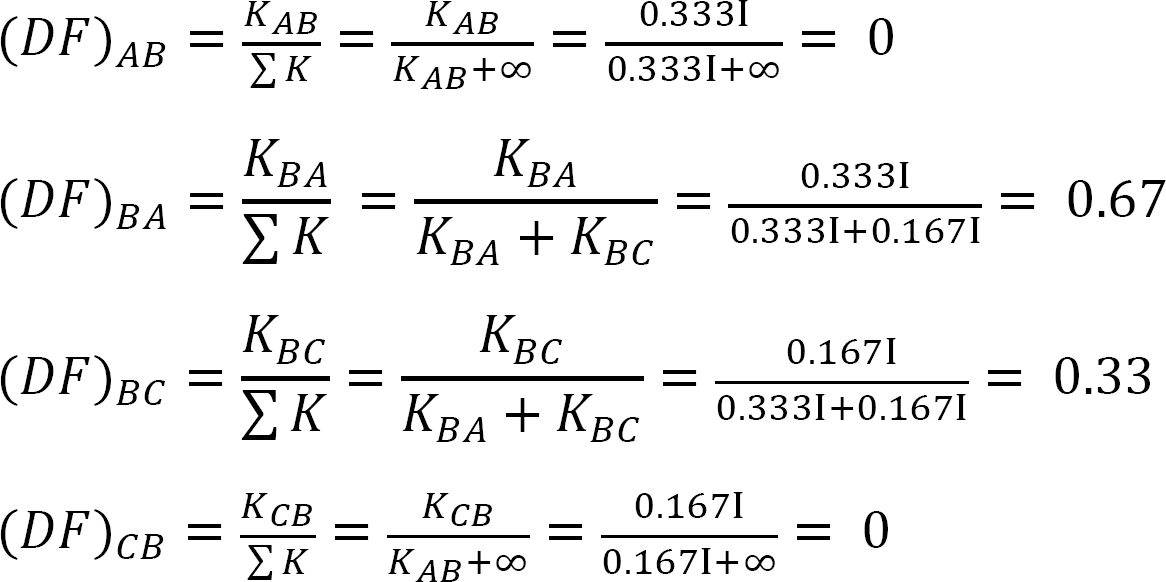
taulukko 12.1 Jakelutaulukko.
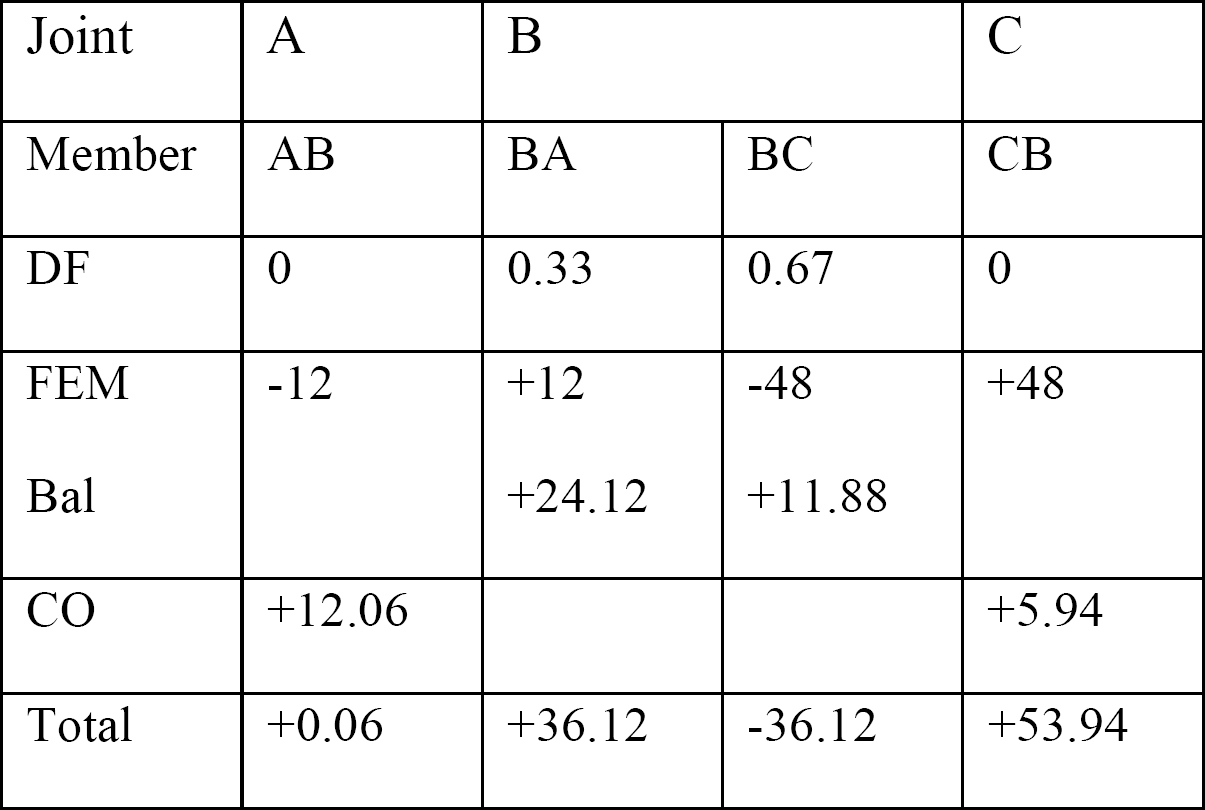
leikkausvoima ja taivutus momenttikaaviot.
esimerkki 12.2
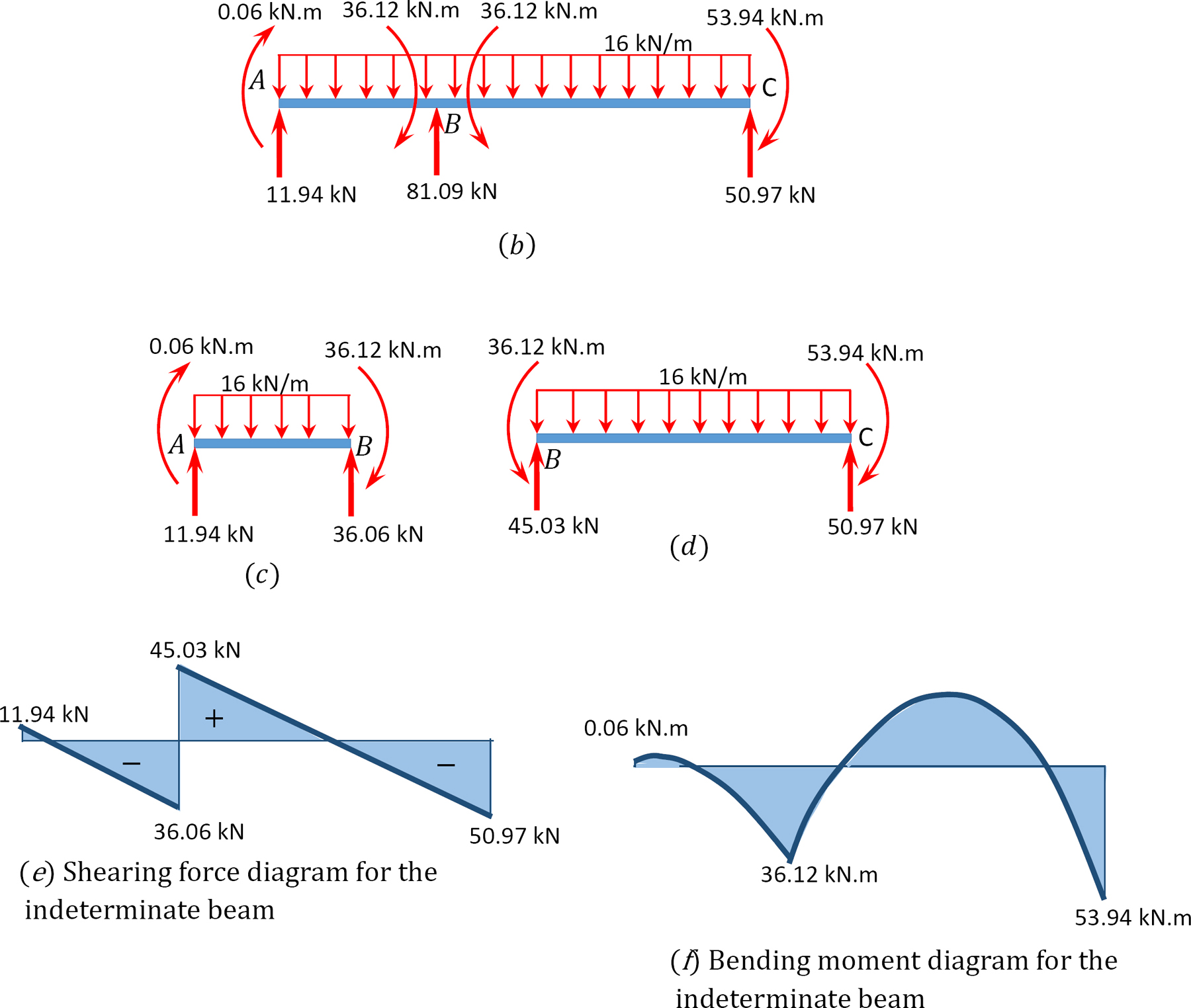
momenttijakaumamenetelmän avulla määritetään loppumomentit ja reaktiot kuvassa 12.7 a esitetyn säteen tukiin. Piirrä leikkausvoima ja taivutusmomenttikaaviot.
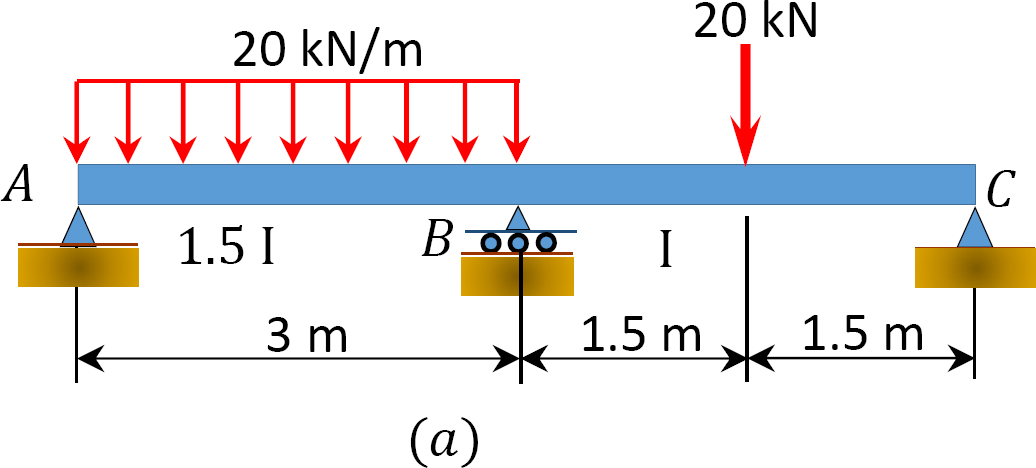
Kuva. 12.7. Lasersäde.
ratkaisu
kiinteä loppumomentti.
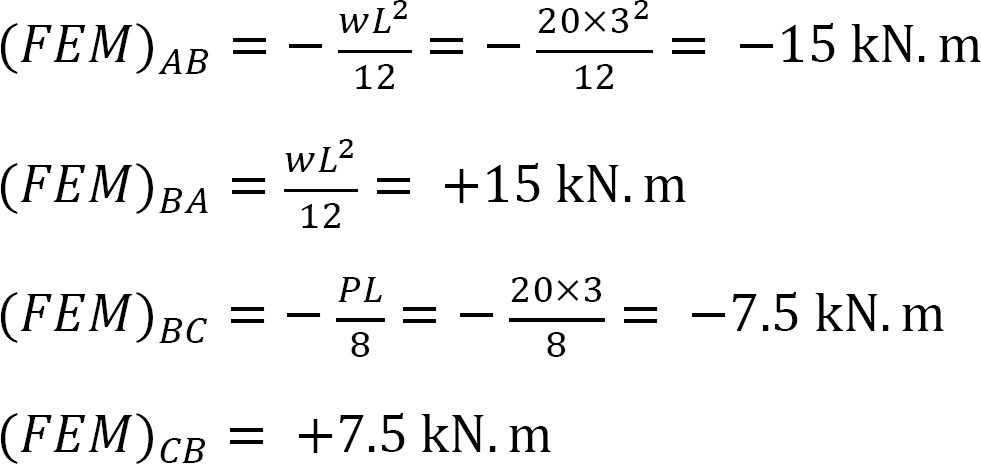
Jäykkyystekijä.
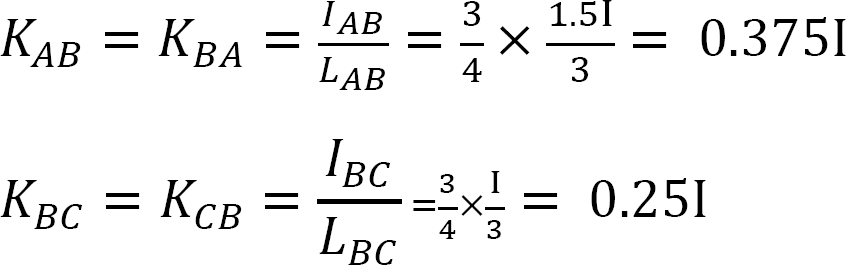
Jakelukerroin.
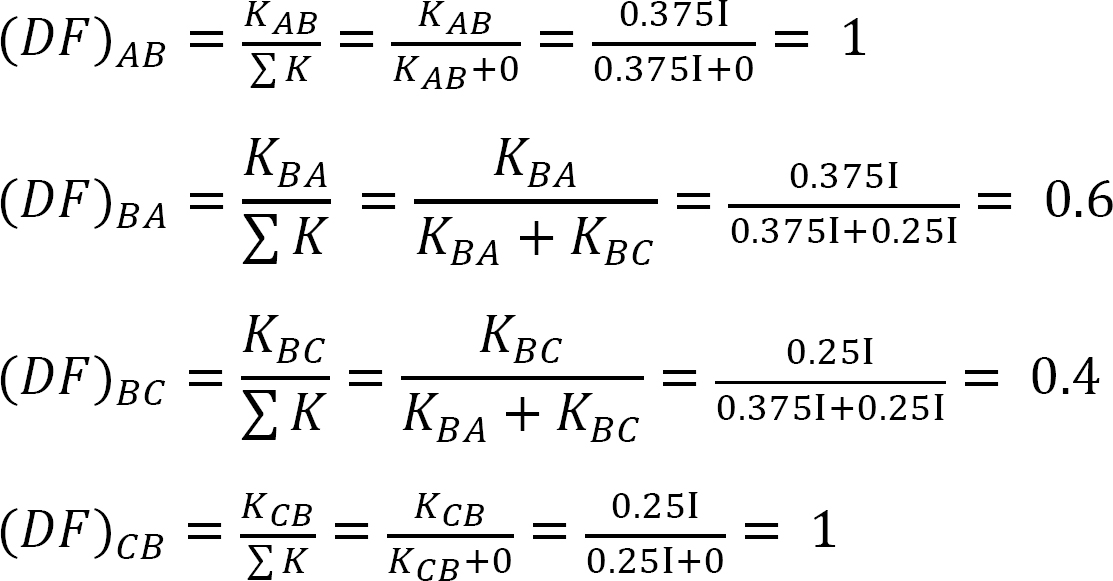
taulukko 12.2 Jakelutaulukko.
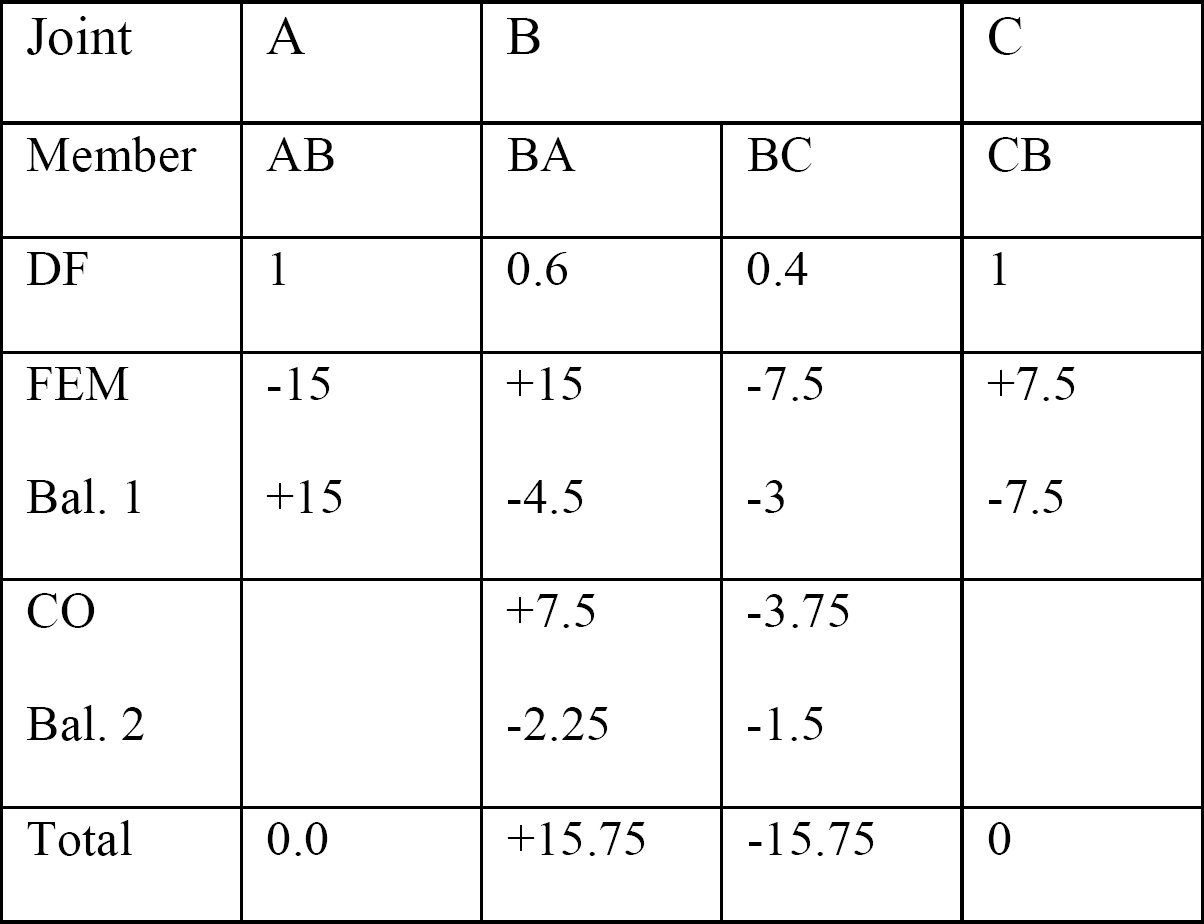
leikkausvoima ja taivutus momenttikaaviot.
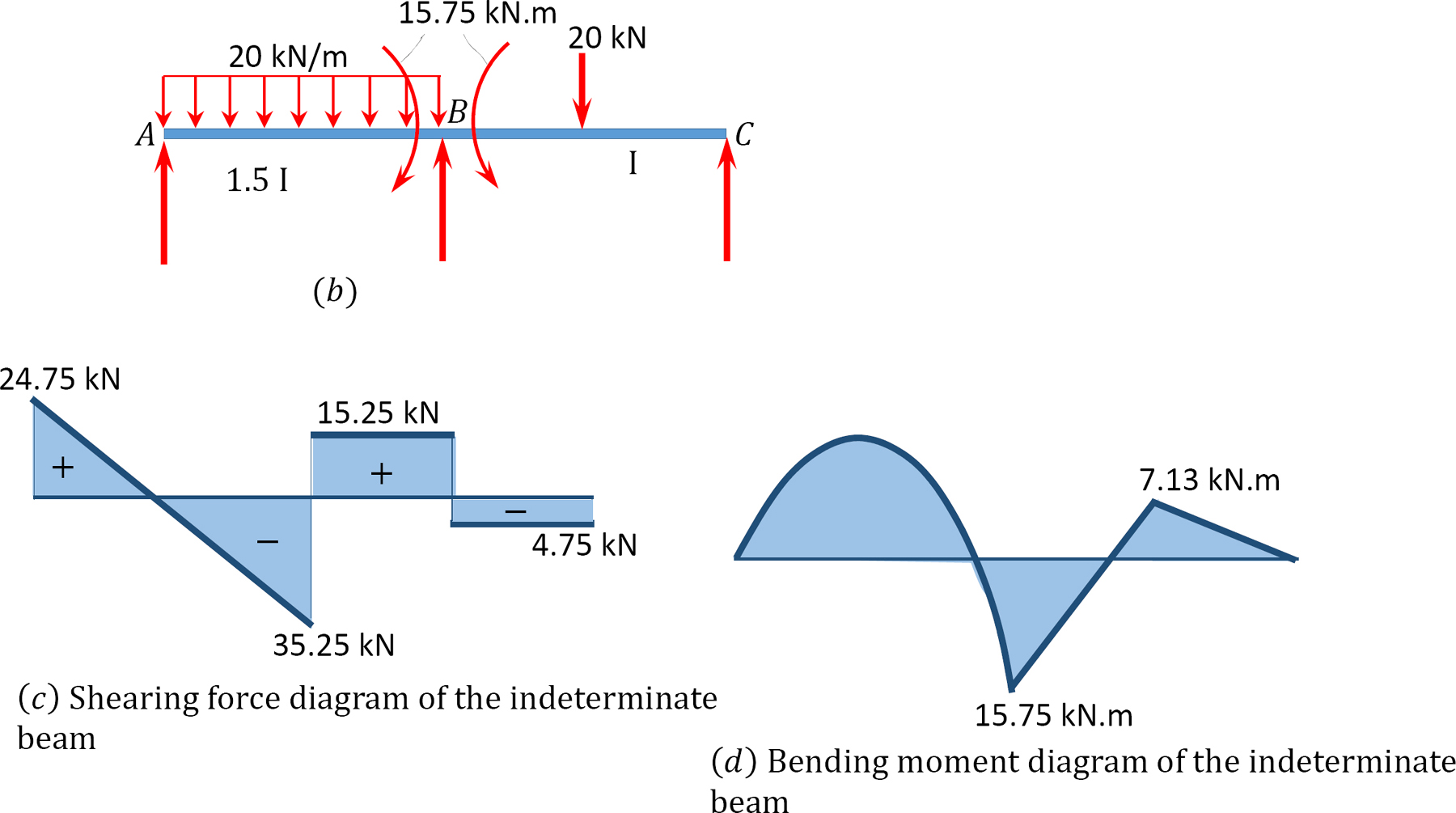
12.6 määrittelemättömien kehysten analyysi
kehysten analysointi momenttijakaumamenetelmällä riippuu analysoitavan kehyksen tyypistä. Kehykset luokitellaan huojuviksi tai ei-huojuviksi kehyksiksi. Ei-huojuvien kehysten analysointimenettely on samanlainen kuin epämääräisten palkkien. Mutta huojuvien kehysten analysoinnissa menettely on erilainen. Sway-kehysten analysointiin liittyy kaksi vaihetta, eli ei-sway-vaihe ja sway-stage-analyysi. Nämä vaiheet on kuvattu alla.
menettely epämääräisten Huojumiskehysten analysoimiseksi Momenttijakaumamenetelmällä
A. Ei-huojuva vaiheanalyysi
* oletetaan ensin, että on olemassa kuvitteellinen rekvisiitta, joka estää kehystä huojumasta.
* laske vaakasuuntaiset reaktiot rungon tukirakenteissa ja huomaa ero X. Tämä on voima, joka estää huojumisen.
B. Huojuva vaiheanalyysi
* oleta mielivaltaisia momentteja toimimaan kehyksen sarakkeissa. Näiden momenttien suuruus vaihtelee sarakkeesta toiseen suhteessa 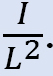
•arvot oletetaan M2: lle, ja M1 määritetään.
* lasketaan vaakareaktioiden suuruus huojuvan ehdon tukirakenteissa. Näiden reaktioiden yhteenlasku antaa mielivaltaisen siirtymävoiman Y.
* määritä suhde 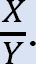 tätä suhdetta kutsutaan huojumiskertoimeksi.
tätä suhdetta kutsutaan huojumiskertoimeksi.
* käytä huojuntakerrointa kertoaksesi huojunnan jakautuneet momentit. Tämä antaa oikaistun hetken huojumiselle.
* kehyksen viimeiset momentit ovat huojumattomassa vaiheessa saatujen momenttien yhteenlasku ja huojumisvaiheessa korjattu momentti.
esimerkki 12.3
momenttijakauman avulla määritetään kuvassa 12.8 esitetyn kehyksen jäsenten loppumomentit. EI = vakio.
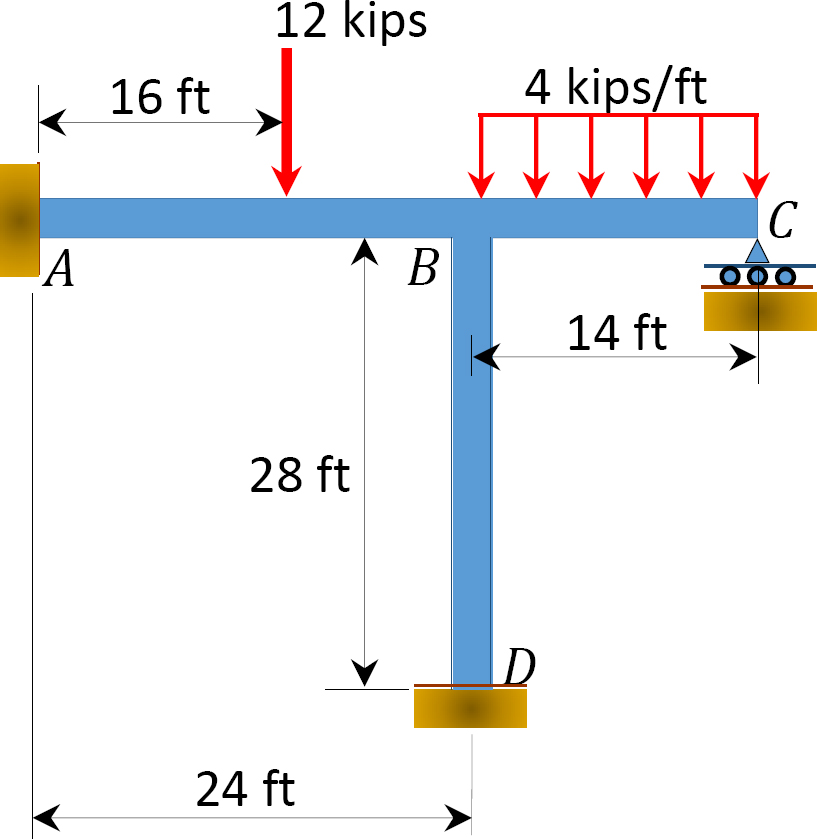
Kuva. 12.8. Kehys.
ratkaisu
kiinteä loppumomentti.
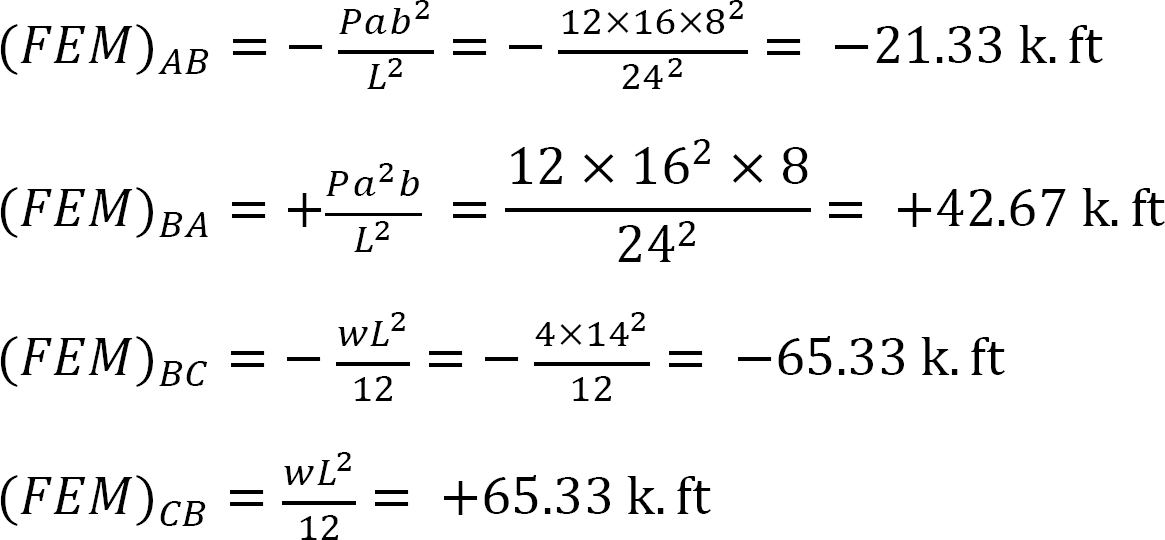
Jäykkyystekijä.
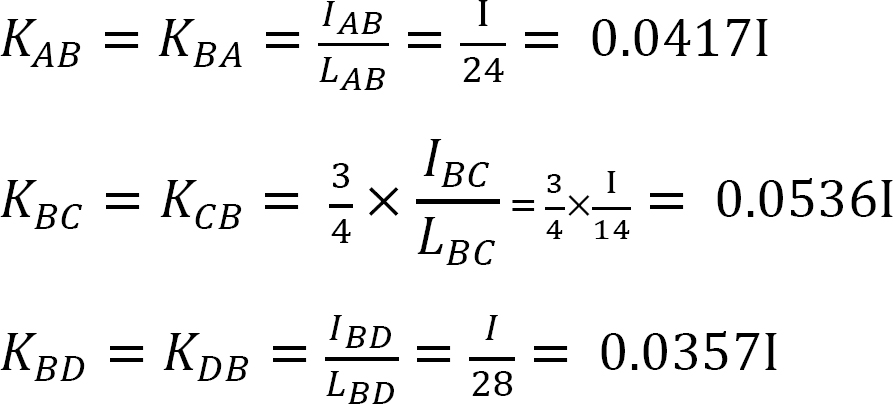
Jakelukerroin.
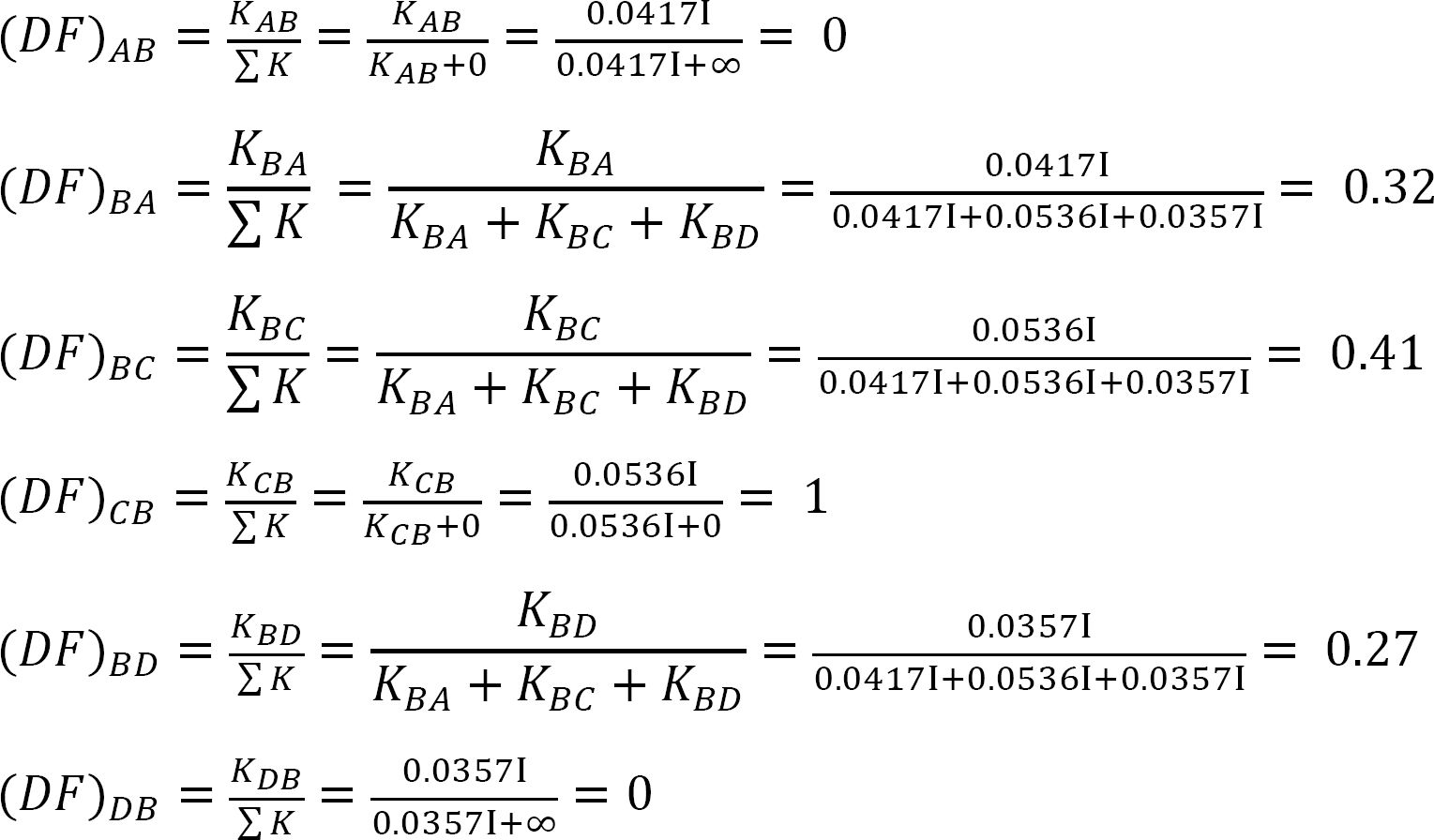
taulukko 12.3. Jakelutaulukko.
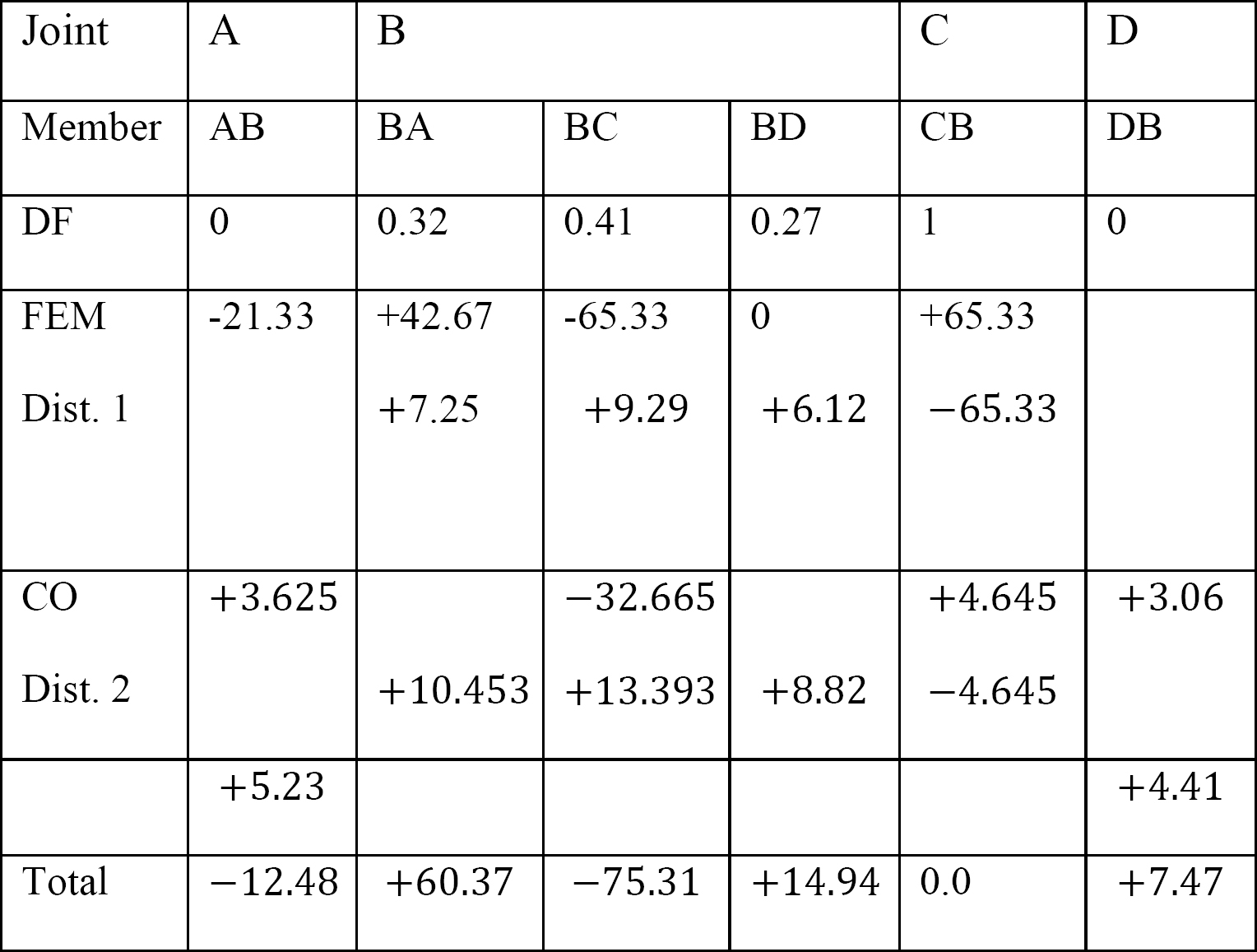
viimeiset jäsenten loppuhetket.
ekθb: n, EKθC: n ja EK∆: n saatujen arvojen korvaaminen jäsenloppumomenttiyhtälöillä viittaa seuraavaan:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14,94 K. Ft
MCB = 0
MDB = +7,47 K. Ft
esimerkki 12.4
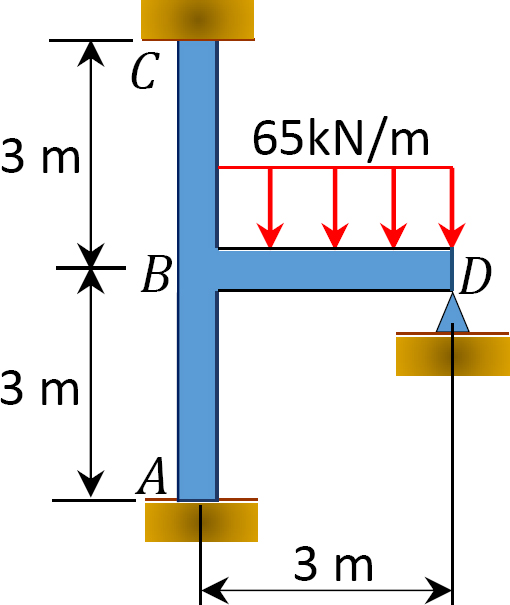
momenttijakauman avulla määritetään loppumomentit kuvassa 12.9 esitetyn kehyksen tukiin. EI = vakio.
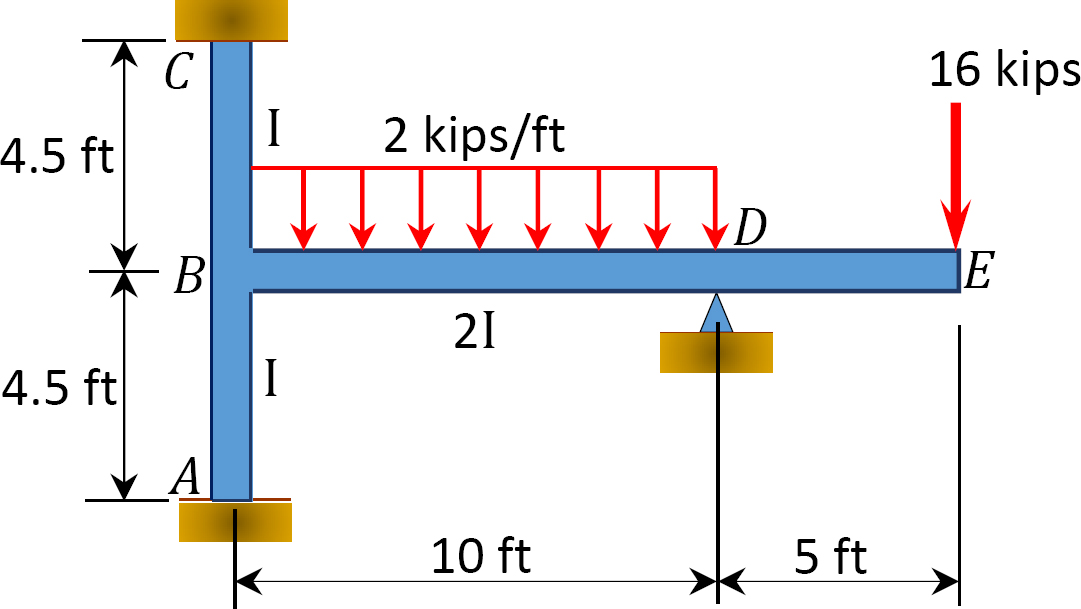
Kuva. 12.9. Kehys.
ratkaisu
kiinteä loppumomentti.
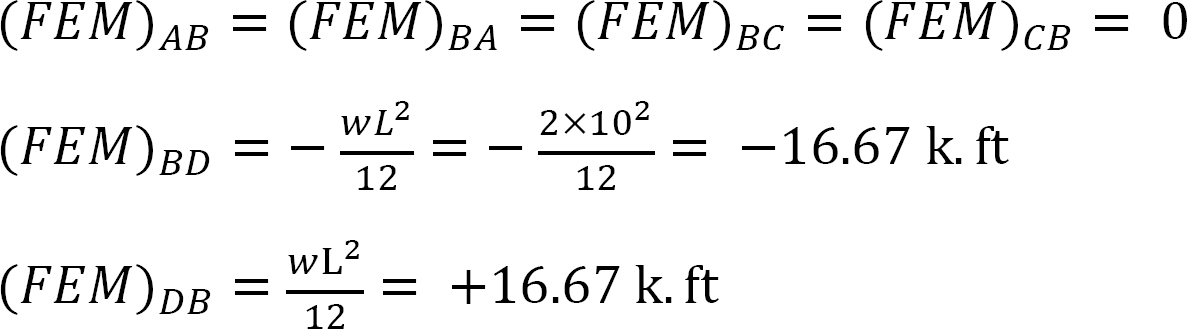
Jäykkyystekijä.
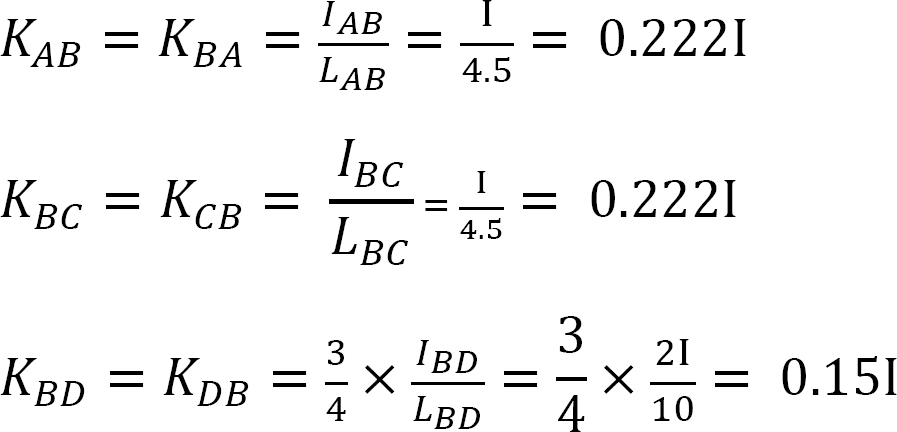
Jakelukerroin.

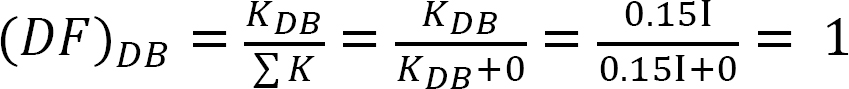
taulukko 12.4. Jakelutaulukko.
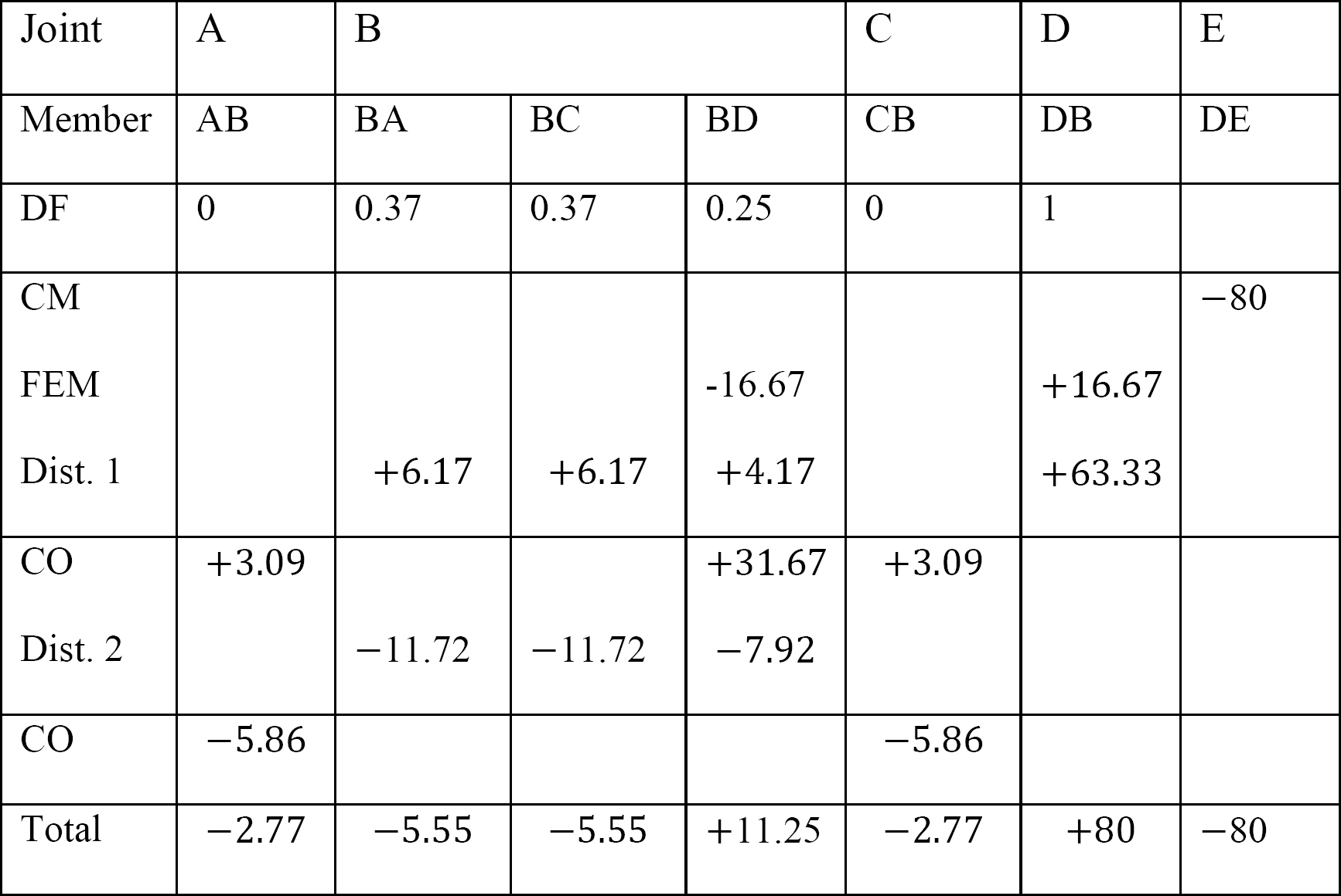
viimeiset jäsenten loppuhetket.
MAB = -2,77 k. ft
MBA = -5,55 k. Ft
MBC = -5,55 k. ft
MBD = +11,25 k. ft
MCB = -2,77
MDB = + 80 k. Ft
MDE = -80 k. ft
esimerkki 12.5
momenttijakauman avulla määritetään loppumomentit kuvassa 12.10 esitetyn kehyksen tukiin. EI = vakio.
Kuva. 12.10. Kehys.
ratkaisu
kiinteä loppumomentti.
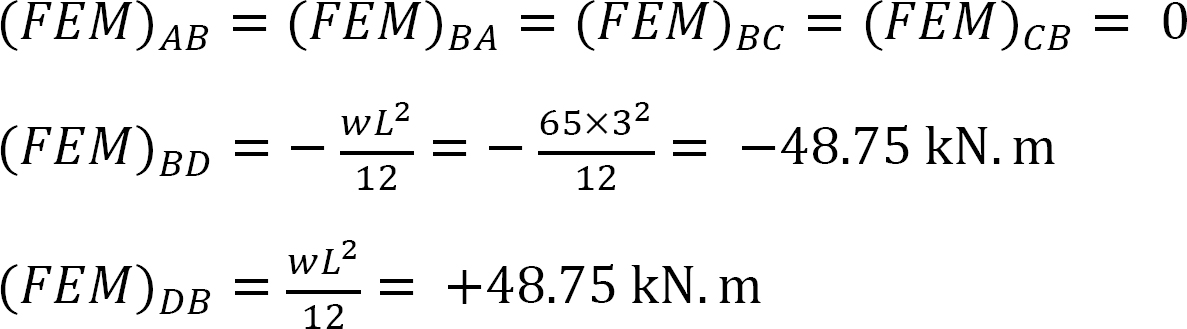
Jäykkyystekijä.
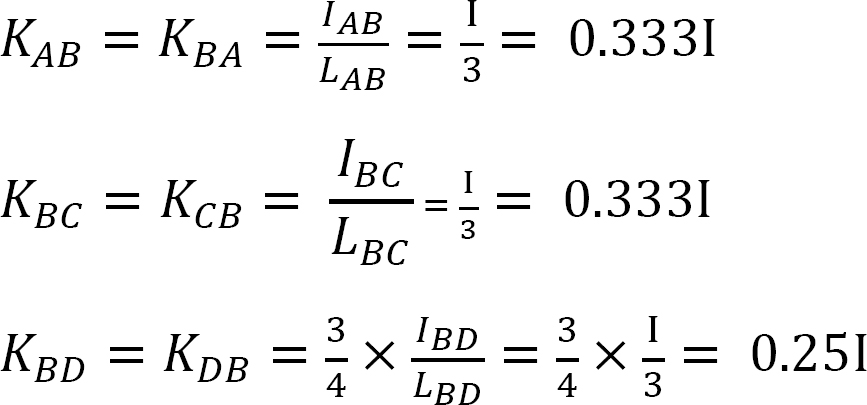
Jakelukerroin.
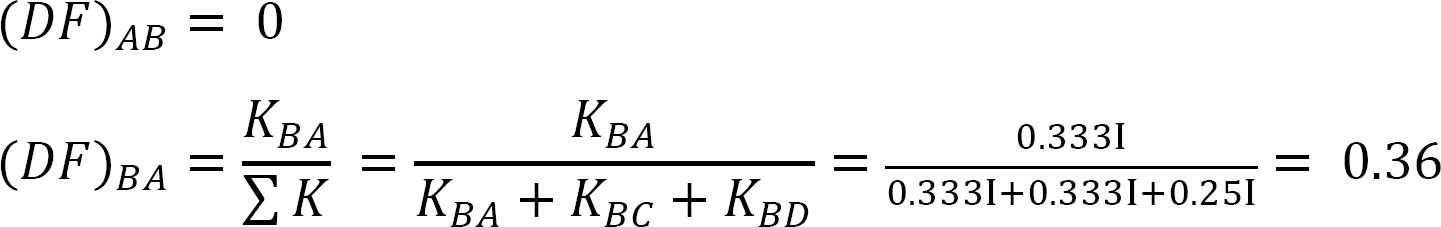

taulukko 12.5. Jakelutaulukko.
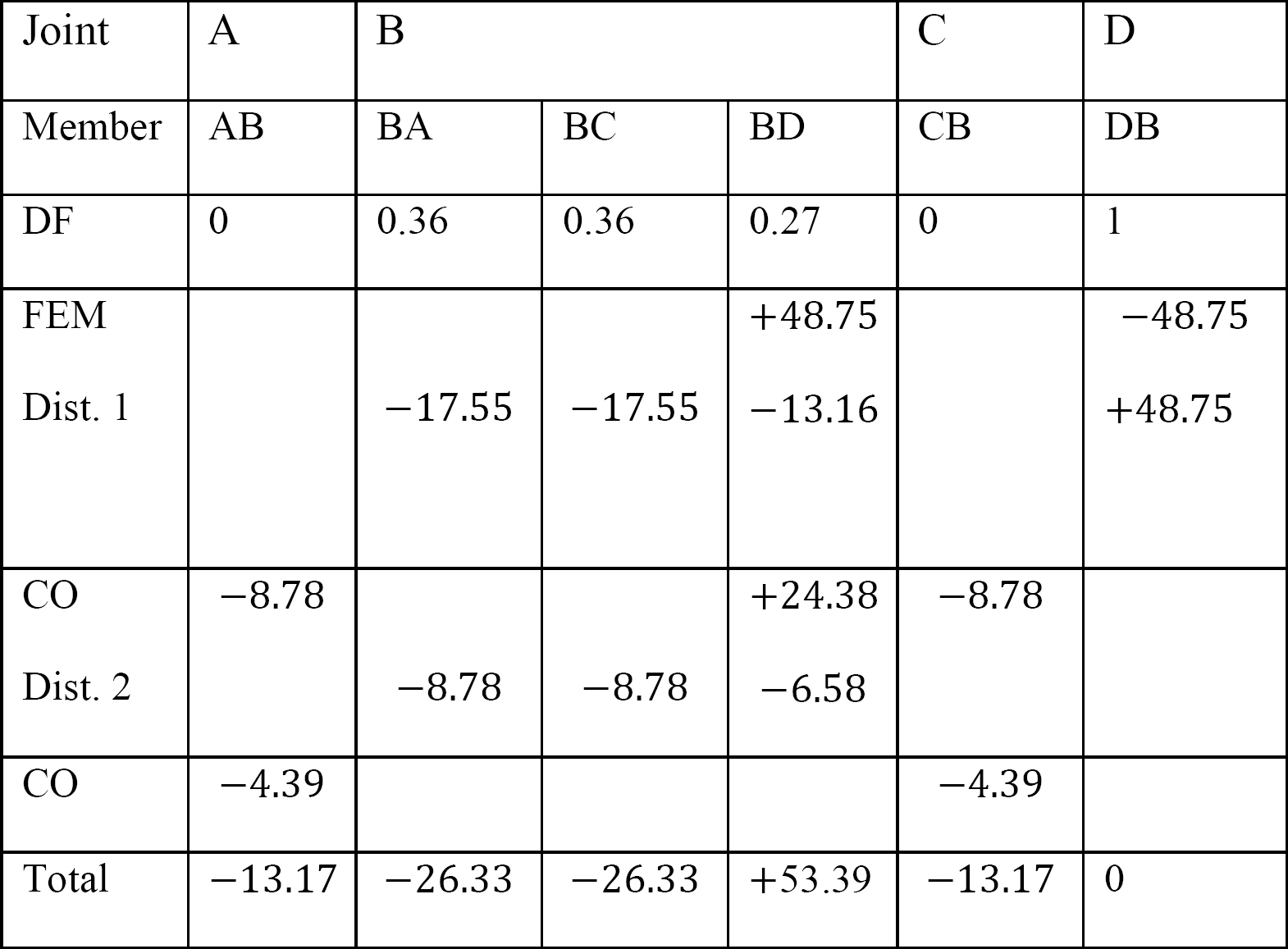
viimeiset jäsenten loppuhetket.
MAB = -13,17 k. ft
MBA = -26,33 k. ft
MBC = -26,33 k. ft
MBD = +53,39 k. ft
MCB = -13,17 k. ft
MDB = 0
esimerkki 12.6
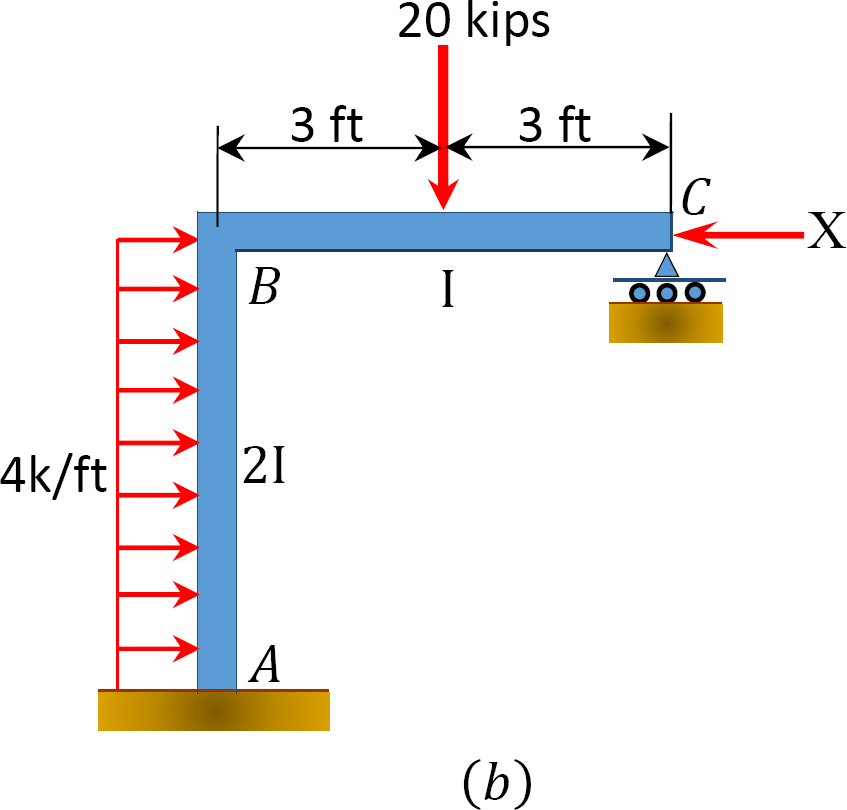
momenttijakaumamenetelmän avulla määritetään kehyksen päättymismomentit, joissa on kuvassa 12.11 a esitetty sivu-sway.
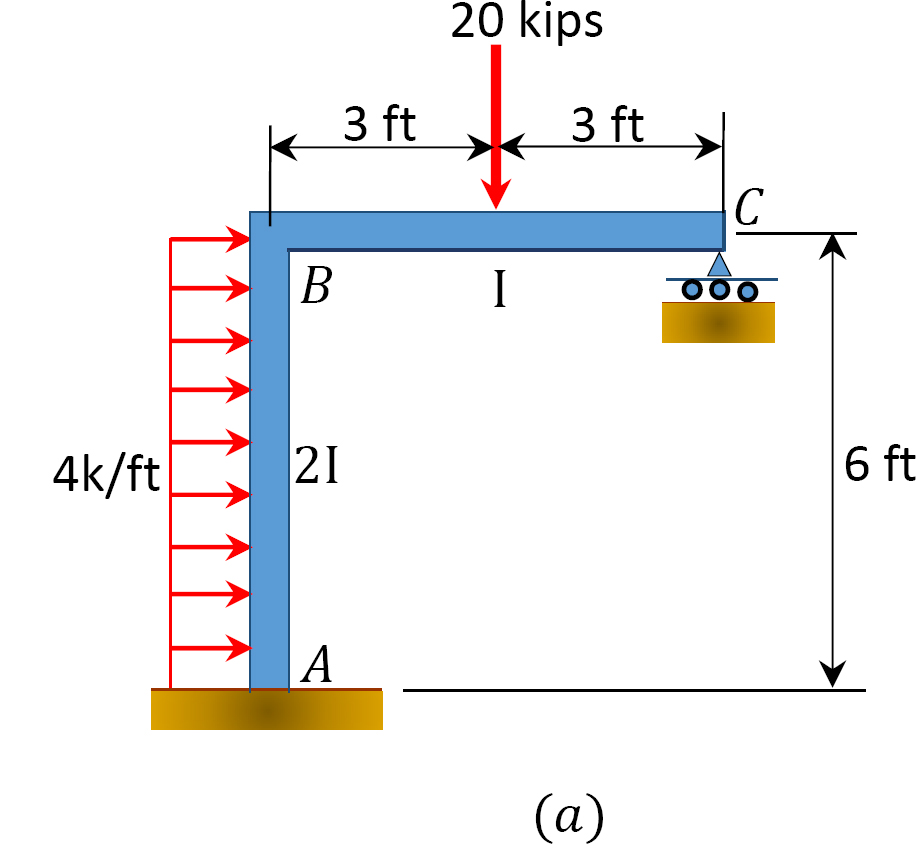
Kuva. 12.11. Runko sivuheijastimella.
ratkaisu
kiinteä loppumomentti.
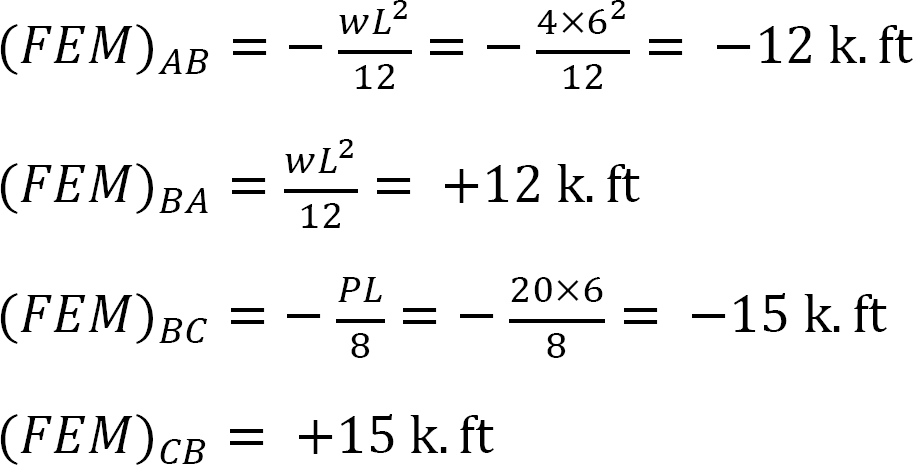
Jäykkyystekijä.
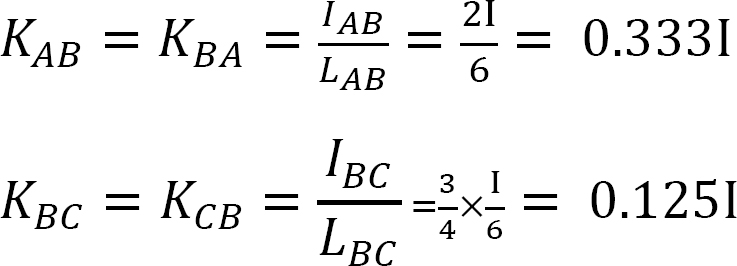
Jakelukerroin.
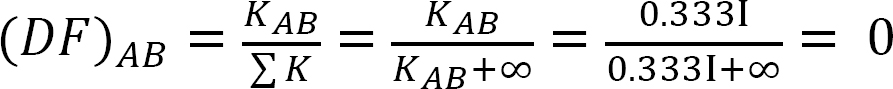

analyysi runko ilman puoli-huojunta.
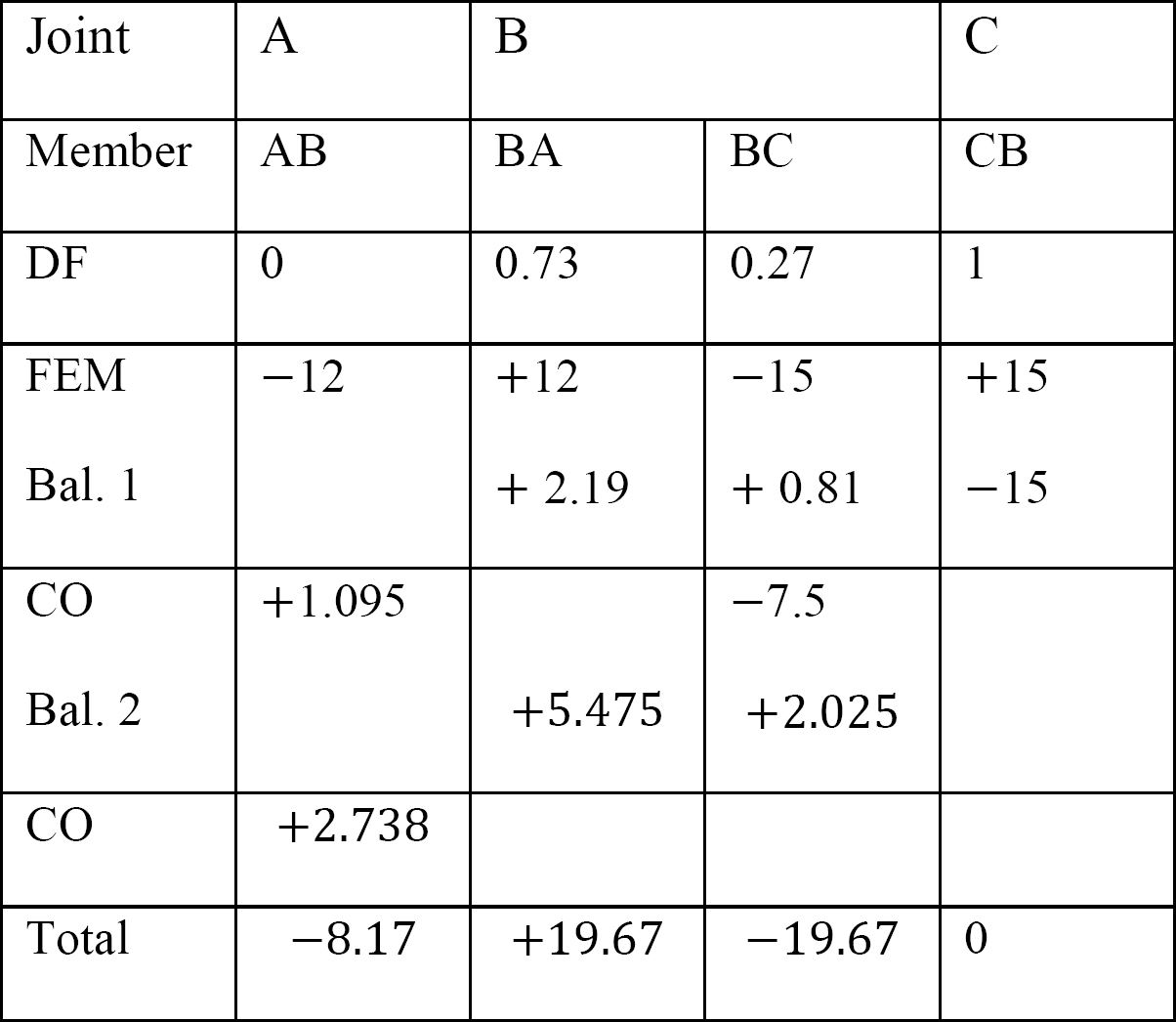
taulukko 12.6. Jakelutaulukko (ei huojuvaa kehystä).
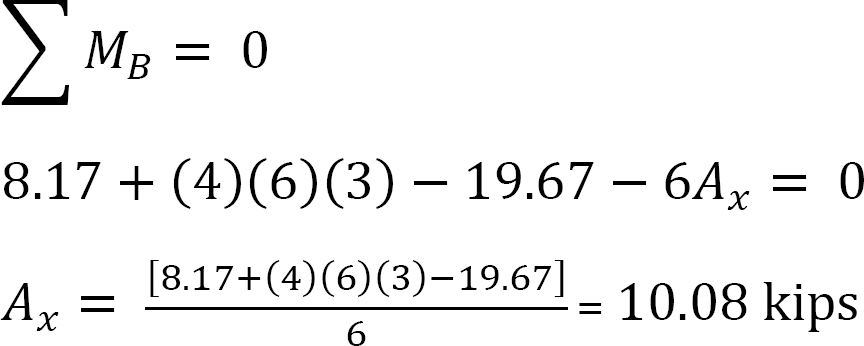
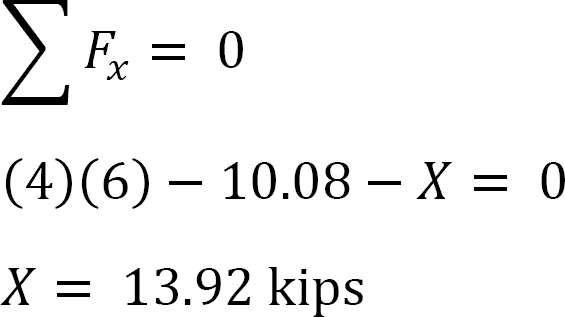
analyysi runko puoli-sway.
Oletetaan, että MAB = + 20 k. ft
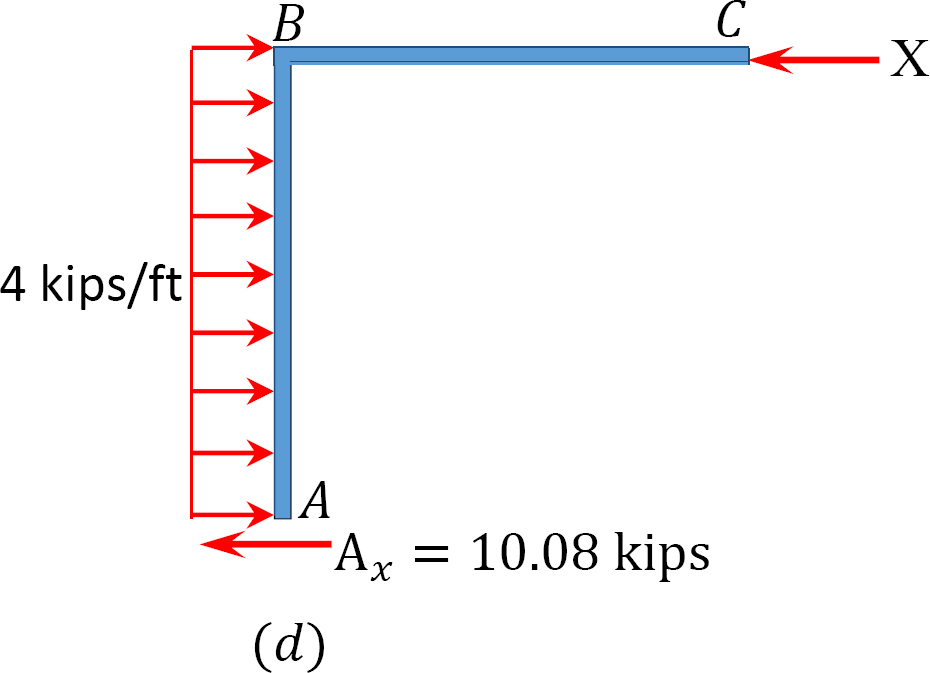
taulukko 12.7. Jakotaulukko (sway frame).
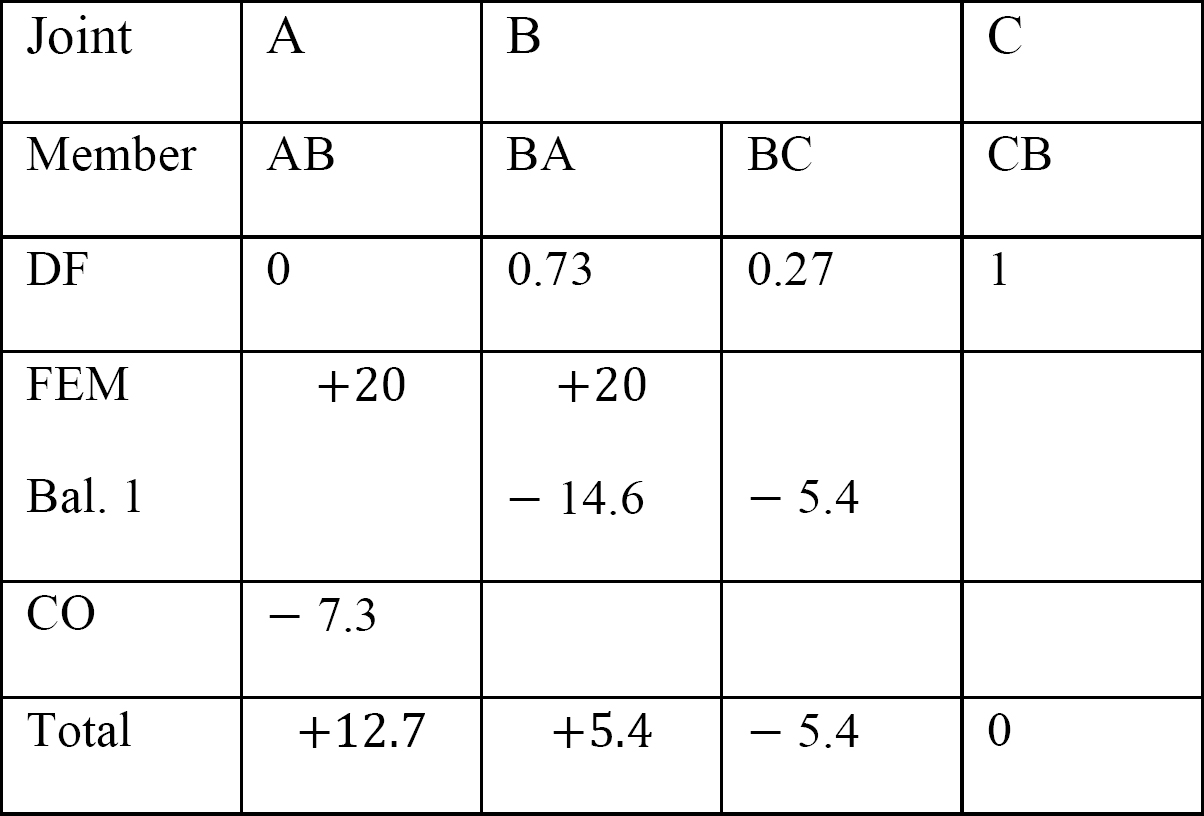
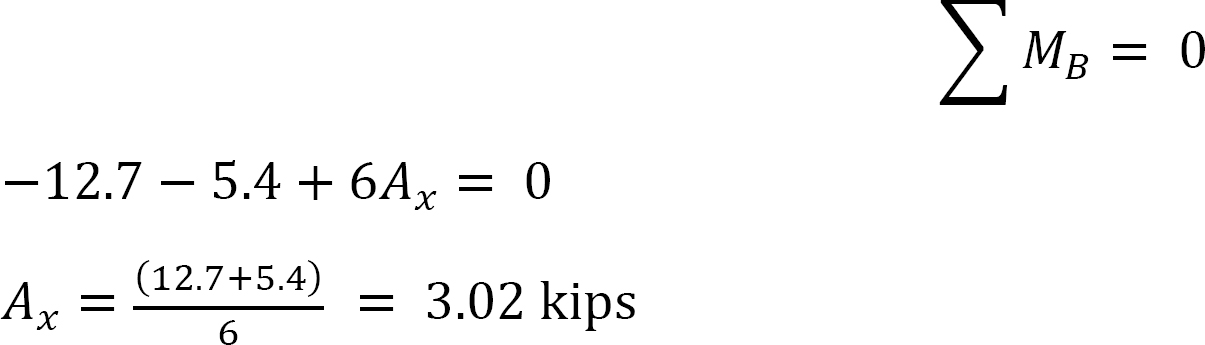
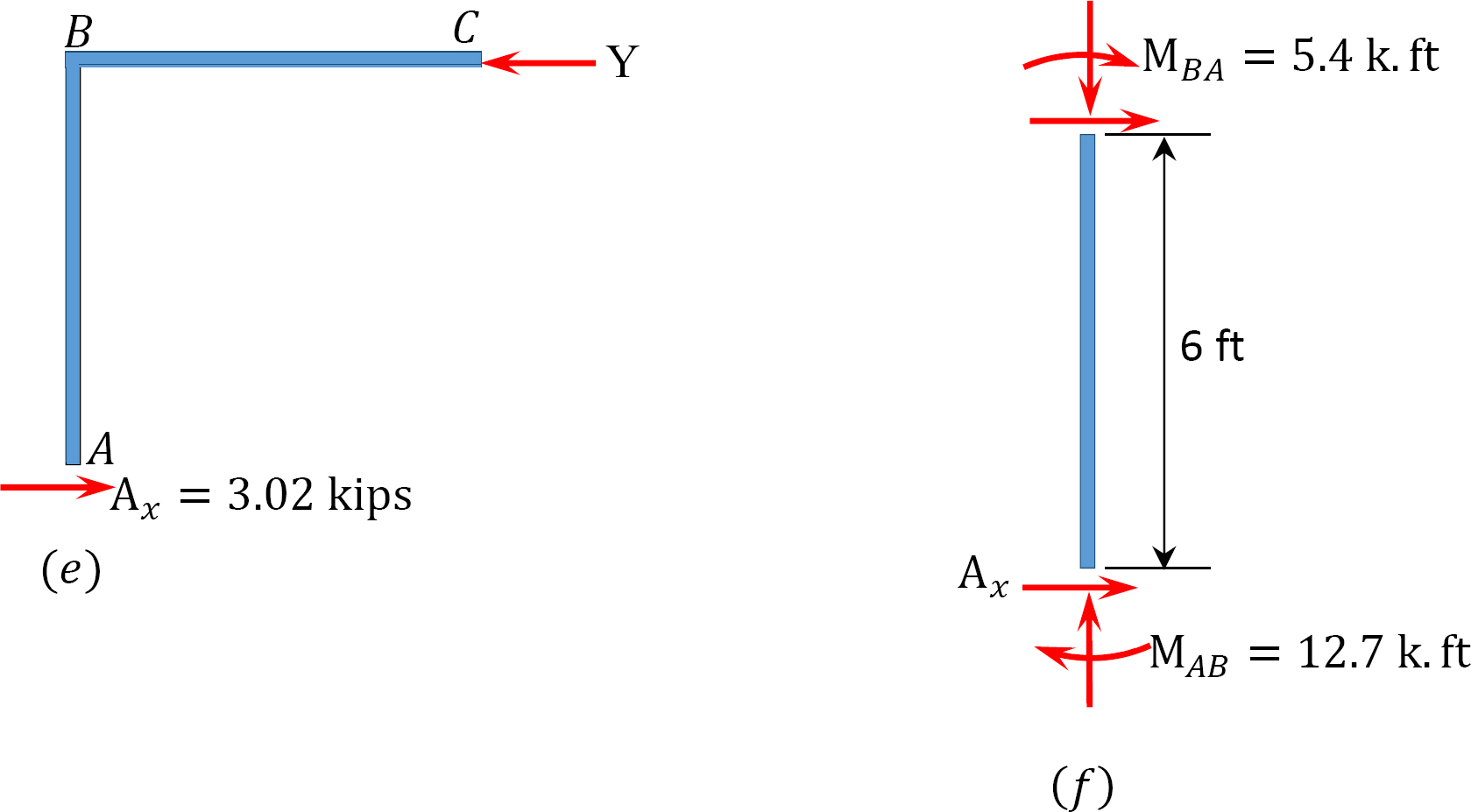
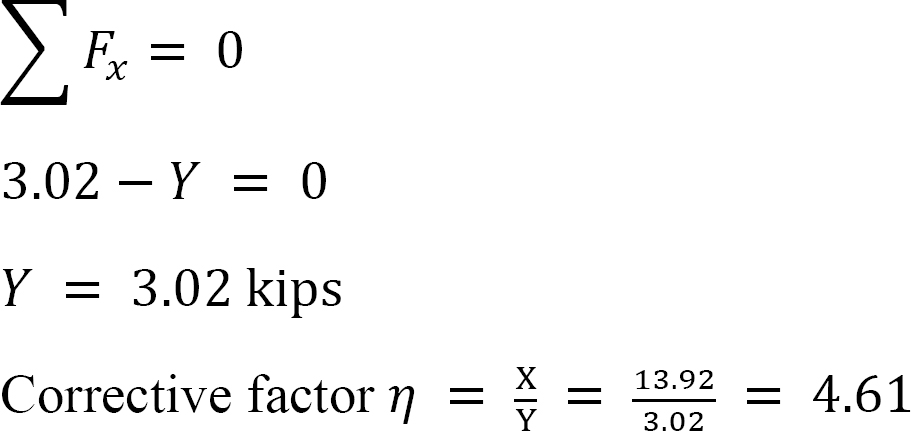
viimeiset loppuhetket.
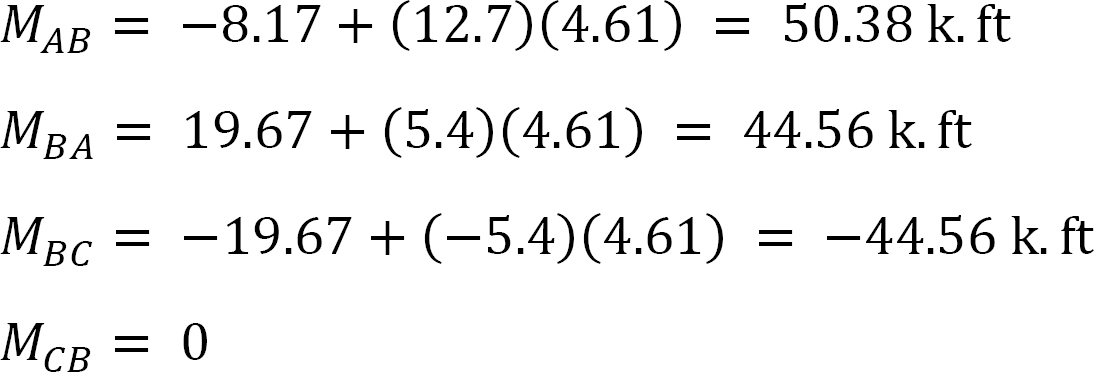
esimerkki 12.7
huojuva kehys Ladataan Kuvan 12.12 a mukaisesti. määritetään momenttijakaumamenetelmällä kehyksen jäsenten loppumomentit.
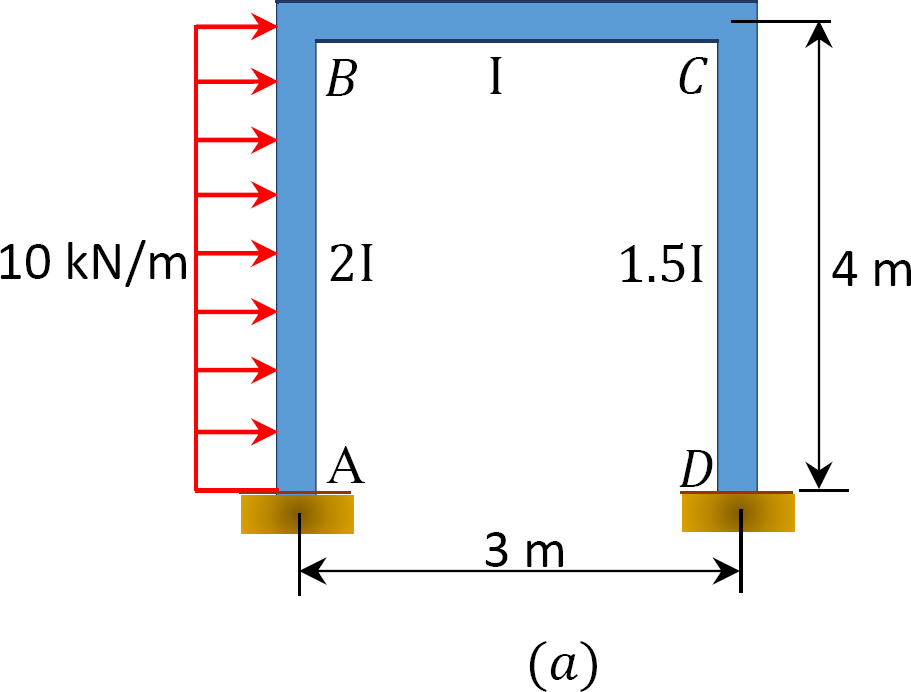
Kuva. 12.12. Ladattu keinukehys.
ratkaisu
kiinteä loppumomentti.
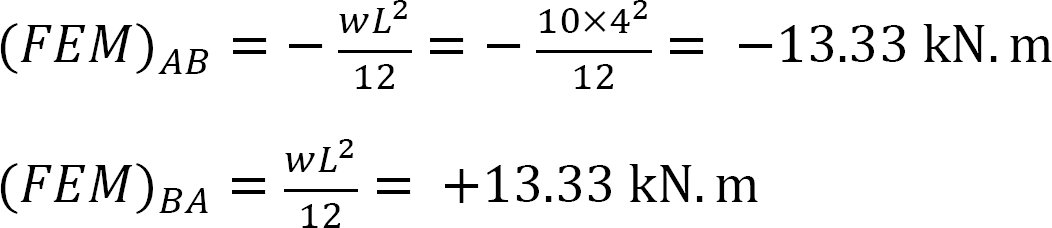
Jäykkyystekijä.
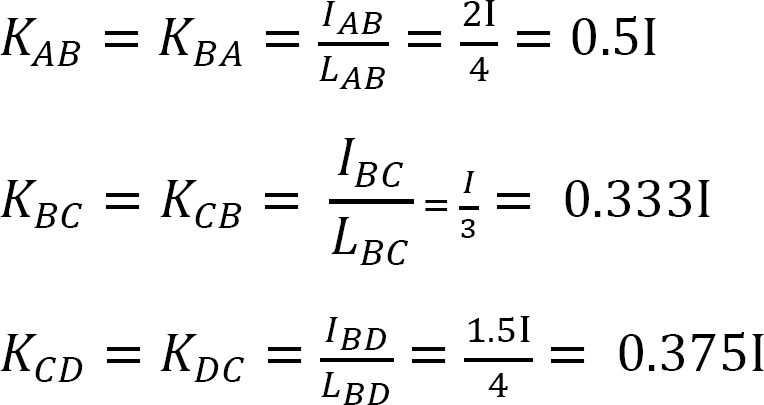
Jakelukerroin.

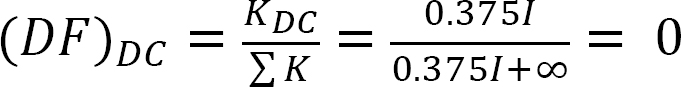
analyysi runko ilman puoli-huojunta.
taulukko 12.8. Jakelutaulukko (ei huojuvaa kehystä).
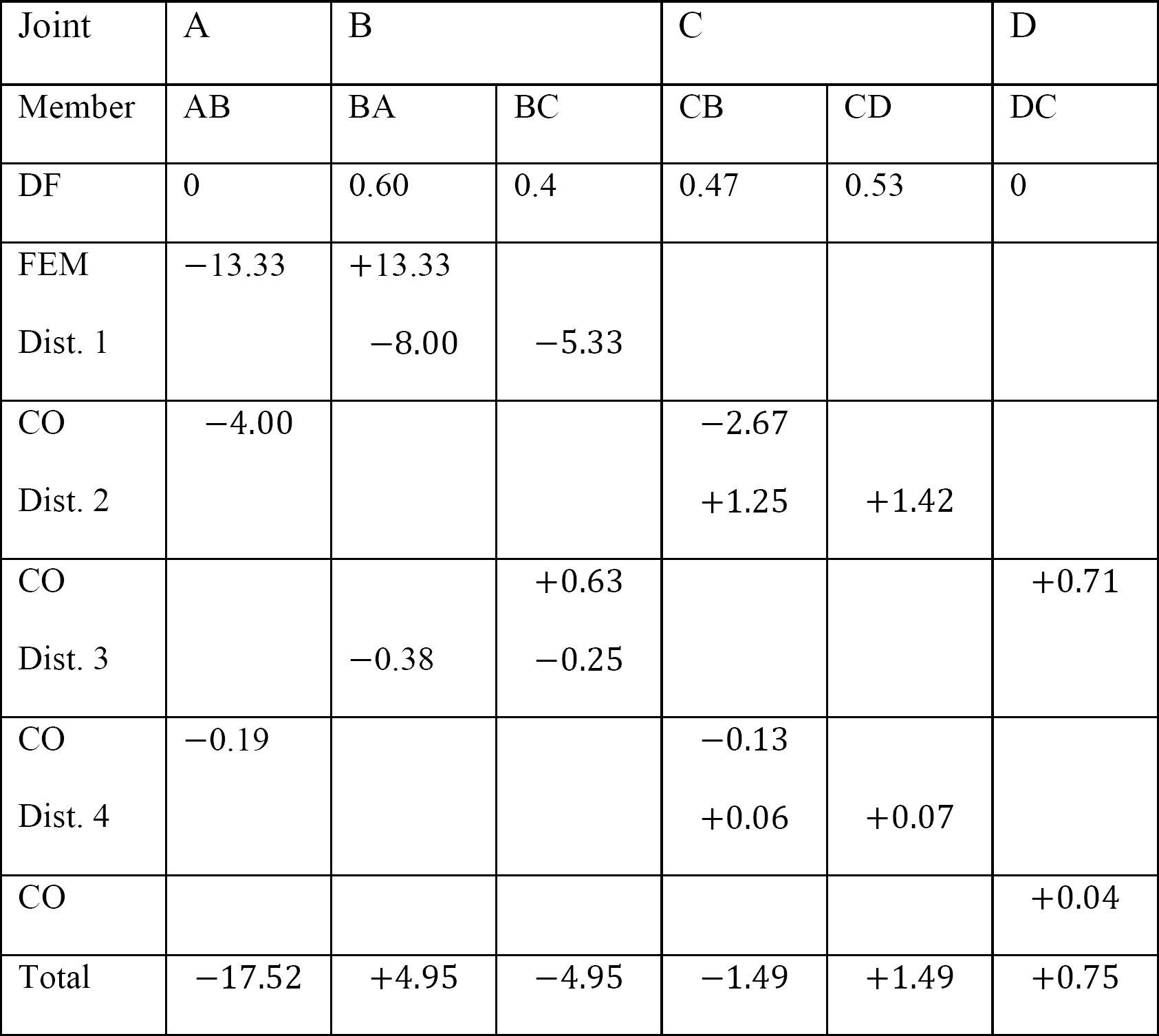
taulukko 12.9. Jakotaulukko (sway frame).
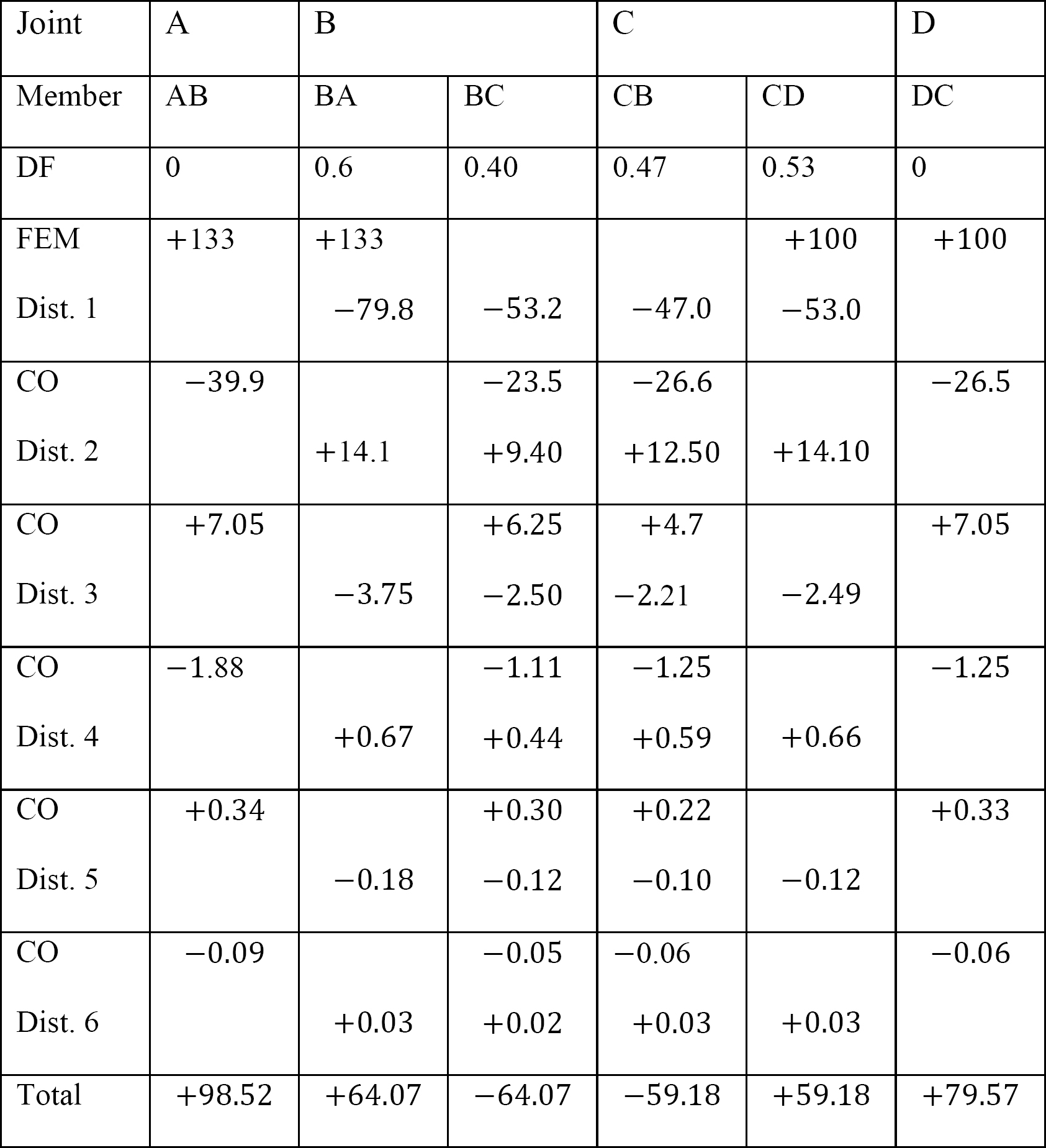
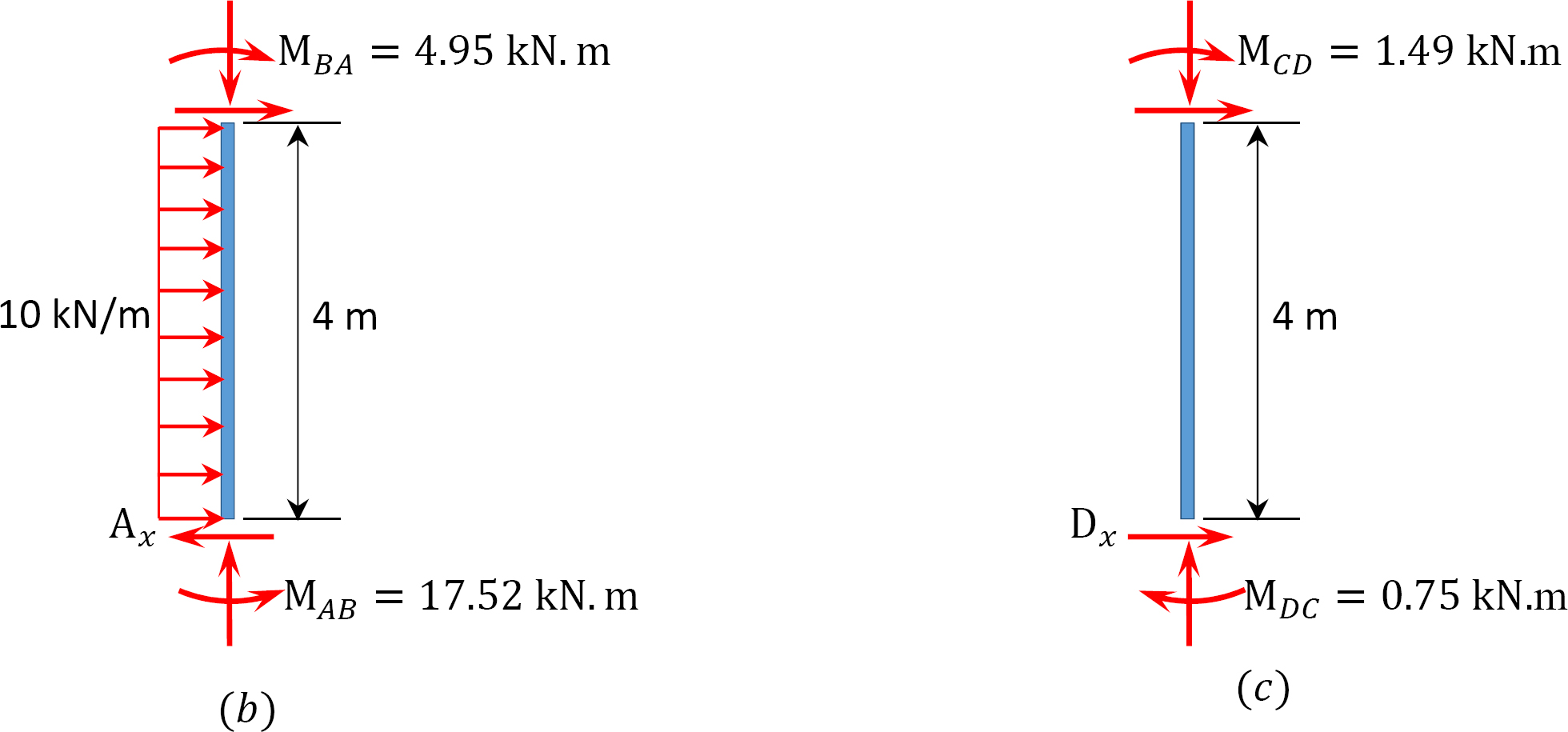
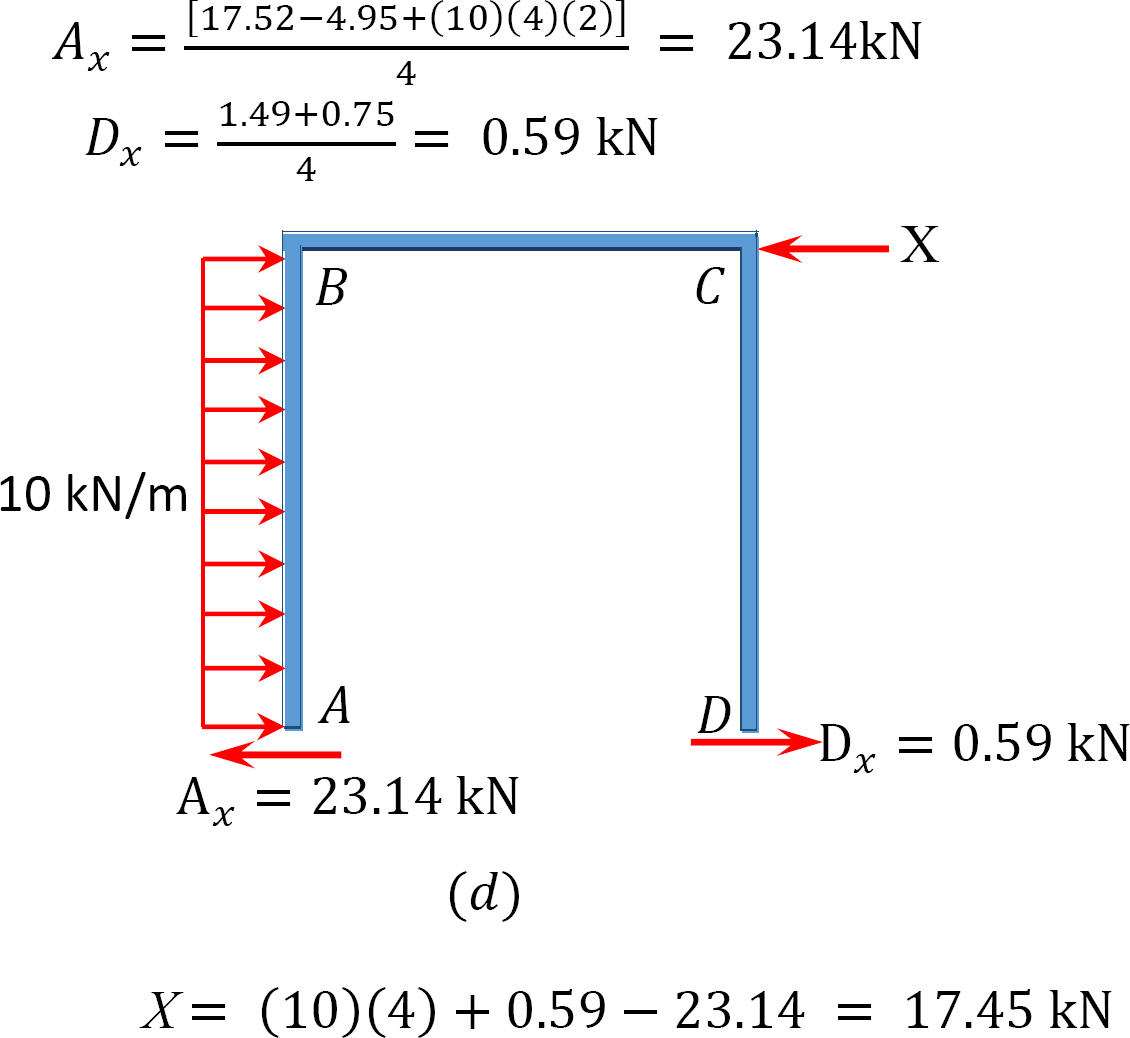
analyysi runko puoli-sway.
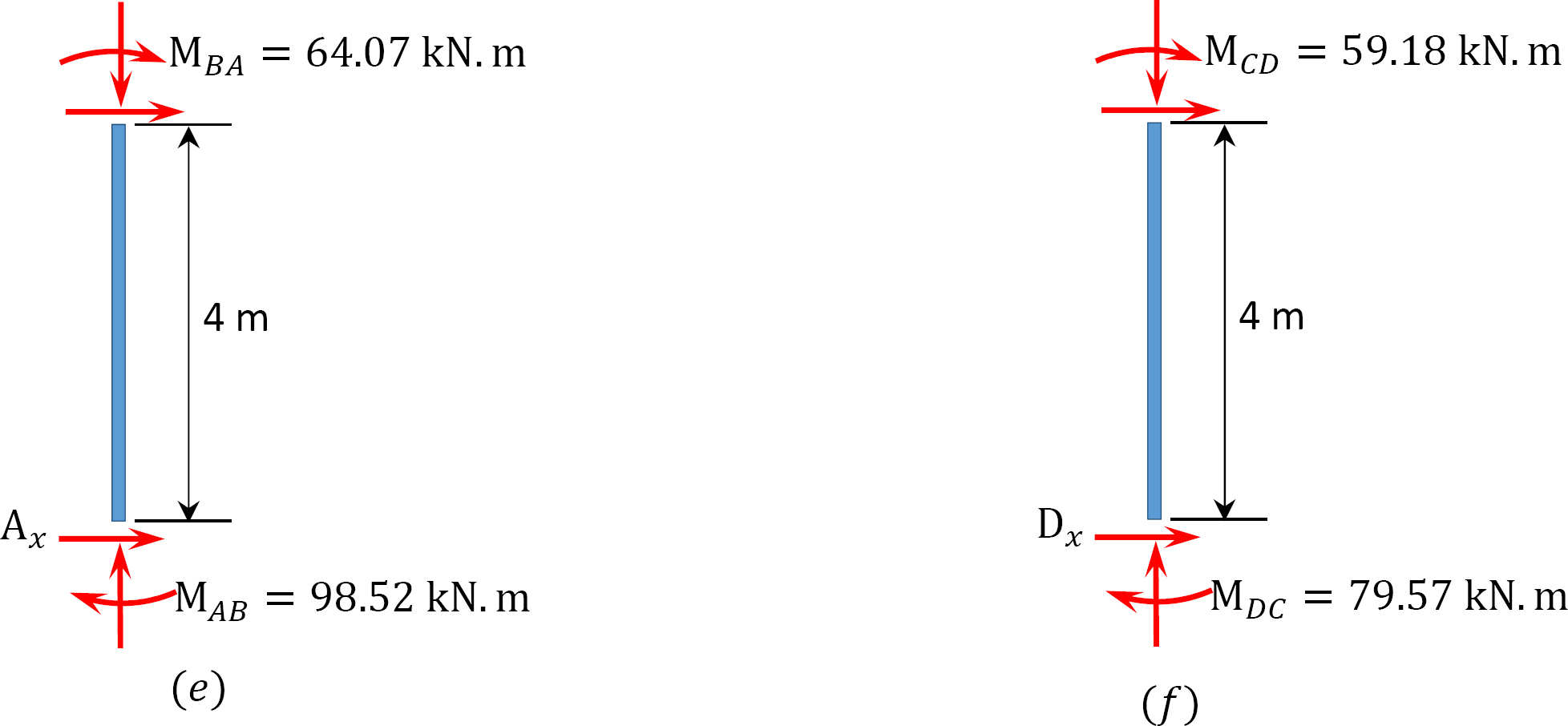

viimeinen loppuhetki.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. M
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Lukuyhteenveto
Momenttijakaumamenetelmä määrittelemättömien rakenteiden analysoimiseksi: momenttijakaumamenetelmä on likimääräinen analyysimenetelmä. Sen tarkkuus riippuu iteraatioiden määrästä. Tässä menetelmässä oletetaan, että kaikki rakenteen liitokset ovat väliaikaisesti lukkiutuneita tai kiinnittyneitä ja siten estyvät mahdollisesta pyörimisestä. Kuormitukset kohdistetaan jäseniin, ja momentit, jotka on kehitetty jäsen päättyy fixity määritetään. Liitokset rakenteessa avataan sitten peräkkäin, ja epätasapainoinen hetki kussakin liitoksessa jaetaan jäsenille, jotka kokoontuvat kyseisessä liitoksessa. Siirrettävät momentit jäsenten ääripäissä määritetään, ja tasapainoprosessia jatketaan, kunnes haluttu tarkkuus on saavutettu. Jäsenten loppuhetket määritetään laskemalla yhteen kiinteä loppuhetki, jaettu hetki ja siirtohetki. Kun jäsenten loppuhetket on määritetty, rakenne muuttuu determinatiiviseksi.
Käytännön Ongelmat
12.1 Käytä momenttijakaumamenetelmää laskemaan palkkien jäsenten loppumomentti Kuvassa P12.1 kautta Kuvassa P12.12 ja piirrä taivutus momentti ja leikkausvoima kaaviot. EI = vakio.
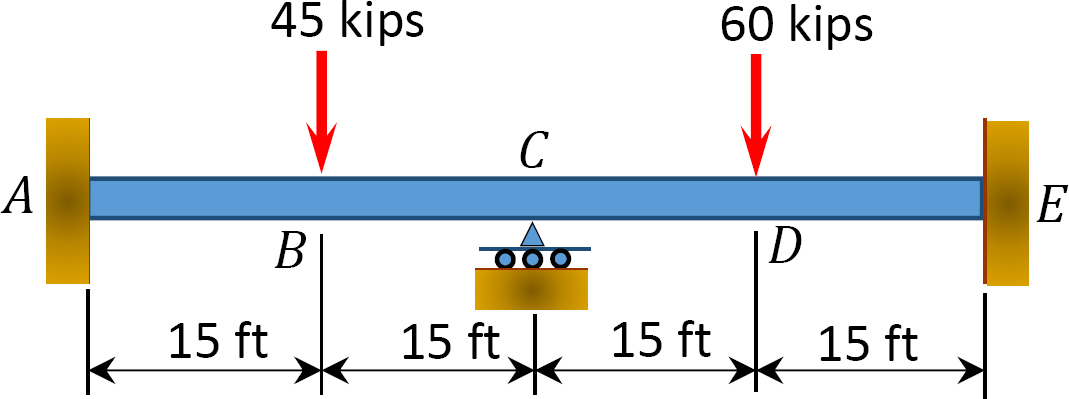
Kuva. P12.1. Lasersäde.
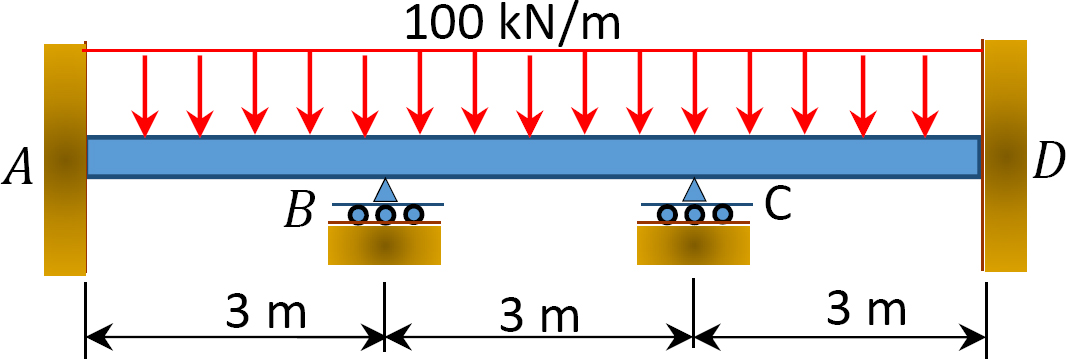
Kuva. P12.2. Lasersäde.
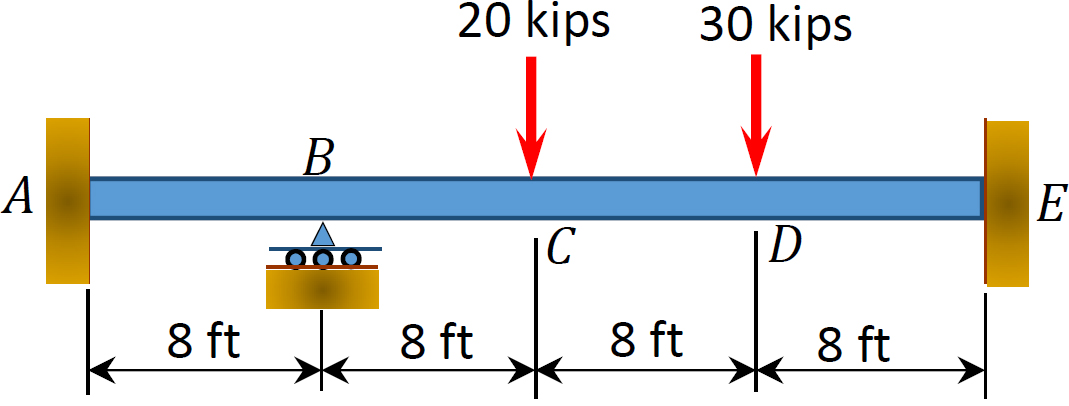
Kuva. P12.3. Lasersäde.
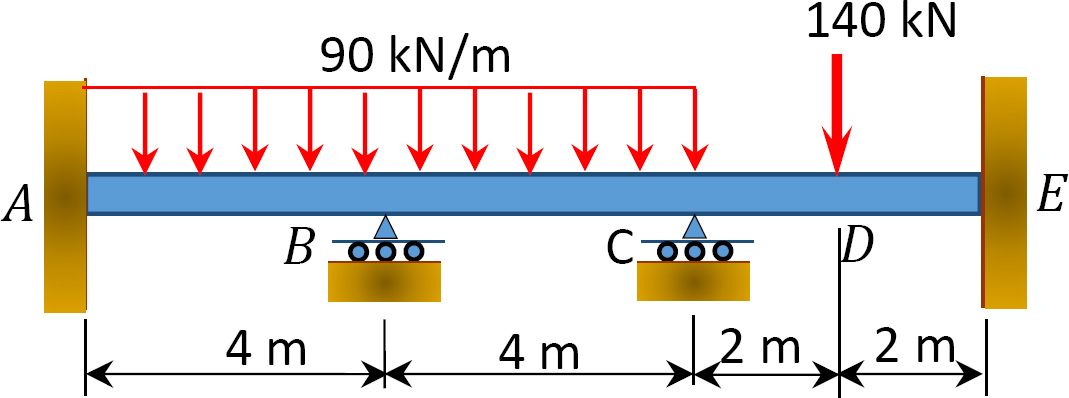
Kuva. P12.4. Lasersäde.
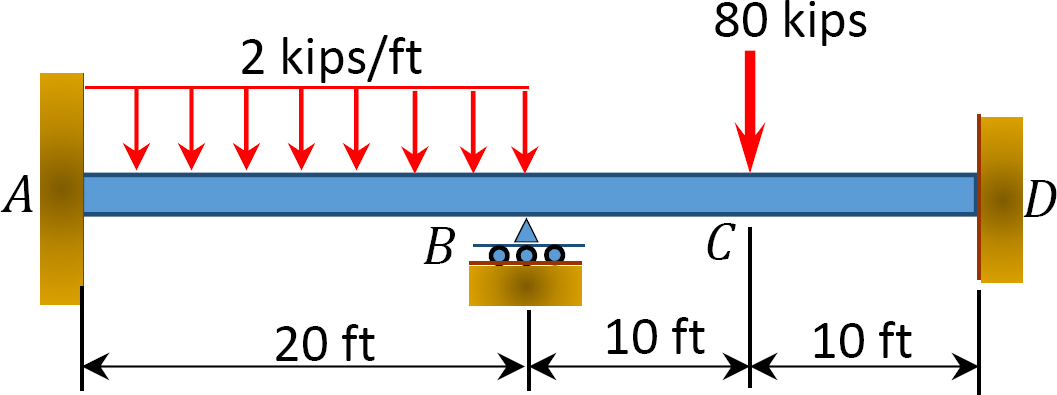
Kuva. P12.5. Lasersäde.
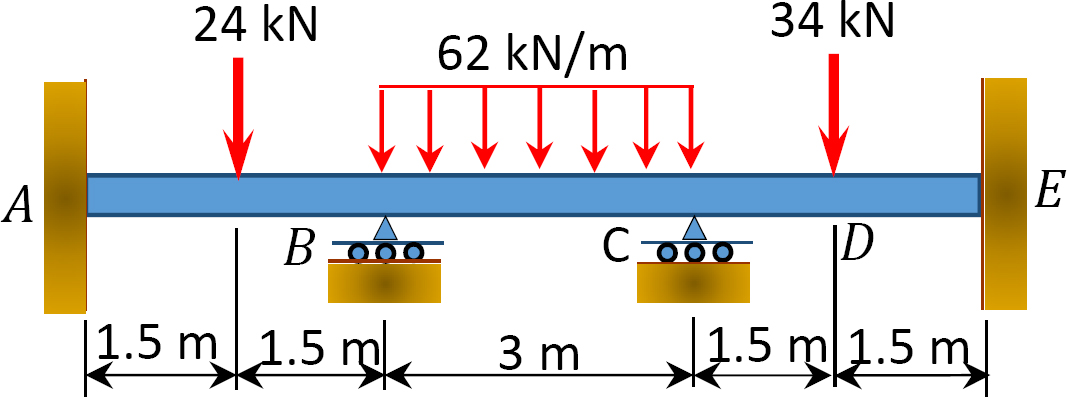
Kuva. P12.6. Lasersäde.
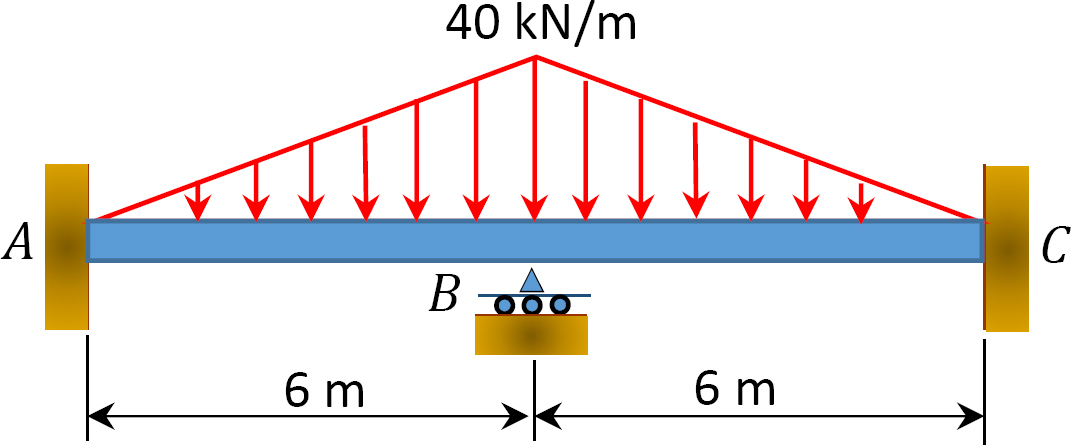
Kuva. P12.7. Lasersäde.
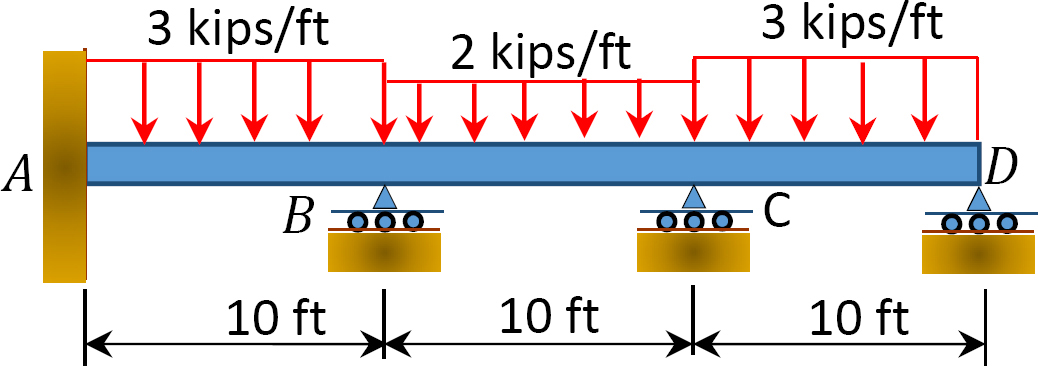
Kuva. P12.8. Lasersäde.
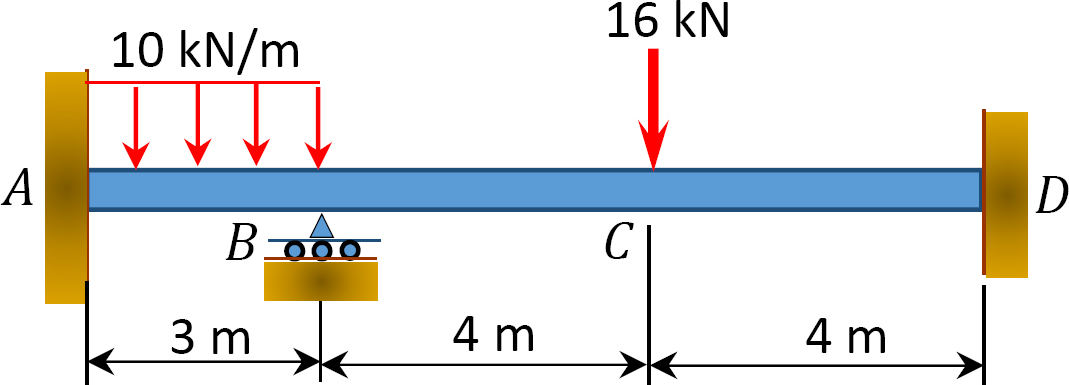
Kuva. P12.9. Lasersäde.
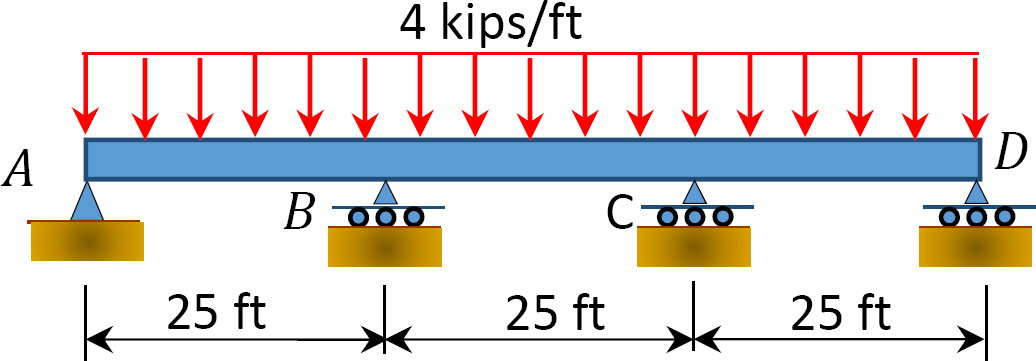
Kuva. P12.10. Lasersäde.
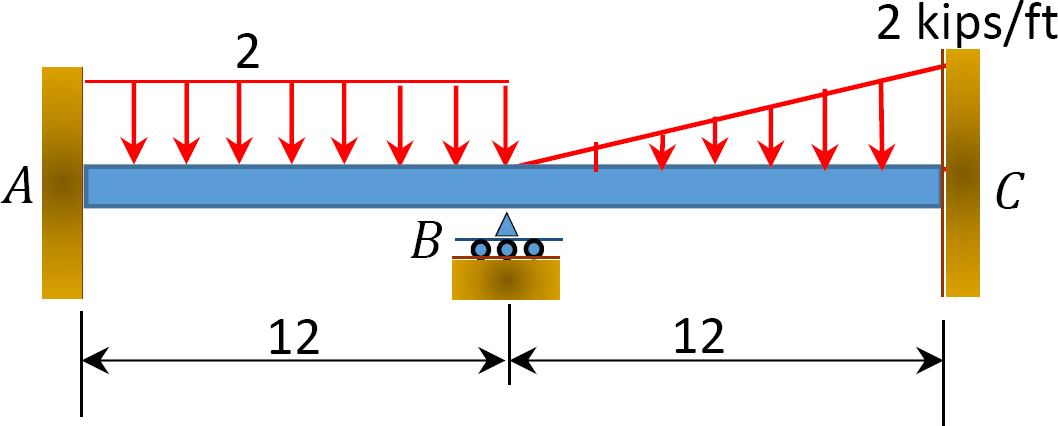
Kuva. P12.11. Lasersäde.
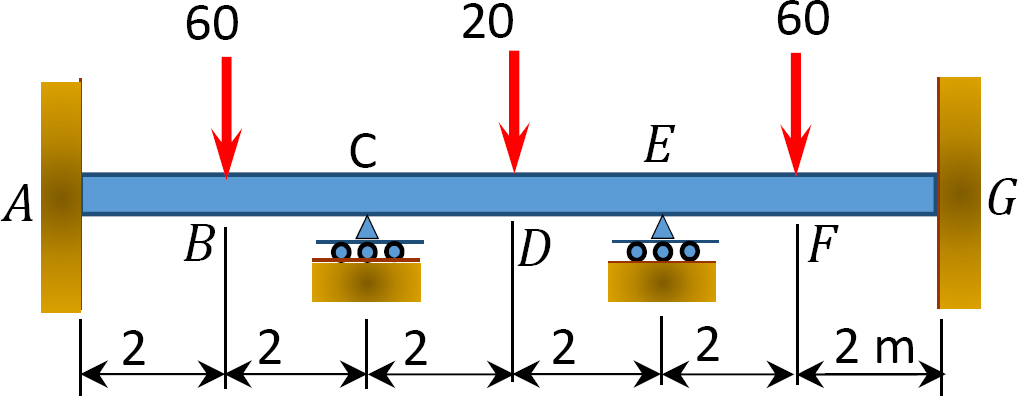
Kuva. P12.12. Lasersäde.
12.2 laske momenttijakaumamenetelmällä Kuvassa P12.13 esitettyjen kehysten jäsenten loppumomentti kuvioon 12.20 ja piirrä taivutusmomentti ja leikkausvoimakaaviot. EI = vakio.
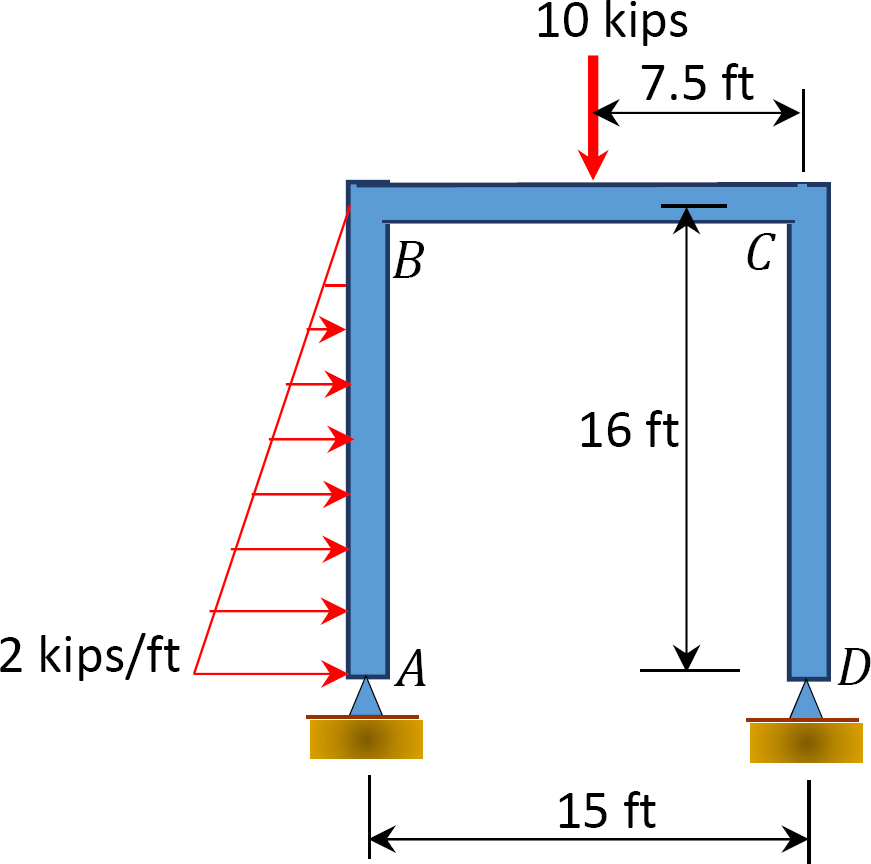
Kuva. P12.13. Kehys.
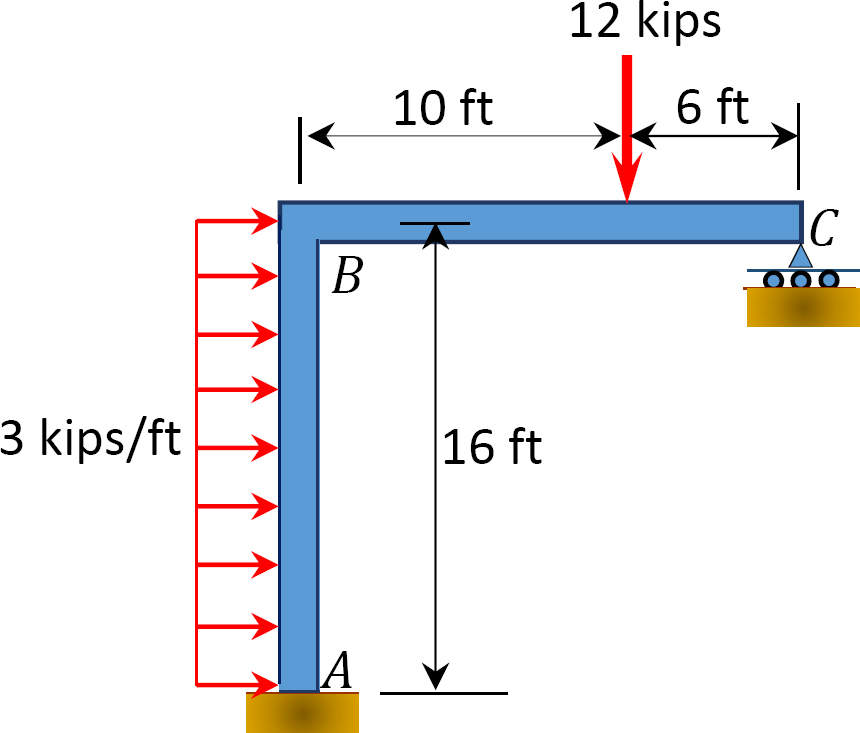
Kuva. P12.14. Kehys.
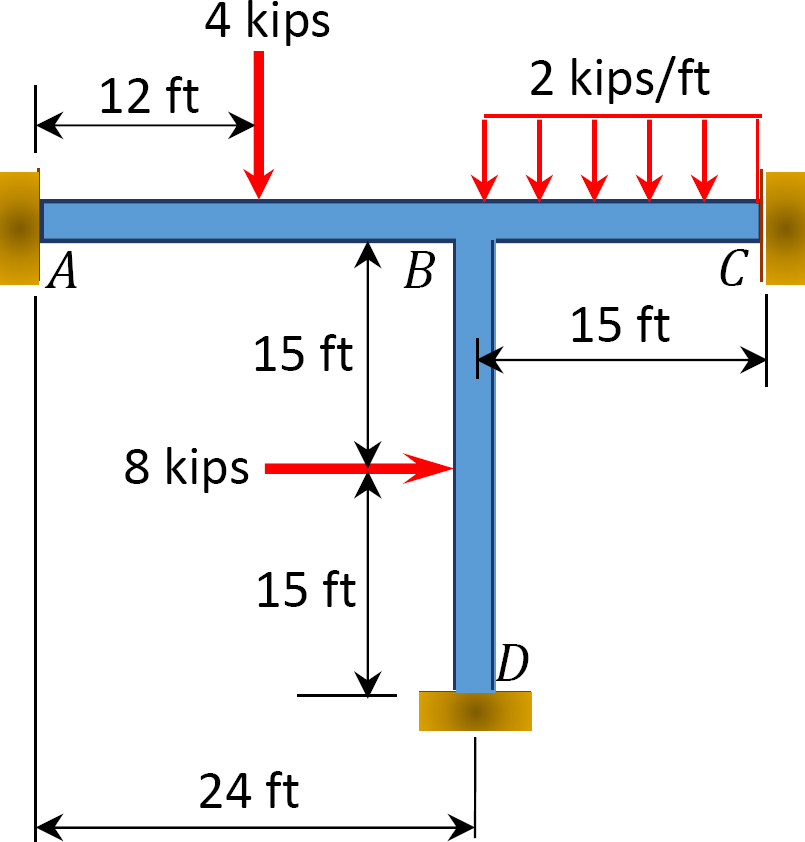
Kuva. P12.15. Kehys.
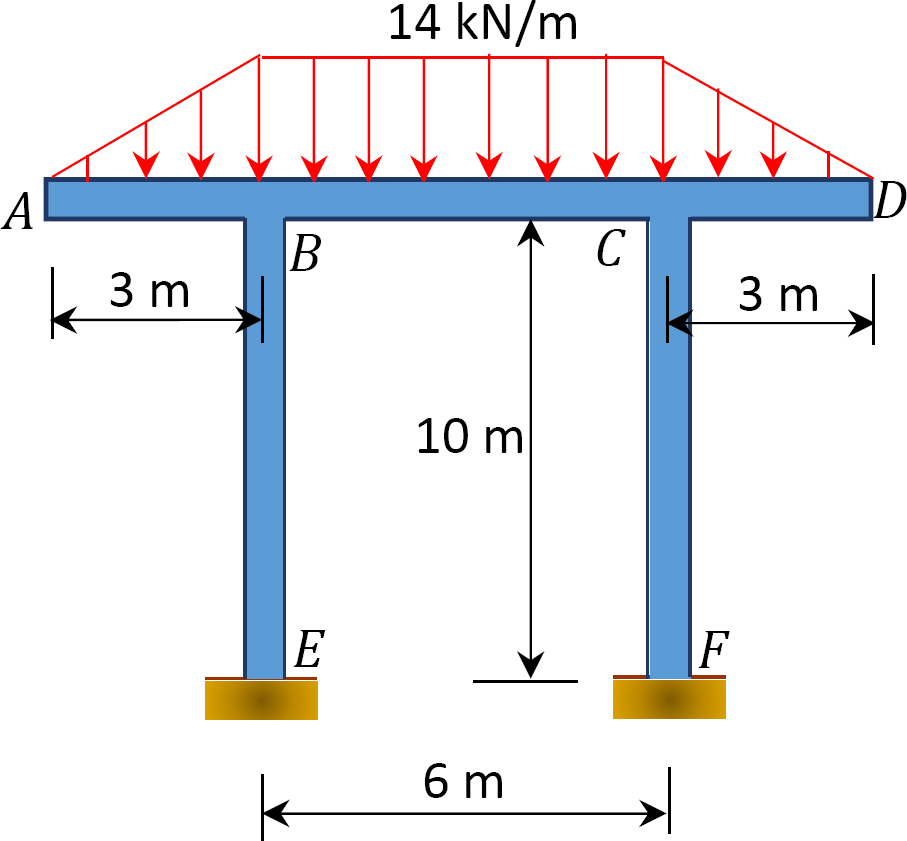
Fig. P12.16. Frame.
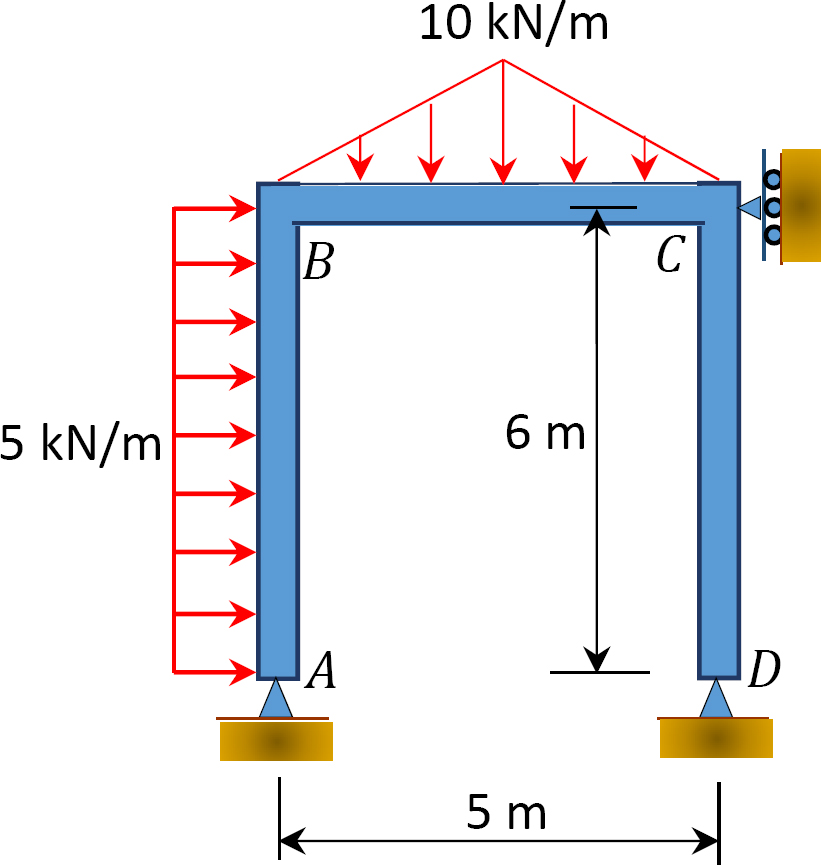
Fig. P12.17. Frame.
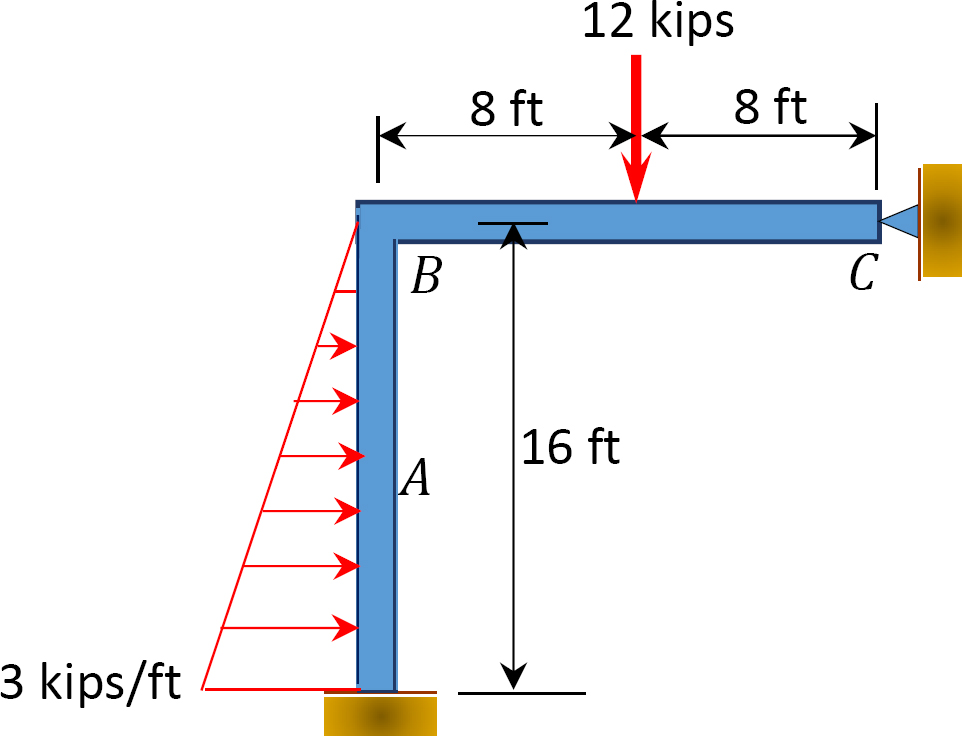
Fig. P12.18. Frame.
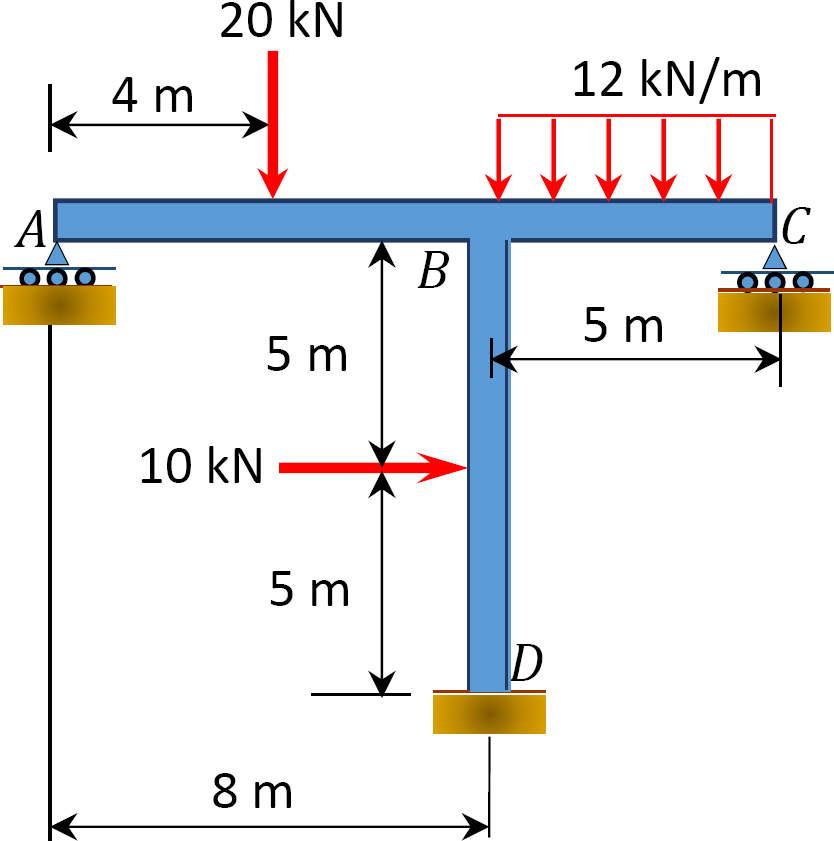
Fig. P12.19. Frame.
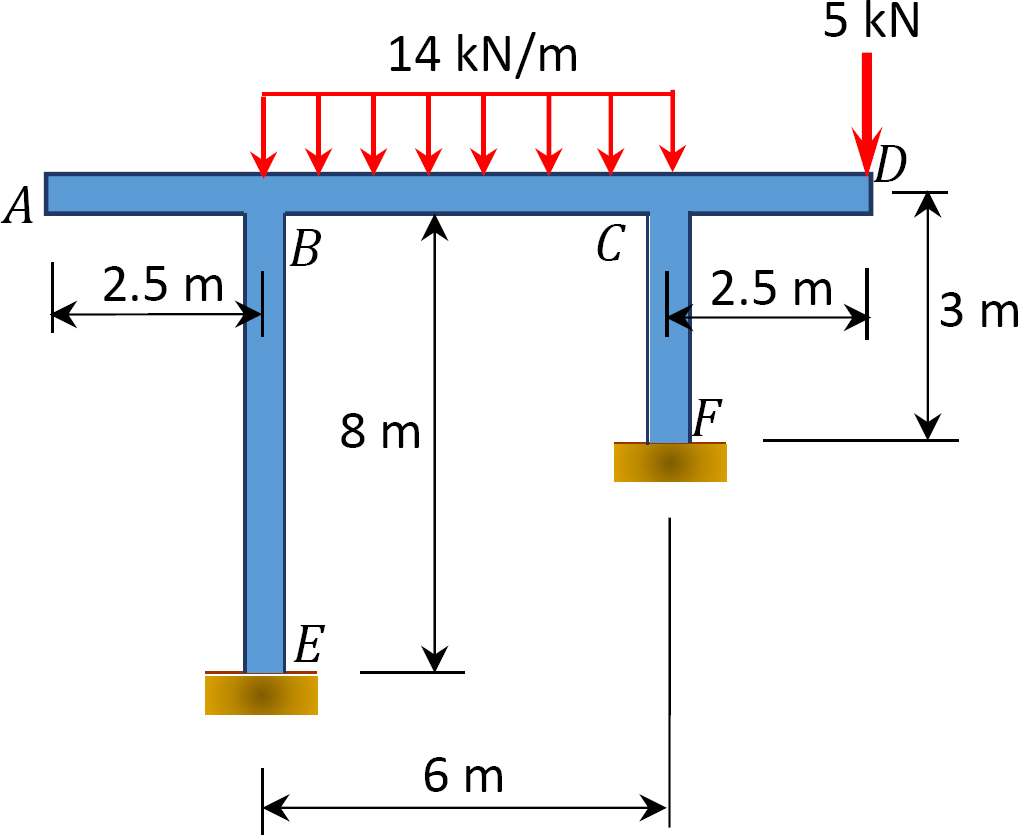
Fig. P12.20. Frame.