Capítulo 12
Momento Método de Distribuição de Análise de Estruturas
12.1 Conceitos Básicos
O momento de distribuição de um método de análise de vigas e quadros foi desenvolvido por Hardy Cross e formalmente apresentado em 1930. Embora este método seja um método de deformação como o método da deflexão da inclinação, é um método aproximado e, portanto, não requer resolução simultânea de equações, como foi o caso com este último método. O grau de precisão dos resultados obtidos pelo método de distribuição de momento depende do número de aproximações sucessivas ou do processo de iteração.
para ilustrar o conceito do método de distribuição do momento, considere o quadro apresentado na figura 12.1. Os membros do quadro são prismáticos e presumem-se que não deformam axialmente nem se traduzem em relação uns aos outros. As juntas ACD do quadro são fixas, enquanto a junta B pode rodar ligeiramente devido à carga aplicada. Primeiro, antes de realizar a distribuição de momento entre os membros, todas as articulações são consideradas temporariamente bloqueadas usando um grampo.
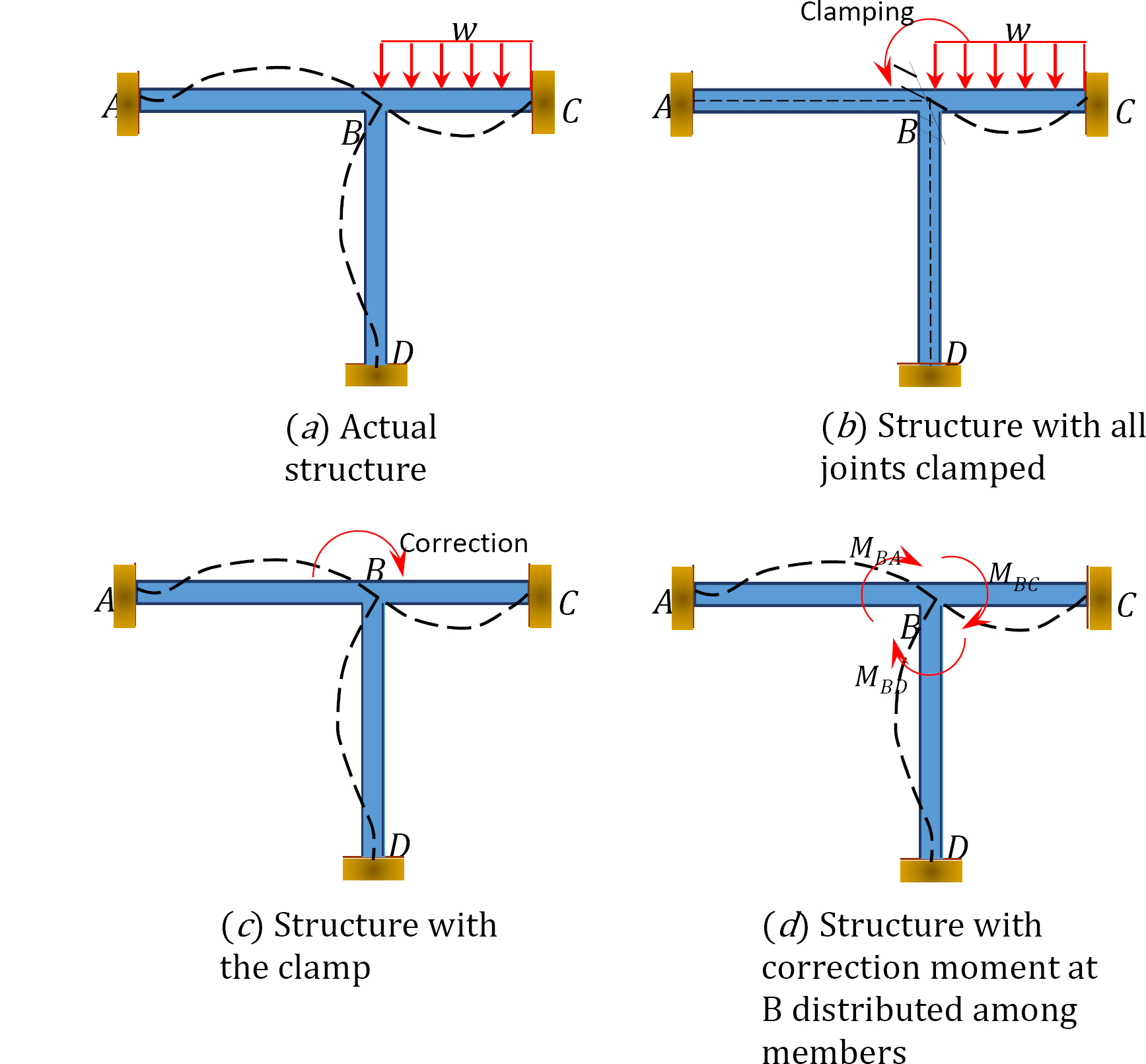
Fig. 12.1. Quadro.
12.2 Convenção de sinais
a Convenção de sinais para o método de distribuição de momento é semelhante ao estabelecido para o método de deflexão do declive; ou seja, o momento no final de um membro é considerado positivo se ele tende a rodar o fim do Membro no Sentido DOS ponteiros do relógio e negativo se ele tende a rodar no sentido contrário aos ponteiros do relógio.
12.3 definições
momentos desequilibrados: este método de análise assume que as articulações de uma estrutura são inicialmente fixadas ou bloqueadas e, em seguida, liberadas sucessivamente. Uma vez que um conjunto é liberado, uma rotação ocorre, uma vez que a soma dos momentos finais fixos dos Membros reunidos naquele conjunto não é zero. O valor da soma dos momentos finais obtidos é o momento desequilibrado dessa articulação.Momentos de transição: os momentos distribuídos nas extremidades dos Membros reunidos em uma causa conjunta momentos nas outras extremidades, que se supõe serem fixos. Estes momentos induzidos nas outras extremidades são chamados momentos de transição.
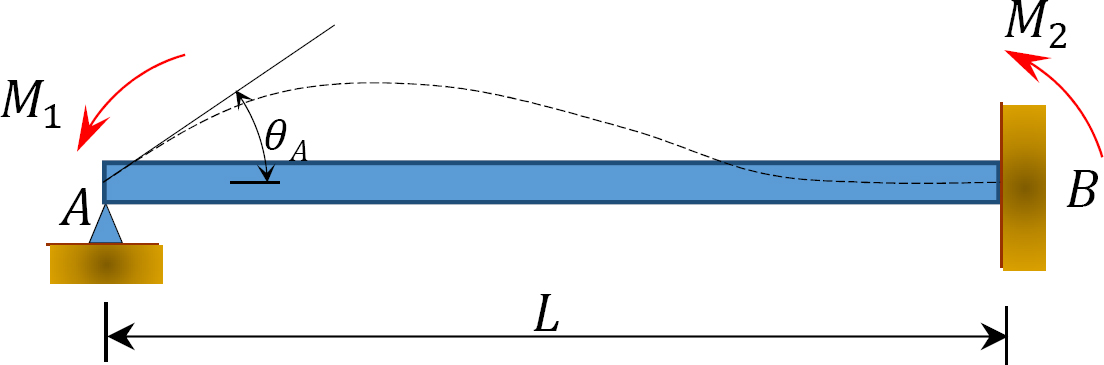
Fig. 12.2. Feixe prismático descarregado.
considerar um feixe prismático sem carga fixado na extremidade B, como ilustrado na figura 12.2. Se um momento M1 for aplicado à extremidade esquerda do feixe, as equações de inclinação e deflexão para ambas as extremidades do feixe podem ser escritas do seguinte modo::


Substituindo 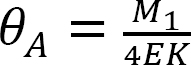 a partir da equação 12.1 na equação 12.2 sugerem o seguinte:
a partir da equação 12.1 na equação 12.2 sugerem o seguinte:

Equação 12.3 sugere que o momento transportados para o fixo extremidade de uma viga devido a um momento aplicado na outra extremidade é igual à metade da aplicada momento.Factor de reporte :a relação entre o momento induzido e o momento aplicado é referida como factor de reporte. Para o feixe indicado na figura 12.2, o Fator de transição é o seguinte::

factor distribuído (DF): O factor distribuído é um factor utilizado para determinar a proporção do momento desequilibrado transportado por cada um dos Membros reunidos numa Assembleia Paritária. Para os membros reunidos em conjunto O do quadro apresentado na figura 12.3, os seus factores de distribuição são calculados da seguinte forma: :
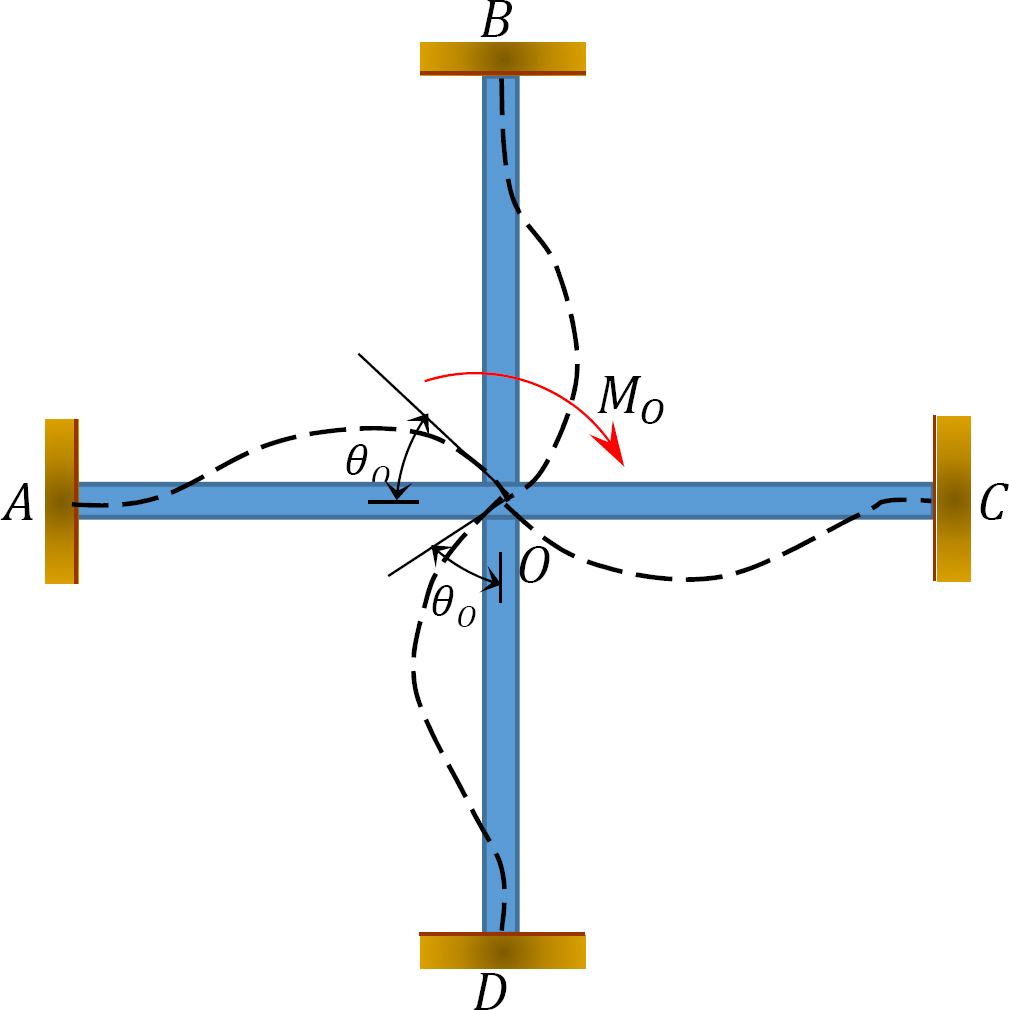
Fig. 12.3. Quadro.

momentos distribuídos: após a liberação do grampo imaginário em uma articulação, o momento desequilibrado nessa articulação faz com que ela gire. A rotação distorce o fim da reunião dos membros na junta, resultando no desenvolvimento de momentos de resistência. Estes momentos de resistência são chamados momentos distribuídos. Distribuído momentos para os membros do quadro mostrado na Figura 12.3 são calculadas da seguinte forma:
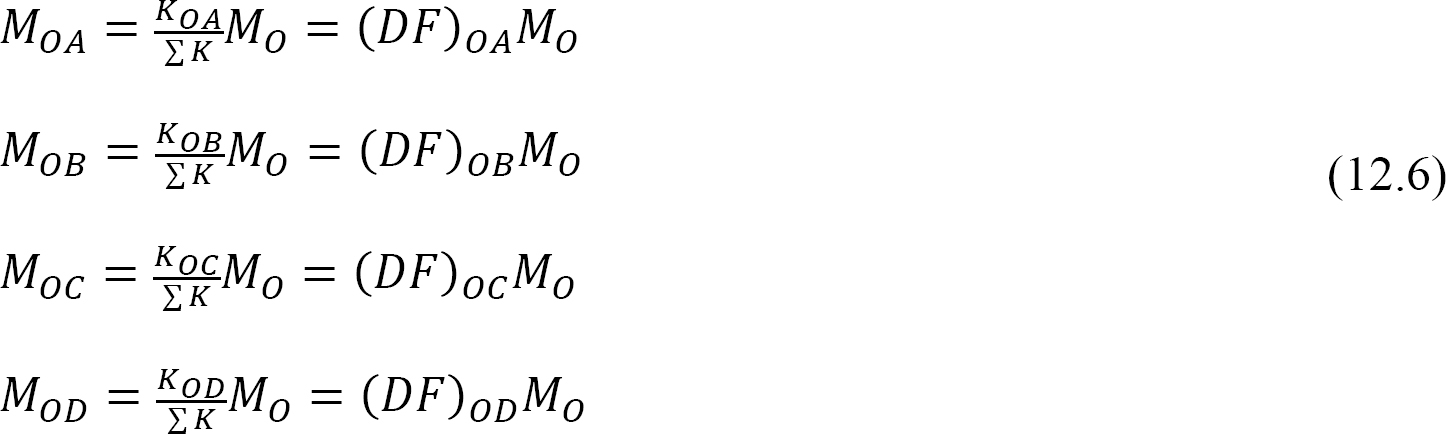
12.4 Modificação de Rigidez do elemento
às Vezes, o processo de iteração no momento método de distribuição pode ser significativamente reduzida ajustando-se a rigidez à flexão de alguns membros do indeterminado estrutura. Esta seção considera a influência de um suporte fixo – e um pino-end na rigidez flexural de um feixe indeterminado.Processo 1: Um feixe articulado numa extremidade e fixado na outra
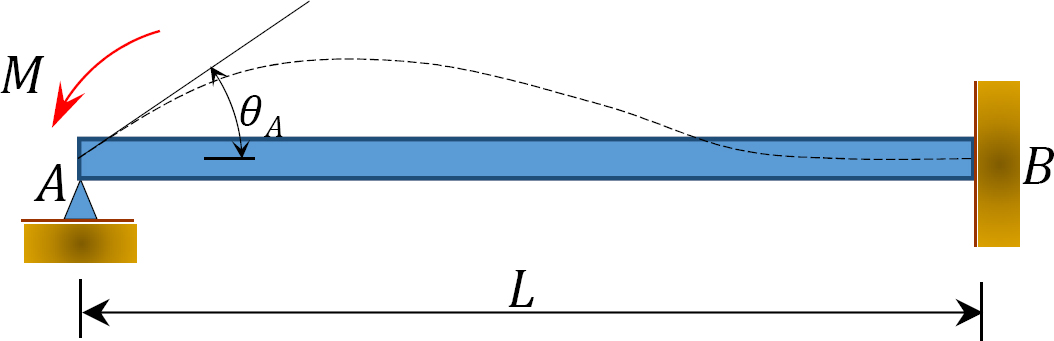
Fig. 12.4. Feixe
considerar um feixe articulado na extremidade a e fixado na extremidade B, conforme ilustrado na figura 12.4. A aplicação de um momento M roda a extremidade da dobradiça por um montante θ. Escrito encosta-deflexão da equação para o final de Um dos estados-e observando que a 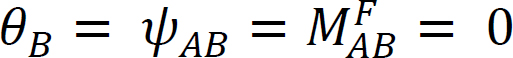 sugere o seguinte:
sugere o seguinte:
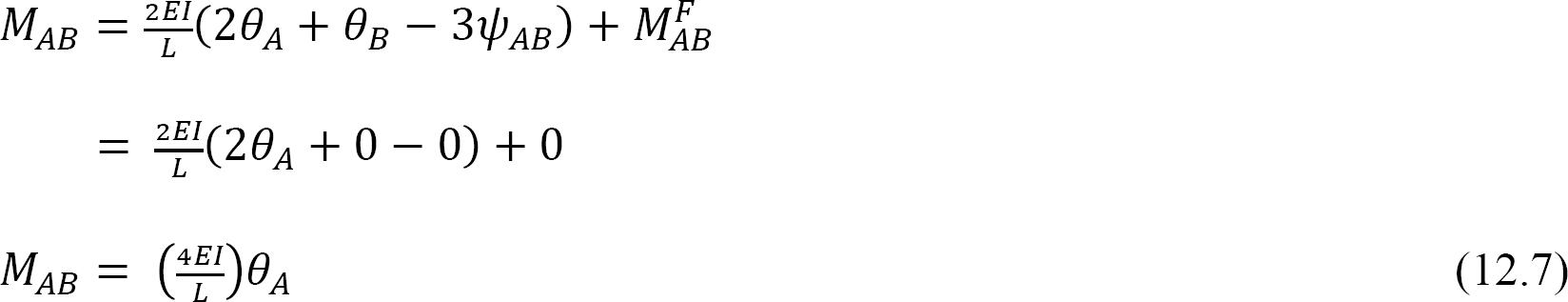
Por definição, a rigidez de flexão de um membro estrutural é o momento em que deve ser aplicado ao fim de cada membro, causa uma unidade de rotação do fim. A seguinte expressão para a rigidez de flexão para o membro com um fixo de extremidade é expressa da seguinte forma, ao substituir θA = 1 na equação 12.7:

Por definição, a relativa rigidez de flexão de um membro é determinado dividindo-se a rigidez de flexão do membro por 4E. Dividindo a equação de 12,8 por 4E sugere a seguinte expressão para a rigidez relativa para o caso a ser considerado:

Caso 2: Uma viga articulada em ambas as extremidades
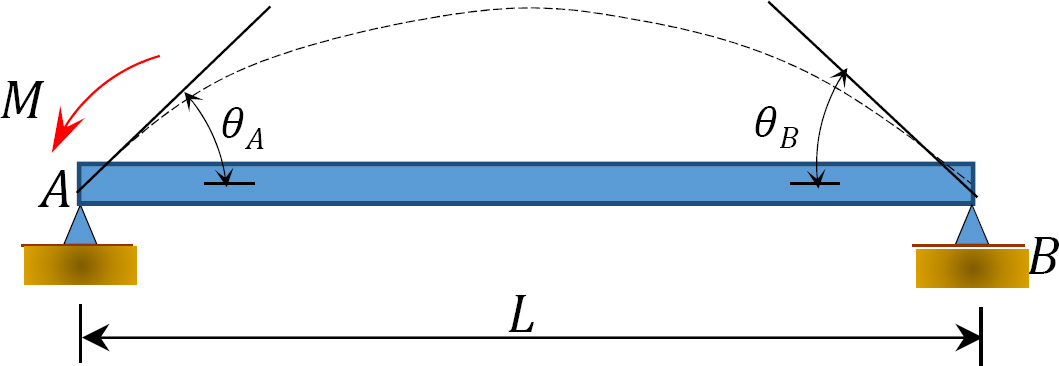
Fig. 12.5. Feixe simplesmente suportado.
aplicar um momento M na extremidade A do feixe simplesmente suportado indicado na figura 12.5 roda o feixe por um ângulo θA na extremidade articulada. Usando a modificação encosta-deflexão da equação derivada no ponto 11.4 do Capítulo 11 e observando que a 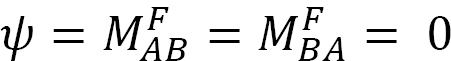 sugere a seguinte expressão para o momento na extremidade articulada, onde a carga é aplicada:
sugere a seguinte expressão para o momento na extremidade articulada, onde a carga é aplicada:
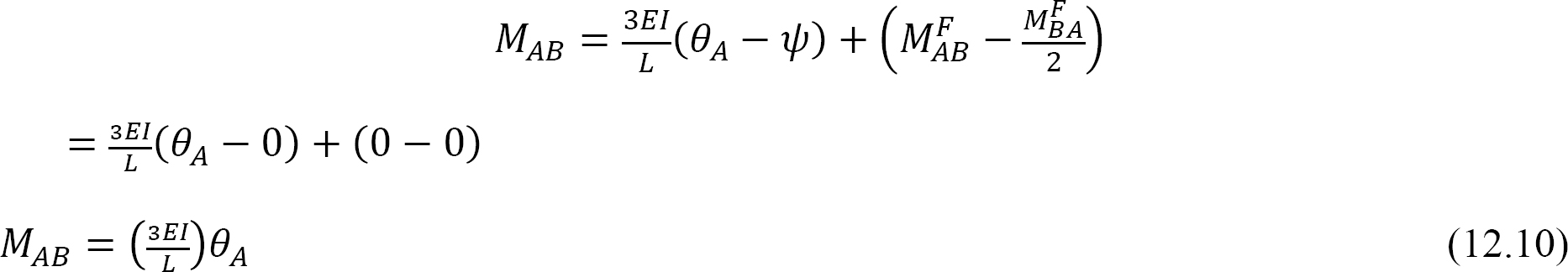
Substituindo θA = 1 na equação 12.10 sugere a seguinte expressão para a rigidez de flexão de um membro com uma extremidade articulada:

A rigidez relativa de um membro com uma dobradiça de extremidade é obtido dividindo-se a equação 12.11 por 4E, como segue:

Comparando as equações 12.12 e 12,9 sugere que um membro com uma dobradiça de extremidade é de três quarto tão duro como o membro com a mesma geometria, mas fixa bem no final. Este fato estabelecido pode reduzir substancialmente o número de iteração ao analisar feixes ou quadros com um extremo de hinged usando o método de distribuição de momento. Nesses casos, a rigidez relativa do feixe na extremidade próxima é primeiramente ajustada de acordo com a equação 12.12, e seu fator de distribuição é calculado com a rigidez ajustada. Durante a operação de equilíbrio, o fim próximo será equilibrado apenas uma vez, sem mais Transferência de momentos de ou para o seu fim.
12.5 Análise de vigas indeterminadas
o procedimento para a análise de vigas indeterminadas pelo método de distribuição do momento é resumido brevemente da seguinte forma ::Processo de Análise de vigas indeterminadas pelo método de distribuição do momento
•calcular os momentos de fim fixo para os membros, assumindo que as articulações são fixadas contra a rotação.
•calcular o factor de distribuição para cada um dos membros ligados na junta
•calcular o momento desequilibrado em cada junta e distribuir o mesmo aos fins dos membros ligados nessa junta.
•Transferir metade do momento distribuído para os outros fins dos membros.
•Adicionar ou subtrair estes últimos momentos (momentos obtidos nos passos três e quatro) para ou dos momentos finais fixos originais.
•aplicar os momentos finais determinados nas articulações da estrutura indicada.
•desenhar o diagrama do corpo livre de cada extensão do feixe, mostrando as cargas e momentos nas articulações obtidos pelo método de distribuição do momento.
•determinar as reacções de suporte para cada intervalo.
•calcular e construir os diagramas de força de cisalhamento e momento de flexão para cada período.
•desenhar um momento Flector e um diagrama de força de cisalhamento para o feixe em questão, combinando os diagramas no passo 9.Exemplo 12.1
utilizando o método de distribuição do momento, determinar os momentos finais e as reacções nos suportes do feixe indicadas na figura 12.6 A. desenhar a força de cisalhamento e os diagramas do momento Flector. EI = constante.
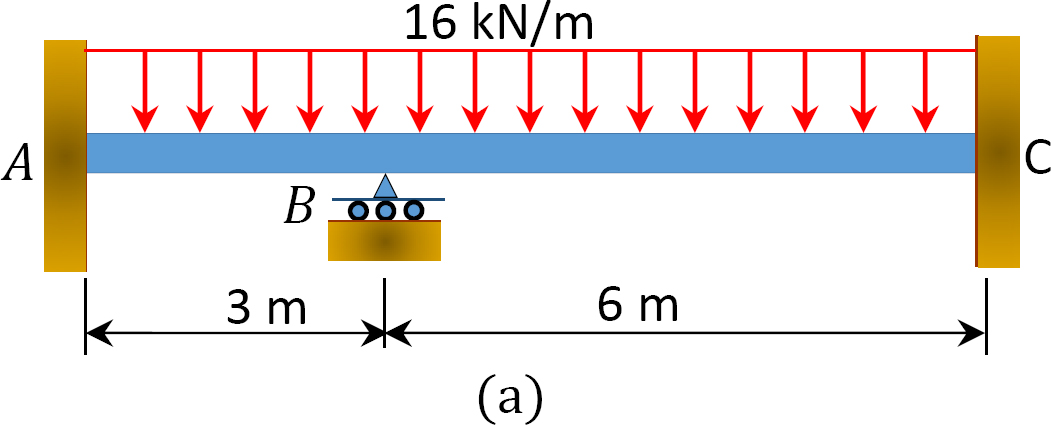
Fig. 12.6. Feixe.
solução
momento final fixo.
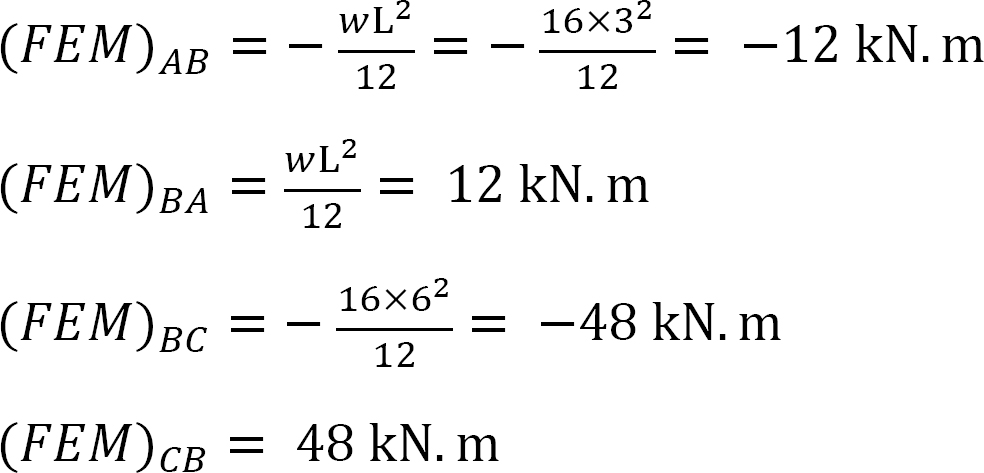
Factor de rigidez.
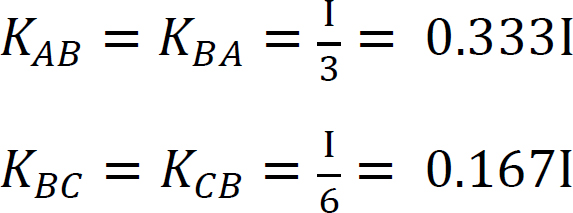
factor de distribuição.
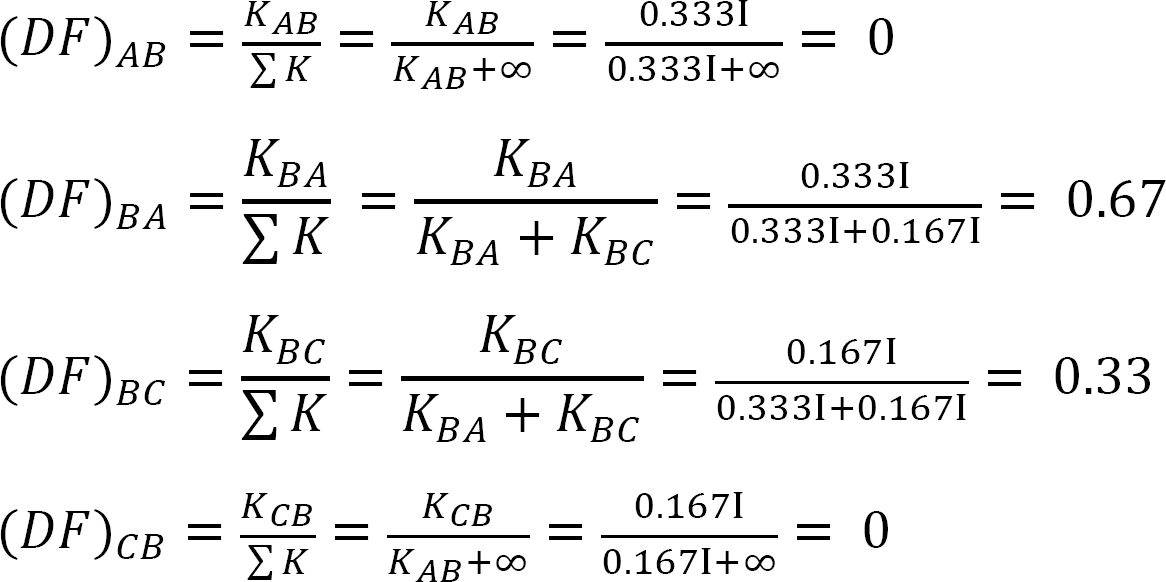
quadro 12.1. Tabela de distribuição.
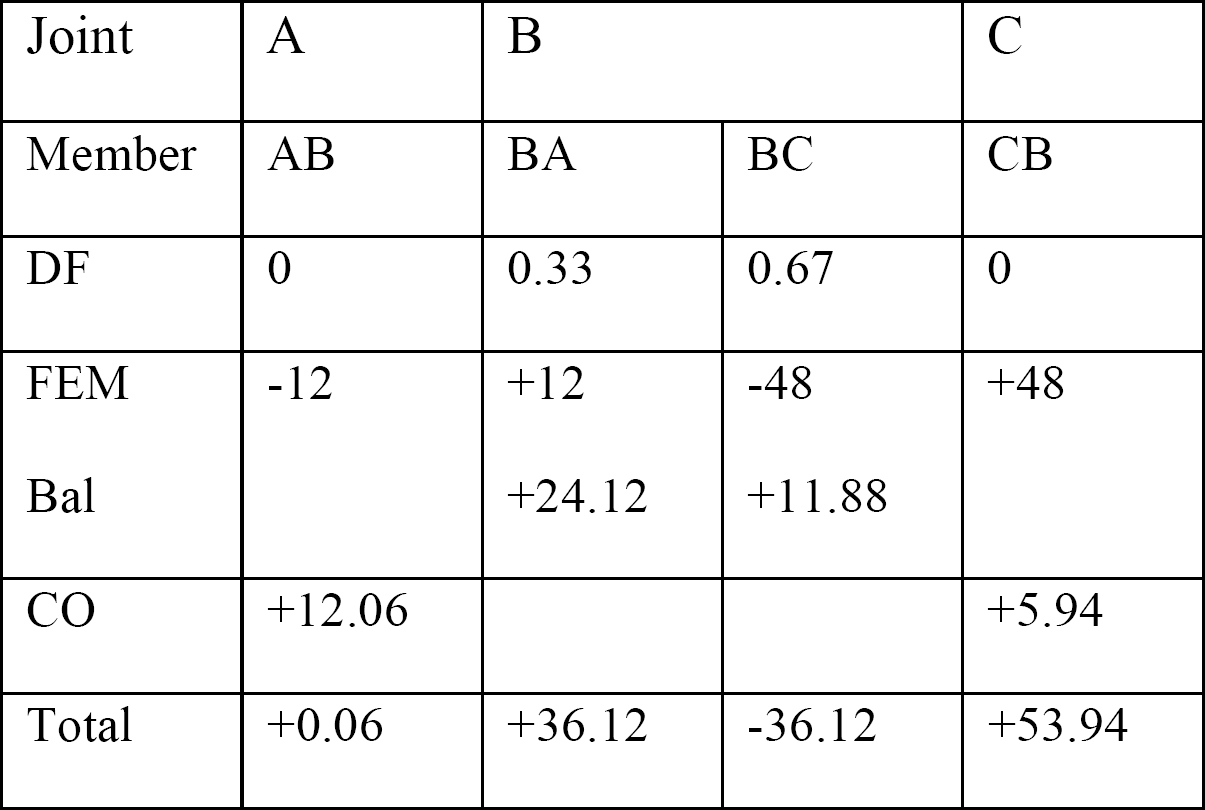
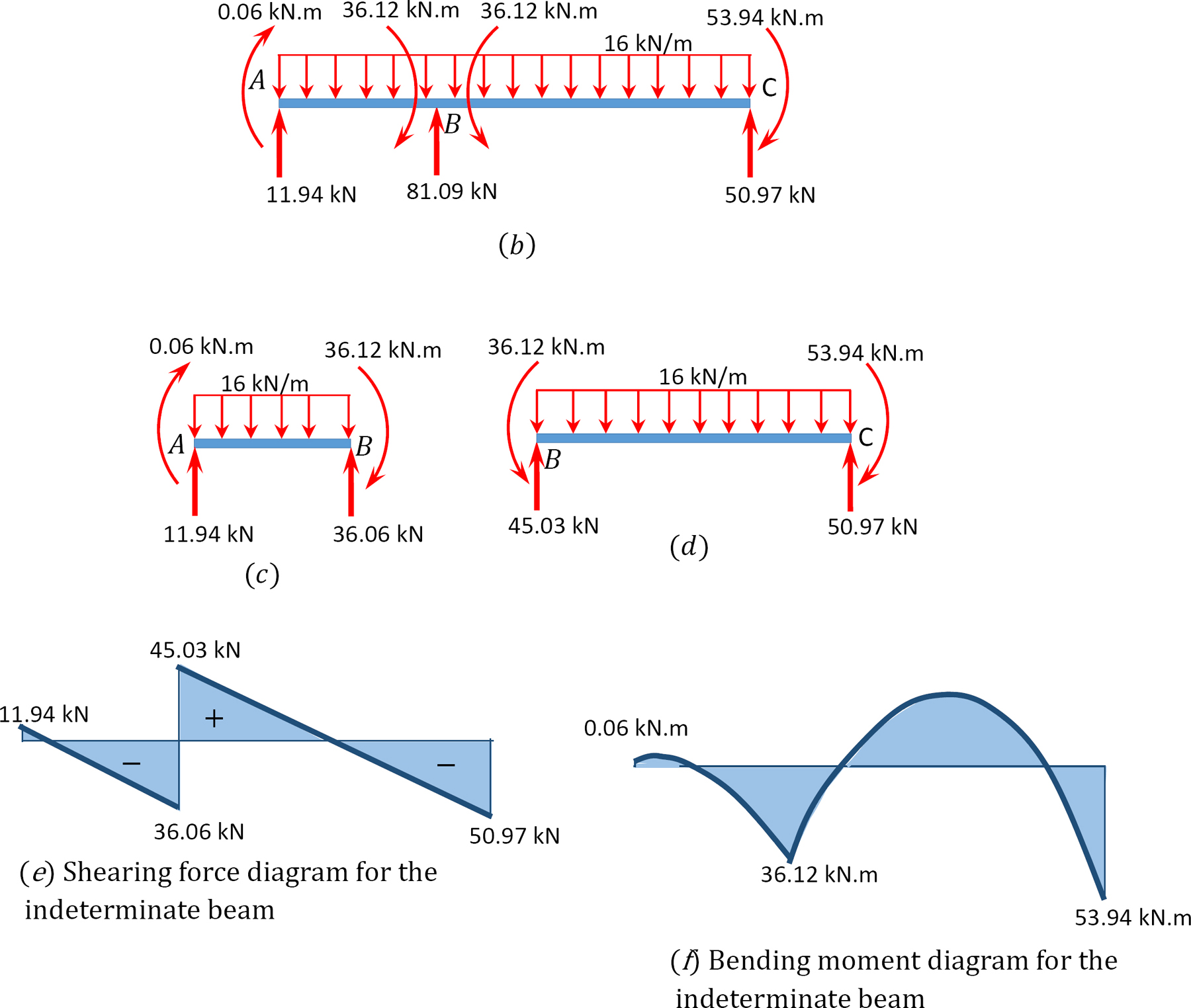
diagramas de força de corte e momento de flexão.
Exemplo 12.2
Usando o momento método de distribuição, para determinar o termo momentos e reações em apoios da viga mostrada na Figura 12.7. Desenhe a força de cisalhamento e momento fletor diagramas.
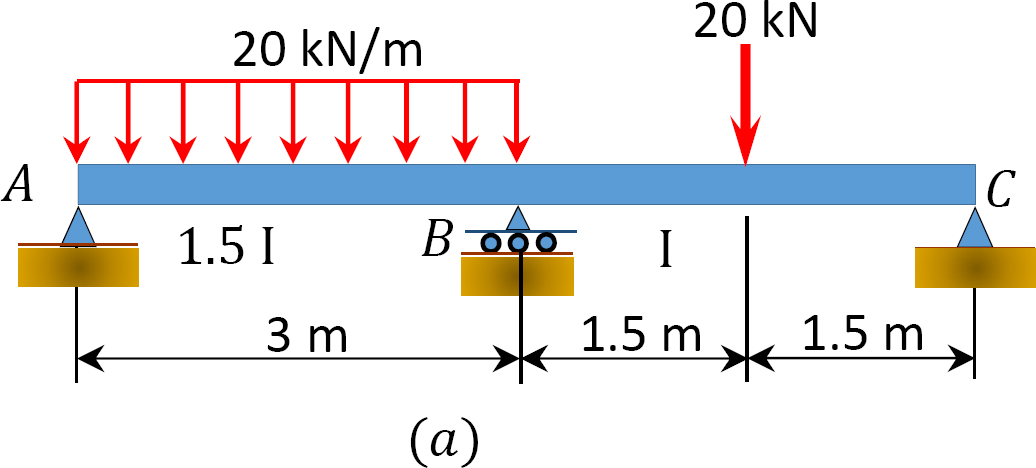
Fig. 12.7. Feixe.
solução
momento final fixo.
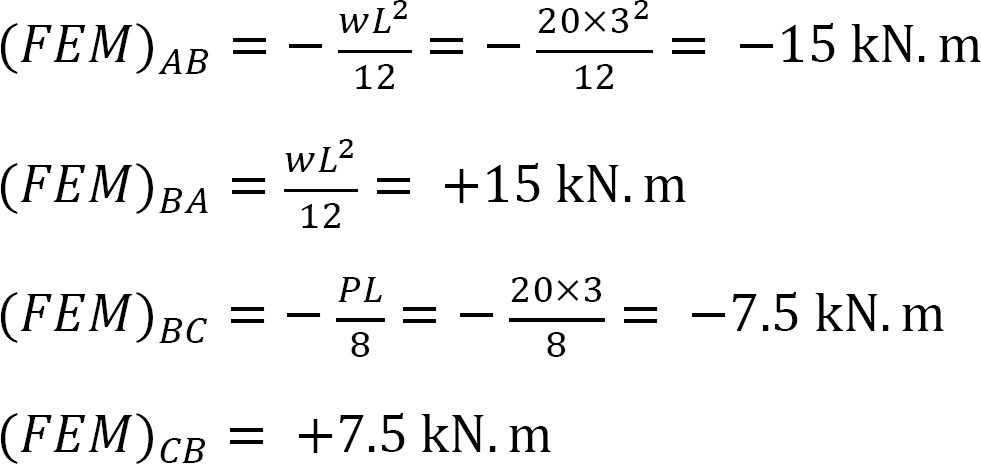
Factor de rigidez.
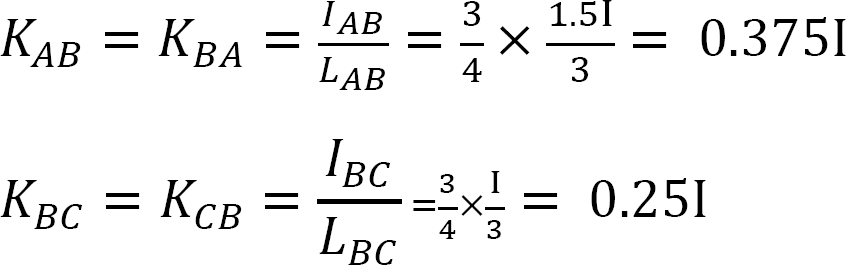
factor de distribuição.
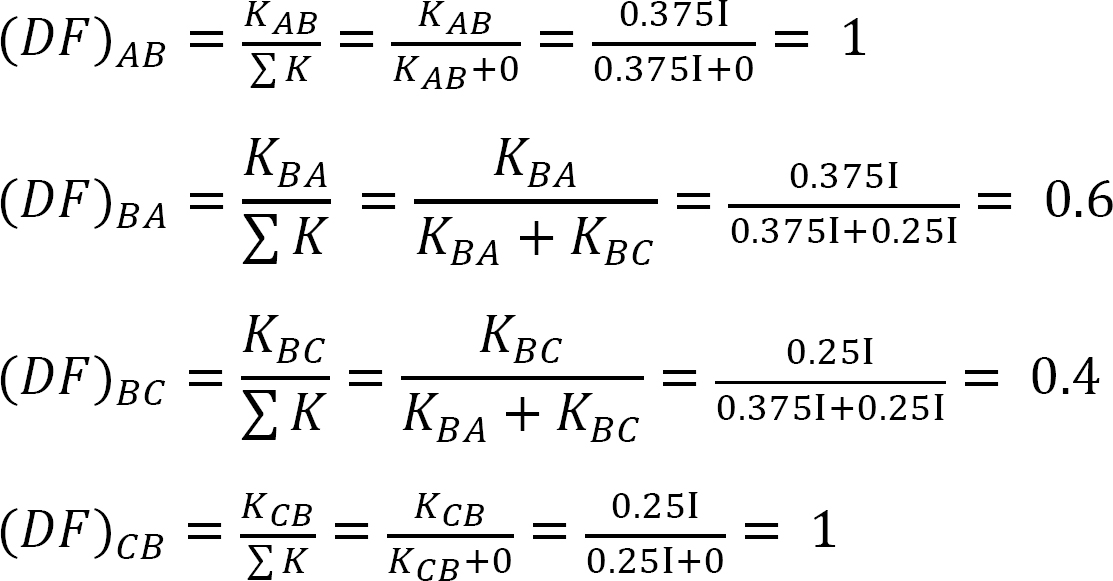
quadro 12.2. Tabela de distribuição.
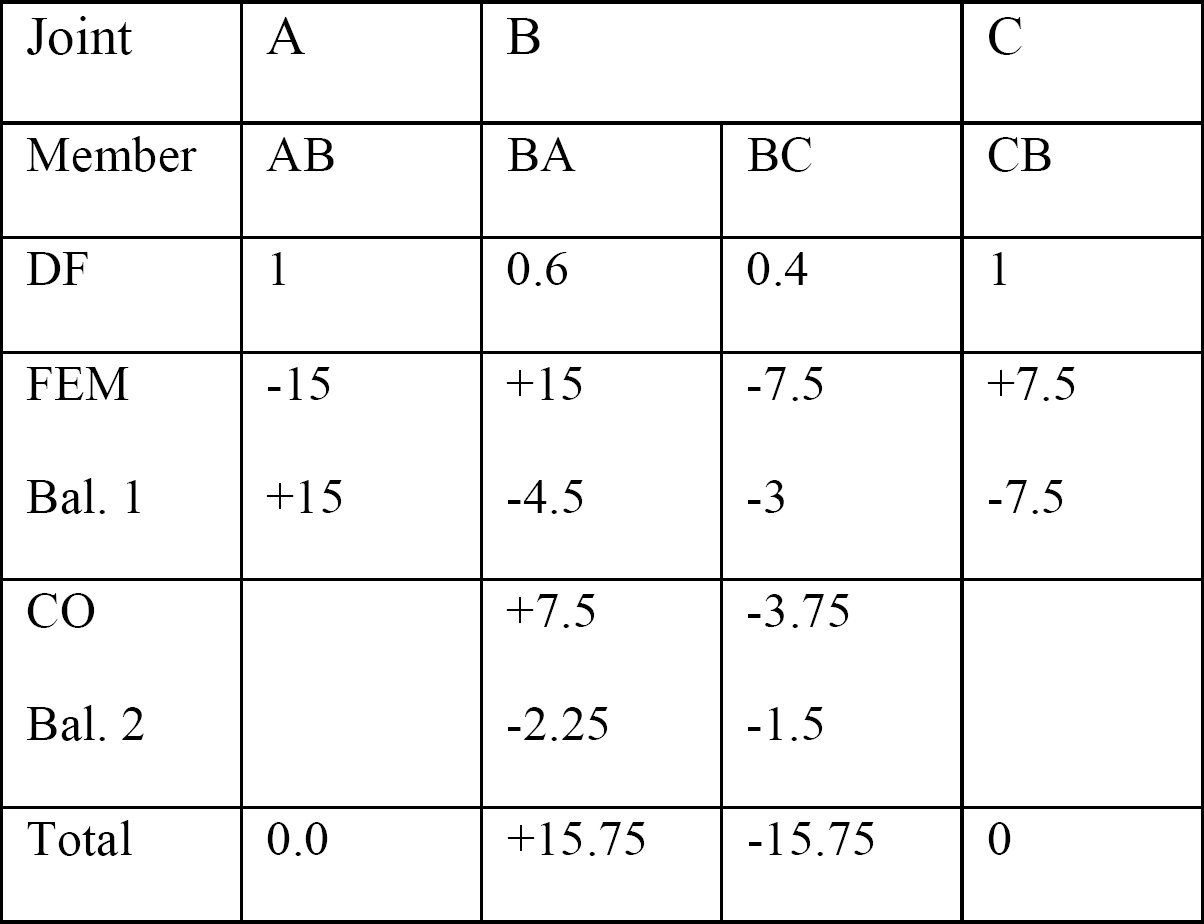
diagramas de força de corte e momento de flexão.
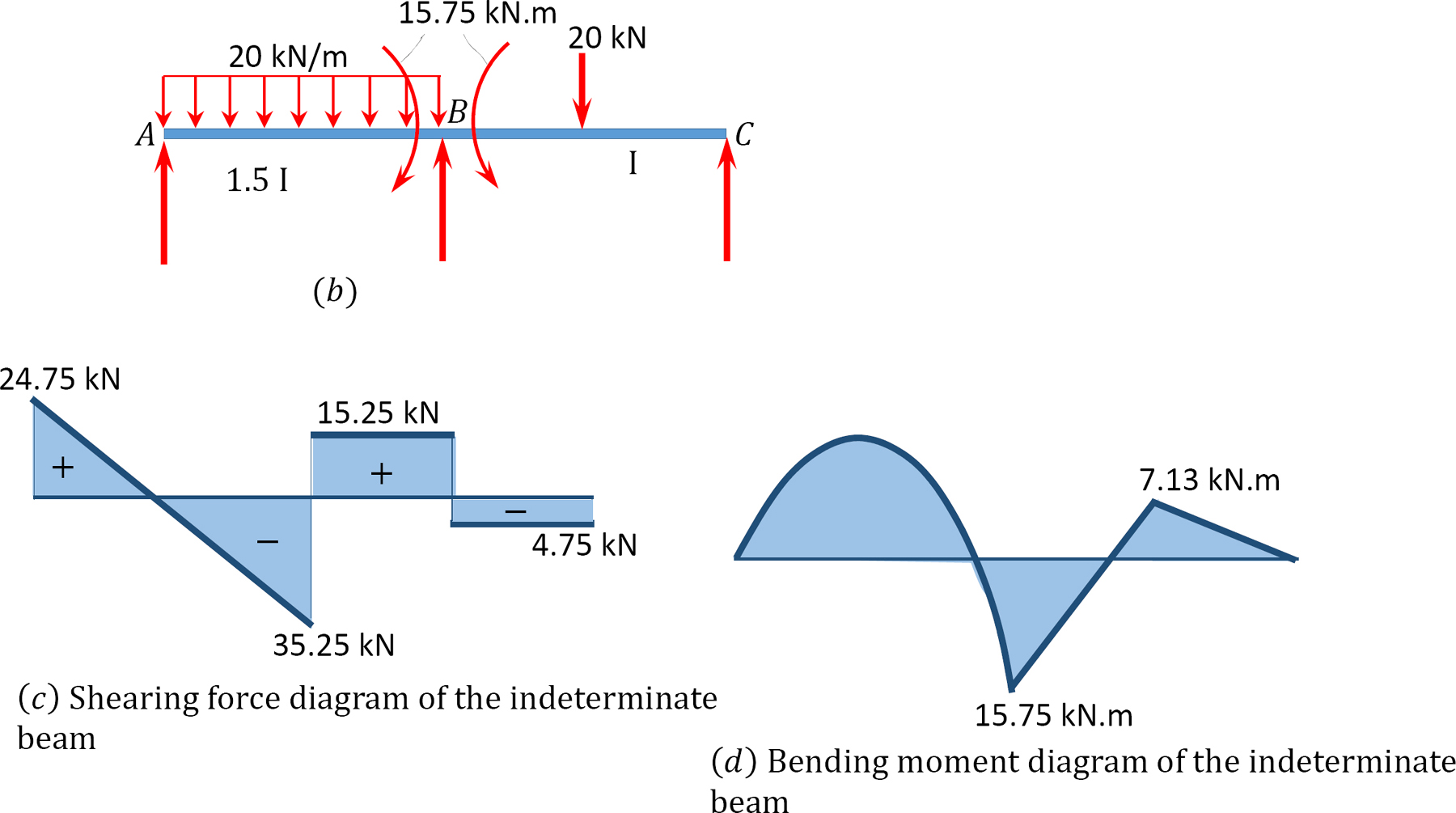
12.6 Análise de quadros indeterminados
o procedimento para a análise de quadros usando o método de distribuição de momento depende do tipo de quadro que está sendo analisado. As molduras são categorizadas como baloiços ou não baloiços. O procedimento para a análise de quadros de não-oscilação é semelhante ao das vigas indeterminadas. Mas para a análise de quadros de balanço, o procedimento é diferente. Há duas fases envolvidas na análise de quadros de oscilação, nomeadamente a fase de não oscilação e a fase de oscilação. Estas etapas são descritas abaixo.
Procedure for Analysis of Indeterminate Sway-Frames by the Moment Distribution Method
A. Non-sway stage analysis
•Calcule as reacções horizontais nos suportes do quadro e observe a diferença X. Esta é a força para evitar oscilações.
B. Análise do estágio de oscilação
•os valores são assumidos para M2 E M1 é determinado.
•os momentos arbitrários são então distribuídos como para a condição de não-oscilação
•Calcule a magnitude das reacções horizontais nos suportes para a condição de oscilação. The summation of these reactions gives the arbitrary displacing force Y.
* Determine the ratio 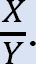 This ratio is called the sway factor.
This ratio is called the sway factor.
•utilize o factor de sway para multiplicar os momentos distribuídos da sway. Isto dá o momento corrigido para o balanço.
utilizando o método de distribuição do momento, determinar os momentos finais dos membros da moldura mostrada na figura 12.8. EI = constante.
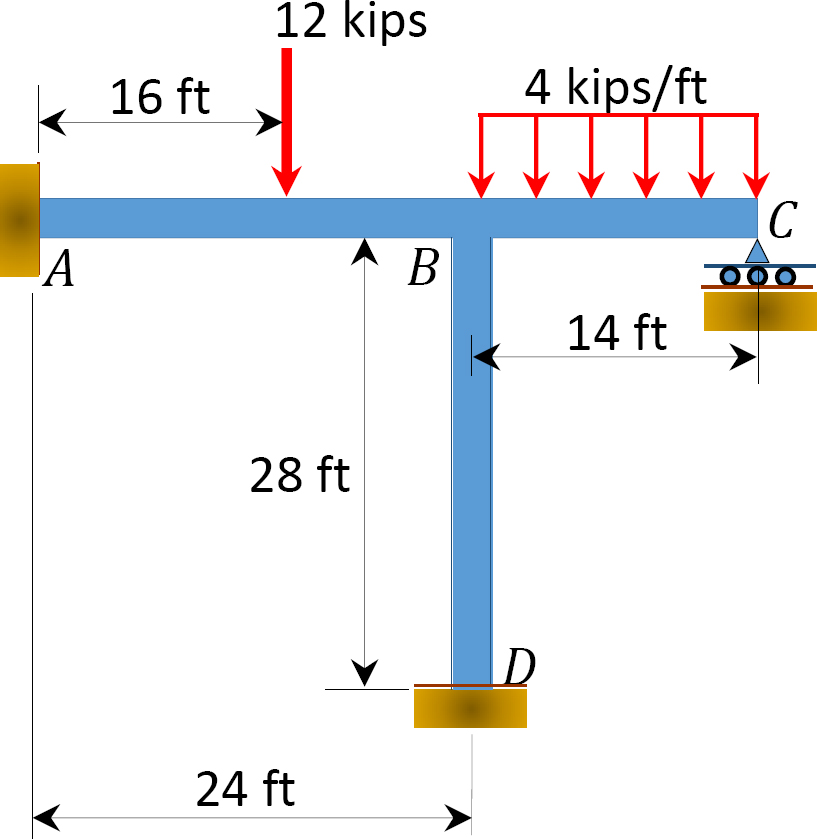
Fig. 12.8. Quadro.
solução
momento final fixo.
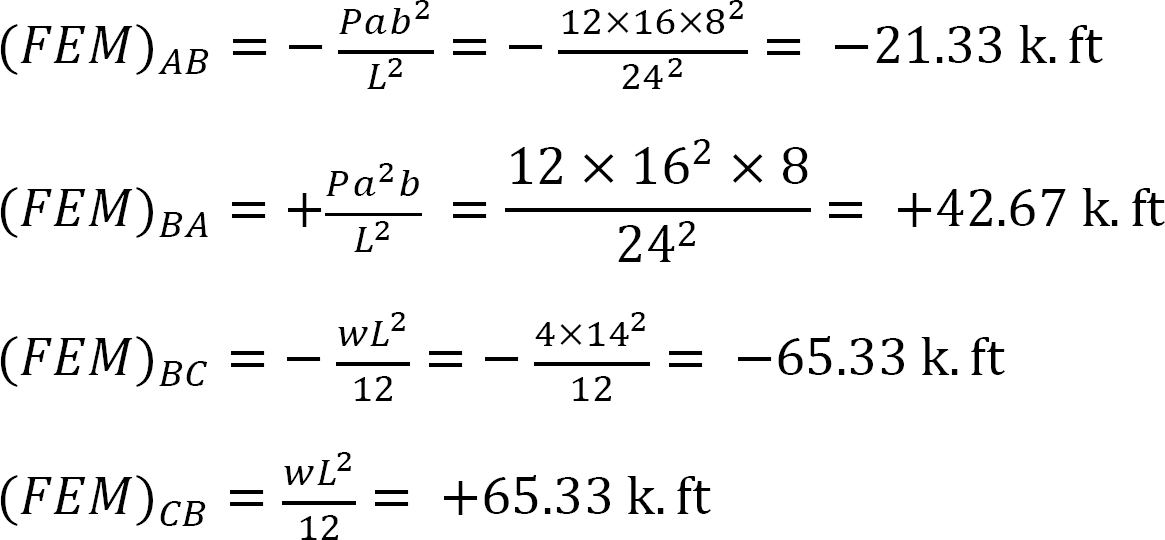
Factor de rigidez.
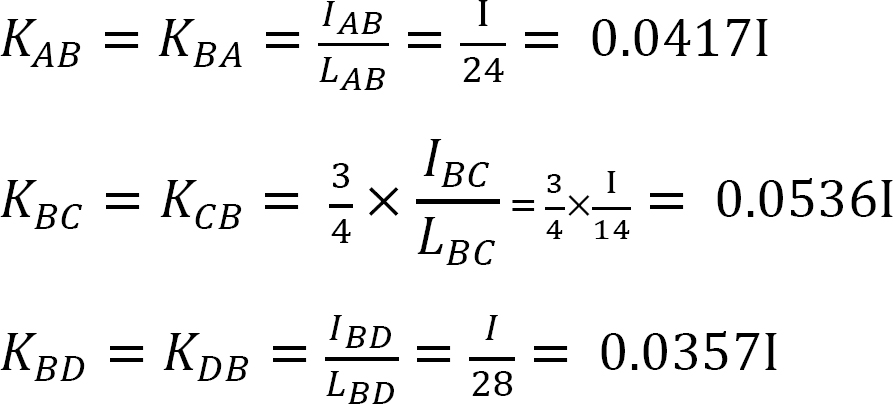
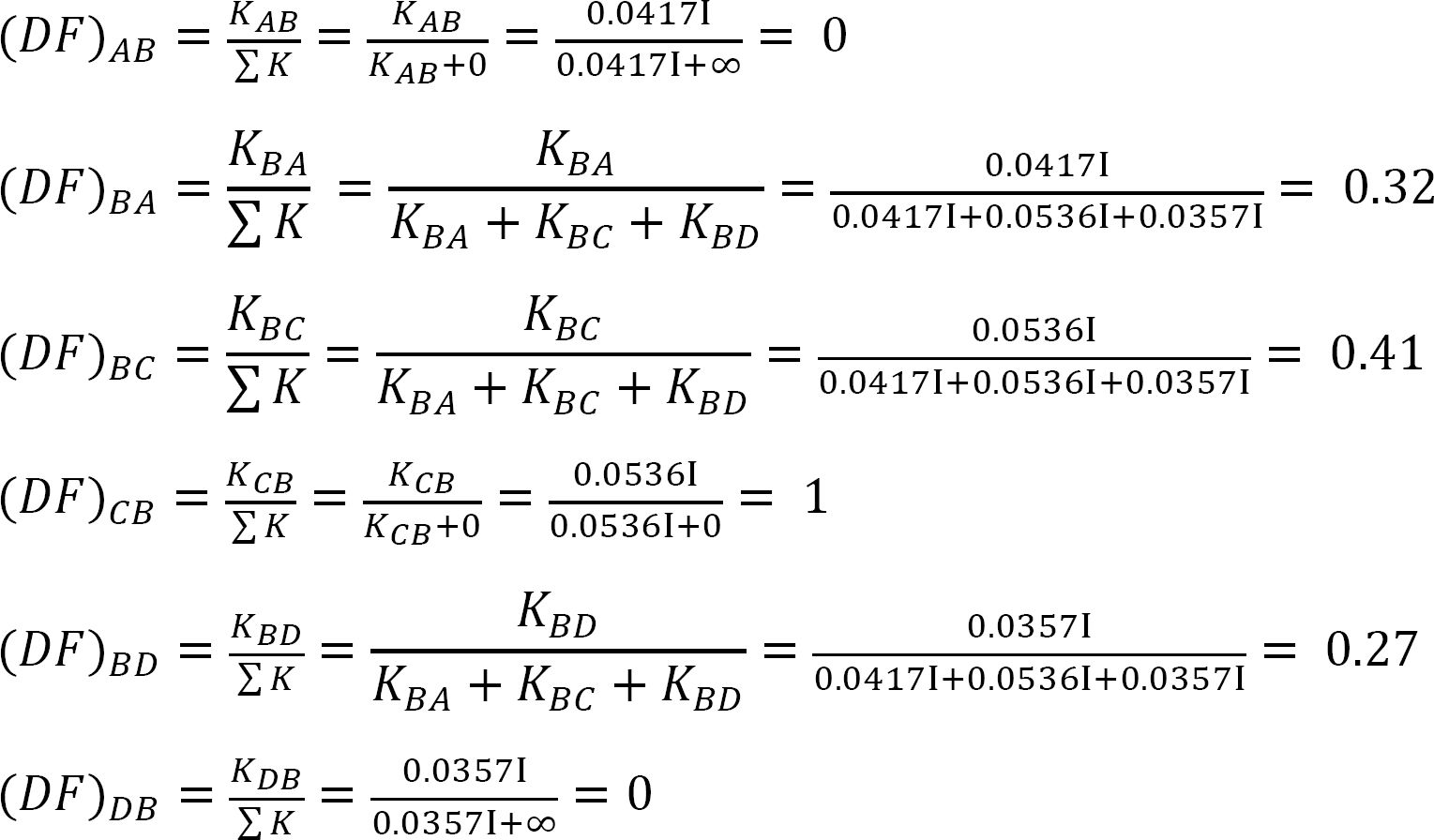
factor de distribuição.
quadro 12.3. Tabela de distribuição.
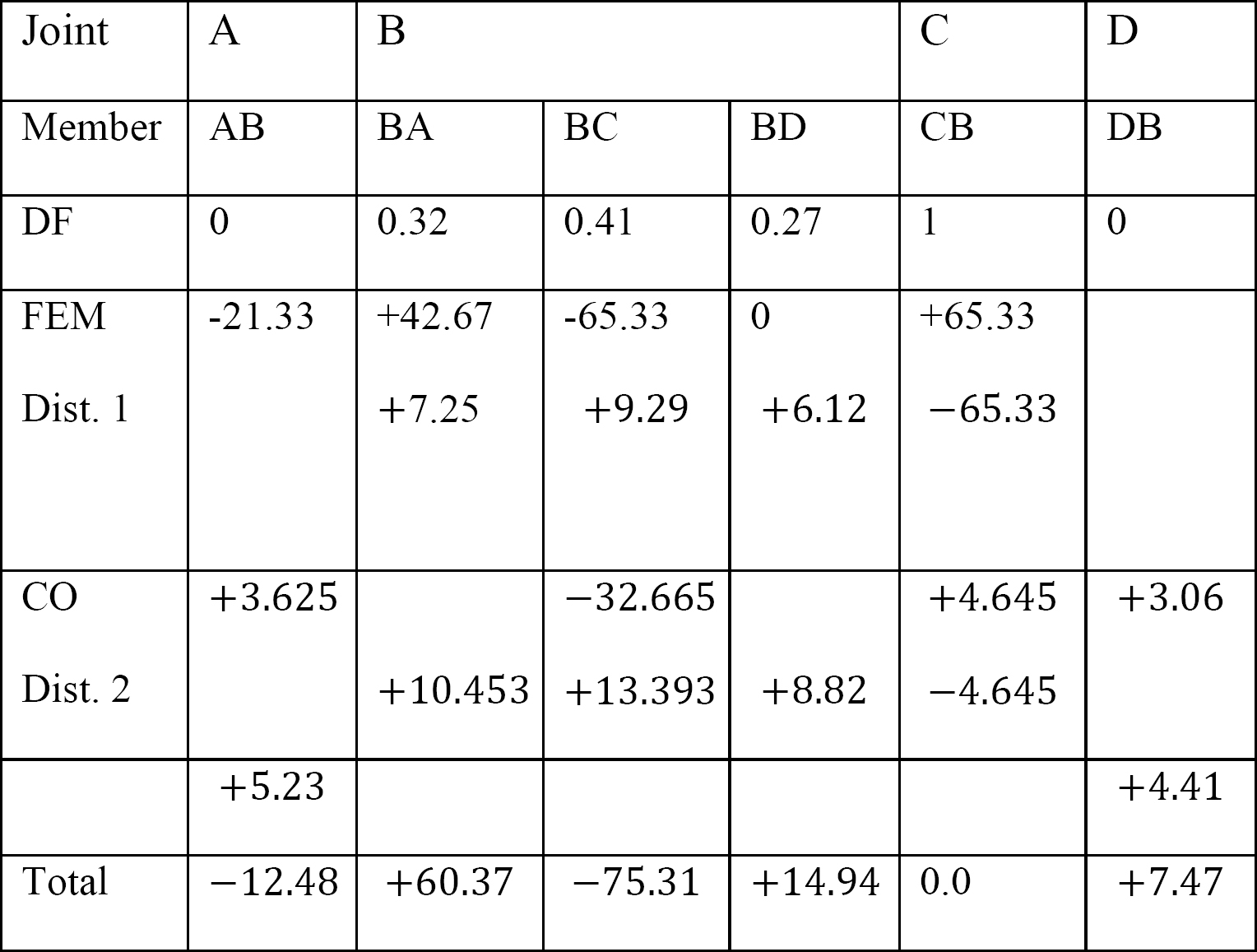
últimos momentos do membro final.
Substituindo os valores obtidos de EKθB, EKθC, e EK∆ para o membro momento final equações sugere o seguinte:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Exemplo 12.4
usando o método de distribuição de momento, determinar os momentos finais nos suportes da moldura mostrada na figura 12.9. EI = constante.
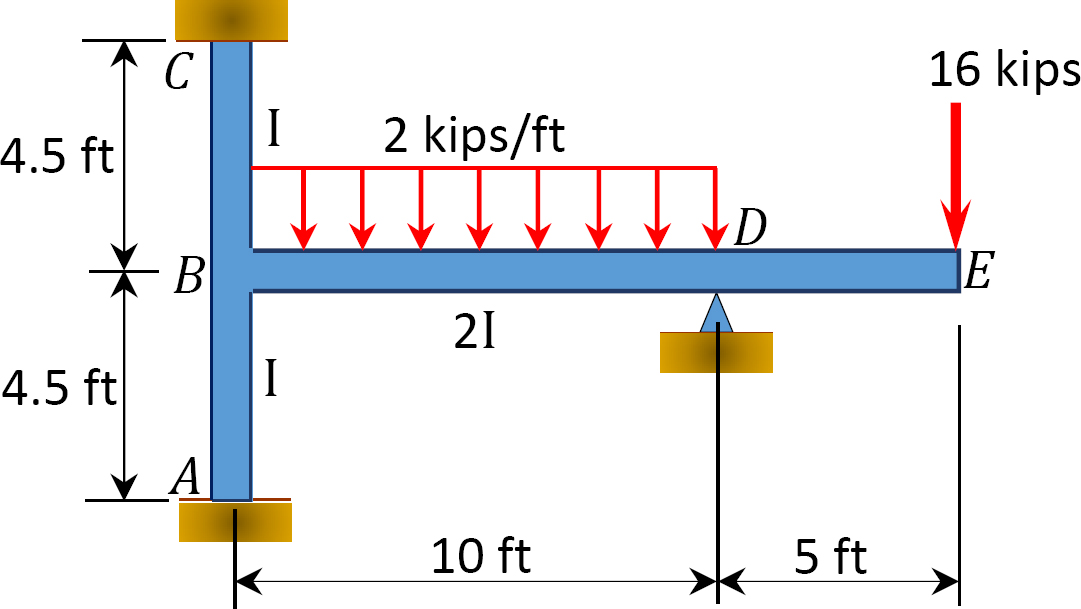
Fig. 12.9. Quadro.
solução
momento final fixo.
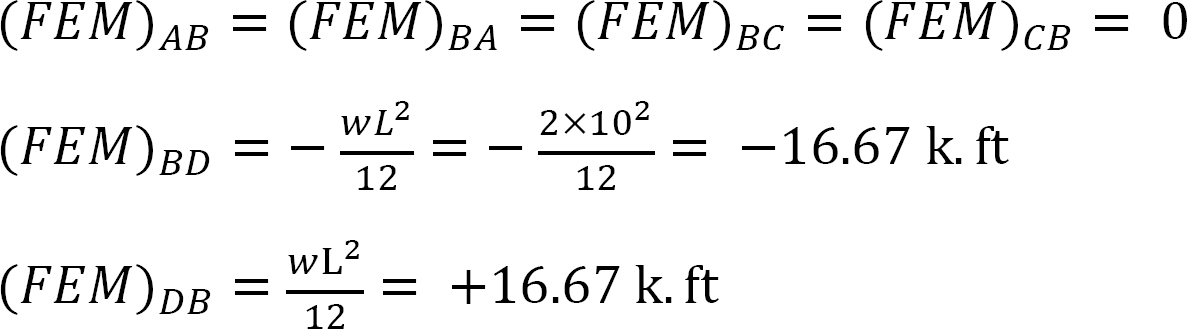
Factor de rigidez.
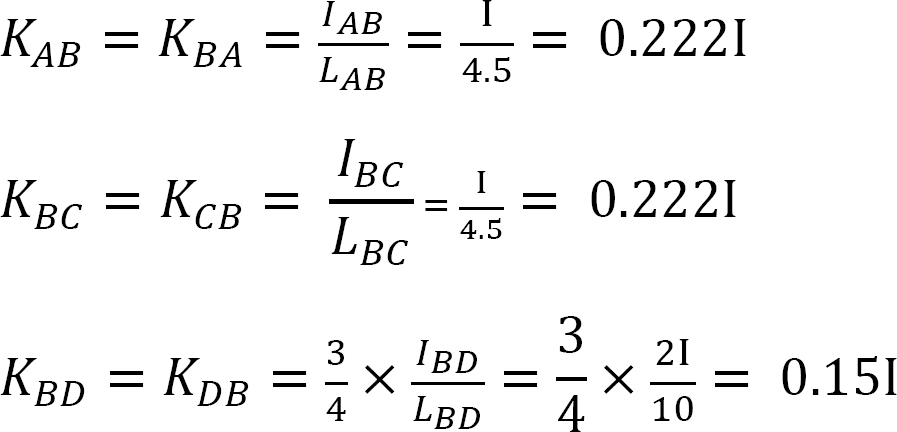
factor de distribuição.

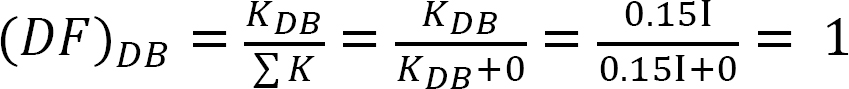
quadro 12.4. Tabela de distribuição.
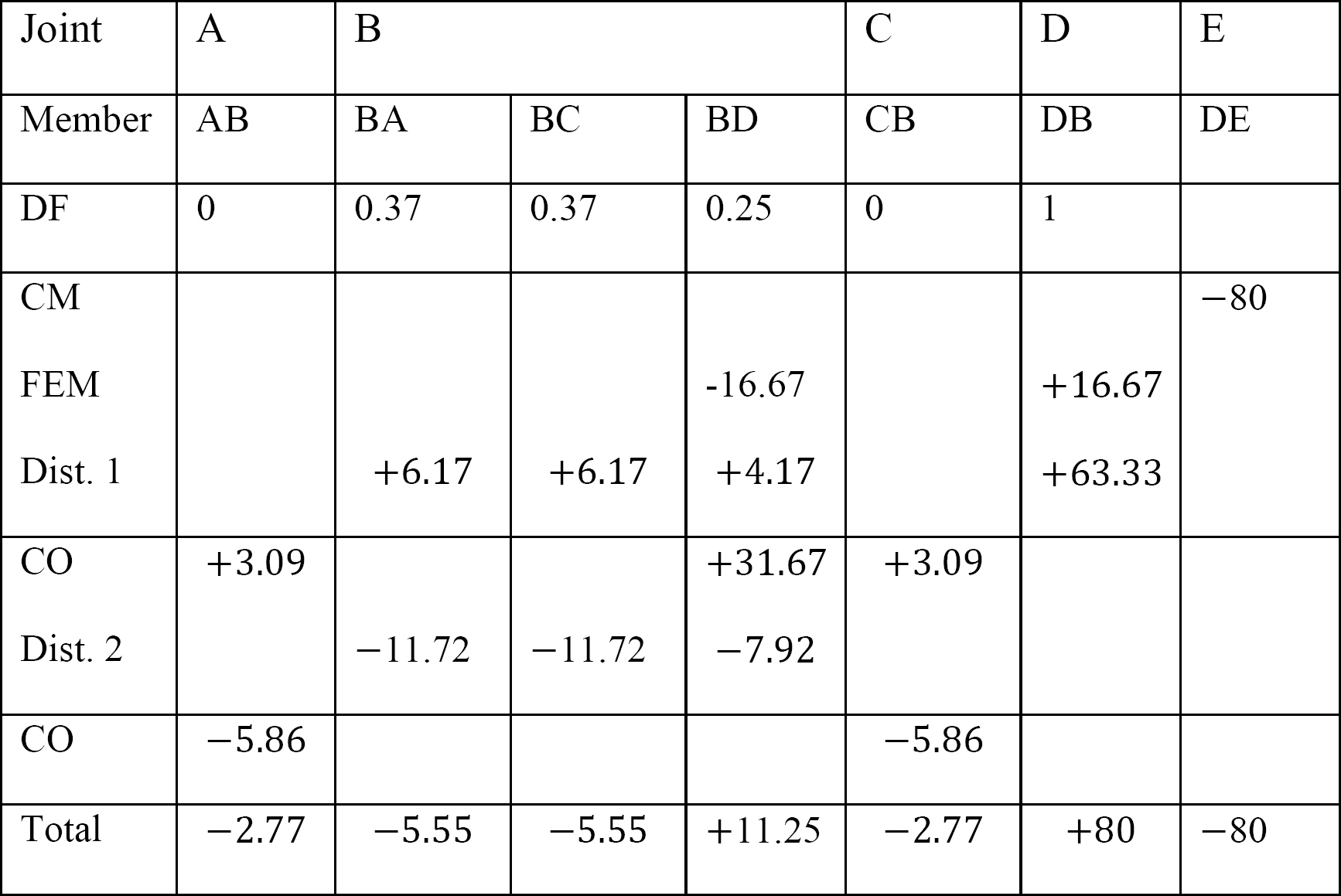
últimos momentos do membro final.
MAB = -2.77 k. ft
MBA = -5.55 k. ft
MBC = -5.55 k. ft
MBD = +11.25 k. ft
MCB = -2.77
MDB = +80 k. ft
MDE = -80 k. ft
Exemplo 12.5
Usando o momento método de distribuição, para determinar o termo momentos no suporte do quadro mostrado na Figura 12.10. EI = constante.
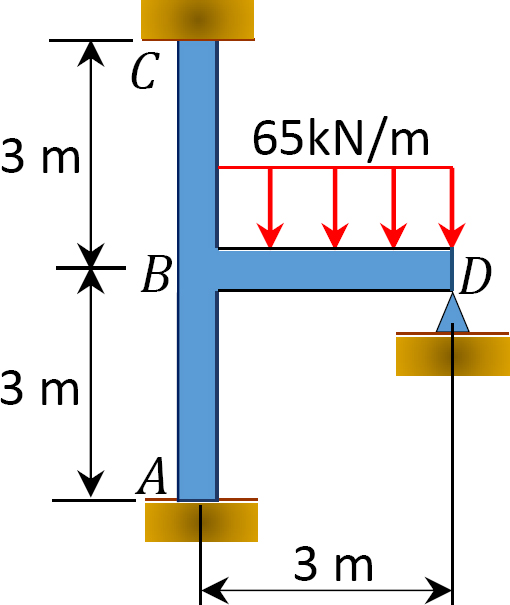
Fig. 12.10. Quadro.
solução
momento final fixo.
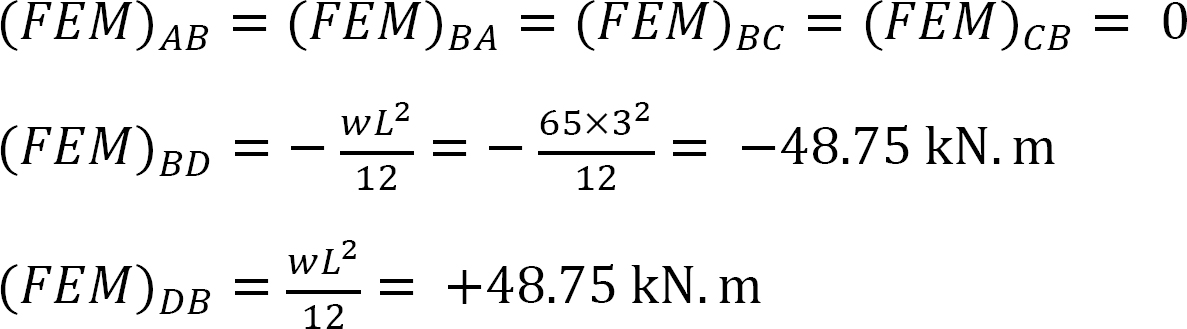
Factor de rigidez.
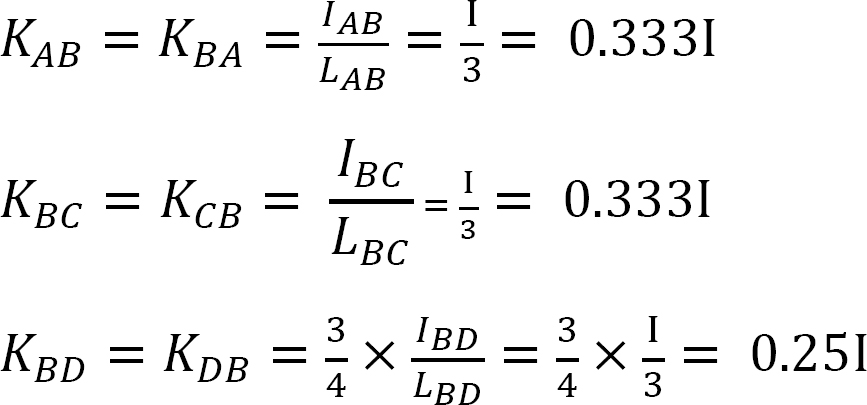
factor de distribuição.
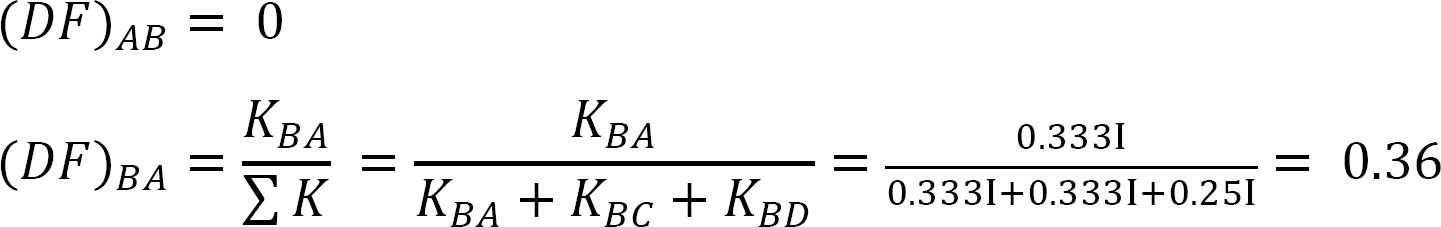

mesa 12.5. Tabela de distribuição.
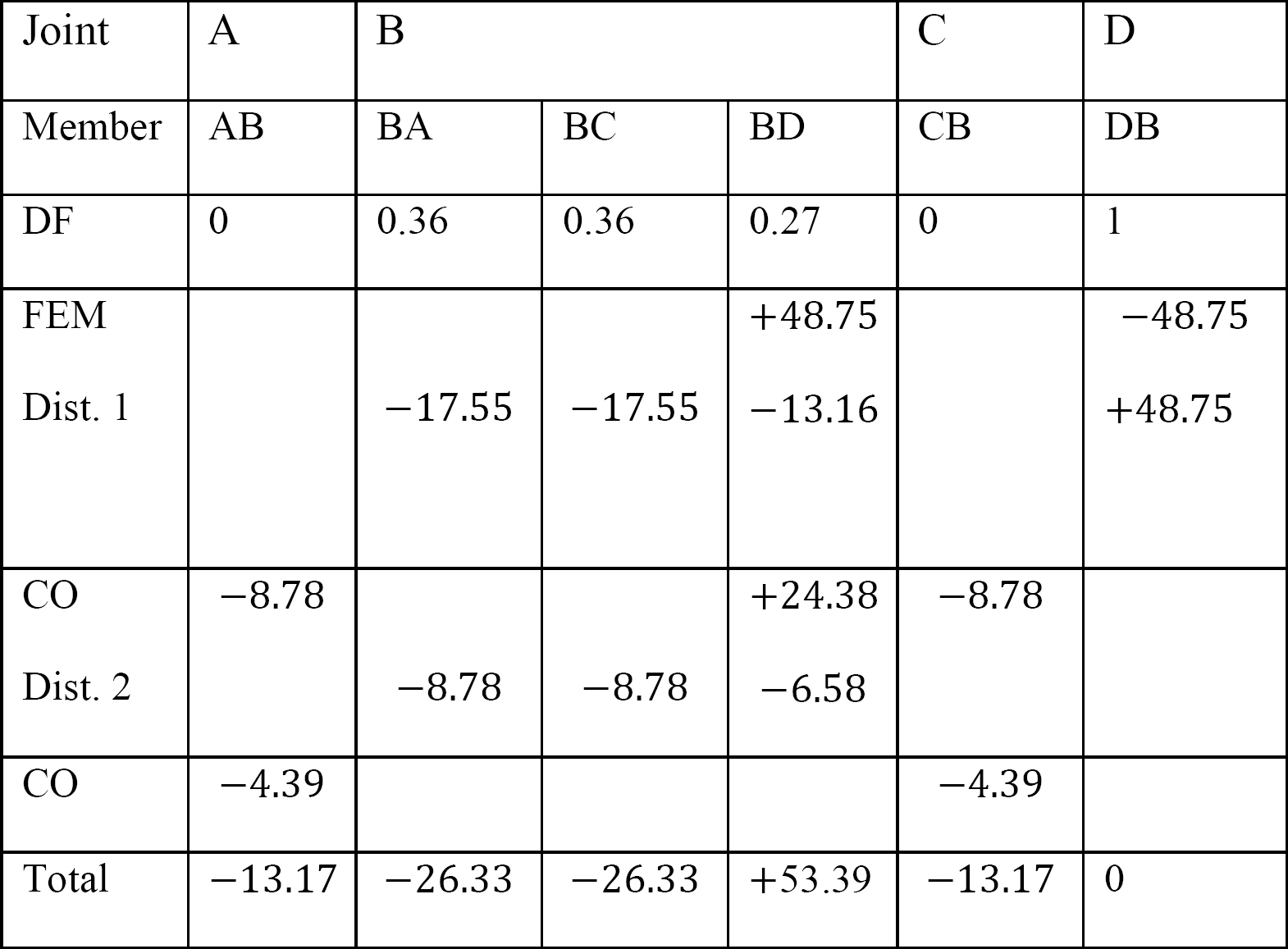
últimos momentos do membro final.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +53.39 k. ft
MCB = -13.17 k. ft
MDB = 0
Exemplo 12.6
Usando o momento método de distribuição, determinar o membro final-momentos do quadro com a face de oscilação mostrado na Figura 12.11 um.
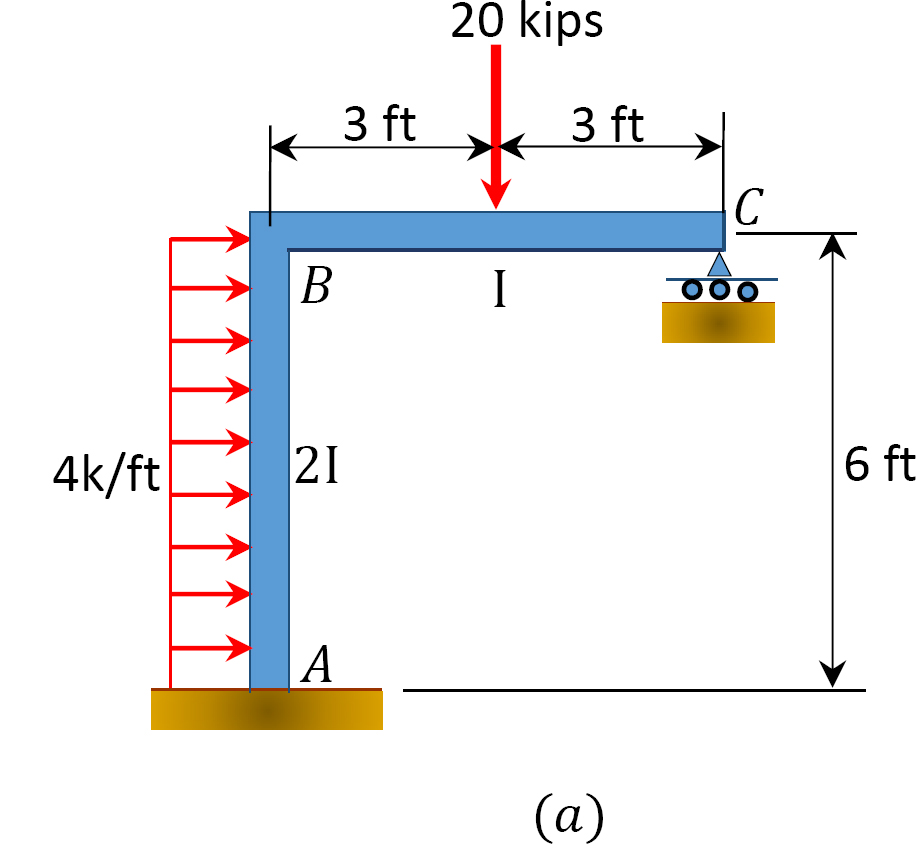
Fig. 12.11. Moldura com baloiço lateral.
solução
momento final fixo.
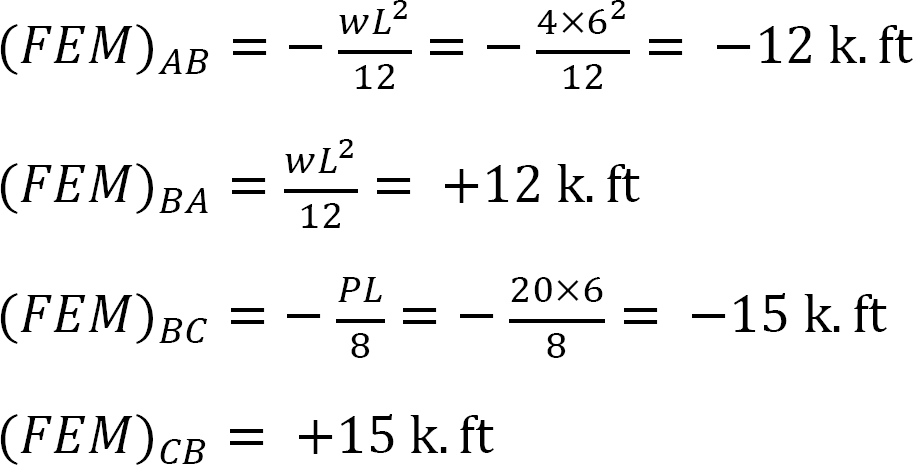
Factor de rigidez.
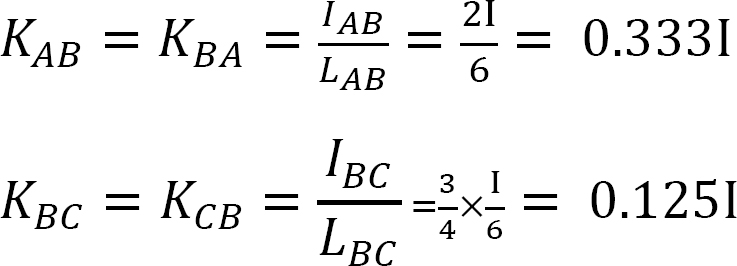
factor de distribuição.
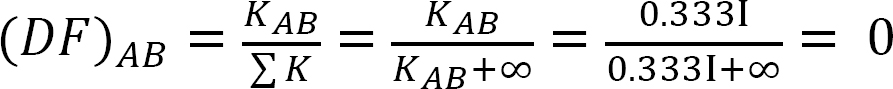

análise da moldura sem oscilação lateral.
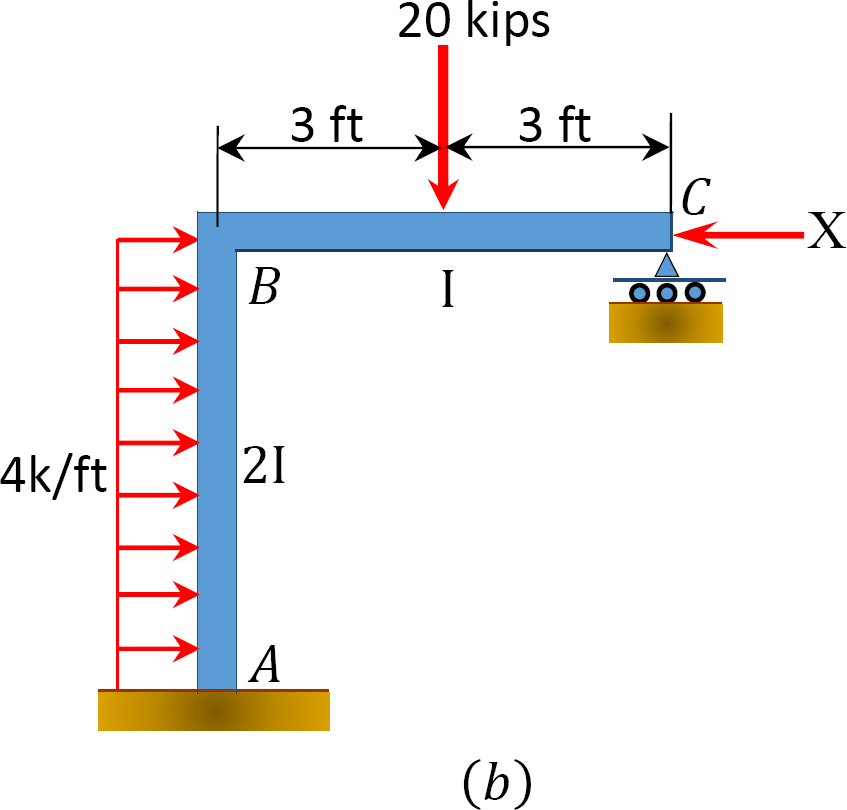
quadro 12.6. Tabela de distribuição (sem oscilação).
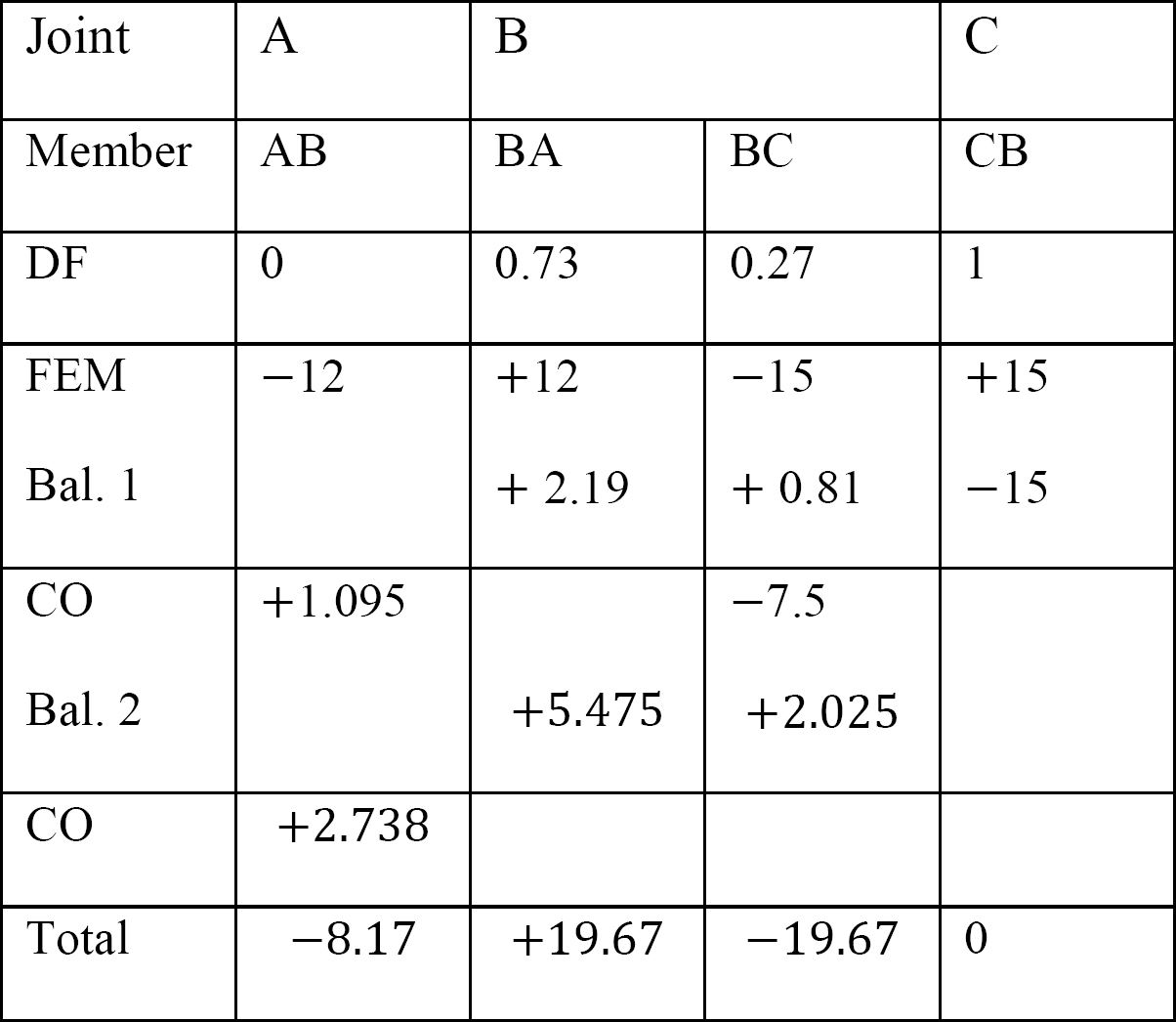
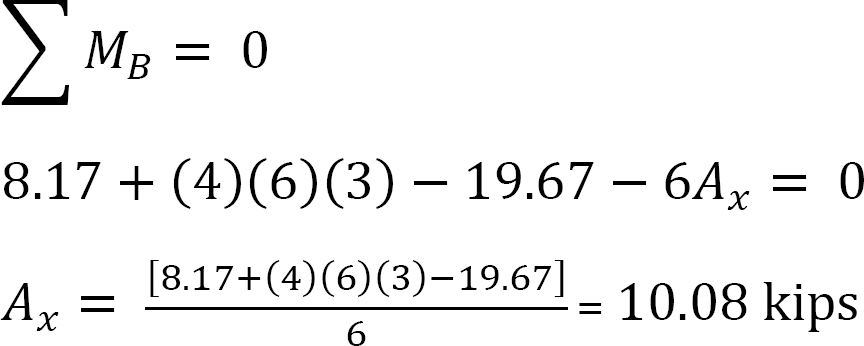
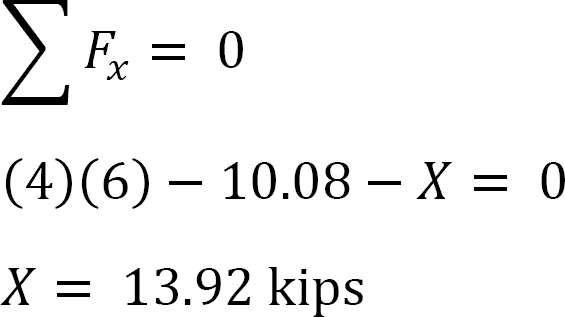
análise da moldura com baloiço lateral.
assumir que MAB = + 20 K. ft
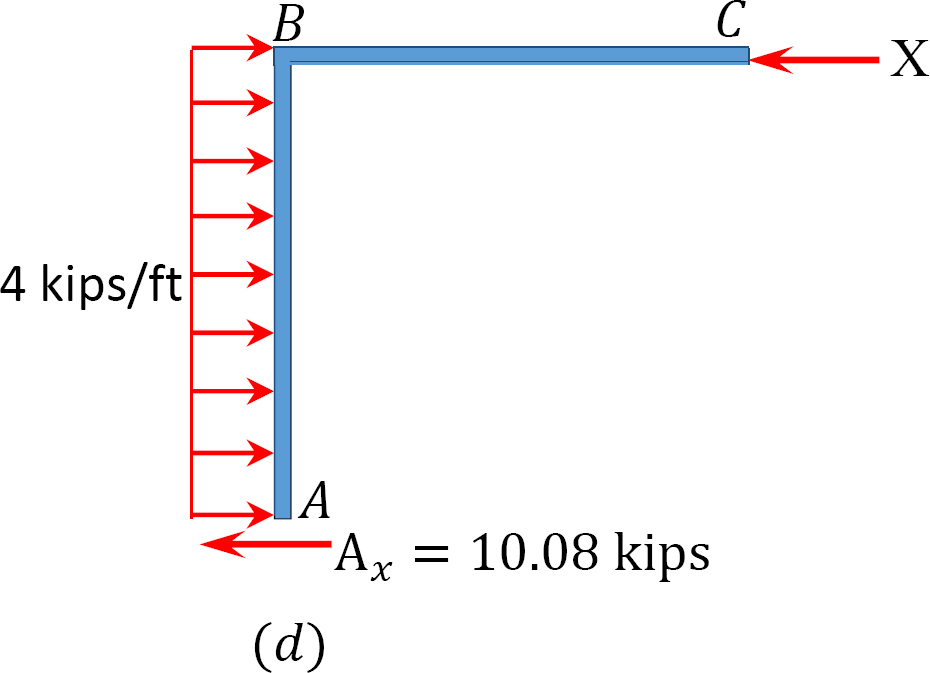
quadro 12.7. Tabela de distribuição (sway frame).
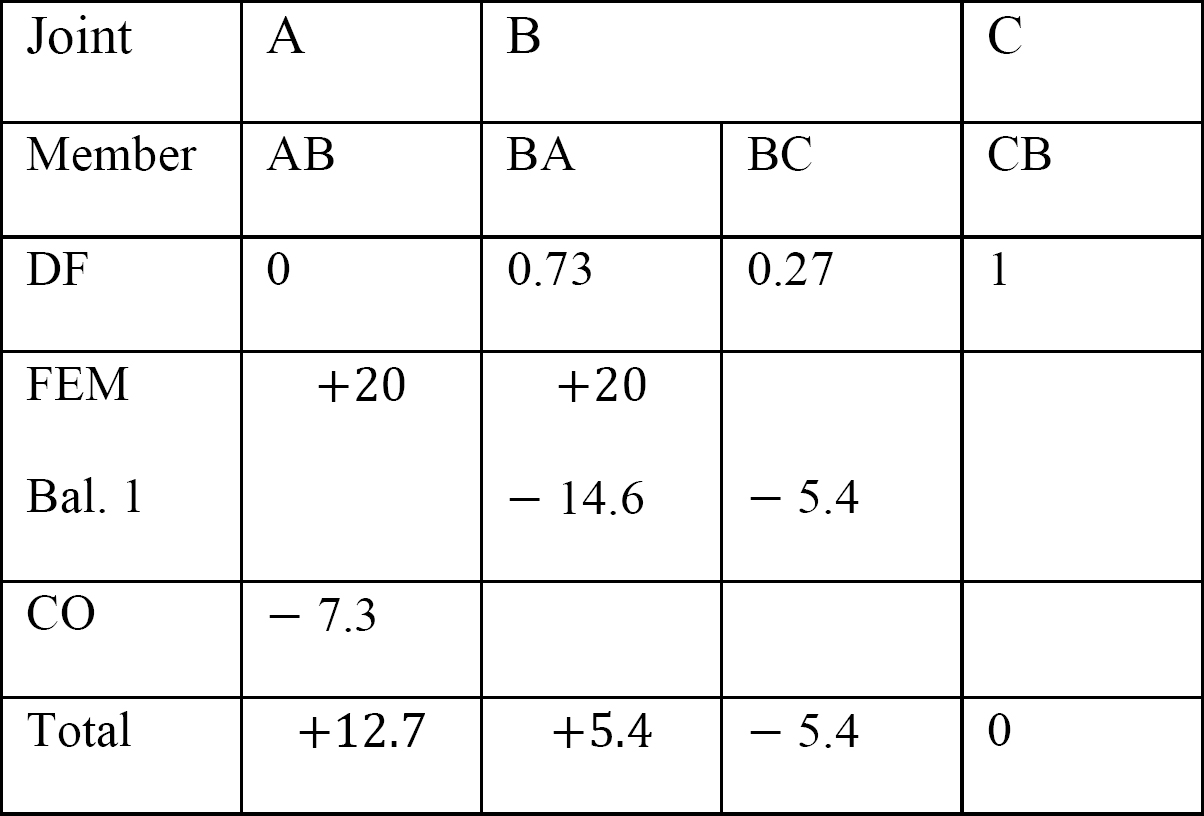
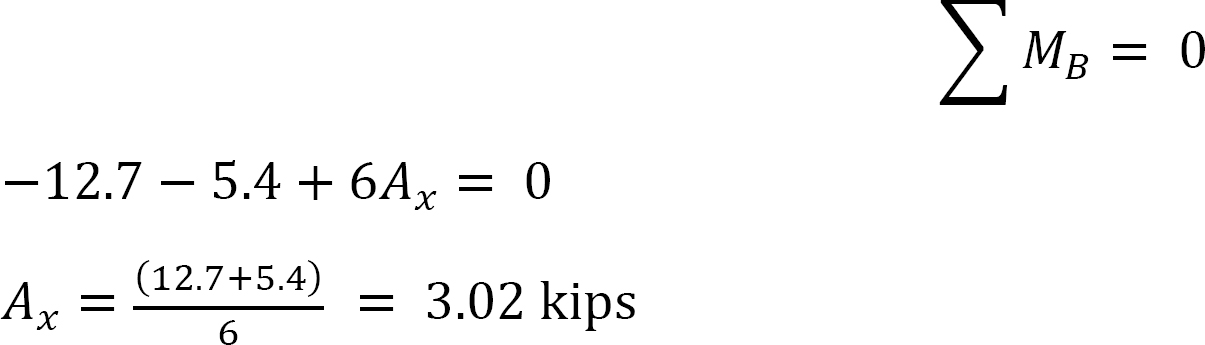
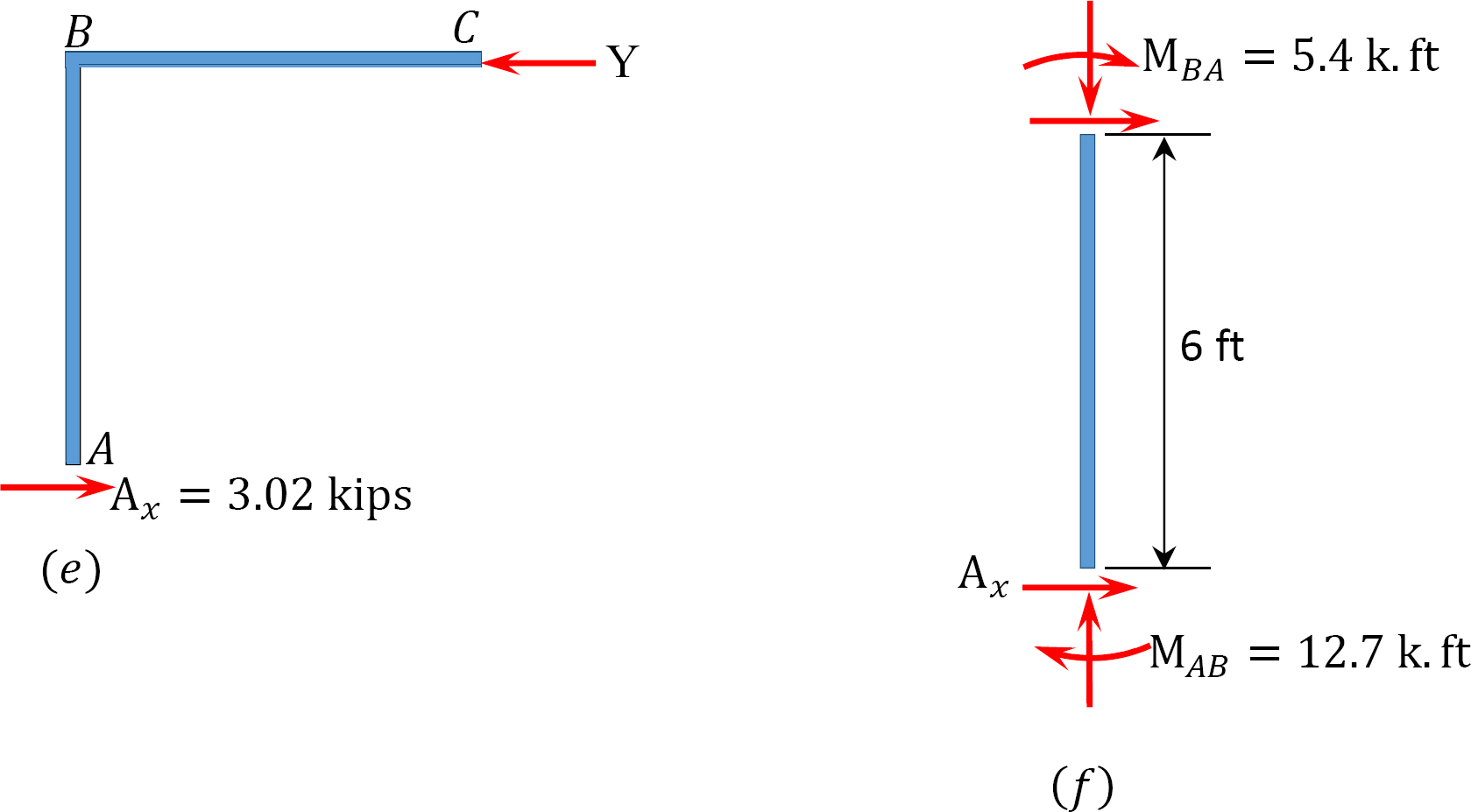
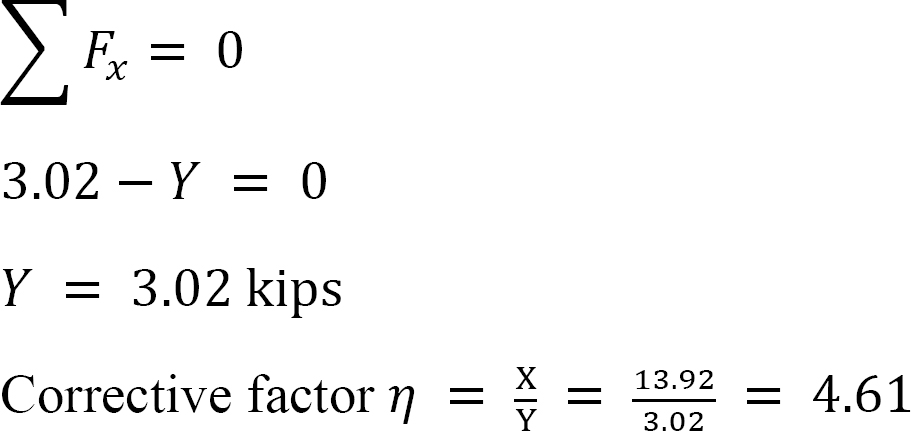
Final de momentos.
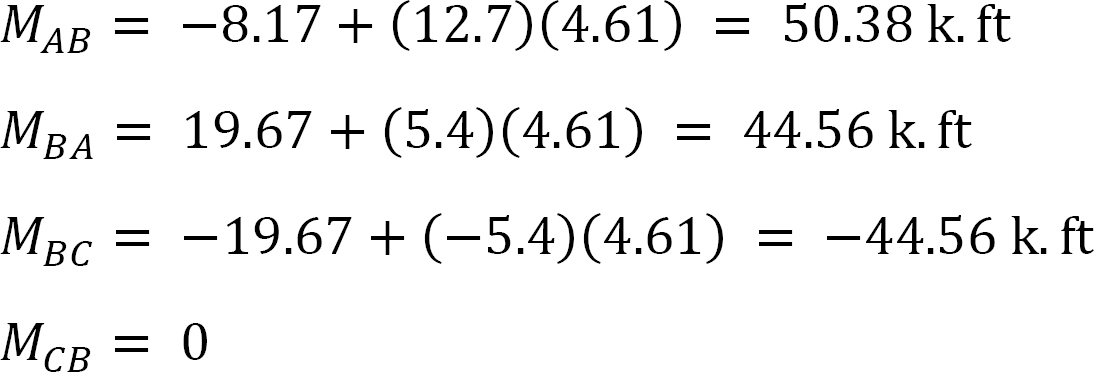
Exemplo 12.7
uma moldura de balanço é carregada como mostrado na figura 12.12 A. Usando o método de distribuição de momento, determinar os momentos finais dos membros da moldura.
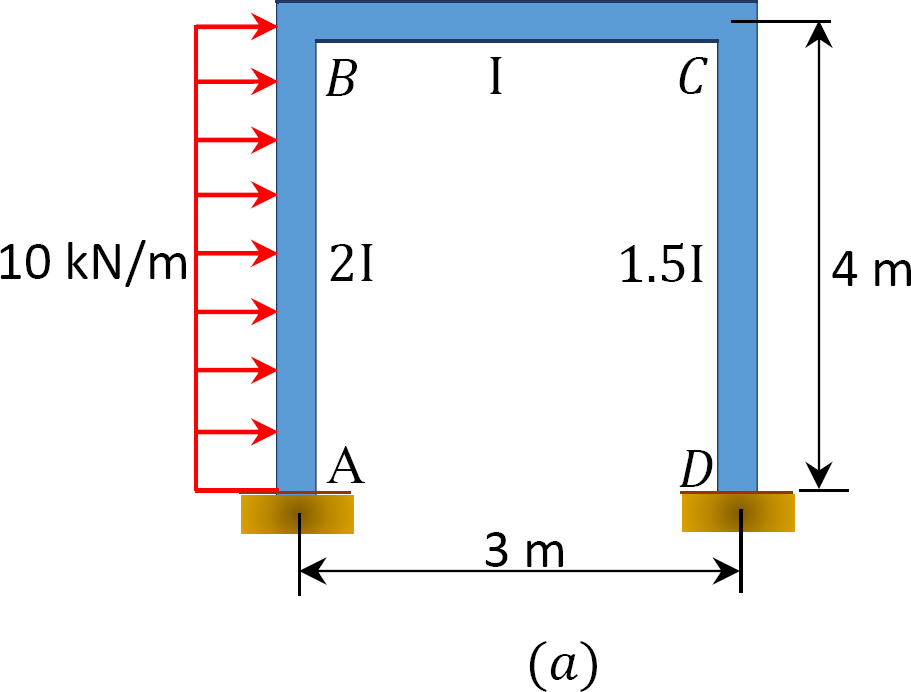
Fig. 12.12. Baloiço carregado.
solução
momento final fixo.
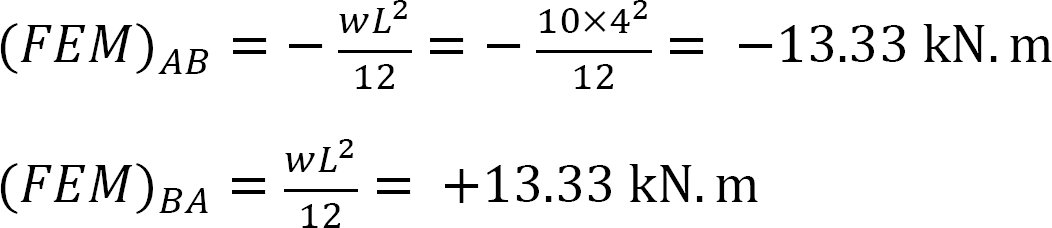
Factor de rigidez.
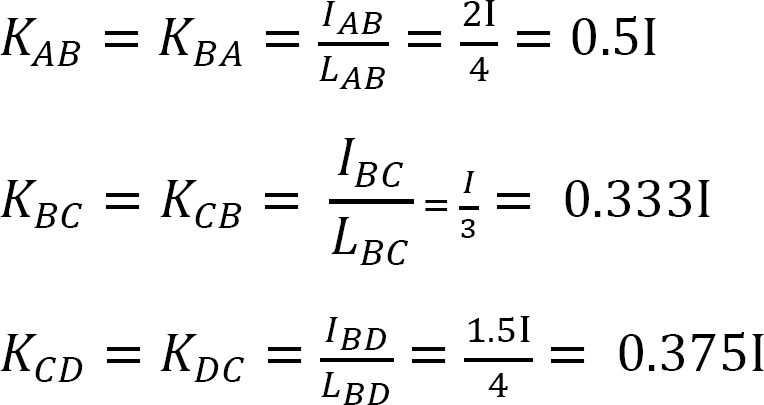
factor de distribuição.

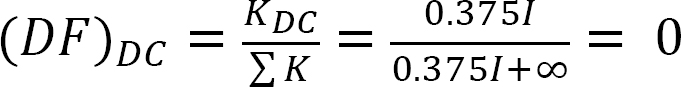
análise da moldura sem oscilação lateral.
quadro 12.8. Tabela de distribuição (sem oscilação).
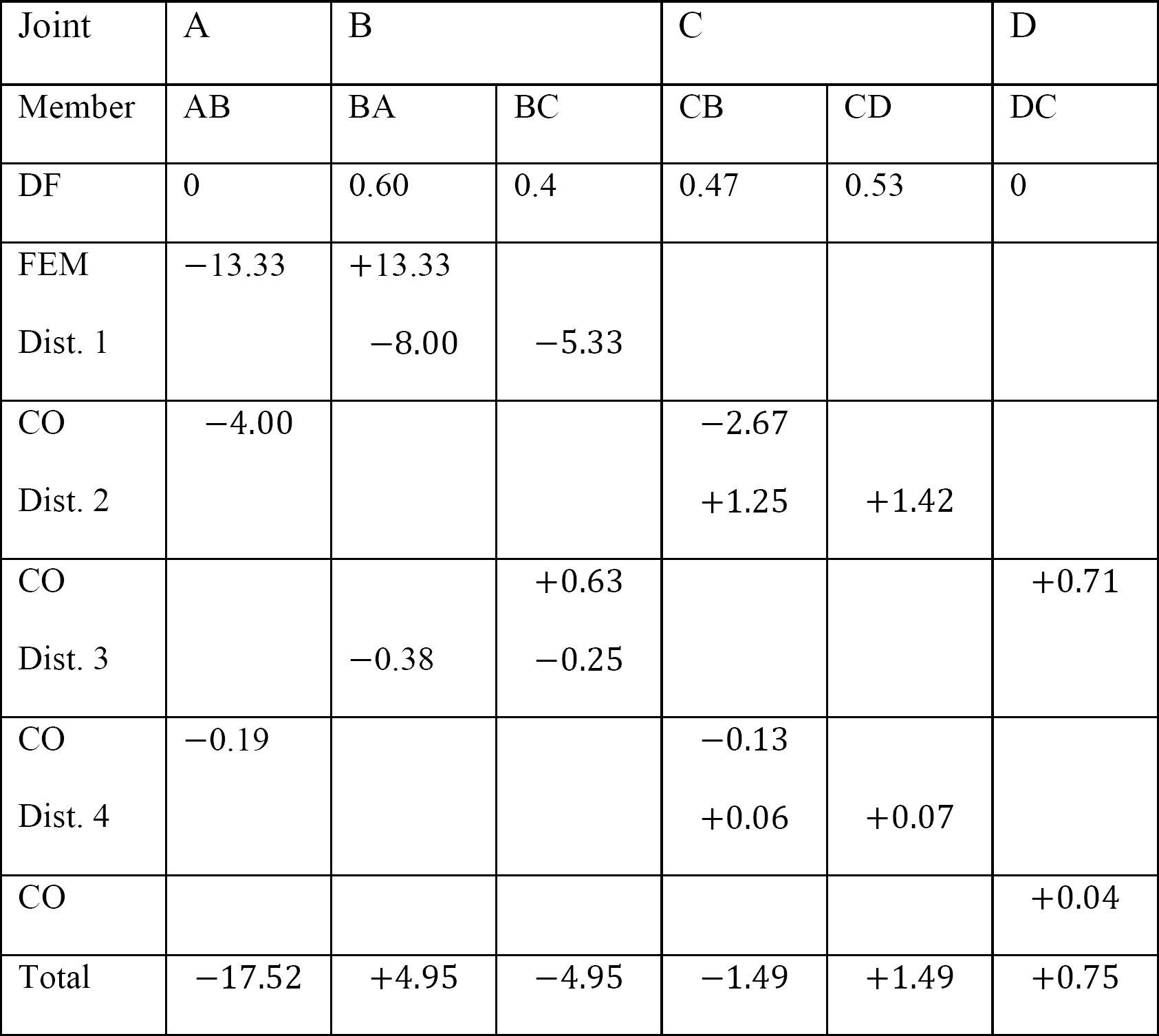
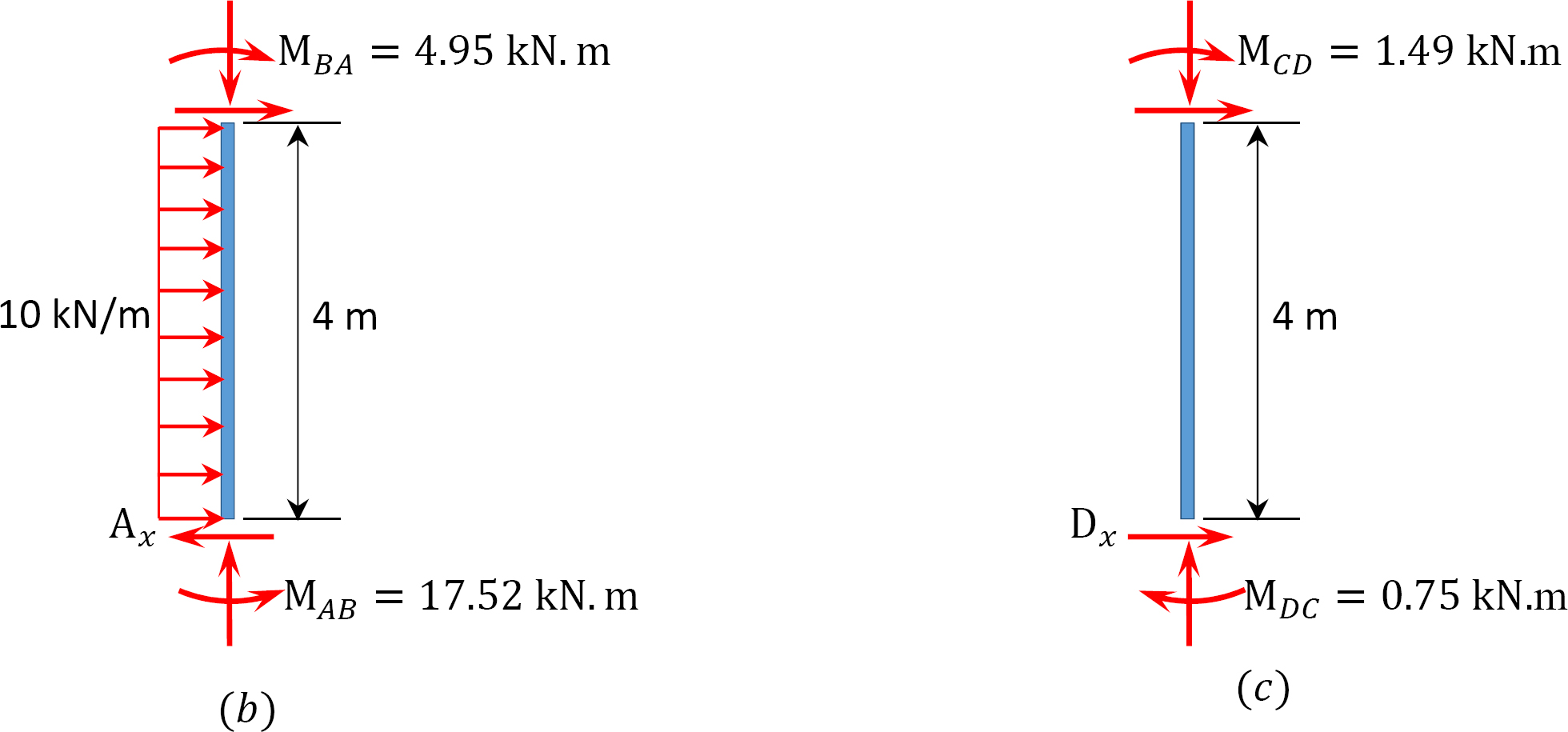
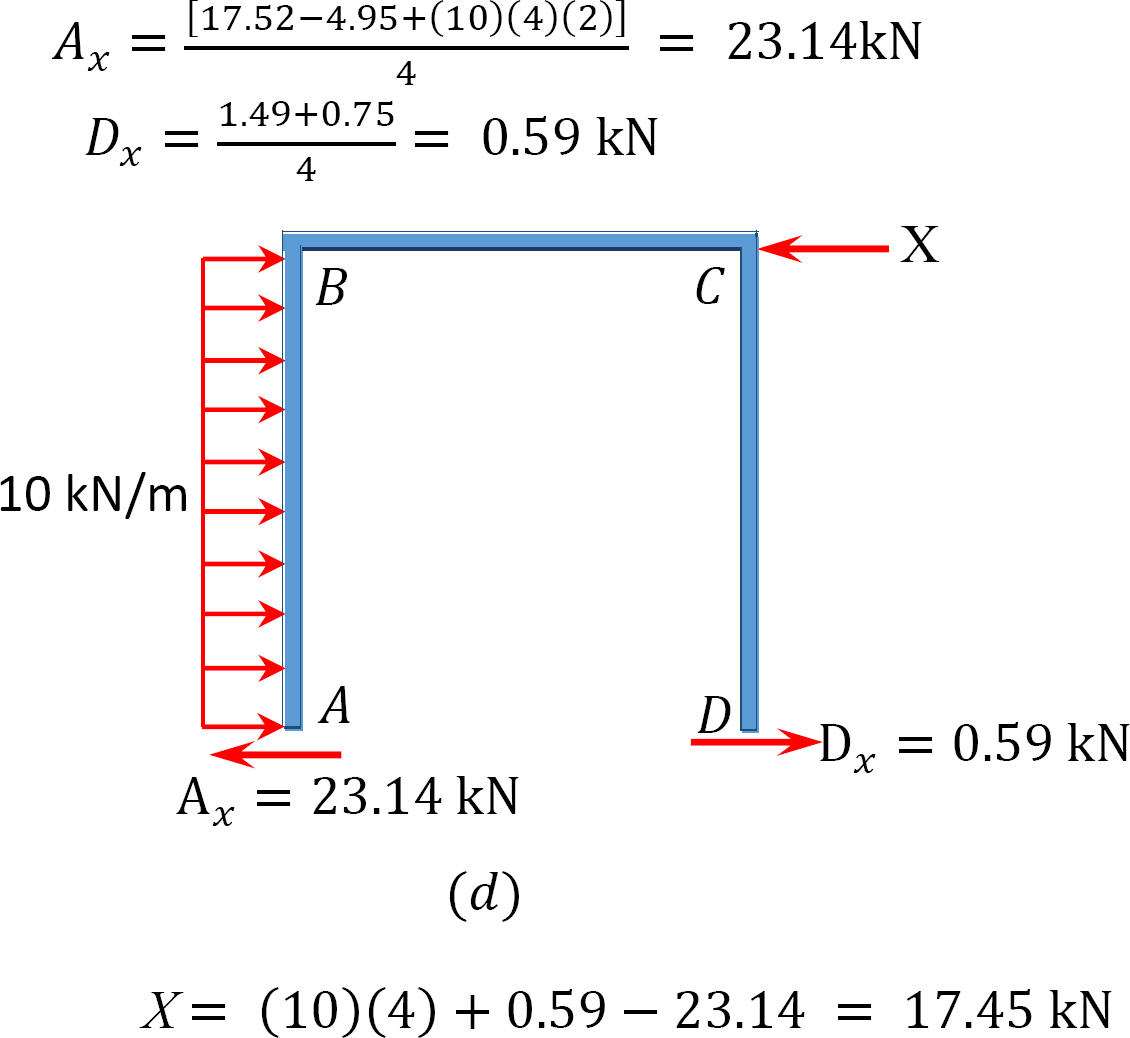
Tabela 12.9. Tabela de distribuição (sway frame).
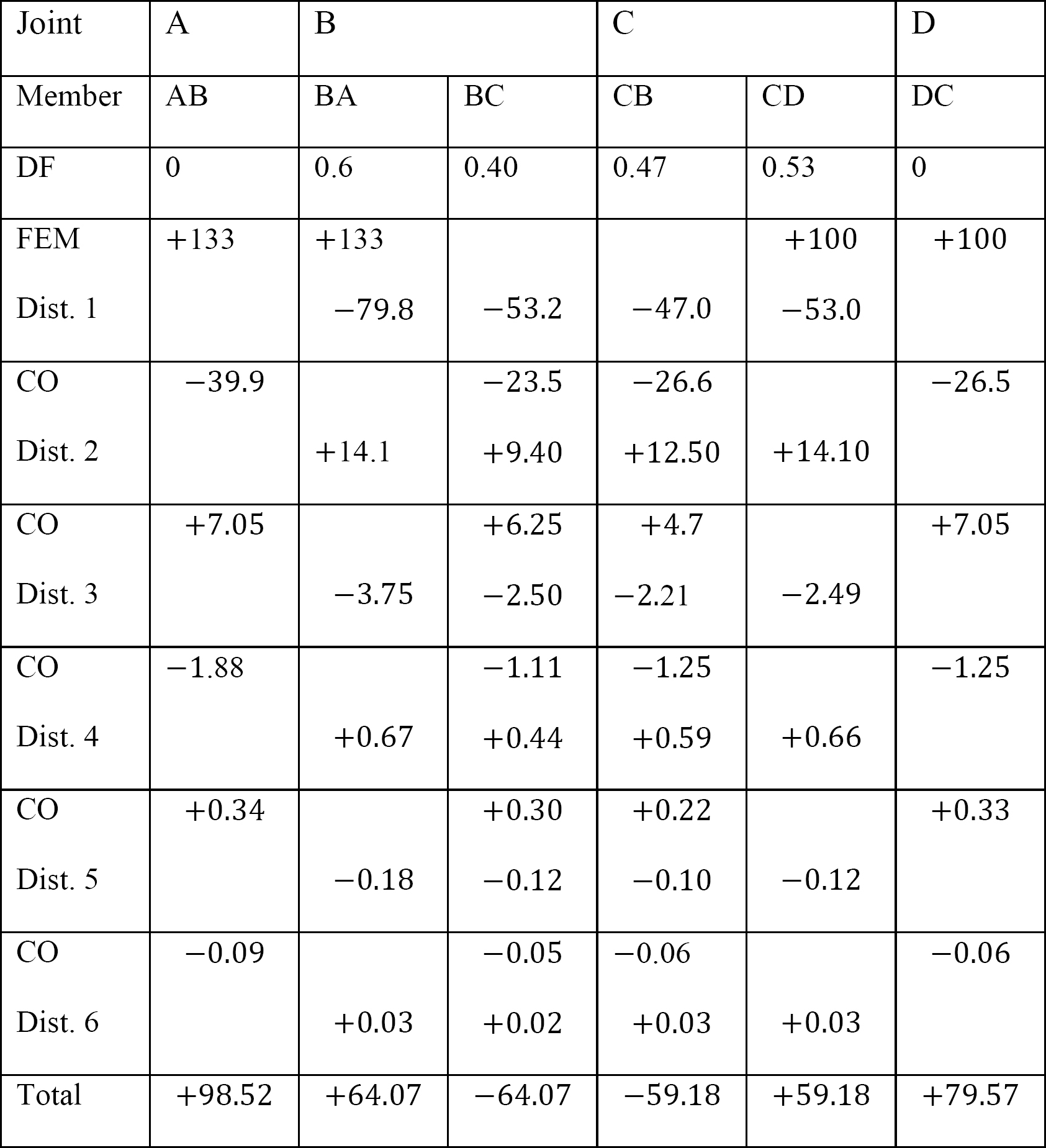
análise da moldura com baloiço lateral.
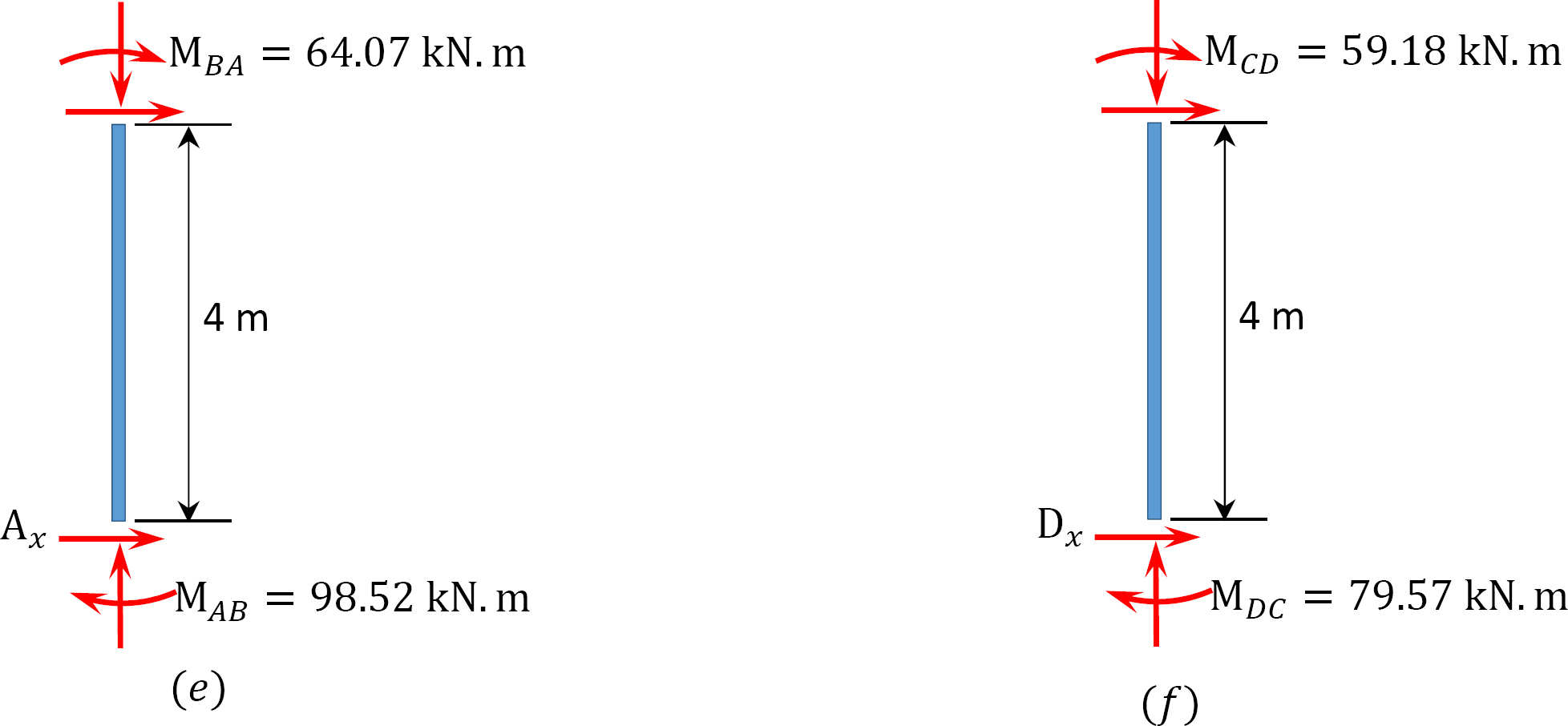

último momento.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Chapter Summary
Moment distribution method of analysis of indeterminate structures: The moment distribution method of analysis is an approximate method of analysis. Seu grau de precisão depende do número de iterações. Neste método, assume-se que todas as juntas de uma estrutura são temporariamente bloqueadas ou presas e, portanto, são impedidas de uma possível rotação. Cargas são aplicadas aos Membros, e os momentos desenvolvidos nos membros terminam devido à fixidade são determinados. As juntas na estrutura são então desbloqueadas sucessivamente, e o momento desequilibrado em cada junta é distribuído aos membros que se reúnem nessa junta. Os momentos de transição nas extremidades mais distantes dos membros são determinados, e o processo de equilíbrio é continuado até o nível desejado de precisão. Os momentos finais dos membros são determinados somando o momento fixo, o momento distribuído e o momento de transição. Uma vez determinados os momentos finais dos Membros, a estrutura torna-se determinada.
Problemas Práticos
12.1 Utilizar o método de distribuição do momento para calcular o momento final dos elementos dos feixes indicados na figura P12.1 através da figura P12.12 e desenhar os diagramas de momento Flector e força de corte. EI = constante.
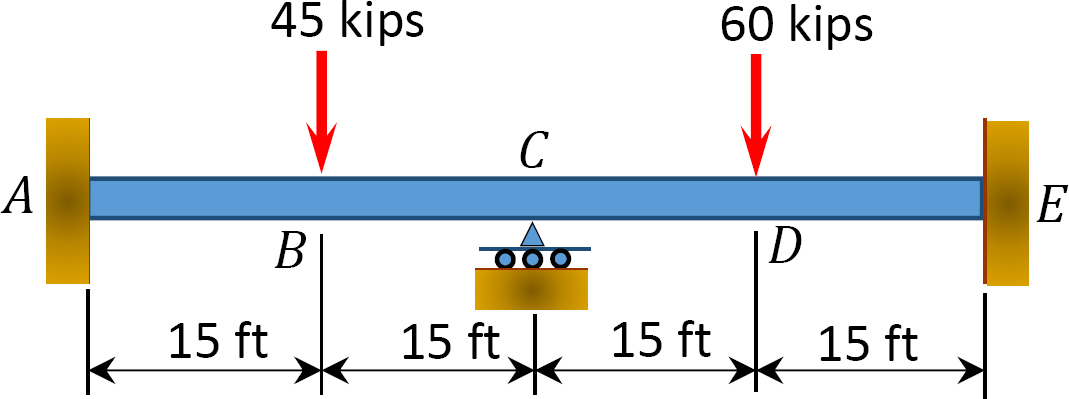
Fig. P12. 1. Feixe.
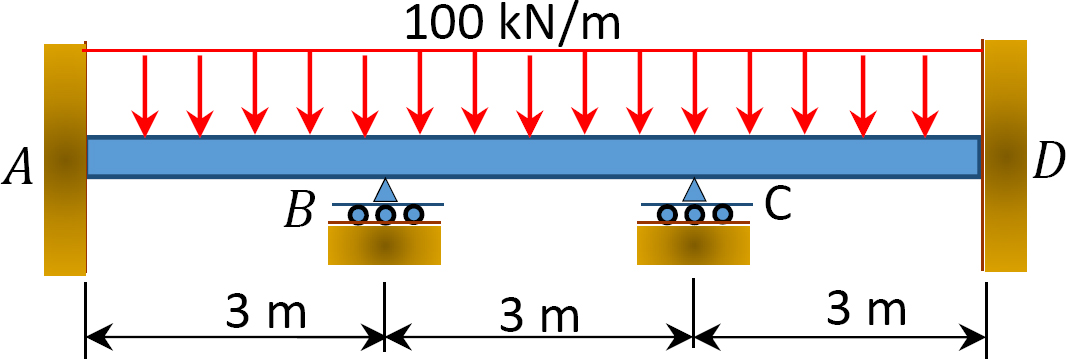
Fig. P12. 2. Feixe.
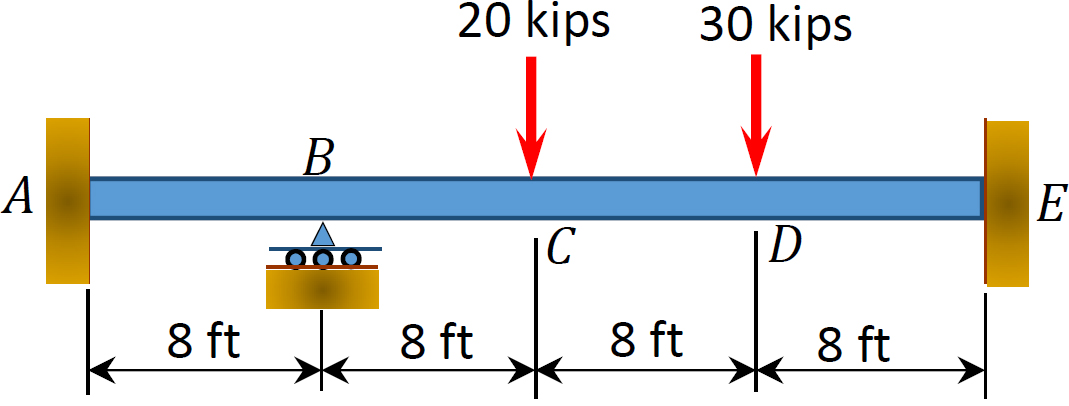
Fig. P12. 3. Feixe.
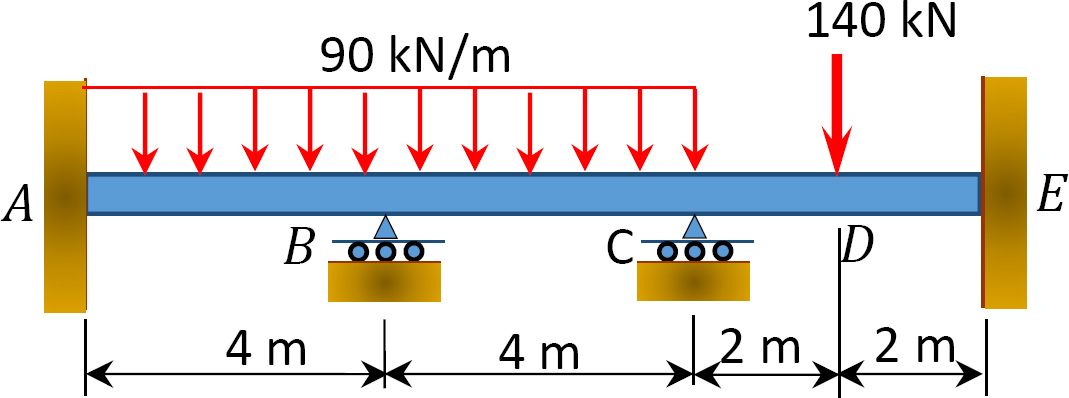
Fig. P12. 4. Feixe.
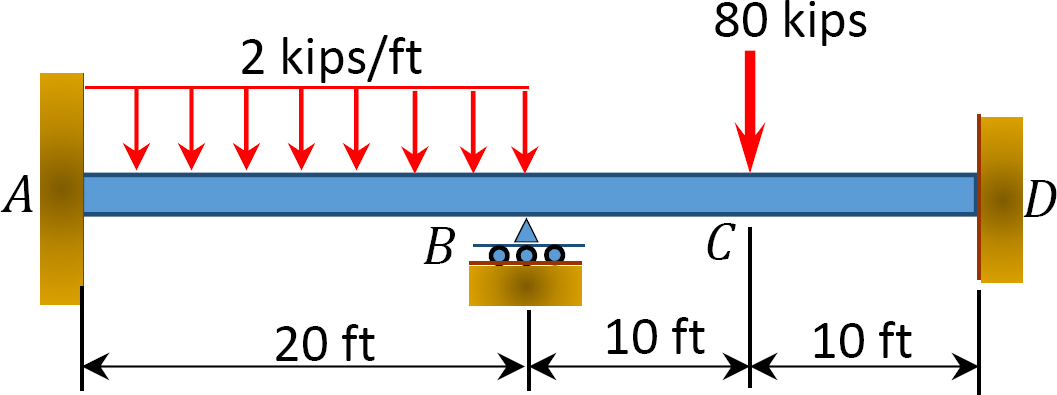
Fig. P12. 5. Feixe.
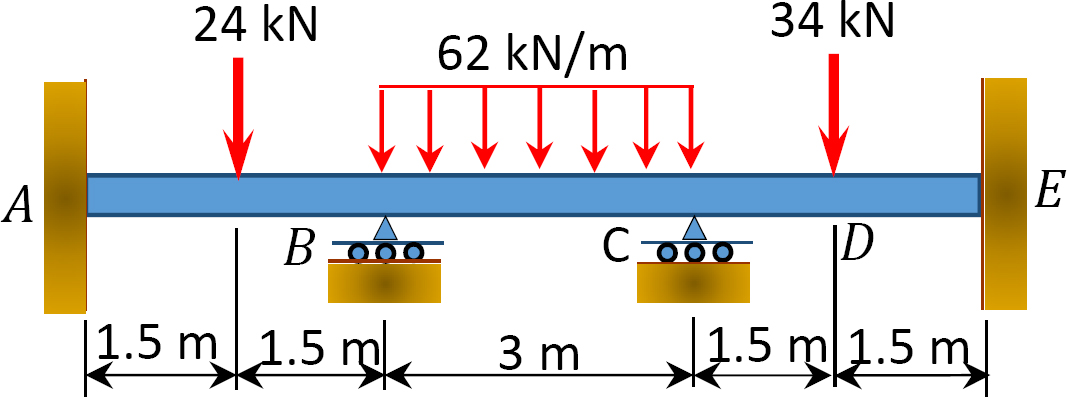
Fig. P12. 6. Feixe.
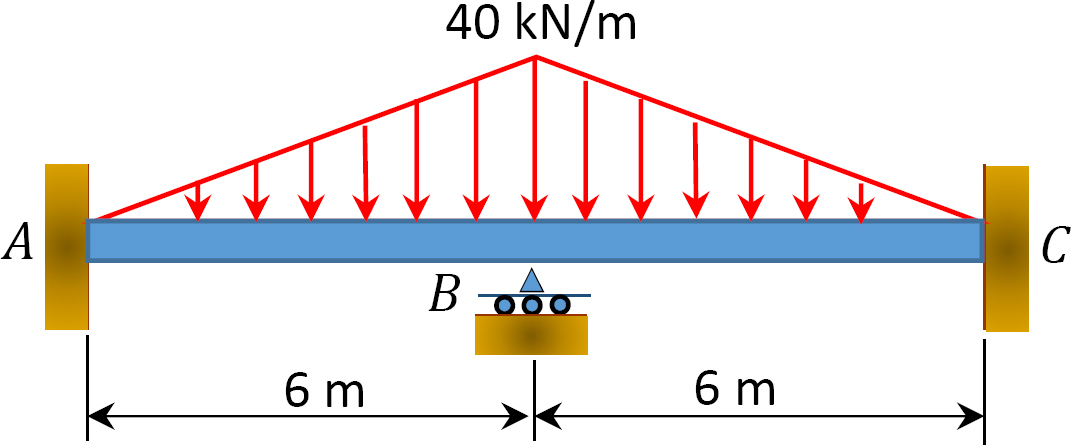
Fig. P12. 7. Feixe.
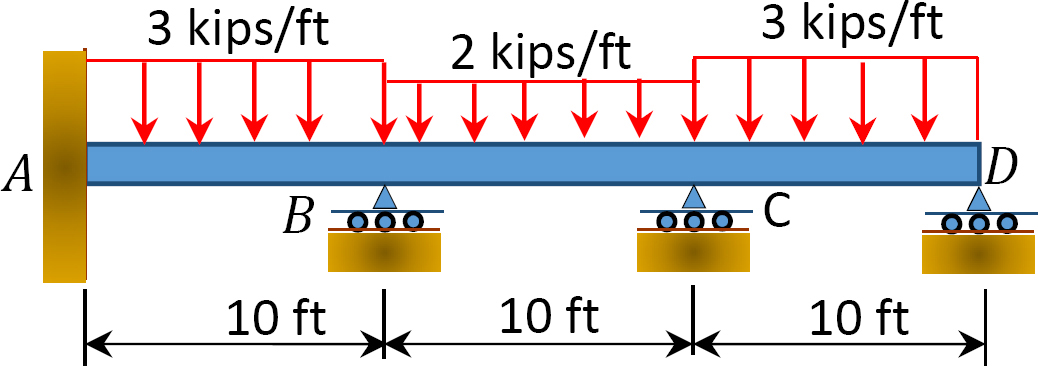
Fig. P12. 8. Feixe.
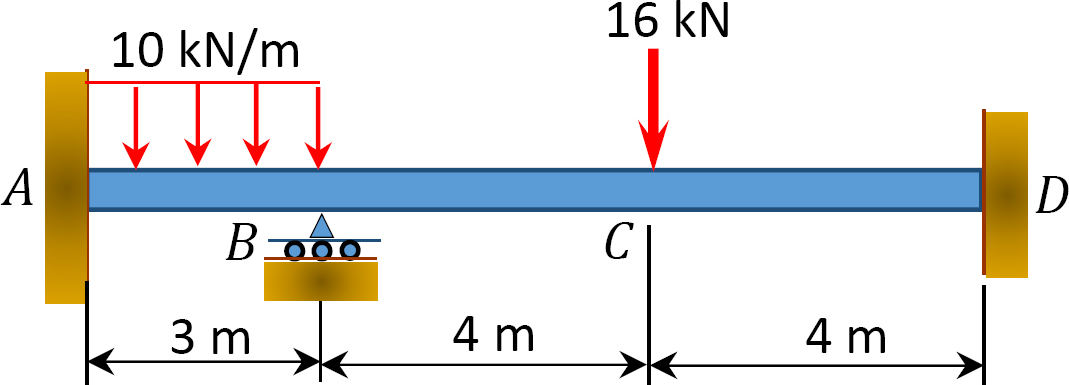
Fig. P12. 9. Feixe.
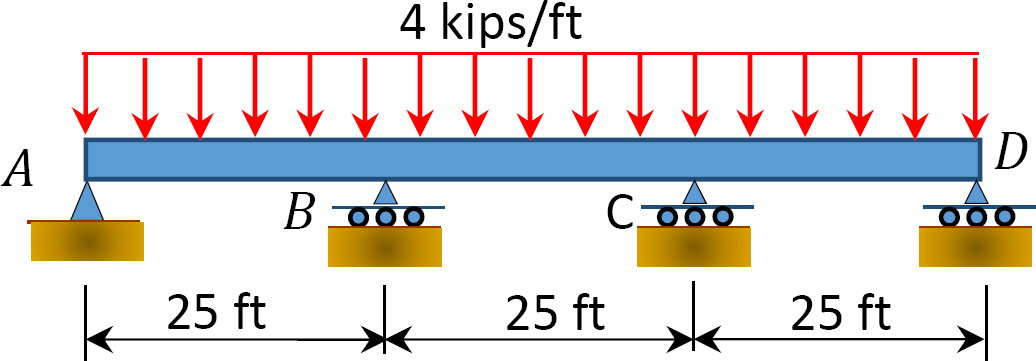
Fig. P12. 10. Feixe.
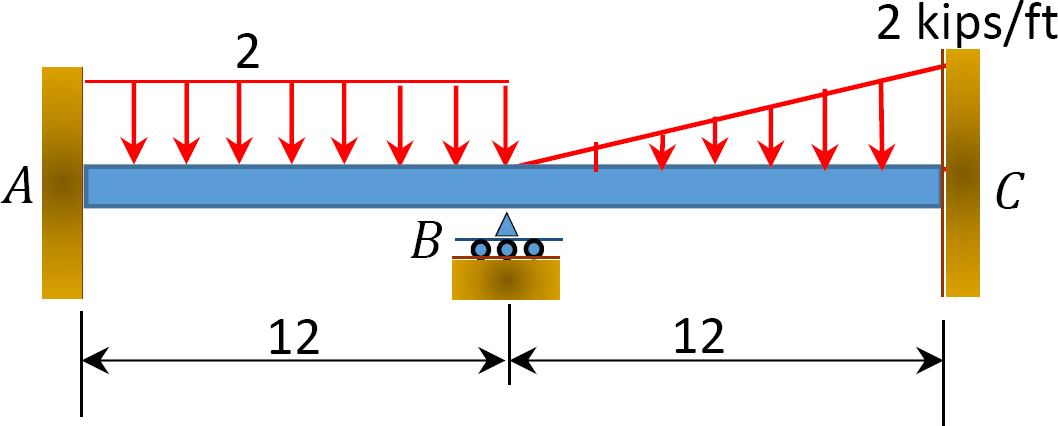
Fig. P12. 11. Feixe.
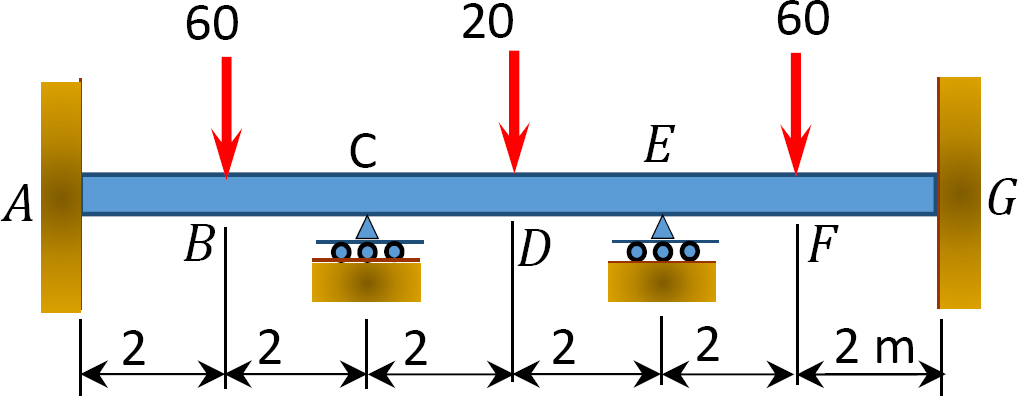
Fig. P12. 12. Feixe.
12.2 utilizar o método de distribuição do momento para calcular o momento final dos membros dos quadros ilustrados na figura P12.13 através da figura 12.20 e desenhar os diagramas de momento Flector e força de corte. EI = constante.
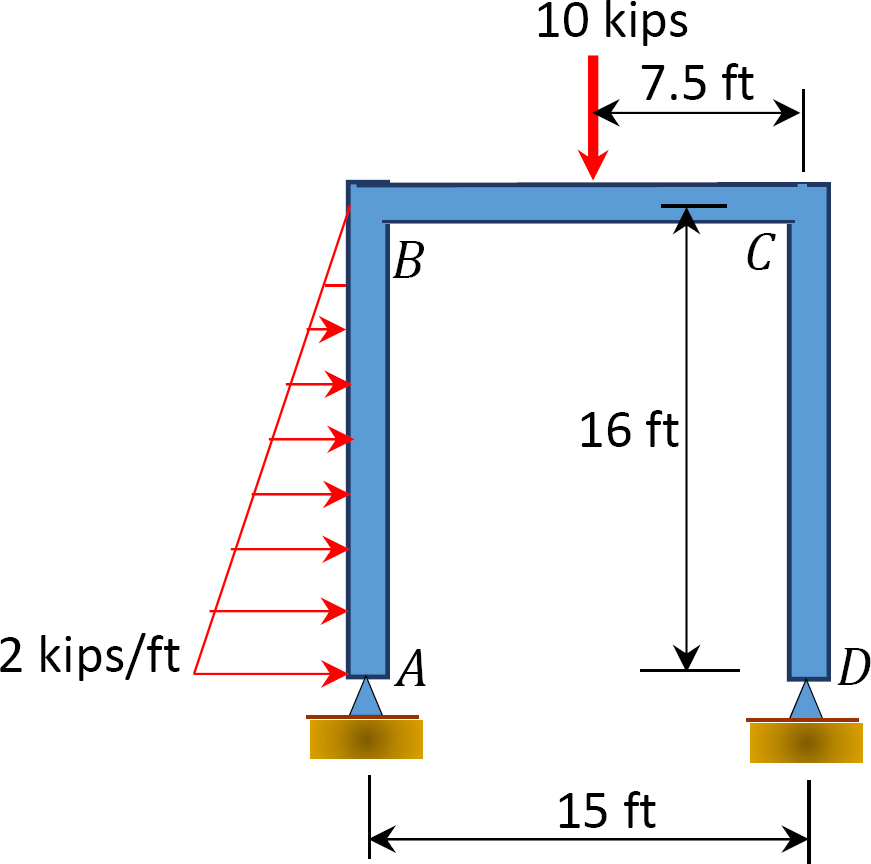
Fig. P12. 13. Quadro.
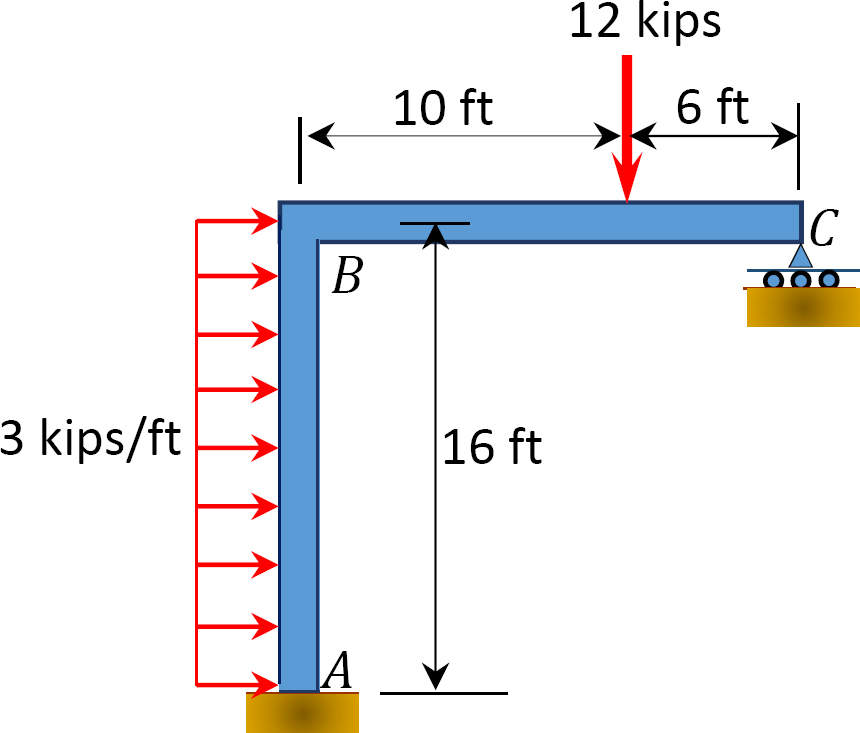
Fig. P12. 14. Quadro.
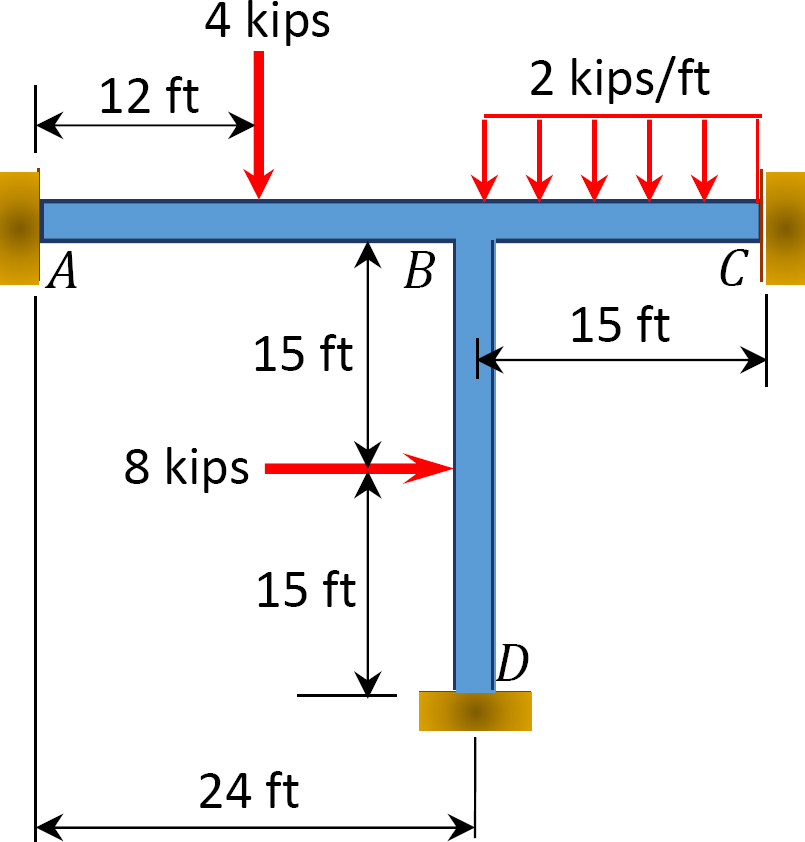
Fig. P12. 15. Quadro.
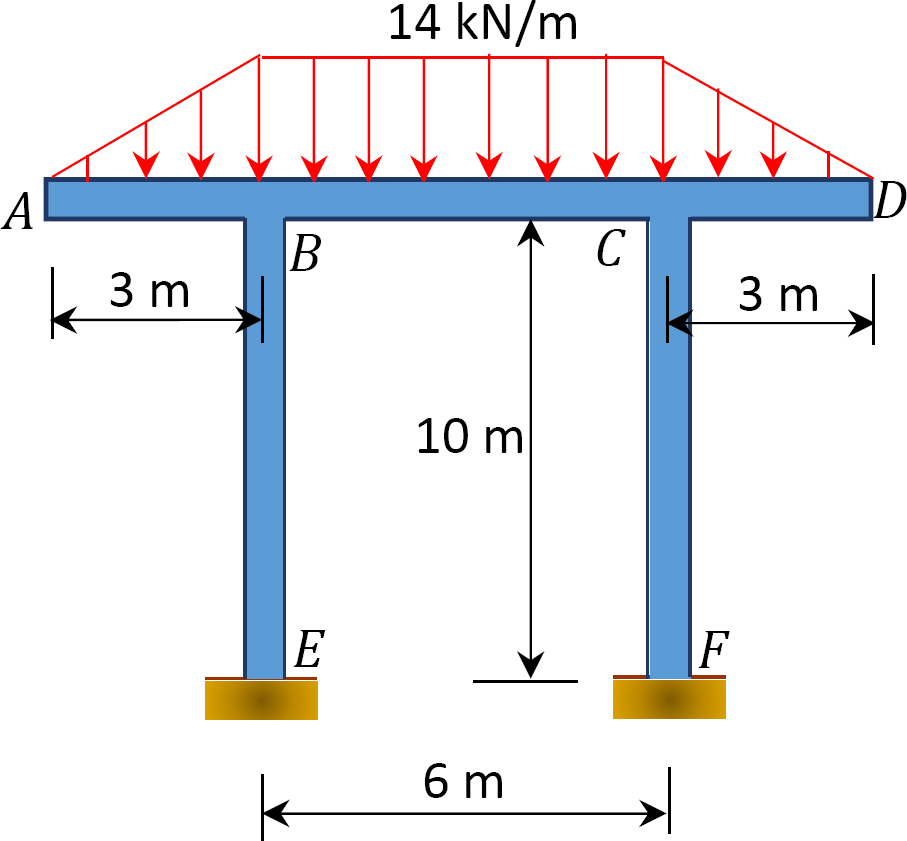
Fig. P12.16. Frame.
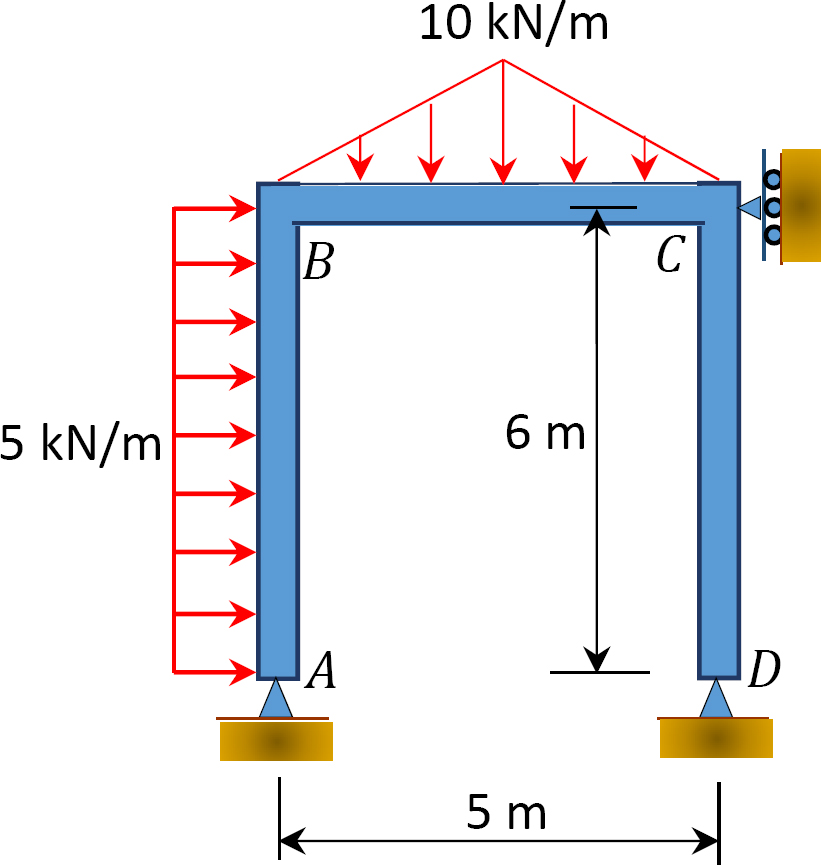
Fig. P12.17. Frame.
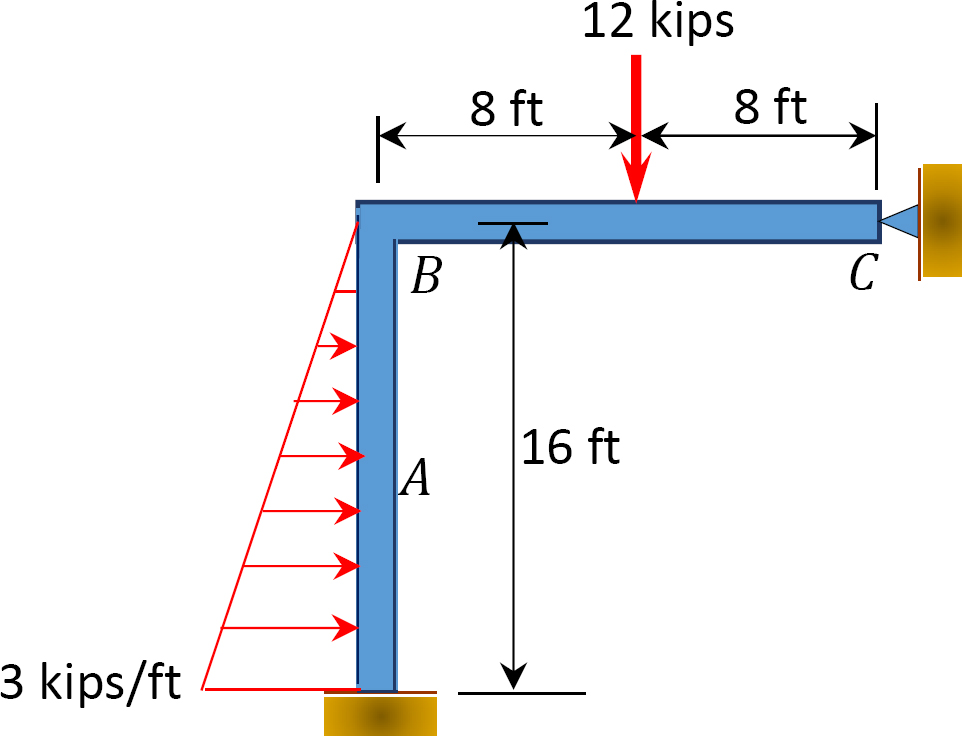
Fig. P12.18. Frame.
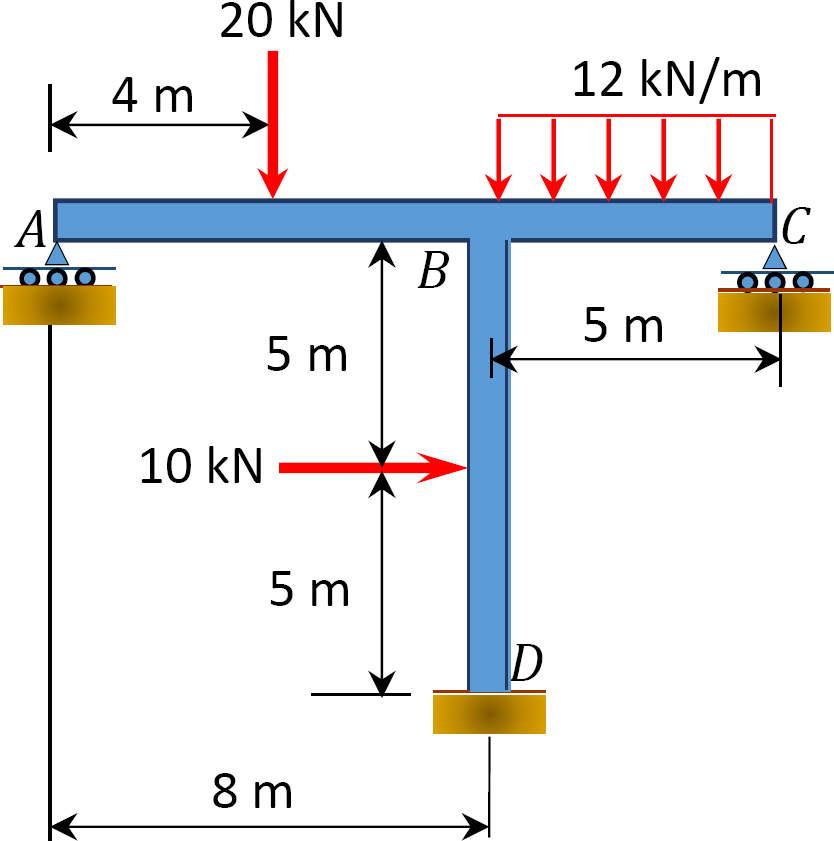
Fig. P12.19. Frame.
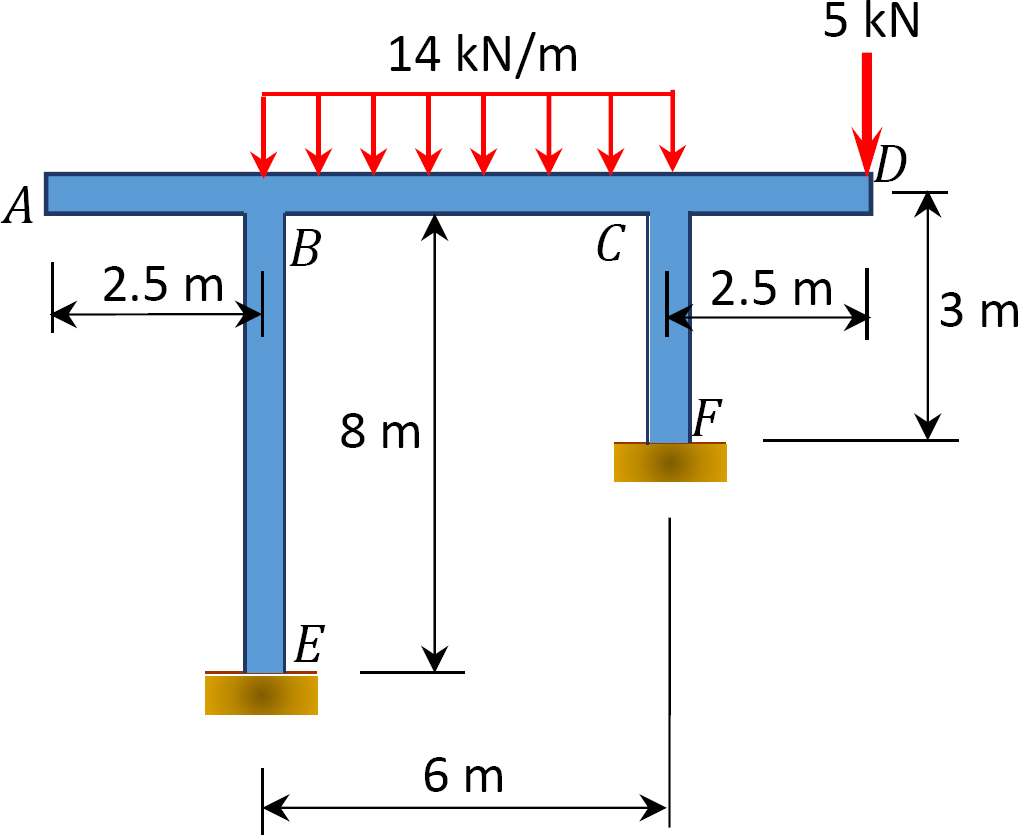
Fig. P12.20. Frame.