Capitolul 12
metoda distribuției momentului de analiză a structurilor
12.1 concepte de bază
metoda distribuției momentului de analiză a grinzilor și cadrelor a fost dezvoltată de Hardy Cross și prezentată oficial în 1930. Deși această metodă este o metodă de deformare ca metoda de deviere a pantei, este o metodă aproximativă și, prin urmare, nu necesită rezolvarea ecuațiilor simultane, așa cum a fost cazul celei de-a doua metode. Gradul de precizie al rezultatelor obținute prin metoda distribuției momentului depinde de numărul de aproximări succesive sau de procesul de iterație.
pentru a ilustra conceptul metodei de distribuție a momentului, luați în considerare cadrul prezentat în figura 12.1. Membrii cadrului sunt prismatici și se presupune că nu se deformează axial și nici nu se traduc unul față de celălalt. Îmbinările ACD ale cadrului sunt fixe, în timp ce articulația B se poate roti ușor datorită sarcinii aplicate. În primul rând, înainte de a efectua distribuția momentului între membri, se presupune că toate îmbinările sunt blocate temporar folosind o clemă.
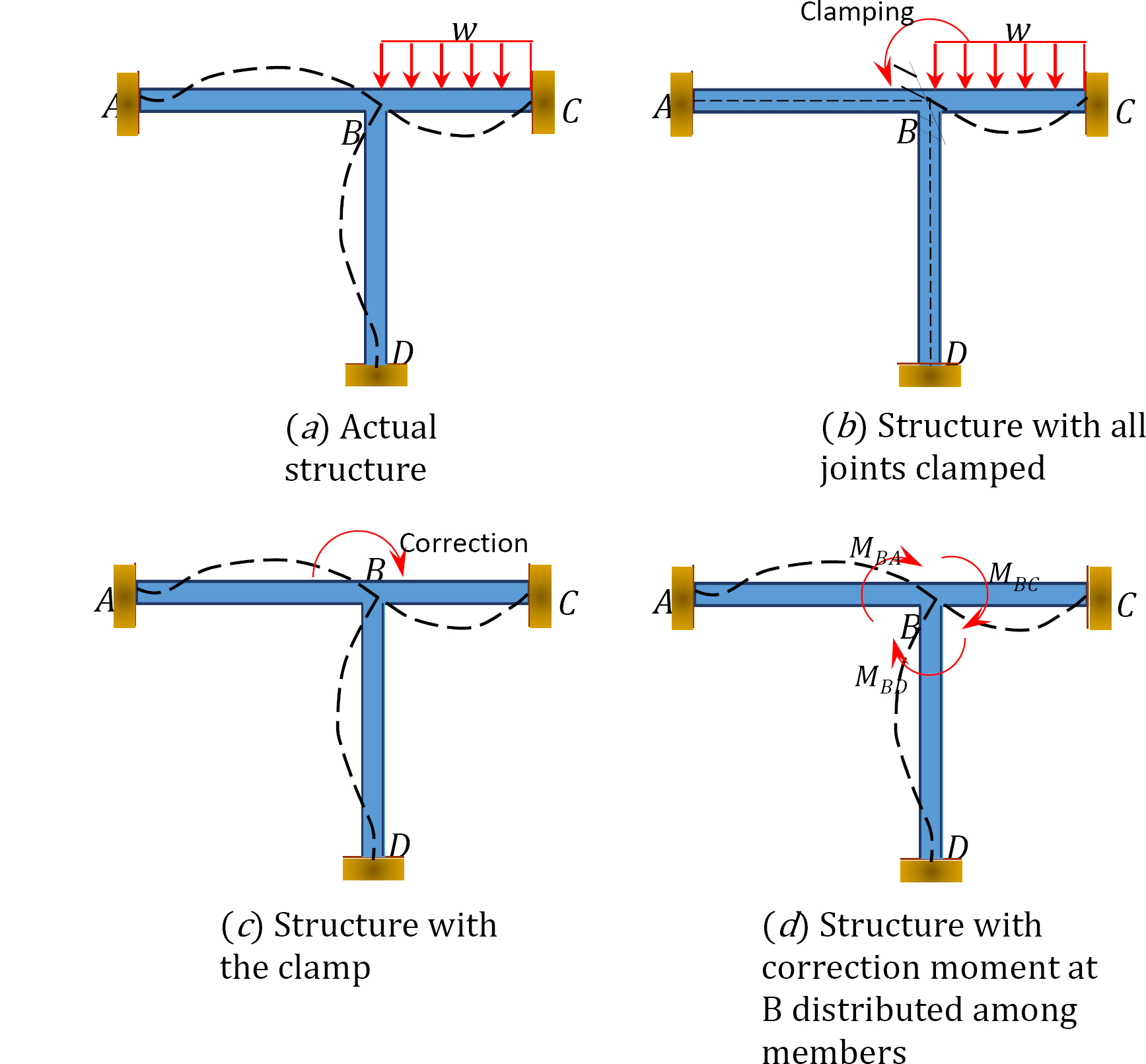
Fig. 12.1. Cadru.
12.2 Convenția semnului
Convenția semnului pentru metoda de distribuție a momentului este similară cu cea stabilită pentru metoda de deviere a pantei; adică, momentul de la sfârșitul unui membru este considerat pozitiv dacă tinde să întoarcă capătul membrului în sensul acelor de ceasornic și negativ dacă tinde să-l întoarcă în sens invers acelor de ceasornic.
12.3 definiții
momente neechilibrate: această metodă de analiză presupune că îmbinările dintr-o structură sunt inițial fixate sau blocate și apoi eliberate succesiv. Odată ce o articulație este eliberată, are loc o rotație, deoarece suma momentelor finale fixe ale membrilor care se întâlnesc la acea articulație nu este zero. Valoarea sumei momentelor finale obținute este momentul dezechilibrat la acea articulație.
momente de reportare: momentele distribuite în capetele membrilor care se întâlnesc la o cauză comună momente în celelalte capete, care se presupune că sunt fixate. Aceste momente induse la celelalte capete sunt numite momente de reportare.
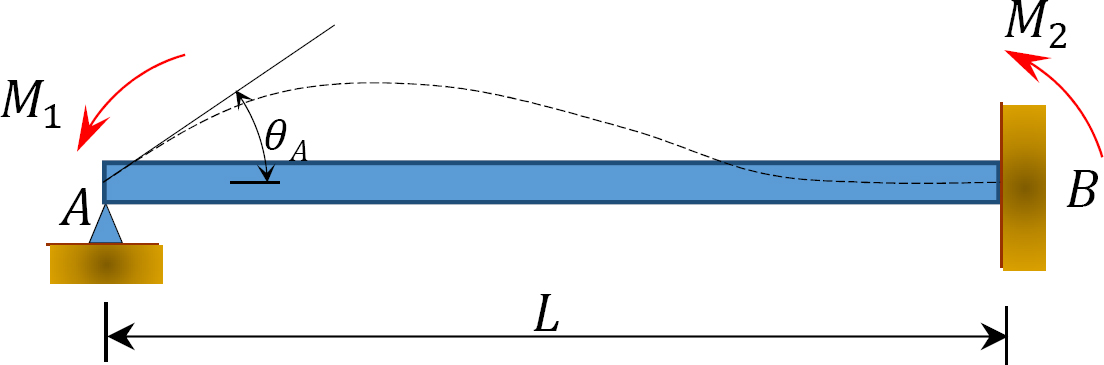
Fig. 12.2. Fascicul prismatic descărcat.
luați în considerare un fascicul prismatic descărcat fixat la capătul B, așa cum se arată în figura 12.2. Dacă un moment M1 este aplicat la capătul stâng al fasciculului, ecuațiile de deviere a pantei pentru ambele capete ale fasciculului pot fi scrise după cum urmează:


înlocuirea 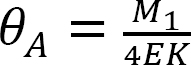 din ecuația 12.1 în ecuația 12.2 sugerează următoarele:
din ecuația 12.1 în ecuația 12.2 sugerează următoarele:

ecuația 12.3 sugerează că momentul reportat la capătul fix al unui fascicul datorită unui moment aplicat la celălalt capăt este egal cu jumătate din momentul aplicat.
factor de reportare: raportul dintre momentul indus și momentul aplicat este denumit factor de reportare. Pentru fasciculul prezentat în figura 12.2, factorul de reportare este următorul:

factorul distribuit (DF): Factorul distribuit este un factor utilizat pentru a determina proporția momentului dezechilibrat purtat de fiecare dintre membrii reuniți la o comună. Pentru membrii reuniți la o comună a cadrului prezentat în figura 12.3, factorii lor de distribuție sunt calculați după cum urmează:
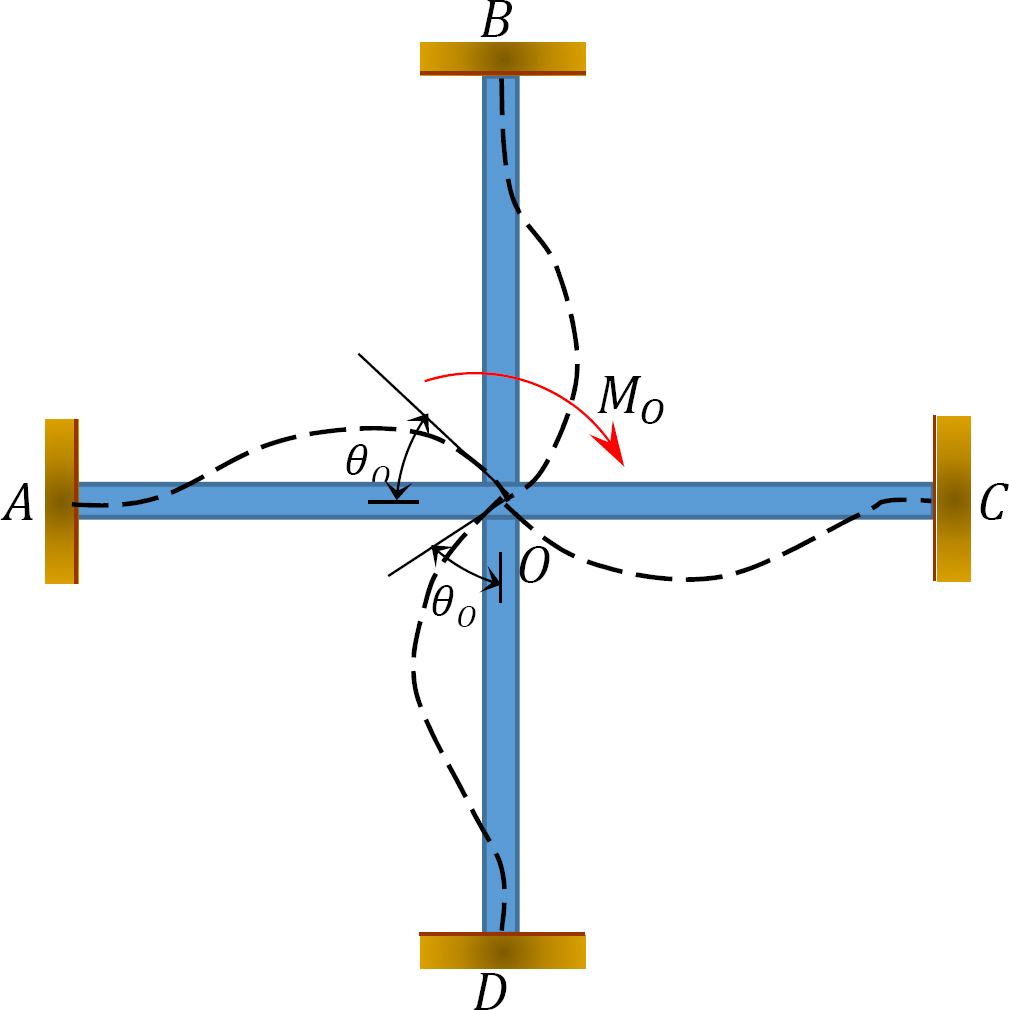
Fig. 12.3. Cadru.

momente distribuite: la eliberarea clemei imaginare la o articulație, momentul dezechilibrat la acea articulație determină rotirea acesteia. Rotația răsucește sfârșitul întâlnirii membrilor la articulație, ducând la dezvoltarea momentelor rezistente. Aceste momente rezistente sunt numite momente distribuite. Momentele distribuite pentru membrii cadrului prezentate în figura 12.3 sunt calculate după cum urmează:
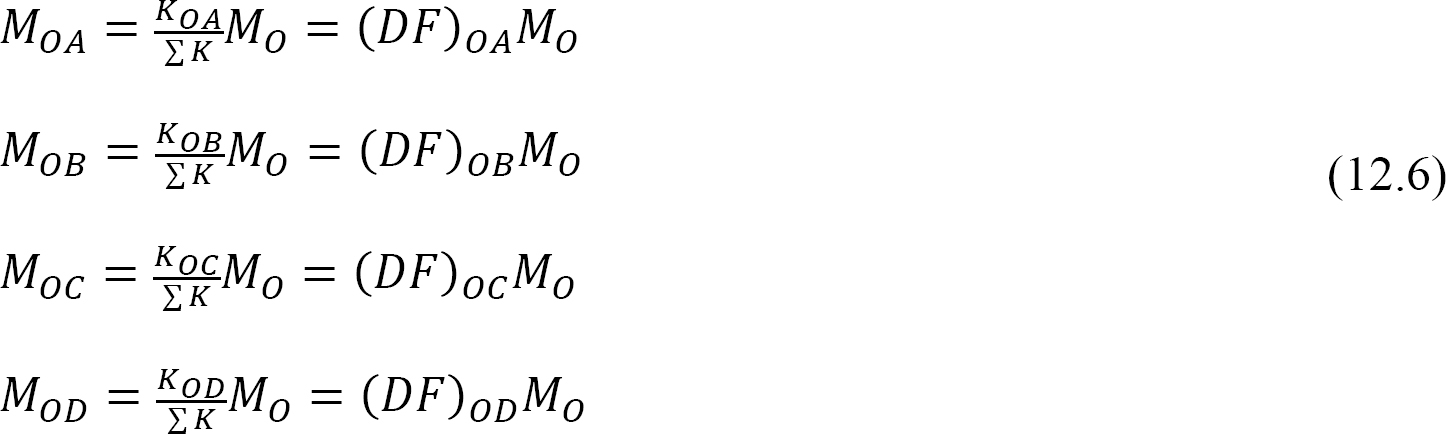
12.4 modificarea rigidității membrilor
uneori procesul de iterație în metoda de distribuție a momentului poate fi redus semnificativ prin ajustarea rigidității la încovoiere a unor membri ai structurii nedeterminate. Această secțiune ia în considerare influența unui suport fix și a unui vârf de fixare asupra rigidității la încovoiere a unui fascicul nedeterminat.
cazul 1: Un fascicul articulat la un capăt și fixat la celălalt
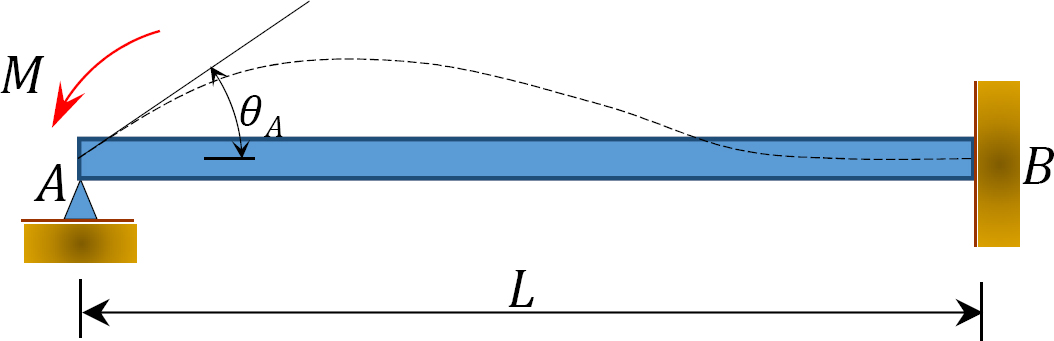
Fig. 12.4. Fasciculul
se consideră un fascicul articulat la capătul a și fixat la capătul B, așa cum se arată în figura 12.4. Aplicarea unui moment m roteste capatul balamalei cu o cantitate de X-X. Scrierea ecuației pantă-deviere pentru capătul A al membrului și menționarea faptului că 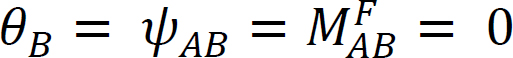 sugerează următoarele:
sugerează următoarele:
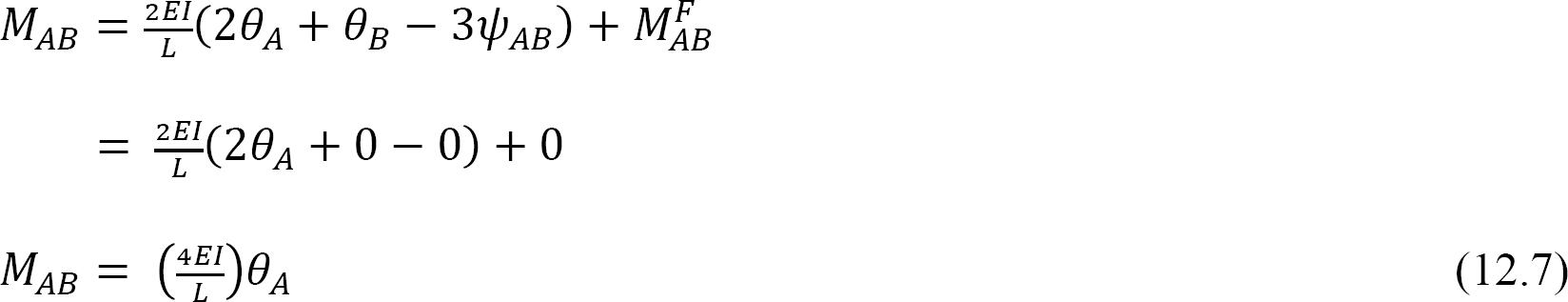
prin definiție, rigiditatea la încovoiere a unui element structural este momentul care trebuie aplicat unui capăt al elementului pentru a determina o rotație a unității acelui capăt. Următoarea expresie a rigidității la încovoiere pentru elementul cu capăt îndepărtat fix este exprimată după cum urmează atunci când se substituie INQUA = 1 în ecuație 12.7:

prin definiție, rigiditatea relativă la încovoiere a unui membru este determinată prin împărțirea rigidității la încovoiere a membrului la 4E. împărțirea ecuației 12.8 la 4E sugerează următoarea expresie pentru rigiditatea relativă pentru cazul luat în considerare:

Cazul 2: o grindă articulată la ambele capete
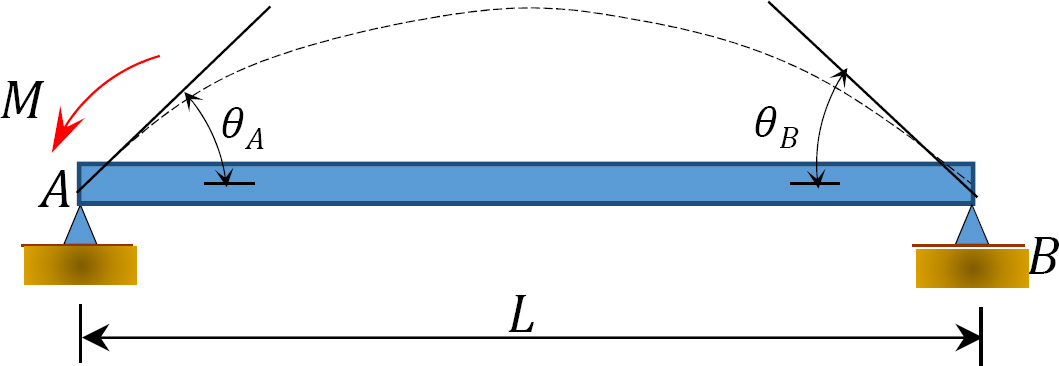
Fig. 12.5. Pur și simplu a sprijinit fascicul.
aplicarea unui moment M la capătul A al fasciculului simplu susținut prezentat în figura 12.5 rotește fasciculul cu un unghi xqua la capătul articulat. Folosind ecuația modificată pantă-deviere derivată în secțiunea 11.4 din capitolul 11 și menționând că 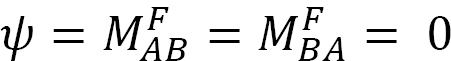 sugerează următoarea expresie pentru momentul de la capătul articulat unde se aplică sarcina:
sugerează următoarea expresie pentru momentul de la capătul articulat unde se aplică sarcina:
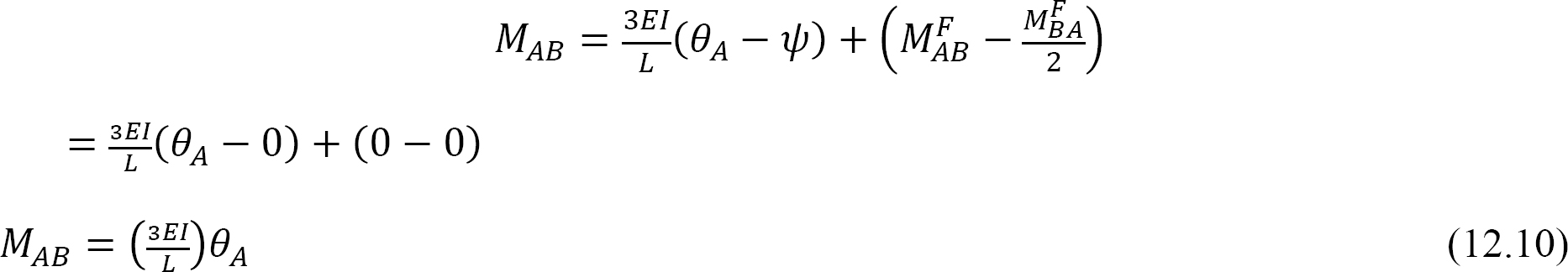
Substituirea xqua = 1 în ecuația 12.10 sugerează următoarea expresie pentru rigiditatea la încovoiere pentru un element cu capăt îndepărtat articulat:

rigiditatea relativă pentru un membru cu capăt îndepărtat articulat se obține prin împărțirea ecuației 12.11 la 4E, după cum urmează:

comparând ecuațiile 12.12 și 12.9 sugerează că un membru cu un capăt îndepărtat articulat este de trei sferturi la fel de rigid ca un membru cu aceeași geometrie, dar fixat la capătul îndepărtat. Acest fapt stabilit poate reduce substanțial numărul de iterații atunci când se analizează grinzi sau cadre cu un capăt îndepărtat articulat folosind metoda distribuției momentului. În astfel de cazuri, rigiditatea relativă a fasciculului la capătul apropiat este ajustată mai întâi conform ecuației 12.12, iar factorul său de distribuție este calculat cu rigiditatea ajustată. În timpul operației de echilibrare, capătul apropiat va fi echilibrat o singură dată, fără a mai fi reportate momente de la sau până la capăt.
12.5 analiza grinzilor nedeterminate
procedura de analiză a grinzilor nedeterminate prin metoda distribuției momentului este rezumată pe scurt după cum urmează:
procedura de analiză a fasciculelor nedeterminate prin metoda distribuției momentului
•calculați momentele de capăt fix pentru membri, presupunând că îmbinările sunt fixate împotriva rotației.
•calculați factorul de distribuție pentru fiecare dintre membrii conectați la articulație
•calculați momentul dezechilibrat la fiecare articulație și distribuiți-l la capetele membrilor conectați la acea articulație.
•transferă jumătate din momentul distribuit către celelalte capete ale membrilor.
•adăugați sau scădeți aceste ultime momente (momente obținute în pașii trei și patru) la sau de la momentele finale fixe originale.
•aplicați momentele finale determinate la îmbinările structurii date.
•desenați diagrama corpului liber a fiecărei întinderi a fasciculului dat, arătând sarcinile și momentele la îmbinările obținute prin metoda distribuției momentului.
•determinați reacțiile de suport pentru fiecare interval.
•calculați și construiți forța de forfecare și diagramele momentului de îndoire pentru fiecare interval.
•desenați un moment de încovoiere și o diagramă a forței de forfecare pentru fasciculul dat prin combinarea diagramelor de la PASUL 9.
exemplu 12.1
folosind metoda distribuției momentului, determinați momentele finale și reacțiile la suporturile fasciculului prezentate în figura 12.6 a. desenați diagramele forței de forfecare și ale momentului de îndoire. EI = constantă.
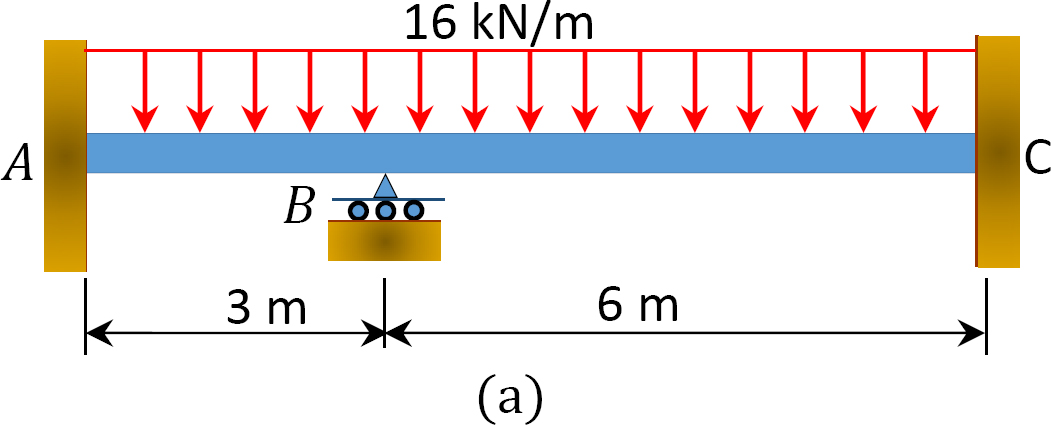
Fig. 12.6. Beam.
soluție
moment final fix.
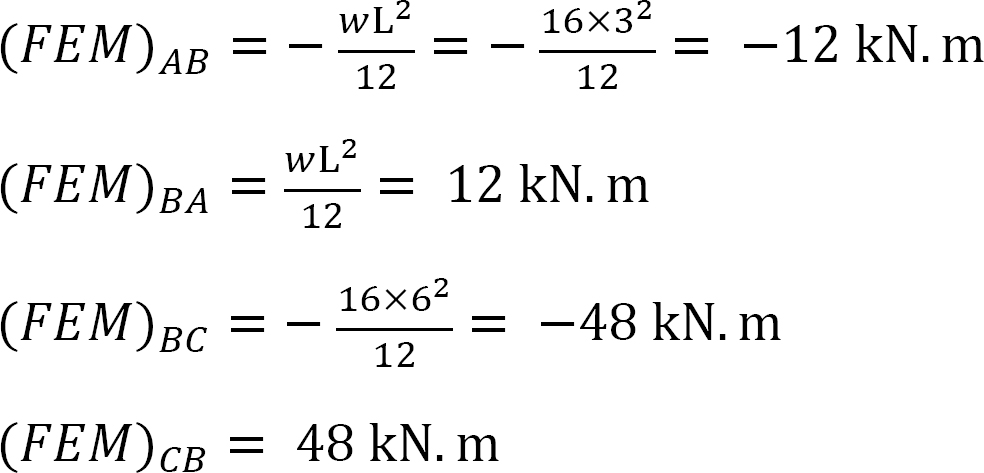
factorul de rigiditate.
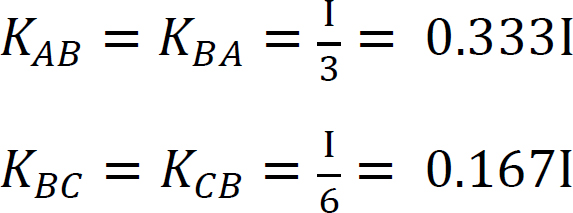
factorul de distribuție.
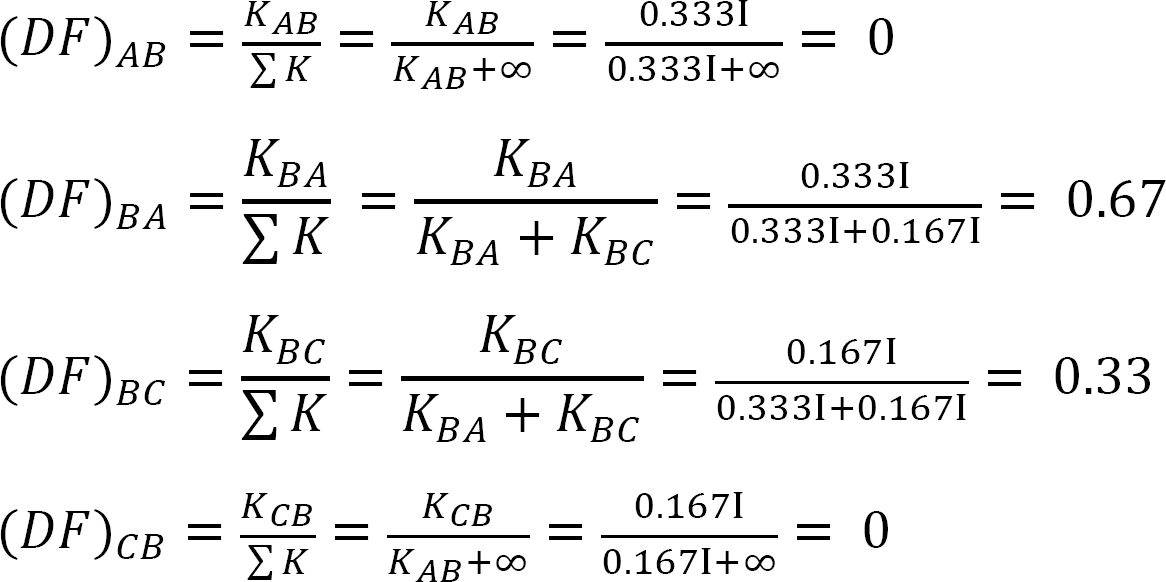
tabelul 12.1. Tabel de distribuție.
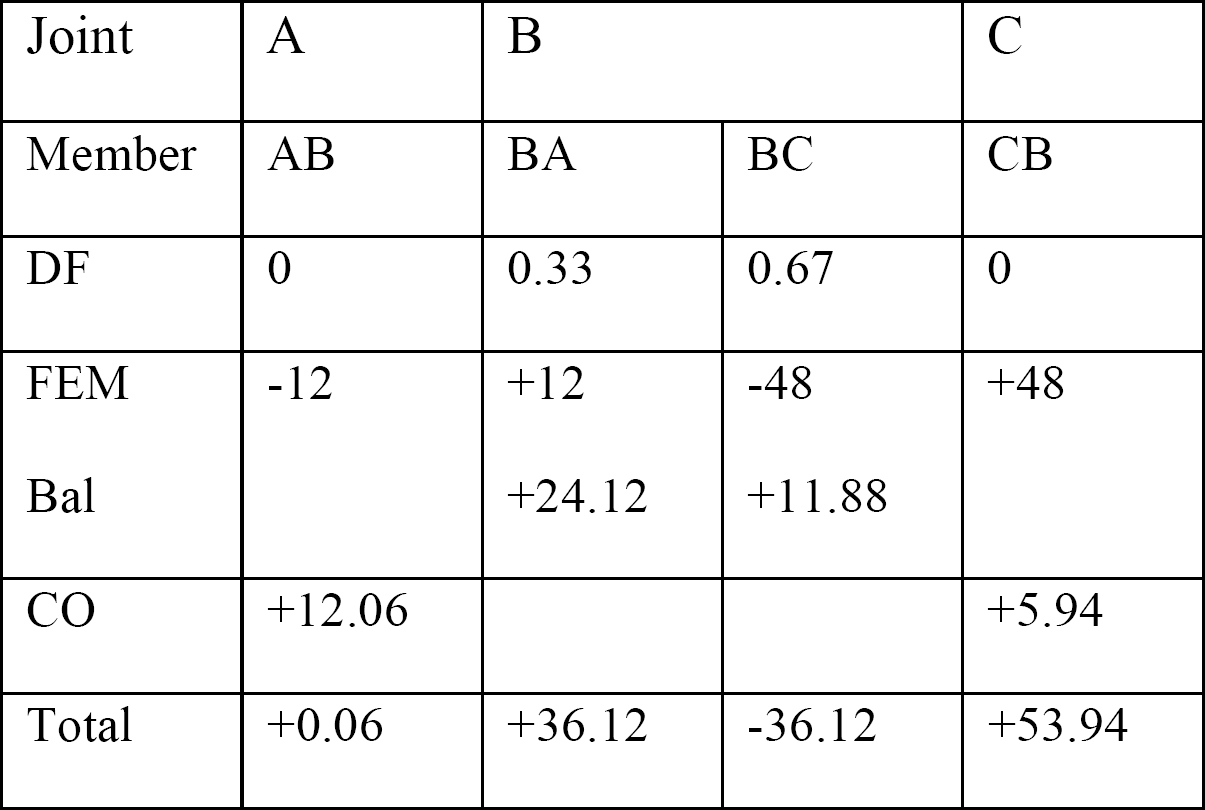
forța de forfecare și diagramele momentului de îndoire.
exemplu 12.2
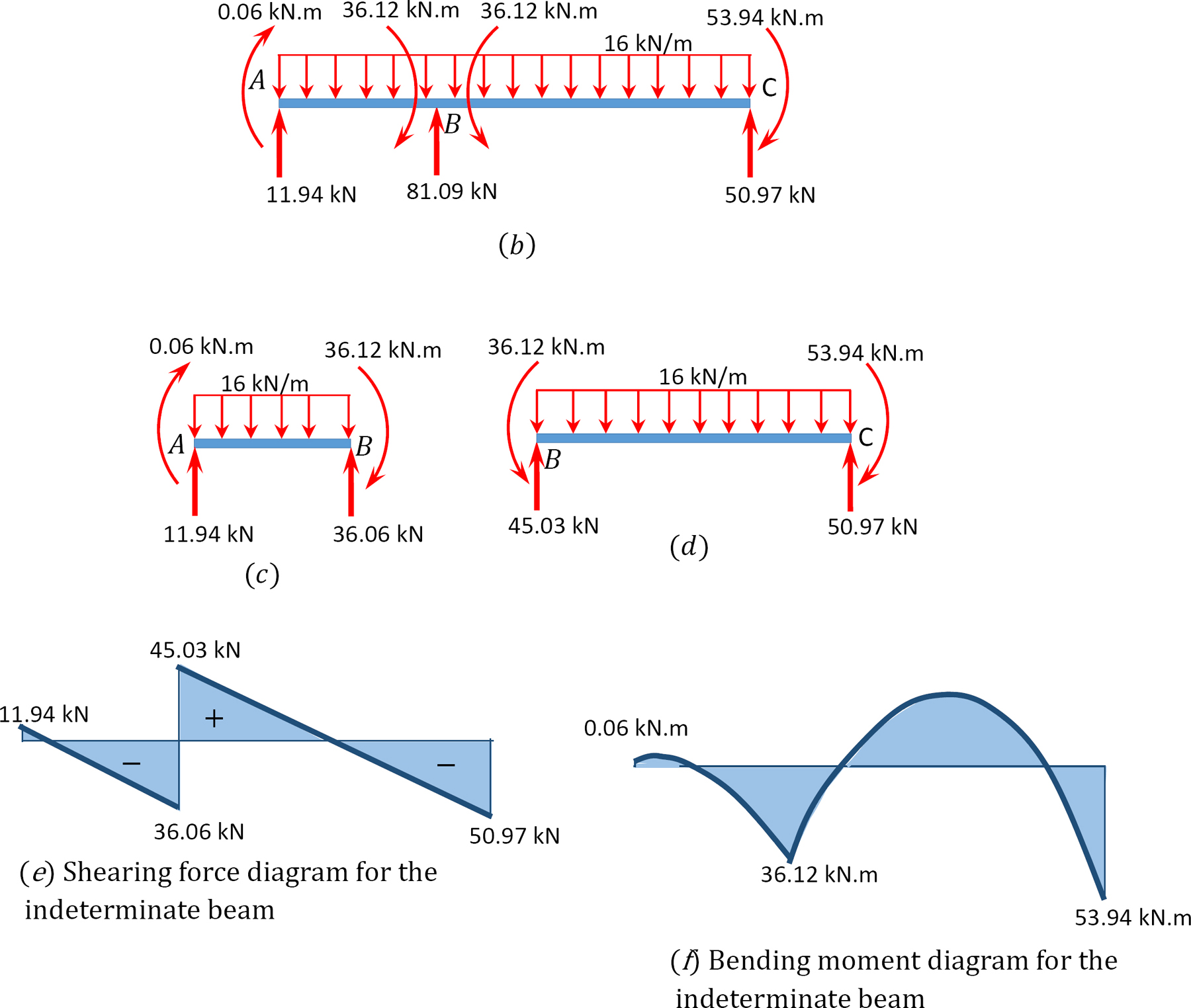
folosind metoda distribuției momentului, determinați momentele finale și reacțiile la suporturile fasciculului prezentate în figura 12.7 a. desenați diagramele forței de forfecare și ale momentului de îndoire.
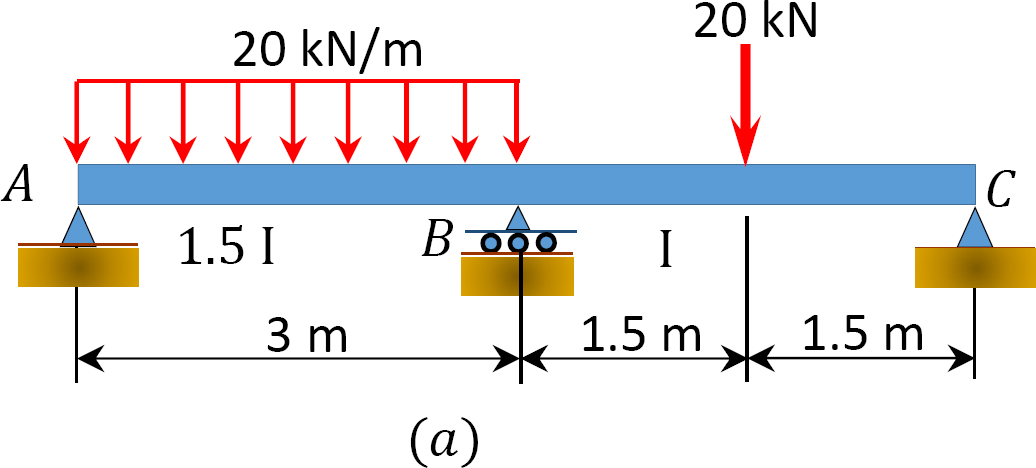
Fig. 12.7. Beam.
soluție
moment final fix.
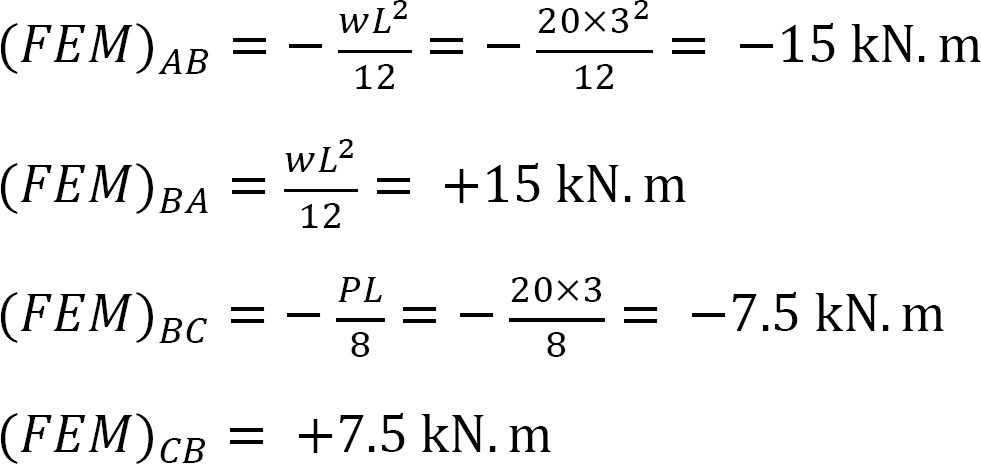
factorul de rigiditate.
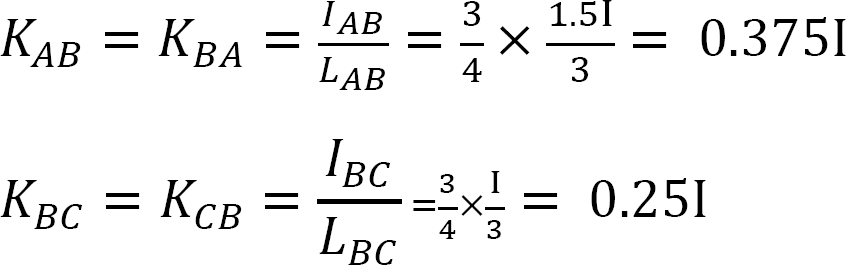
factorul de distribuție.
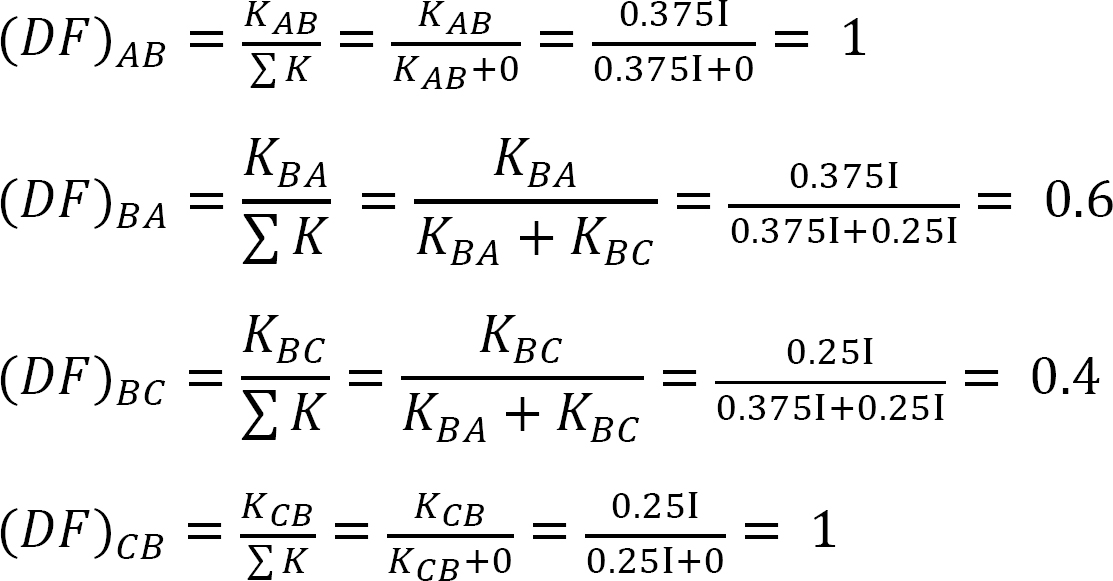
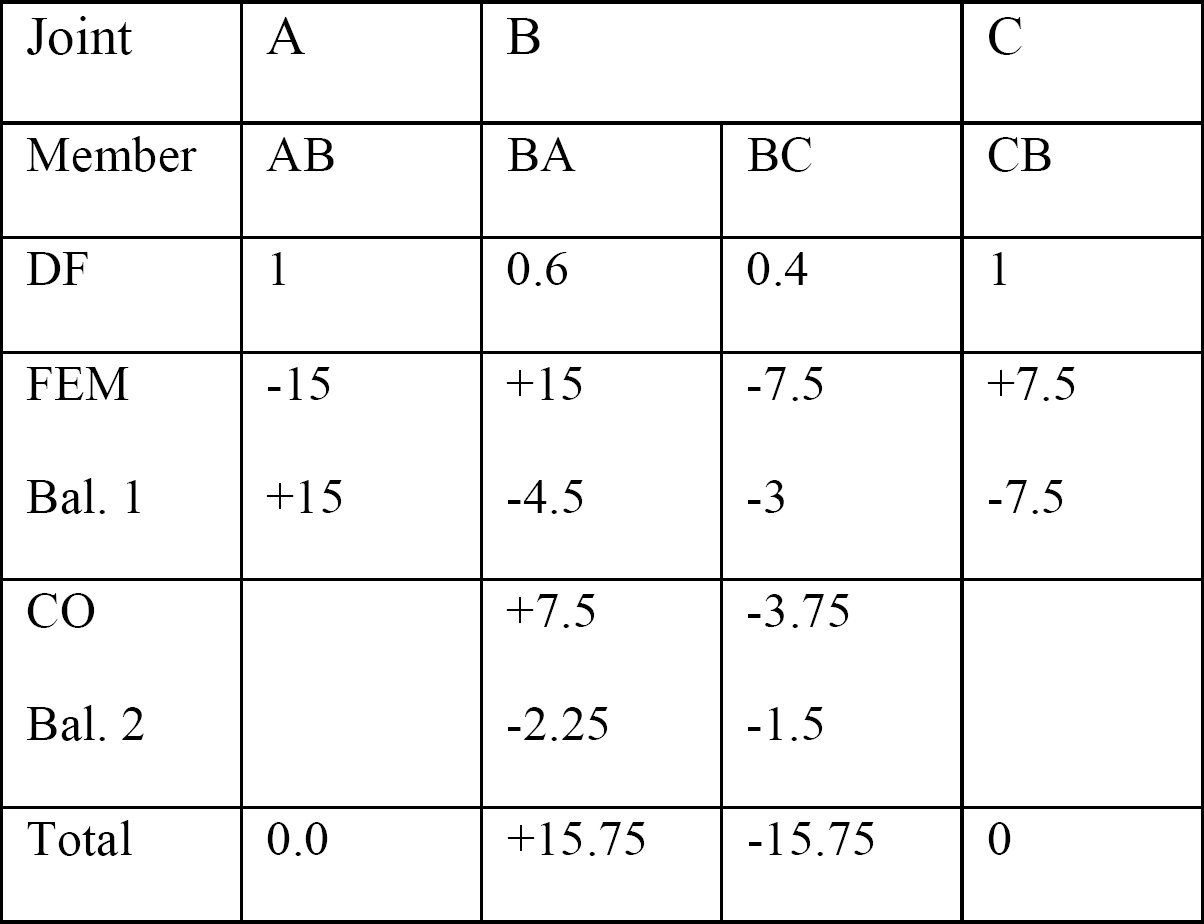
tabelul 12.2. Tabel de distribuție.
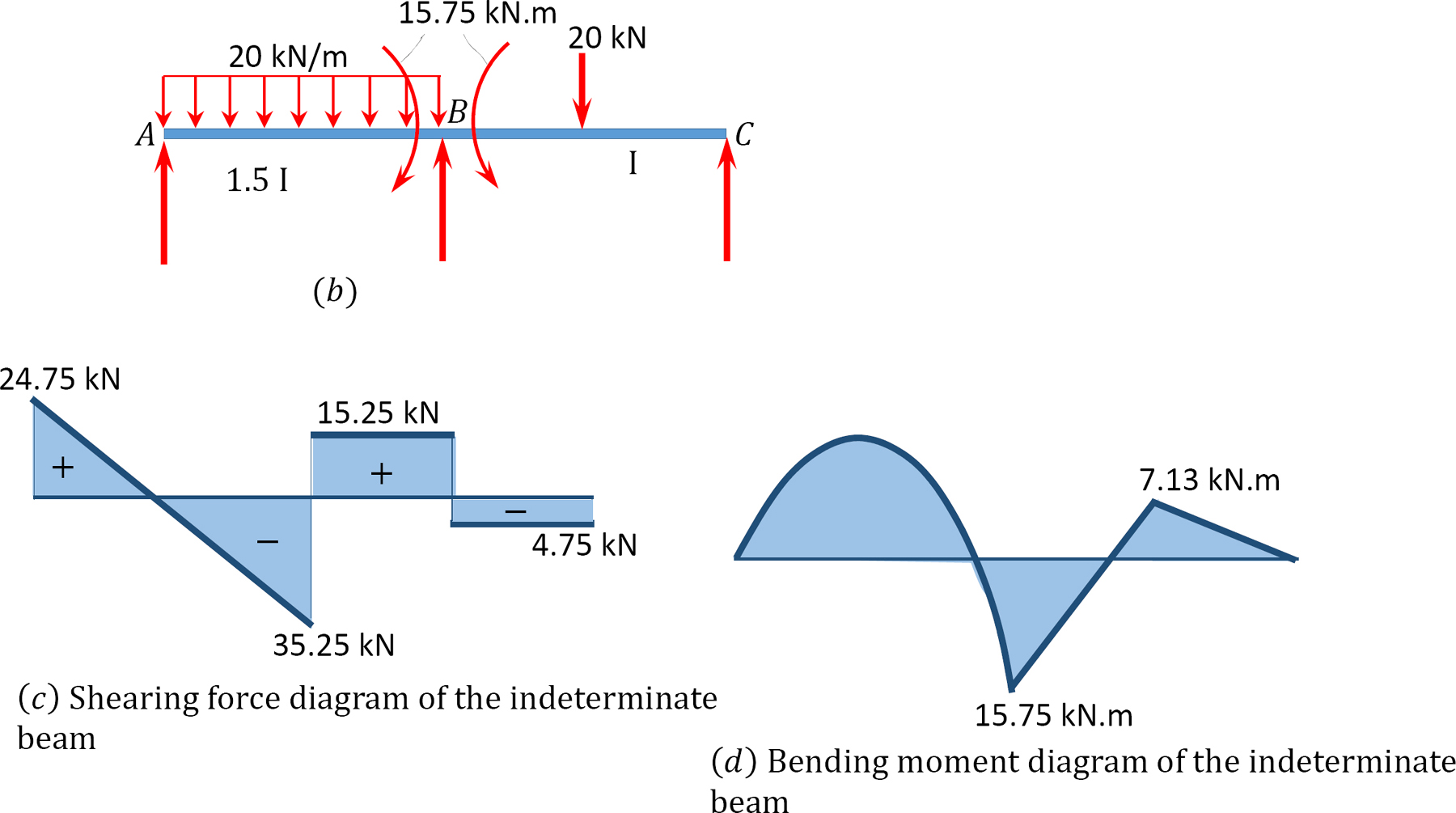
forța de forfecare și diagramele momentului de îndoire.
12.6 analiza cadrelor nedeterminate
procedura de analiză a cadrelor folosind metoda distribuției momentului depinde de tipul de cadru care este analizat. Cadrele sunt clasificate ca cadre sway – sau non-sway. Procedura de analiză a cadrelor non-sway este similară cu cea a grinzilor nedeterminate. Dar pentru analiza cadrelor sway, procedura este diferită. Există două etape implicate în analiza cadrelor sway, și anume etapa non-sway și analizele sway-stage. Aceste etape sunt descrise mai jos.
procedura de analiză a cadrelor Sway nedeterminate prin metoda distribuției momentului
A. Analiza etapei non-sway
•presupuneți mai întâi existența unui suport imaginar care împiedică balansarea cadrului.
•calculați reacțiile orizontale la suporturile cadrului și notați diferența X. Aceasta este forța pentru a preveni balansarea.
B. Analiza etapei Sway
•asumați momente arbitrare pentru a acționa asupra coloanelor cadrului. Magnitudinea acestor momente va varia de la coloană la coloană proporțional cu 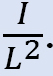
•valorile sunt asumate pentru M2, iar M1 este determinat.
•momentele arbitrare sunt apoi distribuite ca pentru condiția non-sway
•calculați magnitudinea reacțiilor orizontale la suporturile pentru condiția sway. Însumarea acestor reacții dă forța de deplasare arbitrară Y.
•determinați raportul 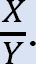 acest raport se numește factorul de balansare.
acest raport se numește factorul de balansare.
•utilizați factorul sway pentru a multiplica momentele distribuite ale sway. Acest lucru oferă momentul corectat pentru balansare.
•momentele finale pentru cadru sunt însumarea momentelor obținute în etapa non-sway și momentul corectat pentru etapa sway.
exemplu 12.3
folosind metoda de distribuție a momentului, determinați momentele finale ale membrilor cadrului prezentate în figura 12.8. EI = constantă.
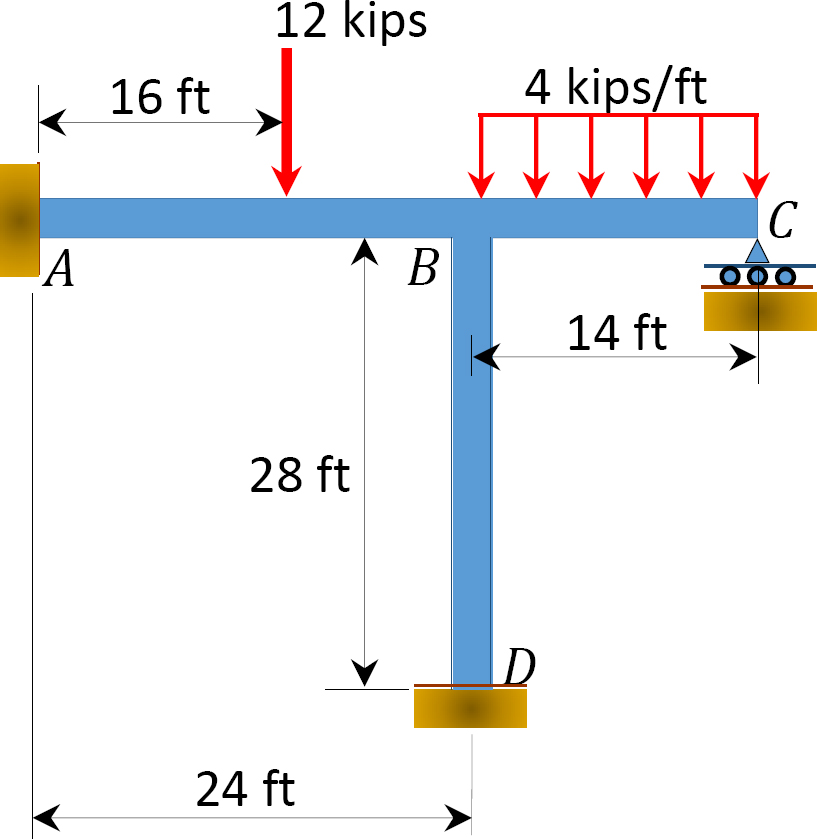
Fig. 12.8. Cadru.
soluție
moment final fix.
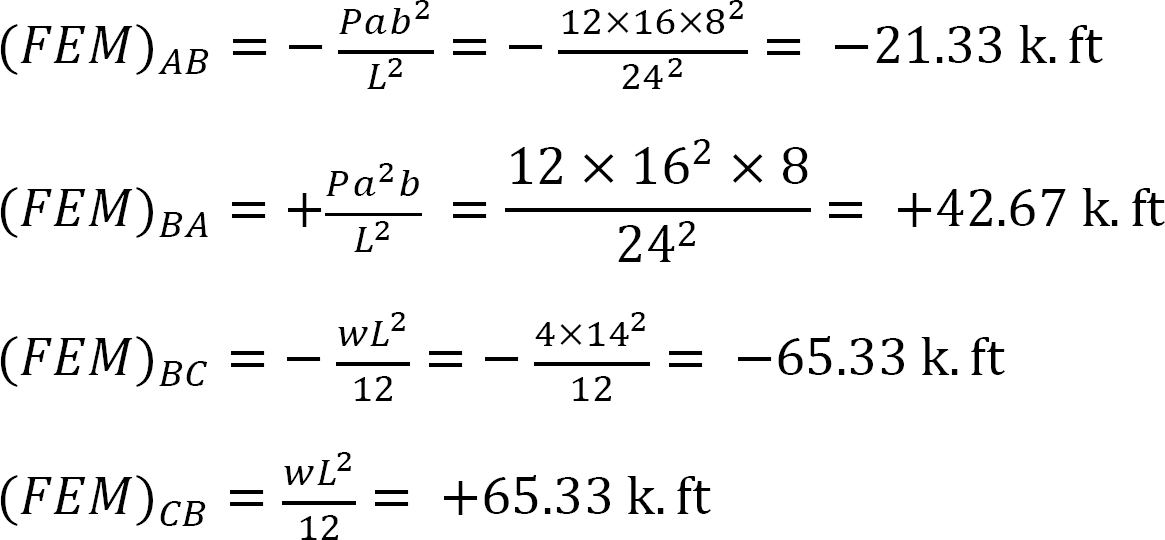
factorul de rigiditate.
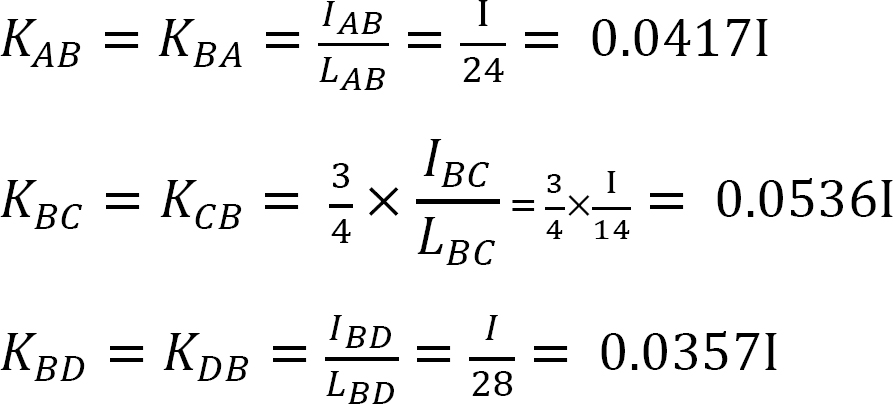
factorul de distribuție.
tabelul 12.3. Tabel de distribuție.
momentele finale ale membrilor.
Substituirea valorilor obținute de la EK la EK în ecuațiile momentului final sugerează următoarele:
MAB = -12.48 K. ft
MBA = +60.37 K. ft
MBC = -75.31 K. ft
MBD = +14,94 K. ft
MCB = 0
MDB = +7,47 K. ft
exemplul 12.4
folosind metoda de distribuție a momentului, determinați momentele finale la suporturile cadrului prezentate în figura 12.9. EI = constantă.
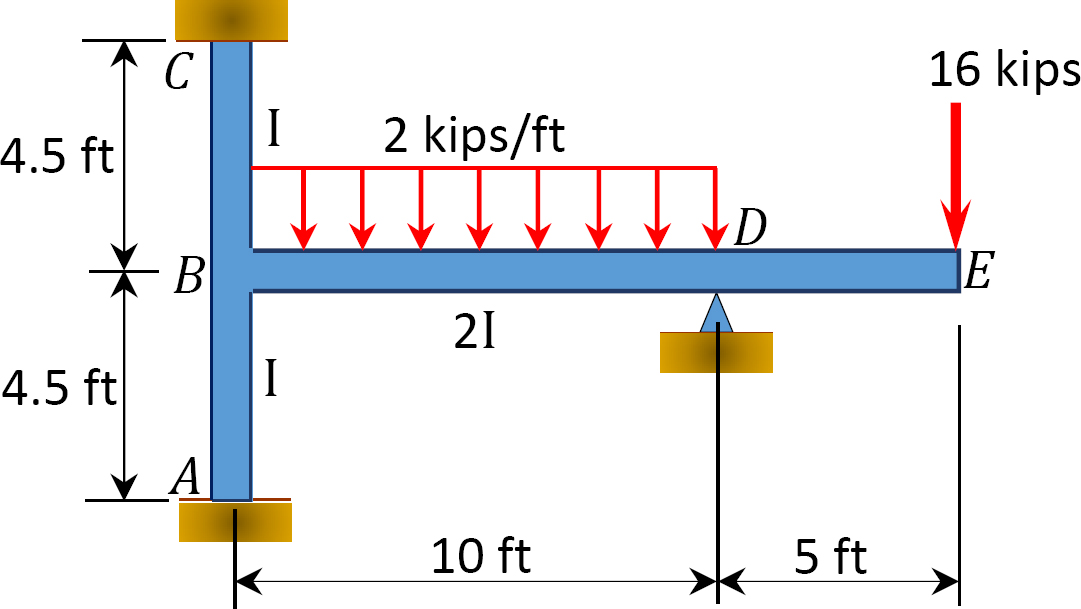
Fig. 12.9. Cadru.
soluție
moment final fix.
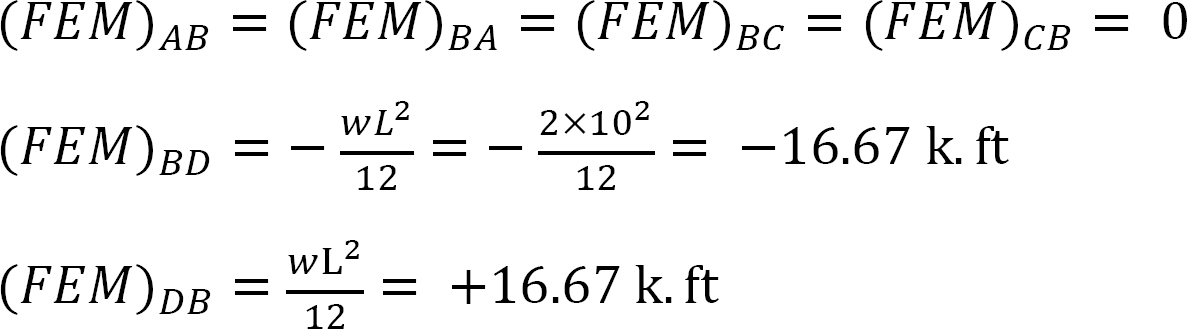
factorul de rigiditate.
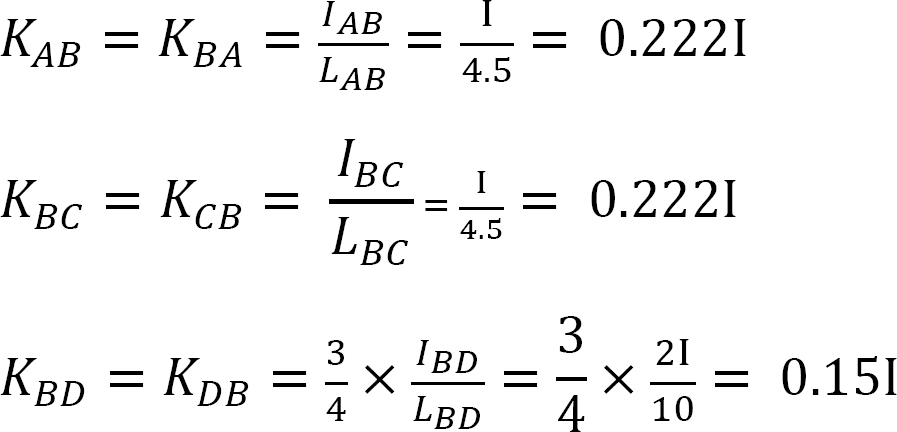
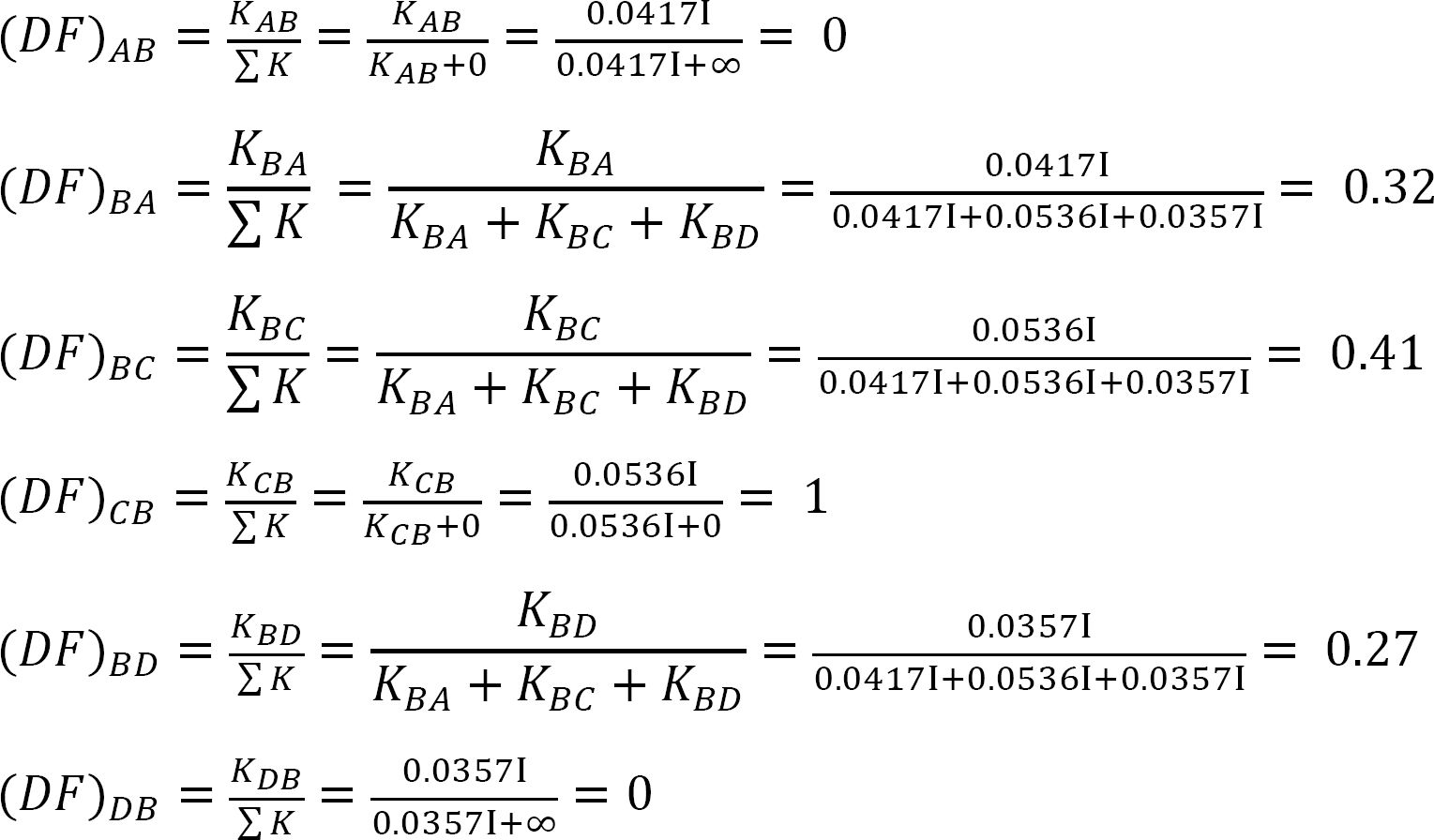
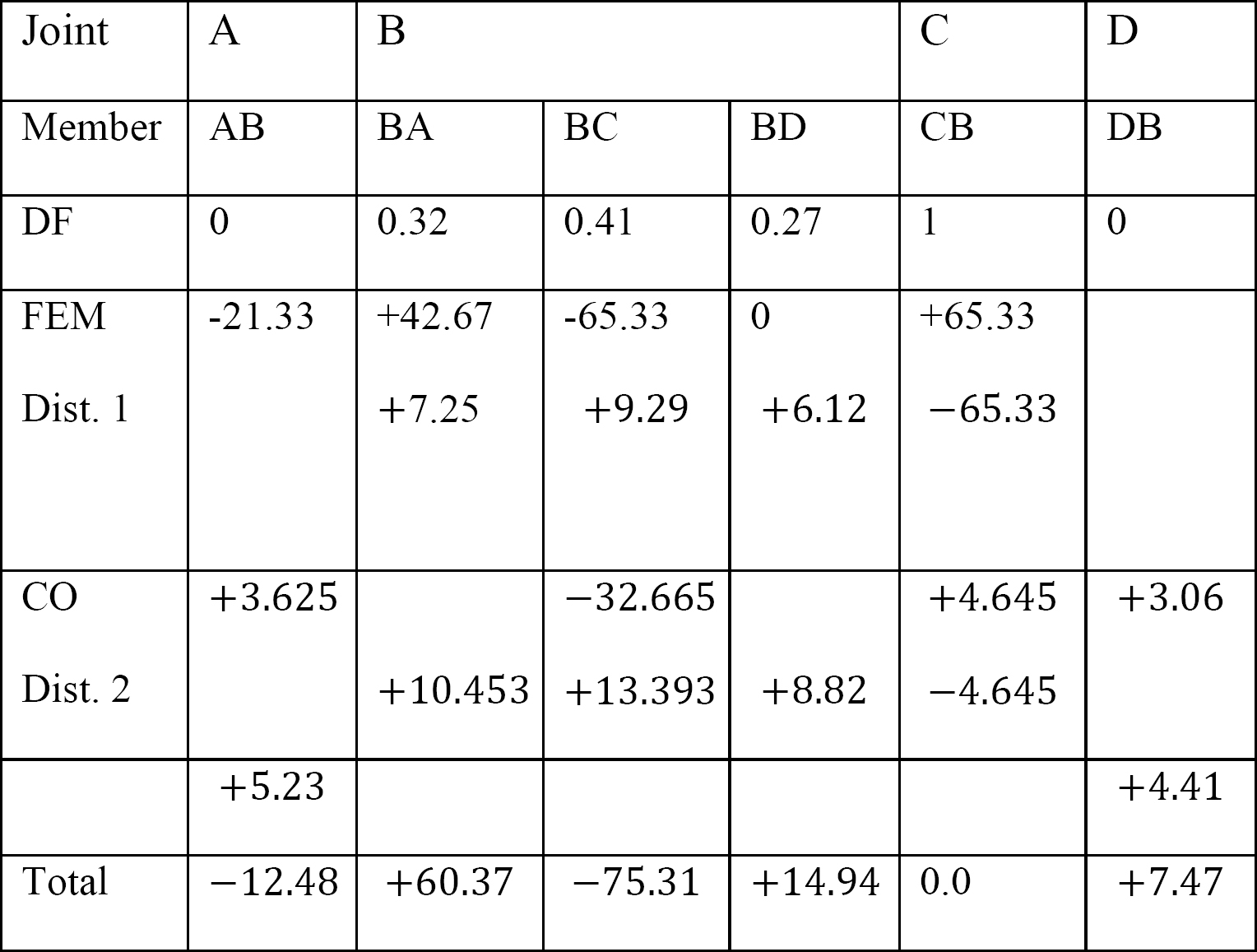
factorul de distribuție.

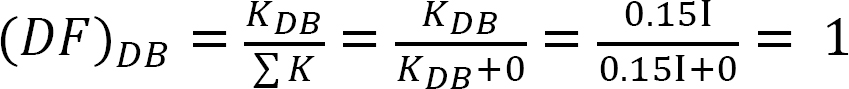
tabelul 12.4. Tabel de distribuție.
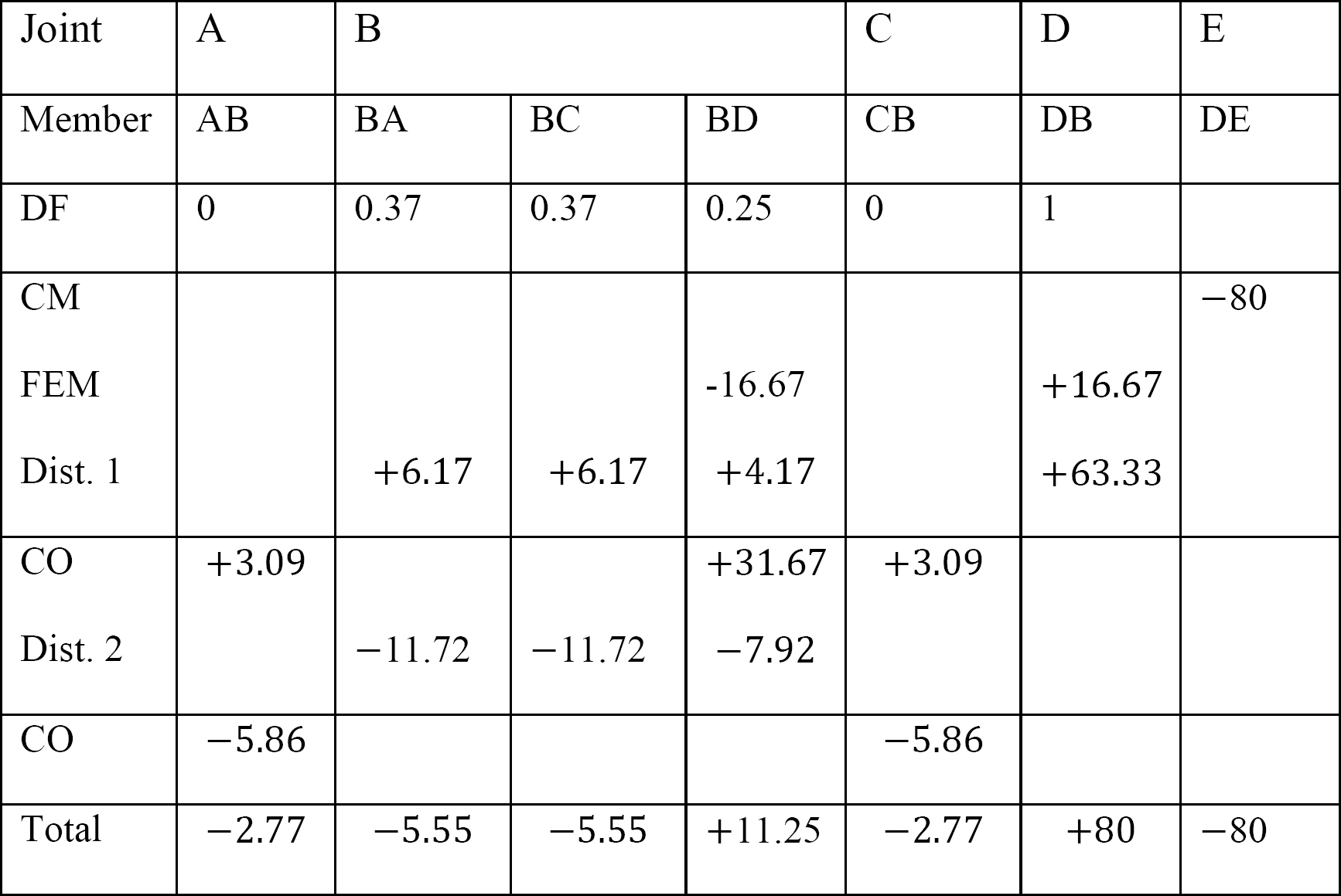
momentele finale ale membrilor.
MAB = -2.77 K. ft
MBA = -5.55 K. ft
MBC = -5.55 k. ft
MBD = +11,25 K. ft
MCB = -2,77
MDB = + 80 K. ft
MDE = -80 K. ft
exemplu 12.5
folosind metoda de distribuție a momentului, determinați momentele finale la suporturile cadrului prezentate în figura 12.10. EI = constantă.
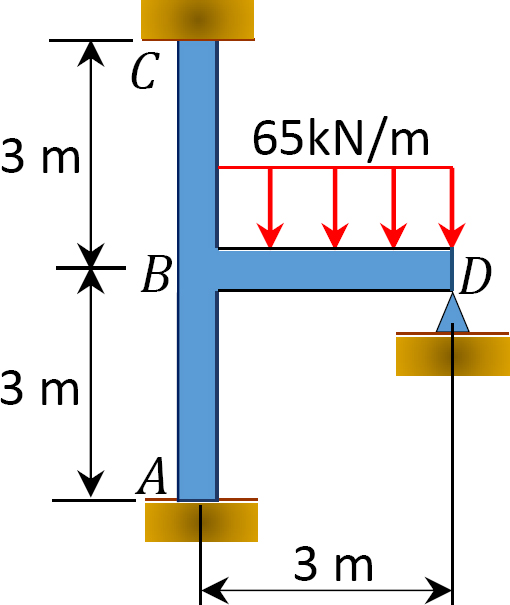
Fig. 12.10. Cadru.
soluție
moment final fix.
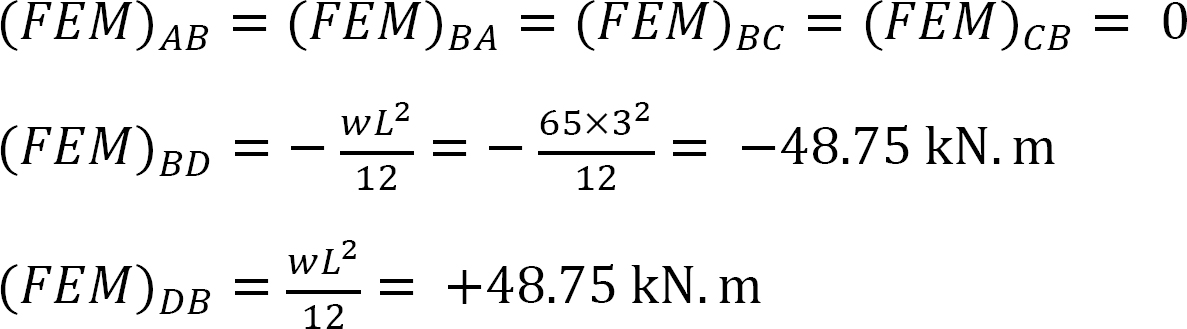
factorul de rigiditate.
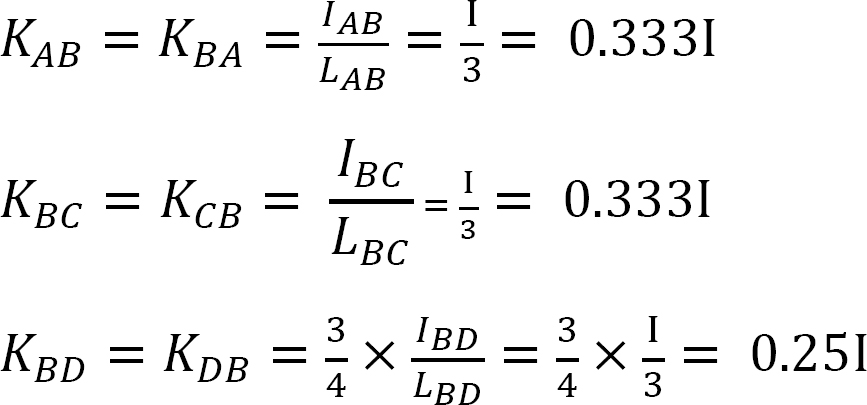
factorul de distribuție.
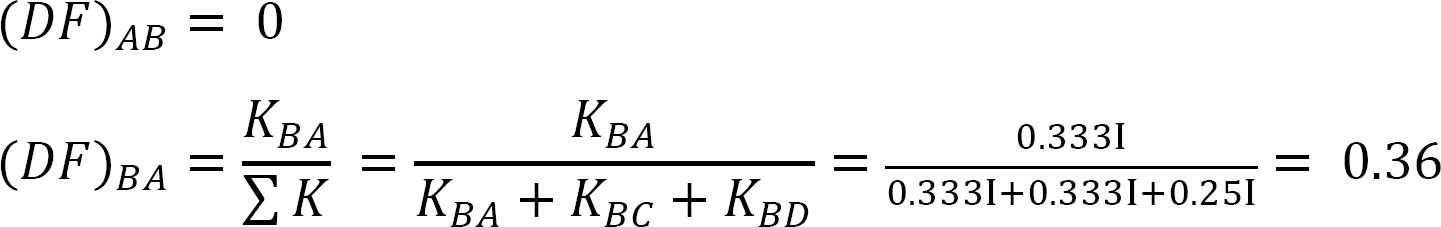

tabelul 12.5. Tabel de distribuție.
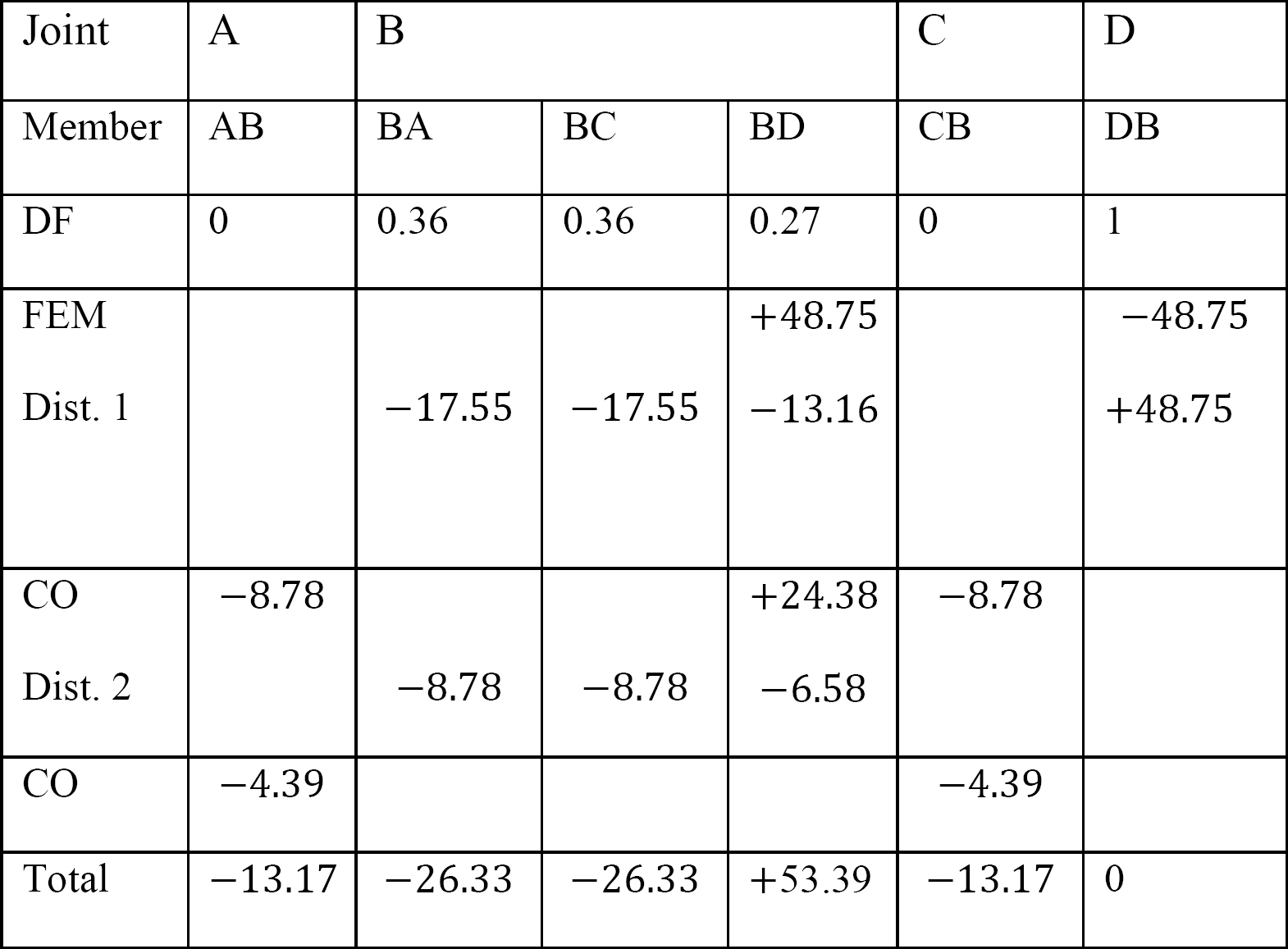
momentele finale ale membrilor.
MAB = -13.17 K. ft
MBA = -26.33 K. ft
MBC = -26.33 K. ft
MBD = +53.39 K. ft
MCB = -13.17 K. ft
MDB = 0
exemplu 12.6
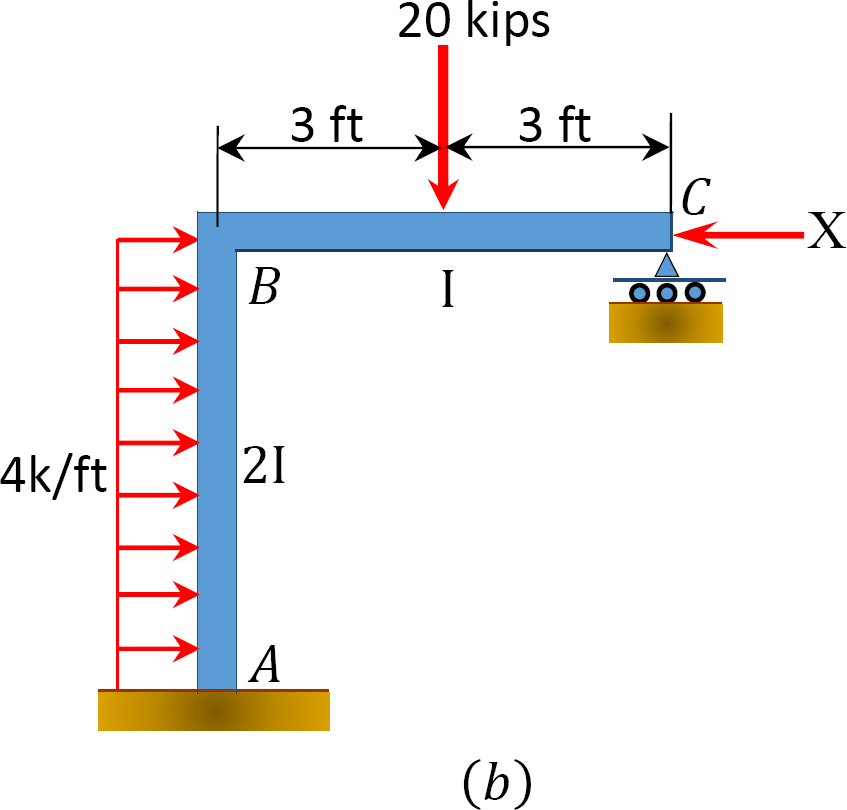
folosind metoda de distribuție a momentului, determinați momentele finale ale cadrului cu balansare laterală prezentate în figura 12.11 a.
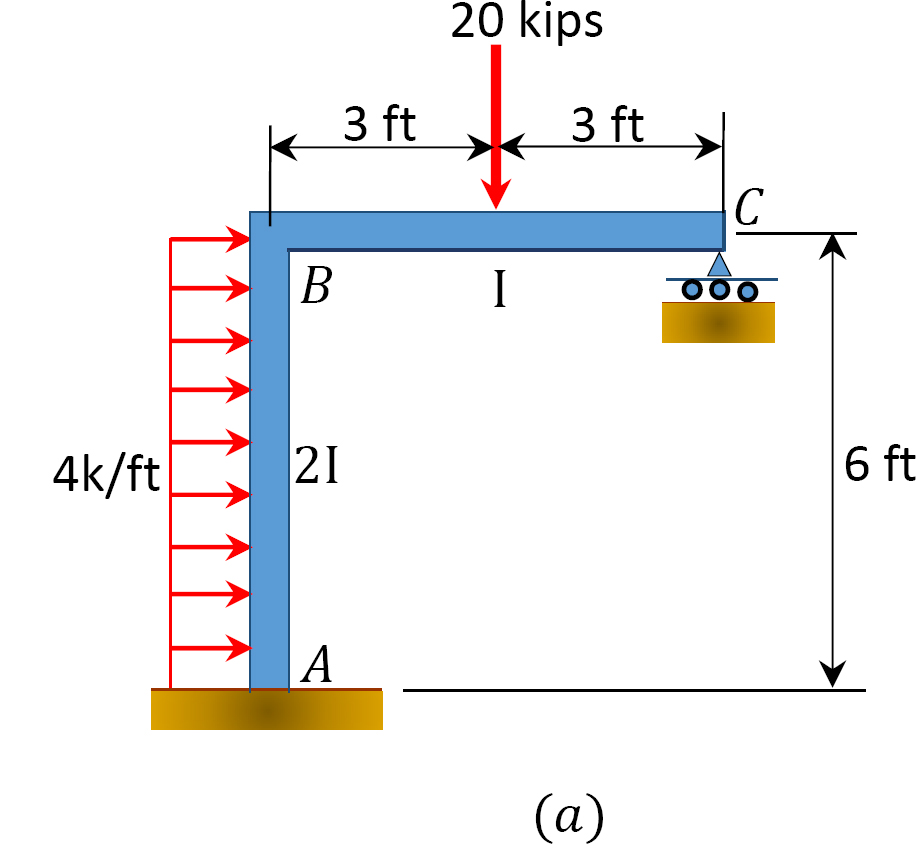
Fig. 12.11. Cadru cu balansare laterală.
soluție
moment final fix.
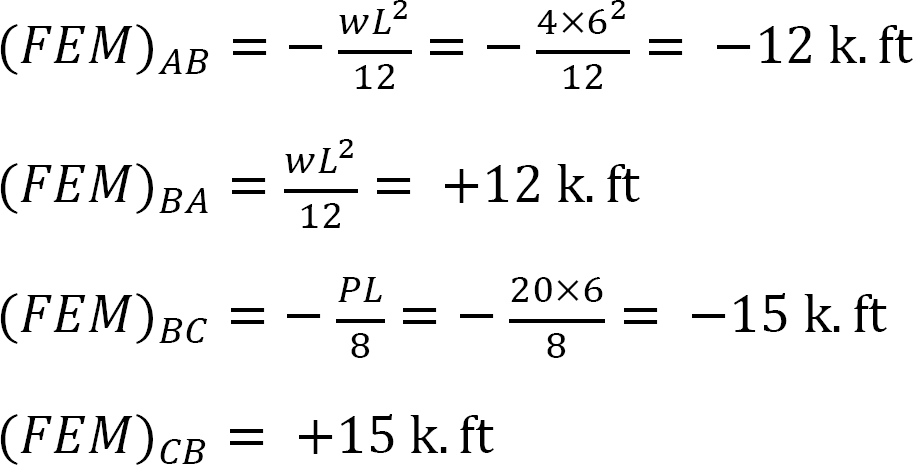
factorul de rigiditate.
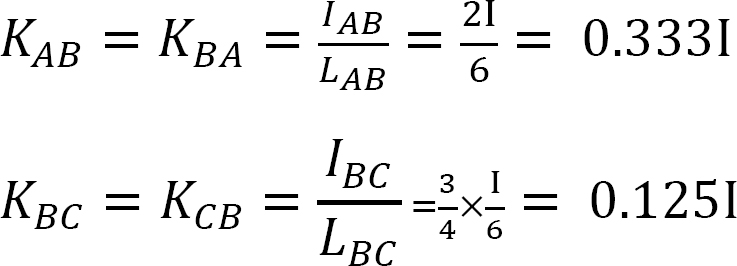
factorul de distribuție.
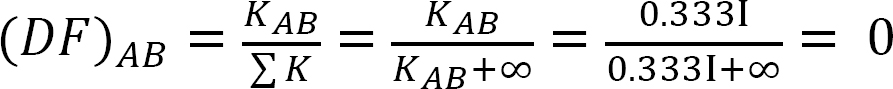

Analiza cadrului fără balansare laterală.
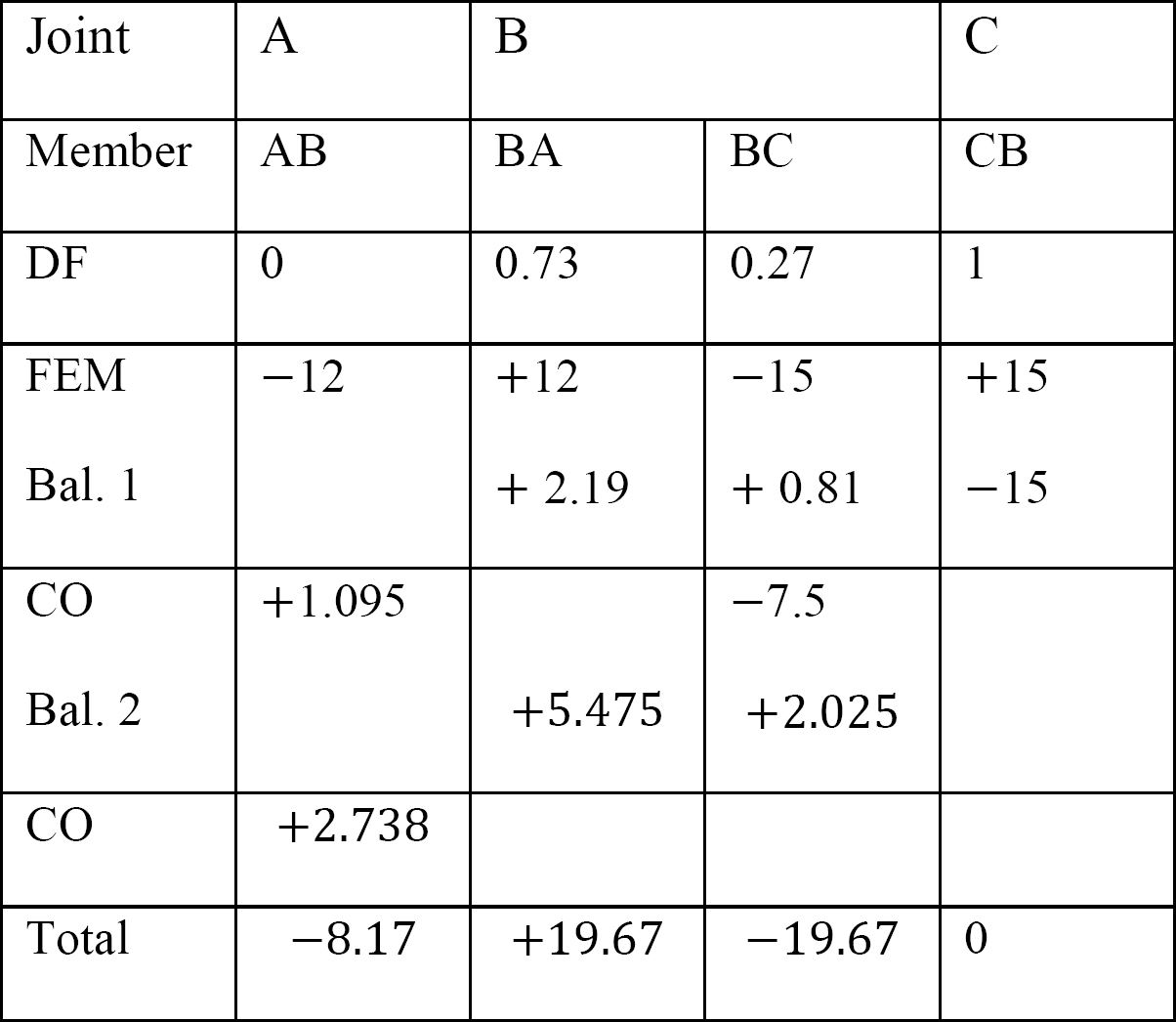
tabelul 12.6. Tabel de distribuție (fără cadru de balansare).
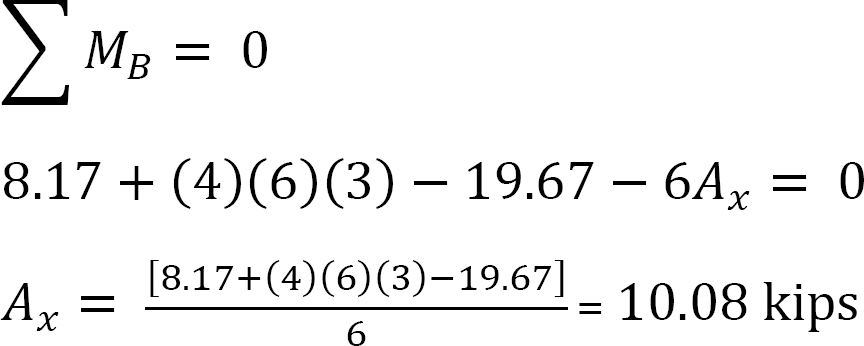
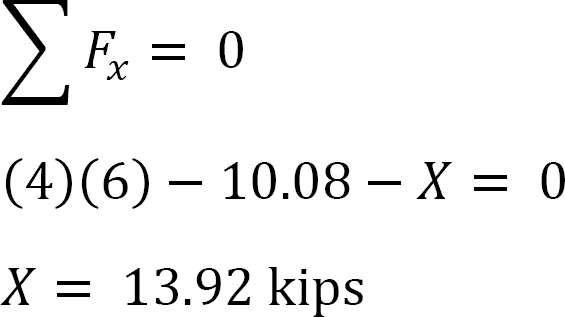
Analiza cadrului cu balansare laterală.
să presupunem că MAB = + 20 K. ft
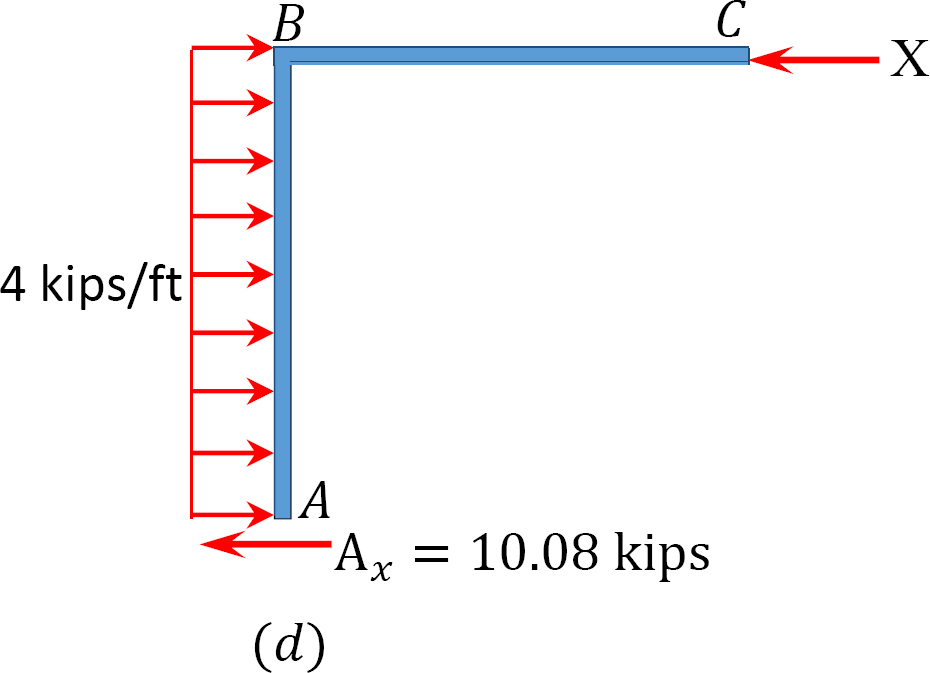
tabelul 12.7. Tabel de distribuție (cadru sway).
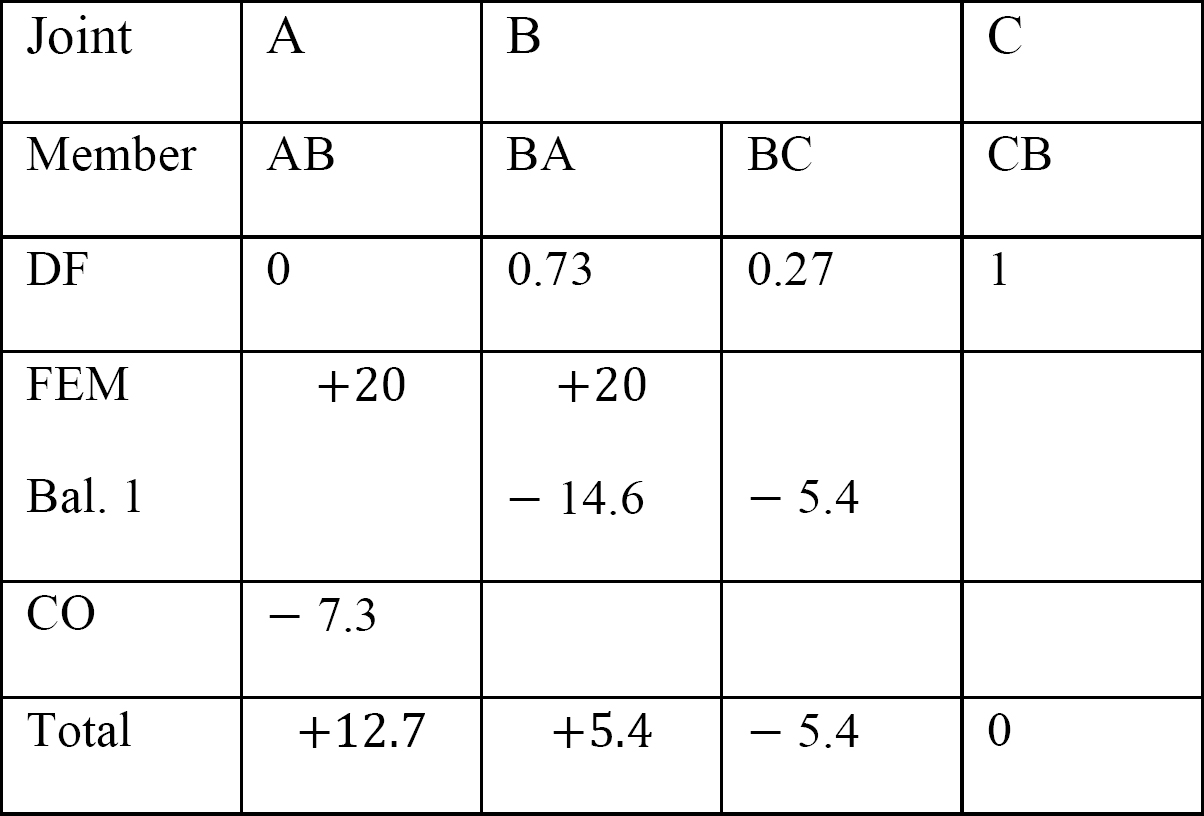
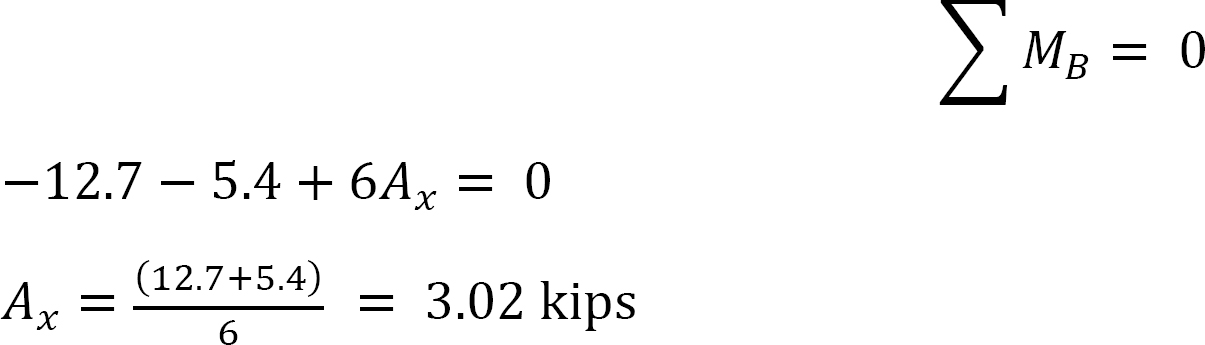
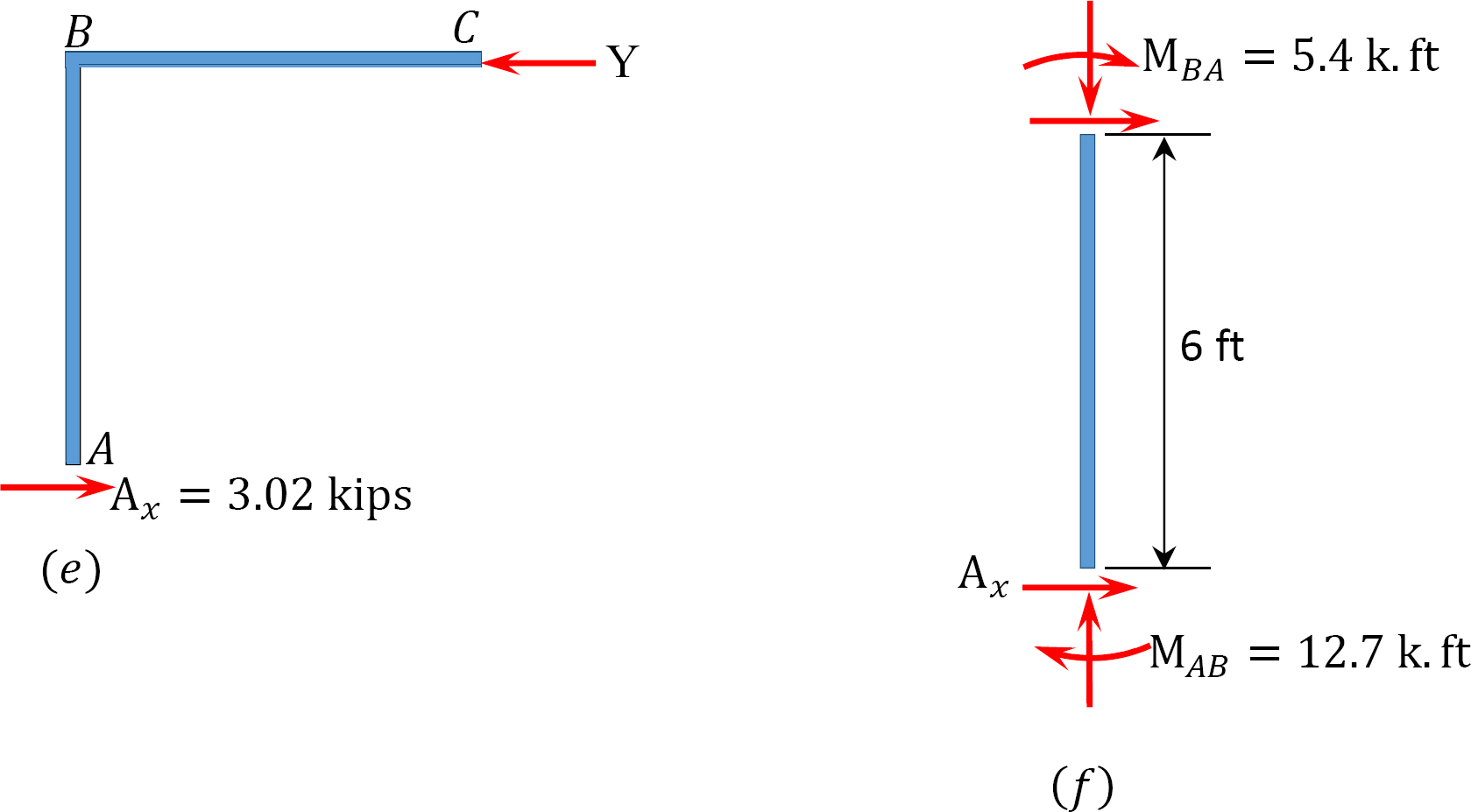
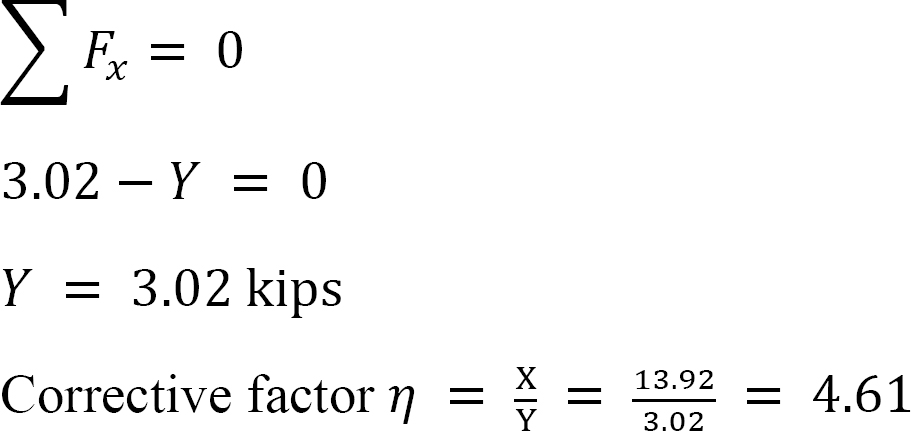
momente finale.
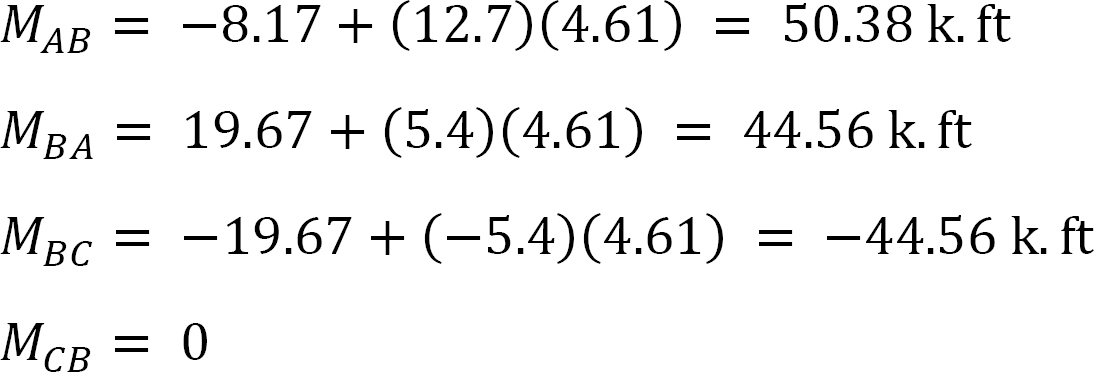
exemplu 12.7
un cadru de balansare este încărcat așa cum se arată în figura 12.12 a. folosind metoda distribuției momentului, determinați momentele finale ale membrilor cadrului.
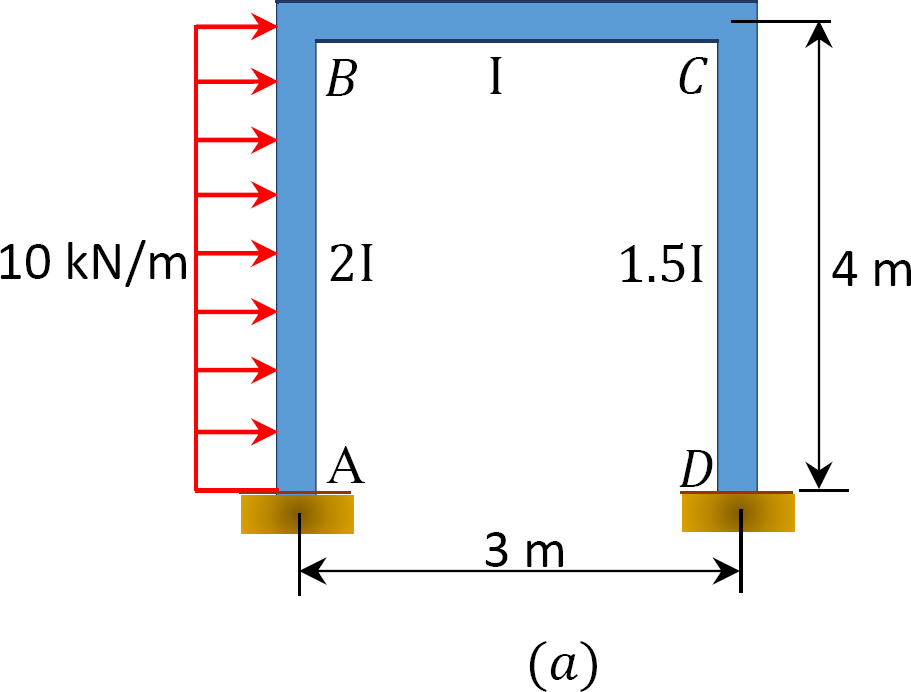
Fig. 12.12. Cadru sway încărcat.
soluție
moment final fix.
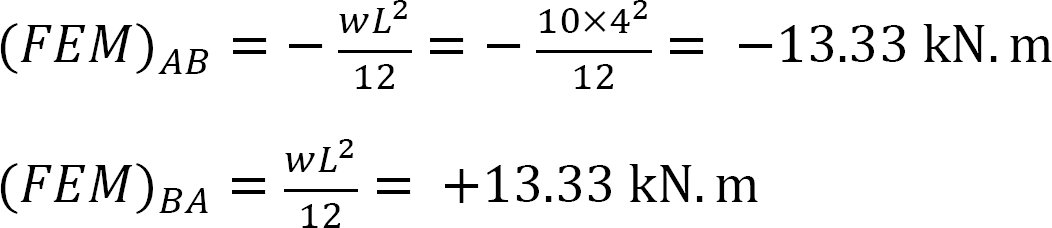
factorul de rigiditate.
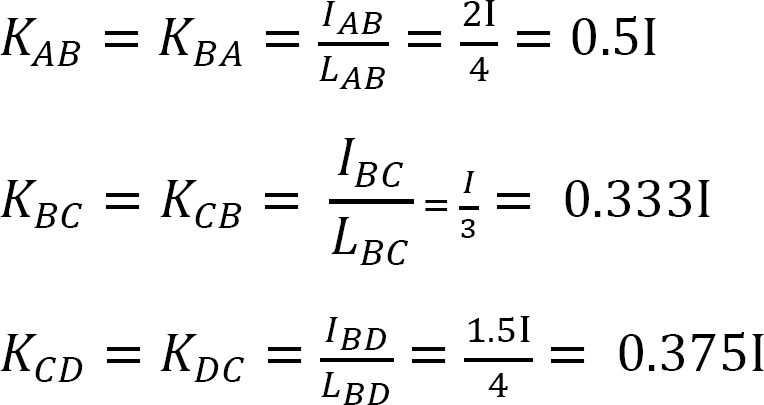
factorul de distribuție.

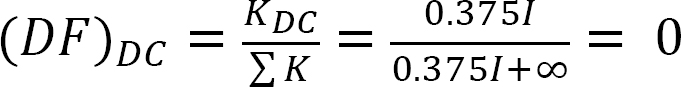
Analiza cadrului fără balansare laterală.
tabelul 12.8. Tabel de distribuție (fără cadru de balansare).
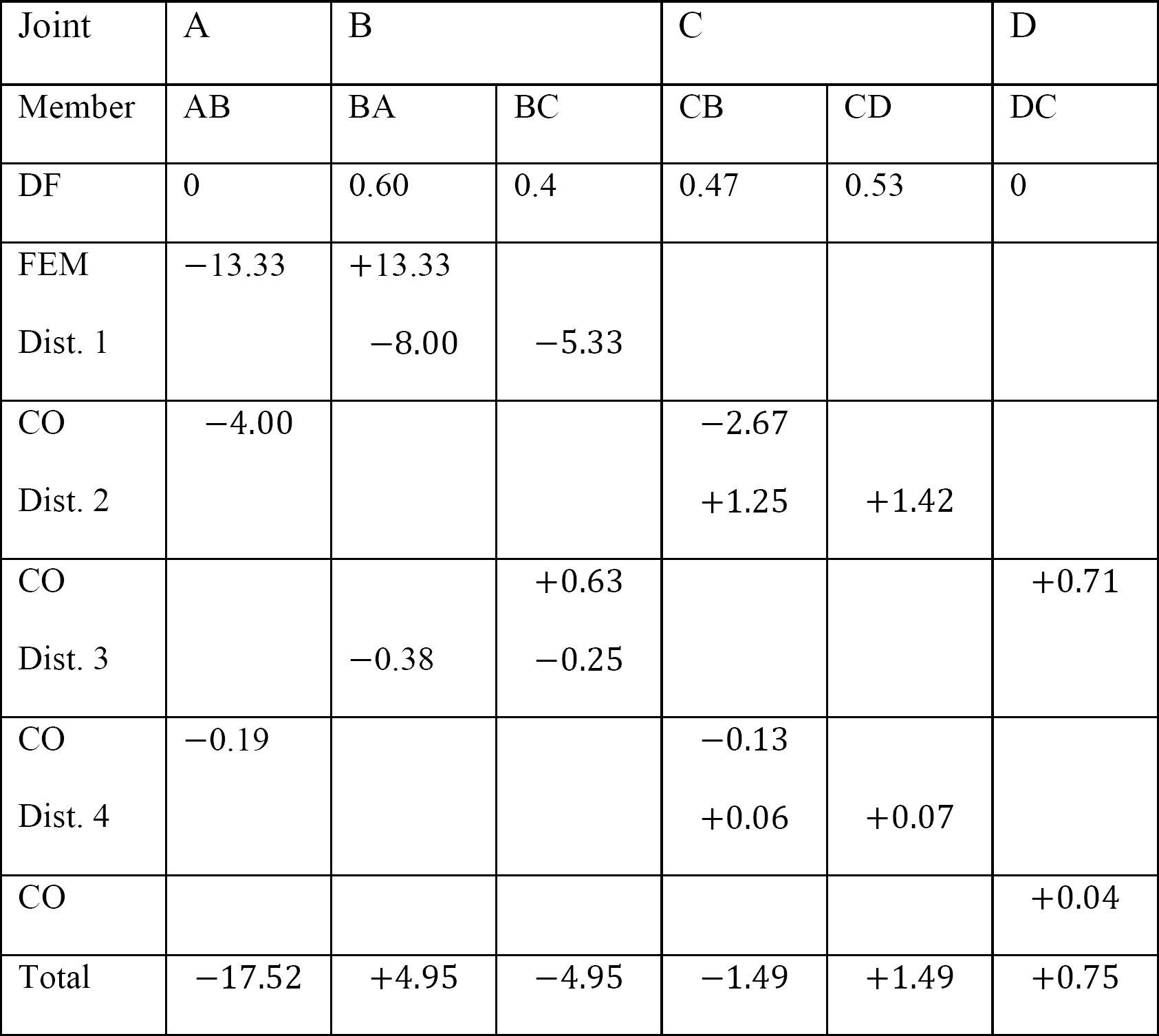
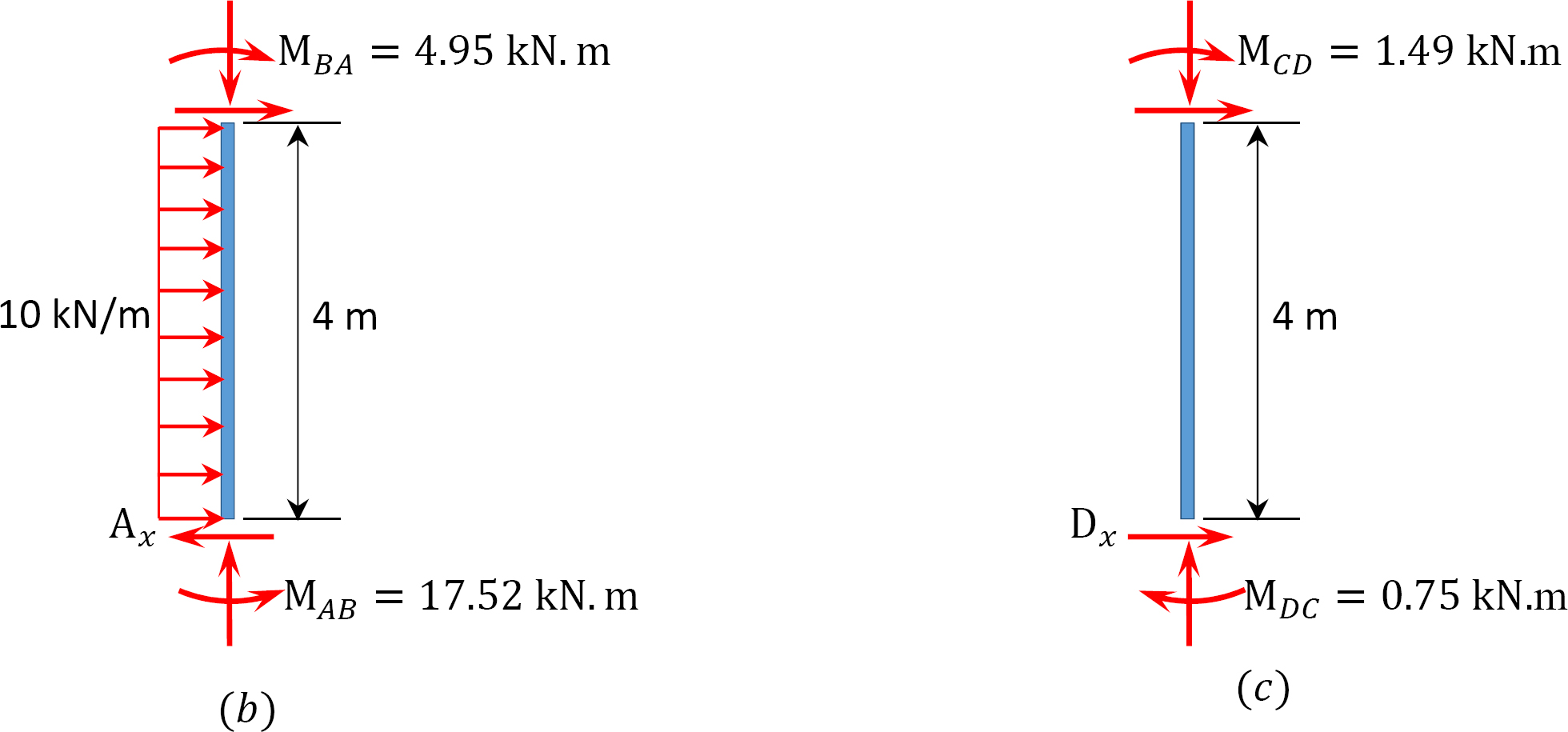
tabelul 12.9. Tabel de distribuție (cadru sway).
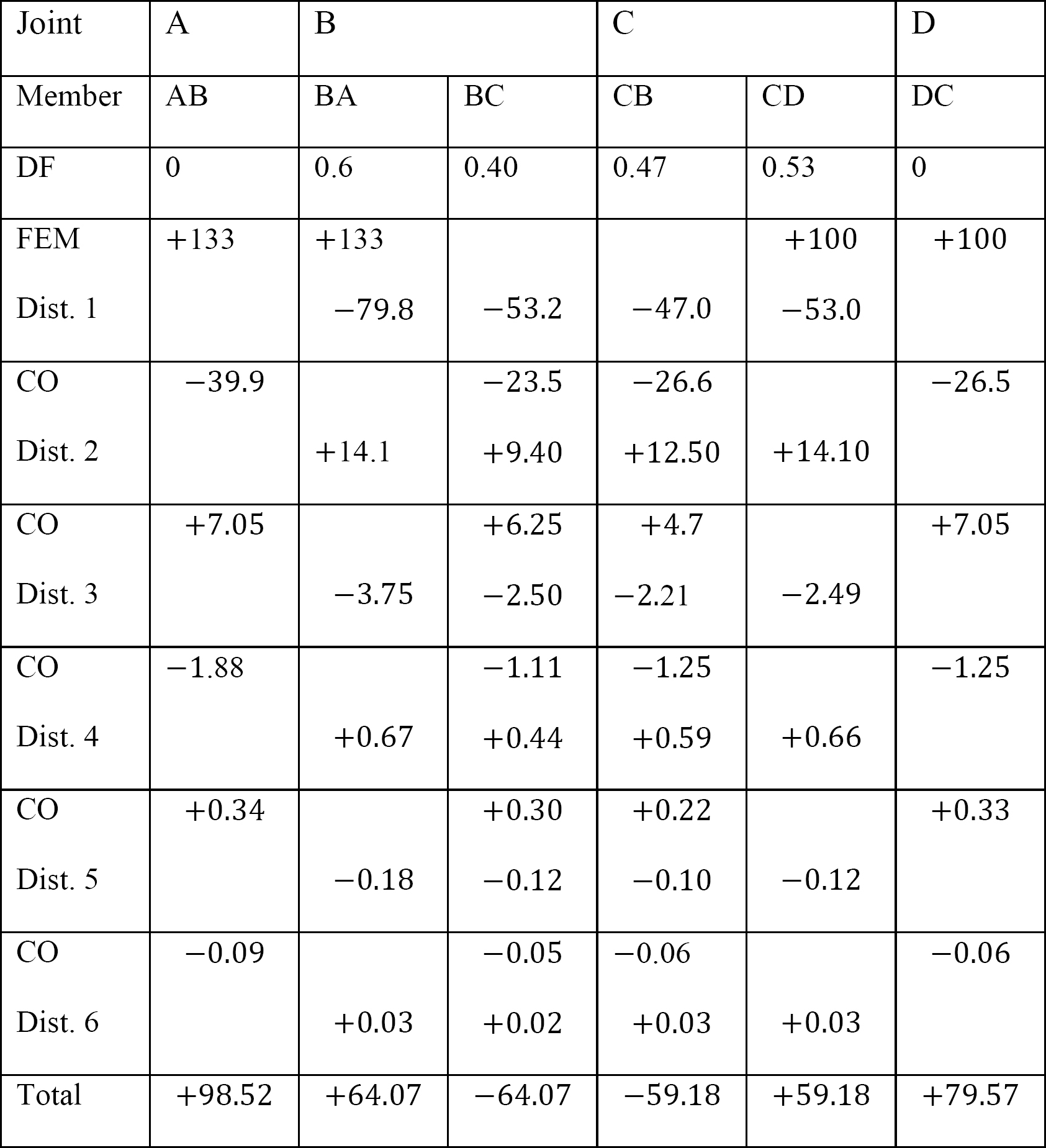
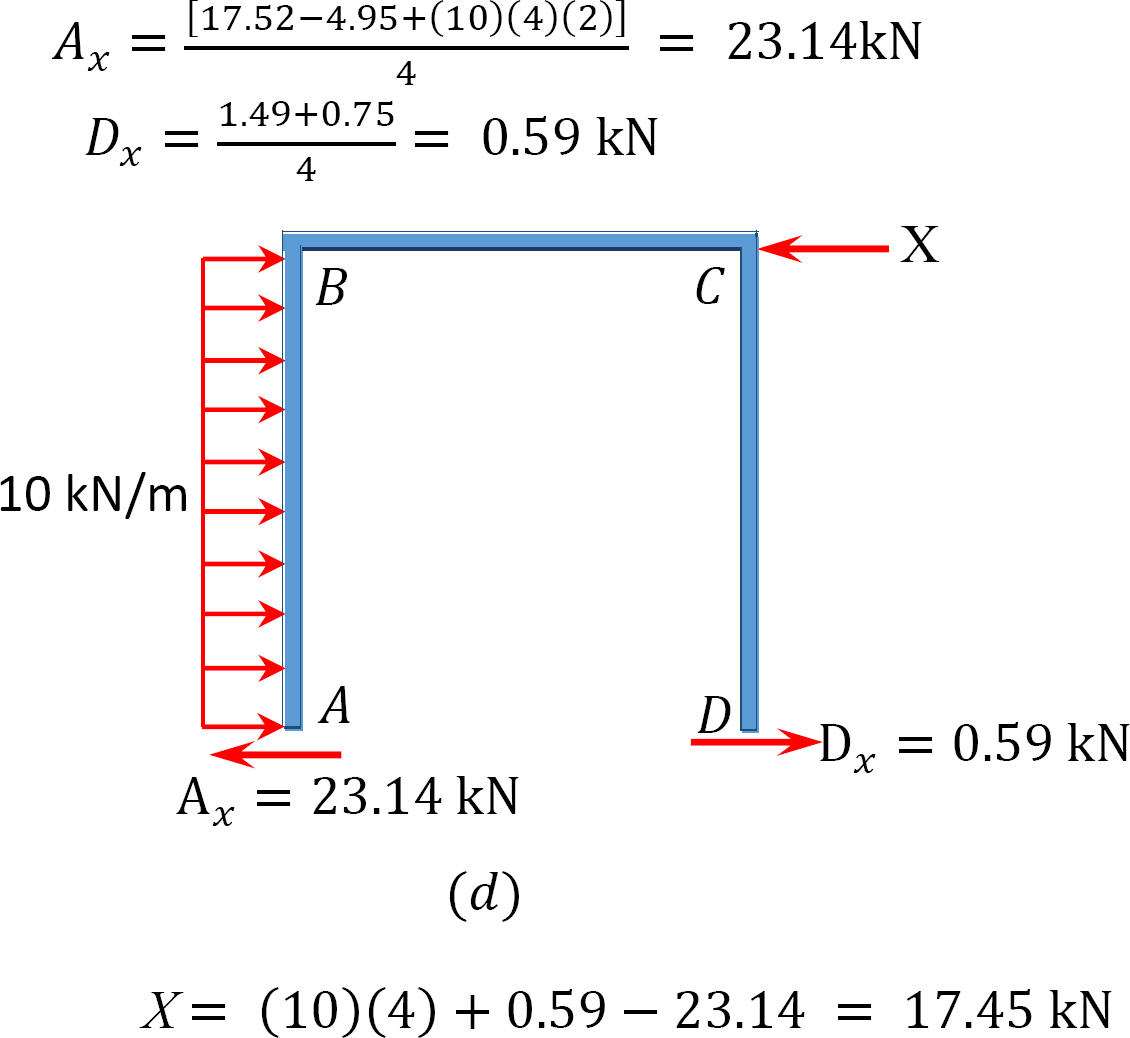
Analiza cadrului cu balansare laterală.
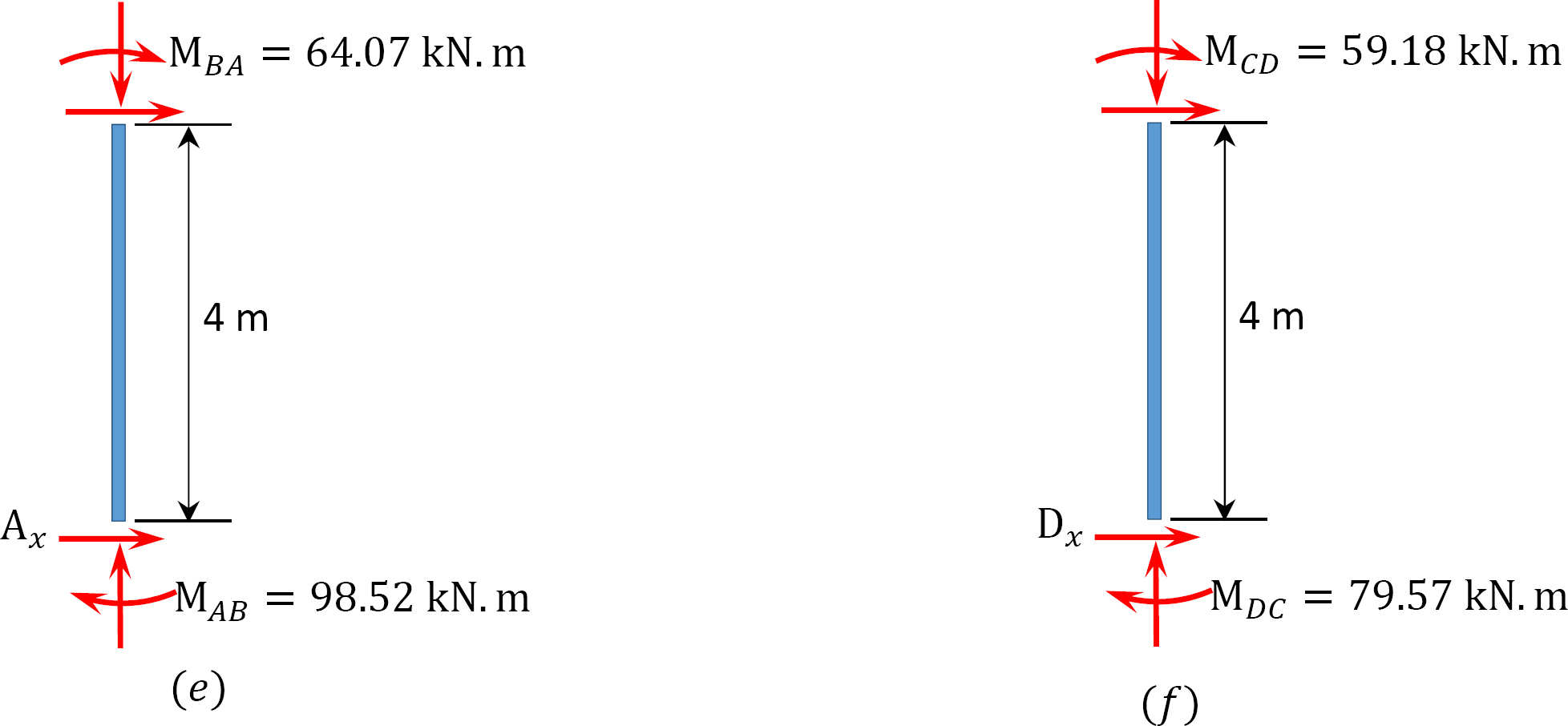

momentul final final.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Rezumatul capitolului
metoda distribuției momentului de analiză a structurilor nedeterminate: metoda distribuției momentului de analiză este o metodă aproximativă de analiză. Gradul său de precizie depinde de numărul de iterații. În această metodă, se presupune că toate îmbinările dintr-o structură sunt blocate temporar sau fixate și, astfel, sunt împiedicate să se rotească posibil. Sarcinile sunt aplicate membrilor, iar momentele dezvoltate la capetele membrilor datorită fixității sunt determinate. Îmbinările din structură sunt apoi deblocate succesiv, iar momentul dezechilibrat la fiecare articulație este distribuit membrilor care se întâlnesc la acea articulație. Reportarea momentelor la capetele îndepărtate ale membrilor este determinată, iar procesul de echilibrare este continuat până la nivelul dorit de precizie. Momentele finale ale membrilor sunt determinate prin adăugarea momentului final fix, momentul distribuit și momentul reportării. Odată ce momentele finale ale membrilor sunt determinate, structura devine determinată.
Probleme De Practică
12.1 utilizați metoda de distribuție a momentului pentru a calcula momentul final al elementelor grinzilor prezentate în figura P12.1 până în figura P12.12 și desenați diagramele momentului de îndoire și forței de forfecare. EI = constantă.
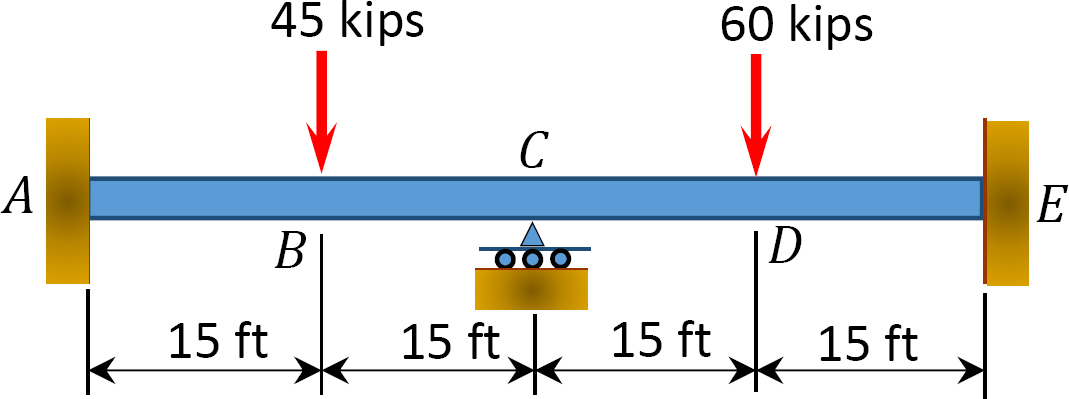
Fig. P12. 1. Beam.
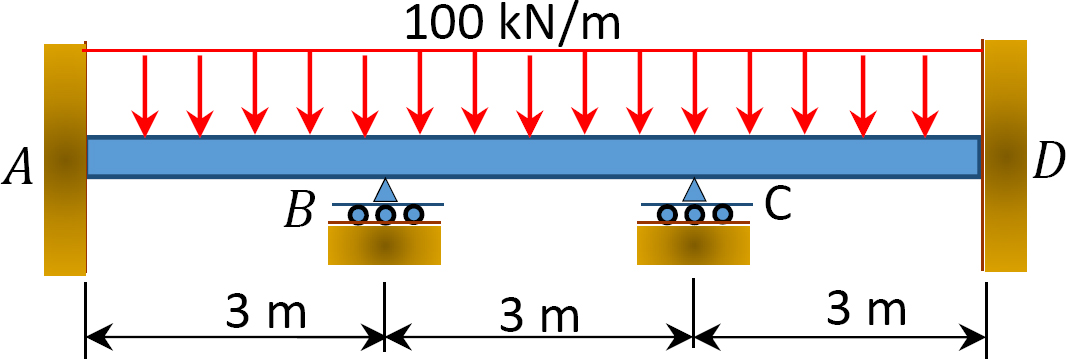
Fig. P12. 2. Beam.
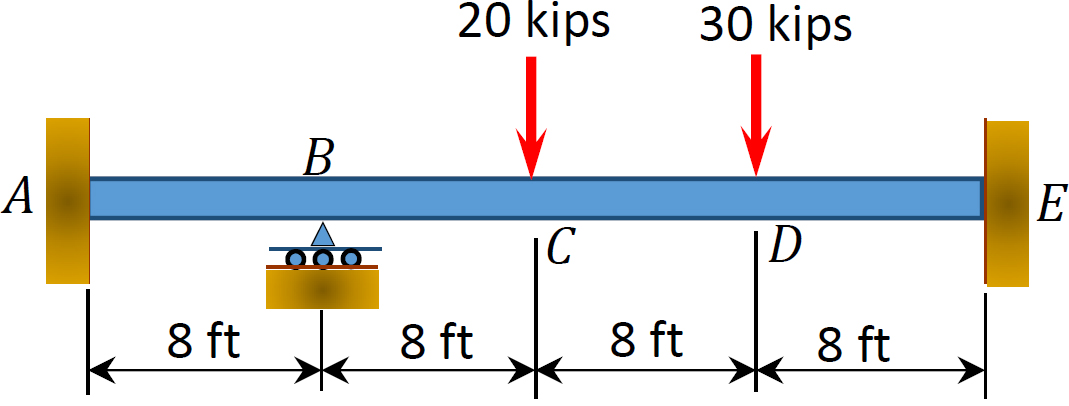
Fig. P12. 3. Beam.
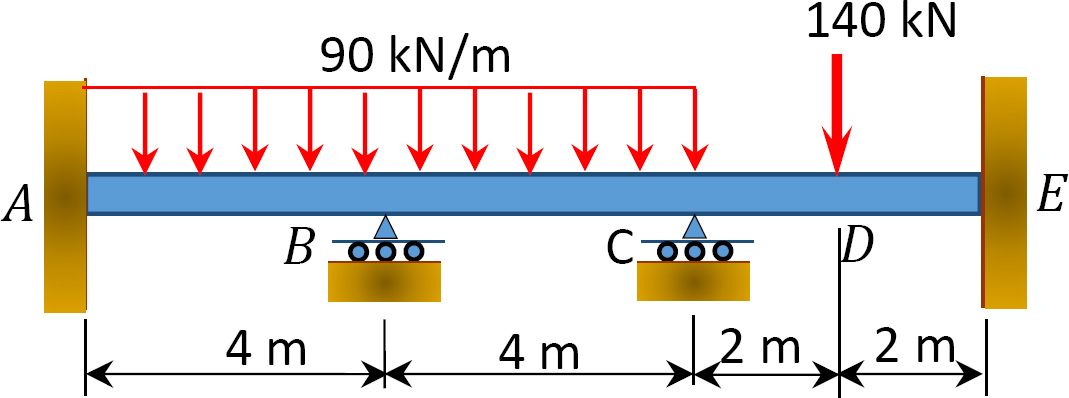
Fig. P12. 4. Beam.
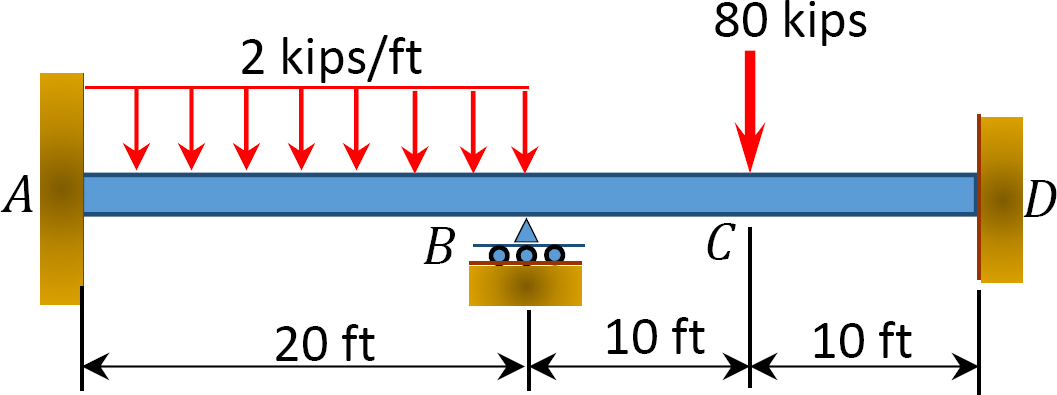
Fig. P12. 5. Beam.
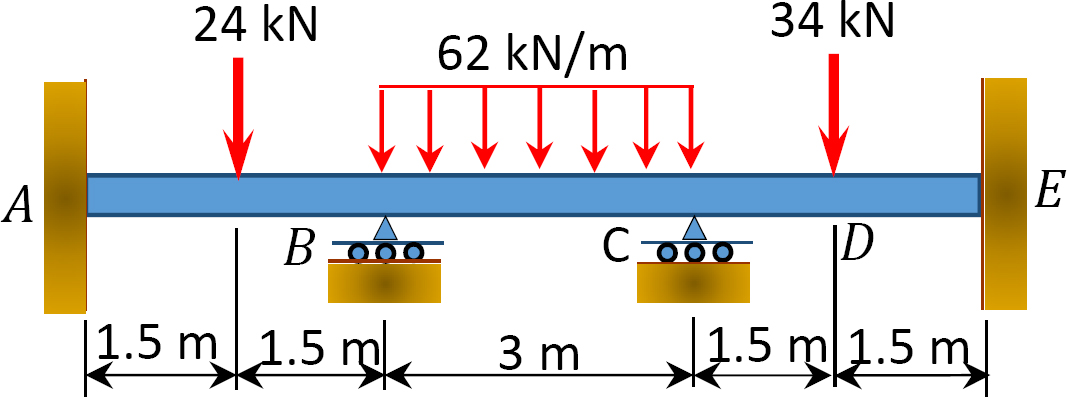
Fig. P12. 6. Beam.
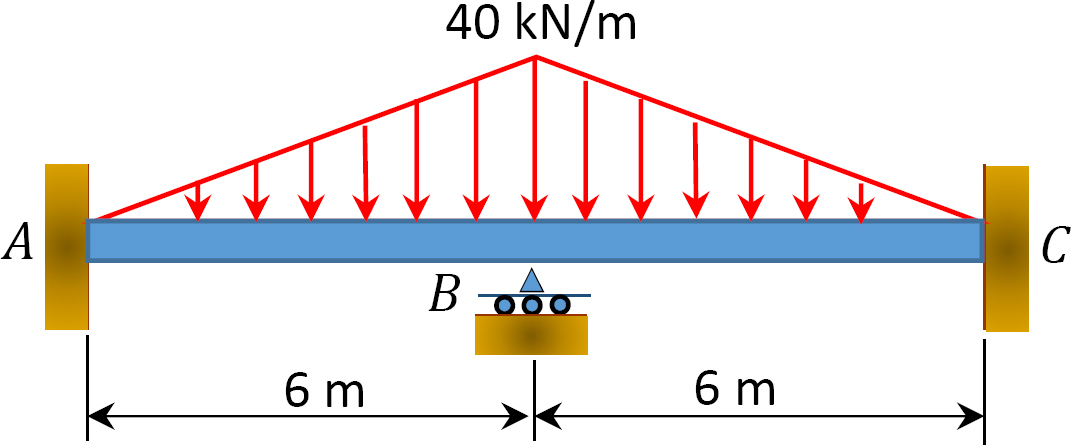
Fig. P12. 7. Beam.
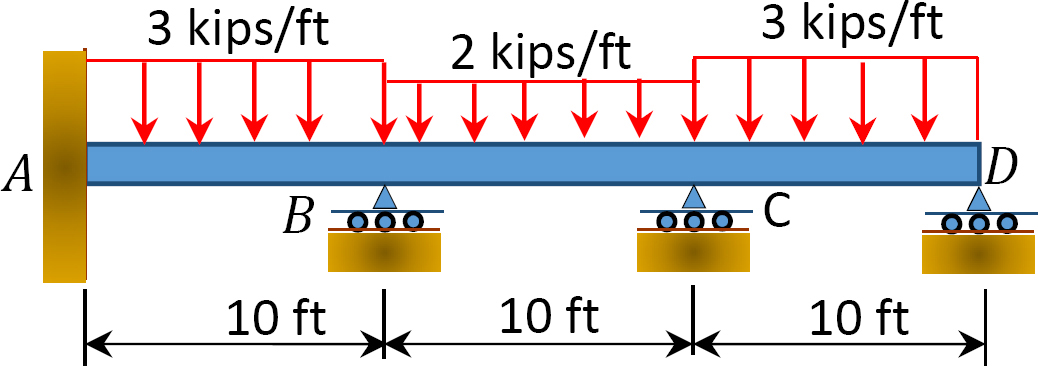
Fig. P12. 8. Beam.
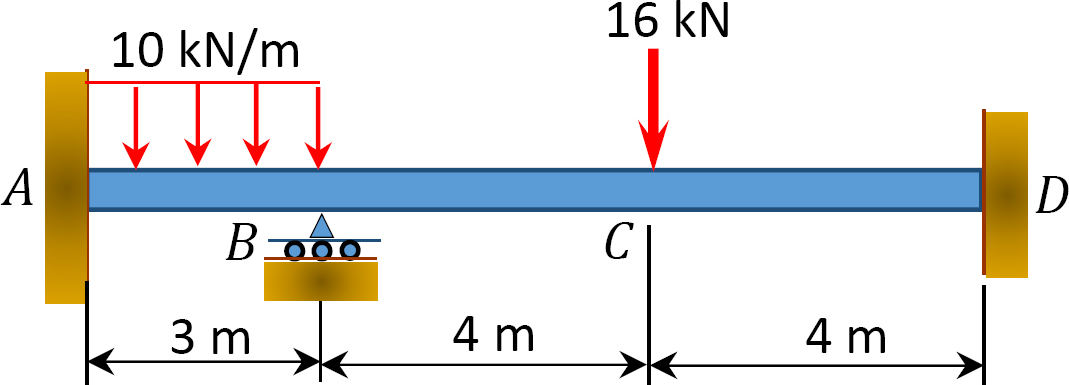
Fig. P12. 9. Beam.
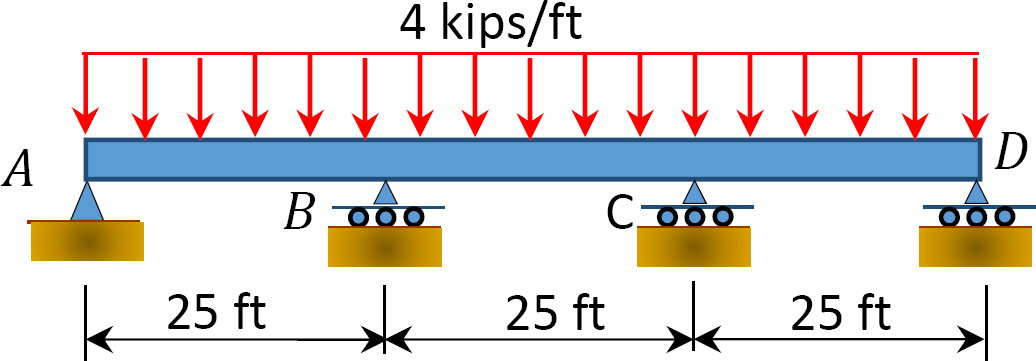
Fig. P12. 10. Beam.
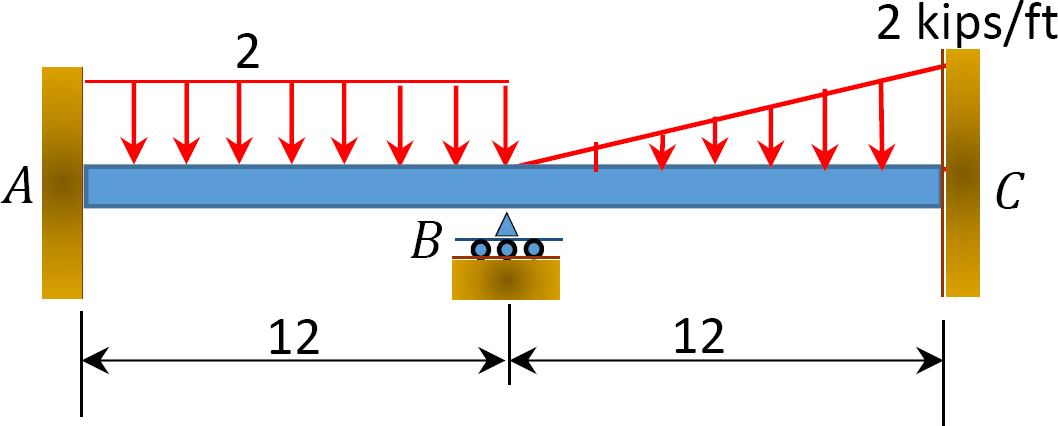
Fig. P12. 11. Beam.
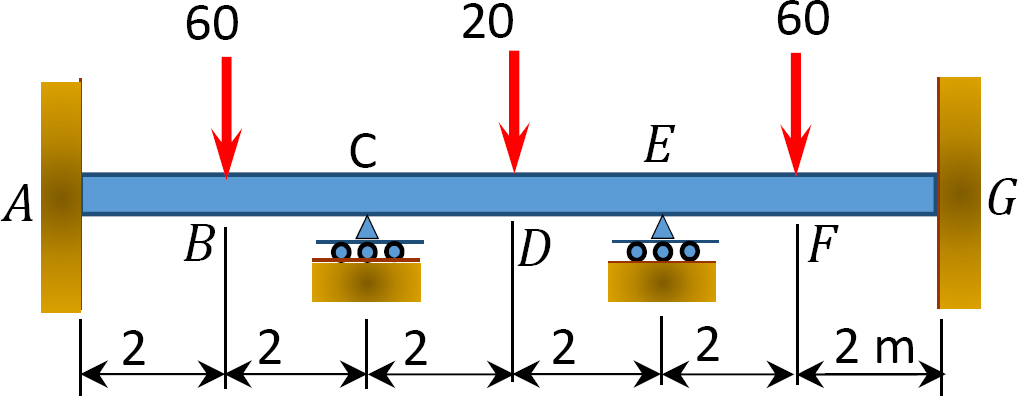
Fig. P12. 12. Beam.
12.2 utilizați metoda de distribuție a momentului pentru a calcula momentul final al membrilor cadrelor prezentate în figura P12.13 până în figura 12.20 și desenați diagramele momentului de îndoire și forței de forfecare. EI = constantă.
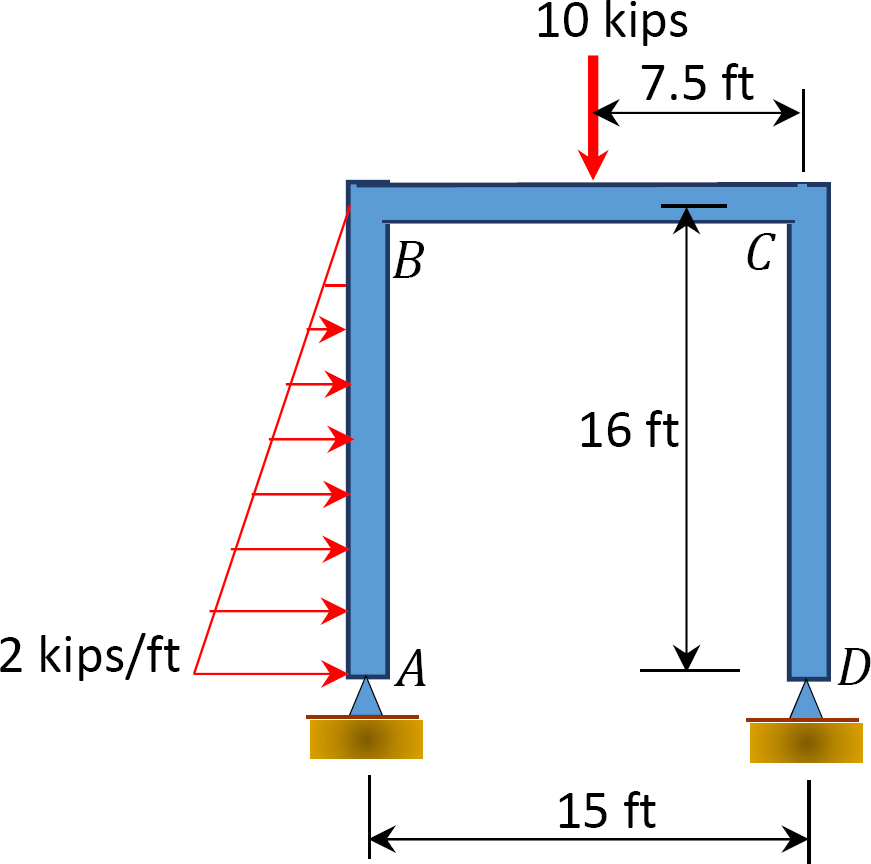
Fig. P12. 13. Cadru.
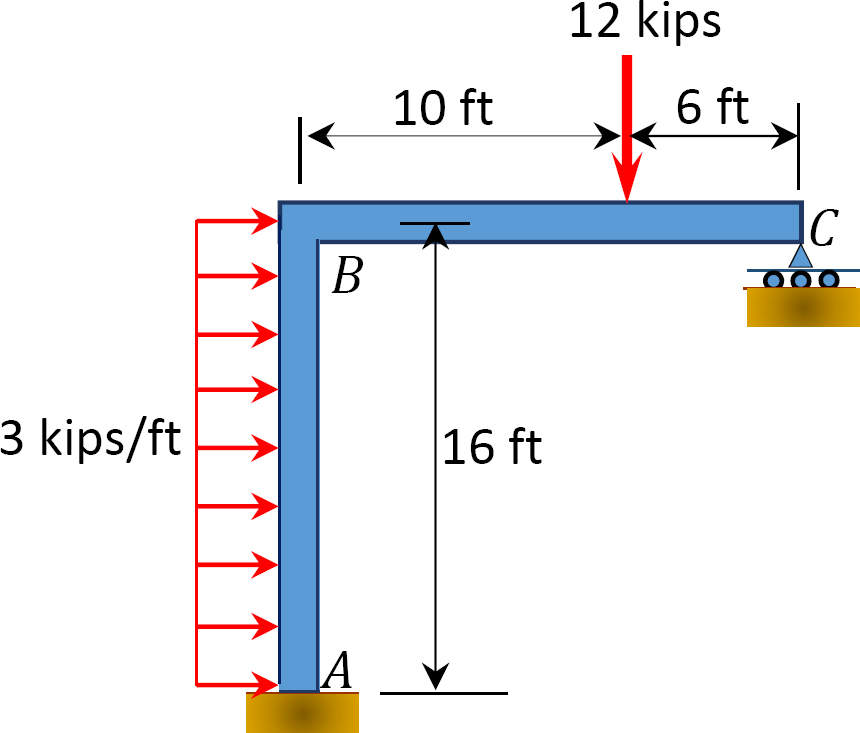
Fig. P12. 14. Cadru.
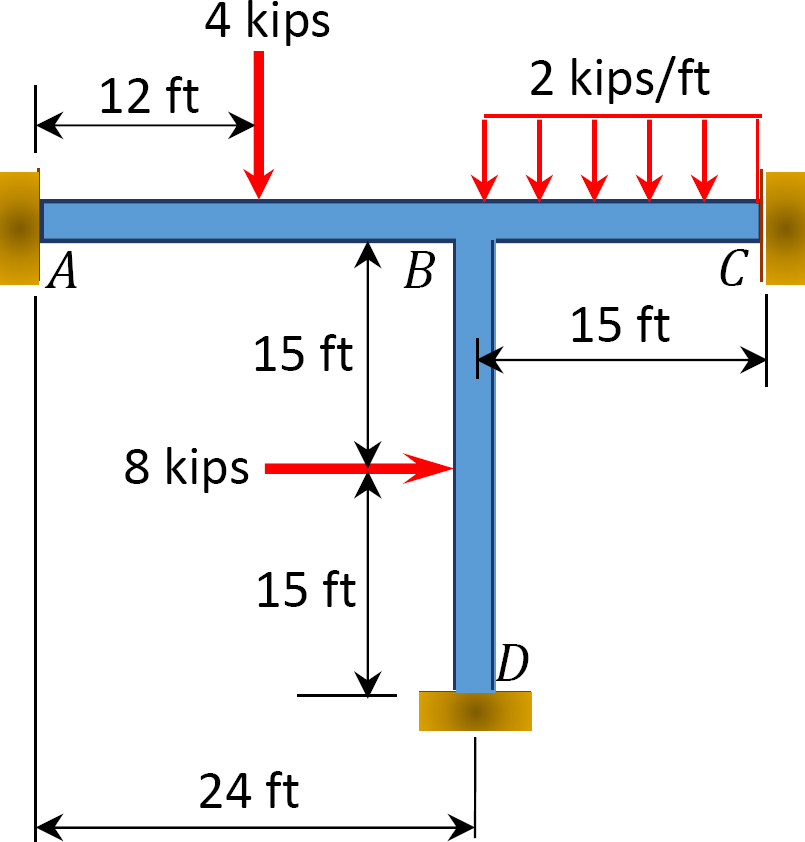
Fig. P12. 15. Cadru.
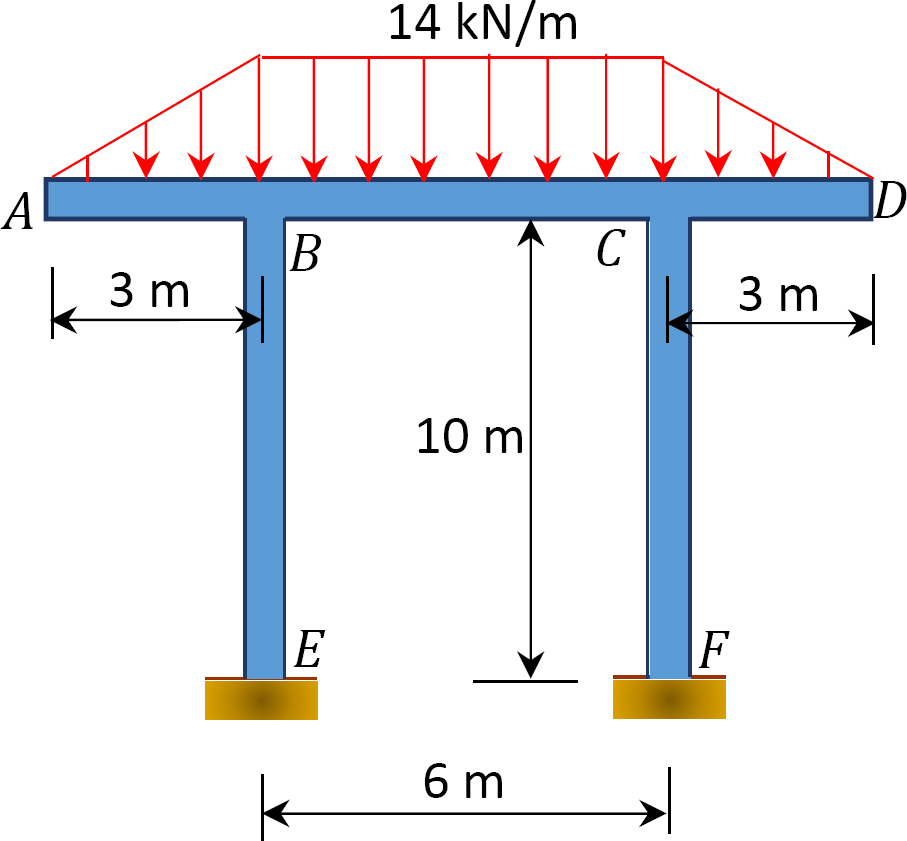
Fig. P12.16. Frame.
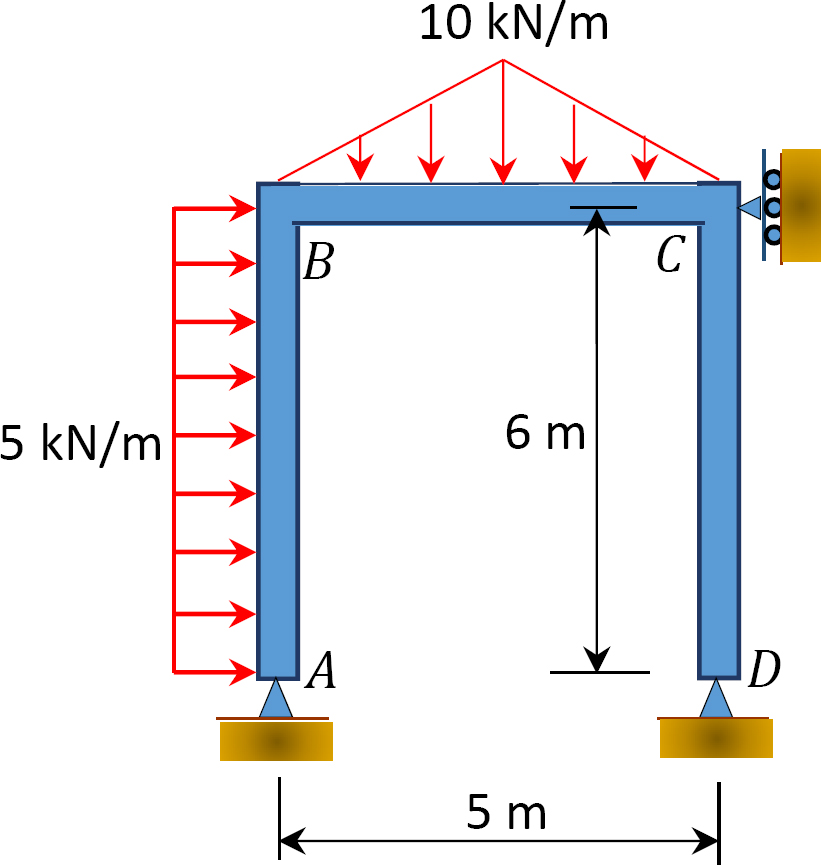
Fig. P12.17. Frame.
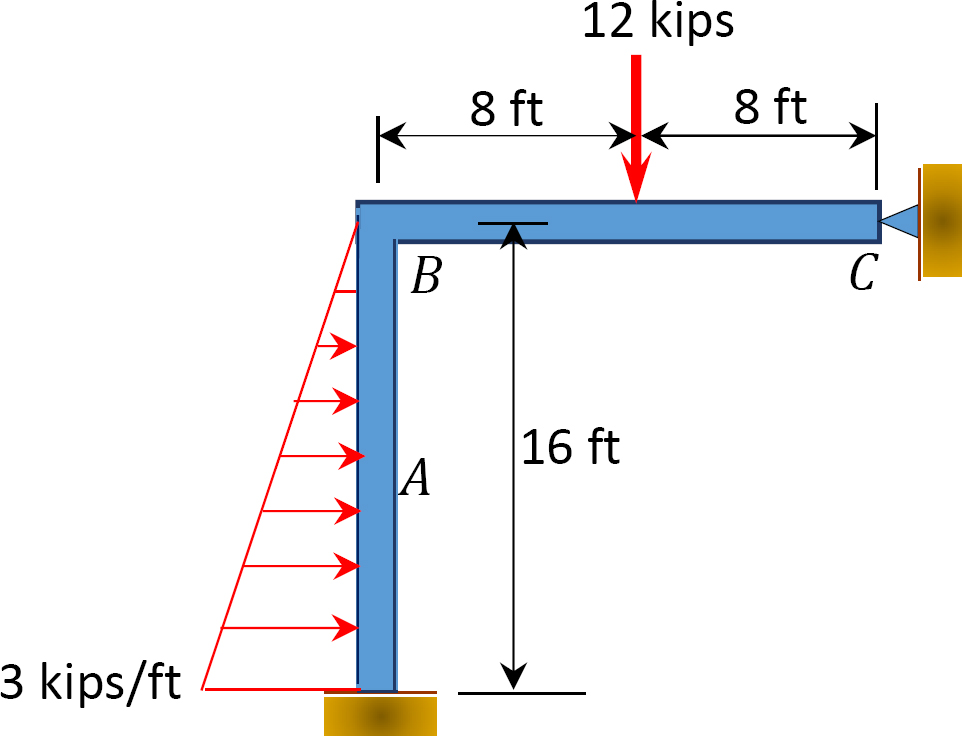
Fig. P12.18. Frame.
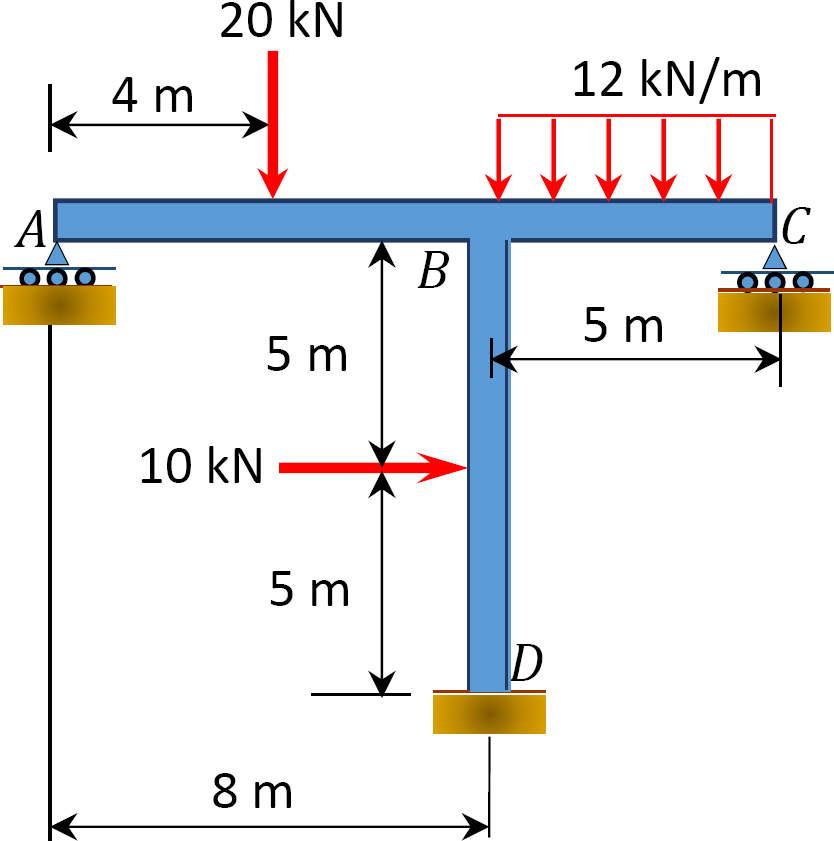
Fig. P12.19. Frame.
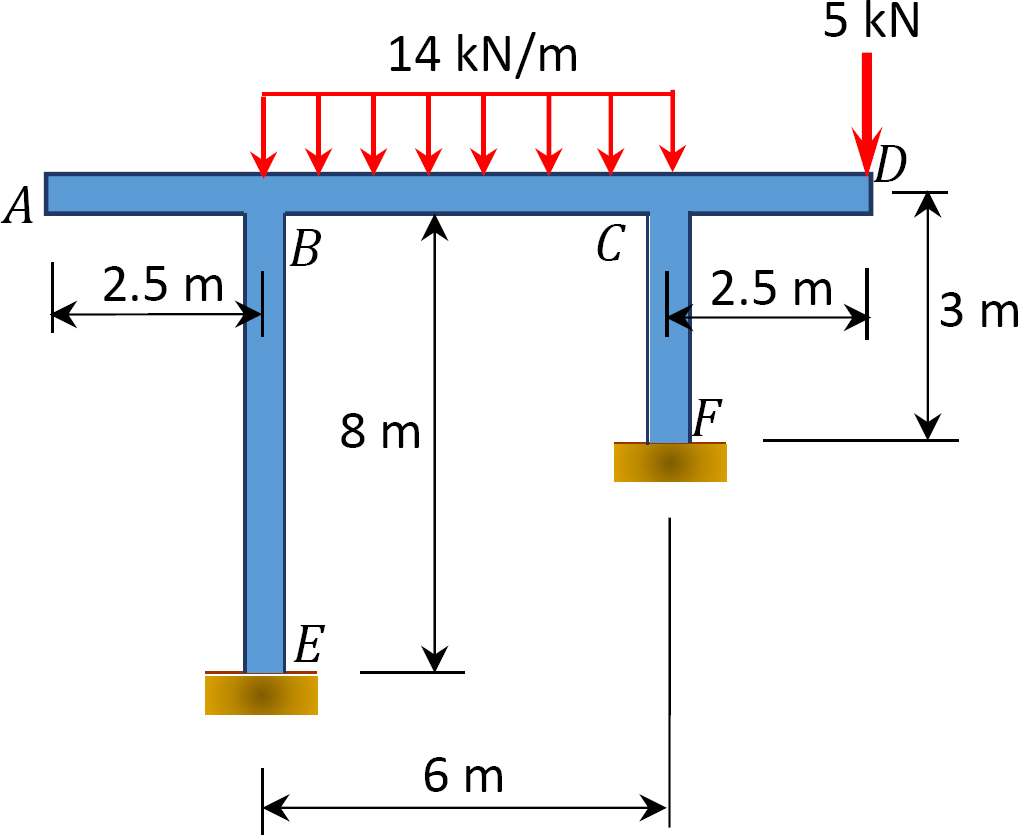
Fig. P12.20. Frame.