Capítulo 12
Método de Distribución de Momentos para el Análisis de Estructuras
12.1 Conceptos básicos
El método de distribución de momentos para el análisis de vigas y marcos fue desarrollado por Hardy Cross y presentado formalmente en 1930. Aunque este método es un método de deformación como el método de desviación de pendiente, es un método aproximado y, por lo tanto, no requiere resolver ecuaciones simultáneas, como fue el caso con este último método. El grado de precisión de los resultados obtenidos por el método de distribución de momentos depende del número de aproximaciones sucesivas o del proceso de iteración.
Para ilustrar el concepto del método de distribución de momentos, considere el marco que se muestra en la Figura 12.1. Los miembros del marco son prismáticos y se supone que no se deforman axialmente ni se traducen entre sí. Las juntas ACD del bastidor son fijas, mientras que la junta B puede girar ligeramente debido a la carga aplicada. En primer lugar, antes de llevar a cabo la distribución de momentos entre los miembros, se supone que todas las articulaciones están bloqueadas temporalmente mediante una abrazadera.
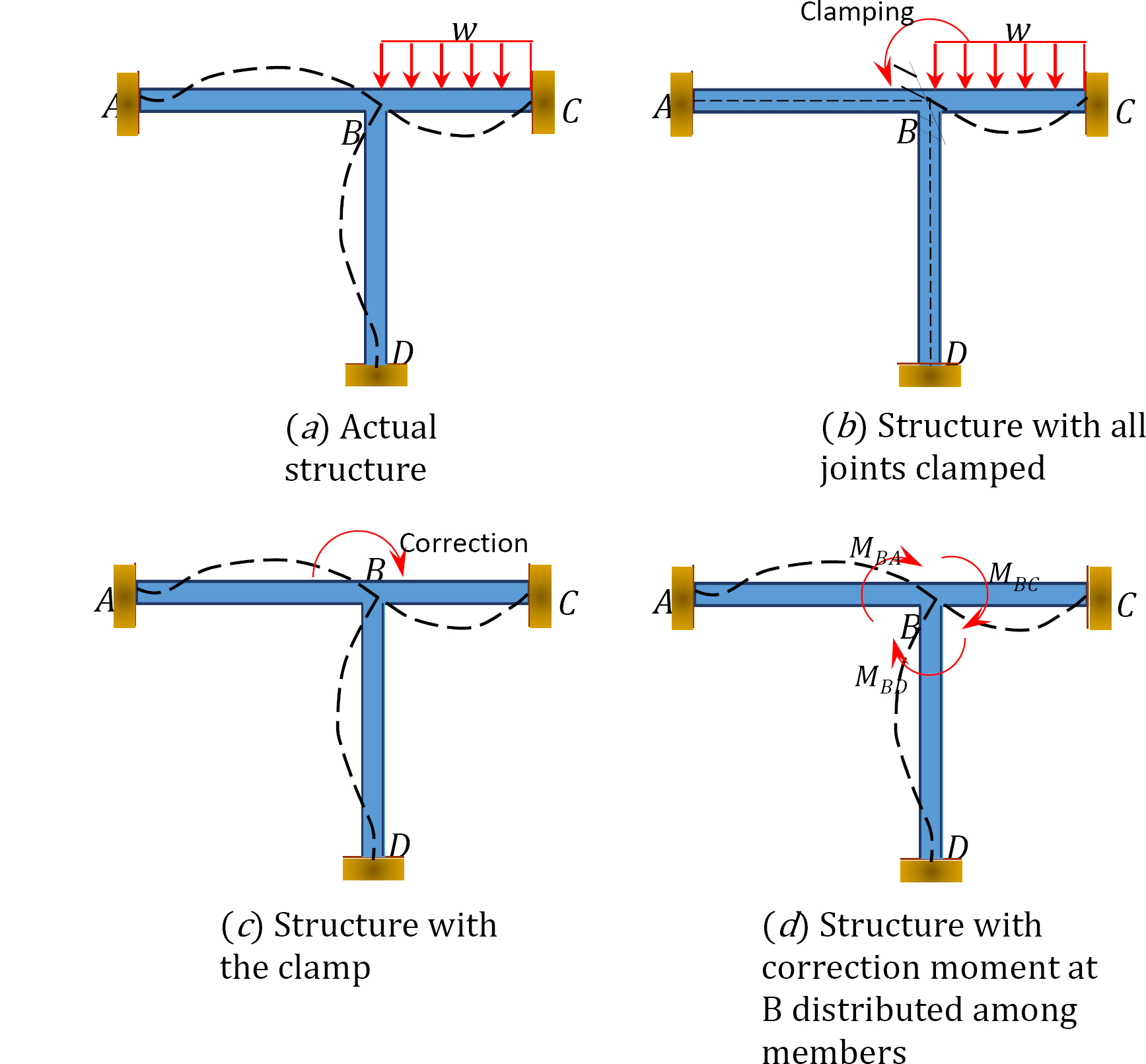
Fig. 12.1. Marco.
12.2 Convención de signos
La convención de signos para el método de distribución de momento es similar a la establecida para el método de desviación de pendiente; es decir, el momento al final de un miembro se considera positivo si tiende a girar el extremo del miembro en el sentido de las agujas del reloj y negativo si tiende a girarlo en el sentido contrario a las agujas del reloj.
12.3 Definiciones
Momentos desequilibrados: Este método de análisis asume que las juntas en una estructura se sujetan o bloquean inicialmente y luego se liberan sucesivamente. Una vez que se libera una articulación, se produce una rotación, ya que la suma de los momentos finales fijos de los miembros que se reúnen en esa articulación no es cero. El valor de la suma de los momentos finales obtenidos es el momento desequilibrado en esa articulación.
Momentos de arrastre: Los momentos distribuidos en los extremos de la reunión de miembros en una causa conjunta momentos en los otros extremos, que se supone que son fijos. Estos momentos inducidos en los otros extremos se llaman momentos de arrastre.
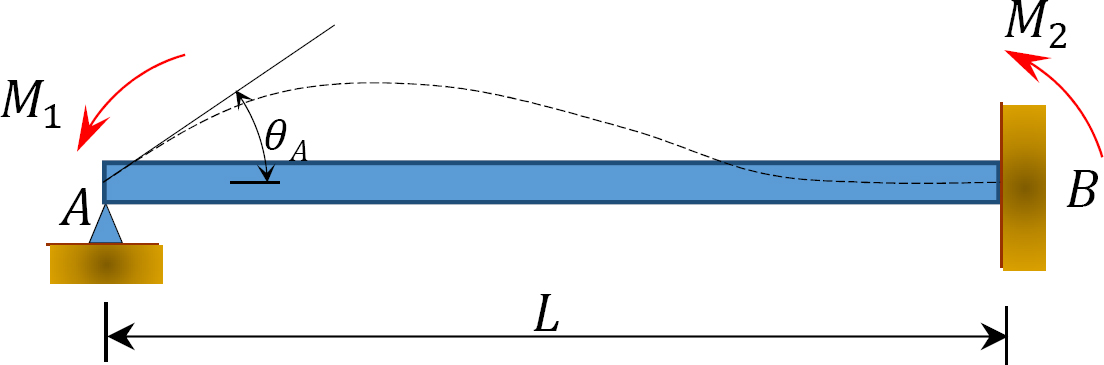
Fig. 12.2. Haz prismático sin carga.
Considere un haz prismático sin carga fijado en el extremo B, como se muestra en la Figura 12.2. Si se aplica un momento M1 al extremo izquierdo de la viga, las ecuaciones de pendiente-desviación para ambos extremos de la viga se pueden escribir de la siguiente manera:


Sustituir 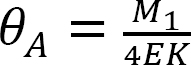 de la ecuación 12.1 a la ecuación 12.2 sugiere lo siguiente:
de la ecuación 12.1 a la ecuación 12.2 sugiere lo siguiente:

La ecuación 12.3 sugiere que el momento transferido al extremo fijo de una viga debido a un momento aplicado en el otro extremo es igual a la mitad del momento aplicado.Factor de arrastre
: La relación entre el momento inducido y el momento aplicado se conoce como factor de arrastre. Para la viga que se muestra en la figura 12.2, el factor de arrastre es el siguiente:

Factor distribuido (DF): El factor distribuido es un factor utilizado para determinar la proporción del momento desequilibrado llevado por cada uno de los miembros reunidos en una junta. Para los miembros reunidos en la junta O del marco que se muestra en la Figura 12.3, sus factores de distribución se calculan de la siguiente manera:
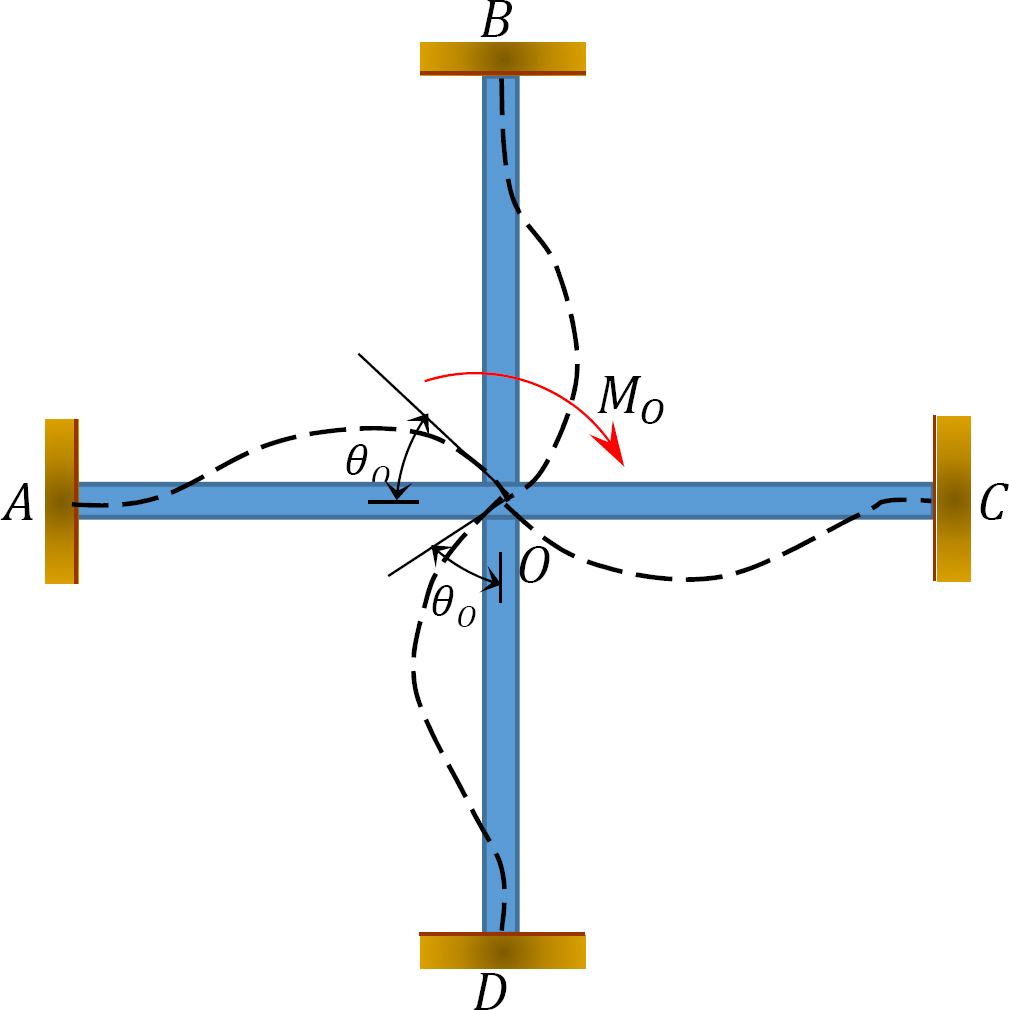
Fig. 12.3. Marco.

Momentos distribuidos: Al soltar la pinza imaginaria en una articulación, el momento desequilibrado en esa articulación hace que gire. La rotación retuerce el final de la reunión de los miembros en la articulación, lo que resulta en el desarrollo de momentos de resistencia. Estos momentos de resistencia se llaman momentos distribuidos. Los momentos distribuidos para los miembros del marco que se muestran en la Figura 12.3 se calculan de la siguiente manera:
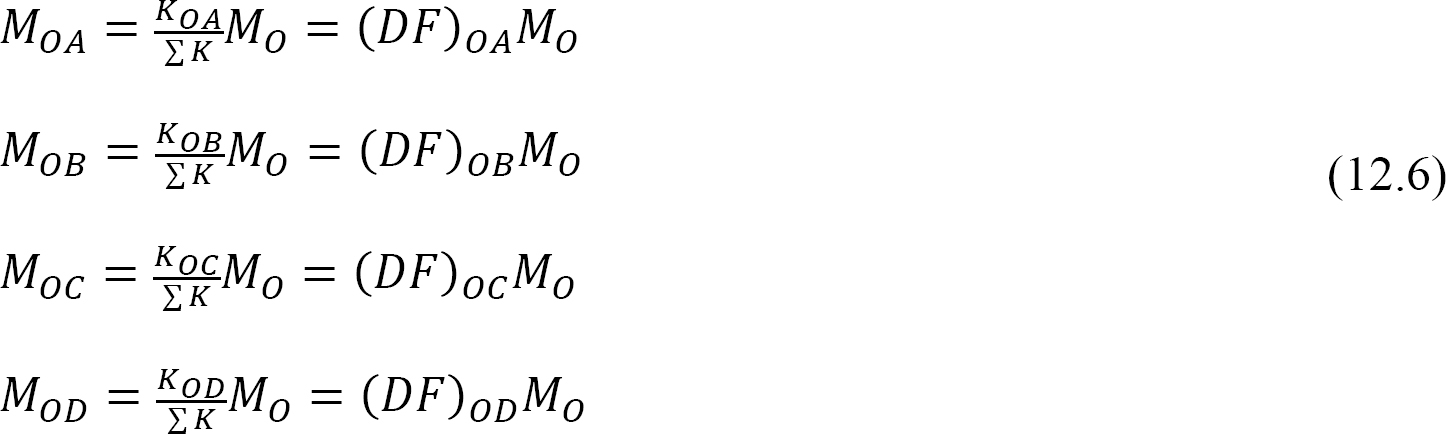
12.4 Modificación de la Rigidez de la barra
A veces, el proceso de iteración en el método de distribución de momentos se puede reducir significativamente ajustando la rigidez a flexión de algunos miembros de la estructura indeterminada. En esta sección se considera la influencia de un soporte fijo y un pasador en la rigidez a flexión de una viga indeterminada.
Caso 1: Una viga articulada en un extremo y fijada en el otro
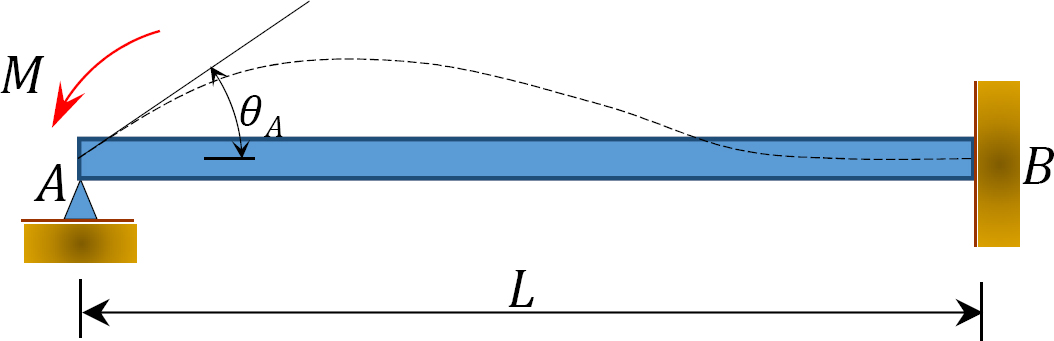
Fig. 12.4. Viga
Considere una viga articulada en el extremo A y fija en el extremo B, como se muestra en la Figura 12.4. Aplicando un momento M gira el extremo de la bisagra en una cantidad θ. Escribir la ecuación pendiente-desviación para el extremo A de la barra y observar que 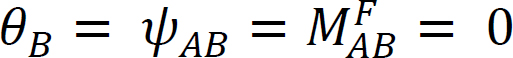 sugiere lo siguiente:
sugiere lo siguiente:
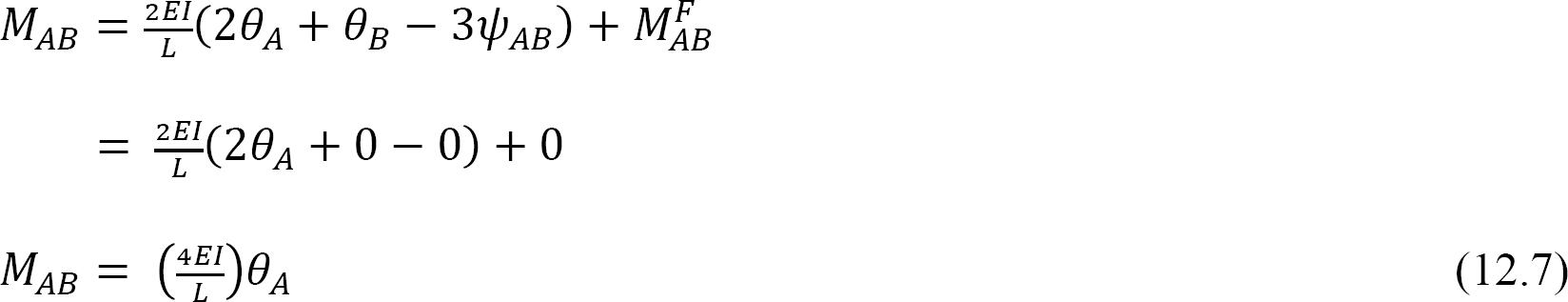
Por definición, la rigidez de flexión de un miembro estructural es el momento que se debe aplicar a un extremo del miembro para causar una rotación unitaria de ese extremo. La siguiente expresión para la rigidez de flexión del miembro con un extremo lejano fijo se expresa de la siguiente manera al sustituir θA = 1 en la ecuación 12.7:

Por definición, la rigidez de flexión relativa de una barra se determina dividiendo la rigidez de flexión de la barra por 4E. Dividir la ecuación 12.8 por 4E sugiere la siguiente expresión de rigidez relativa para el caso considerado:

Caso 2: Una viga con bisagras en ambos extremos
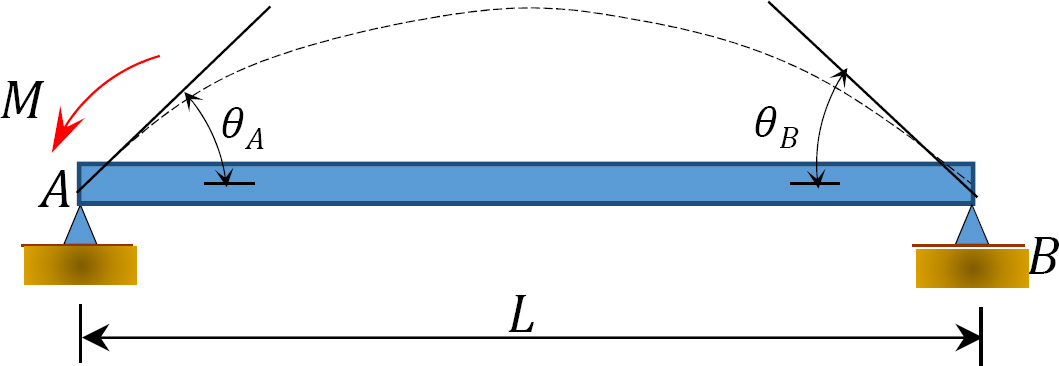
Fig. 12.5. Viga simplemente soportada.
Aplicando un momento M en el extremo A de la viga simplemente apoyada que se muestra en la Figura 12.5, la viga gira en un ángulo θA en el extremo articulado. Utilizando la ecuación de inclinación-desviación modificada derivada de la sección 11.4 del capítulo 11 y observando que 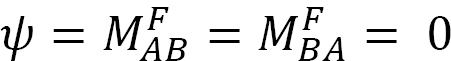 sugiere la siguiente expresión para el momento en el extremo articulado donde se aplica la carga:
sugiere la siguiente expresión para el momento en el extremo articulado donde se aplica la carga:
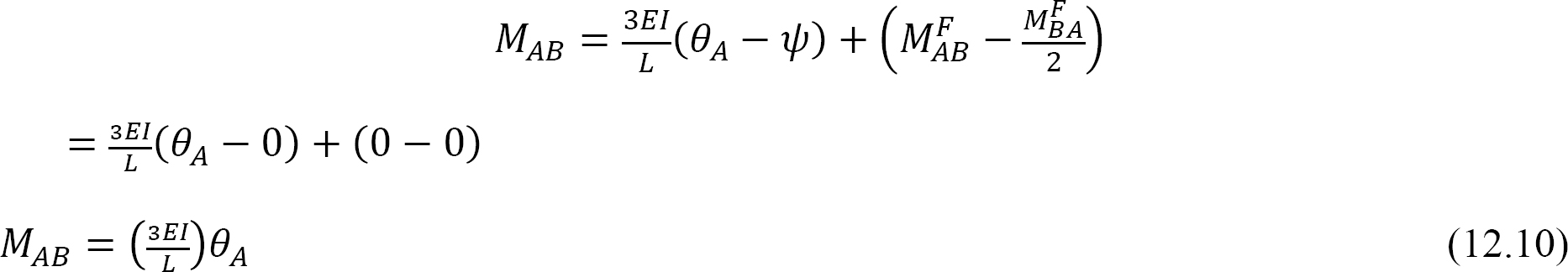
La sustitución de θA = 1 en la ecuación 12.10 sugiere la siguiente expresión para la rigidez de flexión de un miembro con un extremo abisagrado:

La rigidez relativa de un miembro con un extremo trasero articulado se obtiene dividiendo la ecuación 12.11 por 4E, de la siguiente manera:

La comparación de las ecuaciones 12.12 y 12.9 sugiere que un miembro con un extremo con bisagras es tres cuartos tan rígido como un miembro con la misma geometría pero fijo en el extremo lejano. Este hecho establecido puede reducir sustancialmente el número de iteraciones al analizar vigas o marcos con un extremo abisagrado utilizando el método de distribución de momentos. En tales casos, la rigidez relativa de la viga en el extremo cercano se ajusta primero de acuerdo con la ecuación 12.12, y su factor de distribución se calcula con la rigidez ajustada. Durante la operación de equilibrado, el extremo cercano se equilibrará una sola vez sin que se trasladen más momentos desde o hasta su final.
12.5 Análisis de haces Indeterminados
El procedimiento para el análisis de haces indeterminados por el método de distribución de momentos se resume brevemente de la siguiente manera:
Procedimiento para el Análisis de Haces Indeterminados por el Método de Distribución de Momentos
•Calcule los momentos de extremo fijo para los miembros, suponiendo que las articulaciones estén sujetas contra la rotación.
•Calcule el momento desequilibrado en cada junta y distribuya el mismo a los extremos de los miembros conectados en esa junta.
* Lleve más de la mitad del momento distribuido a los otros extremos de los miembros.
* Sumar o restar estos últimos momentos (momentos obtenidos en los pasos tres y cuatro) a o desde los momentos fijos originales.
* Aplicar los momentos finales determinados en las articulaciones de la estructura dada.
•Dibuje el diagrama de cuerpo libre de cada tramo de la viga dada, mostrando las cargas y los momentos en las articulaciones obtenidos por el método de distribución de momentos.
•Determine las reacciones de soporte para cada intervalo.
* Calcule y construya los diagramas de fuerza de corte y momento de flexión para cada tramo.
•Dibuje un momento de flexión y un diagrama de fuerza de corte para la viga dada combinando los diagramas del paso 9.
Ejemplo 12.1
Utilizando el método de distribución de momentos, determine los momentos finales y las reacciones en los soportes de la viga que se muestran en la Figura 12.6 a. Dibuje los diagramas de fuerza de corte y momento de flexión. EI = constante.
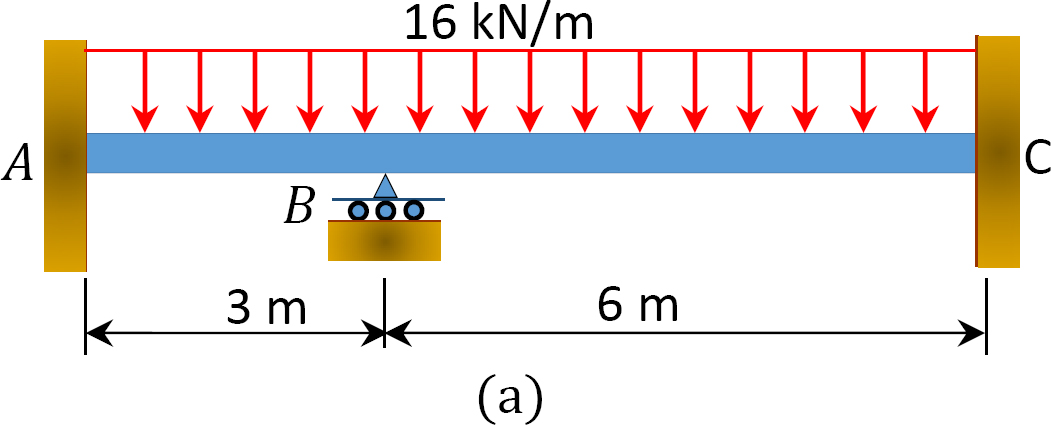
Fig. 12.6. Viga.
Solución
Momento final fijo.
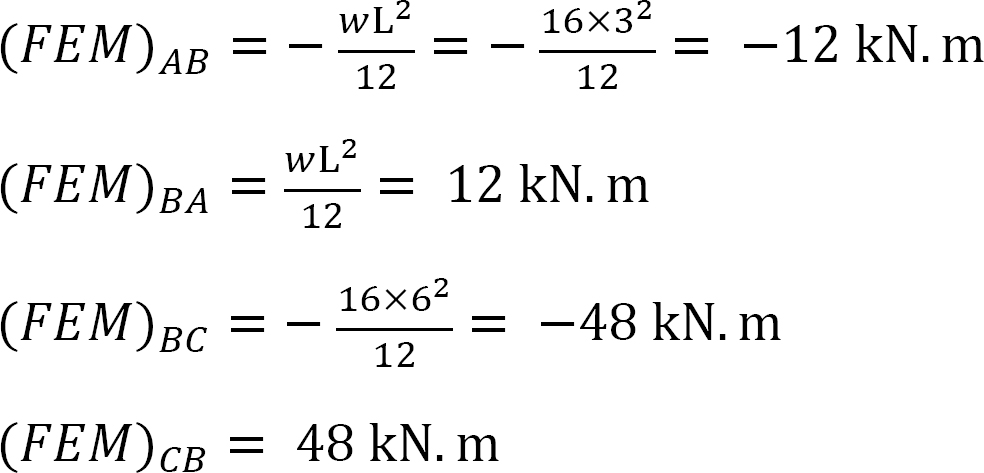
Factor de rigidez.
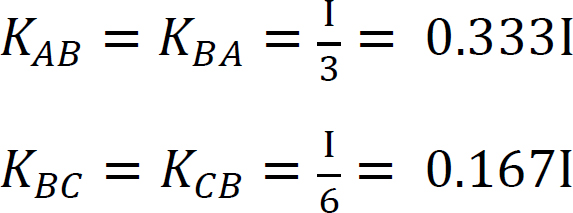
factor de Distribución.
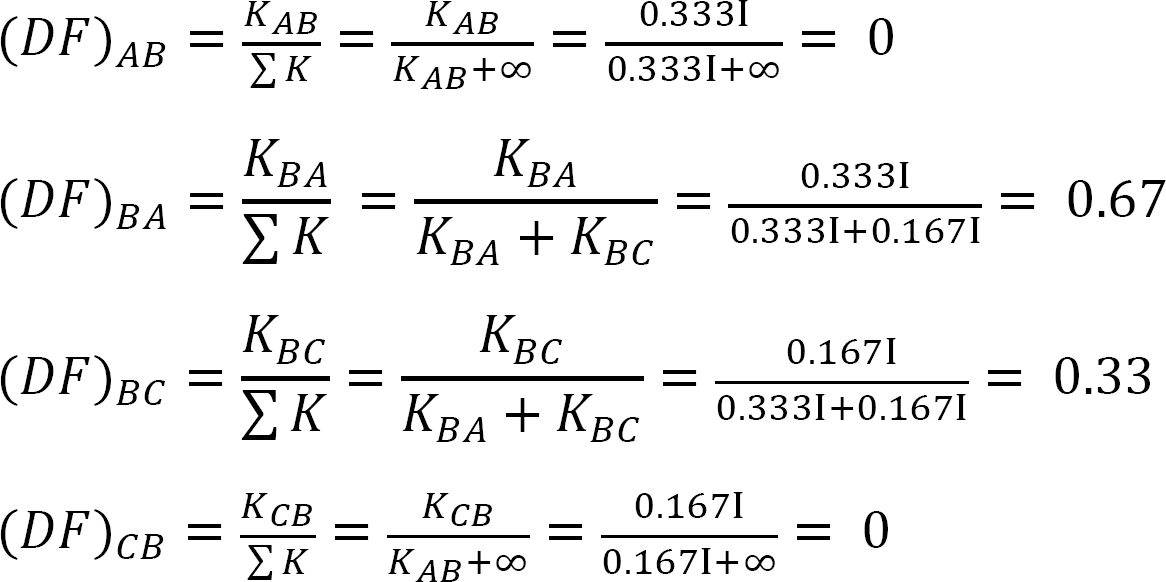
Tabla 12.1. Tabla de distribución.
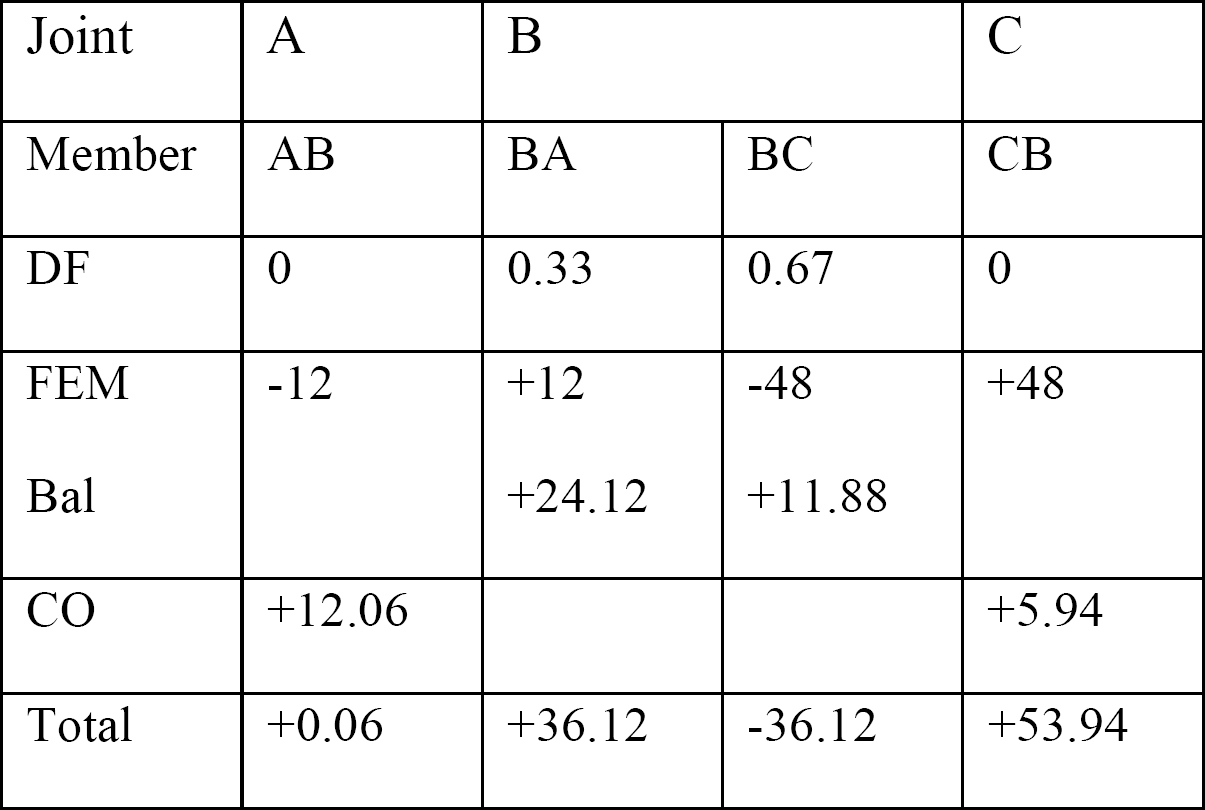
fuerza Cortante y momento de flexión diagramas.
Ejemplo 12.2
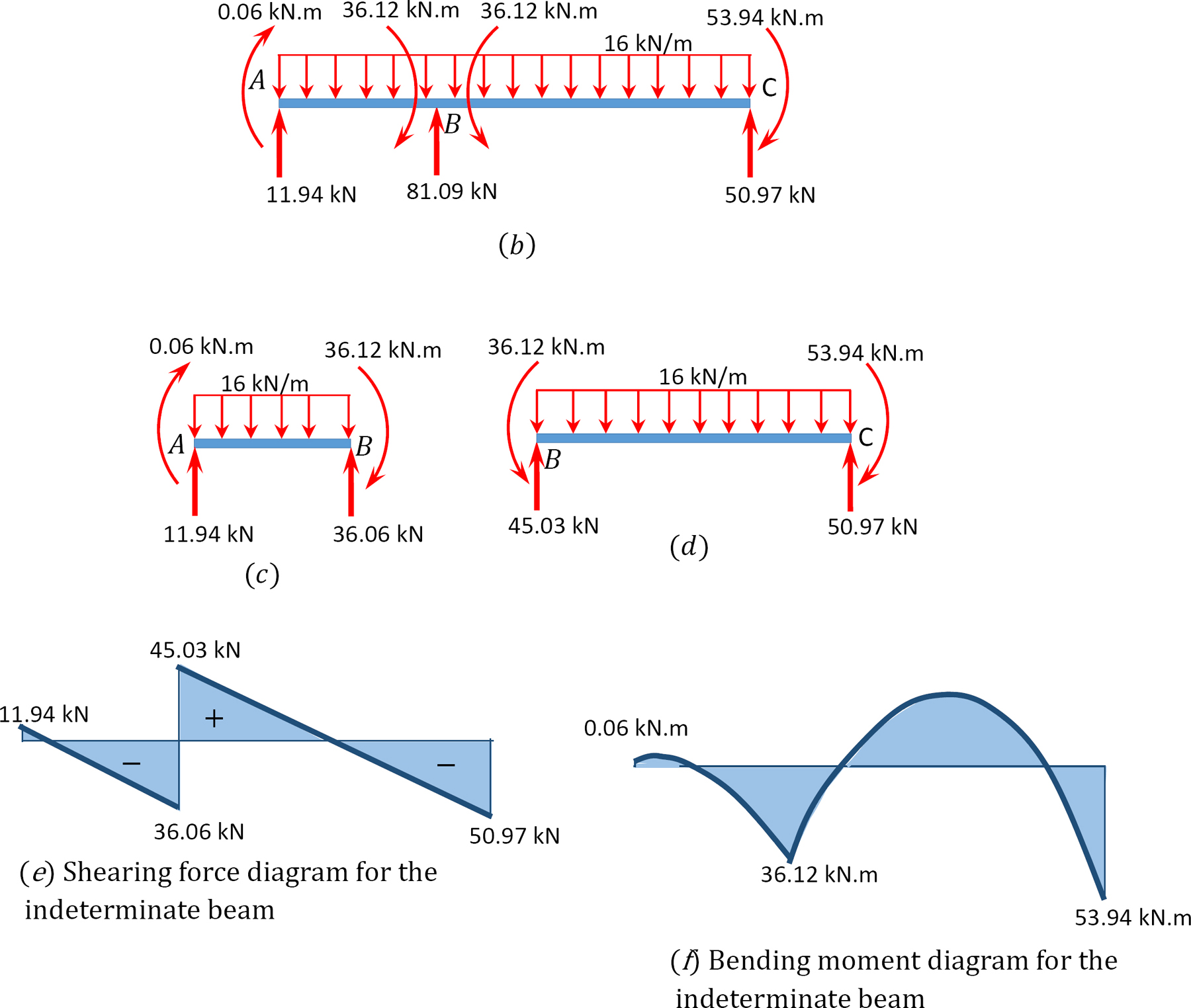
Utilizando el método de distribución de momentos, determine los momentos finales y las reacciones en los soportes de la viga que se muestran en la Figura 12.7 a. Dibuje los diagramas de fuerza de corte y momento de flexión.
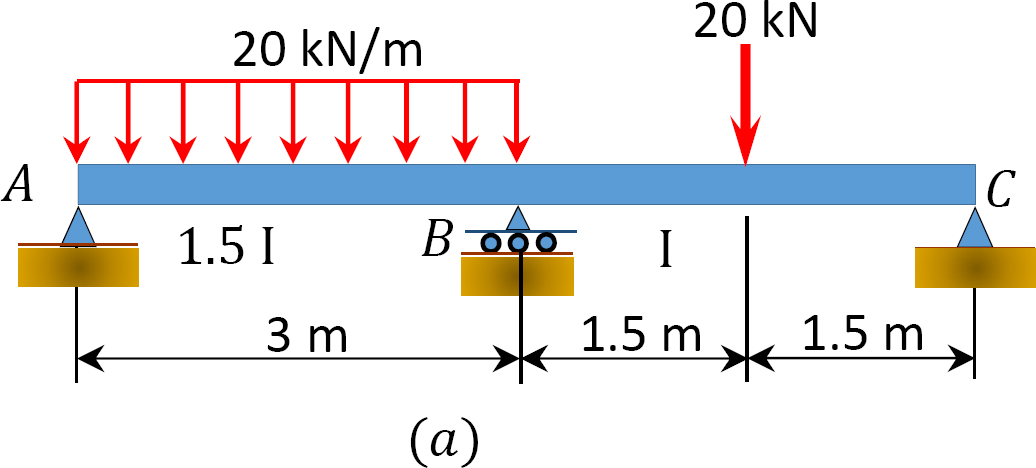
Fig. 12.7. Viga.
Solución
Momento final fijo.
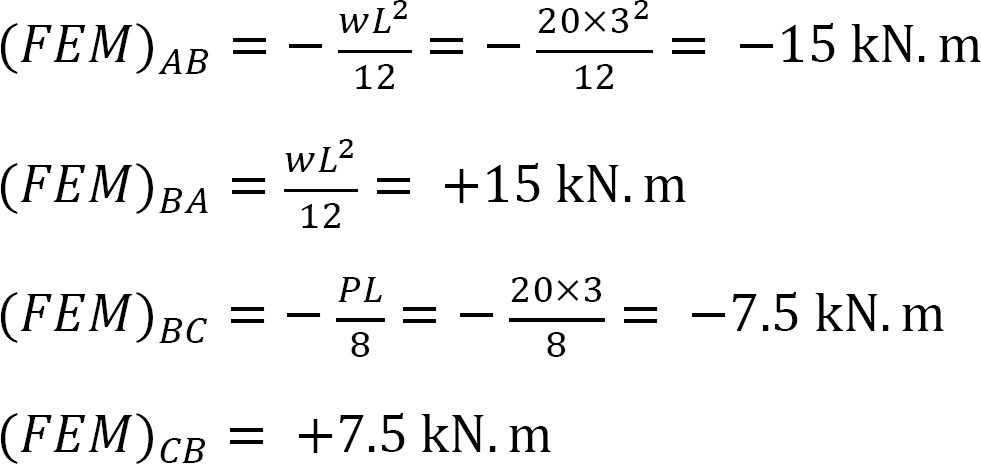
Factor de rigidez.
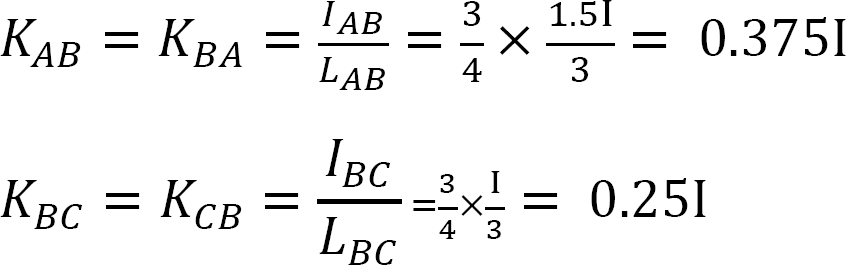
factor de Distribución.
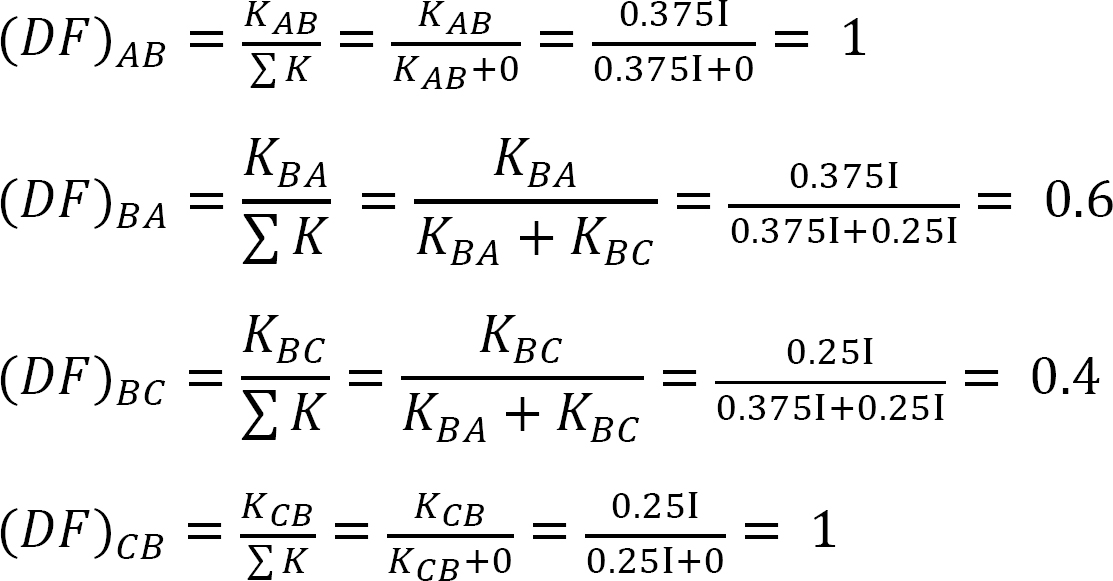
Tabla 12.2. Tabla de distribución.
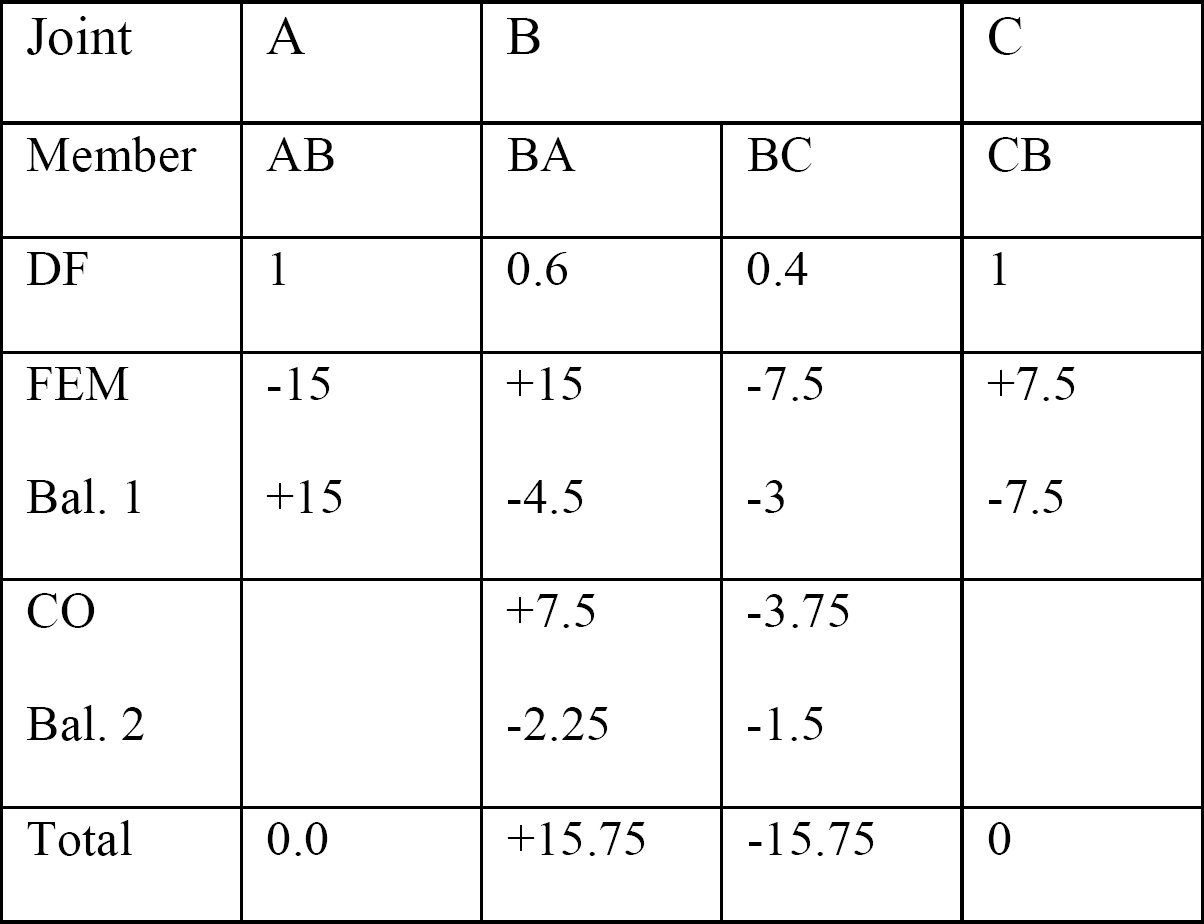
fuerza Cortante y momento de flexión diagramas.
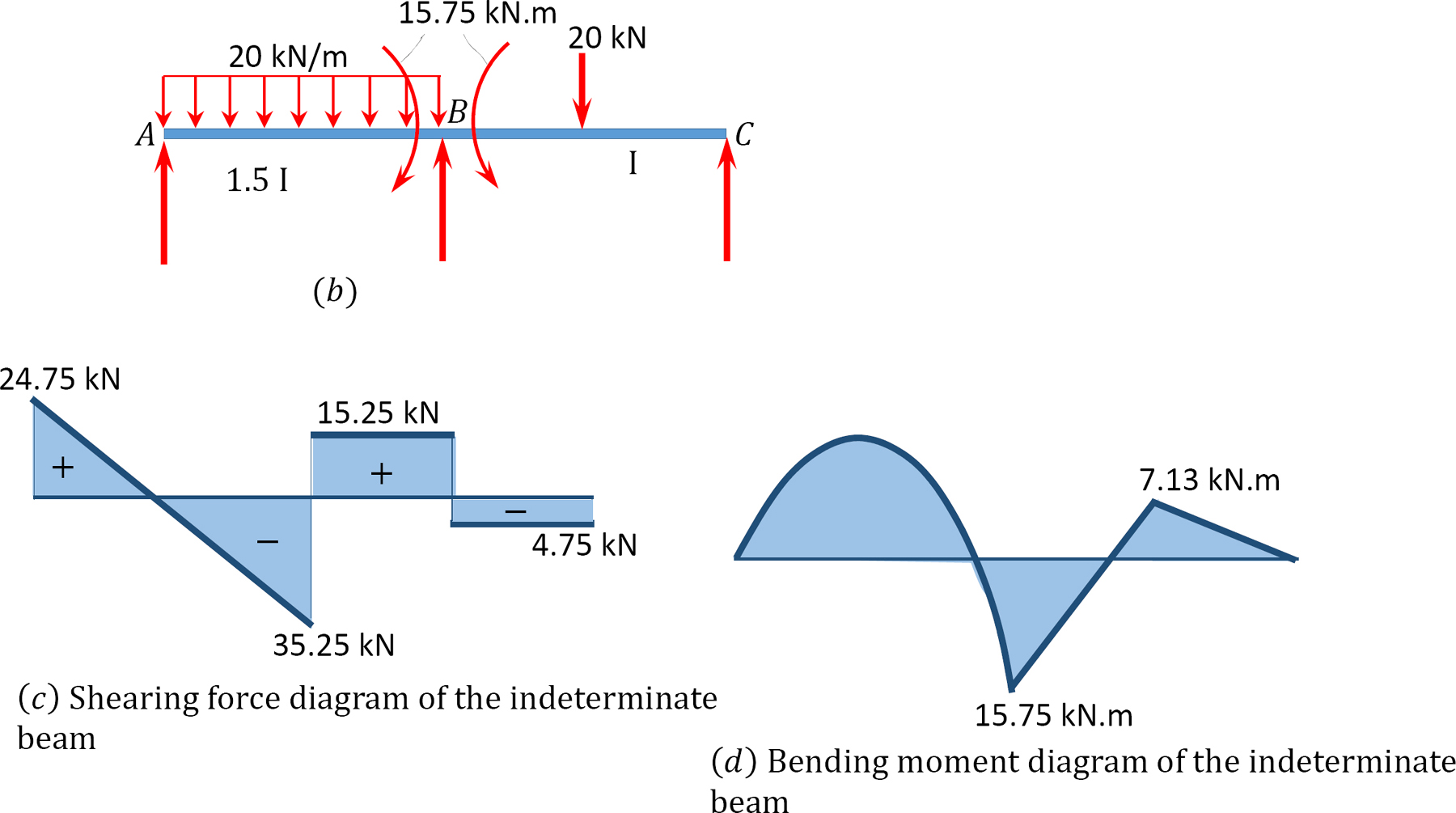
12.6 Análisis de Fotogramas Indeterminados
El procedimiento para el análisis de fotogramas utilizando el método de distribución de momentos depende del tipo de fotograma que se está analizando. Los marcos se clasifican como marcos oscilantes o no oscilantes. El procedimiento para el análisis de los marcos no oscilantes es similar al de los haces indeterminados. Pero para el análisis de los marcos de oscilación, el procedimiento es diferente. Hay dos etapas involucradas en el análisis de los marcos de balanceo, a saber, el análisis de la etapa sin balanceo y el análisis de la etapa de balanceo. Estas etapas se describen a continuación.
Procedimiento para el Análisis de Marcos de Oscilación Indeterminados por el Método de Distribución de Momentos
A. Análisis de etapas sin oscilación
* Primero asuma la existencia de un soporte imaginario que evita que el marco se balancee.
•Calcule las reacciones horizontales en los soportes del marco y anote la diferencia X. Esta es la fuerza para evitar el balanceo.
B. Análisis de la etapa de balanceo
* Asuma momentos arbitrarios para actuar sobre las columnas del marco. La magnitud de estos momentos variará de columna a columna en proporción a 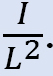
•Se asumen valores para M2 y se determina M1.
* Calcule la magnitud de las reacciones horizontales en los soportes para la condición de balanceo. La suma de estas reacciones da la fuerza de desplazamiento arbitraria Y.
•Determina la relación 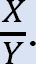 Esta relación se denomina factor de balanceo.
Esta relación se denomina factor de balanceo.
* Utilice el factor de balanceo para multiplicar los momentos distribuidos del balanceo. Esto da el momento corregido para el balanceo.
* Los momentos finales para el cuadro son la suma de los momentos obtenidos en la etapa de no balanceo y el momento corregido para la etapa de balanceo.
Ejemplo 12.3
Utilizando el método de distribución de momentos, determine los momentos finales de los miembros del cuadro que se muestra en la Figura 12.8. EI = constante.
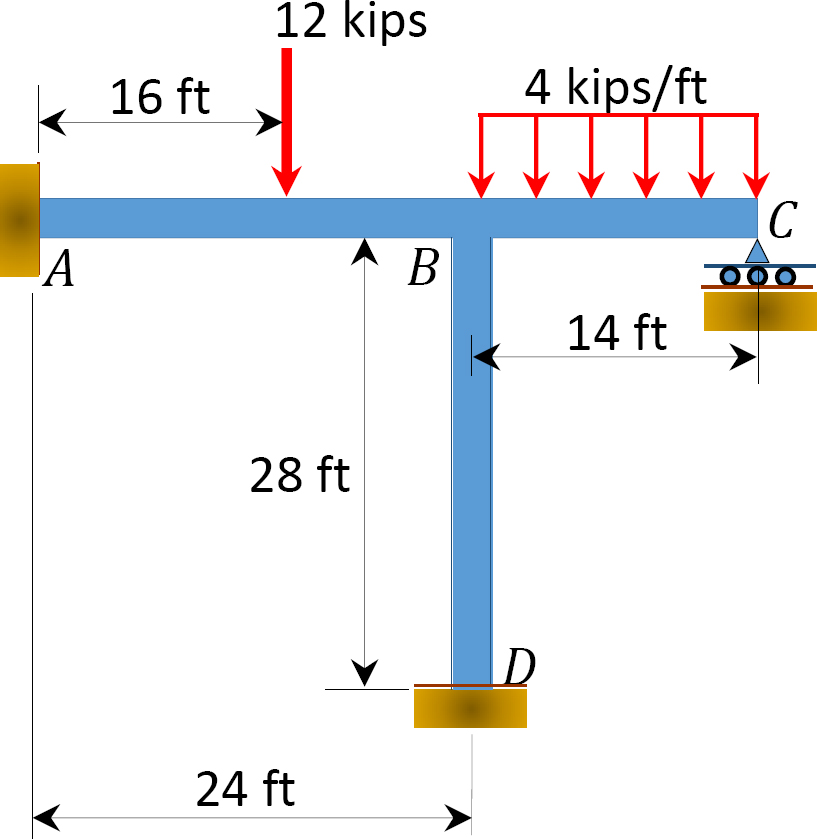
Fig. 12.8. Marco.
Solución
Momento final fijo.
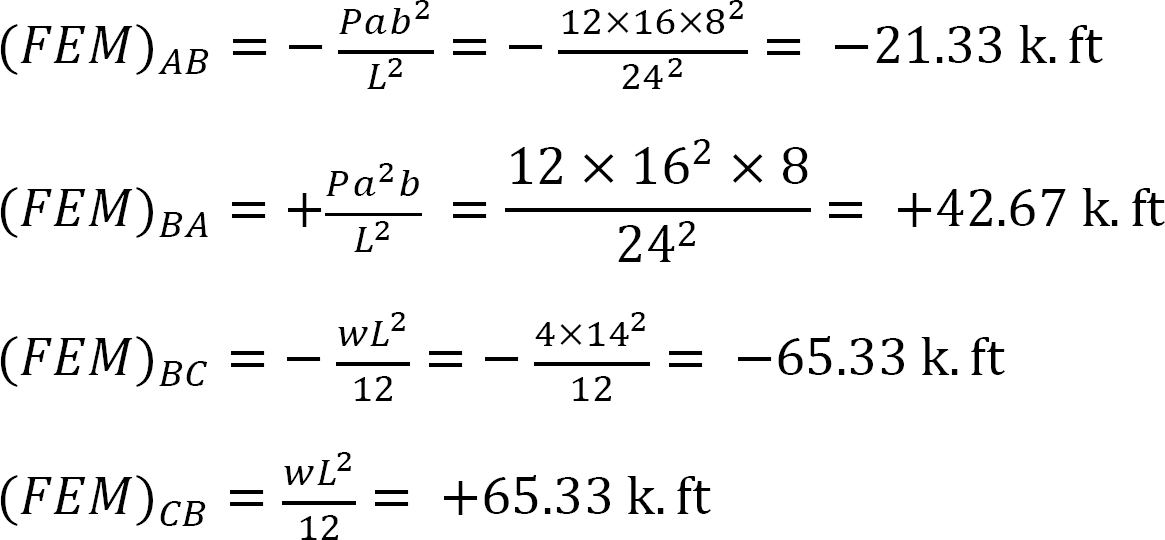
Factor de rigidez.
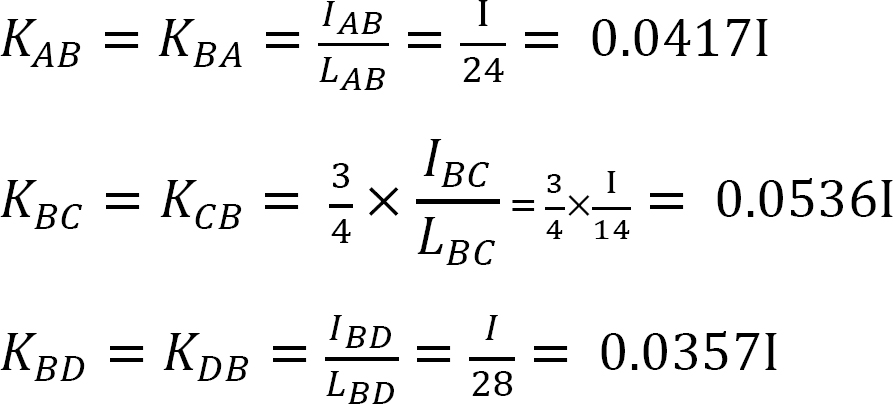
factor de Distribución.
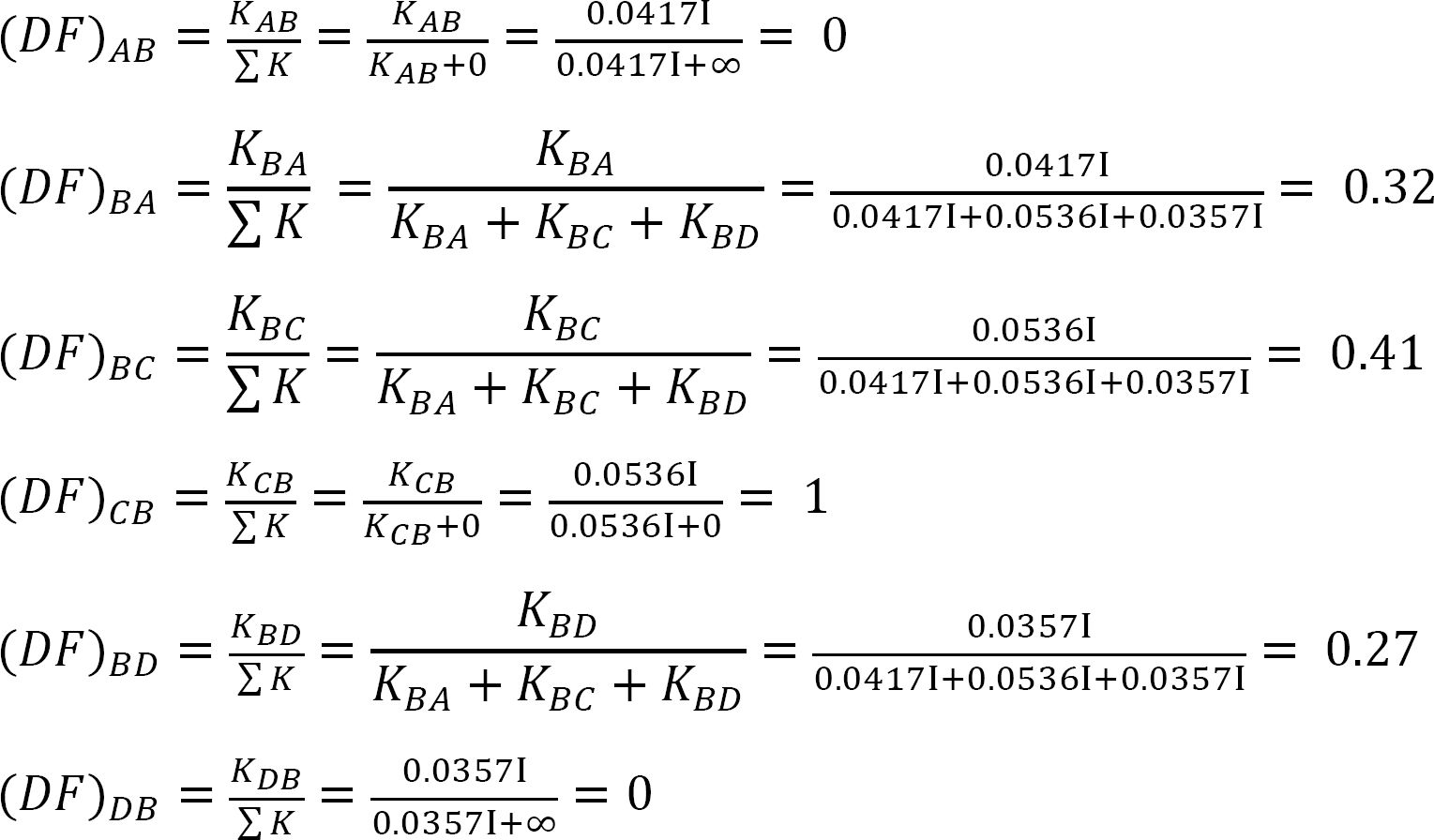
Tabla 12.3. Tabla de distribución.
Momentos finales de los miembros.
Sustituyendo los valores obtenidos de EKθB, EKθC, y EK∆ en los estados finales momento ecuaciones sugiere la siguiente:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Ejemplo 12.4
Utilizando el método de distribución de momentos, determine los momentos finales en los soportes del marco que se muestran en la Figura 12.9. EI = constante.
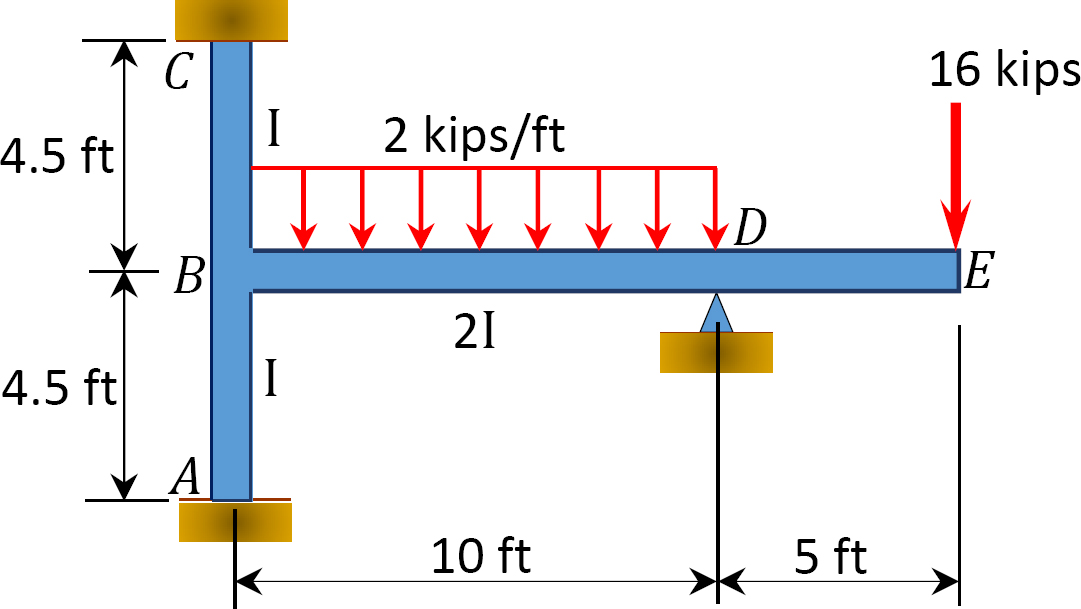
Fig. 12.9. Marco.
Solución
Momento final fijo.
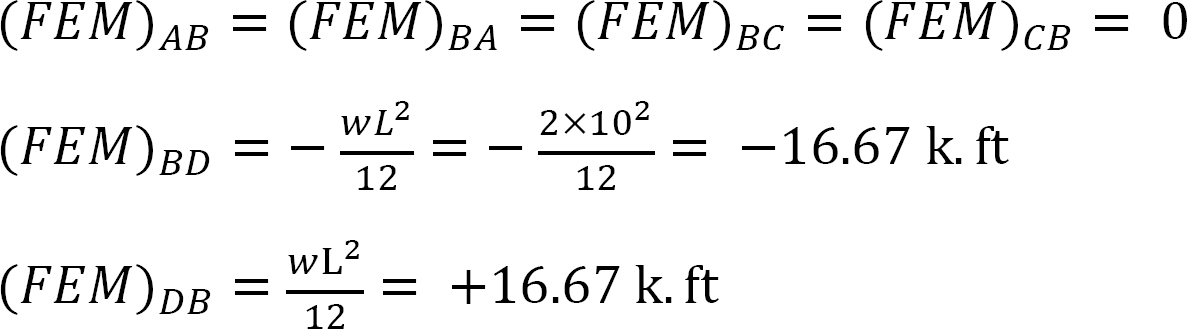
Factor de rigidez.
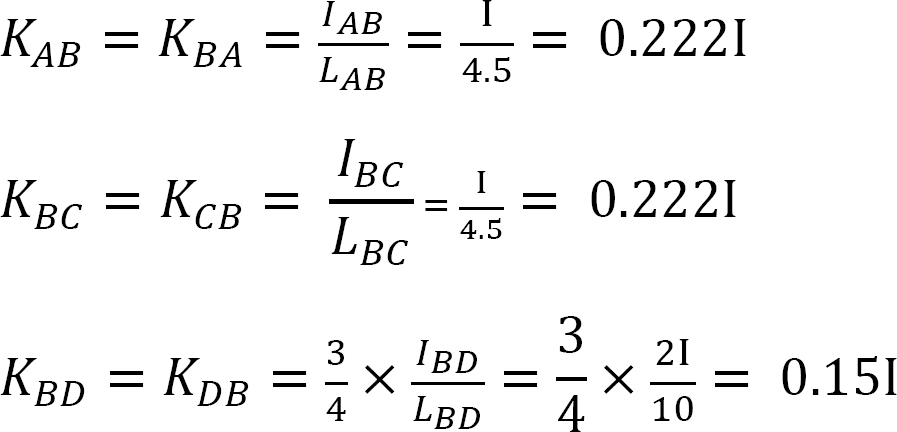
factor de Distribución.

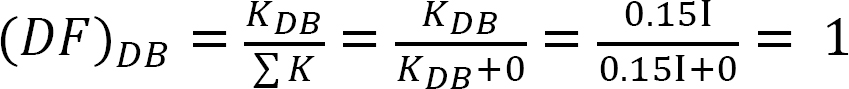
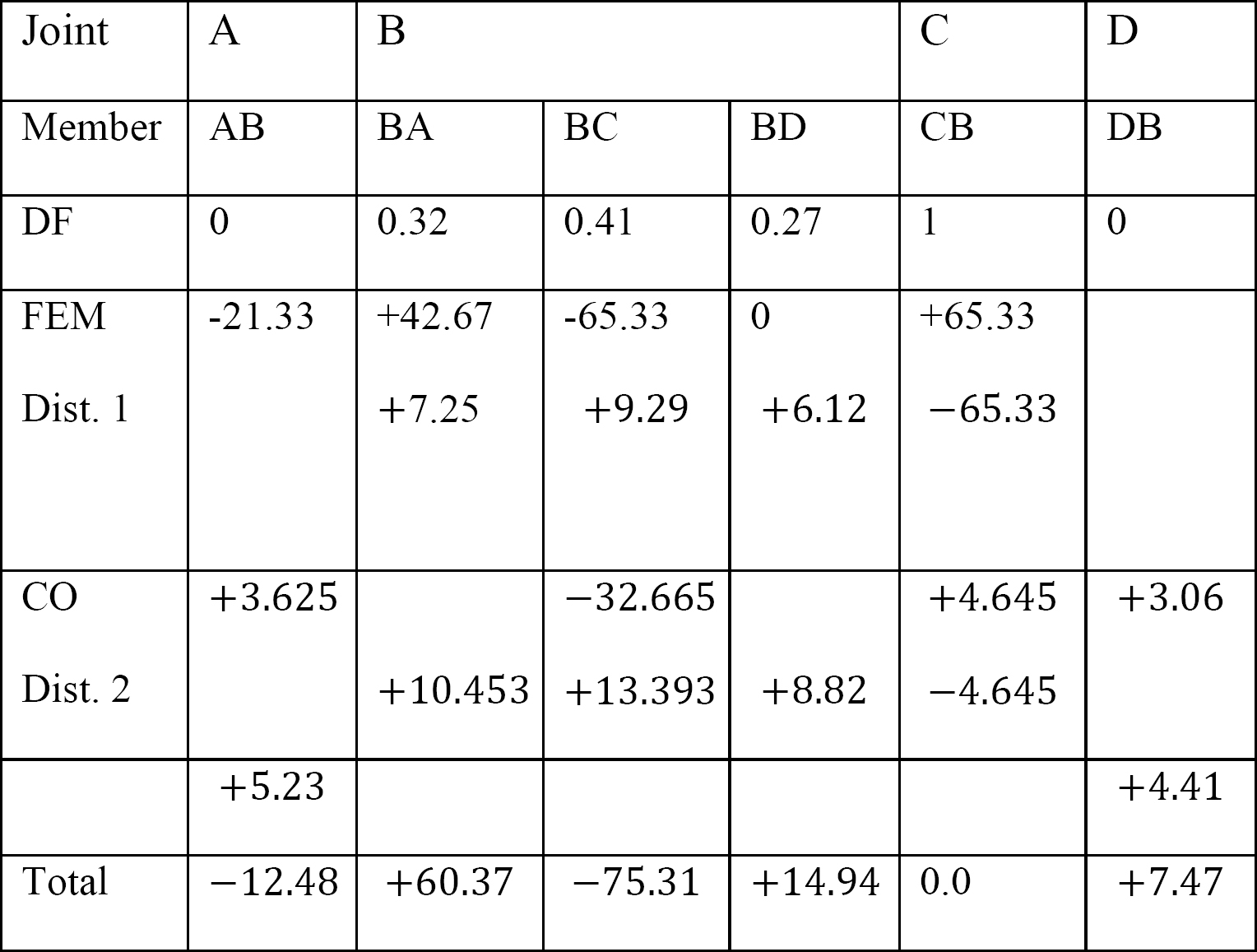
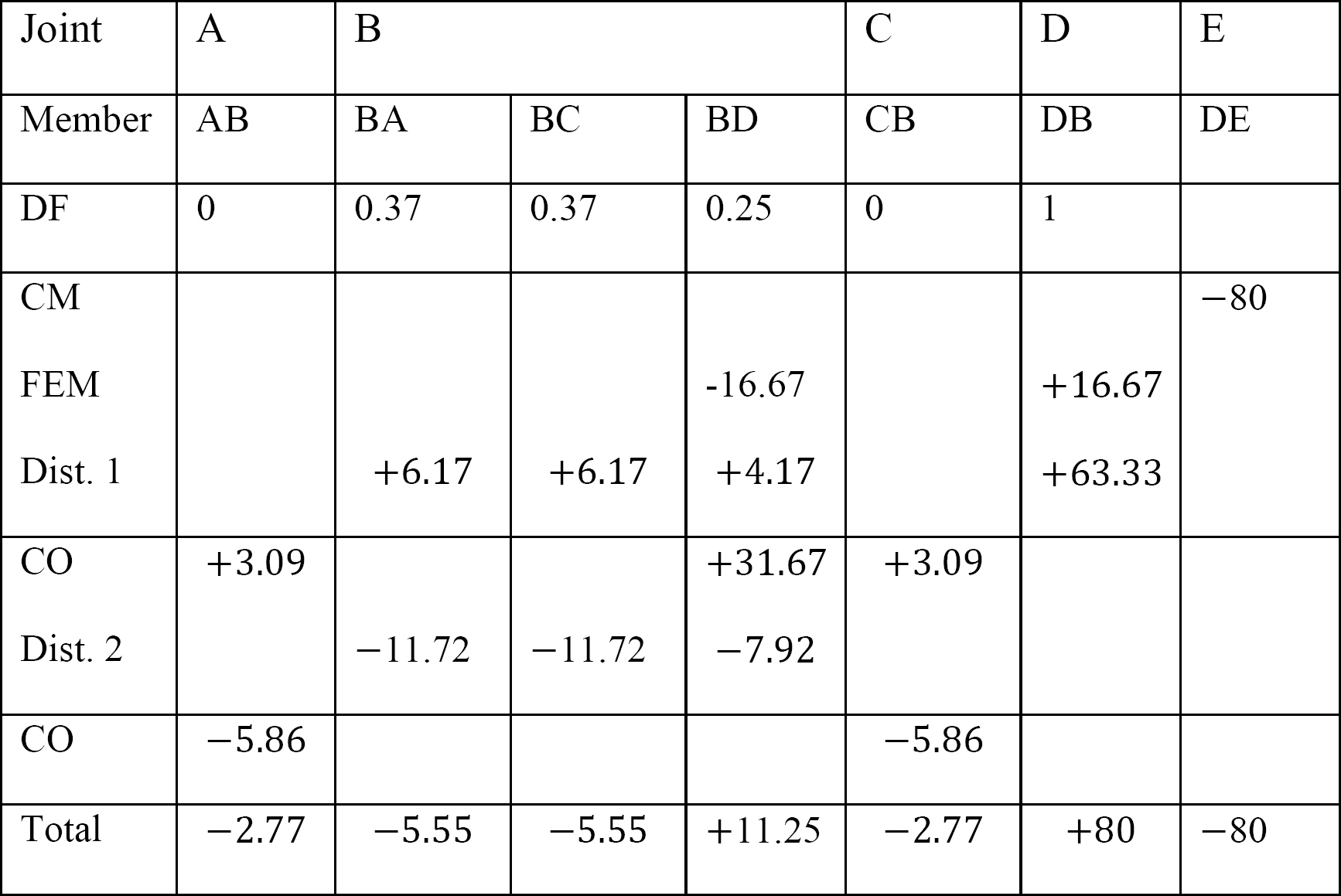
Tabla 12.4. Tabla de distribución.
Momentos finales de los miembros.
MAB = -2.77 k. ft
MBA = -5.55 k. ft
MBC = -5.55 k. ft
MBD = +11,25 k. ft
MCB = -2,77
MDB = + 80 k. ft
MDE = -80 k. ft
Ejemplo 12.5
Utilizando el método de distribución de momentos, determine los momentos finales en los soportes del marco que se muestran en la Figura 12.10. EI = constante.
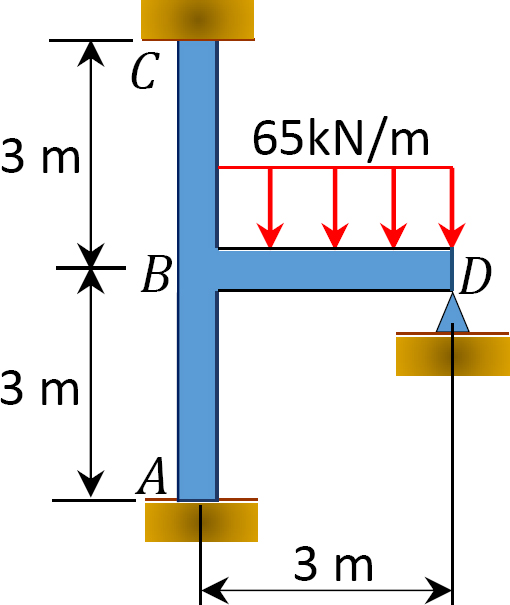
Fig. 12.10. Marco.
Solución
Momento final fijo.
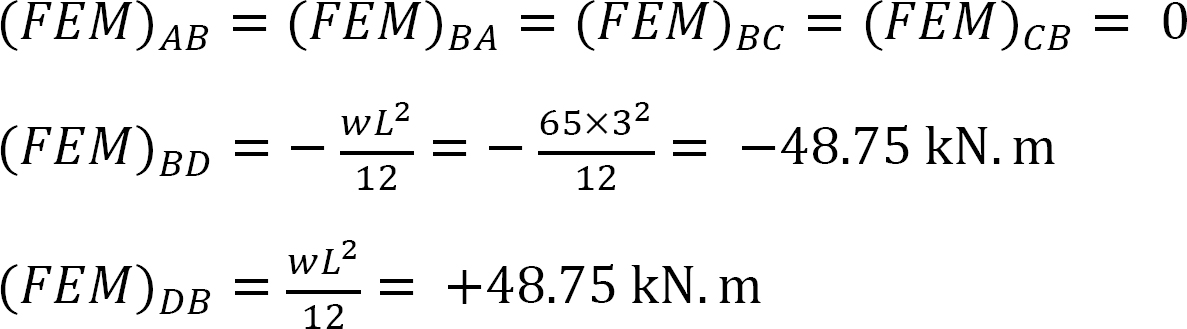
Factor de rigidez.
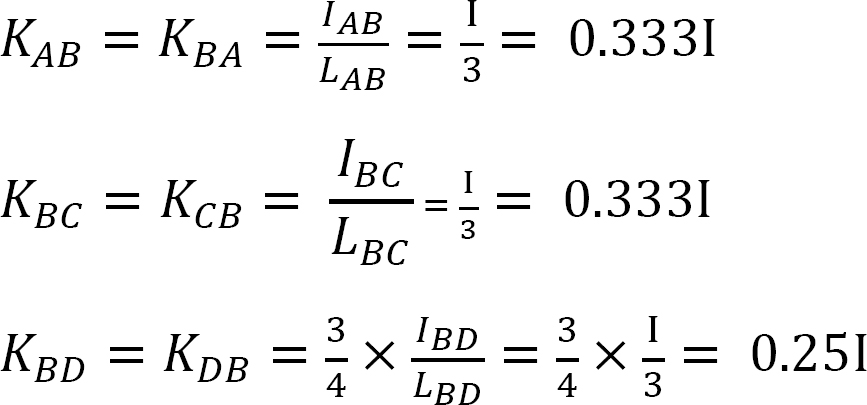
factor de Distribución.
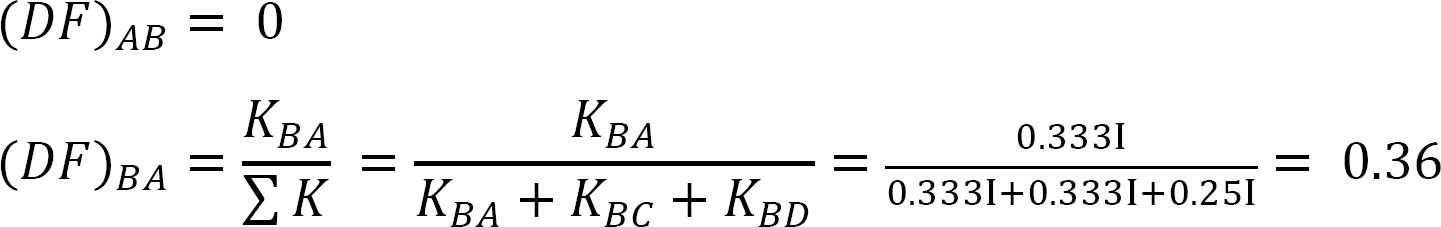

Tabla 12.5. Tabla de distribución.
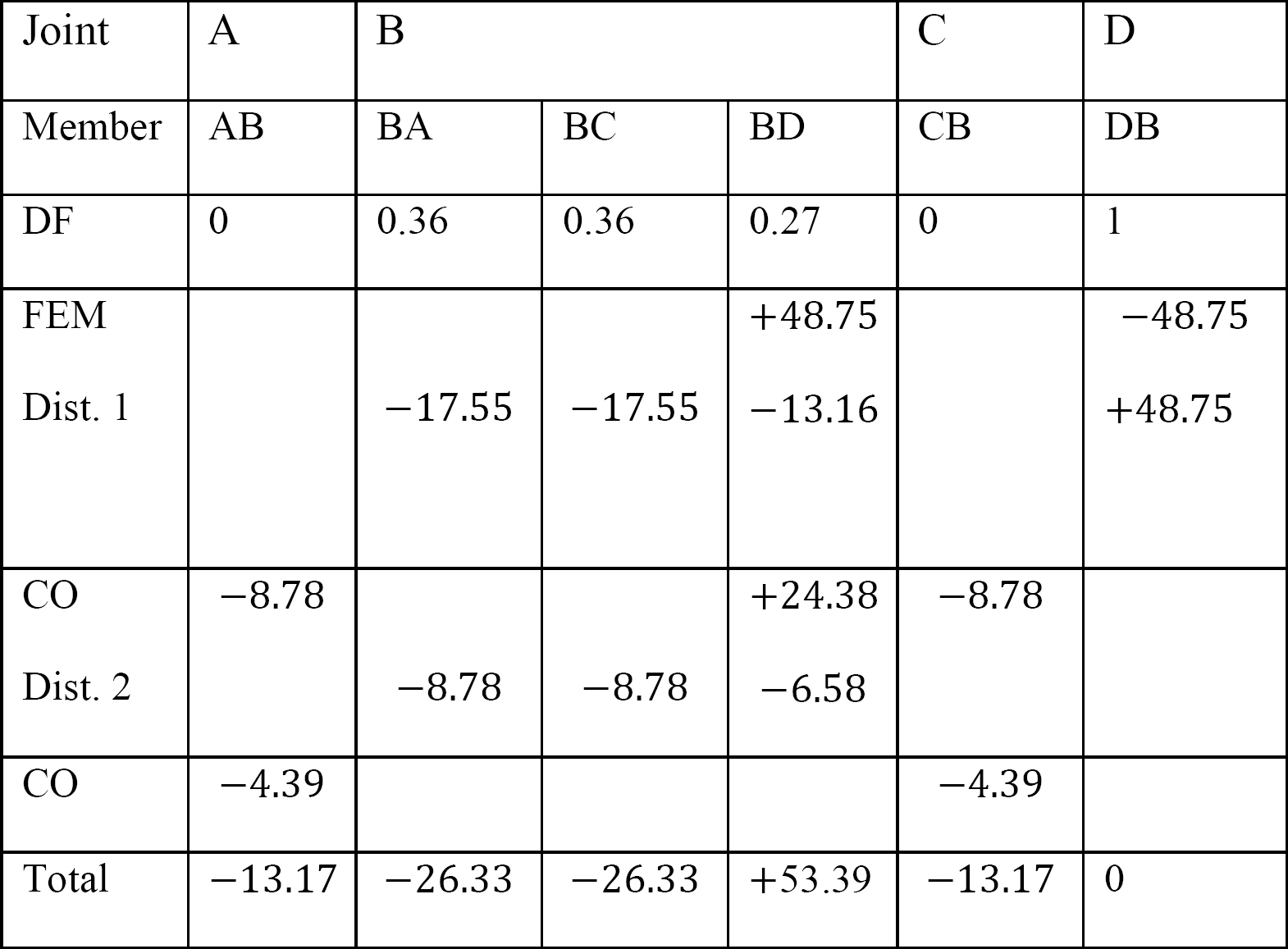
Momentos finales de los miembros.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +un 53,39 k. ft
MCB = -13.17 k. ft
MDB = 0
Ejemplo 12.6
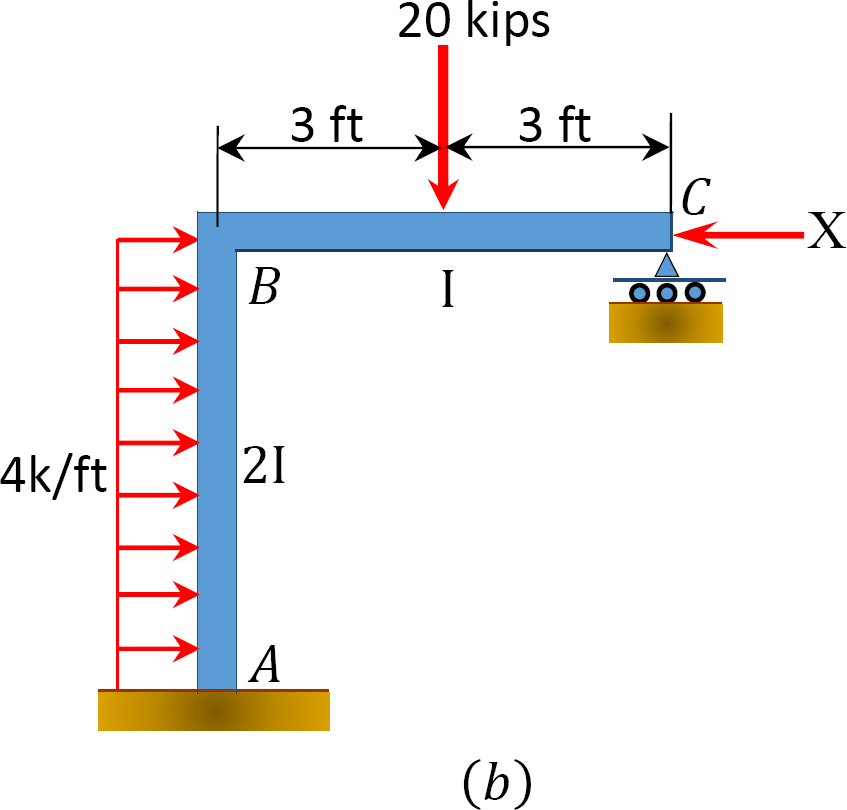
Utilizando el momento en el método de distribución, determinar el miembro final-momentos de la trama con el lado de balanceo se muestra en la Figura 12.11 un.
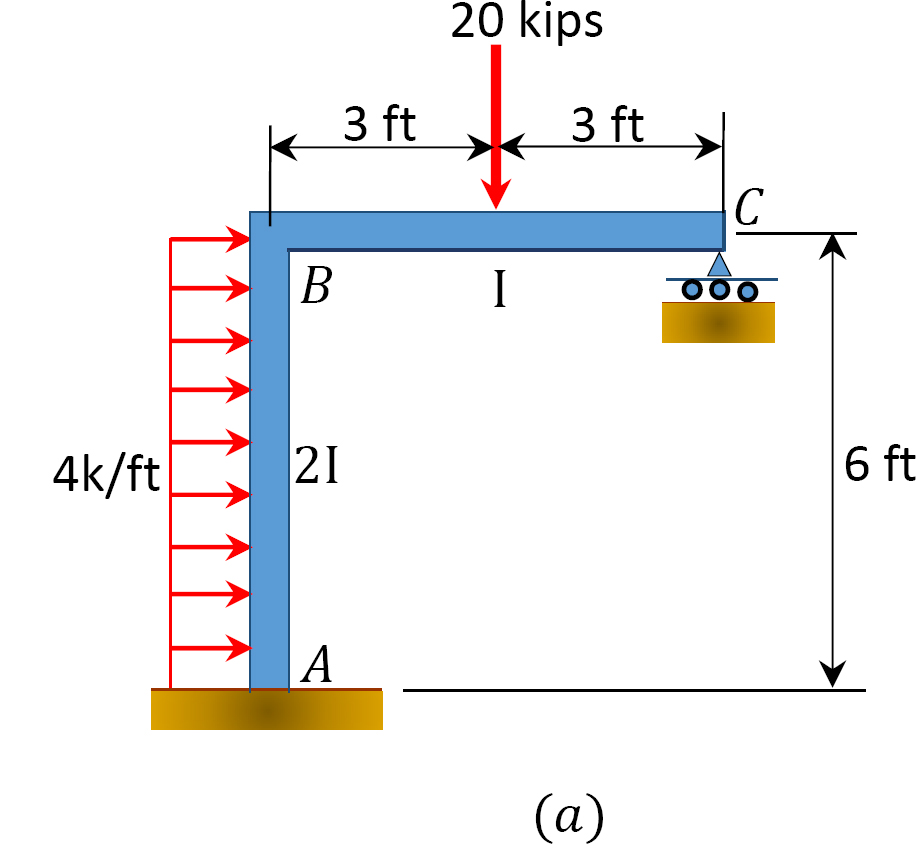
Fig. 12.11. Marco con balanceo lateral.
Solución
Momento final fijo.
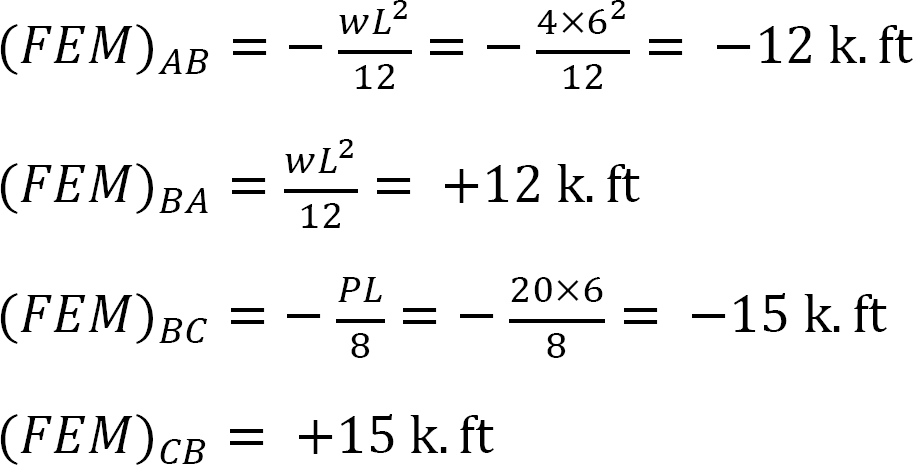
Factor de rigidez.
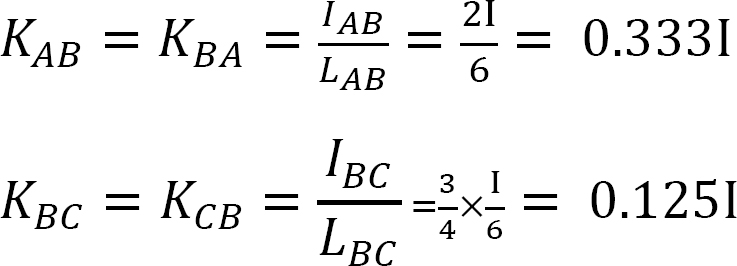
factor de Distribución.
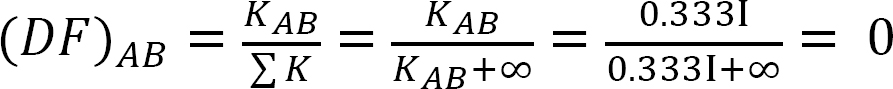

Análisis de marco sin el lado de balanceo.
la Tabla 12.6. Mesa de distribución (sin marco oscilante).
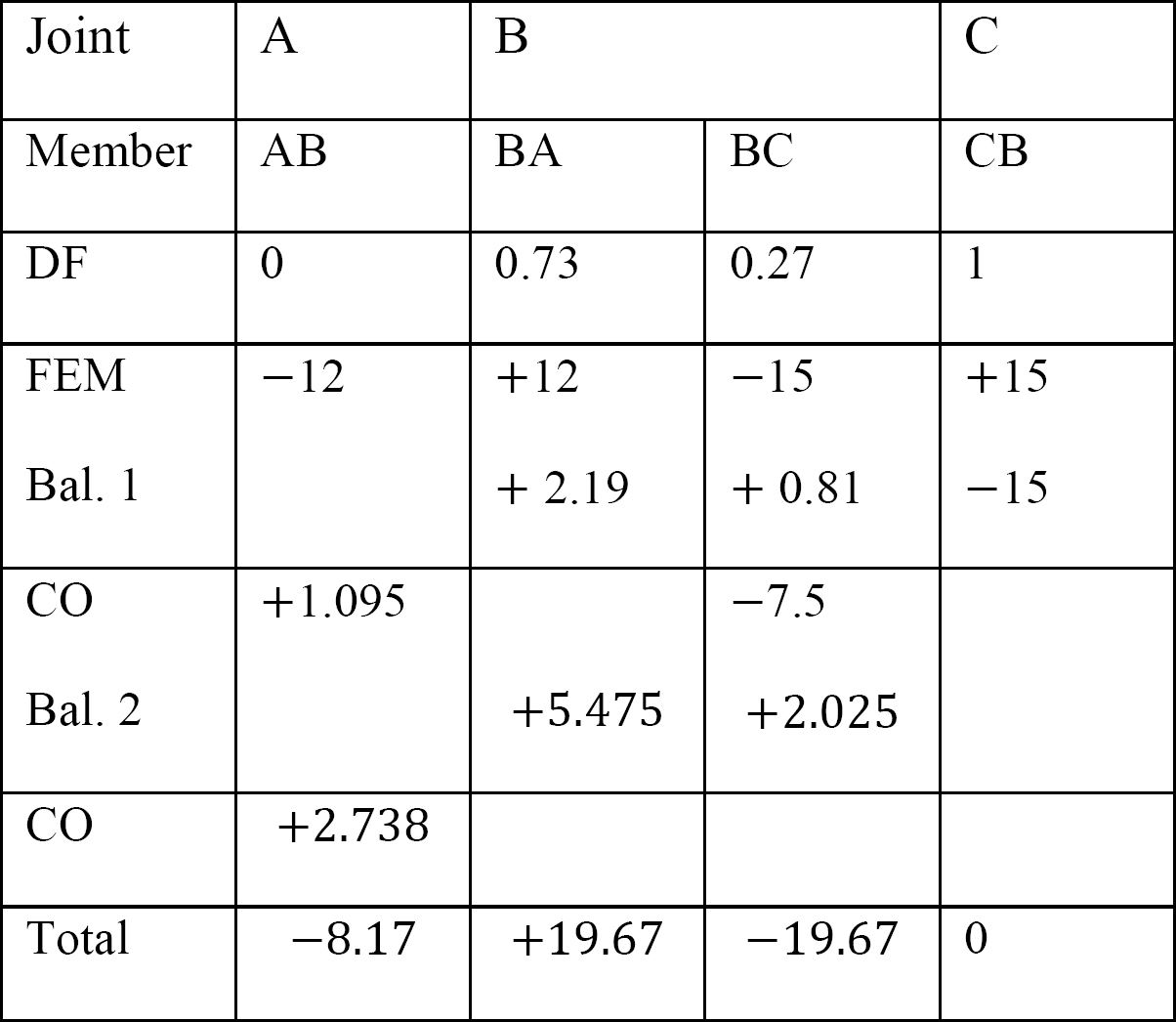
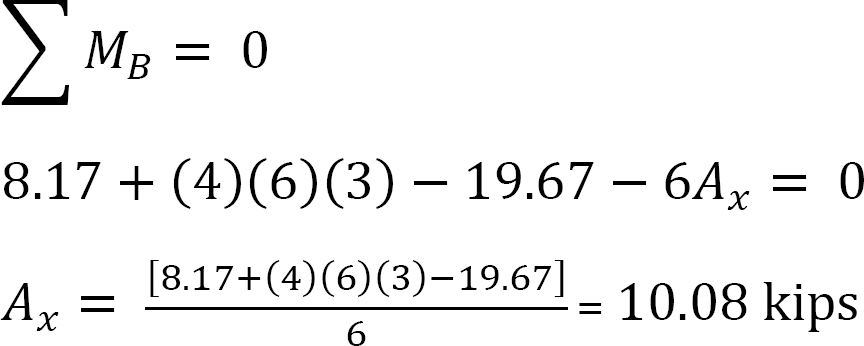
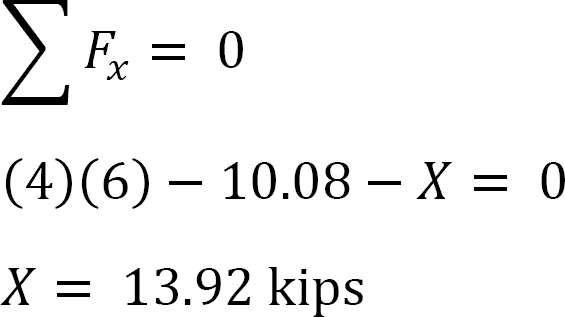
Análisis de marco con el lado de balanceo.
Supongamos que MAB = + 20 k. ft
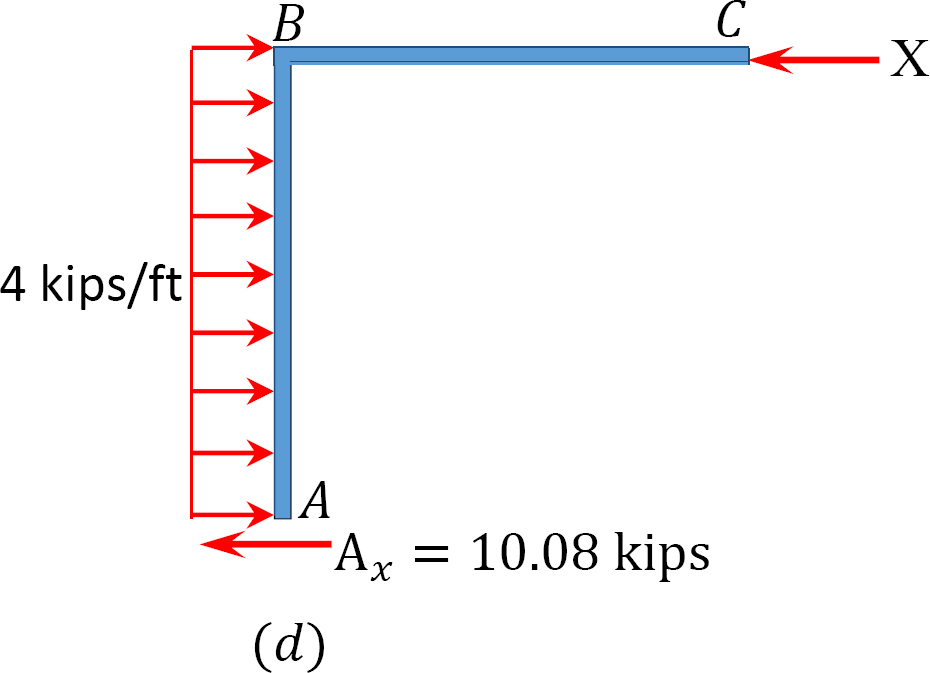
Cuadro 12.7. Mesa de distribución (marco oscilante).
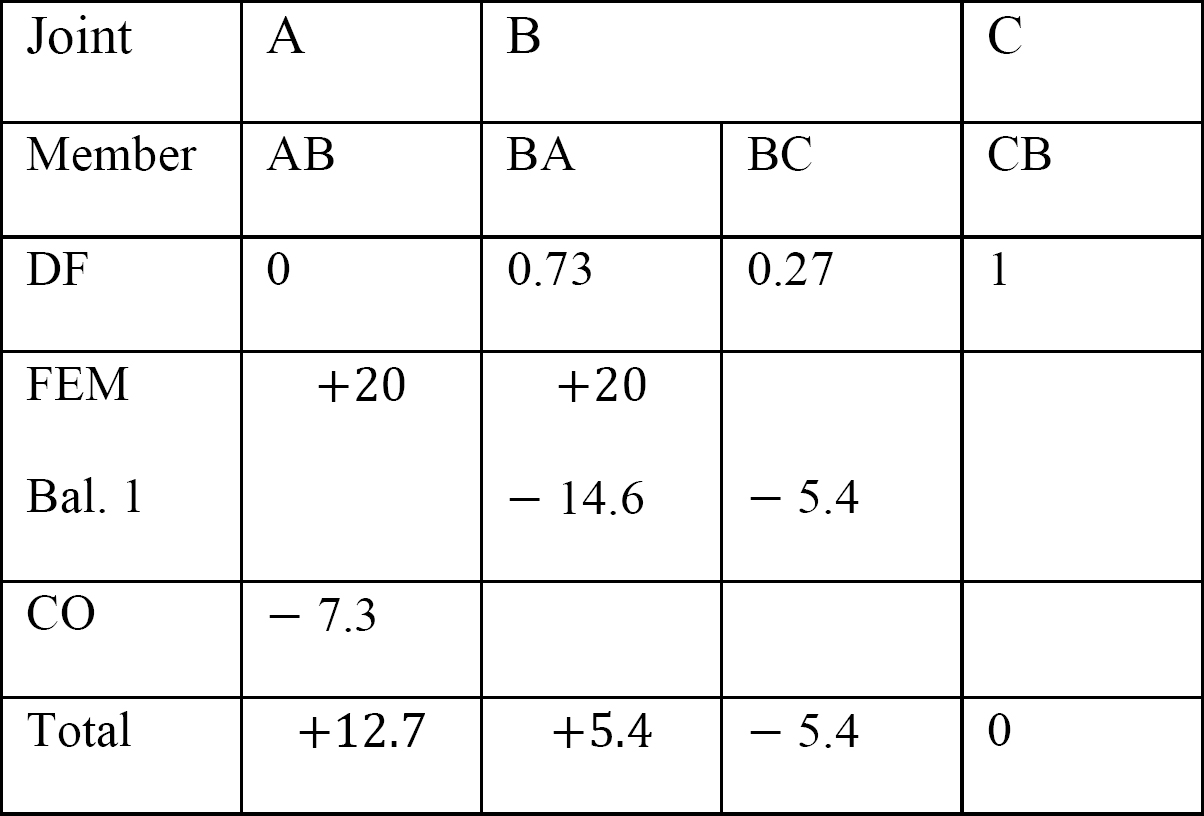
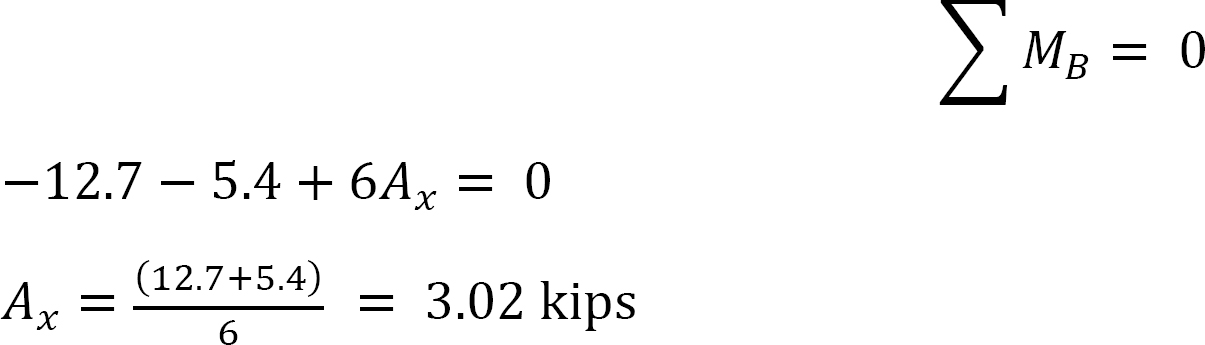
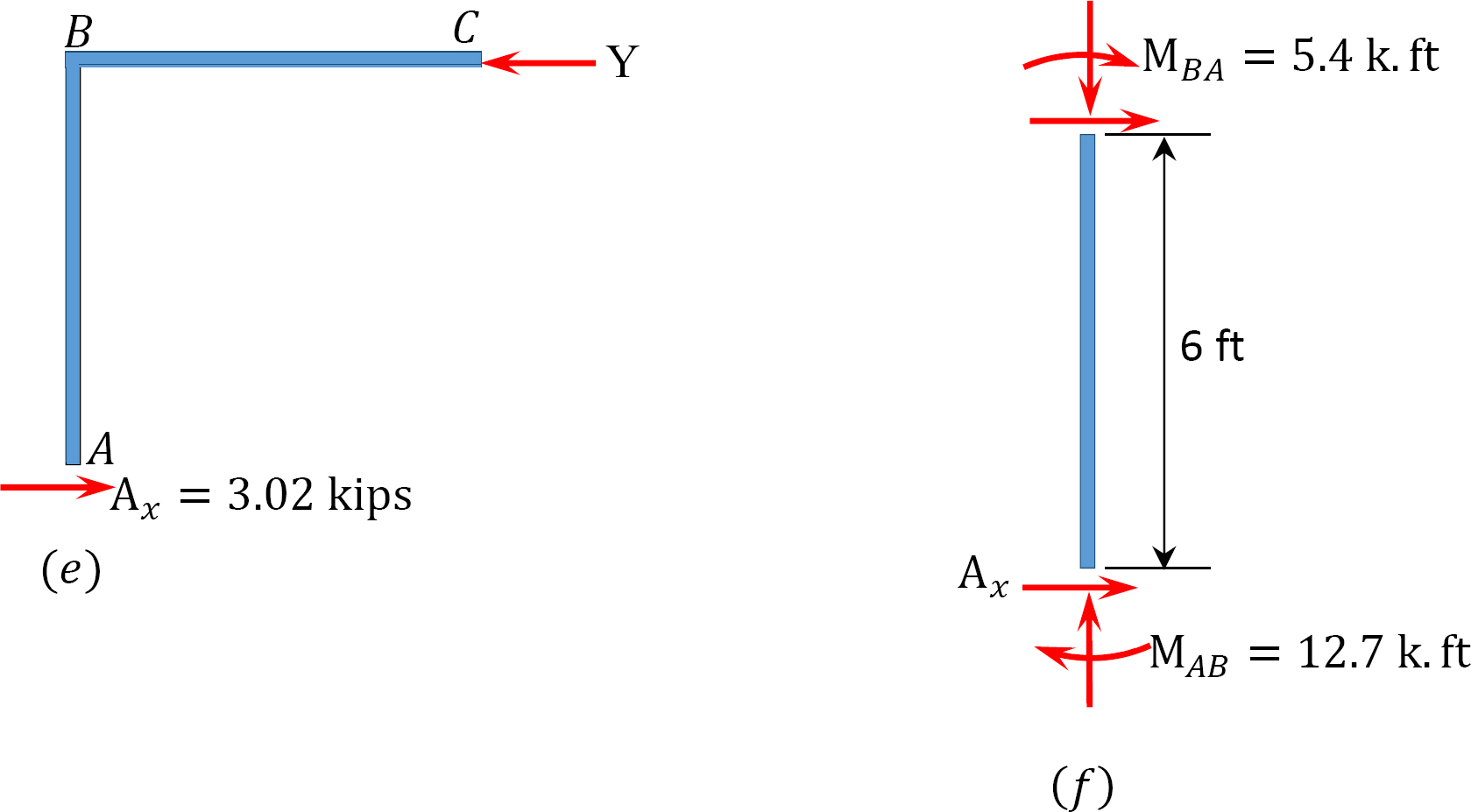
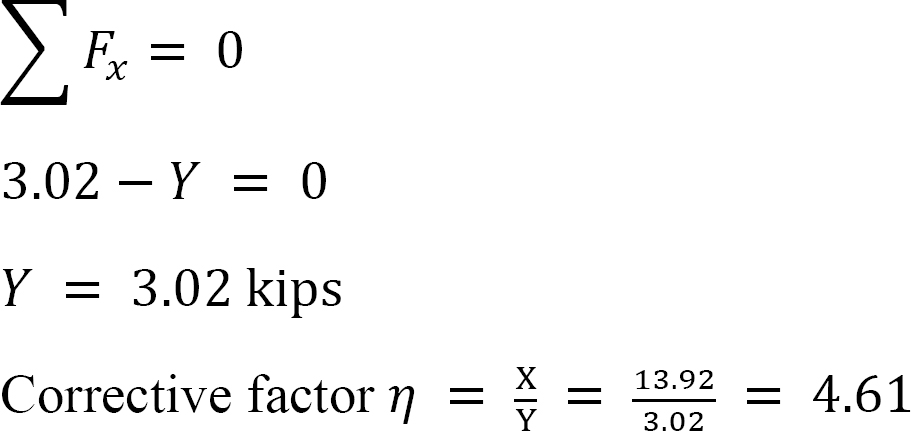
Final momentos.
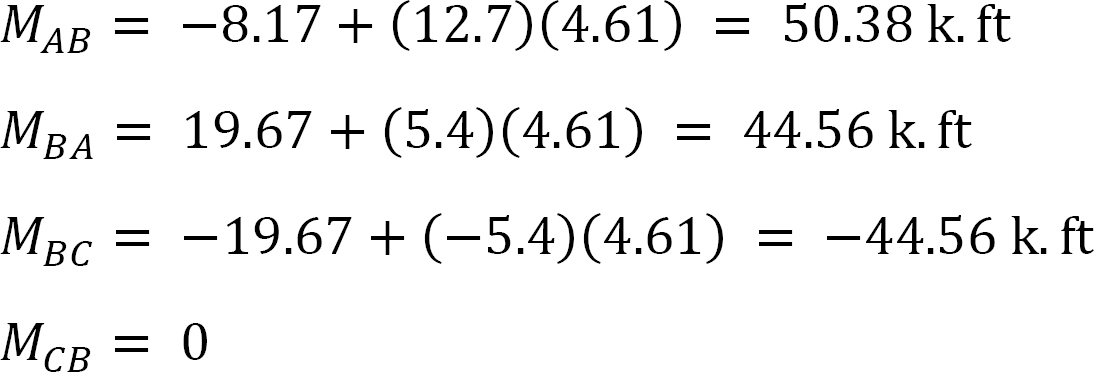
Ejemplo 12.7
Se carga un marco de balanceo como se muestra en la Figura 12.12 a. Utilizando el método de distribución de momentos, determine los momentos finales de los miembros del marco.
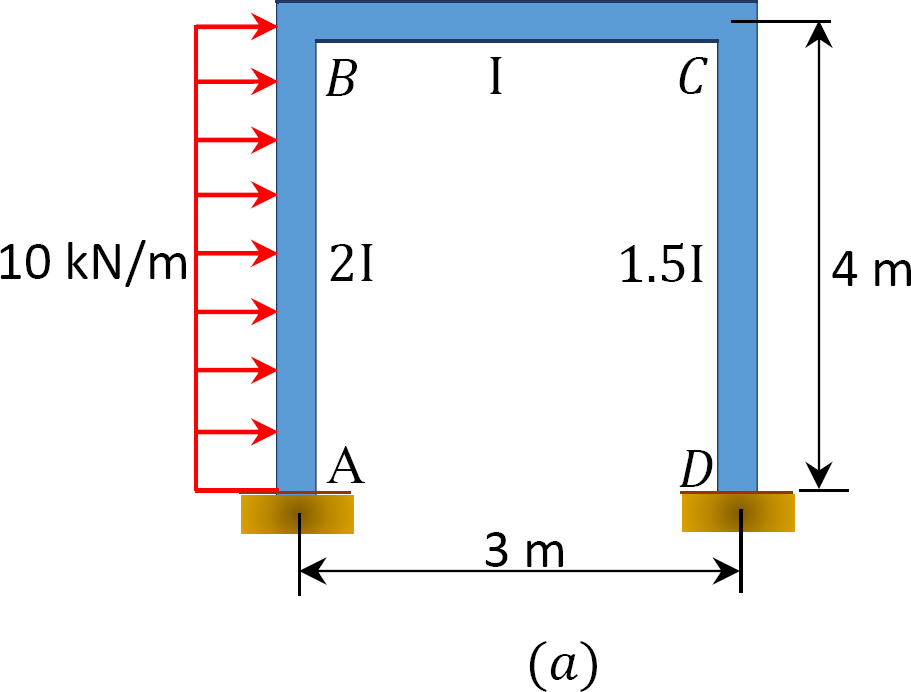
Fig. 12.12. Marco oscilante cargado.
Solución
Momento final fijo.
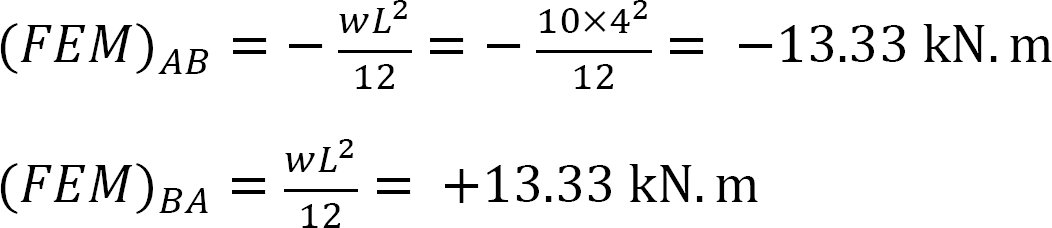
Factor de rigidez.
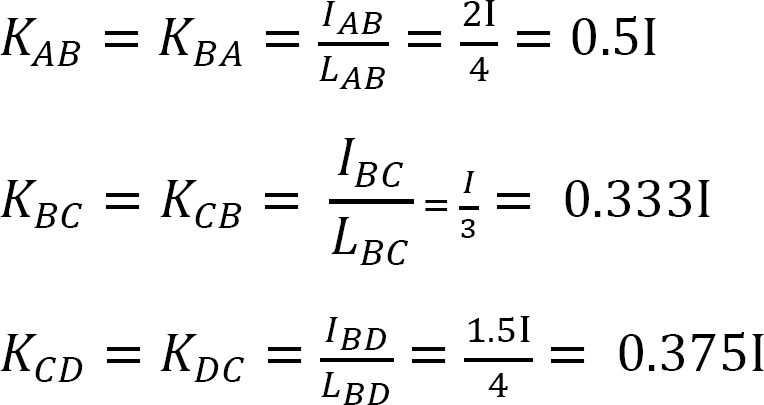
factor de Distribución.

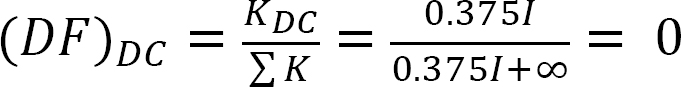
Análisis de marco sin el lado de balanceo.
Cuadro 12.8. Mesa de distribución (sin marco oscilante).
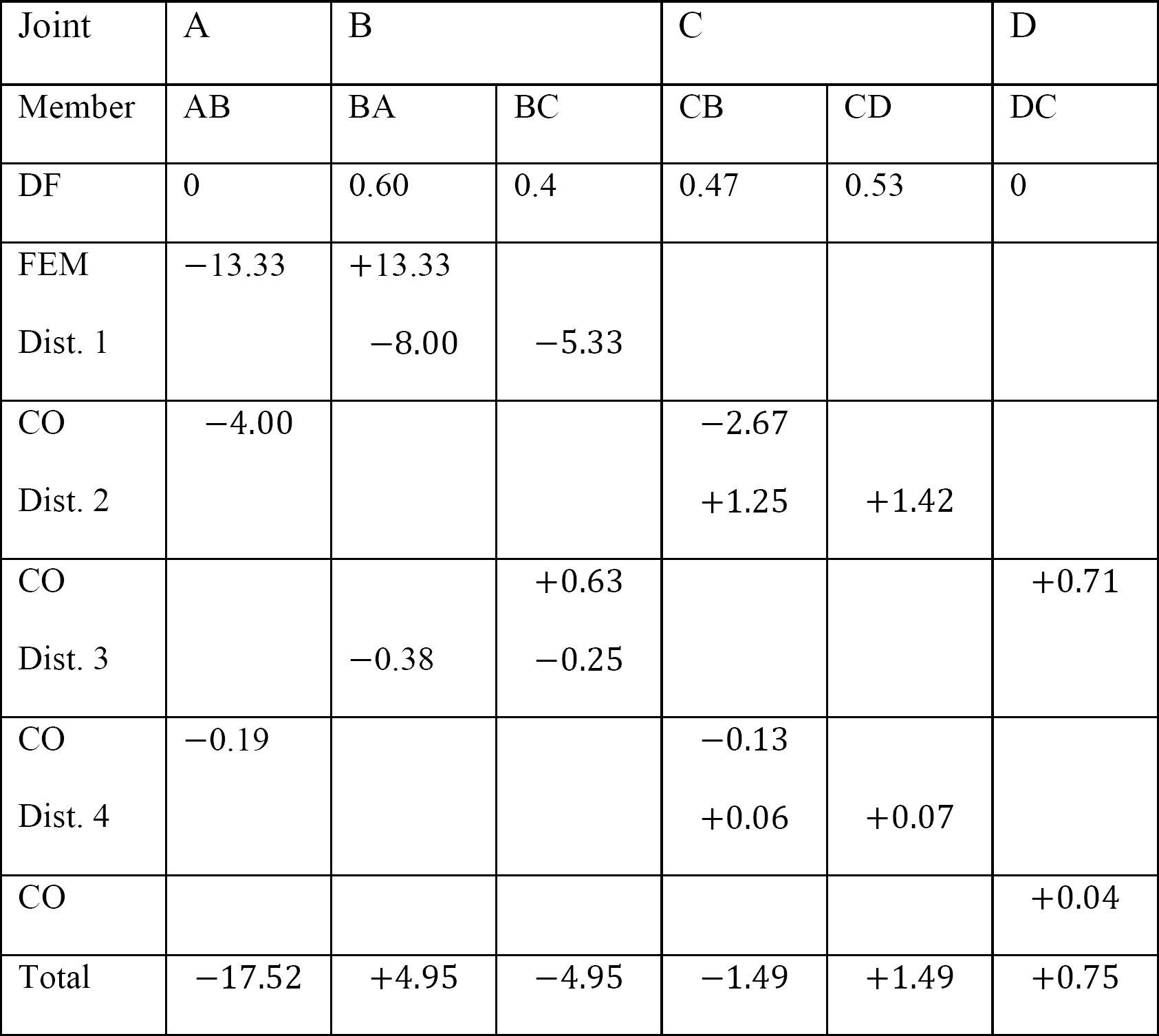
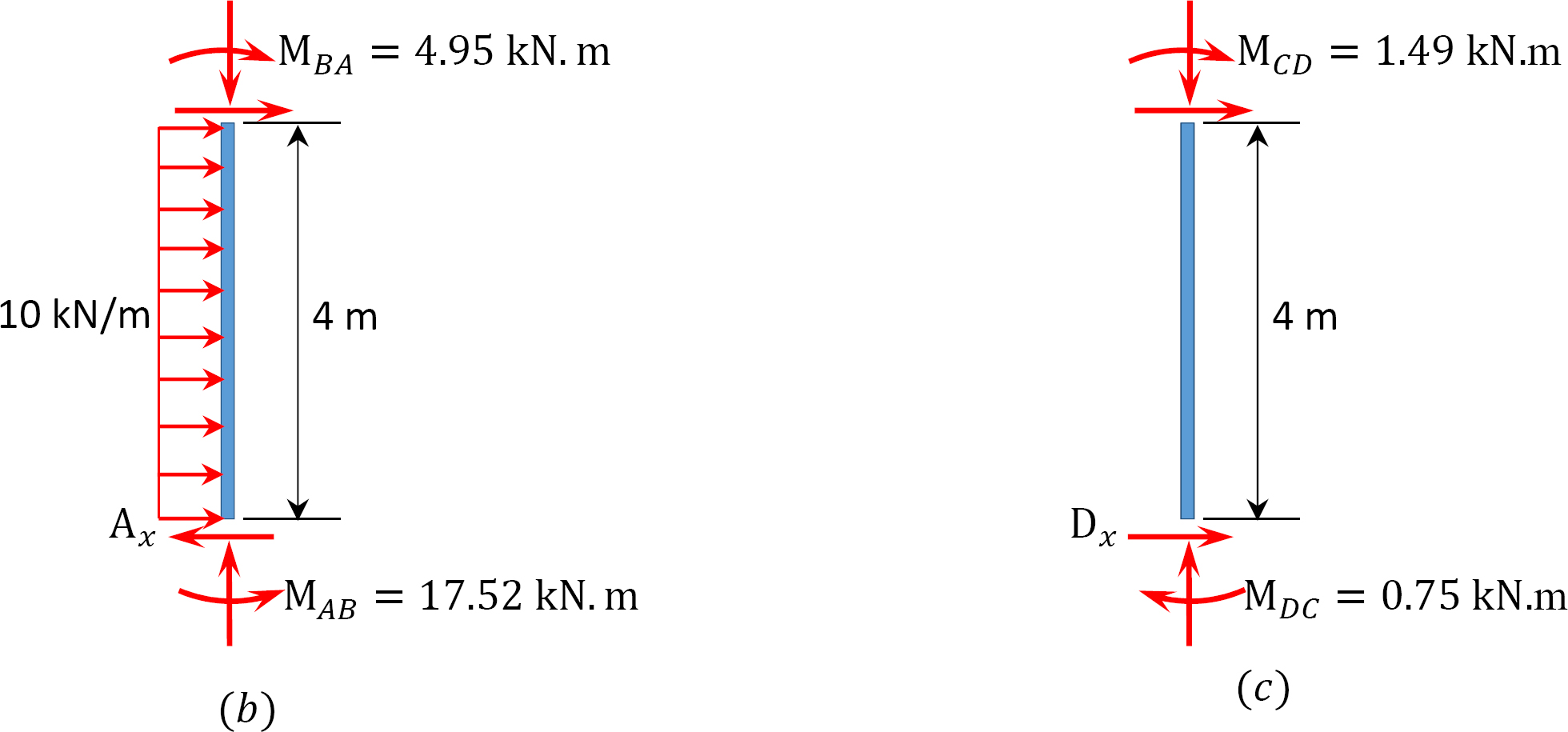
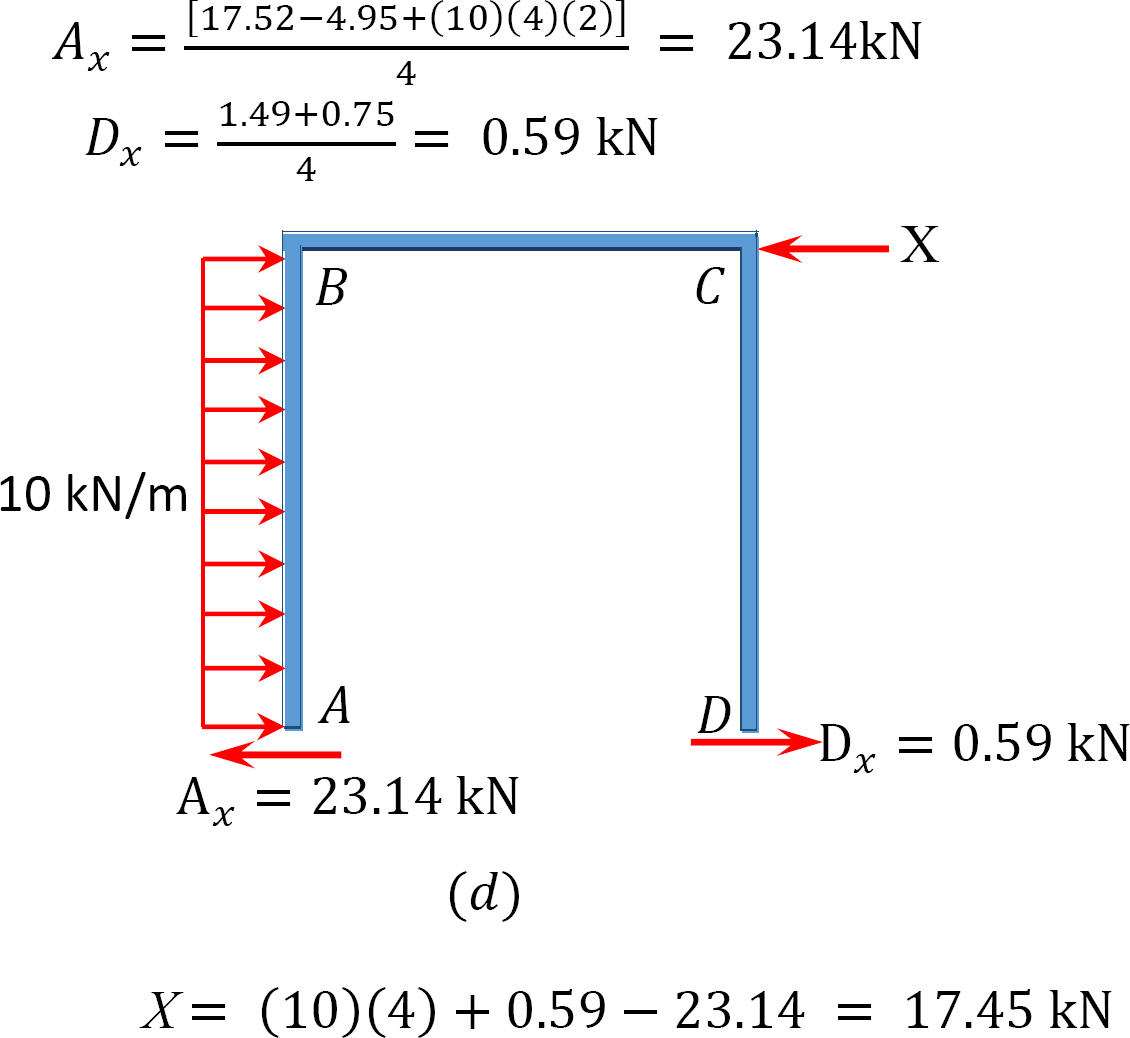
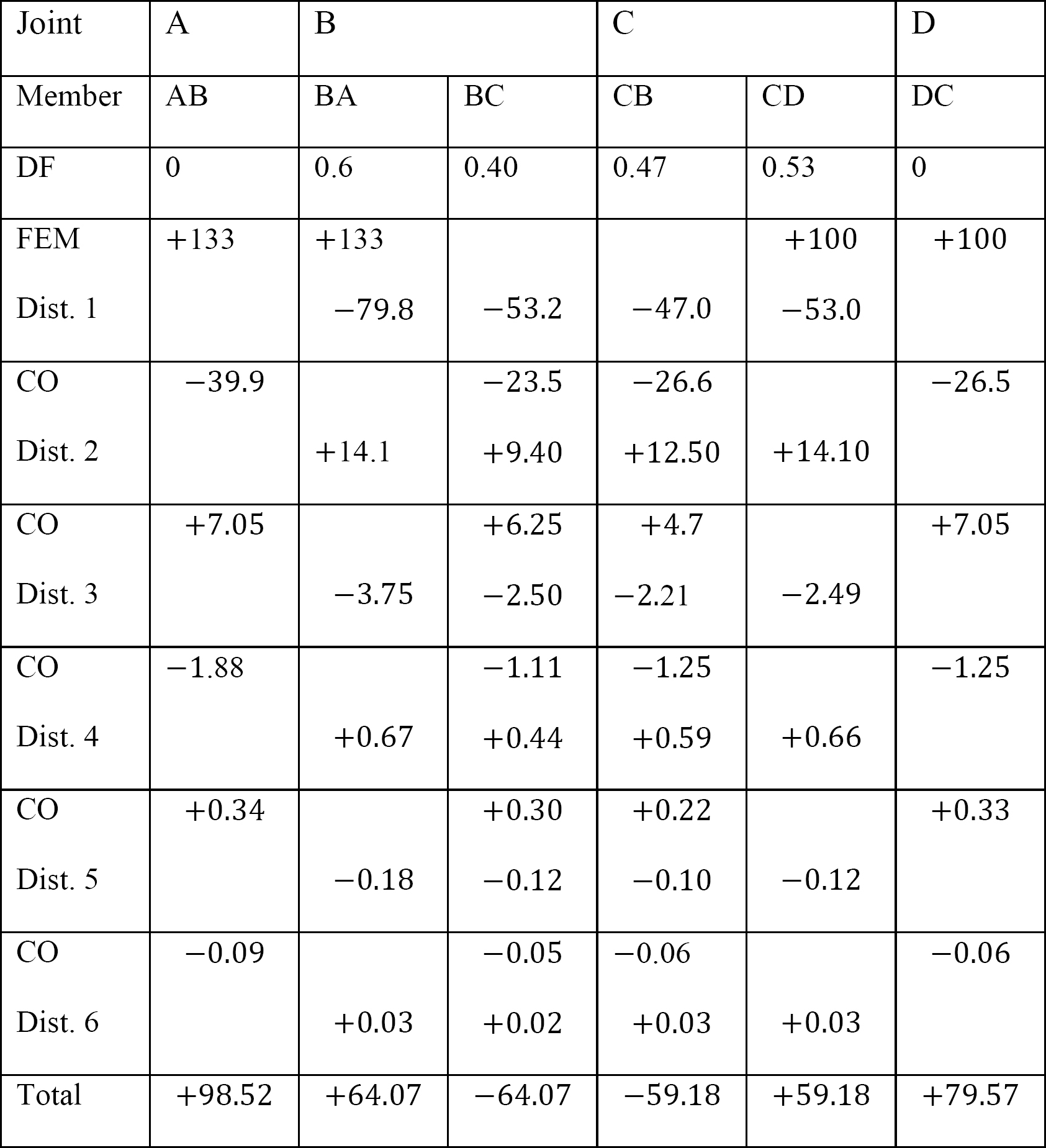
Tabla 12.9. Mesa de distribución (marco oscilante).
Análisis de bastidor con balanceo lateral.
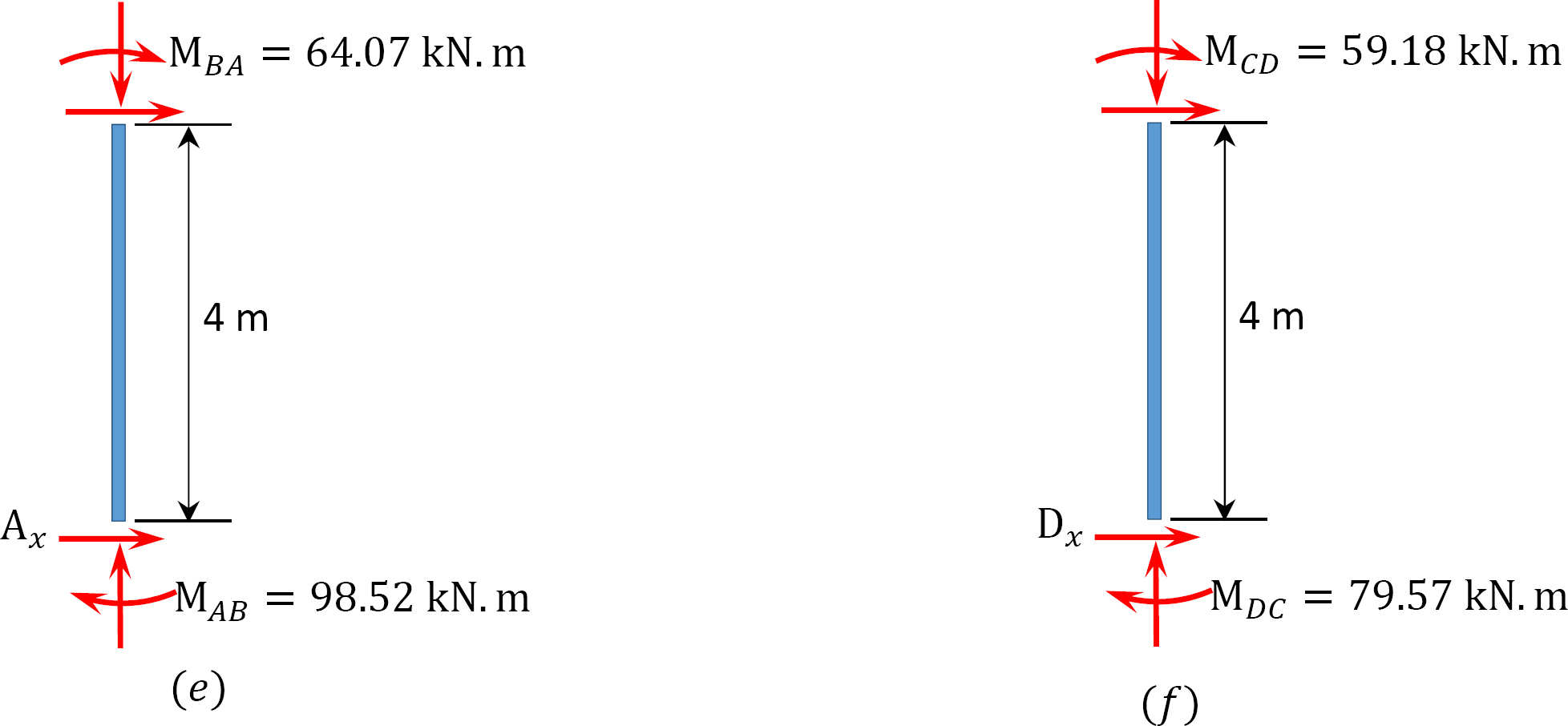

fin último momento.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
CMM = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Resumen del capítulo
Método de análisis de distribución de momentos de estructuras indeterminadas: El método de análisis de distribución de momentos es un método de análisis aproximado. Su grado de precisión depende del número de iteraciones. En este método, se supone que todas las juntas de una estructura están bloqueadas o sujetas temporalmente y, por lo tanto, se evita la posible rotación. Se aplican cargas a las barras y se determinan los momentos desarrollados en los extremos de las barras debido a la fijación. Las articulaciones de la estructura se desbloquean sucesivamente, y el momento de desequilibrio en cada articulación se distribuye a los miembros que se reúnen en esa articulación. Se determinan los momentos de arrastre en los extremos lejanos de los miembros, y el proceso de equilibrio continúa hasta el nivel deseado de precisión. Los momentos finales de los miembros se determinan sumando el momento de final fijo, el momento distribuido y el momento de arrastre. Una vez que se determinan los momentos finales de los miembros, la estructura se vuelve determinada.
Problemas de práctica
12.1 Utilice el método de distribución de momentos para calcular el momento final de las barras de las vigas que se muestran en la Figura P12.1 hasta la Figura P12.12 y dibuje los diagramas de momento de flexión y fuerza de corte. EI = constante.
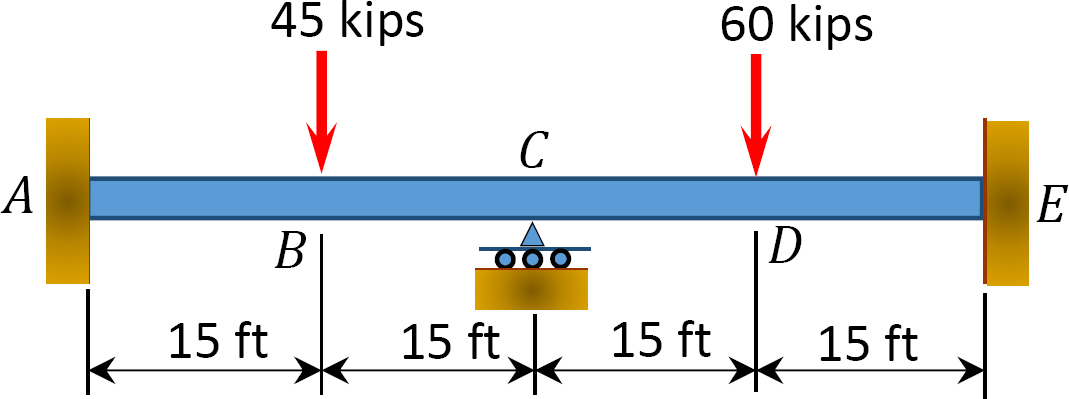
Fig. P12.1. Viga.
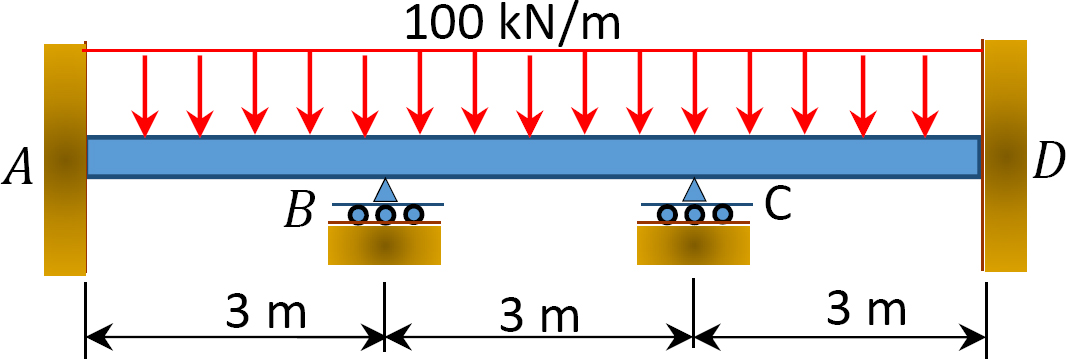
Fig. P12. 2. Viga.
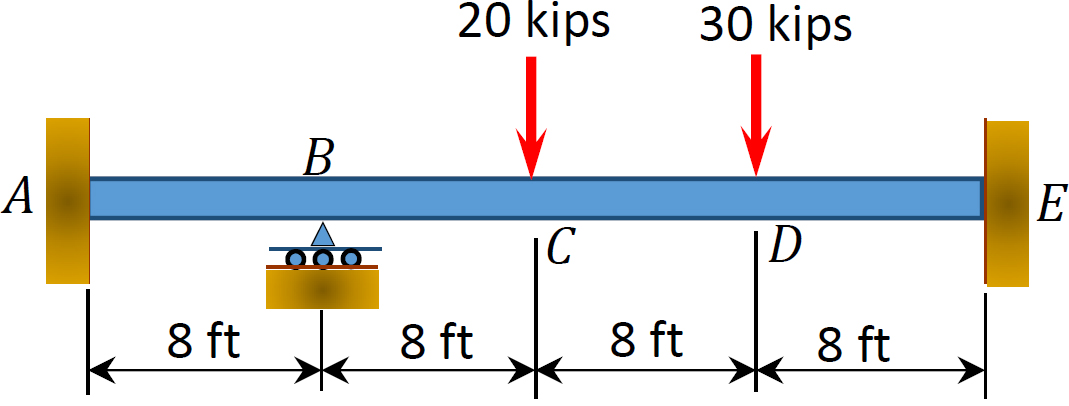
Fig. P12. 3. Viga.
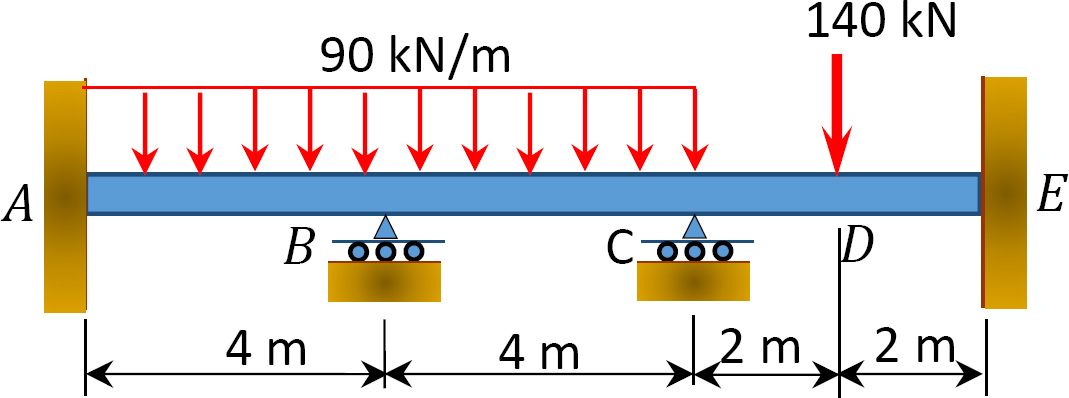
Fig. P12. 4. Viga.
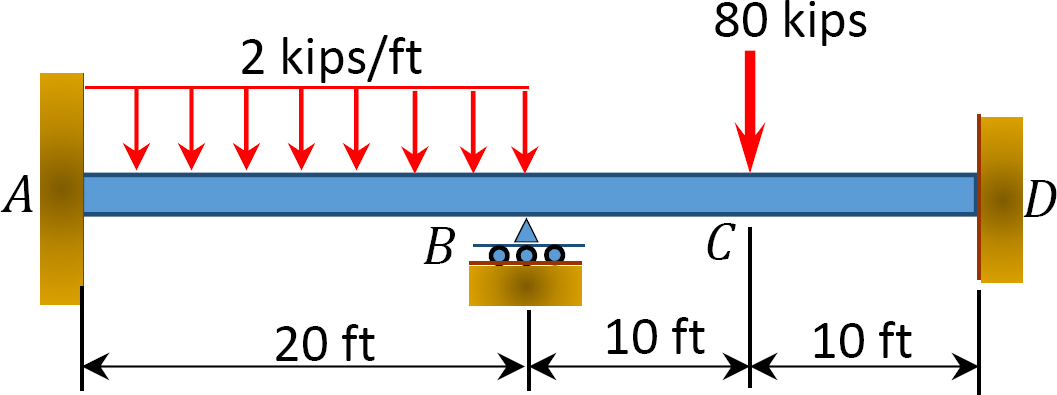
Fig. P12. 5. Viga.
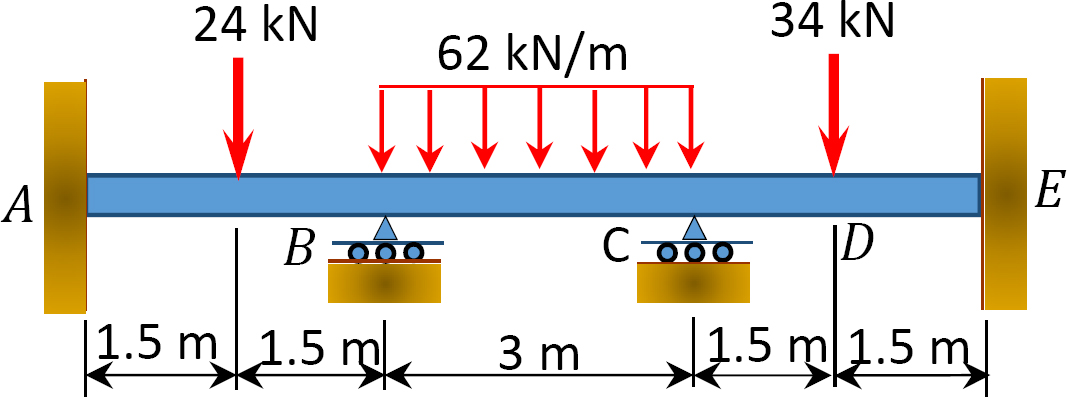
Fig. P12. 6. Viga.
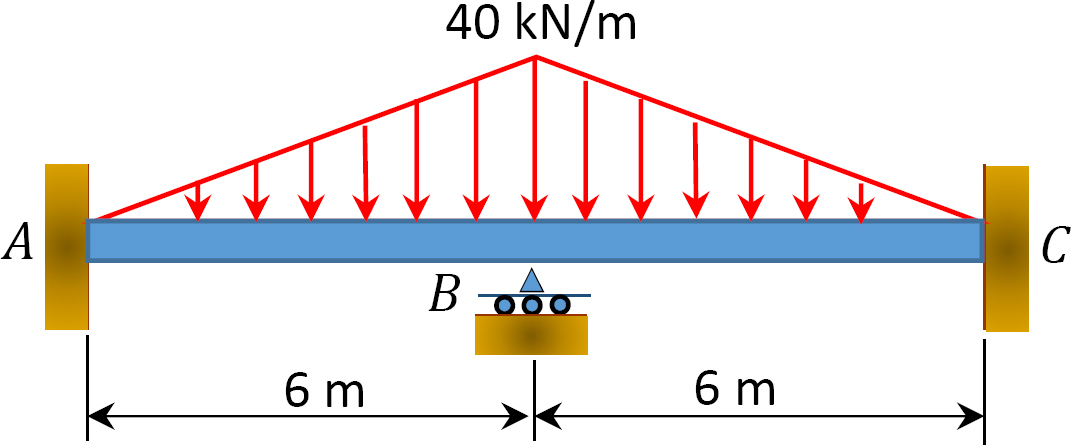
Fig. P12. 7. Viga.
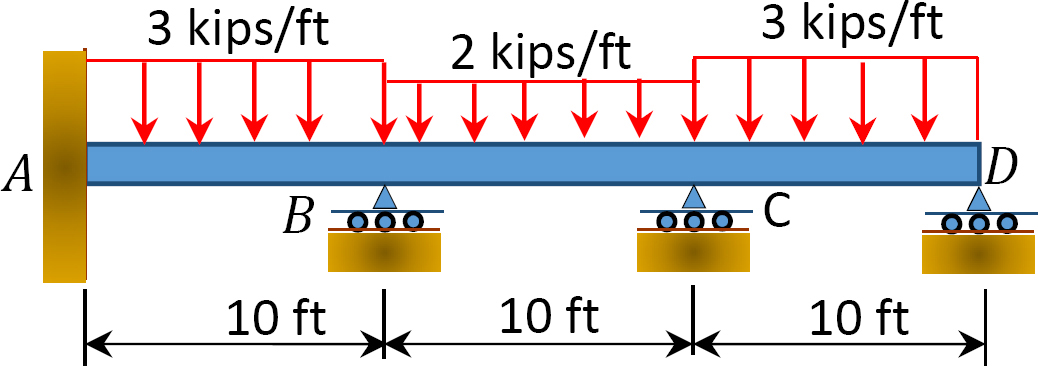
Fig. P12. 8. Viga.
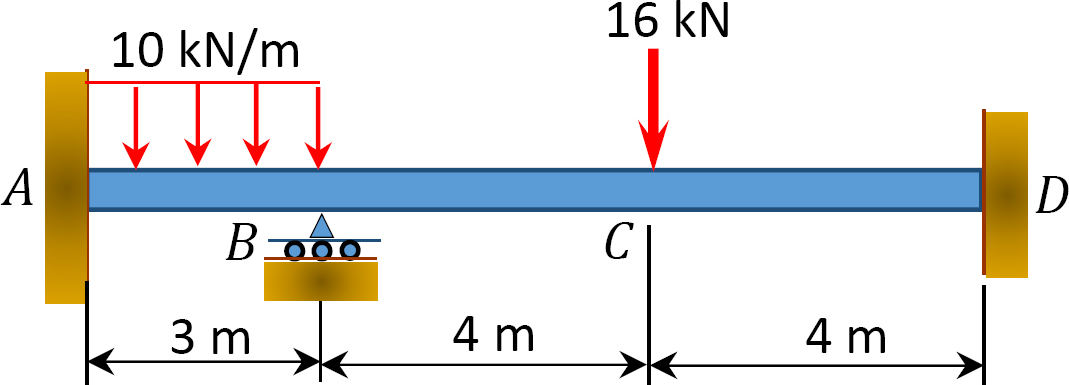
Fig. P12. 9. Viga.
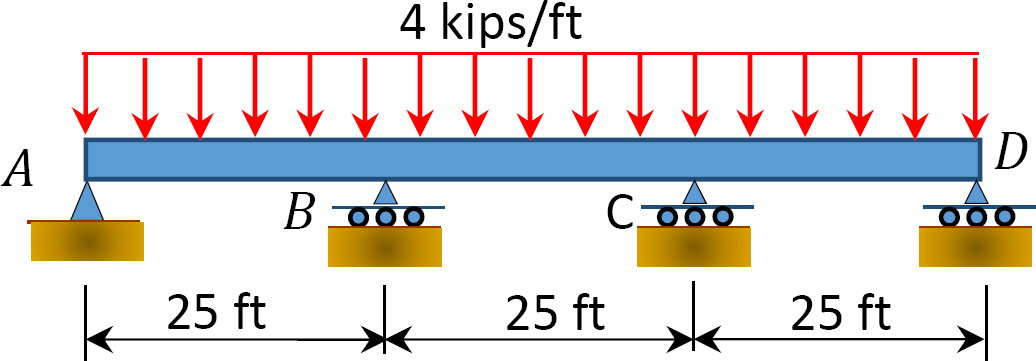
Fig. P12. 10. Viga.
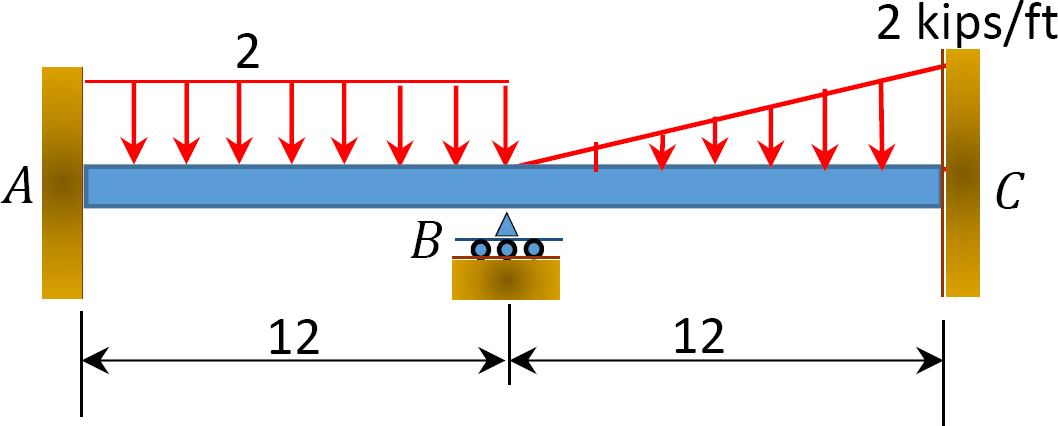
Fig. P12.11. Viga.
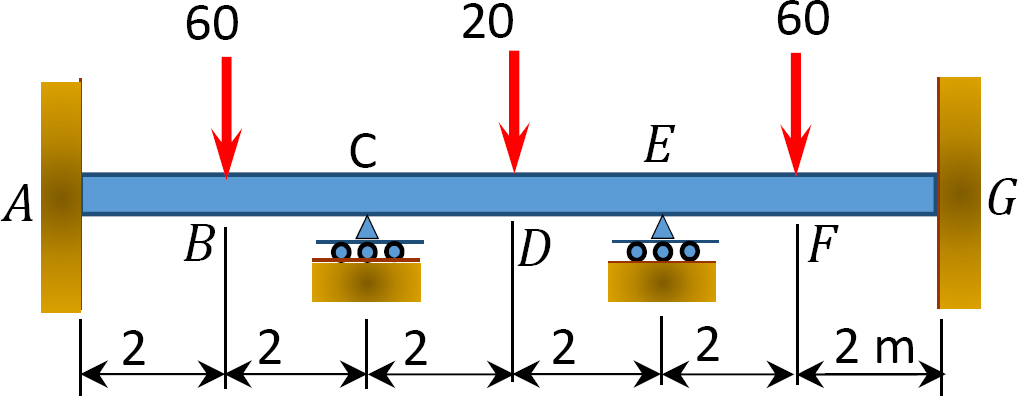
Fig. P12.12. Viga.
12.2 Utilice el método de distribución de momentos para calcular el momento final de los miembros de los marcos mostrados en la Figura P12.13 hasta la Figura 12.20 y dibuje los diagramas de momento de flexión y fuerza de corte. EI = constante.
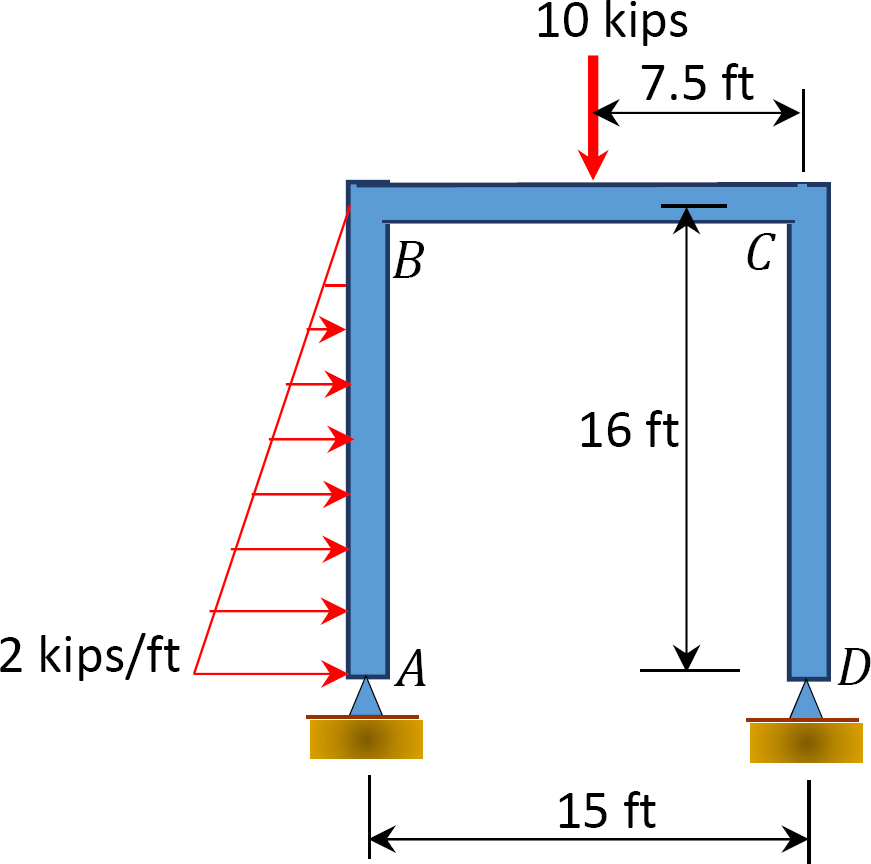
Fig. P12. 13. Marco.
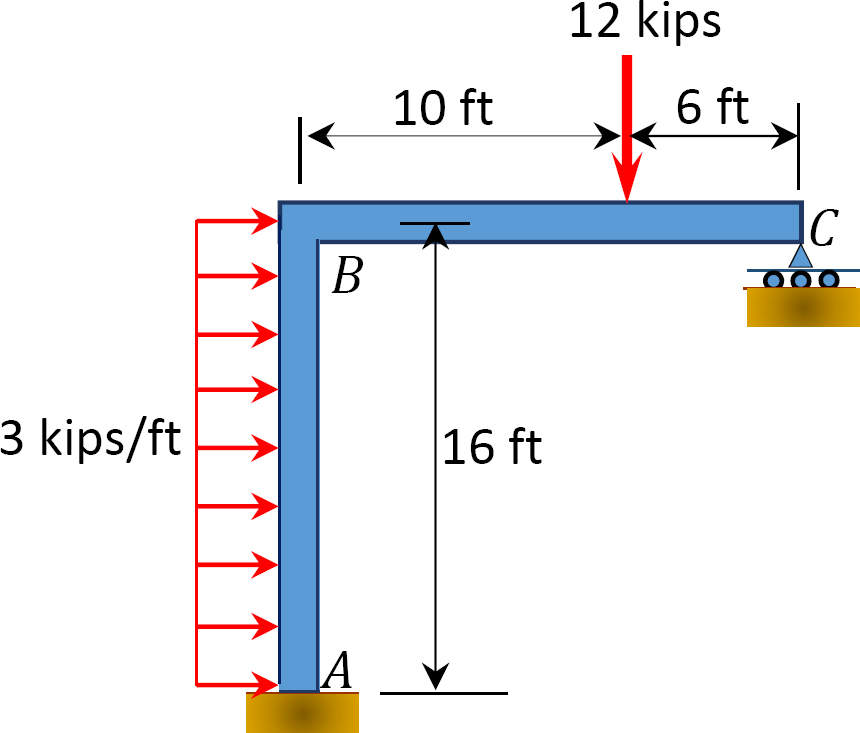
Fig. P12. 14. Marco.
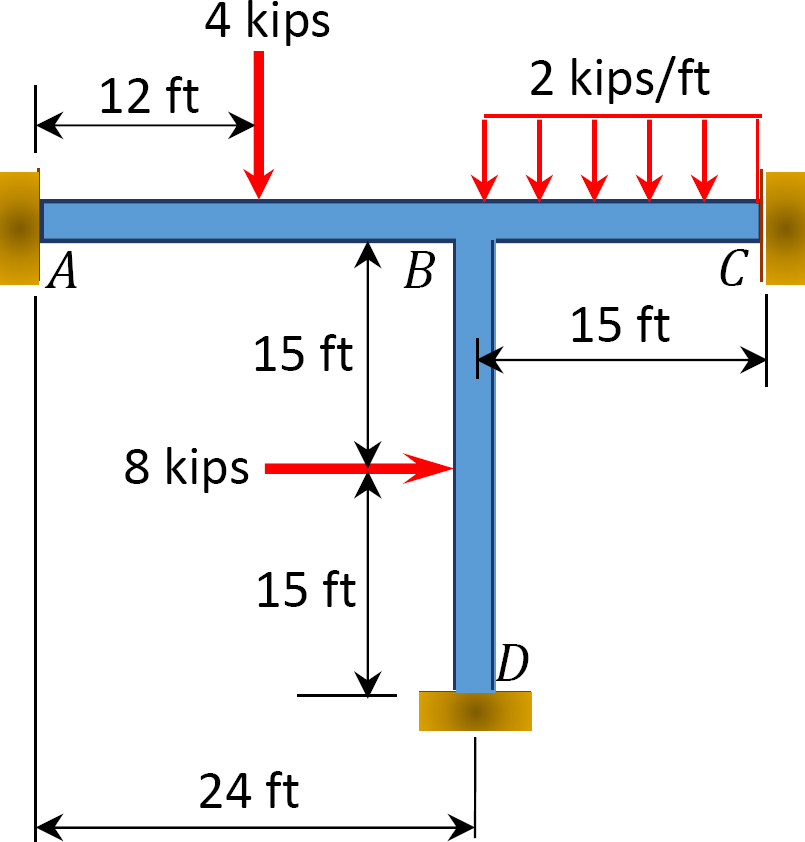
Fig. P12. 15. Marco.
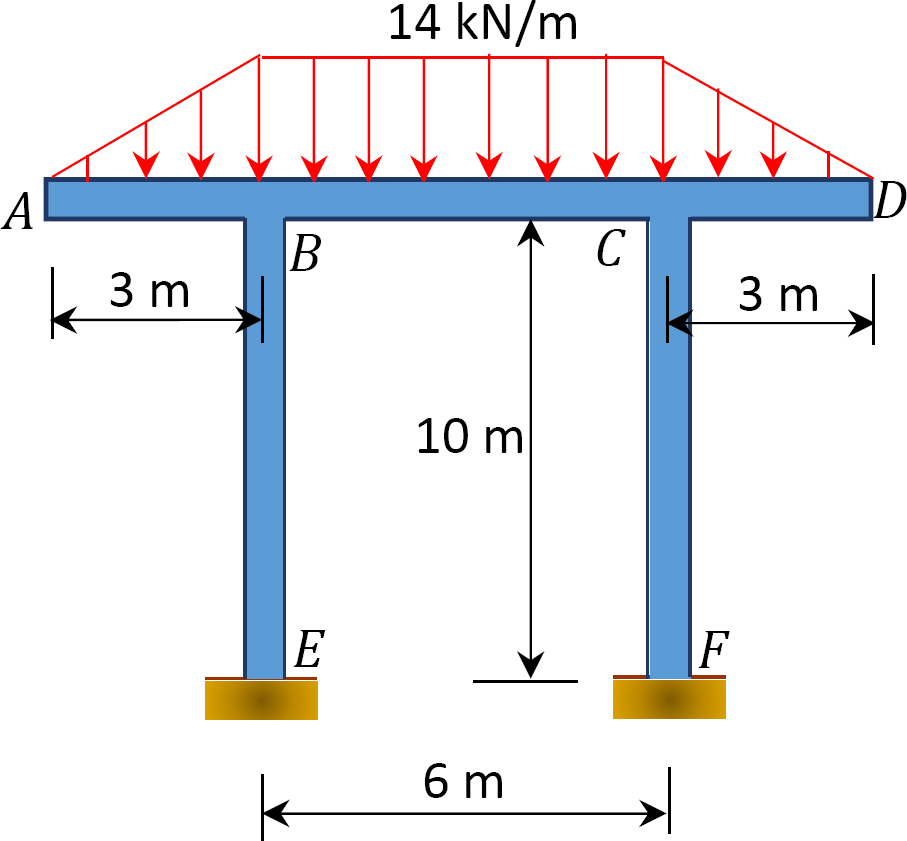
Fig. P12.16. Frame.
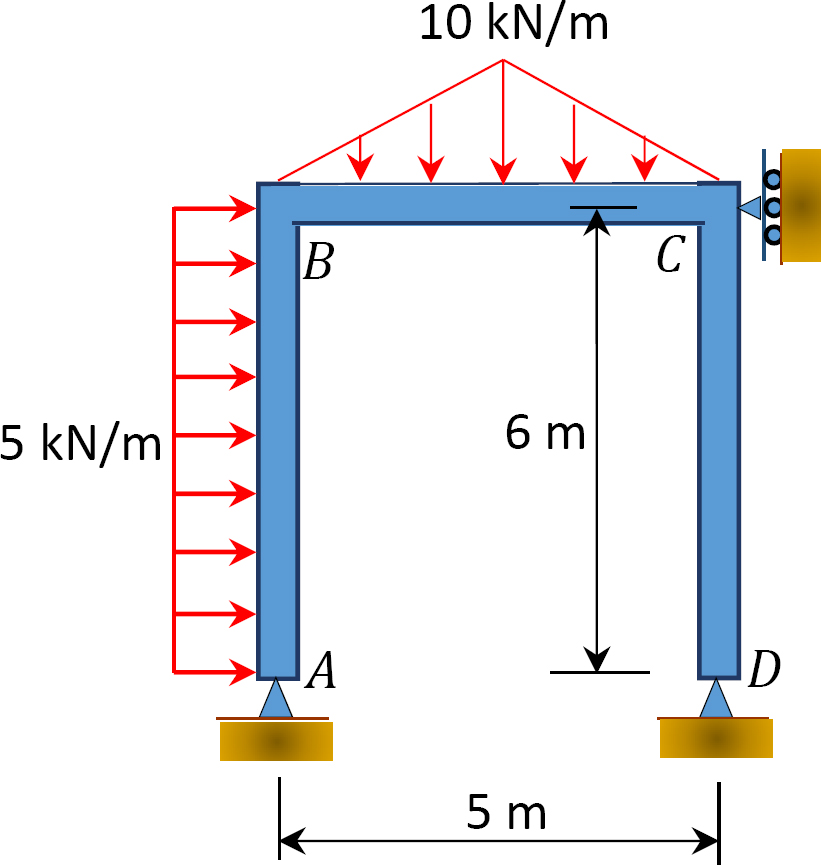
Fig. P12.17. Frame.
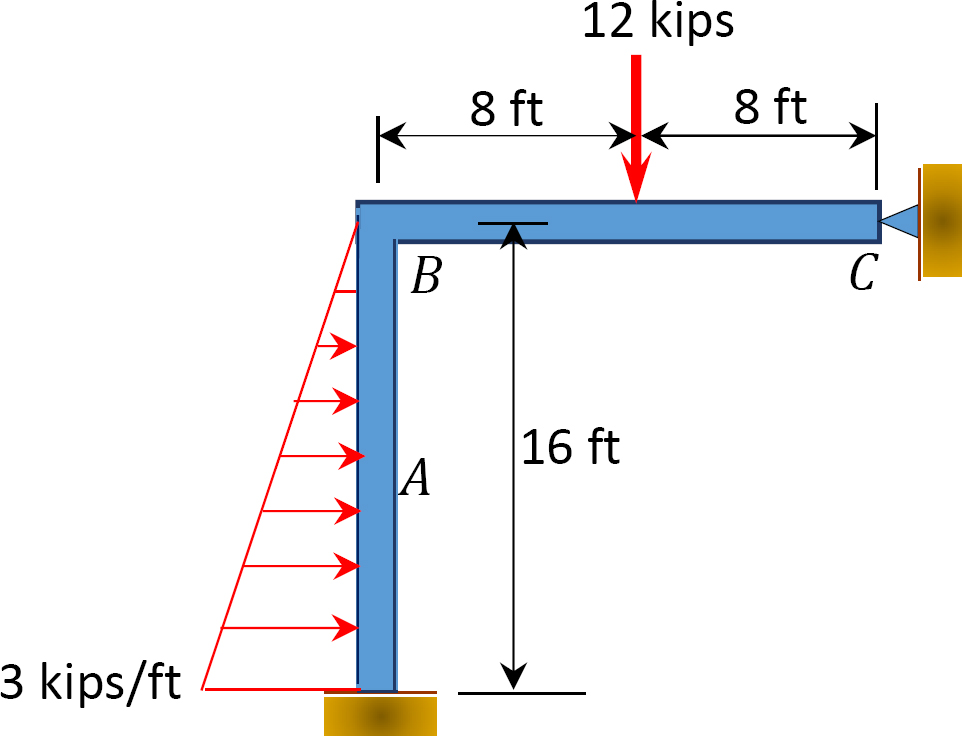
Fig. P12.18. Frame.
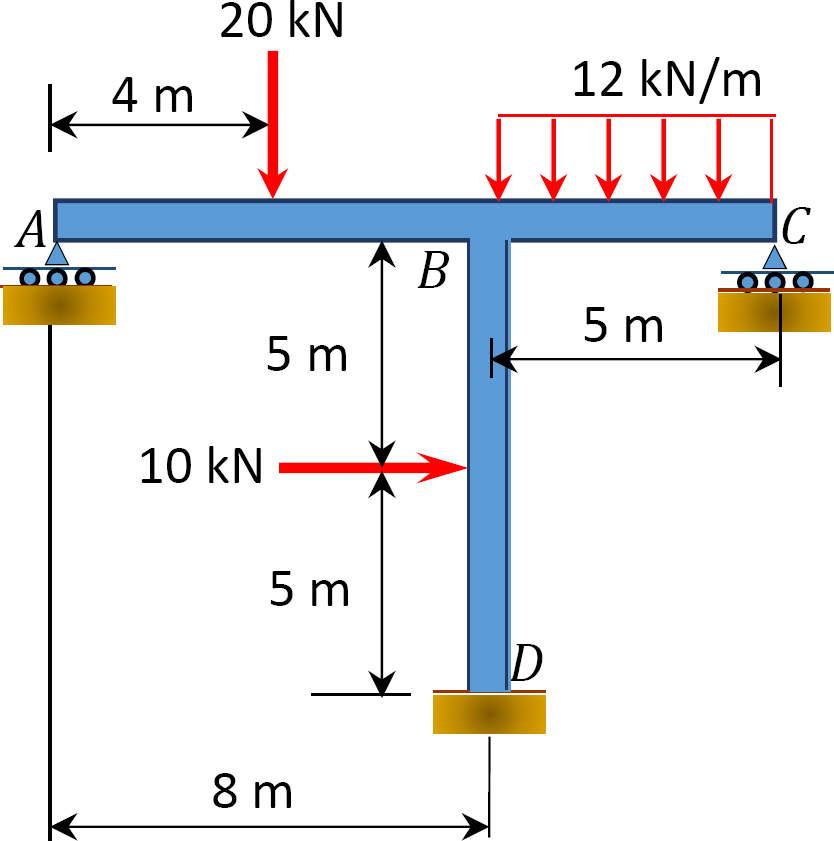
Fig. P12.19. Frame.
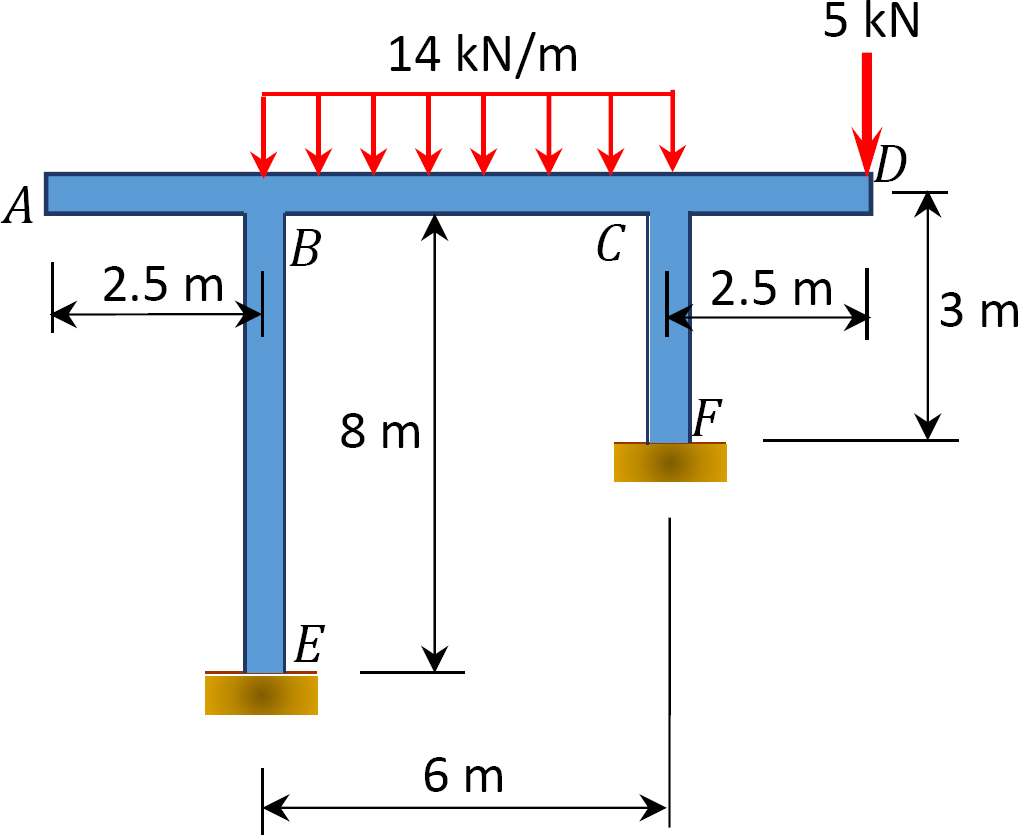
Fig. P12.20. Frame.