Saint-Venantin periaatteen soveltaminen ja tulkitseminen

kaikki rakennesuunnittelijat käyttävät Saint-Venantin periaatetta joko aktiivisesti tai alitajuisesti. Voit löytää tämän periaatteen eri muotoiluja useimmissa rakenteellisissa mekaniikan oppikirjoissa, mutta sen tarkka merkitys ei ole ilmeinen. Saint-Venantin periaate kertoo, että kuorman tarkka jakautuminen ei ole tärkeää kaukana kuormatusta alueesta, kunhan kuorman tulos on oikea. Tässä blogikirjoituksessa tutustumme Saint-Venantin periaatteeseen erityisesti finite element (Fe) – analyysin yhteydessä.

Saint-Venantin periaatteen historia

ranskalainen tiedemies Barré de Saint-Venant muotoili kuuluisan periaatteensa vuonna 1855, mutta se oli enemmän havainto kuin tiukka matemaattinen toteamus:

”jos elastisen kappaleen pieneen osaan vaikuttavat voimat korvataan toisella staattisesti ekvivalentilla pinnan samaan osaan vaikuttavien voimien järjestelmällä, tämä kuormituksen uudelleenjako aiheuttaa merkittäviä muutoksia jännityksissä paikallisesti, mutta sillä on merkityksetön vaikutus jännityksiin etäisyyksillä, jotka ovat suuria verrattuna sen pinnan lineaarisiin mittoihin, jolla voimat muuttuvat.”

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Saint-Venantin muotokuva. Kuva public domainissa Wikimedia Commonsissa.

monet suuret ajattelijat soveltavan mekaniikan alalla-Boussinesq, Love, von Mises, Toupin ja muut-olivat mukana toteamassa Saint-Venantin periaatetta tarkemmassa muodossa ja antamassa sille matemaattisia todisteita. Kuten on käynyt ilmi, tämä on melko vaikeaa yleisemmissä tapauksissa, ja tutkimus aiheesta on edelleen käynnissä. (Argumentointi on ollut ajoittain varsin eloisaa.)

yksinkertainen esimerkki: jännitysten analysointi etäältä

aloitetaan jostakin melko yksinkertaisesta: ohut suorakulmainen levy, jossa on pyöreä reikä jonkin matkan päässä kuormitetusta reunasta, jota vedetään aksiaalisesti. Jos olemme kiinnostuneita stressin keskittymisestä reikään, niin kuinka tärkeää on todellinen kuormituksen jakautuminen?

oikeanpuoleisella rajalla sovelletaan kolmea eri kuormitustyyppiä:

1. jatkuva aksiaalinen jännitys 100 MPa
2. symmetrinen parabolinen jännitysjakauma, jonka huippuamplitudi on 150 MPa
3. keskitetty pistekuorma, jonka tulos on sama kuin kahdessa edellisessä kuormitustapauksessa

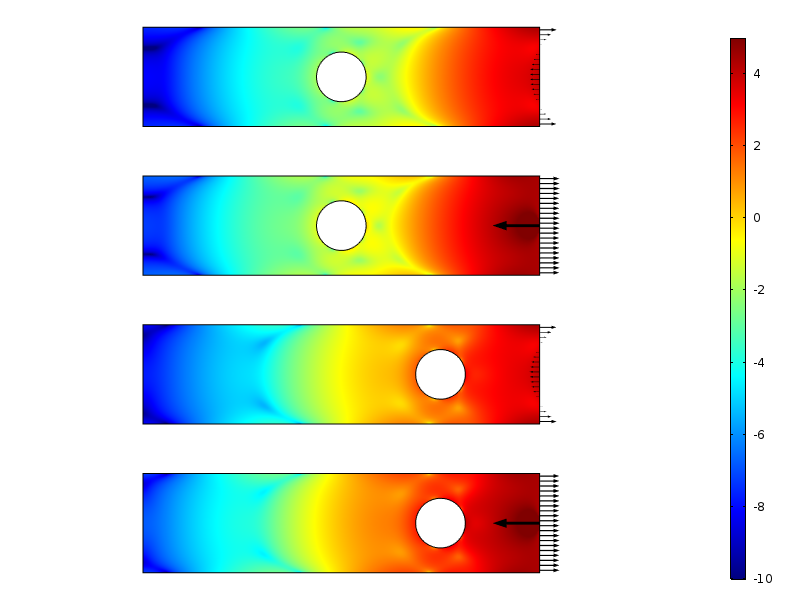
kuten alla olevista kuvioista nähdään, kuormituksen kohdistaminen ei vaikuta reiän jännitysjakaumaan. Olennaista tässä on tietysti se, että reikä on riittävän kaukana kuormasta.

Von Mises jännitysmuodot kolmelle kuormitustapaukselle.

toinen tapa visualisoida tämä skenaario on käyttää pääasiallisia jännitysnuolia. Tällainen juoni korostaa stressikenttää virtana ja antaa hyvän tunteen uudelleenjaolle.

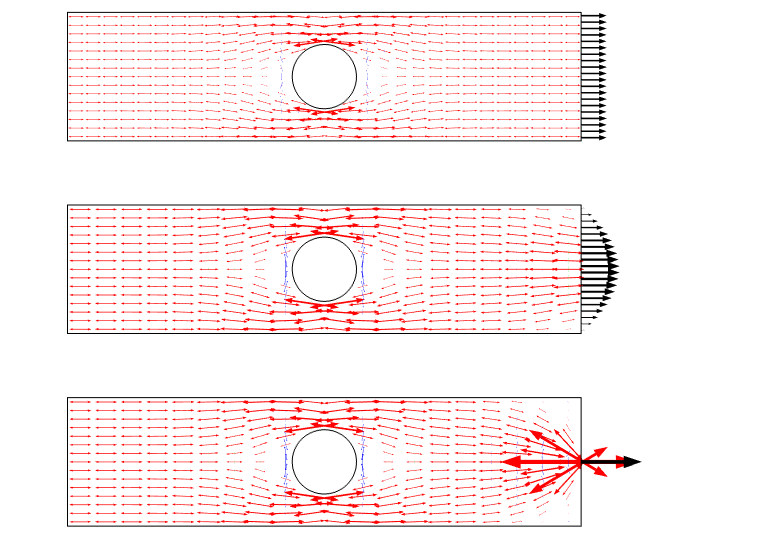
kolmen kuormitustapauksen pääasiallinen rasituskäyrä. Huomaa, että on olemassa singulariteetti, kun käytetään pistekuormaa.

piirtämällä jännitettä viivaa pitkin voimme nähdä, että kaikki kolme tapausta yhtyvät toisiinsa etäisyydellä reunasta, joka on suunnilleen sama kuin levyn leveys.

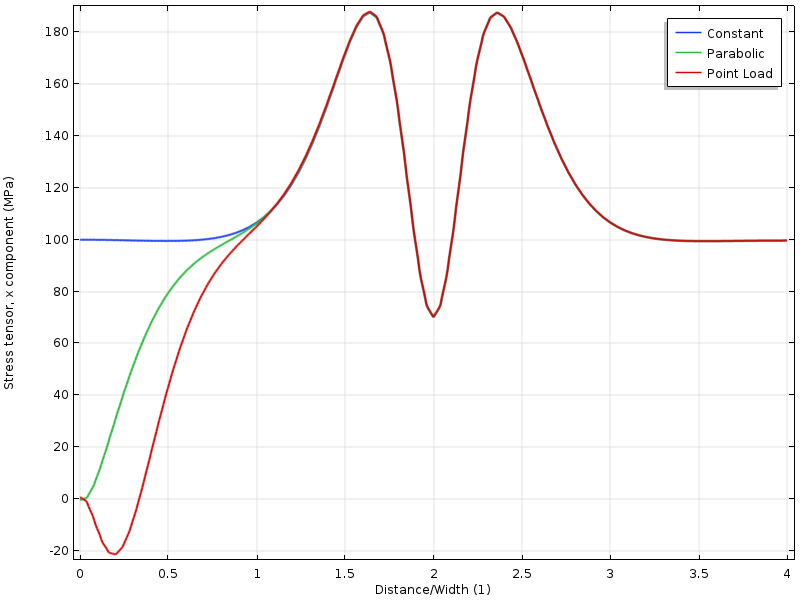
jännitys yläreunaa pitkin etäisyyden funktiona kuormitetusta rajasta. Etäisyys normalisoidaan levyn leveydellä.

jos reikää siirretään lähemmäs ladattua rajaa, saadaan toinen tilanne. Rasitustila reiän ympärillä riippuu nyt kuorman jakautumisesta. Vielä mielenkiintoisempaa on kuitenkin se, että etäisyys siihen, missä kolme stressikenttää ovat nyt yhtä mieltä, on kaksi kertaa niin kaukana kuormitetusta rajasta. Saint-Venantin periaatteen soveltaminen edellyttää, että paineet voidaan jakaa vapaasti uudelleen. Tässä tapauksessa, että uudelleenjako on osittain estetty reikä.

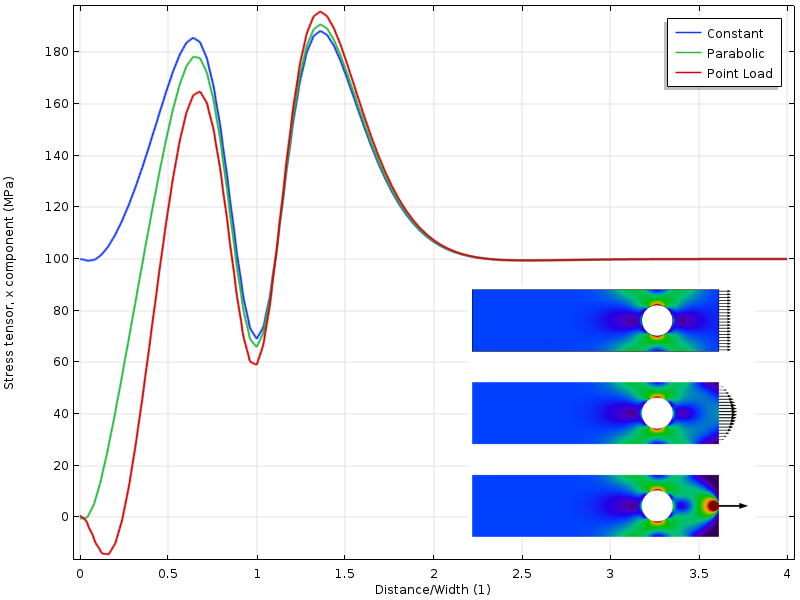
rasitus yläreunaa pitkin reiän ollessa lähempänä kuormitettua rajaa.

huomaa, että Saint-Venantin periaate kertoo, ettei jännitystilassa ole eroa etäisyydellä, joka on kuormitetun alueen lineaarisen ulottuvuuden luokkaa. Huomioitava kuormattu alue ei kuitenkaan välttämättä ole se alue, joka on todellisuudessa kuormattu! Tämä lausunto voi kuulostaa oudolta, mutta ajattele sitä näin: kun reikä on kaukana, voimme laskea stressikonsentraatiokertoimen käsikirjalla (omani sanoo 4.32) eikä FE-ratkaisulla. Käsikirjan lähestymistapa sisältää implisiittisen oletuksen, että kuorma jakautuu tasaisesti kuten ensimmäisessä kuormitustapauksessa. Joten vaikka todellinen kuormitus kohdistettaisiin vain pieneen osaan rajaa, kriittinen etäisyys siinä tapauksessa on suhteessa koko rajan kokoon.

ratkaistaessa ongelmaa äärellisen elementin menetelmällä (FEM), niin reikä voi olla mielivaltaisen lähellä kuormaa. Rajan asettaa se, että fyysisestä näkökulmasta kuorman jakautuminen on hyvin määritelty. Heti kun teemme oletuksia uudelleenjaosta, on kuitenkin implisiittinen oletus kuorman jakautumisesta, joka voi poiketa todellisesta.

Nollatulosjärjestelmät ja jännityksen energiatiheys

tähän mennessä olemme sanoneet, että jännitykset ovat samat riippumatta kuormituksen yksityiskohdista jollakin sopivalla etäisyydellä. Koska käsittelemme tässä lineaarista elastisuutta, on aina mahdollista asettaa kuormatapauksia päällekkäin. Saint-Venantin periaatteen todistusten kanssa työskenneltäessä on helpompi muotoilla periaate tämän suuntaisesti: kuormitusjärjestelmän aiheuttamat rasitukset, joihin ei liity voimaa tai momenttia, ovat pieniä etäisyydellä, joka on samaa suuruusluokkaa kuin kuormitetun rajan koko.

näin tutkimme kahden kuormitusjärjestelmän erosta aiheutuvaa stressiä yhtäläisillä tuloksilla. Useimmat nykyaikaiset todisteet perustuvat arvioihin kannan energiatiheyden hajoamisesta tällaiselle nollatulosjärjestelmälle.

palataksemme edellä olevaan ongelmaan voimme laskea kuormitustapausten erotuksen. Näin voimme tutkia stressin tai rasitusenergian tiheyden todellista hajoamista stressikenttien erotukselle.

kannan energiatiheyden logaritmi nollatuloksisissa kuormitustapauksissa.

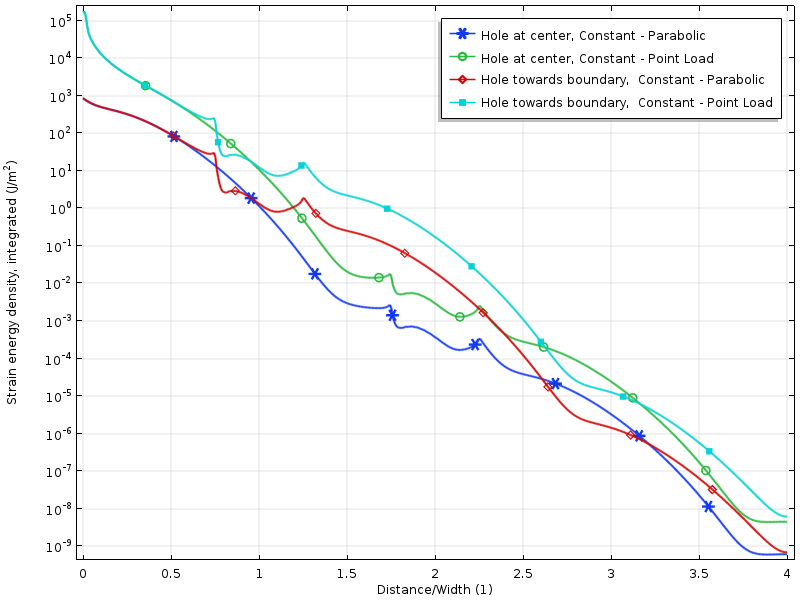
kannan energiatiheys levyn suuntaisesti nollakuormitustapauksissa. Energia integroidaan pystysuuntaan, jotta saadaan aikaan määrä, joka on vain etäisyyden funktio kuormituksesta.

kannan energiatiheyden logaritmin hajoaminen on enemmän tai vähemmän lineaarista etäisyyden kanssa kuormitetusta rajasta. Tämä on itse asiassa linjassa sen kanssa, mitä nykyaikaiset todisteet ennustavat: kannan energiatiheyden eksponentiaalinen hajoaminen. Voimme myös selvästi nähdä, miten reikä tilapäisesti vähentää hajoamisnopeutta.

soveltamalla Saint-Venantin periaatetta ohuisiin rakenteisiin

ohuempiin rakenteisiin, kuten kuoriin, palkkeihin ja ristikoihin, tiedetään hyvin, ettei Saint-Venantin periaatetta voi soveltaa samalla tavalla kuin ”kiinteämpään” kappaleeseen. Häiriöt kulkevat odotettua pidempiä matkoja, sillä ohuessa rakenteessa kuormitusreitit ovat paljon rajoitetumpia. Tämä on sama ilmiö, jonka näemme edellä olevassa esimerkissä olevan reiän kanssa, mutta näkyvämmin.

tässä tutkitaan sädettä, jonka poikkileikkaus on ipe100-standardin mukainen. Säteen päähän kohdistuu aksiaalinen jännitys, jonka amplitudilla on lineaarinen jakauma molemmissa poikkileikkaussuunnissa.

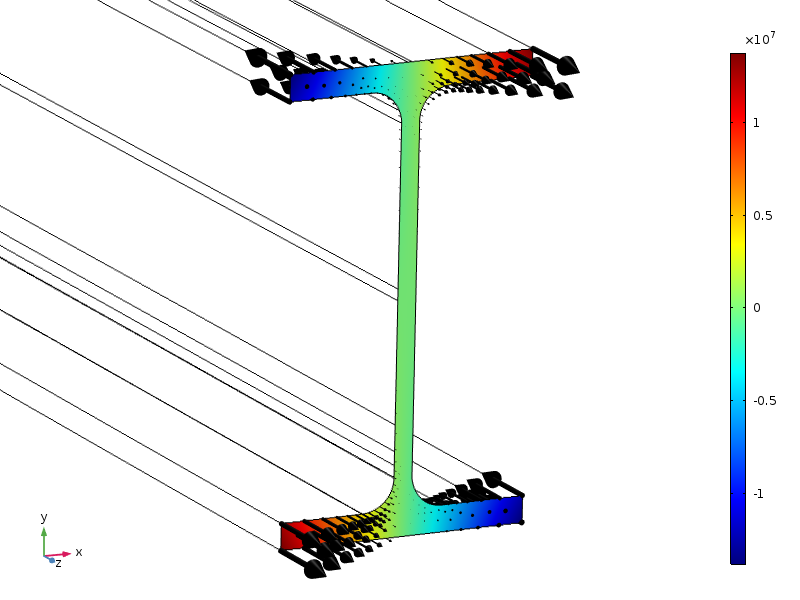
kuorman jakautuminen, näytetään ääriviivoina ja nuolina.

symmetrioista johtuen tällä kuormituksella on nollasta johtuva voima sekä nollamomentti kaikkien akselien ympärillä. Poikkileikkauksen korkeus on 100 mm, joten jos sovelletaan Saint-Venantin periaatteen vakiomuotoa, jännitysten tulisi olla pieniä noin 100 mm: n etäisyydellä loppuosasta.

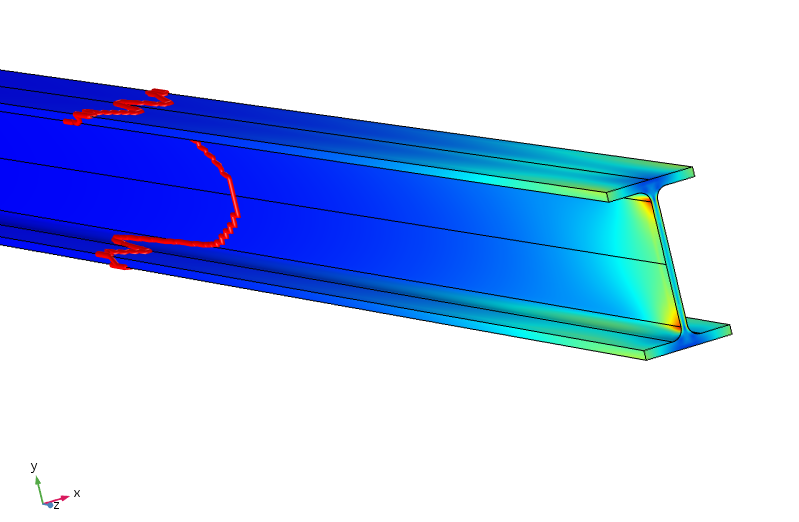
ekvivalenttijännitys säteessä. Punainen ääriviivat osoittaa, missä jännitys on alle 5% kohdistetusta huippujännityksestä.

on käynyt ilmi, että jotta jännitys olisi alle 5% kohdistetusta kuormitushuipusta, meidän on kuljettava lähes metri sädettä pitkin. Näin ollen kuorman uudelleenjako on paljon tehottomampi tässä, koska ylä-ja alalaipojen välinen tasapainotus vaatii momenttisiirtoa ohuen rainan läpi.

jos tunnet teorian palkkien nonuniformisesta vääntymisestä (eli vääntymisteoriasta tai Vlasov-teoriasta), huomaat, että sovelletulla kuormituksella on merkittävä bimomentti. Bimomentti on poikkileikkausmäärä, jonka fysikaalinen ulottuvuusvoima X pituus2.

ehkä (tämä on vain henkilökohtainen spekulaationi), tehokas Saint-Venantin periaate tässä tapauksessa vaatinee voiman ja momentin lisäksi myös nollan bimomentin. Tämä voidaan saada aikaan lisäämällä neljä pistekuormaa, jotka antavat vastapainoksi bimomentin. Tällaisen analyysin tulos on esitetty alla.

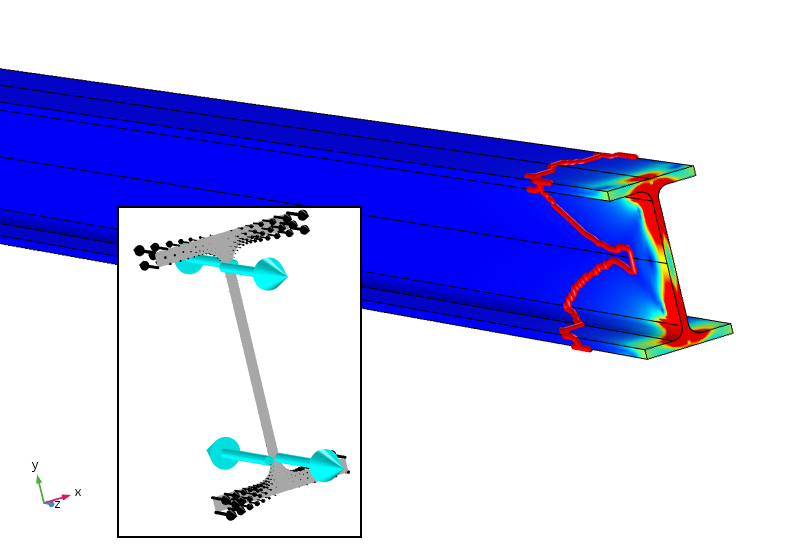
Ekvivalenttijännitys, jossa on neljä pistekuormaa, jotka tuottavat myös nollabimomentin. 5%: n stressikäyrä on nyt paljon lähempänä ladattua rajaa.

kohdistetut pistekuormitukset, joita ei ole sijoitettu optimaalisesti tarkoitukseen, aiheuttavat erittäin suuria (itse asiassa yksittäisiä) paikallisia jännityksiä. Jännitys kuitenkin putoaa pois paljon nopeammin ja on alle 5% noin 100 mm: n jälkeen. 5%: n raja on edelleen levitetyn kuormituksen suhteen, joten sitä ei säädetä uusiin paikallisiin rasituksiin. Kannan energiatiheyden logaritminen hajoamisnopeus on kolme kertaa nopeampi pistekuormitusten lisäämisen jälkeen.

Saint-Venantin periaate äärellisessä Elementtianalyysissä

joissakin tapauksissa voidaan intuitiivisesti katsoa Saint-Venantin periaatteen soveltuvan FE: n diskretointiongelmaan. Tässä tarkastellaan hajautettuja kuormia ja sopimattomia silmiä.

hajautetut kuormat

Fe-mallissa kuormat kohdistetaan aina mesh-solmuihin, vaikka ne määriteltäisiin jatkuvaksi rajakuormaksi. Kuorma jaetaan sisäisesti elementin solmuihin virtuaalityön periaatteella, kuten alla olevassa esimerkissä on esitetty.

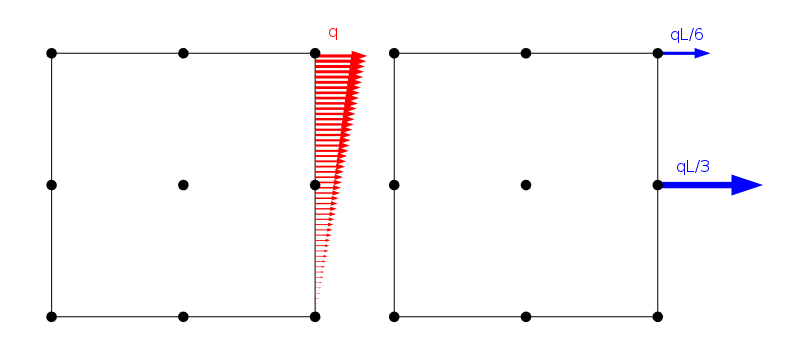
lineaarisesti jakautunut kuorma ja miten sitä sovelletaan toisen kertaluvun Lagrangen elementin solmuihin, joiden sivun pituus on L.

on kuitenkin olemassa ääretön määrä kuormitusjakaumia, jotka antavat samat solmukohdat, kunhan niillä on sama resultoiva voima ja momentti. On selvää, ratkaisu äärellinen Elementti ongelma on sama kaikissa näissä tapauksissa. Saint-Venantin periaatteesta voimme kuitenkin päätellä, että kaikkien tällaisten kuormien pitäisi antaa periaatteessa sama stressikenttä heti, kun olemme jonkin matkan päässä.

koska kuormien uudelleenjaon kohteena olevan alueen koko on elementtipinta, lineaarinen ulottuvuus, jonka jälkeen ei ole eroa, on oleellisesti yksi elementtikerros rakenteen sisällä. Näin ollen ratkaisu uloimman kerroksen elementtejä ei välttämättä vastaa todellista kuormitusta, mutta edelleen, se ei.

esimerkkinä voidaan ladata suorakulmainen levy, jonka rajakuormitus on eksponentiaalinen jännitysjakauma. Jännitys lasketaan hieno verkko on esitetty alla.

aksiaalisen jännitysjakauman ääriviivat.

Saint-Venantin periaatteen vuoksi jännityskenttä jaetaan uudelleen puhtaaseen taivutustilaan jonkin matkan päässä kuormitetusta reunasta, aivan kuten oletammekin. Tämä ei kuitenkaan ole nykyisen keskustelun kohde. Sen sijaan tutkimme eroa yllä olevan stressijakauman ja sen välillä, mitä saamme useilla karkeilla silmillä.

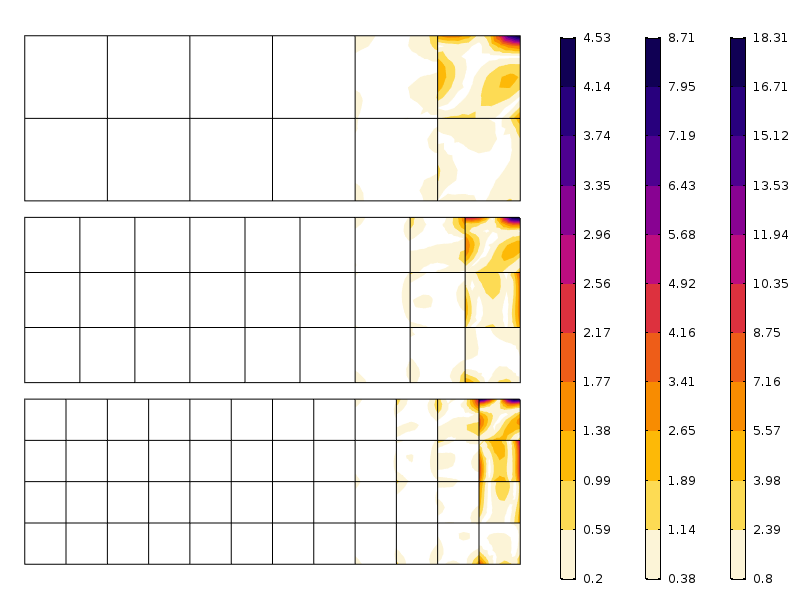
virhe aksiaalisessa rasituksessa kolmessa eri silmässä. Huomaa eri asteikot. Odotetusti virhe on pienempi, kun verkko on hienompi.

kuten kuvasta näkyy, virhe vähenee nopeasti ensimmäisen elementtikerroksen jälkeen. Tässä on itse asiassa kyse mesh-lähentymisen ja Saint-Venantin periaatteeseen sisältyvän paineiden uudelleenjaon yhdistelmästä.

Nonconforming Mesh

nonconforming mesh syntyy, kun muodon toiminnot kahdessa toisiinsa liitetyssä elementissä eivät täsmää. Yleisin tapaus on, kun kokoonpano yhdistetään identiteettiparien ja jatkuvuusehtojen avulla. Esimerkkinä tästä voimme tutkia suoraa baaria, jossa on tarkoituksellisesti yhteensopimaton verkko. Yksinkertaisella kuormitustapauksella, kuten yksiakselisella jännityksellä, on mahdollista tutkia siirtymän aiheuttamia rasitushäiriöitä.

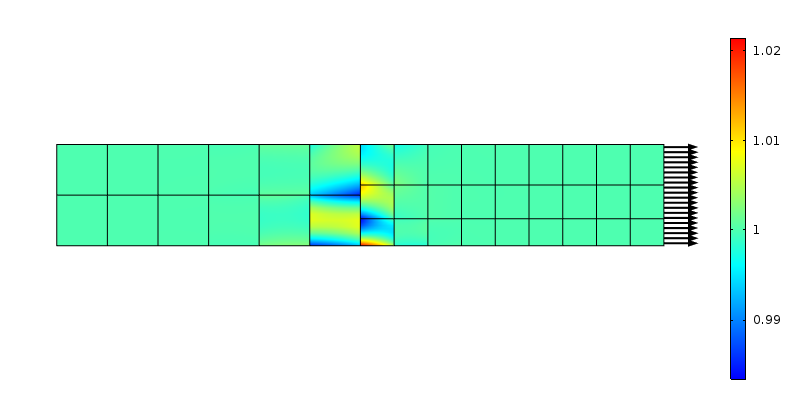
aksiaalinen rasitus ei-yhteensopivassa mesh-siirtymässä. Käytetään toisen kertaluvun alkuaineita.

solmujen lähettämät voimat eivät vastaa oletusta jatkuvasta rasituksesta. Jälleen tämä voidaan nähdä paikallisena kuormituksen uudelleenjakona elementin kokoiselle alueelle. Saint-Venantin päättelyä käyttäen häiriön pitäisi häipyä ”elementtikokoisella” etäisyydellä siirtymästä. Tutkitaan, mitä tapahtuu, jos verkko on puhdistettu aksiaaliseen suuntaan.

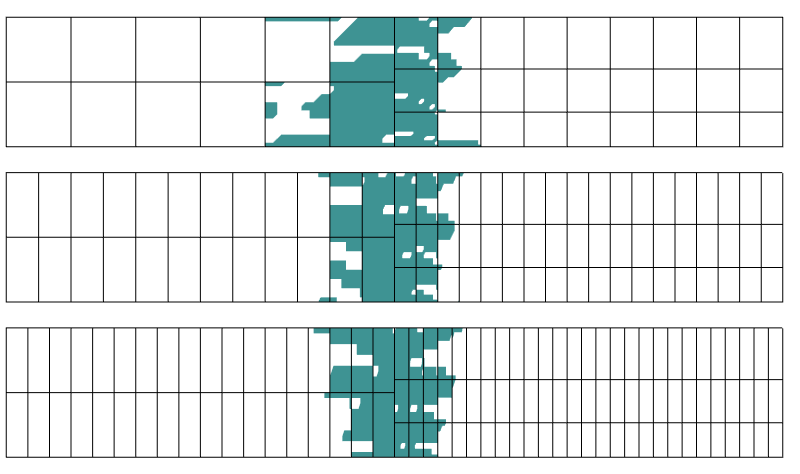
alue, jossa stressivirhe on yli 0, 1%. Aksiaalisessa suunnassa käytetään kolmea eri diskretaatiota.

on käynyt ilmi, että häiriöalueeseen ei juuri vaikuta diskretointi suuntaan, joka on kohtisuorassa siirtymärajaan nähden. Juuri tästä Saint-Venantin periaate kertoo.

Loppuhuomautukset

hyödyntämättä Saint-Venantin periaatetta monet rakenteelliset analyysit ovat vaikeita tehdä yksinkertaisesti siksi, että tarkkaa kuormituksen jakautumista ei tunneta.

periaate pätee muodollisesti vain lineaarisille elastisille materiaaleille. Käytännössä käytämme sitä intuitiivisesti myös päivittäin muihin tilanteisiin. Jos esimerkiksi ”reikälevyn” materiaali olisi elastoplastista, odottaisimme kahden jaetun kuormituksen antavan vastaavat tulokset, kunhan myötörasitus on yli rajalla kohdistetun jännityksen niin, että reiän ympärillä on vain plastista muodonmuutosta. Pistekuormitus antaa kuitenkin aina erilaisen ratkaisun, koska materiaali saa satoa kuormitetun pisteen ympärillä. Pidempään keskusteluun, lue tämä blogikirjoitus singularities at point loads.

Next Steps

Lue lisää COMSOL Multiphysics® – ohjelmiston käytöstä FEA: lle.

Further Reading

• Y. C. Fung and P. Tong, Classical and Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.