Tous les ingénieurs en structure utilisent le principe de Saint-Venant, que ce soit activement ou inconsciemment. Vous pouvez trouver diverses formulations de ce principe dans la plupart des manuels de mécanique des structures, mais sa signification exacte n’est pas évidente. Le principe de Saint-Venant nous dit que la répartition exacte d’une charge n’est pas importante loin de la région chargée, tant que les résultantes de la charge sont correctes. Dans ce billet de blog, nous explorerons le principe de Saint-Venant, en particulier dans le contexte de l’analyse par éléments finis (FE).
- L’histoire du Principe de Saint-Venant
- Exemple simple: Analyse des contraintes à distance
- Systèmes Résultants nuls et Densité d’Énergie de déformation
- Application du Principe de Saint-Venant aux Structures minces
- Principe de Saint-Venant en Analyse par éléments Finis
- Charges distribuées
- Maillage non conforme
- Remarques finales
- Prochaines étapes
- Lectures complémentaires
L’histoire du Principe de Saint-Venant
Le scientifique français Barré de Saint-Venant a formulé son célèbre principe en 1855, mais c’était plus une observation qu’un énoncé mathématique strict:
» Si les efforts agissant sur une petite partie de la surface d’un corps élastique sont remplacés par un autre système statiquement équivalent de forces agissant sur la même partie de la surface, cette redistribution des charges produit localement des variations importantes des contraintes, mais a un effet négligeable sur les contraintes à des distances importantes par rapport aux dimensions linéaires de la surface sur laquelle les efforts sont modifiés. »
B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Portrait de Saint-Venant. Image dans le domaine public, via Wikimedia Commons.
De nombreux grands esprits du domaine de la mécanique appliquée — Boussinesq, Love, von Mises, Toupin et d’autres — ont participé à énoncer le principe de Saint-Venant sous une forme plus exacte et à en fournir des preuves mathématiques. Il s’avère que cela est assez difficile pour des cas plus généraux, et des recherches sur le sujet sont toujours en cours. (L’argumentation a parfois été assez vive.)
Exemple simple: Analyse des contraintes à distance
Commençons par quelque chose d’assez simple: une plaque rectangulaire mince avec un trou circulaire à une certaine distance du bord chargé, qui est tiré axialement. Si nous nous intéressons à la concentration de contraintes au niveau du trou, quelle est l’importance de la répartition réelle de la charge?
Trois types de charge différents sont appliqués à la limite la plus à droite:
- Une contrainte axiale constante de 100 MPa
- Une distribution de contrainte parabolique symétrique avec une amplitude de crête de 150 MPa
- Une charge ponctuelle centrée avec la même résultante que les deux cas de charge précédents
Comme on le voit dans les graphiques ci-dessous, la distribution de contrainte au niveau du trou n’est pas affectée par la façon dont la charge est appliquée. La clé ici est, bien sûr, que le trou est suffisamment éloigné de la charge.

Contours de contraintes de Von Mises pour les trois cas de charge.
Une autre façon de visualiser ce scénario consiste à utiliser les flèches de contrainte principales. Un tel tracé met l’accent sur le champ de contrainte en tant que flux et donne un bon sentiment de redistribution.
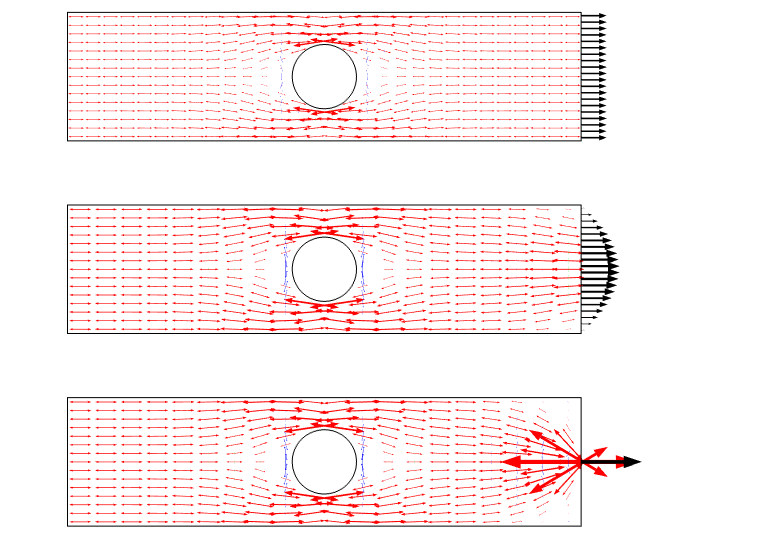
Diagramme de contrainte principal pour les trois cas de charge. Notez qu’il existe une singularité lorsqu’une charge ponctuelle est utilisée.
En représentant graphiquement la contrainte le long d’une ligne, nous pouvons voir que les trois cas convergent l’un vers l’autre à une distance du bord, qui est approximativement égale à la largeur de la plaque.
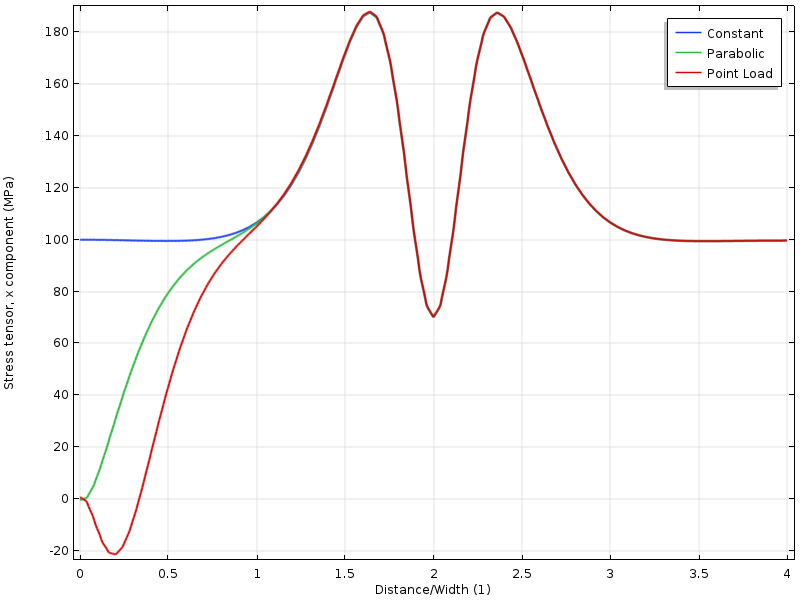
Contrainte le long du bord supérieur en fonction de la distance par rapport à la limite chargée. La distance est normalisée par la largeur de la plaque.
Si le trou est rapproché de la limite chargée, nous obtenons une autre situation. L’état de contrainte autour du trou dépend maintenant de la répartition de la charge. Mais encore plus intéressant est que la distance à laquelle les trois champs de contrainte s’accordent maintenant est deux fois plus éloignée de la limite chargée. L’application du principe de Saint-Venant exige que les contraintes soient libres de se redistribuer. Dans ce cas, cette redistribution est partiellement bloquée par le trou.
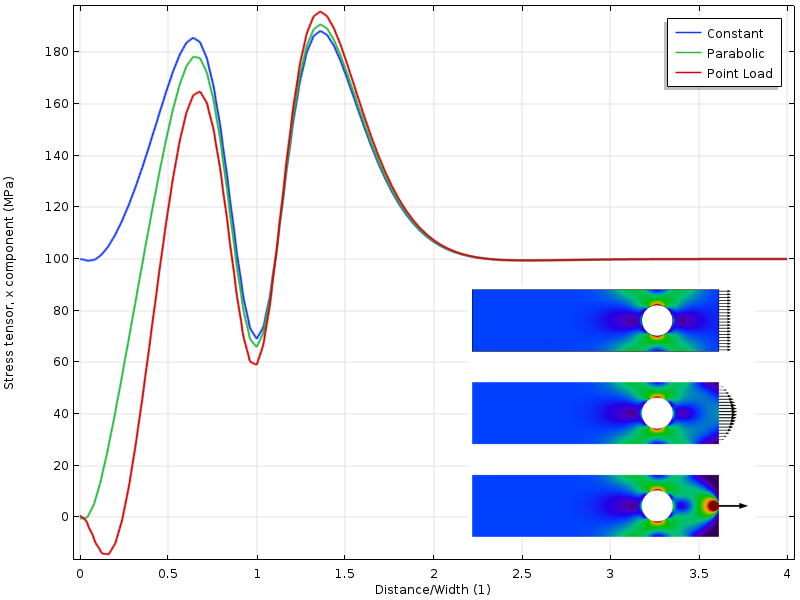
Contrainte le long du bord supérieur avec le trou plus près de la limite chargée.
Notez que le principe de Saint-Venant nous dit qu’il n’y a pas de différence dans l’état de contrainte à une distance qui est de l’ordre de la dimension linéaire de la zone chargée. La zone chargée à prendre en compte, cependant, peut ne pas être la zone réellement chargée! Cette affirmation peut sembler étrange, mais pensez-y de cette façon: Lorsque le trou est loin, nous pouvons calculer le facteur de concentration de contrainte à l’aide d’un manuel (le mien dit 4.32) plutôt que par une solution FE. L’approche du manuel contient une hypothèse implicite que la charge est répartie uniformément comme dans le premier cas de charge. Ainsi, même si la charge réelle n’a été appliquée qu’à une petite partie de la limite, la distance critique dans ce cas est liée à la taille de la limite entière.
Lors de la résolution du problème en utilisant la méthode des éléments finis (FEM), le trou peut être arbitrairement proche de la charge. Ce qui fixe la limite, c’est que du point de vue physique, la répartition de la charge est bien définie. Dès que nous faisons des hypothèses sur la redistribution, cependant, il existe une hypothèse implicite sur la répartition de la charge, qui peut différer de la répartition réelle.
Systèmes Résultants nuls et Densité d’Énergie de déformation
Jusqu’à présent, nous avons dit que les contraintes sont les mêmes indépendamment des détails de la charge à une distance appropriée. Puisqu’il s’agit ici d’élasticité linéaire, il est toujours possible de superposer des cas de charge. Lorsque l’on travaille avec des preuves du principe de Saint-Venant, il est plus facile de formuler un principe selon ces lignes: Les contraintes causées par un système de charge sans force ni moment résultants seront faibles à une distance du même ordre de grandeur que la taille de la limite chargée.
Ainsi, nous étudions la contrainte causée par la différence entre les deux systèmes de charge avec des résultantes égales. La plupart des preuves modernes sont basées sur des estimations de la décroissance de la densité d’énergie de déformation pour un tel système à résultat nul.
En revenant au problème ci-dessus, nous pouvons calculer la différence entre les cas de charge. Cela nous permet d’étudier la décroissance réelle de la densité d’énergie de contrainte ou de contrainte pour la différence des champs de contrainte.
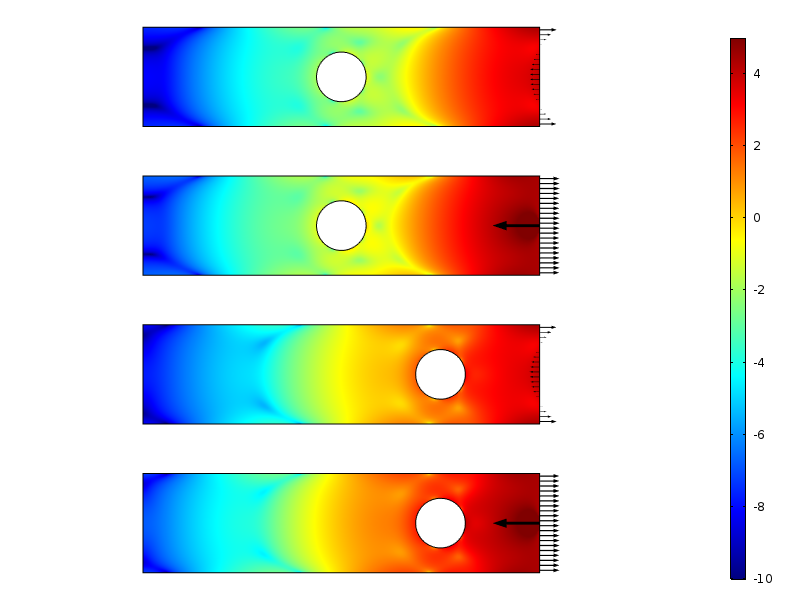
Logarithme de densité d’énergie de déformation pour les cas de charge à résultat nul.
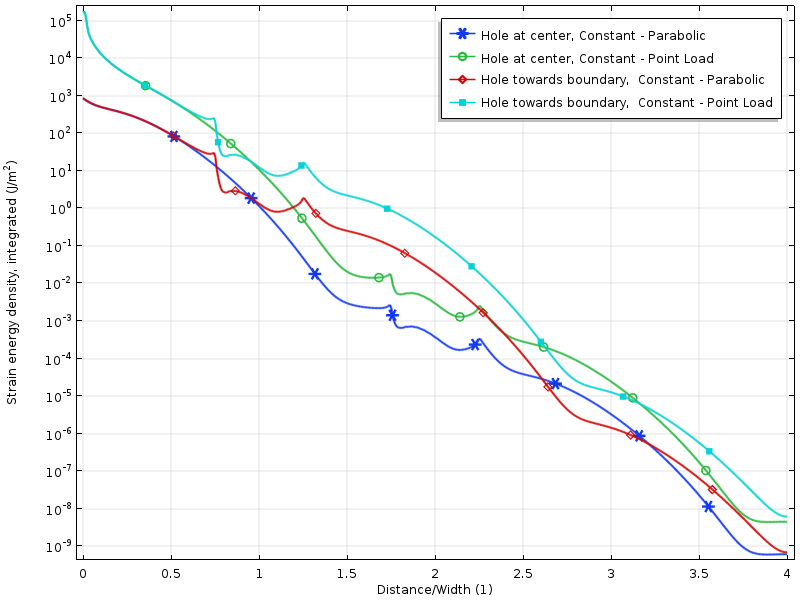
La densité d’énergie de déformation le long de la plaque pour les cas de charge résultants nuls. L’énergie est intégrée le long de la direction verticale afin de produire une quantité qui n’est qu’une fonction de la distance de la charge.
La décroissance dans le logarithme de la densité d’énergie de déformation est plus ou moins linéaire avec la distance de la limite chargée. Ceci est en fait conforme à ce que les preuves modernes prédisent: une décroissance exponentielle de la densité d’énergie de déformation. Nous pouvons également voir clairement comment le trou réduit temporairement le taux de désintégration.
Application du Principe de Saint-Venant aux Structures minces
Pour les structures plus minces comme les coquilles, les poutres et les fermes, il est bien connu que le principe de Saint-Venant ne peut pas être appliqué de la même manière que pour un objet plus « solide ». Les perturbations parcourent des distances plus longues que ce à quoi nous nous attendons, car les trajets de charge dans une structure mince sont beaucoup plus limités. C’est le même phénomène que nous voyons avec le trou dans l’exemple ci-dessus, mais plus en évidence.
Ici, nous étudions une poutre de section standard IPE100. L’extrémité de la poutre est soumise à une contrainte axiale, avec une amplitude qui a une distribution linéaire dans les deux directions de section transversale.
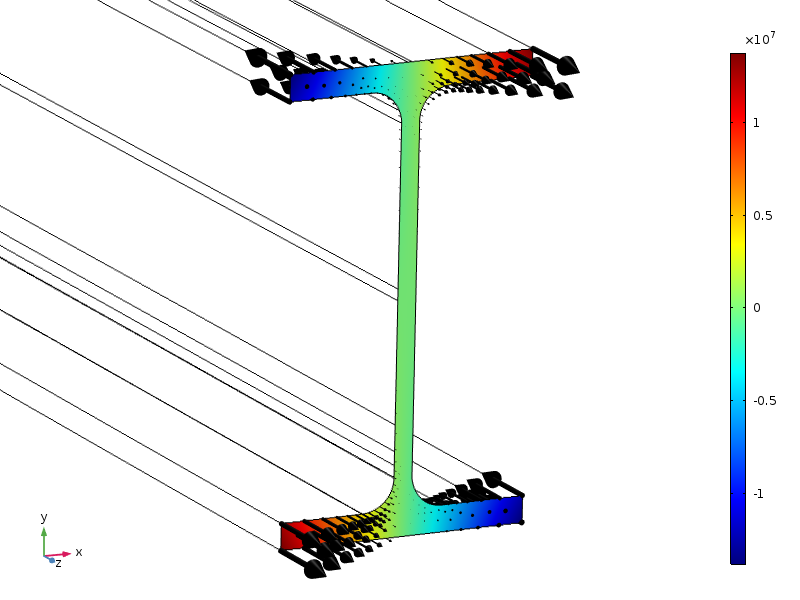
Répartition de la charge, affichée sous forme de contours et de flèches.
En raison des symétries, cette charge a une force résultante nulle, ainsi qu’un moment nul autour de tous les axes. La hauteur de la section transversale est de 100 mm, donc si la forme standard du principe de Saint-Venant est applicable, les contraintes doivent être faibles à une distance d’environ 100 mm de la section terminale.
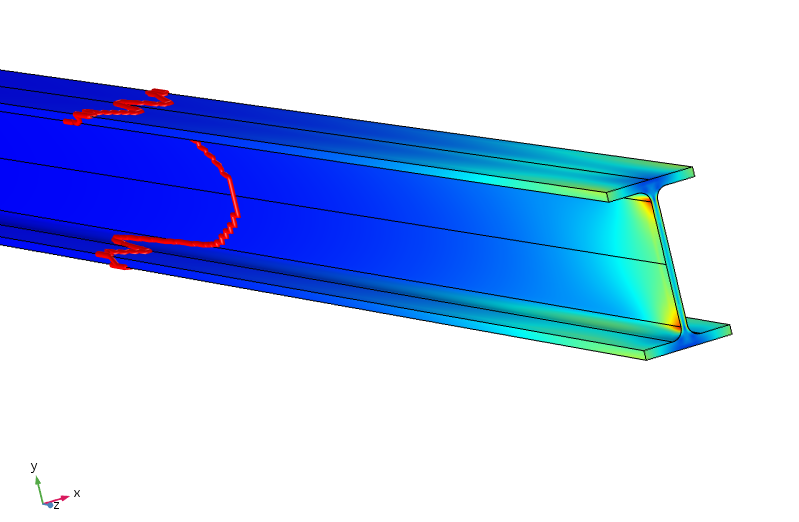
Contrainte équivalente dans la poutre. Le contour rouge indique où la contrainte est inférieure à 5% de la contrainte maximale appliquée.
Il s’avère que pour que la contrainte soit inférieure à 5% de la contrainte maximale appliquée, nous devons parcourir près d’un mètre le long de la poutre. Ainsi, la redistribution des charges est ici beaucoup moins efficace, car l’équilibrage entre les brides supérieure et inférieure nécessite un transfert de moment à travers la bande mince.
Si vous connaissez la théorie de la torsion non uniforme des poutres (c’est-à-dire la théorie du gauchissement ou la théorie de Vlasov), vous reconnaîtrez que la charge appliquée a un bimoment significatif. Le bimoment est une grandeur de section avec la force de dimension physique X longueur 2.
Peut-être (ce n’est que ma spéculation personnelle), un principe de Saint-Venant efficace pour ce cas devrait exiger non seulement la force et le moment, mais aussi un bimoment de zéro. Cela peut être accompli en ajoutant quatre charges ponctuelles qui fournissent un bimoment contrecarrant. Le résultat d’une telle analyse est présenté ci-dessous.
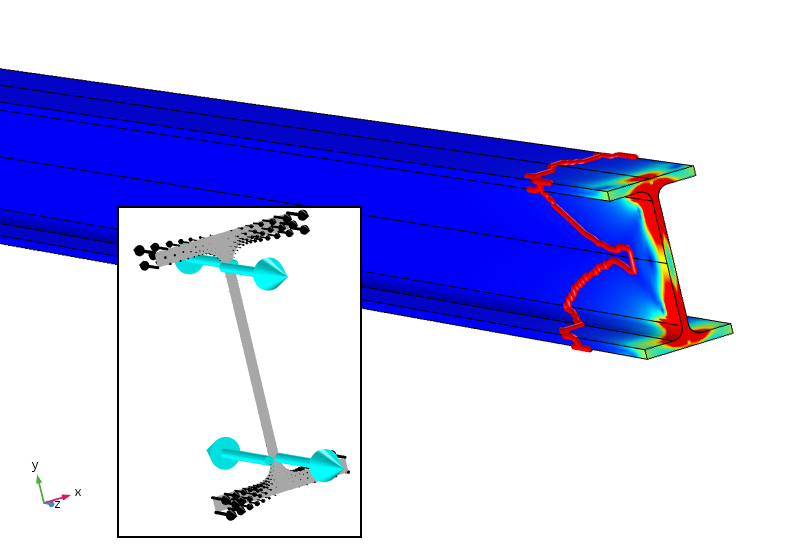
Contrainte équivalente avec quatre charges ponctuelles qui fournissent également un bimoment nul. Le contour de contrainte de 5% est maintenant beaucoup plus proche de la limite chargée.
Les charges ponctuelles appliquées, qui ne sont pas placées de manière optimale, donnent des contraintes locales extrêmement élevées (en fait singulières). Cependant, la contrainte diminue beaucoup plus rapidement et est inférieure à 5% après environ 100 mm. La limite de 5% est toujours en termes de charge répartie appliquée, elle n’est donc pas ajustée pour les nouvelles contraintes locales. Le taux de désintégration logarithmique de la densité d’énergie de déformation est trois fois plus rapide après l’ajout des charges ponctuelles.
Principe de Saint-Venant en Analyse par éléments Finis
Dans certains cas, on peut considérer intuitivement que le principe de Saint-Venant s’applique au problème discrétisé par FE. Ici, nous examinons les charges distribuées et les maillages non conformes.
Charges distribuées
Dans le modèle FE, les charges sont toujours appliquées aux nœuds de maillage, même si vous les spécifiez comme une charge limite continue. La charge est distribuée en interne aux nœuds de l’élément en utilisant le principe du travail virtuel, comme indiqué dans l’exemple ci-dessous.
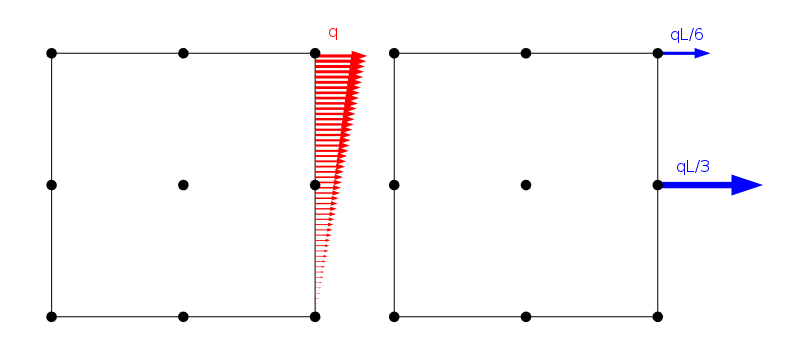
Une charge distribuée linéairement et comment elle est appliquée aux nœuds d’un élément de Lagrange du second ordre de longueur latérale L.
Il existe cependant un nombre infini de distributions de charge qui donnent les mêmes charges nodales tant qu’elles partagent la même force et le même moment résultants. De toute évidence, la solution au problème des éléments finis est la même pour tous ces cas. Du principe de Saint-Venant, cependant, nous pouvons conclure que toutes ces charges devraient donner essentiellement le même champ de contrainte dès que nous sommes à une certaine distance.
Étant donné que la taille de la zone sur laquelle nous redistribuons les charges est une face d’élément, la dimension linéaire après laquelle il n’y a pas de différence est essentiellement une couche d’élément à l’intérieur de la structure. Ainsi, la solution dans la couche d’éléments la plus externe peut ne pas correspondre à la charge réelle, mais plus loin, elle le fait.
À titre d’exemple, nous pouvons charger une plaque rectangulaire avec une charge limite qui a une distribution de contrainte exponentielle. La contrainte calculée avec un maillage fin est illustrée ci-dessous.

Tracé de contour de la distribution des contraintes axiales.
En raison du principe de Saint-Venant, le champ de contrainte est redistribué à un état de flexion pure à une certaine distance du bord chargé, comme nous l’attendons. Ce n’est cependant pas l’objectif de la discussion actuelle. Nous étudions plutôt la différence entre la distribution des contraintes ci-dessus et ce que nous obtenons avec un certain nombre de mailles grossières.
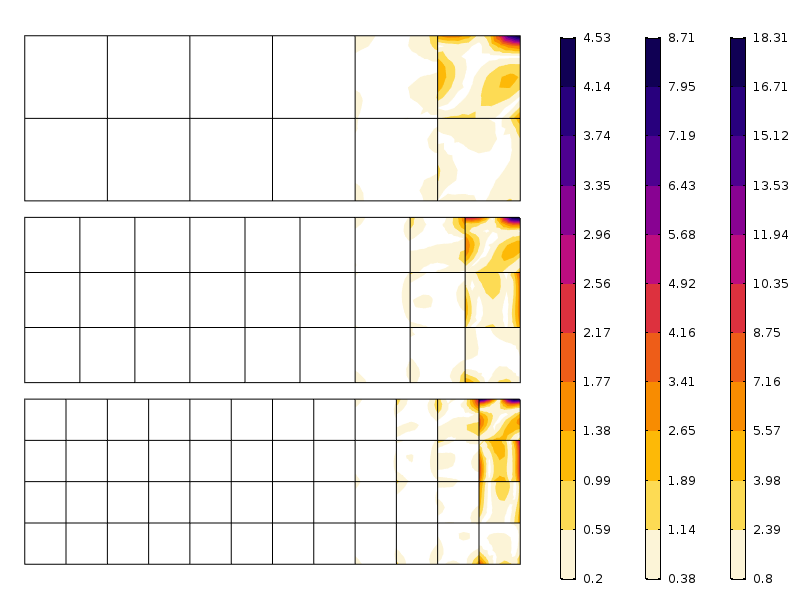
Erreur de contrainte axiale pour trois mailles différentes. Notez les différentes échelles. Comme prévu, l’erreur est plus petite lorsque le maillage est plus fin.
Comme on peut le voir sur la figure, l’erreur diminue rapidement après la première couche d’élément. Ce que nous voyons ici est en fait une combinaison de convergence des mailles et de redistribution des contraintes impliquées par le principe de Saint-Venant.
Maillage non conforme
Un maillage non conforme se produit lorsque les fonctions de forme de deux éléments connectés ne correspondent pas. Le cas le plus courant est lorsqu’un assemblage est connecté à l’aide de paires d’identités et de conditions de continuité. Pour illustrer cela, nous pouvons étudier une barre droite avec un maillage intentionnellement non apparié. Avec un cas de charge simple, tel qu’une tension uniaxiale, il est possible d’étudier les perturbations de contrainte provoquées par la transition.
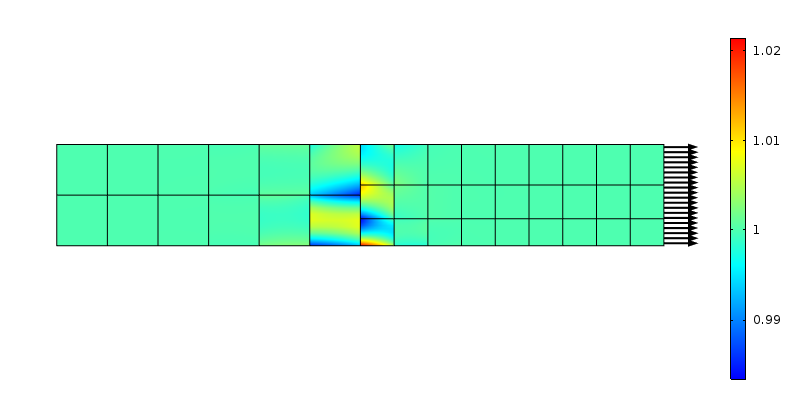
Contrainte axiale à une transition de maille non conforme. Des éléments de second ordre sont utilisés.
Les forces transmises par les nœuds des deux côtés ne correspondent pas à l’hypothèse d’une contrainte constante. Encore une fois, cela peut être vu comme une redistribution de charge locale sur une zone correspondant à la taille de l’élément. En utilisant le raisonnement de Saint-Venant, la perturbation devrait s’estomper à une distance » de la taille de l’élément » de la transition. Étudions ce qui se passe si le maillage est affiné dans le sens axial.
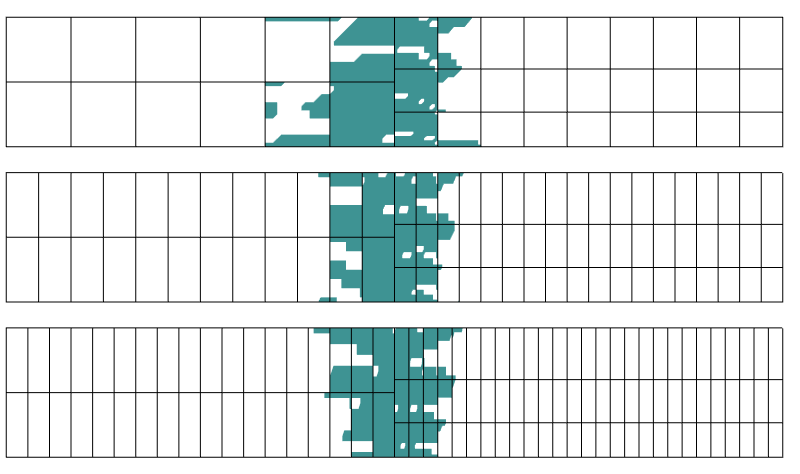
Région avec plus de 0,1% d’erreur dans le stress. Trois discrétisations différentes sont utilisées dans le sens axial.
Il s’avère que la région de perturbation n’est pas beaucoup affectée par la discrétisation dans la direction perpendiculaire à la limite de transition. C’est exactement ce que nous dit le principe de Saint-Venant.
Remarques finales
Sans utiliser le principe de Saint-Venant, de nombreuses analyses structurales sont difficiles à réaliser, tout simplement parce que la répartition détaillée des charges n’est pas connue.
Le principe n’est formellement valable que pour les matériaux élastiques linéaires. En pratique, nous l’utilisons également intuitivement au quotidien pour d’autres situations. Si, par exemple, le matériau de l’exemple « plaque avec trou » était élastoplastique, on s’attendrait à ce que les deux charges réparties donnent des résultats équivalents, tant que la limite d’élasticité est supérieure à la contrainte appliquée à la limite de sorte qu’il n’y ait que déformation plastique autour du trou. La charge ponctuelle, cependant, donne toujours une solution différente, car le matériau cède autour du point chargé. Pour une discussion plus longue, lisez cet article de blog sur les singularités aux charges ponctuelles.
Prochaines étapes
En savoir plus sur l’utilisation du logiciel COMSOL Multiphysics® pour FEA.
Lectures complémentaires
- Y.C. Fung et P. Tong, Mécanique classique et informatique des Solides, World Scientific Publishing Co. Ept. Ltd., 2001.