12.fejezet
Moment Distribution analysis of Structures
12.1 alapfogalmak
a moment distribution analysis of structures-Engineering LibreTexts
1930-ban került bemutatásra. Bár ez a módszer olyan deformációs módszer, mint a lejtés-elhajlás módszer, hozzávetőleges módszer, ezért nem igényel egyidejű egyenletek megoldását, mint az utóbbi módszer esetében. A pillanatnyi Eloszlás módszerével kapott eredmények pontosságának mértéke az egymást követő közelítések számától vagy az iterációs folyamattól függ.
a momentumeloszlás módszerének szemléltetéséhez vegye figyelembe a 12.1. ábrán látható keretet. A keret tagjai prizmásak, és feltételezzük, hogy nem deformálódnak tengelyirányban, és nem fordulnak egymáshoz képest. A keret ACD illesztései rögzítve vannak, míg a B kötés az alkalmazott terhelés miatt kissé elfordulhat. Először is, mielőtt a tagok közötti pillanatnyi eloszlást elvégeznénk, feltételezzük, hogy az összes illesztést ideiglenesen rögzítik egy bilincs segítségével.
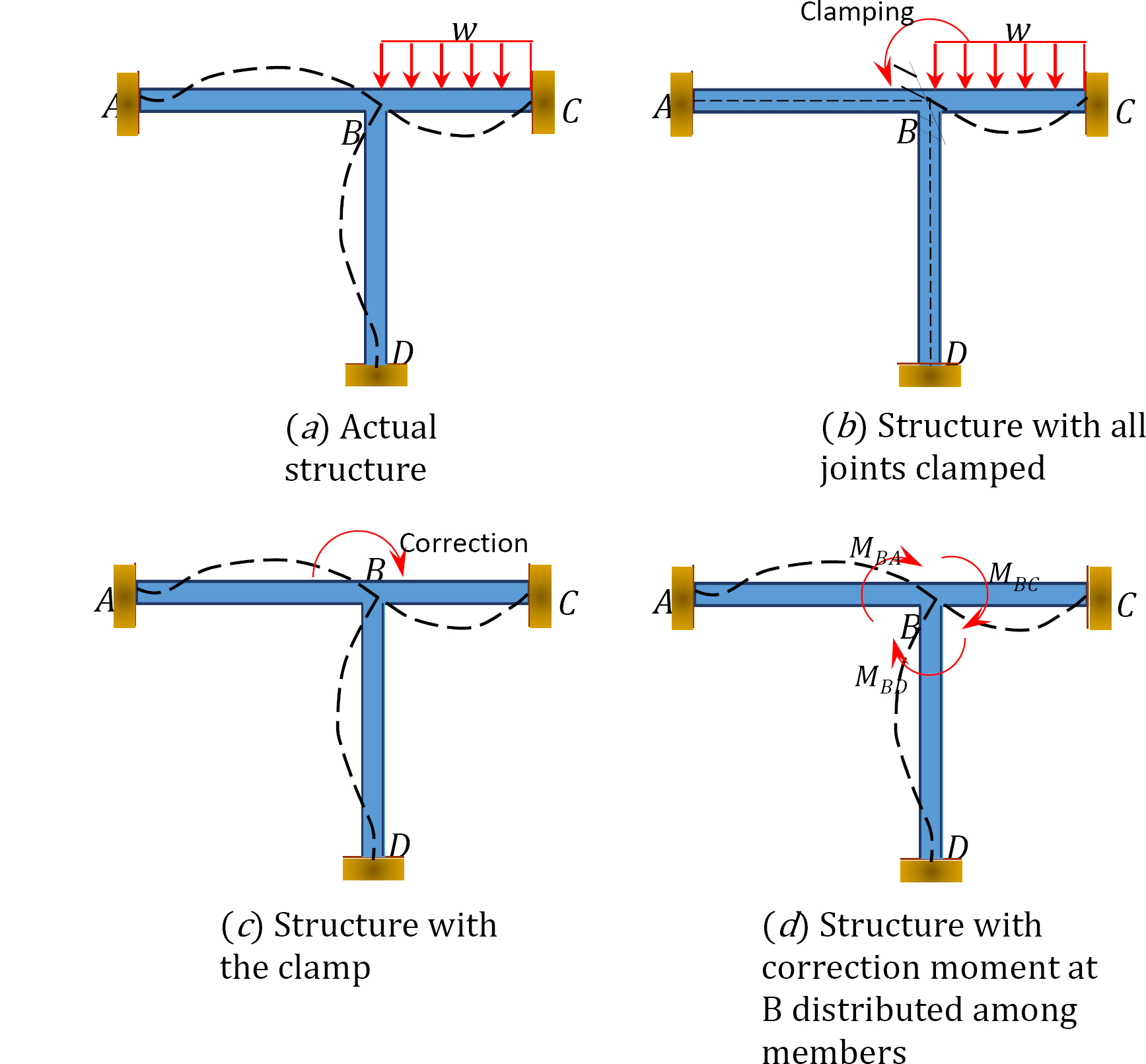
Fig. 12.1. Keret.
12.2 jel konvenció
a jel konvenció a pillanateloszlási módszerhez hasonló a lejtés-elhajlás módszeréhez; vagyis a tag végén lévő pillanat akkor tekinthető pozitívnak, ha hajlamos a tag végét az óramutató járásával megegyező irányba, negatívnak, ha az óramutató járásával ellentétes irányba fordítani.
12.3 meghatározások
kiegyensúlyozatlan pillanatok: Ez az elemzési módszer azt feltételezi, hogy a szerkezet ízületeit kezdetben rögzítik vagy rögzítik, majd egymás után elengedik. Miután elengedtek egy ízületet, rotációra kerül sor, mivel az adott ízületben ülésező tagok rögzített végpillanatainak összege nem nulla. A kapott végmomentumok összegének értéke az adott ízület kiegyensúlyozatlan pillanata.
átvitt pillanatok: az elosztott pillanatok a tagok találkozásának végén egy közös ügynél, a többi végén, amelyek feltételezhetően rögzítettek. Ezeket az indukált pillanatokat a másik végén átvitt pillanatoknak nevezzük.
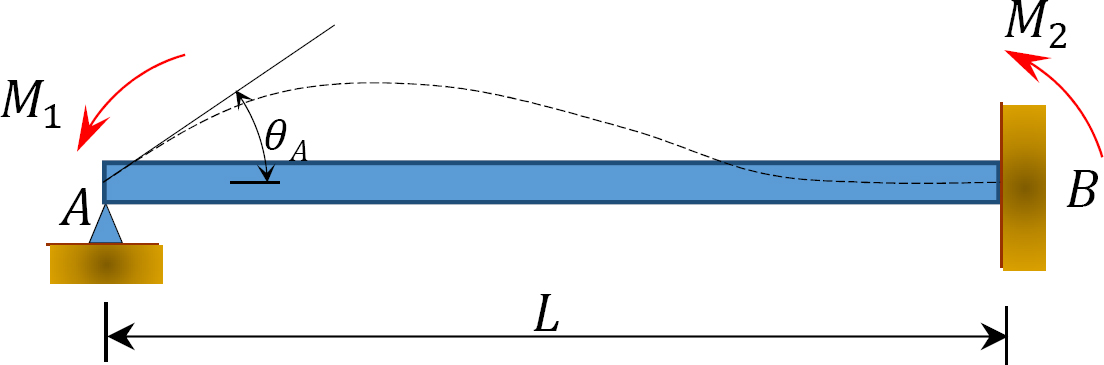
Fig. 12.2. Terheletlen prizmás gerenda.
Vegyünk egy terheletlen prizmás gerendát, amely a B végén van rögzítve, amint azt a 12.2.ábra mutatja. Ha egy M1 pillanatot alkalmazunk a gerenda bal végére, akkor a gerenda mindkét végére a lejtés-elhajlás egyenletek a következőképpen írhatók:


az 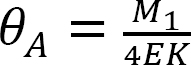 helyettesítése a 12.1 egyenletből a 12.2 egyenletbe a következőket javasolja:
helyettesítése a 12.1 egyenletből a 12.2 egyenletbe a következőket javasolja:

a 12.3 egyenlet azt sugallja, hogy a gerenda rögzített végére átvitt momentum a másik végén alkalmazott Momentum miatt megegyezik az alkalmazott Momentum felével.
átviteli tényező: az indukált Momentumnak az alkalmazott momentumhoz viszonyított arányát átviteli tényezőnek nevezzük. A 12.2. ábrán látható fénysugár esetében az átviteli tényező a következő:

elosztott tényező (DF): Az elosztott tényező egy olyan tényező, amelyet a kiegyensúlyozatlan pillanat arányának meghatározására használnak, amelyet az egyes tagok közösen üléseznek. A 12.3. ábrán látható keret o közös ülésén ülésező tagok eloszlási tényezőit a következőképpen kell kiszámítani:
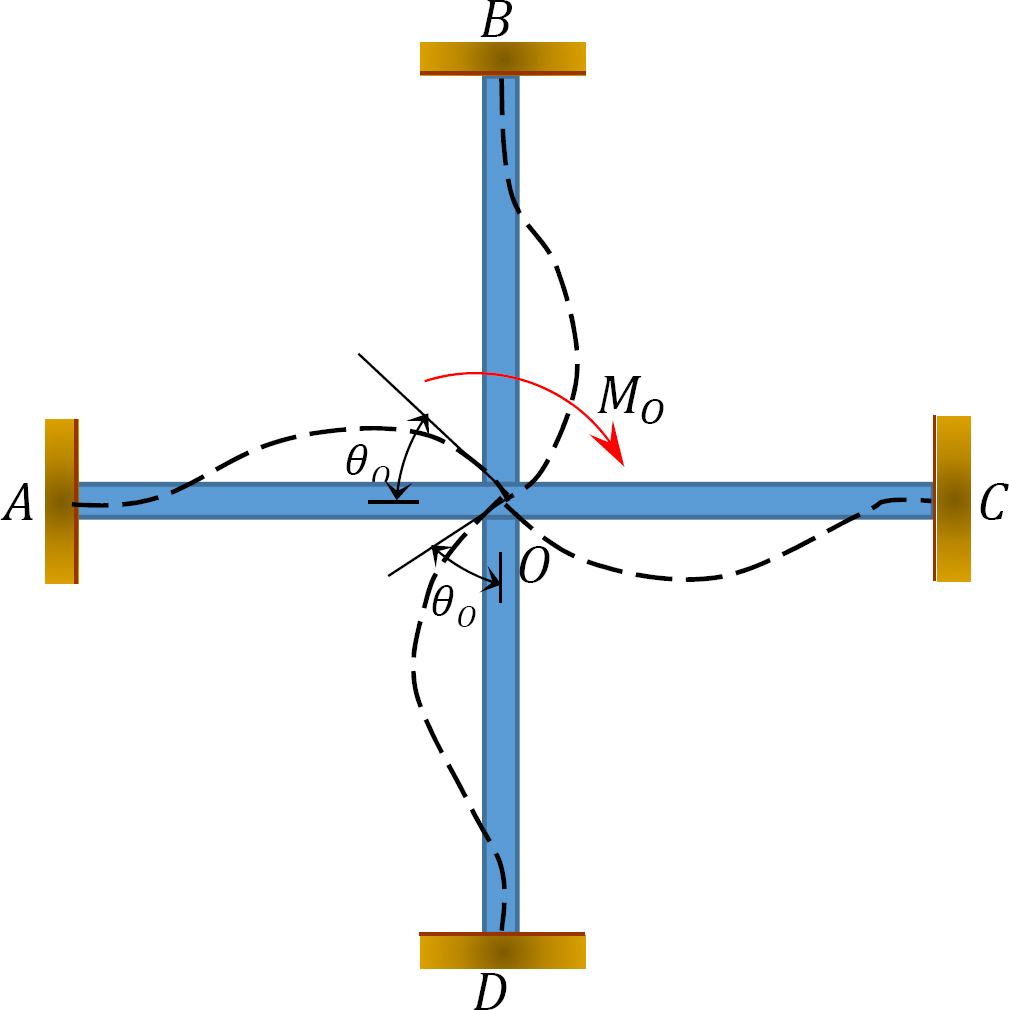
Fig. 12.3. Keret.

elosztott pillanatok: a képzeletbeli bilincs elengedésekor egy ízületnél az adott ízület kiegyensúlyozatlan pillanata elfordul. A forgatás megfordítja a tagok találkozójának végét az ízületben, ami ellenállási pillanatok kialakulását eredményezi. Ezeket az ellenálló pillanatokat elosztott pillanatoknak nevezzük. A 12.3. ábrán látható keret tagjai számára elosztott momentumokat a következőképpen számítjuk ki:
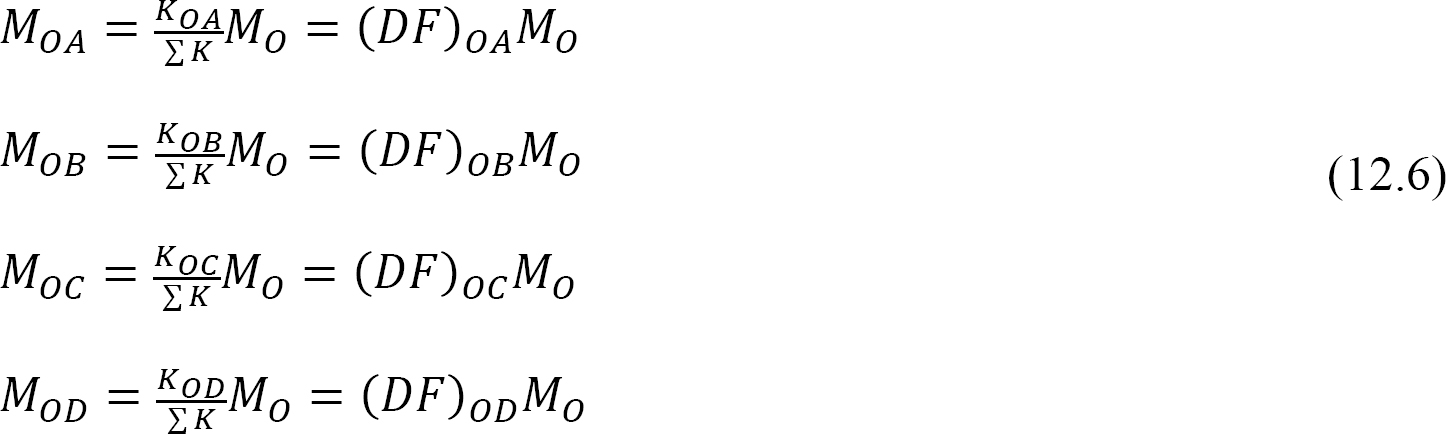
12.4 A Tagmerevség módosítása
néha a momentumelosztási módszerben az iterációs folyamat jelentősen csökkenthető a határozatlan szerkezet egyes tagjainak hajlítási merevségének beállításával. Ez a szakasz egy rögzített és egy csapvégű támasz hatását vizsgálja egy határozatlan gerenda hajlítási merevségére.
1. eset: Az egyik végén csuklós, a másikban rögzített gerenda
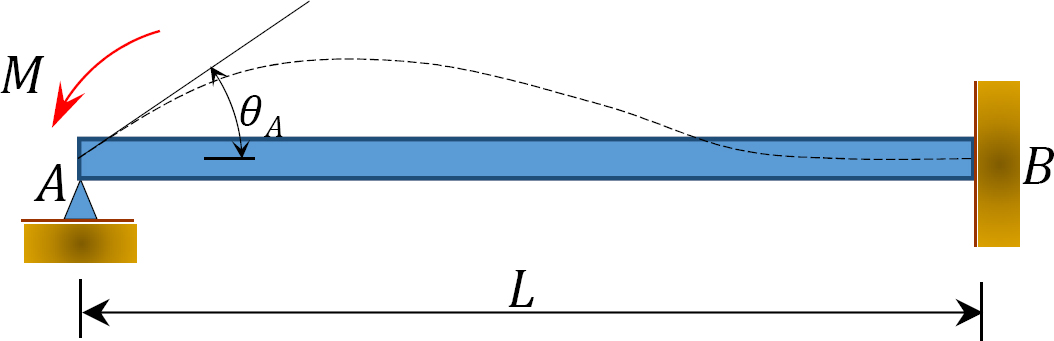
Fig. 12.4. Gerenda
Vegyünk egy gerendát, amely az A végén csuklós és a B végén rögzített, a 12.4. ábrán látható módon. Egy pillanat alkalmazása M elforgatja a csuklópánt végét egy összeggel Ft. A tag a végének meredekség-elhajlási egyenletének megírása, megjegyezve, hogy 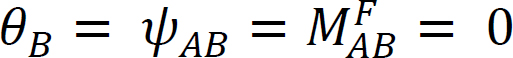 a következőket javasolja:
a következőket javasolja:
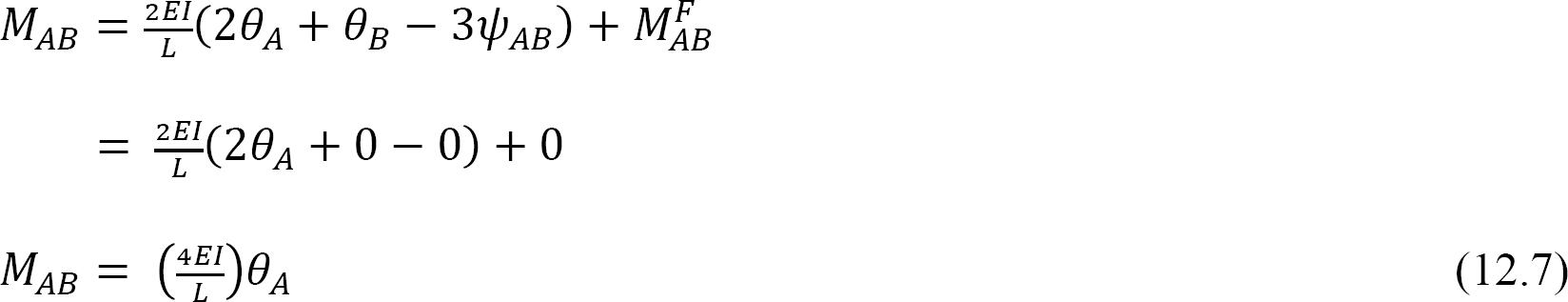
definíció szerint a szerkezeti elem hajlítási merevsége az a pillanat, amelyet a tag végére kell alkalmazni, hogy ennek a végnek egységnyi forgása legyen. A rögzített távolabbi végű tag hajlítási merevségének következő kifejezését a következőképpen fejezzük ki, ha az on-napot = 1 egyenletbe helyettesítjük 12.7:

definíció szerint egy tag relatív hajlítási merevségét úgy határozzuk meg, hogy elosztjuk a tag hajlítási merevségét 4E-vel. a 12.8 egyenlet elosztása 4E-vel a következő kifejezésre utal relatív merevség a vizsgált esetre:

2. eset: mindkét végén csuklós gerenda
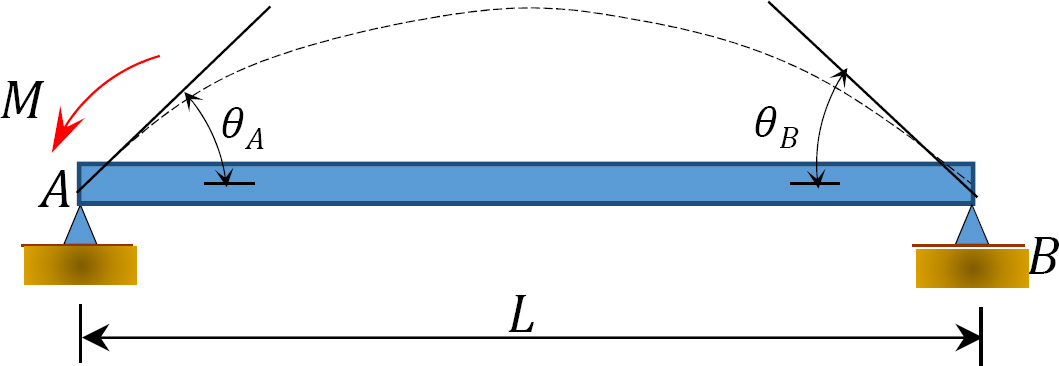
Fig. 12.5. Egyszerűen támogatott gerenda.
ha a 12.5.ábrán bemutatott, egyszerűen támasztott gerenda A végén egy M Momentumot alkalmazunk, a gerendát a csuklós végnél egy na-a szöggel forgatjuk el. A 11. fejezet 11.4. szakaszában levezetett módosított meredekség-elhajlás egyenlet alkalmazásával, megjegyezve, hogy 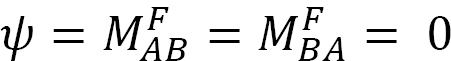 a következő kifejezést javasolja arra a pillanatra, amikor a terhelést a csuklós végén alkalmazzák:
a következő kifejezést javasolja arra a pillanatra, amikor a terhelést a csuklós végén alkalmazzák:
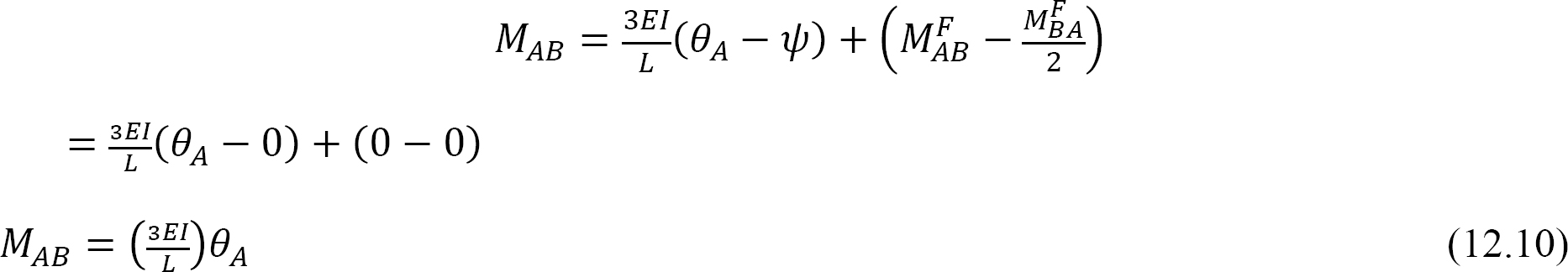
ha az Ong = 1 – et behelyettesítjük a 12.10 egyenletbe, akkor a következő kifejezést javasoljuk a csuklós távoli végű tag hajlítási merevségére:

a csuklós távoli végű tag relatív merevségét a 12.11 egyenlet 4E-vel történő elosztásával kapjuk meg, az alábbiak szerint:

a 12.12 és a 12.9 egyenletek összehasonlítása azt sugallja, hogy egy csuklós távoli végű tag háromnegyede olyan merev, mint egy ugyanolyan geometriájú, de a távoli végén rögzített tag. Ez a megállapított tény jelentősen csökkentheti az iteráció számát, amikor a gerendákat vagy kereteket csuklós távoli véggel elemezzük a momentumeloszlás módszerével. Ilyen esetekben a gerenda relatív merevségét a közeli végén először a 12.12 egyenlet szerint állítjuk be, majd eloszlási tényezőjét a beállított merevséggel számítjuk ki. A kiegyenlítő művelet során a közeli vég csak egyszer kerül kiegyensúlyozásra, a pillanatok további átvitele nélkül a végétől vagy a végéig.
12.5 meghatározatlan gerendák elemzése
a meghatározatlan gerendák analízisének eljárását a pillanateloszlás módszerével röviden összefoglaljuk a következőképpen:
eljárás Határozatlan gerendák elemzésére a Momentumeloszlás módszerével
•Számítsa ki a tagok rögzített végű momentumait, feltételezve, hogy az illesztések a forgás ellen vannak rögzítve.
•Számítsa ki az elosztási tényezőt az ízülethez kapcsolódó minden egyes tag esetében
•Számítsa ki az egyes ízületeknél a kiegyensúlyozatlan pillanatot, és ossza el ugyanazt az adott ízülethez kapcsolódó tagok végein.
•vigye át az elosztott pillanat felét a tagok másik végére.
•összeadja vagy kivonja ezeket az utóbbi pillanatokat (a harmadik és negyedik lépésben kapott pillanatokat) az eredeti rögzített végű pillanatokhoz vagy azokhoz.
•alkalmazza a meghatározott végmomentumokat az adott szerkezet ízületein.
•rajzolja meg az adott gerenda minden fesztávolságának szabadtest-diagramját, bemutatva a momentumelosztási módszerrel kapott kötések terhelését és momentumait.
•határozza meg az egyes tartományok támogatási reakcióit.
•rajzoljon egy hajlítónyomatékot és egy nyíróerő-diagramot az adott gerendára a 9.lépésben szereplő diagramok kombinálásával.
példa 12.1
a momentumeloszlás módszerével határozzuk meg a 12.6 A. ábrán látható fénynyaláb tartóinál a végnyomatékokat és a reakciókat.rajzoljuk meg a nyíróerőt és a hajlítónyomaték diagramjait. Ei = állandó.
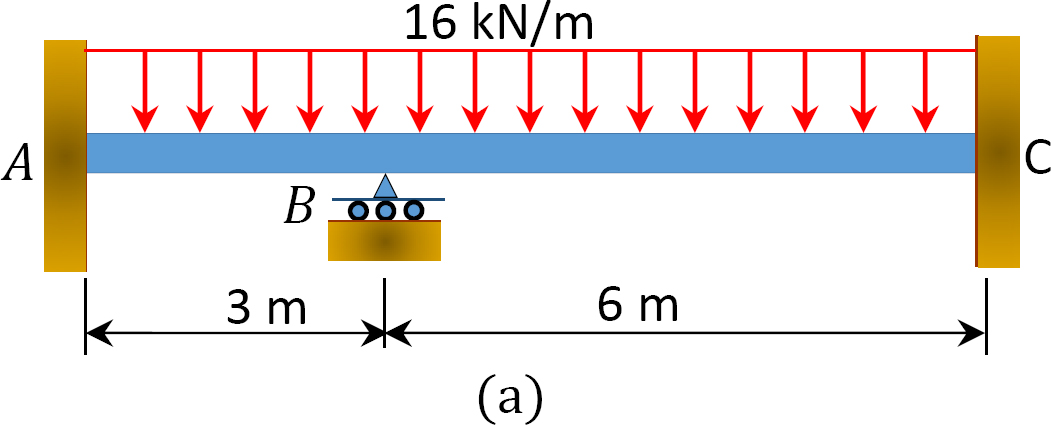
Fig. 12.6. Beam.
megoldás
rögzített végnyomaték.
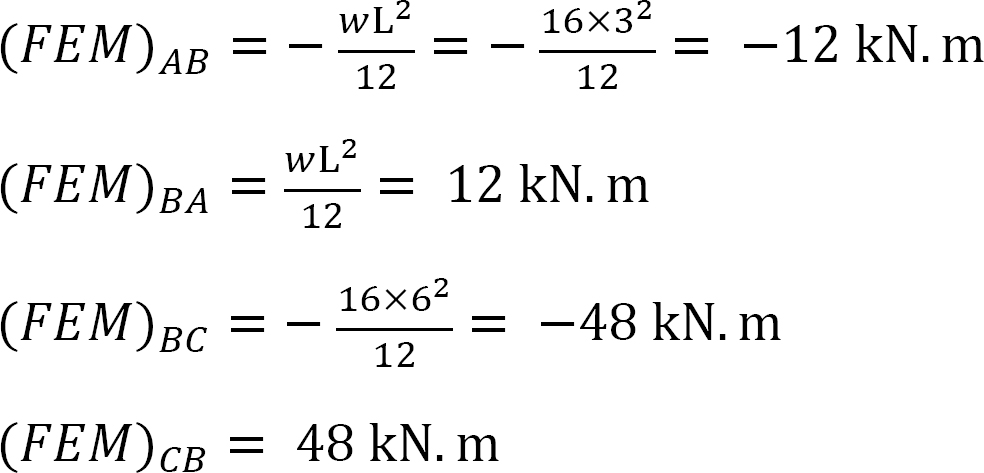
merevségi tényező.
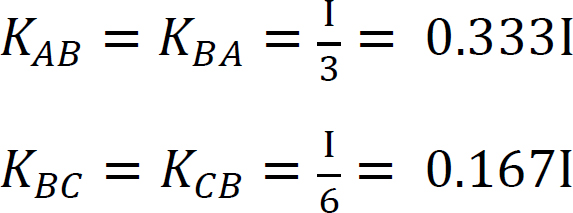
elosztási tényező.
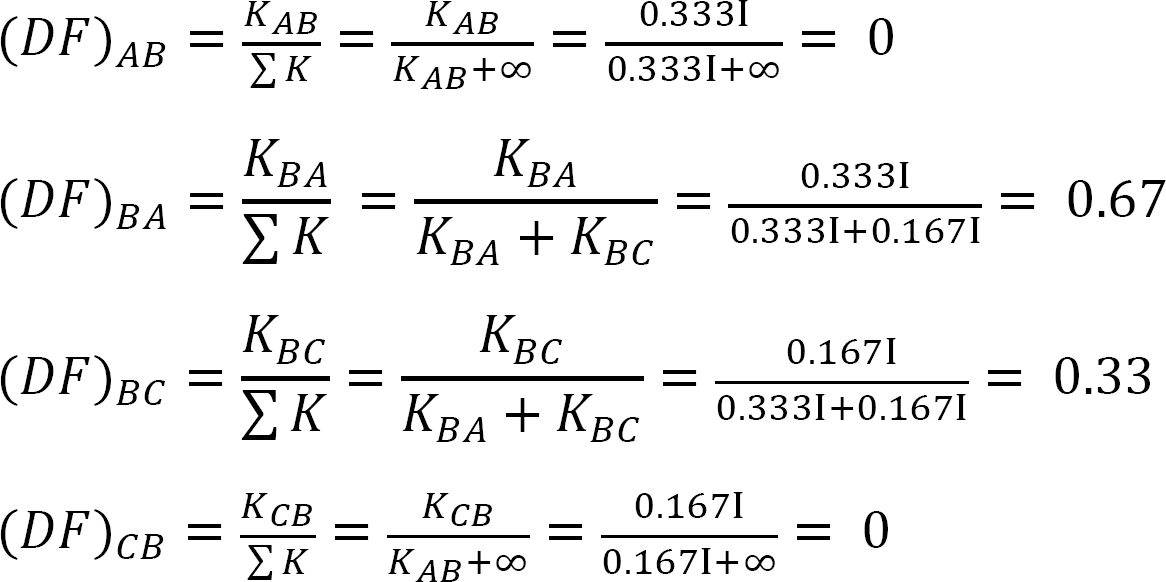
táblázat 12.1. Terjesztési táblázat.
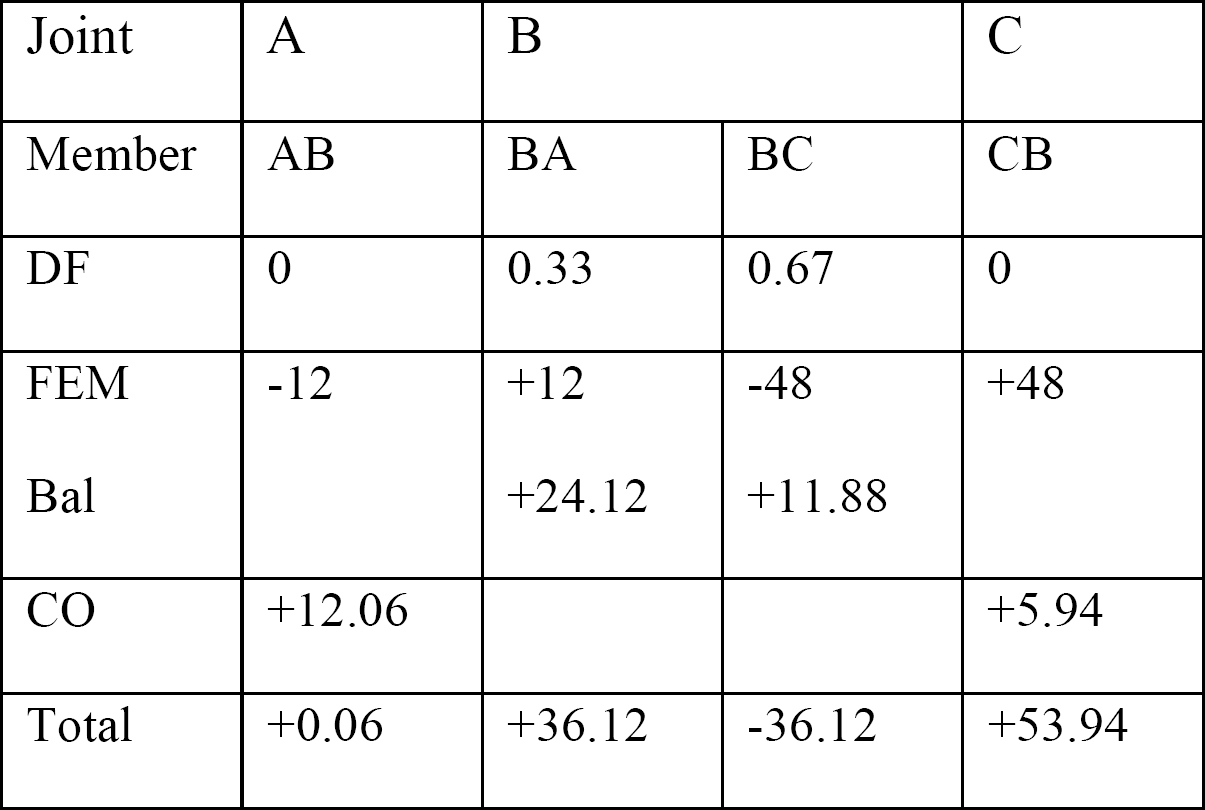
nyíróerő és hajlítónyomaték diagramok.
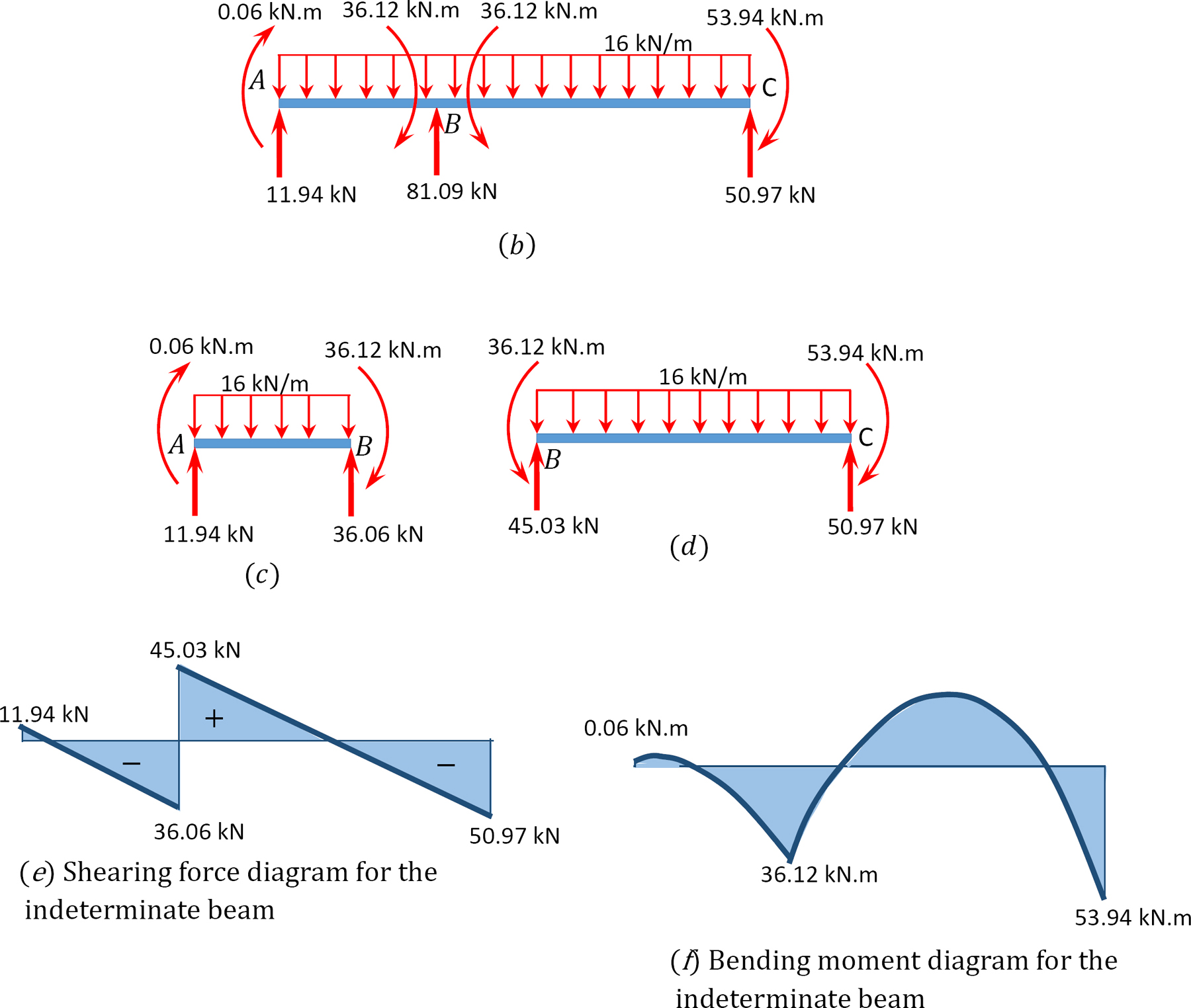
példa 12.2
a momentumeloszlás módszerével határozzuk meg a 12.7 A. ábrán látható fénynyaláb tartóinál a végnyomatékokat és a reakciókat.rajzoljuk meg a nyíróerő és a hajlítónyomaték diagramjait.
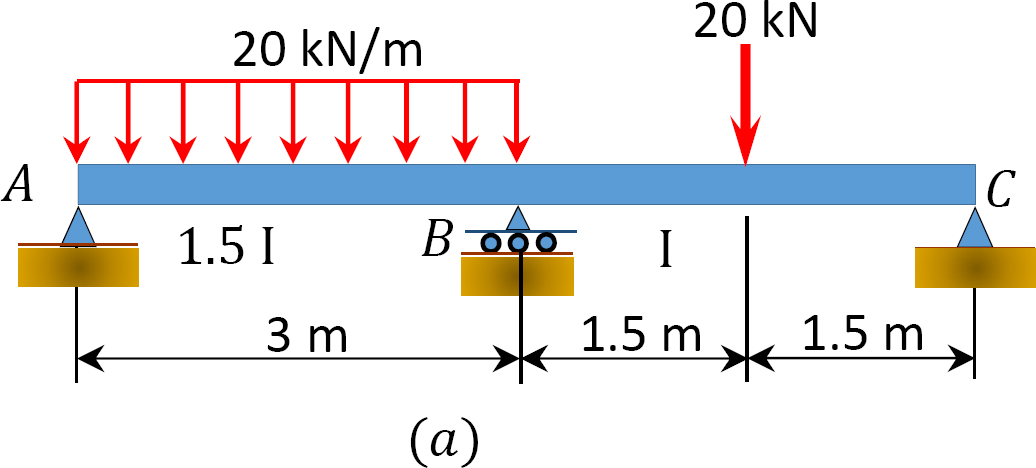
Fig. 12.7. Beam.
megoldás
rögzített végnyomaték.
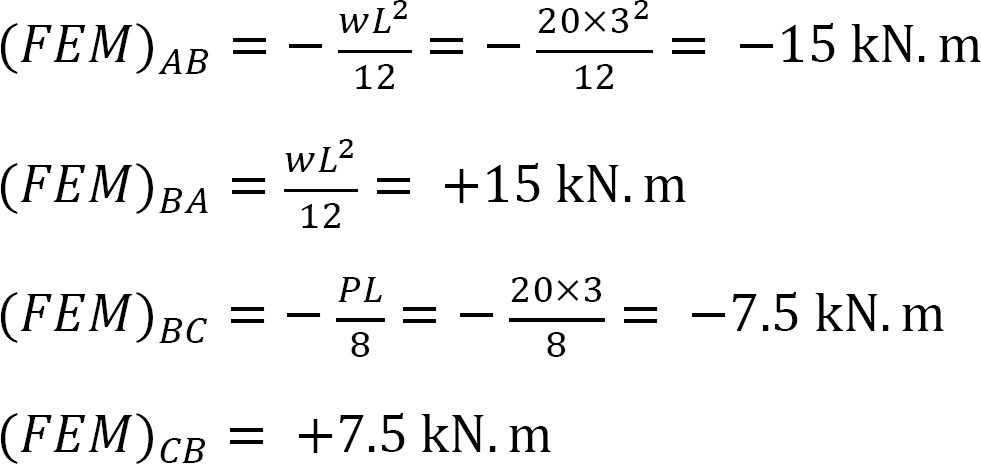
merevségi tényező.
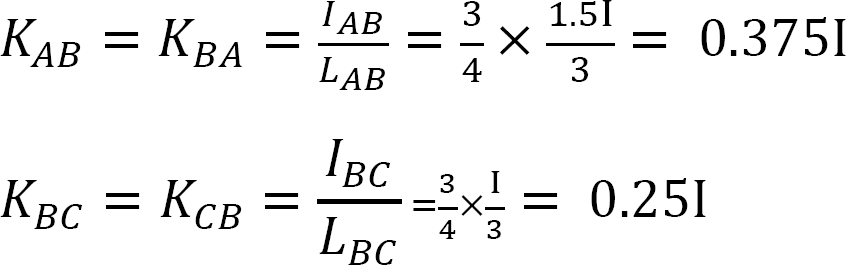
elosztási tényező.
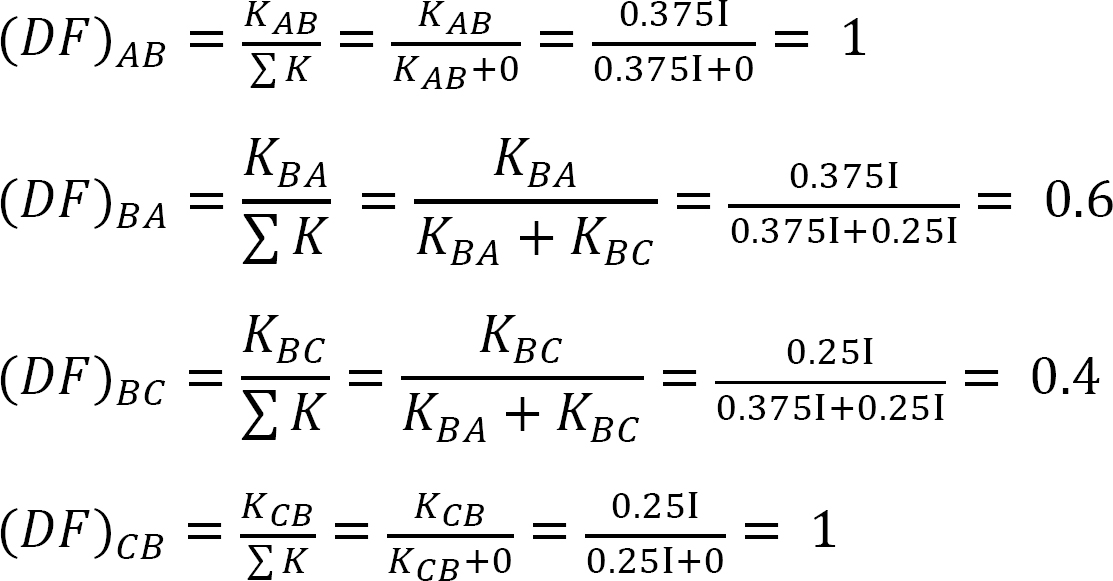
táblázat 12.2. Terjesztési táblázat.
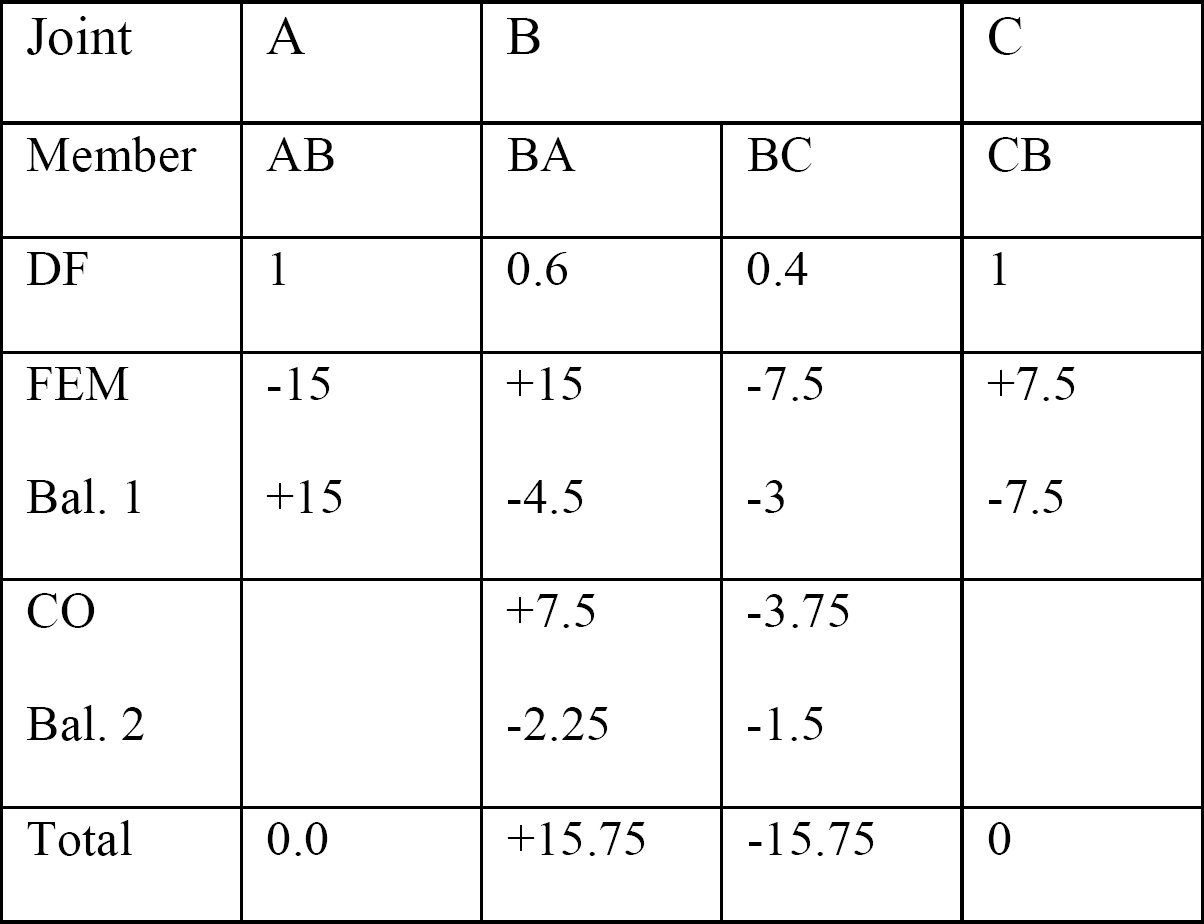
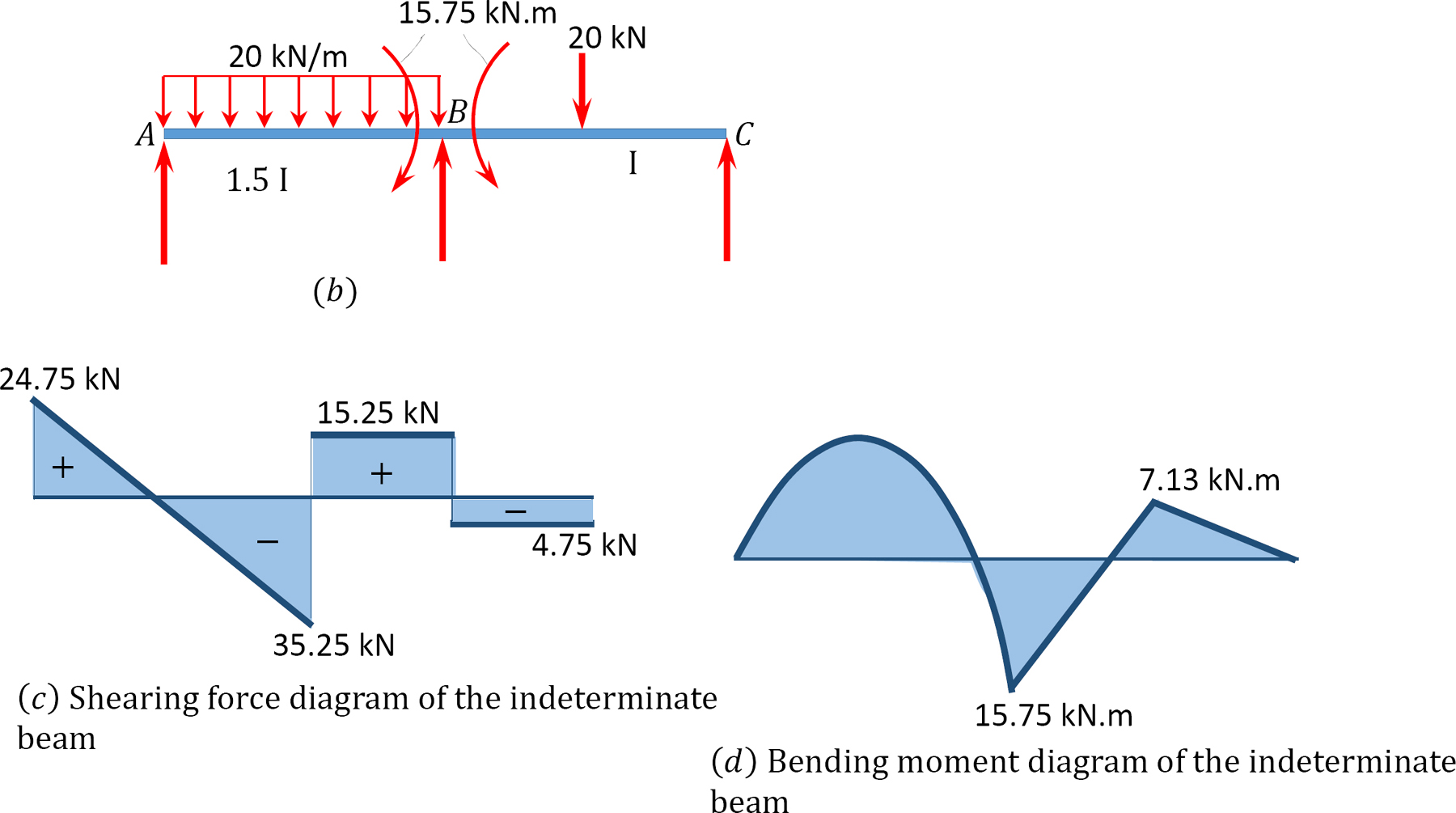
nyíróerő és hajlítónyomaték diagramok.
12.6 Határozatlan keretek elemzése
a keretek elemzésének eljárása a pillanatelosztási módszerrel az elemzett keret típusától függ. A kereteket sway-vagy nem sway-keretek közé sorolják. A nem lengő keretek elemzésének eljárása hasonló a határozatlan gerendákéhoz. De a sway keretek elemzéséhez az eljárás más. A lengési keretek elemzésének két szakasza van, nevezetesen a nem lengési szakasz és a lengési szakasz elemzése. Ezeket a szakaszokat az alábbiakban ismertetjük.
eljárás meghatározatlan lengési keretek elemzésére a Momentumelosztási módszerrel
A. Nem lengési szakasz elemzés
•először tegyük fel, hogy létezik egy képzeletbeli támasz, amely megakadályozza a keret imbolygását.
B. Sway stage analysis
•az M2 értékeket feltételezzük, az M1 értéket pedig meghatározzuk.
•ezután a tetszőleges momentumokat elosztjuk, mint a nem lengési feltételhez
•számítsuk ki a vízszintes reakciók nagyságát a lengési feltétel támaszainál. Ezeknek a reakcióknak az összegzése megadja az önkényes kiszorító erőt Y.
ezt az arányt lengési tényezőnek nevezzük.
•használja a sway tényezőt a sway elosztott pillanatainak szorzásához. Ez megadja a korrigált pillanatot a lengéshez.
•a keret utolsó pillanatai a nem sway szakaszban kapott pillanatok összegzése és a korrigált pillanat a sway szakaszban.
példa 12.3
a momentumelosztás módszerével határozzuk meg a 12.8.ábrán látható keret tagjainak végmomentumait. Ei = állandó.
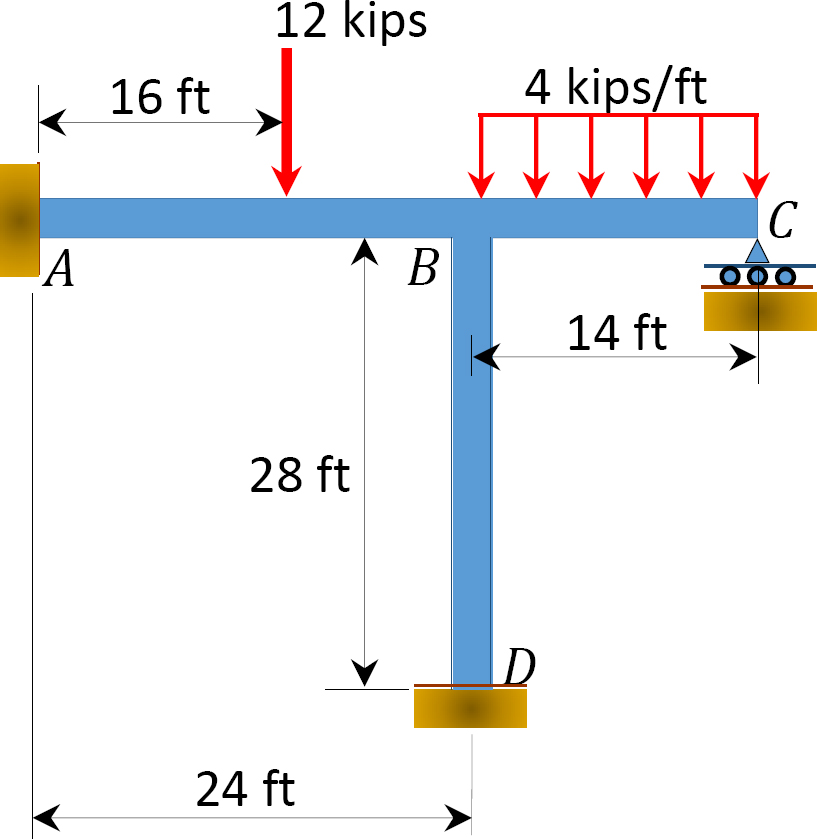
Fig. 12.8. Keret.
megoldás
rögzített végnyomaték.
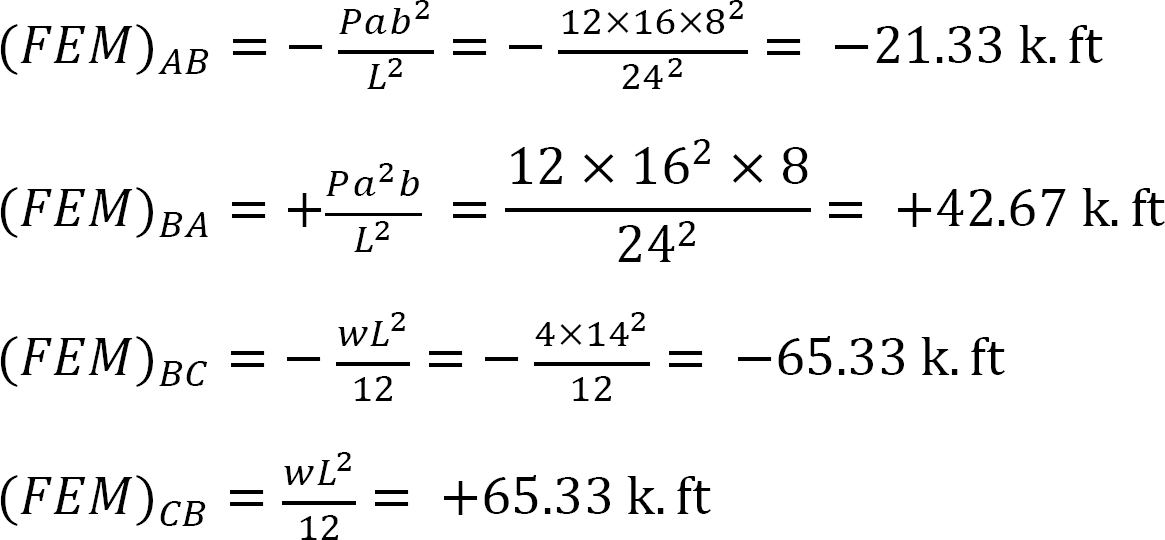
merevségi tényező.
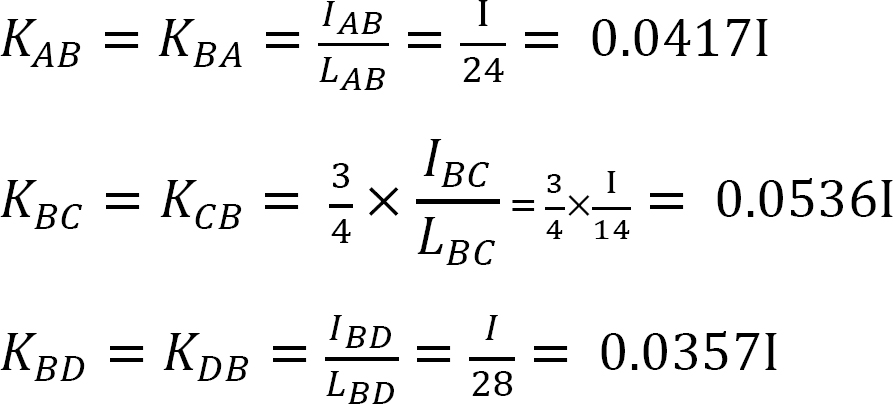
elosztási tényező.
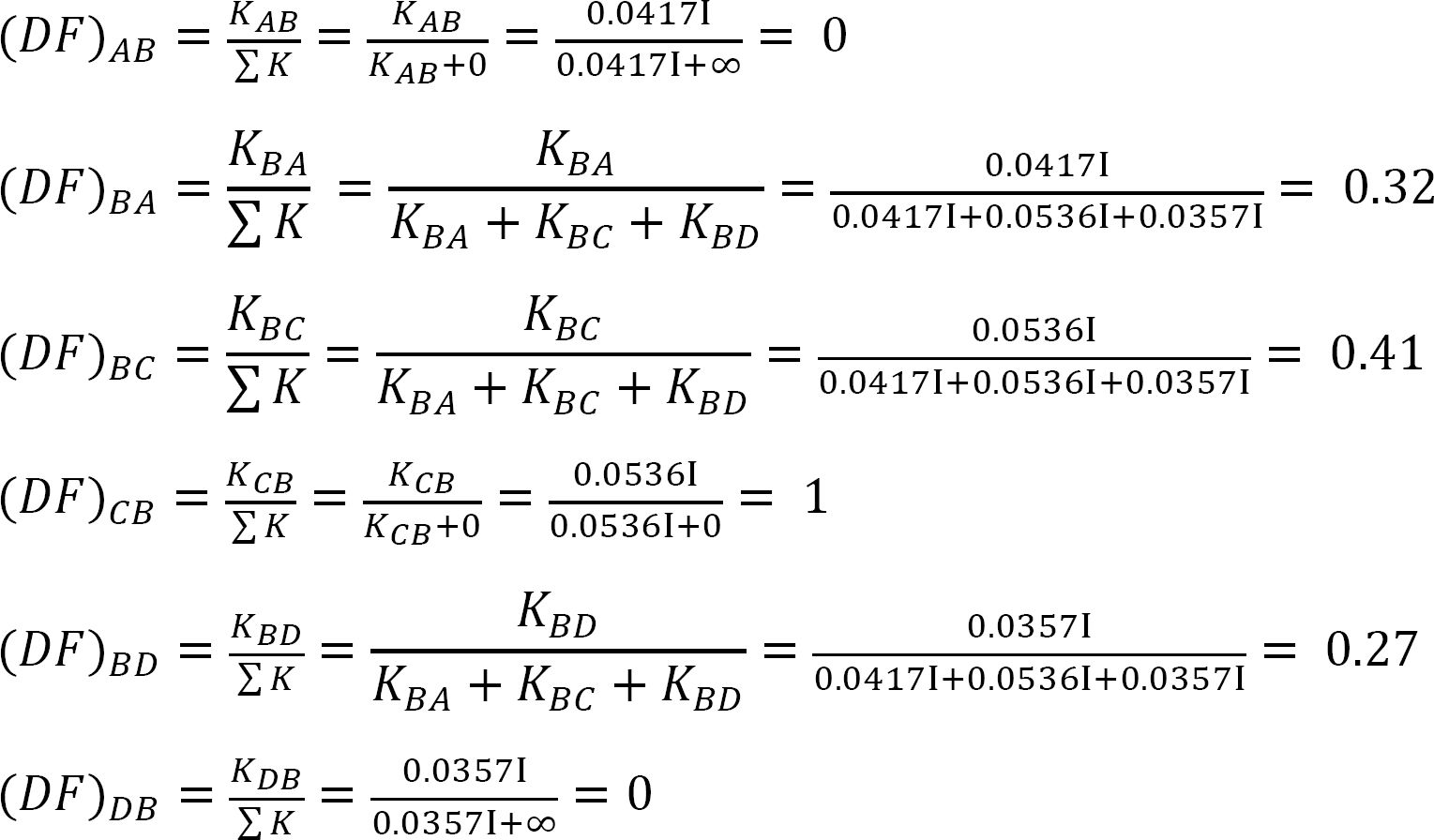
táblázat 12.3. Terjesztési táblázat.
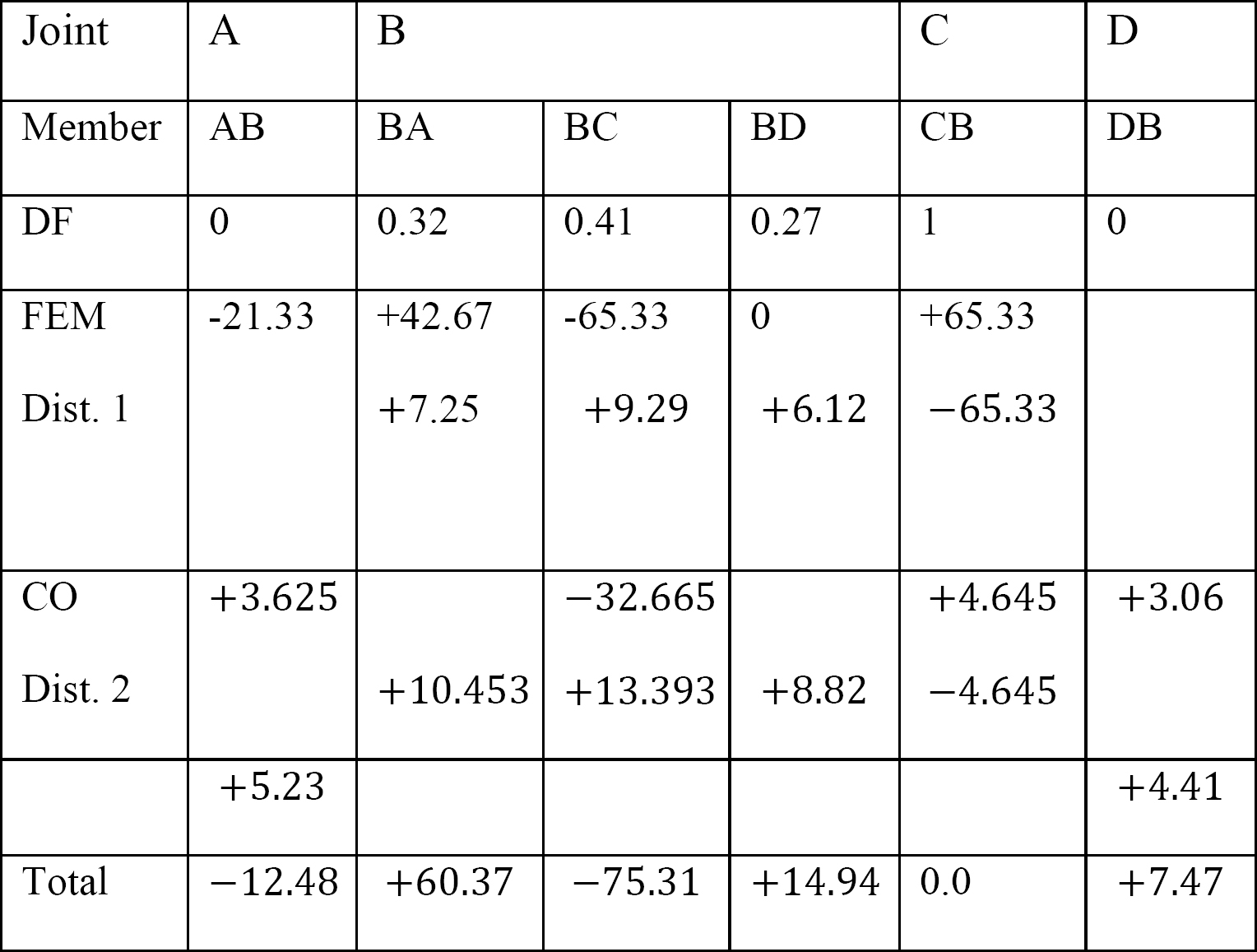
utolsó tag vége pillanatok.
az EK (ek), ek (ek), és ek (ek) (ek) (ek) értékeinek helyettesítése a tagvégi Momentum egyenletekben a következőket sugallja:
MAB = -12,48 k. ft
MBA = +60,37 k. ft
MBC = -75,31 K. ft
MBD = +14,94 k. Ft
MCB = 0
MDB = +7,47 k. Ft
12.példa.4
a momentumelosztási módszerrel határozzuk meg a 12.9.ábrán látható keret tartóinál a végnyomatékokat. Ei = állandó.
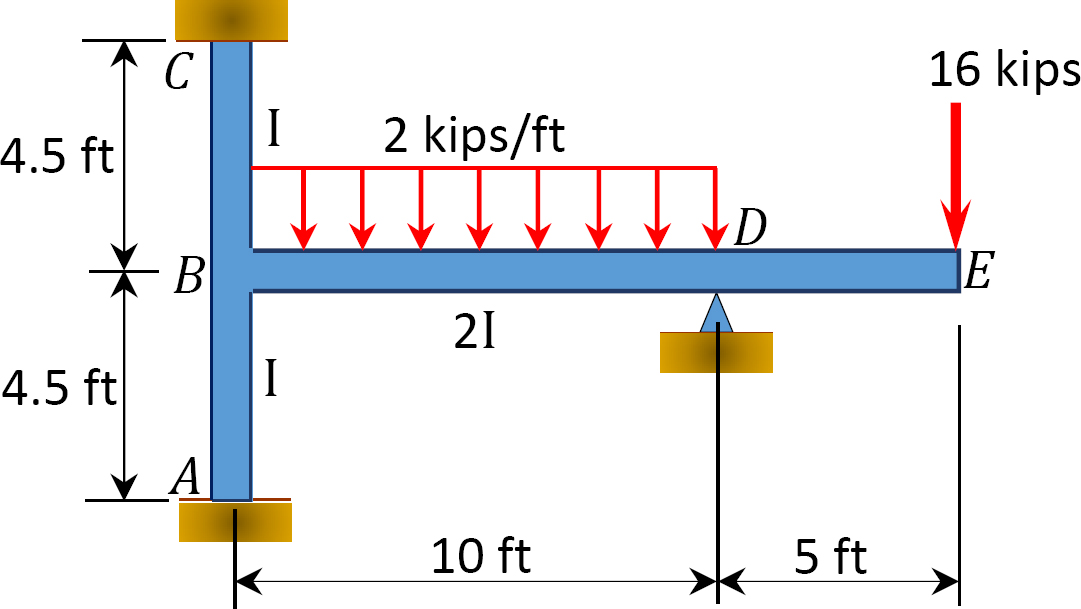
Fig. 12.9. Keret.
megoldás
rögzített végnyomaték.
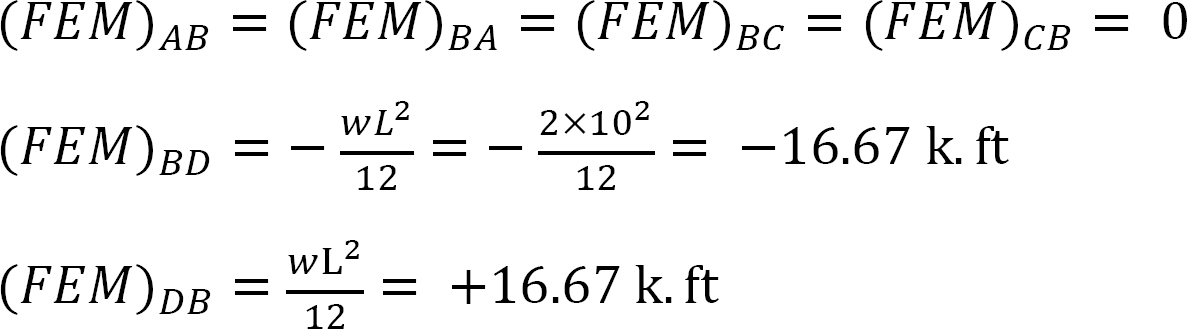
merevségi tényező.
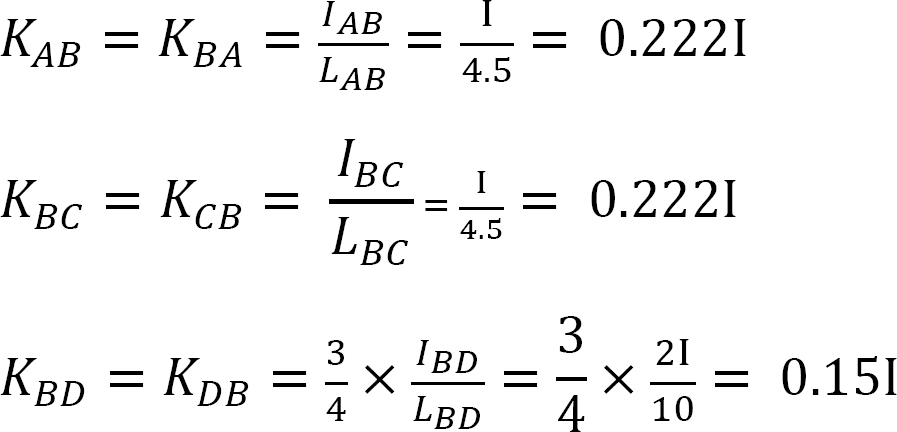
elosztási tényező.

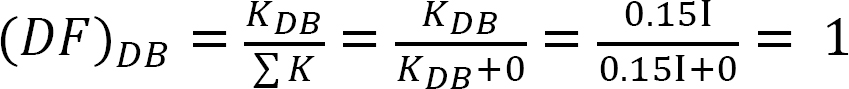
táblázat 12.4. Terjesztési táblázat.
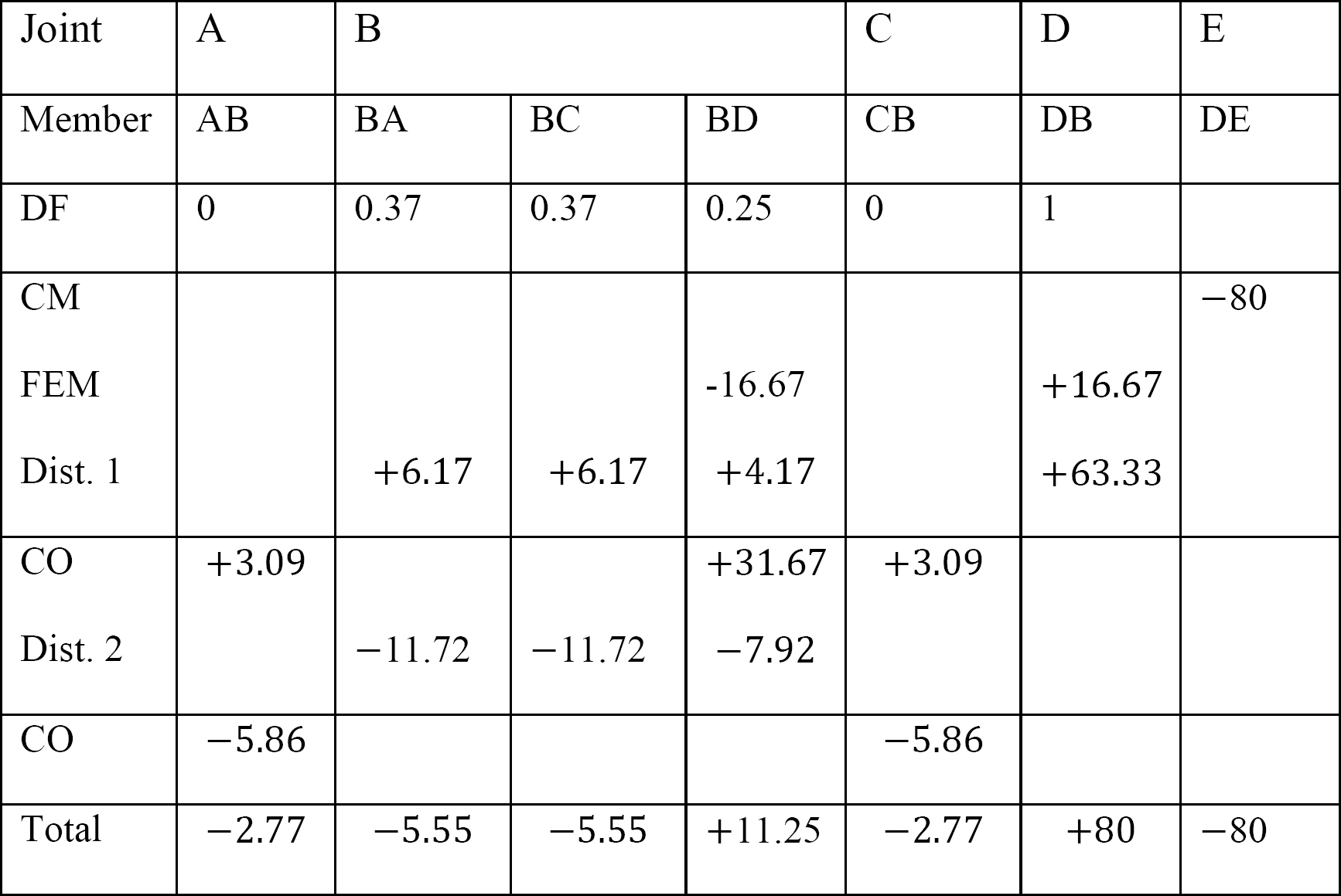
utolsó tag vége pillanatok.
MAB = -2,77 k. ft
MBA = -5,55 k. ft
MBC = -5,55 k. ft
MBD = +11,25 k. ft
MCB = -2,77
MDB = +80 k. ft
mde = -80 k. ft
példa 12.5
a momentumelosztási módszerrel határozzuk meg a 12.10.ábrán látható keret tartóinál a végmomentumokat. Ei = állandó.
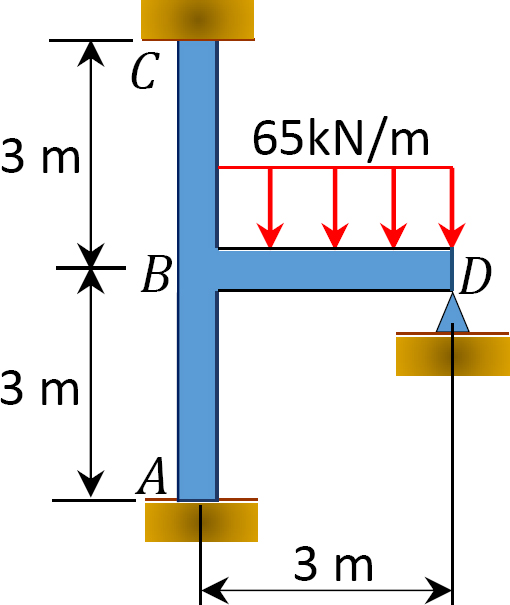
Fig. 12.10. Keret.
megoldás
rögzített végnyomaték.
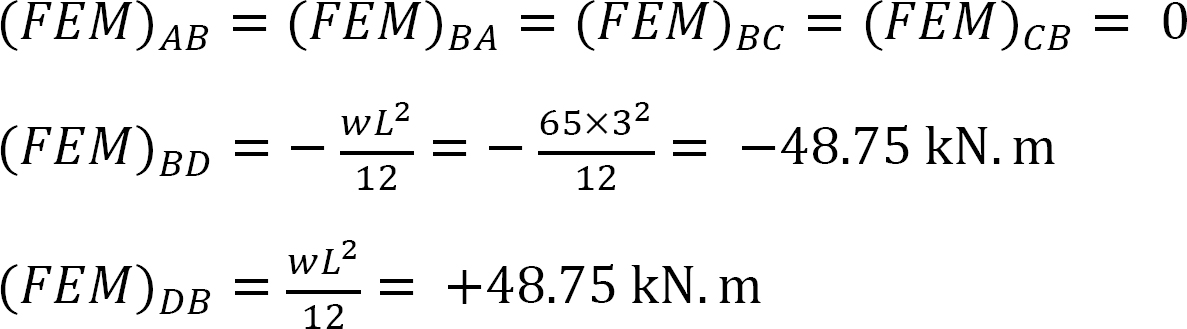
merevségi tényező.
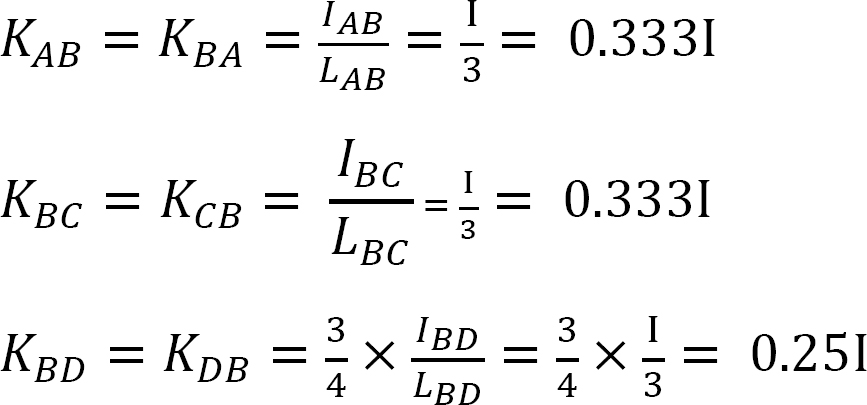
elosztási tényező.
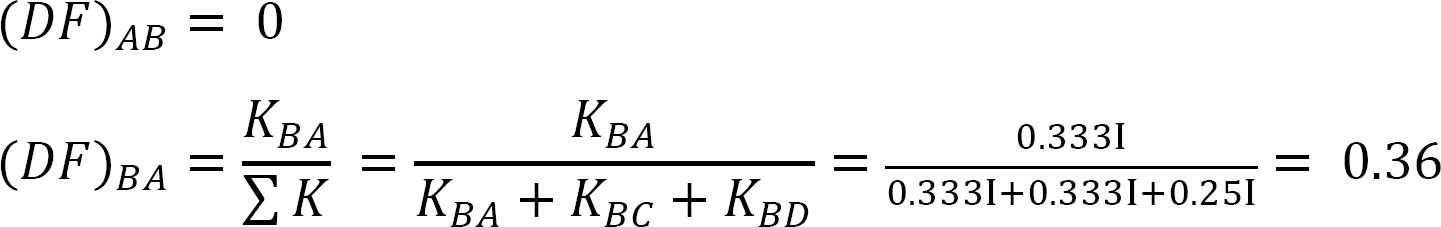

táblázat 12.5. Terjesztési táblázat.
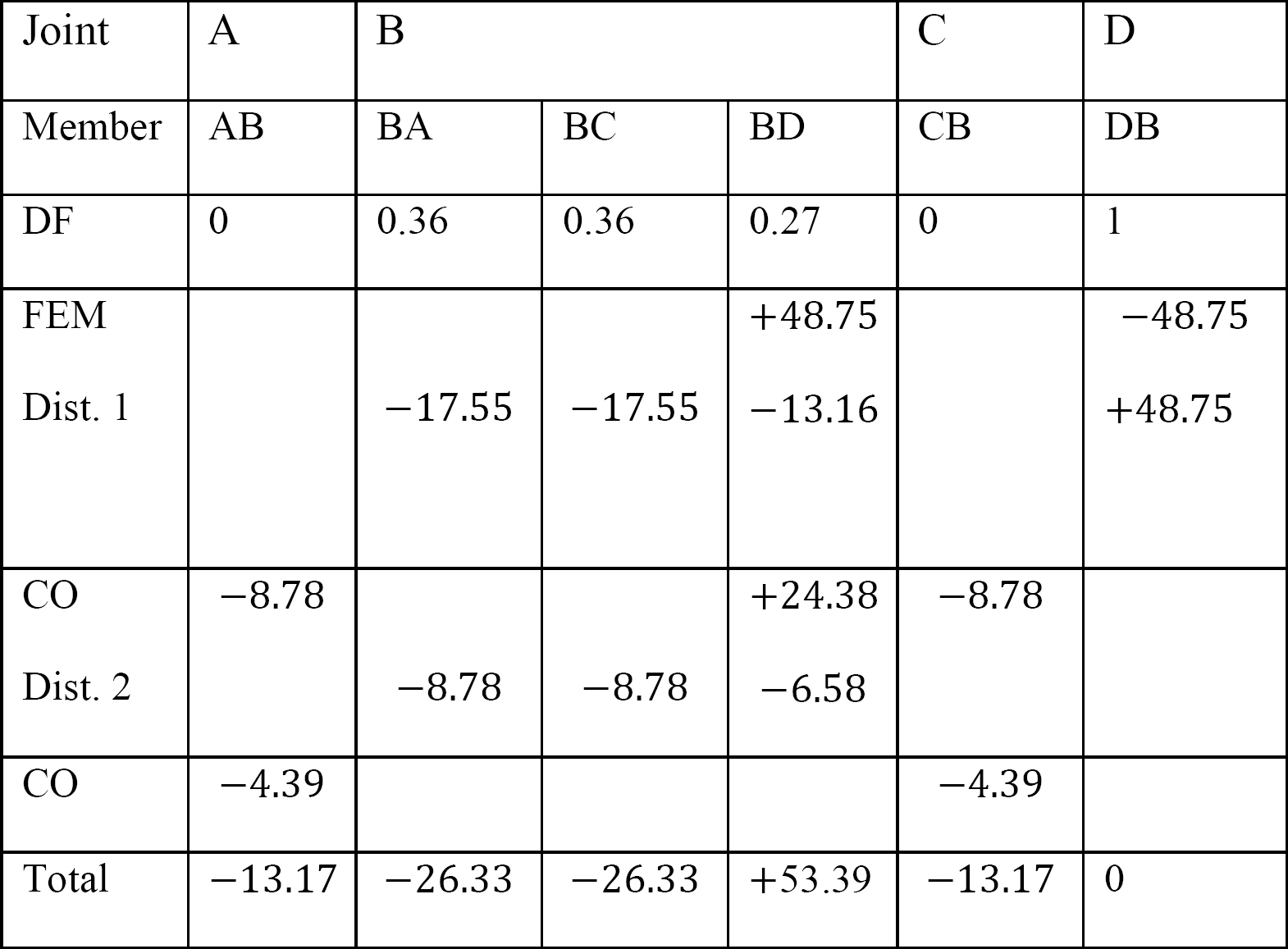
utolsó tag vége pillanatok.
MAB = -13,17 k. ft
MBA = -26,33 k. ft
MBC = -26,33 k. ft
MBD = +53,39 k. ft
MCB = -13,17 k. ft
MDB = 0
példa 12.6
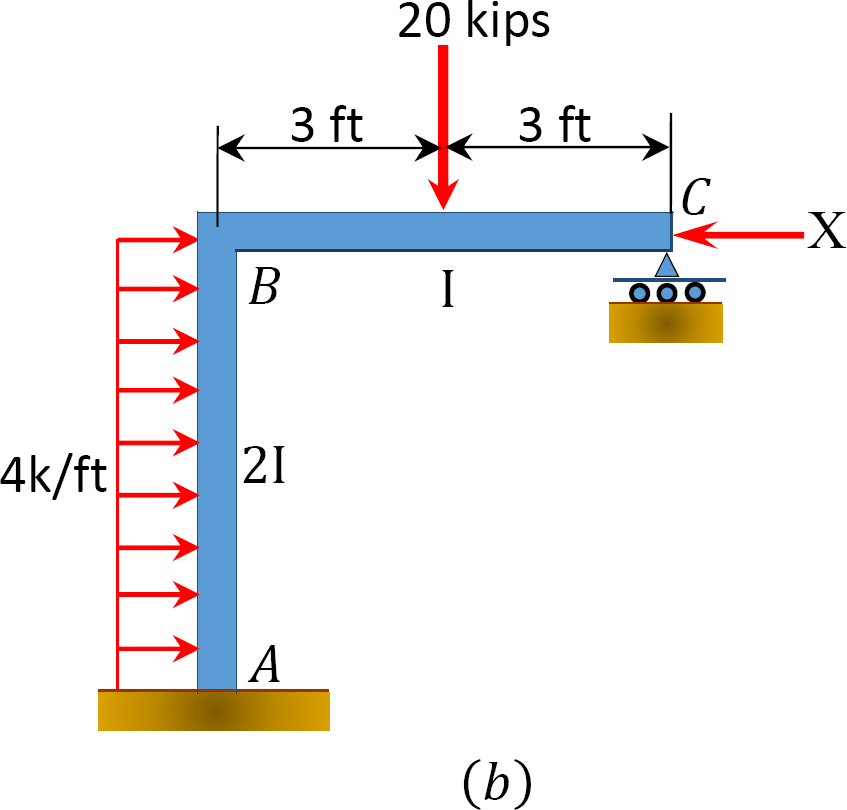
a momentumeloszlás módszerével határozzuk meg a keret tagvégmomentumait a 12.11 A ábrán látható oldalsó lengéssel.
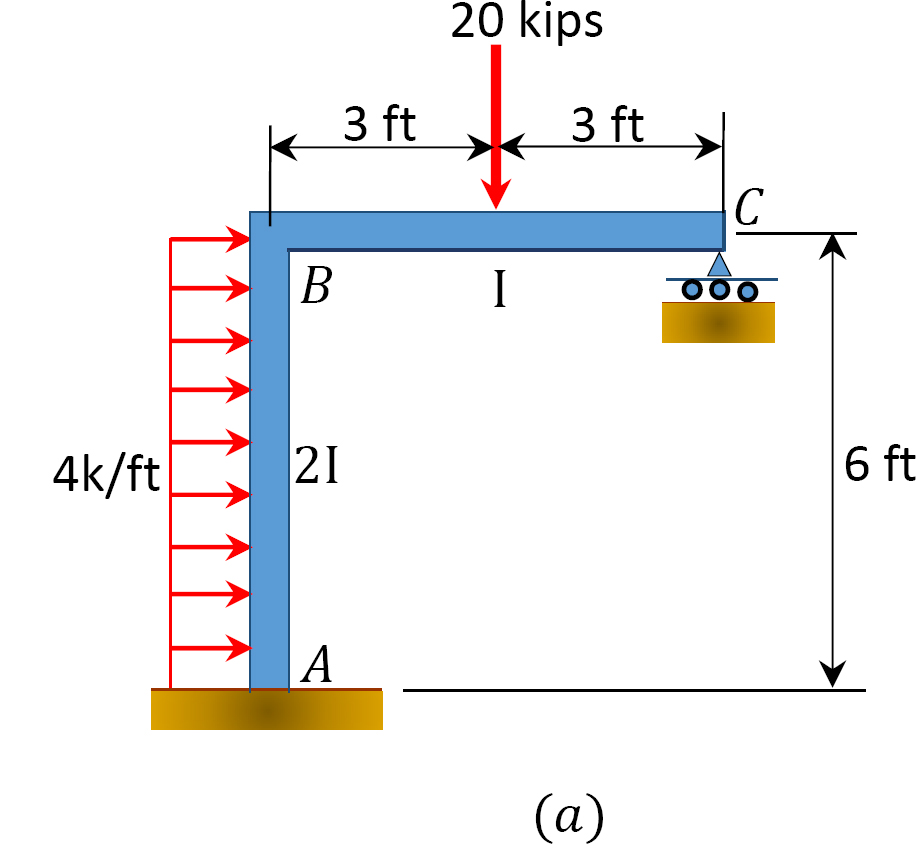
Fig. 12.11. Keret oldalsó lengéssel.
megoldás
rögzített végnyomaték.
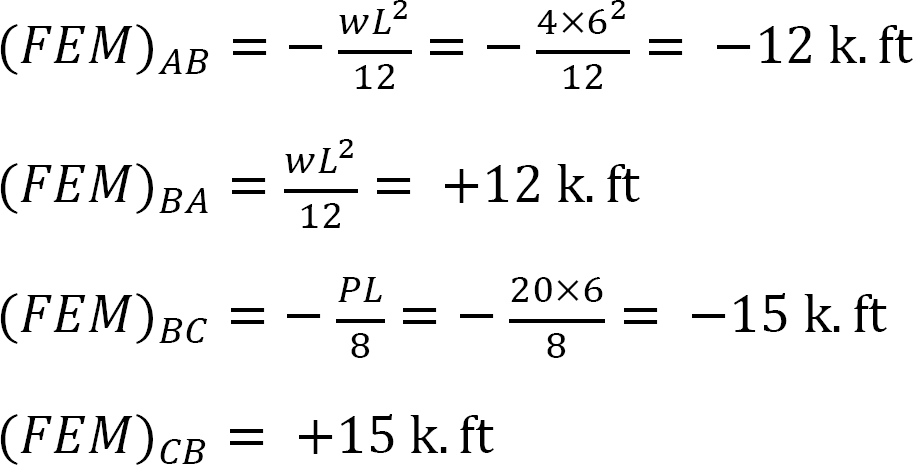
merevségi tényező.
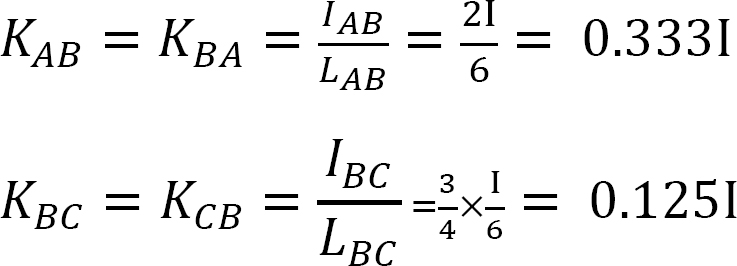
elosztási tényező.
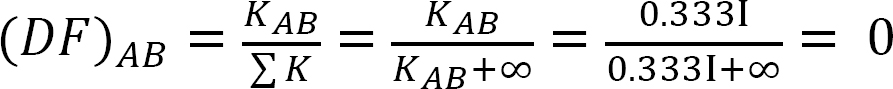

a keret elemzése oldalsó lengés nélkül.
táblázat 12.6. Elosztási táblázat (nincs lengőkeret).
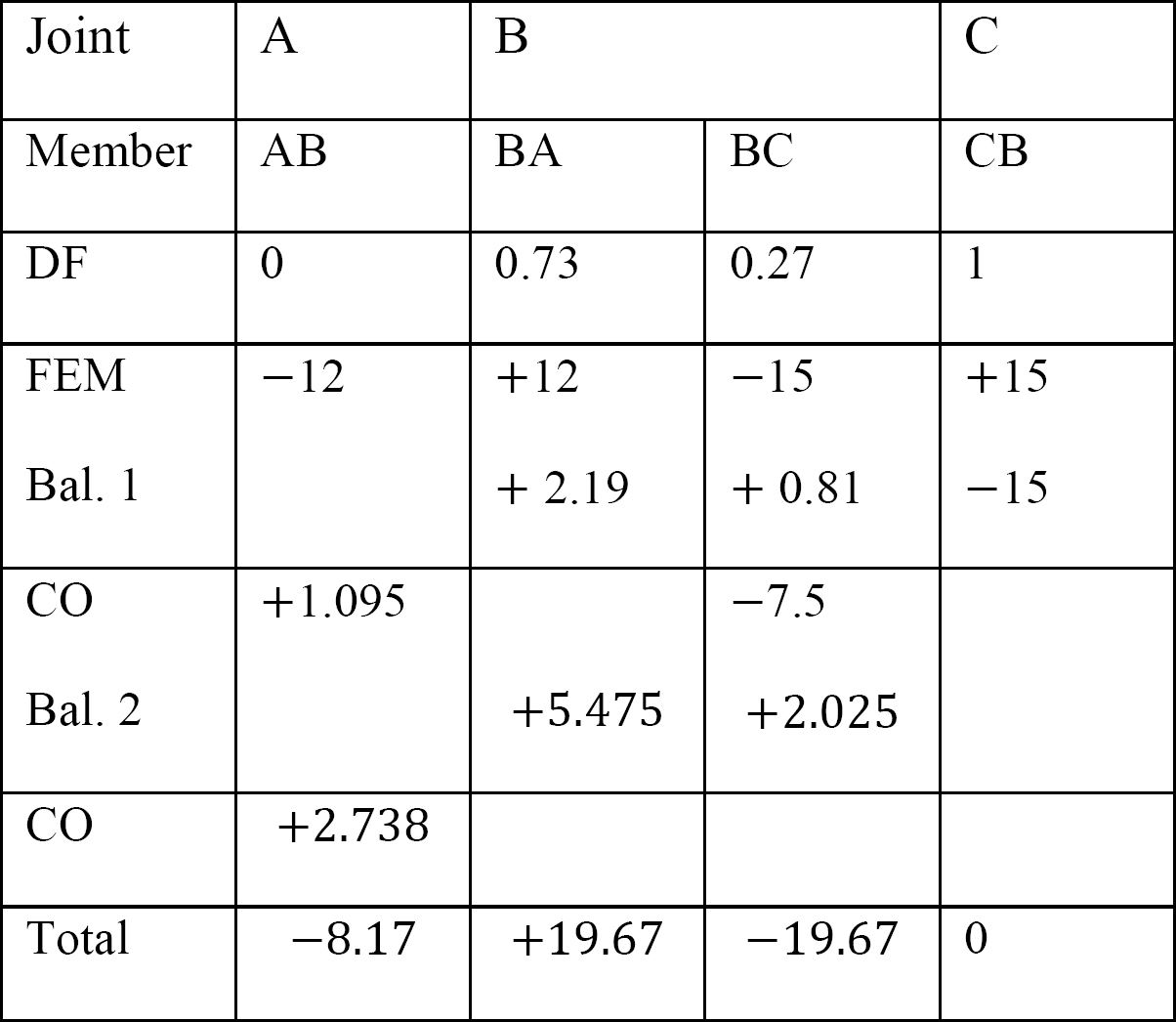
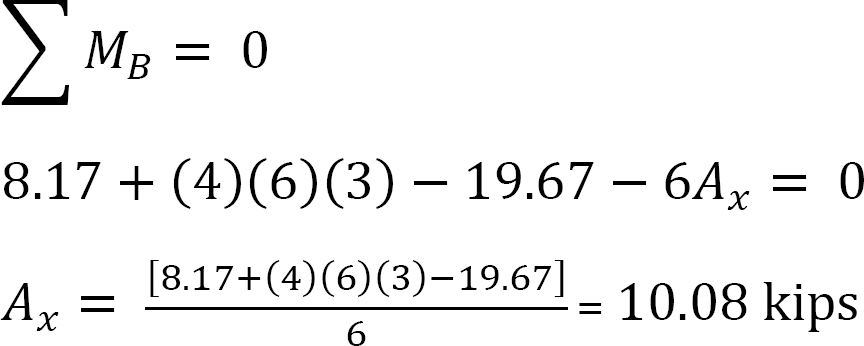
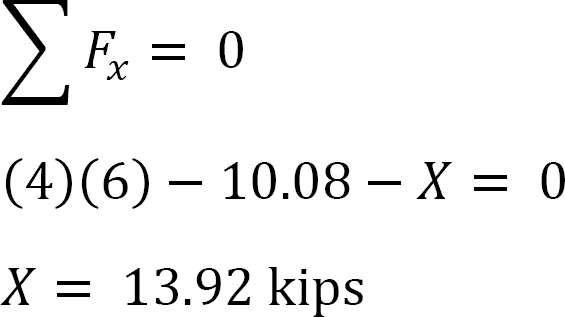
a keret elemzése oldalsó lengéssel.
tegyük fel, hogy MAB = +20 k. ft
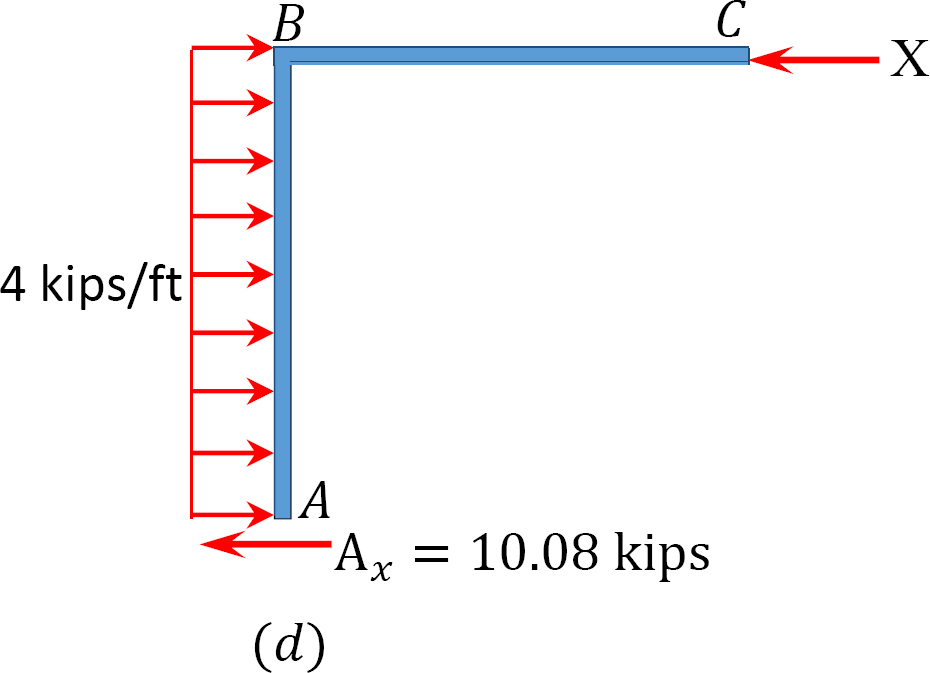
táblázat 12.7. Elosztási táblázat (sway keret).
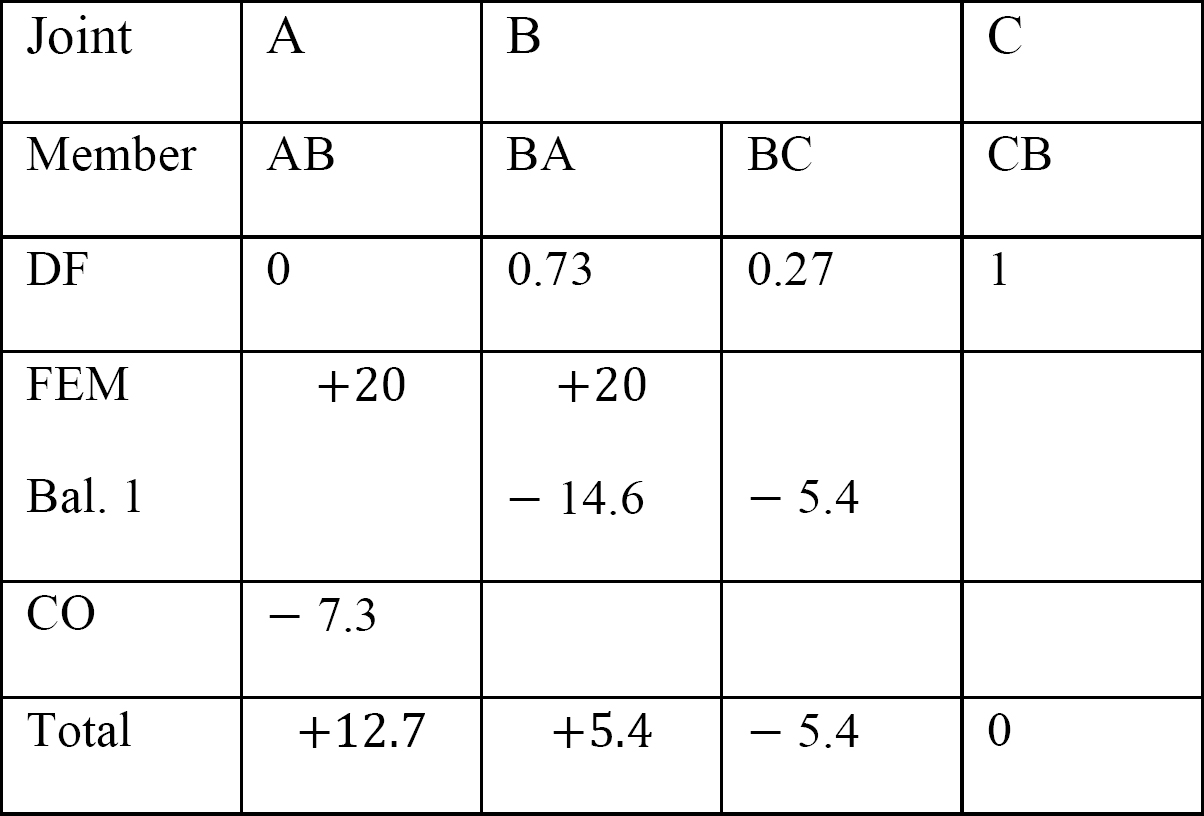
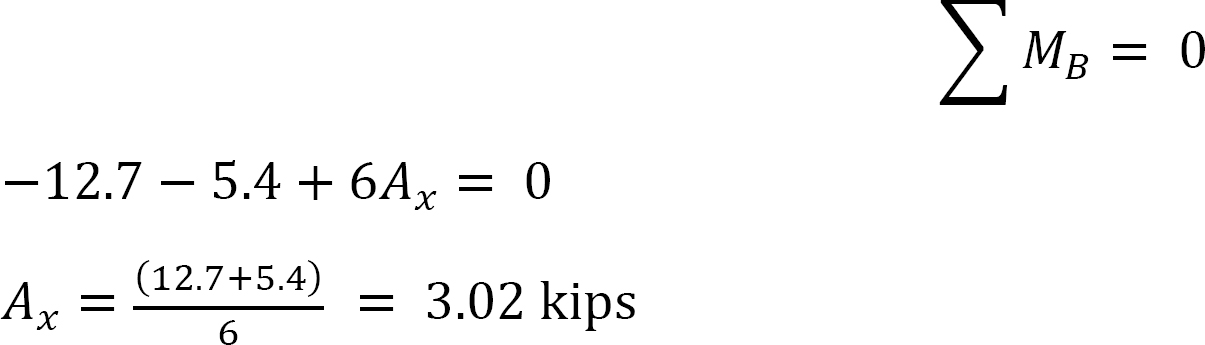
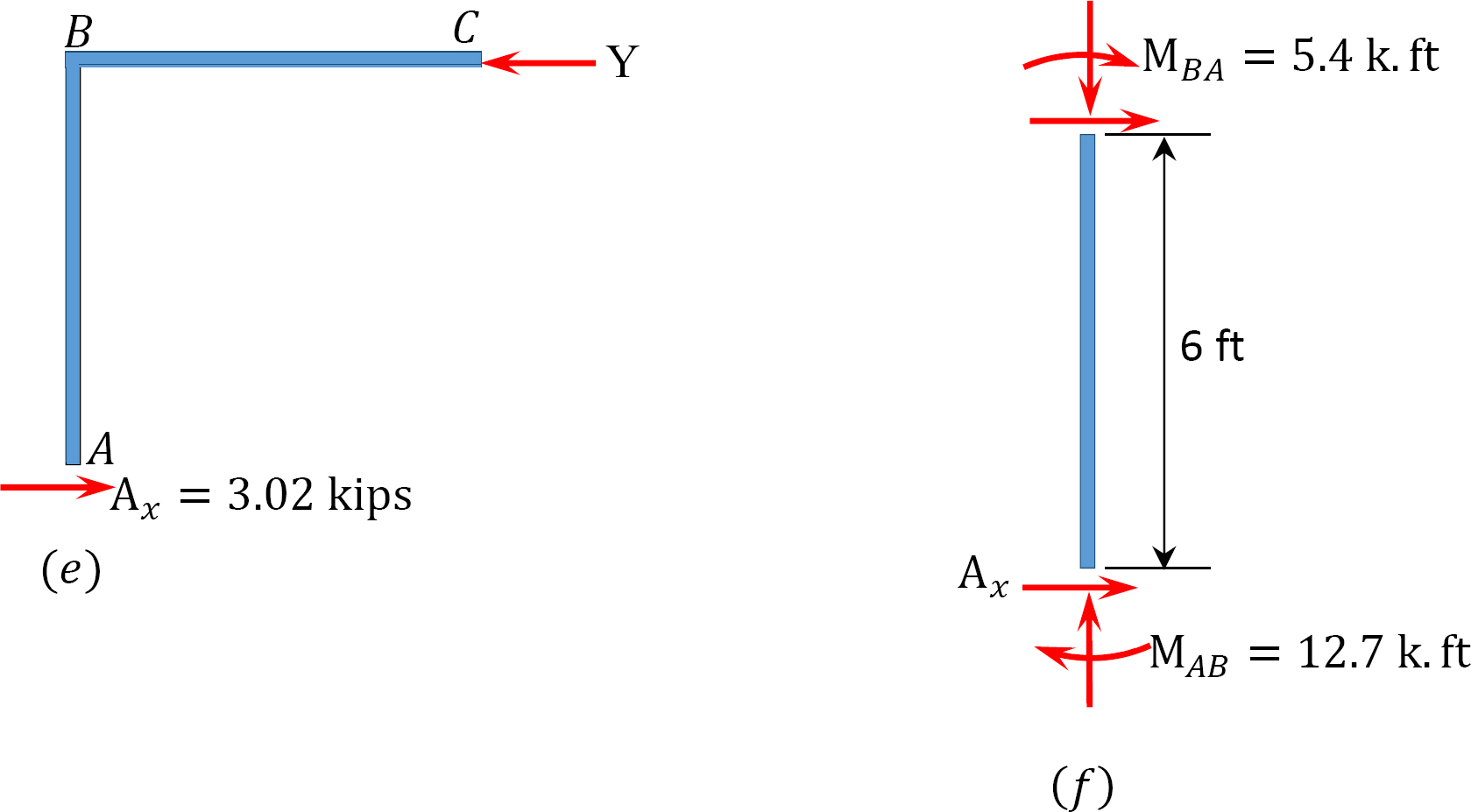
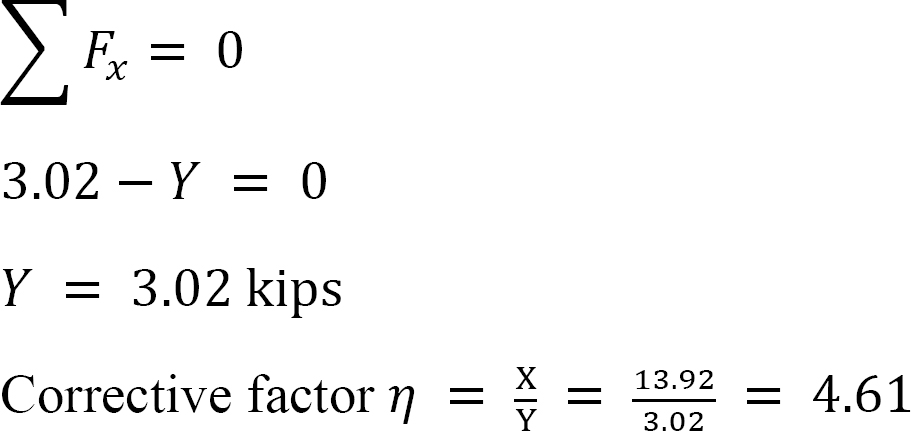
az utolsó pillanatokban.
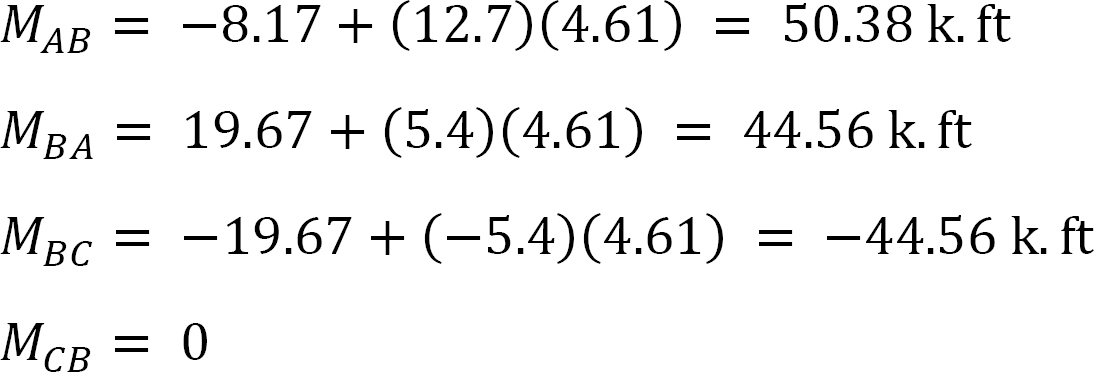
példa 12.7
a lengőkeret betöltése a 12.12 A. ábrán látható módon történik. a momentumelosztási módszerrel határozzuk meg a keret tagjainak végnyomatékait.
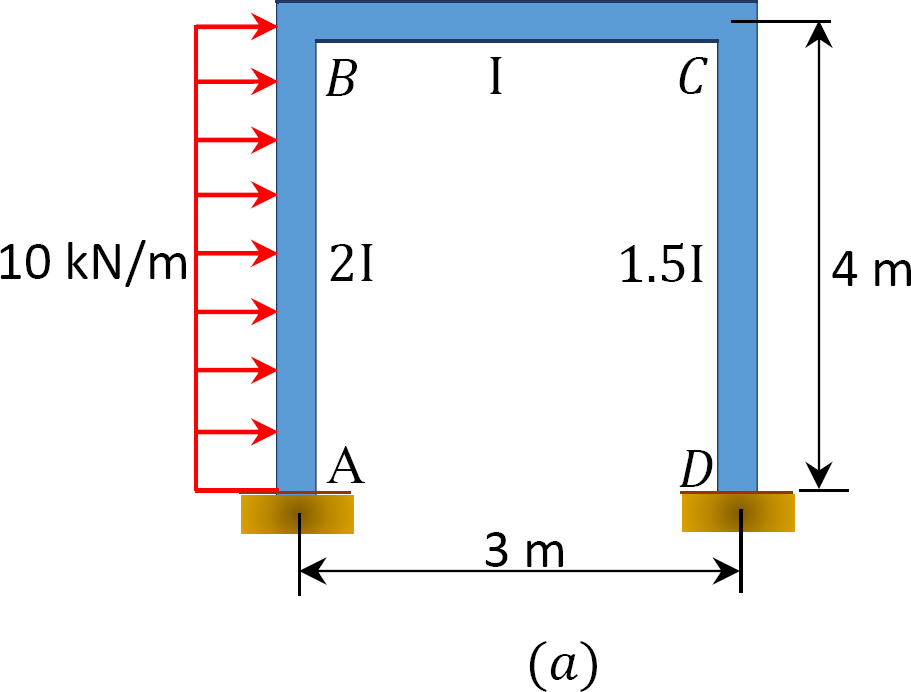
Fig. 12.12. Betöltött sway keret.
megoldás
rögzített végnyomaték.
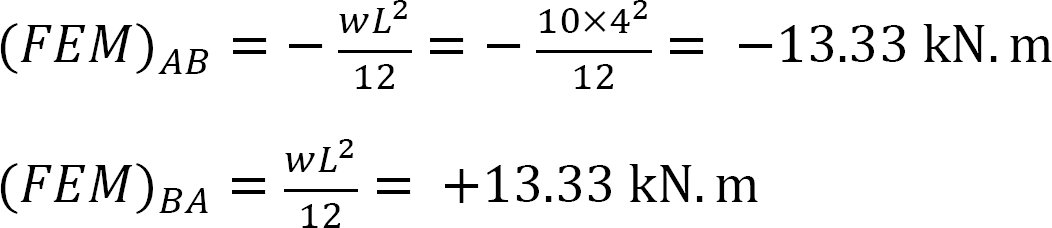
merevségi tényező.
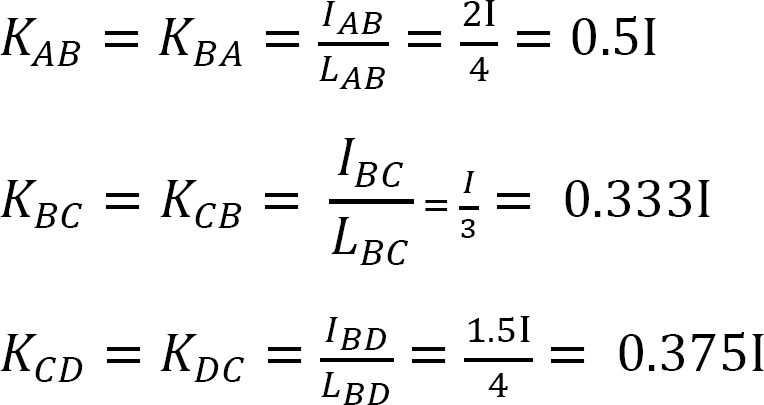
elosztási tényező.

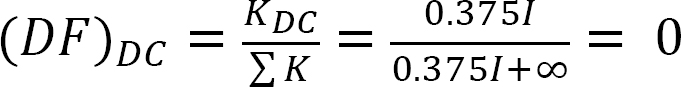
a keret elemzése oldalsó lengés nélkül.
12.8.táblázat. Elosztási táblázat (nincs lengőkeret).
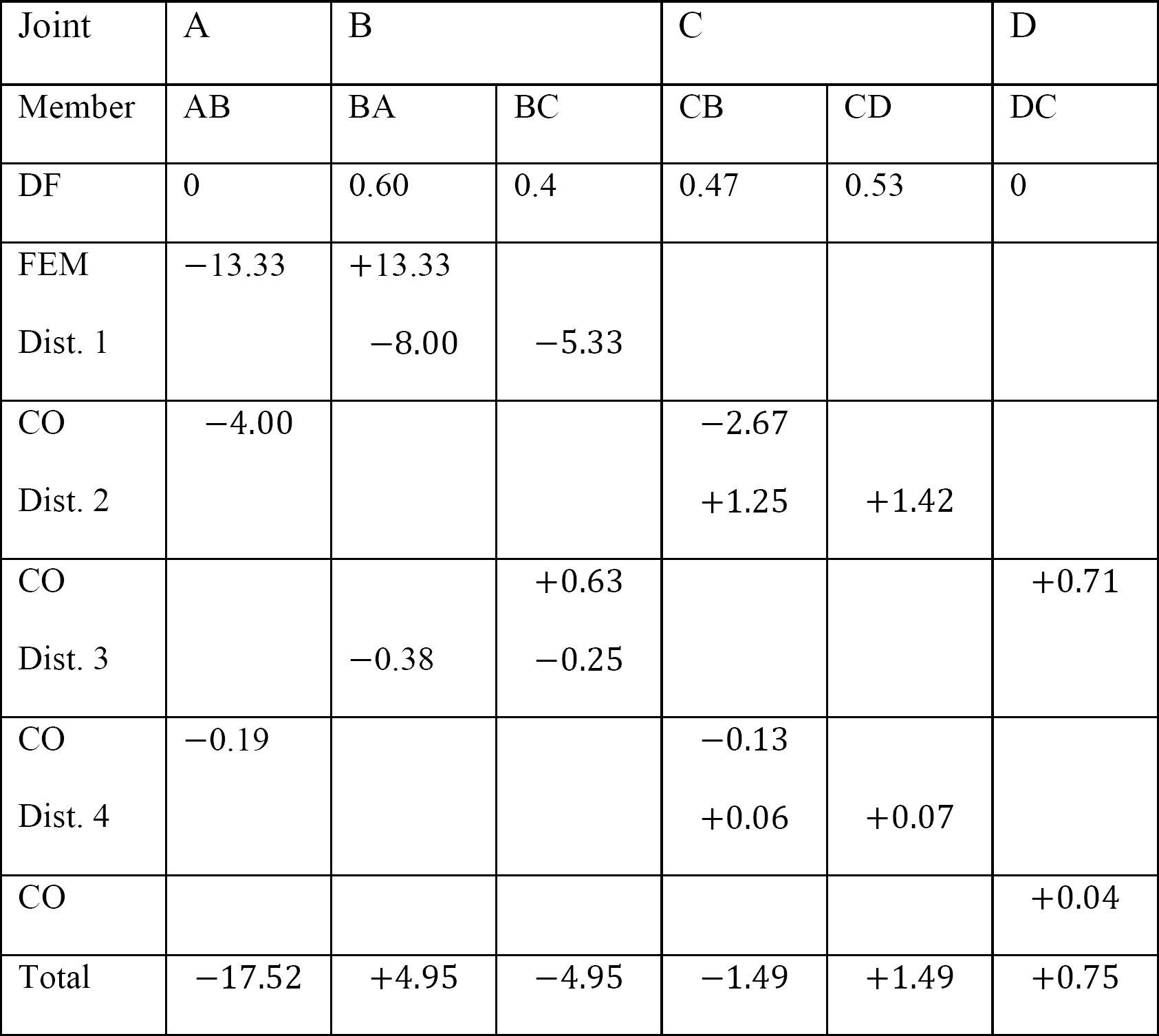
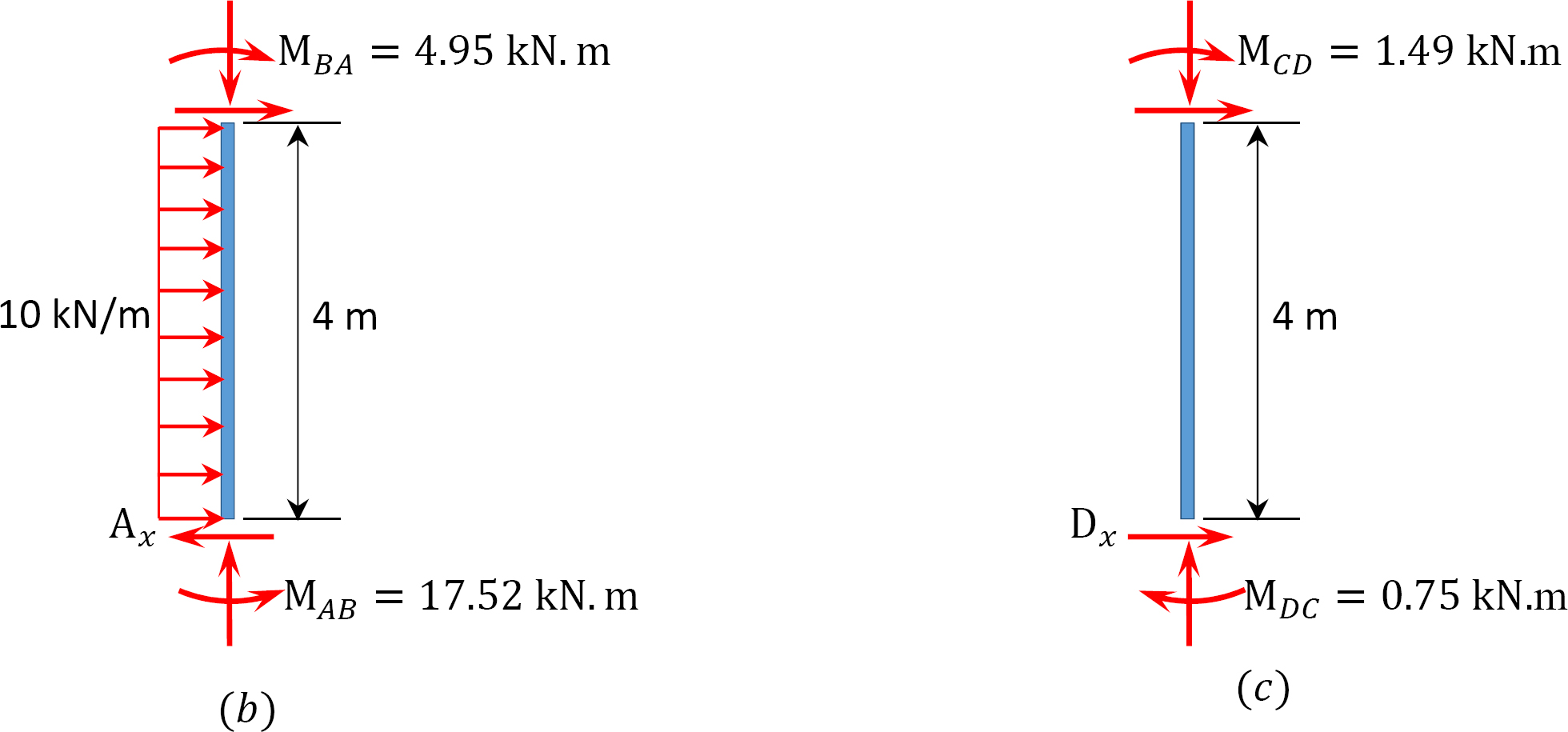
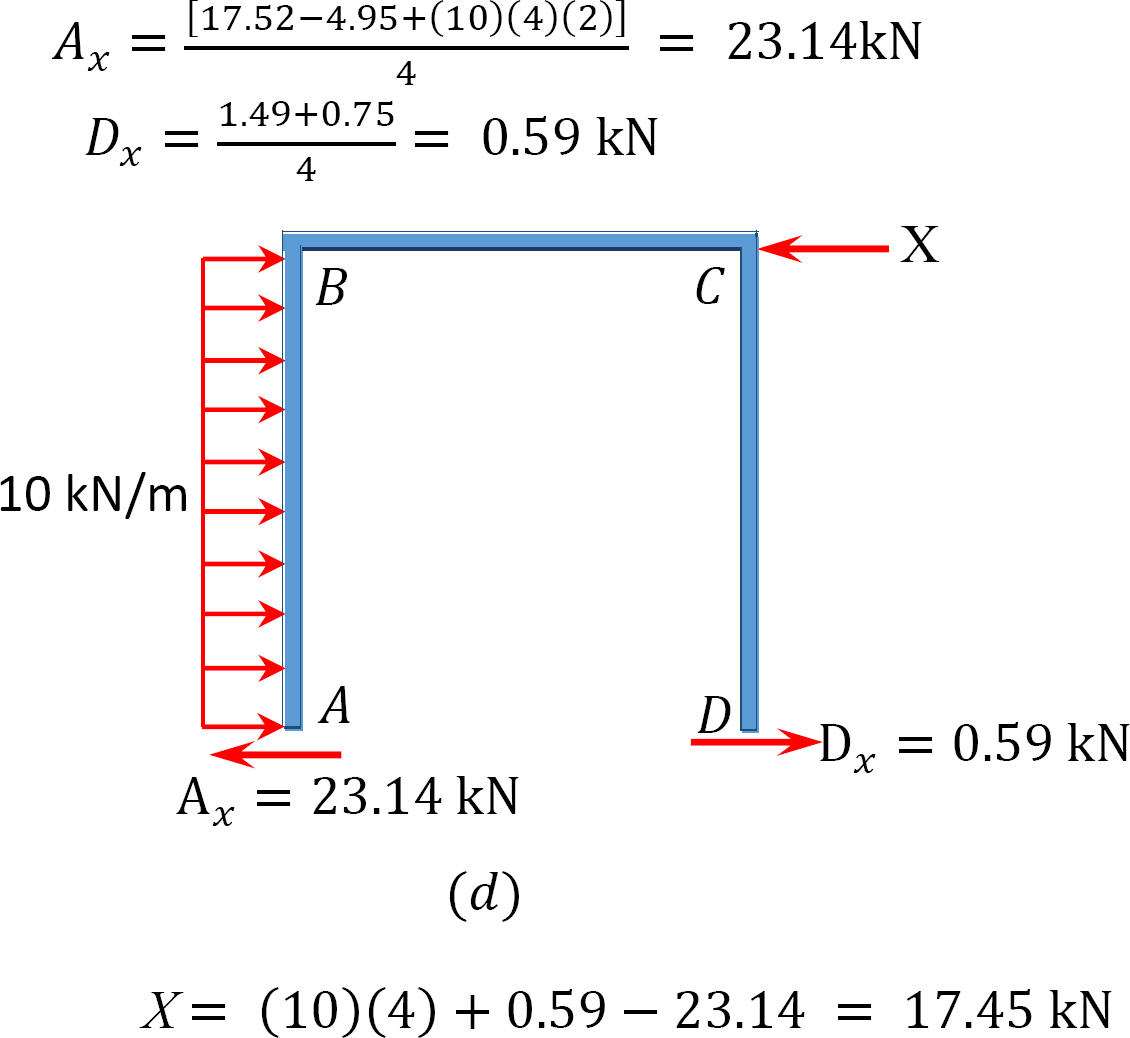
táblázat 12.9. Elosztási táblázat (sway keret).
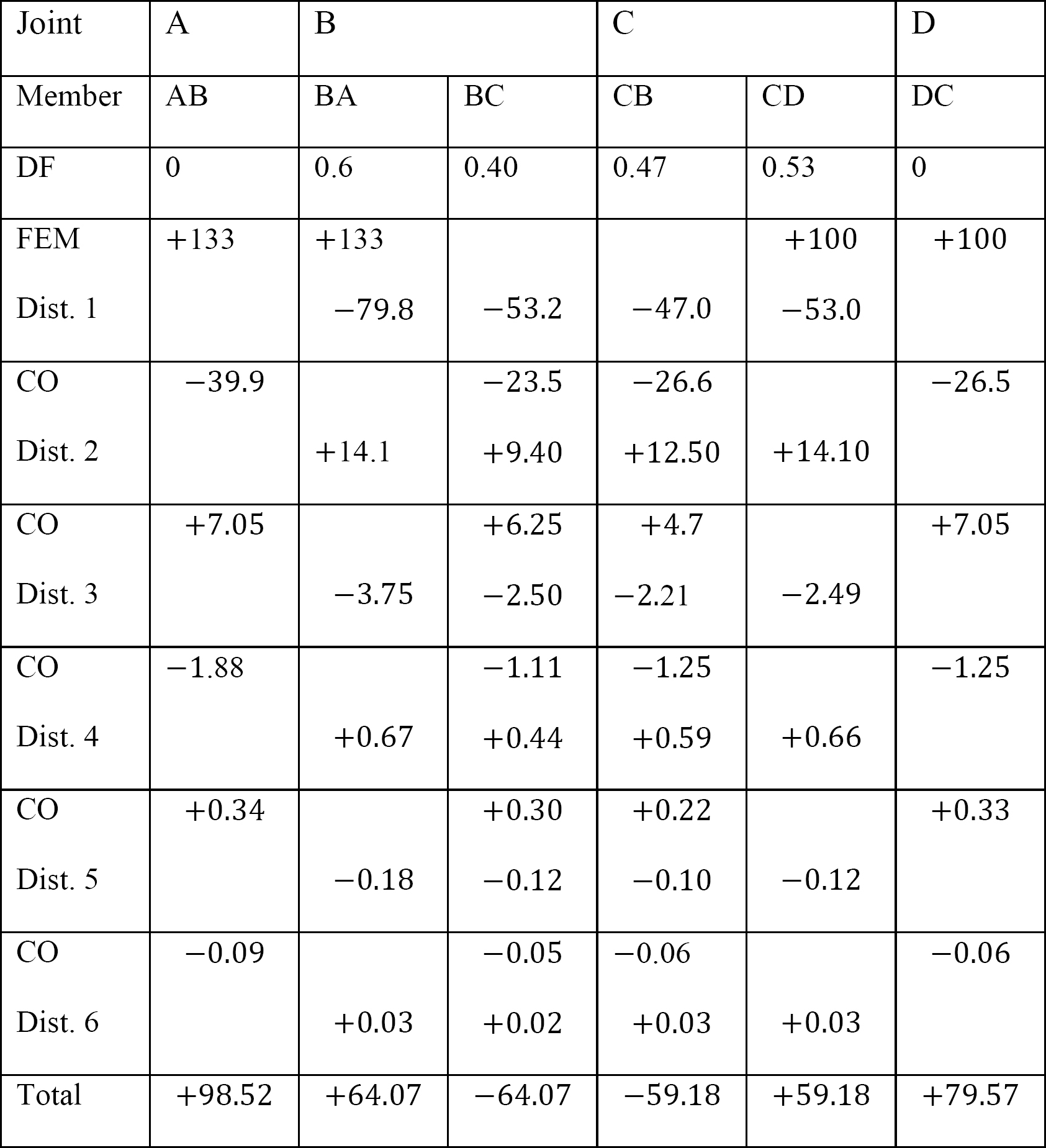
a keret elemzése oldalsó lengéssel.
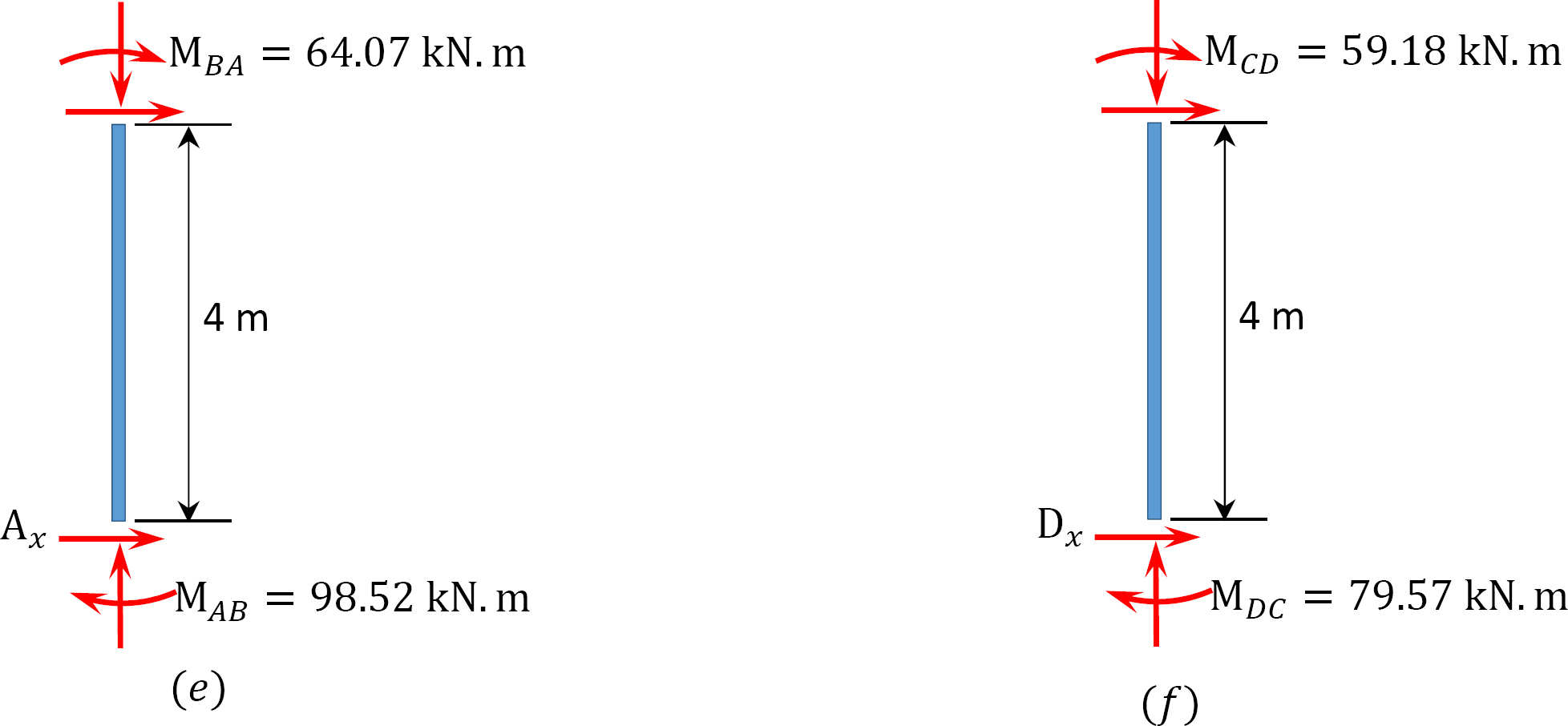

utolsó pillanat.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
fejezet összefoglaló
Moment Eloszlás meghatározatlan struktúrák elemzési módszere: a moment Eloszlás elemzési módszere hozzávetőleges elemzési módszer. Pontossága az iterációk számától függ. Ebben a módszerben azt feltételezzük, hogy a szerkezet összes illesztése ideiglenesen reteszelve vagy rögzítve van, így megakadályozva az esetleges elfordulást. A tagokra terheléseket alkalmaznak, és meghatározzák a tagvégeken a fixitás miatt kialakult pillanatokat. A szerkezet ízületeit ezután egymás után oldják fel, és az egyes ízületeknél a kiegyensúlyozatlan pillanatot elosztják az adott ízületben ülésező tagok között. Meghatározzák a tagok távoli végein lévő pillanatok átvitelét, és az egyensúlyozás folyamatát a kívánt pontossági szintig folytatják. A tagok végső pillanatait a rögzített vég pillanat, az elosztott pillanat és az átvitel pillanat összeadásával határozzuk meg. Miután meghatározták a tagok végső pillanatait, a szerkezet meghatározóvá válik.
Gyakorlati Problémák
12.1 A nyomatékeloszlás módszerével számítsa ki a P12.1-P12.12 ábrán látható gerendák tagjainak végnyomatékát, és rajzolja meg a hajlítónyomaték és a nyíróerő diagramjait. Ei = állandó.
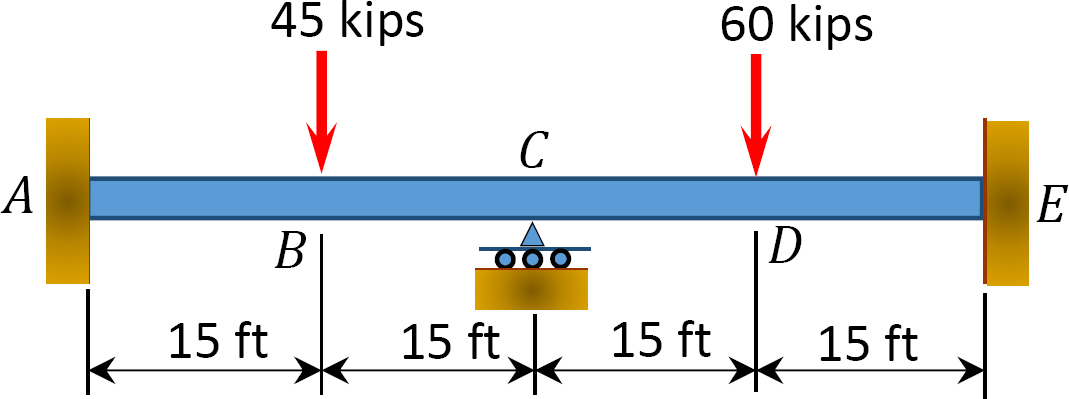
Fig. P12.1. Beam.
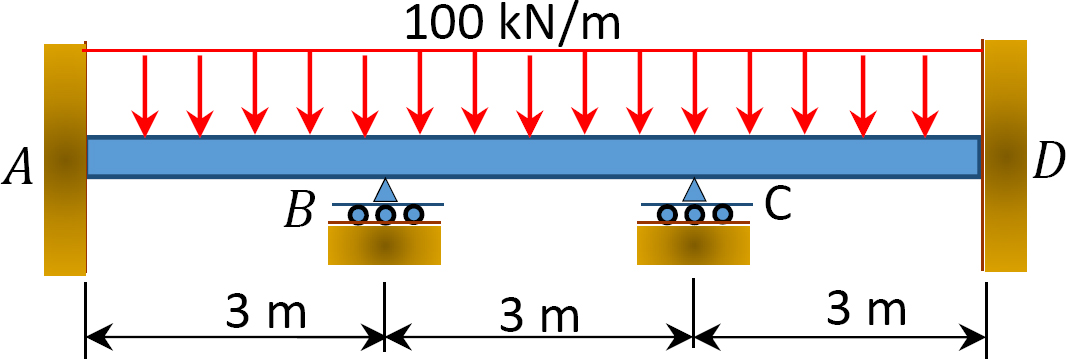
Fig. P12.2. Beam.
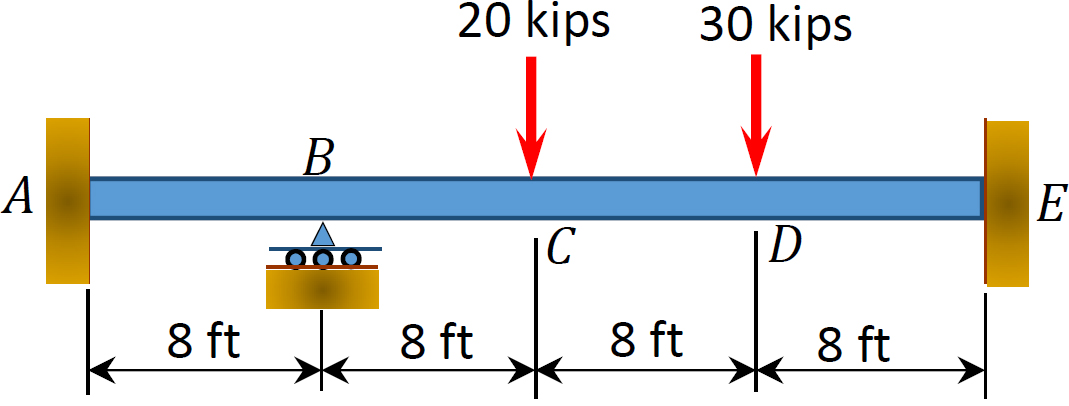
Fig. P12.3. Beam.
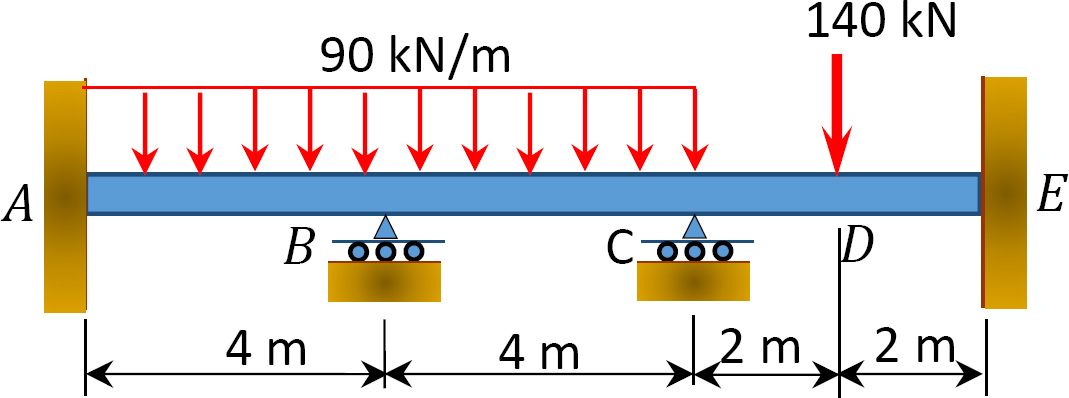
Fig. P12. 4. Beam.
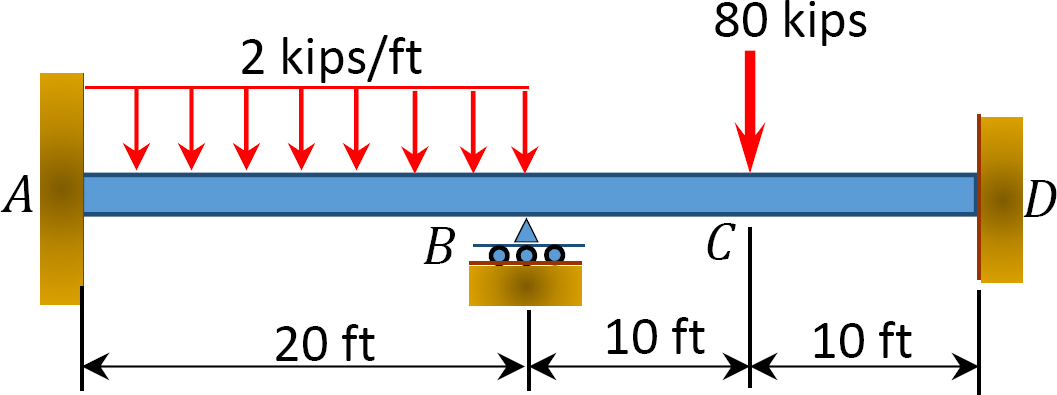
Fig. 12.5. o. Beam.
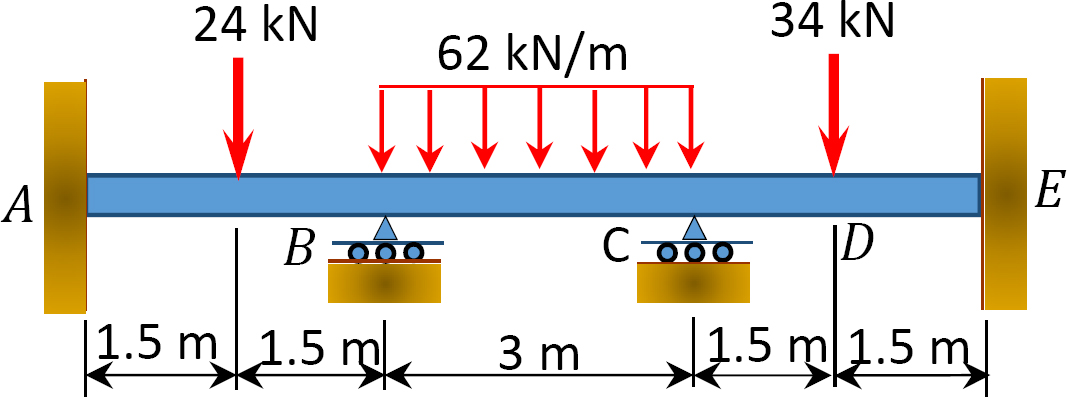
Fig. P12. 6. Beam.
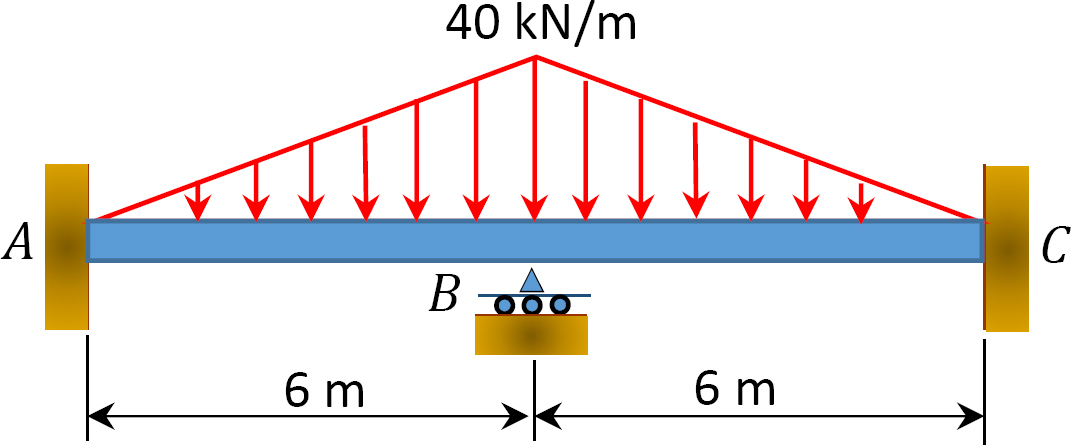
Fig. P12. 7. Beam.
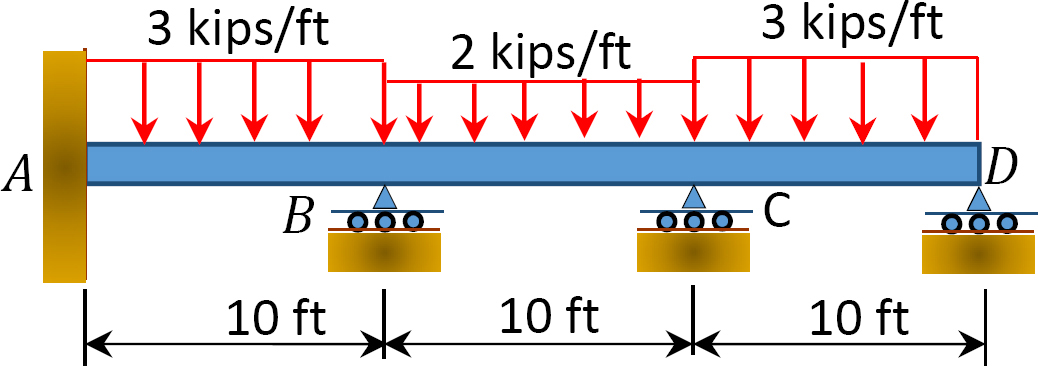
Fig. 12.8. o. Beam.
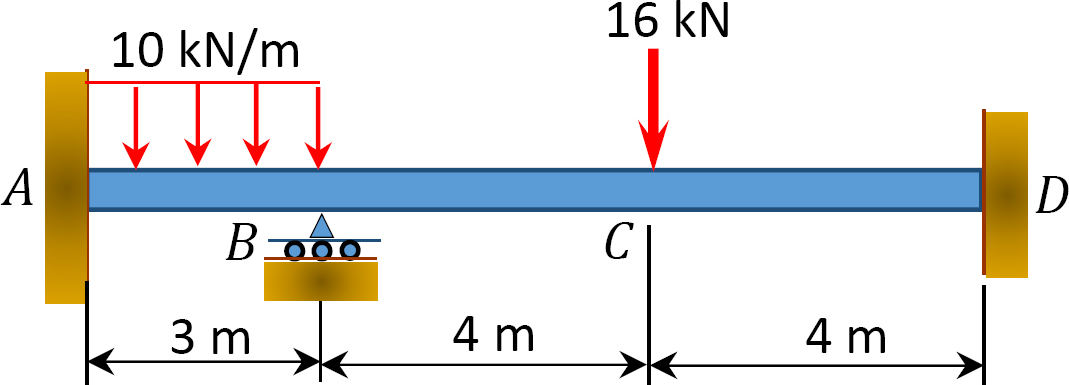
Fig. 12.9. o. Beam.
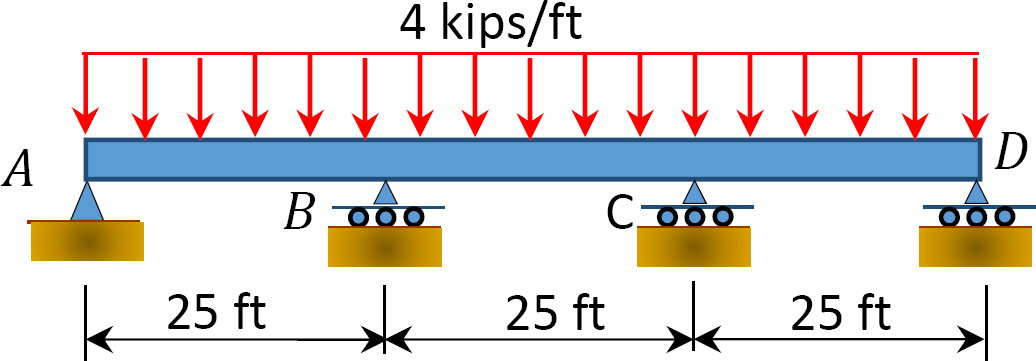
Fig. 12. 10. o. Beam.
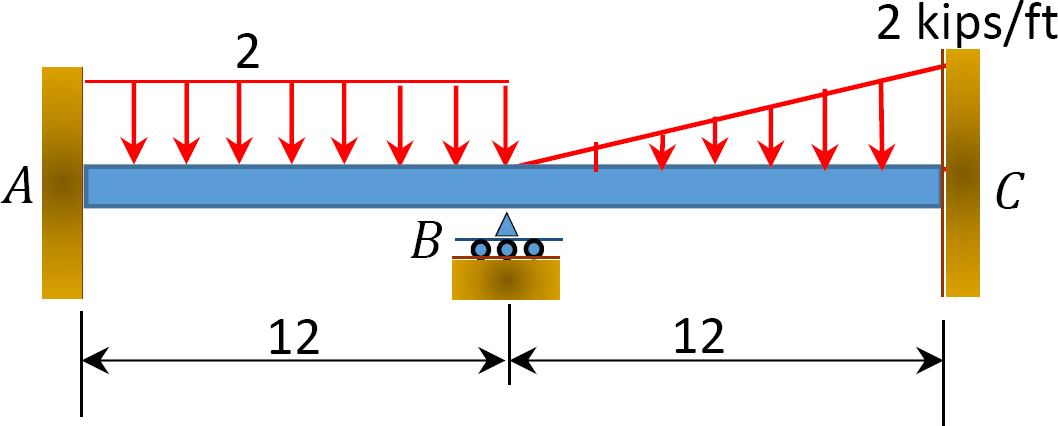
Fig. 12. 11. o. Beam.
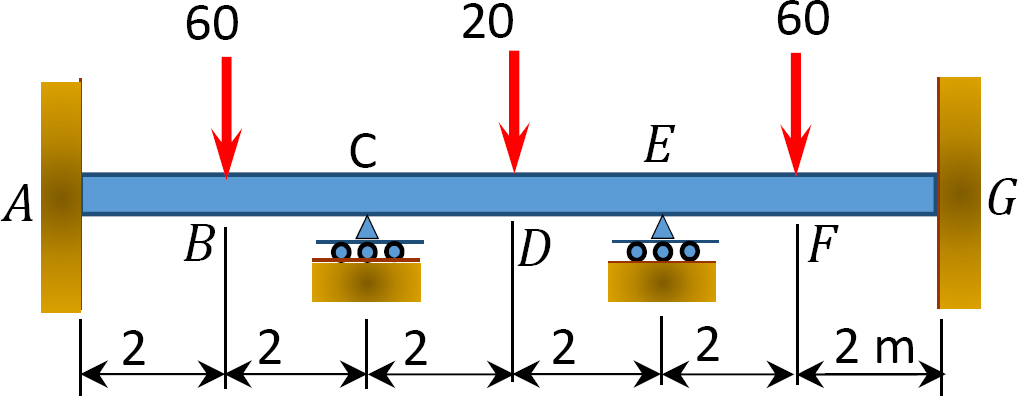
Fig. 12. 12. o. Beam.
12.2 a pillanateloszlás módszerével számítsa ki a P12.13-12.20.ábrán látható keretek tagjainak végnyomatékát, és rajzolja meg a hajlítónyomaték és a nyíróerő diagramjait. Ei = állandó.
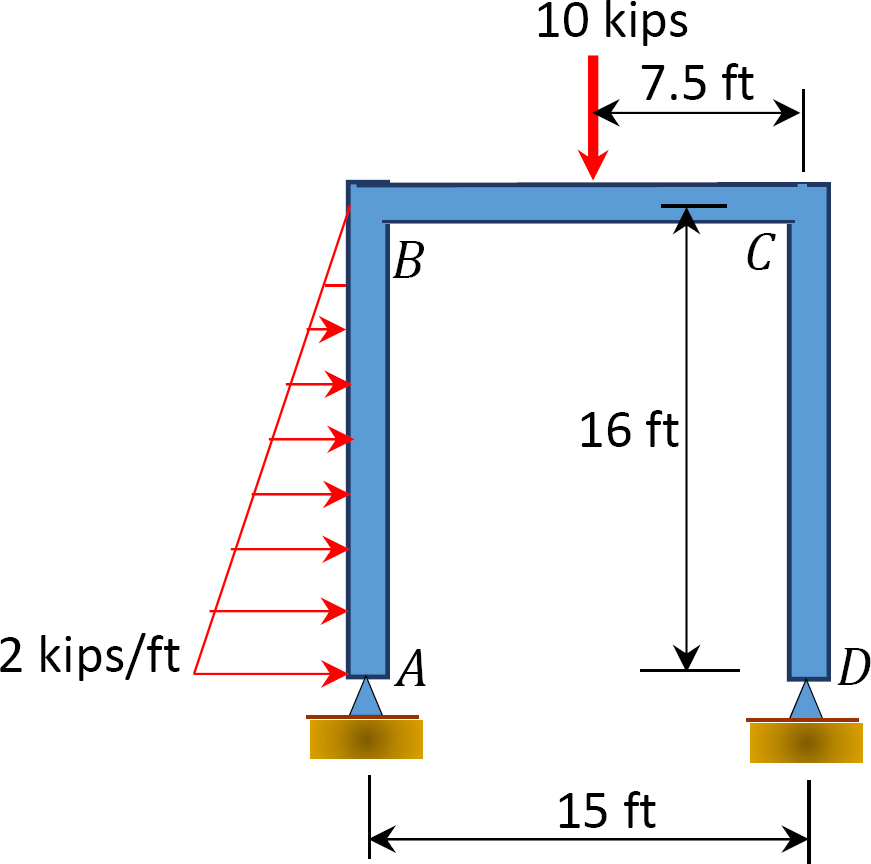
Fig. 12. 13. O. Keret.
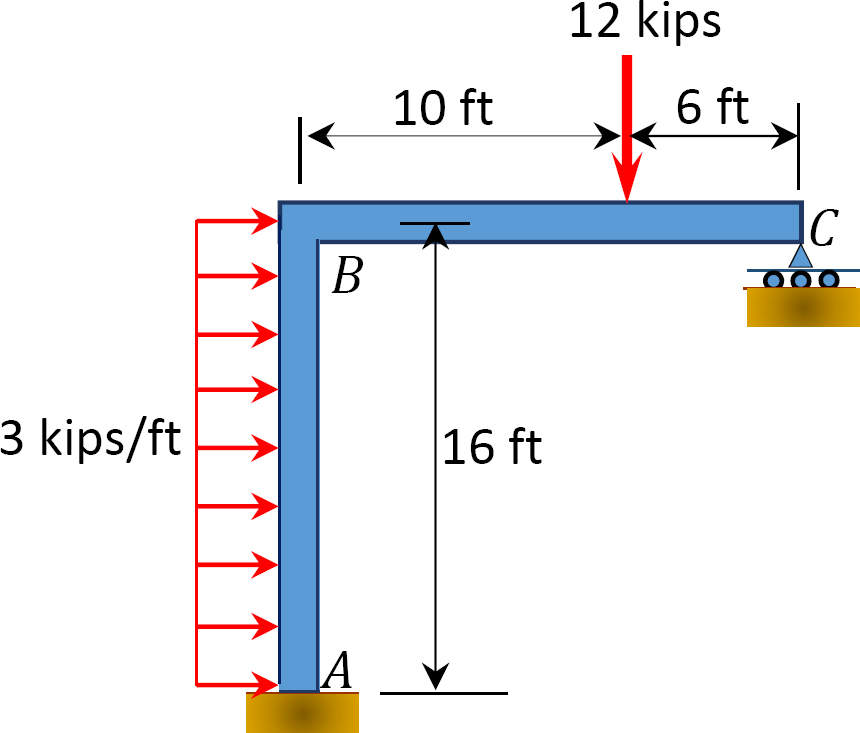
Fig. 12. 14. o. Keret.
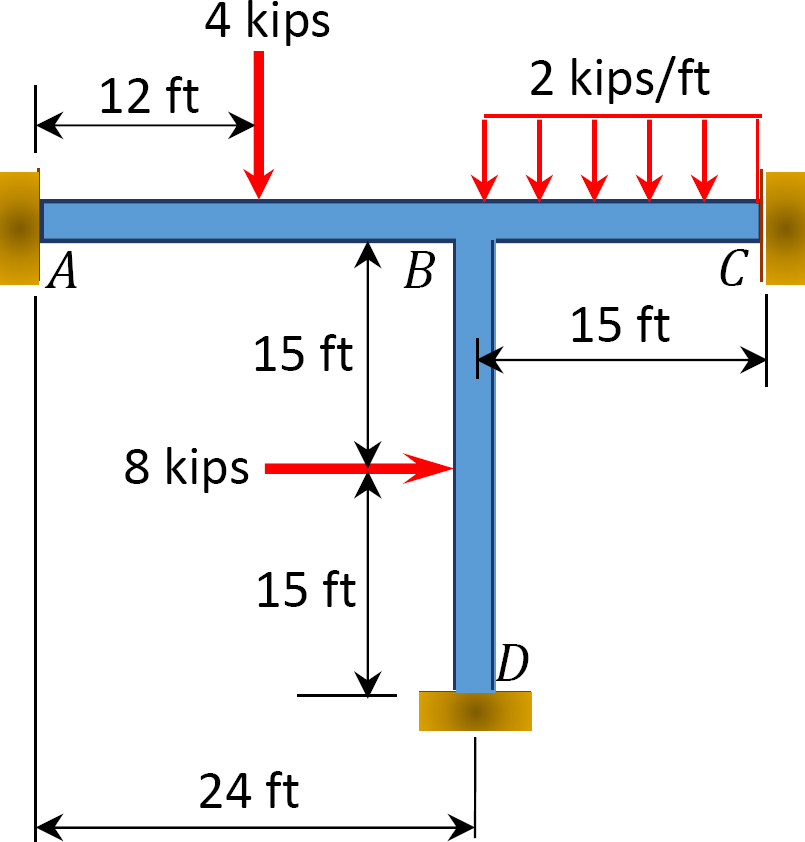
Fig. 12. 15. o. Keret.
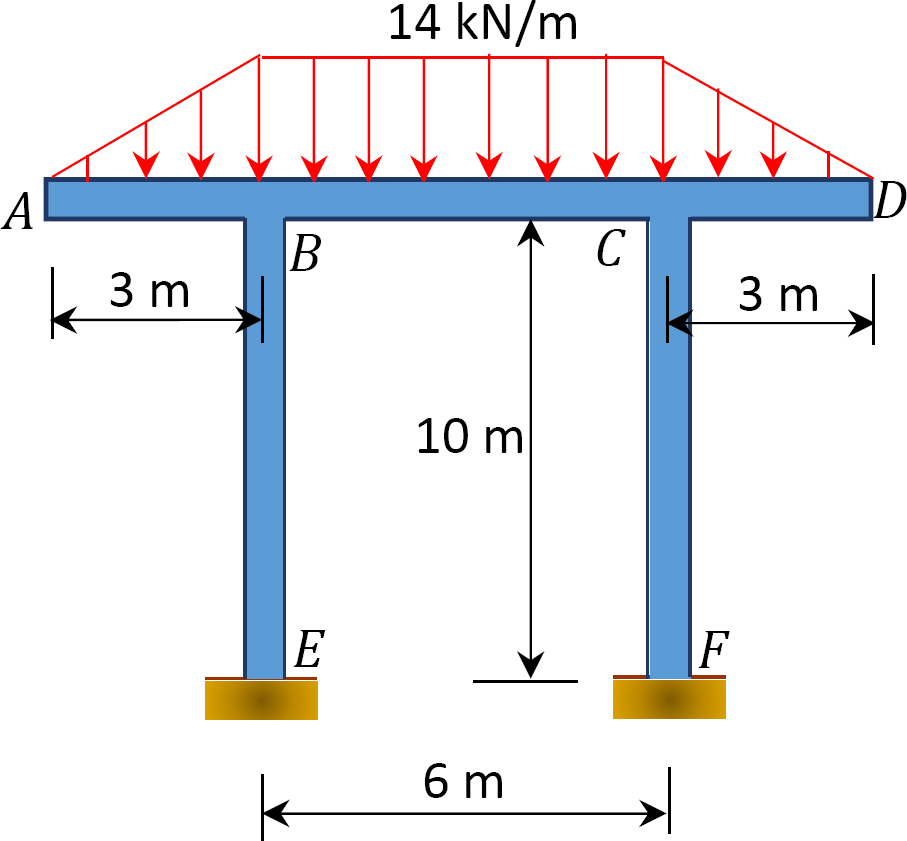
Fig. P12.16. Frame.
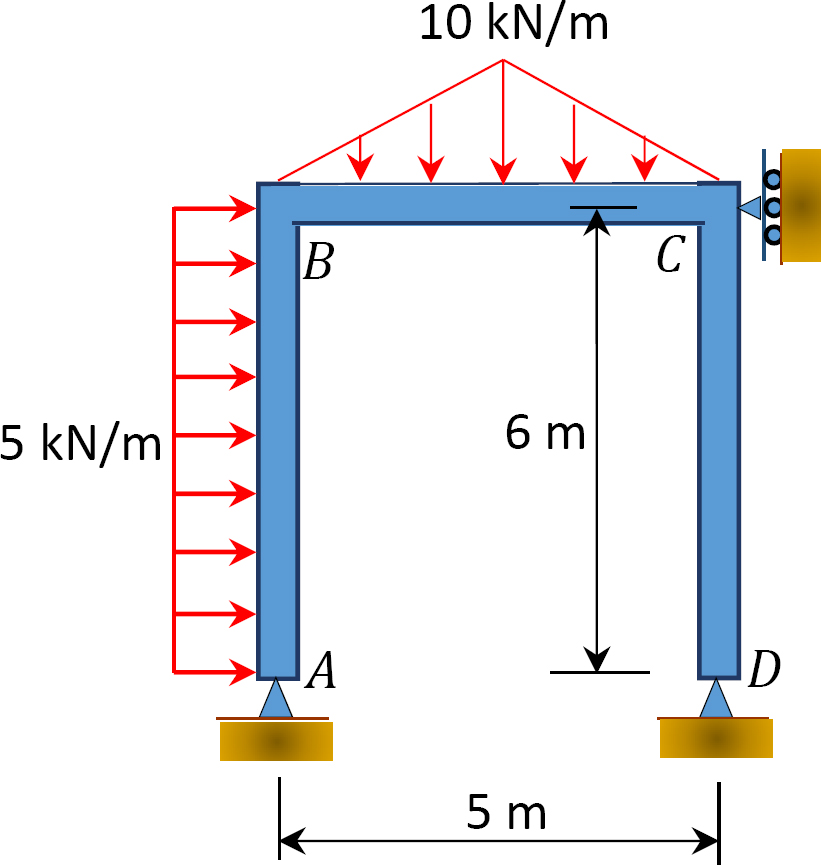
Fig. P12.17. Frame.
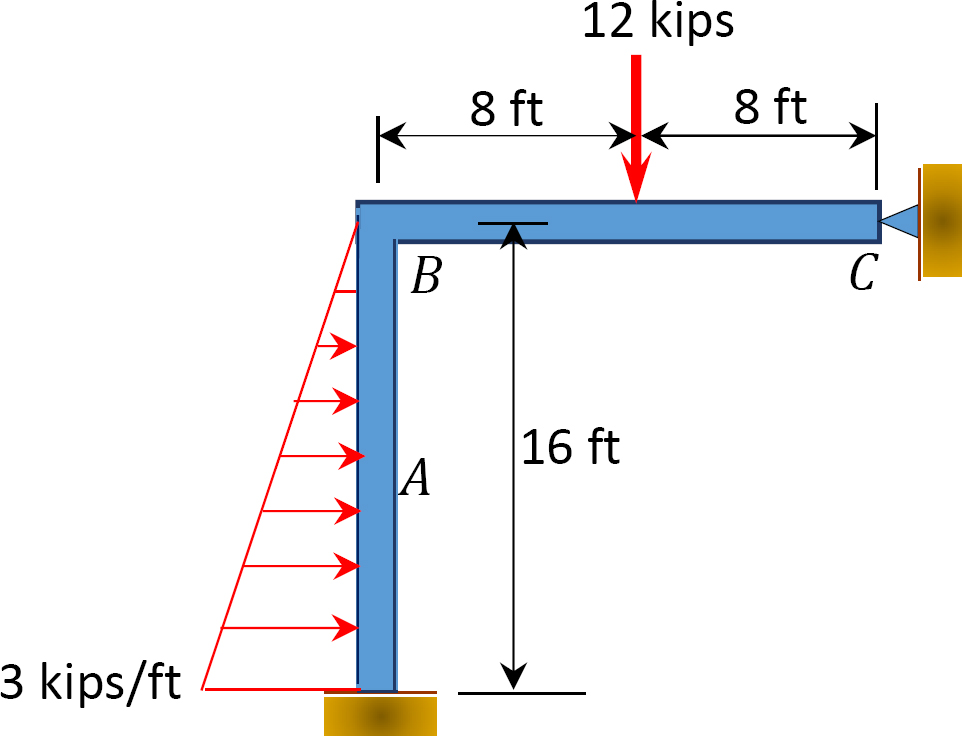
Fig. P12.18. Frame.
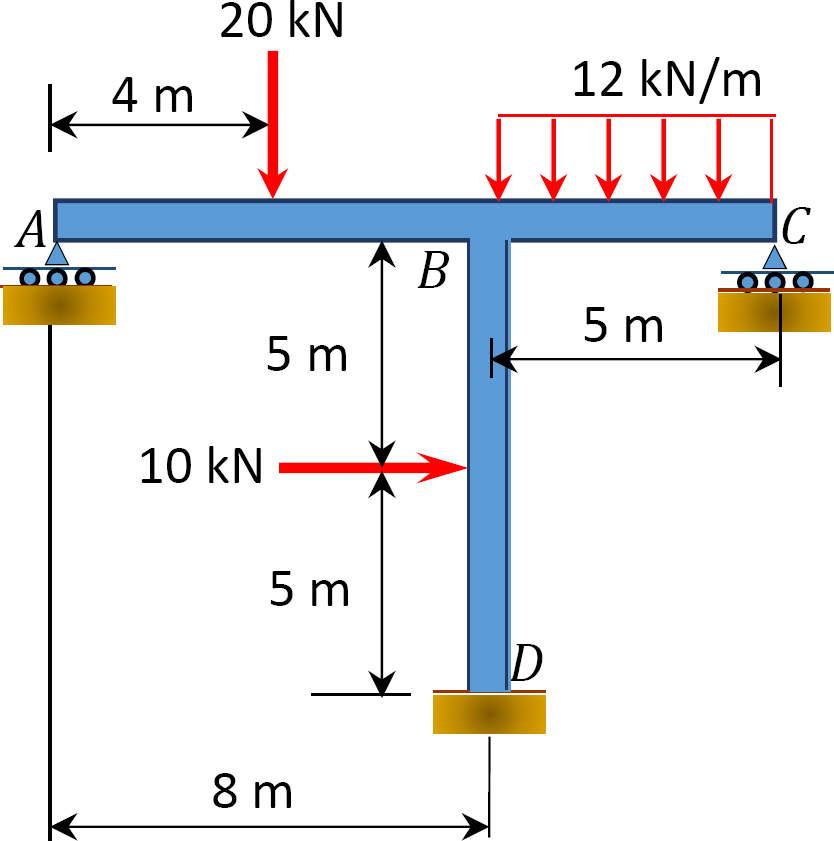
Fig. P12.19. Frame.
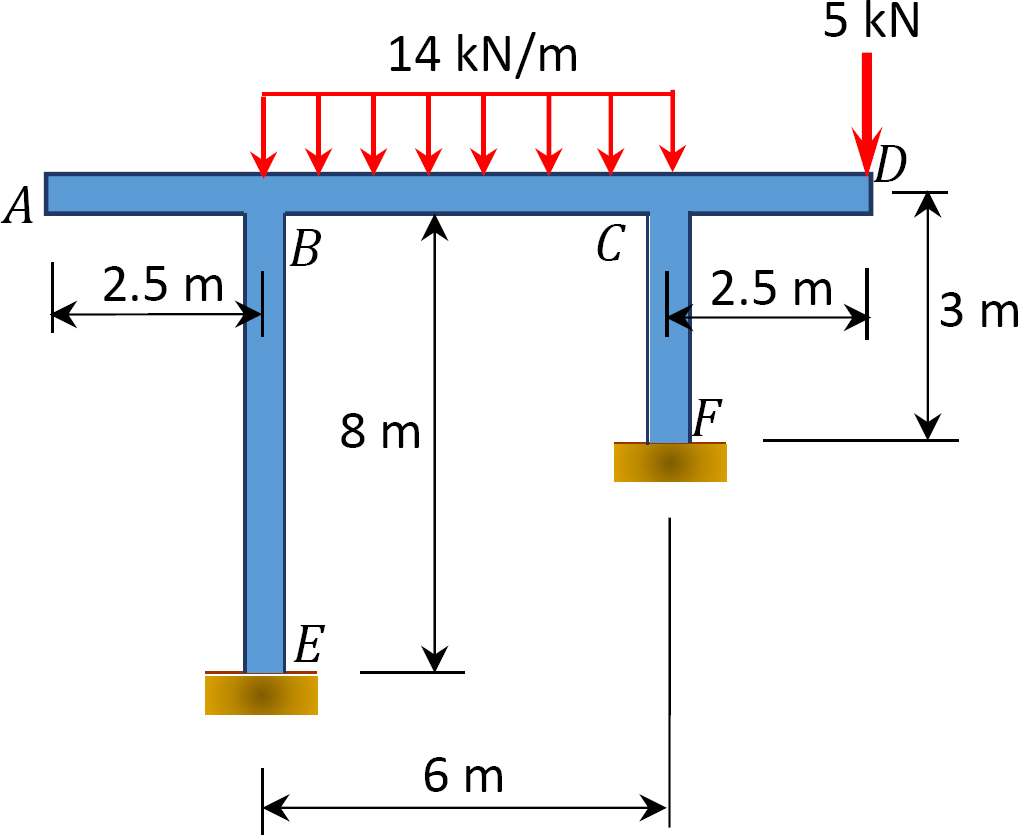
Fig. P12.20. Frame.