![]()
La forma forzata più generale dell’equazione di Duffing è
|
(1)
|
A seconda dei parametri scelti, l’equazione può assumere una serie di forme speciali. Ad esempio, senza smorzamento e senza forzatura, ![]() e prendendo il segno più, l’equazione diventa
e prendendo il segno più, l’equazione diventa
|
(2)
|
(Bender e Orszag 1978, p. 547; Zwillinger 1997, p.122). Questa equazione può visualizzare un comportamento caotico. Per ![]() , l’equazione rappresenta una “molla dura” e per
, l’equazione rappresenta una “molla dura” e per ![]() , rappresenta una “molla morbida.”Se
, rappresenta una “molla morbida.”Se ![]() , le curve di ritratto di fase sono chiuse.
, le curve di ritratto di fase sono chiuse.
Se invece prendiamo ![]() ,
, ![]() , reimpostare l’orologio in modo che
, reimpostare l’orologio in modo che ![]() , e utilizzare il segno meno, l’equazione è quindi
, e utilizzare il segno meno, l’equazione è quindi
|
(3)
|
Questo può essere scritto come un sistema di equazioni differenziali ordinarie del primo ordine come
|
(4)
|
|||
|
(5)
|
(Wiggins, 1990, p. 5) che, in unforced caso, si riduce a
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, p. 6; Ott 1993, p. 3).
I punti fissi di questo insieme di equazioni differenziali accoppiate sono dati da
|
(8)
|
quindi ![]() , e
, e
|
(9)
|
|||
|
(10)
|
mi ![]() . I punti fissi sono quindi
. I punti fissi sono quindi ![]() ,
, ![]() , e
, e ![]() .
.
Analisi della stabilità dei punti fissi può essere punto linearizzando le equazioni. Differenziare dà
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
che può essere scritto come equazione della matrice
|
(14)
|
Esame della stabilità del punto (0,0):
|
(15)
|
|
(16)
|
Ma ![]() , quindi
, quindi ![]() è reale. Poiché
è reale. Poiché ![]() , ci sarà sempre una radice positiva, quindi questo punto fisso è instabile. Ora guarda (
, ci sarà sempre una radice positiva, quindi questo punto fisso è instabile. Ora guarda (![]() , 0). L’equazione caratteristica è
, 0). L’equazione caratteristica è
|
(17)
|
che ha radici
|
(18)
|
Per ![]() ,
, ![]() , quindi il punto è asintoticamente stabile. Se
, quindi il punto è asintoticamente stabile. Se ![]() ,
, ![]() , quindi il punto è linearmente stabile (Wiggins 1990, p. 10). Tuttavia, se
, quindi il punto è linearmente stabile (Wiggins 1990, p. 10). Tuttavia, se ![]() , il radicale dà una parte immaginaria e la parte reale è
, il radicale dà una parte immaginaria e la parte reale è ![]() , quindi il punto è instabile. Se
, quindi il punto è instabile. Se ![]() ,
, ![]() , che ha una radice reale positiva, quindi il punto è instabile. Se
, che ha una radice reale positiva, quindi il punto è instabile. Se ![]() , allora
, allora ![]() , quindi entrambe le radici sono positive e il punto è instabile.
, quindi entrambe le radici sono positive e il punto è instabile.
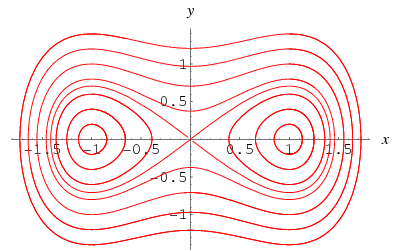
È interessante notare che il caso speciale ![]() senza forzatura,
senza forzatura,
|
(19)
|
|||
|
(20)
|
può essere integrato da quadrature. Differenziare (19) e pluggingin (20) dà
|
(21)
|
Moltiplicando entrambi i lati per ![]() dà
dà
|
(22)
|
Ma questo può essere scritto
|
(23)
|
quindi abbiamo un invariante di movimento ![]() ,
,
|
(24)
|
Risolvere per ![]() dà
dà
|
(25)
|
|
(26)
|
so
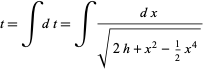 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
quindi le equazioni dell’oscillatore Duffing sono date dall’Hamiltoniansistema