Legge di Metcalfe 101

La spiegazione tldr della legge di Metcalfe è che man mano che le reti diventano più grandi, crescono di valore molto più grandi e più velocemente della base di utenti. Voglio andare un livello più profondo e fornire una spiegazione usando una semplice matematica.

Prima di tutto, aiuta a pensare alla legge di Metcalfe come un quadro su come pensare al valore di una rete. Proprio come in Econ 101, si impara a conoscere l’offerta e la domanda in perfetta concorrenza (niente è perfetto), si dovrebbe trattare questo come un modello per pensare al valore della rete e non un’equazione che è possibile utilizzare direttamente dalla scatola nella vita reale.

Ecco alcune ipotesi di base per semplificare il modello:

• Pensa a questo esempio come a una rete di comunicazione (ad es. telefoni o fax)
• Il valore della rete è semplicemente misurato dal numero di connessioni che puoi effettuare
• Il valore di ogni connessione è lo stesso

Usiamo l’esempio dei fax. L’idea semplice è che se più dei miei amici hanno fax, possiamo tutti fax ogni altra roba e tutti noi ottenere valore da questo.

Quindi, contiamo il numero di possibili connessioni tra le macchine fax:

Ecco alcuni esempi illustrativi:

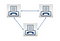
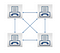
Se vuoi continuare a ripetere questo, si finisce con una tabella come questa:

Avrei potuto andare avanti ma mi sono fermato a 15 perché è chiaro che il numero di possibili connessioni sta crescendo molto più velocemente del numero di fax. La relazione tra il numero nella colonna 1 e la colonna 2 risulta essere:

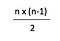
Quindi se testiamo questo usando 15 dalla tabella sopra, dovremmo ottenere 105:

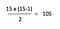
Quindi, come si passa dall’equazione sopra a “n^2”? Bene, la legge afferma che il valore della rete è “proporzionale a n ^2”. Il modo più semplice per pensarci è che man mano che n diventa più grande, non c’è molta differenza tra e .

Quindi è davvero così.

Una volta compreso il framework, possiamo quindi iniziare a farlo a pezzi: P

“Cosa succede se possiedo uno dei due fax nel mondo e l’altro è di proprietà del mio acerrimo nemico e non ottengo alcun valore da quella connessione?”

” Cosa succede se più persone si uniscono alla rete, più il mio sistema di comunicazione sembra essere inquinato?”

” Se uso questo framework per cercare di capire il valore monetizzabile (o enterprise value) di una rete, sto confondendo due cose molto diverse?”

” Come funziona questo modello quando lo applico ai social network e non ai fax?”