ダッフィング方程式の最も一般的な強制形式は次のとおりです
 |
(1)
|
選択されたパラメータに応じて、方程式はいくつかの特別な形式を取ることができます。 たとえば、減衰がなく強制がない場合、
となり、プラス記号を取ると、方程式は次のようになります
 |
(2)
|
(ＢｅｎｄｅｒおよびＯｒｓｚａｇ１ ９ ７ ８，ｐ． この方程式は、カオス的な挙動を示すことができます。 
の場合、式は「硬ばね」を表し、
の場合、「軟ばね」を表します。”
の場合、位相曲線は閉じています。
代わりに
、
を取る場合、クロックをリセットして
となり、マイナス記号を使用すると、式は次のようになります
 |
(3)
|
これは、一次常微分方程式のシステムとして書くことができます
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
(Wiggins1990,p.5)これは、予期されない場合には、に減少します
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
(Wiggins1990,p.6;Ott1993,p.3）。
この結合された微分方程式の集合の不動点は次式で与えられる
 |
(8)
|
したがって、
、および
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
. したがって、固定小数点は次のようになります
, 
, と
.
固定小数点の安定性の解析は、方程式を線形化することによって点にすることができます。 差別化は与える
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
これは行列方程式として書くことができます
 |
(14)
|
点の安定性を調べる(0,0):
 |
(15)
|
 |
(16)
|
しかし、
なので、
本物です。 
なので、常に正の根が1つあるので、この固定小数点は不安定です。 今見てください(
, 0). 特性方程式は次のようになります
 |
(17)
|
根を持っています
 |
(18)
|
,
の場合、ポイントは漸近的に安定です。 
の場合、ラムダ_+/-^((+/-1,0))=+/-したがって、点は線形安定である(Wiggins1990,p.10)。 ただし、
, 根基は虚数部を与え、実数部は
なので、点は不安定です。 If
, 
、これは正の実根を持つので、点は不安定です。 もし
ならば
なので、両方の根は正であり、点は不安定です。
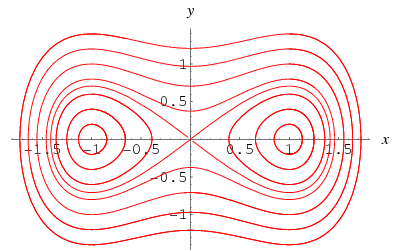
興味深いことに、強制なしの特殊ケース
,
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
直交によって統合することができます。 差別化(19)とプラグイン(20)を与える
 |
(21)
|
両側に
 |
(22)
|
しかし、これは書くことができます
 |
(23)
|
だから我々は運動の不変性を持っています
,
 |
(24)
|
 |
(25)
|
 |
(26)
|
so
 |
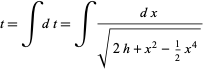(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion 
satisfies
 |
(28)
|
 |
(29)
|
したがって、ダフリング発振器の方程式はハミルトニアン系
によって与えられる。