![]()
더핑 방정식의 가장 일반적인 강제 형태는 다음과 같습니다
|
(1)
|
선택한 매개 변수에 따라 방정식은 여러 가지 특별한 형태를 취할 수 있습니다. 예를 들어,감쇠가없고 강제력이 없으면![]() 더하기 기호를 사용하면 방정식이 됩니다
더하기 기호를 사용하면 방정식이 됩니다
|
(2)
|
(1978 년,547 쪽;즈윌링거 1997 년,122 쪽). 이 방정식은 혼란스러운 행동을 나타낼 수 있습니다. ![]() 의 경우 방정식은”하드 스프링”을 나타내고
의 경우 방정식은”하드 스프링”을 나타내고![]() 의 경우”소프트 스프링”을 나타냅니다.”
의 경우”소프트 스프링”을 나타냅니다.”![]() 이면 위상 세로 곡선이 닫힙니다.
이면 위상 세로 곡선이 닫힙니다.
대신![]() ,
,![]() ,
,![]() ,마이너스 기호를 사용 하 여 시계를 다시 설정 하는 경우 방정식은 다음
,마이너스 기호를 사용 하 여 시계를 다시 설정 하는 경우 방정식은 다음
|
(3)
|
이것은 첫번째 순서 상미분 방정식의 체계로 것과 같이 쓰여질 수 있다
|
(4)
|
|||
|
(5)
|
(위 긴스 1990,피.5)어떤,강제되지 않은 경우,로 감소
|
(6)
|
|||
|
(7)
|
(1990 년,피.6;오트 1993,피.3).
이 결합 된 미분 방정식 세트의 고정 점은 다음과 같습니다
|
(8)
|
그리고 그 결과는 다음과 같습니다.
|
(9)
|
|||
|
(10)
|
제공![]() . 따라서 고정 점은 다음과 같습니다
. 따라서 고정 점은 다음과 같습니다![]() ,
, ![]() , 그리고
, 그리고![]() .
.
고정점의 안정성 분석은 방정식을 선형화하여 포인트가 될 수 있습니다. 차별화 제공
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
행렬 방정식으로 쓸 수 있습니다
|
(14)
|
점의 안정성 검토(0,0):
|
(15)
|
|
(16)
|
그러나![]() ,그래서
,그래서![]() 진짜.
진짜. ![]() 이후 항상 하나의 양의 루트가 있으므로이 고정점은 불안정합니다. 이제 봐(
이후 항상 하나의 양의 루트가 있으므로이 고정점은 불안정합니다. 이제 봐(![]() , 0). 특성 방정식은
, 0). 특성 방정식은
|
(17)
|
뿌리가 있는
|
(18)
|
따라서 점근 적으로 안정적입니다. 만약![]() ,람다_+/-^((+/-1,0))=+/-이 점들은 선형 적으로 안정적입니다. 그러나,만약
,람다_+/-^((+/-1,0))=+/-이 점들은 선형 적으로 안정적입니다. 그러나,만약![]() , 라디칼은 허수 부분을 제공하고 실수 부분은
, 라디칼은 허수 부분을 제공하고 실수 부분은![]() 이므로 점이 불안정합니다. 100000000000(2),
이므로 점이 불안정합니다. 100000000000(2), ![]() 은 양의 실제 루트를 가지므로 점이 불안정합니다. 따라서 두 근 모두 양수이고 점은 불안정합니다.
은 양의 실제 루트를 가지므로 점이 불안정합니다. 따라서 두 근 모두 양수이고 점은 불안정합니다.
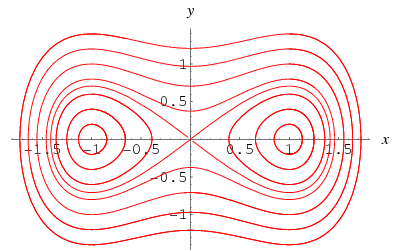
흥미롭게도 특별한 경우![]() ,
,
|
(19)
|
|||
|
(20)
|
구적법에 의해 통합될 수 있습니다. (19)및 플러그 인(20)차별화
|
(21)
|
양변에![]() 제공
제공
|
(22)
|
그러나 이것은 쓸 수 있습니다
|
(23)
|
그래서 우리는 운동의 불변성을 가지고 있습니다![]() ,
,
|
(24)
|
에 대한 해결![]() 제공
제공
|
(25)
|
|
(26)
|
so
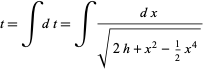 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
그래서 더핑 오실레이터의 방정식은 해밀턴 시스템에 의해 주어집니다.