제 12 장
구조 분석 모멘트 분포 방법
12.1 기본 개념
빔 및 프레임 분석의 모멘트 분포 방법은 하디 크로스에 의해 개발되었으며 1930 년에 공식적으로 발표되었습니다. 이 방법은 경사 편향 방법과 같은 변형 방법이지만 대략적인 방법이므로 후자의 방법과 마찬가지로 연립 방정식을 풀 필요가 없습니다. 모멘트 분포 방법에 의해 얻어진 결과의 정확도는 연속적인 근사 수 또는 반복 프로세스에 따라 달라집니다.
모멘트 분포 방법의 개념을 설명하기 위해 그림 12.1 에 표시된 프레임을 고려하십시오. 프레임의 구성원은 프리즘이며 축 방향으로 변형되거나 서로 상대적으로 변환되지 않는 것으로 간주됩니다. 관절 고정 프레임의 관절 비 적용된 하중으로 인해 약간 회전 할 수 있습니다. 첫째,구성원 간의 모멘트 분배를 수행하기 전에 모든 조인트는 클램프를 사용하여 일시적으로 잠기는 것으로 가정합니다.
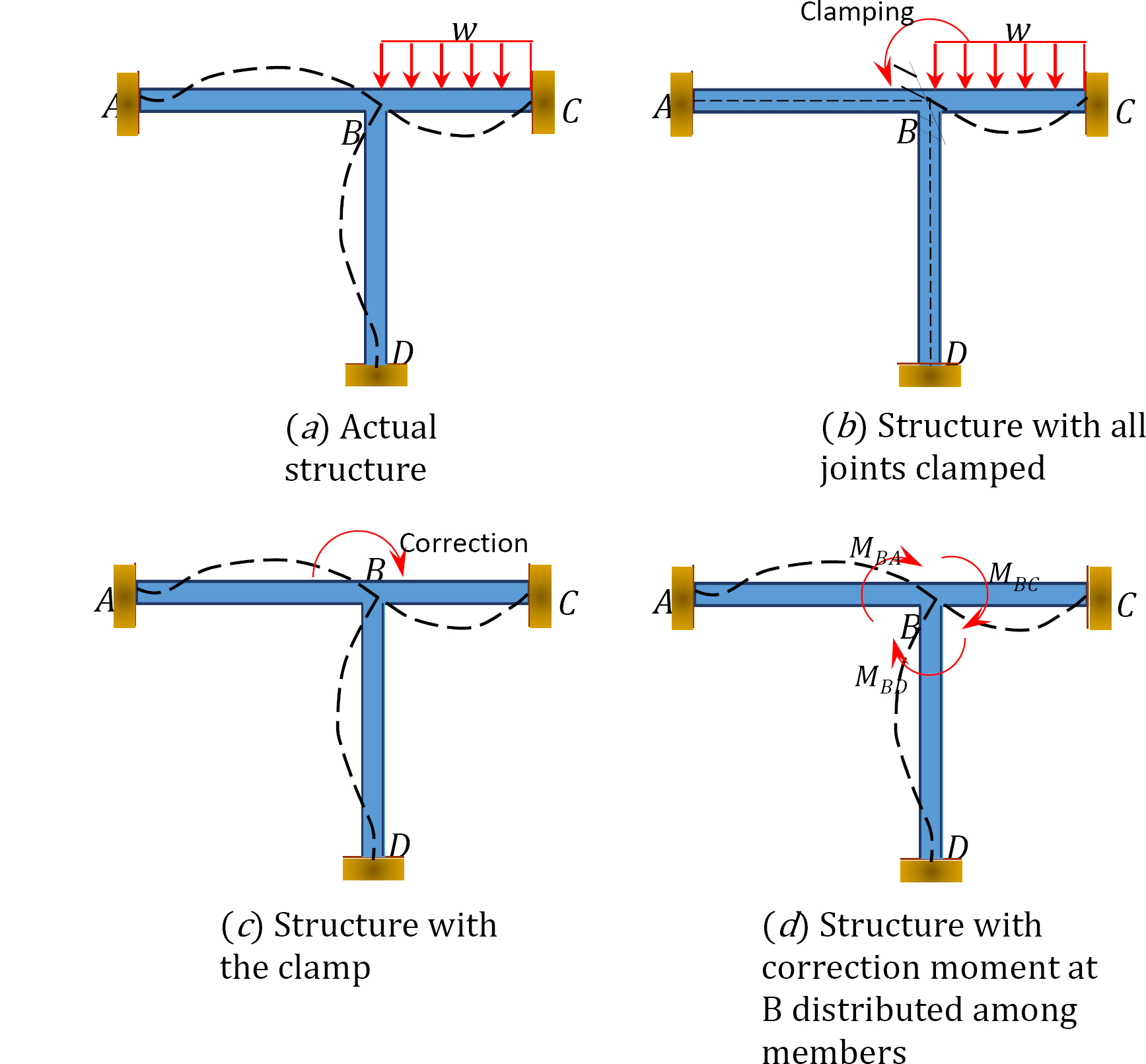
그림. 12.1. 프레임.
12.2 부호 협약
모멘트 분포 방법에 대한 부호 협약은 기울기-편향 방법에 대해 설정된 것과 유사합니다; 즉,멤버의 끝부분의 순간은 멤버의 끝을 시계 방향으로 돌리는 경향이 있다면 양수로 간주되고,멤버를 시계 반대 방향으로 돌리는 경향이 있다면 음수로 간주됩니다.
12.3 정의
불균형 모멘트:이 분석 방법은 구조의 조인트가 처음에 클램핑되거나 고정 된 다음 연속적으로 해제된다고 가정합니다. 합동이 풀어 놓으면 하자마자,저 합동에 만나는 일원의 조정 끝 순간의 합계가 0 이지 않기 때문에,교체는 일어난다. 얻은 끝 모멘트의 합 값은 해당 조인트에서의 불균형 모멘트입니다.
이월 모멘트:고정되는 것으로 추정되는 다른 끝의 공동 원인 모멘트에서 만나는 회원의 끝에서 분산 된 순간. 다른 끝에 이 유도한 순간은 이월 순간에게 불립니다.
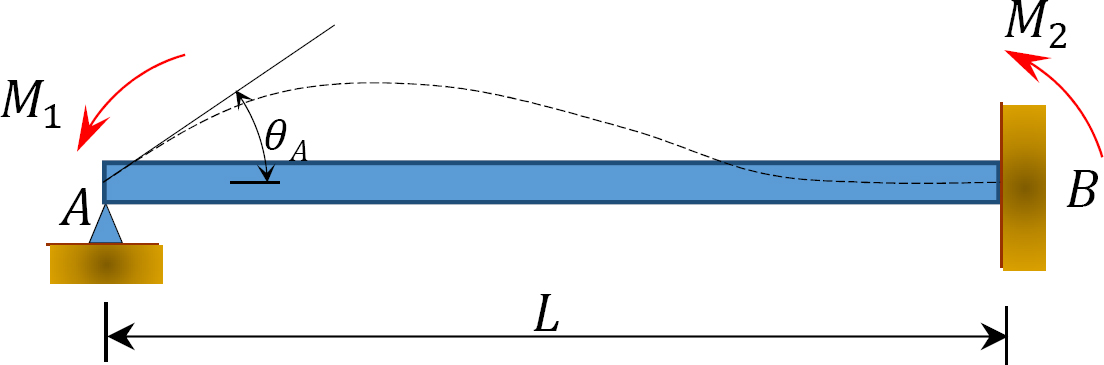
그림. 12.2. 언로드 된 프리즘 빔.
도 12.2 에 도시 된 바와 같이,단부에 고정 된 언로드 된 프리즘 빔을 고려한다. 모멘트 미디엄 1 이 빔의 왼쪽 끝에 적용되면 빔의 양쪽 끝에 대한 기울기-편향 방정식을 다음과 같이 작성할 수 있습니다:


방정식 12.1 에서 방정식 12.2 로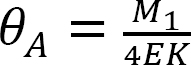 를 대입하면 다음을 제안합니다:
를 대입하면 다음을 제안합니다:

방정식 12.3 은 다른 쪽 끝에 적용된 모멘트로 인해 빔의 고정 된 끝으로 이월 된 모멘트가 적용된 모멘트의 절반과 같음을 나타냅니다.
이월 인자:적용된 모멘트에 대한 유도 모멘트의 비율을 이월 인자라고합니다. 그림 12.2 에 표시된 빔의 경우 이월 계수는 다음과 같습니다:

분산 인자(디에프): 분산 요인은 공동에서 만나는 각 구성원이 수행하는 불균형 모멘트의 비율을 결정하는 데 사용되는 요소입니다. 그림 12.3 에 나와 있는 프레임의 공동 오에서 만나는 회원들의 분포 인자는 다음과 같이 계산됩니다:
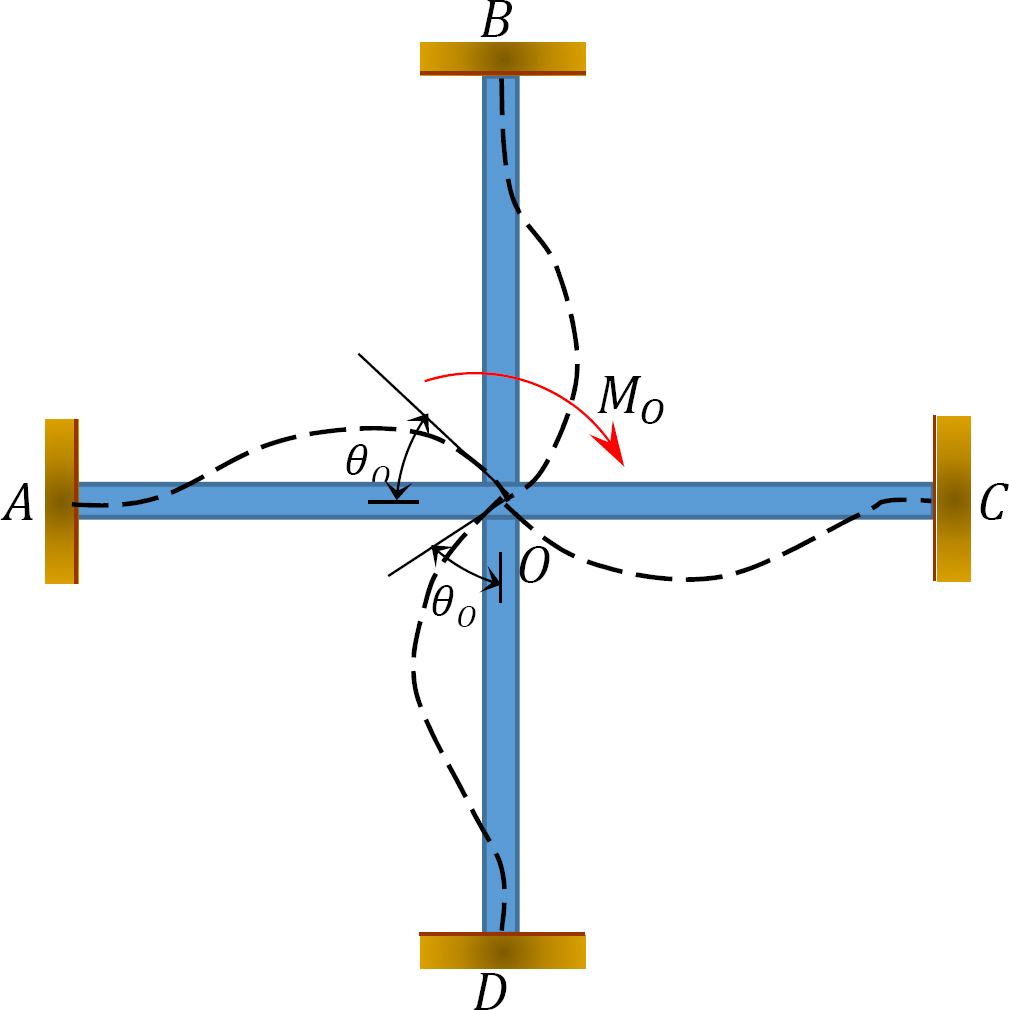
그림. 12.3. 프레임.

분산 모멘트:조인트에서 가상 클램프가 해제되면 해당 조인트에서 불균형 한 모멘트가 회전합니다. 회전은 저항 순간의 개발의 결과로,공동에서 회의 회원의 끝을 왜곡. 이러한 저항 순간을 분산 순간이라고합니다. 그림 12.3 에 표시된 프레임 멤버의 분산 모멘트는 다음과 같이 계산됩니다:
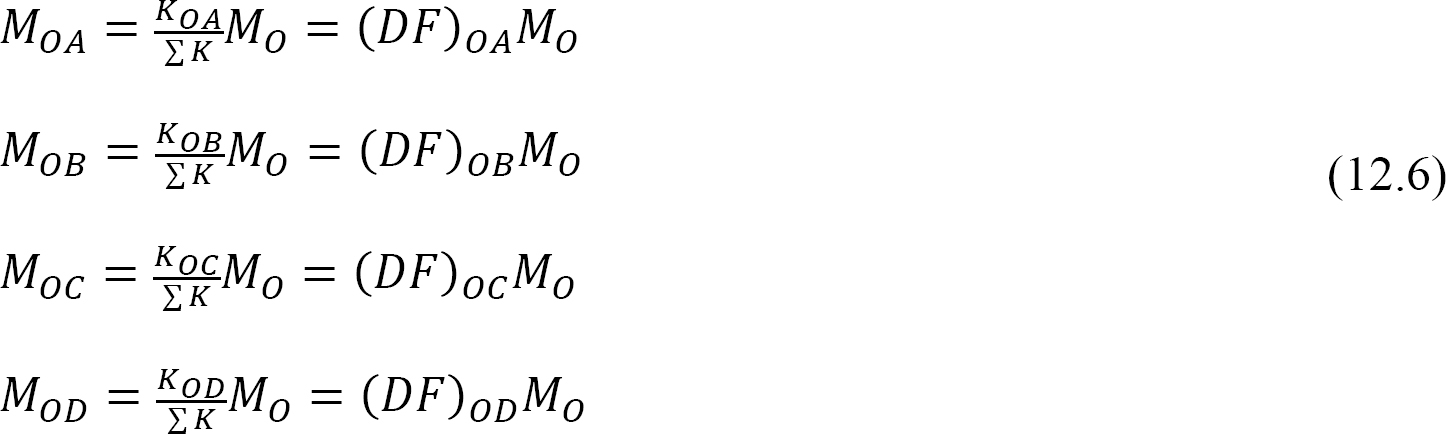
12.4 부재 강성의 변형
때때로 모멘트 분포 방법에서의 반복 과정은 불확실한 구조의 일부 부재들의 굴곡 강성을 조정함으로써 현저하게 감소될 수 있다. 이 섹션에서는 불확실한 빔의 굴곡 강성에 대한 고정 및 핀 엔드 지지대의 영향을 고려합니다.
사례 1: 1 개의 끝에 경첩을 달고 다른 사람에 고쳐지는 광속
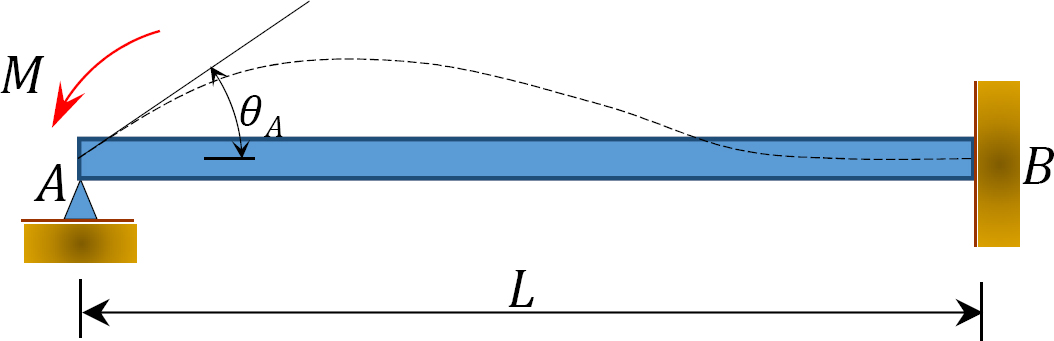
그림. 12.4. 빔
그림 12.4 와 같이 단부에 힌지 및 단부에 고정 된 빔을 고려하십시오. 모멘트 적용 미디엄 힌지 끝을 양만큼 회전시킵니다. 끝 부분에 대한 기울기-편향 방정식을 작성하고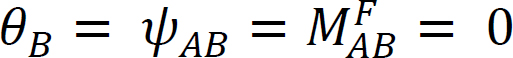 는 다음을 암시합니다:
는 다음을 암시합니다:
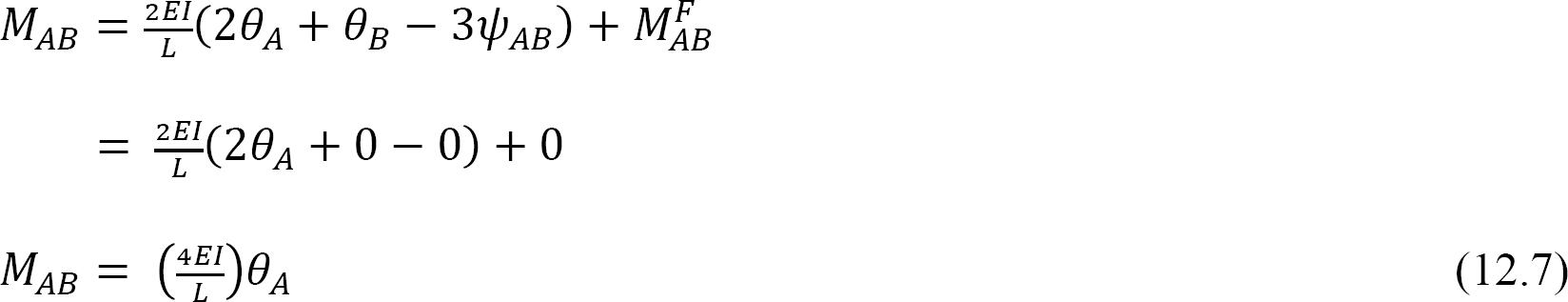
정의에 따르면,구조 부재의 굽힘 강성은 그 단부의 단위 회전을 유발하기 위해 부재의 단부에 적용되어야 하는 순간이다. 고정 파단을 갖는 부재에 대한 굽힘 강성에 대한 다음 식은 다음과 같이 표현된다.12.7:

방정식 12.8 을 4 로 나누면 고려되는 경우에 대한 상대 강성에 대한 다음 표현이 제시됩니다:

사례 2:양쪽 끝에 힌지 된 빔
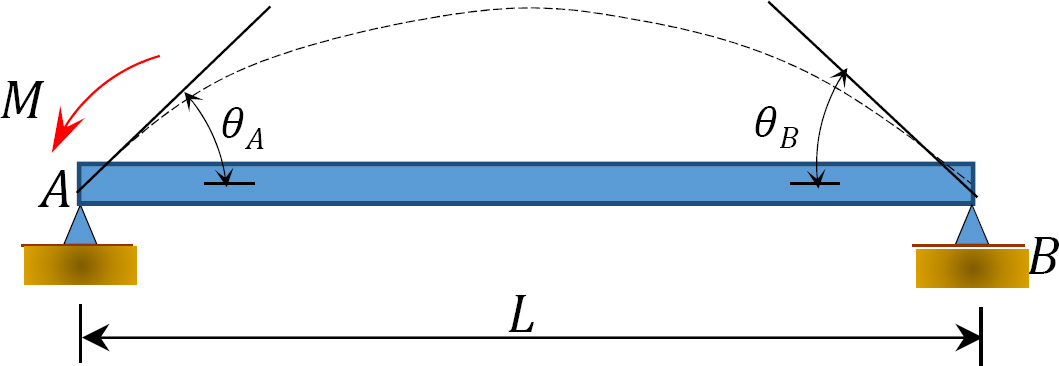
그림. 12.5. 단순히 지원 빔.
도 12.5 에 도시된 단순하게 지지된 빔의 끝부분에 모멘트를 적용하면 힌지 끝부분에 빔이 비스듬히 회전한다. 11 장의 섹션 11.4 에서 파생 된 수정 된 기울기-편향 방정식을 사용하고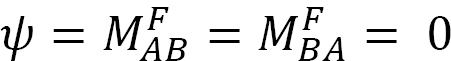 는 하중이 가해지는 힌지 끝 부분에서 다음 표현을 제안합니다:
는 하중이 가해지는 힌지 끝 부분에서 다음 표현을 제안합니다:
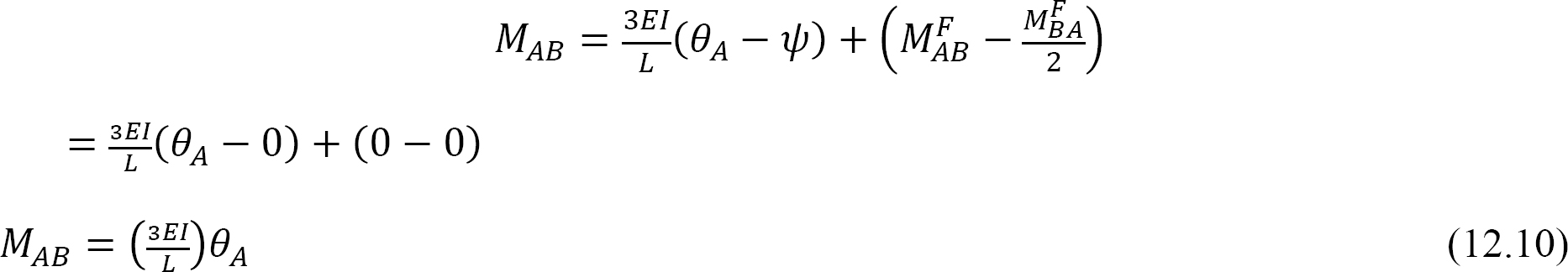
식 12.10 에 제 12.10=1 을 대입하면 경첩이 달린 맨 끝을 가진 부재에 대한 굽힘 강성에 대한 다음 식을 제안합니다:

경첩이 달린 맨 끝을 가진 부재에 대한 상대 강성은 다음과 같이 방정식 12.11 을 4 로 나눔으로써 얻어진다:

방정식 12.12 와 12.9 를 비교하면 경첩이 달린 맨 끝을 가진 부재는 동일한 지오메트리를 가진 부재만큼 뻣뻣하지만 맨 끝에 고정 된 3/4 임을 알 수 있습니다. 이 확립 된 사실은 모멘트 분포 방법을 사용하여 힌지 된 파 엔드가있는 빔 또는 프레임을 분석 할 때 반복 횟수를 실질적으로 줄일 수 있습니다. 이러한 경우,니어 엔드에서의 빔의 상대 강성은 먼저 수학식 12.12 에 따라 조정되고,그 분포 인자는 조정 된 강성으로 계산된다. 균형을 잡는 가동 도중,가까운 끝은 그것의 끝에 순간의 이월 더 없이 다만 한 번 균형을 잡을 것입니다.
12.5 불확정 빔의 분석
모멘트 분포 방법에 의한 불확정 빔의 분석 절차는 다음과 같이 간단히 요약된다:
모멘트 분포 방법에 의한 불확정 빔의 분석 절차
•조인트가 회전에 대해 클램핑된다고 가정하여 멤버에 대한 고정 끝 모멘트를 계산합니다.
•관절에서 연결된 각 부재에 대한 분포 계수 계산
•각 관절에서 불균형 모멘트를 계산하고 그 관절에서 연결된 부재의 끝 부분에 동일하게 분배합니다.
•분산 모멘트의 절반을 멤버의 다른 쪽 끝으로 이월합니다.
•이 후자의 모멘트(3 단계와 4 단계에서 얻은 모멘트)를 원래 고정 끝 모멘트에 추가하거나 뺍니다.
•지정된 구조의 조인트에 결정된 끝 모멘트를 적용합니다.
•주어진 빔의 각 스팬의 자유 몸체 다이어그램을 그려 모멘트 분포 방법으로 얻은 조인트에서의 하중 및 모멘트를 보여줍니다.
•각 스팬에 대한 지지 반응을 결정합니다.
•각 스팬에 대한 전단력 및 굽힘 모멘트 다이어그램을 계산하고 구성합니다.
•단계 9 의 다이어그램을 결합하여 주어진 빔에 대해 하나의 굽힘 모멘트와 하나의 전단력 다이어그램을 그립니다.
예 12.1
모멘트 분포 방법을 사용하여 그림 12.6 에 표시된 빔의 지지대에서 끝 모멘트와 반응을 결정합니다. 상수입니다.
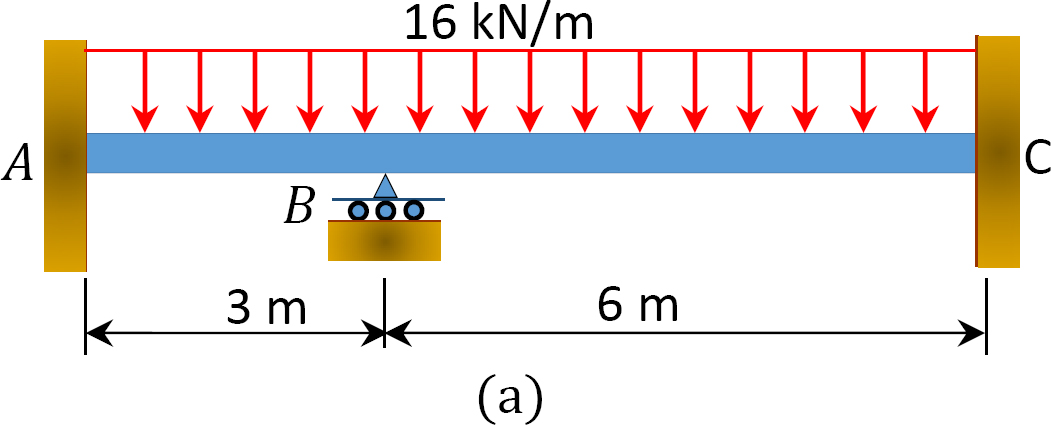
그림. 12.6. 빔.
솔루션
고정 종료 순간.
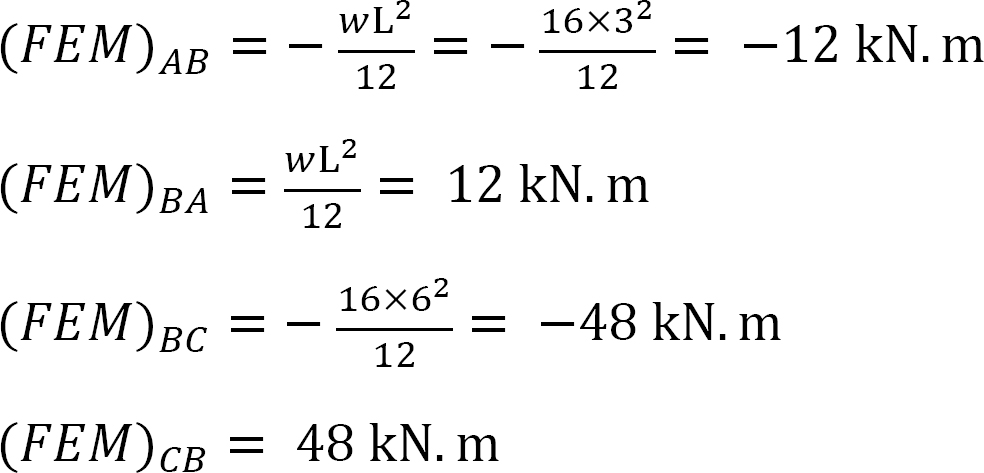
강성 계수.
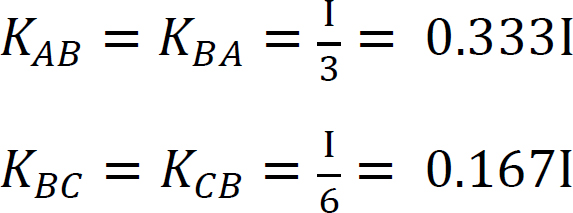
분포 계수.
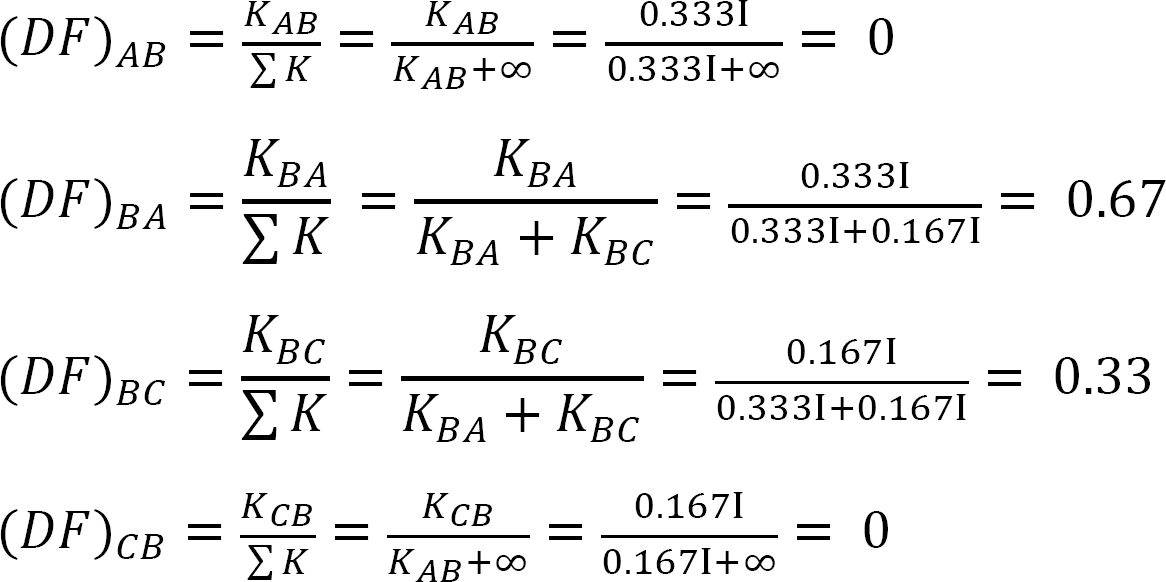
표 12.1. 배포 테이블.
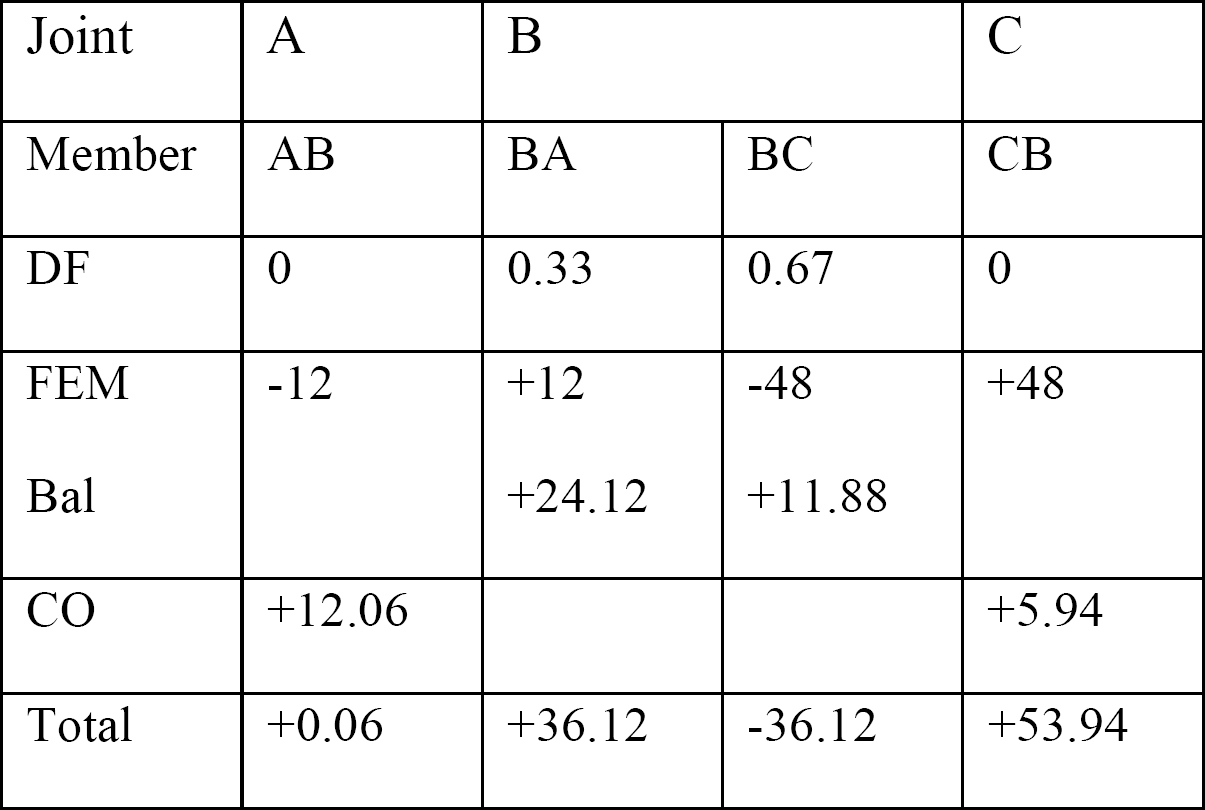
전단력 및 굽힘 모멘트 다이어그램.
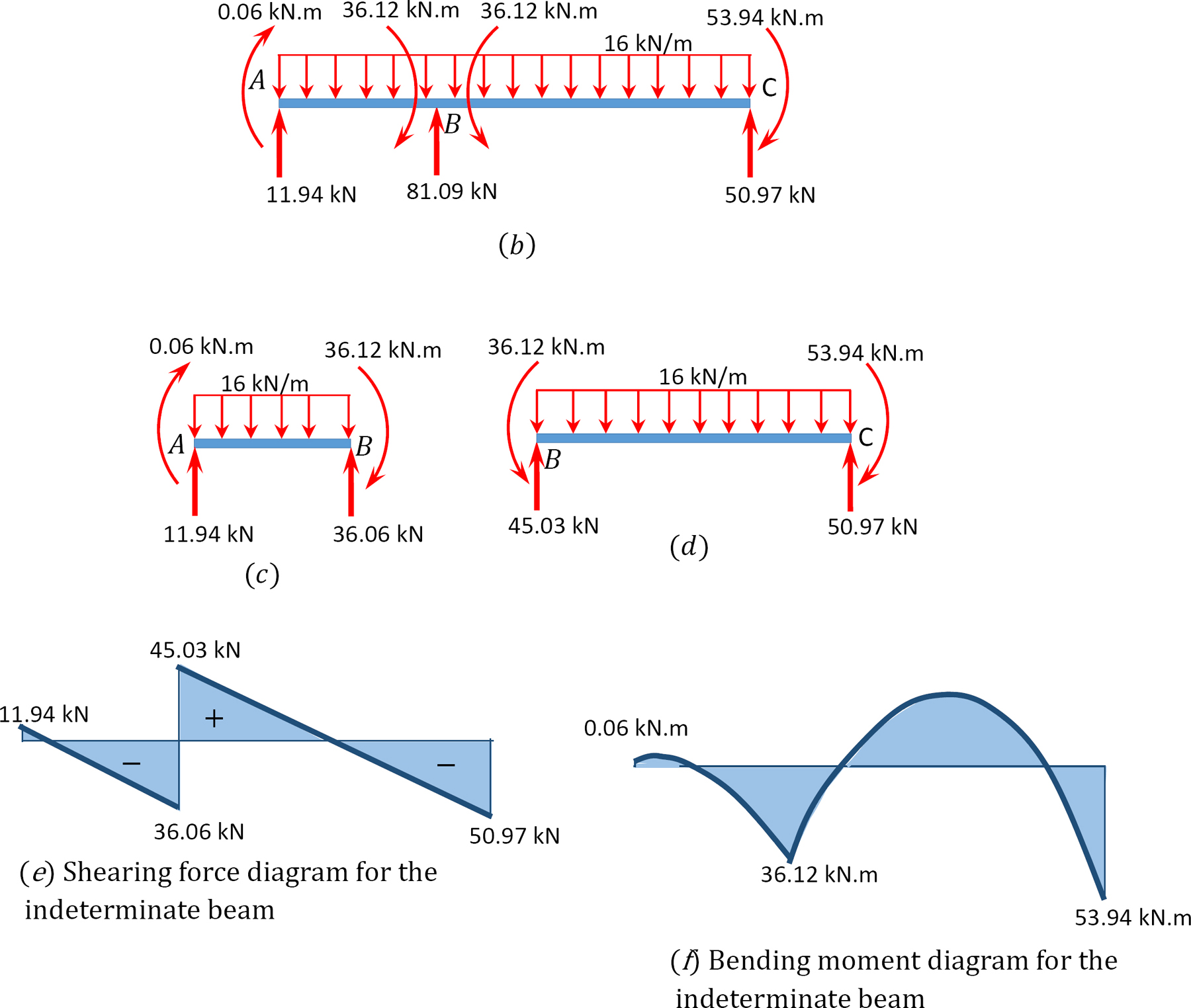
예:12.2
모멘트 분포 방법을 사용하여 그림 12.7 에 표시된 빔의 지지대에서 끝 모멘트와 반응을 결정합니다.
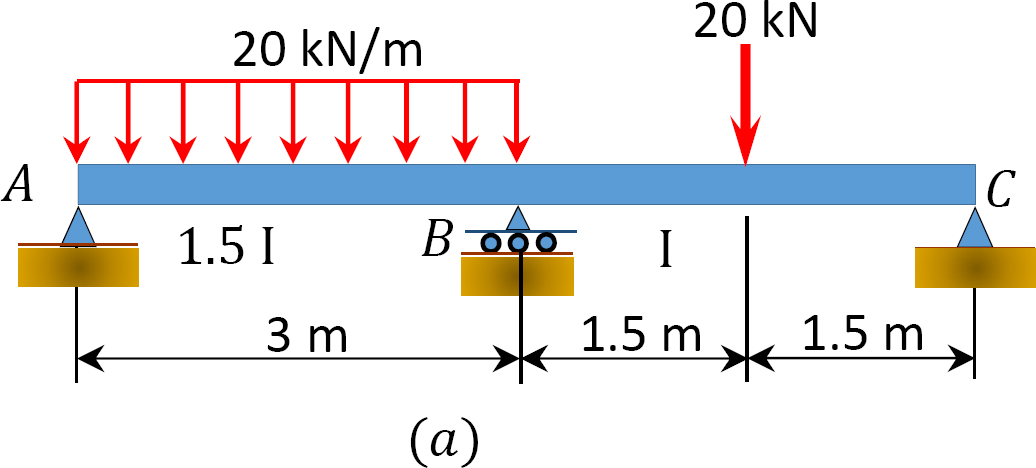
그림. 12.7. 빔.
솔루션
고정 종료 순간.
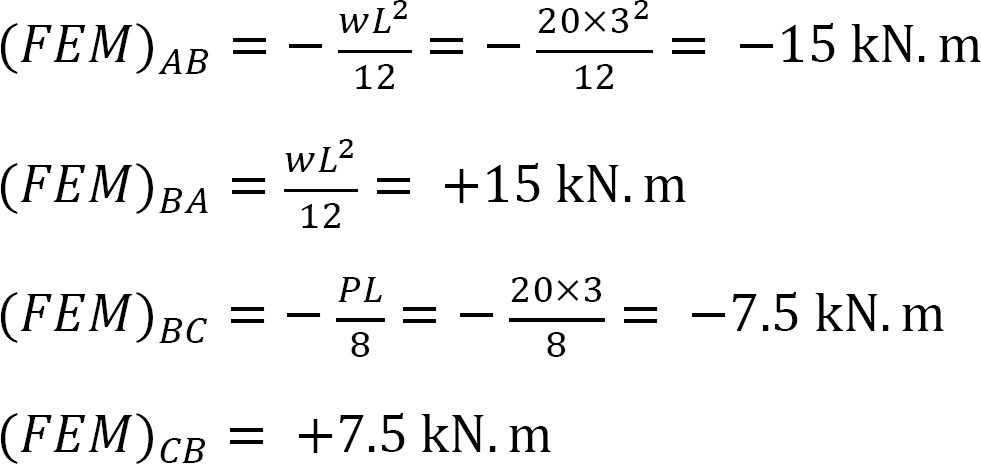
강성 계수.
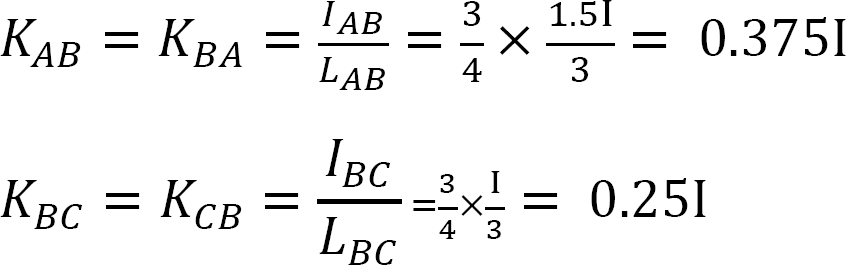
분포 계수.
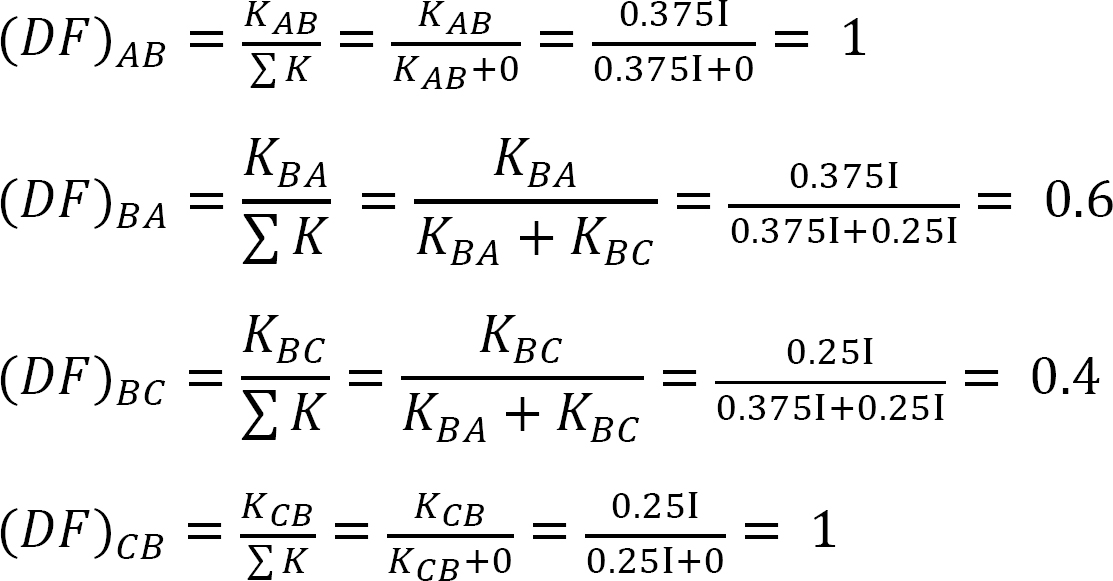
표 12.2. 배포 테이블.
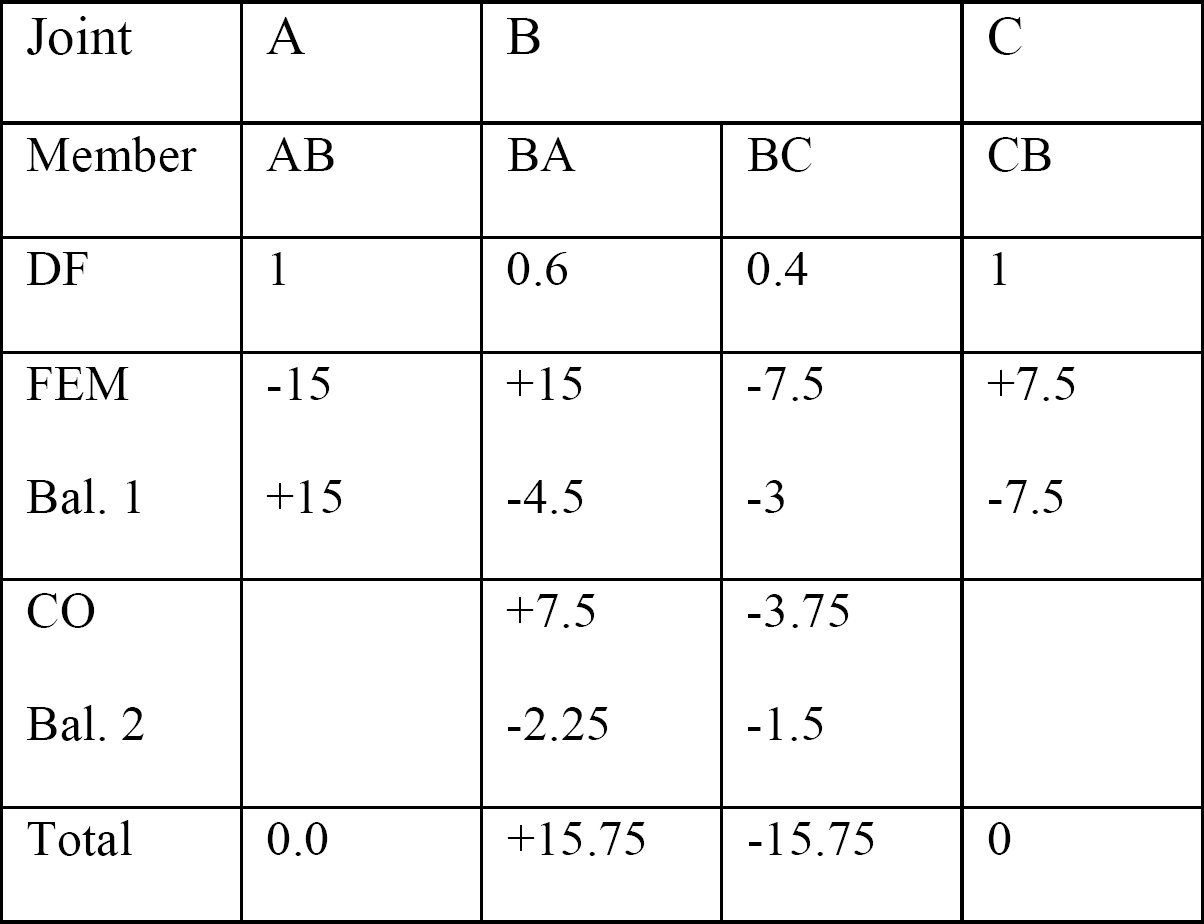
전단력 및 굽힘 모멘트 다이어그램.
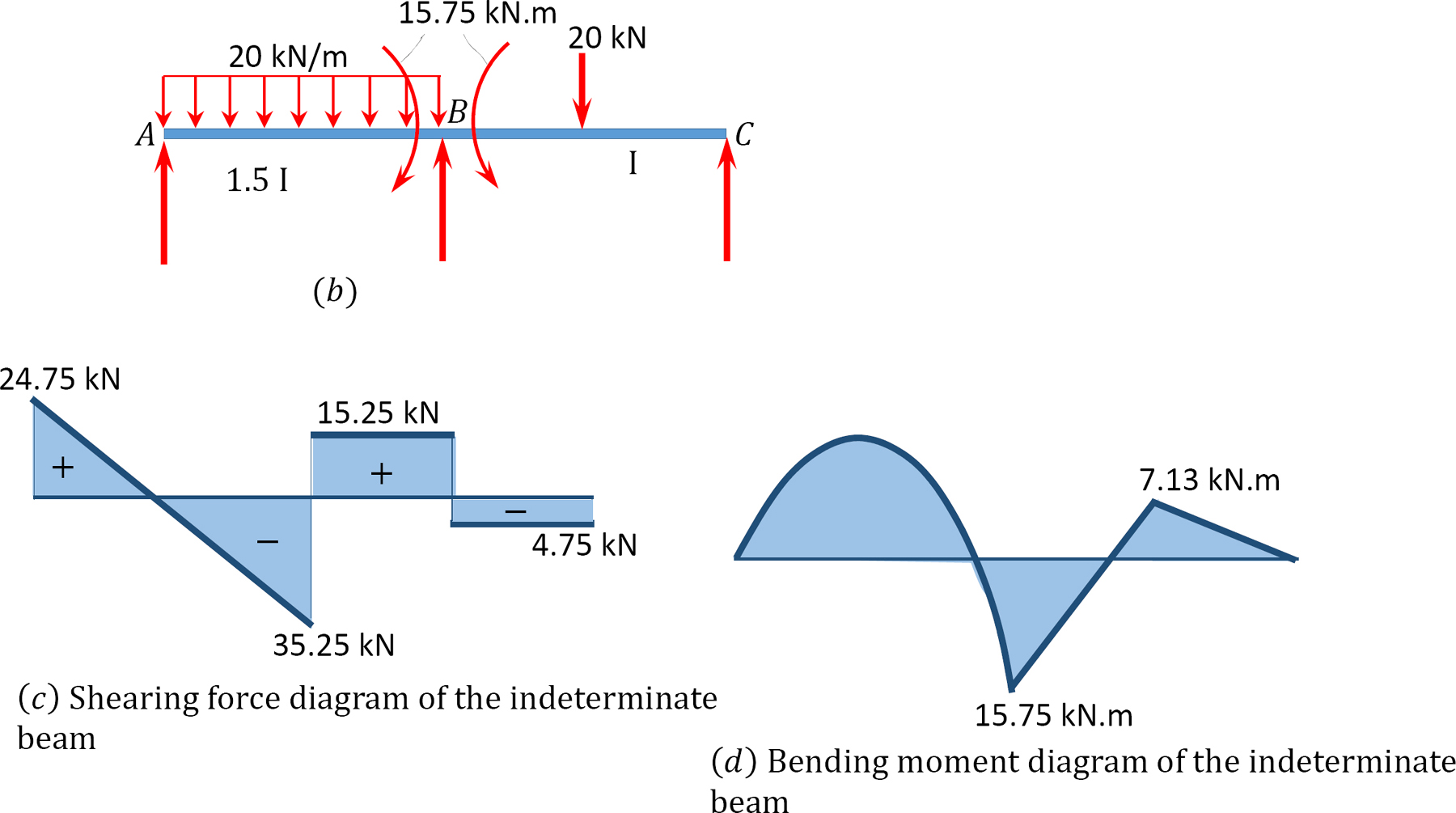
12.6 불확정 프레임 분석
모멘트 분포 방법을 사용한 프레임 분석 절차는 분석 중인 프레임의 유형에 따라 달라집니다. 프레임은 동요 또는 비 동요 프레임으로 분류됩니다. 흔들리지 않는 프레임의 분석 절차는 불확실한 빔의 분석과 유사합니다. 그러나 동요 프레임 분석을 위해 절차가 다릅니다. 동요 프레임의 분석에 관련된 두 단계,즉 비 동요 단계와 동요 단계 분석이 있습니다. 이러한 단계는 아래에 설명되어 있습니다.
모멘트 분포 방법에 의한 불확정 동요프레임의 분석 절차
가.비동요 단계 분석
•먼저 프레임이 흔들리는 것을 방지하는 가상의 소품이 존재한다고 가정한다.
•프레임의 지지대에서 수평 반응을 계산하고 차이를 주목하십시오.
비. 동요 단계 분석
•프레임의 열에 작용하는 임의의 순간을 가정합니다. 이 모멘트의 크기는 열에 비례하여 열에 따라 다릅니다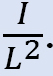
•값은 미디엄 2 에 대해 가정되고 미디엄 1 이 결정됩니다.
•임의 모멘트는 비동요 조건
에 대해 분포한다•동요조건에 대한 지지대에서의 수평반응의 크기를 계산한다. 이러한 반응의 합계는 임의의 변위력을 제공합니다 와이.
•비율 결정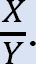 이 비율을 동요 요인이라고합니다.
이 비율을 동요 요인이라고합니다.
•흔들림 계수를 사용하여 흔들림의 분산 모멘트를 곱합니다. 이 동요에 대한 수정 된 순간을 제공합니다.
•프레임의 마지막 순간은 흔들리지 않는 단계에서 얻은 모멘트와 흔들리지 않는 단계에 대한 수정 된 모멘트의 합계입니다.
예 12.3
모멘트 분배 방법을 사용하여 그림 12.8 에 표시된 프레임의 멤버의 끝 모멘트를 결정합니다. 상수입니다.
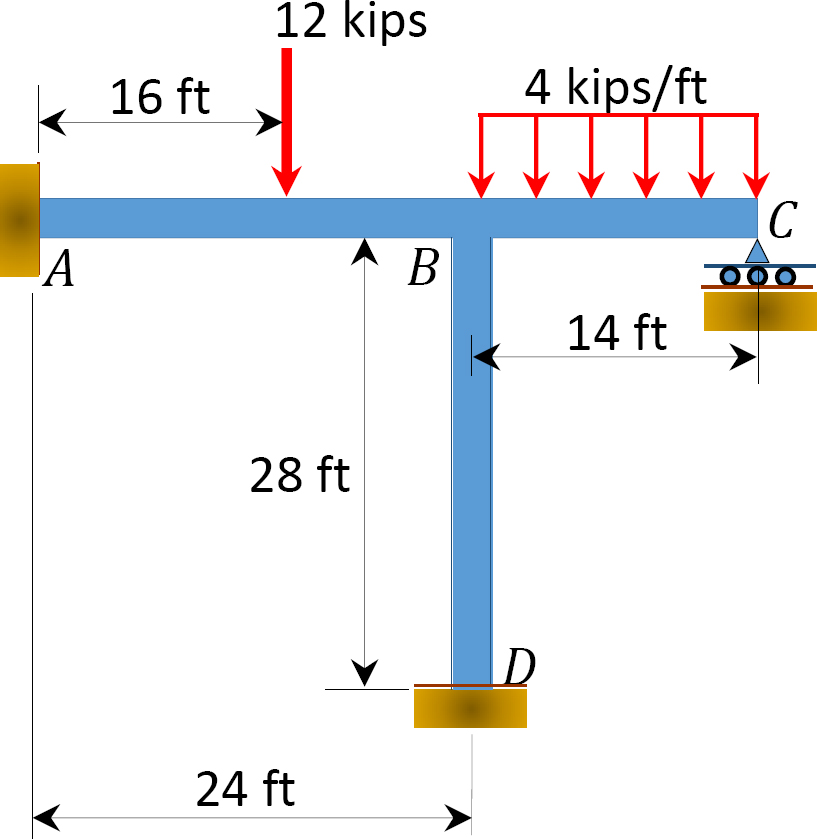
그림. 12.8. 프레임.
솔루션
고정 종료 순간.
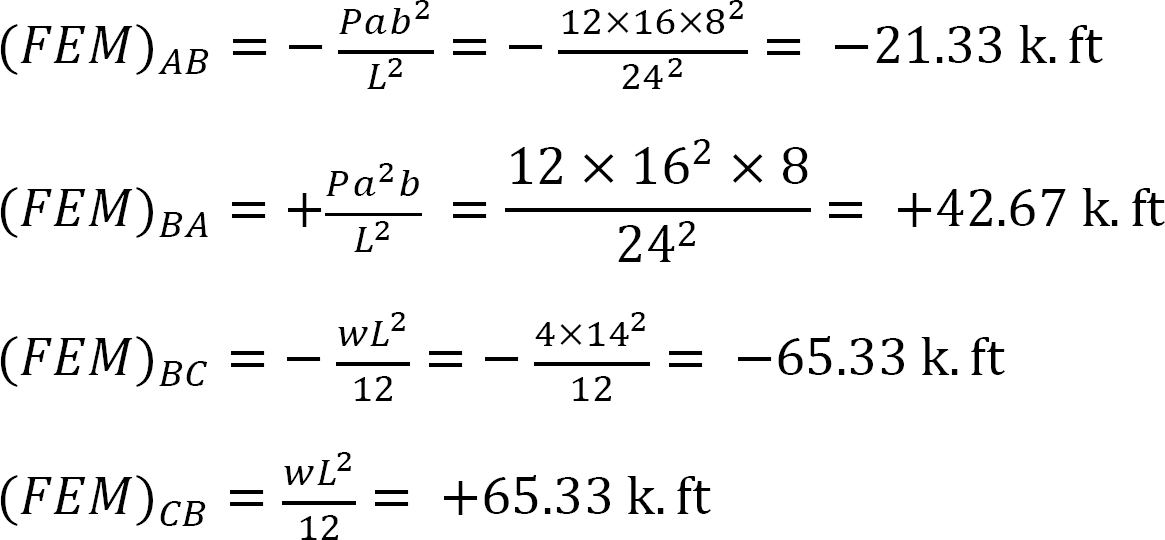
강성 계수.
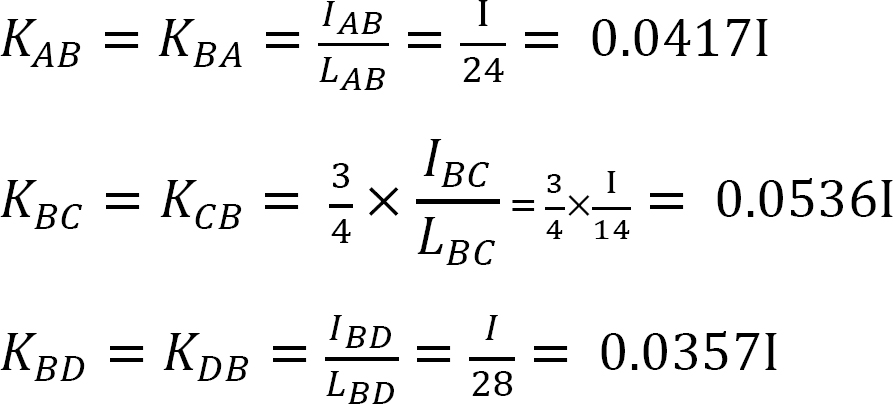
분포 계수.
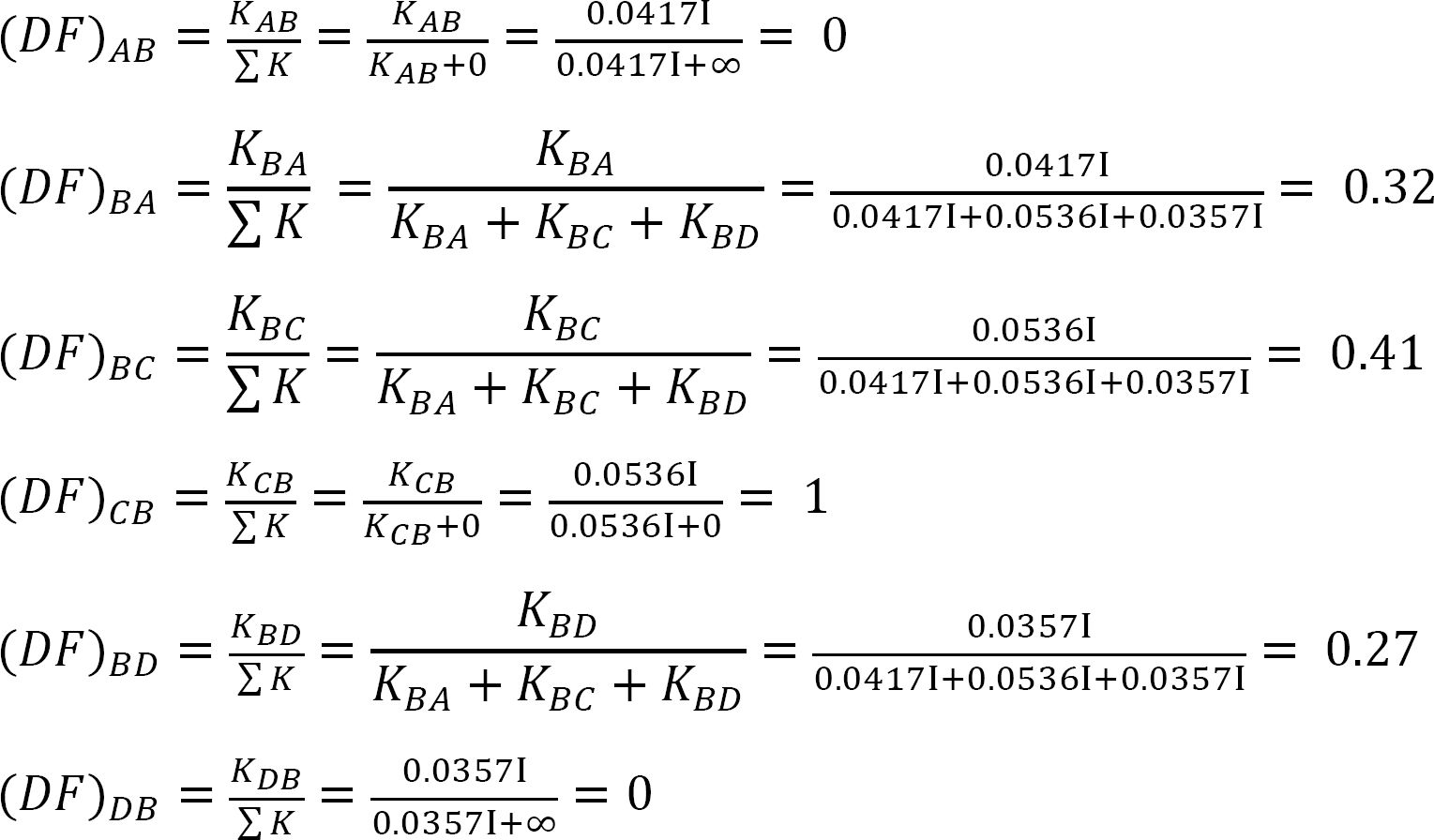
표 12.3. 배포 테이블.
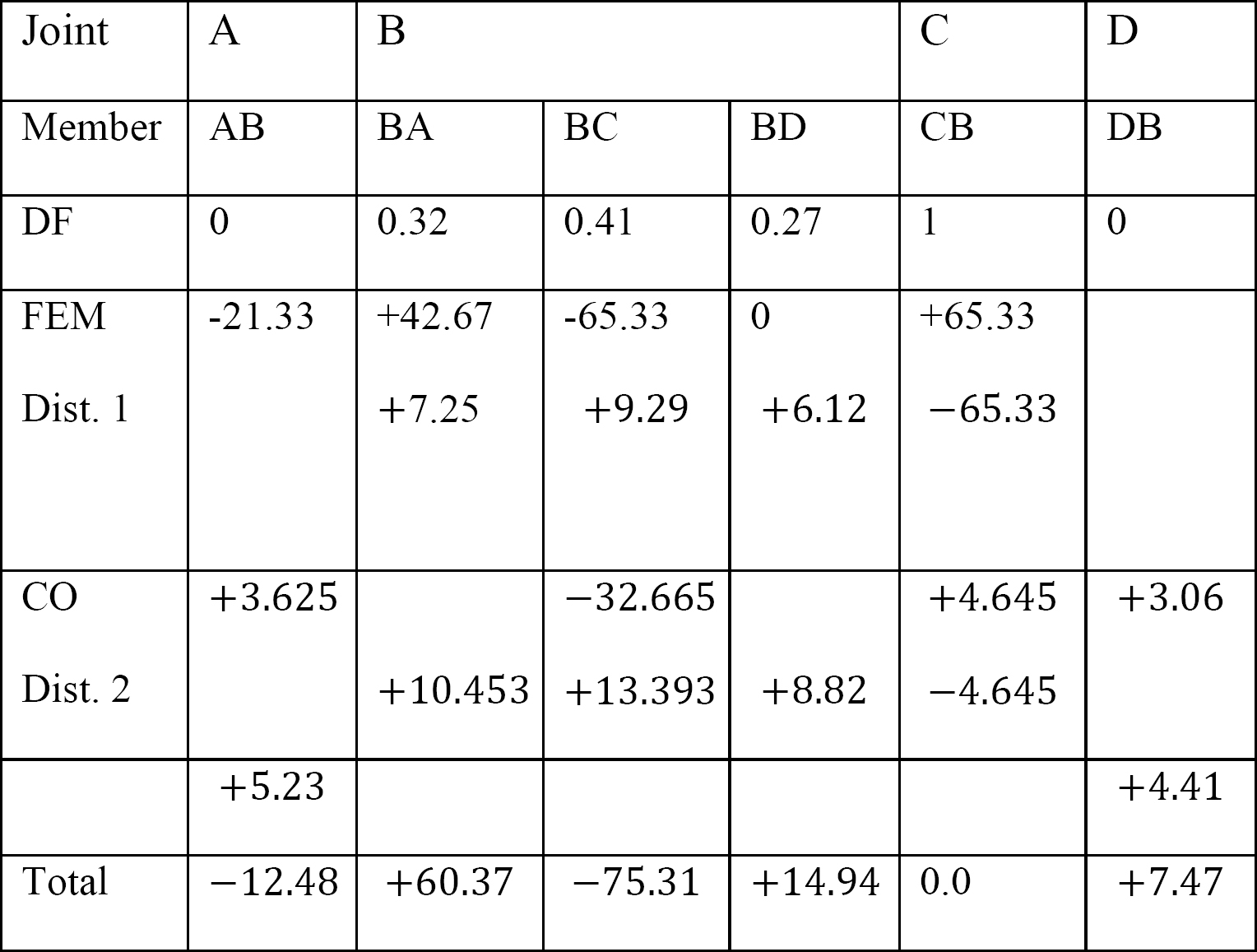
최종 멤버 끝 순간.
얻은 값을 멤버 끝 모멘트 방정식에 대입하면 다음과 같은 것을 알 수 있습니다.
예를 들어,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트,14.94 피트.4
모멘트 분포 방법을 사용하여 그림 12.9 에 표시된 프레임의 지지대에서 끝 모멘트를 결정합니다. 상수입니다.
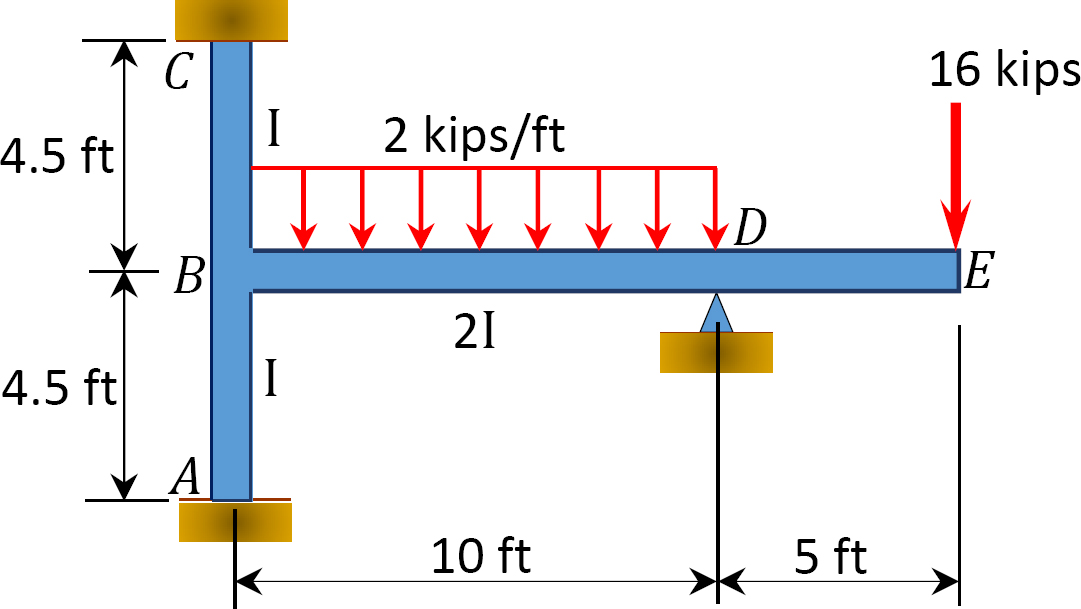
그림. 12.9. 프레임.
솔루션
고정 종료 순간.
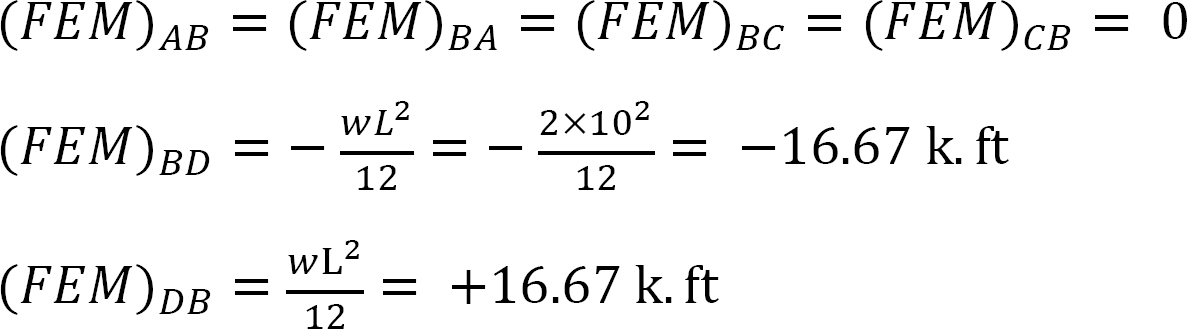
강성 계수.
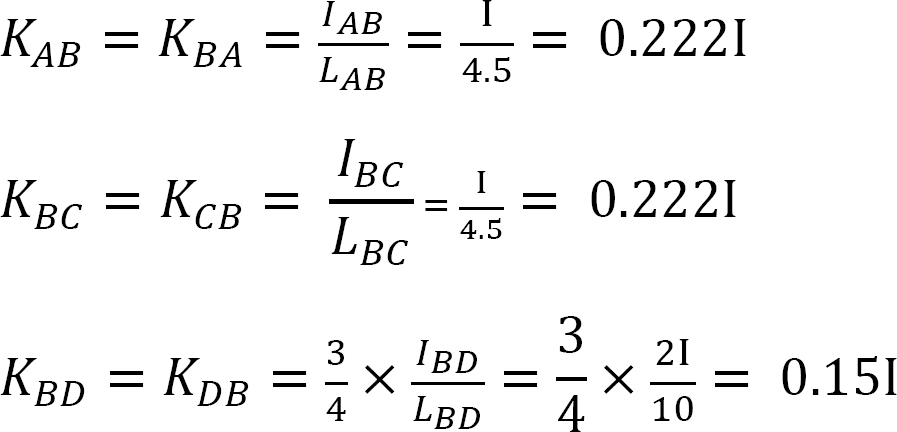
분포 계수.

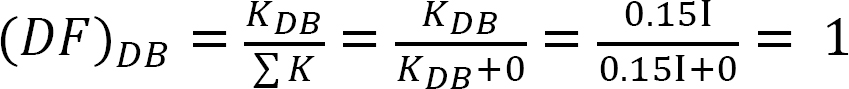
표 12.4. 배포 테이블.
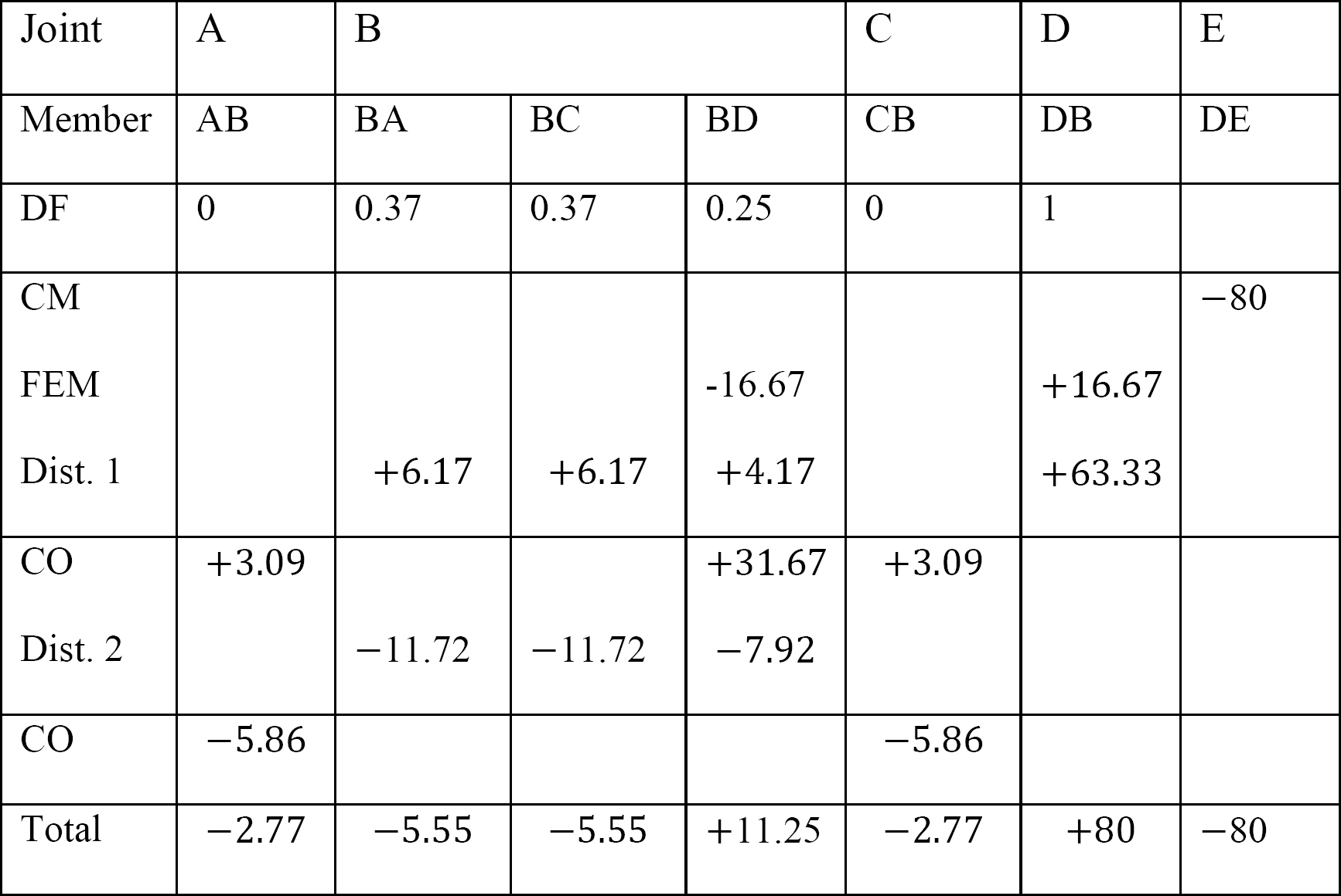
최종 멤버 끝 순간.2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 15 일-2016 년 10 월 이 예제에서는 다음과 같은 예제들을 사용할 수 있습니다:-2.77
모멘트 분포 방법을 사용하여 그림 12.10 에 표시된 프레임의 지지대에서 끝 모멘트를 결정합니다. 상수입니다.
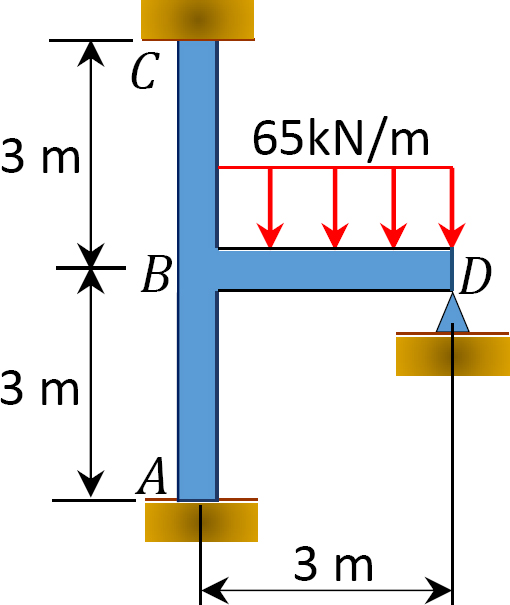
그림. 12.10. 프레임.
솔루션
고정 종료 순간.
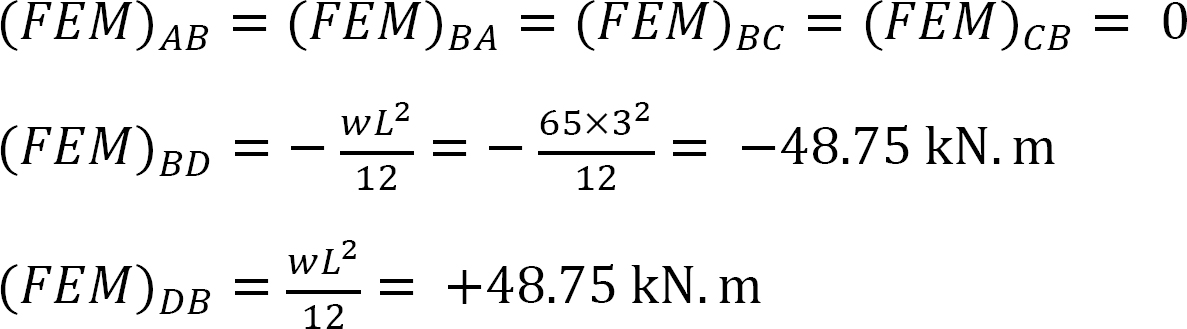
강성 계수.
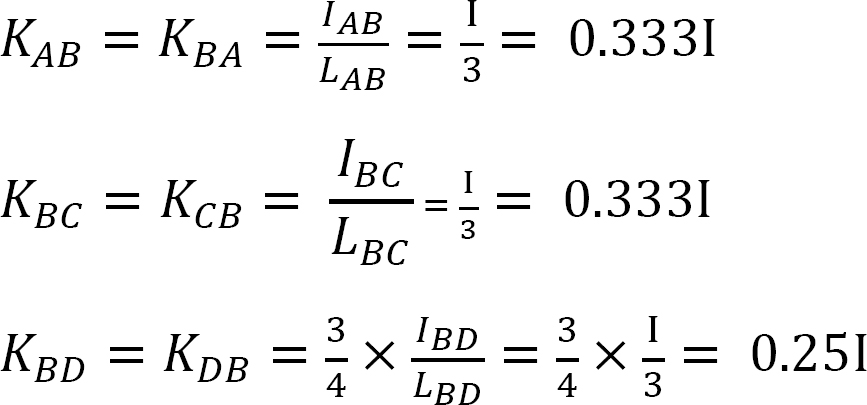
분포 계수.
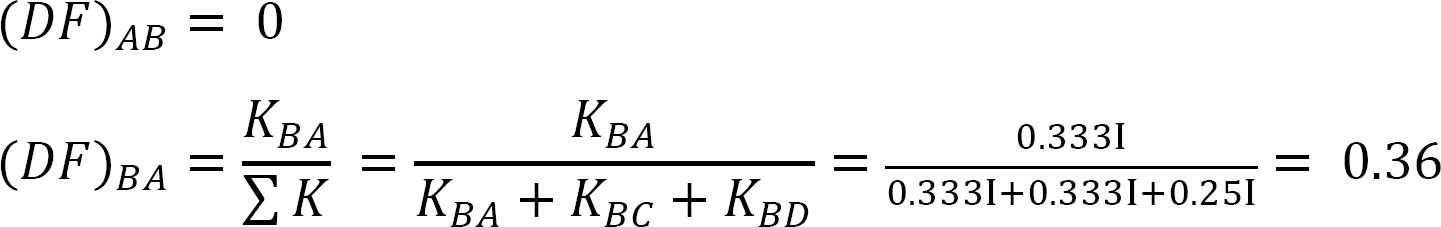

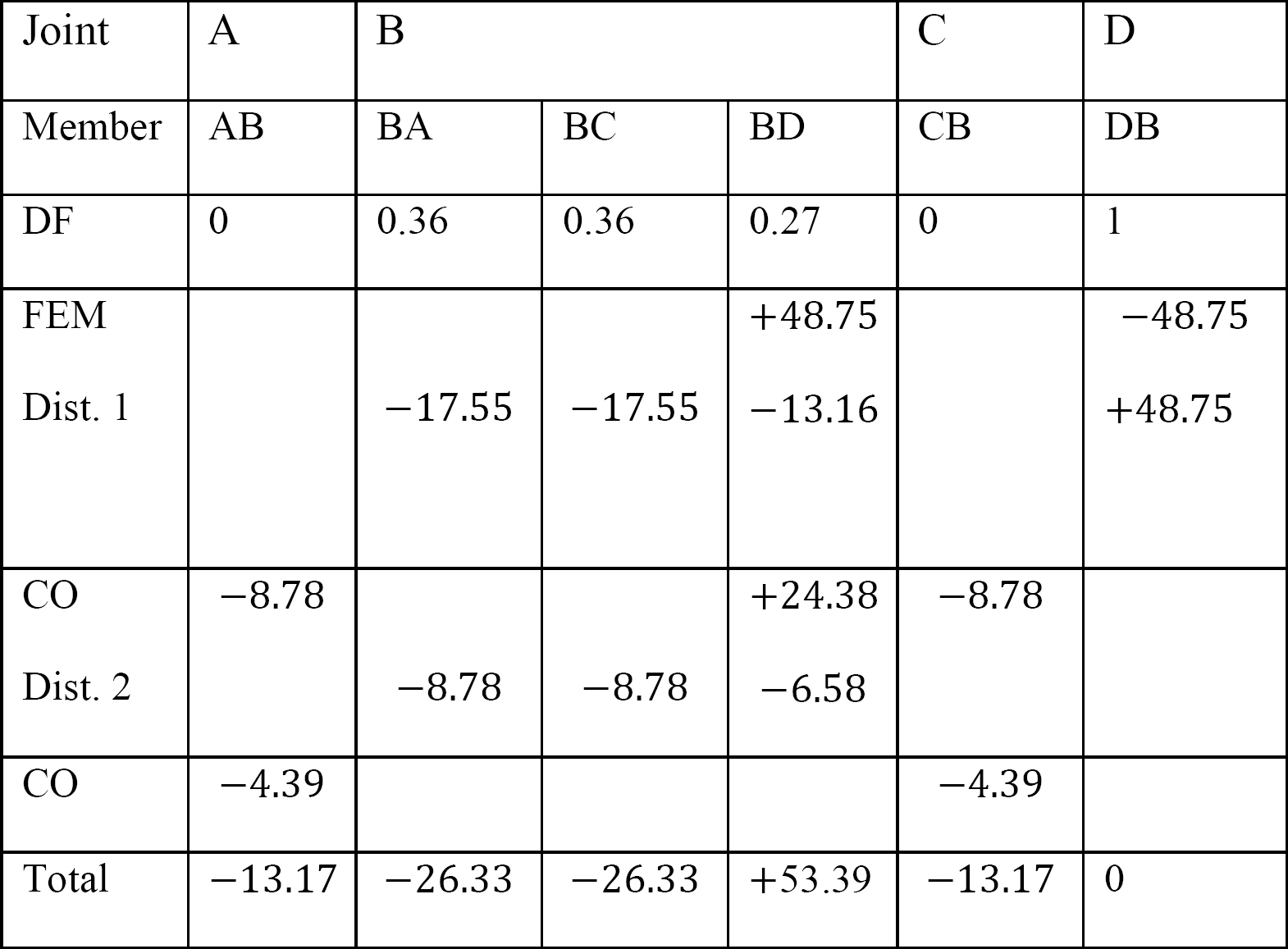
표 12.5. 배포 테이블.
최종 멤버 끝 순간.2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 12 월 1 일,2016 년 7016>
= 0
예:12.6
모멘트 분포 방법을 사용하여 그림 12.11 에 표시된 측면 동요를 사용하여 프레임의 멤버 끝 모멘트를 결정합니다..
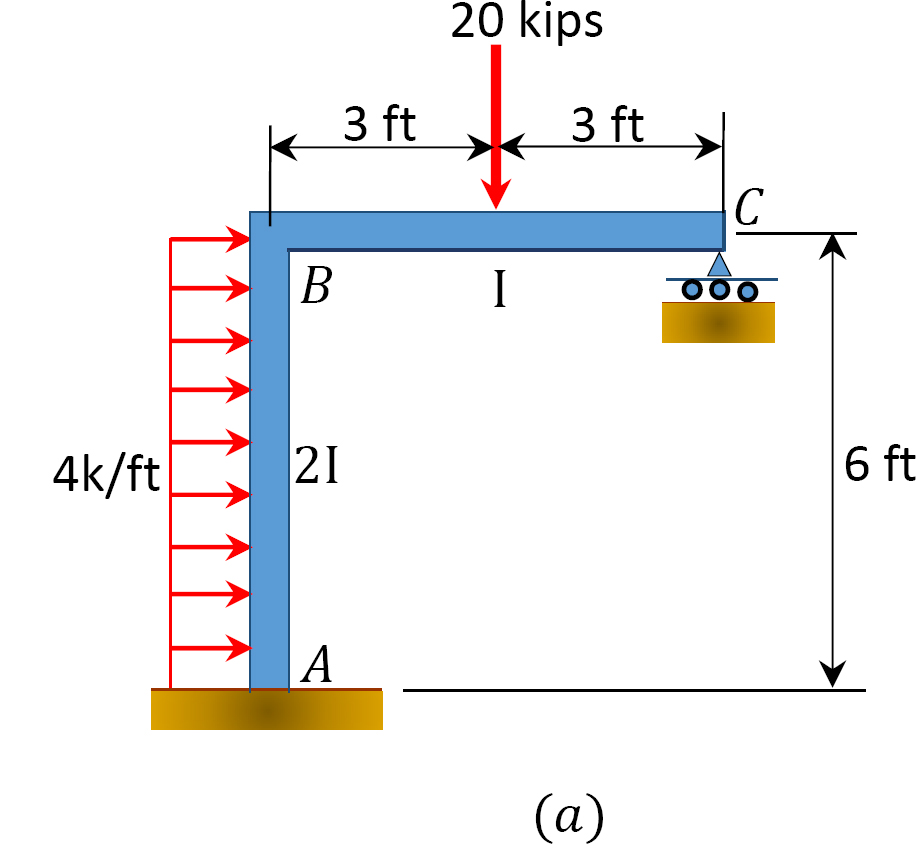
그림. 12.11. 사이드 스웨이가있는 프레임.
솔루션
고정 종료 순간.
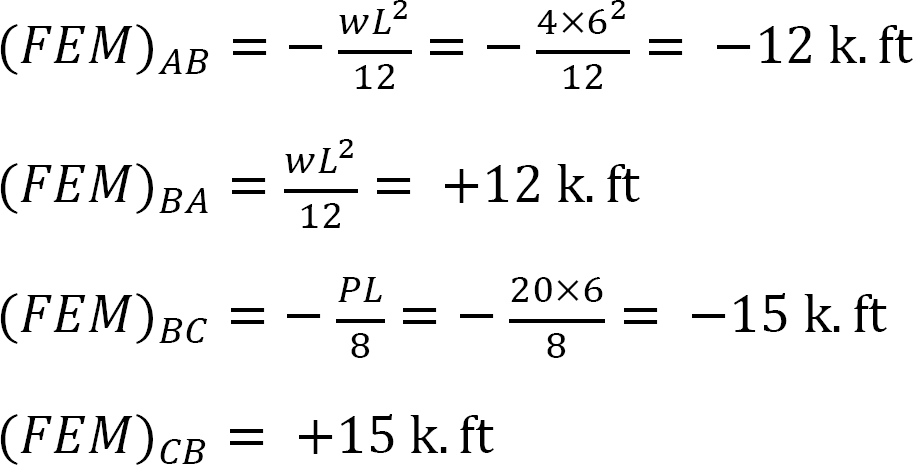
강성 계수.
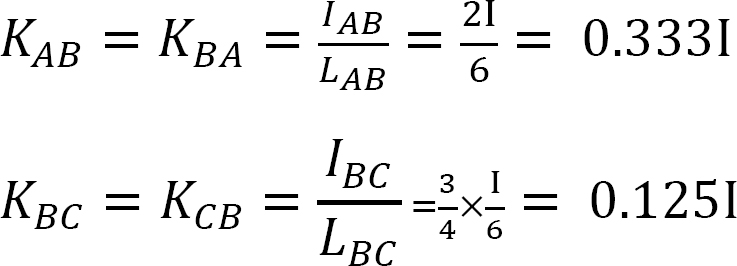
분포 계수.
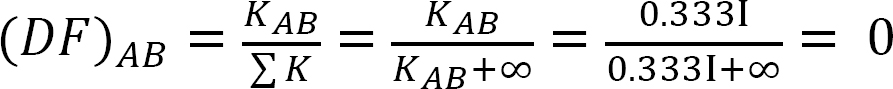

측 동요 없는 구조의 분석.
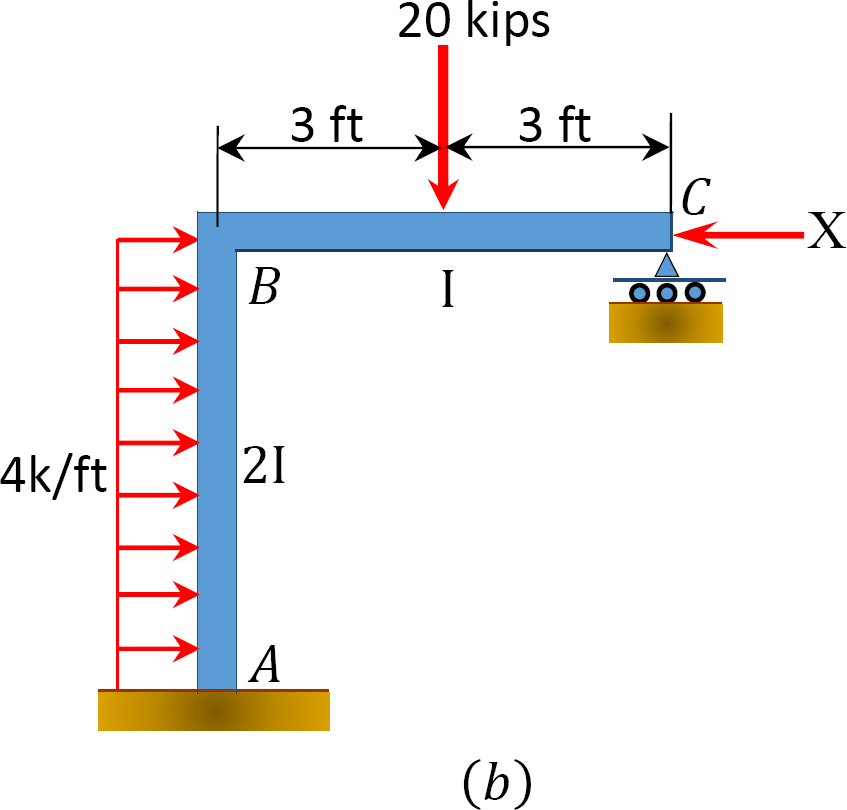
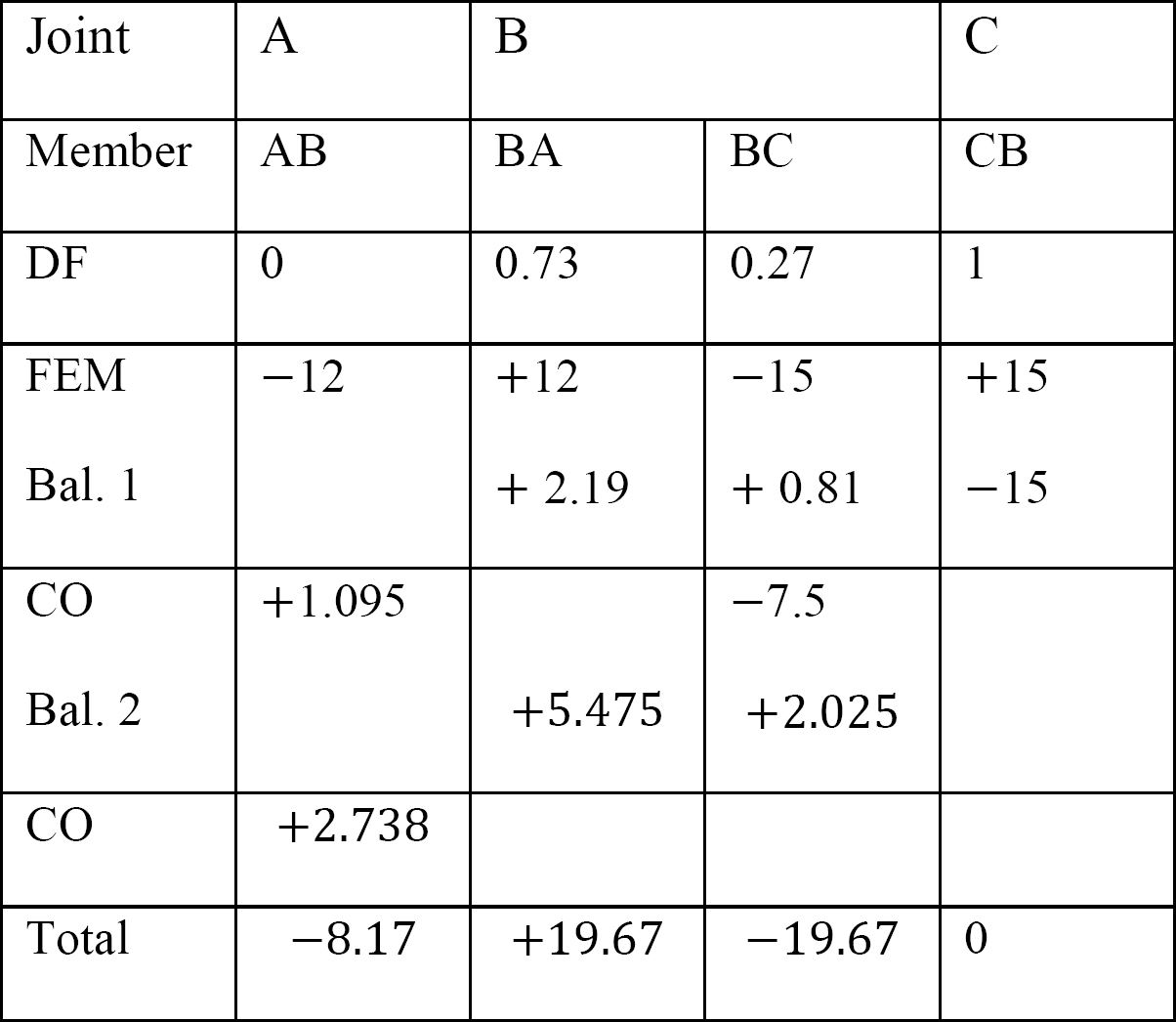
표 12.6. 배급 테이블(동요 구조 없음).
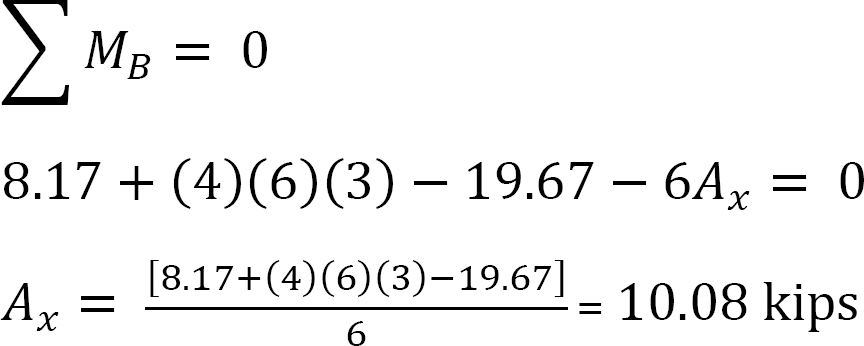
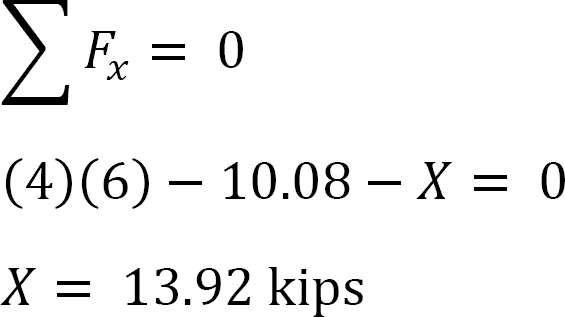
측 동요를 가진 구조의 분석.
정 MAB=+20k. ft
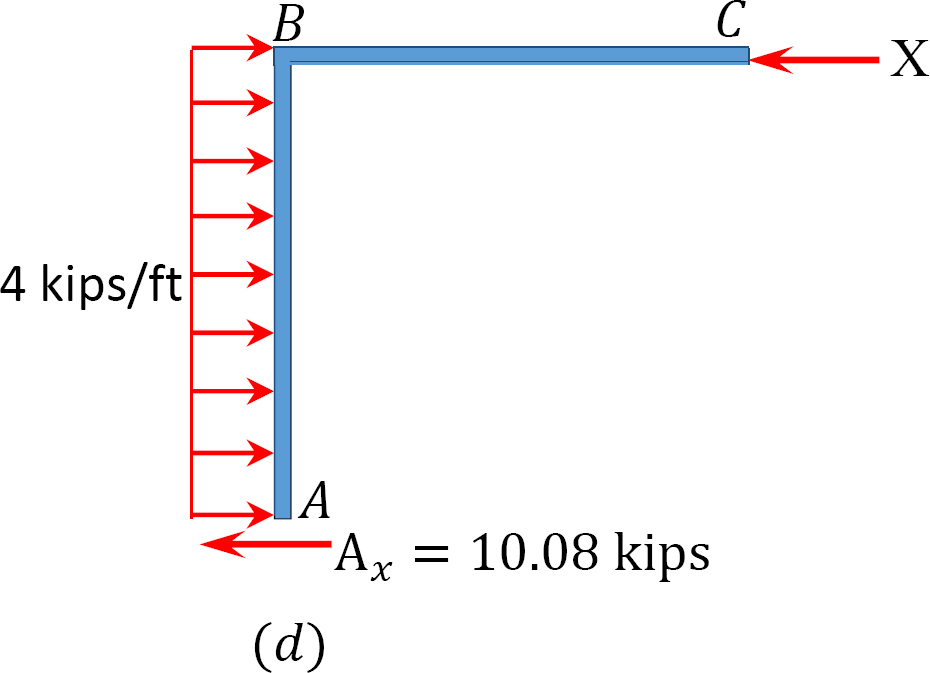
테이블 12.7. 배급 테이블(동요 구조).
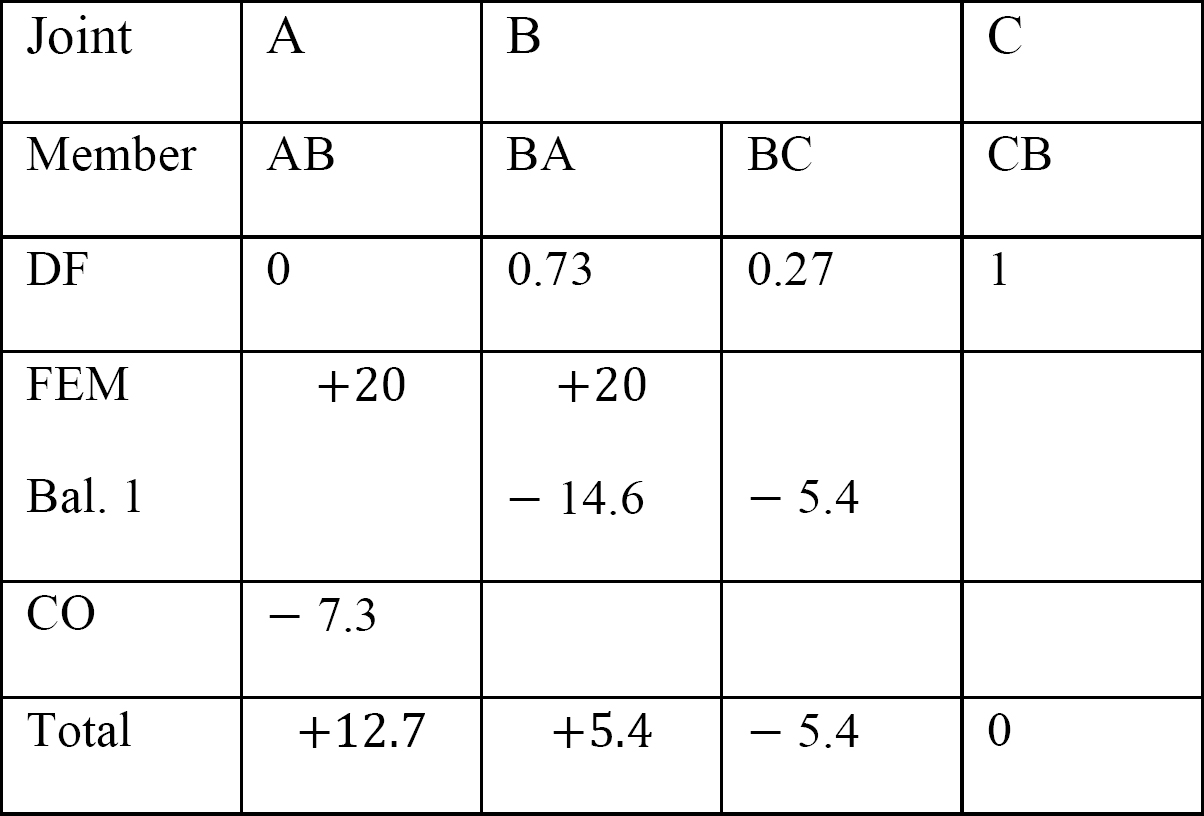
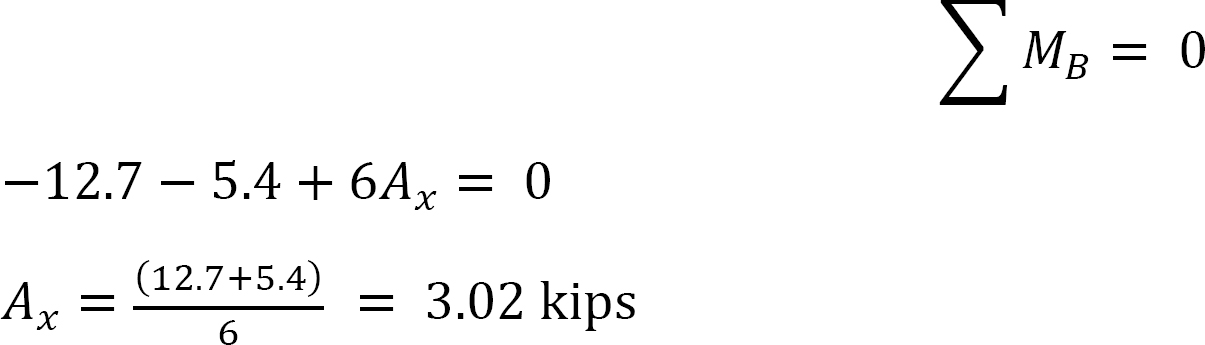
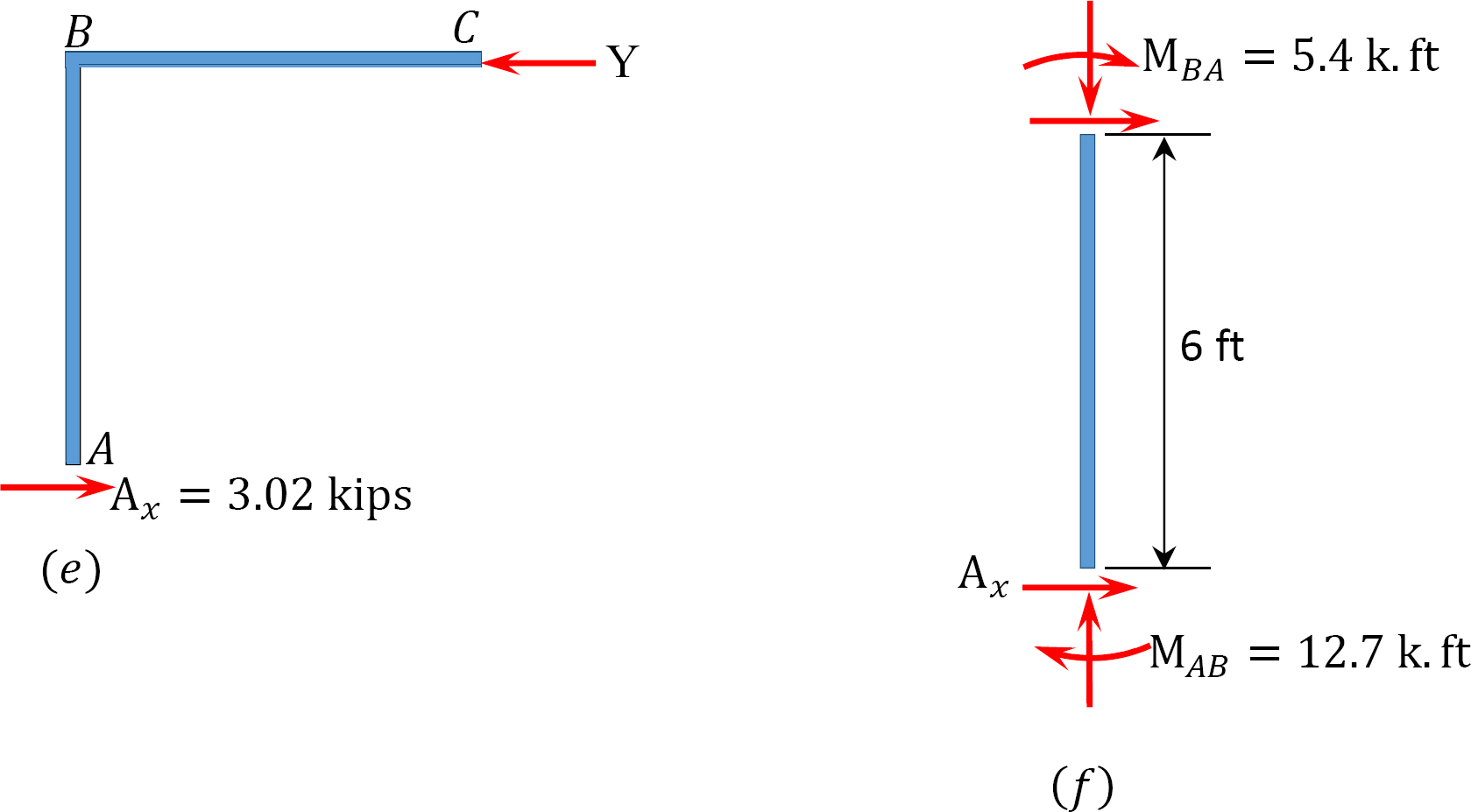
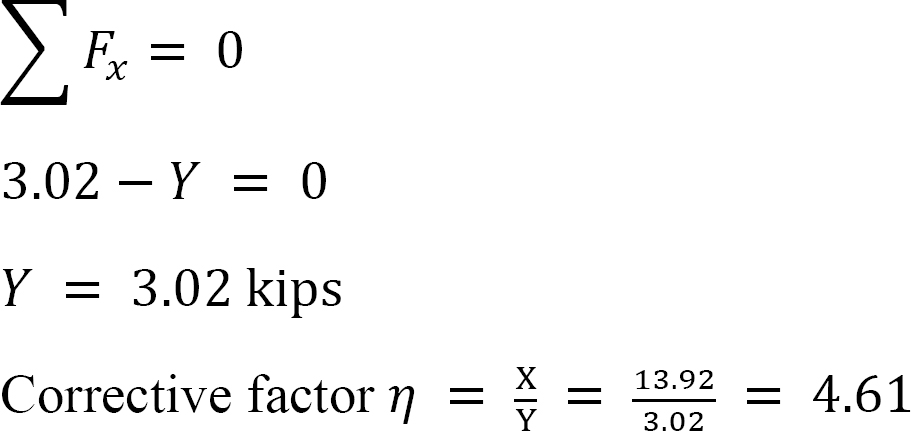
마지막 끝 순간.
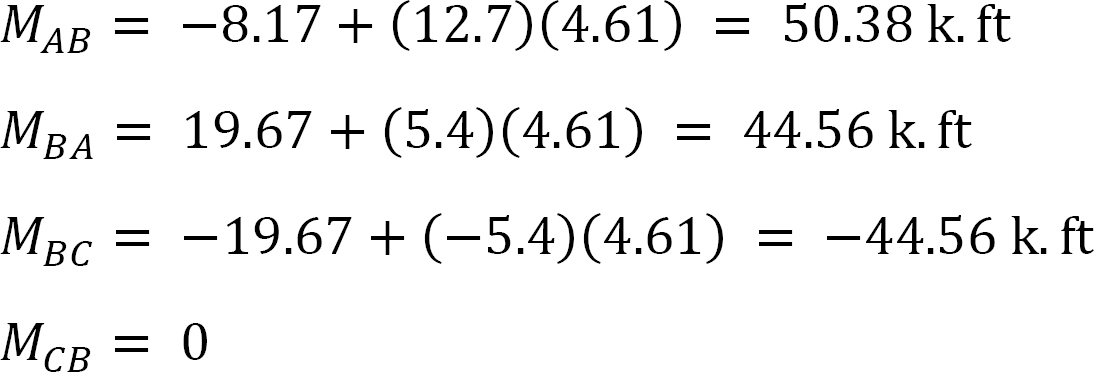
예 12.7
모멘트 분배 방법을 사용하여 프레임 멤버의 끝 모멘트를 결정합니다.
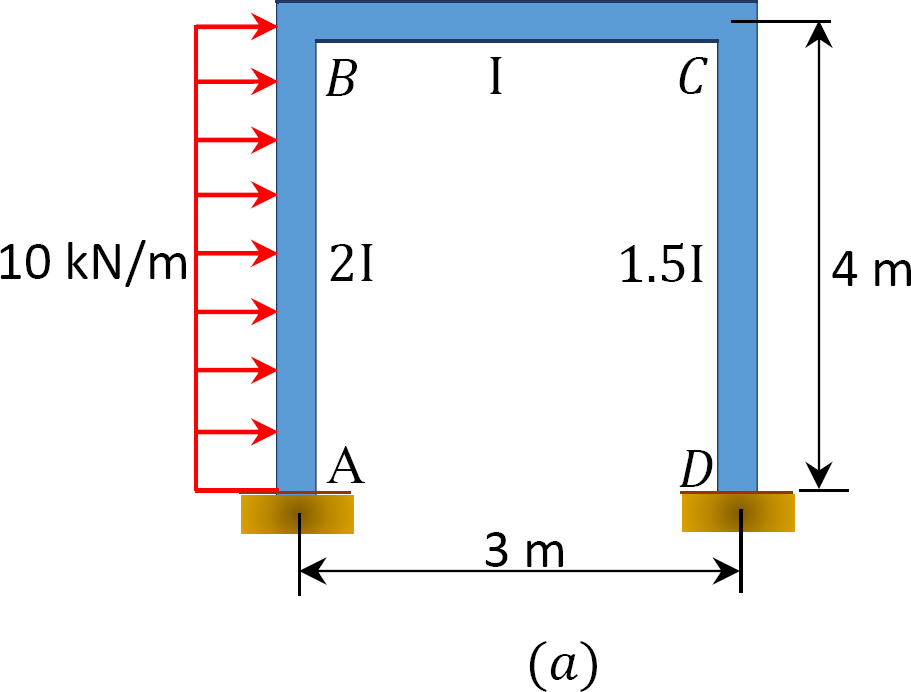
그림. 12.12. 로드 동요 프레임.
솔루션
고정 종료 순간.
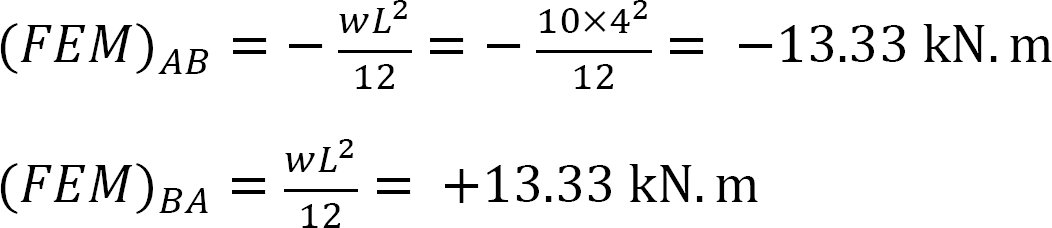
강성 계수.
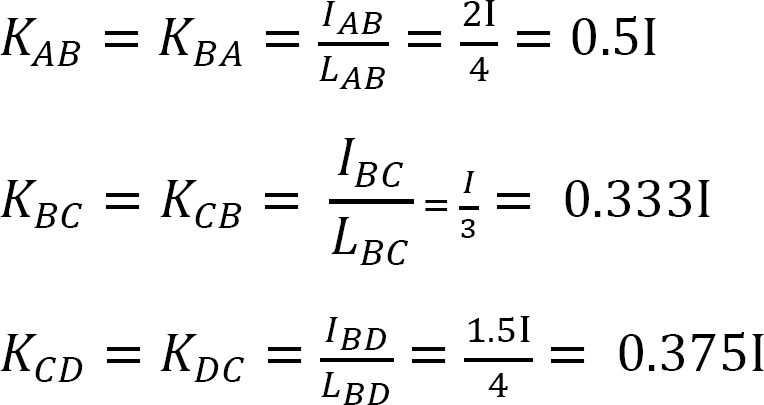
분포 계수.

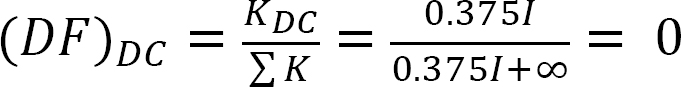
측 동요 없는 구조의 분석.
표 12.8. 배급 테이블(동요 구조 없음).
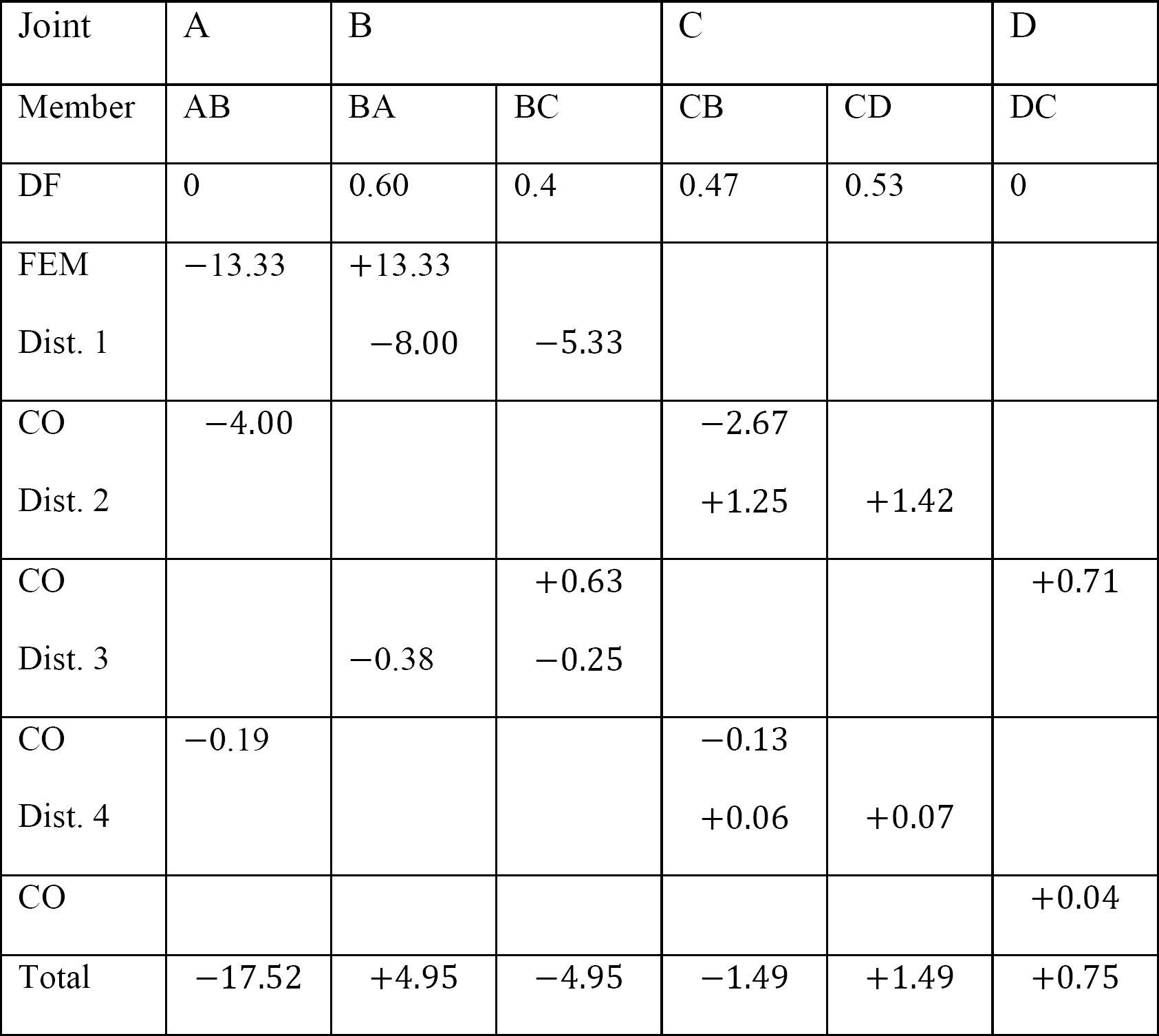
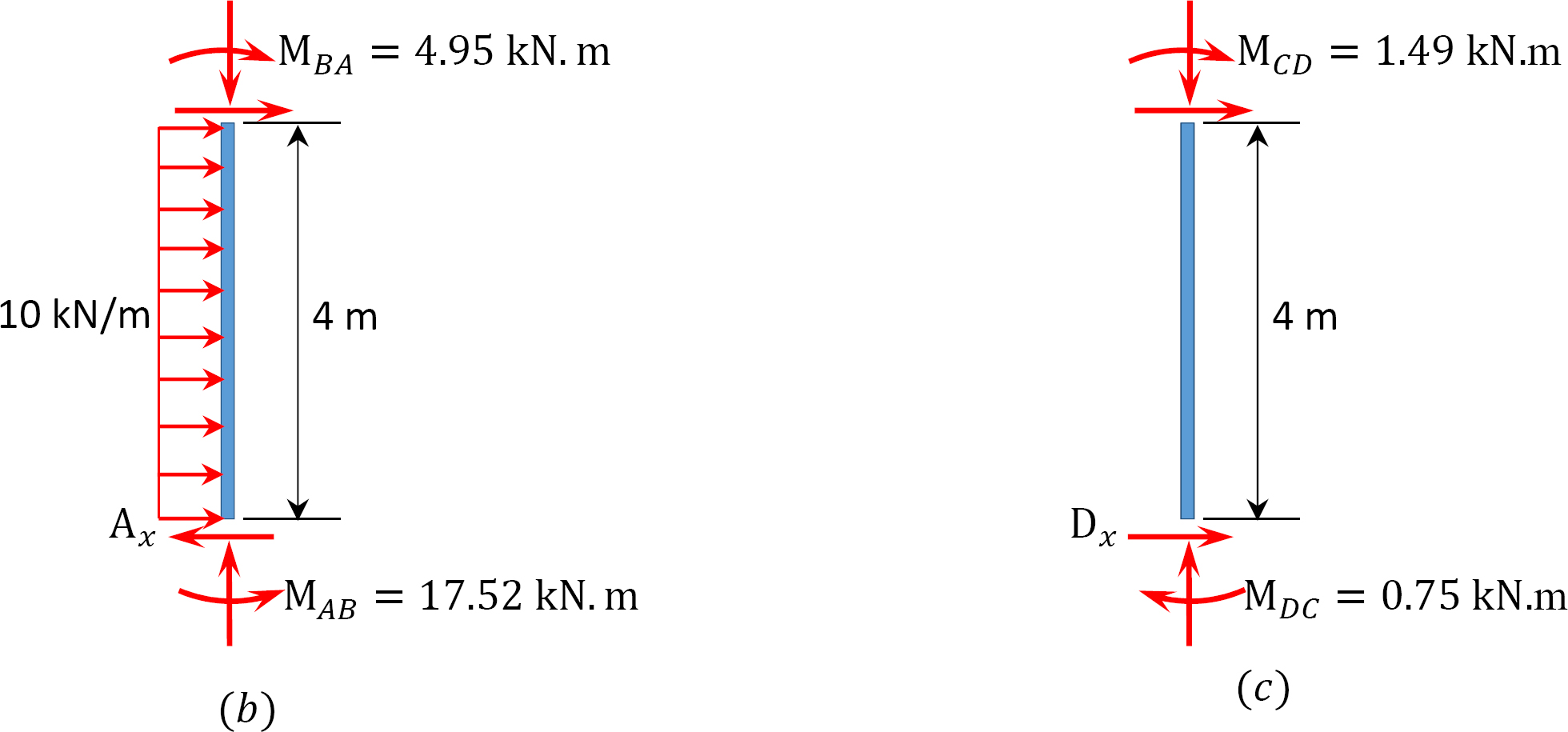
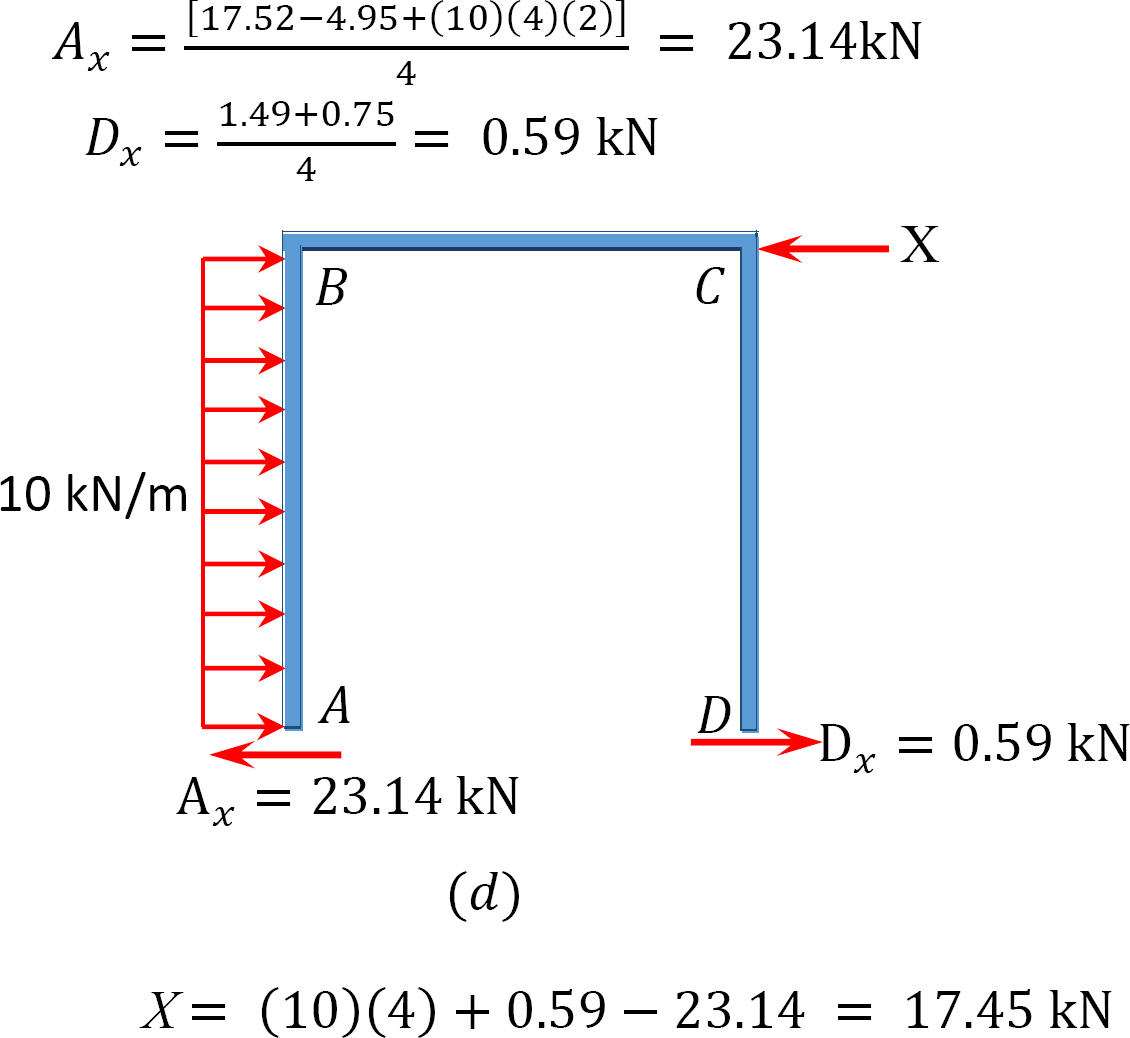
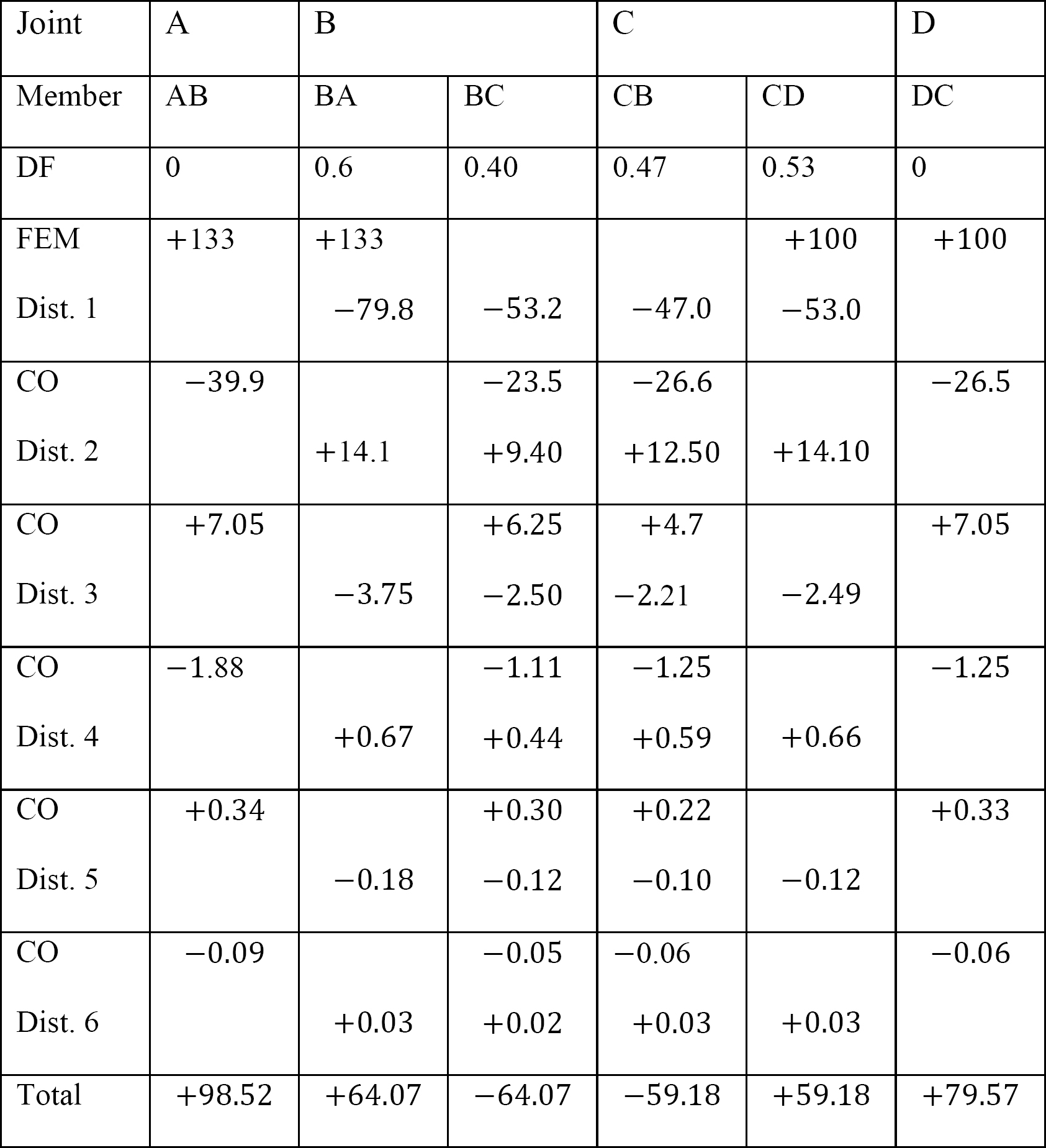
표 12.9. 배급 테이블(동요 구조).
측 동요를 가진 구조의 분석.
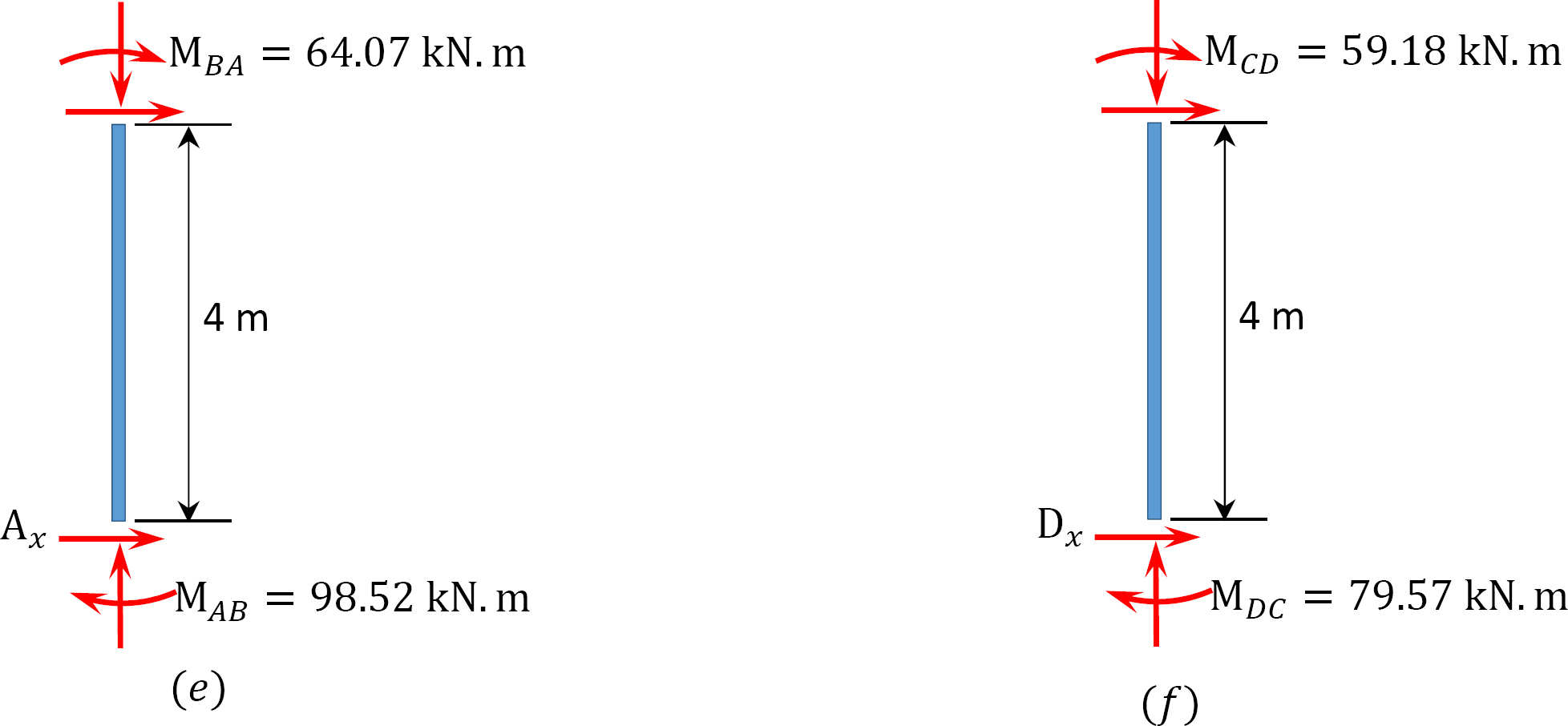

마지막 끝 순간.
= -17.52 + (98.52)(0.23) = 5.14 케인
= 4.95 + (64.07)(0.23) = 19.69 케인
= -4.95 + (-64.07)(0.23) = -19.69 케인
= -1.49 + (-59.18)(0.23) = -15.10 케인 전화 번호:+86-755-86100000= 1.49 + (59.18)(0.23) = 15.10 케인
= 0.75 + (79.57)(0.23) = 19.05 케인
장 요약
불확정 구조의 모멘트 분포 분석 방법:분석의 모멘트 분포 방법은 대략적인 분석 방법입니다. 정확도는 반복 횟수에 따라 달라집니다. 이 방법에서는 구조의 모든 조인트가 일시적으로 잠기거나 클램핑되어 가능한 회전을 방지한다고 가정합니다. 로드가 멤버에 적용되고 고정성으로 인해 멤버 끝에서 개발된 모멘트가 결정됩니다. 구조에 있는 합동은 그 때 연속적으로 자물쇠로 열리고,각 합동에 균형이 잡히지 않는 순간은 그 합동에 만나는 일원에게 배부됩니다. 멤버들의 먼 끝에서의 이월 모멘트가 결정되고,밸런싱 과정은 원하는 수준의 정확도까지 계속된다. 멤버의 종료 모멘트는 고정 종료 모멘트,분산 모멘트 및 이월 모멘트를 추가하여 결정됩니다. 멤버의 종료 모멘트가 결정되면 구조가 확정됩니다.
연습 문제
12.1 모멘트 분포 방법을 사용하여 그림 12.1 에서 그림 12.12 까지의 보 멤버의 끝 모멘트를 계산하고 굽힘 모멘트 및 전단력 다이어그램을 그립니다. 상수입니다.
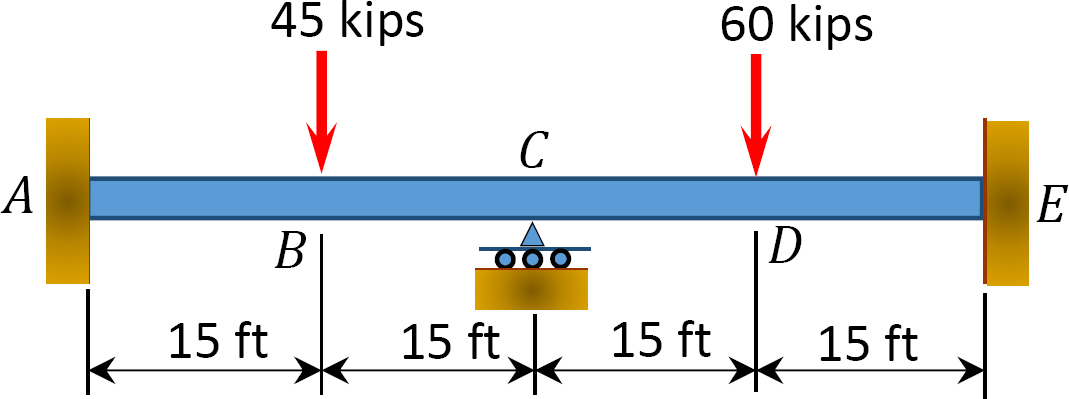
그림. 12.1 쪽 빔.
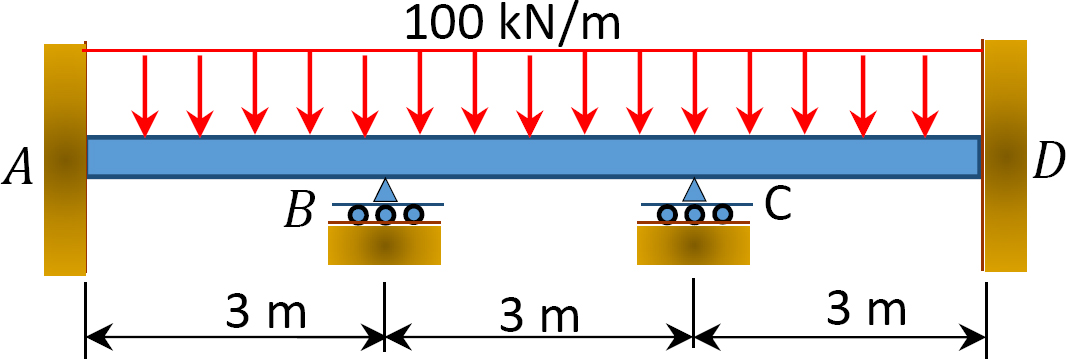
그림. 12.2 쪽 빔.
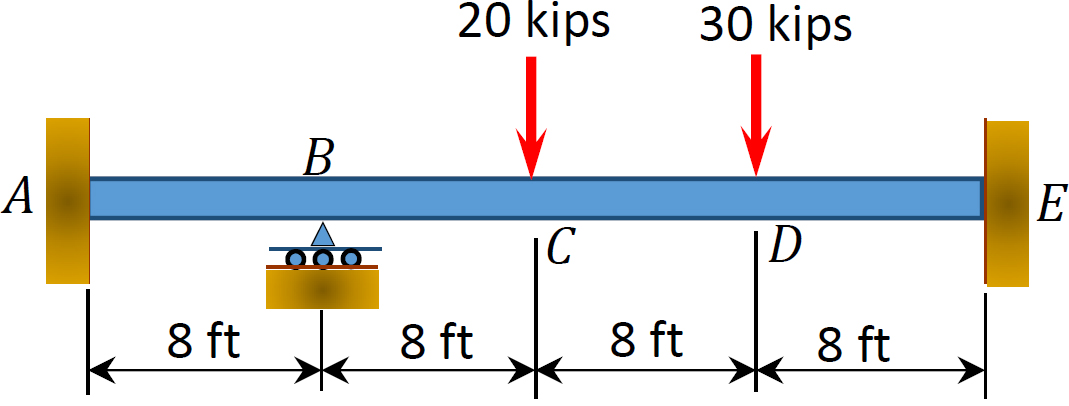
그림. 12.3 쪽 빔.
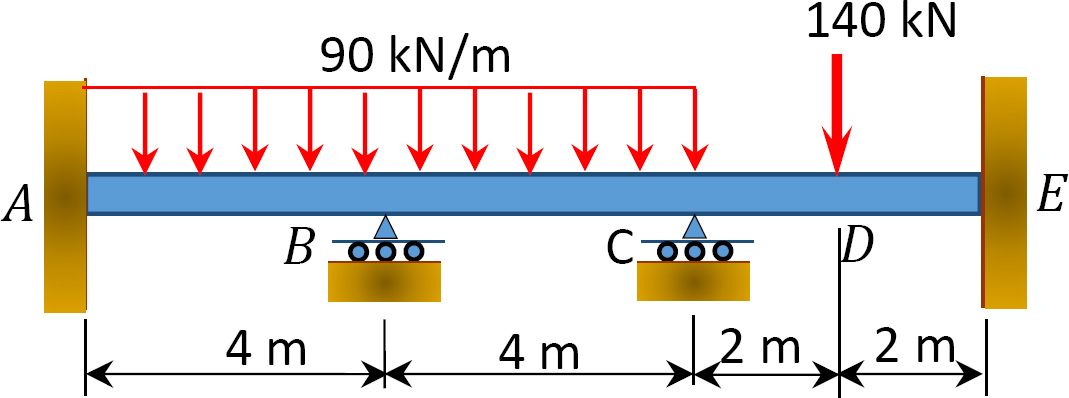
그림. 12.4 쪽 빔.
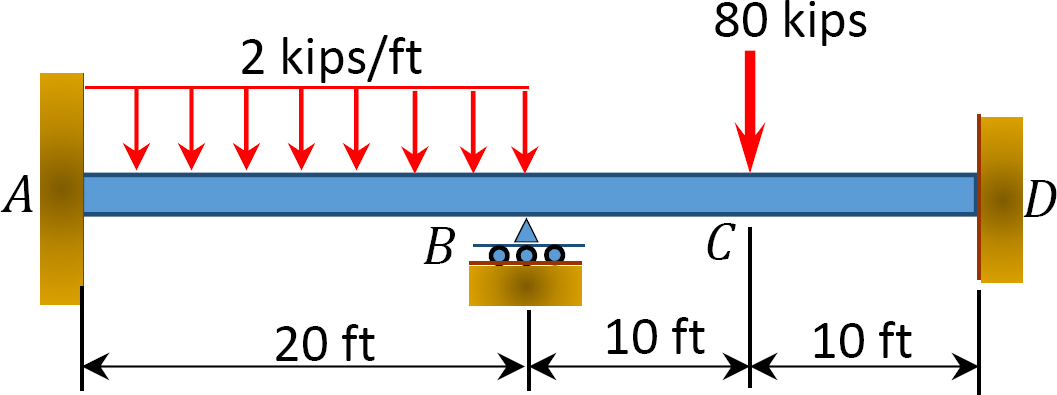
그림. 12.5 쪽 빔.
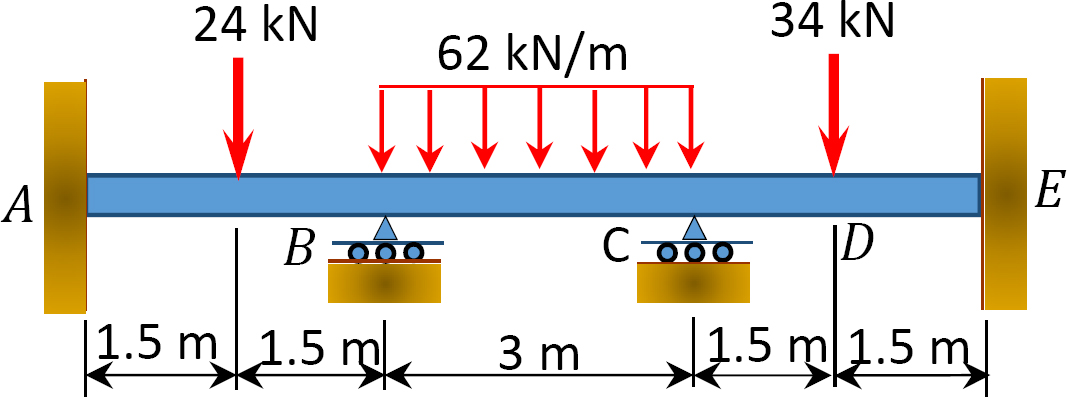
그림. 12.6 쪽 빔.
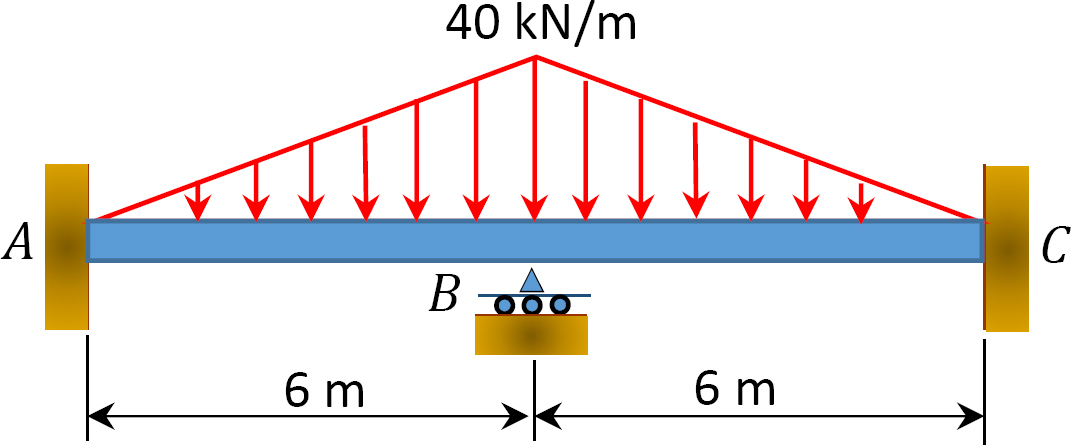
그림. 12.7 쪽 빔.
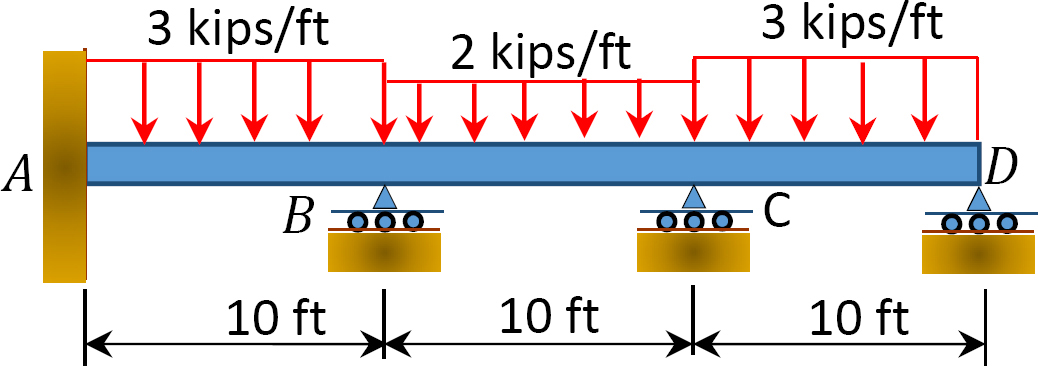
그림. 12.8 쪽 빔.
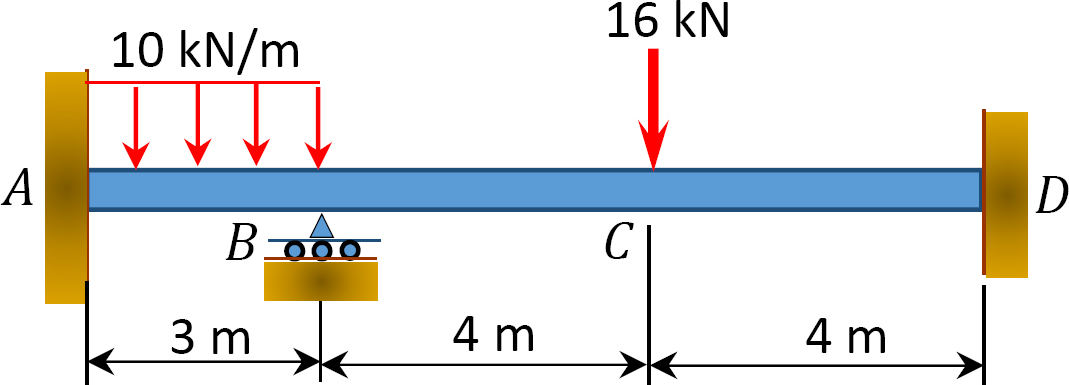
그림. 12.9 쪽 빔.
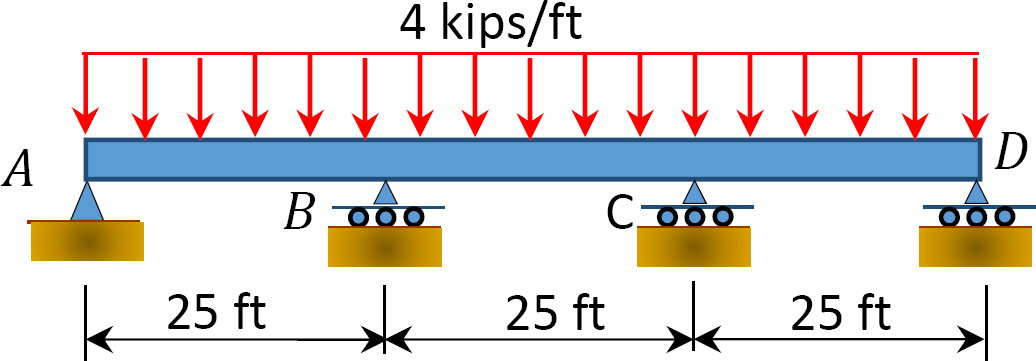
그림. 12.10 쪽 빔.
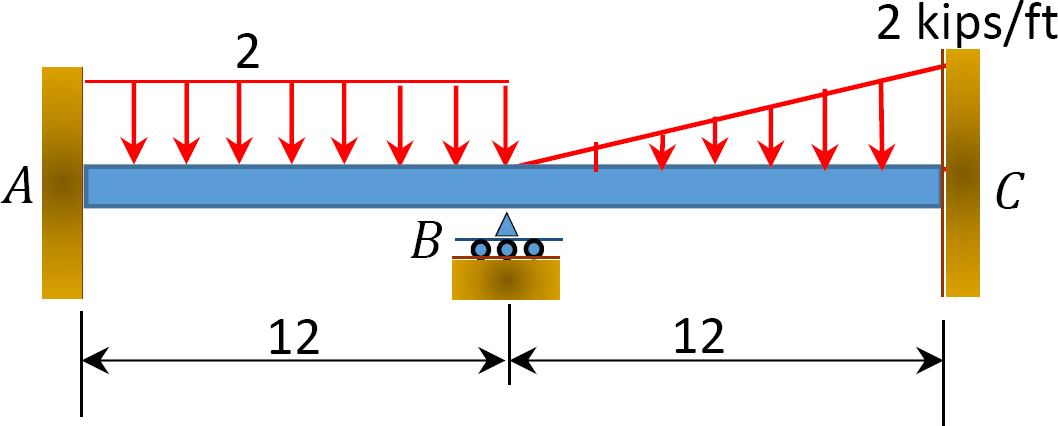
그림. 12.11 쪽 빔.
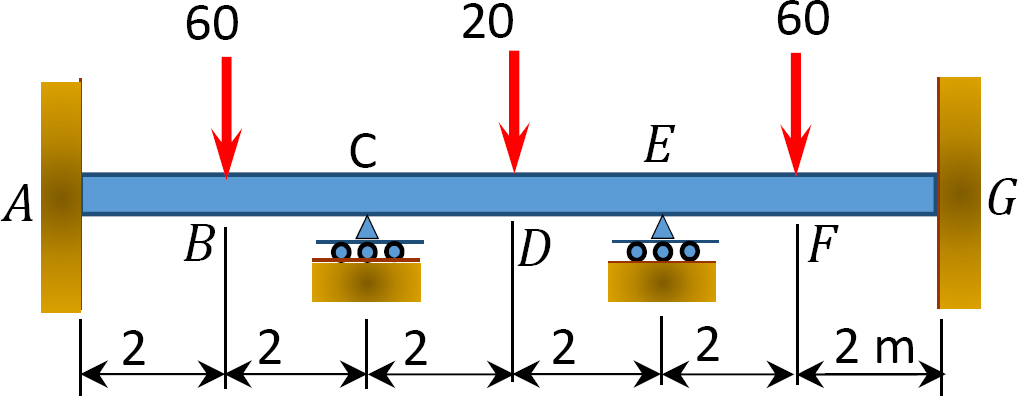
그림. 12.12 쪽 빔.12.2 모멘트 분포 방법을 사용하여 그림 12.13 에서 그림 12.20 에 표시된 프레임 멤버의 끝 모멘트를 계산하고 굽힘 모멘트와 전단력 다이어그램을 그립니다. 상수입니다.
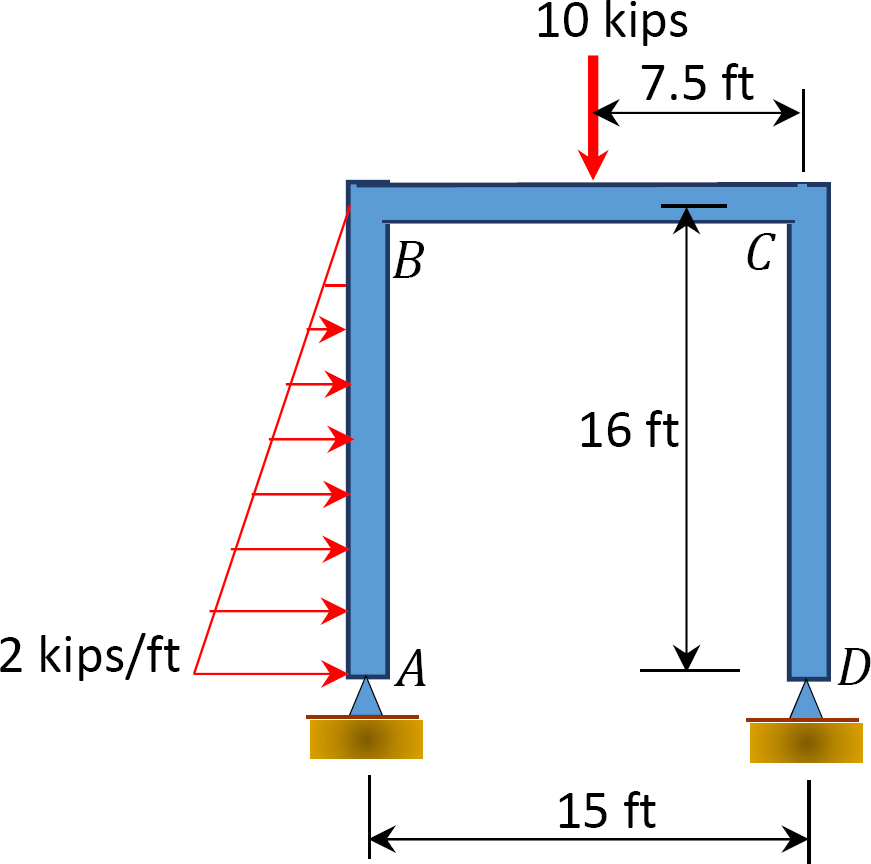
그림. 12.13 쪽 프레임.
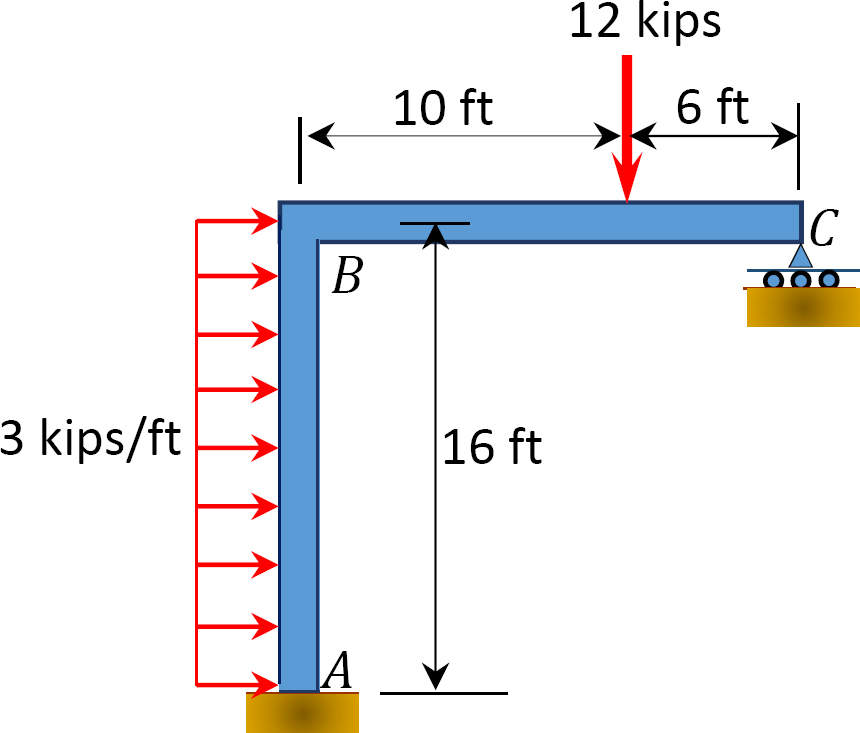
그림. 12.14 쪽 프레임.
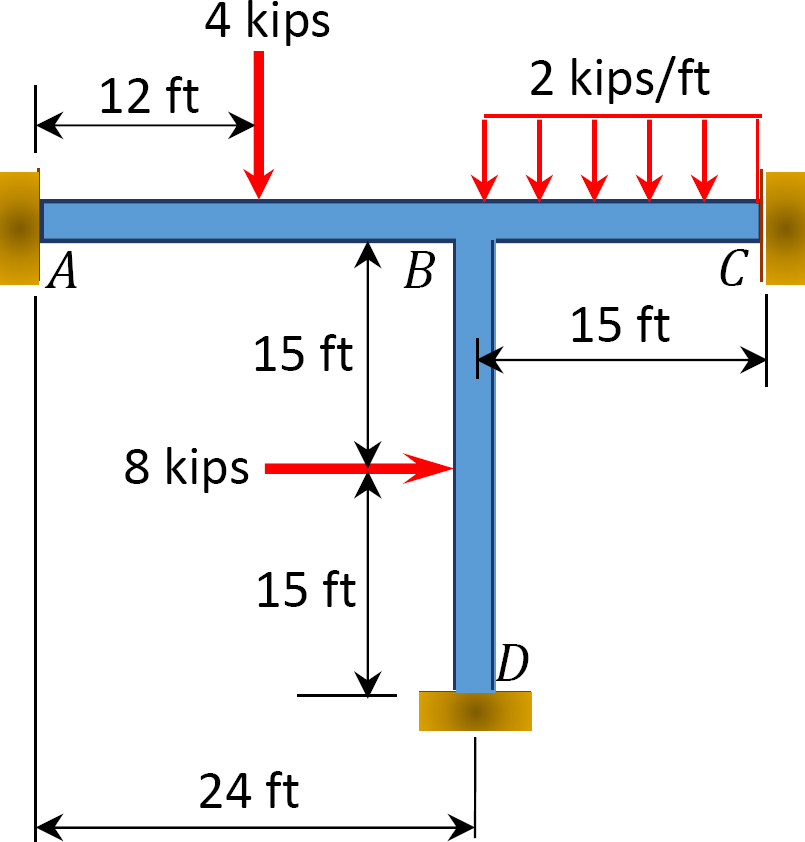
그림. 12.15 쪽 프레임.
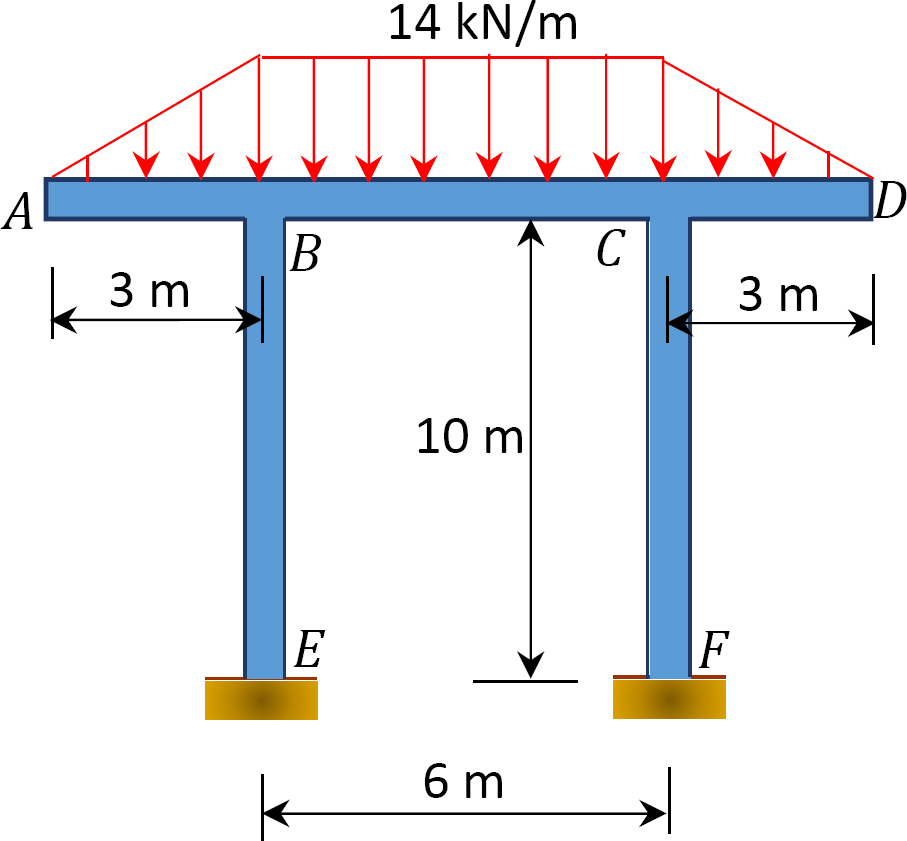
Fig. P12.16. Frame.
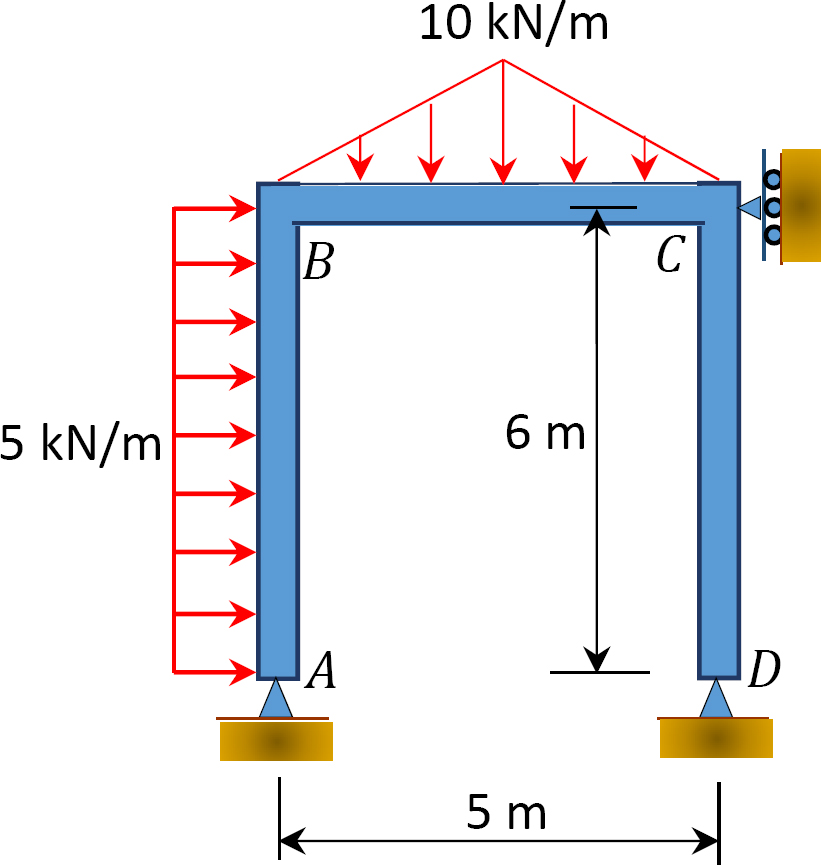
Fig. P12.17. Frame.
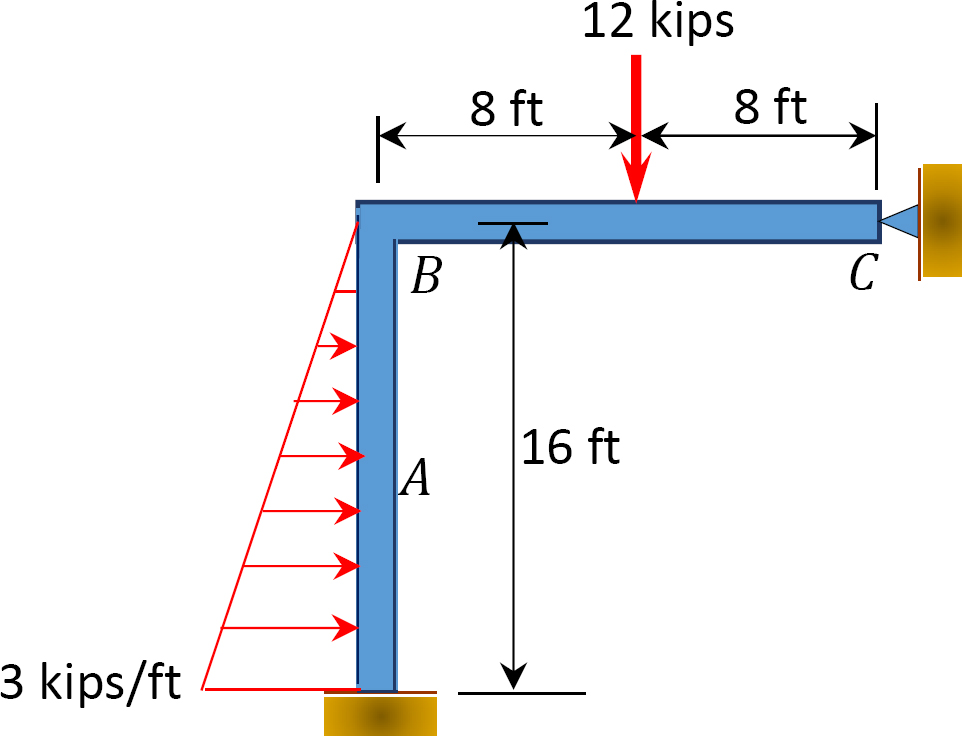
Fig. P12.18. Frame.
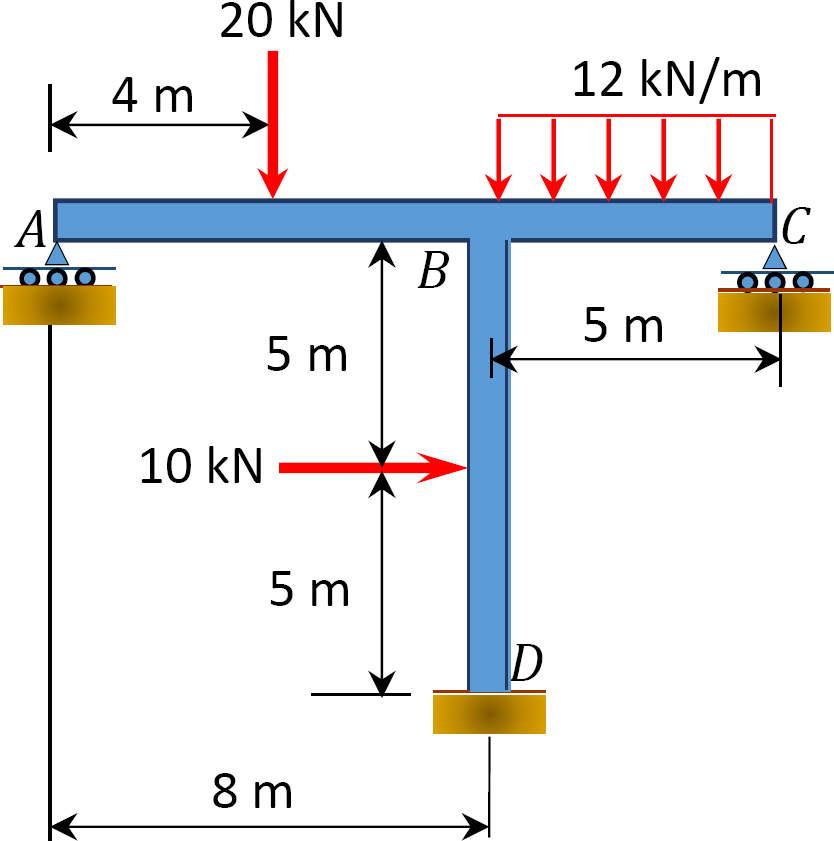
Fig. P12.19. Frame.
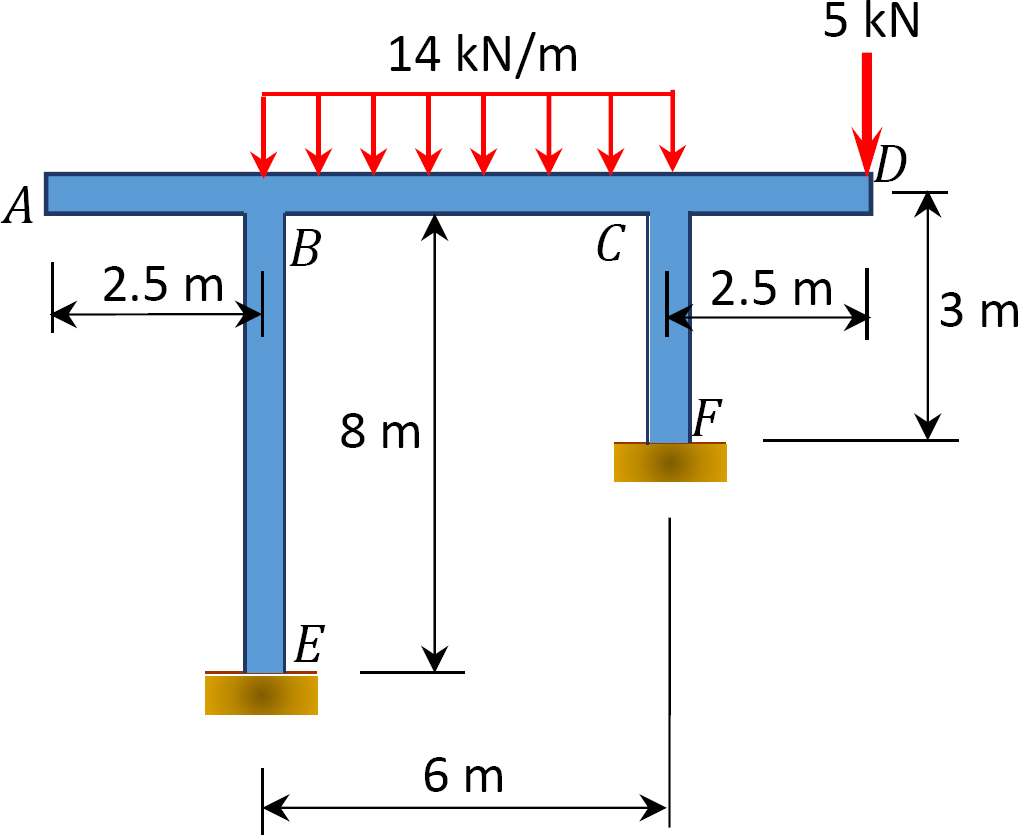
Fig. P12.20. Frame.