Modelos simples de Ornstein-Uhlenbeck

Estimación de los óptimos Evolutivos

Este tutorial muestra cómo especificar un modelo de Ornstein-Uhlenbeck en el que se supone que el fenotipo óptimo es constante entre ramas de una filogenia calibrada en el tiempo (referencia faltante) utilizando los conjuntos de datos de tamaño corporal (logarítmico) a través de clados de vertebrados (referencia faltante). Proporcionamos la representación gráfica probabilística de cada componente para este tutorial. Después de especificar el modelo, estimará los parámetros de la evolución de Ornstein-Uhlenbeck utilizando Markov chain Monte Carlo (MCMC).

Modelo de Ornstein-Uhlenbeck

Bajo el modelo simple de Ornstein-Uhlenbeck (OU), se asume que un carácter continuo evoluciona hacia un valor óptimo, $\theta th. El carácter evoluciona estocásticamente de acuerdo con un parámetro de deriva, $\sigma^2$. El carácter es empujado hacia el óptimo por la tasa de adaptación, \ \ alpha$; valores más grandes de alfa indican que el carácter se tira más fuertemente hacia $\theta th. A medida que el carácter se aleja de $\theta,, el parámetro alpha\alpha determines determina la fuerza con la que se retira el carácter. Por esta razón, $\alpha sometimes a veces se conoce como un parámetro de «banda elástica». Cuando el parámetro de velocidad de adaptación \ \ alpha = 0$, el modelo de unidad organizativa se contrae en el modelo BM. El modelo gráfico resultante es bastante simple, ya que la probabilidad de los caracteres continuos depende solo de la filogenia (que asumimos que se conoce en este tutorial) y los tres parámetros de OU ().

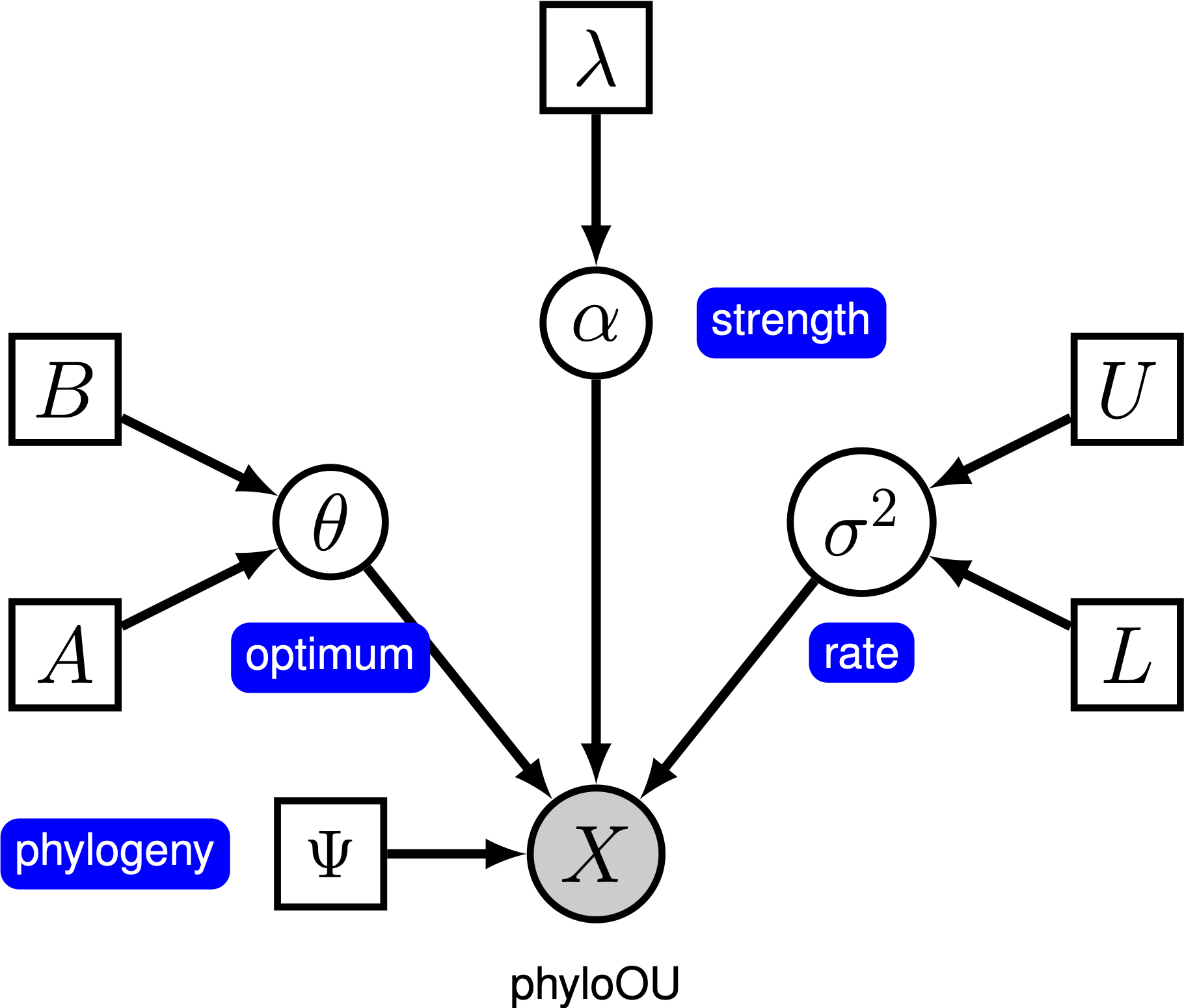
En este tutorial, utilizamos los 66 conjuntos de datos de tamaño corporal (log) y filogenias de vertebrados de (Landis y Schraiber 2017).

The La especificación completa del modelo de unidad organizativa se encuentra en el archivo llamado mcmc_OU.Rev.

Leer los datos

Comenzamos decidiendo cuál de los 66 conjuntos de datos de vertebrados usar. Aquí, asumimos que estamos analizando el primer conjunto de datos (Acanthuridae), pero debe sentirse libre de elegir cualquiera de los conjuntos de datos.

dataset <- 1

Ahora, leemos en el árbol (calibrado en el tiempo) correspondiente a nuestro conjunto de datos elegido.

T <- readTrees("data/trees.nex")

A continuación, leemos en los datos de caracteres para el mismo conjunto de datos.

data <- readContinuousCharacterData("data/traits.nex")

Además, inicializamos una variable para nuestros vectores de cámaras y monitores:

moves = VectorMoves()monitors = VectorMonitors()

Especificando el modelo

Modelo de árbol

En este tutorial, asumimos que el árbol se conoce sin área. Creamos un nodo constante para el árbol que corresponde a la filogenia observada.

tree <- T

Parámetro de velocidad

La velocidad estocástica de evolución está controlada por el parámetro de velocidad, $ \ sigma^2$. Dibujamos el parámetro de velocidad de un prior loguniforme. Este prior es uniforme en la escala logarítmica, lo que significa que representa ignorancia sobre el orden de magnitud de la tasa.

sigma2 ~ dnLoguniform(1e-3, 1)

Para estimar la distribución posterior de $\sigma^2$, debemos proporcionar un mecanismo de propuesta MCMC que opere en este nodo. Debido a que $ \ sigma^2 is es un parámetro de velocidad, y por lo tanto debe ser positivo, usamos un movimiento de escala llamado mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Parámetro de adaptación

La velocidad de adaptación hacia el óptimo está determinada por el parámetro alpha \ alpha alpha. Extraemos \ \ alpha from de una distribución anterior exponencial y le colocamos una propuesta de escala.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Óptimo

Extraemos el valor óptimo de un prior uniforme vago que va de -10 a 10 (debes cambiar este prior si tu personaje está fuera de este rango). Debido a que este parámetro puede ser positivo o negativo, usamos un movimiento de diapositiva para proponer cambios durante MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Modelo de Ornstein-Uhlenbeck

Ahora que hemos especificado los parámetros del modelo, podemos dibujar los datos de caracteres del modelo filogenético OU correspondiente. En este ejemplo, usamos el algoritmo REML para calcular eficientemente la probabilidad (Felsenstein 1985). Asumimos que el carácter comienza en el valor óptimo en la raíz del árbol.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Observando que $X is es el dato observado (), sujetamos el data a este nodo estocástico.

X.clamp(data)

Finalmente, creamos un objeto de espacio de trabajo para todo el modelo con model(). Recuerde que los objetos de espacio de trabajo se inicializan con el operador = y no forman parte del modelo gráfico bayesiano. La función model() recorre todo el gráfico del modelo y encuentra todos los nodos del modelo que especificamos. Este objeto proporciona una forma conveniente de referirse a todo el objeto del modelo, en lugar de a un solo nodo DAG.

mymodel = model(theta)

Ejecutar un análisis MCMC

Especificar monitores

Para nuestro análisis MCMC, necesitamos configurar un vector de monitores para registrar los estados de nuestra cadena de Markov. Todas las funciones del monitor se denominan mn*, donde * es el comodín que representa el tipo de monitor. En primer lugar, inicializaremos el monitor del modelo utilizando la función mnModel. Esto crea una nueva variable de monitor que genera los estados de todos los parámetros del modelo cuando se pasa a una función MCMC.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

Además, cree un monitor de pantalla que reportará los estados de variables específicas a la pantalla con mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Inicializando y ejecutando la simulación MCMC

Con un modelo completamente especificado, un conjunto de monitores y un conjunto de movimientos, ahora podemos configurar el algoritmo MCMC que muestreará los valores de los parámetros en proporción a su probabilidad posterior. La función mcmc() creará nuestro objeto MCMC:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Ahora, ejecute el MCMC:

mymcmc.run(generations=50000)

Cuando se complete el análisis, tendrá los archivos monitoreados en el directorio yourutput.

file El archivo Rev para realizar este análisis: mcmc_OU.Rev

Los caracteres que evolucionan bajo el proceso OU tenderán a una distribución estacionaria, que es una distribución normal con media \\theta.y varianza^\sigma ^ 2\div 2 \ alpha alpha. Por lo tanto, si las tasas de evolución son altas (o las ramas en el árbol son relativamente largas), puede ser difícil estimar separately\sigma^2 separately y separately\alpha separately por separado, ya que ambos determinan la varianza a largo plazo del proceso. Podemos ver si esto afecta nuestro análisis examinando la distribución posterior de las articulaciones de los parámetros en Tracer. Cuando los parámetros están correlacionados positivamente, debemos dudar en interpretar sus distribuciones marginales (es decir, no hacer inferencias sobre la tasa de adaptación o el parámetro de varianza por separado).

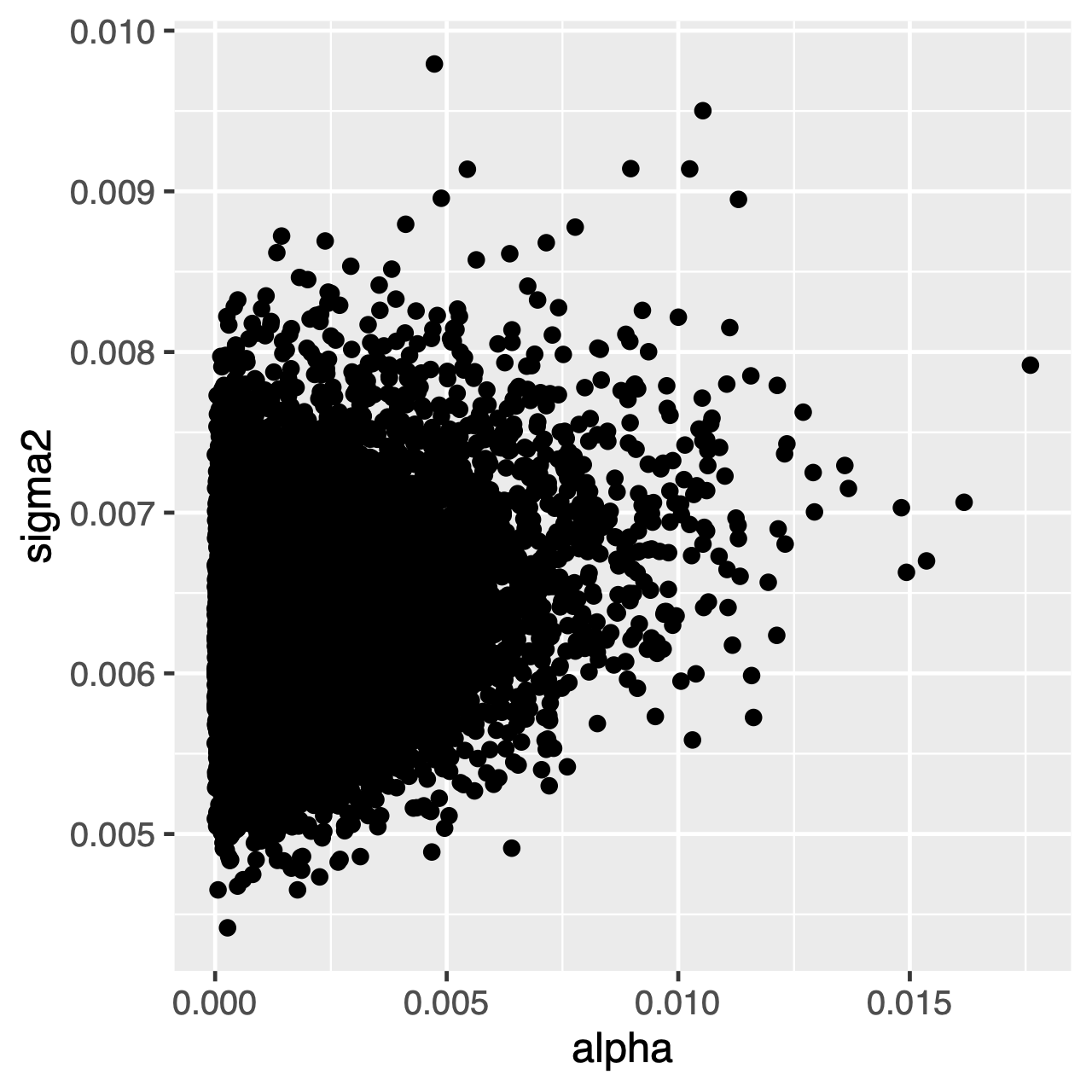
Ejercicio 1

• Ejecute una simulación MCMC para estimar la distribución posterior del óptimo de unidad organizativa (theta).
• Cargue el archivo de salida generado en Tracer: ¿Cuál es la estimación posterior media de theta y cuál es el HPD estimado?
• Use Tracer para comparar las distribuciones posteriores de las articulaciones de alpha y sigma2. ¿Estos parámetros están correlacionados o no correlacionados?
• Compare la media previa con la media posterior. (Sugerencia: Utilice el argumento opcional underPrior=TRUE en la función mymcmc.run()) ¿Son diferentes (por ejemplo,)? ¿La media posterior está fuera del intervalo de probabilidad del 95% anterior?

Comparar modelos OU y BM

Ahora que podemos encajar tanto en modelos BM como en modelos OU, es posible que, naturalmente, queramos saber qué modelo se ajusta mejor. En esta sección, aprenderemos a usar la cadena Markov Montecarlo de salto reversible para comparar el ajuste de los modelos OU y BM.

Selección de modelos utilizando el salto reversible MCMC

Para probar la hipótesis de que un personaje evoluciona hacia un óptimo selectivo, imaginamos dos modelos. El primer modelo, donde no hay adaptación hacia el óptimo, es el caso cuando $\alpha = 0$. El segundo modelo corresponde al modelo de unidad organizativa con $ \ alpha > 0$. Esto funciona porque el movimiento browniano es un caso especial del modelo OU cuando la tasa de adaptación es 0. Desafortunadamente, debido a que $ \ alpha is es un parámetro continuo, una cadena de Markov estándar nunca visitará estados en los que cada valor sea exactamente igual a 0. Afortunadamente, podemos usar salto reversible para permitir que la cadena Markov considere visitar el modelo de movimiento browniano. Esto implica especificar la probabilidad previa en cada uno de los dos modelos, y proporcionar la distribución previa para $\alpha for para el modelo OU.

El uso de rjMCMC permite a la cadena Markov visitar los dos modelos en proporción a su probabilidad posterior. La probabilidad posterior del modelo i i is es simplemente la fracción de muestras donde la cadena visitaba ese modelo. Debido a que también especificamos un prior en los modelos, podemos calcular un factor de Bayes para el modelo de unidad organizativa como:

\

donde $P( \text{modelo de unidad organizativa} \mid X) are y P P( \text{modelo de unidad organizativa}) are son la probabilidad posterior y la probabilidad anterior del modelo de unidad organizativa, respectivamente.

Salto reversible entre modelos OU y BM

Para habilitar rjMCMC, simplemente tenemos que colocar un salto reversible antes en el parámetro relevante, $ \ alpha$. Podemos modificar el prior en alpha para que tome un valor constante de 0, o se extraiga de una distribución anterior. Finalmente, especificamos una probabilidad previa en el modelo de unidad organizativa de p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

A continuación, proporcionamos una propuesta de salto reversible en alpha que propone cambios entre los dos modelos.

moves.append( mvRJSwitch(alpha, weight=1.0) )

Además, proporcionamos la propuesta mvScale normal para cuando el MCMC visita el modelo de unidad organizativa.

moves.append( mvScale(alpha, weight=1.0) )

Incluimos una variable que tiene un valor de 1 cuando la cadena está visitando el modelo de unidad organizativa, y una variable correspondiente que tiene un valor de 1 cuando está visitando el modelo de BM. Esto nos permitirá calcular fácilmente la probabilidad posterior de los modelos porque simplemente necesitamos calcular el valor medio posterior de este parámetro.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

Fracción de muestras para la que is_OU = 1 es la probabilidad posterior del modelo de unidad organizativa. Alternativamente, la estimación media posterior de esta variable indicadora corresponde a la probabilidad posterior del modelo de unidad organizativa. Estos valores se pueden usar en la ecuación del factor de Bayes anterior para calcular el soporte del Factor de Bayes para cualquiera de los modelos.

1. Felsenstein J. 1985. Phylogenies and the comparative method (en inglés). El Naturalista Americano.:1-15.10.1086/284325
2. Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Representación de Modelos Gráficos Probabilísticos en Filogenética. Biología Sistemática. 63: 753-771.10.1093/sysbio/syu039
3. Landis M. J., Schraiber J. G. 2017. Evolución pulsada en forma de tamaños de cuerpo de vertebrados modernos. Actas de la Academia Nacional de Ciencias. 114: 13224-13229.10.1073/pnas.1710920114