Kapittel 12
Moment Distribusjon Metode For Analyse Av Strukturer
12.1 Grunnleggende Begreper
moment distribusjon metode for analyse av bjelker og rammer ble utviklet Av Hardy Cross og formelt presentert i 1930. Selv om denne metoden er en deformasjonsmetode som hellingsbøyningsmetoden, er den en omtrentlig metode og krever dermed ikke å løse samtidige ligninger, slik det var tilfelle med sistnevnte metode. Graden av nøyaktighet av resultatene oppnådd ved metoden for momentfordeling avhenger av antall suksessive tilnærminger eller iterasjonsprosessen.
for å illustrere konseptet med metoden for momentfordeling, vurder rammen vist I Figur 12.1. Medlemmer av rammen er prismatiske og antas ikke å deformere aksialt eller oversette i forhold til hverandre. Leddene ACD av rammen er faste, mens felles B kan rotere litt på grunn av den påførte belastningen. Først, før du utfører momentfordeling blant medlemmer, antas alle leddene å være midlertidig låst ved hjelp av en klemme.
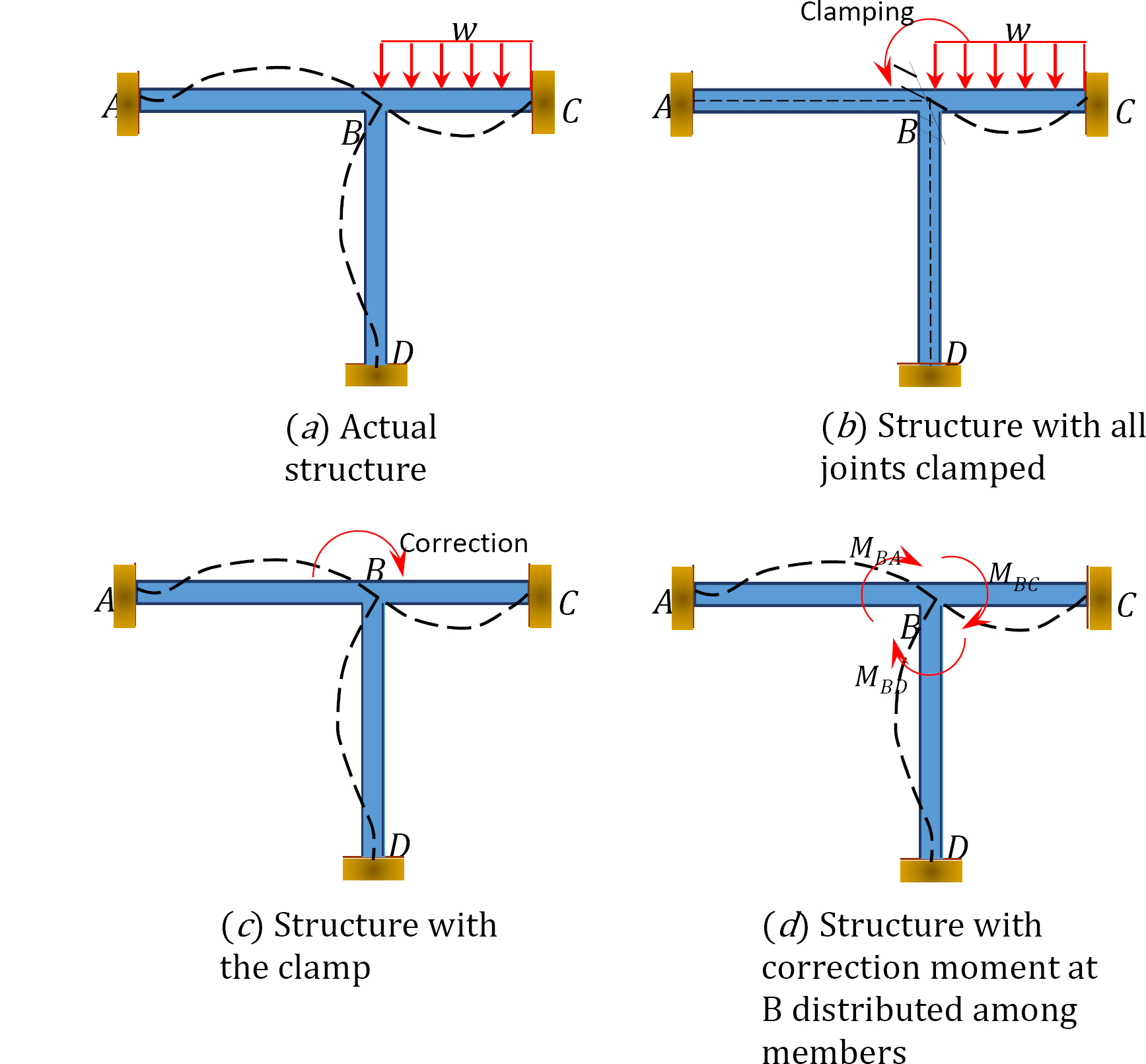
Fig. 12.1. Ramme.
12.2 Tegnkonvensjon
tegnkonvensjonen for øyeblikksfordelingsmetoden ligner den som er etablert for skråning-avbøyningsmetoden; det vil si at øyeblikket på slutten av et medlem anses som positivt hvis det har en tendens til å snu enden av medlemmet med urviseren og negativ hvis det har en tendens til å snu den mot klokka.
12.3 Definisjoner
Ubalanserte øyeblikk: denne analysemetoden antar at leddene i en struktur først klemmes eller låses og deretter frigjøres suksessivt. Når en felles er utgitt, finner en rotasjon sted, siden summen av de faste sluttmomentene til medlemsmøtet på den felles ikke er null. Verdien av summen av sluttmomentene som er oppnådd, er det ubalanserte øyeblikket ved den felles.
Overføringsmomenter: de distribuerte øyeblikkene i slutten av medlemsmøtet i en felles årsaksmomenter i den andre enden, som antas å være faste. Disse induserte øyeblikkene i den andre enden kalles overføringsmomenter.
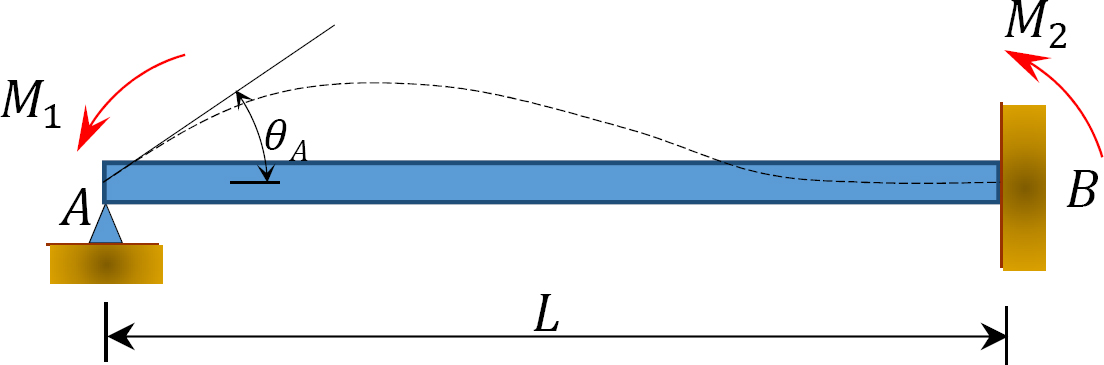
Fig. 12.2. Losset prismatisk stråle.
Vurder en losset prismatisk stråle festet til ende B, som vist i Figur 12.2. Hvis Et øyeblikk m1 påføres på venstre ende av strålen, kan skrånings-avbøyningsligningene for begge ender av strålen skrives som følger:


Å Erstatte 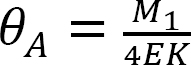 fra ligning 12.1 til ligning 12.2 foreslår følgende:
fra ligning 12.1 til ligning 12.2 foreslår følgende:

Ligning 12.3 antyder at øyeblikket overført til den faste enden av en stråle på grunn av et øyeblikk påført i den andre enden er lik halvparten av det påførte øyeblikket.
Overføringsfaktor: forholdet mellom det induserte øyeblikket og det anvendte øyeblikket refereres til som overføringsfaktoren. For strålen vist i Figur 12.2 er overføringsfaktoren som følger:

Distribuert faktor (DF): Den distribuerte faktor er en faktor som brukes til å bestemme andelen av ubalansert øyeblikk båret av hvert av medlemmene møte på en felles. For medlemsmøtet på felles O av rammen vist i Figur 12.3, beregnes deres fordelingsfaktorer som følger:
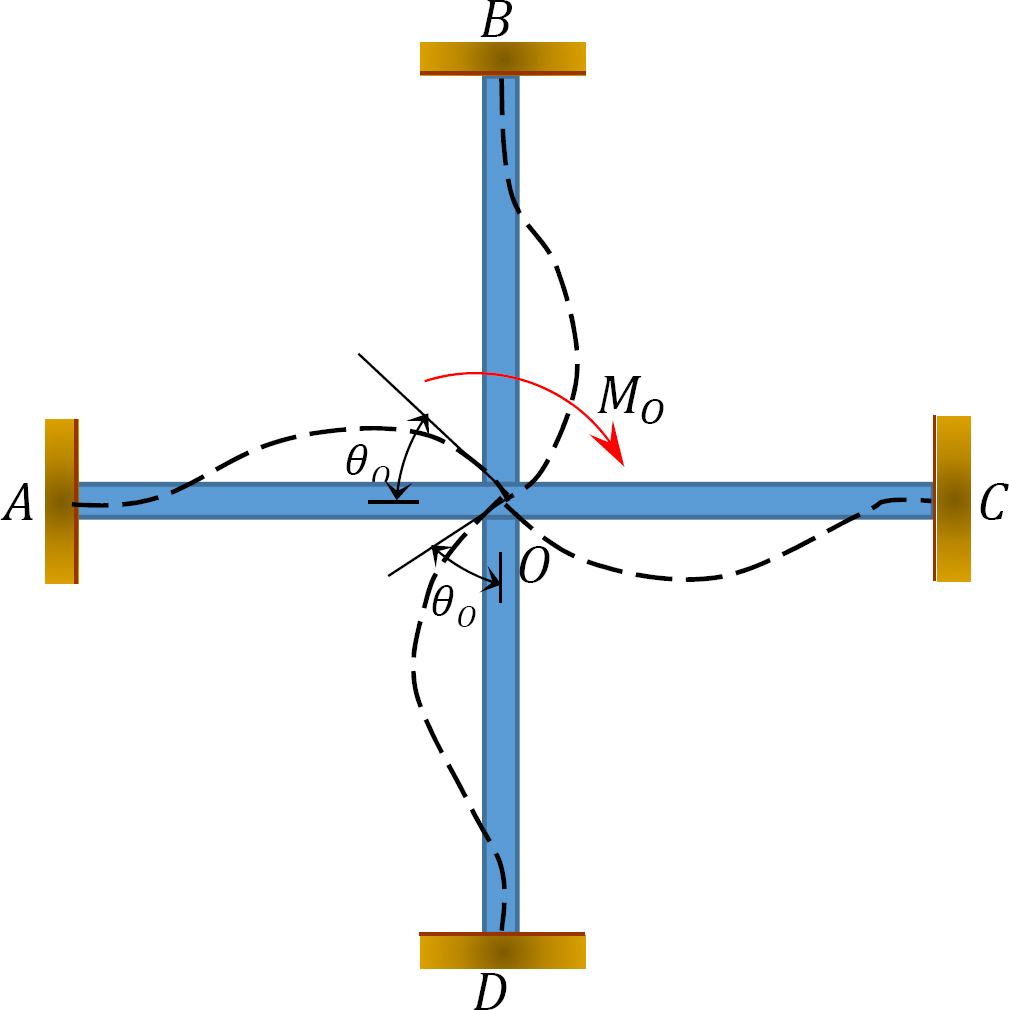
Fig. 12.3. Ramme.

Distribuerte øyeblikk: ved frigjøring av den imaginære klemmen i en ledd, forårsaker det ubalanserte øyeblikket ved det leddet at det roterer. Rotasjonen vrir slutten av medlemsmøtet i leddet, noe som resulterer i utvikling av motstående øyeblikk. Disse motstandsmomentene kalles distribuerte øyeblikk. De distribuerte øyeblikkene for medlemmene av rammen vist i Figur 12.3 beregnes som følger:
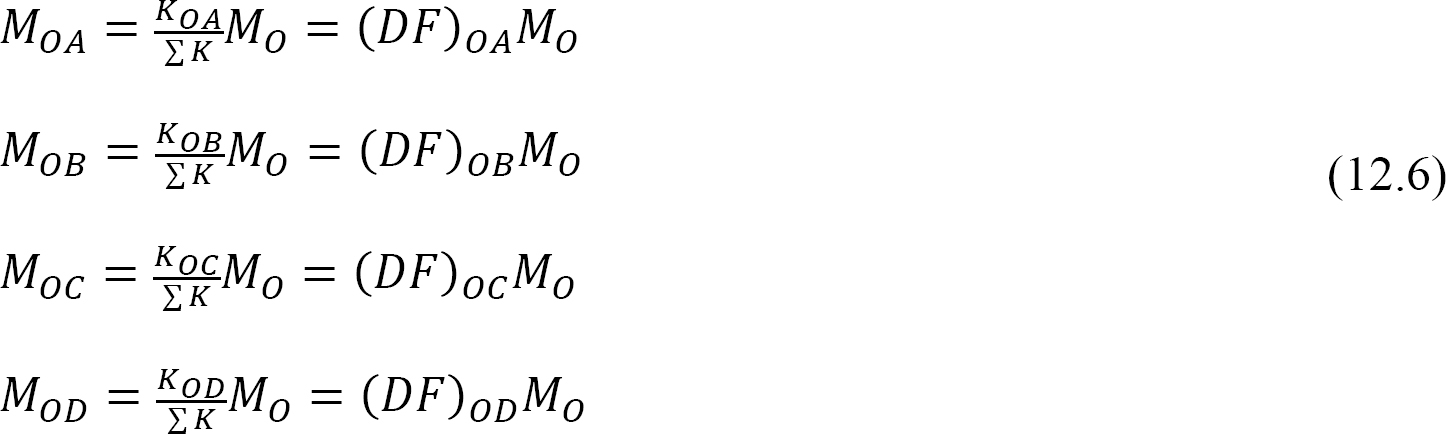
12.4 Modifikasjon Av Medlemsstivhet
Noen ganger kan iterasjonsprosessen i øyeblikksfordelingsmetoden reduseres betydelig ved å justere bøyestivheten til noen medlemmer av den ubestemte strukturen. Denne delen vurderer innflytelsen av en fast – og en pin-end-støtte på bøyestivheten til en ubestemt stråle.
Tilfelle 1: En bjelke hengslet i den ene enden og festet på den andre
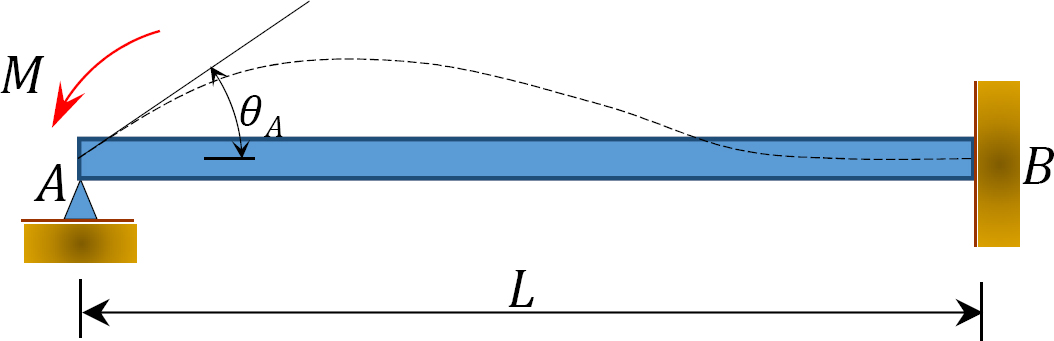
Fig. 12.4. Beam
Vurder en bjelke hengslet på ende A og festet til ende B, som vist i Figur 12.4. Påføring av et øyeblikk m roterer hengselenden med en mengde θ. Skrive skrånings-avbøyningsligningen for slutten A av medlemmet og merke seg at 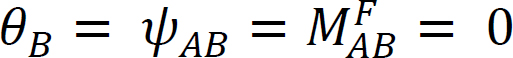 antyder følgende:
antyder følgende:
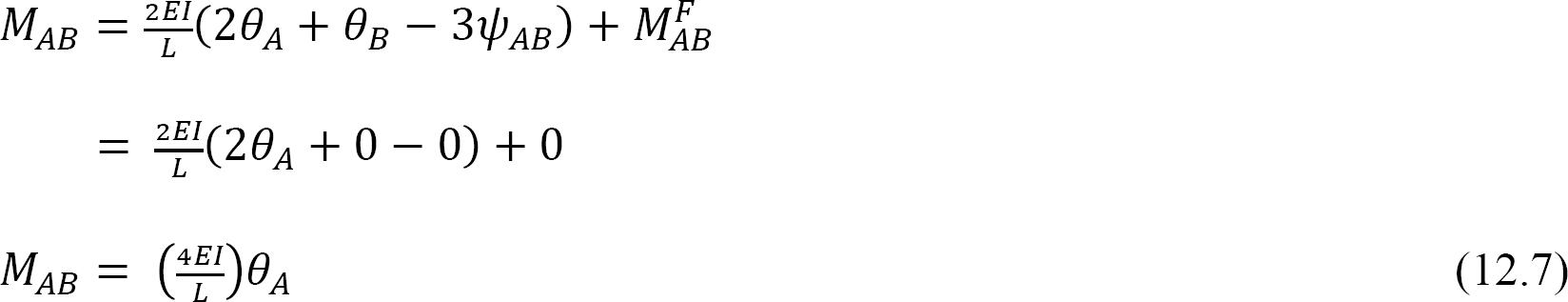
per definisjon er bøyestivheten til et strukturelt medlem det øyeblikket som må påføres en ende av medlemmet for å forårsake en enhetsrotasjon av den enden. Følgende uttrykk for bøyestivheten for medlemmet med en fast fjern ende uttrykkes som følger når du erstatter θ = 1 i ligning 12.7:

per definisjon bestemmes den relative bøyestivheten til et medlem ved å dele bøyestivheten TIL medlemmet MED 4E. Å Dele ligningen 12,8 med 4E antyder følgende uttrykk for relativ stivhet for saken som vurderes:

Sak 2: en bjelke hengslet i begge ender
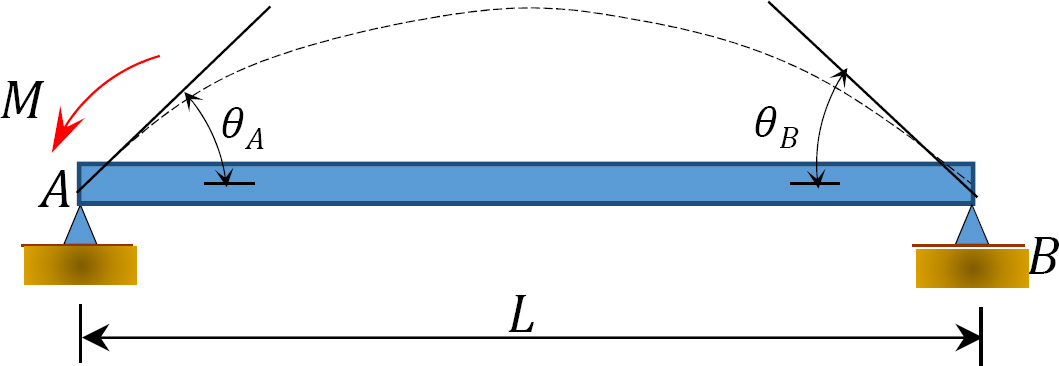
Fig. 12.5. Bare støttet beam.
Ved å Bruke et øyeblikk M På enden A av den enkelt støttede bjelken vist i Figur 12.5 roterer bjelken med en vinkel θ ved den hengslede enden. Ved å bruke den modifiserte skrånings-avbøyningsligningen avledet i seksjon 11.4 I Kapittel 11 og merke seg at 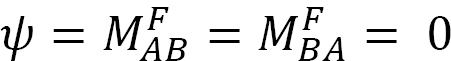 antyder følgende uttrykk for øyeblikket ved den hengslede enden der lasten påføres:
antyder følgende uttrykk for øyeblikket ved den hengslede enden der lasten påføres:
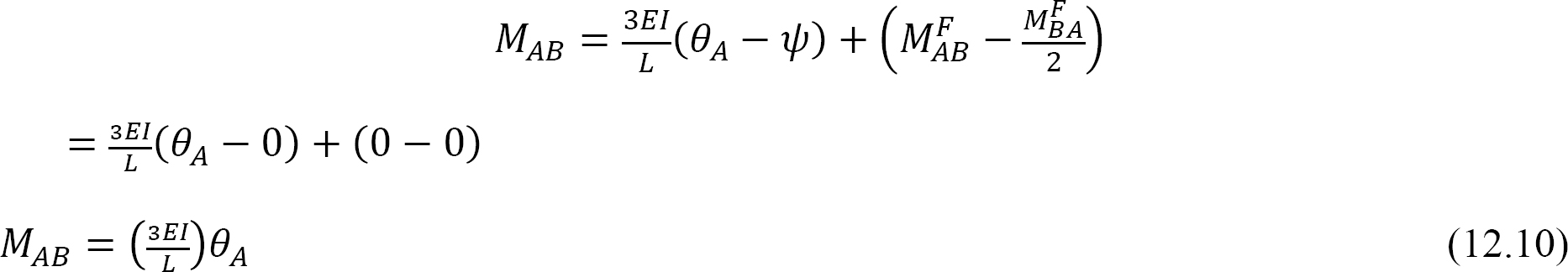
Å Erstatte θ = 1 i ligning 12.10 antyder følgende uttrykk for bøyestivheten for et medlem med en hengslet fjern ende:

den relative stivheten for et medlem med en hengslet langt ende oppnås ved å dividere ligning 12.11 MED 4E, som følger:

Sammenligning av ligningene 12.12 og 12.9 antyder at et medlem med en hengslet fjern ende er tre fjerdedeler så stiv som et medlem med samme geometri, men fast i den fjerne enden. Dette etablerte faktum kan vesentlig redusere antall iterasjon når man analyserer bjelker eller rammer med en hengslet fjern ende ved hjelp av metoden for momentfordeling. I slike tilfeller justeres den relative stivheten til strålen i nærenden først i henhold til ligning 12.12, og dens fordelingsfaktor beregnes med den justerte stivheten. Under balanseringsoperasjonen vil den nære enden bli balansert bare en gang uten videre overføring av øyeblikk fra eller til sin ende.
12.5 Analyse Av Ubestemte Bjelker
prosedyren for analyse av ubestemte bjelker ved metoden for momentfordeling er kort oppsummert som følger:
Prosedyre For Analyse Av Ubestemte Bjelker Ved Øyeblikksfordelingsmetoden
•Beregn de faste øyeblikkene for medlemmer, forutsatt at leddene klemmes mot rotasjon.
* Beregn fordelingsfaktoren for hvert av medlemmene som er koblet til leddet
* Beregn det ubalanserte øyeblikket ved hvert ledd og fordel det samme til endene av medlemmene som er koblet til det leddet.
* Bære over halvparten av det distribuerte øyeblikket til de andre endene av medlemmene.
* Legg til eller trekk fra disse siste øyeblikkene (øyeblikk oppnådd i trinn tre og fire) til eller fra de opprinnelige faste øyeblikkene.
* Bruk de bestemte sluttmomentene på leddene i den oppgitte strukturen.
* Tegn fri kroppsdiagrammet for hvert span av den gitte strålen, som viser belastningene og øyeblikkene i leddene oppnådd ved øyeblikksfordelingsmetoden.
* Bestem støttereaksjonene for hvert span.
•Beregn og konstruer skjærkraften og bøyningsmomentdiagrammer for hvert span.
* Tegn ett bøyemoment og ett skjærkraftdiagram for den gitte strålen ved å kombinere diagrammene i trinn 9.
Eksempel 12.1
ved hjelp av momentfordelingsmetoden bestemmer du sluttmomentene og reaksjonene på bjelkens støtter vist i Figur 12.6 a. Tegn skjærkraften og bøyningsmomentdiagrammer. EI = konstant.
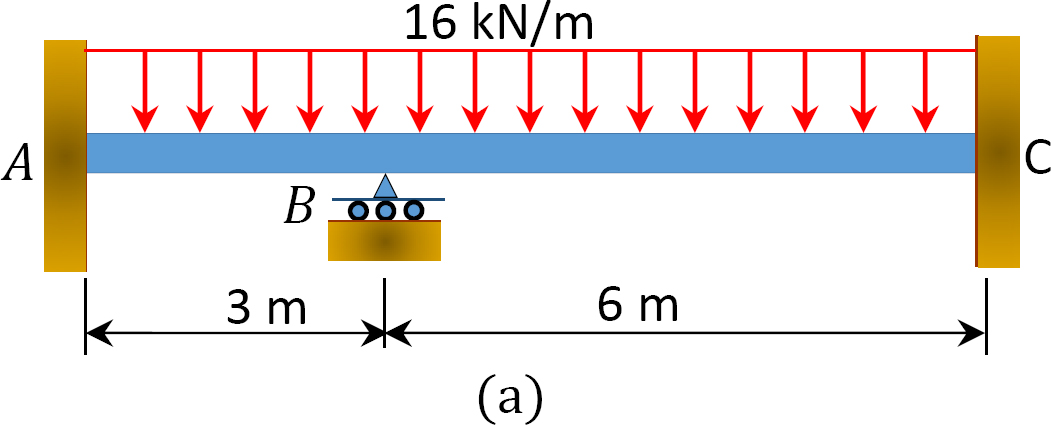
Fig. 12.6. Stråle.
Løsning
Fast sluttmoment.
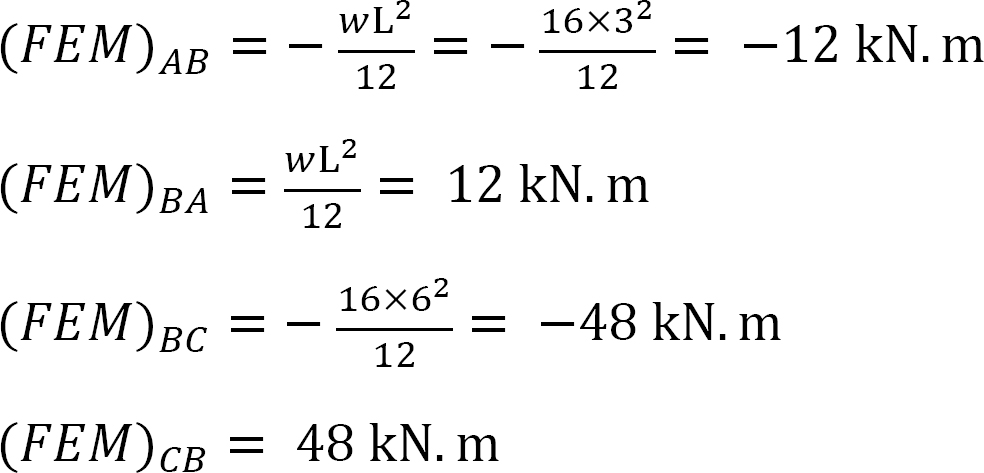
Stivhetsfaktor.
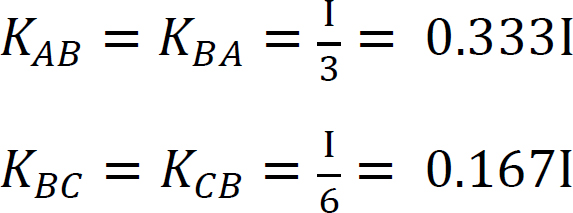
Distribusjonsfaktor.
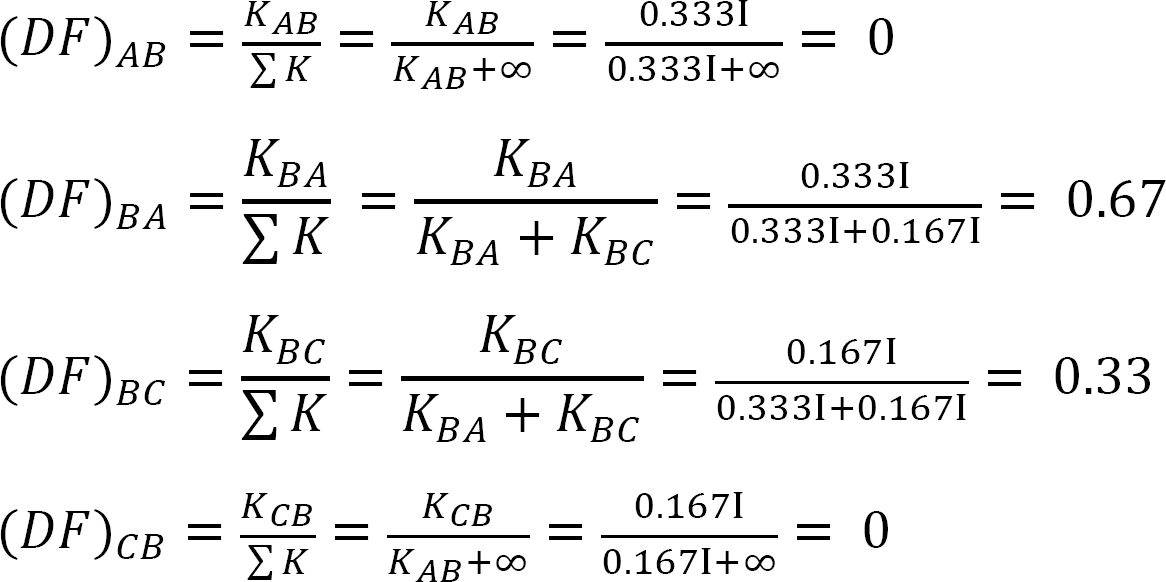
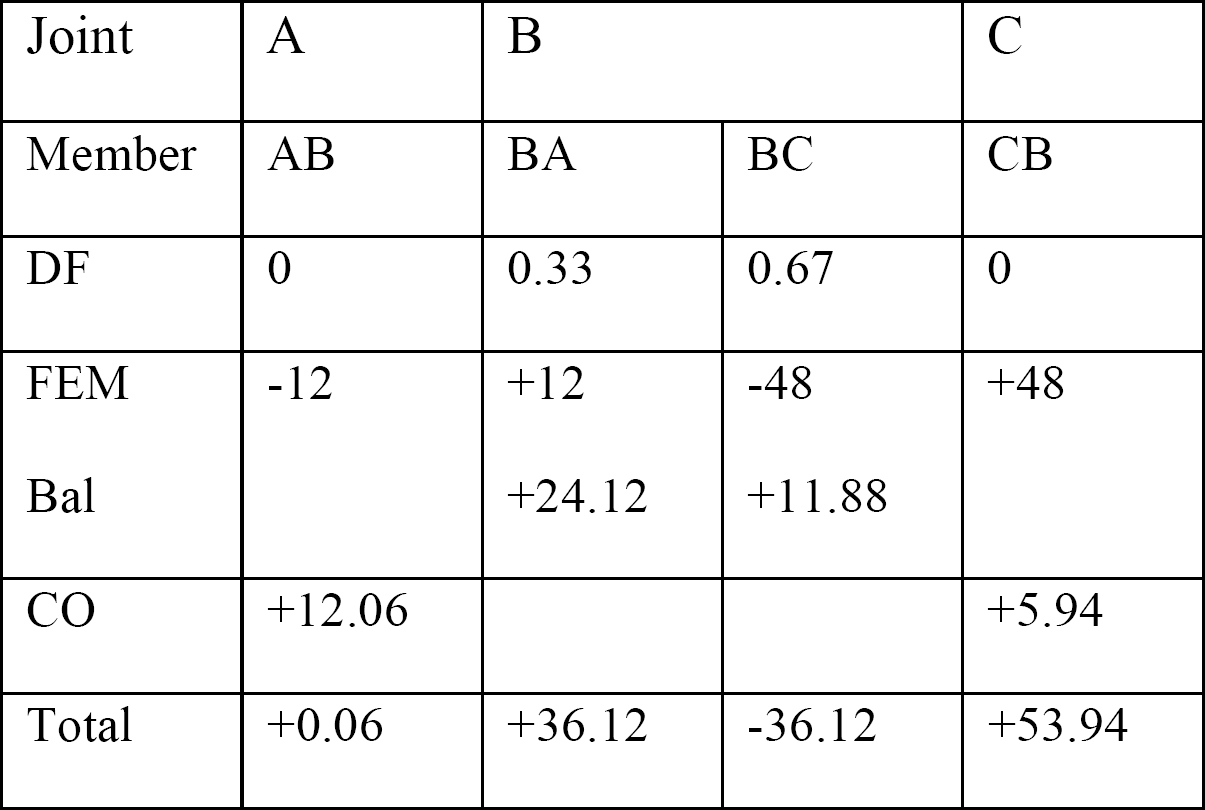
Tabell 12.1. Distribusjonstabell.
Skjærkraft og bøyemomentdiagrammer.
Eksempel 12.2
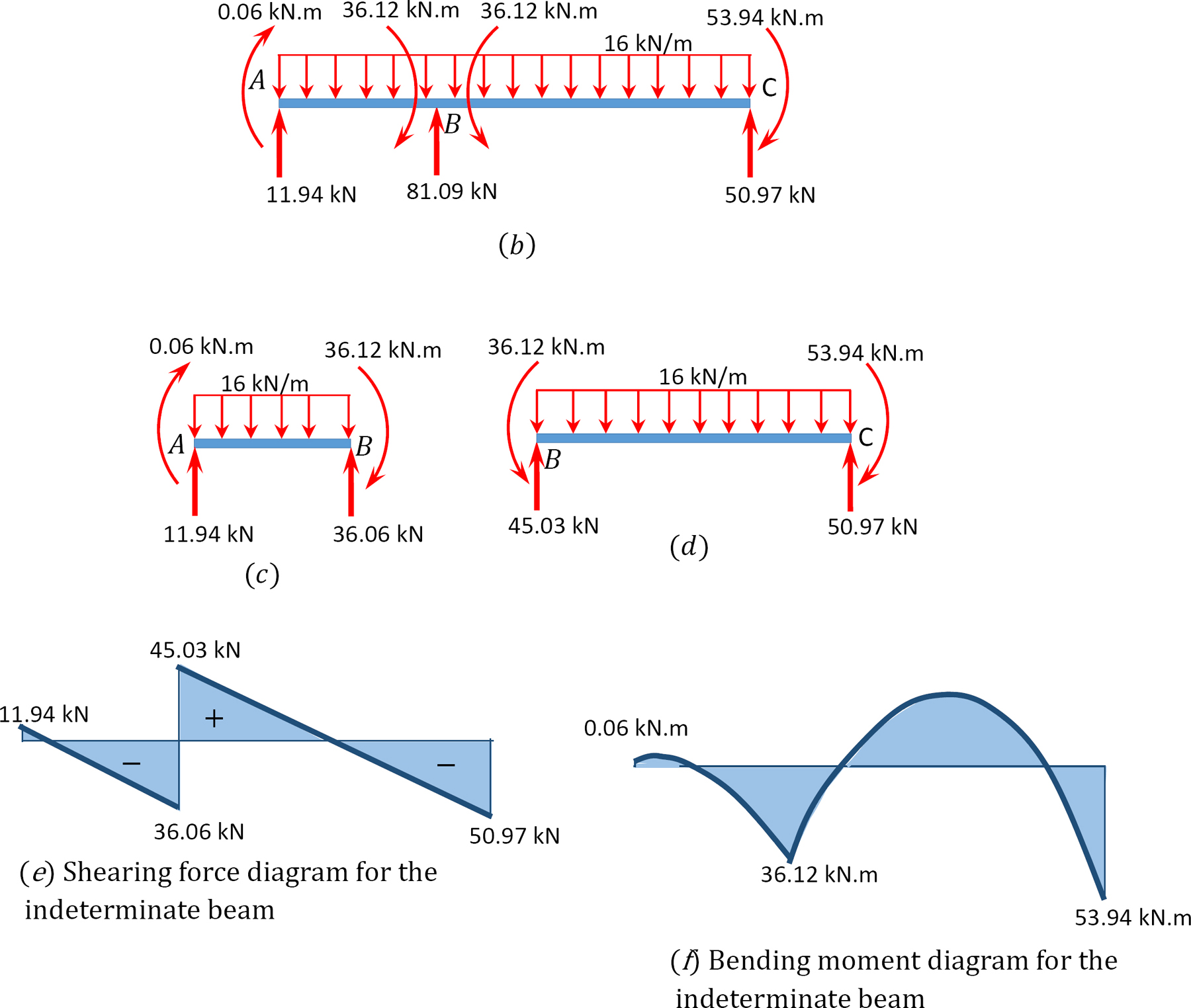
ved hjelp av momentfordelingsmetoden bestemmer du sluttmomentene og reaksjonene på bjelkens støtter vist i Figur 12.7 a. Tegn skjærkraften og bøyningsmomentdiagrammer.
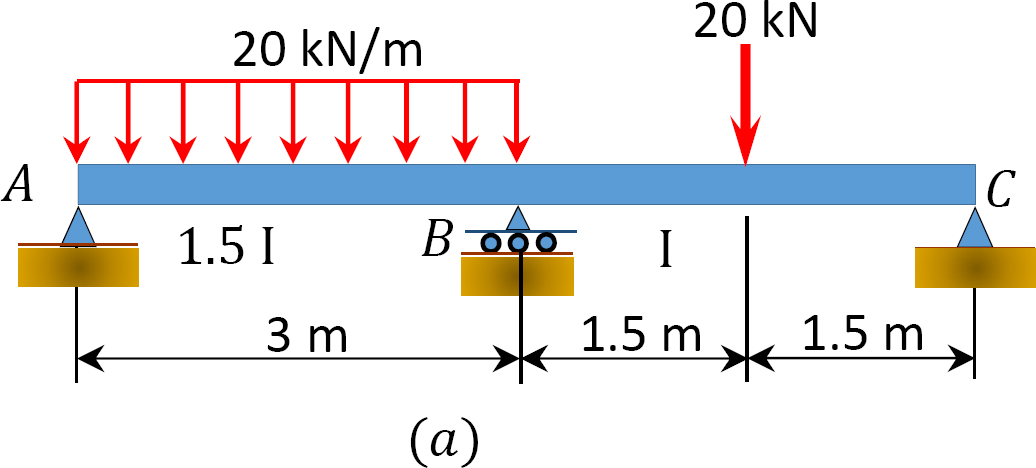
Fig. 12.7. Stråle.
Løsning
Fast sluttmoment.
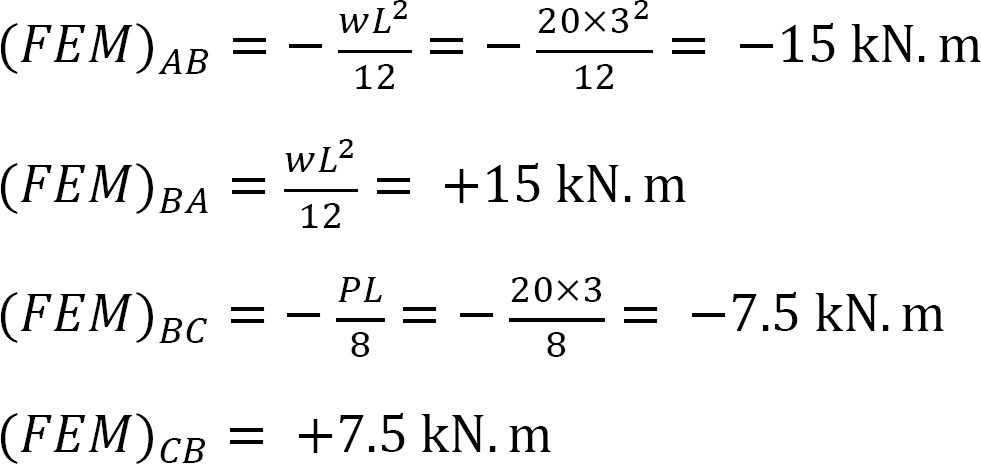
Stivhetsfaktor.
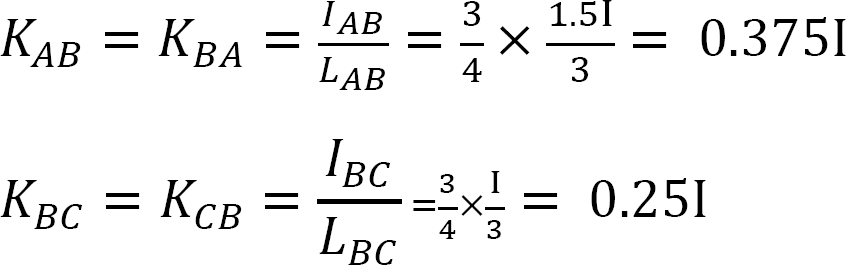
Distribusjonsfaktor.
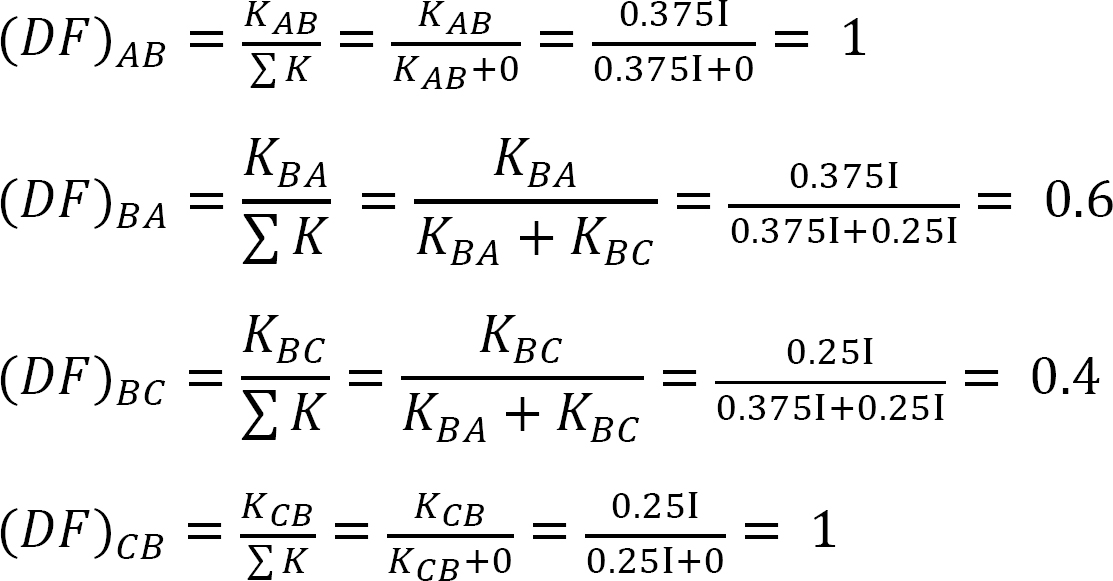
Tabell 12.2. Distribusjonstabell.
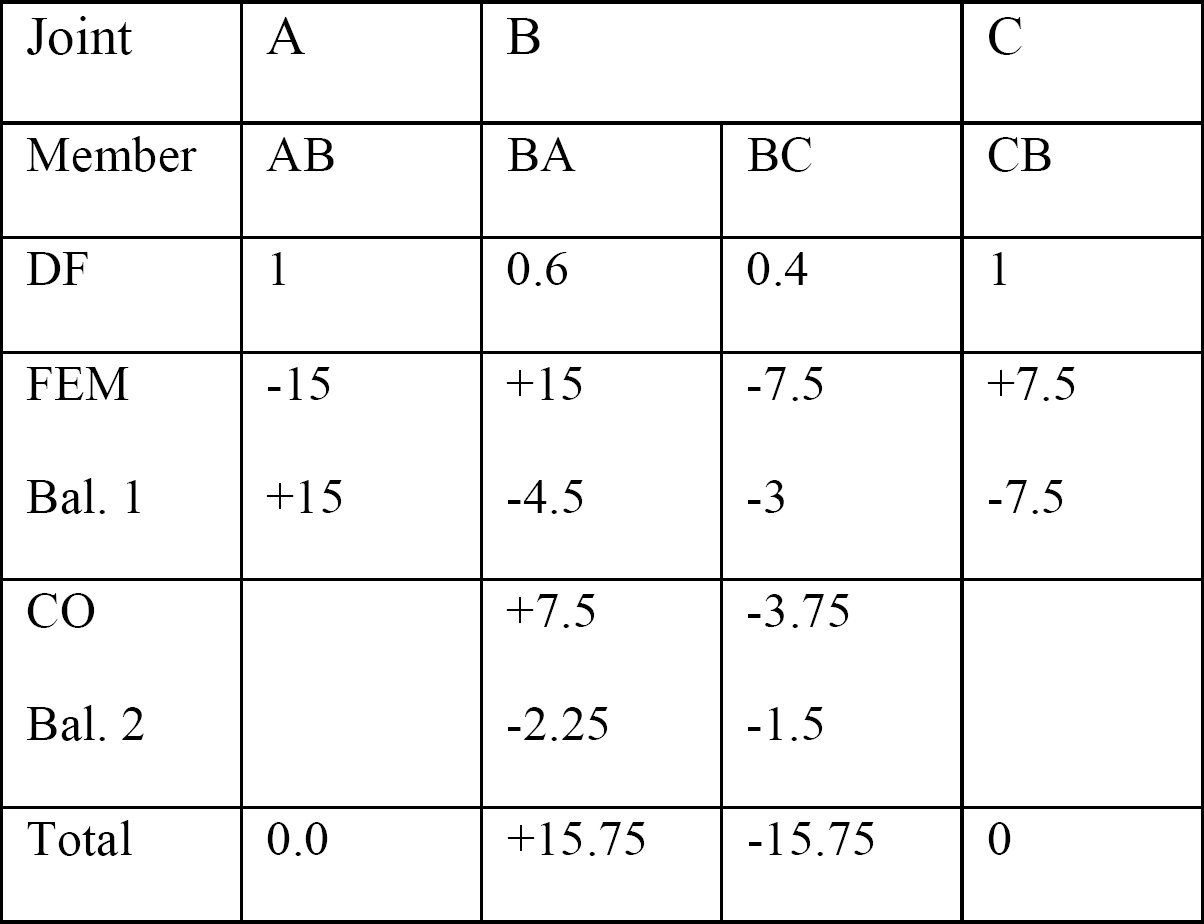
Skjærkraft og bøyemomentdiagrammer.
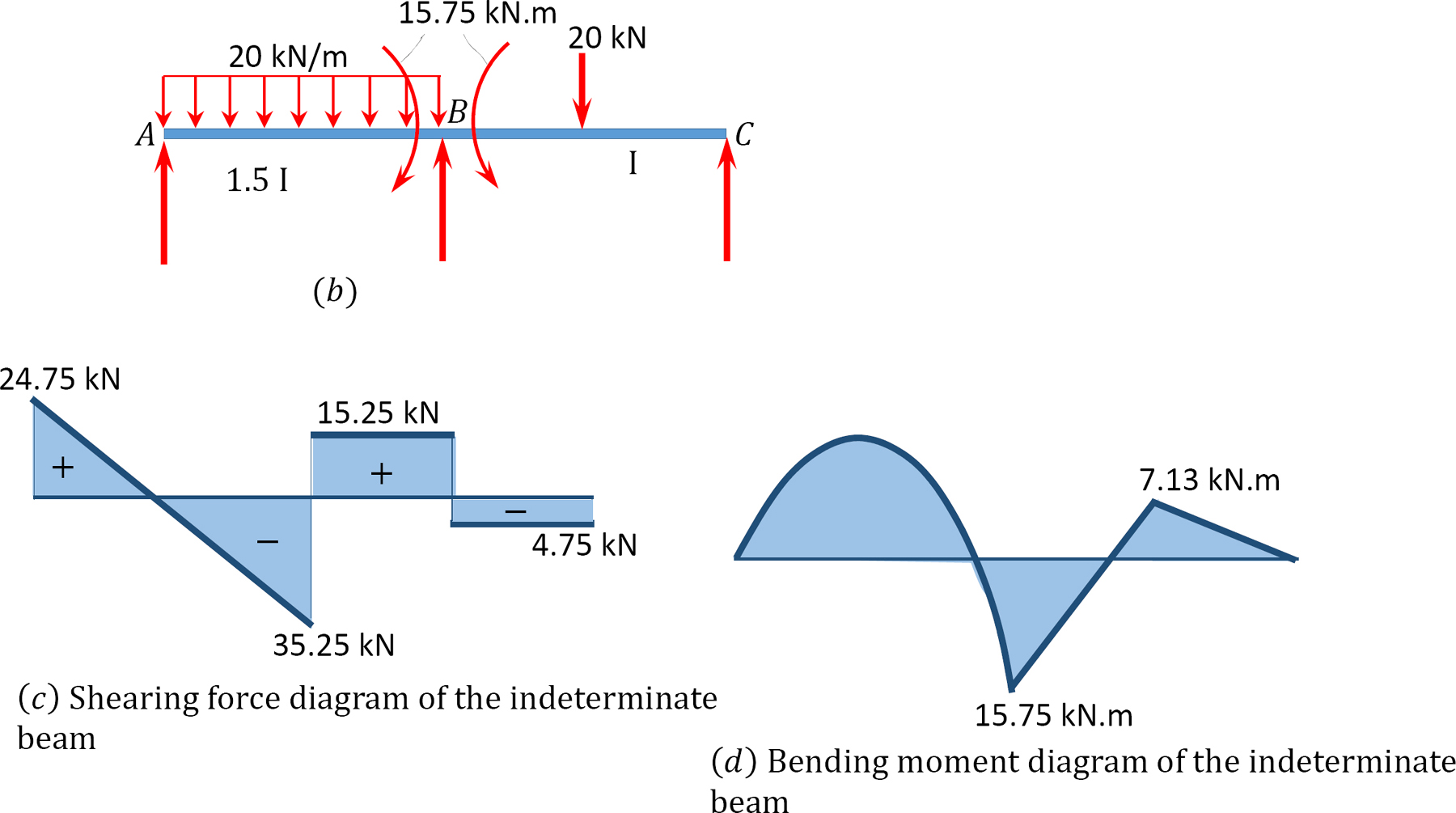
12.6 Analyse Av Ubestemte Rammer
prosedyren for analyse av rammer ved hjelp av øyeblikksfordelingsmetoden avhenger av hvilken type ramme som analyseres. Rammer kategoriseres som sway-eller ikke-sway-rammer. Prosedyren for analyse av ikke – svingrammer er lik den for ubestemte bjelker. Men for analyse av sway rammer, er prosedyren annerledes. Det er to stadier involvert i analysen av sway-rammer, nemlig ikke-sway-scenen og sway-scenen analyser. Disse stadiene er beskrevet nedenfor.
Prosedyre For Analyse Av Ubestemte Sway-Rammer Ved Øyeblikksfordelingsmetoden
A. Ikke-sway-sceneanalyse
•anta først at det finnes en imaginær prop som hindrer rammen i å svinge.
* Beregn de horisontale reaksjonene på støttene på rammen og merk forskjellen X. dette er kraften for å hindre sving.
B. Sway stage analysis
* Anta vilkårlige øyeblikk for å handle på kolonnene i rammen. Størrelsen på disse øyeblikkene vil variere fra kolonne til kolonne i forhold til 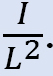
•Verdier antas For M2, Og M1 bestemmes.
* Beregn størrelsen på de vannrette reaksjonene ved støttene for sway-betingelsen. Summeringen av disse reaksjonene gir den vilkårlige forskyvningskraften Y.
* Bestem forholdet 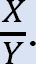 dette forholdet kalles sway-faktoren.
dette forholdet kalles sway-faktoren.
* bruk sway-faktoren til å multiplisere de distribuerte øyeblikkene i sway. Dette gir det korrigerte øyeblikket for sway.
Eksempel 12.3
Bruk øyeblikksfordelingsmetoden til å bestemme medlemmenes sluttmomenter for rammen vist i Figur 12.8. EI = konstant.
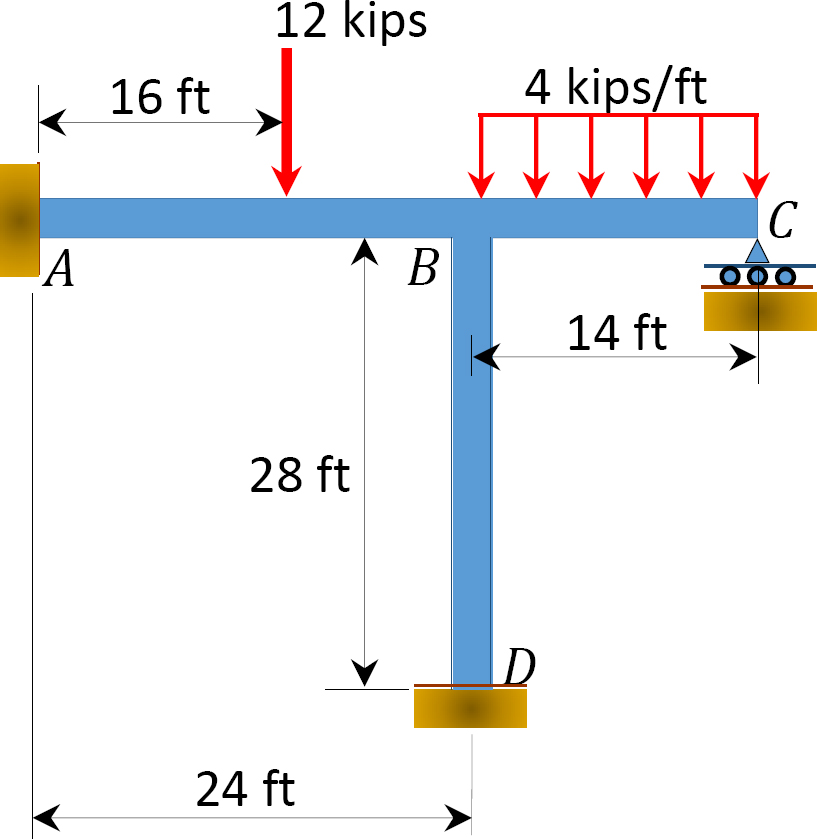
Fig. 12.8. Ramme.
Løsning
Fast sluttmoment.
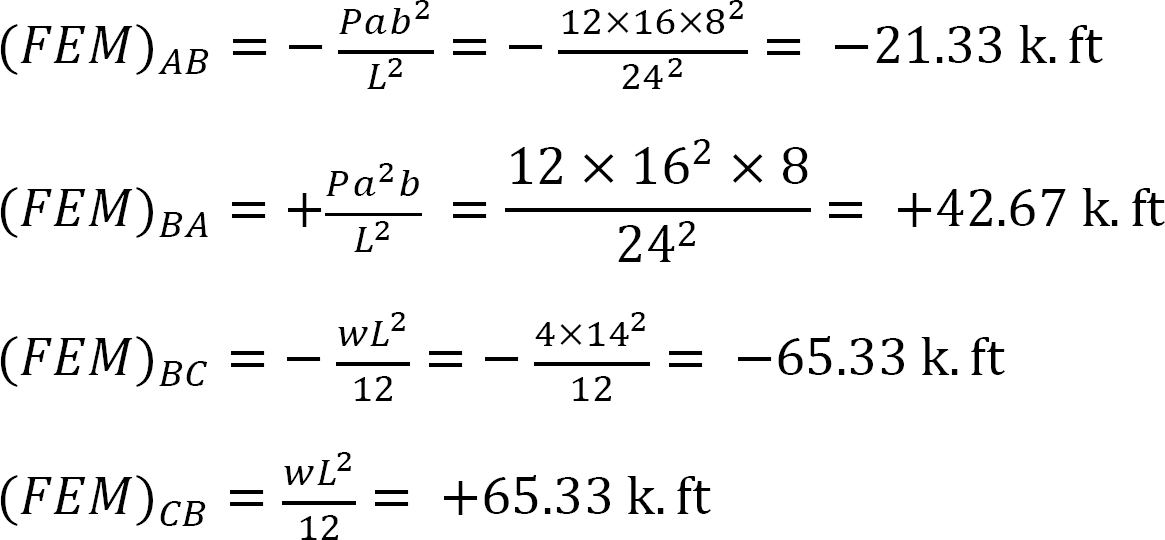
Stivhetsfaktor.
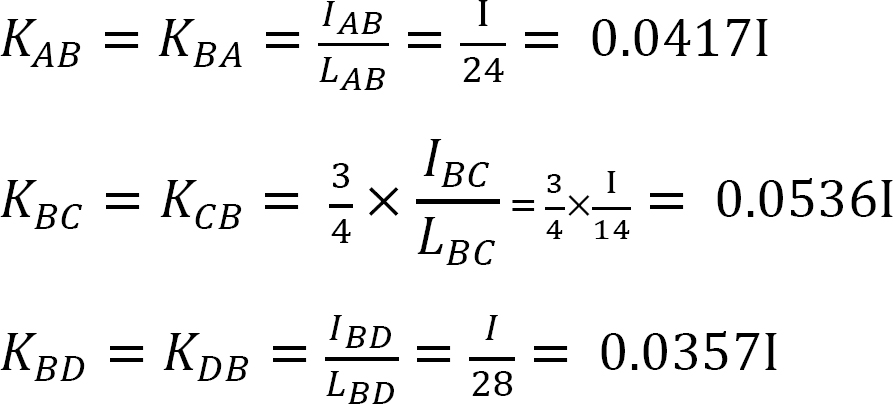
Distribusjonsfaktor.
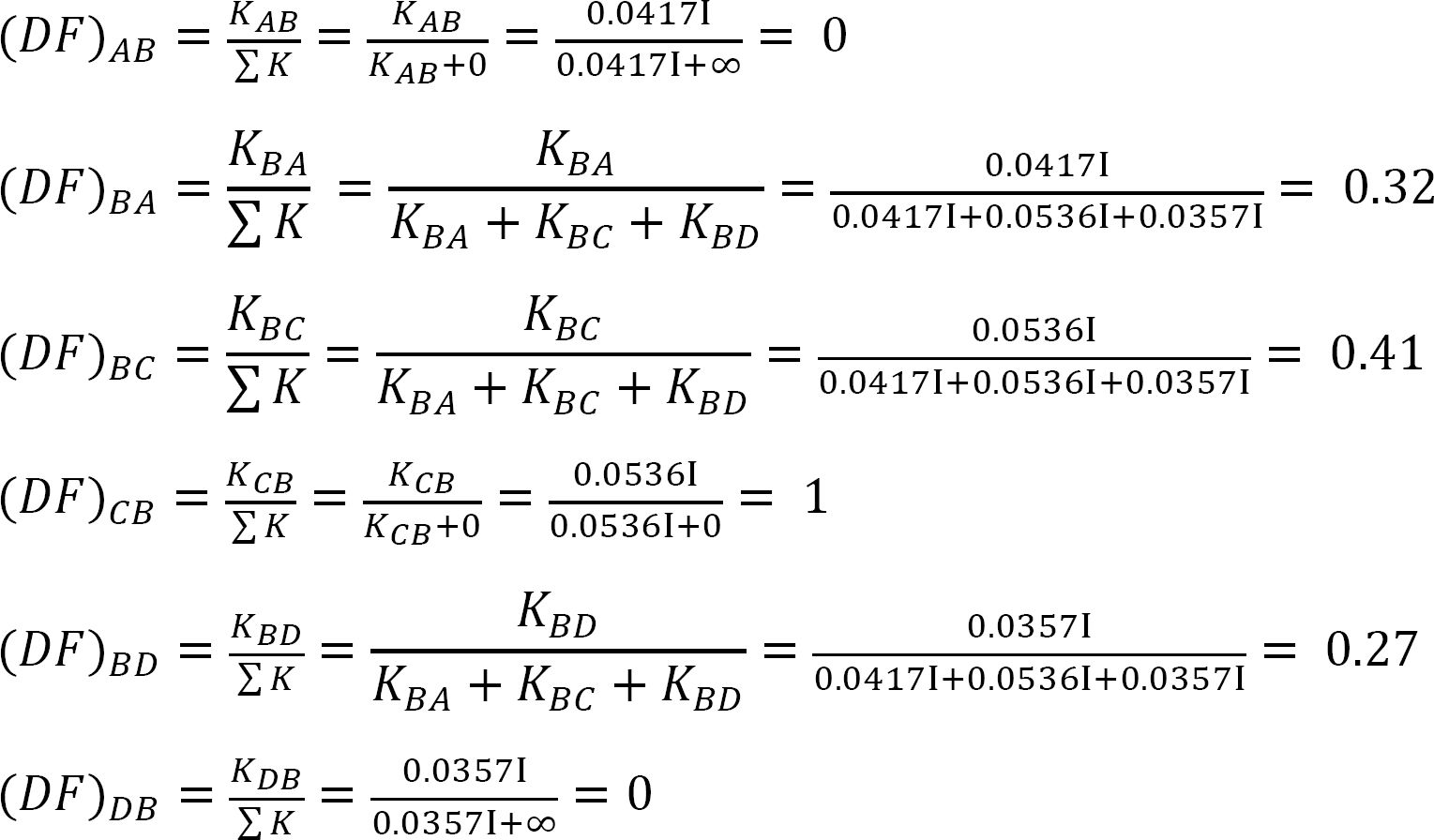
Tabell 12.3. Distribusjonstabell.
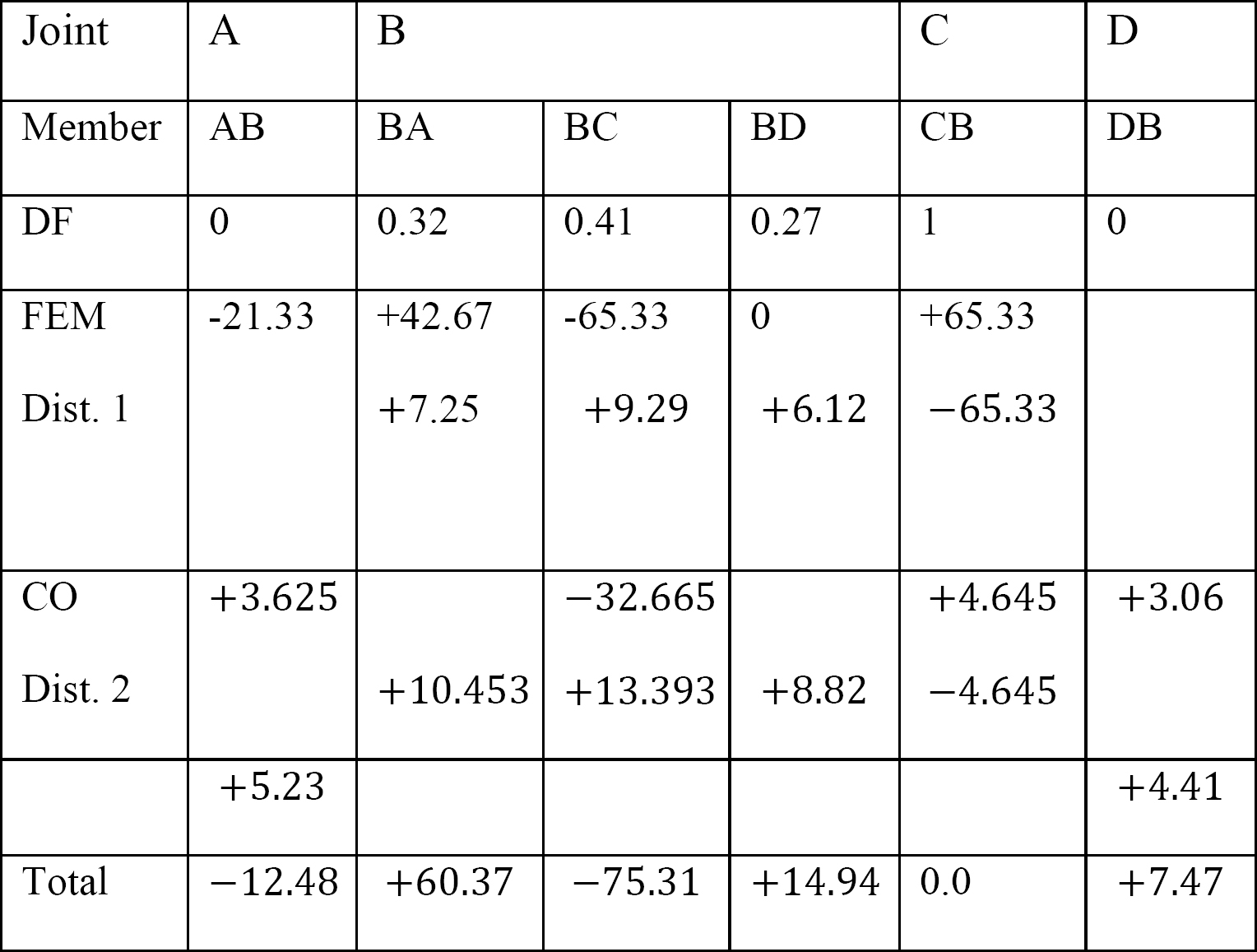
Endelig medlem slutt øyeblikk.
Ved Å Erstatte de oppnådde verdiene Av Ekθ, Ekθ og EK∆ i medlemsendemomentligningene, foreslår følgende:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14,94 k. ft
Mcb = 0
mdb = +7,47 k. ft
eksempel 12.4
ved hjelp av øyeblikksfordelingsmetoden, bestem sluttmomentene på støttene til rammen vist i Figur 12.9. EI = konstant.
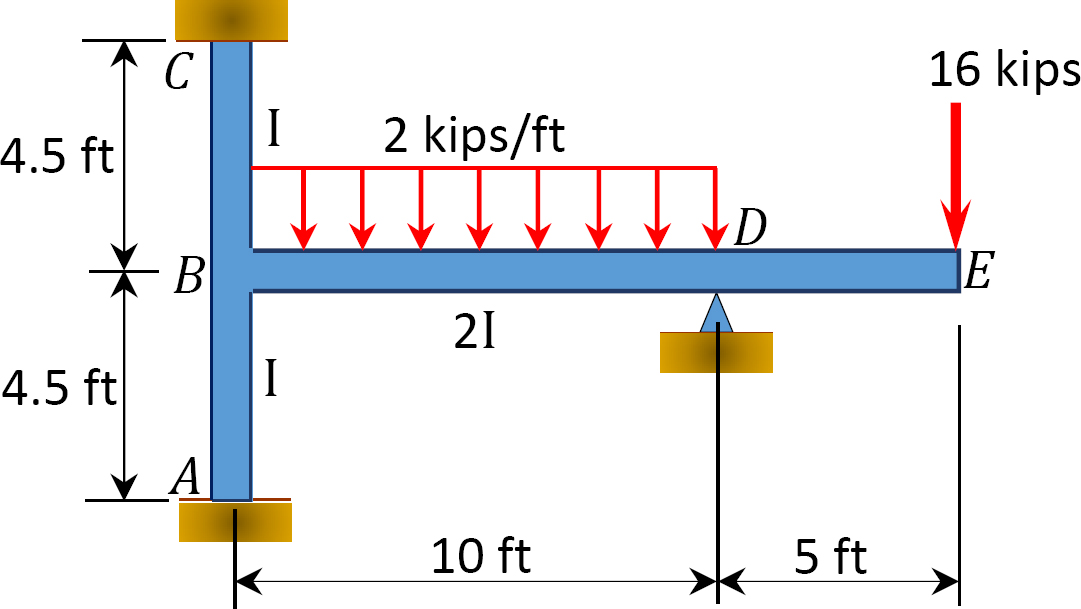
Fig. 12.9. Ramme.
Løsning
Fast sluttmoment.
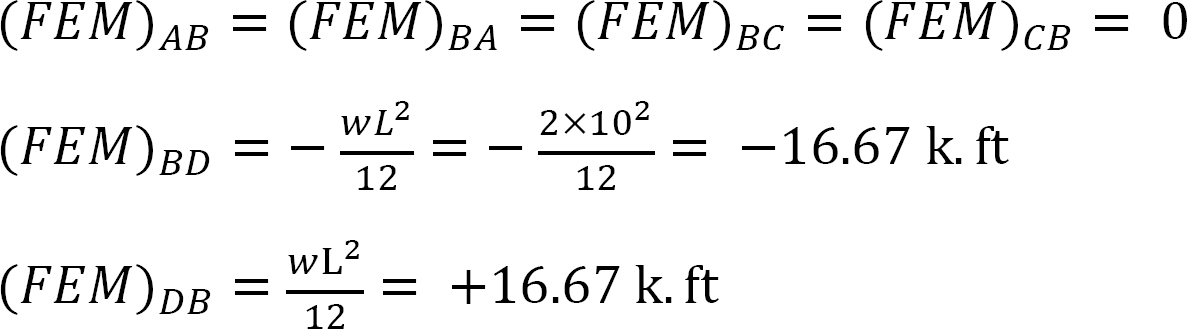
Stivhetsfaktor.
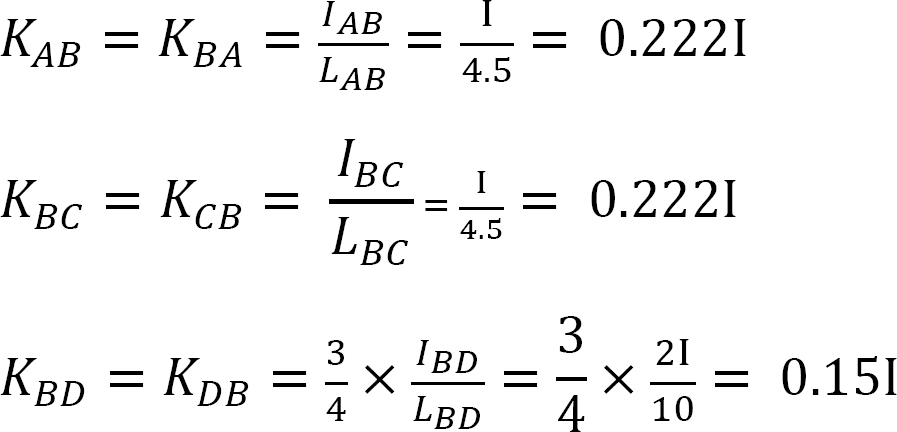
Distribusjonsfaktor.

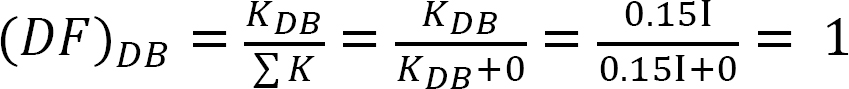
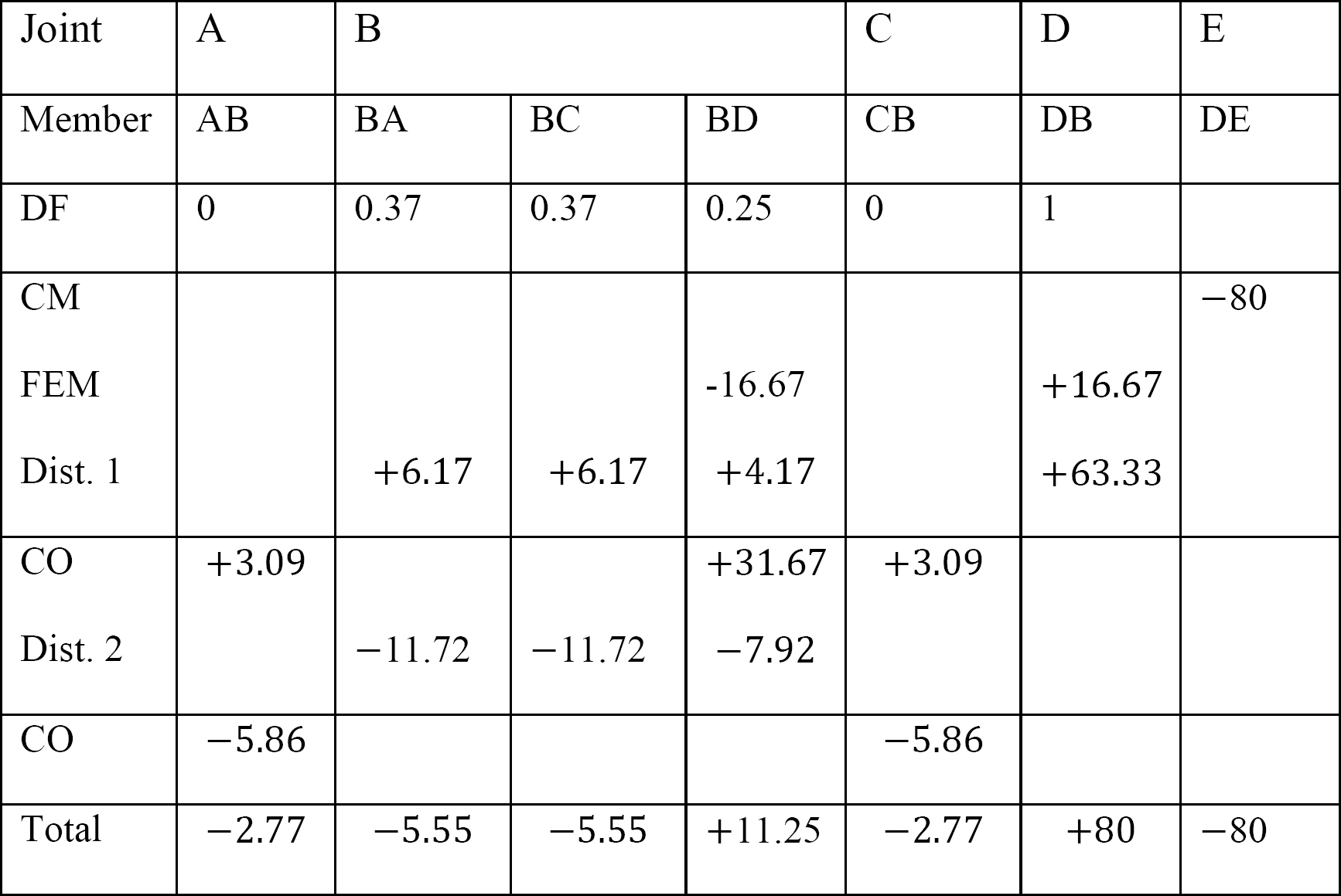
Tabell 12.4. Distribusjonstabell.
Endelig medlem slutt øyeblikk.
MAB = -2,77 k. ft
MBA = -5,55 K. ft
MBC = -5,55 k. ft
MBD = + 11,25 k. ft
MCB = -2,77
MDB = +80 k. ft
Mde = -80 k. ft
Eksempel 12.5
ved hjelp av øyeblikksfordelingsmetoden, bestem sluttmomentene på støttene til rammen vist i Figur 12.10. EI = konstant.
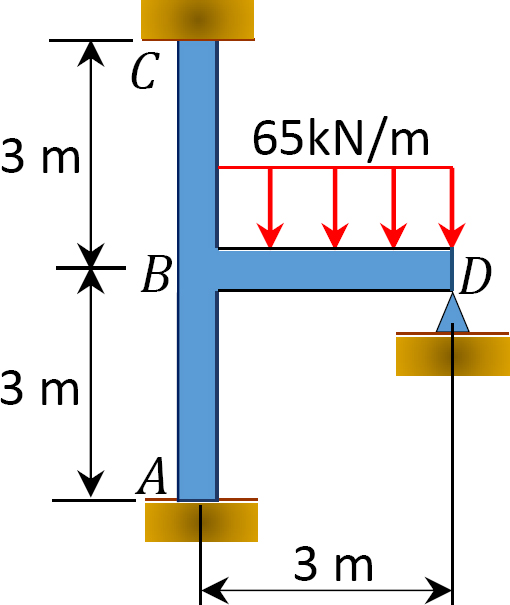
Fig. 12.10. Ramme.
Løsning
Fast sluttmoment.
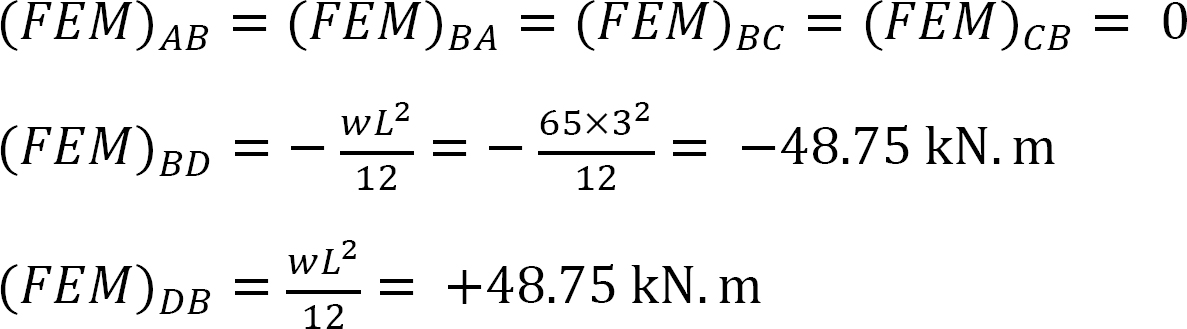
Stivhetsfaktor.
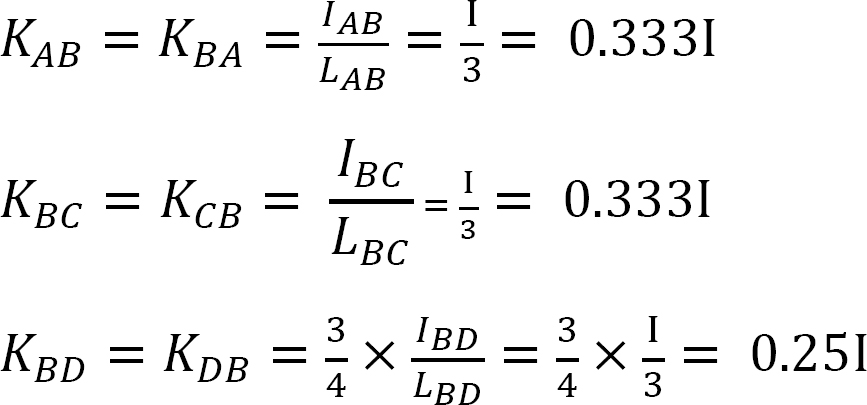
Distribusjonsfaktor.
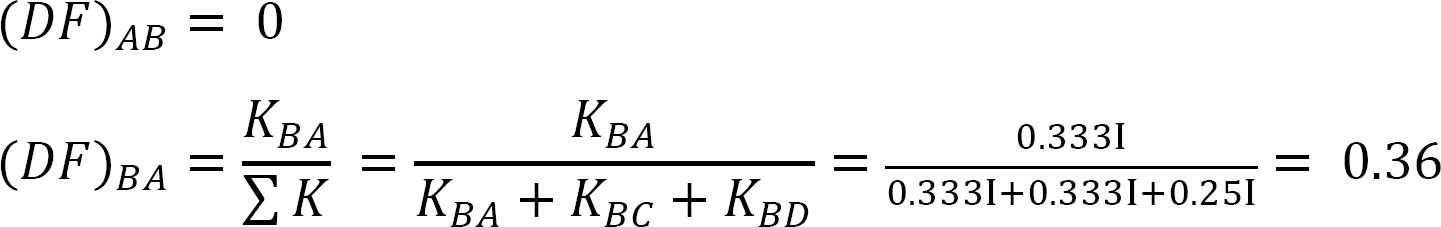

Tabell 12.5. Distribusjonstabell.
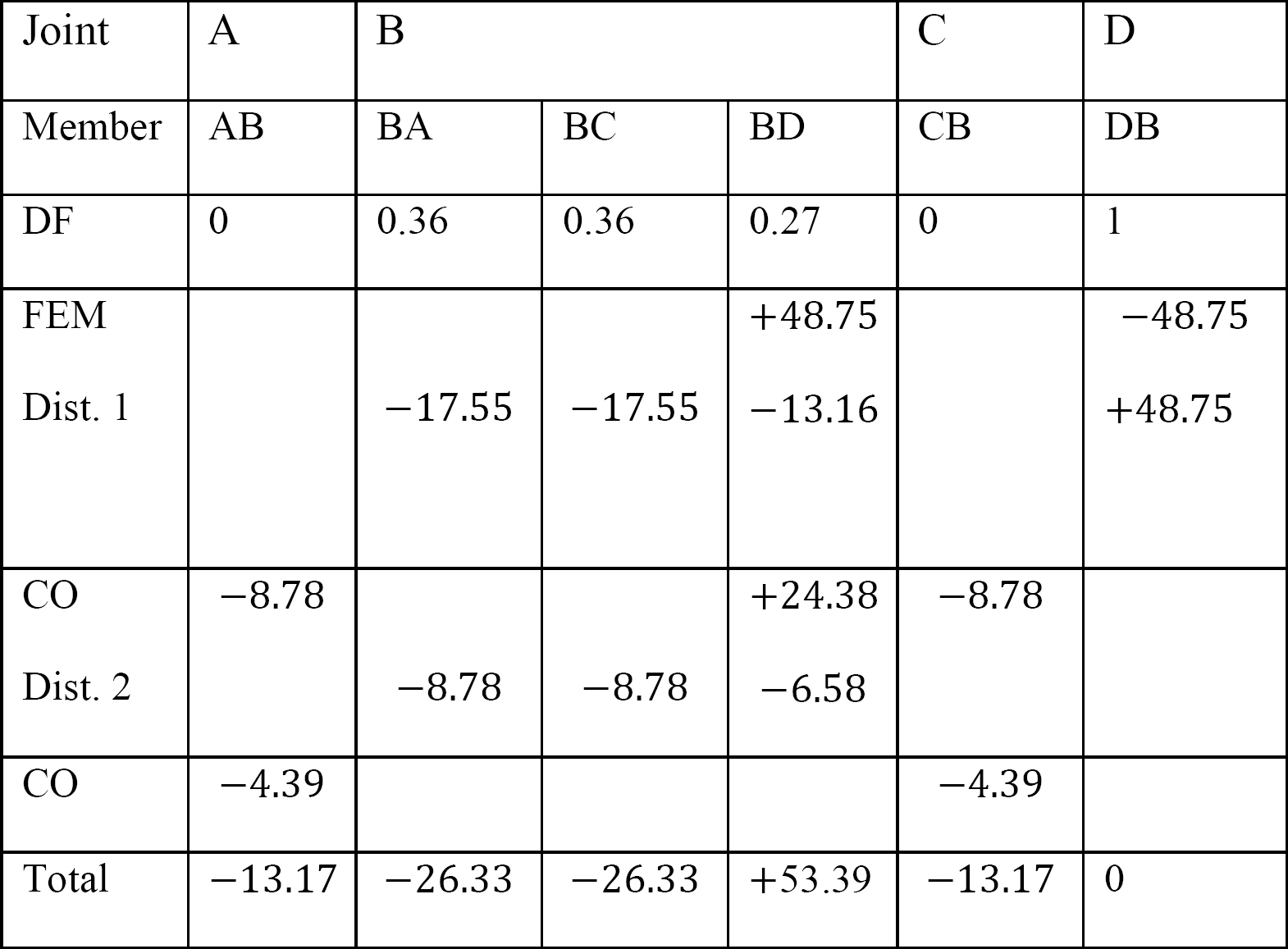
Endelig medlem slutt øyeblikk.
MAB = -13.17 k. ft
MBA = -26.33 K. ft
MBC = -26.33 k. ft
MBD = +53.39 K. ft
MCB = -13.17 k. ft
mdb = 0
Eksempel 12.6
bruk øyeblikksfordelingsmetoden til å bestemme rammens sluttmomenter med sideving som vist i Figur 12.11 a.
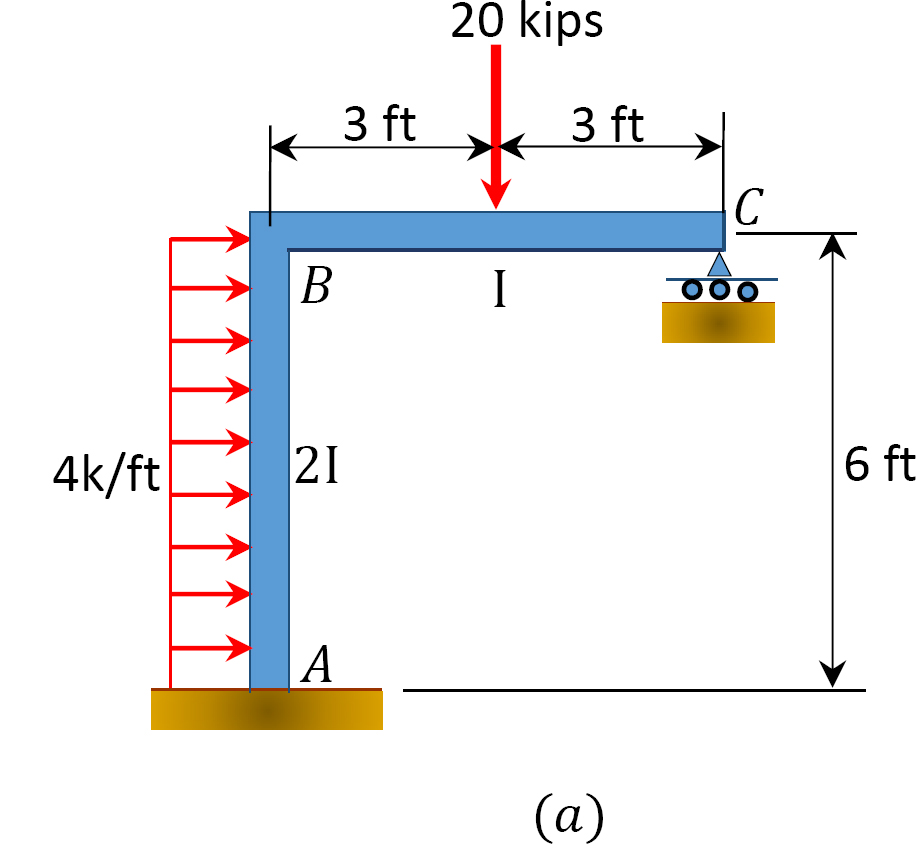
Fig. 12.11. Ramme med sideving.
Løsning
Fast sluttmoment.
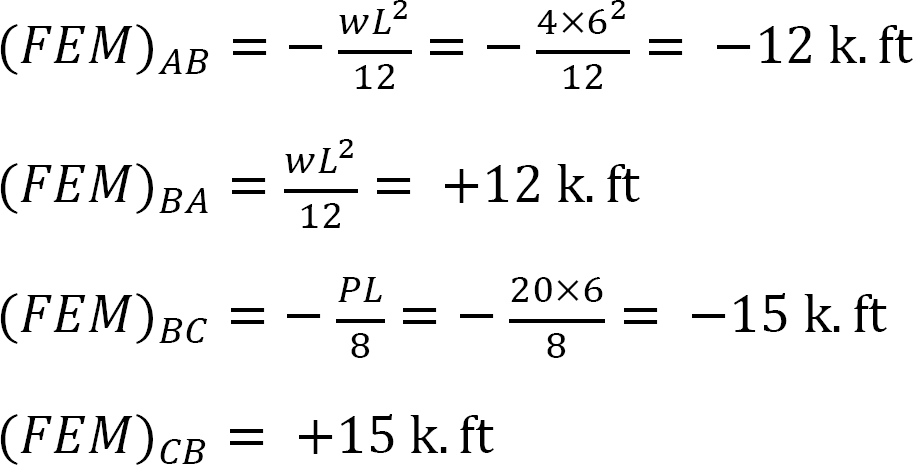
Stivhetsfaktor.
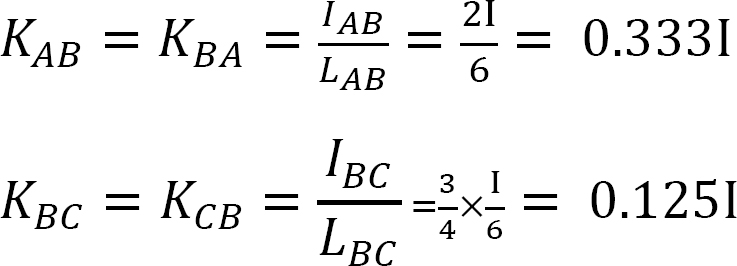
Distribusjonsfaktor.
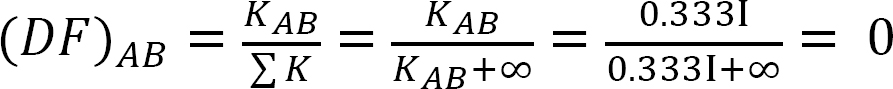

Analyse av ramme uten side-sway.
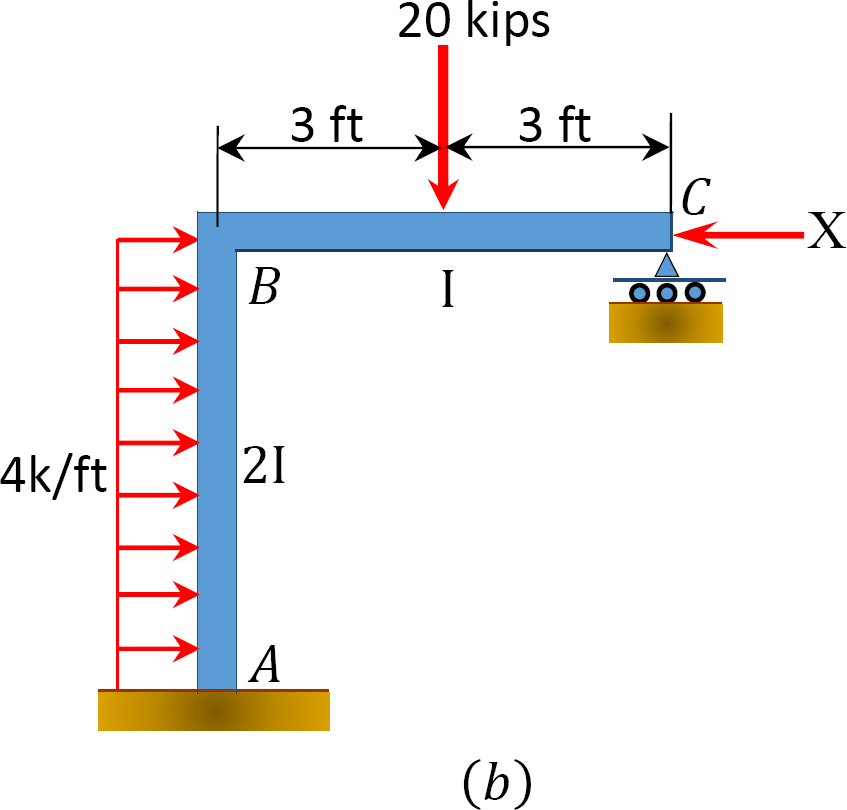
Tabell 12.6. Distribusjonstabell(ingen sway-ramme).
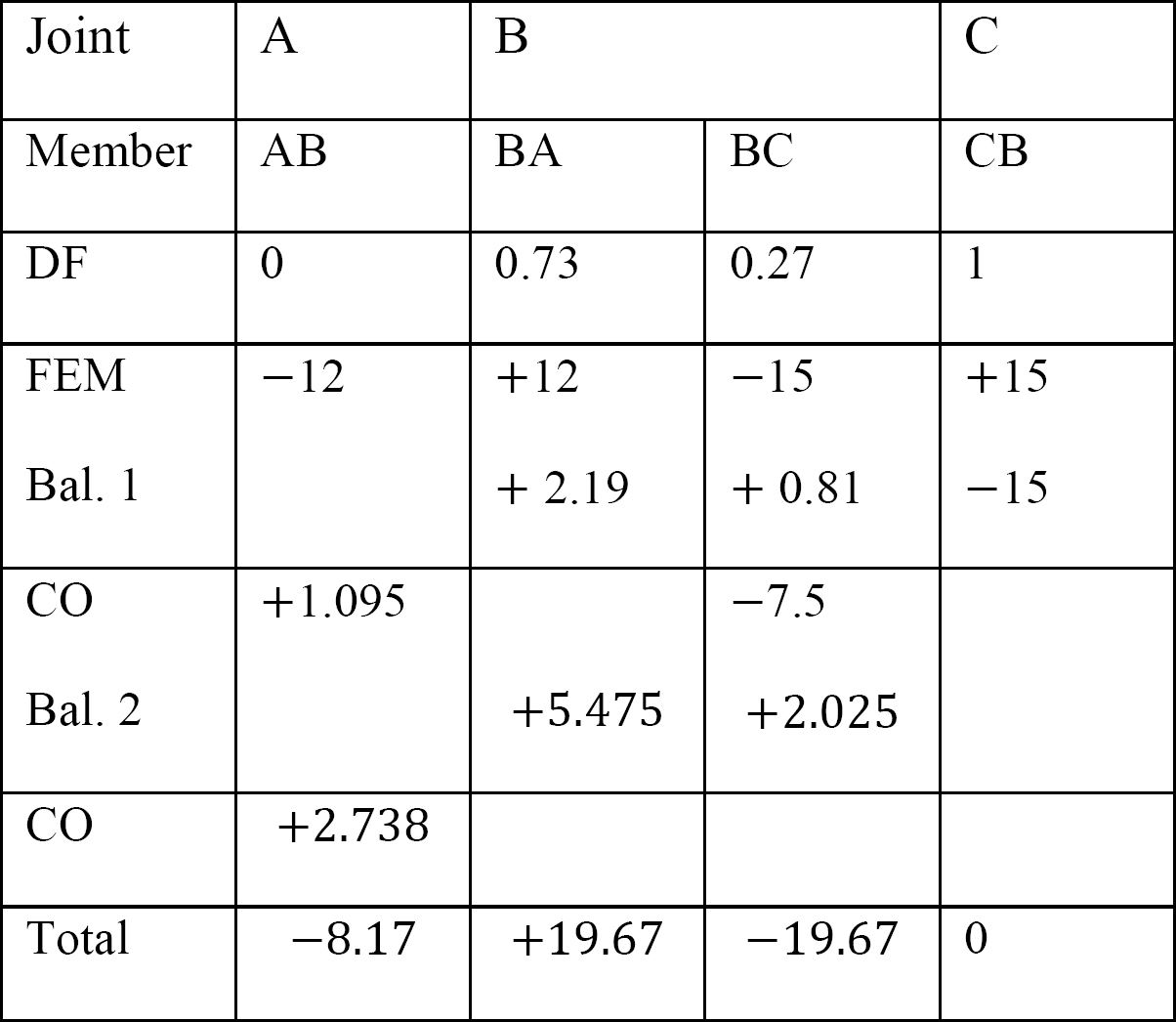
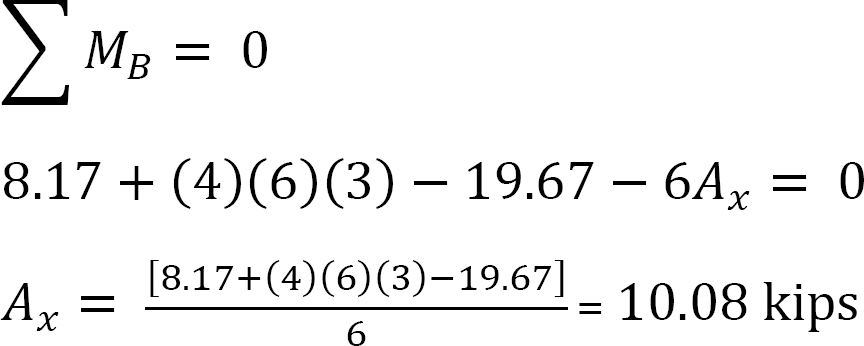
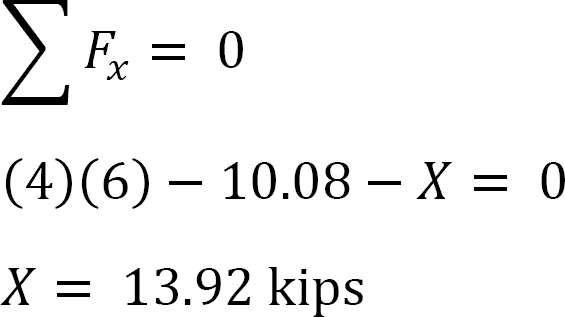
Analyse av ramme med side-sway.
Anta AT MAB = + 20 k. ft
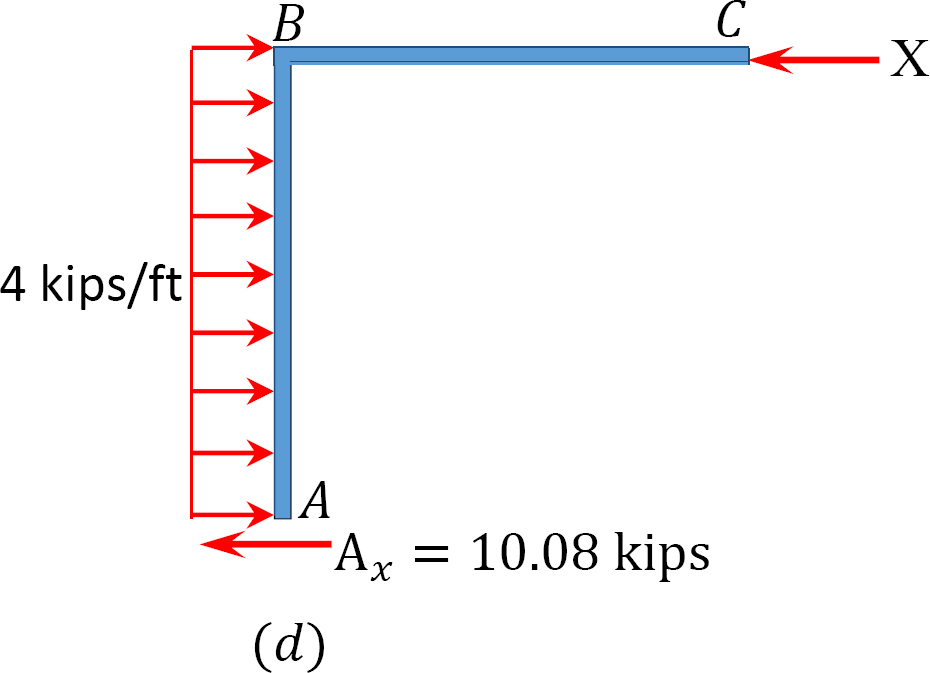
Tabell 12.7. Distribusjonstabell (sway frame).
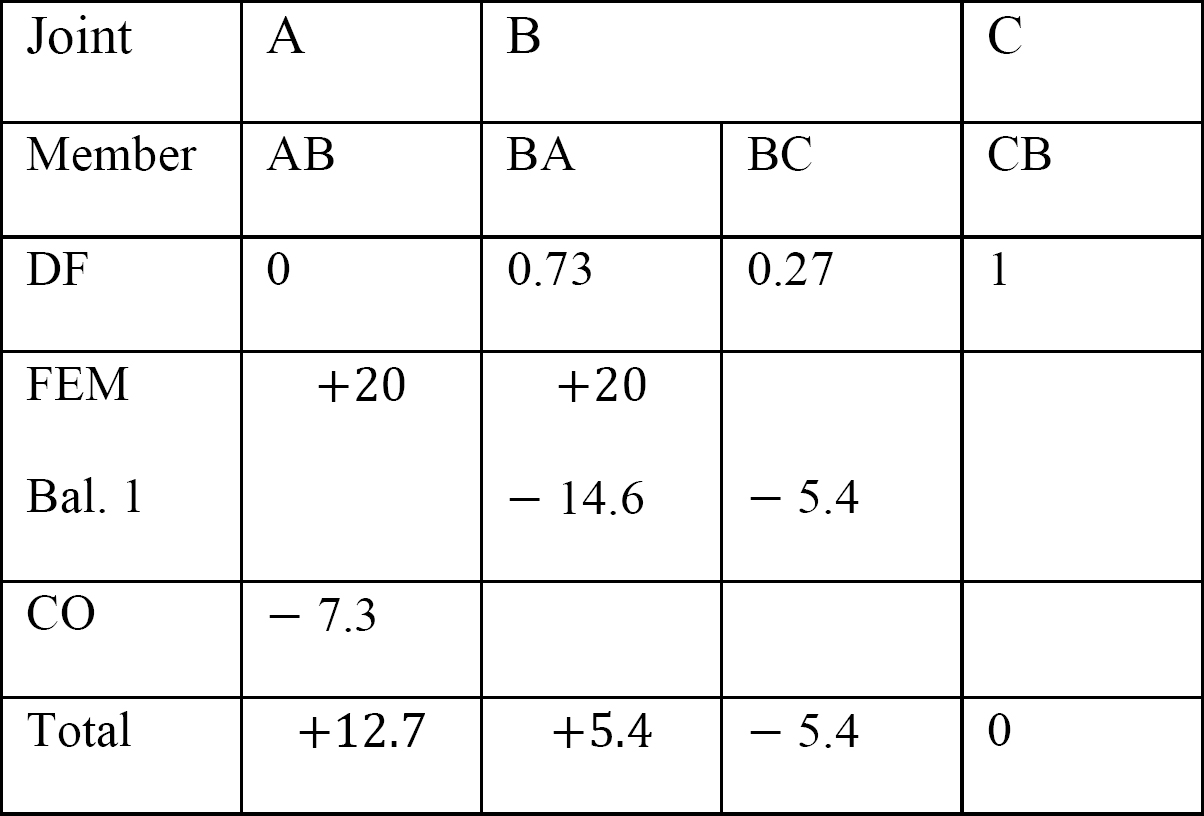
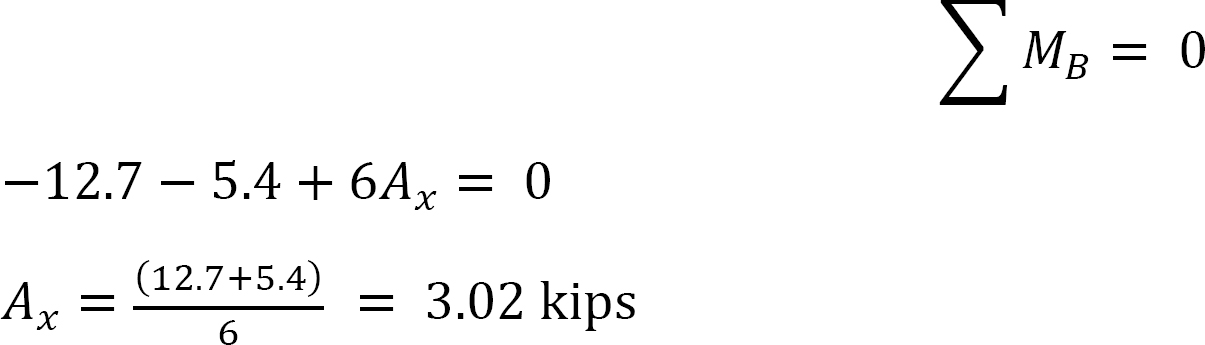
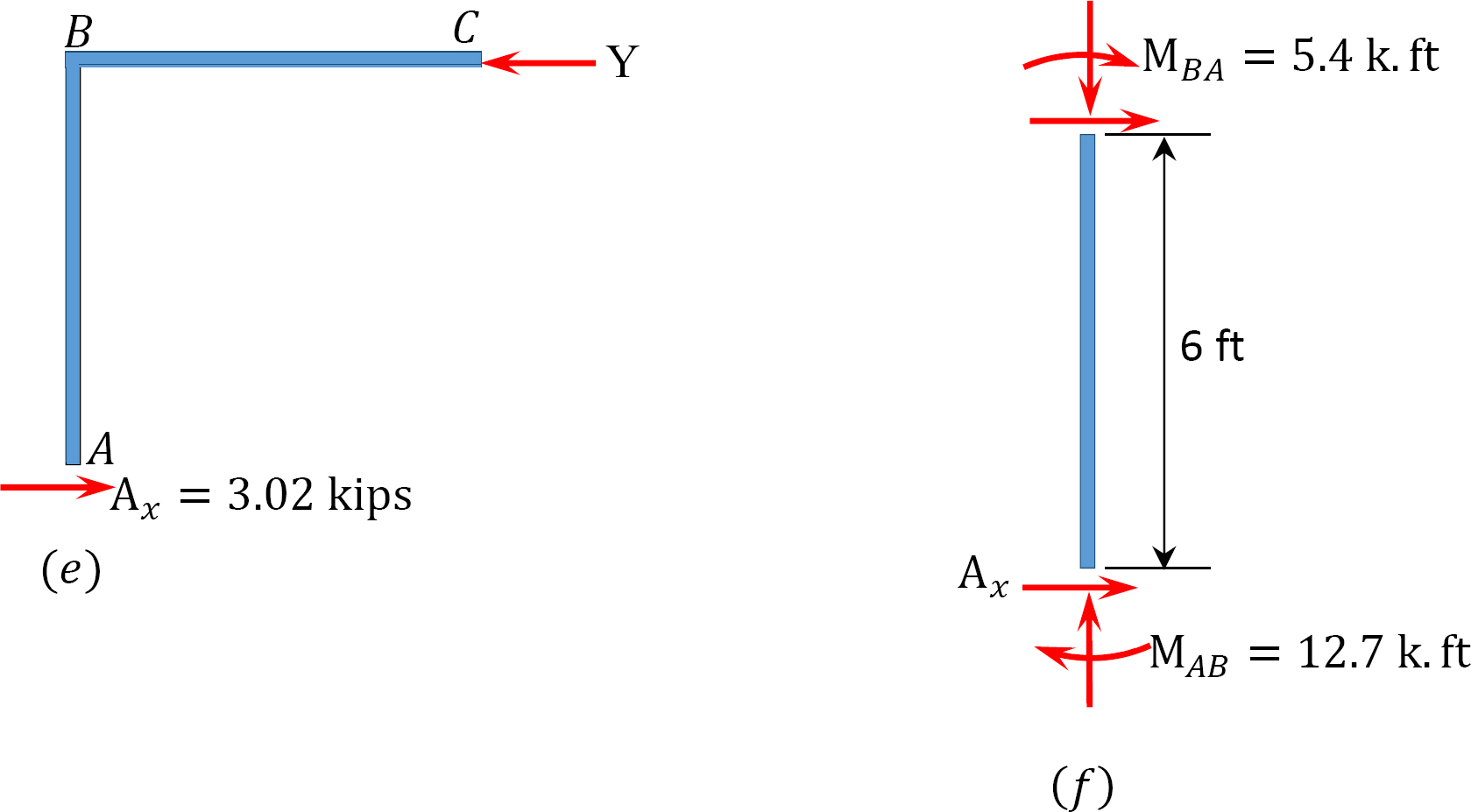
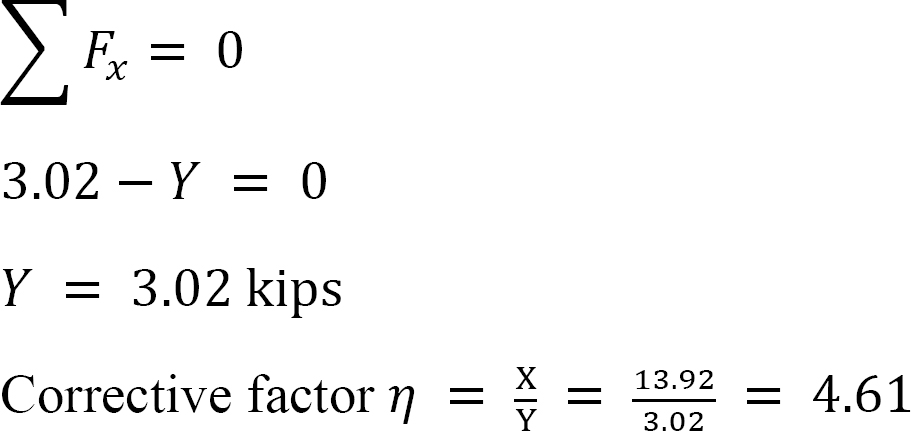
Endelige sluttmomenter.
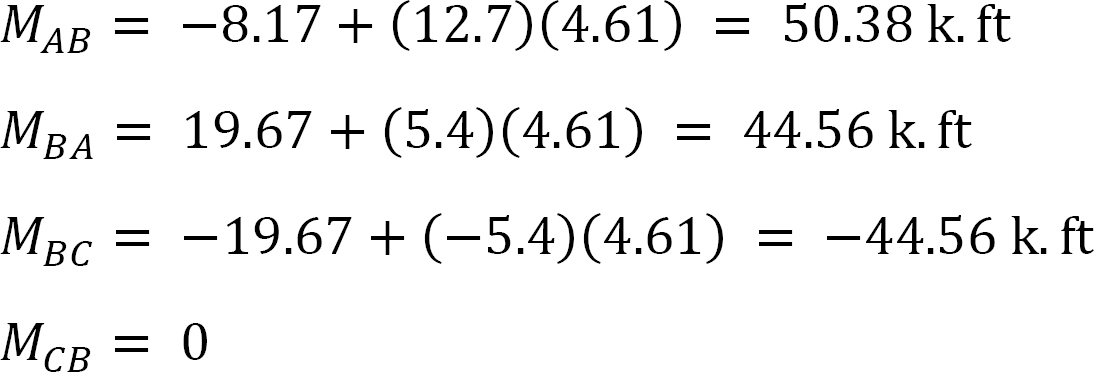
Eksempel 12.7
en sway-ramme lastes inn som vist i Figur 12.12 a. bruk øyeblikksfordelingsmetoden til å bestemme sluttmomentene til rammens medlemmer.
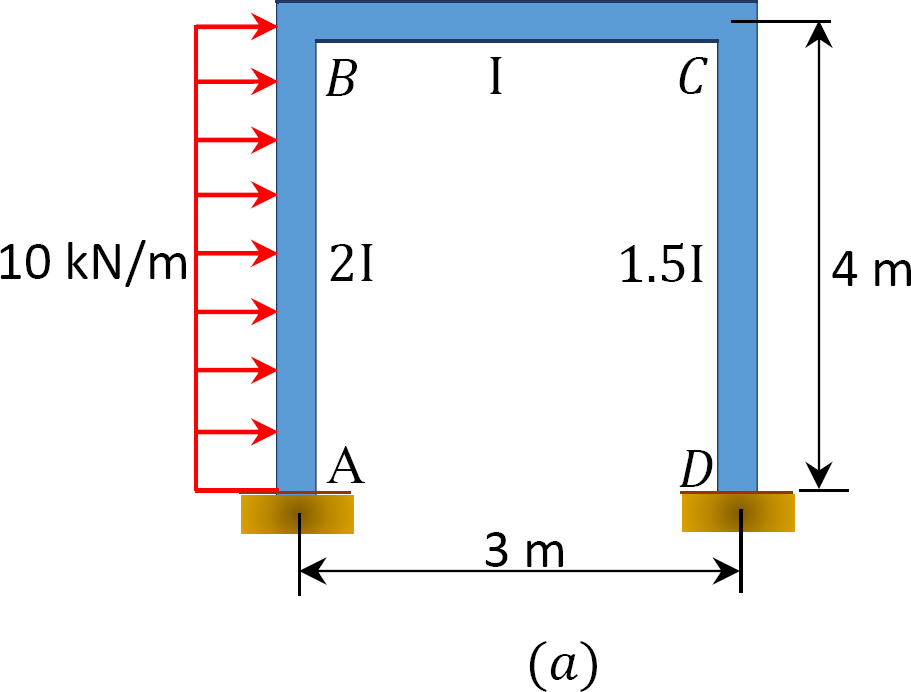
Fig. 12.12. Lastet sway ramme.
Løsning
Fast sluttmoment.
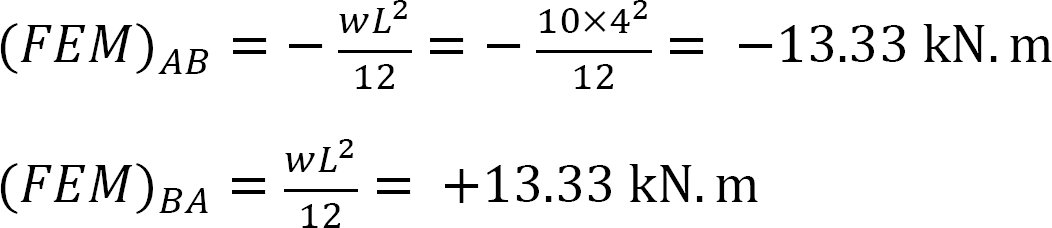
Stivhetsfaktor.
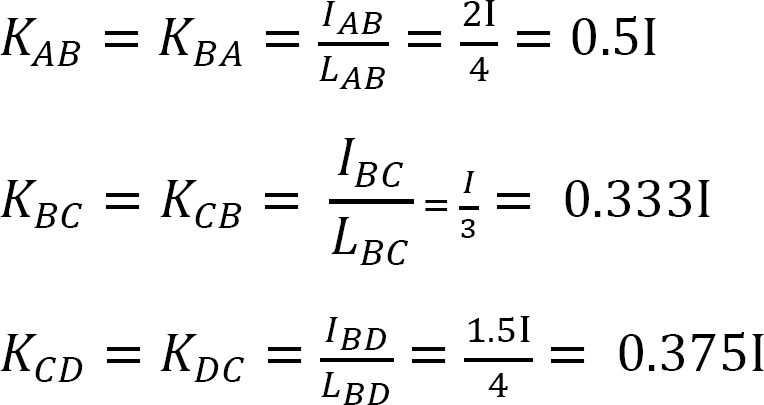
Distribusjonsfaktor.

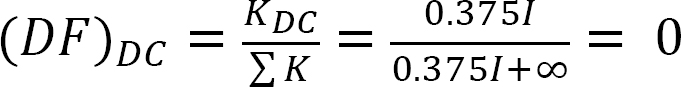
Analyse av ramme uten side-sway.
Tabell 12.8. Distribusjonstabell(ingen sway-ramme).
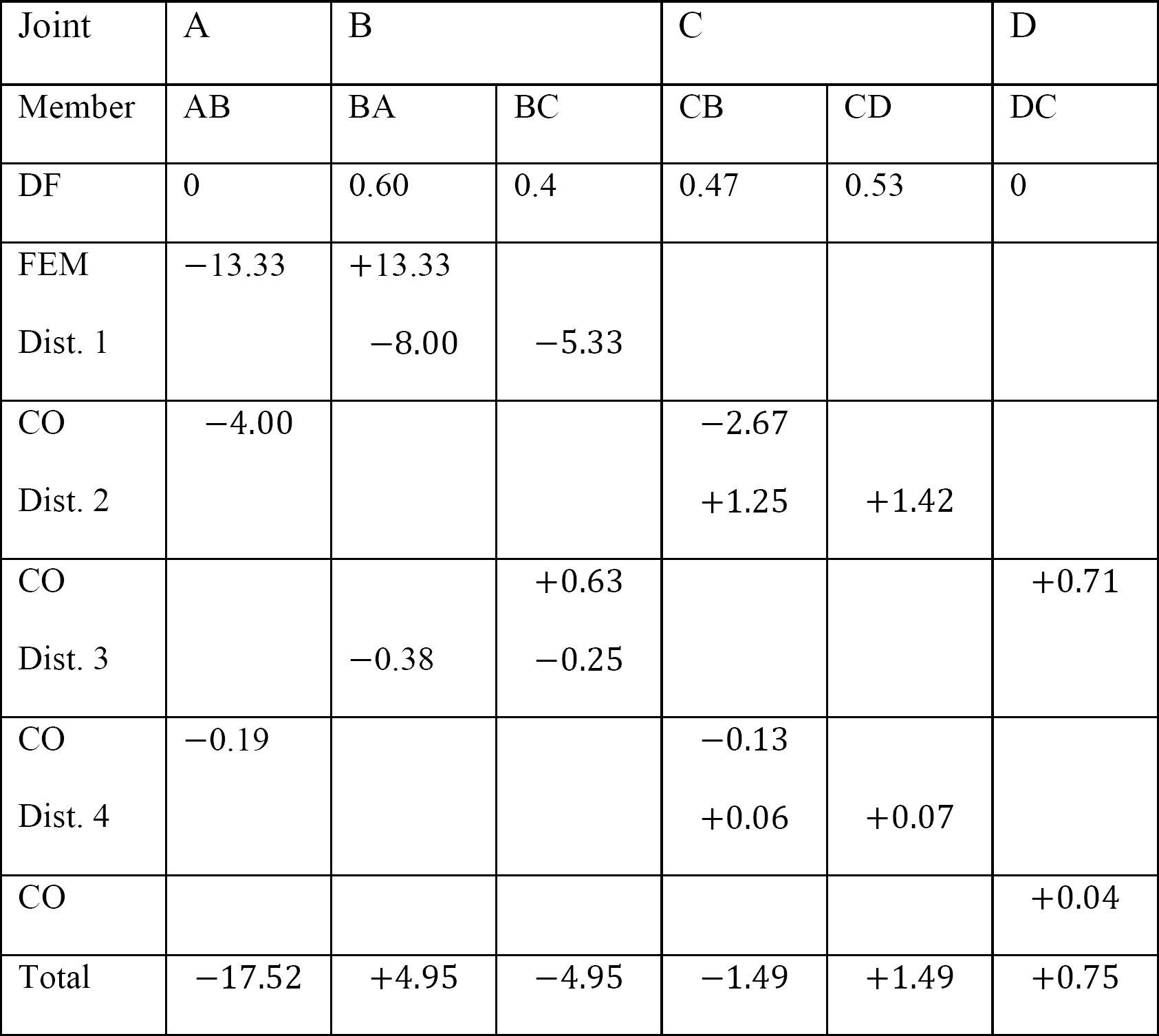
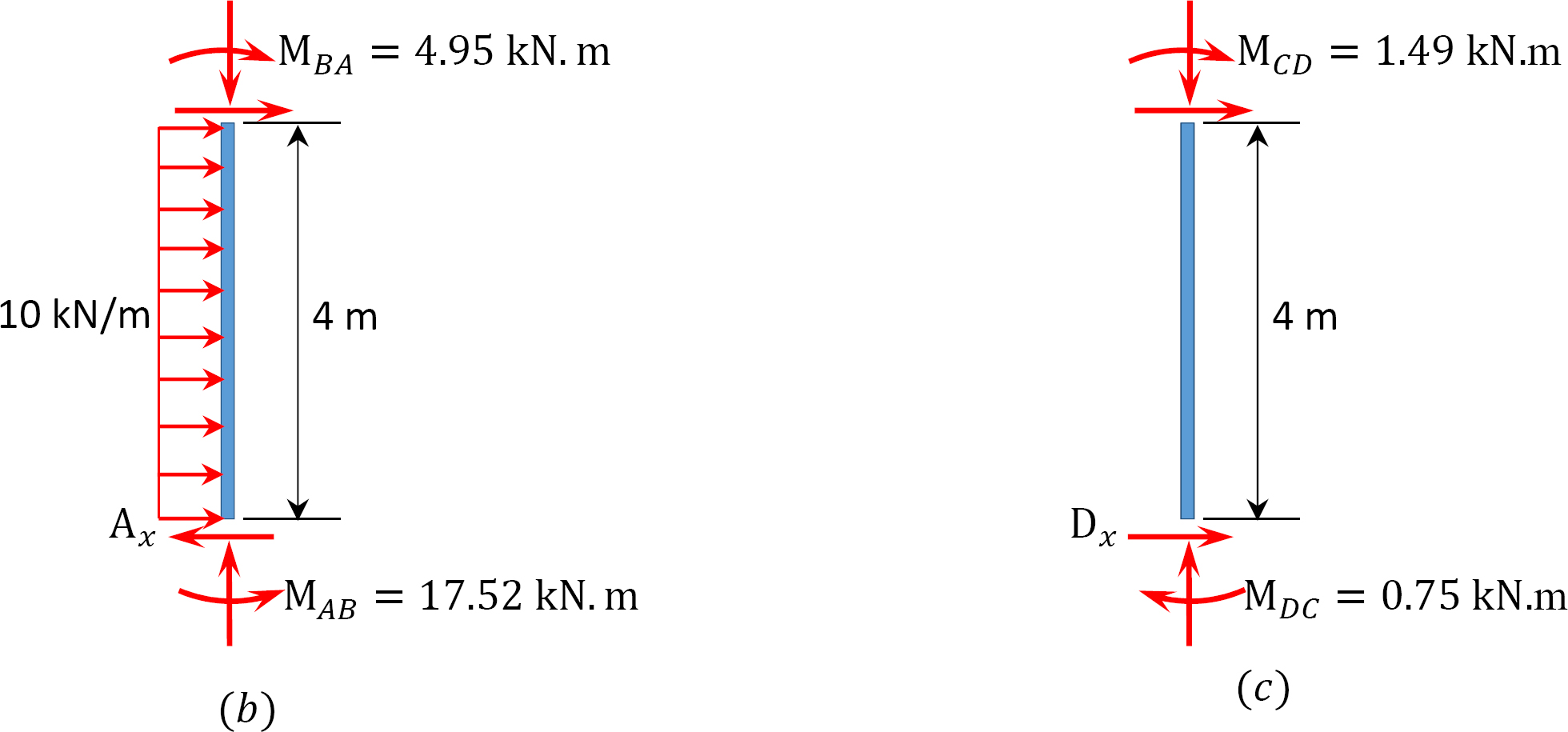
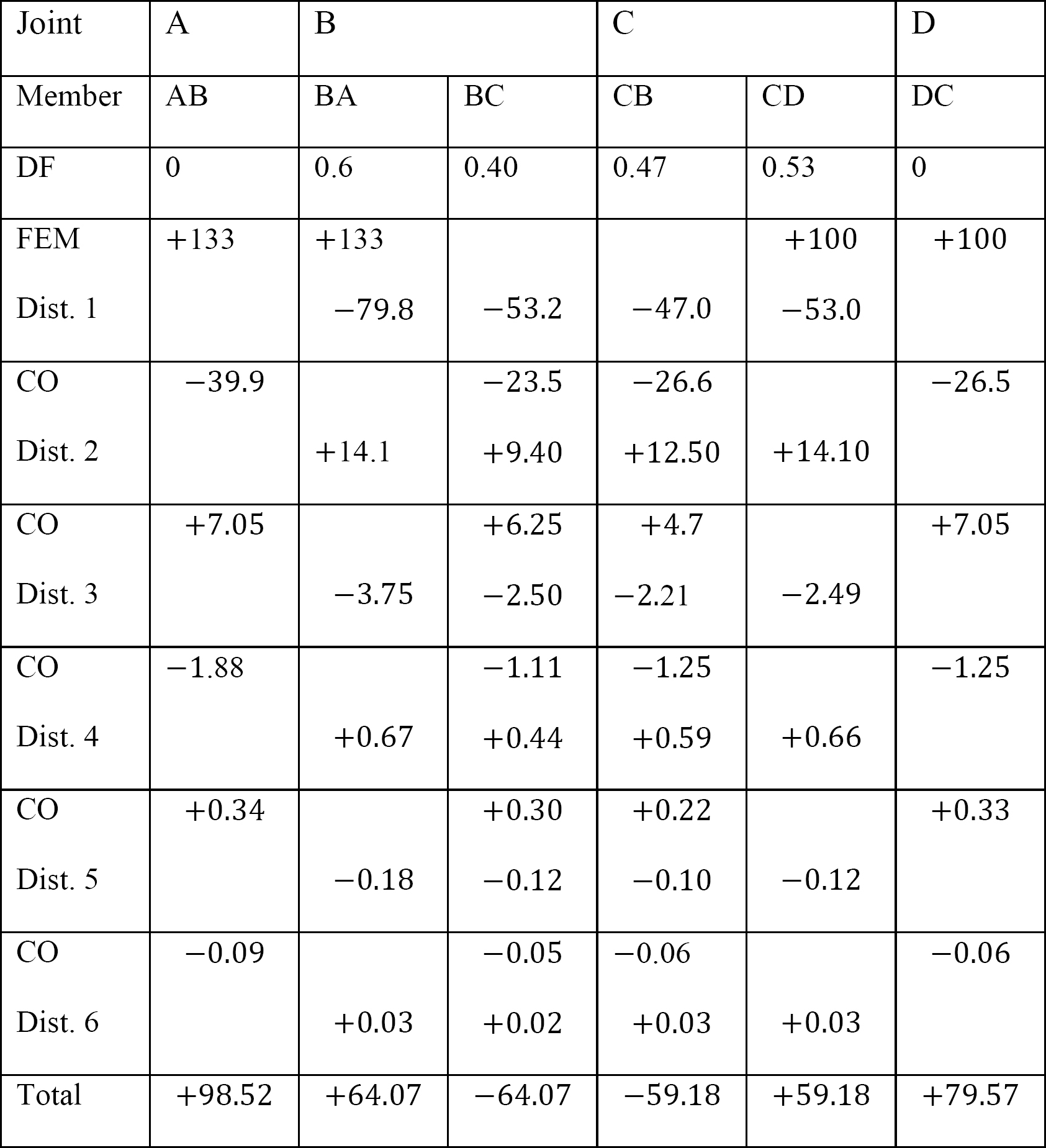
Tabell 12.9. Distribusjonstabell (sway frame).
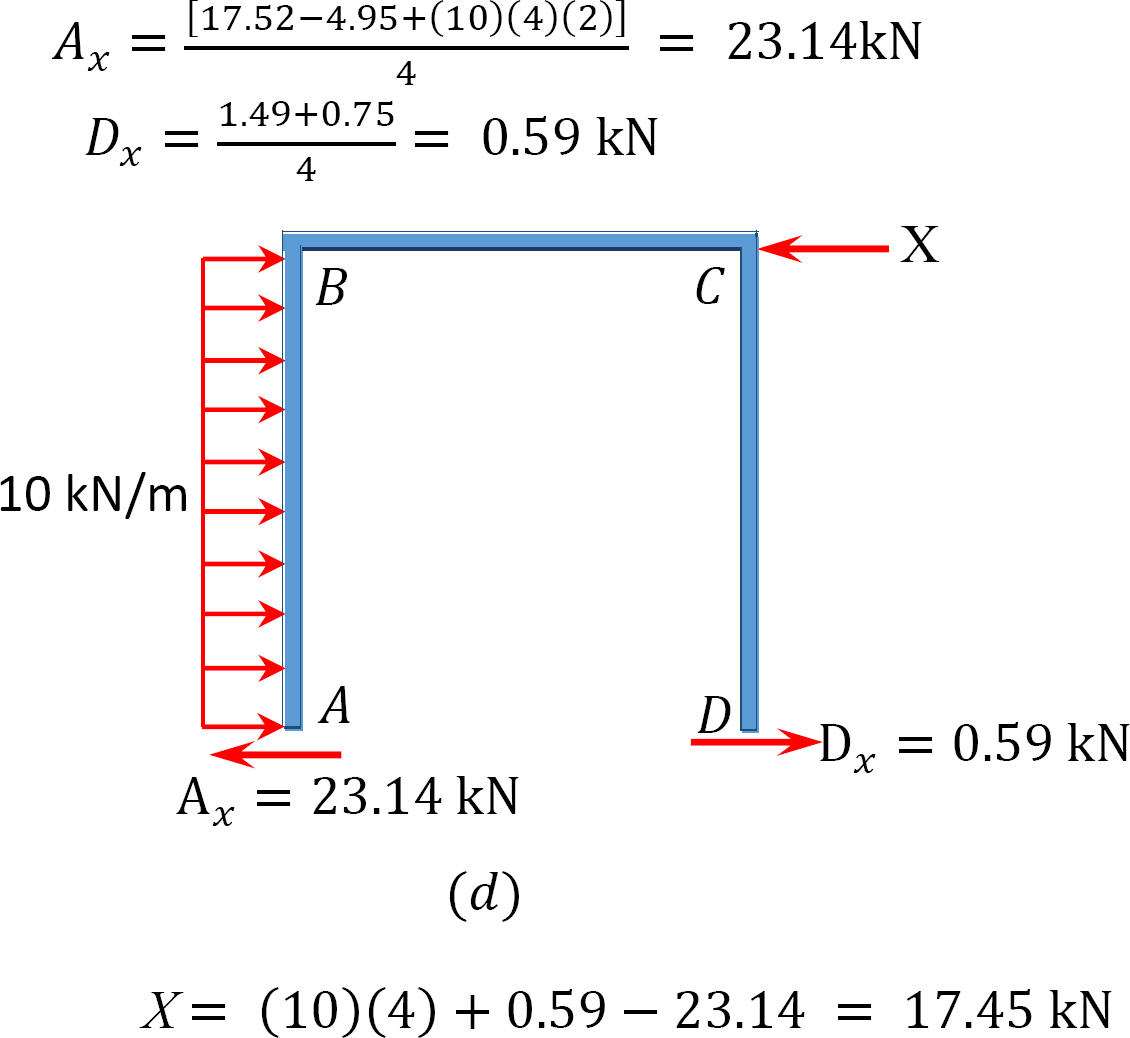
Analyse av ramme med side-sway.
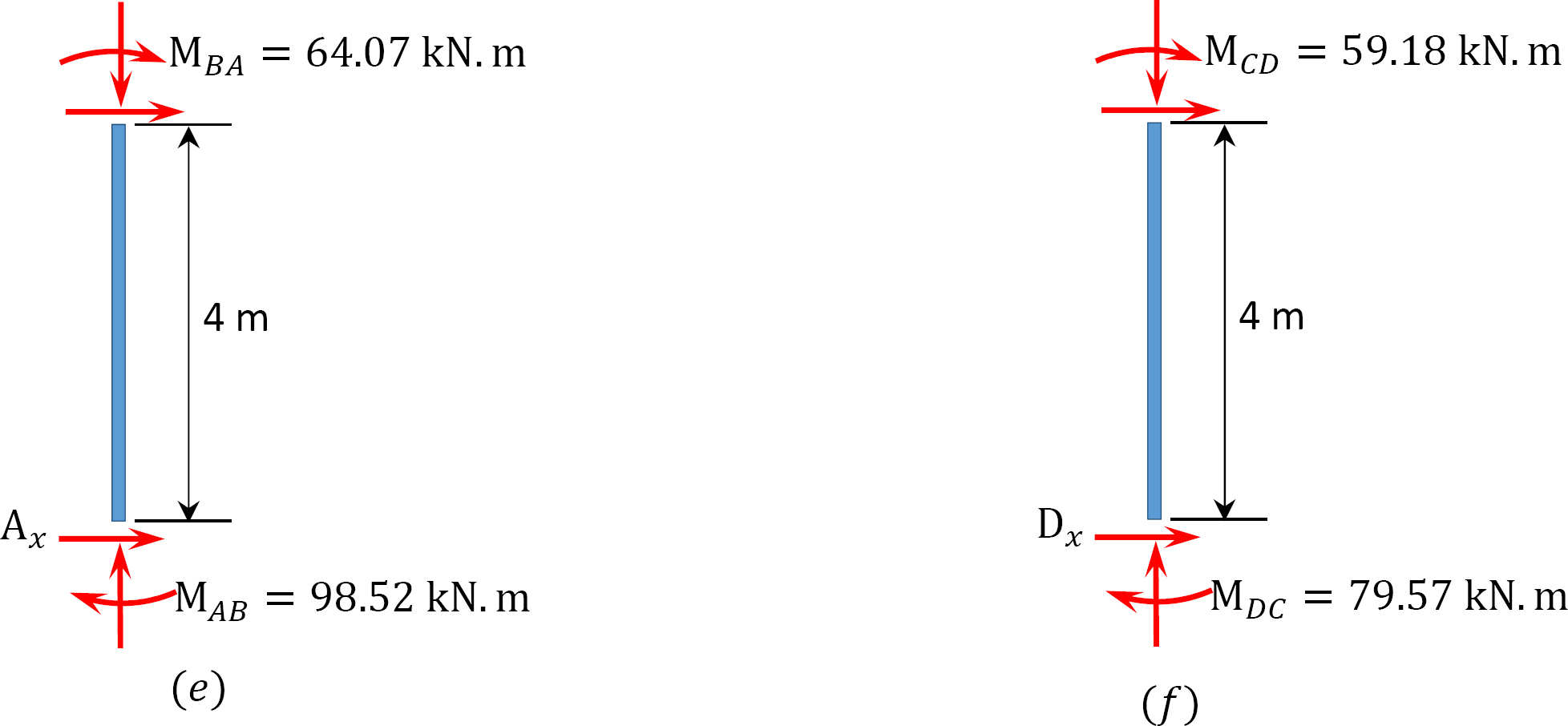

Endelig slutt øyeblikk.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. M
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Kapittelsammendrag
Momentfordelingsmetode for analyse av ubestemte strukturer: momentfordelingsmetoden for analyse er en omtrentlig analysemetode. Dens grad av nøyaktighet er avhengig av antall iterasjoner. I denne metoden antas det at alle leddene i en struktur er midlertidig låst eller klemmet og dermed forhindres i mulig rotasjon. Laster blir brukt på medlemmene, og øyeblikkene utviklet ved medlemsendene på grunn av fixity bestemmes. Leddene i strukturen låses så opp suksessivt, og det ubalanserte øyeblikket ved hvert ledd distribueres til medlemmer som møtes på det leddet. Overføringsmomenter på medlemmenes fjerne ender bestemmes, og balanseringsprosessen fortsetter til ønsket nivå av nøyaktighet. Medlemmenes sluttmomenter bestemmes ved å legge sammen det faste sluttmomentet, det distribuerte øyeblikket og overføringsmomentet. Når medlemmenes sluttmomenter er bestemt, blir strukturen determinant.
Praksis Problemer
12.1 Bruk momentfordelingsmetoden til å beregne sluttmomentet til medlemmer av bjelkene vist I Figur P12.1 Til Figur P12.12 og tegne bøyemomentet og skjærkraftdiagrammer. EI = konstant.
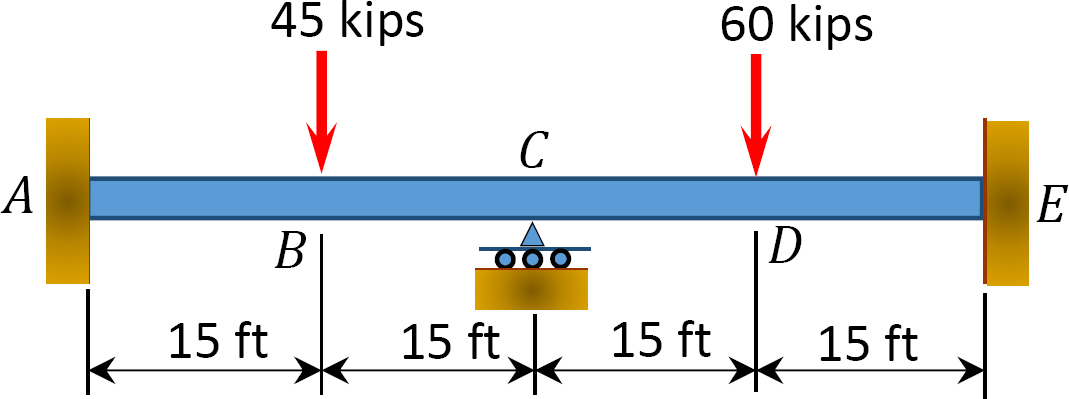
Fig. P12.1. Stråle.
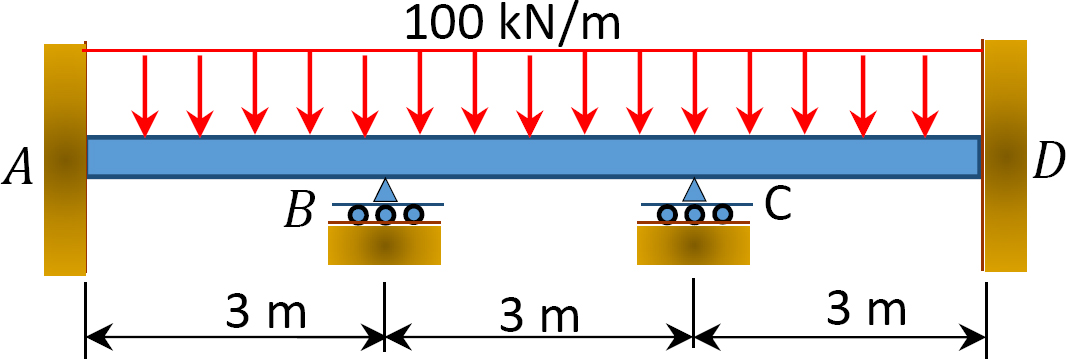
Fig. P12. 2. Stråle.
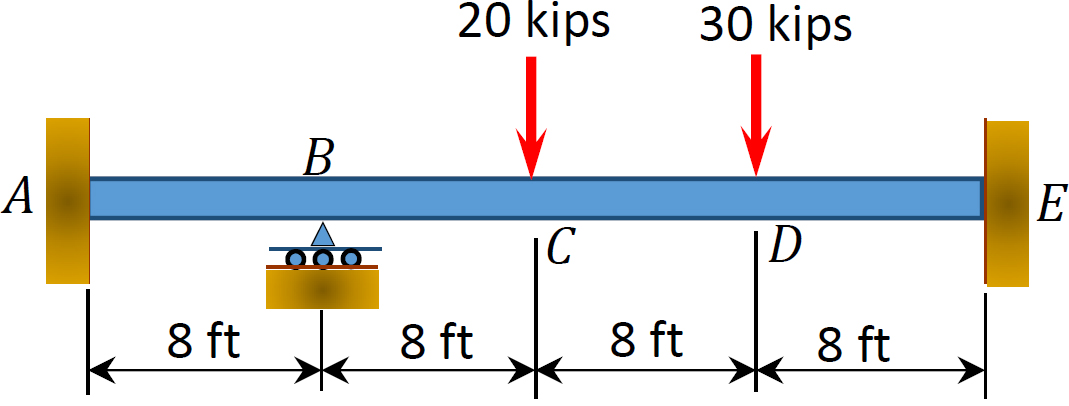
Fig. P12.3. Stråle.
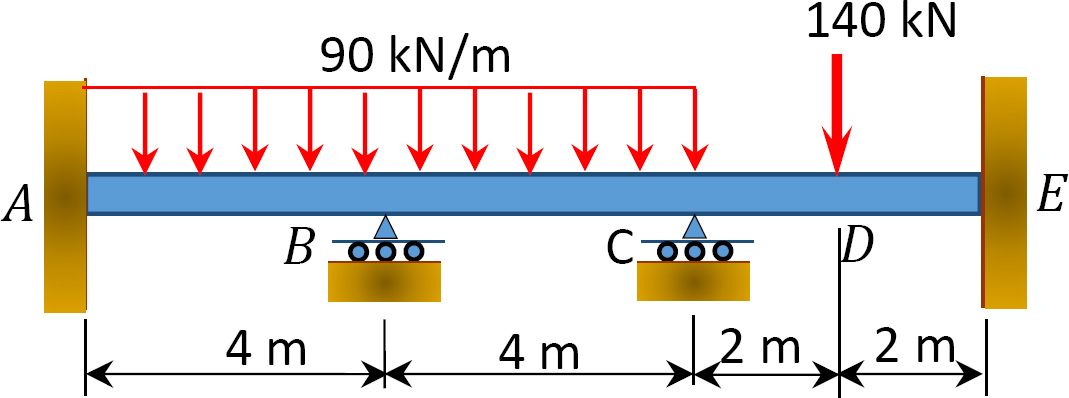
Fig. P12. 4. Stråle.
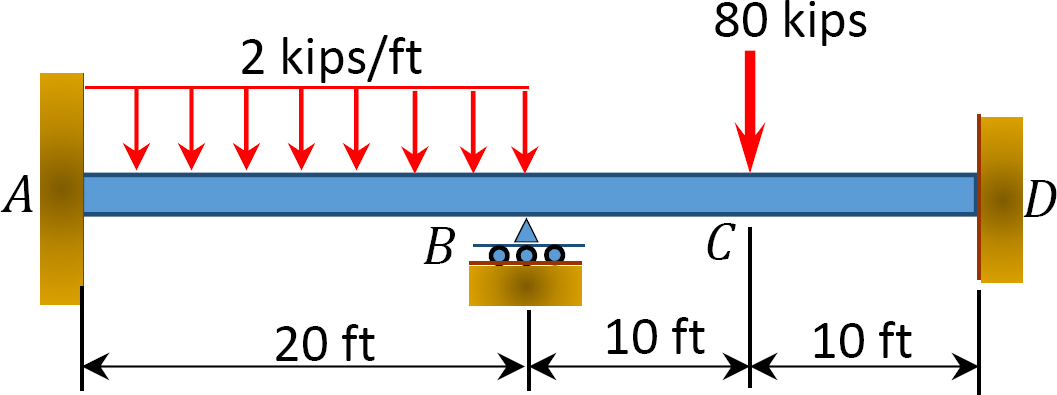
Fig. P12.5. Stråle.
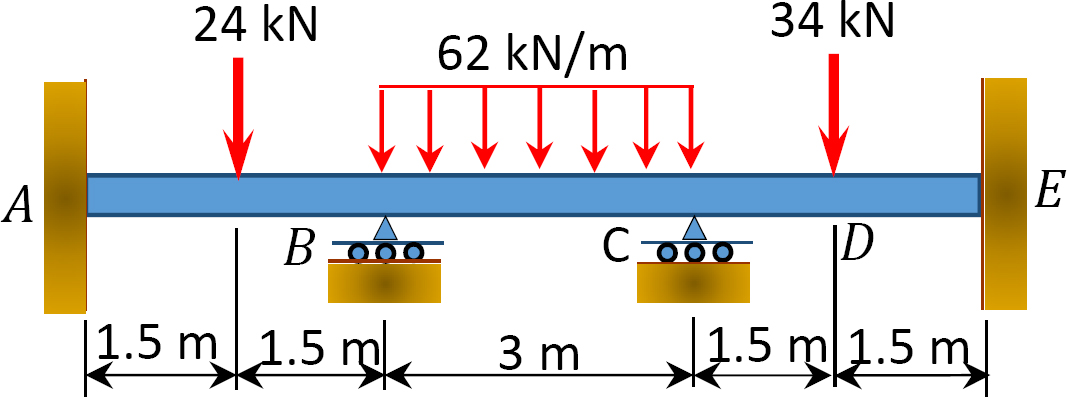
Fig. P12. 6. Stråle.
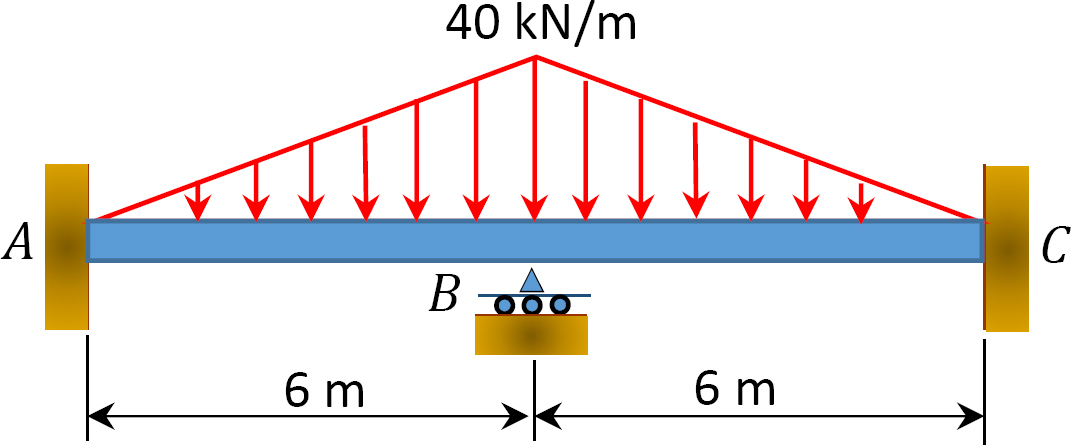
Fig. P12. 7. Stråle.
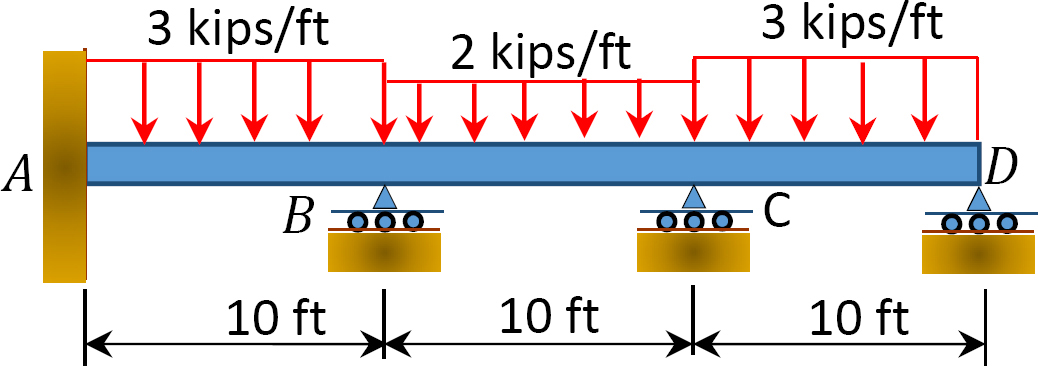
Fig. P12. 8. Stråle.
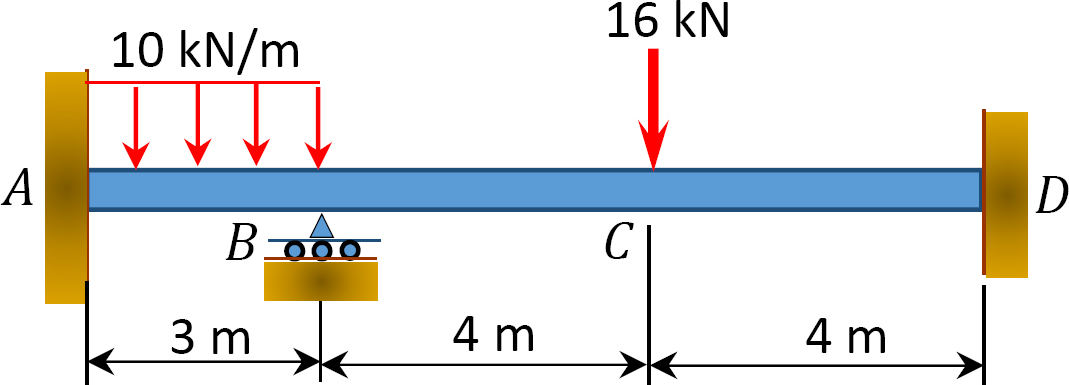
Fig. P12. 9. Stråle.
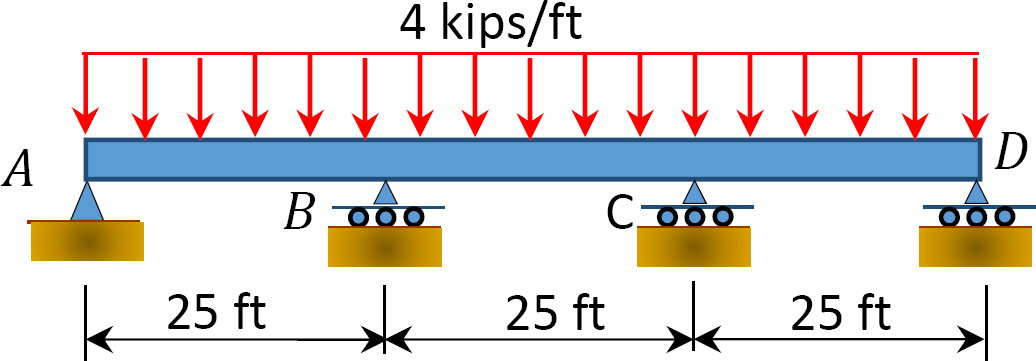
Fig. P12.10. Stråle.
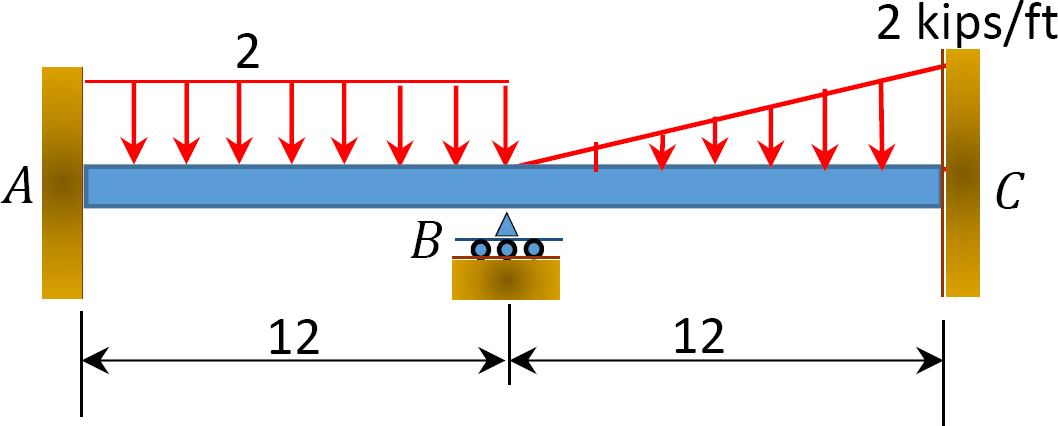
Fig. P12.11. Stråle.
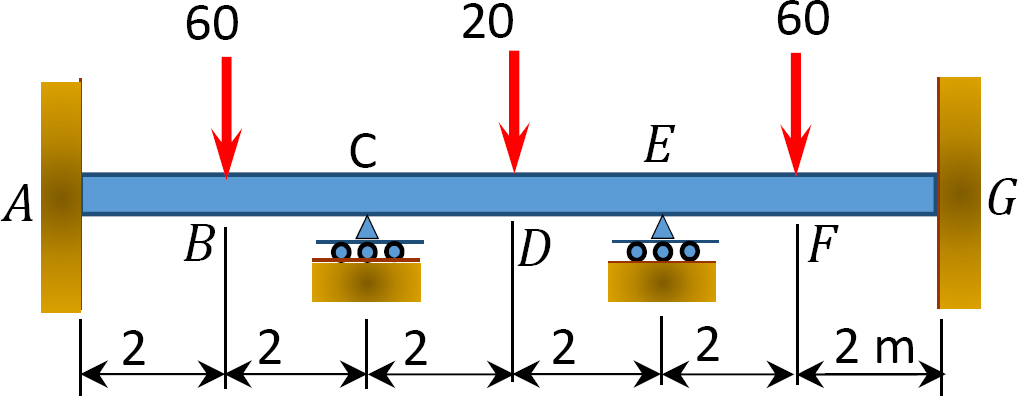
Fig. P12.12. Stråle.
12.2 Bruk momentfordelingsmetoden til å beregne sluttmomentet til medlemmene av rammene vist I Figur P12. 13 Til Figur 12.20 og tegne bøyningsmomentet og skjærkraftdiagrammer. EI = konstant.
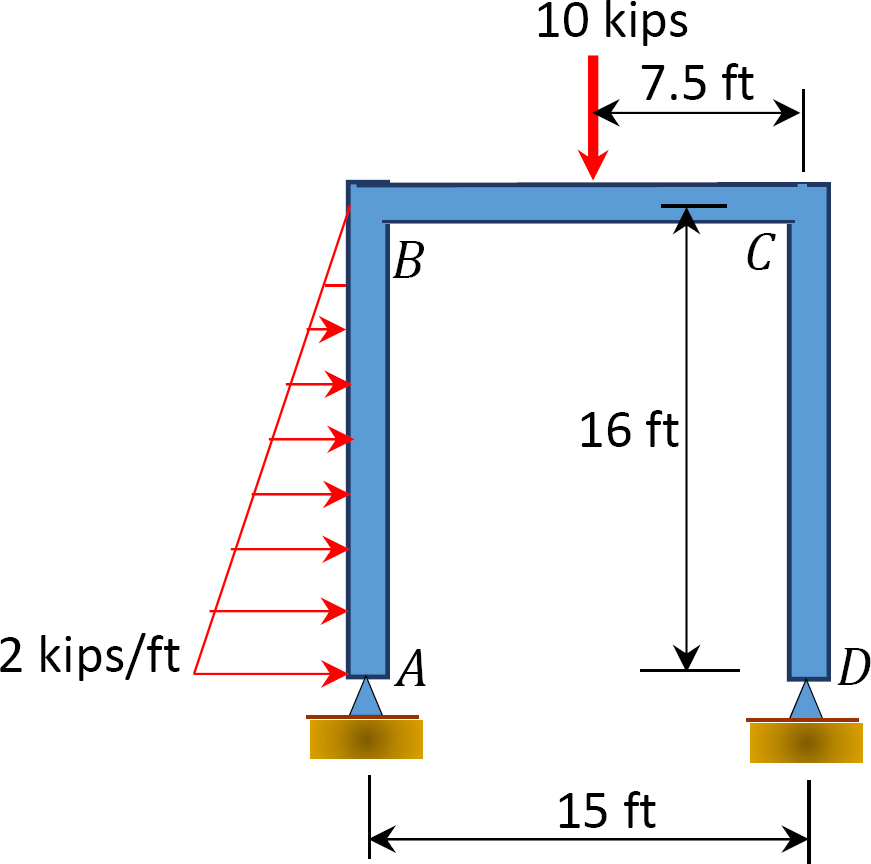
Fig. P12.13. Ramme.
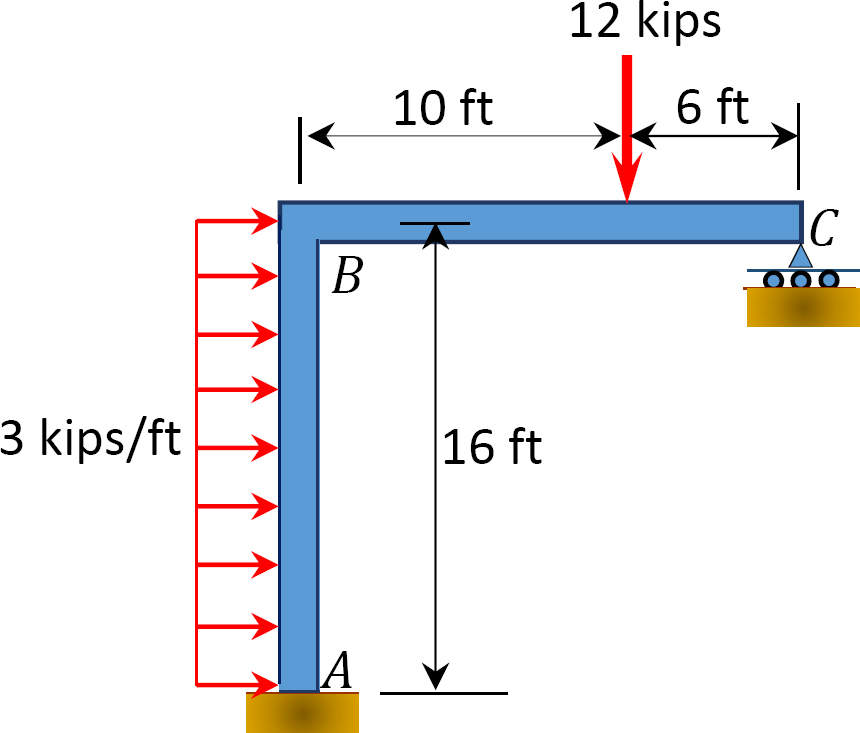
Fig. P12.14. Ramme.
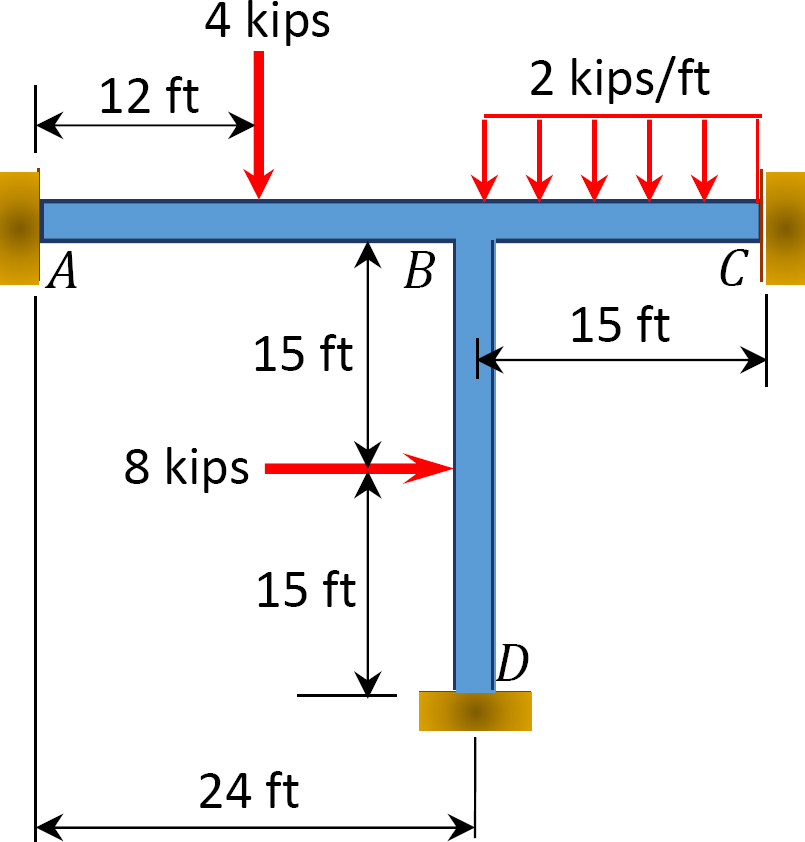
Fig. P12.15. Ramme.
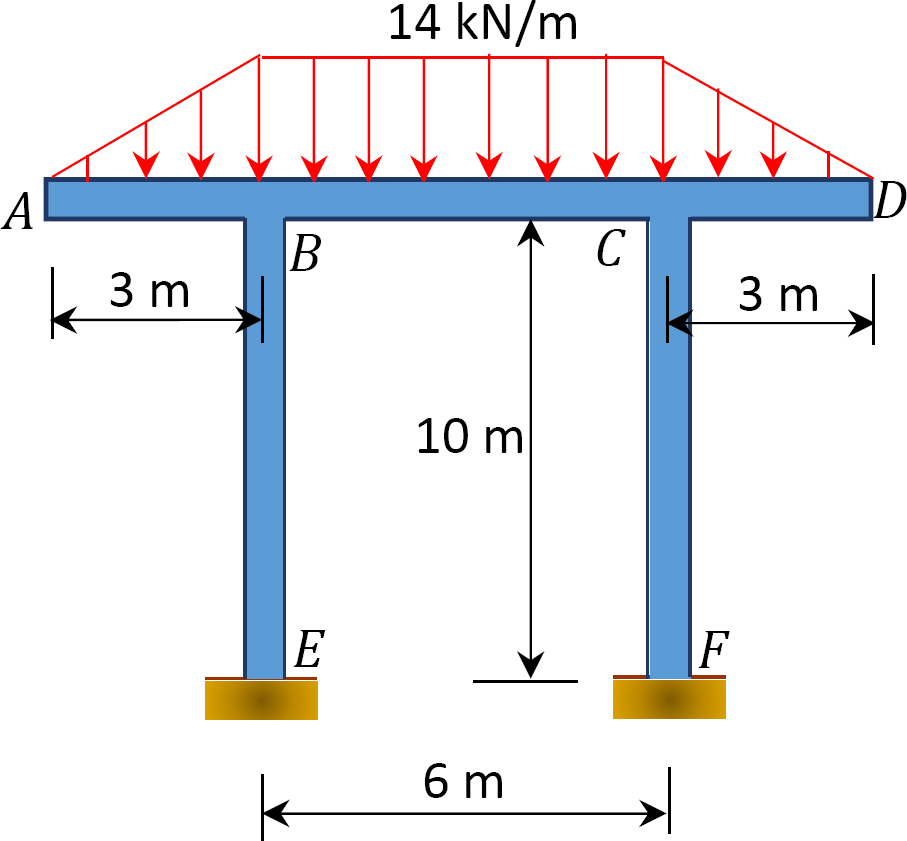
Fig. P12.16. Frame.
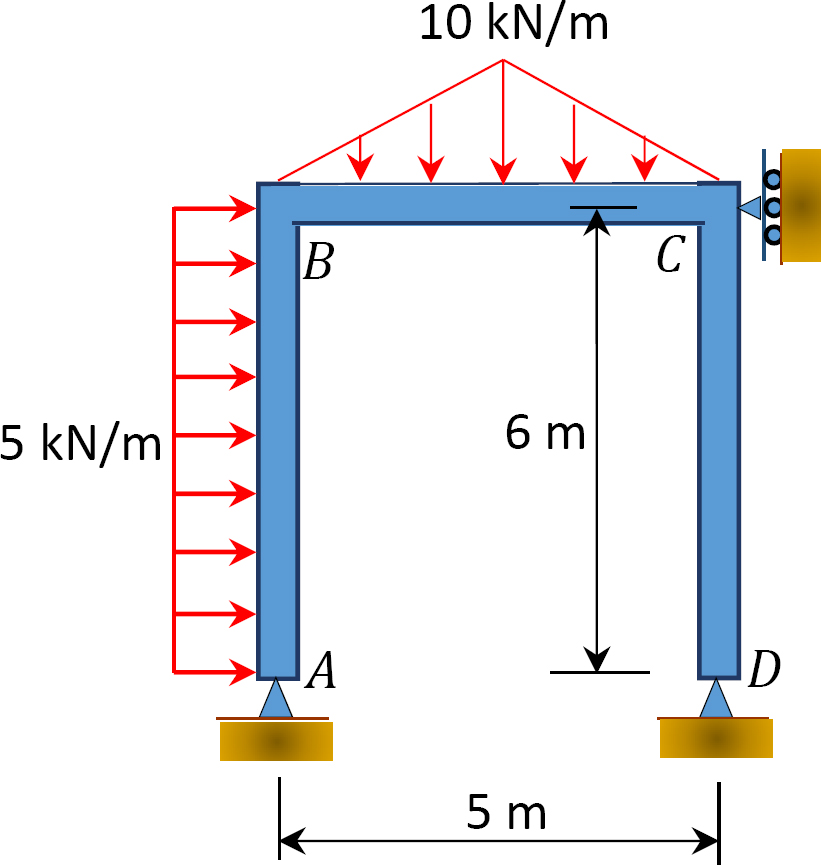
Fig. P12.17. Frame.
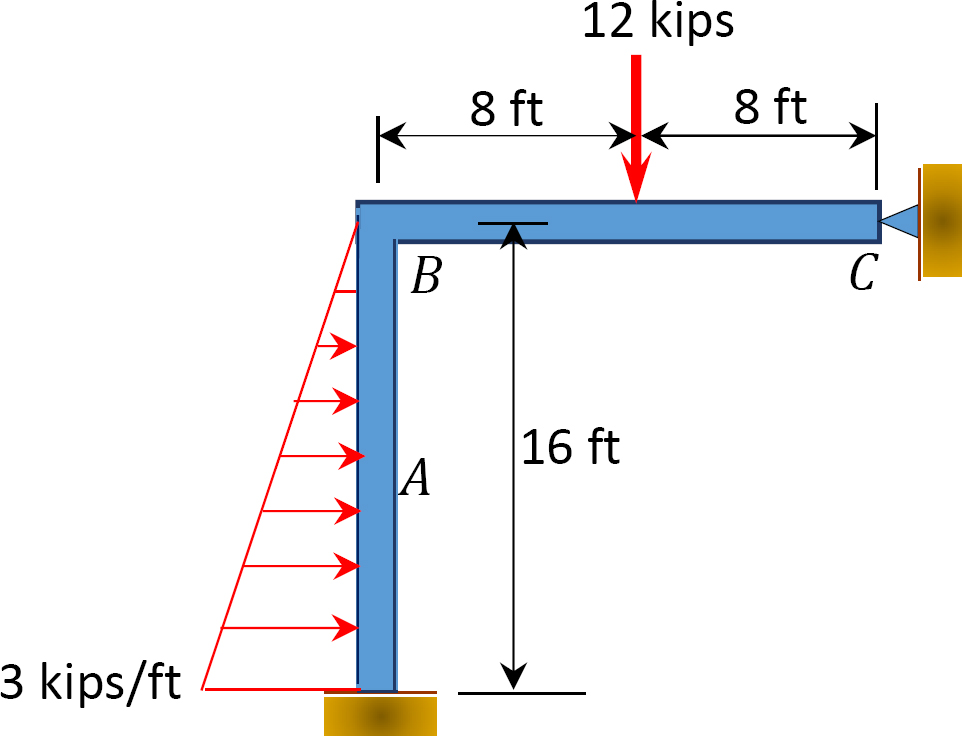
Fig. P12.18. Frame.
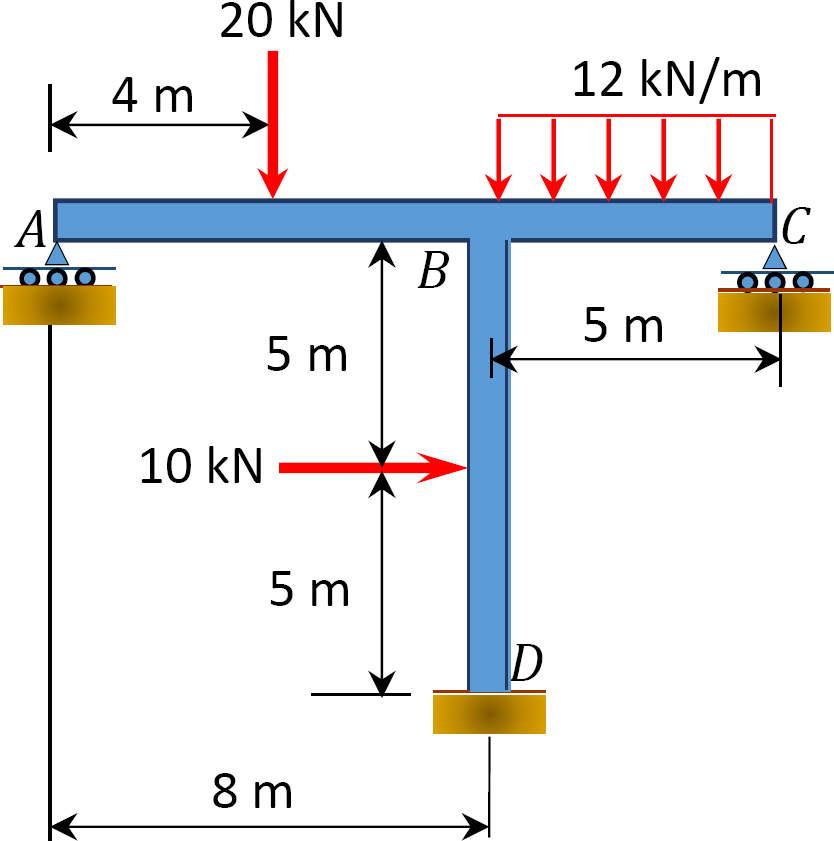
Fig. P12.19. Frame.
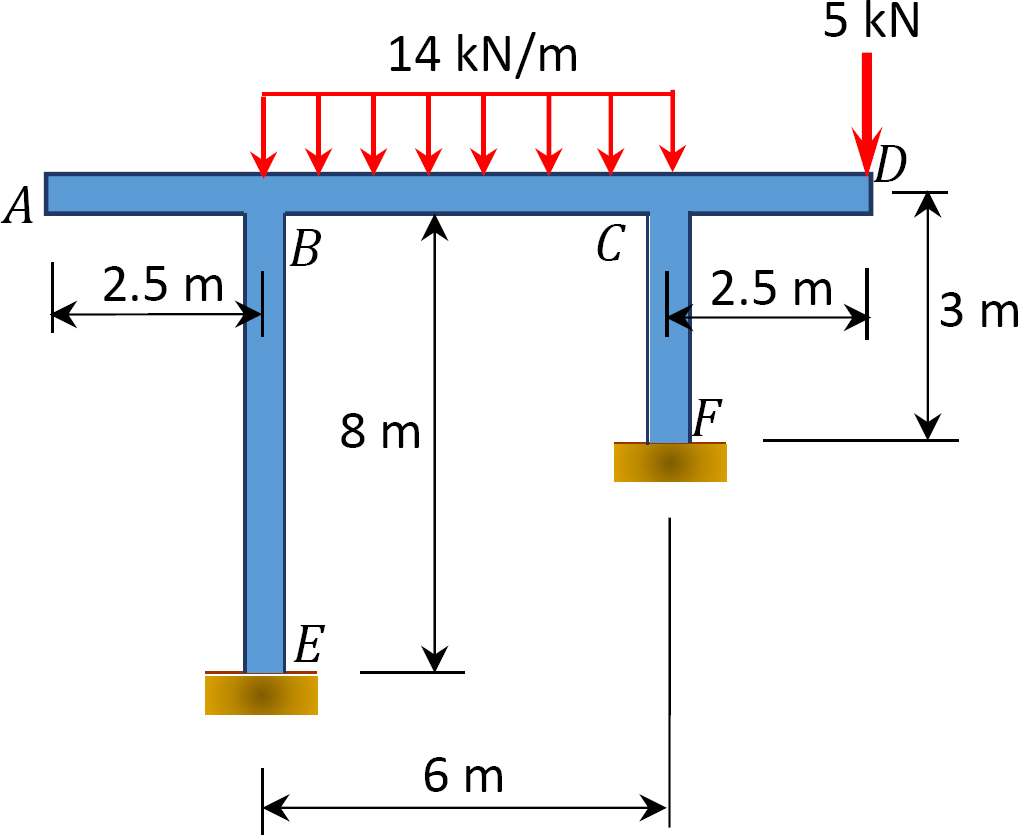
Fig. P12.20. Frame.