Duffing differentiaalvergelijking

de meest algemene geforceerde vorm van de Duffvergelijking is

(1)

afhankelijk van de gekozen parameters kan de vergelijking een aantal speciale vormen aannemen. Bijvoorbeeld, zonder demping en zonder forcering, en het plusteken nemen, wordt de vergelijking

(2)

(Bender en Orszag 1978, blz. 547; Zwillinger 1997, blz. 122). Deze vergelijking kan chaotisch gedrag vertonen. Voor staat de vergelijking voor een “harde veer” en voor staat de vergelijking voor een “zachte veer”.”Als , worden de faseportretkrommen gesloten.

als we in plaats daarvan , nemen, de klok resetten zodat , en gebruik het minteken, dan is de vergelijking

(3)

dit kan worden geschreven als een systeem van de eerste orde gewone differentiaalvergelijkingen als

			(4)
			(5)

(Wiggins 1990, blz. 5), die in het geval unforced tot

			(6)
			(7)

(Wiggins 1990, blz. 6; Ott 1993, blz. 3).

de vaste punten van deze verzameling gekoppelde differentiaalvergelijkingen worden gegeven door

(8)

dus , en

			(9)
			(10)

geeft . De vaste punten zijn dus , , en .

analyse van de stabiliteit van de vaste punten kan punt zijn door de vergelijkingen te lineariseren. Differentiëren geeft

			(11)
			(12)
			(13)

die kan worden geschreven als de matrixvergelijking

(14)

onderzoek naar de stabiliteit van het punt (0,0):

(15)

(16)

maar , dus is echt. Sinds zal er altijd één positieve wortel zijn, dus dit vaste punt is onstabiel. Kijk nu naar (, 0). De karakteristieke vergelijking is

(17)

die wortels heeft

(18)

voor , , dus het punt is asymptotisch stabiel. Indien , , dus het punt is lineair stabiel (Wiggins 1990, p. 10). Indien , het radicaal geeft een imaginair deel en het reële deel is , dus het punt is onstabiel. Indien , , die een positieve reële wortel heeft, dus het punt is onstabiel. Als , dan , dus beide wortels zijn positief en het punt is instabiel.

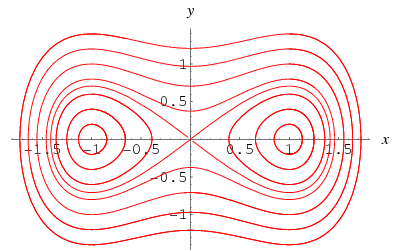
interessant is dat het speciale geval zonder forcering,

			(19)
			(20)

kan worden geïntegreerd door kwadraturen. Differentiëren (19) en pluggen in (20) geeft

(21)

beide zijden vermenigvuldigen met geeft

(22)

maar dit kan geschreven worden

(23)

dus we hebben een invariant van beweging ,

(24)

oplossen voor geeft

(25)

(26)

so

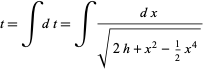(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion satisfies

(28)

(29)

dus de vergelijkingen van de duffing oscillator worden gegeven door het Hamiltoniansystem