aplicarea și interpretarea principiului Saint-Venant

toți inginerii structurali folosesc principiul Saint-Venant, fie activ, fie subconștient. Puteți găsi diverse formulări ale acestui principiu în majoritatea manualelor de mecanică structurală, dar sensul său exact nu este evident. Principiul lui Saint-Venant ne spune că distribuția exactă a unei sarcini nu este importantă departe de regiunea încărcată, atâta timp cât rezultatele sarcinii sunt corecte. În această postare pe blog, vom explora principiul lui Saint-Venant, în special în contextul analizei elementelor finite (FE).

istoria principiului lui Saint-Venant

omul de știință francez Barrul de Saint-Venant și-a formulat faimosul principiu în 1855, dar a fost mai mult o observație decât o afirmație matematică strictă:

„dacă forțele care acționează pe o porțiune mică a suprafeței unui corp elastic sunt înlocuite cu un alt sistem echivalent static de forțe care acționează pe aceeași porțiune a suprafeței, această redistribuire a încărcării produce modificări substanțiale ale tensiunilor la nivel local, dar are un efect neglijabil asupra tensiunilor la distanțe mari în comparație cu dimensiunile liniare ale suprafeței pe care sunt schimbate forțele.”

B. Saint-Venant, M. savants oktiftrangers, vol. 14, 1855.

Portretul lui Saint-Venant. Imagine în domeniul public, prin Wikimedia Commons.

multe minți mari din domeniul mecanicii aplicate — Boussinesq, Love, von Mises, Toupin și alții — au fost implicați în afirmarea principiului lui Saint-Venant într-o formă mai exactă și furnizarea de dovezi matematice pentru acesta. După cum se dovedește, acest lucru este destul de dificil pentru cazuri mai generale, iar cercetările pe această temă sunt încă în desfășurare. (Argumentația a fost uneori destul de vie.)

exemplu simplu: analiza tensiunilor la distanță

să începem cu ceva destul de simplu: o placă dreptunghiulară subțire, cu o gaură circulară la o anumită distanță de marginea încărcată, care este trasă axial. Dacă suntem interesați de concentrația de stres la gaură, atunci cât de importantă este distribuția reală a sarcinii?

trei tipuri diferite de sarcină sunt aplicate la limita din dreapta:

1. o tensiune axială constantă de 100 MPa
2. o distribuție simetrică a stresului parabolic cu amplitudine maximă de 150 MPa
3. o sarcină punctată centrată cu același rezultat ca și cele două cazuri anterioare de încărcare

așa cum se vede în graficele de mai jos, distribuția stresului la gaură nu este afectată de modul în care este aplicată sarcina. Cheia aici este, desigur, că gaura este suficient de departe de sarcină.

Von Mises contururi de stres pentru cele trei cazuri de sarcină.

un alt mod de vizualizare a acestui scenariu este prin utilizarea săgeților principale de stres. Un astfel de complot subliniază câmpul de stres ca un flux și oferă un sentiment bun pentru redistribuire.

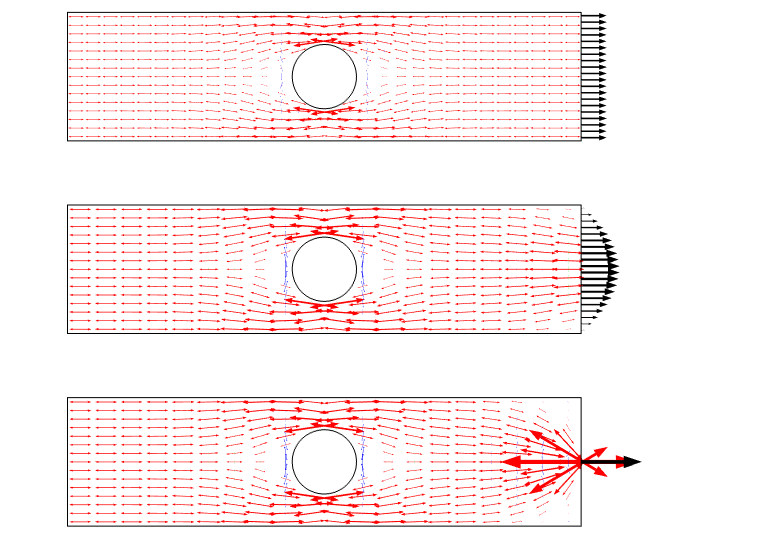
Grafic principal de stres pentru cele trei cazuri de încărcare. Rețineți că există o singularitate atunci când se utilizează o sarcină punctuală.

prin graficarea stresului de-a lungul unei linii, putem vedea că toate cele trei cazuri converg între ele la o distanță de margine, care este aproximativ egală cu lățimea plăcii.

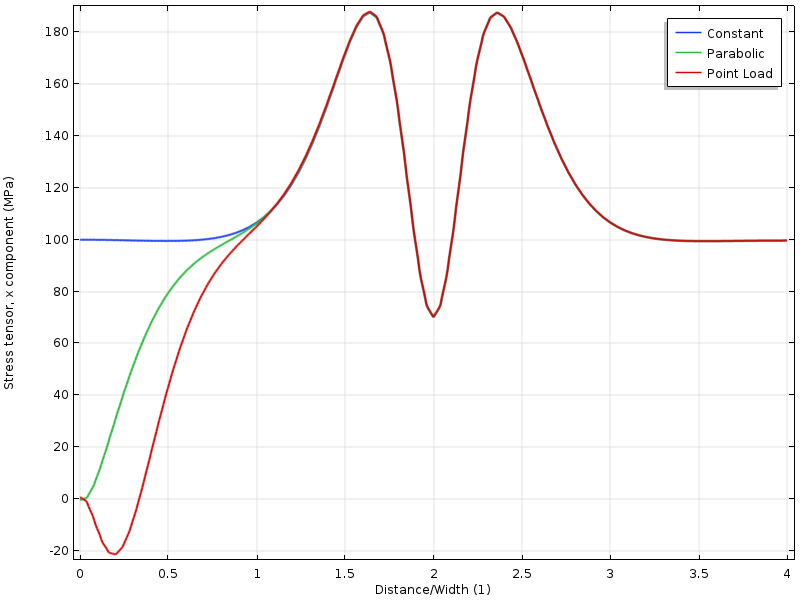
stres de-a lungul marginii superioare în funcție de Distanța de la limita încărcată. Distanța este normalizată de lățimea plăcii.

dacă gaura este mutată mai aproape de limita încărcată, obținem o altă situație. Starea de stres din jurul găurii depinde acum de distribuția sarcinii. Dar și mai interesant este că Distanța până la locul în care cele trei câmpuri de stres sunt de acord acum este de două ori mai departe de limita încărcată. Aplicarea principiului lui Saint-Venant impune ca tensiunile să fie libere să redistribuie. În acest caz, această redistribuire este parțial blocată de gaură.

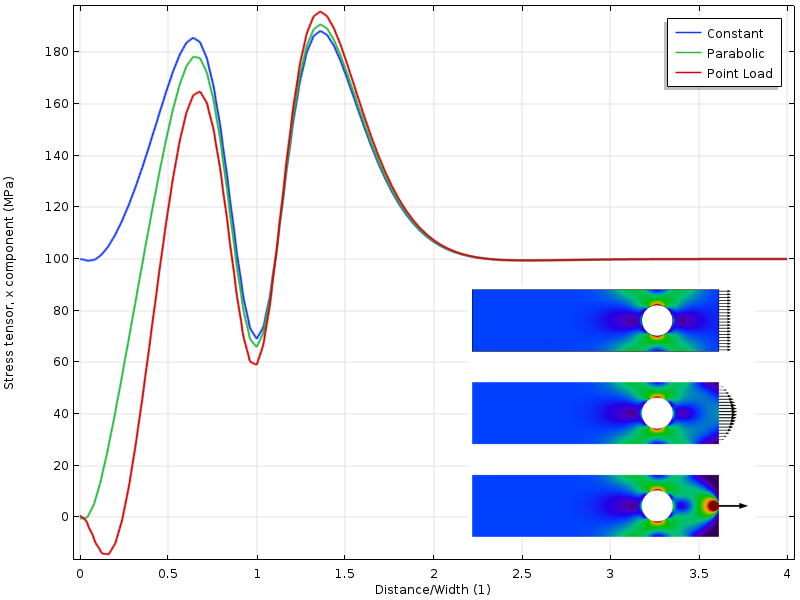
stres de-a lungul marginii superioare cu gaura mai aproape de limita încărcată.

rețineți că principiul lui Saint-Venant ne spune că nu există nicio diferență în starea de stres la o distanță care este de ordinul dimensiunii liniare a zonei încărcate. Cu toate acestea, zona încărcată care trebuie luată în considerare poate să nu fie zona care este de fapt încărcată! Această afirmație poate părea ciudată, dar gândiți-vă astfel: când gaura este departe, putem calcula factorul de concentrare a Stresului folosind un manual (al meu spune 4.32), mai degrabă decât printr-o soluție FE. Abordarea manualului conține o presupunere implicită că sarcina este distribuită uniform ca în primul caz de încărcare. Deci, chiar dacă sarcina reală a fost aplicată doar unei mici părți a limitei, distanța critică în acest caz este legată de dimensiunea întregii limite.

la rezolvarea problemei folosind metoda elementului finit (FEM), atunci gaura poate fi arbitrar aproape de sarcină. Ceea ce stabilește limita este că, din punct de vedere fizic, distribuția sarcinii este bine definită. Cu toate acestea, de îndată ce facem presupuneri despre redistribuire, există o presupunere implicită despre distribuția sarcinii, care poate diferi de cea reală.

sisteme rezultate Zero și densitate de energie a tensiunii

până în prezent, am spus că tensiunile sunt aceleași independente de detaliile sarcinii la o anumită distanță adecvată. Deoarece avem de-a face cu elasticitate liniară aici, este întotdeauna posibilă suprapunerea cazurilor de încărcare. Atunci când se lucrează cu dovezi ale principiului lui Saint-Venant, este mai ușor să se formuleze un principiu de-a lungul acestor linii: tensiunile cauzate de un sistem de încărcare fără forță sau moment rezultat vor fi mici la o distanță care este de același ordin de mărime ca dimensiunea limitei încărcate.

astfel, studiem stresul cauzat de diferența dintre cele două sisteme de încărcare cu rezultate egale. Majoritatea dovezilor moderne se bazează pe estimări ale degradării densității energiei tulpinii pentru un astfel de sistem rezultat zero.

revenind la problema de mai sus, putem calcula diferența dintre cazurile de încărcare. Acest lucru ne permite să studiem decăderea reală a densității de energie a stresului sau a tulpinii pentru diferența câmpurilor de stres.

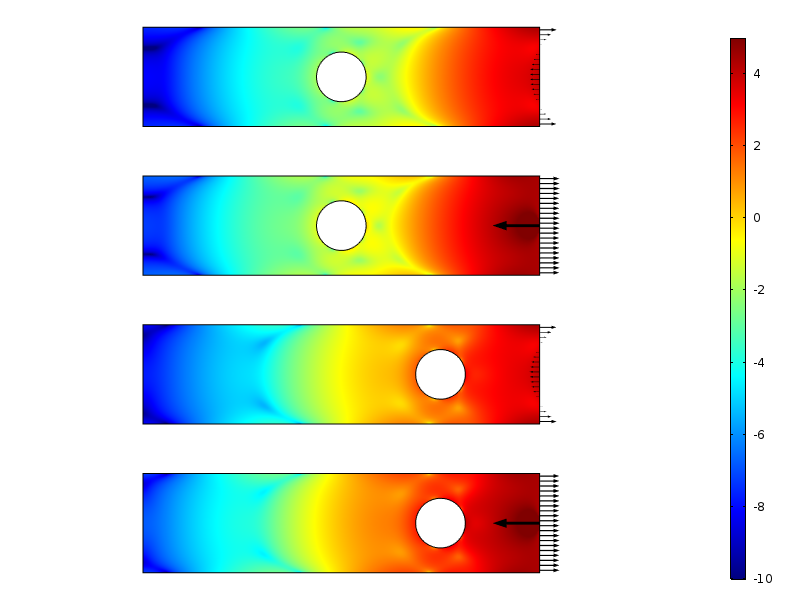
logaritmul densității energetice a tulpinii pentru cazurile de sarcină rezultate zero.

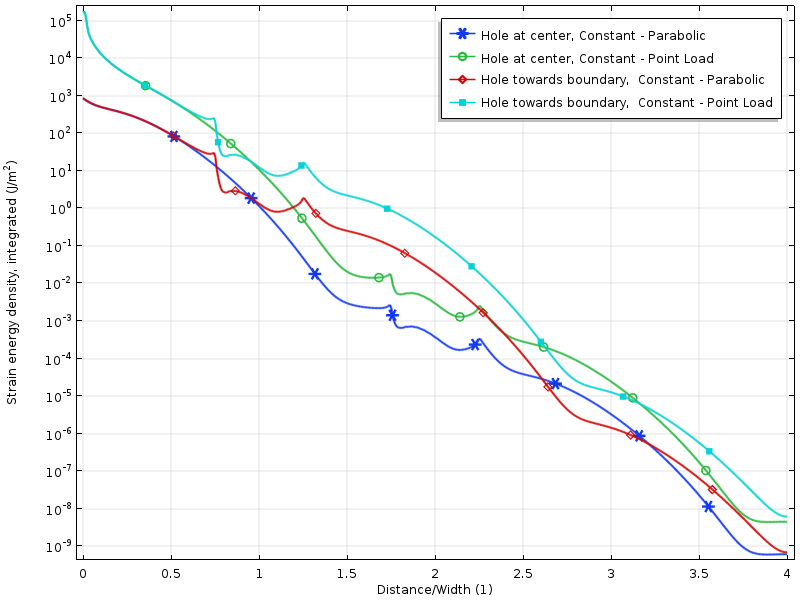
densitatea de energie a tulpinii de-a lungul plăcii pentru cazurile de sarcină rezultate zero. Energia este integrată de-a lungul direcției verticale pentru a produce o cantitate care este doar o funcție a distanței față de sarcină.

decăderea în logaritm a densității energiei tulpinii este mai mult sau mai puțin liniară cu Distanța de la limita încărcată. Acest lucru este de fapt în conformitate cu ceea ce prezic dovezile moderne: o decădere exponențială a densității energiei tulpinii. De asemenea, putem vedea clar cum gaura reduce temporar rata de descompunere.

aplicând principiul lui Saint-Venant la structuri subțiri

pentru structuri mai subțiri, cum ar fi cochilii, grinzi și ferme, este bine cunoscut faptul că principiul lui Saint-Venant nu poate fi aplicat la fel ca pentru un obiect mai „solid”. Perturbațiile parcurg distanțe mai mari decât ceea ce ne așteptăm, deoarece căile de încărcare într-o structură subțire sunt mult mai limitate. Acesta este același fenomen pe care îl vedem cu gaura din exemplul de mai sus, dar mai vizibil.

aici, studiem un fascicul cu o secțiune transversală standard IPE100. Capătul fasciculului este supus unei solicitări axiale, cu o amplitudine care are o distribuție liniară în ambele direcții transversale.

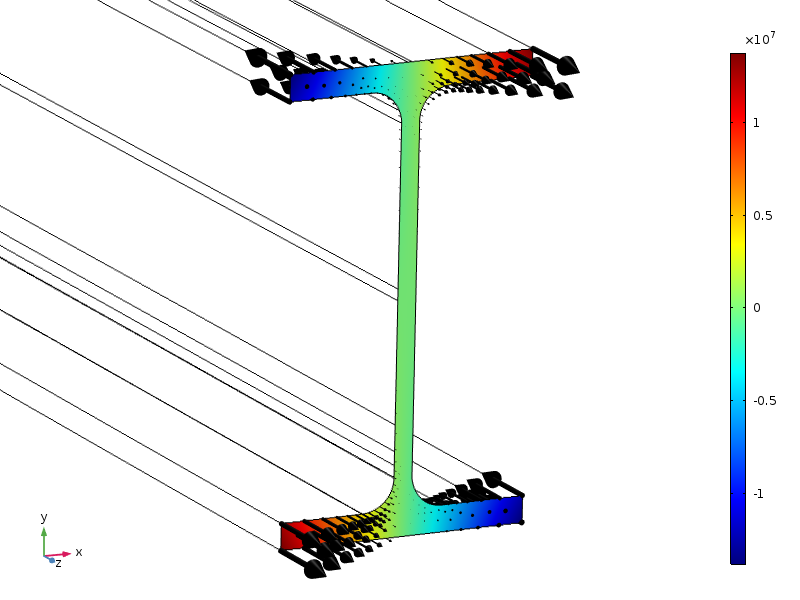
distribuția sarcinii, afișată ca contururi și săgeți.

datorită simetriilor, această sarcină are o forță rezultantă zero, precum și un moment zero în jurul tuturor axelor. Înălțimea secțiunii transversale este de 100 mm, deci dacă se aplică forma standard a principiului Saint-Venant, atunci tensiunile ar trebui să fie mici la o distanță de aproximativ 100 mm de secțiunea finală.

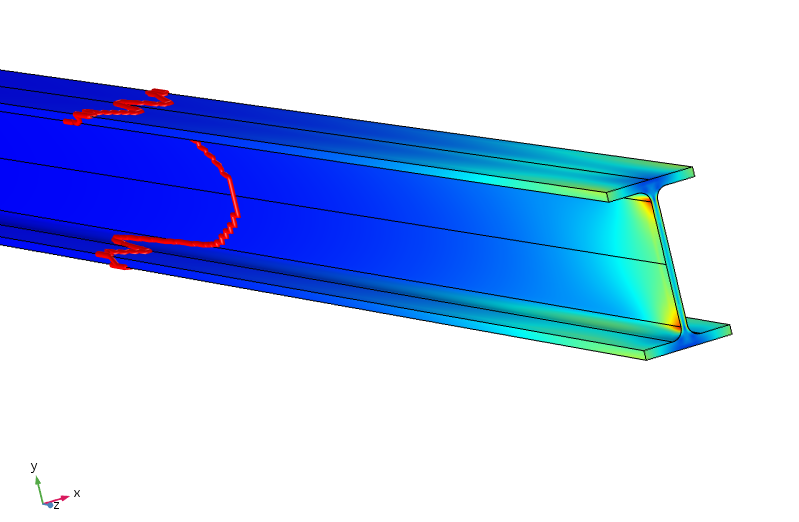
tensiune echivalentă în fascicul. Conturul roșu indică unde tensiunea este mai mică de 5% din tensiunea maximă aplicată.

se pare că, pentru ca stresul să fie sub 5% din tensiunea maximă aplicată, trebuie să călătorim aproape un metru de-a lungul fasciculului. Astfel, redistribuirea sarcinii este mult mai puțin eficientă aici, deoarece echilibrarea dintre flanșele superioare și inferioare necesită transfer de moment prin pânza subțire.

dacă sunteți familiarizați cu teoria torsiunii neuniforme a grinzilor (adică teoria deformării sau teoria Vlasov), veți recunoaște că sarcina aplicată are un bimoment semnificativ. Bimomentul este o cantitate transversală cu forța dimensiunii fizice X lungimea2.

poate (aceasta este doar speculația mea personală), un principiu eficient al lui Saint-Venant pentru acest caz ar trebui să necesite nu numai forță și moment, ci și un bimoment de zero. Acest lucru poate fi realizat prin adăugarea a patru sarcini punctuale care oferă un bimoment contracarant. Rezultatul unei astfel de analize este prezentat mai jos.

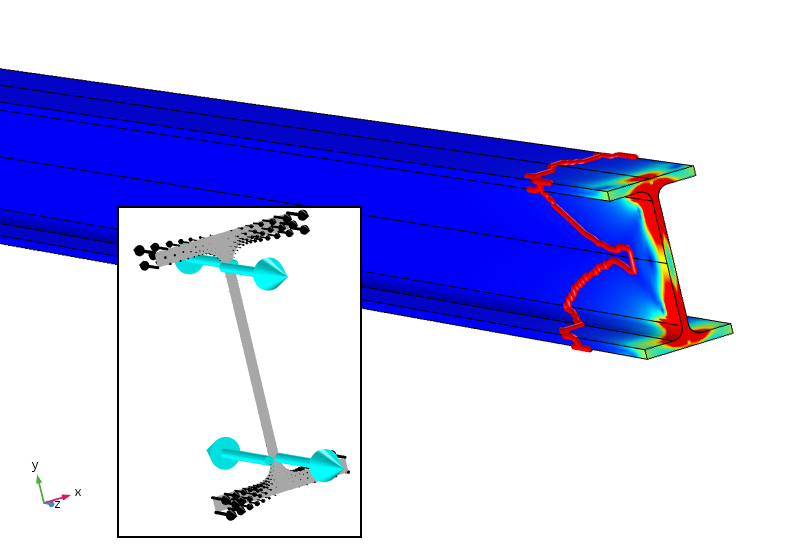
stres echivalent cu sarcini în patru puncte care oferă, de asemenea, un bimoment zero. Conturul de stres de 5% este acum mult mai aproape de limita încărcată.

sarcinile punctuale aplicate, care nu sunt plasate în mod optim în mod intenționat, dau solicitări locale extrem de mari (de fapt singulare). Cu toate acestea, stresul scade mult mai repede și este sub 5% După aproximativ 100 mm. limita de 5% este încă în ceea ce privește sarcina distribuită aplicată, deci nu este ajustată pentru noile solicitări locale. Rata de descompunere logaritmică a densității energiei tulpinii este de trei ori mai rapidă după adăugarea sarcinilor punctuale.

principiul lui Saint-Venant în analiza elementelor Finite

în unele cazuri, puteți considera intuitiv principiul lui Saint-Venant ca fiind aplicabil problemei discretizate de FE. Aici, ne uităm la sarcini distribuite și ochiuri neconforme.

încărcări distribuite

în modelul FE, încărcările sunt întotdeauna aplicate la nodurile mesh, chiar dacă le specificați ca o sarcină limită continuă. Sarcina este distribuită intern la nodurile elementului folosind principiul muncii virtuale, așa cum se arată în exemplul de mai jos.

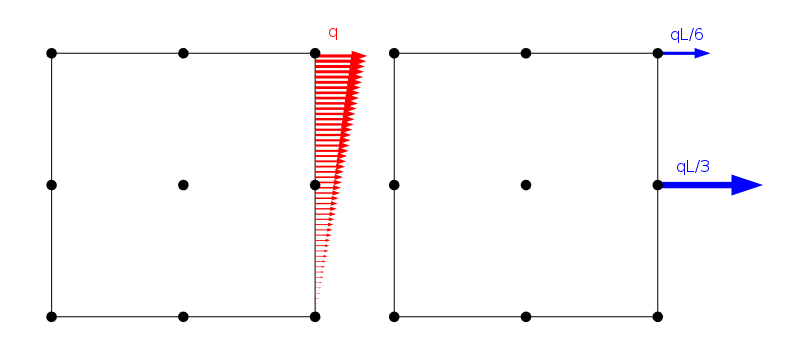
o sarcină distribuită liniar și modul în care este aplicată la nodurile unui element Lagrange de ordinul doi cu lungimea laterală L.

există, totuși, un număr infinit de distribuții de sarcină care dau aceleași sarcini nodale atâta timp cât împărtășesc aceeași forță și moment rezultat. Evident, soluția la problema elementului finit este aceeași pentru toate aceste cazuri. Cu toate acestea, din principiul lui Saint-Venant, putem concluziona că toate aceste sarcini ar trebui să ofere în esență același câmp de stres imediat ce suntem la o anumită distanță.

deoarece dimensiunea zonei peste care redistribuim sarcinile este o față de element, dimensiunea liniară după care nu există nicio diferență este în esență un strat de element în interiorul structurii. Astfel, soluția din stratul exterior al elementelor poate să nu corespundă sarcinii reale, dar mai departe, o face.

de exemplu, putem încărca o placă dreptunghiulară cu o sarcină limită care are o distribuție exponențială a stresului. Stresul calculat cu o plasă fină este prezentat mai jos.

diagrama conturului distribuției stresului axial.

din cauza principiului lui Saint-Venant, câmpul de stres este redistribuit într-o stare pură de îndoire la o anumită distanță de marginea încărcată, așa cum ne așteptăm. Cu toate acestea, aceasta nu este ținta discuției actuale. Mai degrabă, investigăm diferența dintre distribuția stresului de mai sus și ceea ce obținem cu un număr de ochiuri grosiere.

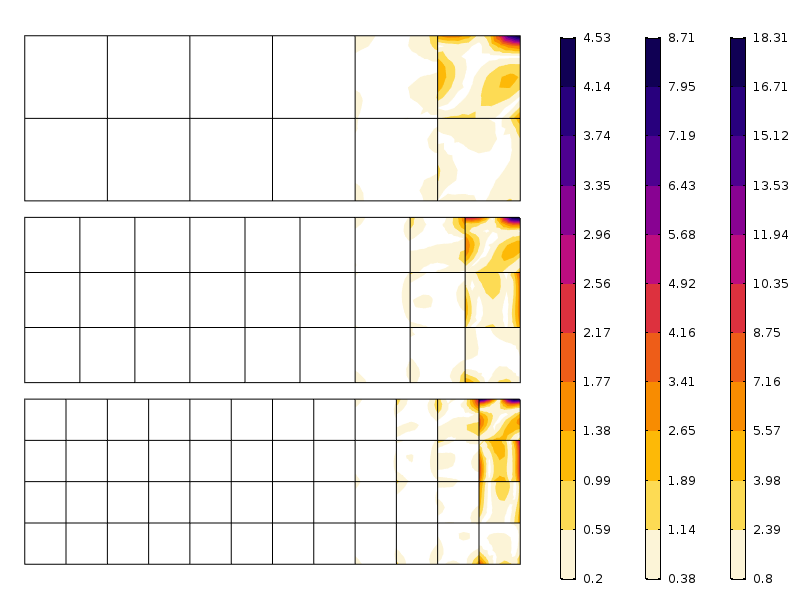
eroare la tensiunea axială pentru trei ochiuri diferite. Rețineți diferitele scale. Așa cum era de așteptat, eroarea este mai mică atunci când Plasa este mai fină.

după cum se poate observa în figură, eroarea scade rapid după primul strat de element. Ceea ce vedem aici este de fapt o combinație de convergență a ochiurilor de plasă și redistribuirea tensiunilor implicate de principiul lui Saint-Venant.

plasă neconformă

o plasă neconformă apare atunci când funcțiile de formă din două elemente conectate nu se potrivesc. Cel mai frecvent caz este atunci când un ansamblu este conectat folosind perechi de identitate și condiții de continuitate. Pentru a exemplifica acest lucru, putem studia o bară dreaptă cu o plasă intenționată care nu se potrivește. Cu un caz simplu de încărcare, cum ar fi tensiunea uniaxială, este posibil să se studieze tulburările de stres cauzate de tranziție.

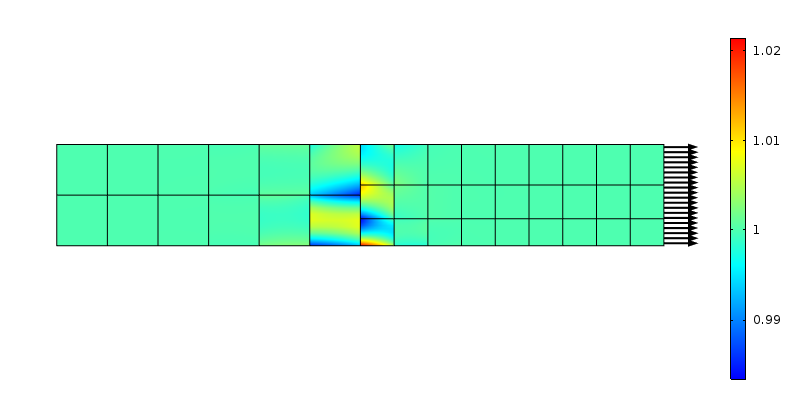
stres Axial la o tranziție de plasă neconformă. Sunt utilizate elemente de ordinul doi.

forțele transmise de nodurile din cele două părți nu se potrivesc cu presupunerea stresului constant. Din nou, acest lucru poate fi văzut ca o redistribuire a sarcinii locale pe o zonă care este dimensiunea elementului. Folosind raționamentul lui Saint-Venant, perturbarea ar trebui să se estompeze la o distanță „de dimensiunea elementului” de tranziție. Să investigăm ce se întâmplă dacă Plasa este rafinată în direcția axială.

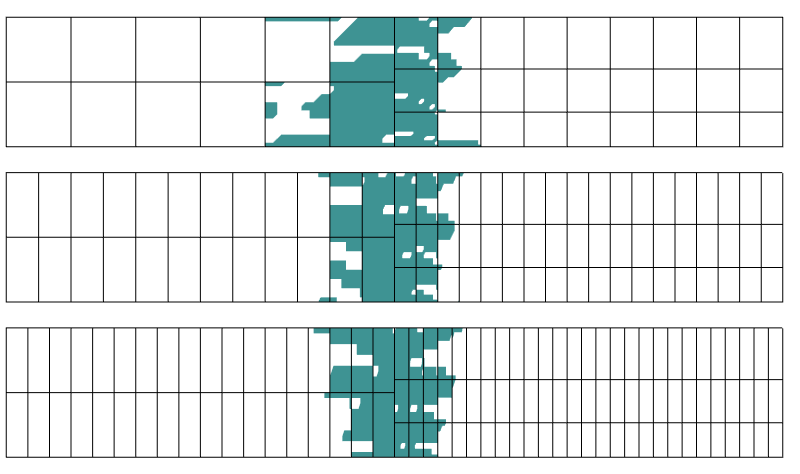
regiune cu mai mult de 0,1% eroare în stres. Trei discretizări diferite sunt utilizate în direcția axială.

se pare că regiunea de perturbare nu este afectată prea mult de discretizarea în direcția perpendiculară pe limita de tranziție. Acesta este exact ceea ce ne spune principiul lui Saint-Venant.

observații finale

fără a folosi principiul lui Saint-Venant, multe analize structurale sunt dificil de realizat, pur și simplu pentru că distribuția detaliată a sarcinii nu este cunoscută.

principiul este formal valabil numai pentru materialele elastice liniare. În practică, îl folosim intuitiv zilnic și pentru alte situații. Dacă, de exemplu, materialul din exemplul „placă cu gaură” ar fi elastoplastic, ne-am aștepta ca cele două sarcini distribuite să dea rezultate echivalente, atâta timp cât tensiunea de randament este peste tensiunea aplicată la limită, astfel încât să existe doar deformare plastică în jurul găurii. Cu toate acestea, sarcina punctuală oferă întotdeauna o soluție diferită, deoarece materialul cedează în jurul punctului încărcat. Pentru o discuție mai lungă, citiți această postare pe blog despre singularități la sarcini punctuale.

pașii următori

Aflați mai multe despre utilizarea software-ului COMSOL multiphysics pentru fea.

lecturi suplimentare

• Y. C. Fung și P. Tong, mecanica solidă clasică și computațională, World Scientific Publishing Co. Pte. Ltd., 2001.