Kapitola 12
Chvíli Distribuční Metoda pro Analýzu Struktur
12.1 Základní Pojmy
V momentě, kdy distribuční metoda analýzy nosníků a rámů byl vyvinut Hardy Cross a formálně předloženy v roce 1930. I když tato metoda je deformace jako metoda svahu-vychýlení metody, je přibližnou metodou a, tak, nevyžaduje řešení rovnic, jako tomu bylo v případě druhé metody. Stupeň přesnosti výsledků získaných metodou chvíli distribuce závisí na počtu po sobě jdoucích aproximací nebo iterační proces.
pro ilustraci konceptu metody rozdělení momentů zvažte rámeček znázorněný na obrázku 12.1. Členové rámu jsou hranolové a se předpokládá, že ne deformovat osově ani přeložit ve vztahu k sobě navzájem. Klouby ACD rámu jsou pevné, zatímco kloub B se může mírně otáčet v důsledku aplikovaného zatížení. Za prvé, před provedením rozdělení momentů mezi členy se předpokládá, že všechny spoje jsou dočasně uzamčeny pomocí svorky.
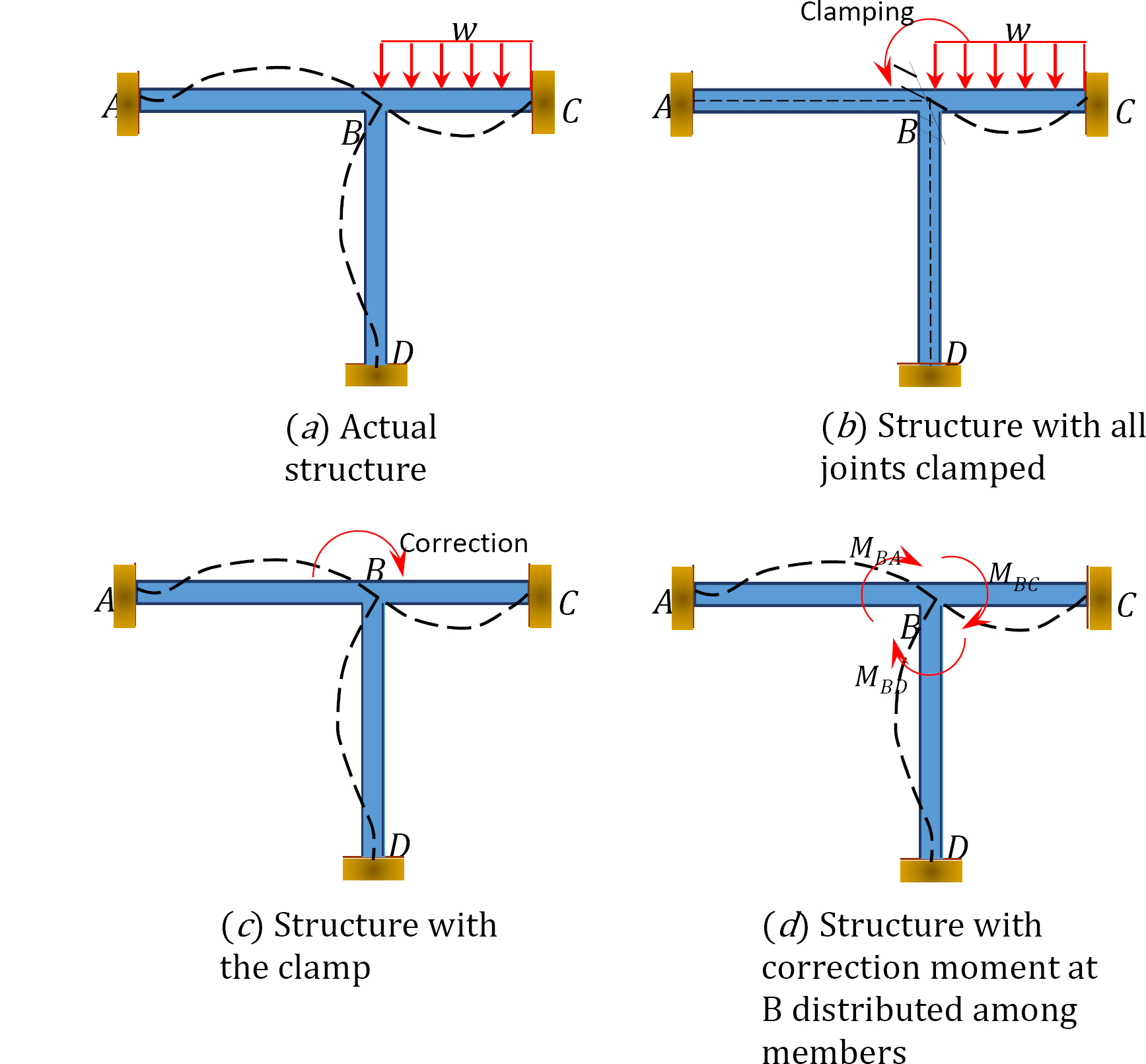
obr. 12.1. Snímek.
12.2 Znamení Úmluvy
podepsat úmluvu o chvíli distribuční metoda je podobná stanovené pro sklon-odklon metoda; to znamená, že okamžik na konci člena je považován za pozitivní, pokud má tendenci otáčet konec člena ve směru hodinových ručiček a negativní, pokud má tendenci jej otáčet proti směru hodinových ručiček.
12.3 Definice
Nevyvážené momenty: Tato metoda analýzy se předpokládá, že spoje ve struktuře jsou původně upnuté nebo uzamčen, a pak se uvolní postupně. Jakmile je kloub uvolněn, dochází k rotaci, protože součet pevných koncových okamžiků schůze členů v tomto kloubu není nulový. Hodnota součtu získaných koncových momentů je nevyvážený okamžik v tomto kloubu.
přenosové momenty: distribuované momenty na koncích členů, které se scházejí ve společné příčině, na ostatních koncích, které se považují za pevné. Tyto indukované momenty na ostatních koncích se nazývají přenosové momenty.
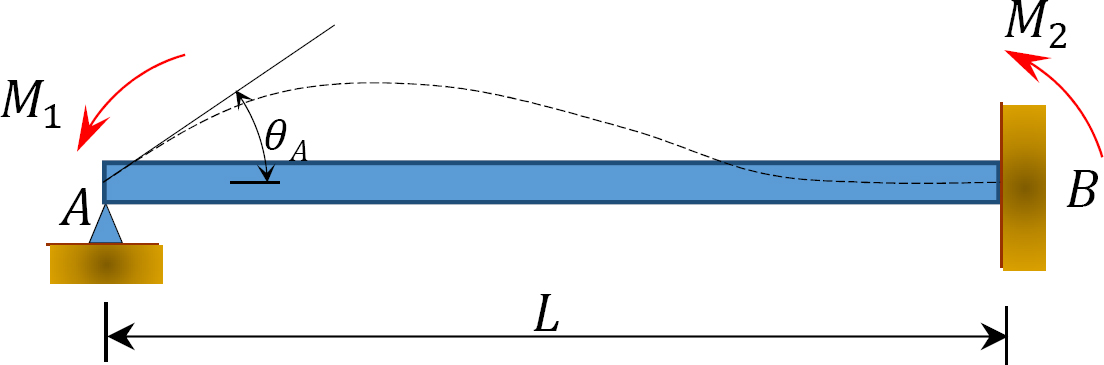
obr. 12.2. Nezatížený hranolový paprsek.
zvažte nezatížený hranolový nosník upevněný na konci B, jak je znázorněno na obrázku 12.2. Pokud je na levý konec nosníku aplikován moment M1, lze rovnice sklonu a vychýlení pro oba konce nosníku zapsat následovně:


Dosazením 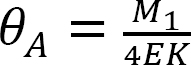 z rovnice 12.1 do rovnice 12.2 navrhnout následující:
z rovnice 12.1 do rovnice 12.2 navrhnout následující:

Rovnice 12.3 naznačuje, že v okamžiku, kdy převedené na pevný konec nosníku vzhledem k okamžiku aplikován na druhém konci je roven jedné-polovina použita chvíli.
přenosový faktor: poměr indukovaného momentu k použitému momentu se označuje jako přenosový faktor. Pro paprsek znázorněný na obrázku 12.2 je faktor přenášení následující:

distribuovaný faktor (DF): Distribuovaný faktor je faktor používaný k určení podílu nevyváženého okamžiku, který nese každý z členů, který se schází v kloubu. 12.3, jejich distribuční faktory jsou vypočteny následovně:
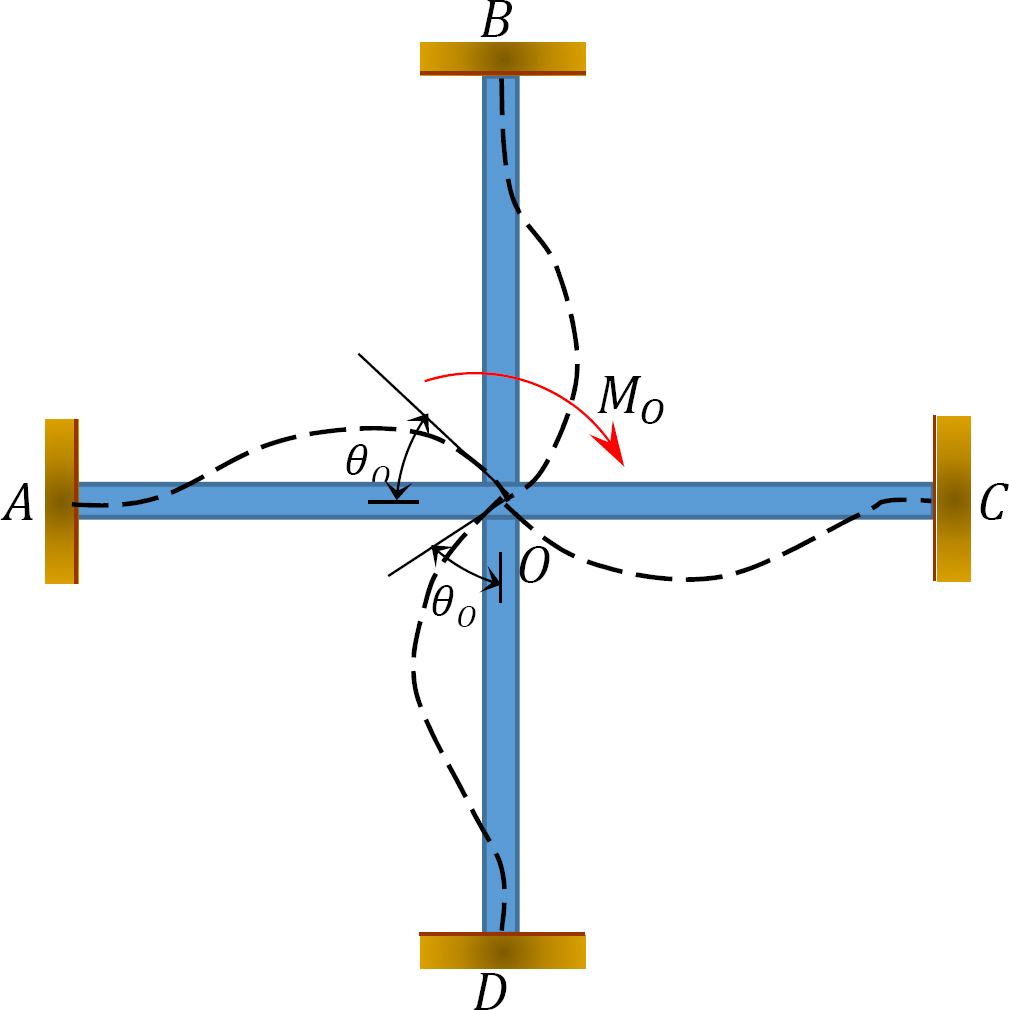
obr. 12.3. Snímek.

distribuované momenty: po uvolnění imaginární svorky v kloubu způsobí nevyvážený okamžik v tomto kloubu jeho otáčení. Rotace překrucuje konec schůze členů na kloubu, což má za následek vývoj odolných momentů. Tyto odporující momenty se nazývají distribuované momenty. Distribuované momenty pro členy rám je znázorněno na Obrázku 12.3 jsou vypočteny následovně:
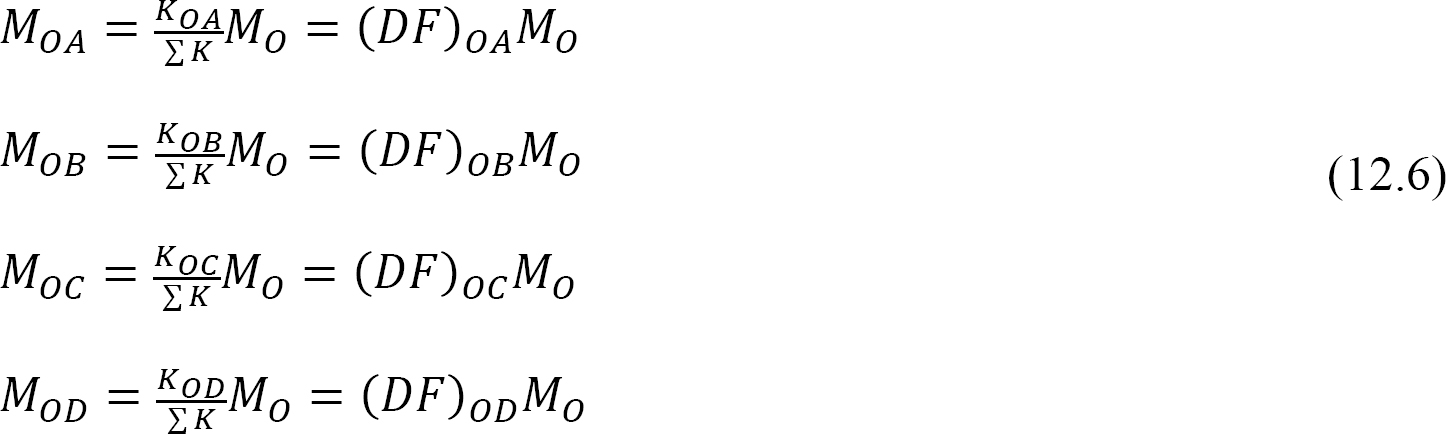
12.4 Změna Členských Tuhost
Někdy iterační proces v okamžiku distribuce metoda může být významně snížena úpravou ohybové tuhosti některých členů neurčité struktury. Tato část se zabývá vlivem pevné-a podpěry na konci čepu na ohybovou tuhost neurčitého nosníku.
případ 1: Nosník zavěšený na jednom konci a upevněný na druhém
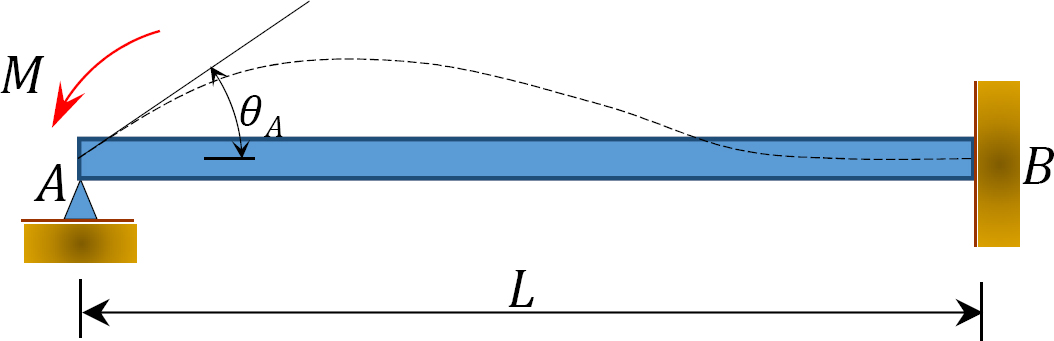
obr. 12.4. Nosník
zvažte nosník zavěšený na konci A a upevněný na konci B, jak je znázorněno na obrázku 12.4. Použití moment M otočí konec závěsu o částku θ. Psaní svahu-průhyb rovnice pro ukončení členských a zmínku, že 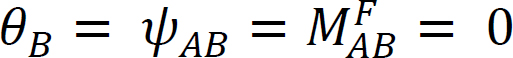 navrhuje následující:
navrhuje následující:
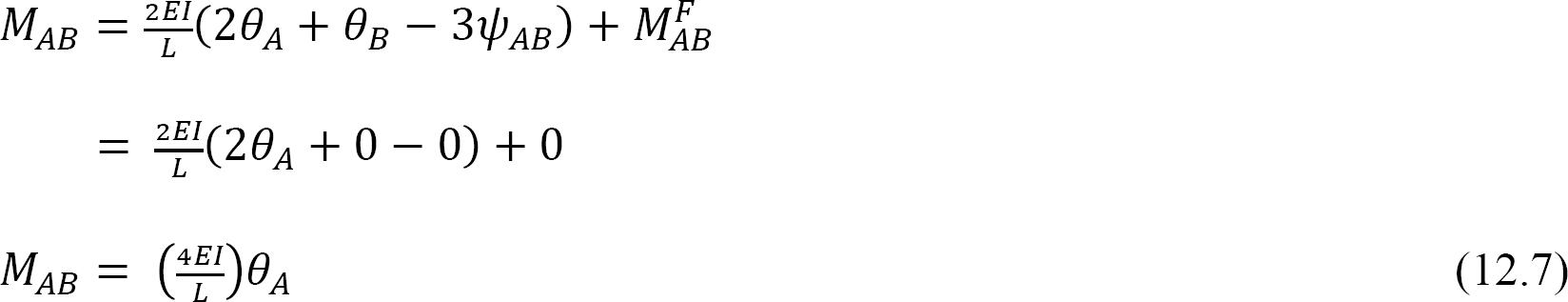
Podle definice, ohýbání tuhost konstrukčního prvku je moment, který musí být aplikován na konci členských způsobit jednotka rotace, která end. Následující výraz pro ohýbání tuhost pro členské s pevnými konci je vyjádřena takto při nahrazování θA = 1 do rovnice 12.7:

Podle definice, relativní tuhost ohýbání člena je stanovena vydělením ohýbání tuhost členských podle 4E. Vydělením rovnice 12.8 tím, že 4E navrhuje následující výraz pro relativní tuhosti pro případ, že za:

Případ 2: nosník kloubově na obou koncích
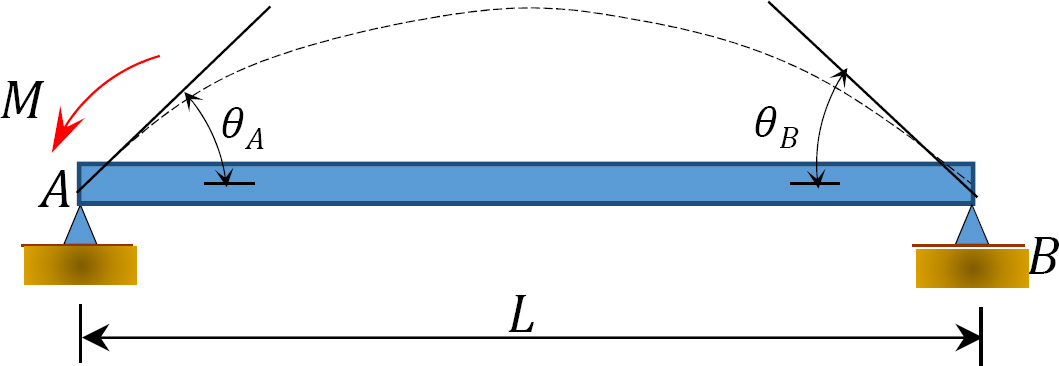
Obr. 12.5. Jednoduše podporovaný paprsek.
Použití momentu M na konci A prostě podepřený nosník je znázorněno na Obrázku 12.5 otočí paprsek o úhel θA na otočné konce. Pomocí upraveného svahu-průhyb rovnice odvozené v kapitole 11.4 Kapitoly 11 a zmínku, že 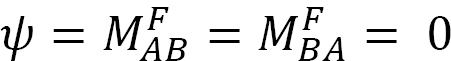 navrhuje následující výraz pro okamžik, odklápěcí konec, kde zatížení se aplikuje:
navrhuje následující výraz pro okamžik, odklápěcí konec, kde zatížení se aplikuje:
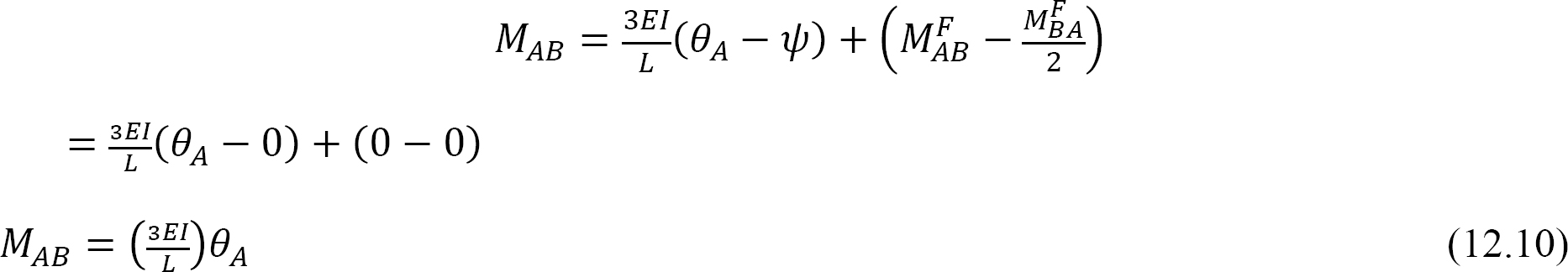
Dosazením θA = 1 do rovnice 12.10 navrhuje následující výraz pro ohýbání tuhost pro člena s odklápěcí daleko end:

relativní tuhosti pro člena s odklápěcí druhém konci se získá vydělením rovnice 12.11 tím, 4E, takto:

Porovnáním rovnic 12.12 a 12,9 naznačuje, že člen s odklápěcí druhém konci je tři-čtvrté tuhá jako člen se stejnou geometrií, ale pevné na druhém konci. Tuto známou skutečnost může podstatně snížit počet opakování při analýze nosníky nebo rámů s odklápěcí vzdáleném konci pomocí metody okamžik rozdělení. V takových případech, relativní tuhost nosníku na blízkém konci je nejprve upravena podle rovnice 12.12, a jeho distribuční koeficient je počítán s upravenou tuhostí. Během vyvažovací operace, blízký konec bude vyvážen jen jednou bez dalšího přenášení okamžiků od nebo do konce.
12.5 Analýza Neurčitých Nosníků
postup pro analýzu neurčitých nosníků metodou chvíli distribuce je stručně shrnout takto:
Postup pro Analýzu Neurčitých Nosníků v Okamžiku, kdy Způsob Distribuce
•Výpočet fixed-end momenty pro členy, za předpokladu, že spoje jsou uchyceny proti otáčení.
* Vypočítejte distribuční faktor pro každý z členů připojených v kloubu
•Vypočítejte nevyvážený moment v každém kloubu a rozdělte jej na konce členů připojených v tomto kloubu.
* přeneste polovinu rozděleného momentu na ostatní konce členů.
* přičtěte nebo odečtěte tyto poslední momenty (momenty získané v krocích tři a čtyři) K nebo z původních okamžiků s pevným koncem.
•aplikujte určené koncové momenty na spoje dané konstrukce.
* nakreslete schéma volného těla každého rozpětí daného paprsku a zobrazte zatížení a momenty ve spojích získané metodou distribuce momentů.
* Určete podpůrné reakce pro každé rozpětí.
* Vypočítejte a vytvořte diagramy střižné síly a ohybového momentu pro každé rozpětí.
* nakreslete jeden ohybový moment a jeden diagram střižné síly pro daný paprsek kombinací diagramů v kroku 9.
Příklad 12.1
Pomocí moment, metody distribuce, určit konec momenty a reakce v místě podpěry nosníku znázorňuje Obrázek 12.6. Nakreslete smyková síla a ohybový moment diagramy. EI = konstanta.
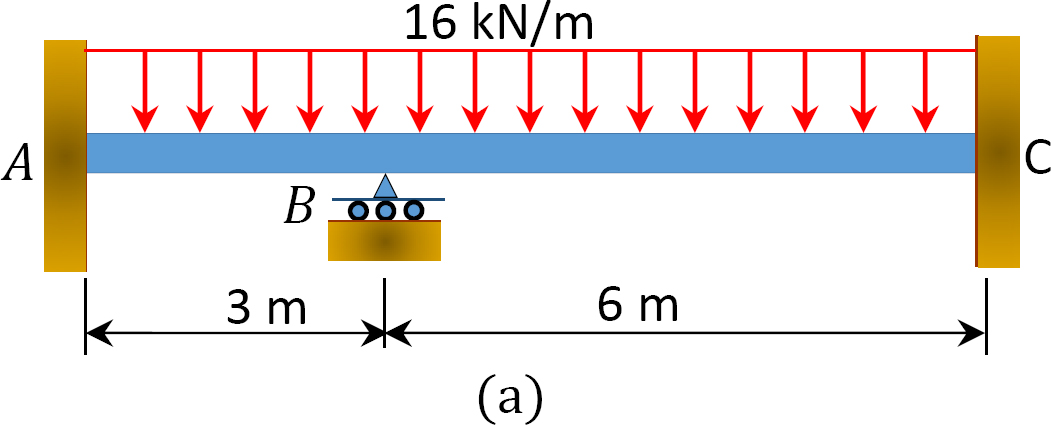
obr. 12.6. Trám.
řešení
pevný koncový moment.
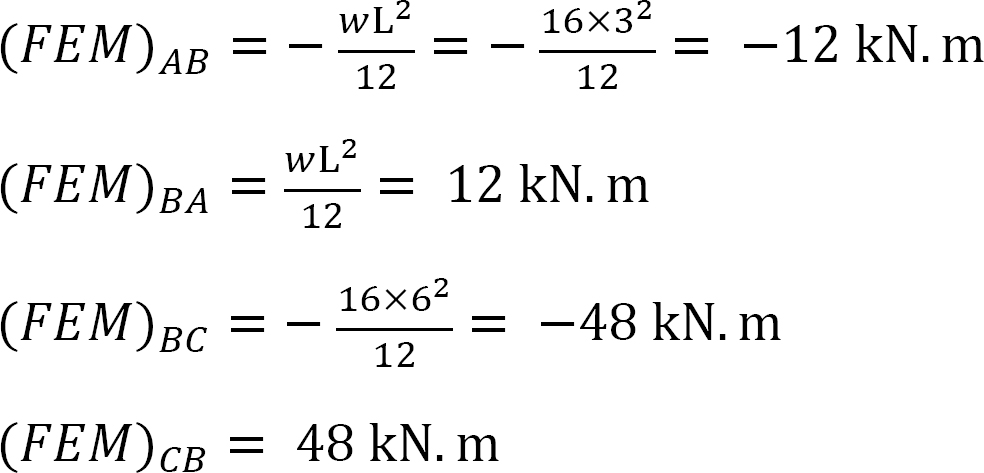
faktor tuhosti.
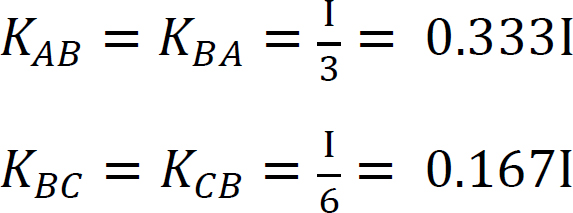
distribuční faktor.
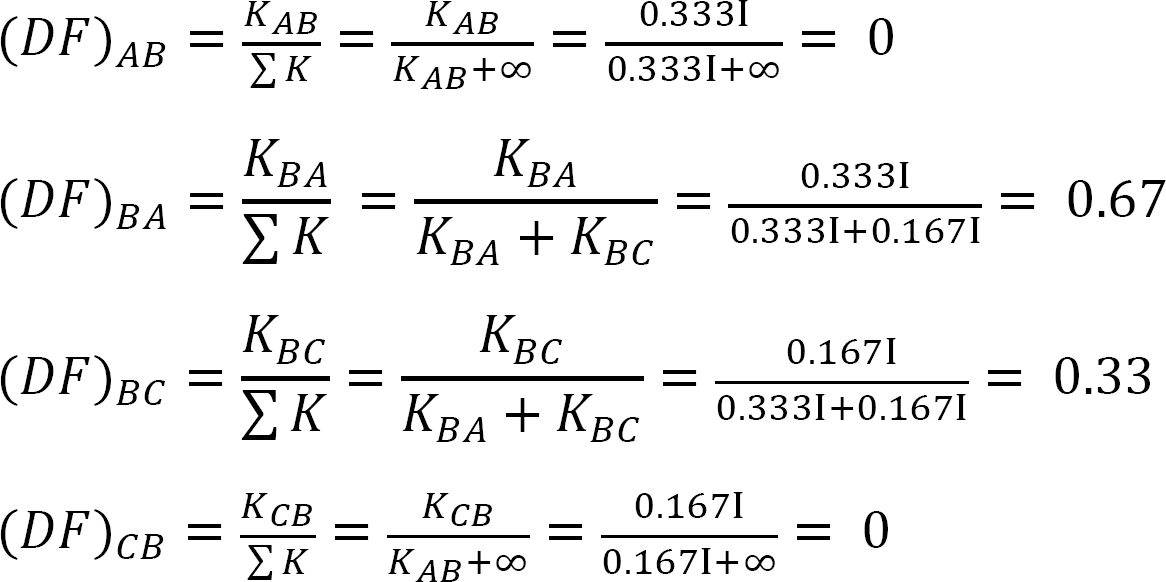
tabulka 12.1 Distribuční tabulka.
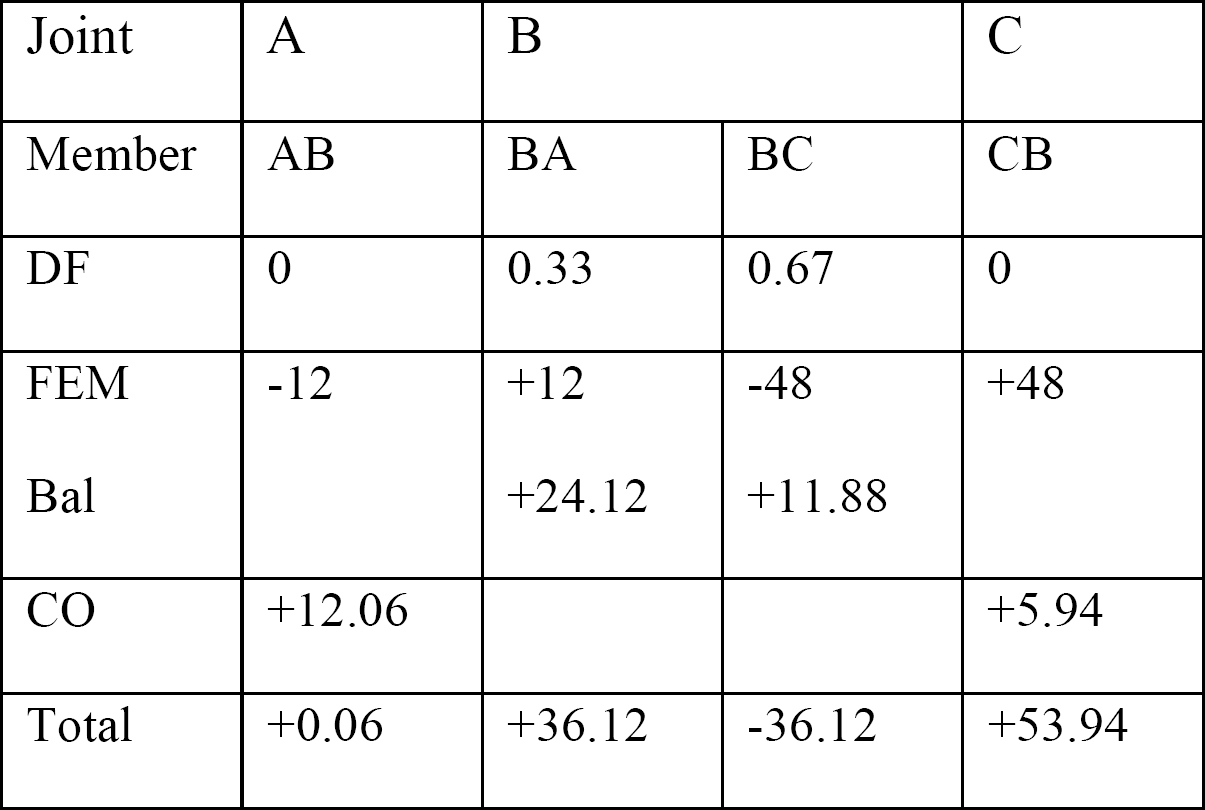
diagramy smykové síly a ohybových momentů.
Příklad 12.2
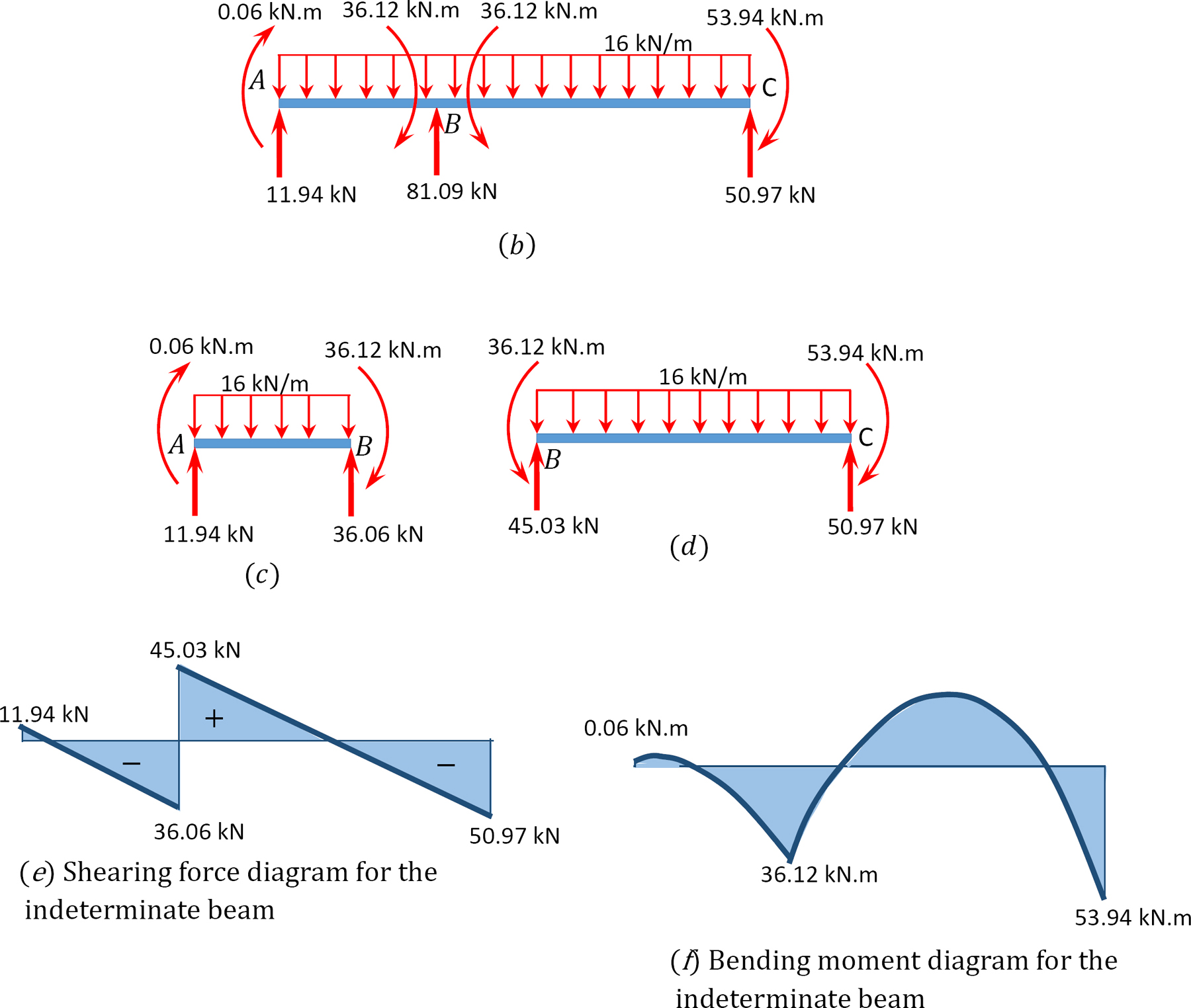
Pomocí moment, metody distribuce, určit konec momenty a reakce na podpěrách paprsku je znázorněno na Obrázku 12.7. Nakreslete smyková síla a ohybový moment diagramy.
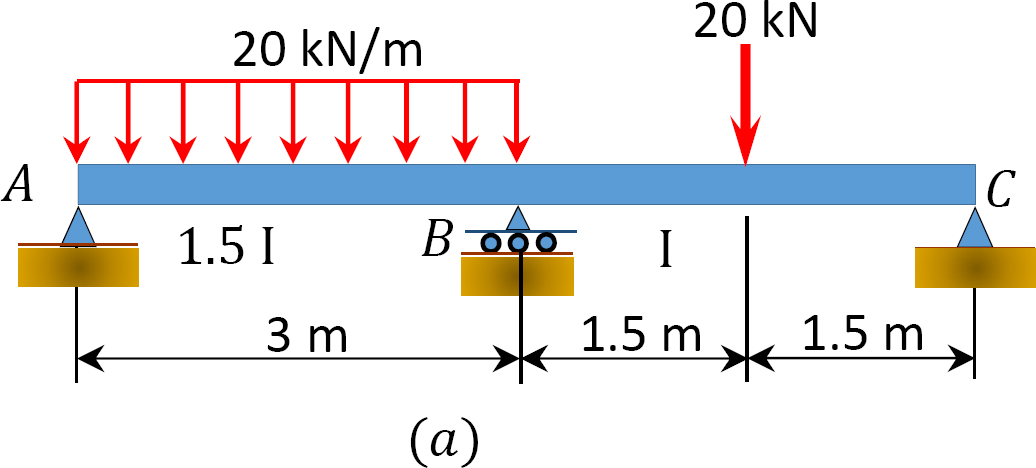
obr. 12.7. Trám.
řešení
pevný koncový moment.
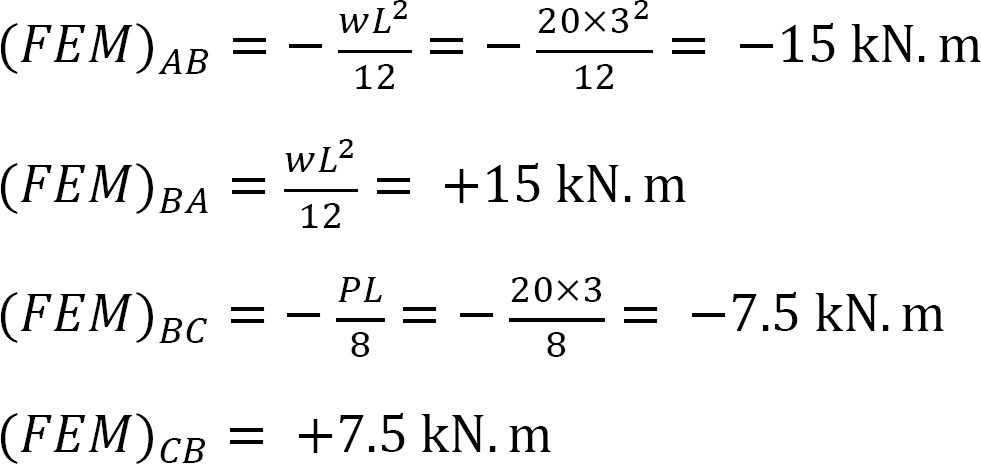
faktor tuhosti.
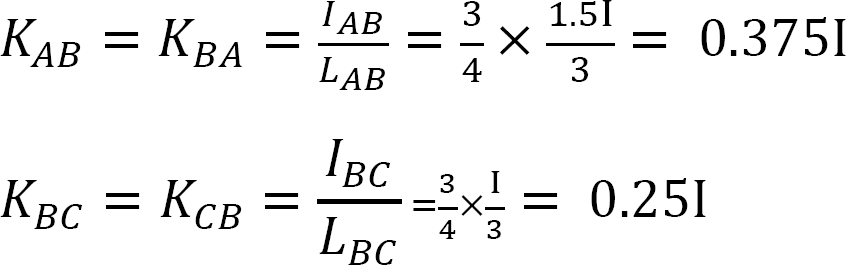
distribuční faktor.
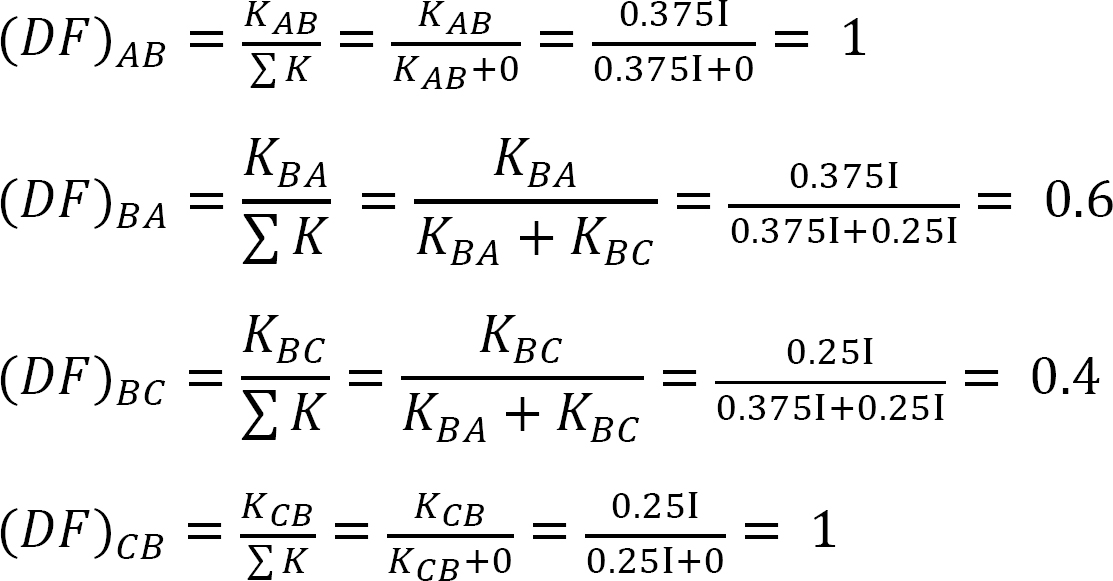
tabulka 12.2 Distribuční tabulka.
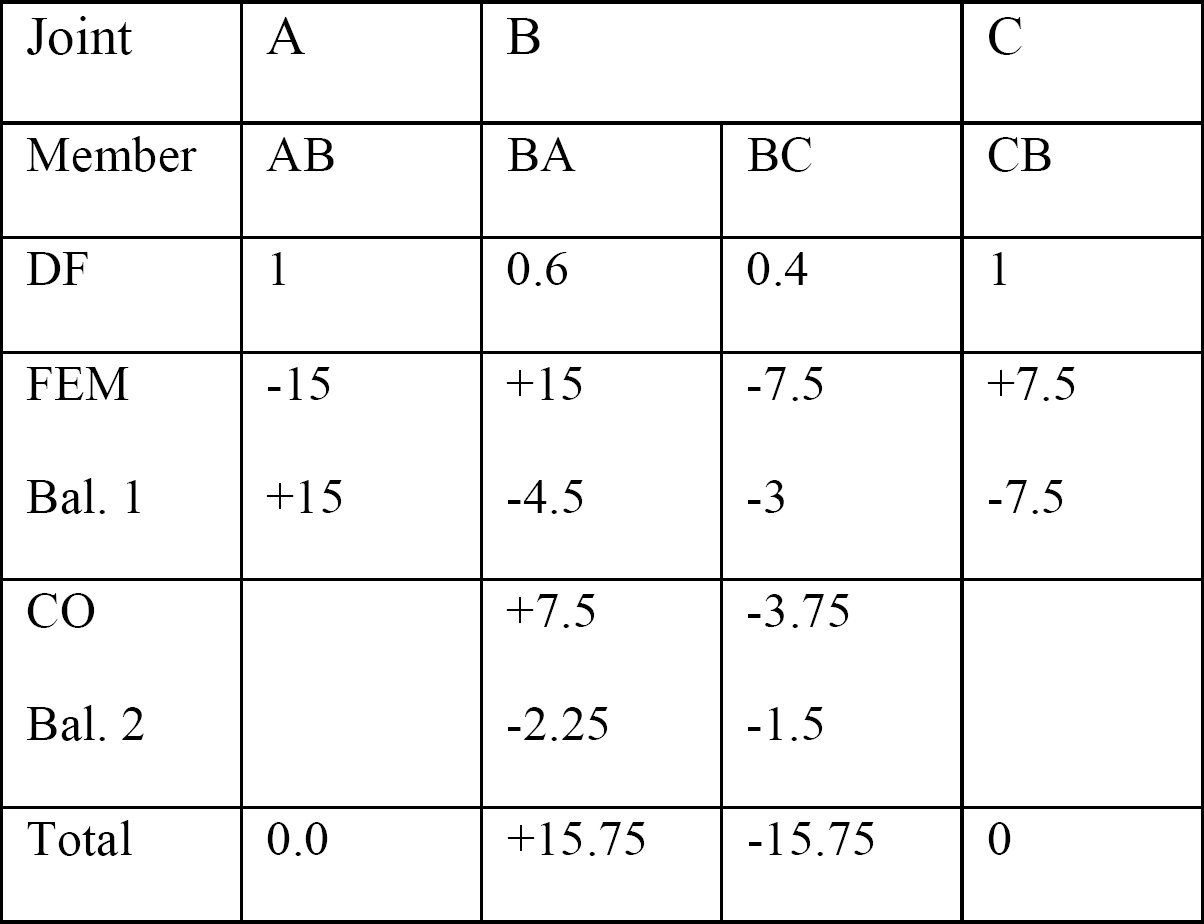
diagramy smykové síly a ohybových momentů.
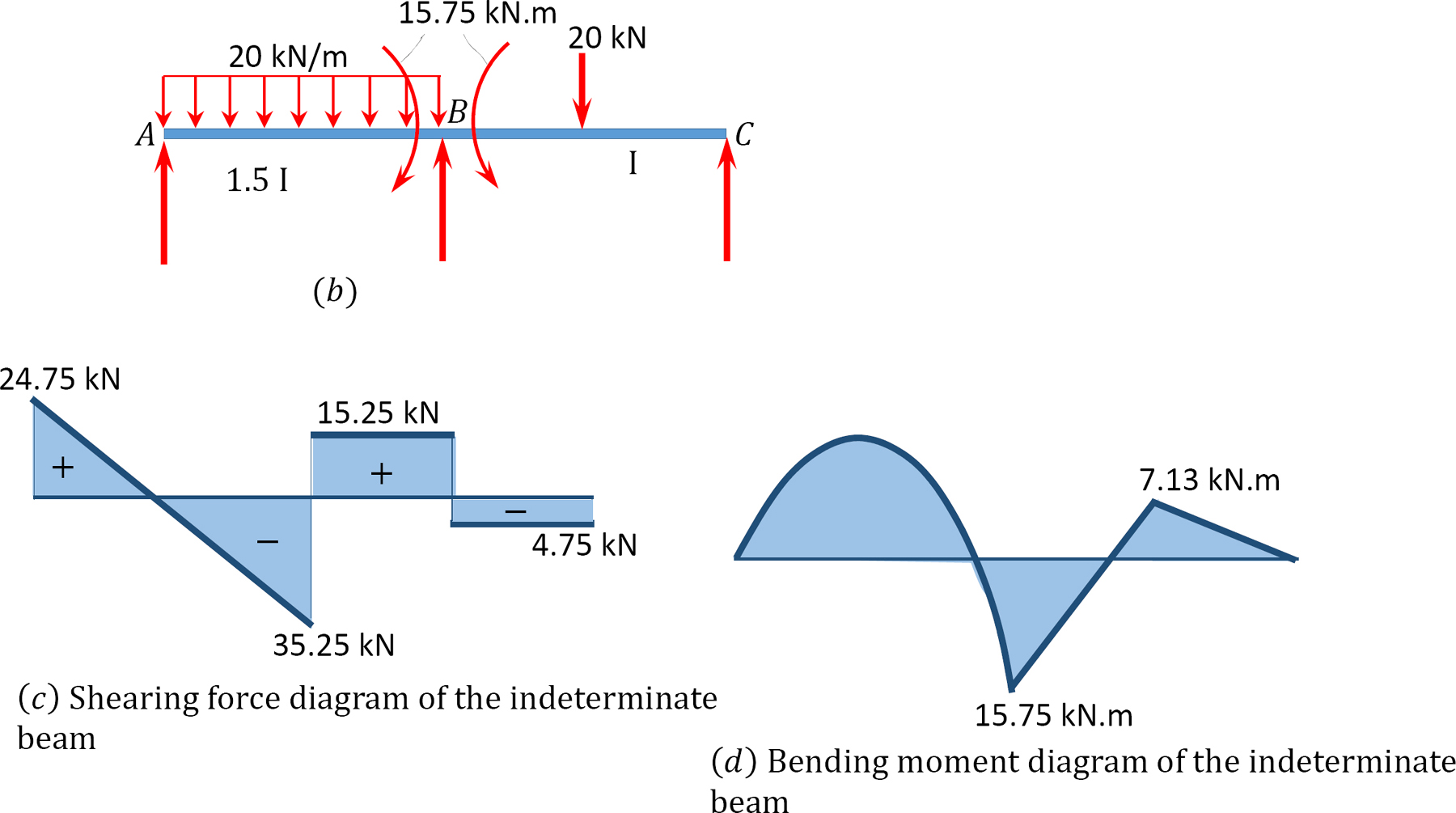
12.6 Analýza Neurčitých Rámů
postup pro analýzu snímků pomocí moment způsob distribuce závisí na typu rámu, který je analyzován. Rámy jsou kategorizovány jako houpat-nebo non-houpat rámy. Postup pro analýzu neklouzavých rámů je podobný postupu neurčitých nosníků. Ale pro analýzu houpacích rámů je postup jiný. Existují dvě fáze zapojené do analýzy houpat rámy, a to non-houpat fáze a houpat fáze analýzy. Tyto fáze jsou popsány níže.
Postup pro Analýzu Neurčitých Sway-Snímky v Okamžiku, kdy Způsob Distribuce
A. Non-sway fázi analýzy
•První předpokládat existenci imaginární rekvizita, která zabraňuje rám z kymácející.
* Vypočítejte horizontální reakce na podpěrách rámu a všimněte si rozdílu X. To je síla, která zabraňuje houpání.
B. Sway stage analysis
* předpokládejte libovolné momenty, které působí na sloupce rámu. Velikost těchto momentů se bude lišit od sloupce ke sloupci v poměru k 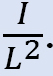
•hodnoty se předpokládají pro M2 a stanoví se M1.
•svévolné momenty jsou pak distribuovány jako pro non-sway stavu
•Výpočet velikosti vodorovné reakce v místě podpěry pro sway stavu. Součet těchto reakcí dává libovolnou posuvnou sílu y.
* Určete poměr 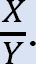 tento poměr se nazývá faktor houpání.
tento poměr se nazývá faktor houpání.
•pomocí koeficientu sway vynásobte rozložené momenty sway. To dává opravený okamžik pro houpání.
•poslední okamžiky na rámu jsou součtové momenty získané v non-sway fázi a opravené chvíli houpat fázi.
příklad 12.3
pomocí metody distribuce momentů určete koncové momenty členů rámce znázorněné na obrázku 12.8. EI = konstanta.
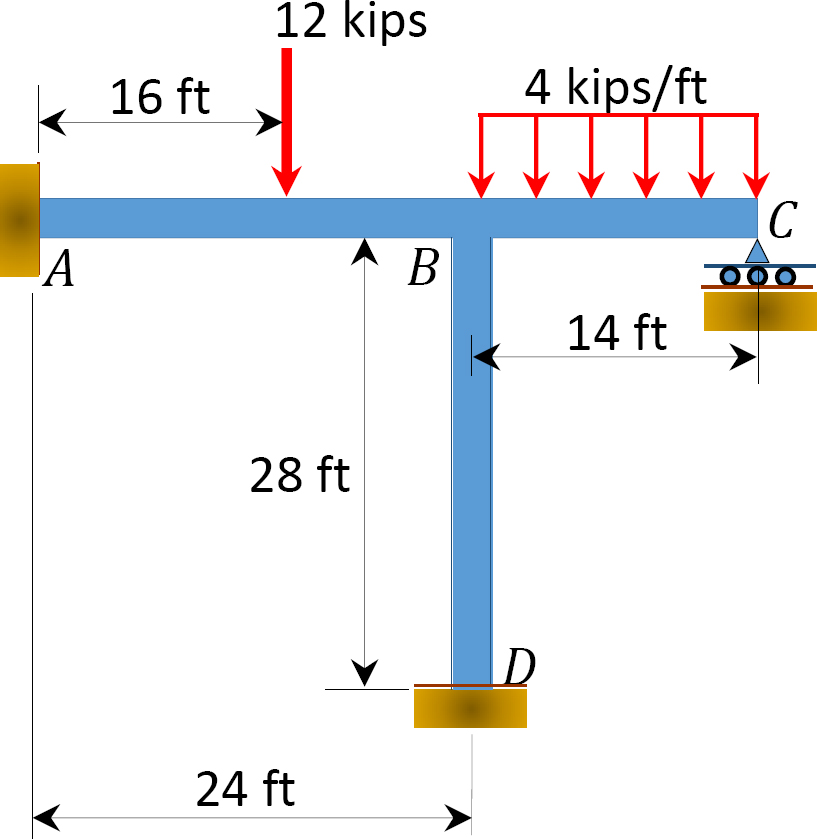
obr. 12.8. Snímek.
řešení
pevný koncový moment.
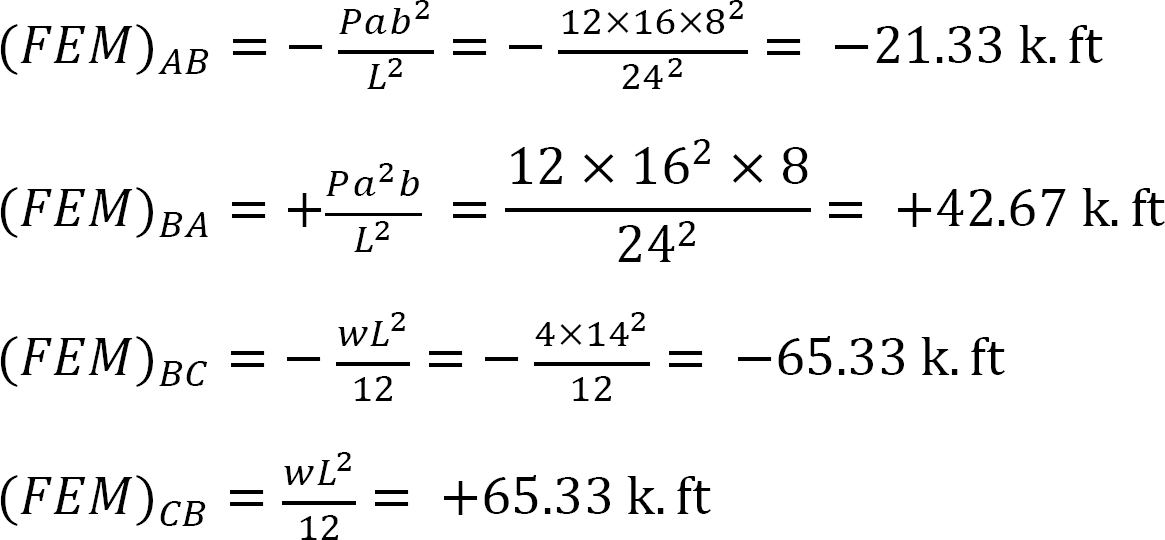
faktor tuhosti.
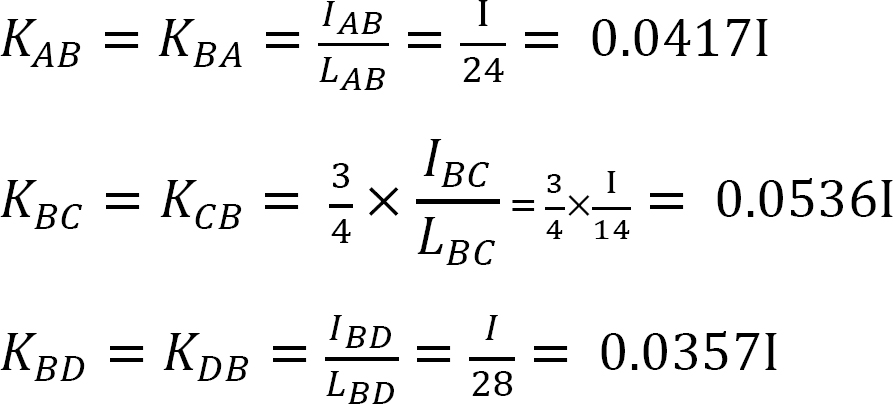
distribuční faktor.
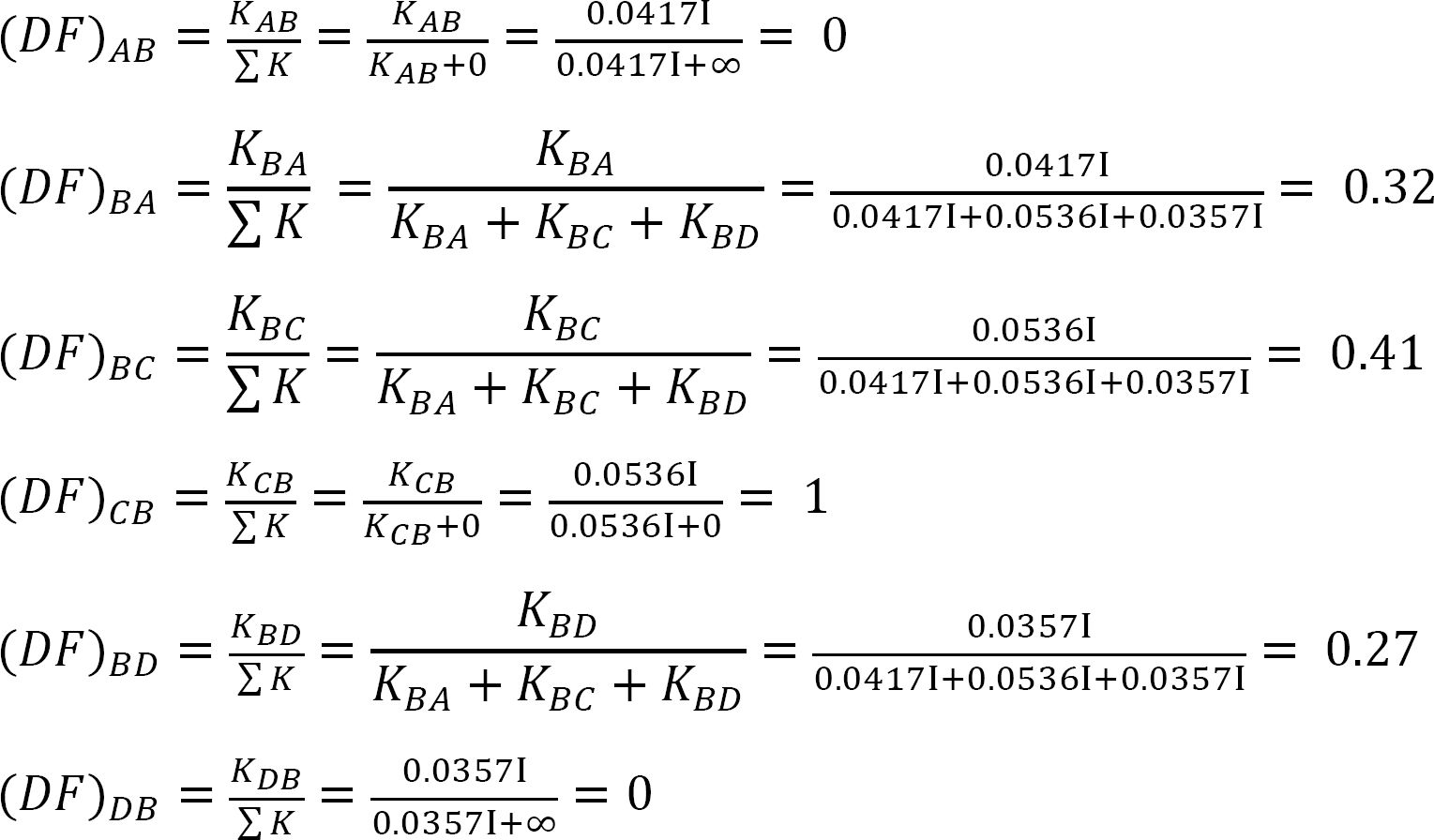
tabulka 12.3. Distribuční tabulka.
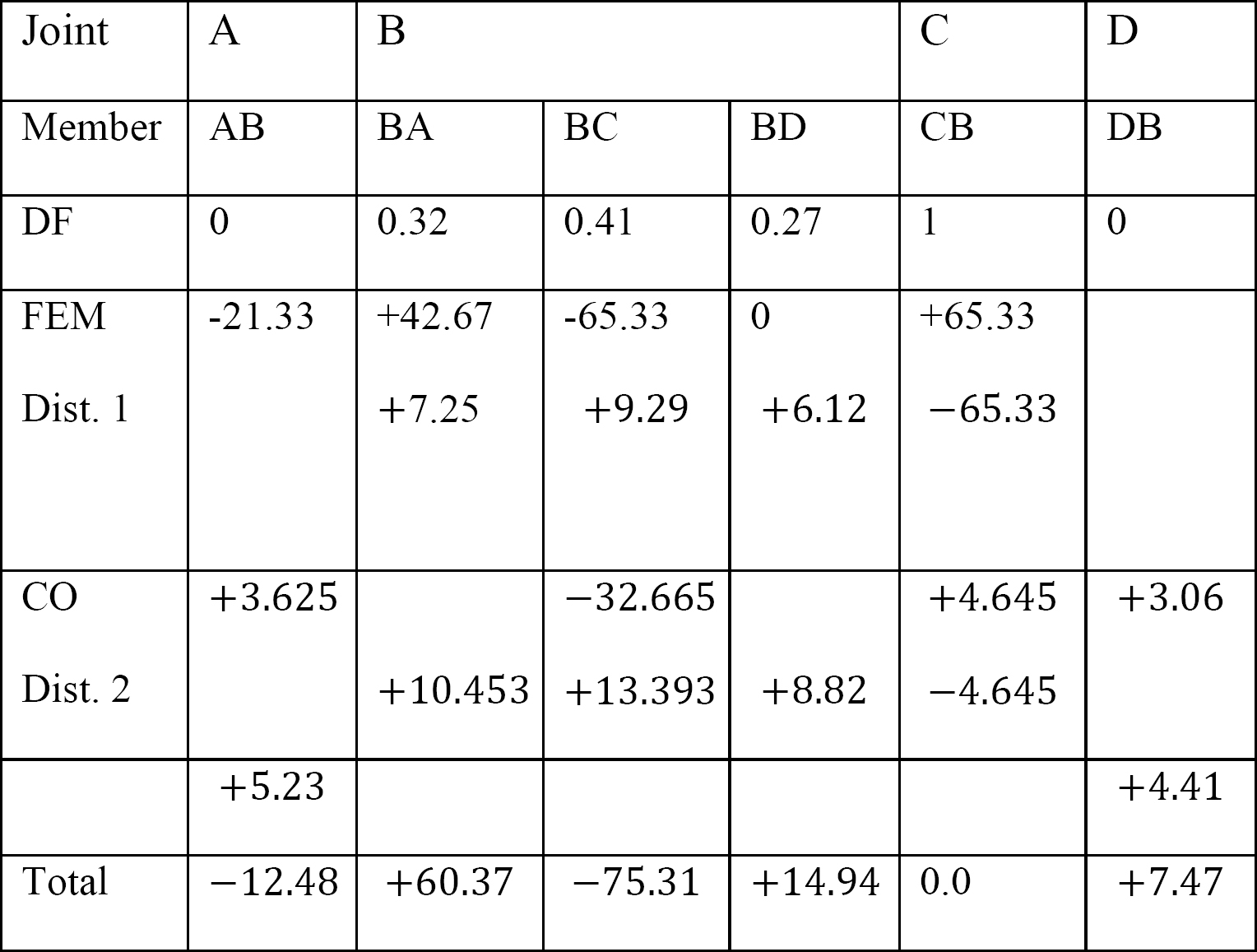
Poslední členské koncové momenty.
Dosazením získaných hodnot EKθB, EKθC, a EK∆ do členských end chvíli rovnice vyplývá následující:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Příklad 12.4
pomocí metody distribuce momentů určete koncové momenty na podpěrách rámu znázorněného na obrázku 12.9. EI = konstanta.
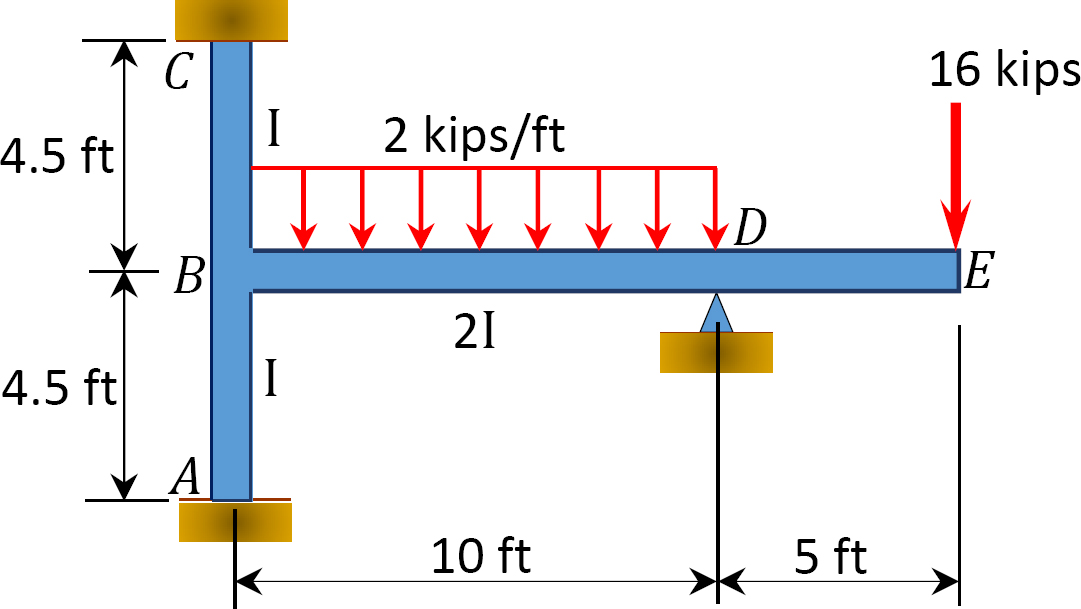
obr. 12.9. Snímek.
řešení
pevný koncový moment.
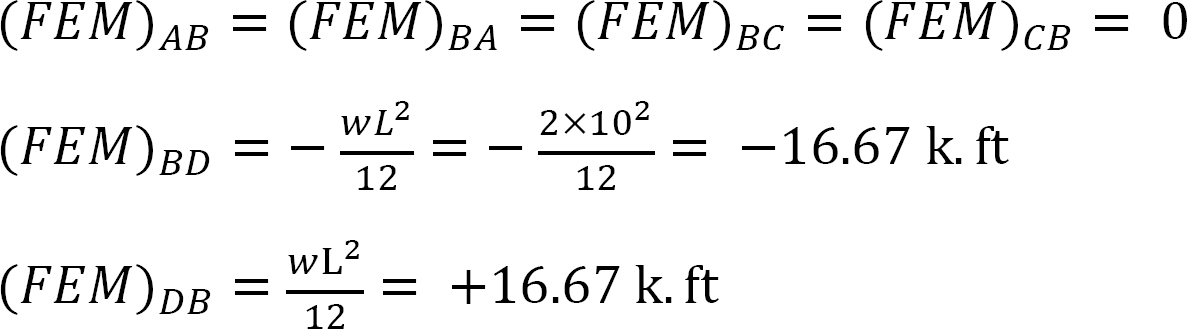
faktor tuhosti.
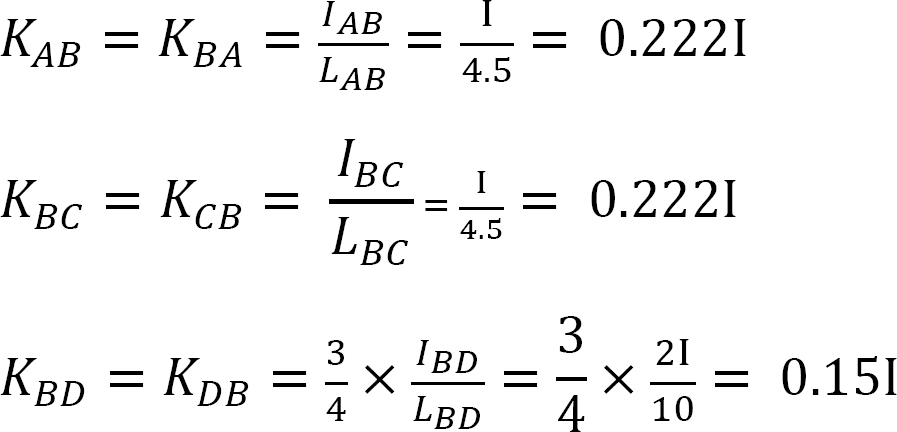
distribuční faktor.

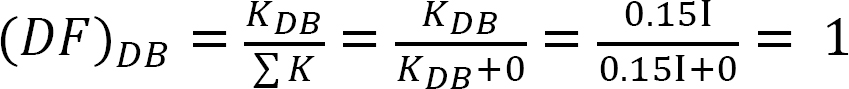
tabulka 12.4 Distribuční tabulka.
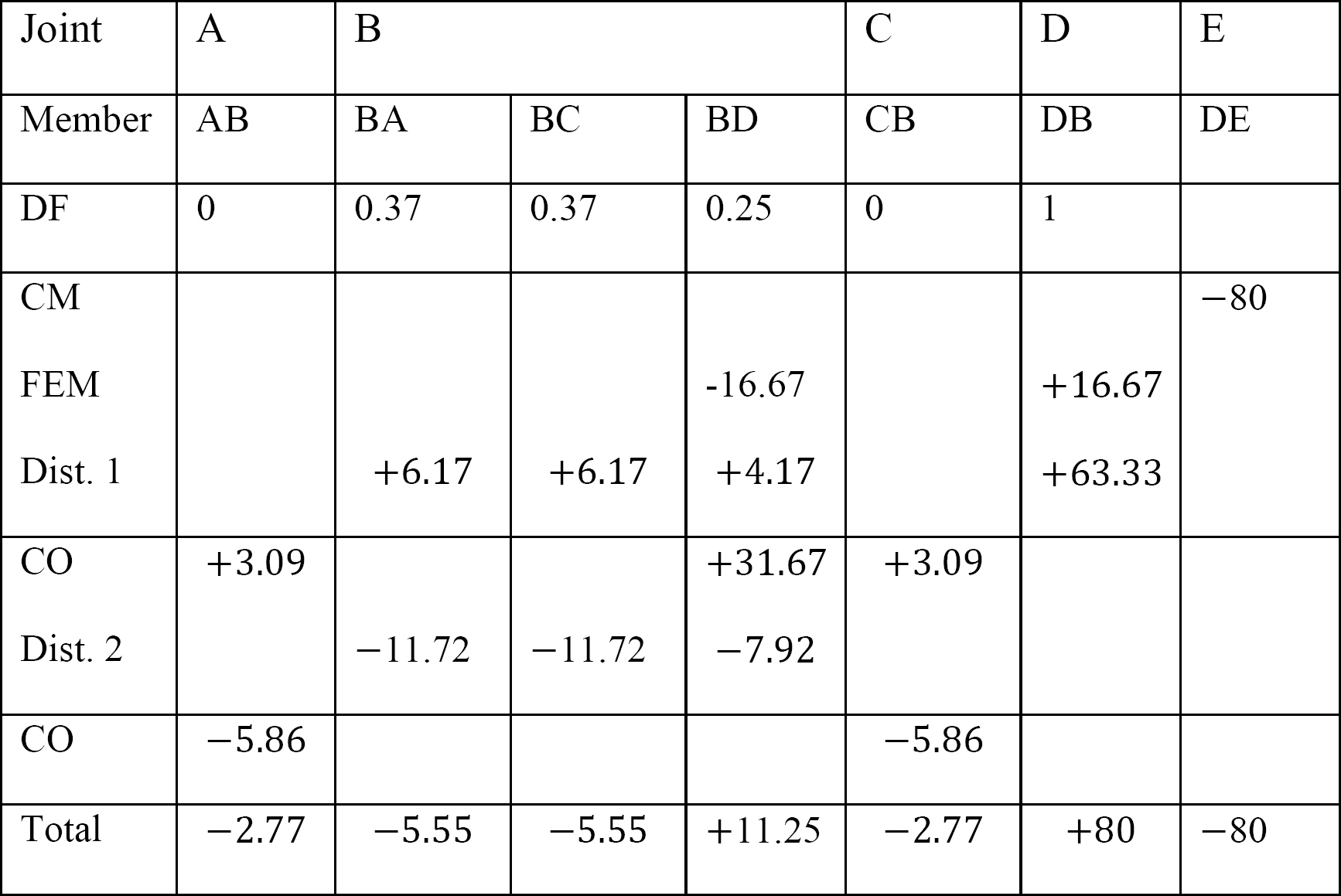
Poslední členské koncové momenty.
MAB = -2.77 k. ft
MBA = -5.55 k. ft
MBC = -5.55 k. ft
MBD = +11.25 k. ft
MCB = -2.77
MDB = +80 k. ft
MDE = -80 k. ft
Příklad 12.5
Pomocí moment, metody distribuce, určit konec okamžiky na podpěry rámu je znázorněno na Obrázku 12.10. EI = konstanta.
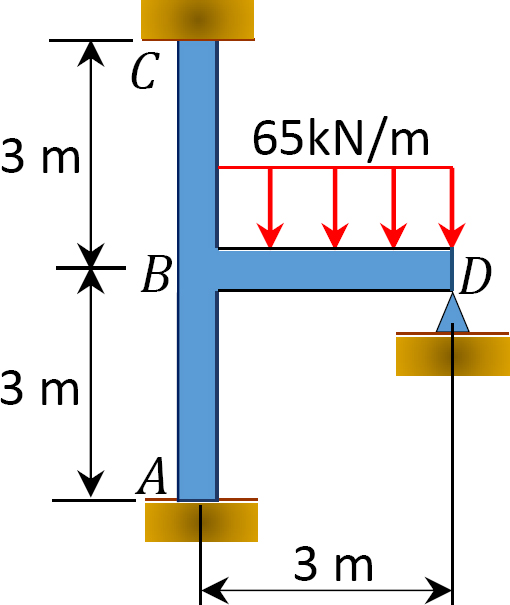
obr. 12.10. Snímek.
řešení
pevný koncový moment.
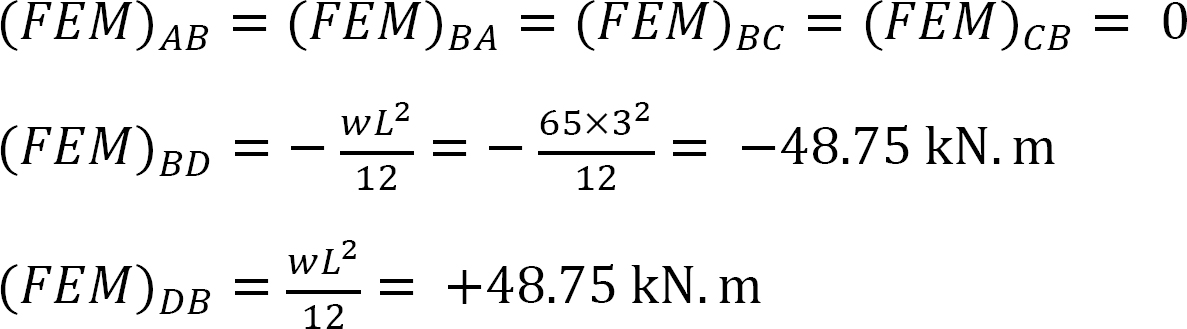
faktor tuhosti.
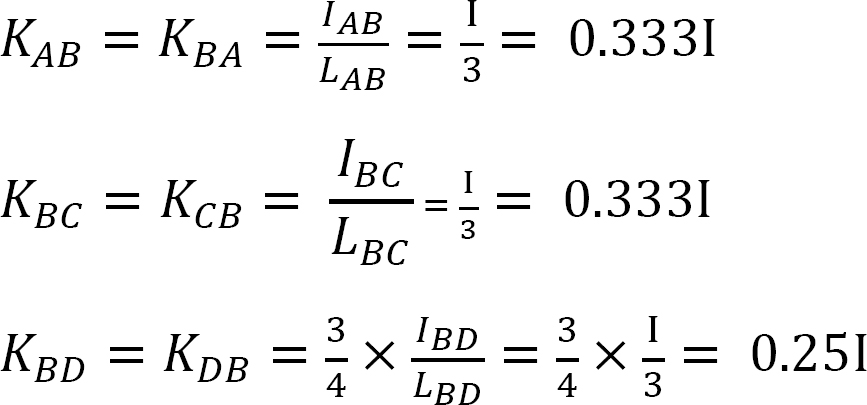
distribuční faktor.
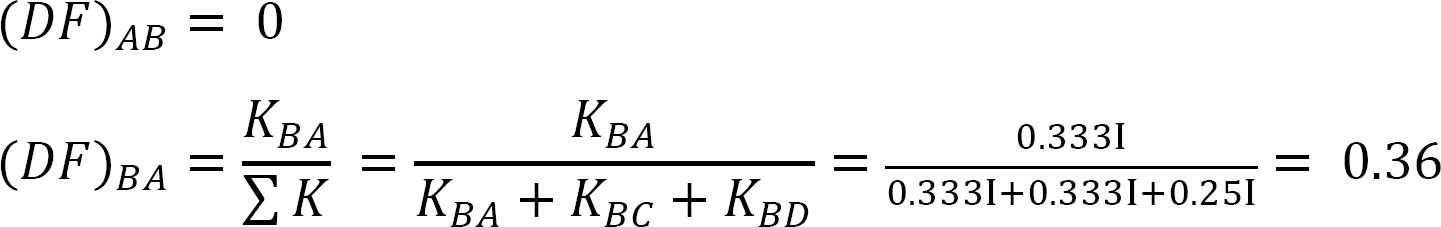

tabulka 12.5. Distribuční tabulka.
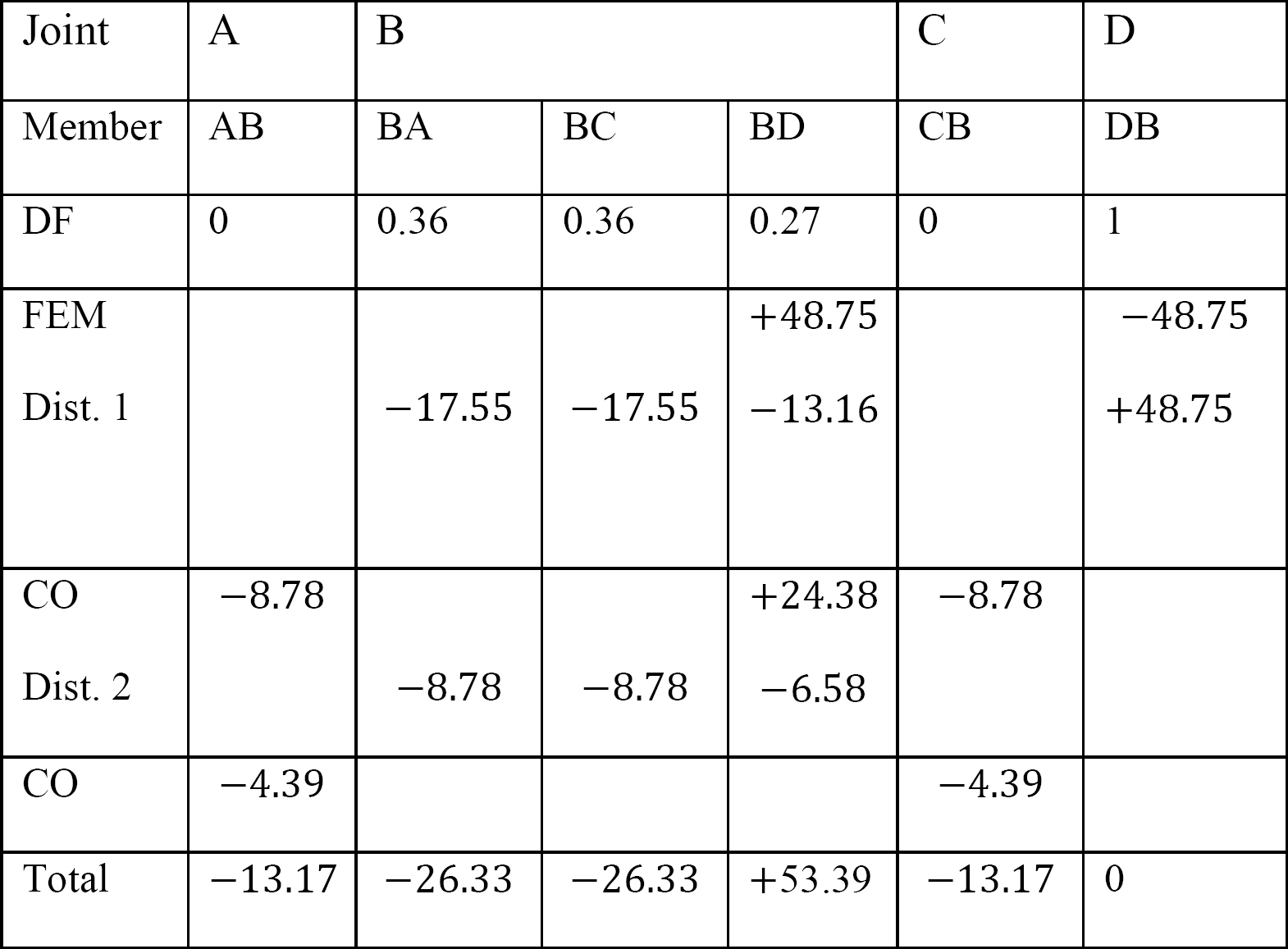
Poslední členské koncové momenty.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +53.39 k. ft
MCB = -13.17 k. ft
MDB = 0
Příklad 12.6
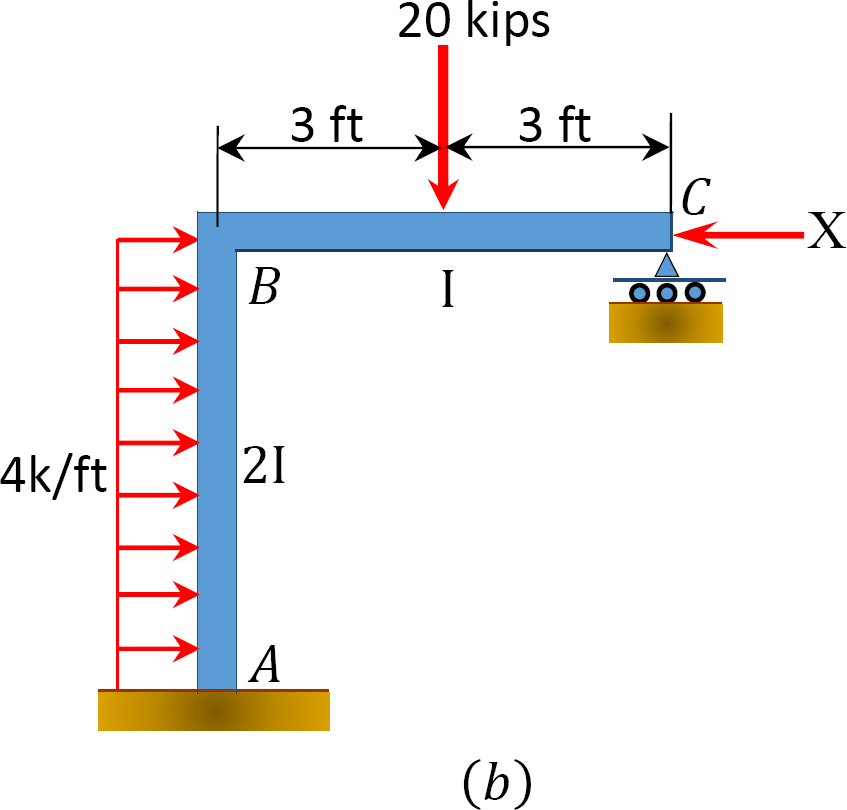
Pomocí moment, metody distribuce, určit členský end-momenty rám s boční-sway ukazuje Obrázek 12.11 a.
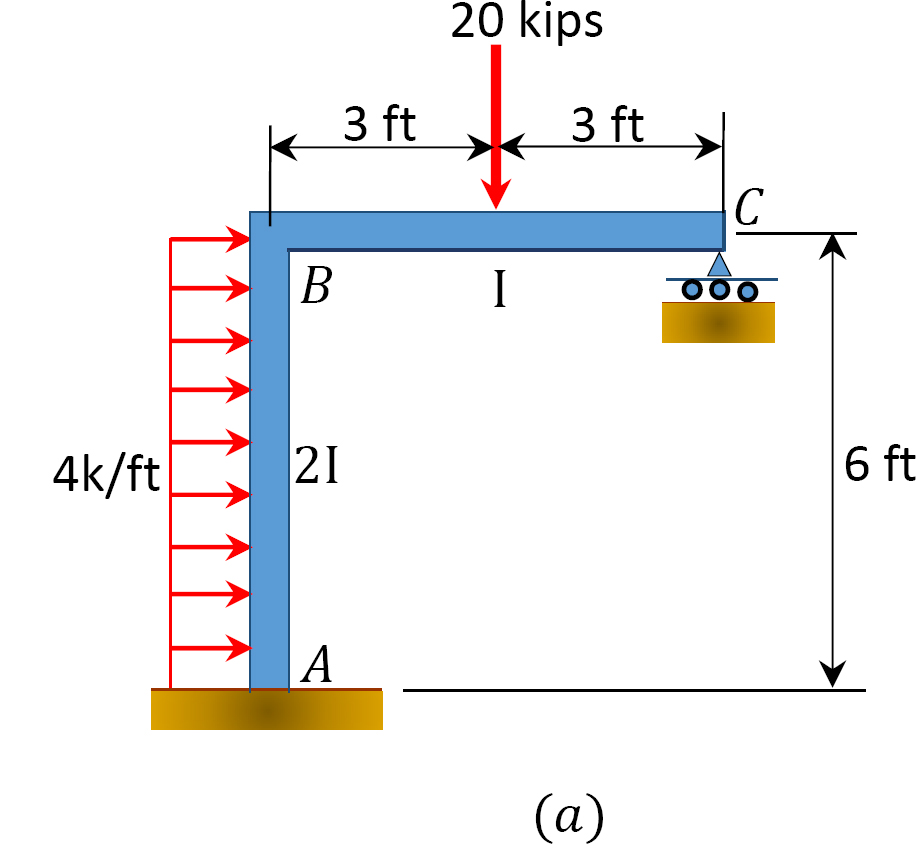
Obr. 12.11. Rám s bočním houpáním.
řešení
pevný koncový moment.
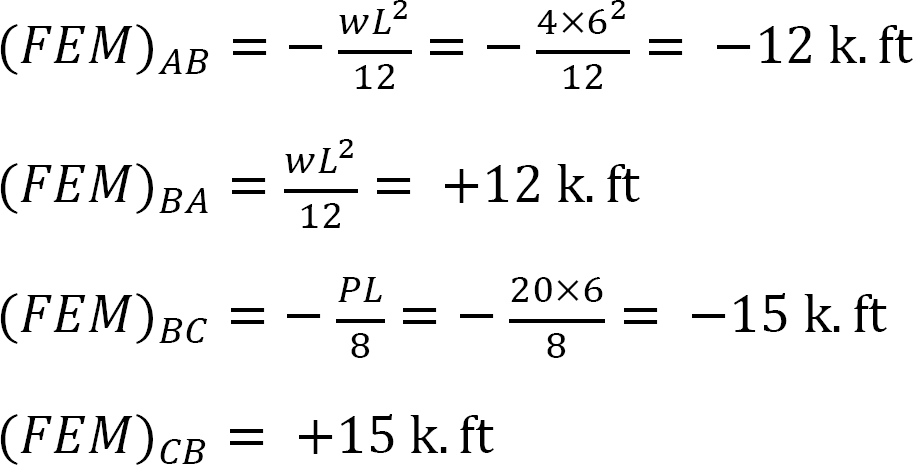
faktor tuhosti.
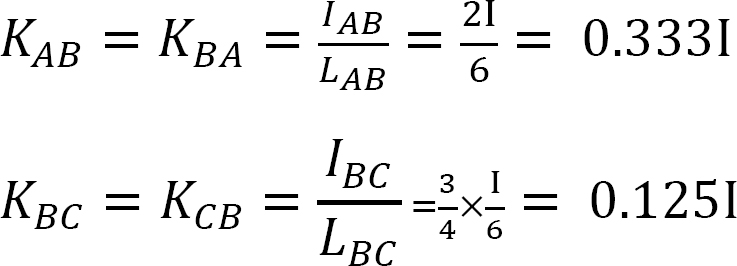
distribuční faktor.
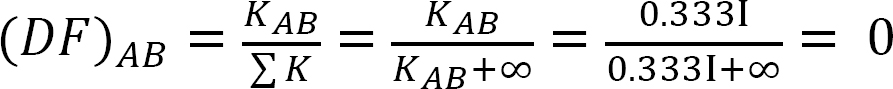

analýza rámu bez bočního houpání.
tabulka 12.6. Distribuční tabulka (bez houpacího rámu).
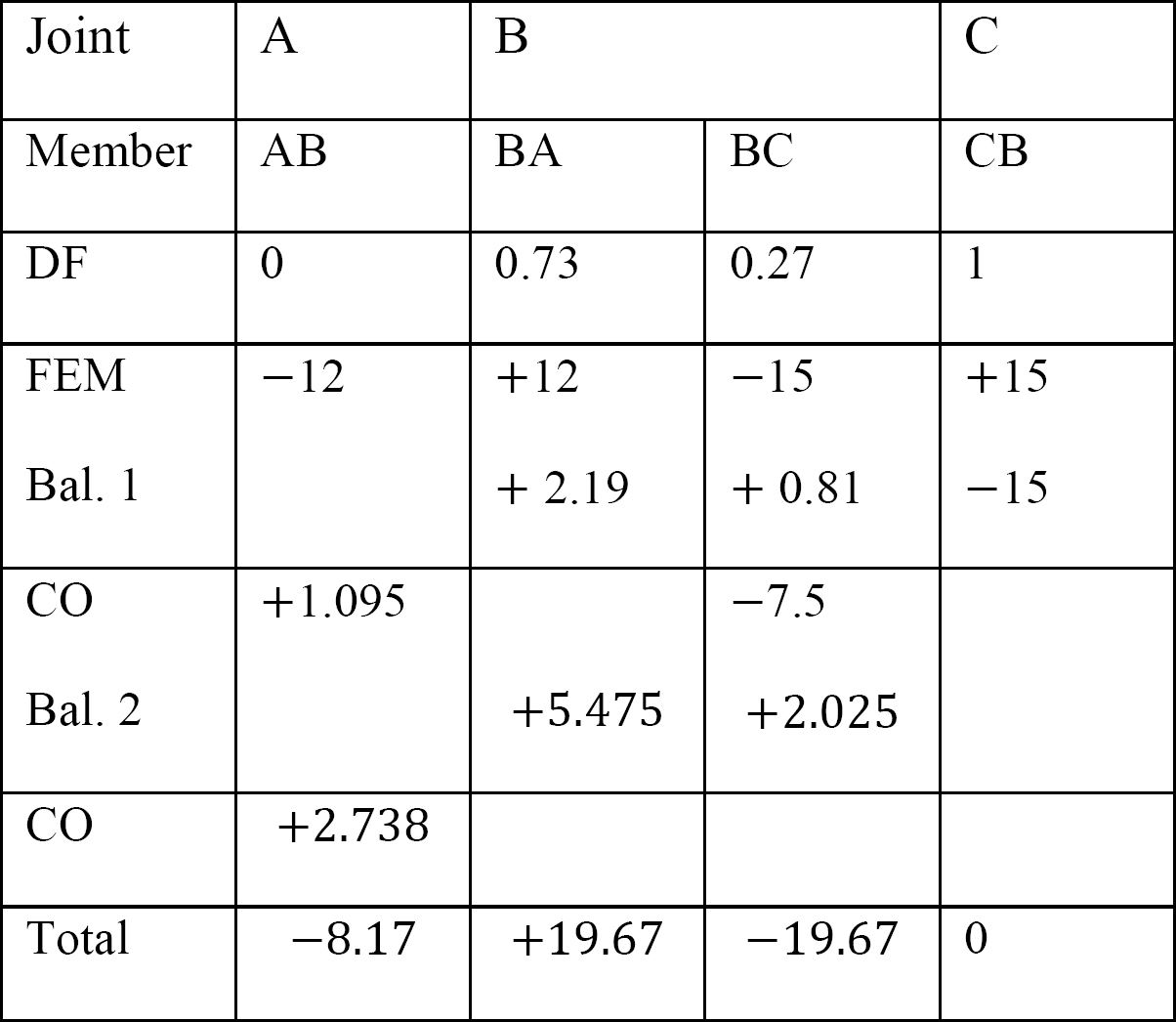
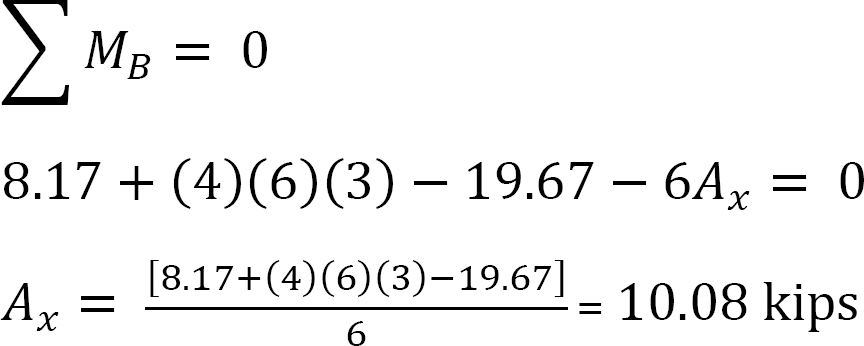
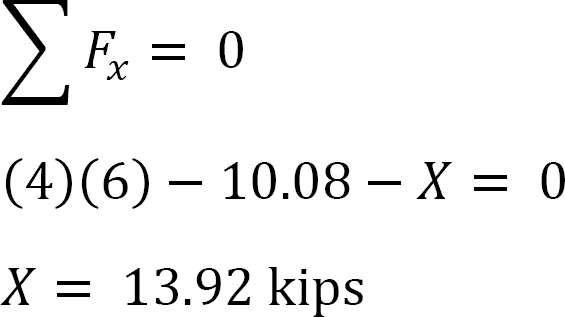
analýza rámu s bočním houpáním.
Předpokládejme, že MAB = + 20 k. ft
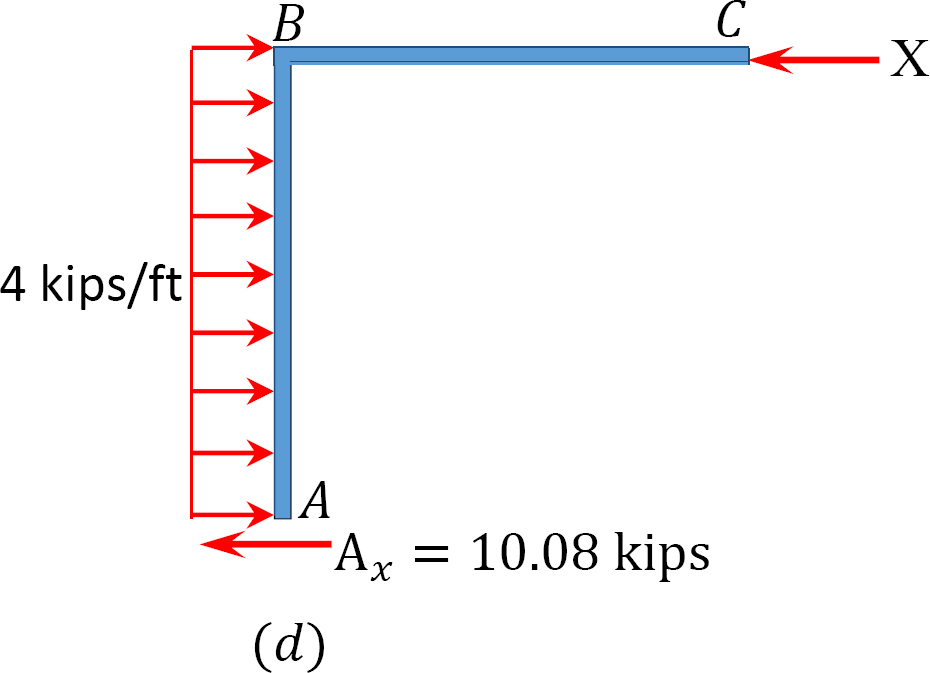
tabulka 12.7. Distribuční tabulka (houpací rám).
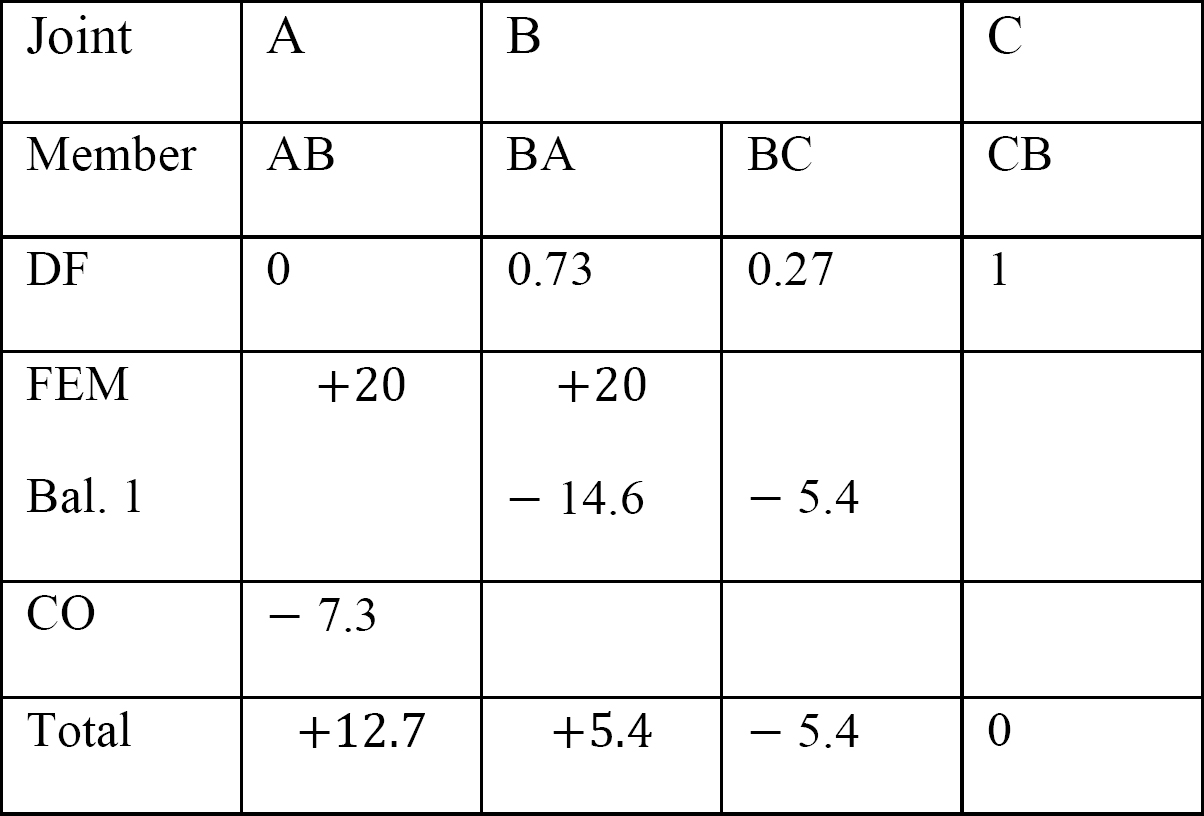
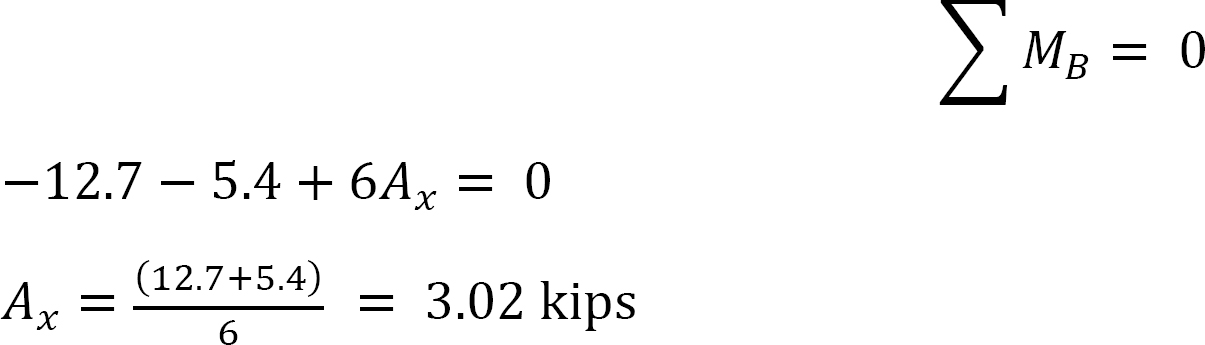
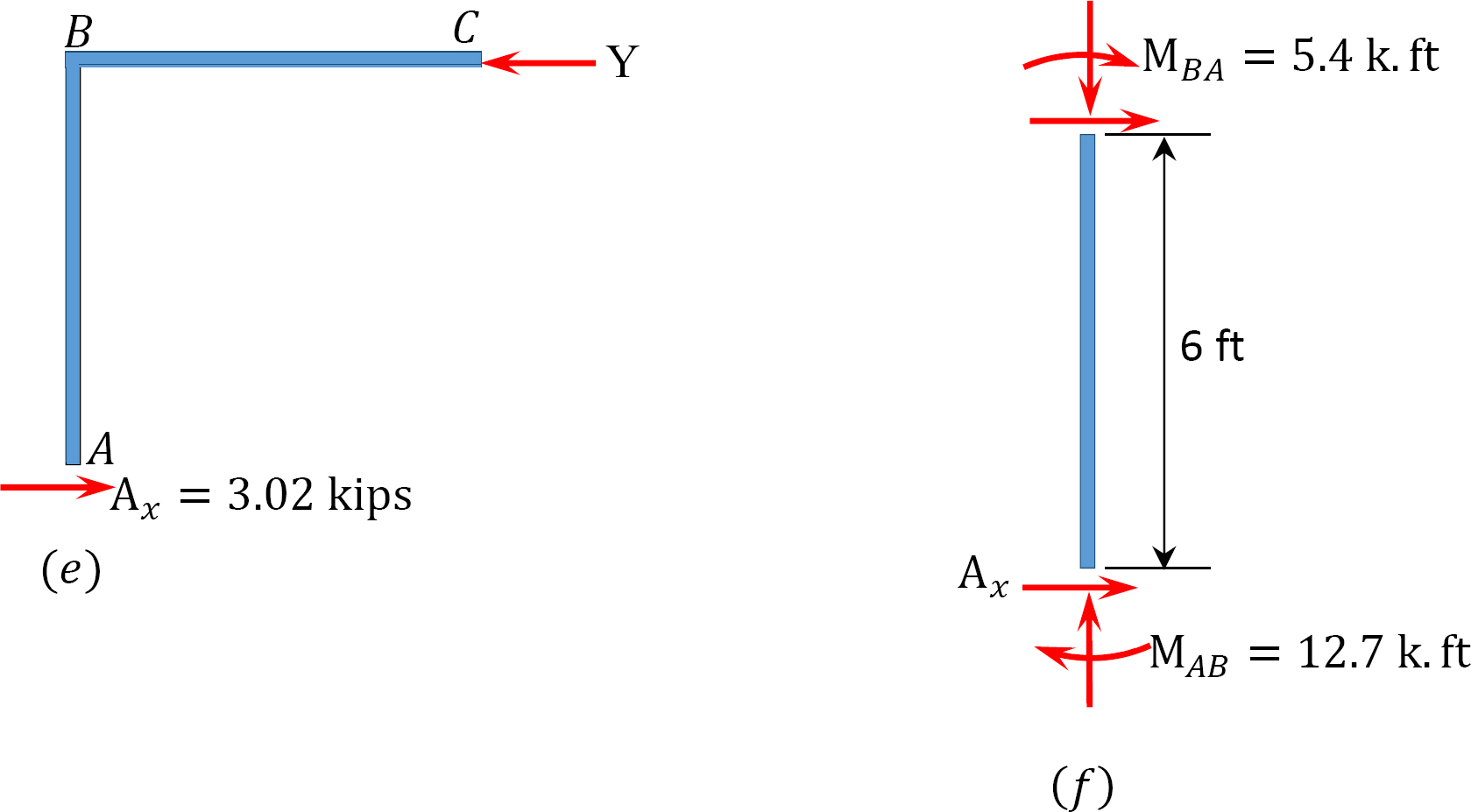
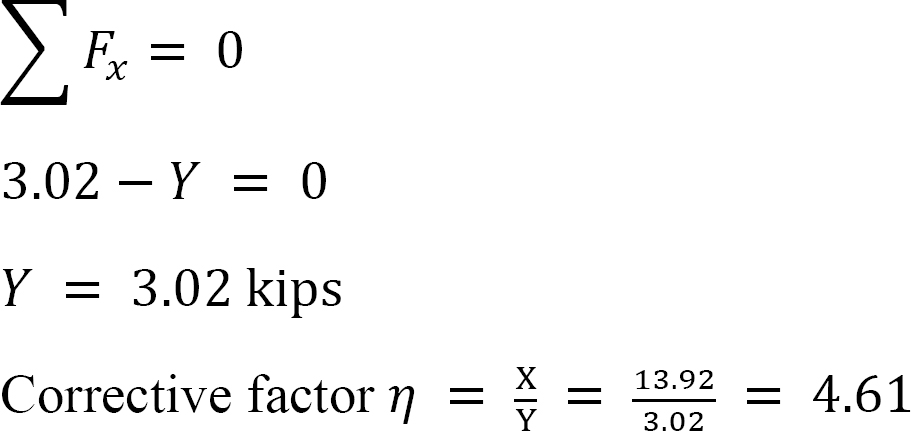
závěrečné momenty.
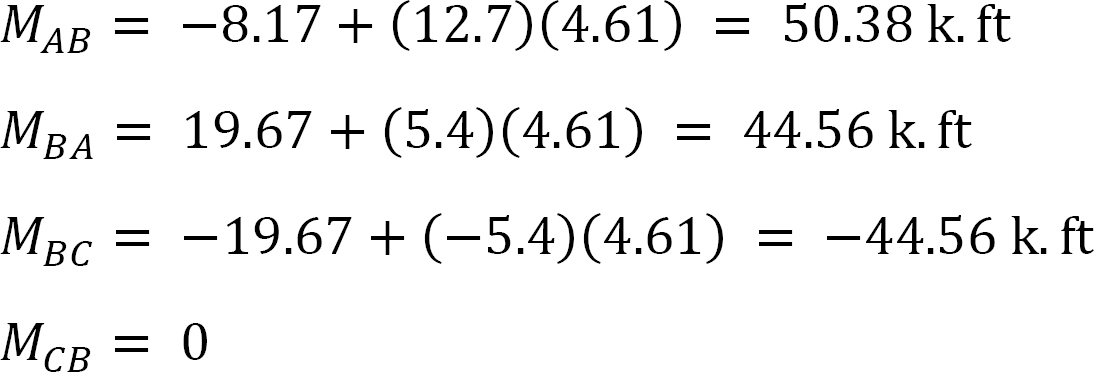
příklad 12.7
12.12 a. pomocí metody distribuce momentů určete koncové momenty členů rámu.
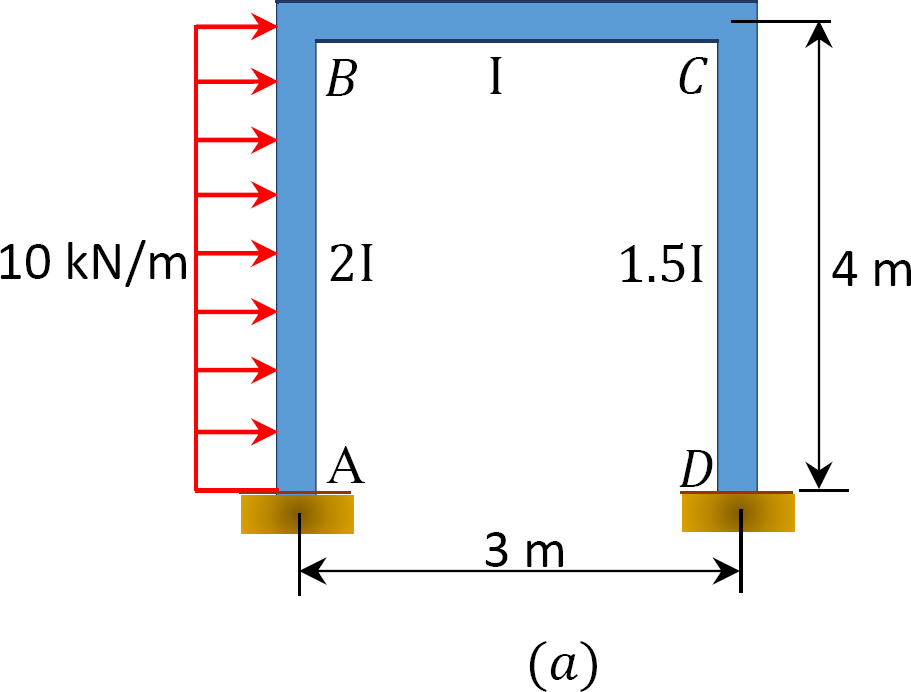
obr. 12.12. Nabitý houpací rám.
řešení
pevný koncový moment.
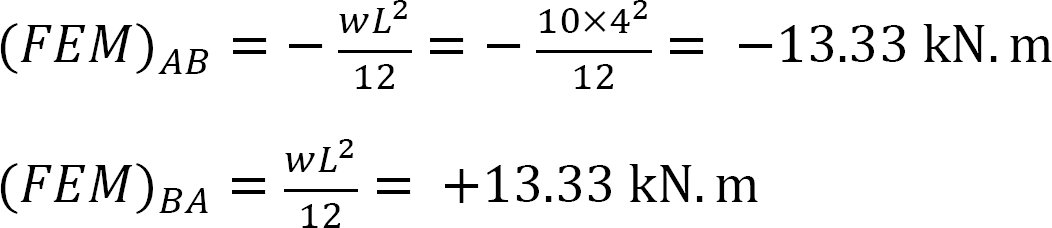
faktor tuhosti.
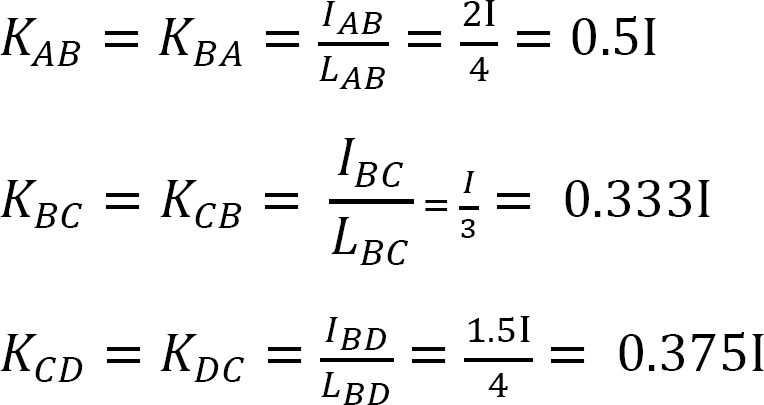
distribuční faktor.

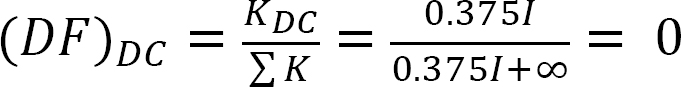
analýza rámu bez bočního houpání.
tabulka 12.8. Distribuční tabulka (bez houpacího rámu).
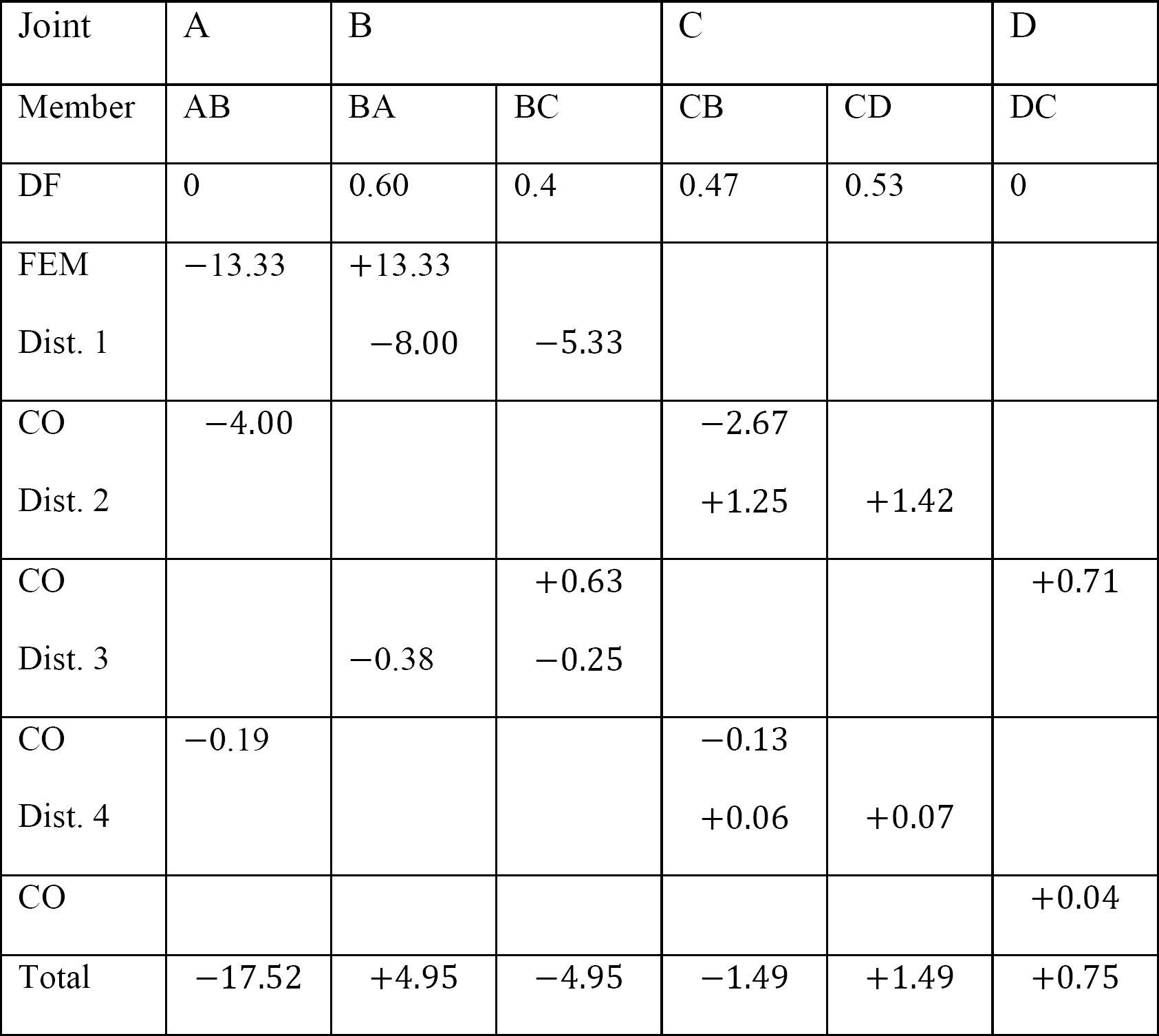
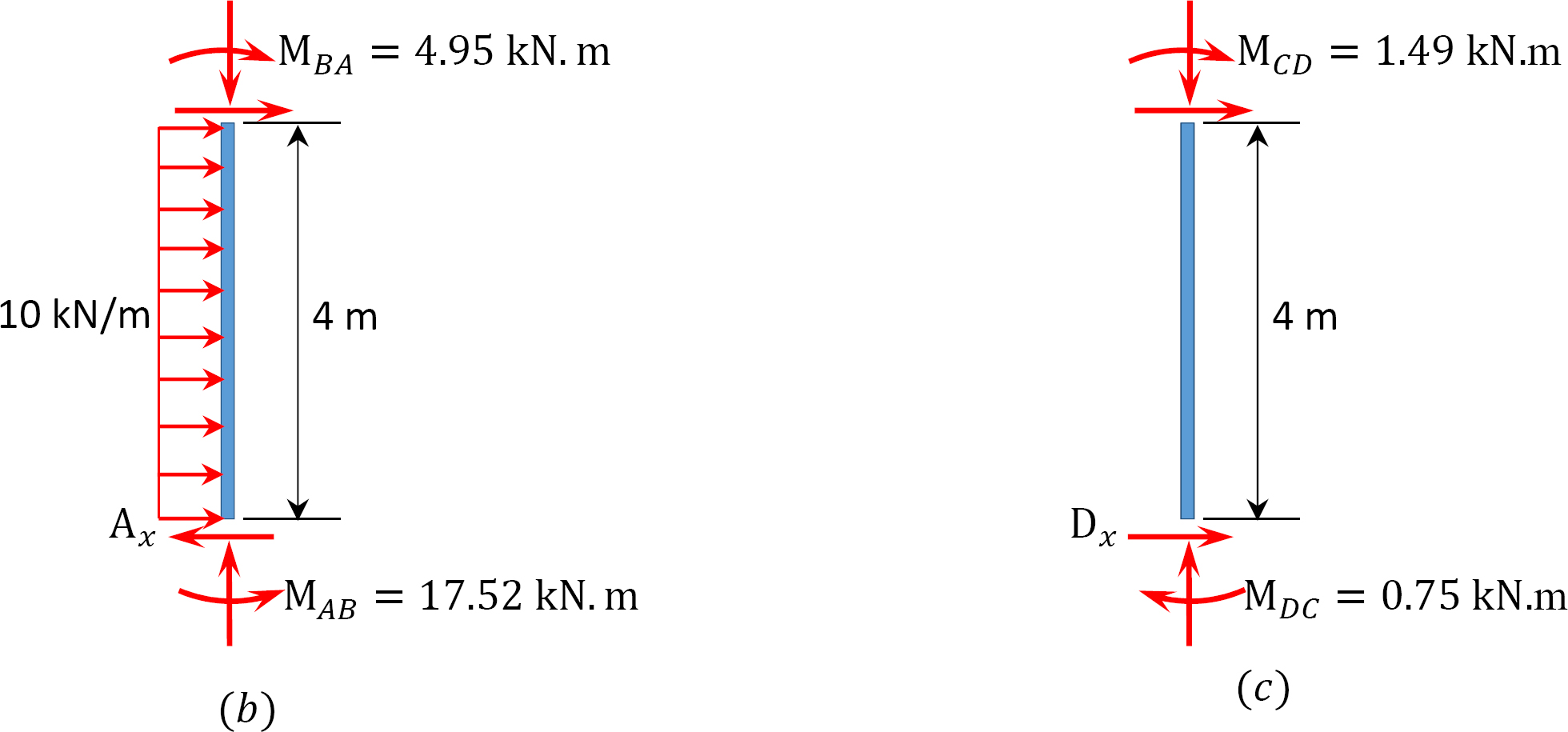
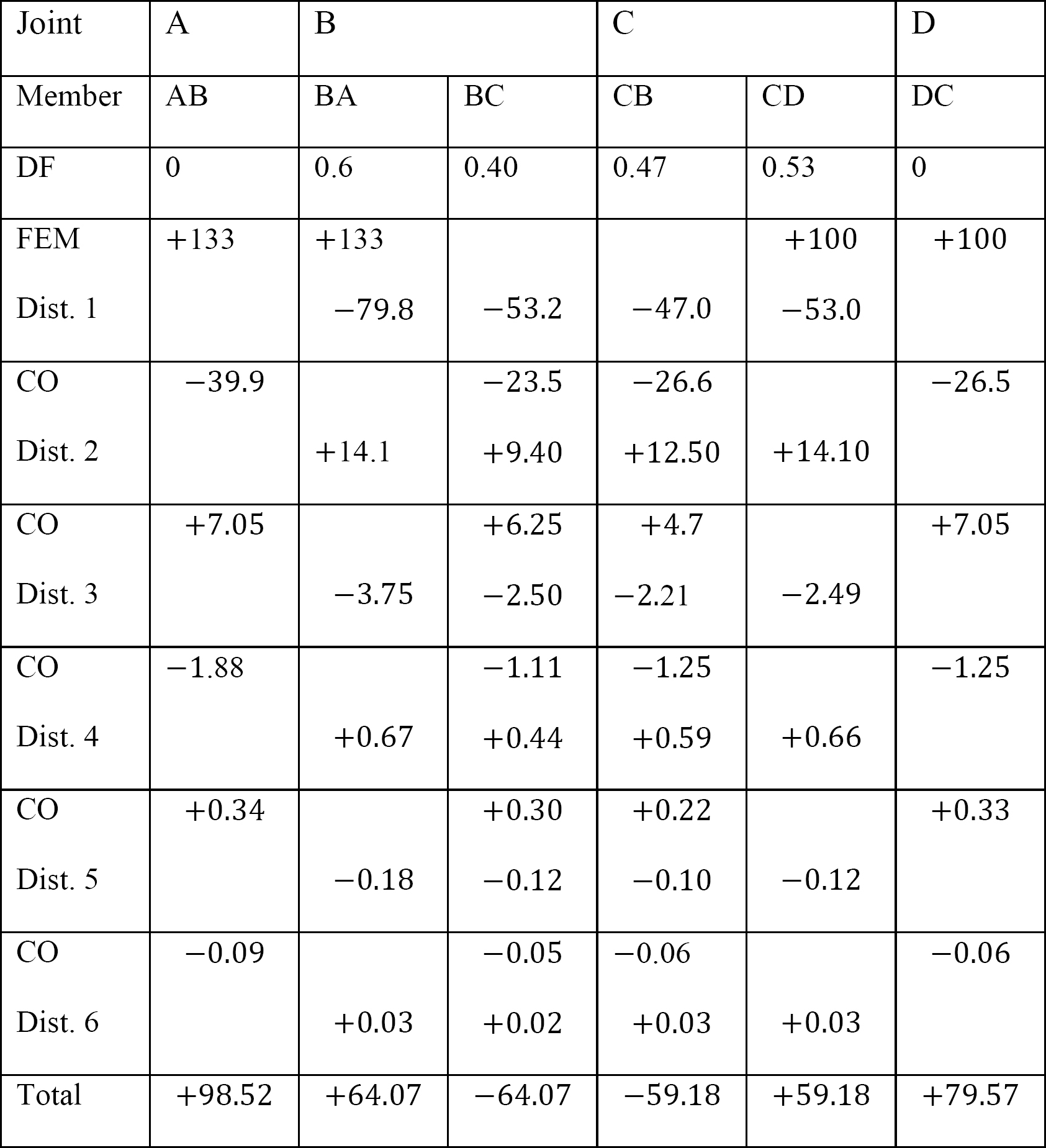
tabulka 12.9. Distribuční tabulka (houpací rám).
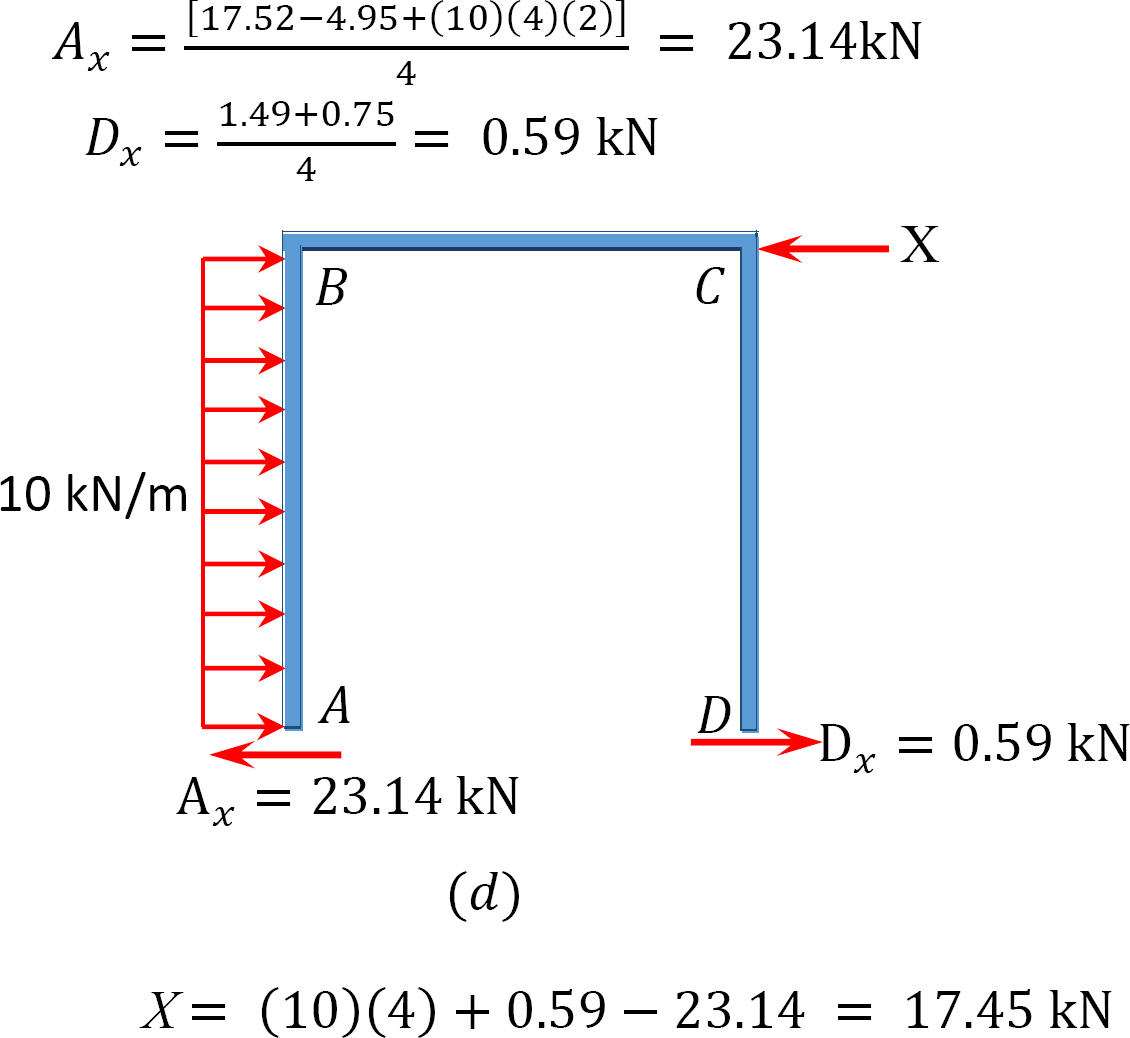
analýza rámu s bočním houpáním.
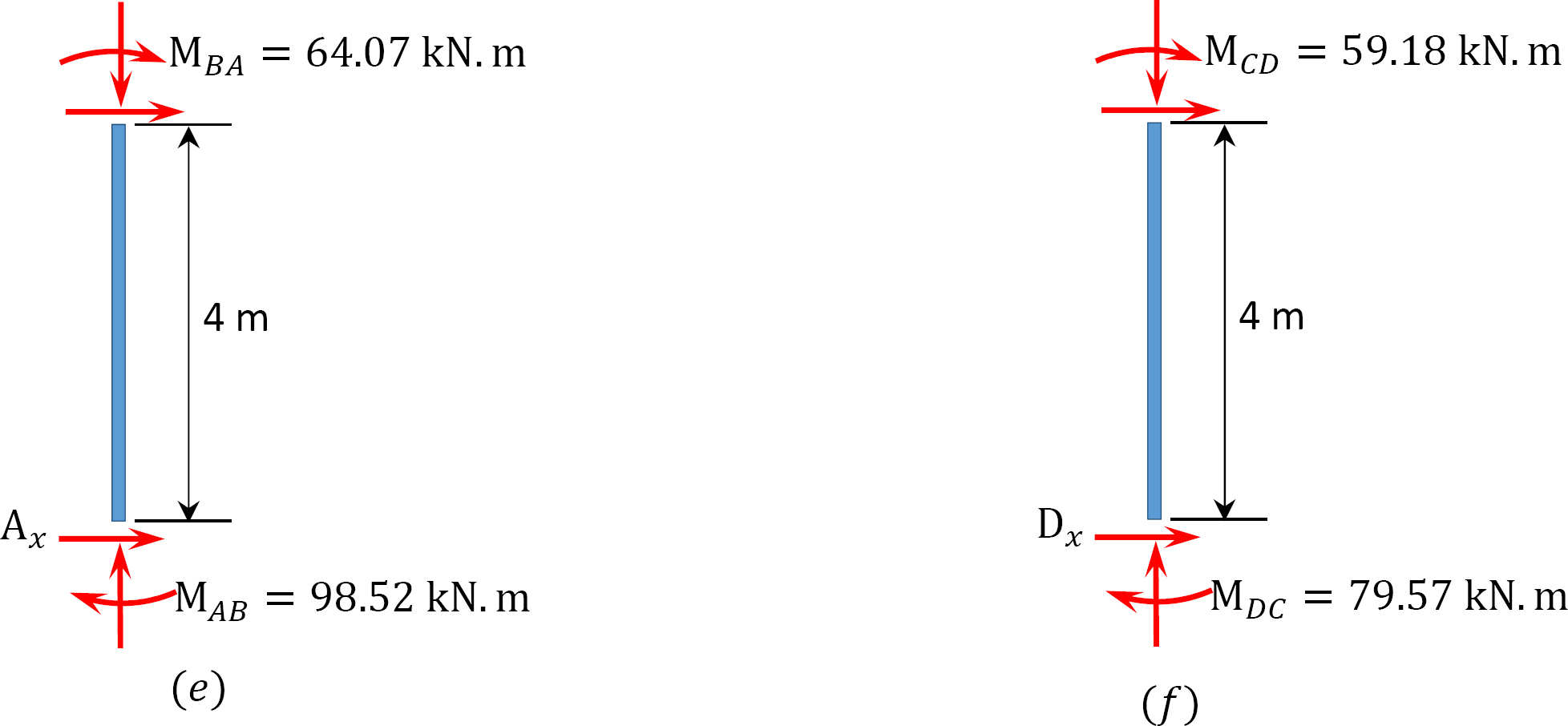

poslední konec.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Shrnutí Kapitoly
Chvíli distribuce metoda analýza neurčitých konstrukcí: V okamžiku, kdy distribuční metoda analýzy, je přibližnou metodou analýzy. Jeho stupeň přesnosti závisí na počtu iterací. Při tomto způsobu se předpokládá, že všechny spoje ve struktuře jsou dočasně uzamčeny nebo upnuty, a tím je zabráněno možnému otáčení. Zatížení se aplikuje na členy, a okamžiky, vyvinutý v členských končí kvůli stálost jsou určeny. Klouby ve struktuře se pak postupně odemykají a nevyvážený okamžik v každém kloubu je distribuován členům, kteří se v tomto kloubu setkávají. Jsou určeny momenty přenosu na vzdálených koncích členů, a proces vyvažování pokračuje až do požadované úrovně přesnosti. Koncové momenty členů jsou určeny sčítáním pevného koncového okamžiku, distribuovaného okamžiku a okamžiku přenosu. Jakmile jsou určeny koncové momenty členů, struktura se stává určující.
Praktické Problémy
12.1 Použití v okamžiku, kdy distribuční metoda pro výpočet end okamžik členy nosníků znázorněno na Obrázku P12.1 až Obrázku P12.12 a kreslení ohybového momentu a posouvající síly diagramy. EI = konstanta.
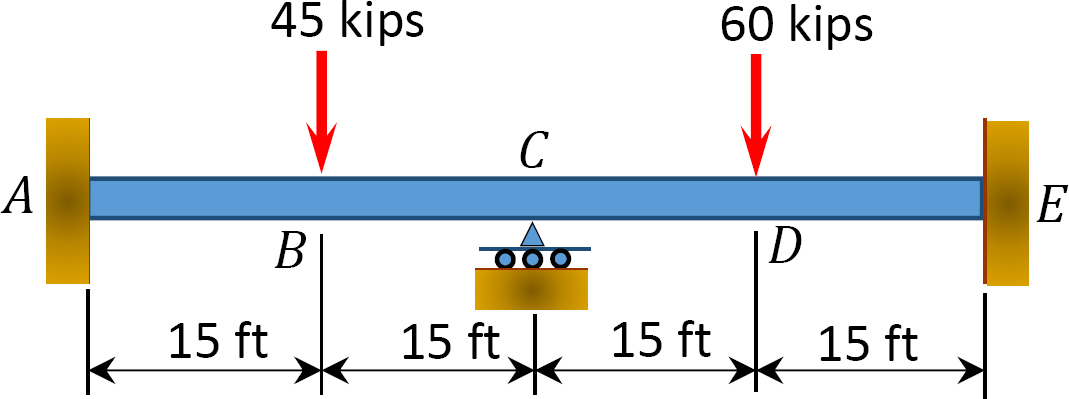
obr. P12.1. Trám.
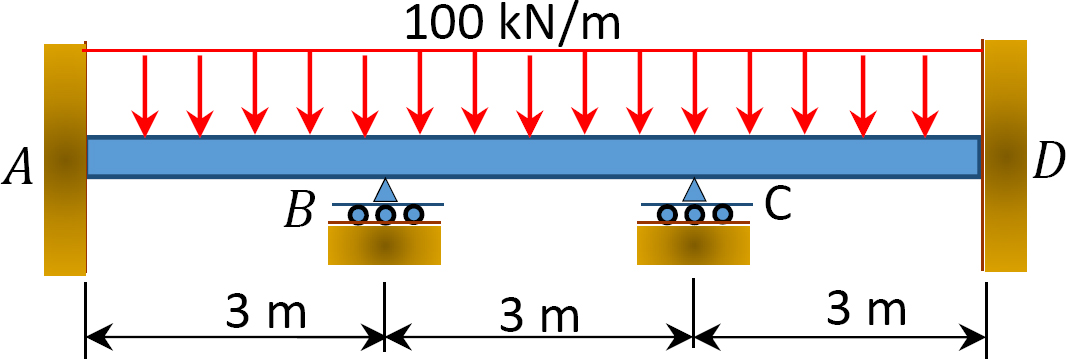
obr. P12, 2. Trám.
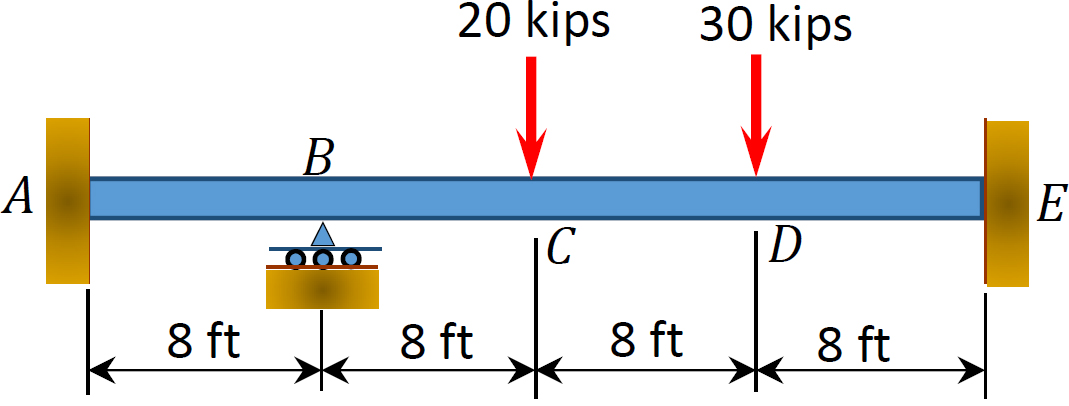
obr. P12, 3. Trám.
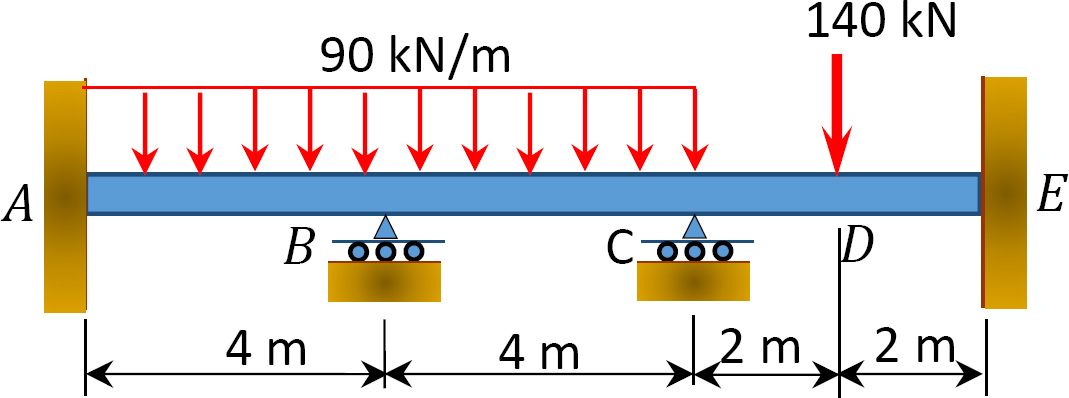
obr. P12, 4. Trám.
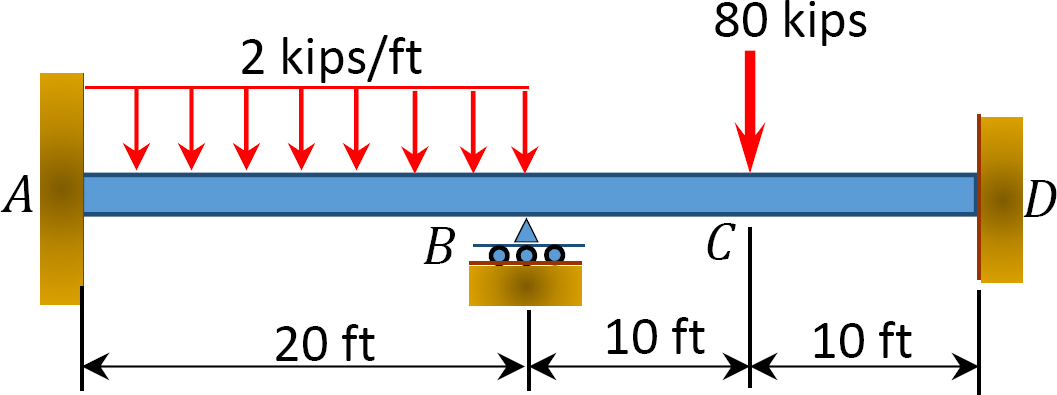
obr. P12, 5. Trám.
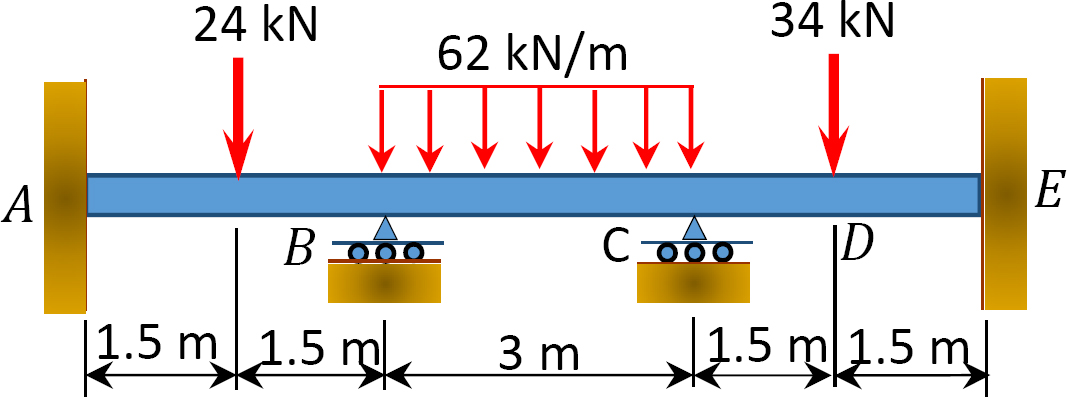
obr. P12, 6. Trám.
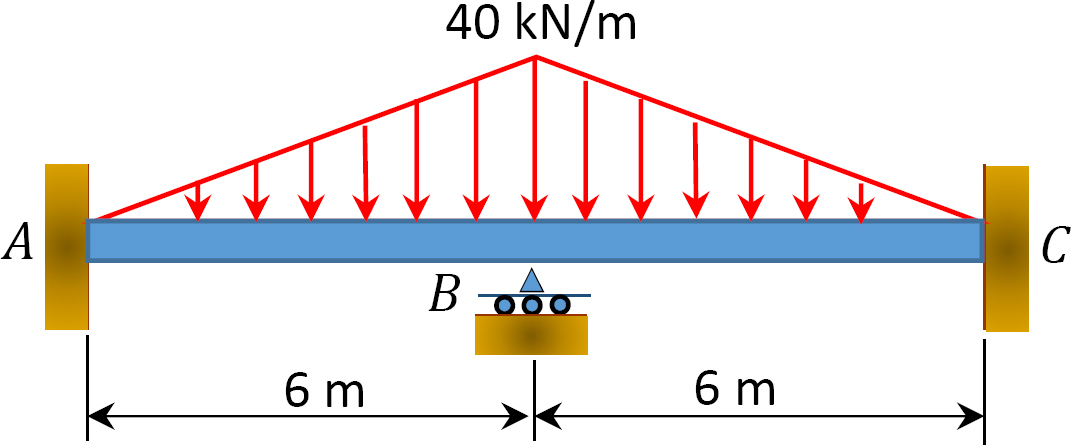
obr. P12, 7. Trám.
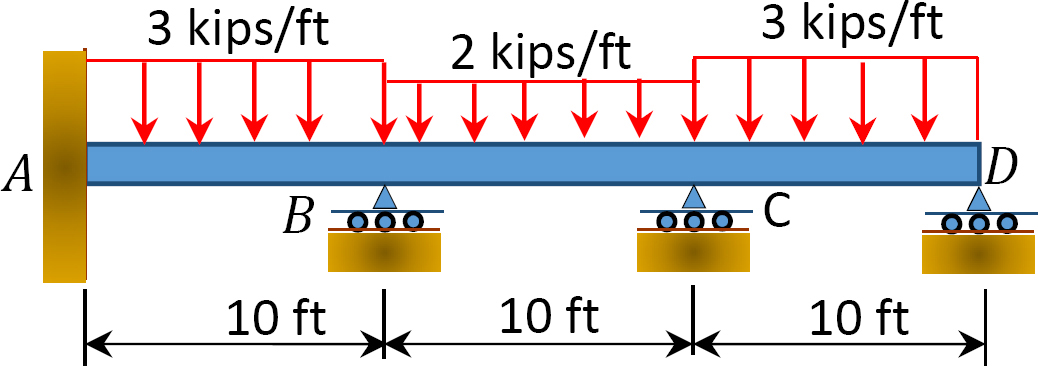
obr. P12, 8. Trám.
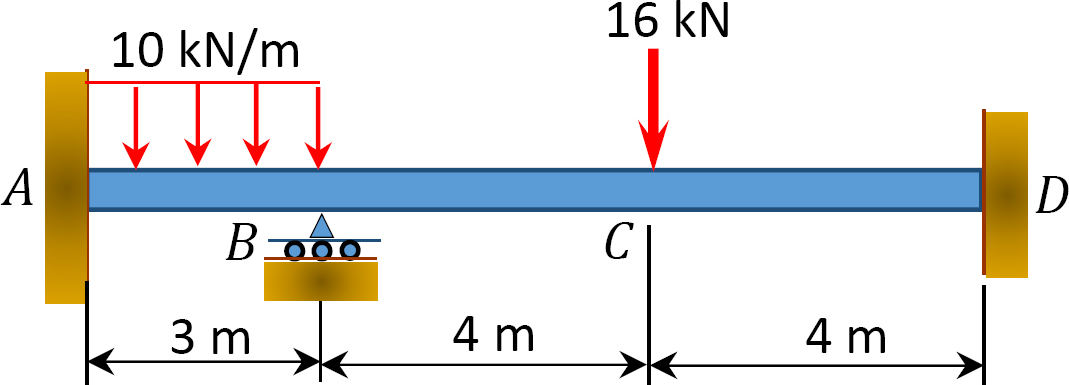
obr. P12, 9. Trám.
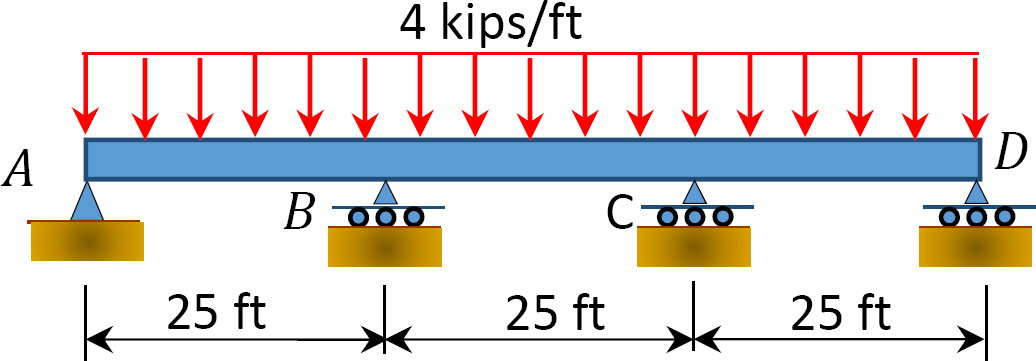
obr. P12.10. Trám.
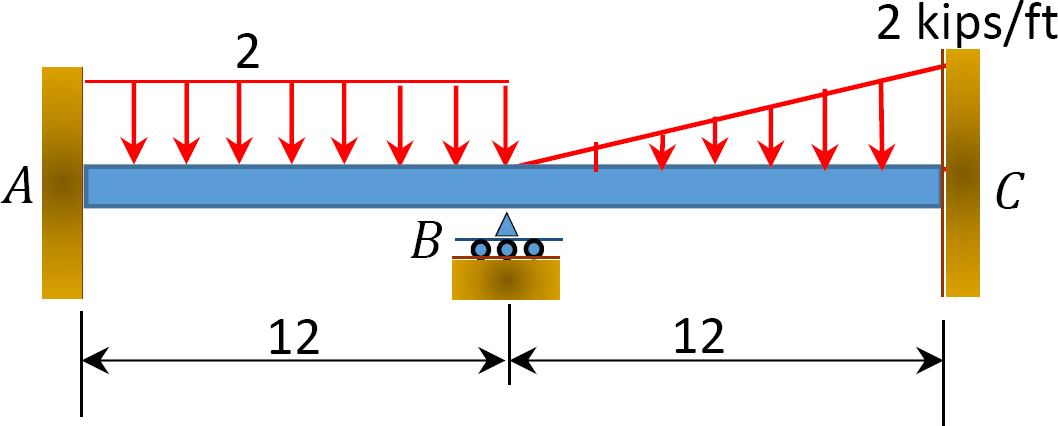
obr. P12.11. Trám.
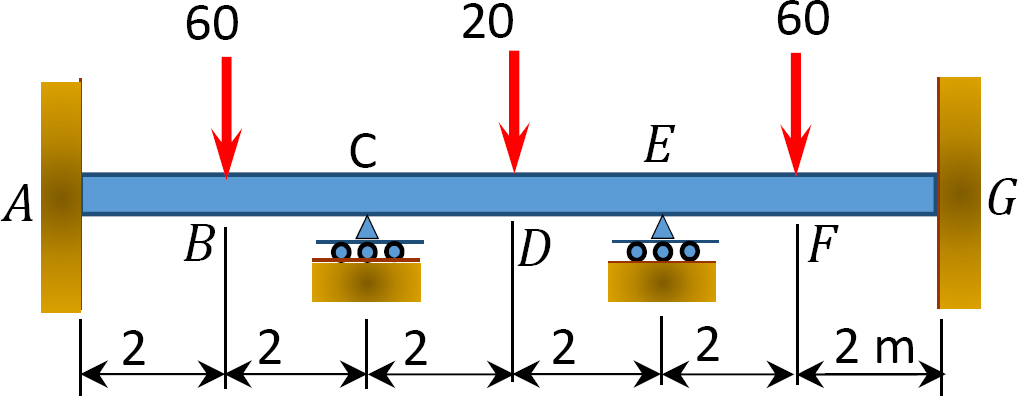
obr. 12.12. Trám.
12.2 Použití v okamžiku, kdy distribuční metoda pro výpočet end okamžik členů rámce je znázorněno na Obrázku P12.13 Obrázek 12.20 a kreslení ohybového momentu a posouvající síly diagramy. EI = konstanta.
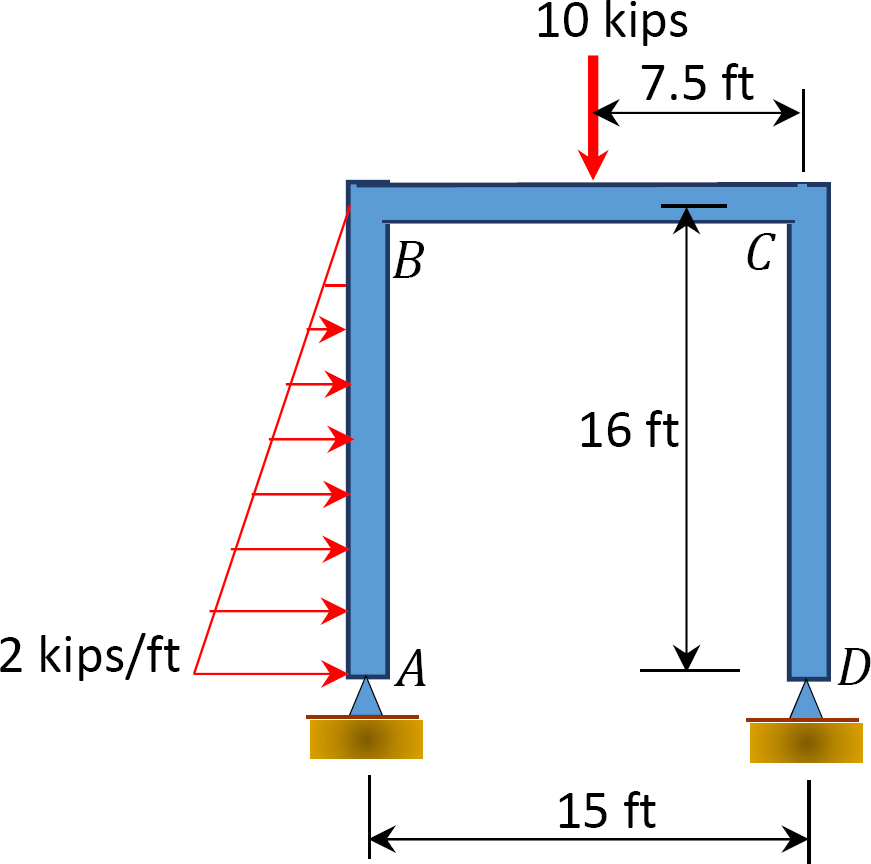
obr. 12.13. Snímek.
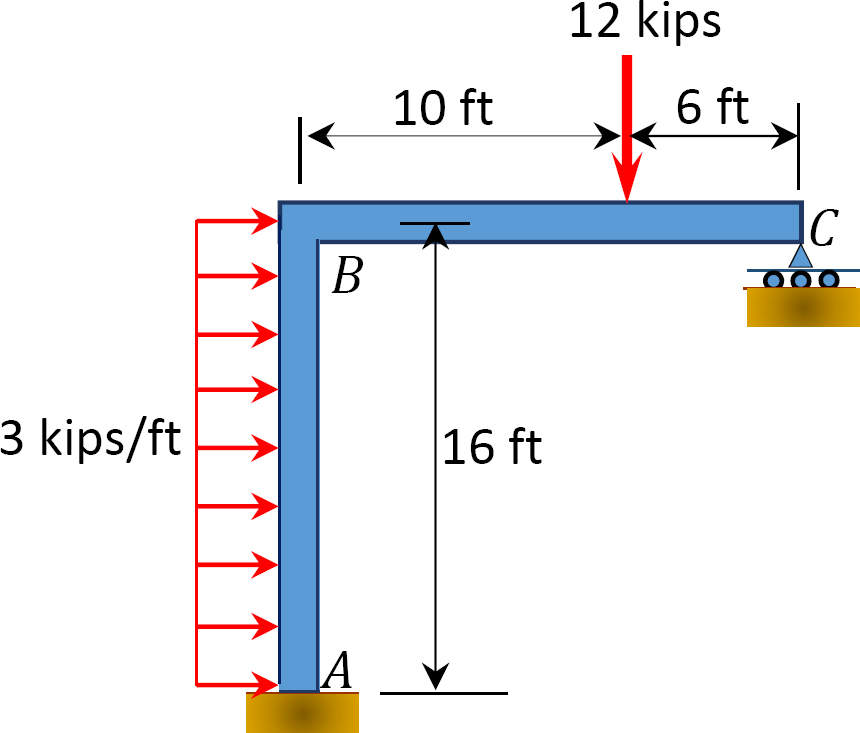
obr. 12.14. Snímek.
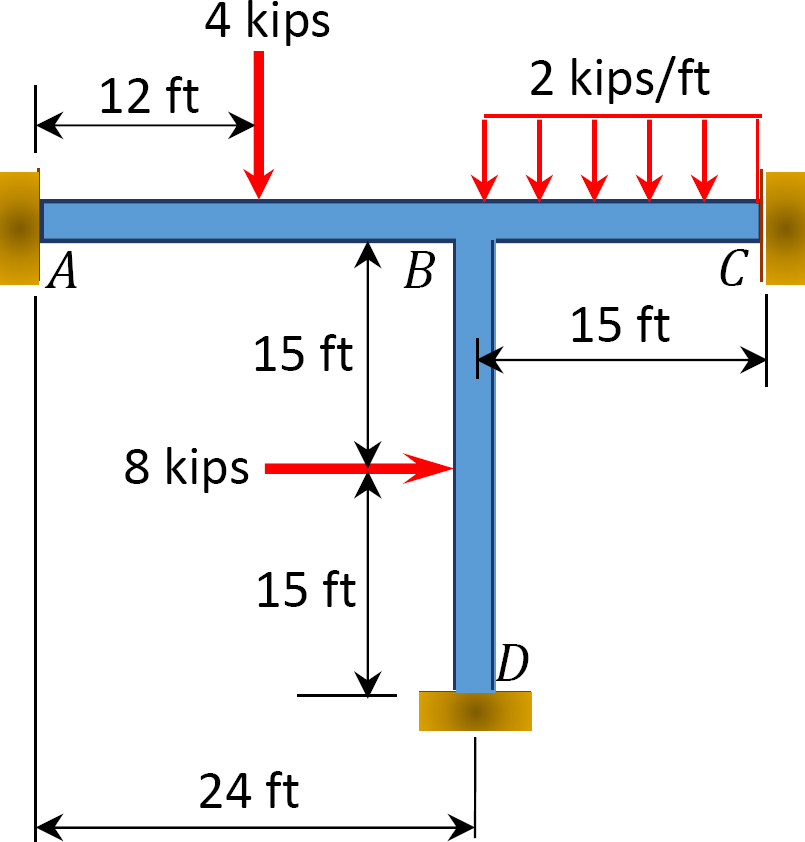
obr. 12.15. Snímek.
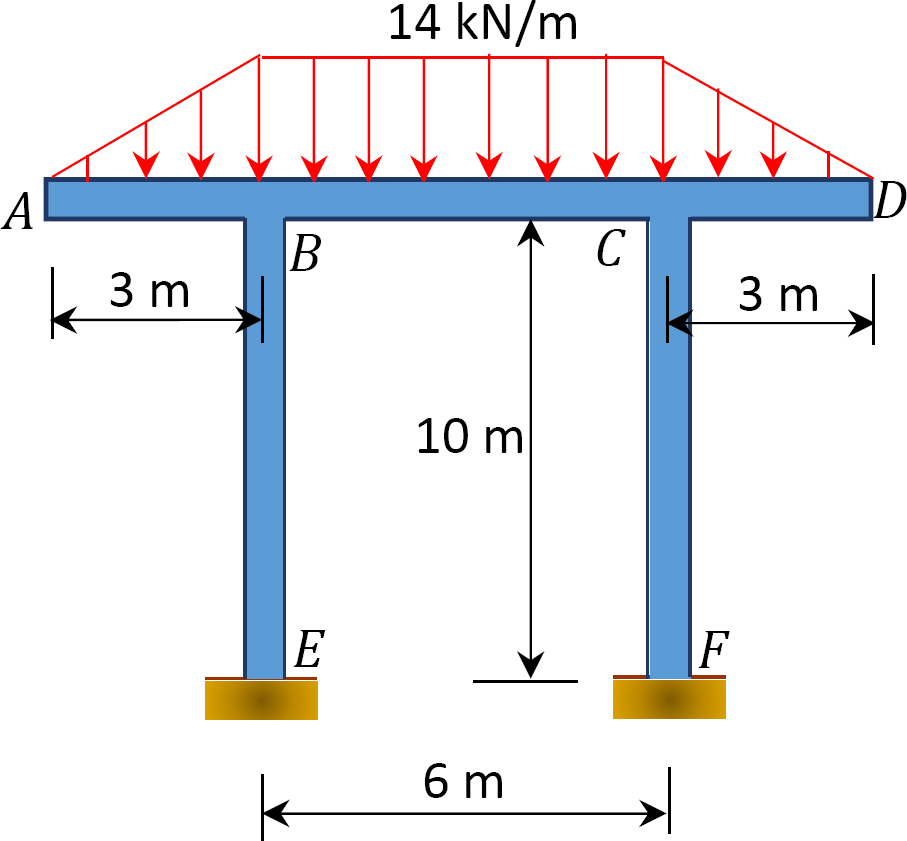
Fig. P12.16. Frame.
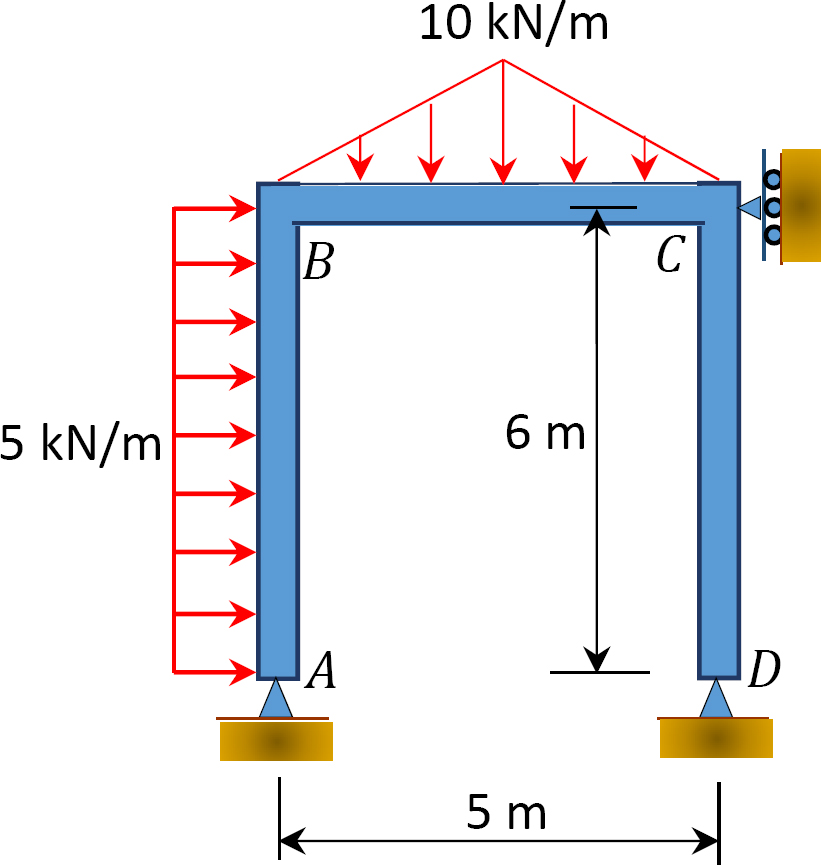
Fig. P12.17. Frame.
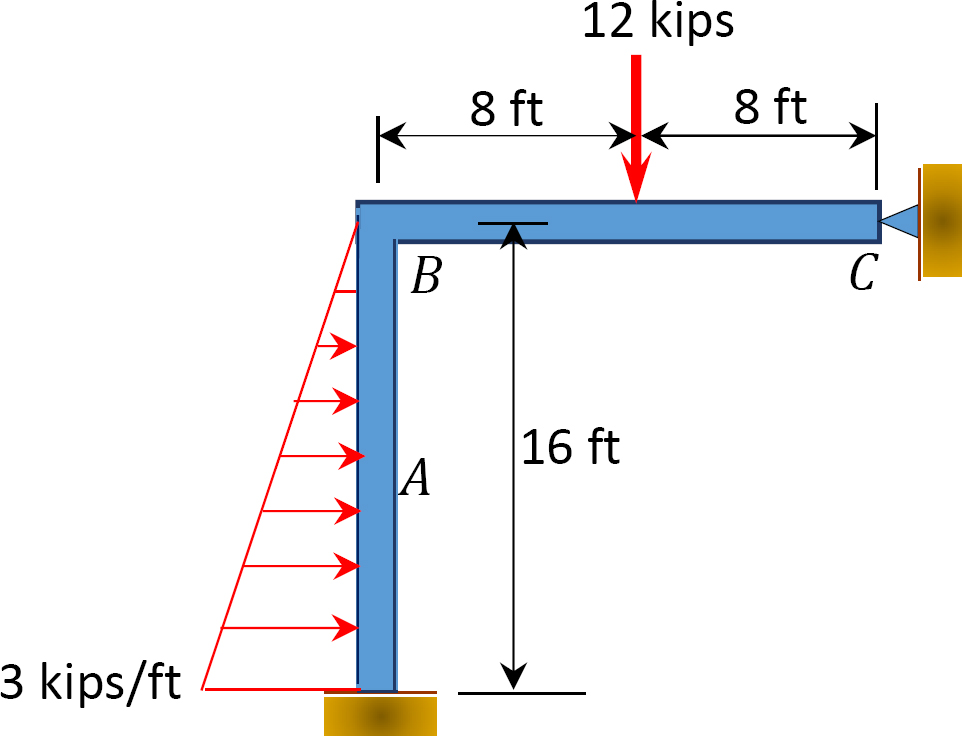
Fig. P12.18. Frame.
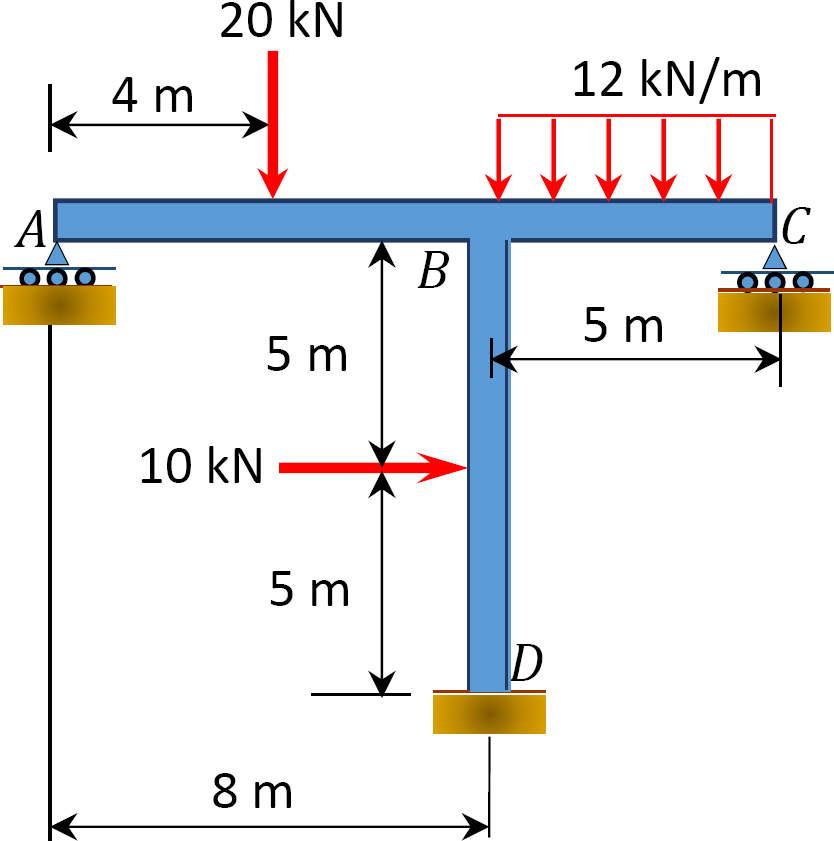
Fig. P12.19. Frame.
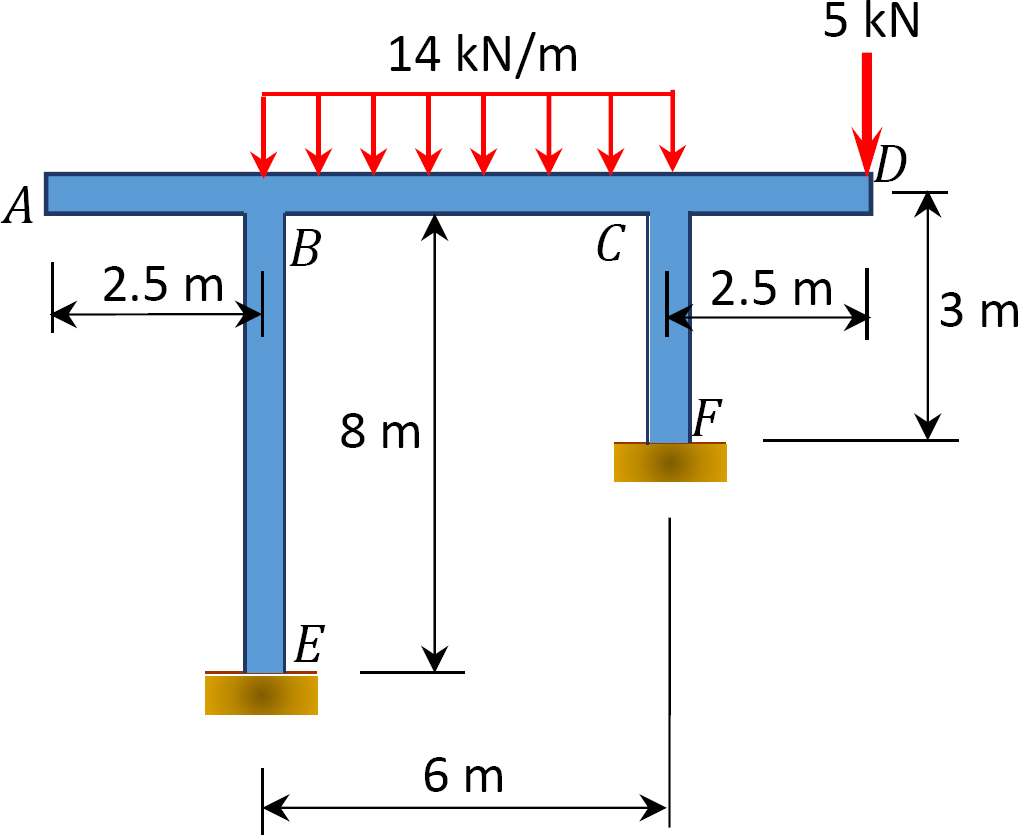
Fig. P12.20. Frame.