Kapitel 12
Moment Distribution metode til analyse af strukturer
12.1 grundlæggende begreber
moment distribution metode til analyse af bjælker og rammer blev udviklet af Hardy Cross og formelt præsenteret i 1930. Selvom denne metode er en deformationsmetode som hældningsafbøjningsmetoden, er den en omtrentlig metode og kræver således ikke løsning af samtidige ligninger, som det var tilfældet med sidstnævnte metode. Graden af nøjagtighed af resultaterne opnået ved metoden til momentfordeling afhænger af antallet af successive tilnærmelser eller iterationsprocessen.
for at illustrere begrebet metoden til momentfordeling skal du overveje rammen vist i figur 12.1. Medlemmer af rammen er prismatiske og antages ikke at deformere aksialt eller oversætte i forhold til hinanden. Samlinger ACD af rammen er faste, mens fælles B kan rotere lidt på grund af den påførte belastning. For det første antages alle leddene at være midlertidigt låst ved hjælp af en klemme, inden de udfører momentfordeling blandt medlemmerne.
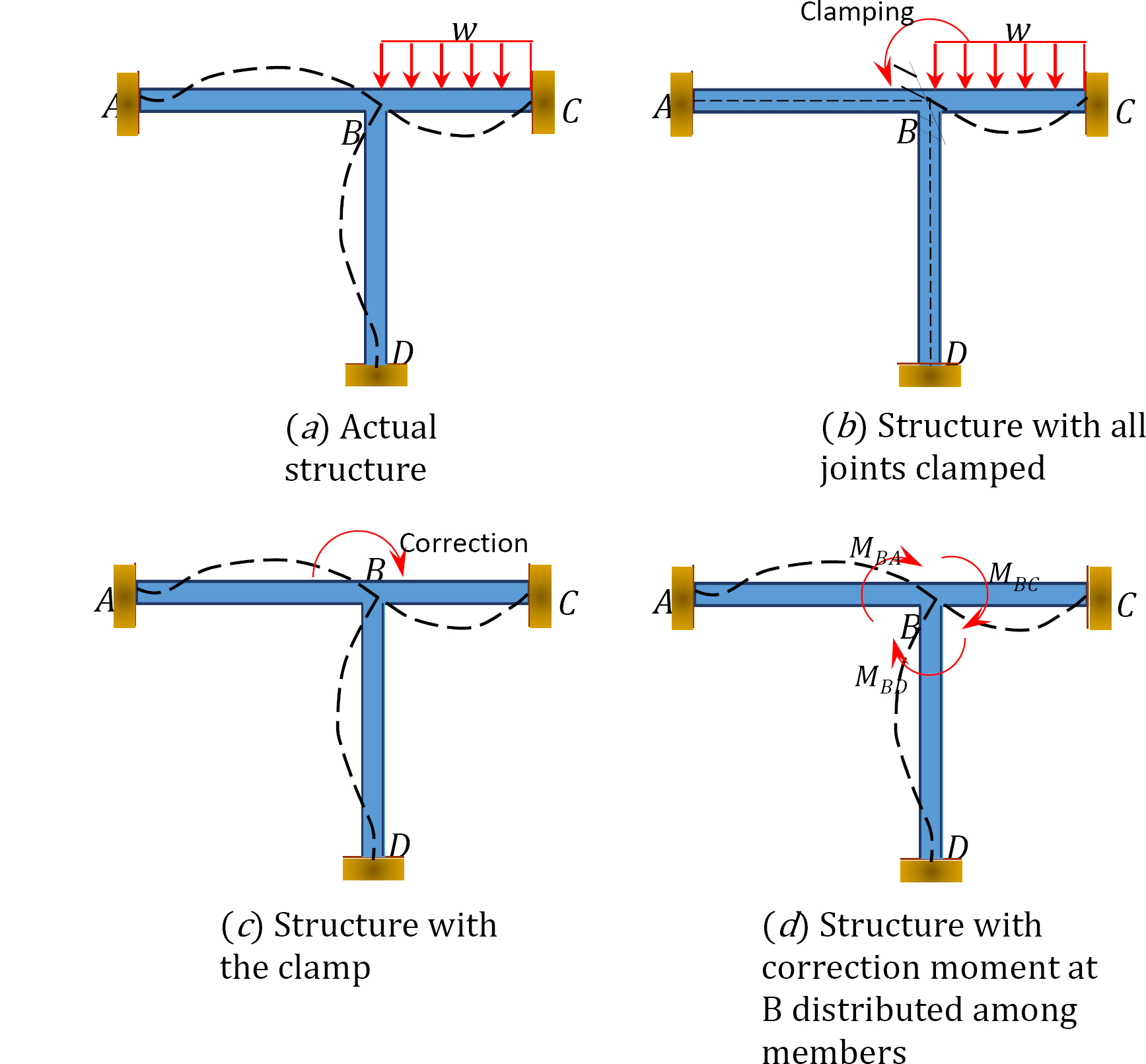
Fig. 12.1. Ramme.
12.2 Sign Convention
sign convention for moment distribution method svarer til den, der er etableret for hældningsafbøjningsmetoden; det vil sige, øjeblikket i slutningen af et medlem betragtes som positivt, hvis det har tendens til at dreje enden af medlemmet med uret og negativt, hvis det har tendens til at dreje det mod uret.
12.3 definitioner
ubalancerede øjeblikke: denne analysemetode antager, at leddene i en struktur oprindeligt klemmes eller låses og derefter frigives successivt. Når en samling er frigivet, finder en rotation sted, da summen af de faste slutmomenter for medlemmerne, der mødes på det fælles, ikke er nul. Værdien af summen af de opnåede slutmomenter er det ubalancerede øjeblik ved det led.
Overførselsmomenter: de distribuerede øjeblikke i enderne af medlemmer, der mødes ved en fælles årsag, øjeblikke i de andre ender, som antages at være rettet. Disse inducerede øjeblikke i de andre ender kaldes overførselsmomenter.
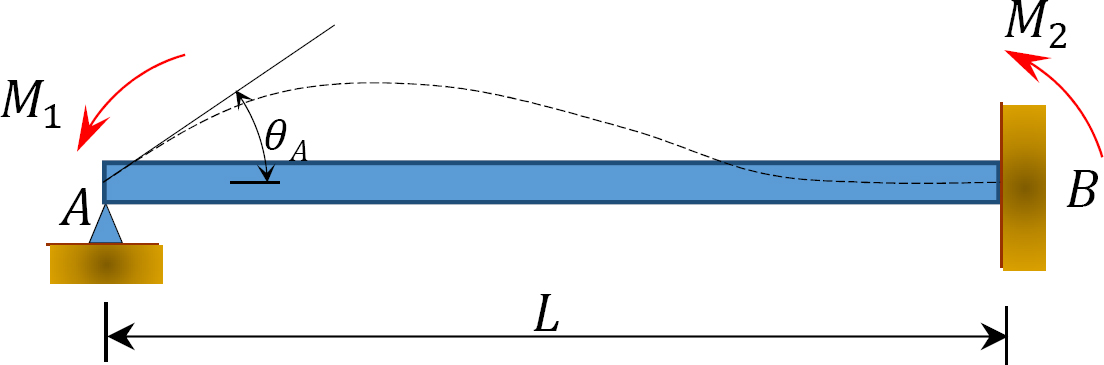
Fig. 12.2. Ubelastet prismatisk stråle.
overvej en ubelastet prismatisk stråle fastgjort i ende B, som vist i figur 12.2. Hvis et øjeblik M1 påføres bjælkens venstre ende, kan hældningsafbøjningsligningerne for begge ender af bjælken skrives som følger:


at erstatte 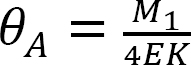 fra ligning 12.1 til ligning 12.2 antyder følgende:
fra ligning 12.1 til ligning 12.2 antyder følgende:

ligning 12.3 antyder, at det øjeblik, der overføres til den faste ende af en bjælke på grund af et øjeblik, der påføres i den anden ende, er lig med halvdelen af det anvendte øjeblik.
overførselsfaktor: forholdet mellem det inducerede øjeblik og det anvendte øjeblik kaldes overførselsfaktoren. For strålen vist i figur 12.2 er fremførselsfaktoren som følger:

distribueret faktor (DF): Den distribuerede faktor er en faktor, der bruges til at bestemme andelen af det ubalancerede øjeblik, der bæres af hvert af medlemmerne, der mødes på et fælles. For medlemmerne, der mødes ved fælles o i rammen vist i figur 12.3, beregnes deres fordelingsfaktorer som følger:
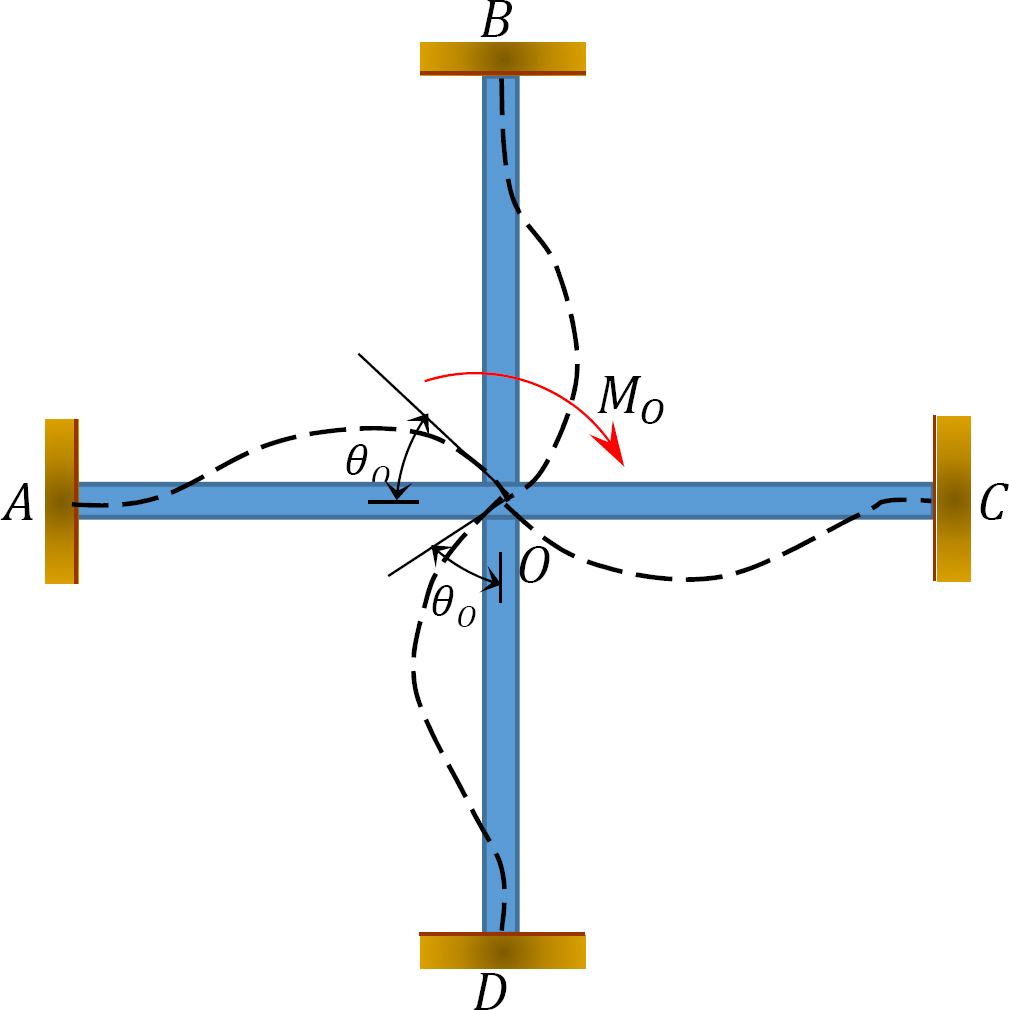
Fig. 12.3. Ramme.

distribuerede øjeblikke: ved frigivelsen af den imaginære klemme ved et led, får det ubalancerede øjeblik ved det led det til at rotere. Rotationen vrider slutningen af medlemmernes møde i leddet, hvilket resulterer i udvikling af modstående øjeblikke. Disse modstående øjeblikke kaldes distribuerede øjeblikke. De distribuerede øjeblikke for medlemmerne af rammen vist i figur 12.3 beregnes som følger:
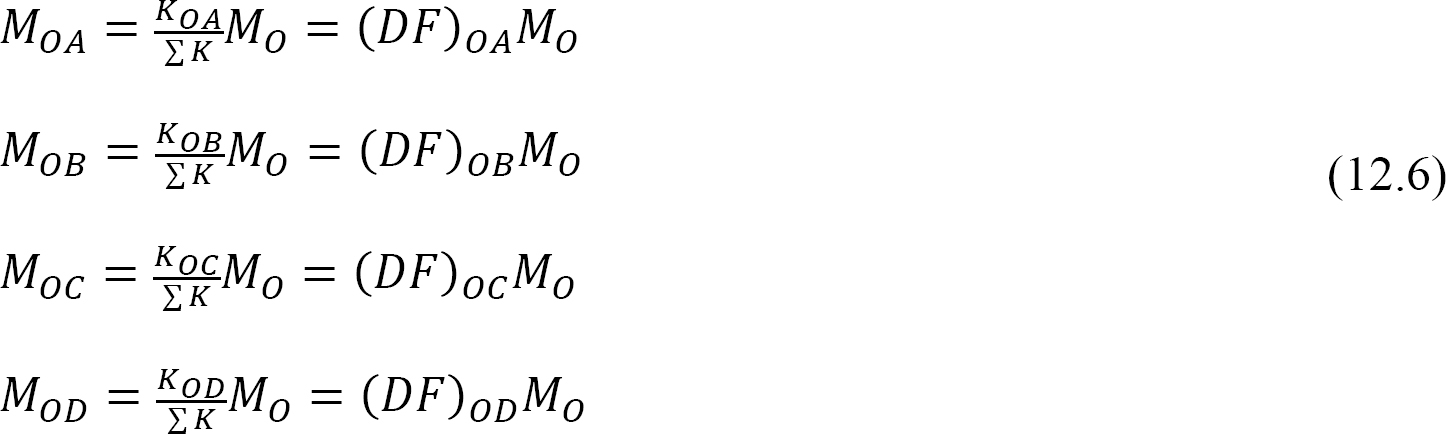
12.4 modifikation af Medlemsstivhed
undertiden kan iterationsprocessen i momentfordelingsmetoden reduceres markant ved at justere bøjningsstivheden for nogle medlemmer af den ubestemte struktur. Dette afsnit overvejer indflydelsen af en fast – og en pin-end-støtte på bøjningsstivheden af en ubestemt stråle.
sag 1: En bjælke hængslet i den ene ende og fastgjort i den anden
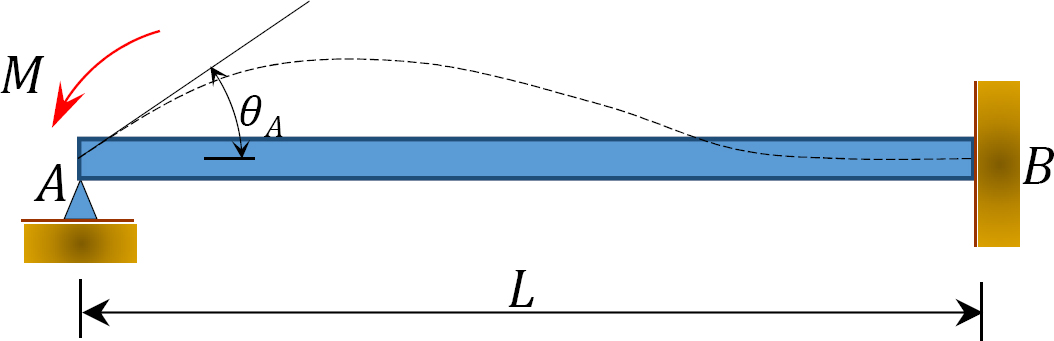
Fig. 12.4. Bjælke
overvej en bjælke hængslet i ende A og fastgjort i ende B, som vist i figur 12.4. Anvendelse af et øjeblik m roterer hængselenden med et beløb pr. Skrivning af hældningsafbøjningsligningen for enden A af medlemmet og bemærker, at 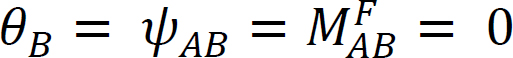 foreslår følgende:
foreslår følgende:
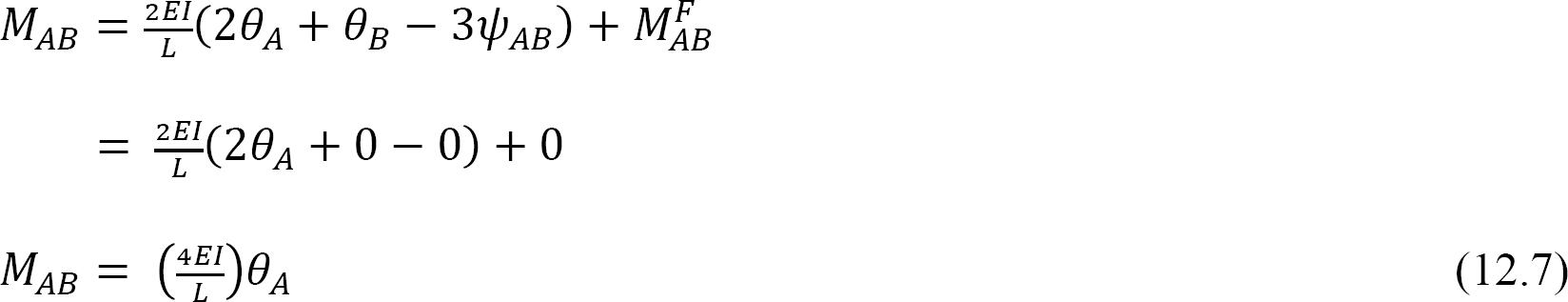
per definition er bøjningsstivheden af et strukturelt element det øjeblik, der skal anvendes på en ende af elementet for at forårsage en enhedsrotation af den ende. Det følgende udtryk for bøjningsstivheden for elementet med en fast fjern ende udtrykkes som følger, når man udskifter Prista = 1 i ligning 12.7:

per definition bestemmes den relative bøjningsstivhed af et medlem ved at dividere bøjningsstivheden af medlemmet med 4E. opdeling af ligningen 12,8 med 4E antyder følgende udtryk for relativ stivhed for den sag, der overvejes:

sag 2: en bjælke hængslet i begge ender
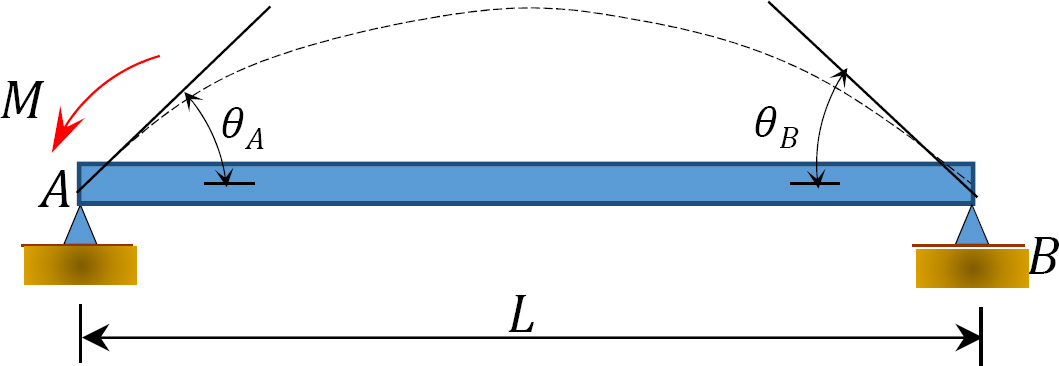
Fig. 12.5. Simpelthen understøttet stråle.
anvendelse af et øjeblik M i enden a af den simpelthen understøttede stråle vist i figur 12.5 roterer strålen med en vinkel, der er rettet mod den hængslede ende. Anvendelse af den modificerede hældningsafbøjningsligning afledt i afsnit 11.4 i kapitel 11 og bemærker, at 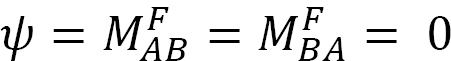 antyder følgende udtryk for øjeblikket i den hængslede ende, hvor belastningen påføres:
antyder følgende udtryk for øjeblikket i den hængslede ende, hvor belastningen påføres:
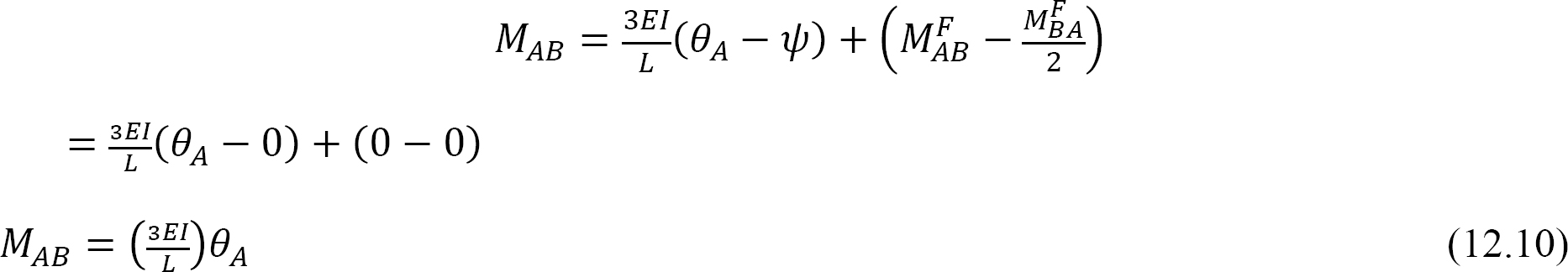
substitution af Karra = 1 i ligning 12.10 antyder følgende udtryk for bøjningsstivheden for et medlem med en hængslet fjern ende:

den relative stivhed for et element med en hængslet fjernende opnås ved at dividere ligning 12.11 med 4E som følger:

sammenligning af ligninger 12.12 og 12.9 antyder, at et medlem med en hængslet fjern ende er tre fjerdedele så stiv som et medlem med samme geometri, men fastgjort i den fjerne ende. Denne etablerede kendsgerning kan betydeligt reducere antallet af iteration ved analyse af bjælker eller rammer med en hængslet fjern ende ved hjælp af metoden til momentfordeling. I sådanne tilfælde justeres den relative stivhed af strålen i den nærmeste ende først i henhold til ligning 12.12, og dens fordelingsfaktor beregnes med den justerede stivhed. Under balanceringsoperationen vil den nærmeste ende blive afbalanceret kun en gang uden yderligere overførsel af øjeblikke fra eller til dens ende.
12.5 analyse af ubestemte bjælker
proceduren for analyse af ubestemte bjælker ved hjælp af momentfordelingsmetoden opsummeres kort som følger:
fremgangsmåde til analyse af ubestemte bjælker ved Momentfordelingsmetoden
•Beregn de faste slutmomenter for medlemmer, forudsat at leddene er fastspændt mod rotation.
•Beregn fordelingsfaktoren for hvert af de medlemmer, der er forbundet ved leddet
•Beregn det ubalancerede øjeblik ved hvert led og fordel det samme til enderne af medlemmer, der er forbundet ved det led.
•Overfør halvdelen af det distribuerede øjeblik til de andre ender af medlemmerne.
•Tilføj eller træk disse sidstnævnte øjeblikke (øjeblikke opnået i trin tre og fire) til eller fra de oprindelige faste øjeblikke.
•Anvend de bestemte slutmomenter ved leddene i den givne struktur.
•tegn frikropsdiagrammet for hvert spænd af den givne stråle, der viser belastninger og øjeblikke ved leddene opnået ved momentfordelingsmetoden.
•Bestem støttereaktionerne for hvert span.
•beregne og konstruere forskydning kraft og bøjning moment diagrammer for hver span.
•Tegn et bøjningsmoment og et forskydningskraftdiagram for den givne stråle ved at kombinere diagrammerne i trin 9.
eksempel 12.1
ved hjælp af momentfordelingsmetoden bestemmes slutmomenterne og reaktionerne ved bjælkens understøtninger vist i figur 12.6 a. tegn forskydningskraften og bøjningsmomentdiagrammerne. Ei = konstant.
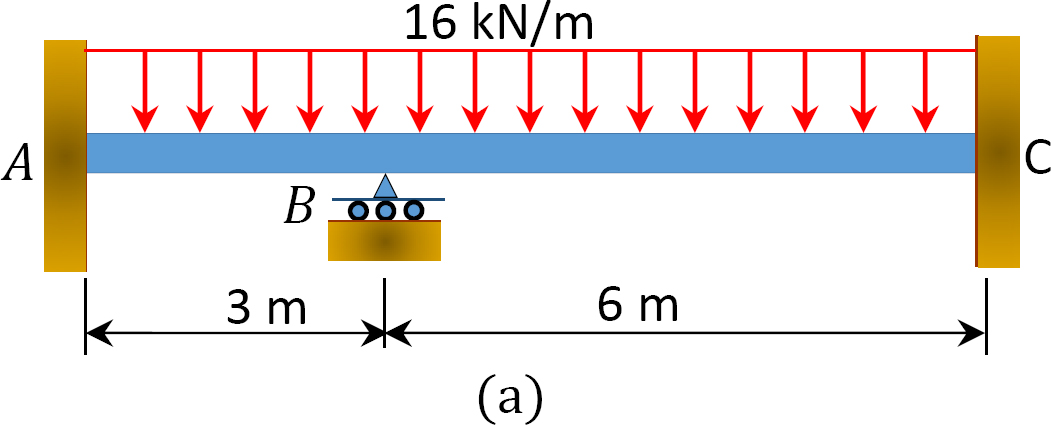
Fig. 12.6. Stråle.
løsning
fast slutmoment.
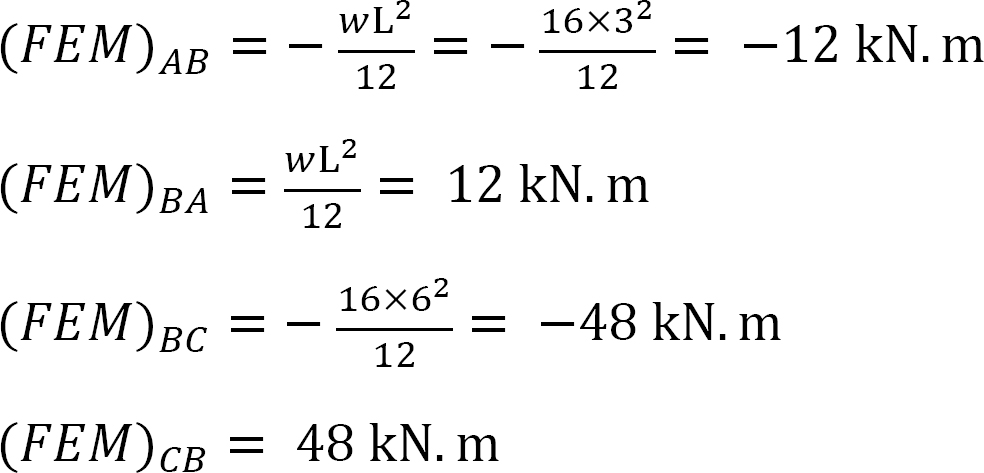
stivhed faktor.
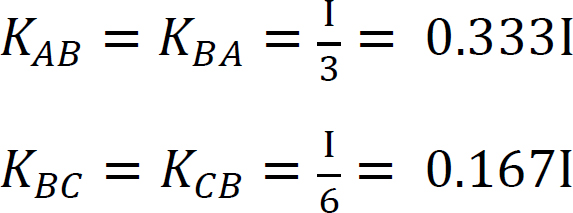
fordeling faktor.
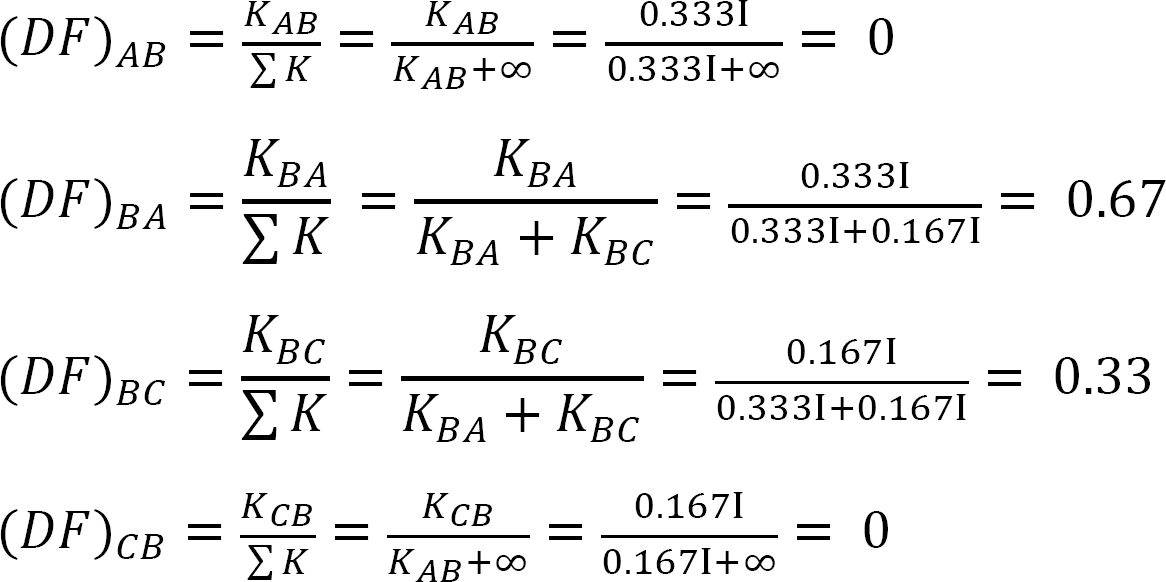
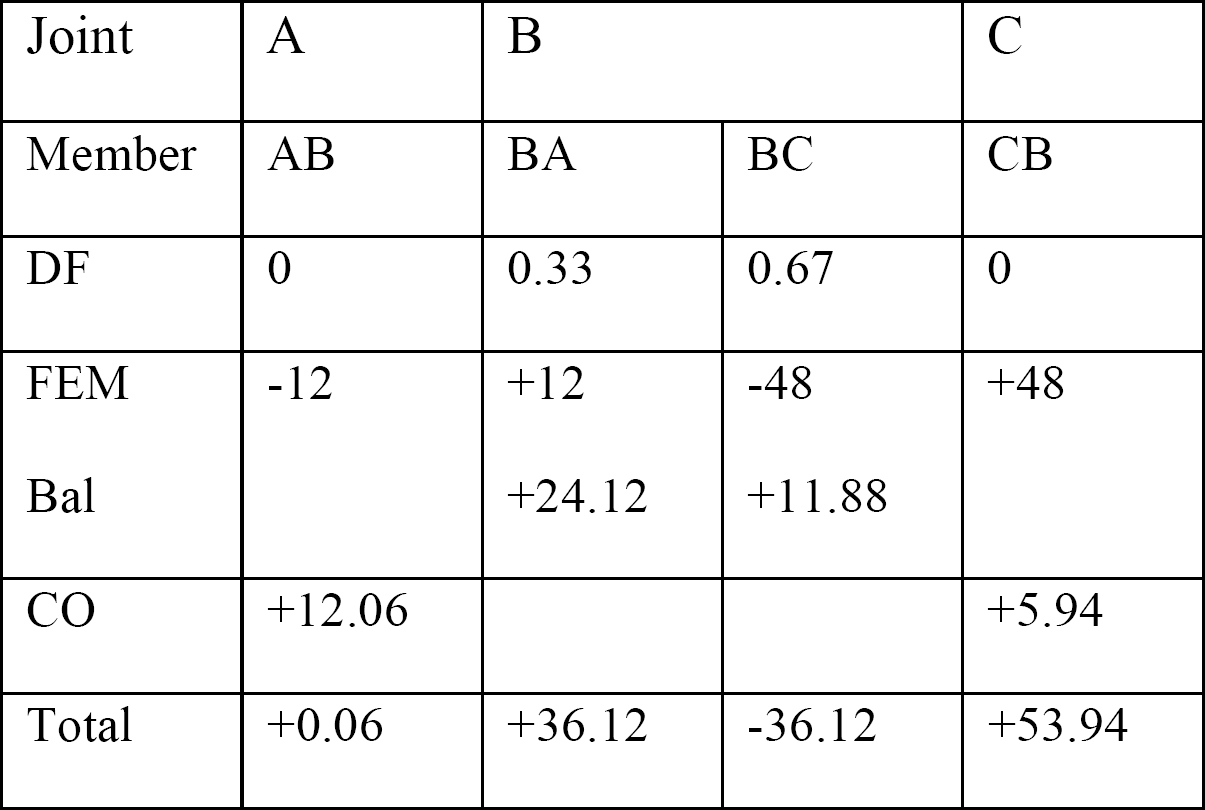
tabel 12.1. Fordeling tabel.
forskydningskraft og bøjningsmomentdiagrammer.
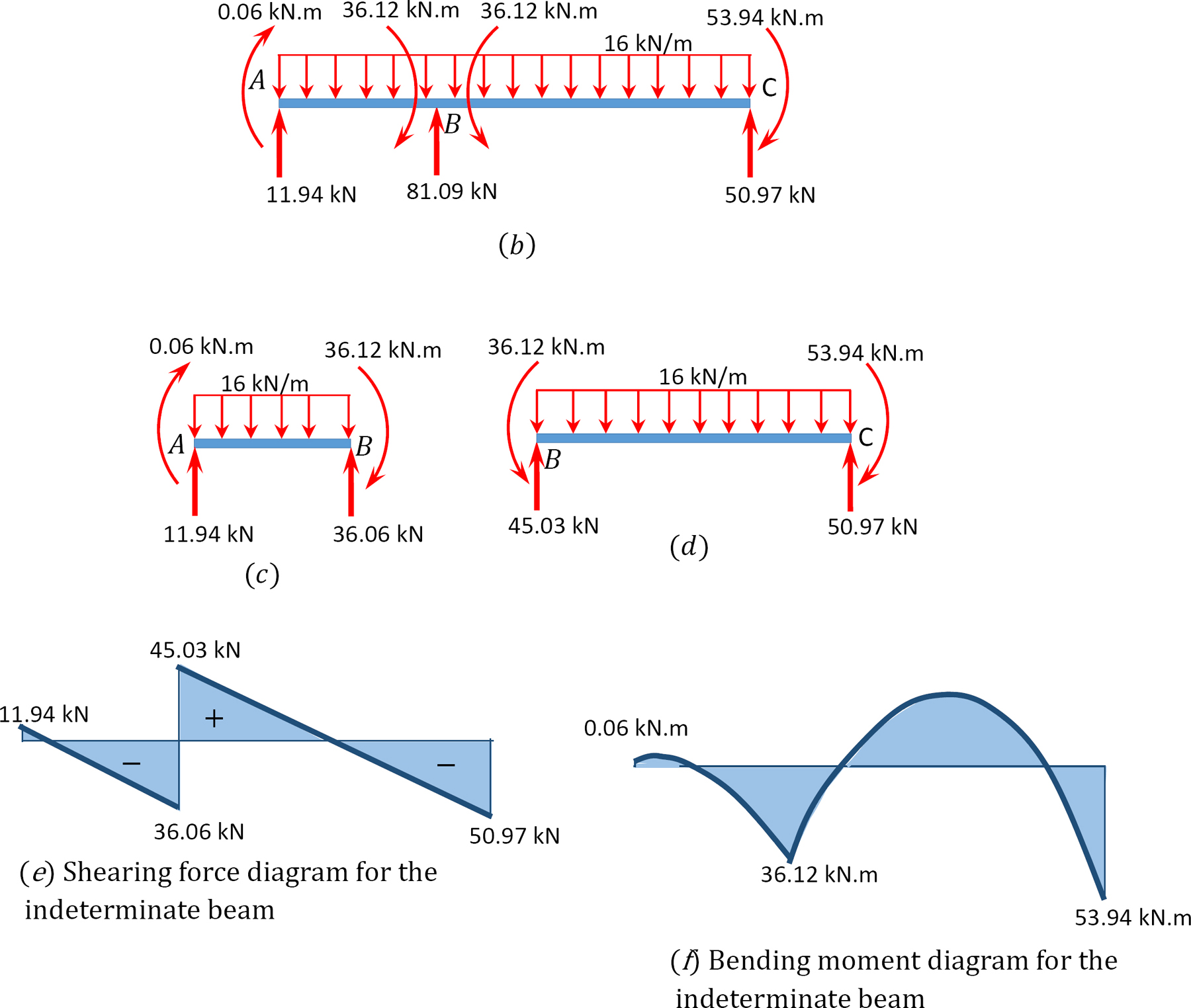
eksempel 12.2
ved hjælp af momentfordelingsmetoden bestemmes slutmomenterne og reaktionerne ved bjælkens understøtninger vist i figur 12.7 a. tegn forskydningskraften og bøjningsmomentdiagrammerne.
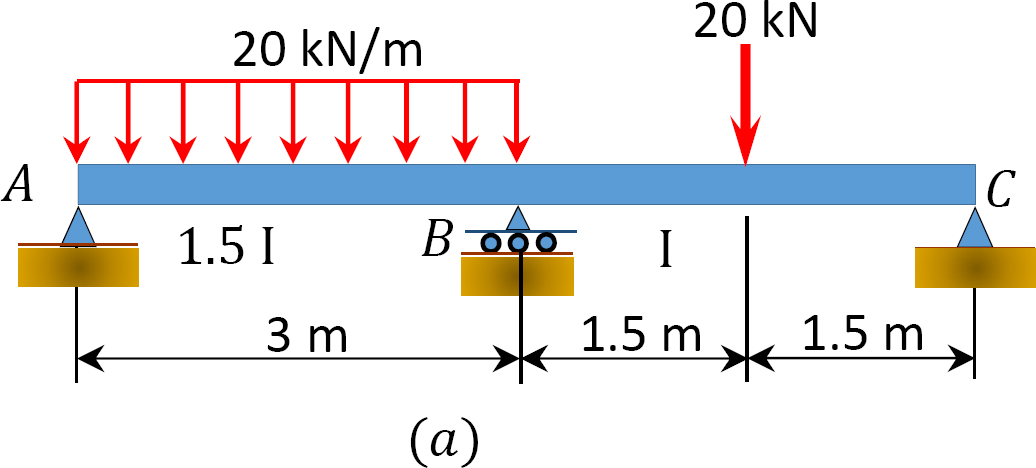
Fig. 12.7. Stråle.
løsning
fast slutmoment.
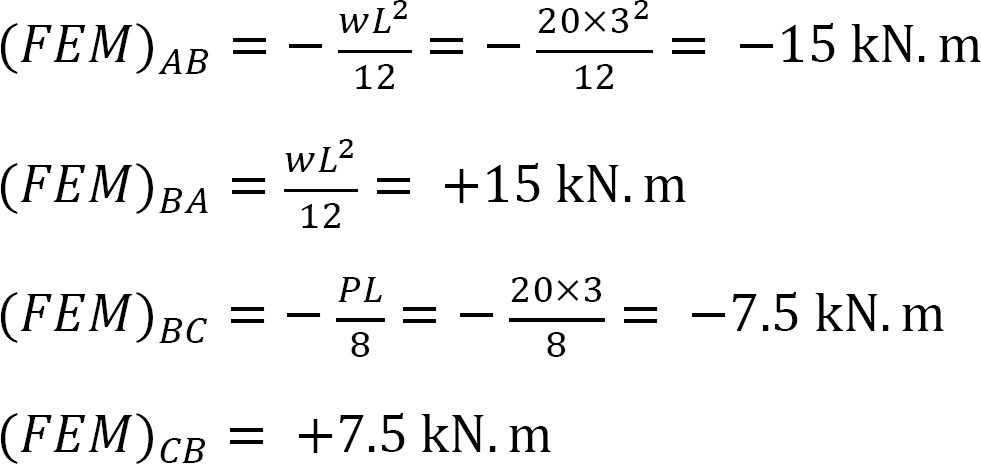
stivhed faktor.
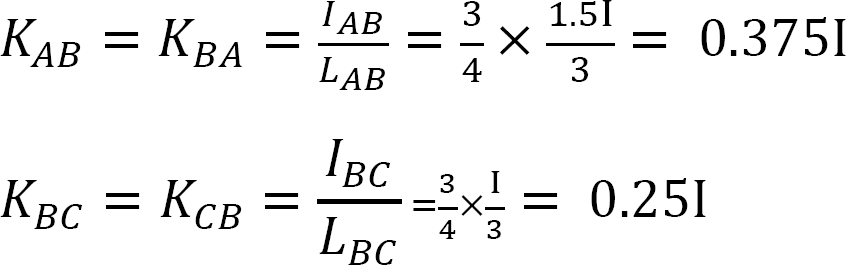
fordeling faktor.
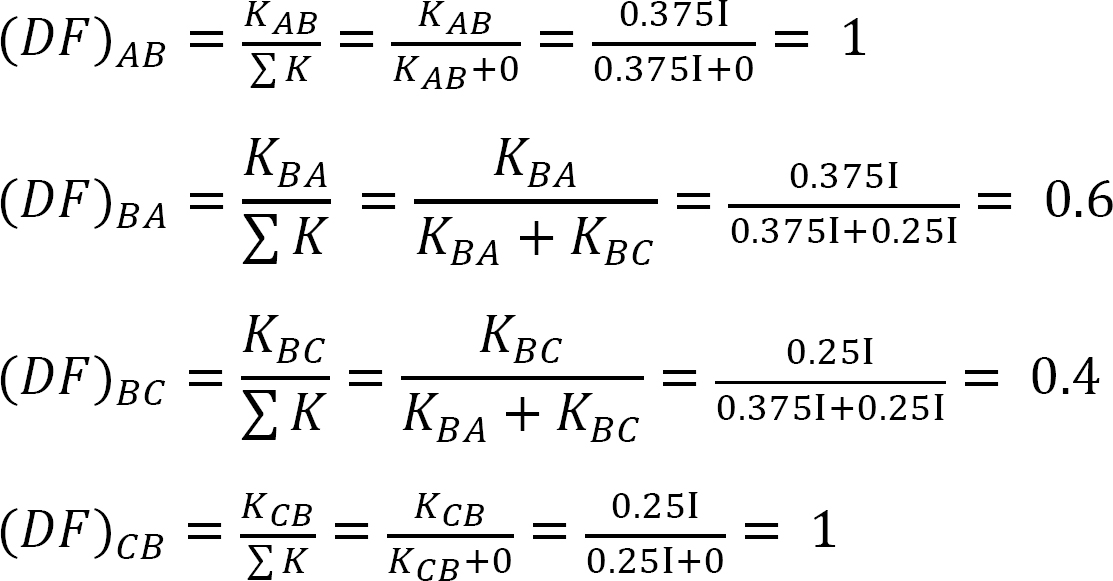
tabel 12.2. Fordeling tabel.
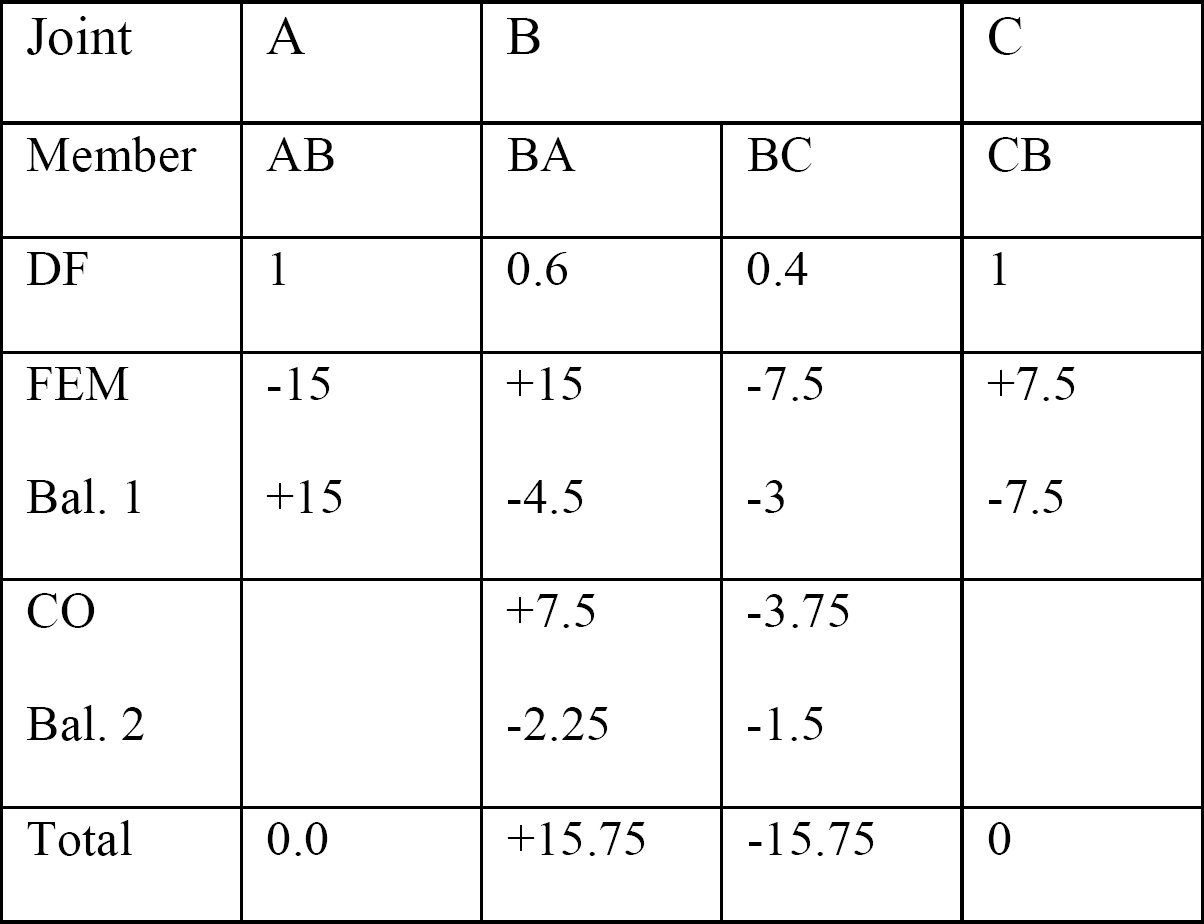
forskydningskraft og bøjningsmomentdiagrammer.
12.6 analyse af ubestemte rammer
proceduren for analyse af rammer ved hjælp af momentfordelingsmetoden afhænger af den type ramme, der analyseres. Rammer er kategoriseret som svaje – eller ikke-svaje rammer. Proceduren for analyse af ikke-svingende rammer svarer til den for ubestemte bjælker. Men for analysen af svingrammer er proceduren anderledes. Der er to faser involveret i analysen af svajerammer, nemlig analyserne ikke-svajende fase og svaj-fase. Disse trin er beskrevet nedenfor.
Procedure for analyse af ubestemte Svingrammer ved Momentfordelingsmetoden
A. ikke-svingende sceneanalyse
•Antag først eksistensen af en imaginær prop, der forhindrer rammen i at svinge.
•Beregn de vandrette reaktioner ved rammens understøtninger og bemærk forskellen.
B. Svaje fase analyse
•Antag vilkårlige øjeblikke til at handle på kolonnerne i rammen. Størrelsen af disse øjeblikke vil variere fra kolonne til kolonne i forhold til 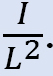
•værdier antages for M2, og M1 bestemmes.
•de vilkårlige øjeblikke fordeles derefter som for den ikke-svingende tilstand
•Beregn størrelsen af de vandrette reaktioner ved understøtningerne for svingtilstanden. Summeringen af disse reaktioner giver den vilkårlige forskydningskraft Y.
•Bestem forholdet 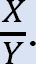 dette forhold kaldes svingfaktoren.
dette forhold kaldes svingfaktoren.
•brug svingfaktoren til at multiplicere de distribuerede øjeblikke af svajen. Dette giver det korrigerede øjeblik for svajen.
•de sidste øjeblikke for rammen er summen af de øjeblikke, der er opnået i det ikke-svingende Stadium og det korrigerede øjeblik for svingetrinnet.
eksempel 12.3
brug momentfordelingsmetoden til at bestemme medlemmernes slutmomenter for rammen vist i figur 12.8. Ei = konstant.
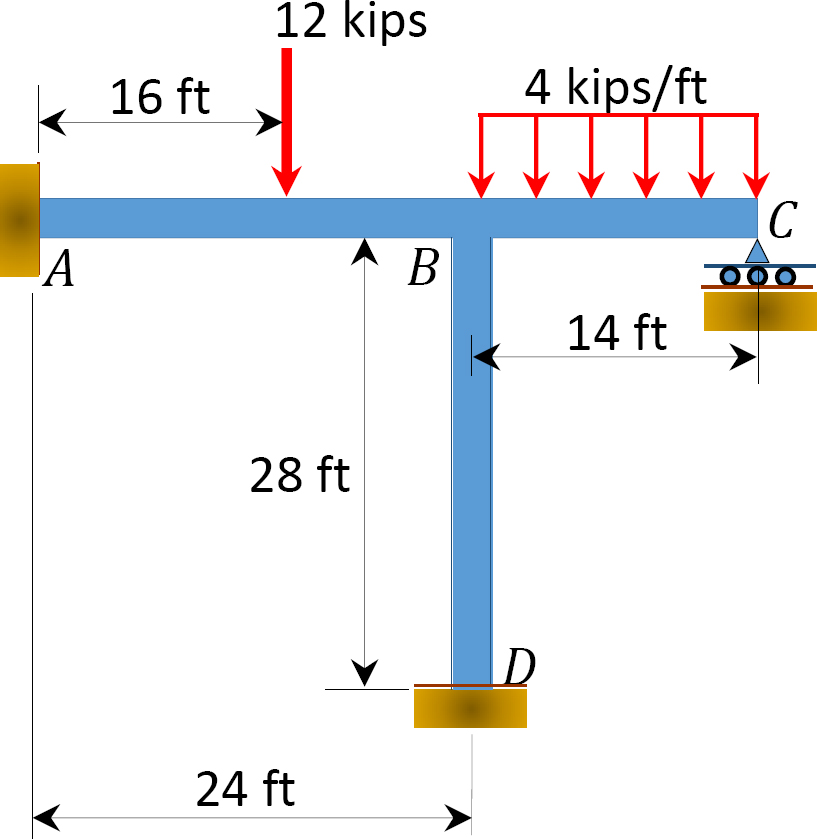
Fig. 12.8. Ramme.
løsning
fast slutmoment.
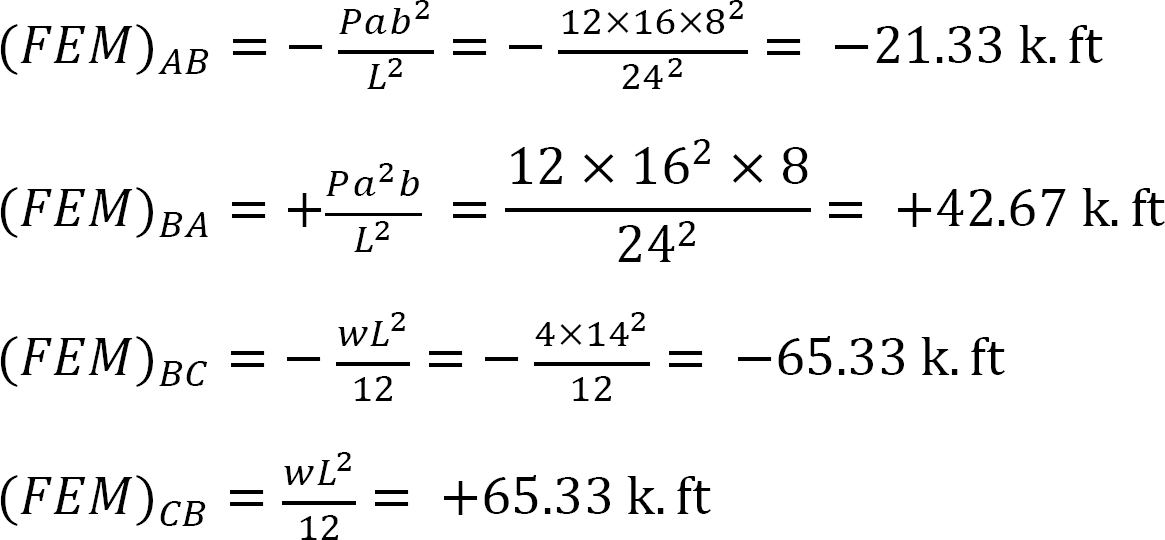
stivhed faktor.
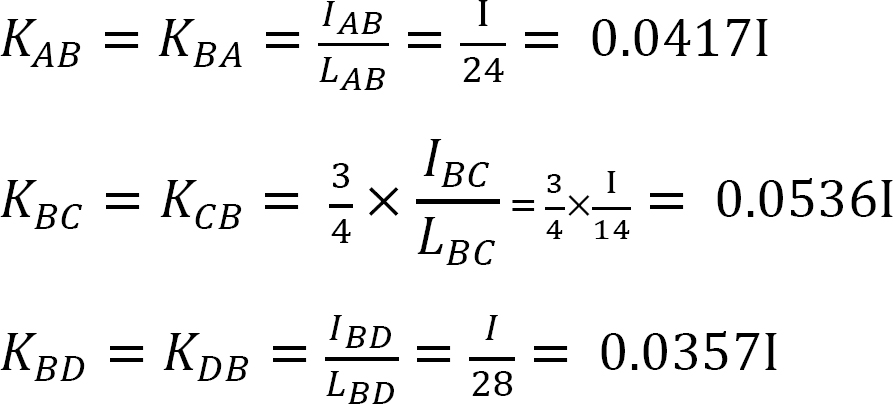
fordeling faktor.
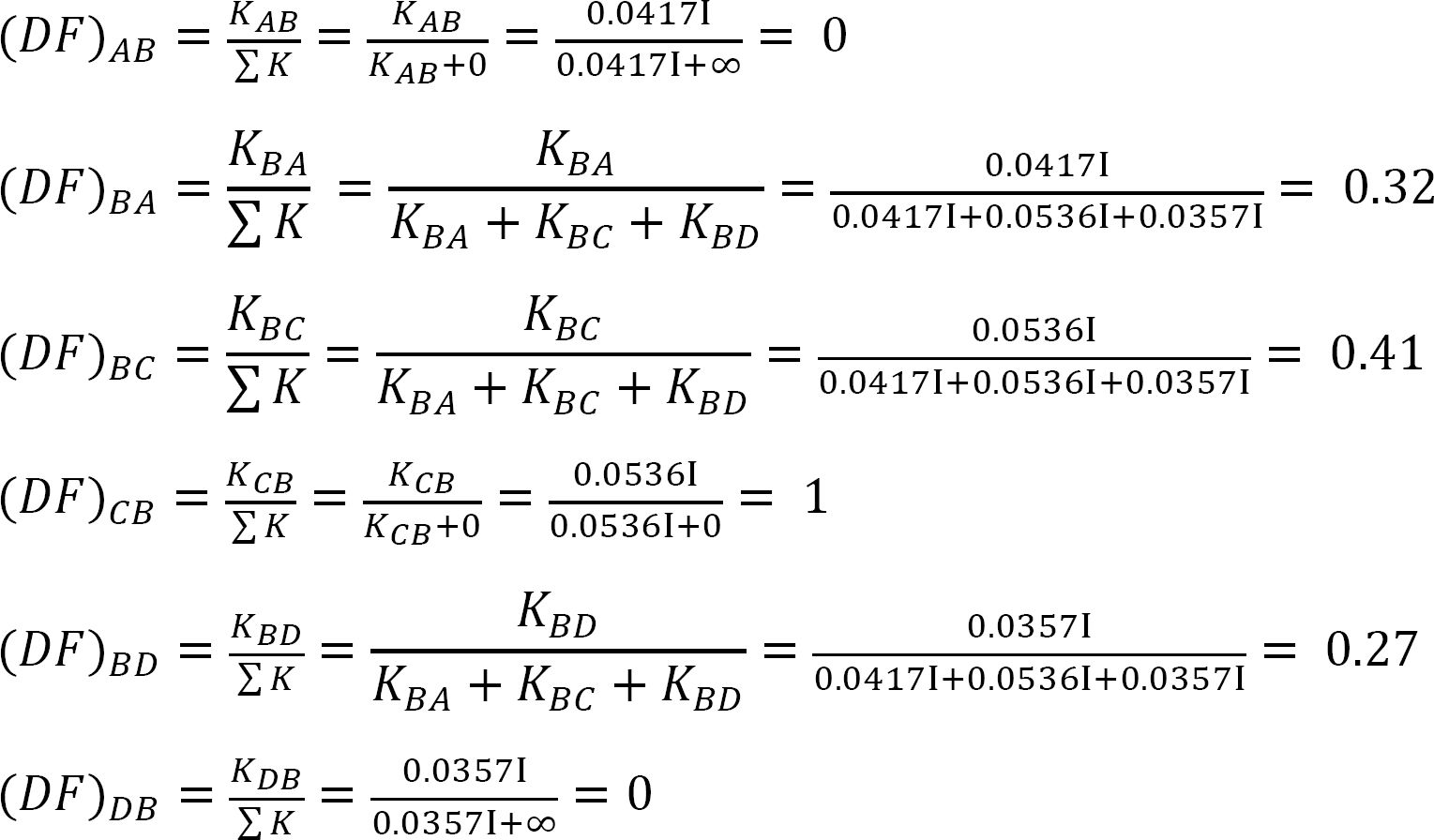
tabel 12.3. Fordeling tabel.
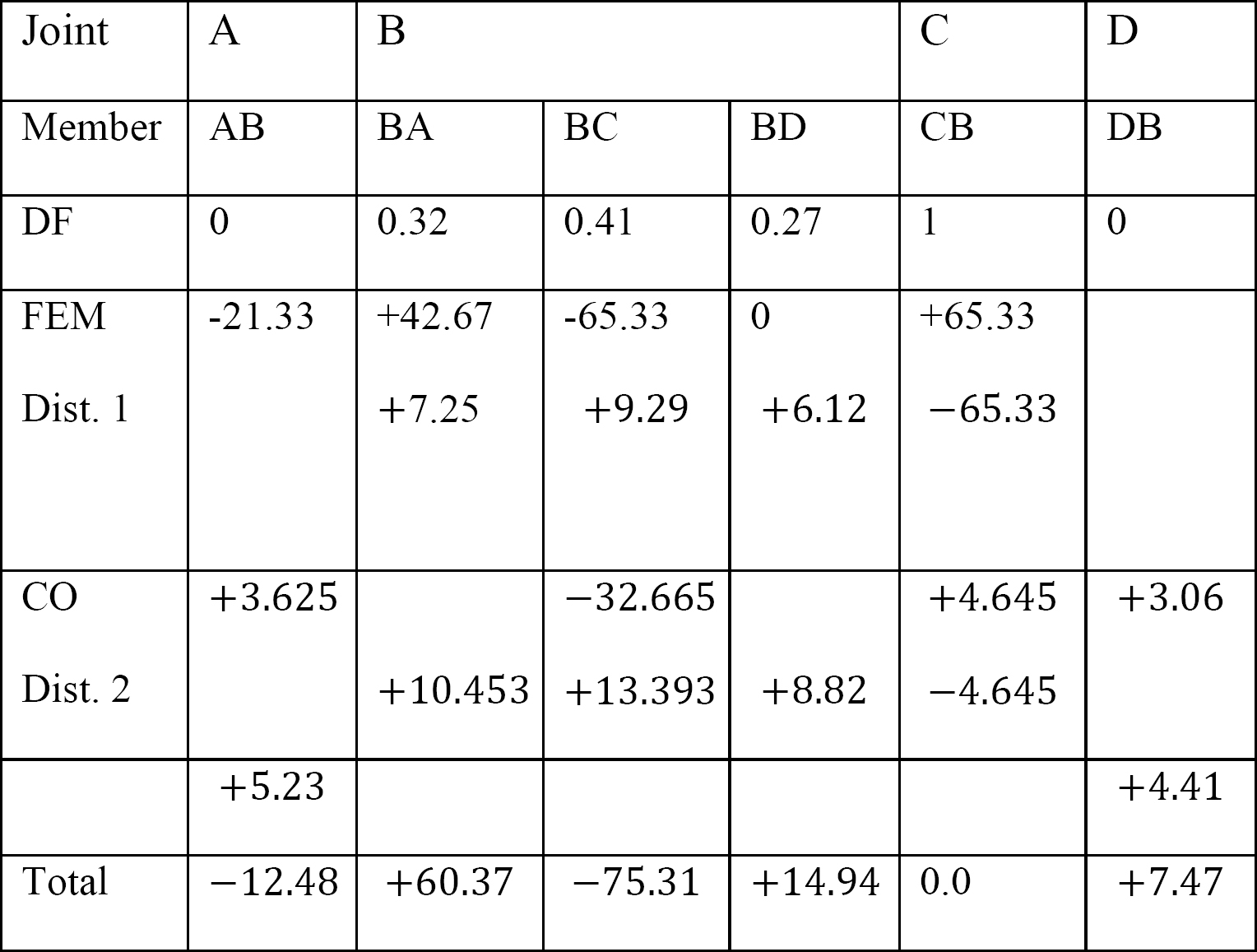
sidste medlems slut øjeblikke.
udskiftning af de opnåede værdier af Ek-karb, Ek-karb og EK-karb i medlemmets slutmomentligninger antyder følgende:
MAB = -12.48 k. karb
MBA = +60.37 k. karb
MBC = -75.31 k. karb
MBD = +14,94 k. ft
MCB = 0
MDB = +7,47 k. ft
eksempel 12.4
ved hjælp af momentfordelingsmetoden skal du bestemme slutmomenterne ved understøtningerne af rammen vist i figur 12.9. Ei = konstant.
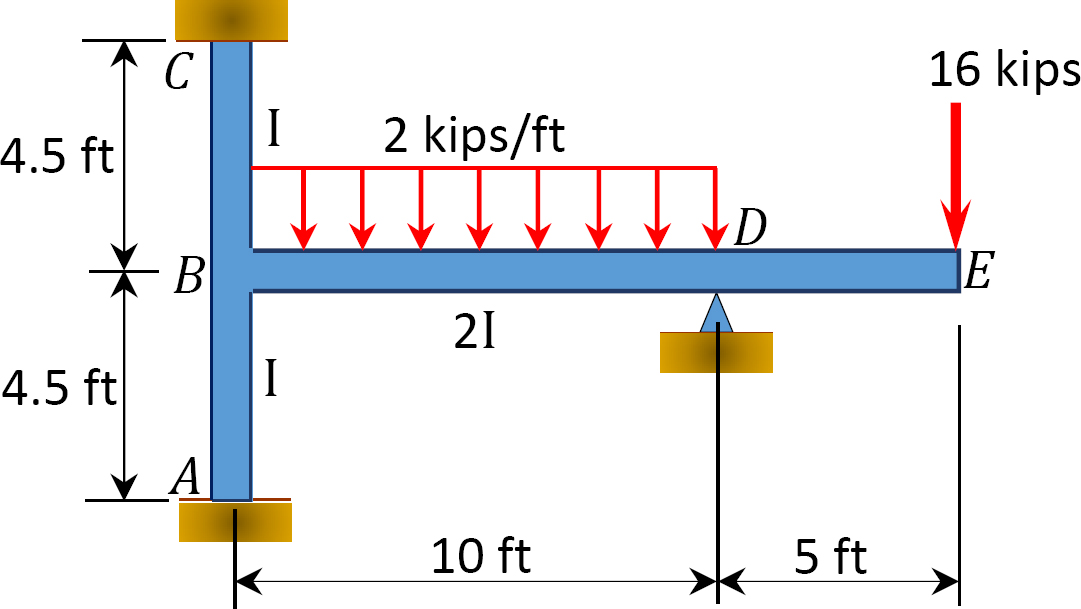
Fig. 12.9. Ramme.
løsning
fast slutmoment.
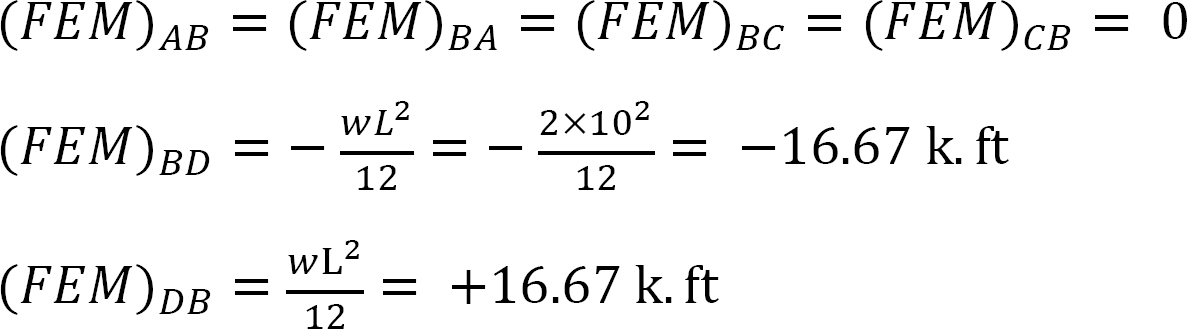
stivhed faktor.
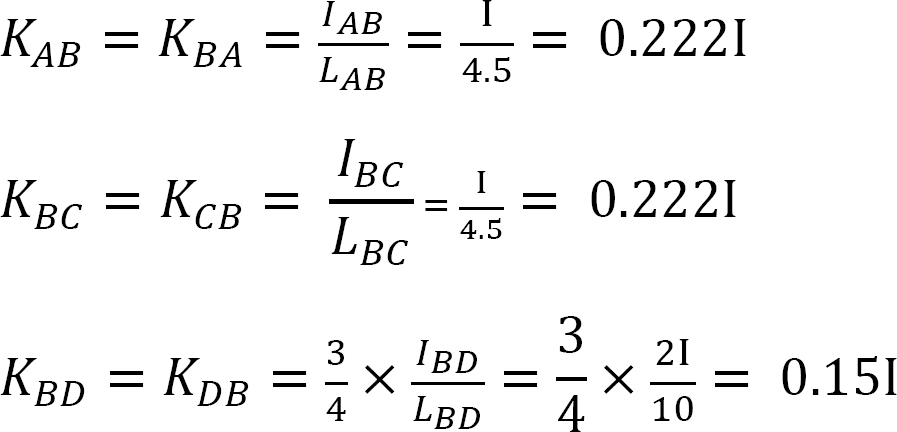
fordeling faktor.

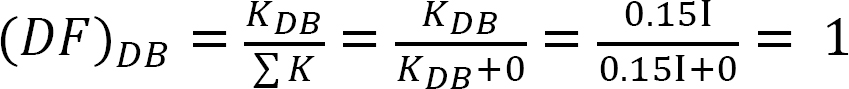
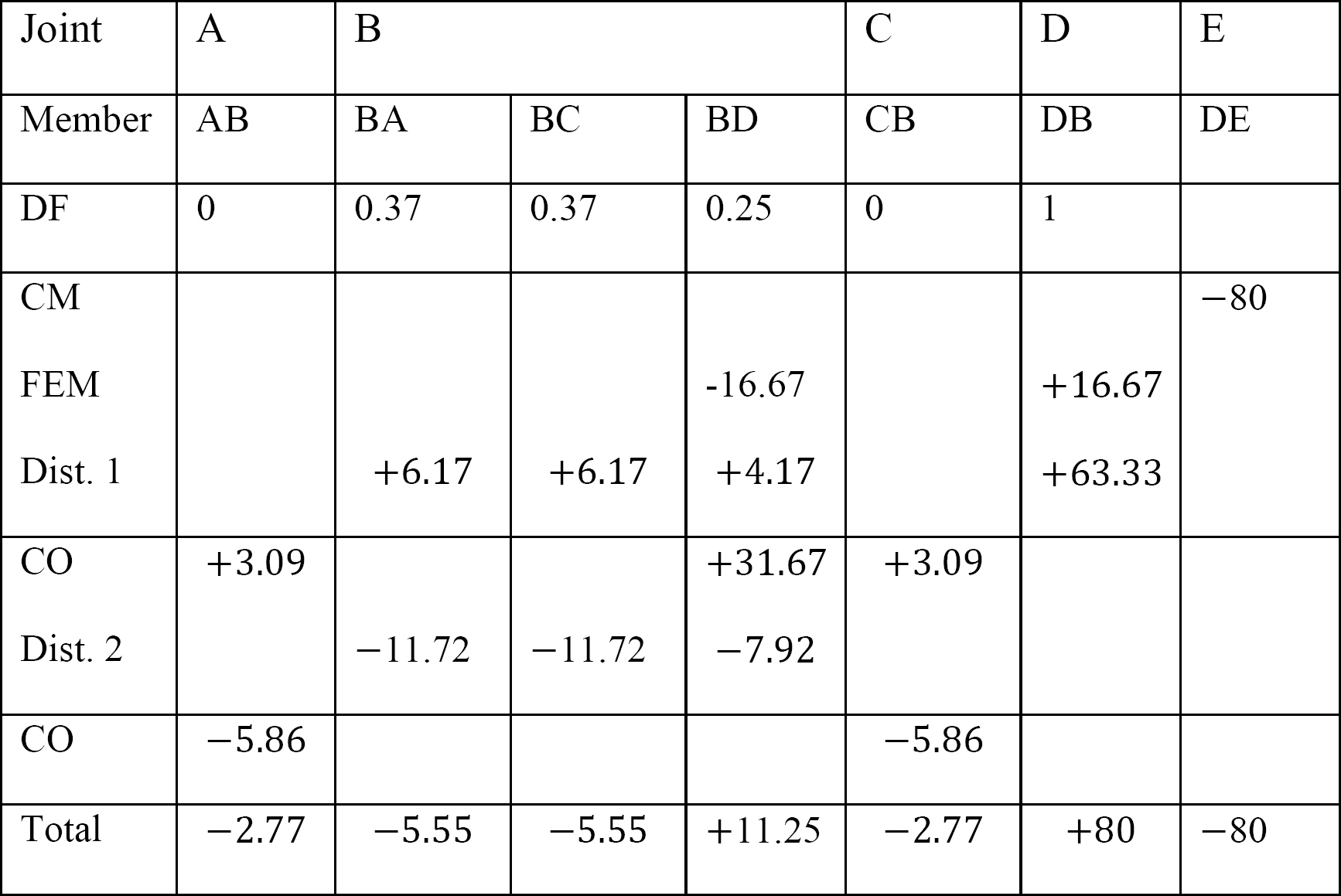
tabel 12.4. Fordeling tabel.
sidste medlems slut øjeblikke.
MAB = -2, 77 k. ft
MBA = -5, 55 k. ft
MBC = -5, 55 k. ft
MBD = +11.25 k. ft
MCB = -2.77
MDB = + 80 k. ft
MDE = -80 k. ft
eksempel 12.5
ved hjælp af momentfordelingsmetoden skal du bestemme slutmomenterne ved understøtningerne af rammen vist i figur 12.10. Ei = konstant.
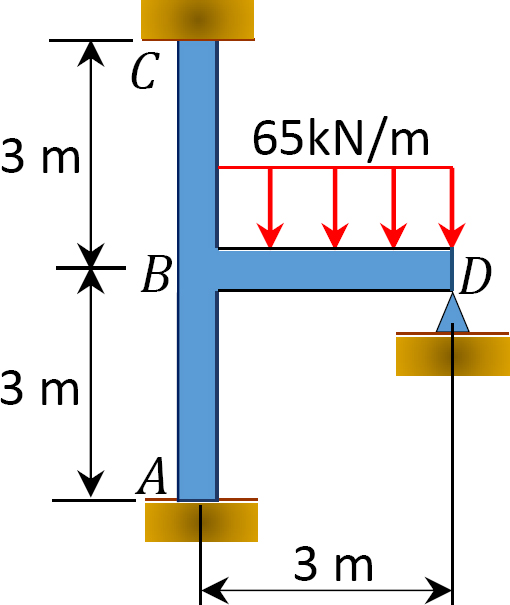
Fig. 12.10. Ramme.
løsning
fast slutmoment.
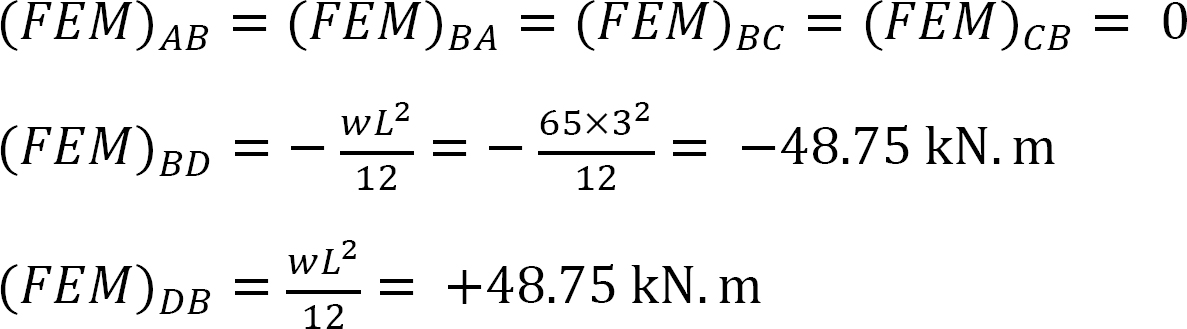
stivhed faktor.
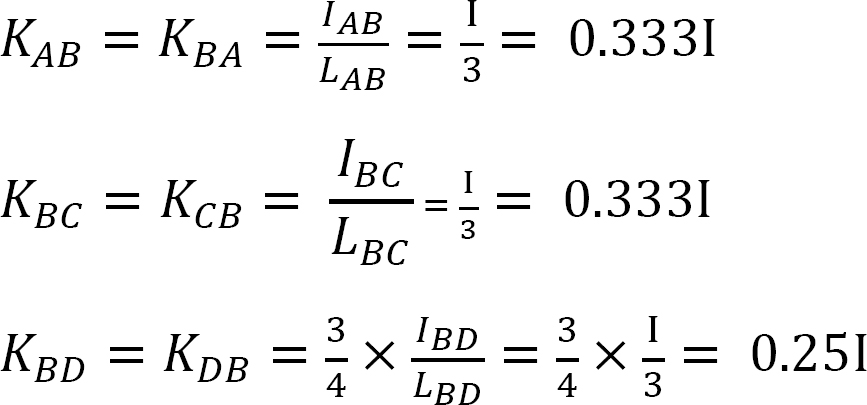
fordeling faktor.
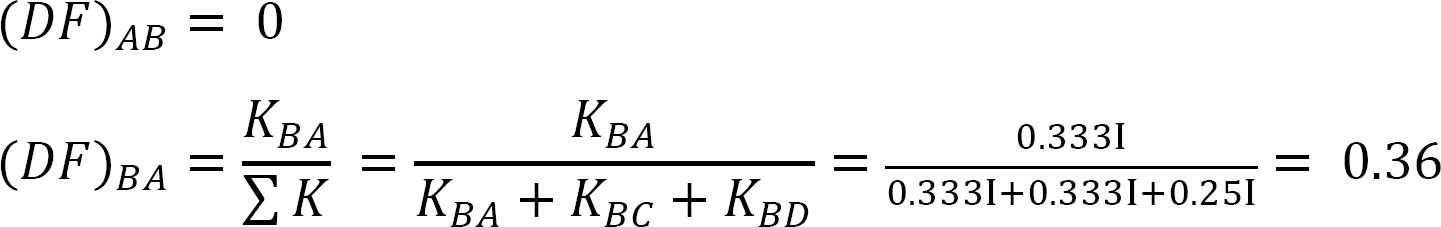

tabel 12.5. Fordeling tabel.
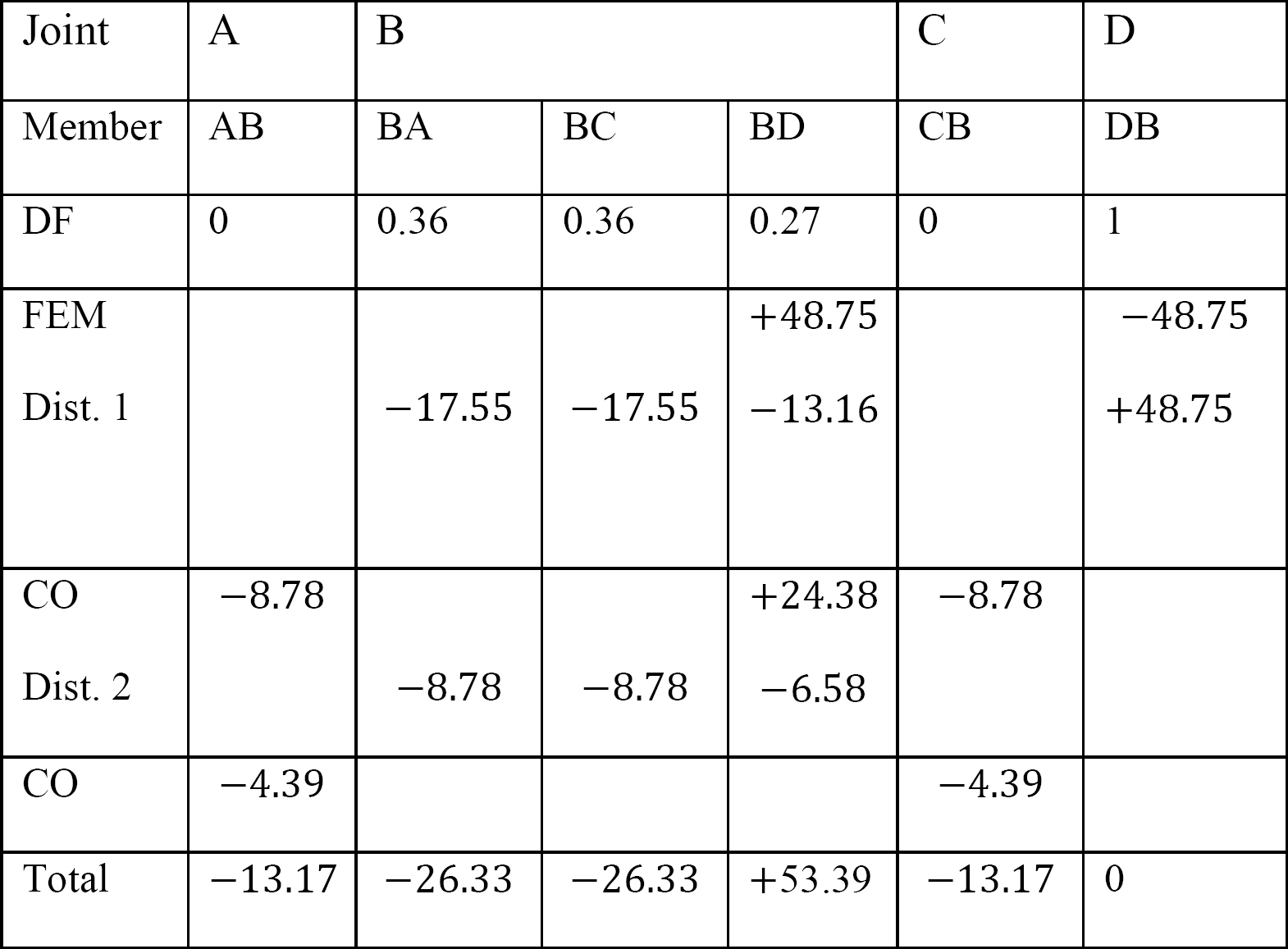
sidste medlems slut øjeblikke.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +53.39 k. ft
MCB = -13.17 k. ft
MDB = 0
eksempel 12.6
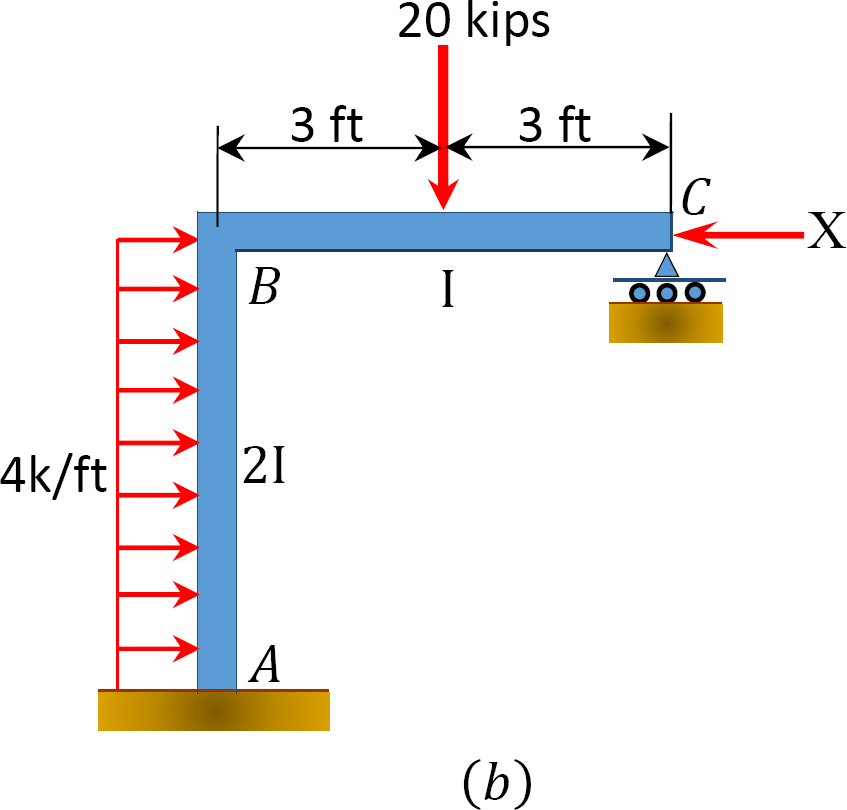
ved hjælp af momentfordelingsmetoden skal du bestemme rammens slutmomenter med sidesving vist i figur 12.11 a.
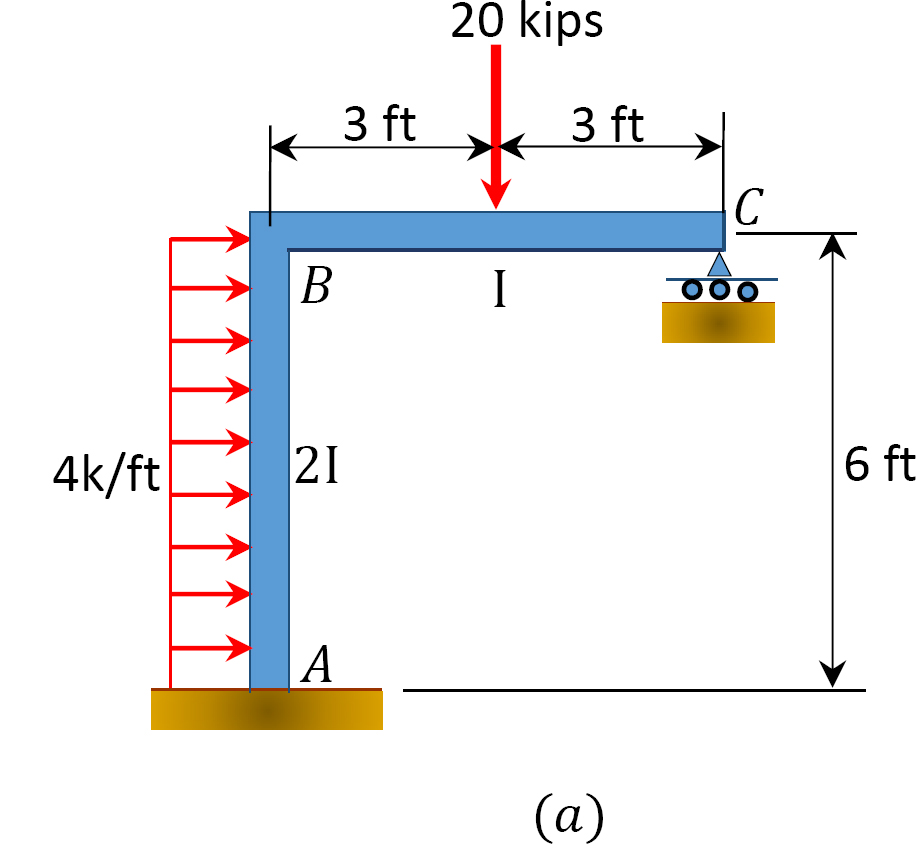
Fig. 12.11. Ramme med sidesving.
løsning
fast slutmoment.
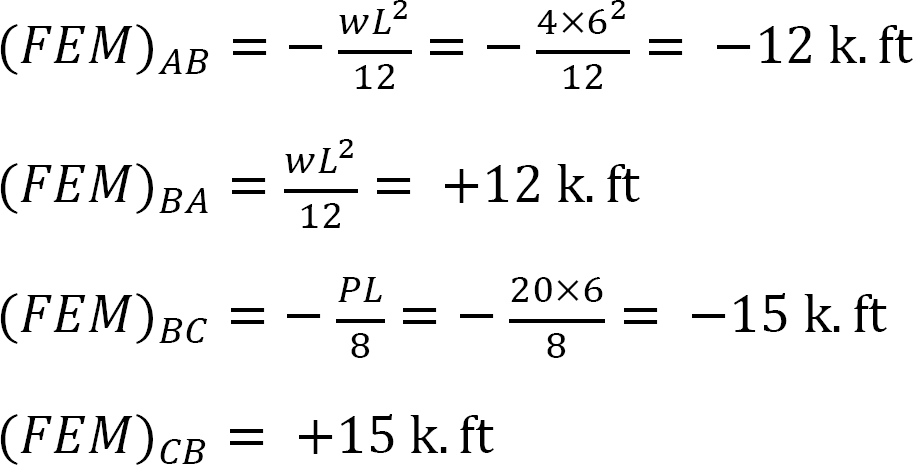
stivhed faktor.
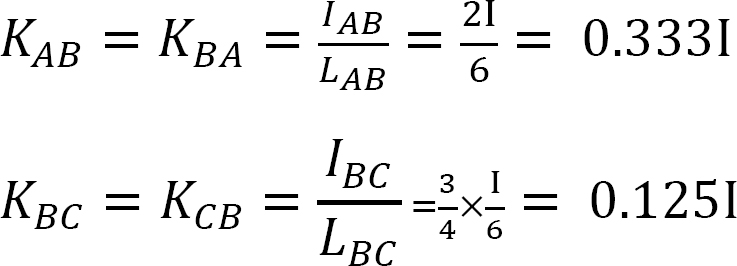
fordeling faktor.
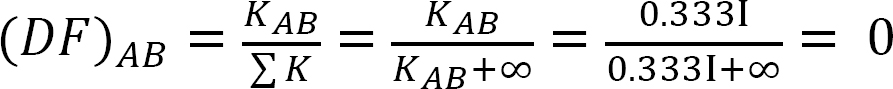

analyse af ramme uden sidesvingning.
tabel 12.6. Fordelingstabel (ingen svingramme).
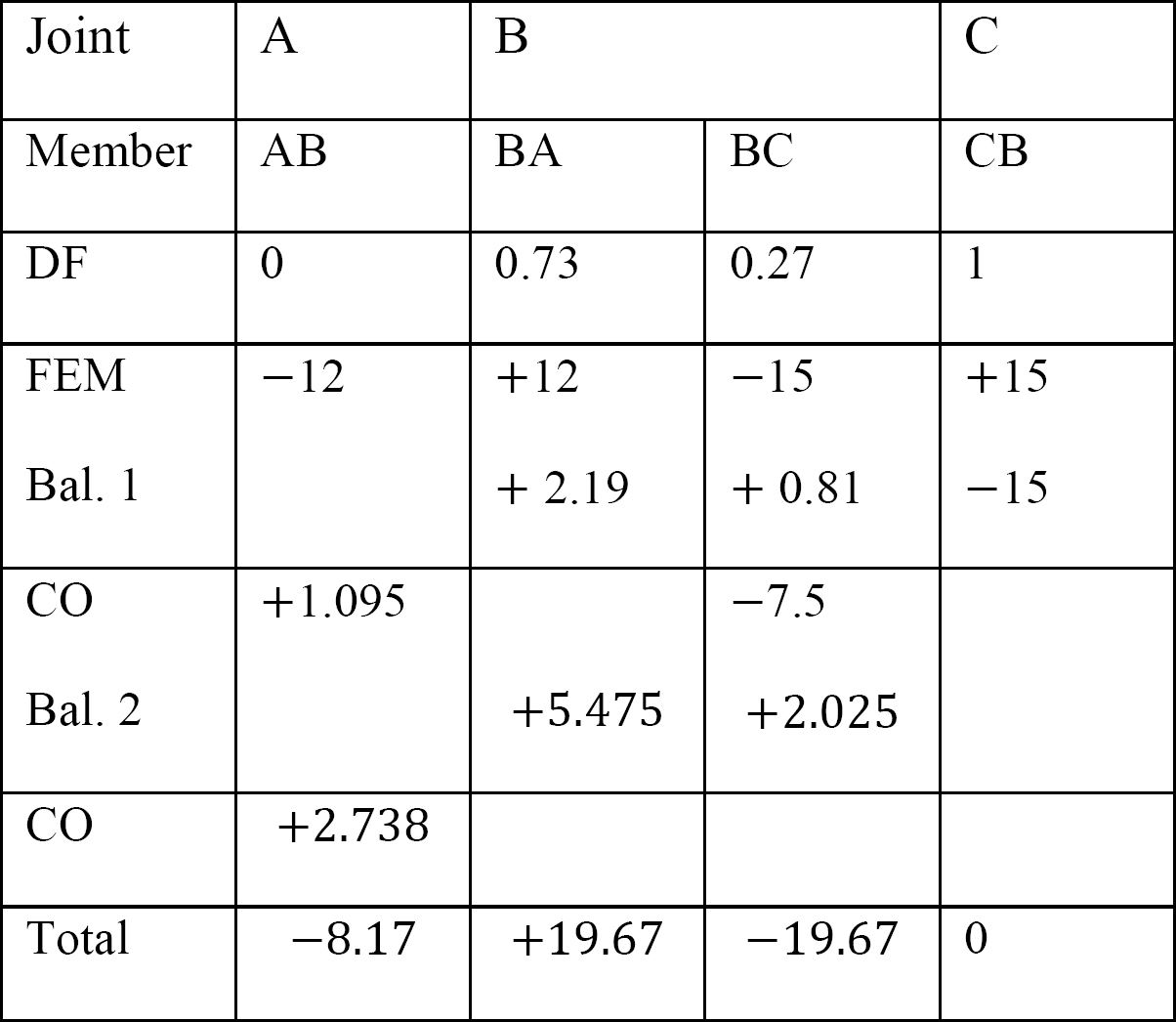
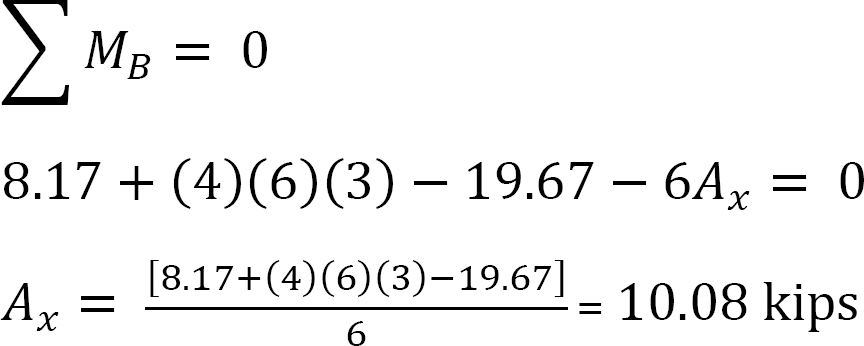
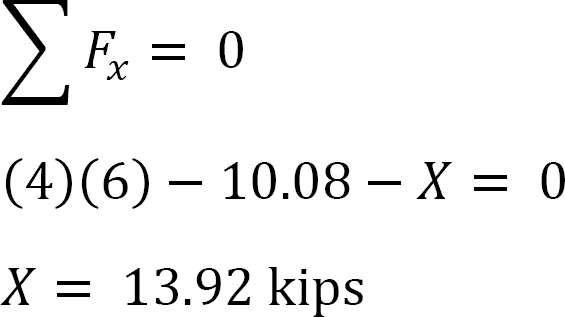
analyse af ramme med sidesvingning.
Antag at MAB = + 20 k. ft
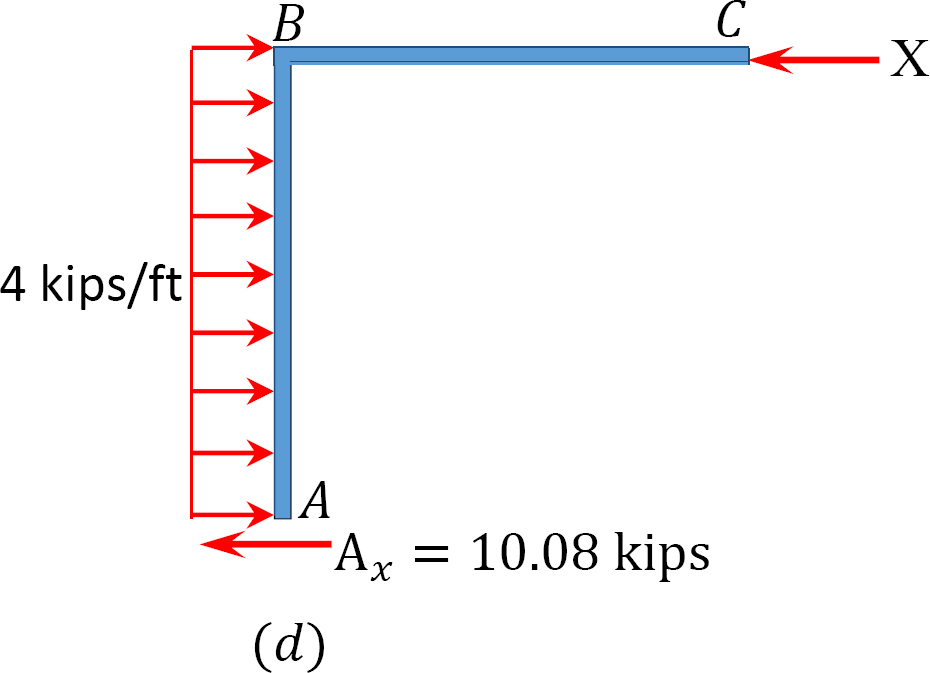
tabel 12.7. Fordelingstabel (svingramme).
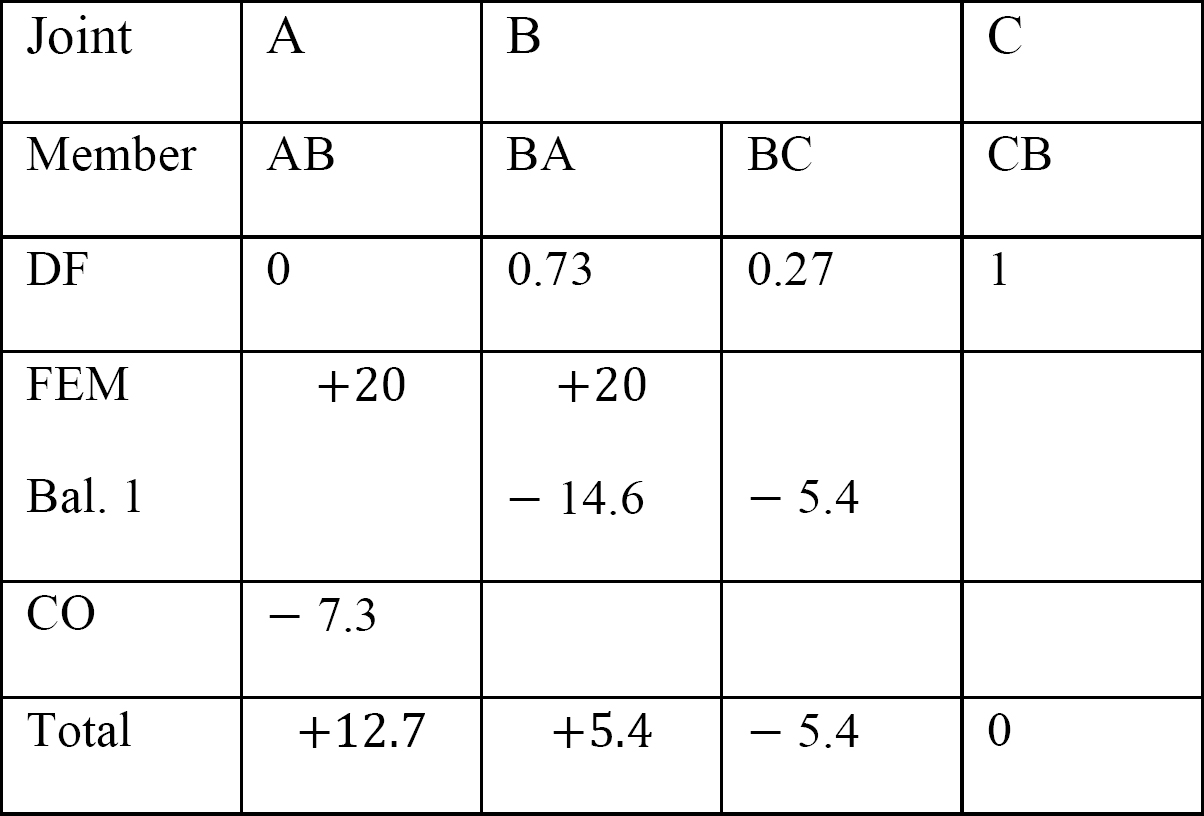
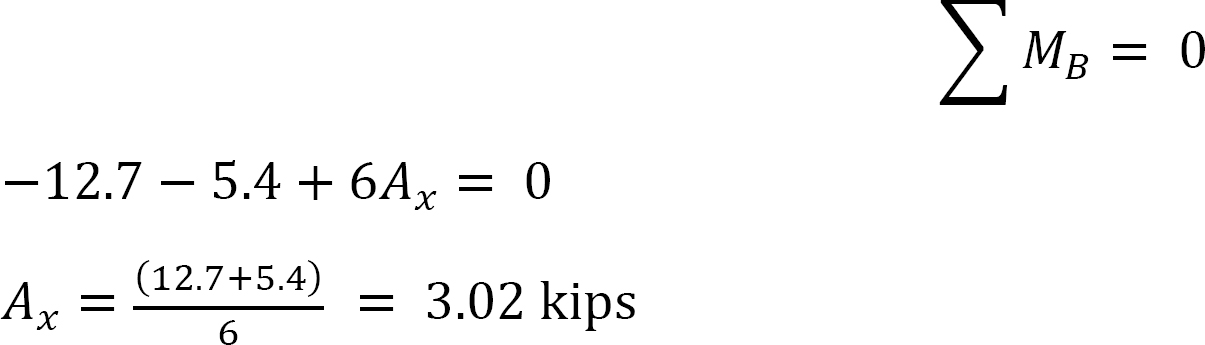
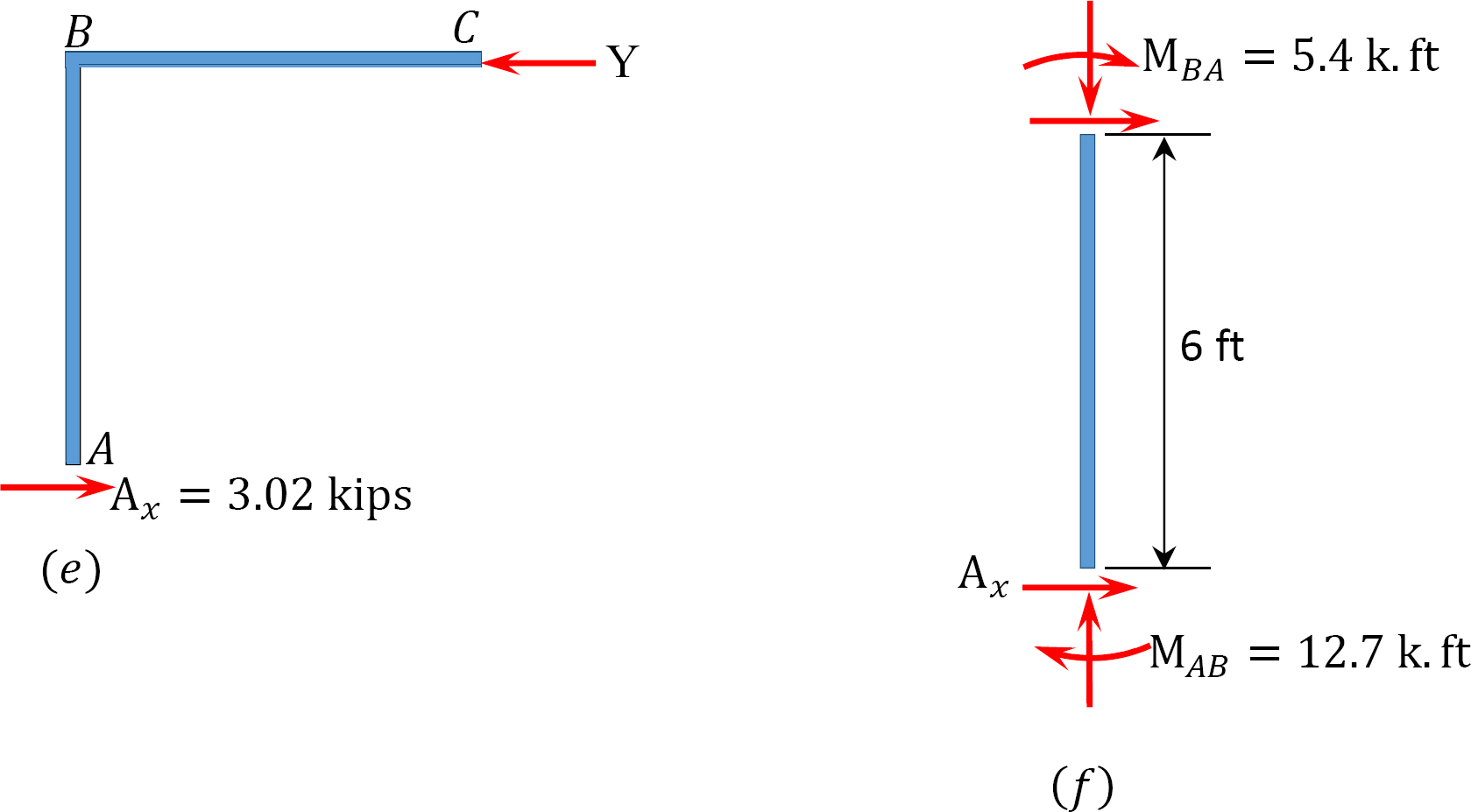
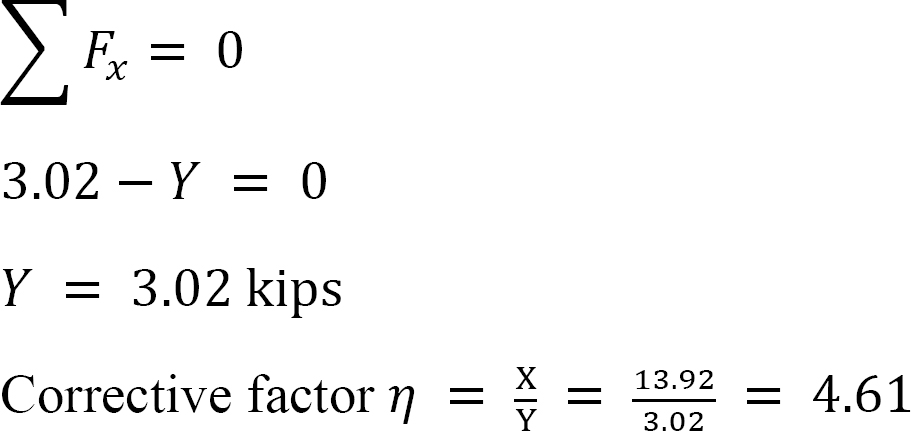
sidste ende øjeblikke.
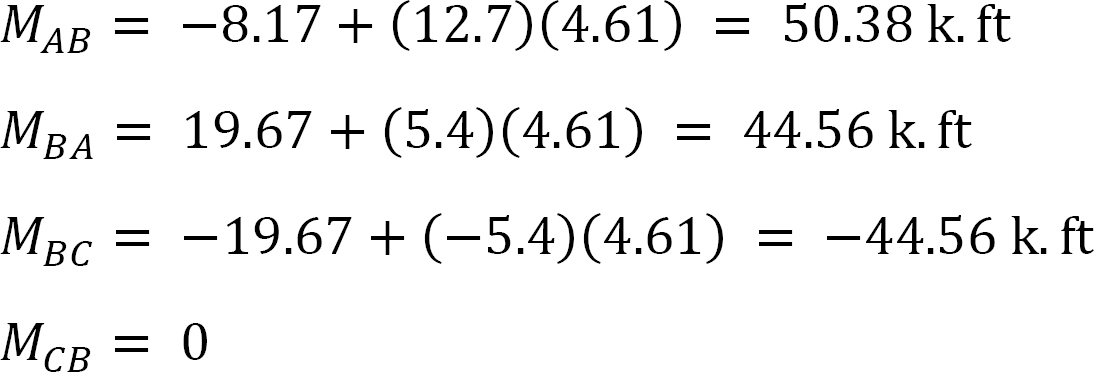
eksempel 12.7
en svingramme indlæses som vist i figur 12.12 A. ved hjælp af momentfordelingsmetoden skal du bestemme slutmomenterne for rammens medlemmer.
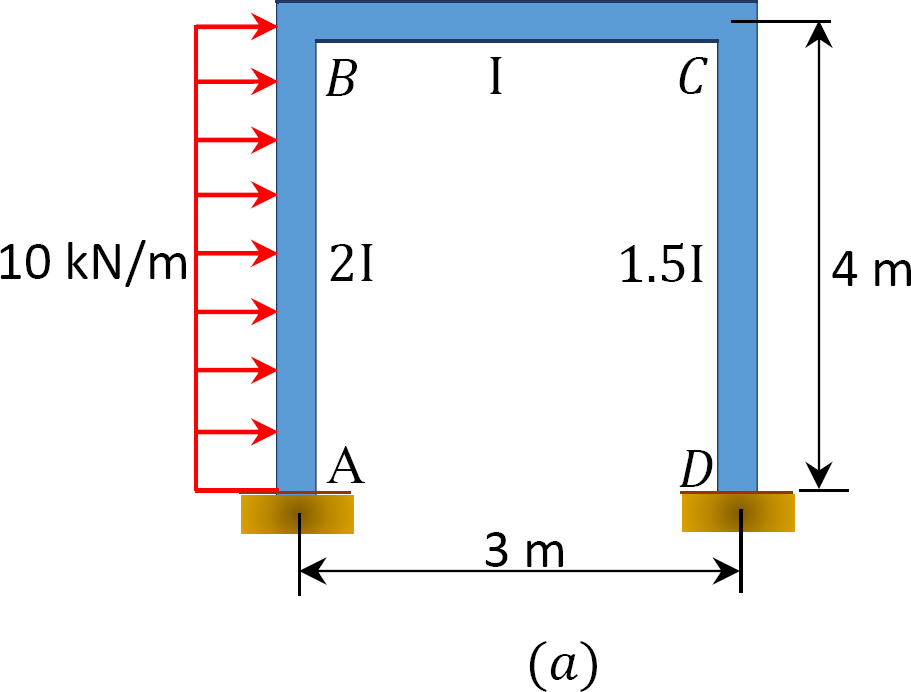
Fig. 12.12. Loaded svaje ramme.
løsning
fast slutmoment.
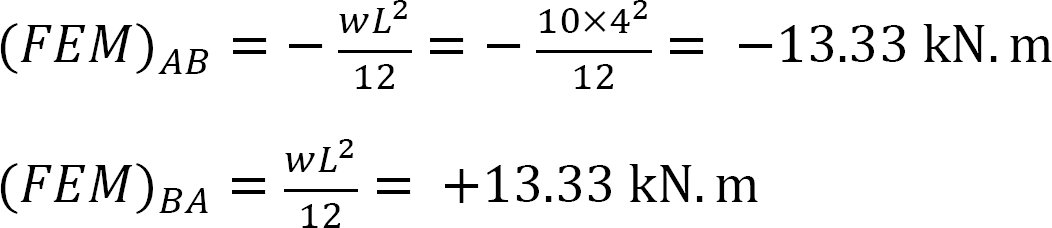
stivhed faktor.
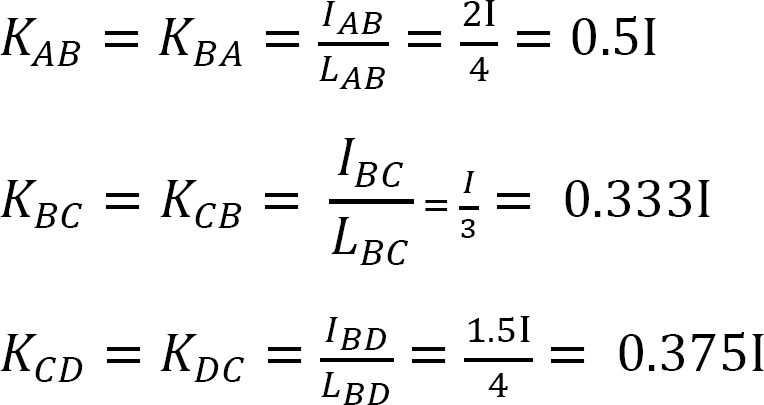
fordeling faktor.

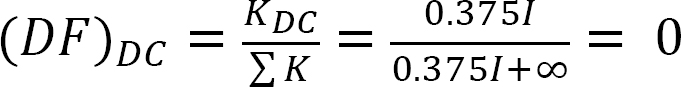
analyse af ramme uden sidesvingning.
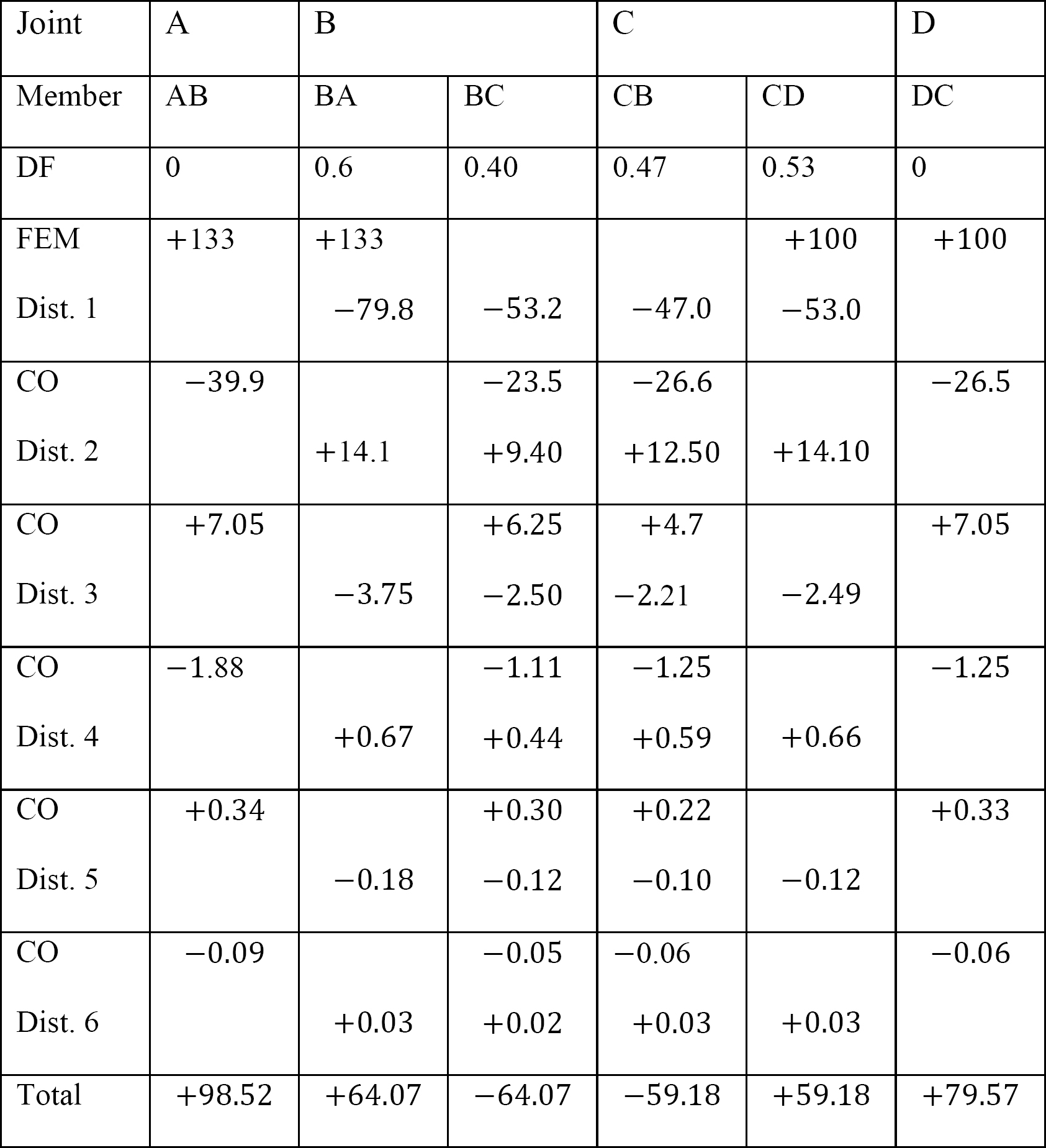
tabel 12.8. Fordelingstabel (ingen svingramme).
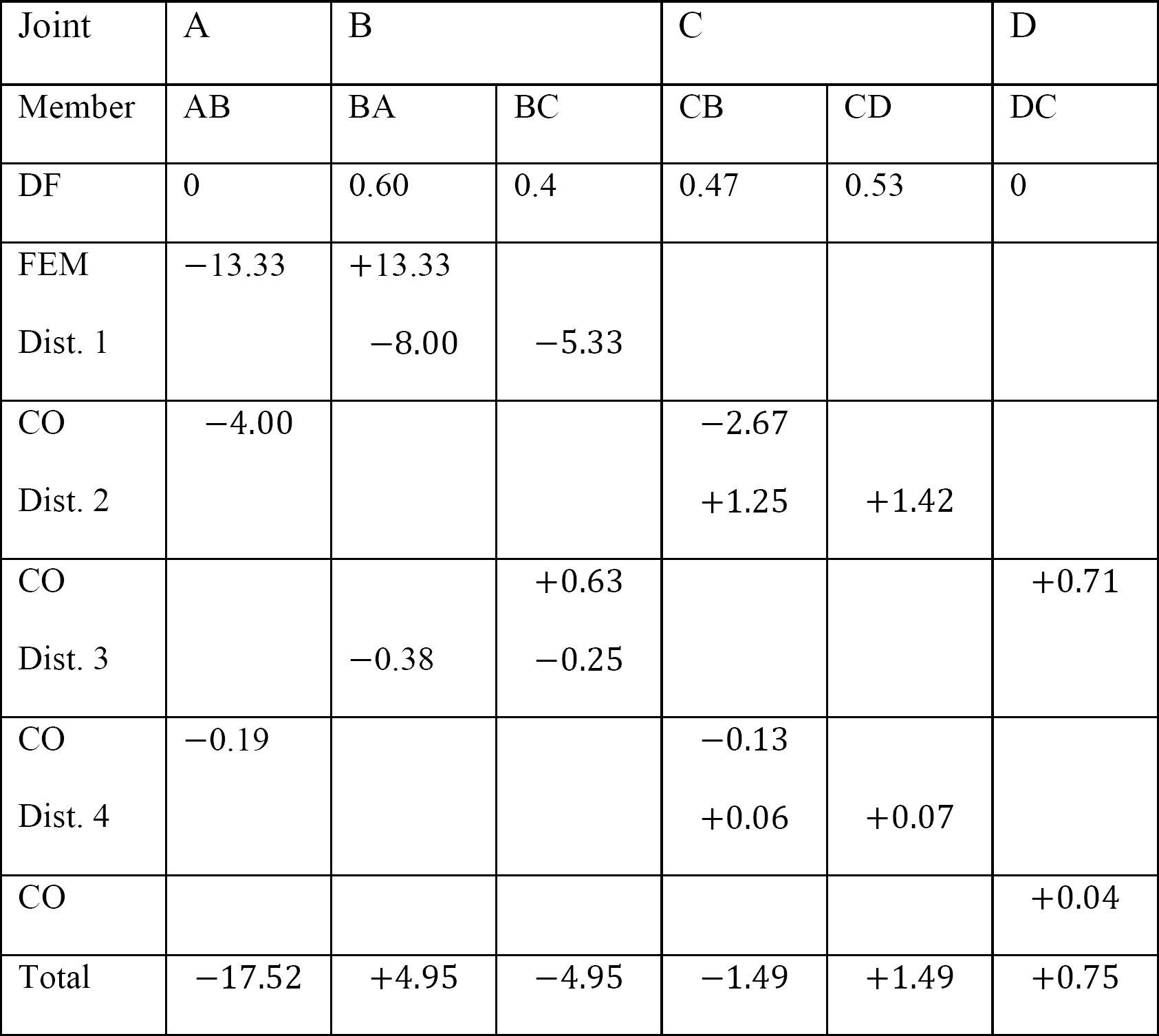
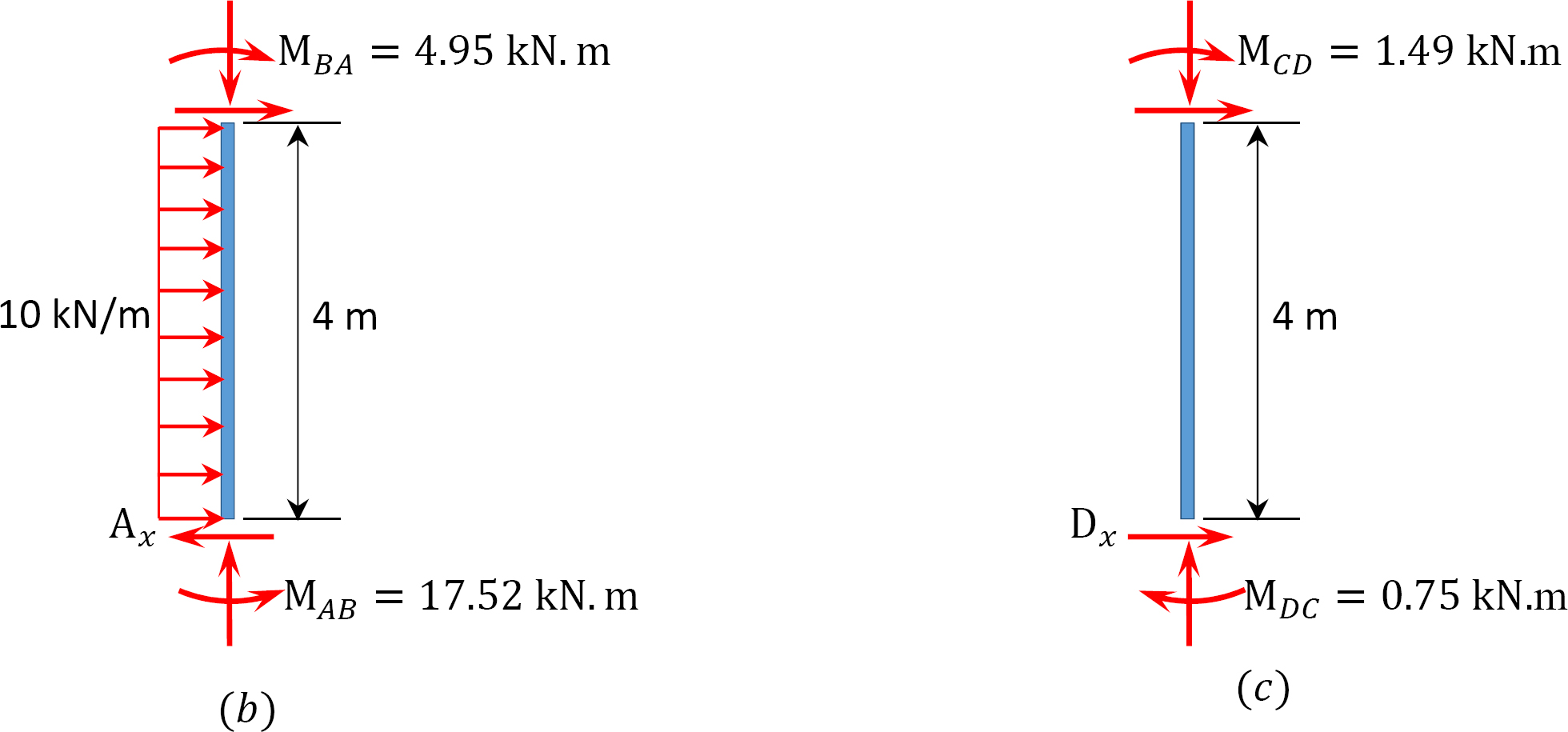
tabel 12.9. Fordelingstabel (svingramme).
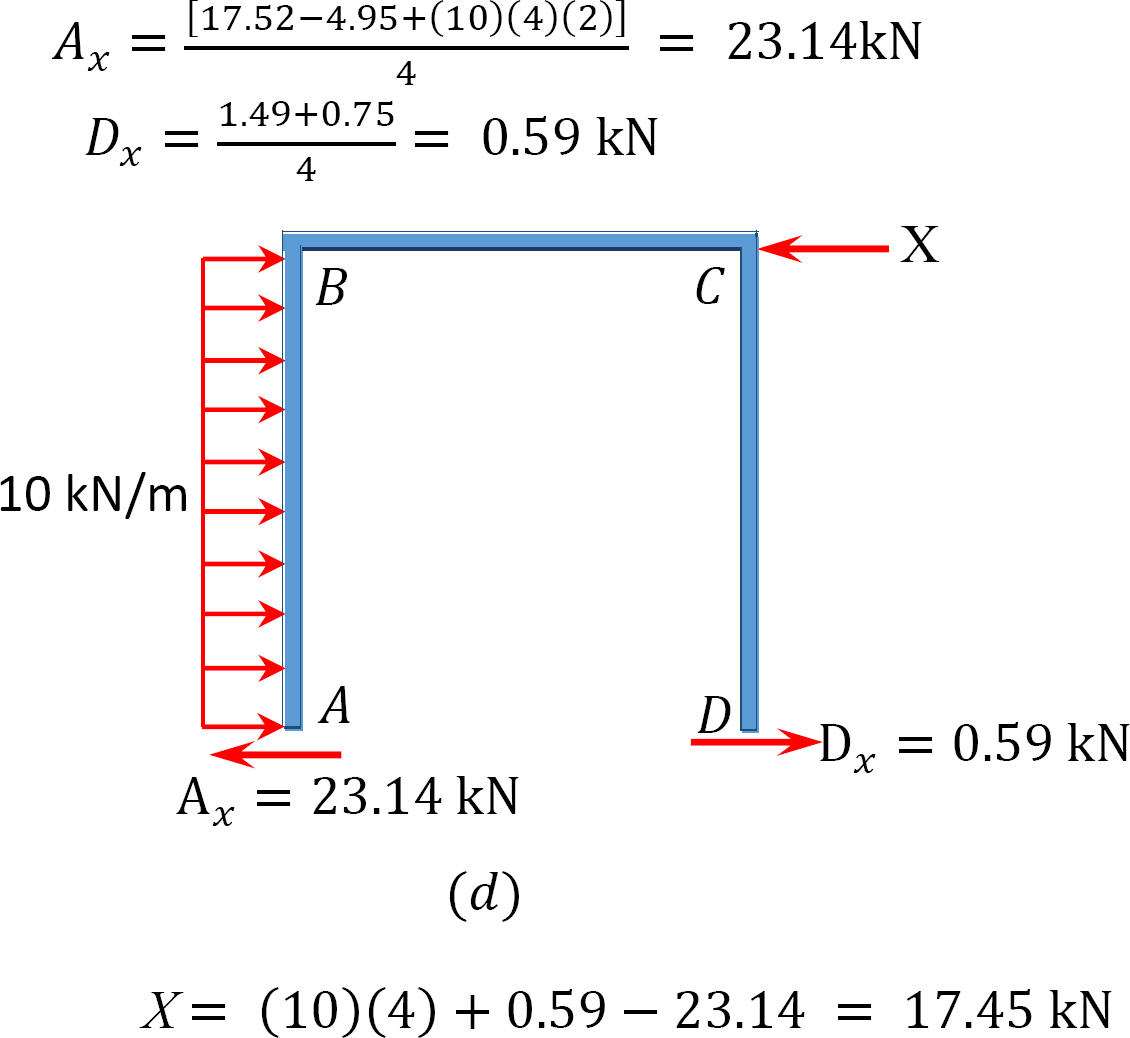
analyse af ramme med sidesvingning.
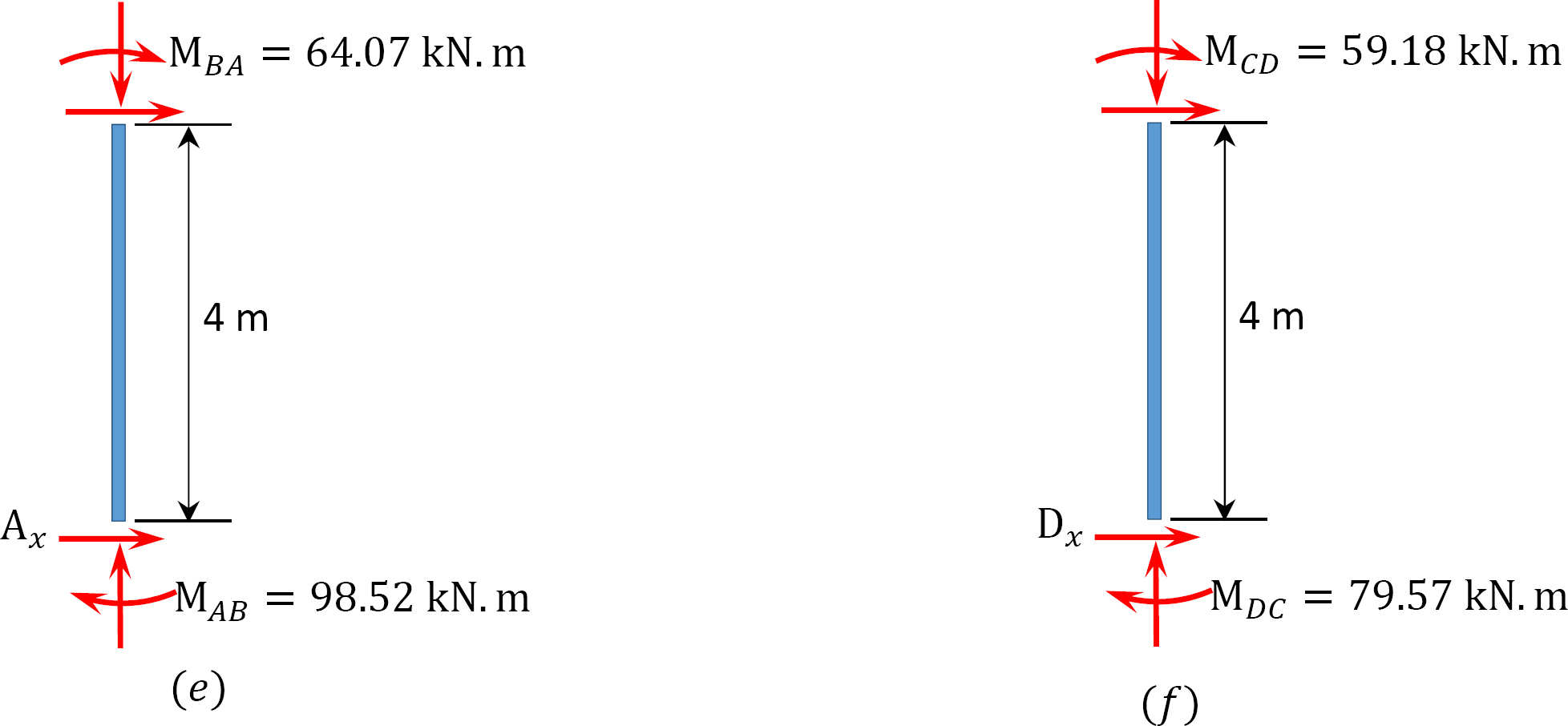

sidste ende øjeblik.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Kapiteloversigt
Momentfordelingsmetode til analyse af ubestemte strukturer: momentfordelingsmetoden til analyse er en omtrentlig analysemetode. Dens grad af nøjagtighed afhænger af antallet af iterationer. Ved denne metode antages det, at alle samlinger i en struktur midlertidigt er låst eller fastspændt og således forhindres i mulig rotation. Belastninger anvendes på medlemmerne, og de øjeblikke, der er udviklet ved medlemsenderne på grund af fasthed, bestemmes. Samlinger i strukturen låses derefter op successivt, og det ubalancerede øjeblik ved hvert led distribueres til medlemmer, der mødes på det led. Overførsel af øjeblikke ved medlemmernes fjerne ender bestemmes, og processen med afbalancering fortsættes indtil det ønskede nøjagtighedsniveau. Medlemmernes slutmomenter bestemmes ved at tilføje det faste slutmoment, det distribuerede øjeblik og overførselsmomentet. Når medlemmernes slutmomenter er bestemt, bliver strukturen bestemt.
Øvelsesproblemer
12.1 brug momentfordelingsmetoden til at beregne slutmomentet for medlemmerne af bjælkerne vist i figur P12.1 til og med figur P12.12 og tegne diagrammerne for bøjningsmoment og forskydningskraft. Ei = konstant.
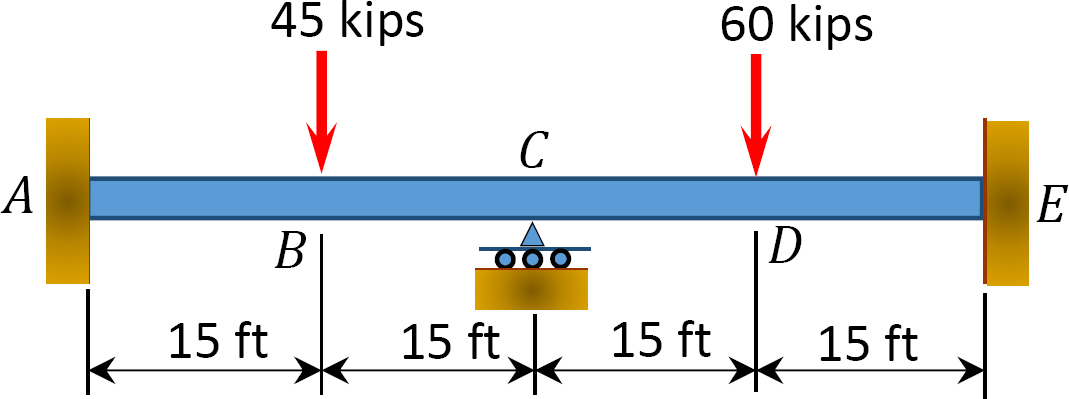
Fig. P12.1. Stråle.
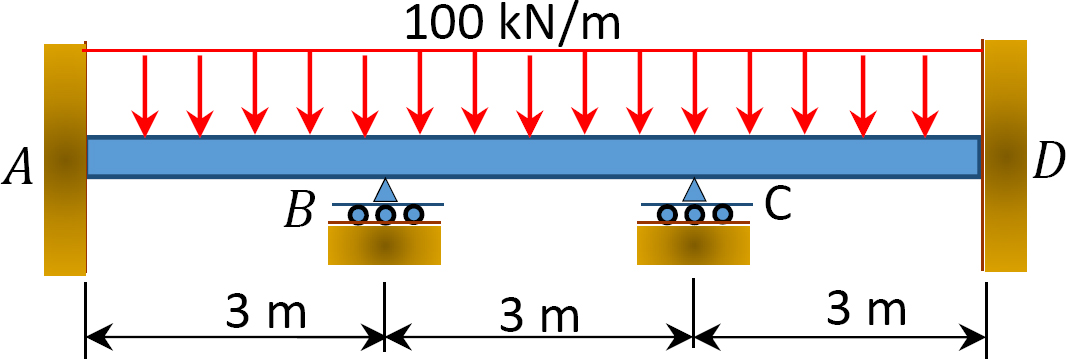
Fig. P12.2. Stråle.
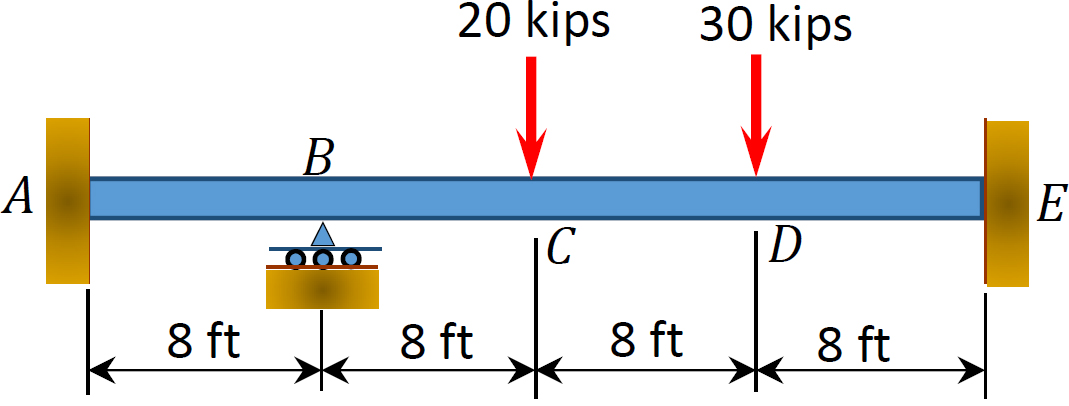
Fig. P12. 3. Stråle.
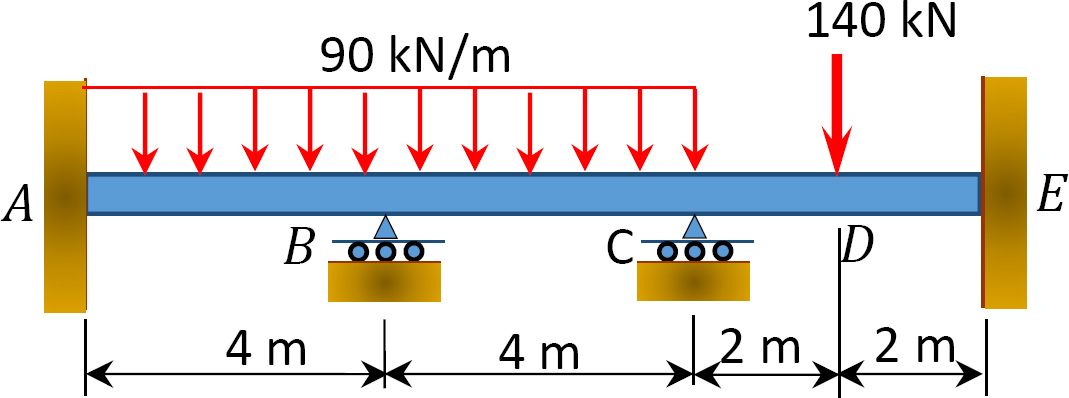
Fig. P12. 4. Stråle.
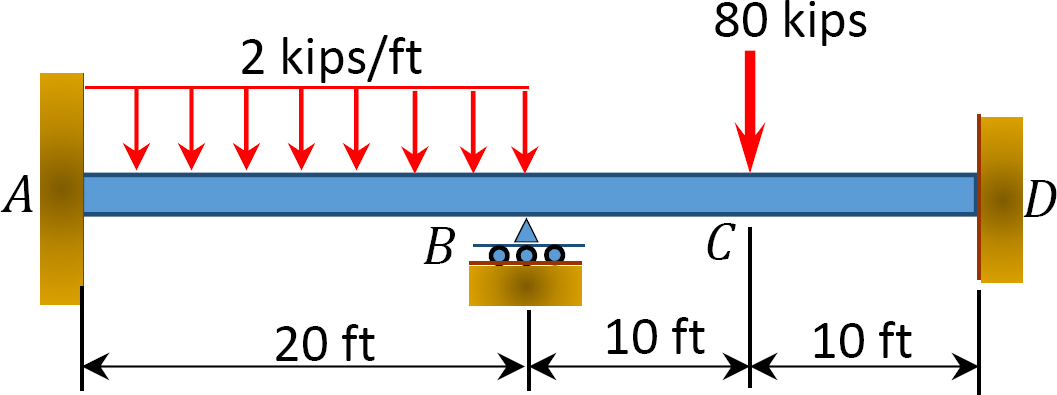
Fig. P12. 5. Stråle.
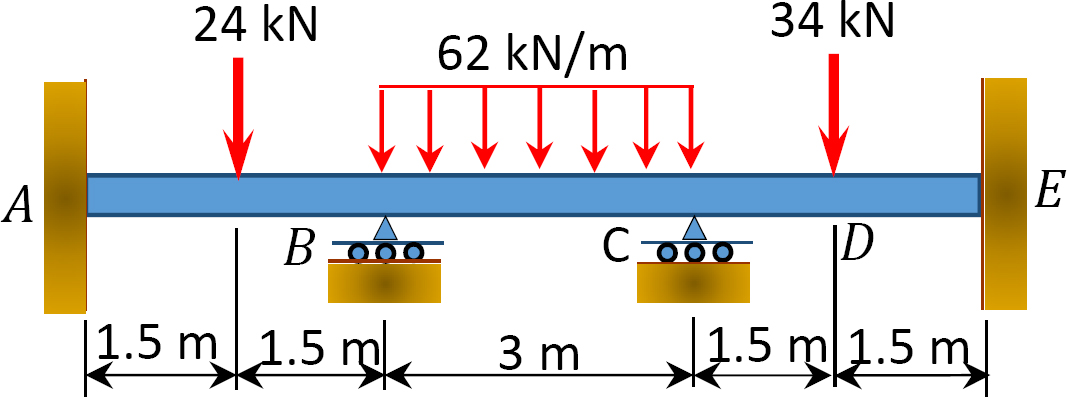
Fig. P12.6. Stråle.
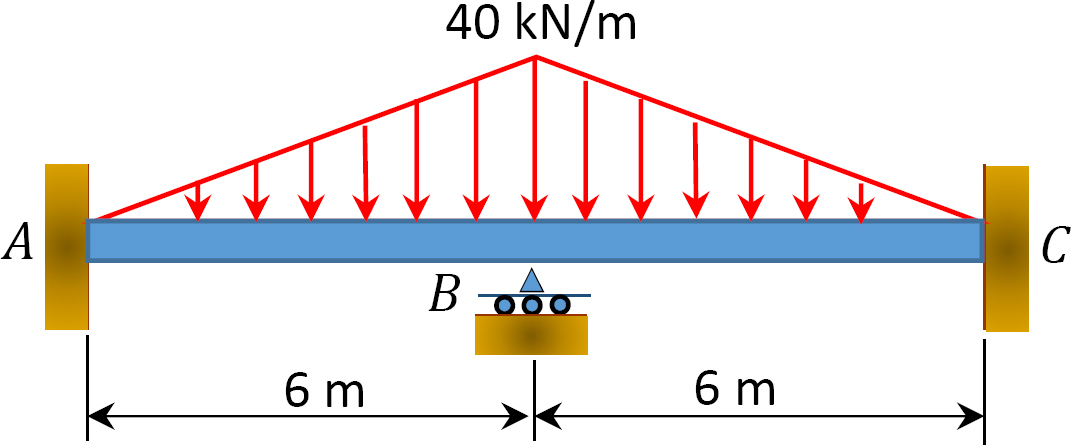
Fig. P12.7. Stråle.
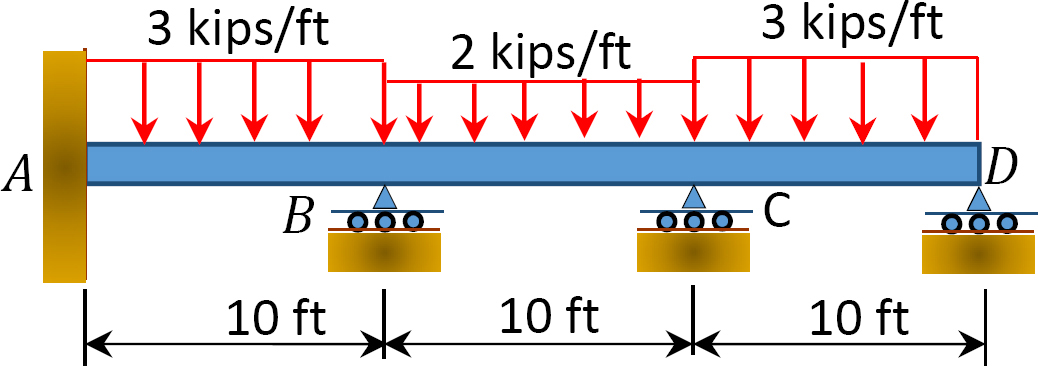
Fig. P12.8. Stråle.
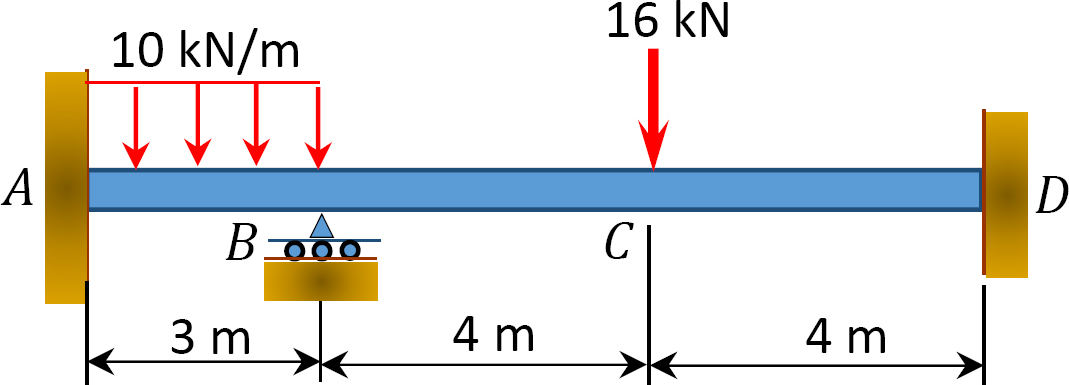
Fig. P12.9. Stråle.
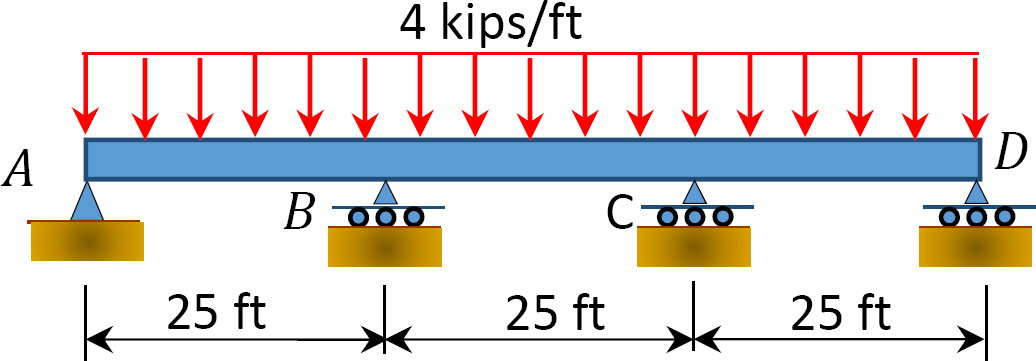
Fig. P12. 10. Stråle.
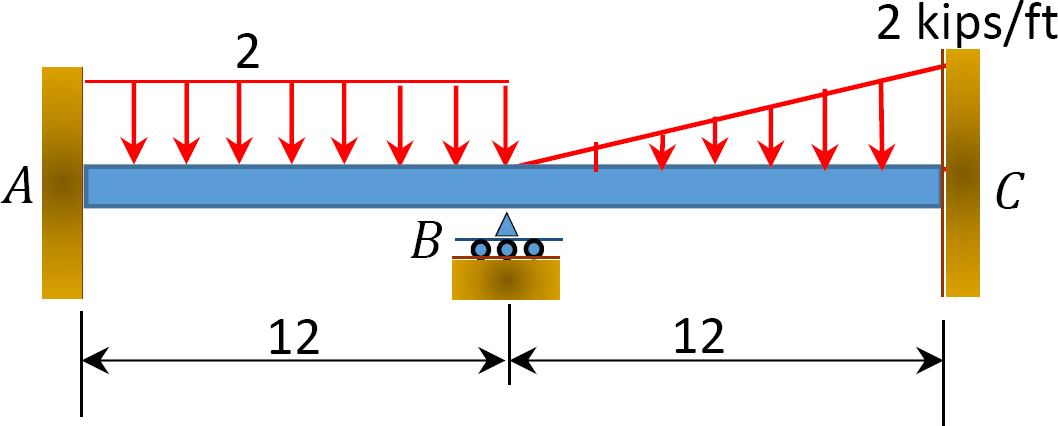
Fig. P12. 11. Stråle.
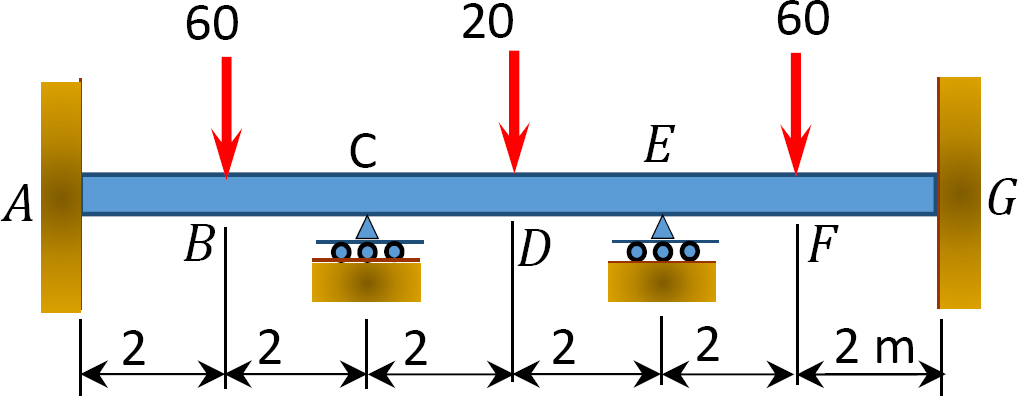
Fig. P12. 12. Stråle.
12.2 brug momentfordelingsmetoden til at beregne slutmomentet for medlemmerne af rammerne vist i figur P12.13 til og med figur 12.20 og tegne diagrammerne for bøjningsmoment og forskydningskraft. Ei = konstant.
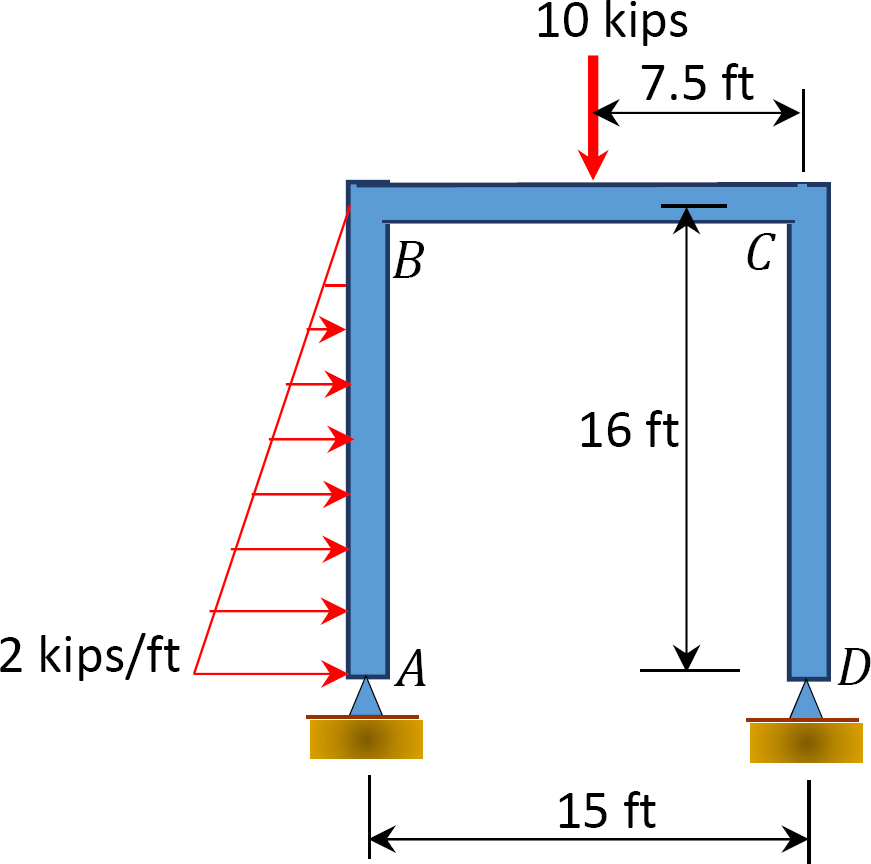
Fig. P12. 13. Ramme.
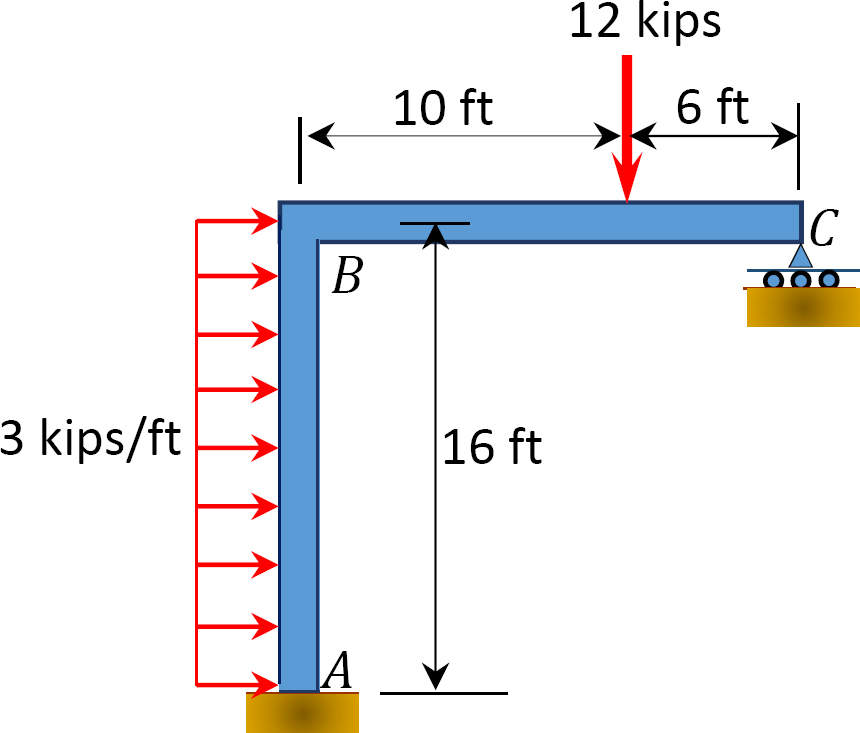
Fig. P12. 14. Ramme.
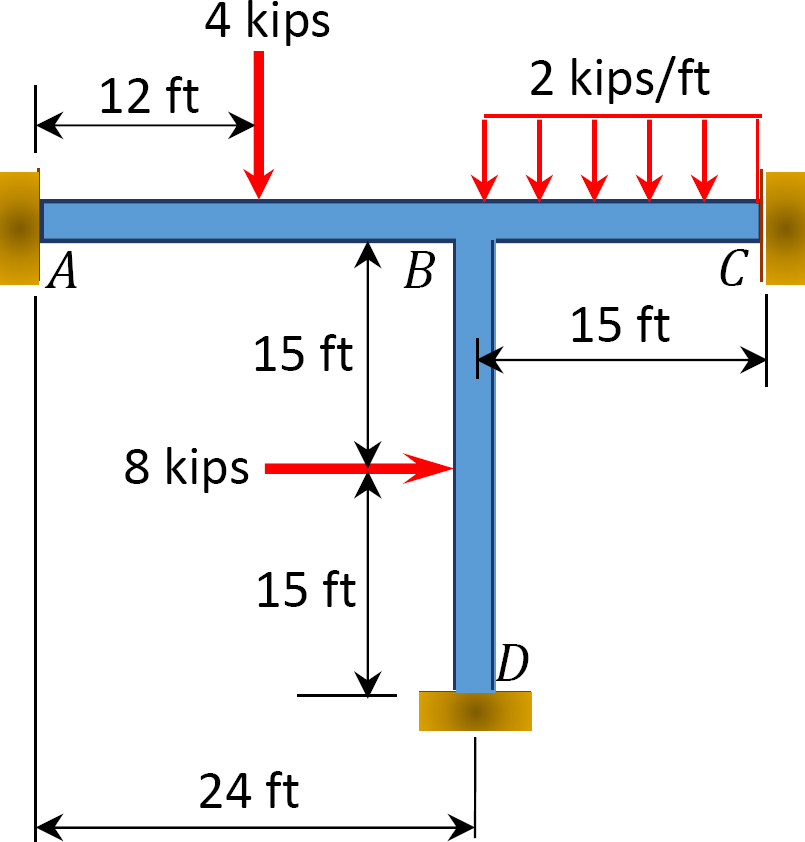
Fig. P12. 15. Ramme.
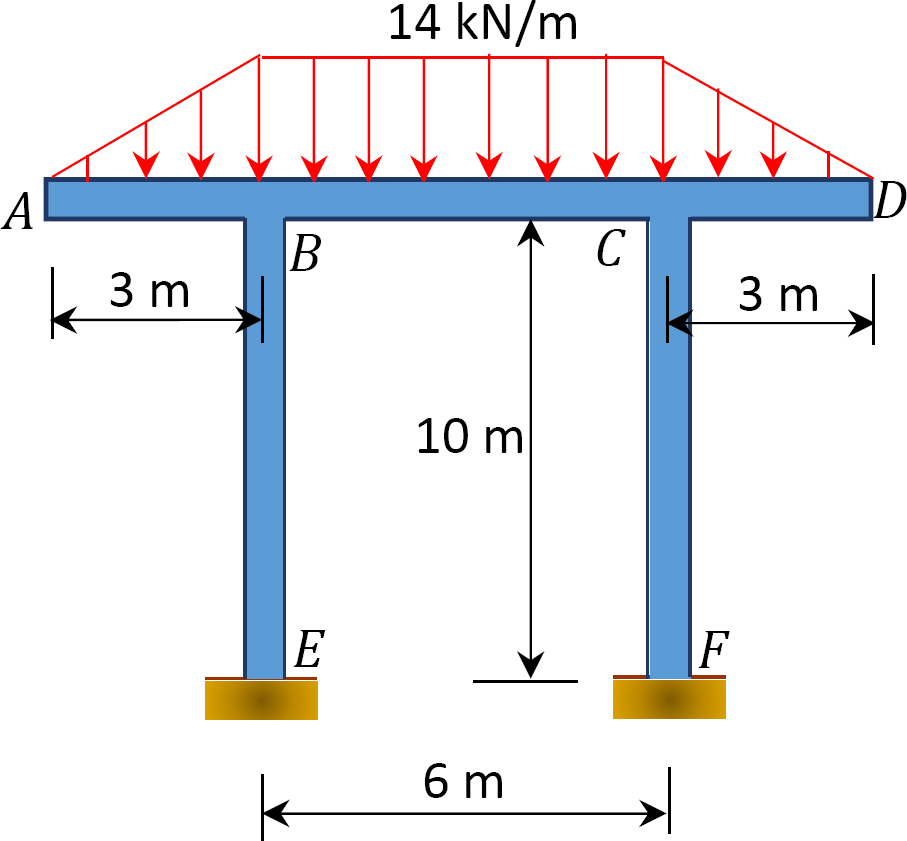
Fig. P12.16. Frame.
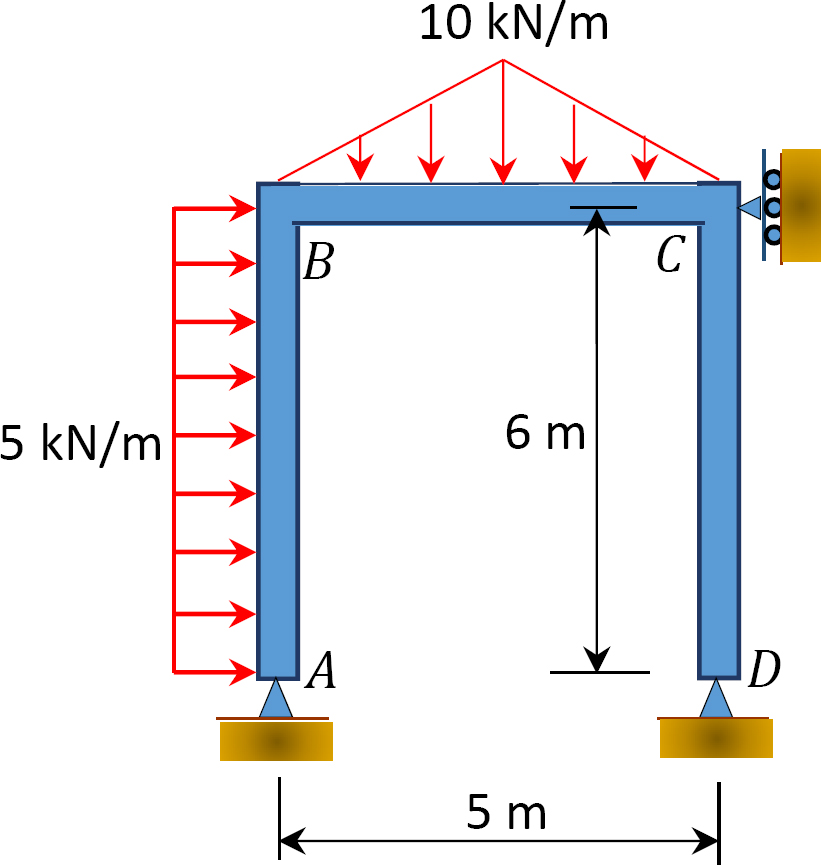
Fig. P12.17. Frame.
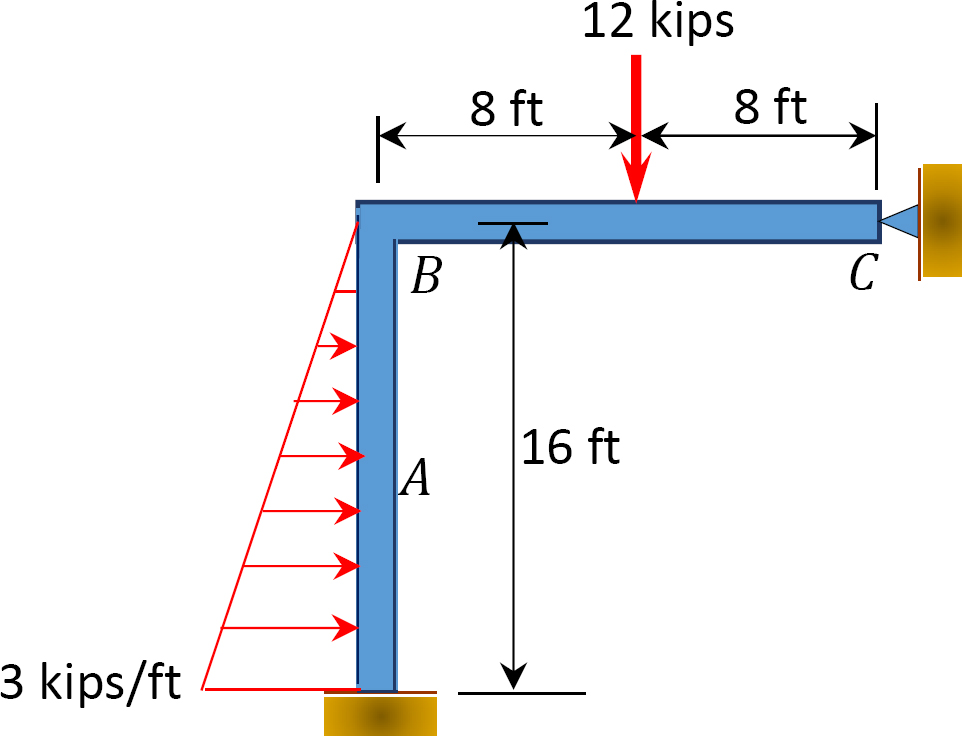
Fig. P12.18. Frame.
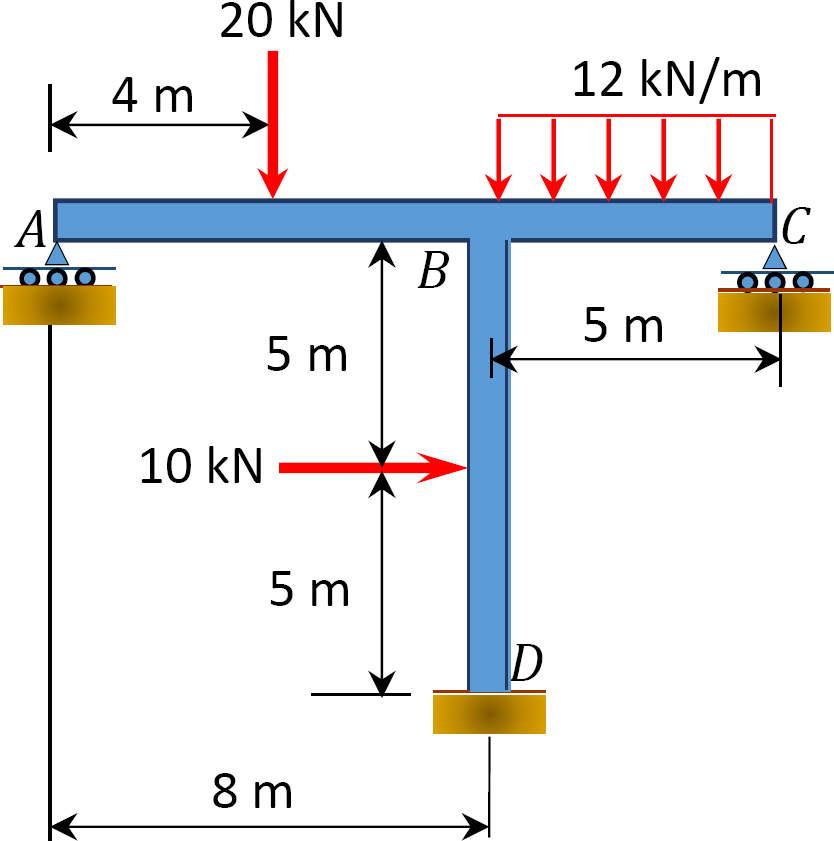
Fig. P12.19. Frame.
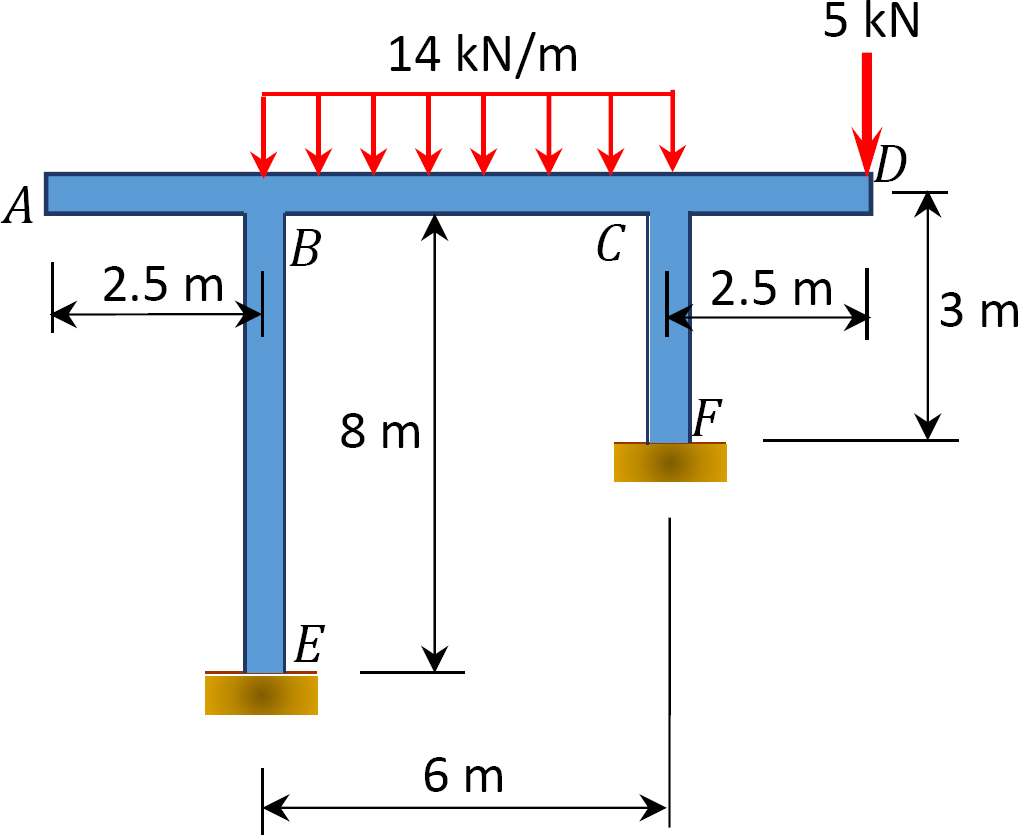
Fig. P12.20. Frame.