![]()
den mest generelle tvungen form af duffing ligning er
|
(1)
|
afhængigt af de valgte parametre kan ligningen tage en række specielle former. For eksempel, uden dæmpning og ingen tvang, ![]() og ved at tage plustegnet bliver ligningen
og ved at tage plustegnet bliver ligningen
|
(2)
|
(1978, s. 547; 1997, s.122). Denne ligning kan vise kaotisk adfærd. For ![]() repræsenterer ligningen en “hård fjeder”, og for
repræsenterer ligningen en “hård fjeder”, og for ![]() repræsenterer den en “blød fjeder.”Hvis
repræsenterer den en “blød fjeder.”Hvis ![]() , er faseportrætkurverne lukket.
, er faseportrætkurverne lukket.
hvis vi i stedet tager ![]() ,
, ![]() , Nulstil uret, så
, Nulstil uret, så ![]() , og brug minustegnet, ligningen er så
, og brug minustegnet, ligningen er så
|
(3)
|
dette kan skrives som et system af første ordens almindelige differentialligninger som
|
(4)
|
|||
|
(5)
|
(1990, s. 5), som i det uforcerede tilfælde reducerer til
|
(6)
|
|||
|
(7)
|
(1990, s. 6; Ott 1993, s.3).
de faste punkter i dette sæt koblede differentialligninger er givet af
|
(8)
|
så ![]() , og
, og
|
(9)
|
|||
|
(10)
|
giver ![]() . De faste punkter er derfor
. De faste punkter er derfor ![]() ,
, ![]() , og
, og ![]() .
.
analyse af stabiliteten af de faste punkter kan være punkt ved linearisering af ligningerne. Differentiering giver
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
som kan skrives som matricen ligning
|
(14)
|
undersøgelse af punktets stabilitet(0,0):
|
(15)
|
|
(16)
|
men ![]() , så
, så ![]() er ægte. Siden
er ægte. Siden ![]() , vil der altid være en positiv rod, så dette faste punkt er ustabilt. Se nu på (
, vil der altid være en positiv rod, så dette faste punkt er ustabilt. Se nu på (![]() , 0). Den karakteristiske ligning er
, 0). Den karakteristiske ligning er
|
(17)
|
som har rødder
|
(18)
|
for ![]() ,
, ![]() , så punktet er asymptotisk stabilt. Hvis
, så punktet er asymptotisk stabilt. Hvis ![]() ,
, ![]() , så punktet er lineært stabilt (1990, s. 10). Men hvis
, så punktet er lineært stabilt (1990, s. 10). Men hvis ![]() , den radikale giver en imaginær del, og den virkelige del er
, den radikale giver en imaginær del, og den virkelige del er ![]() , så punktet er ustabilt. Hvis
, så punktet er ustabilt. Hvis ![]() ,
, ![]() , som har en positiv reel rod, så punktet er ustabilt. Hvis
, som har en positiv reel rod, så punktet er ustabilt. Hvis ![]() , så
, så ![]() , så begge rødder er positive, og punktet er ustabilt.
, så begge rødder er positive, og punktet er ustabilt.
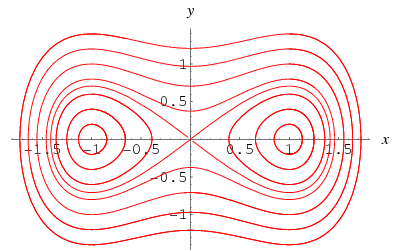
interessant, det specielle tilfælde ![]() uden tvang,
uden tvang,
|
(19)
|
|||
|
(20)
|
kan integreres af kvadraturer. Differentiering (19) og pluggingin (20) giver
|
(21)
|
multiplicere begge sider med ![]() giver
giver
|
(22)
|
men dette kan skrives
|
(23)
|
så vi har en uforanderlig bevægelse ![]() ,
,
|
(24)
|
løsning for ![]() giver
giver
|
(25)
|
|
(26)
|
so
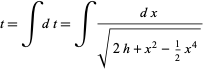 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
så ligningerne af duffing oscillatoren er givet af Hamiltoniansystemet