Kapitel 12
Momentenverteilungsmethode zur Analyse von Strukturen
12.1 Grundbegriffe
Die Momentenverteilungsmethode zur Analyse von Trägern und Rahmen wurde von Hardy Cross entwickelt und 1930 offiziell vorgestellt. Obwohl es sich bei dieser Methode um eine Verformungsmethode wie bei der Slope-Deflection-Methode handelt, handelt es sich um eine ungefähre Methode und erfordert daher keine Lösung simultaner Gleichungen, wie dies bei der letzteren Methode der Fall war. Der Grad der Genauigkeit der Ergebnisse, die durch die Methode der Momentenverteilung erhalten werden, hängt von der Anzahl der aufeinanderfolgenden Näherungen oder dem Iterationsprozess ab.
Um das Konzept der Methode der Momentenverteilung zu veranschaulichen, betrachten Sie den in Abbildung 12.1 gezeigten Rahmen. Die Elemente des Rahmens sind prismatisch und es wird angenommen, dass sie sich weder axial verformen noch relativ zueinander verschieben. Die Gelenke ACD des Rahmens sind fixiert, während sich das Gelenk B aufgrund der aufgebrachten Last leicht drehen kann. Bevor die Momentenverteilung zwischen den Elementen durchgeführt wird, wird zunächst angenommen, dass alle Gelenke vorübergehend mit einer Klemme verriegelt sind.
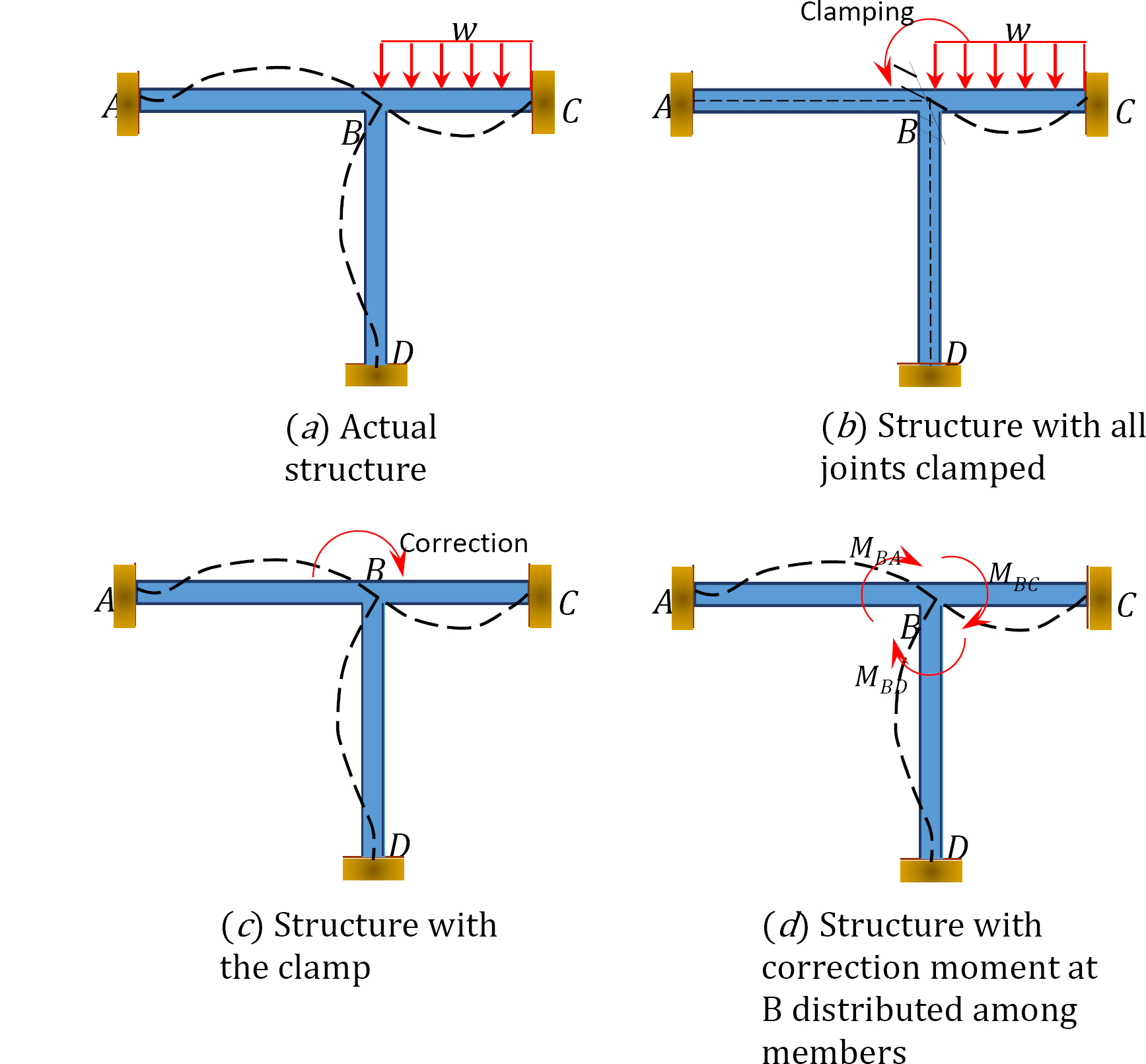
Abb. 12.1. Rahmen.
12.2 Vorzeichenkonvention
Die Vorzeichenkonvention für die Momentenverteilungsmethode ist ähnlich der für die Slope-Deflection-Methode festgelegten; das heißt, der Moment am Ende eines Elements wird als positiv angesehen, wenn er dazu neigt, das Ende des Elements im Uhrzeigersinn zu drehen, und als negativ, wenn er dazu neigt, es gegen den Uhrzeigersinn zu drehen.
12.3 Definitionen
Unwuchtmomente: Bei dieser Analysemethode wird davon ausgegangen, dass die Gelenke in einer Struktur zunächst geklemmt oder verriegelt und dann sukzessive gelöst werden. Sobald ein Gelenk freigegeben wird, findet eine Rotation statt, da die Summe der festen Endmomente der Mitglieder, die sich an diesem Gelenk treffen, nicht Null ist. Der Wert der Summe der erhaltenen Endmomente ist das Unwuchtmoment an diesem Gelenk.
Verschleppungsmomente: Die verteilten Momente an den Enden der Mitgliederversammlung bei einer gemeinsamen Sache Momente an den anderen Enden, die als fest angenommen werden. Diese induzierten Momente an den anderen Enden werden Carry-Over-Momente genannt.
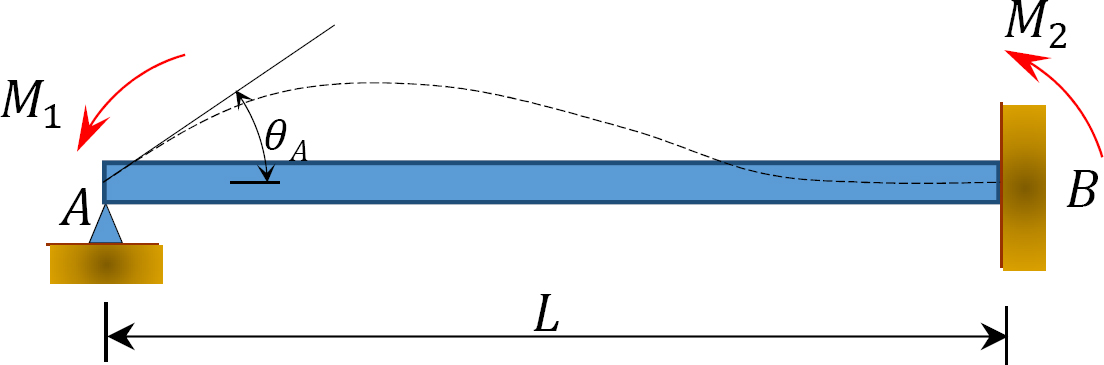
Abb. 12.2. Unbelasteter prismatischer Strahl.
Betrachten Sie einen unbelasteten prismatischen Strahl, der am Ende B befestigt ist, wie in Abbildung 12.2 gezeigt. Wenn ein Moment M1 an das linke Ende des Strahls angelegt wird, können die Steigungsablenkungsgleichungen für beide Enden des Strahls wie folgt geschrieben werden:


Das Ersetzen von 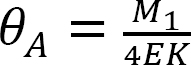 aus Gleichung 12.1 in Gleichung 12.2 schlägt Folgendes vor:
aus Gleichung 12.1 in Gleichung 12.2 schlägt Folgendes vor:

Gleichung 12.3 legt nahe, dass das Moment, das aufgrund eines am anderen Ende angelegten Moments auf das feste Ende eines Strahls übertragen wird, gleich der Hälfte des angelegten Moments ist.
Übertragungsfaktor: Das Verhältnis des induzierten Moments zum angelegten Moment wird als Übertragungsfaktor bezeichnet. Für den in Abbildung 12.2 gezeigten Strahl ist der Übertragungsfaktor wie folgt:

Verteilter Faktor (DF): Der verteilte Faktor ist ein Faktor, der verwendet wird, um den Anteil des unausgeglichenen Moments zu bestimmen, das von jedem der Mitglieder getragen wird, die sich an einem Gelenk treffen. Für die Mitglieder, die sich am gemeinsamen Ende des in Abbildung 12.3 gezeigten Rahmens treffen, werden ihre Verteilungsfaktoren wie folgt berechnet:
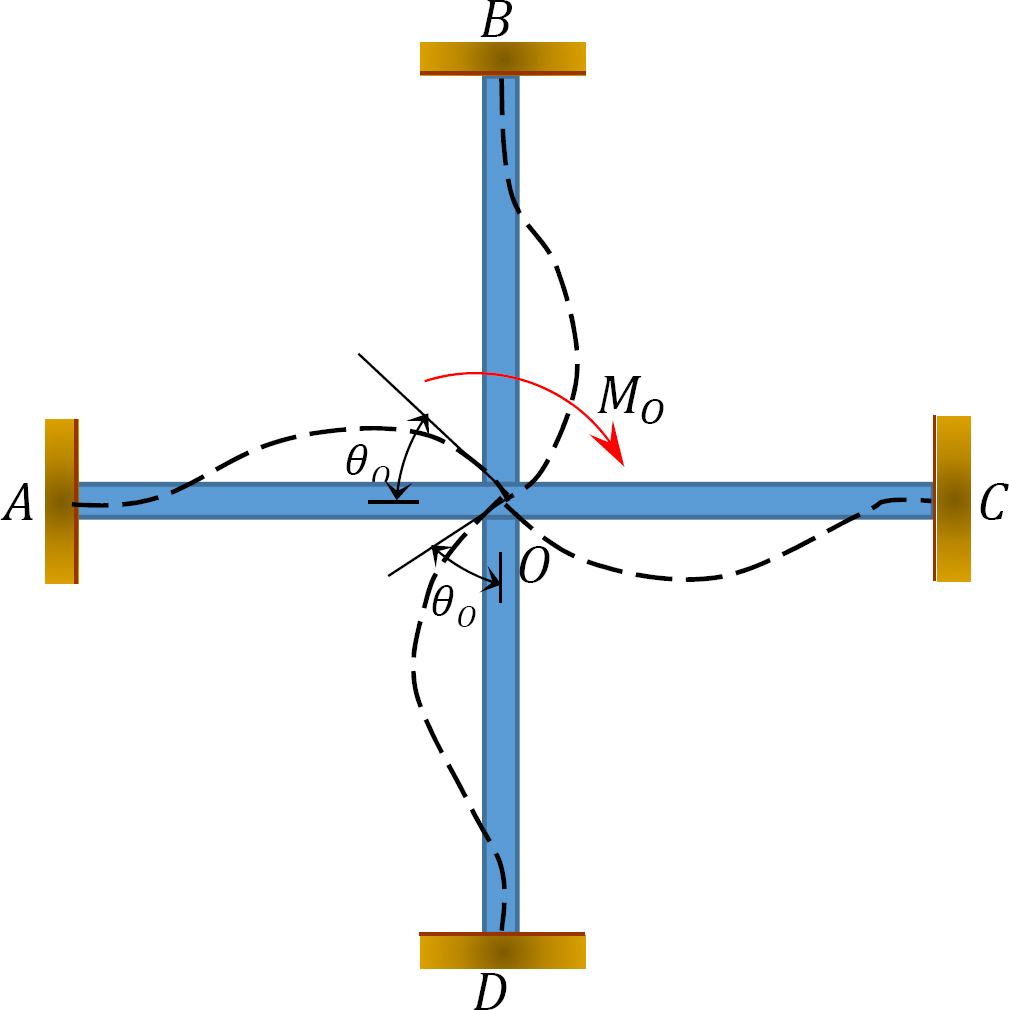
Abb. 12.3. Rahmen.

Verteilte Momente: Beim Lösen der imaginären Klammer an einem Gelenk bewirkt das unausgeglichene Moment an diesem Gelenk, dass es sich dreht. Die Rotation verdreht das Ende der Mitgliederversammlung am Gelenk, was zur Entwicklung von Widerstandsmomenten führt. Diese Widerstandsmomente werden verteilte Momente genannt. Die in Abbildung 12.3 gezeigten verteilten Momente für die Glieder des Rahmens werden wie folgt berechnet:
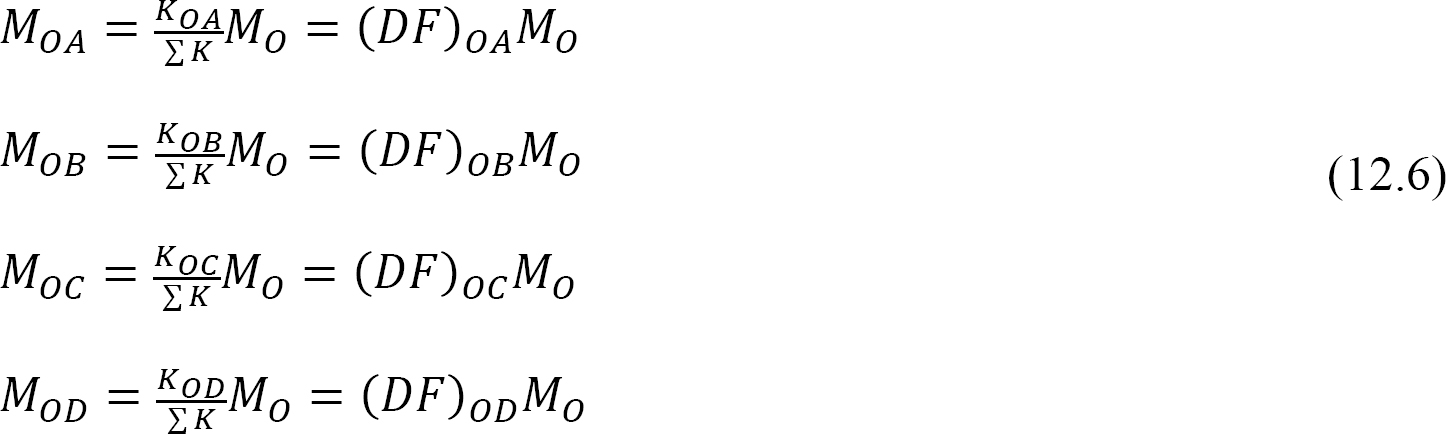
12.4 Änderung der Stabsteifigkeit
Manchmal kann der Iterationsprozess bei der Momentenverteilungsmethode erheblich reduziert werden, indem die Biegesteifigkeit einiger Elemente der unbestimmten Struktur angepasst wird. In diesem Abschnitt wird der Einfluss eines festen und eines stiftförmigen Trägers auf die Biegesteifigkeit eines unbestimmten Trägers betrachtet.
Fall 1: Ein Balken, der an einem Ende angelenkt und am anderen befestigt ist
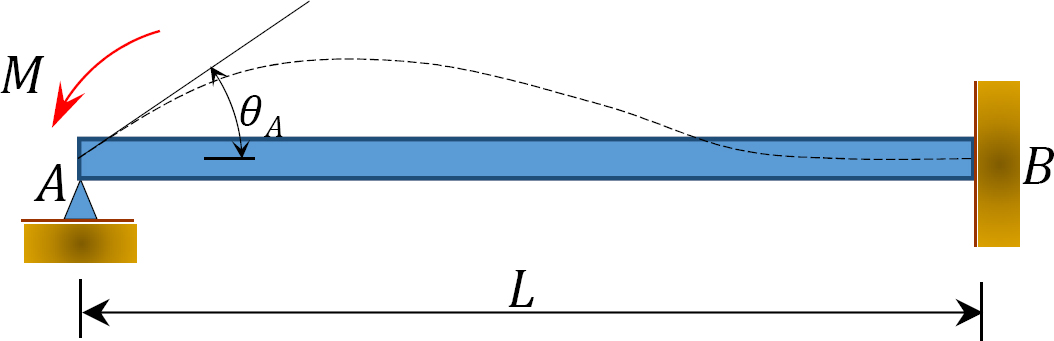
Abb. 12.4. Balken
Betrachten Sie einen Balken, der an Ende A angelenkt und an Ende B befestigt ist, wie in Abbildung 12.4 gezeigt. Durch Anlegen eines Moments M wird das Scharnierende um einen Betrag θ gedreht. Das Schreiben der Steigungs-Ablenkungs-Gleichung für das Ende A des Elements und das Beachten, dass 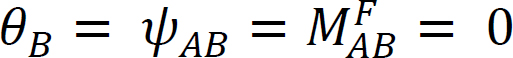 Folgendes vorschlägt:
Folgendes vorschlägt:
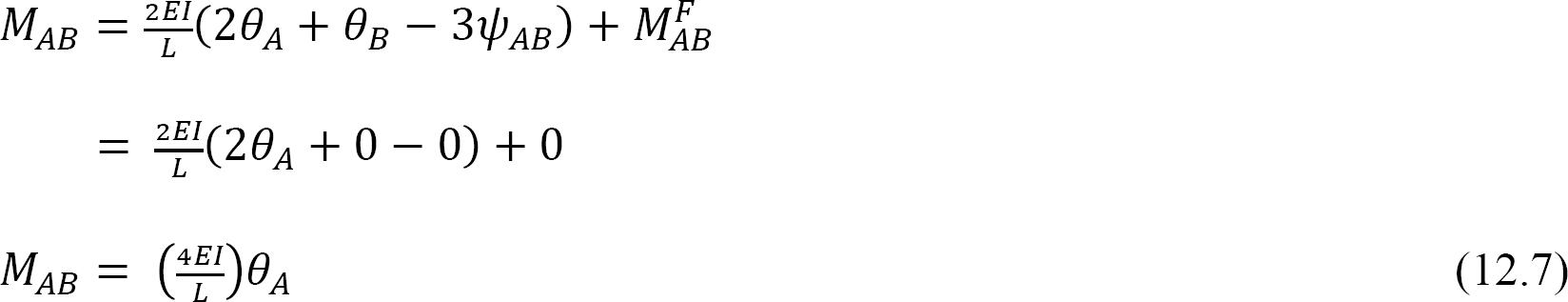
Definitionsgemäß ist die Biegesteifigkeit eines Strukturelements das Moment, das auf ein Ende des Elements aufgebracht werden muss, um eine Einheitsdrehung dieses Endes zu verursachen. Der folgende Ausdruck für die Biegesteifigkeit für das Element mit einem festen fernen Ende wird wie folgt ausgedrückt, wenn θA = 1 in Gleichung 12.7:

Definitionsgemäß wird die relative Biegesteifigkeit eines Elements bestimmt, indem die Biegesteifigkeit des Elements durch 4E dividiert wird. Die Division der Gleichung 12.8 durch 4E legt den folgenden Ausdruck für die relative Steifigkeit für den betrachteten Fall nahe:

Fall 2: Ein an beiden Enden angelenkter Balken
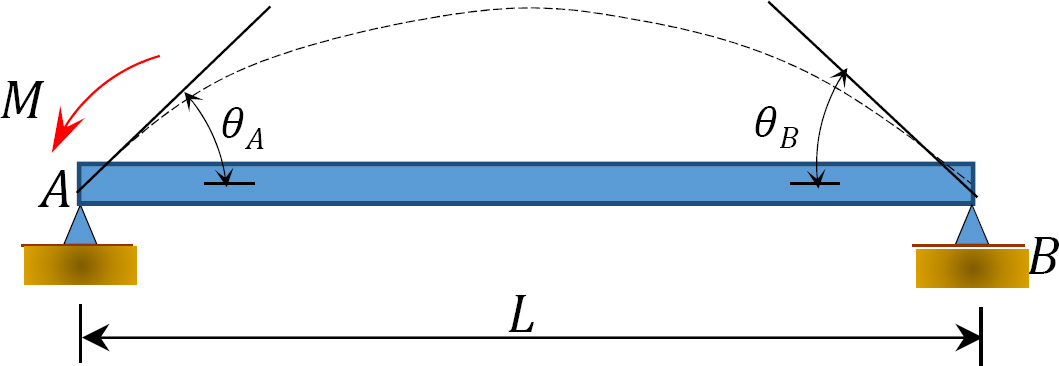
Abb. 12.5. Einfach unterstützter Strahl.
Durch Anlegen eines Moments M am Ende A des in Abbildung 12.5 gezeigten einfach abgestützten Trägers wird der Träger am gelenkigen Ende um einen Winkel θA gedreht. Unter Verwendung der in Kapitel 11 Abschnitt 11.4 abgeleiteten modifizierten Steigungs-Durchbiegungsgleichung und unter Hinweis darauf, dass 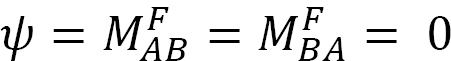 den folgenden Ausdruck für das Moment am gelenkigen Ende vorschlägt, an dem die Last angelegt wird:
den folgenden Ausdruck für das Moment am gelenkigen Ende vorschlägt, an dem die Last angelegt wird:
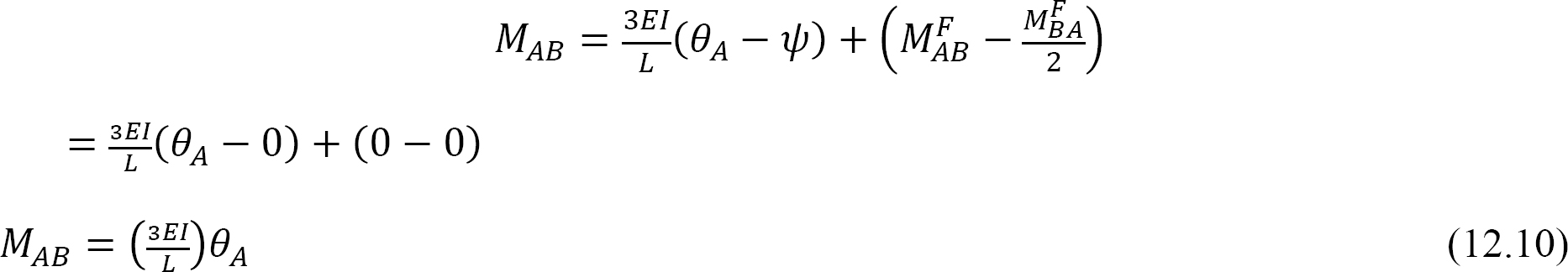
Die Substitution von θA = 1 in Gleichung 12.10 schlägt den folgenden Ausdruck für die Biegesteifigkeit für ein Element mit einem gelenkigen fernen Ende vor:

Die relative Steifigkeit für ein Element mit einem gelenkigen fernen Ende wird erhalten, indem Gleichung 12.11 durch 4E wie folgt dividiert wird:

Der Vergleich der Gleichungen 12.12 und 12.9 legt nahe, dass ein Stab mit einem gelenkigen fernen Ende drei Viertel so steif ist wie ein Stab mit der gleichen Geometrie, aber am fernen Ende fixiert. Diese festgestellte Tatsache kann die Anzahl der Iterationen bei der Analyse von Strahlen oder Rahmen mit einem gelenkigen fernen Ende unter Verwendung der Methode der Momentenverteilung erheblich reduzieren. In solchen Fällen wird zunächst die relative Steifigkeit des Trägers am nahen Ende gemäß Gleichung 12.12 eingestellt und sein Verteilungsfaktor mit der eingestellten Steifigkeit berechnet. Während des Auswuchtvorgangs wird das nahe Ende nur einmal ausgewuchtet, ohne dass weitere Momente von oder zu seinem Ende übertragen werden.
12.5 Analyse unbestimmter Strahlen
Das Verfahren zur Analyse unbestimmter Strahlen nach der Methode der Momentenverteilung wird wie folgt kurz zusammengefasst:
Verfahren zur Analyse unbestimmter Strahlen nach der Momentenverteilungsmethode
• Berechnen Sie die Momente mit festem Ende für Glieder unter der Annahme, dass die Gelenke gegen Drehung geklemmt sind.
*Berechnen Sie den Verteilungsfaktor für jedes der am Gelenk verbundenen Glieder
*Berechnen Sie das Unwuchtmoment an jedem Gelenk und verteilen Sie es auf die Enden der an diesem Gelenk verbundenen Glieder.
* Übertragen Sie die Hälfte des verteilten Moments auf die anderen Enden der Mitglieder.
*Addieren oder subtrahieren Sie diese letzteren Momente (Momente, die in den Schritten drei und vier erhalten wurden) zu oder von den ursprünglichen festen Momenten.
*Wenden Sie die ermittelten Endmomente an den Gelenken der gegebenen Struktur an.
*Zeichnen Sie das Freikörperdiagramm jeder Spannweite des gegebenen Balkens, das die Lasten und Momente an den Gelenken zeigt, die durch die Momentenverteilungsmethode erhalten werden.
*Bestimmen Sie die Stützreaktionen für jede Spanne.
*Berechnen und konstruieren Sie die Scherkraft- und Biegemomentdiagramme für jede Spannweite.
*Zeichnen Sie ein Biegemoment- und ein Scherkraftdiagramm für den gegebenen Träger, indem Sie die Diagramme in Schritt 9 kombinieren.
Beispiel 12.1
Bestimmen Sie mit der Momentenverteilungsmethode die Endmomente und die Reaktionen an den Stützen des Trägers (siehe Abbildung 12.6a). Zeichnen Sie die Scherkraft- und die Biegemomentdiagramme. EI = konstant.
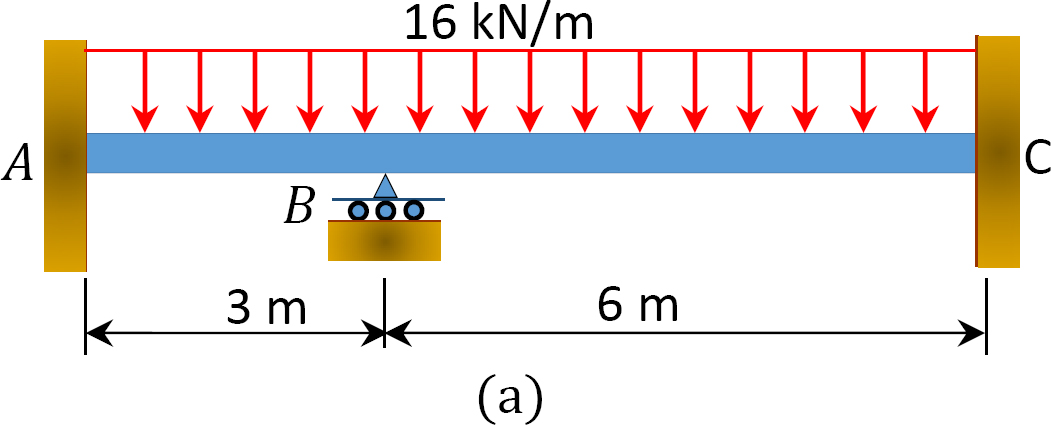
Abb. 12.6. Strahl.
Lösung
Festes Endmoment.
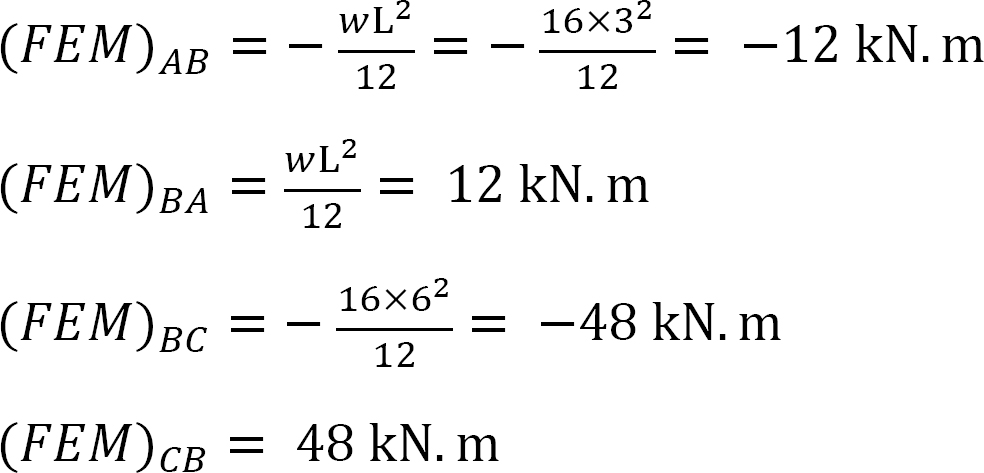
Steifigkeit faktor.
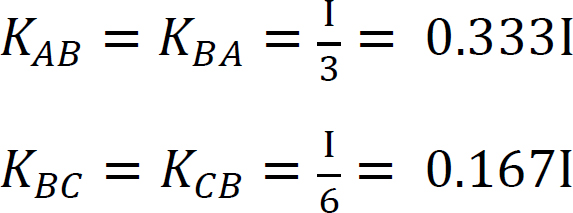
Verteilungsfaktor.
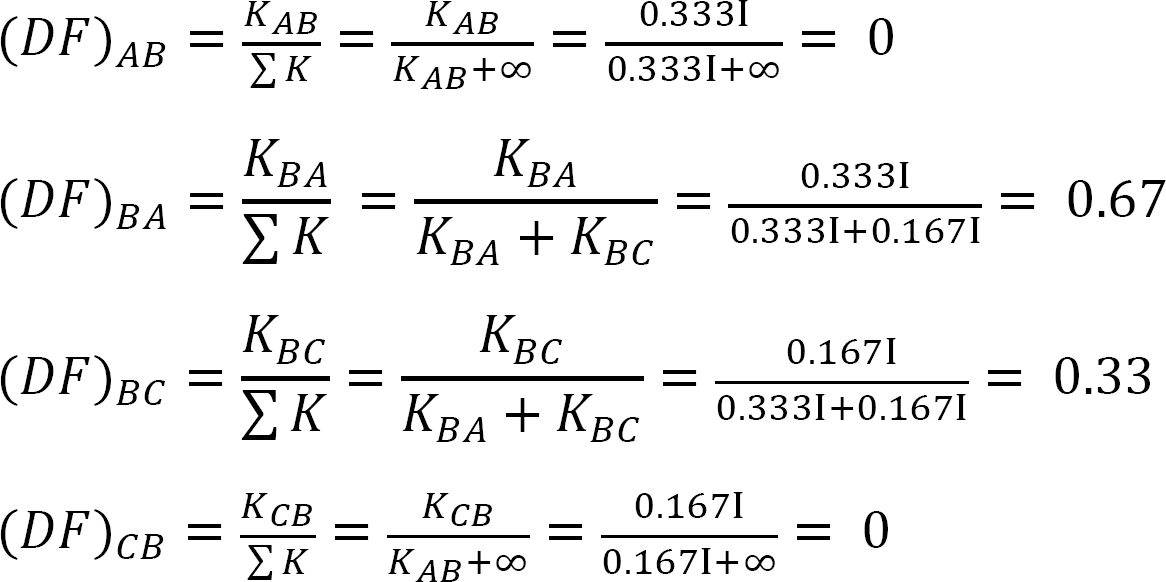
Tabelle 12.1. Verteilungstabelle.
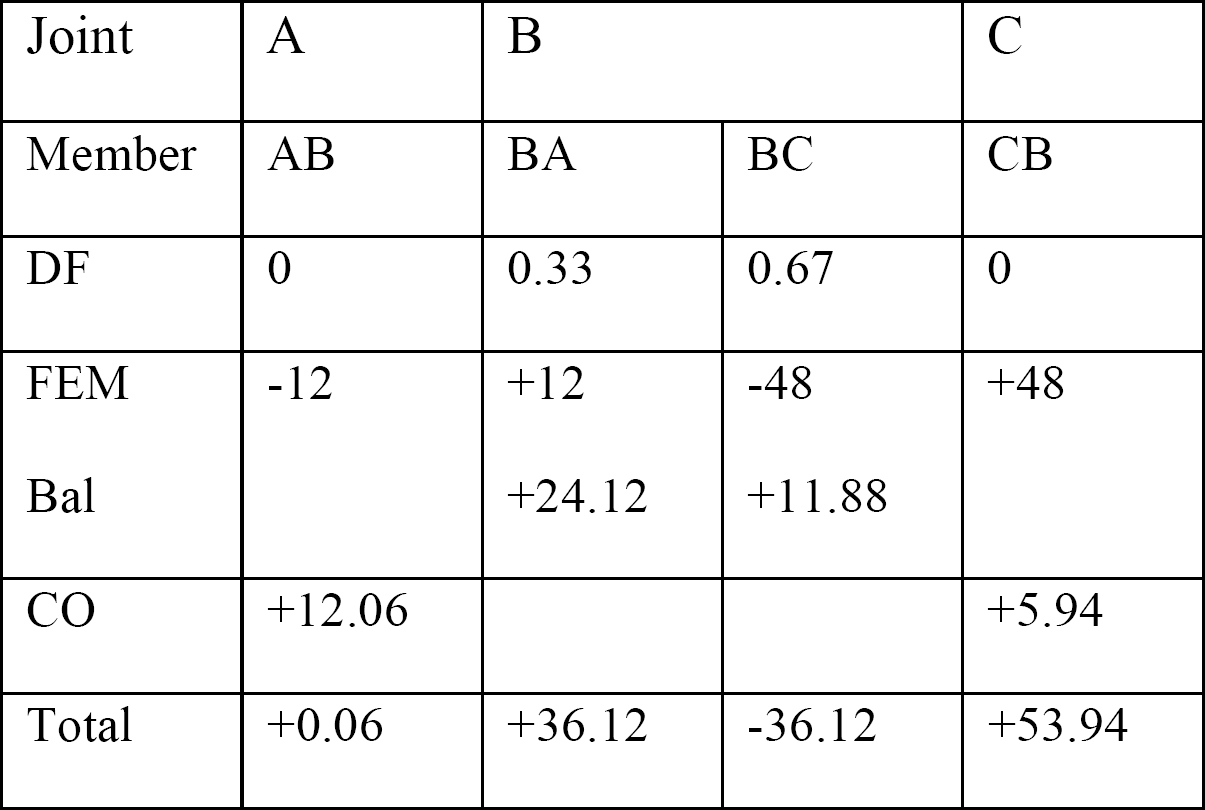
Scherkraft- und Biegemomentdiagramme.
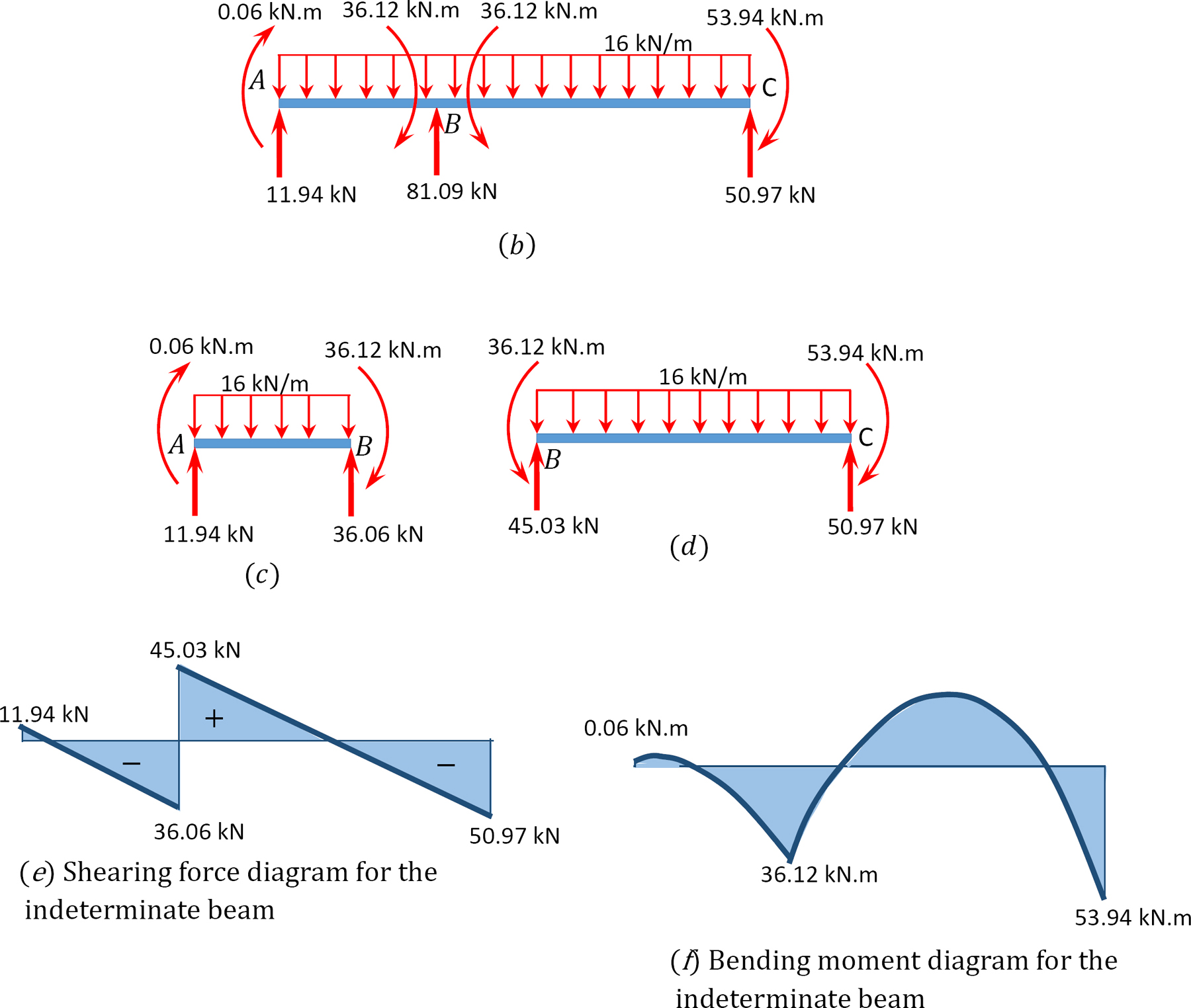
Beispiel 12.2
Bestimmen Sie mit der Momentenverteilungsmethode die Endmomente und die Reaktionen an den Trägern des Trägers (siehe Abbildung 12.7a). Zeichnen Sie die Scherkraft- und die Biegemomentdiagramme.
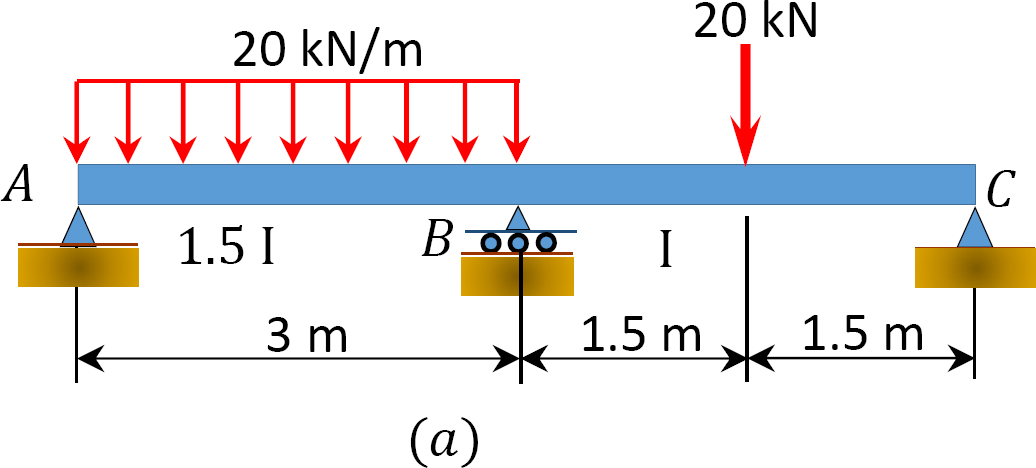
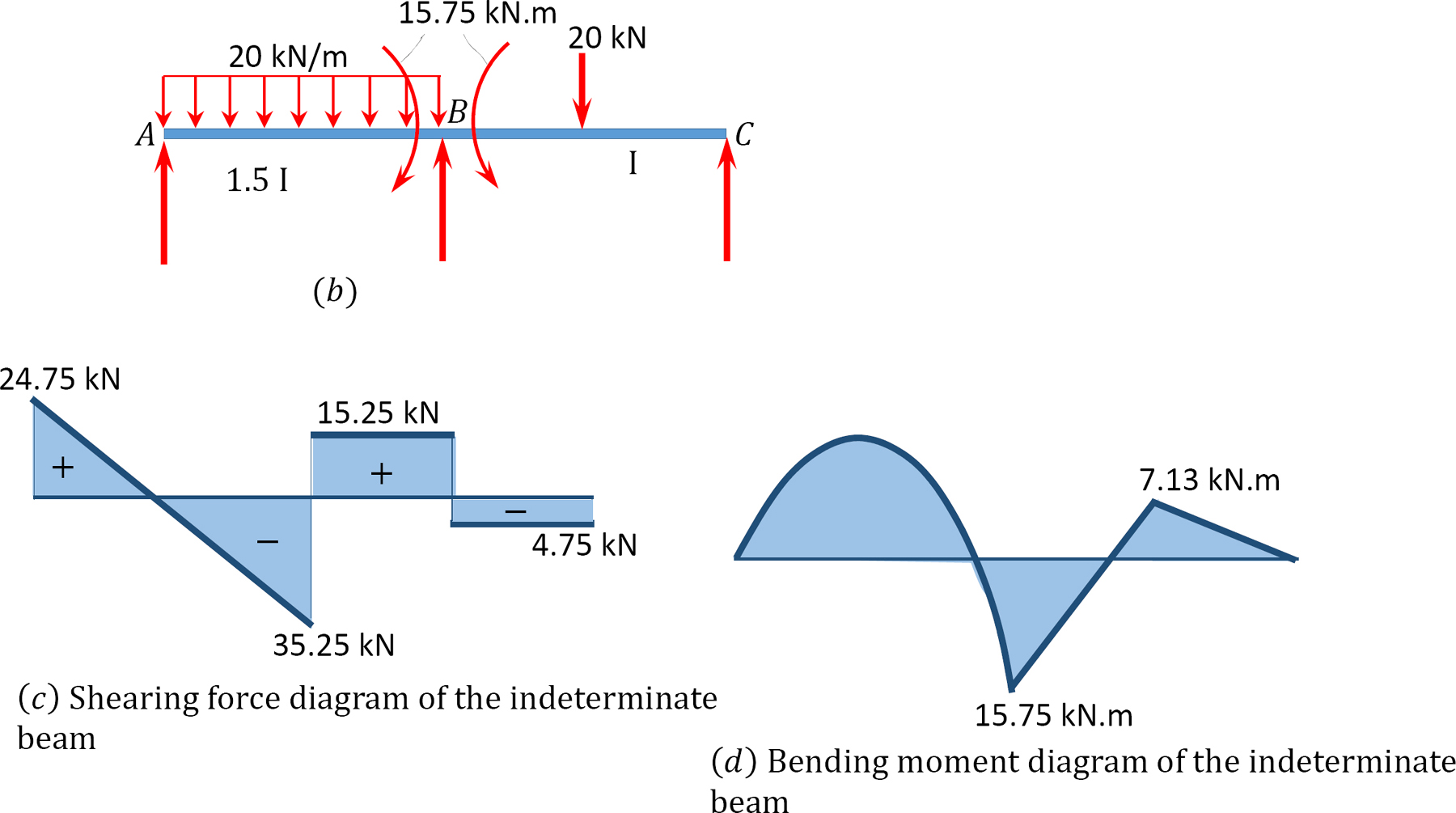
Abb. 12.7. Strahl.
Lösung
Festes Endmoment.
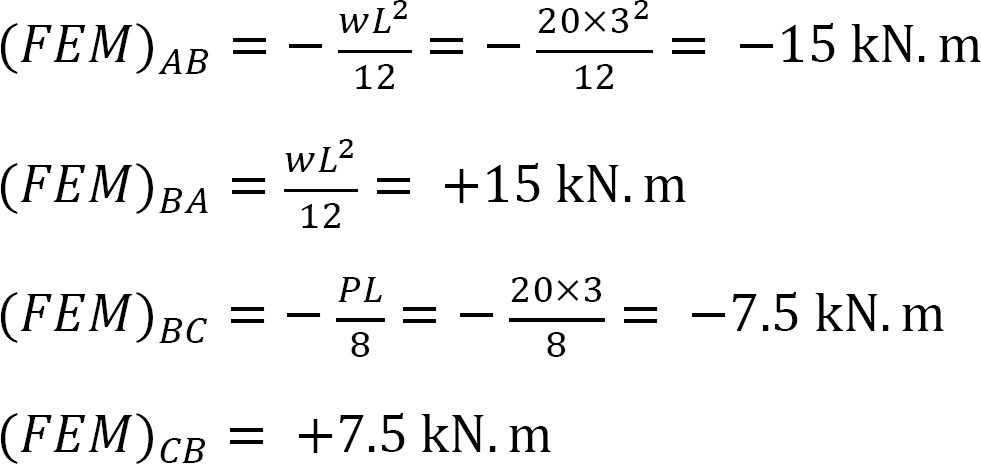
Steifigkeit faktor.
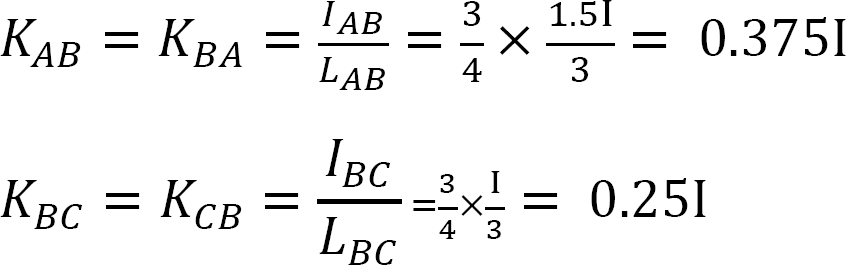
Verteilungsfaktor.
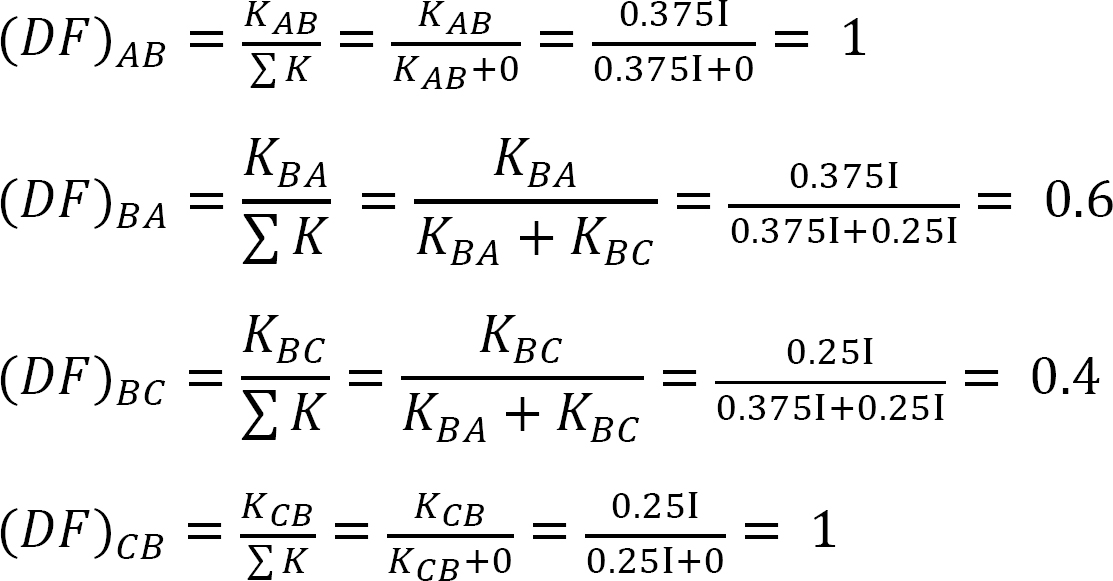
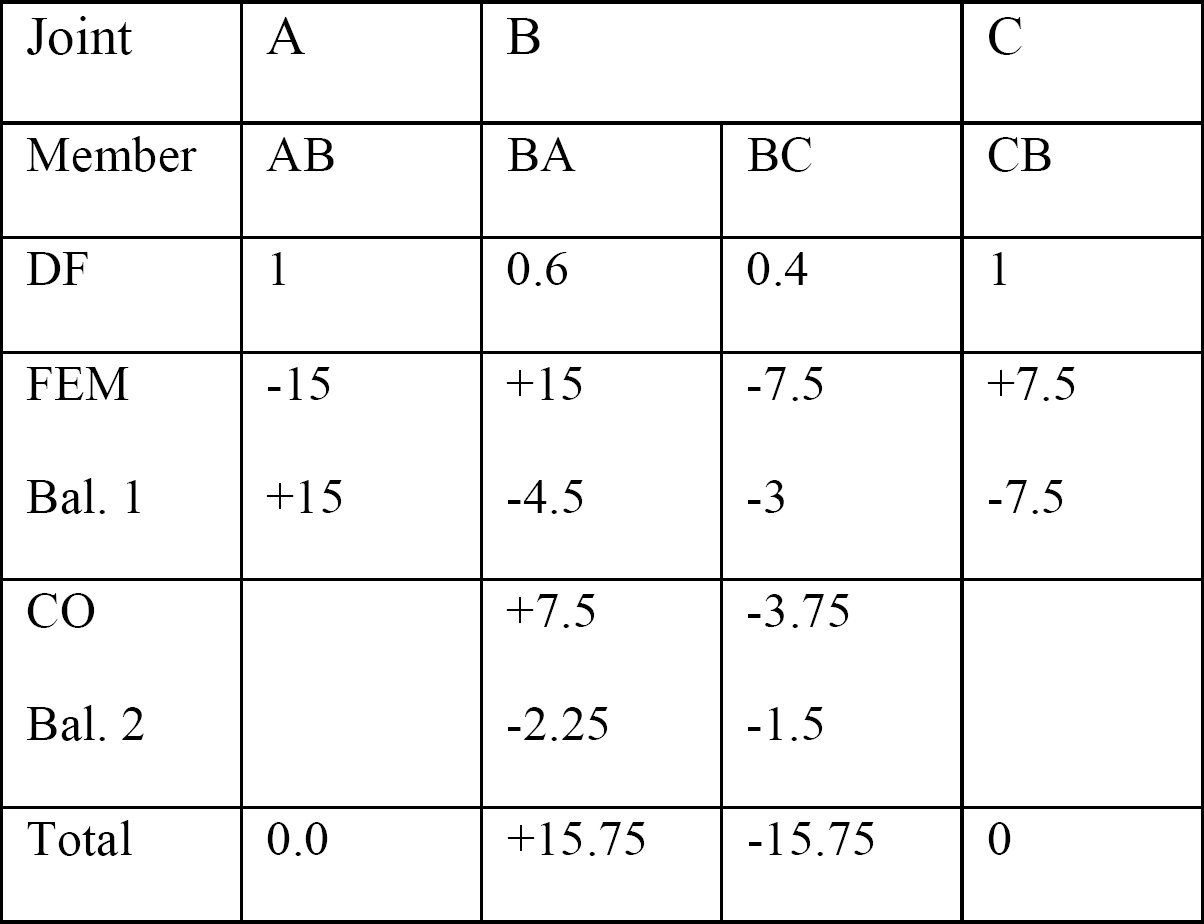
Tabelle 12.2. Verteilungstabelle.
Scherkraft- und Biegemomentdiagramme.
12.6 Analyse unbestimmter Frames
Das Verfahren zur Analyse von Frames mithilfe der Momentverteilungsmethode hängt vom Typ des zu analysierenden Frames ab. Frames werden als Sway- oder Non-Sway-Frames kategorisiert. Das Verfahren zur Analyse von Nicht-Sway-Frames ähnelt dem von unbestimmten Strahlen. Für die Analyse von Sway-Frames ist das Verfahren jedoch anders. Bei der Analyse von Sway Frames gibt es zwei Stufen, nämlich die Nicht-Sway-Stufe und die Sway-Stage-Analyse. Diese Stufen werden im Folgenden beschrieben.
Verfahren zur Analyse unbestimmter Sway-Frames mit der Momentenverteilungsmethode
A. Analyse der Nicht-Sway-Phase
•Nehmen Sie zunächst die Existenz einer imaginären Stütze an, die das Schwanken des Frames verhindert.
*Berechnen Sie die horizontalen Reaktionen an den Stützen des Rahmens und notieren Sie die Differenz X. Dies ist die Kraft, um ein Schwanken zu verhindern.
B. Schwankungsstadienanalyse
*Nehmen Sie beliebige Momente an, um auf die Spalten des Rahmens einzuwirken. Die Größe dieser Momente variiert von Spalte zu Spalte proportional zu 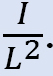
• Für M2 werden Werte angenommen und M1 bestimmt.
•Die willkürlichen Momente werden dann wie für die Nicht-Sway-Bedingung verteilt
*Berechnen Sie die Größe der horizontalen Reaktionen an den Stützen für die Sway-Bedingung. Die Summe dieser Reaktionen ergibt die willkürliche Verschiebekraft Y.
*Bestimmen Sie das Verhältnis 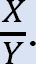 Dieses Verhältnis wird als Schwankungsfaktor bezeichnet.
Dieses Verhältnis wird als Schwankungsfaktor bezeichnet.
*Verwenden Sie den Schwankungsfaktor, um die verteilten Momente des Schwankens zu multiplizieren. Dies gibt den korrigierten Moment für das Schwanken an.
•Die Endmomente für den Rahmen sind die Summe der in der Nicht-Schwankungsstufe erhaltenen Momente und des korrigierten Moments für die Schwankungsstufe.
Beispiel 12.3
Bestimmen Sie mithilfe der Momentenverteilungsmethode die in Abbildung 12.8 gezeigten Endmomente der Stäbe des Rahmens. EI = konstant.
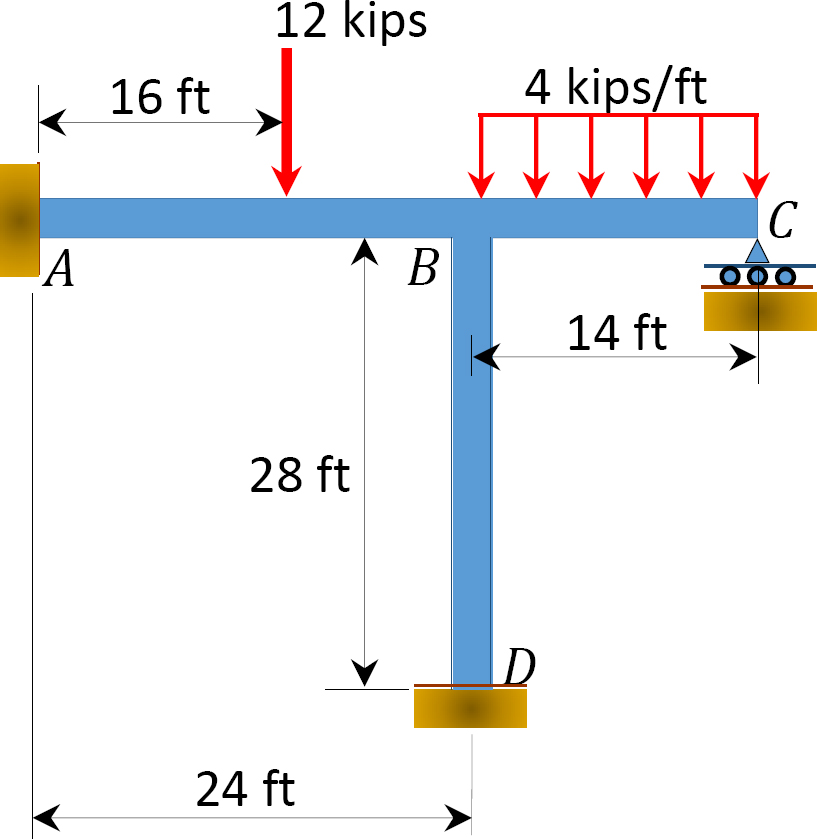
Abb. 12.8. Rahmen.
Lösung
Festes Endmoment.
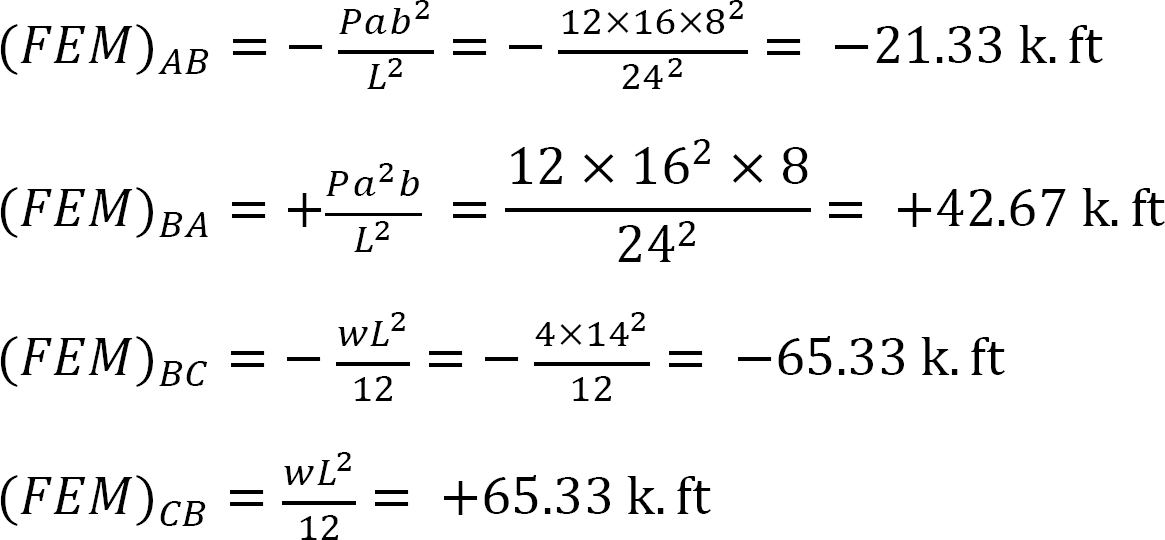
Steifigkeit faktor.
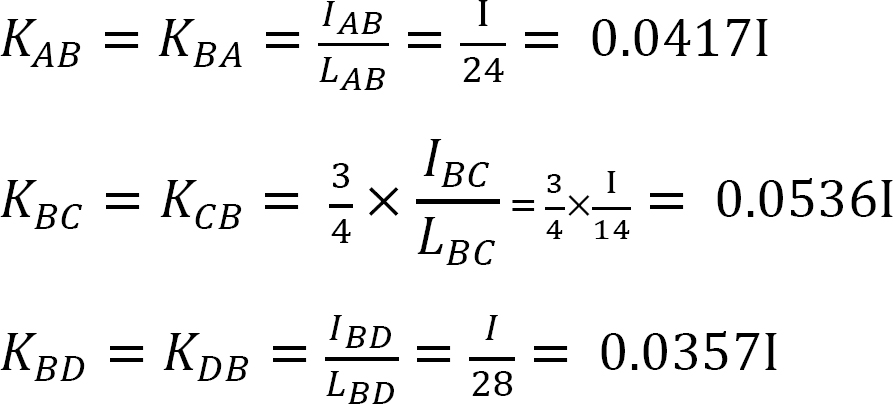
Verteilungsfaktor.
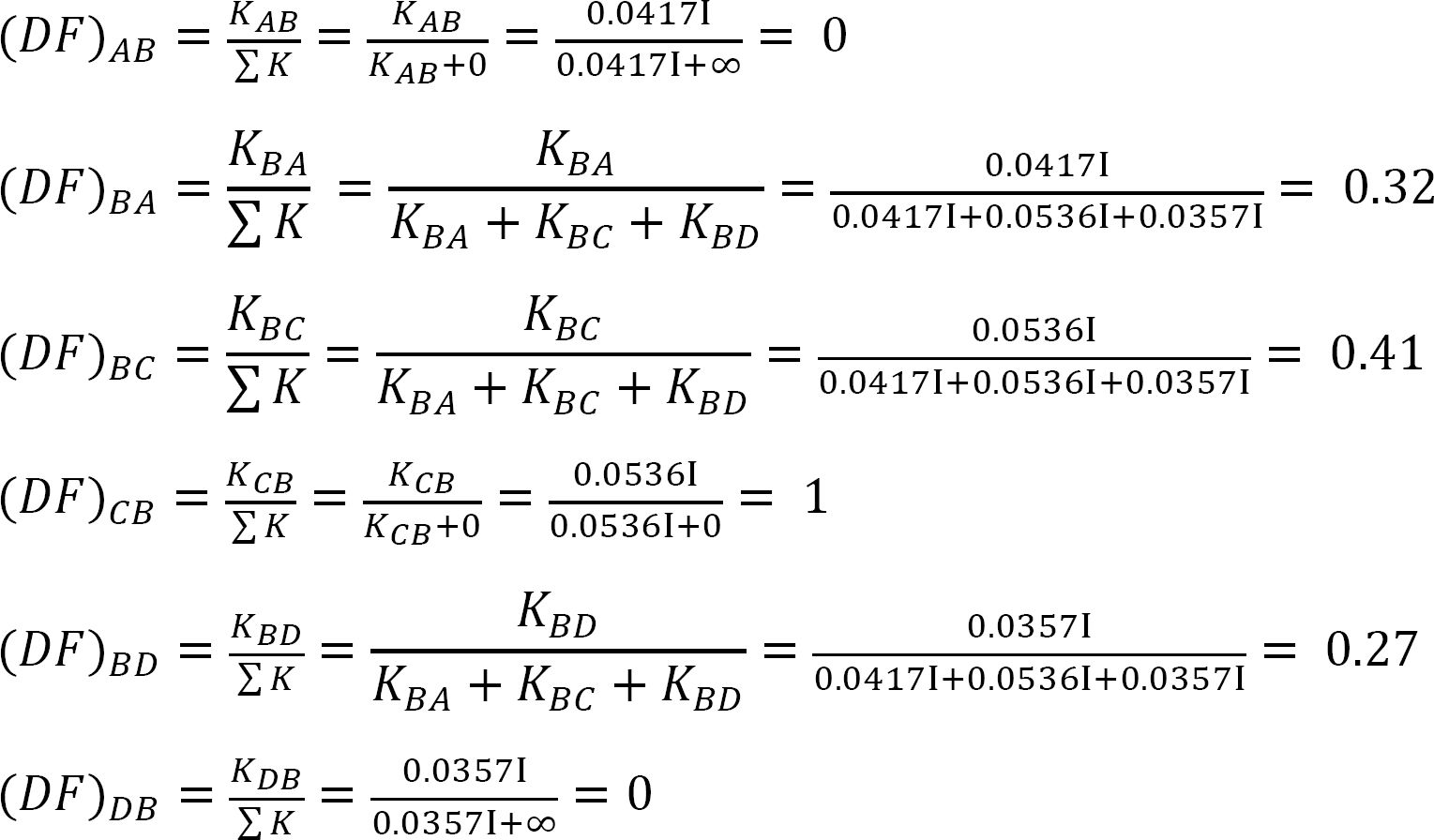
Tabelle 12.3. Verteilungstabelle.
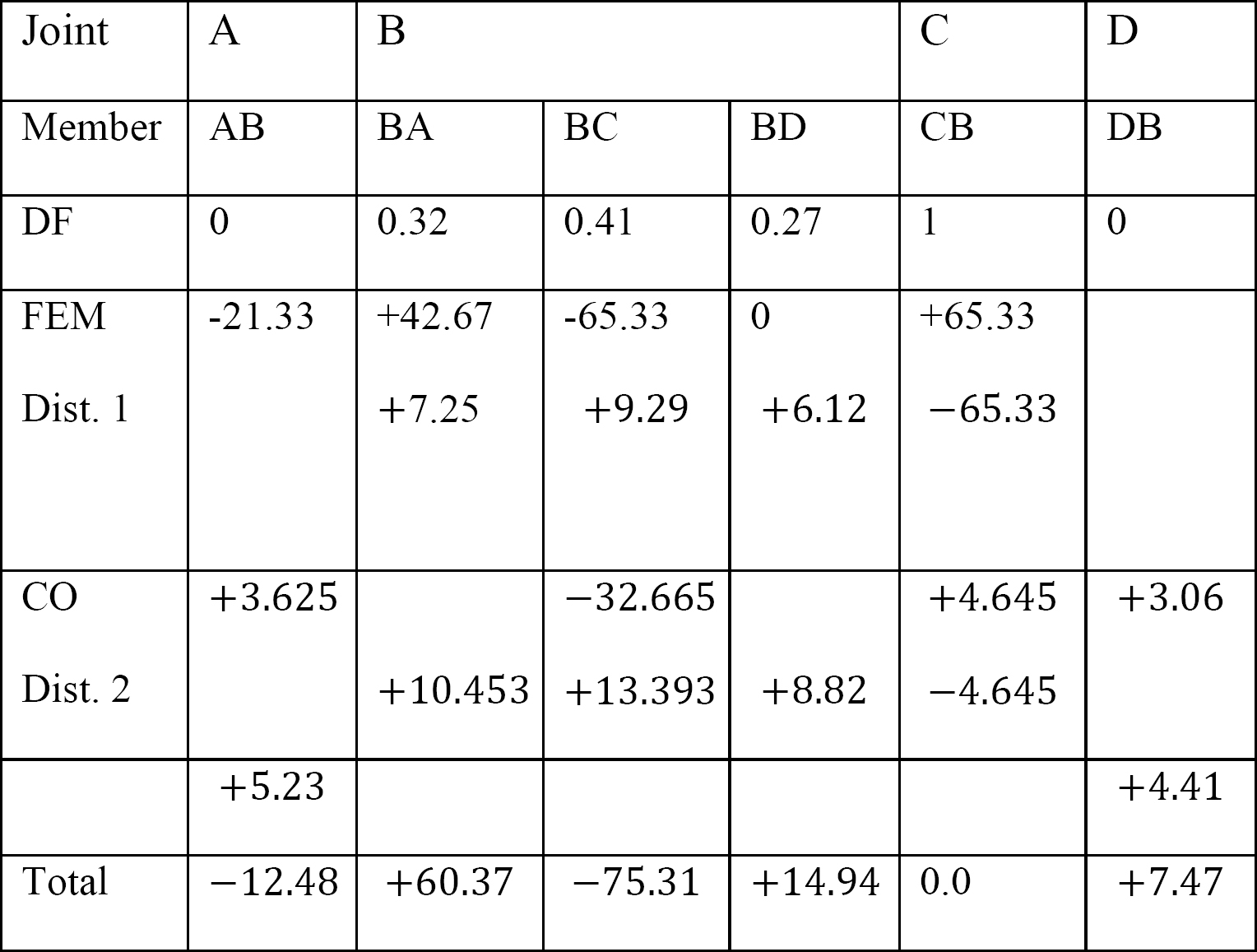
Letzte Mitglied Ende Momente.
Das Einsetzen der erhaltenen Werte von EKθB, EKθC und EK∆ in die Elementendmomentgleichungen legt Folgendes nahe:
MAB = -12,48 k. ft
MBA = +60,37 k. ft
MBC = -75,31 k. ft
MBD = +14,94 k. ft
MCB = 0
MDB = +7,47 k. ft
Beispiel 12.4
Bestimmen Sie mit der Momentenverteilungsmethode die in Abbildung 12.9 gezeigten Endmomente an den Stützen des Rahmens. EI = konstant.
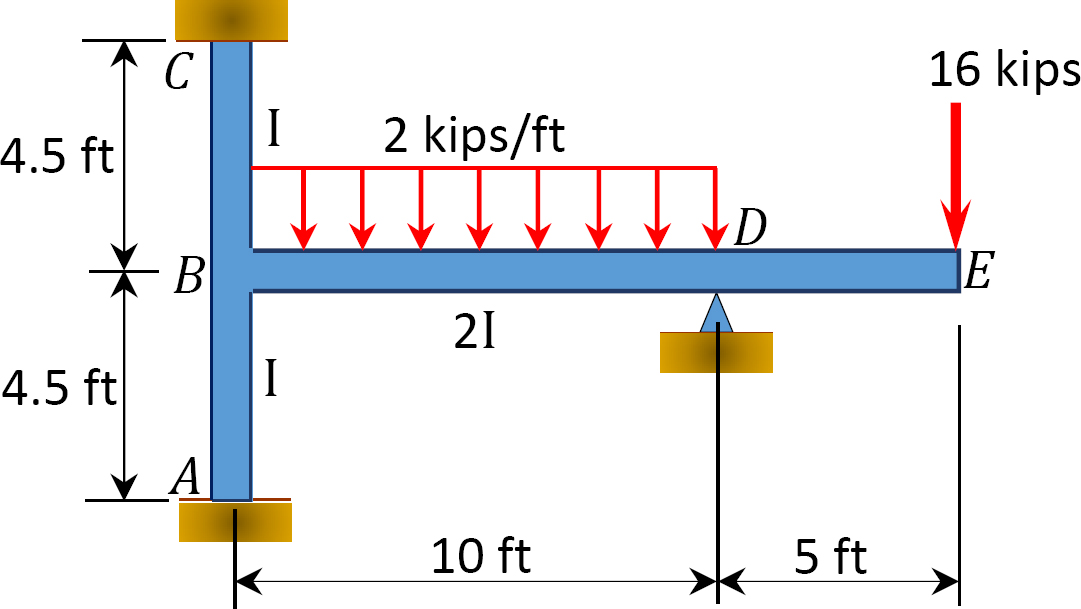
Abb. 12.9. Rahmen.
Lösung
Festes Endmoment.
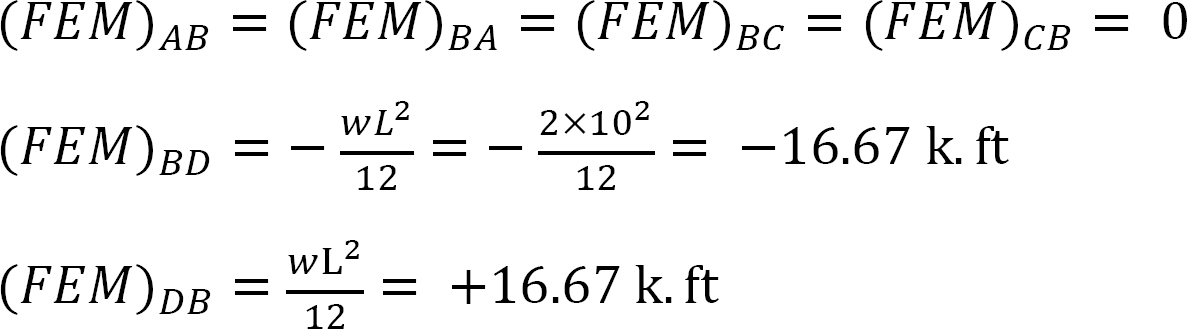
Steifigkeit faktor.
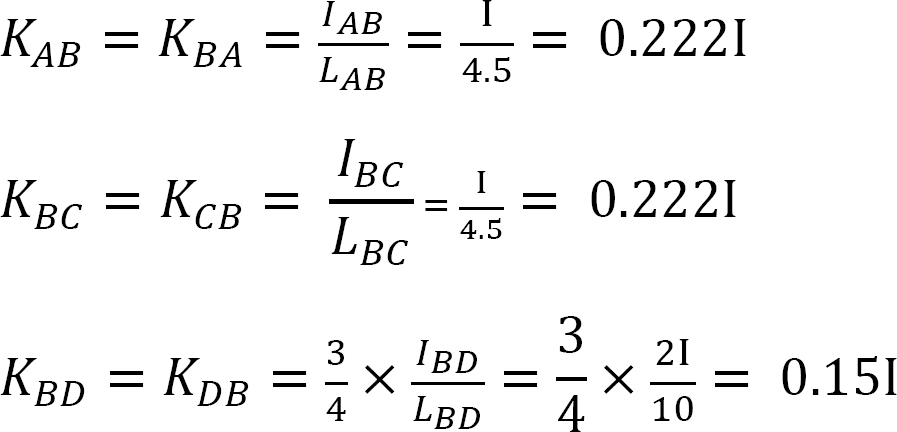
Verteilungsfaktor.

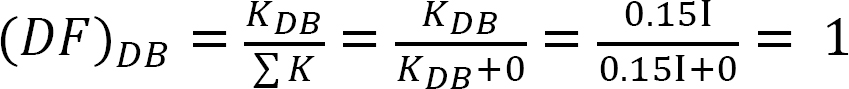
Tabelle 12.4. Verteilungstabelle.
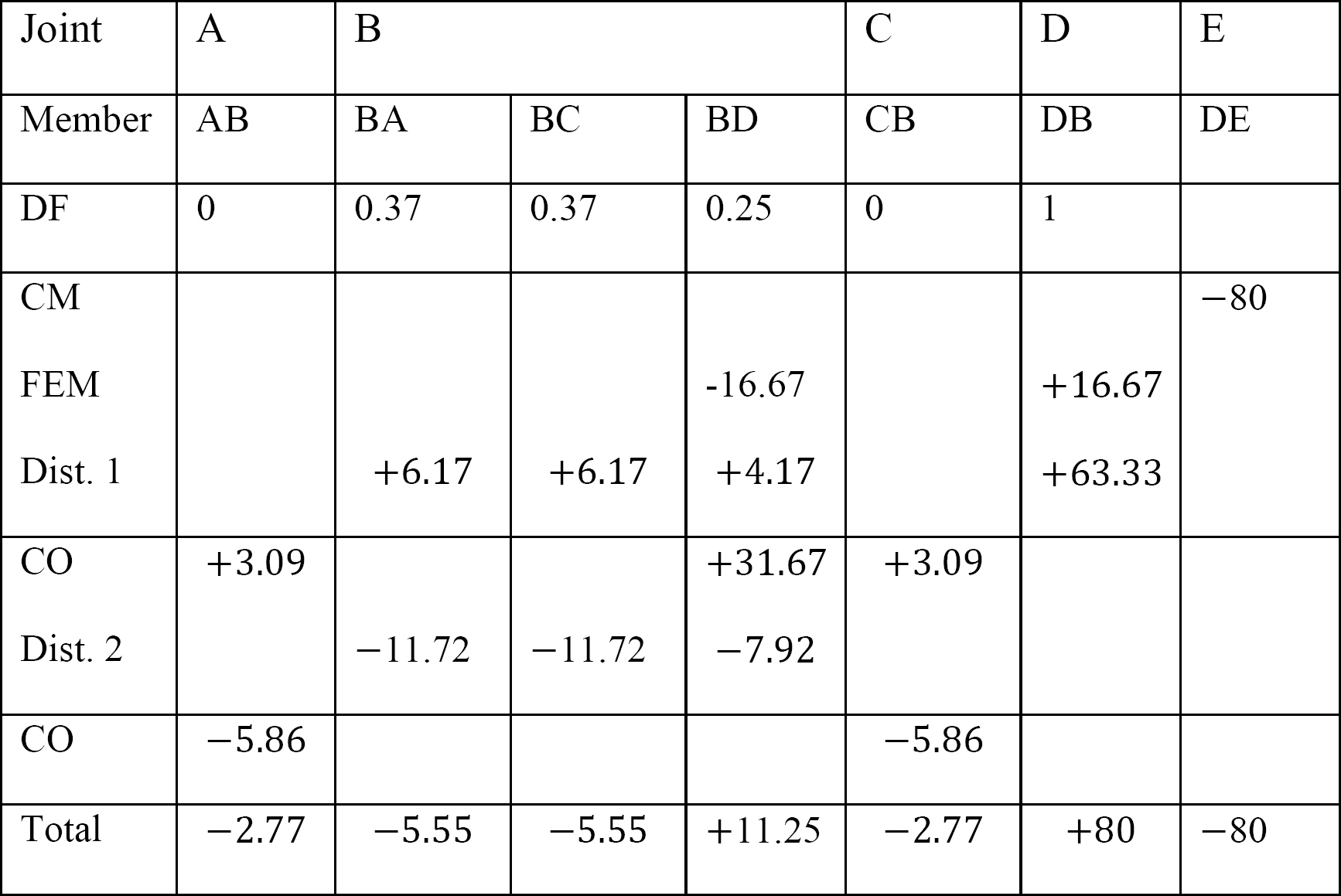
Letzte Mitglied Ende Momente.
MAB = -2,77 Fuß
MBA = -5,55 Fuß
MBC = -5,55 Fuß. ft
MBD = +11,25 k. ft
MCB = -2,77
MDB = +80 k. ft
MDE = -80 k. ft
Beispiel 12.5
Bestimmen Sie mit der Momentenverteilungsmethode die in Abbildung 12.10 gezeigten Endmomente an den Stützen des Rahmens. EI = konstant.
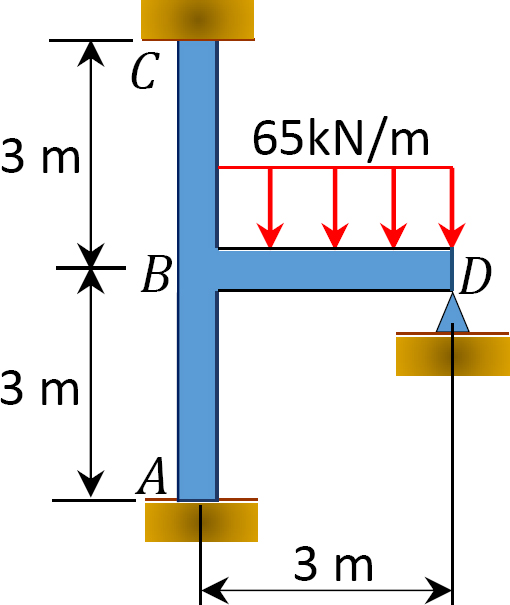
Abb. 12.10. Rahmen.
Lösung
Festes Endmoment.
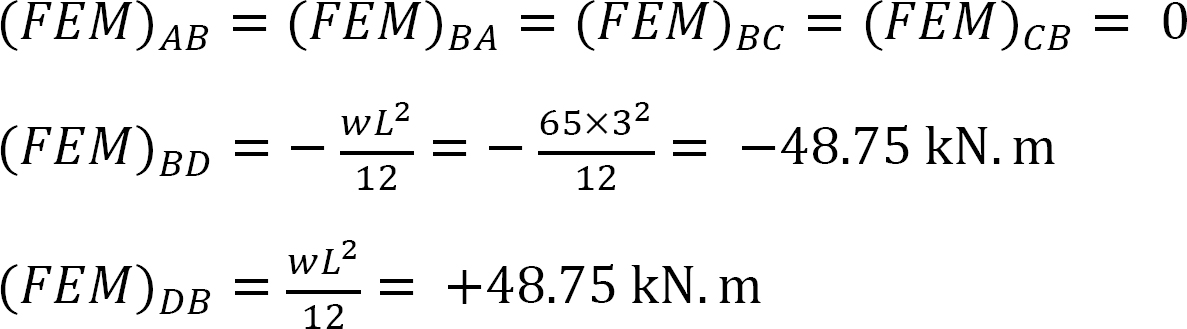
Steifigkeit faktor.
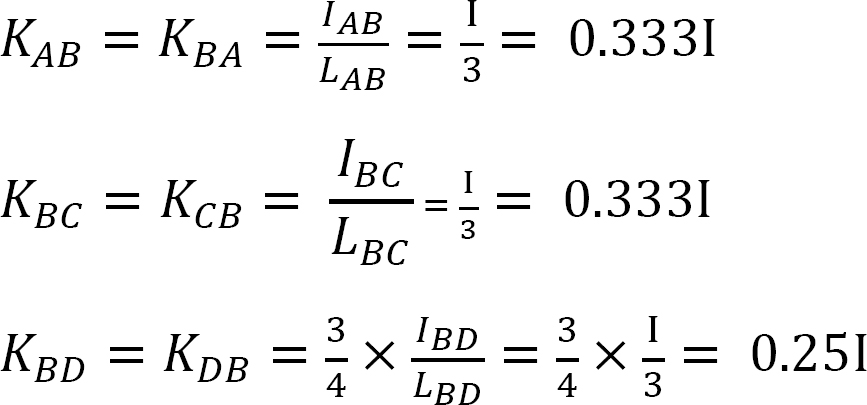
Verteilungsfaktor.
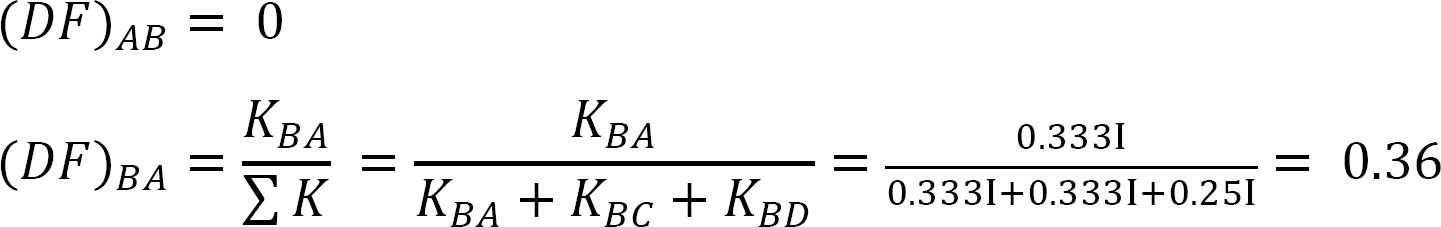

Tabelle 12.5. Verteilungstabelle.
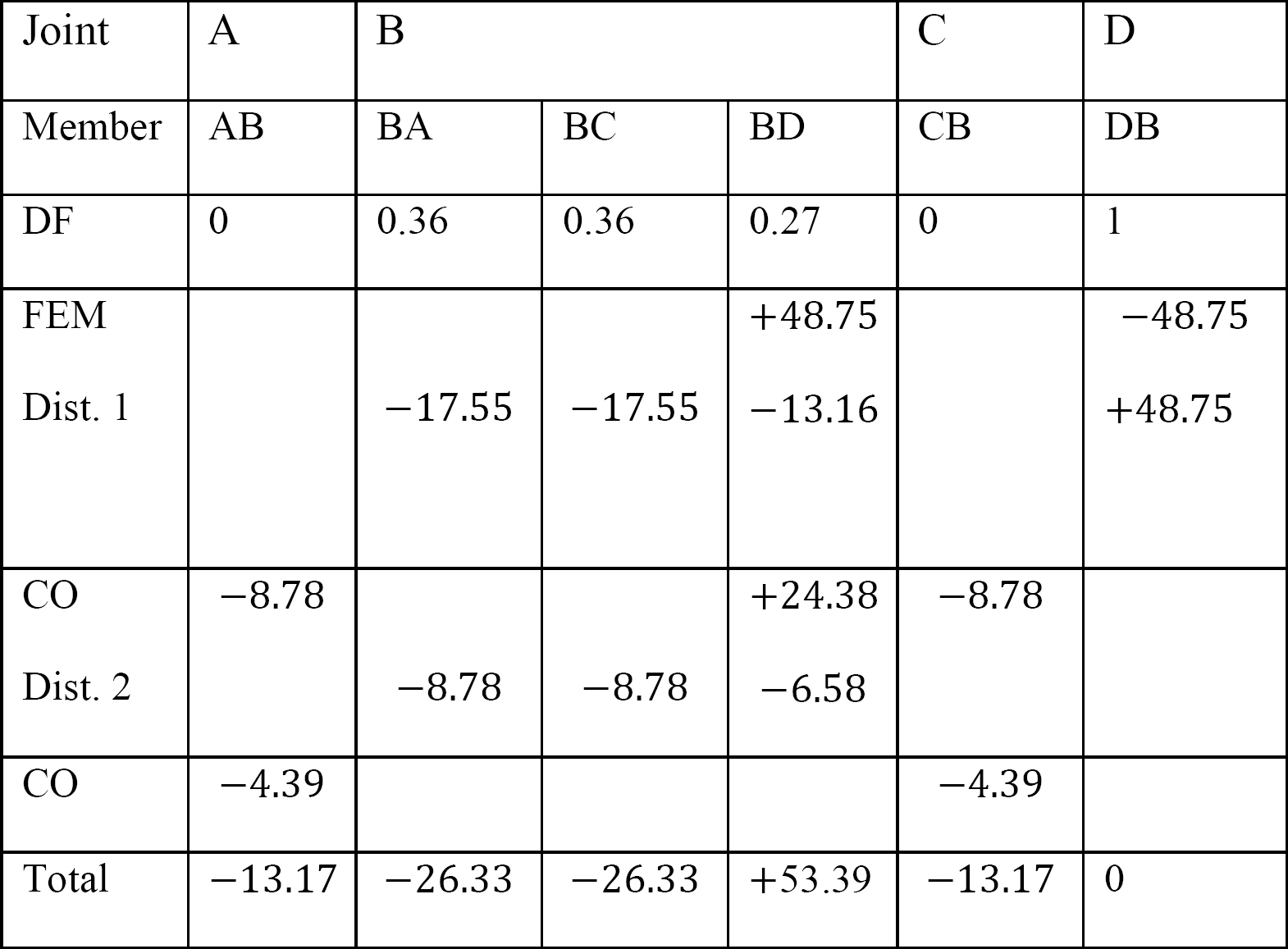
Letzte Mitglied Ende Momente.
MAB = -13,17 Fuß
MBA = -26,33 Fuß
MBC = -26,33 Fuß
MBD = +53,39 Fuß
MCB = -13,17 Fuß
MDB = 0
Beispiel 12.6
Bestimmen Sie mit der Momentenverteilungsmethode die Stabendmomente des Rahmens mit seitlichem Schwanken, wie in Abbildung 12.11a gezeigt.
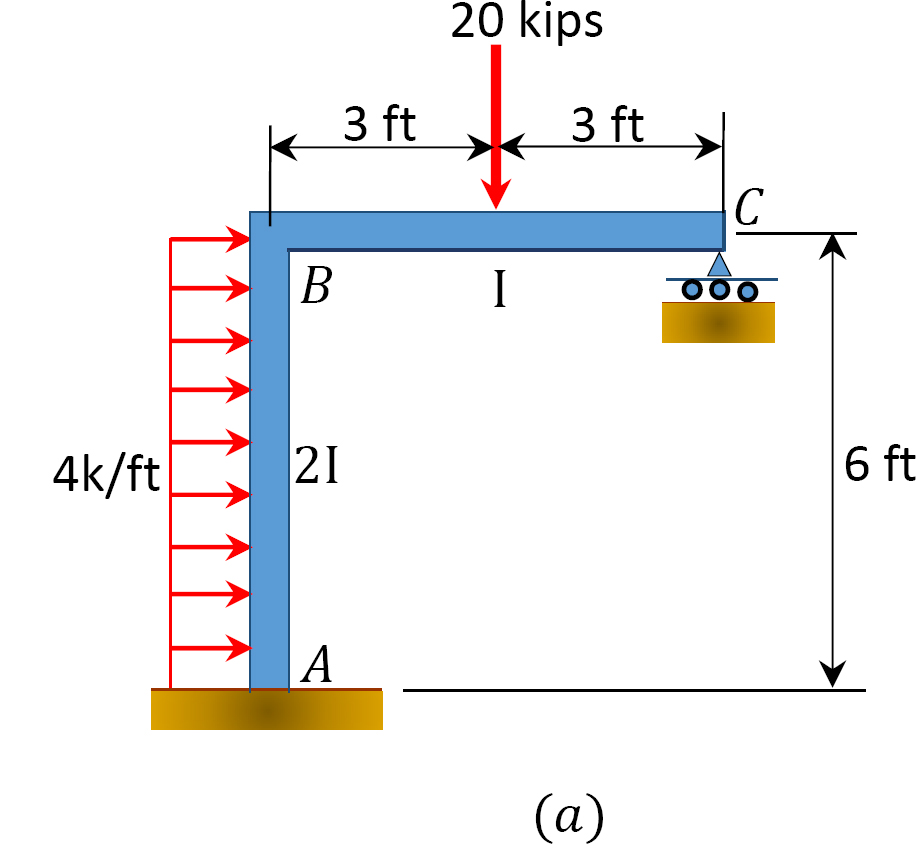
Abb. 12.11. Rahmen mit Side – Sway.
Lösung
Festes Endmoment.
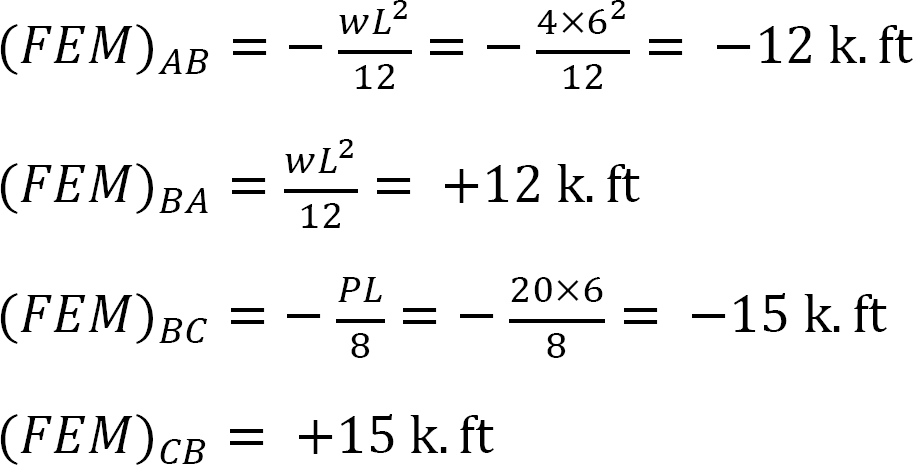
Steifigkeit faktor.
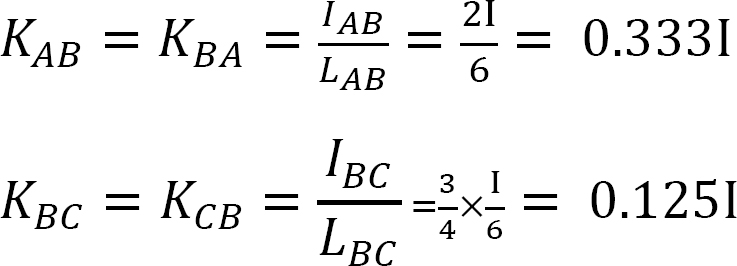
Verteilungsfaktor.
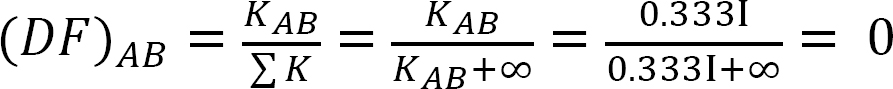

Analyse des Rahmens ohne seitliches Schwanken.
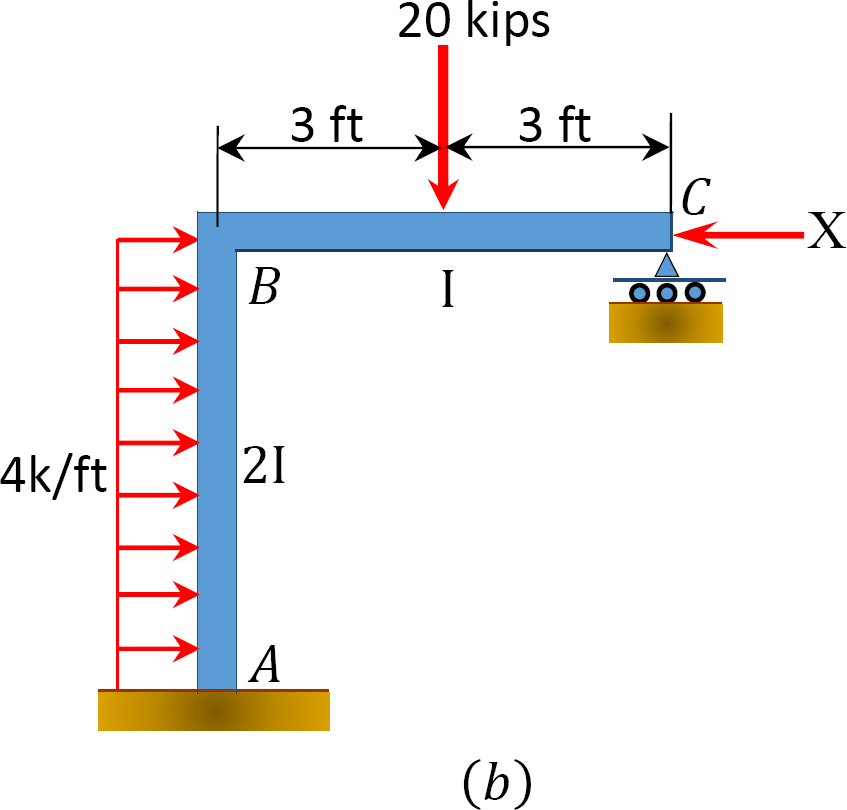
Tabelle 12.6. Verteilungstabelle (kein Schwankungsrahmen).
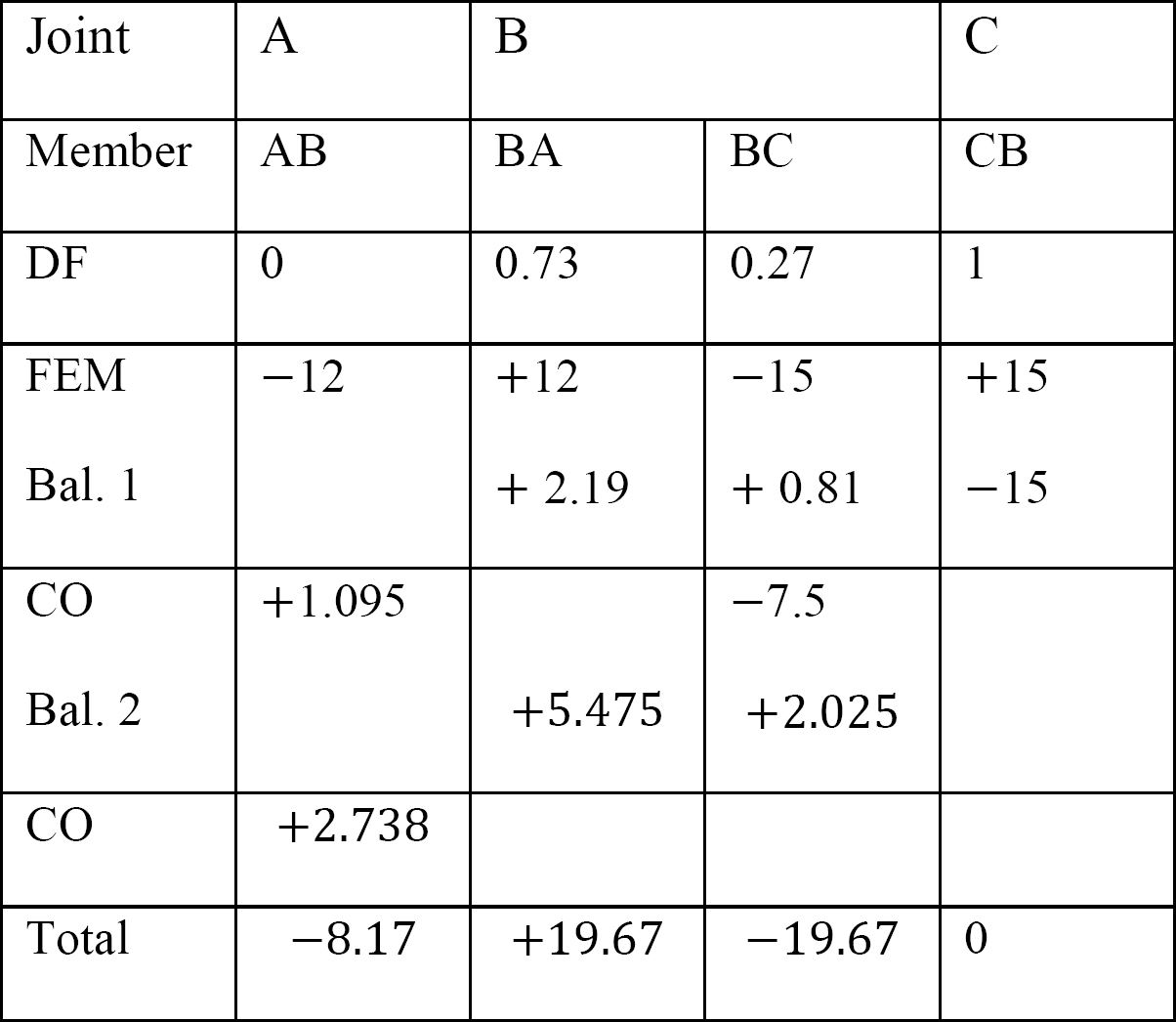
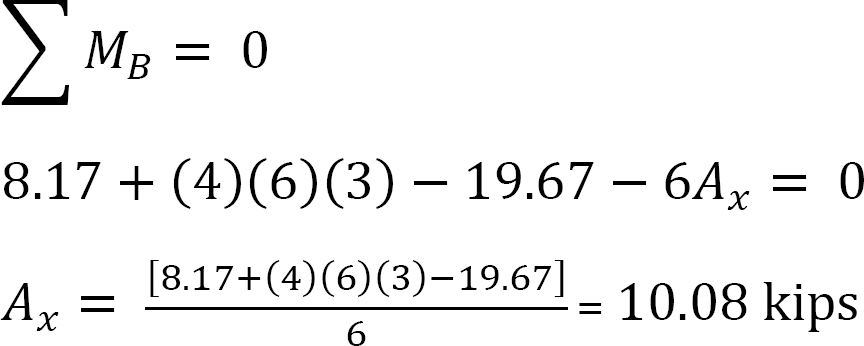
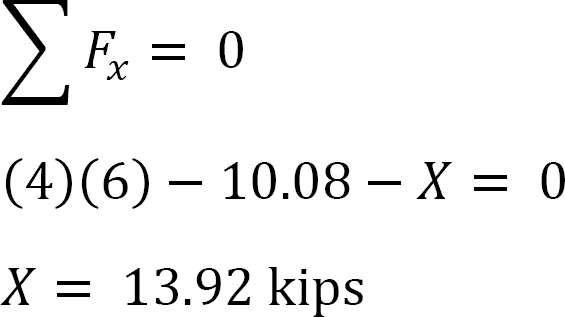
Analyse des Rahmens mit Side-Sway.
Angenommen, MAB = +20 k. ft
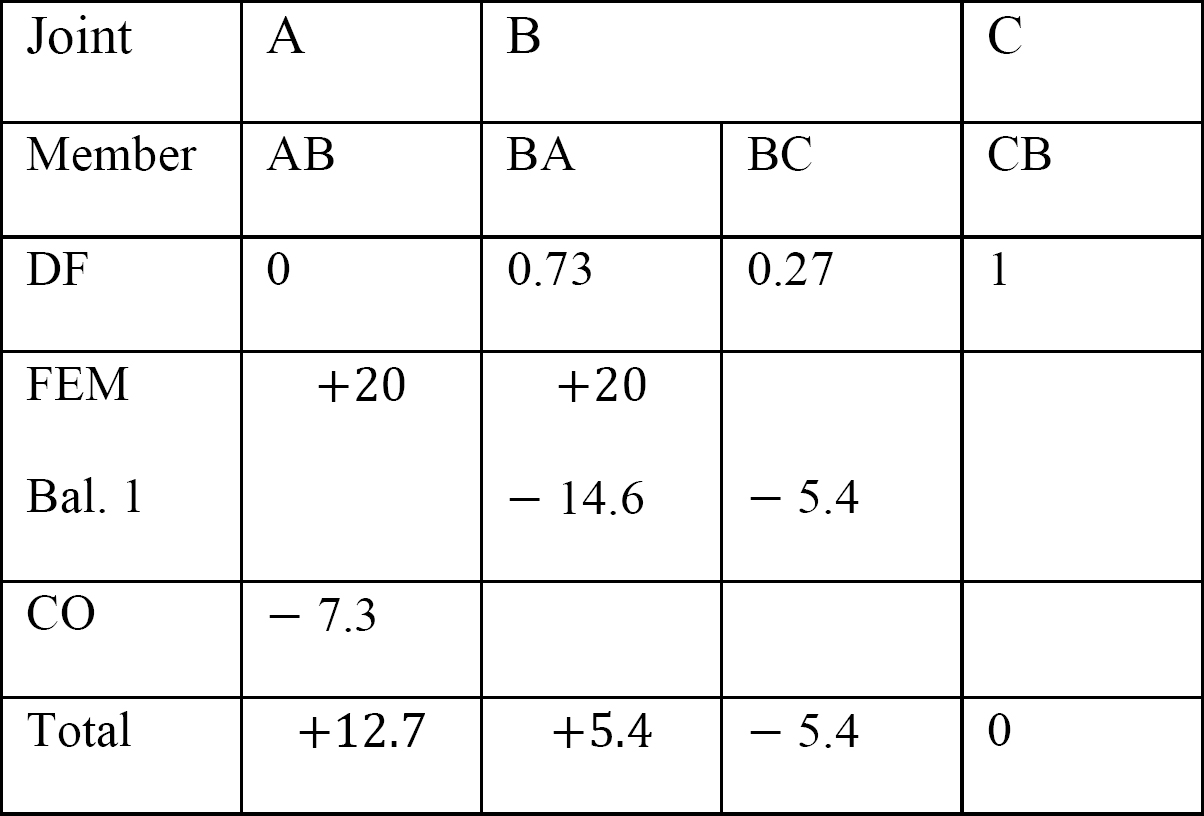
Tabelle 12.7. Verteilungstabelle (Pendelrahmen).
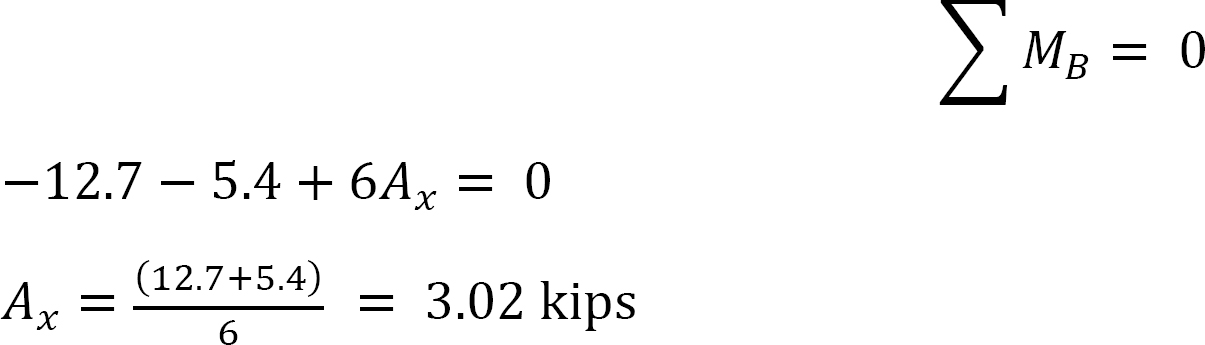
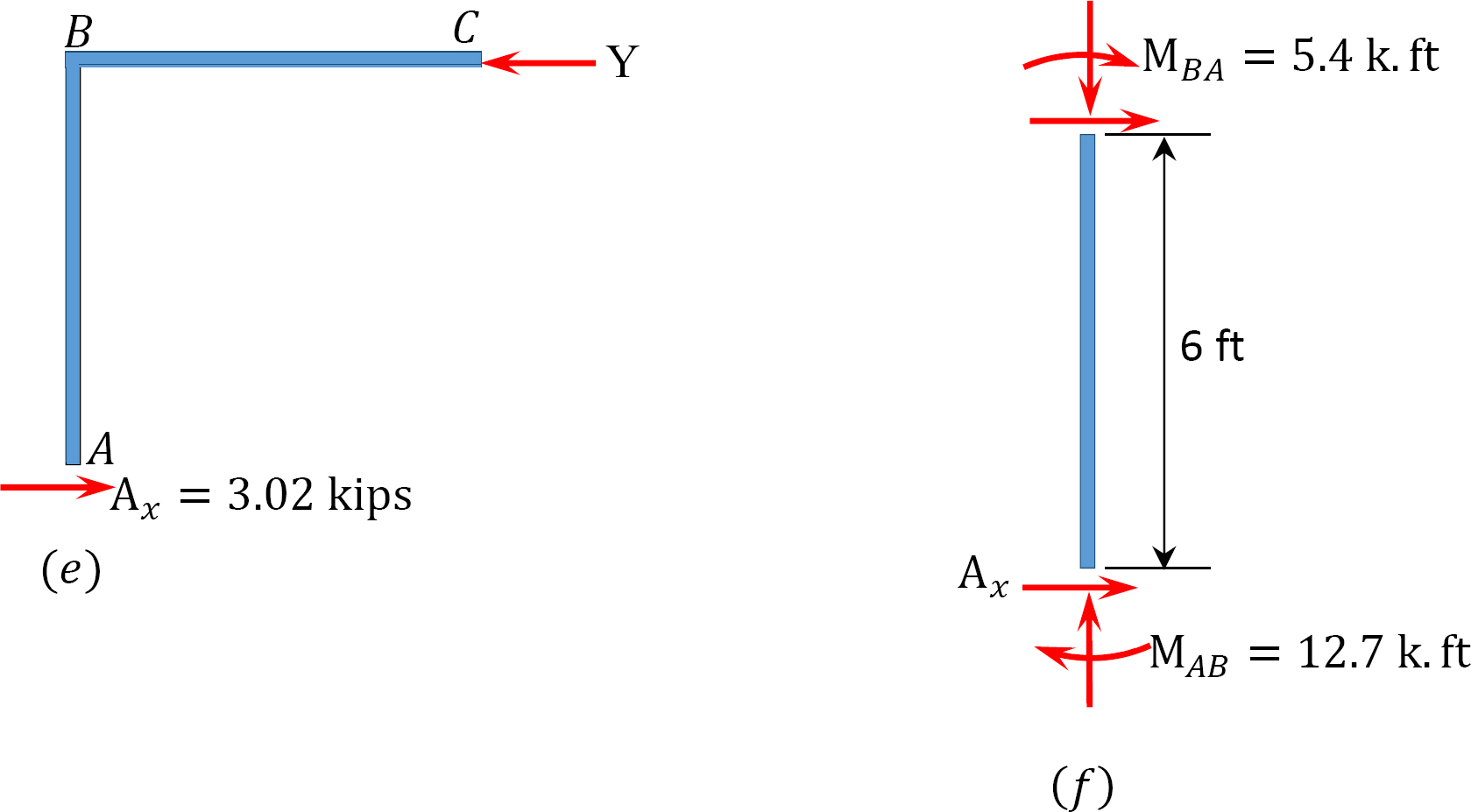
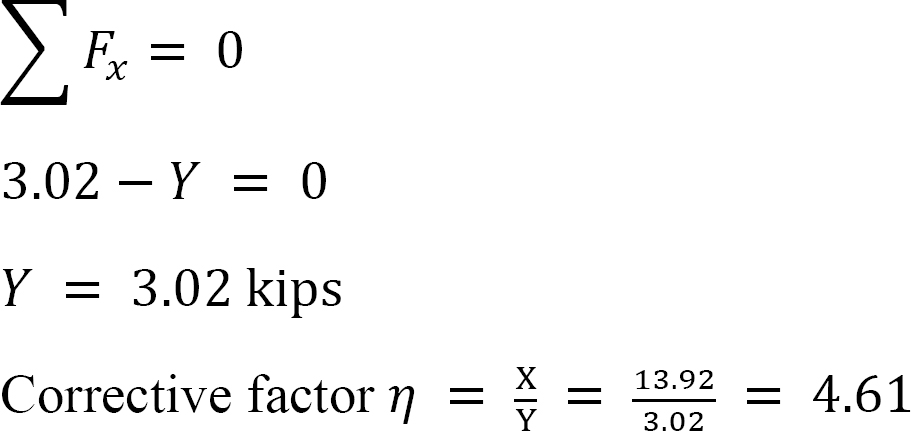
Letzte Endmomente.
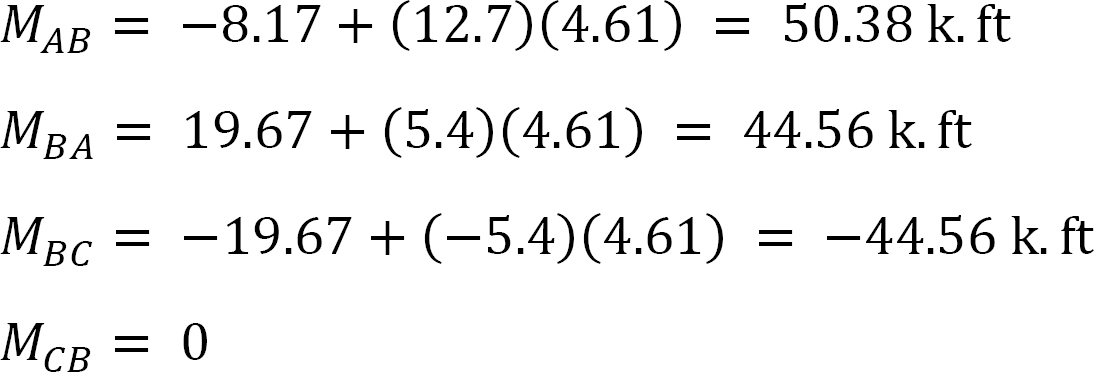
Beispiel 12.7
Ein Pendelrahmen wird wie in Abbildung 12.12a gezeigt geladen. Bestimmen Sie mithilfe der Momentenverteilungsmethode die Endmomente der Glieder des Rahmens.
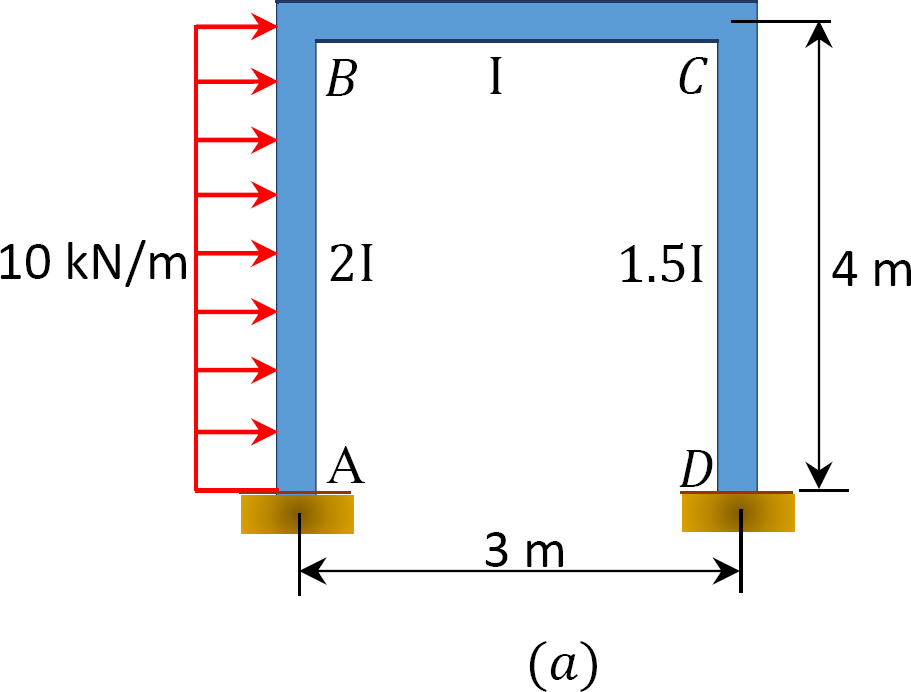
Abb. 12.12. Geladen sway rahmen.
Lösung
Festes Endmoment.
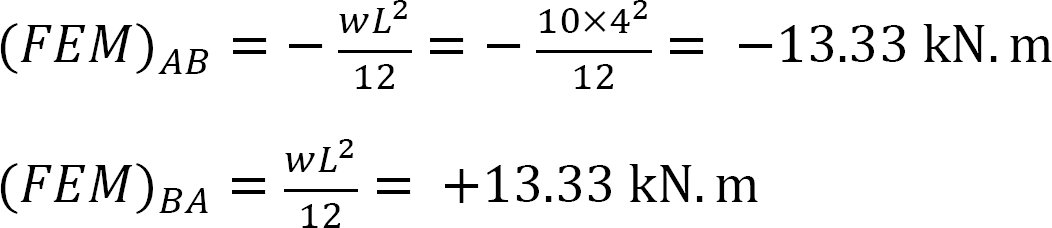
Steifigkeit faktor.
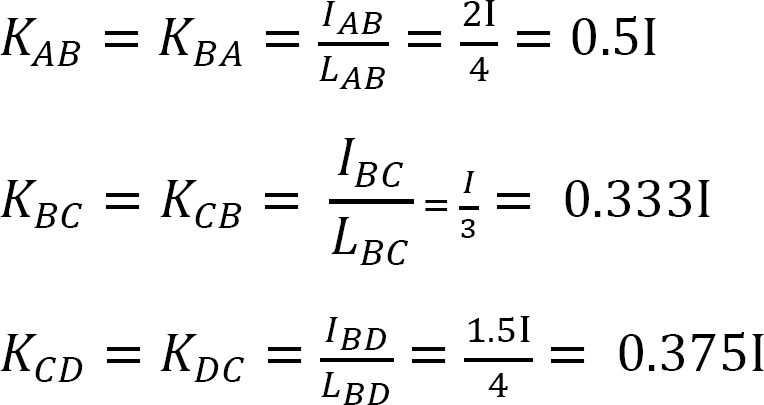
Verteilungsfaktor.

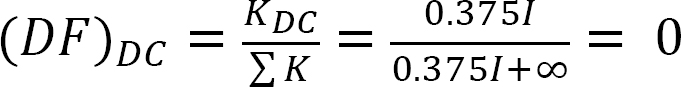
Analyse des Rahmens ohne seitliches Schwanken.
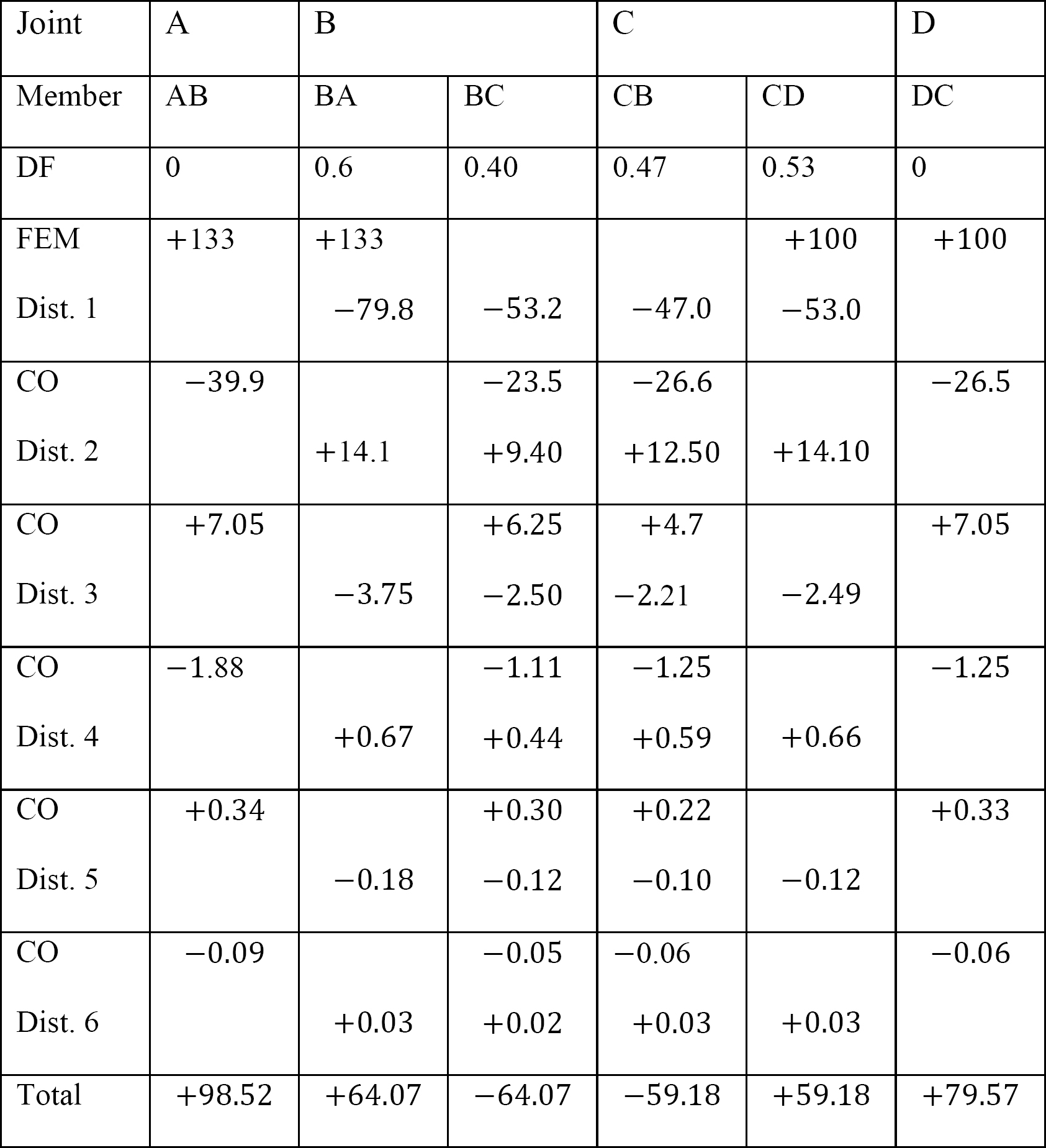
Tabelle 12.8. Verteilungstabelle (kein Schwankungsrahmen).
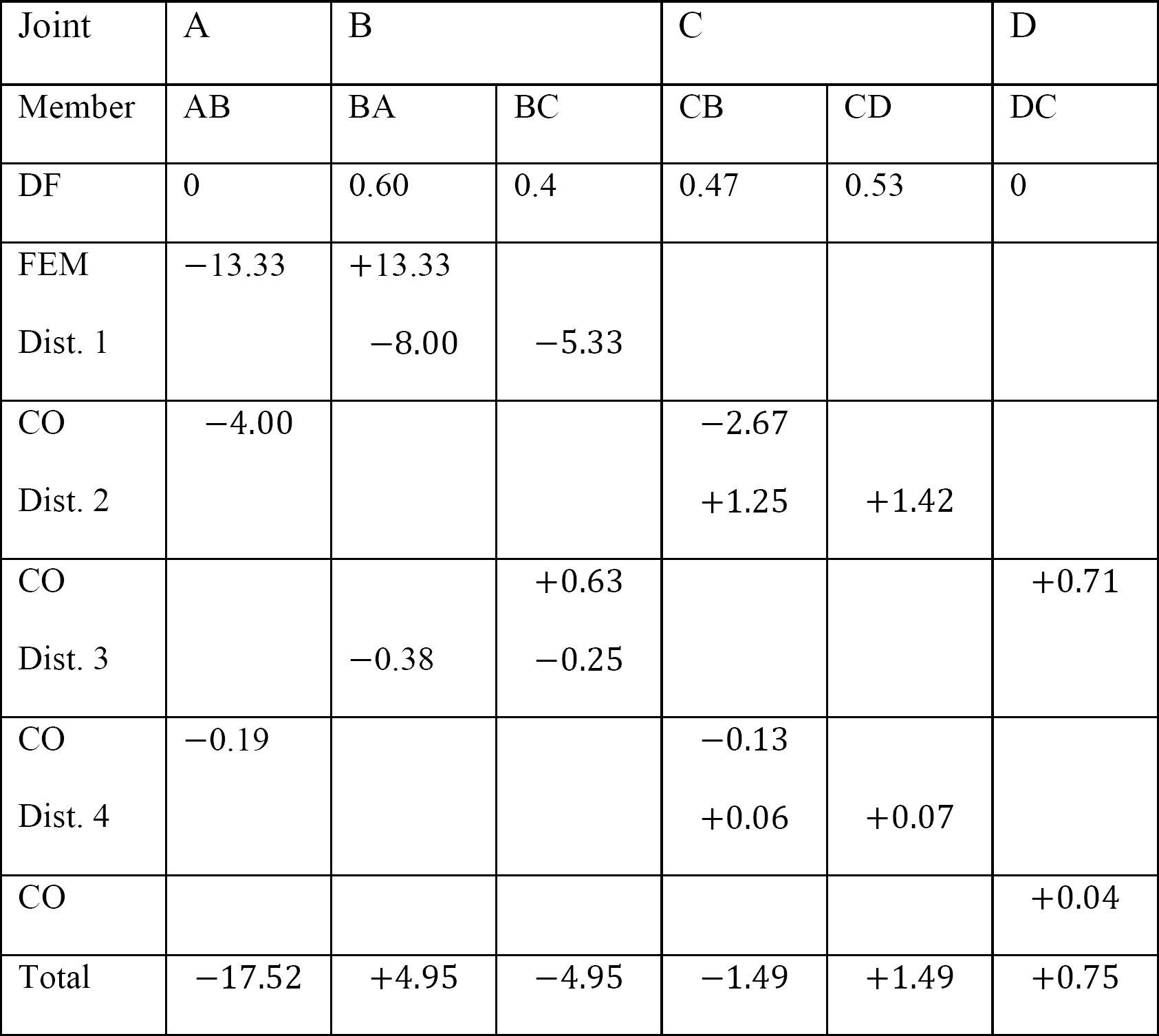
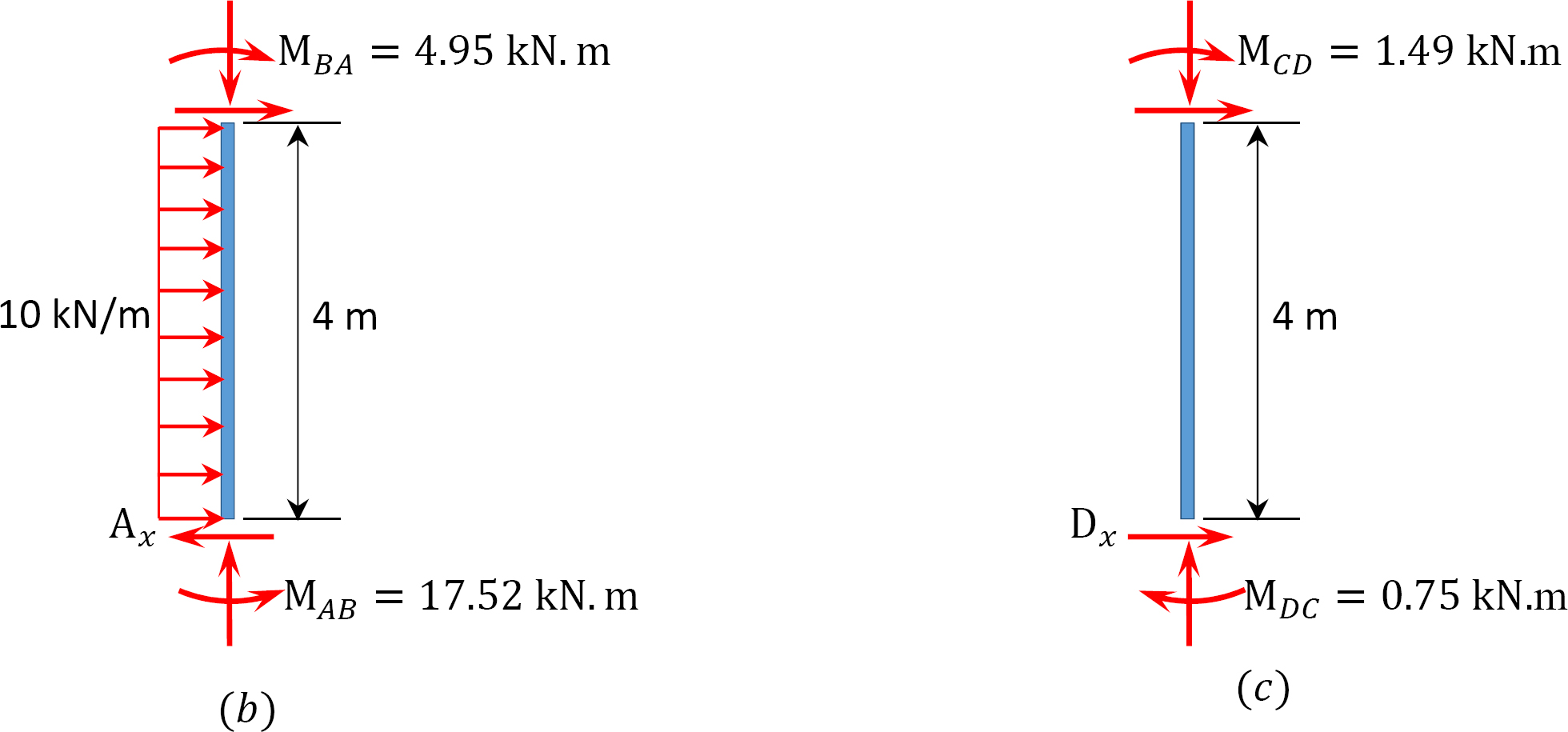
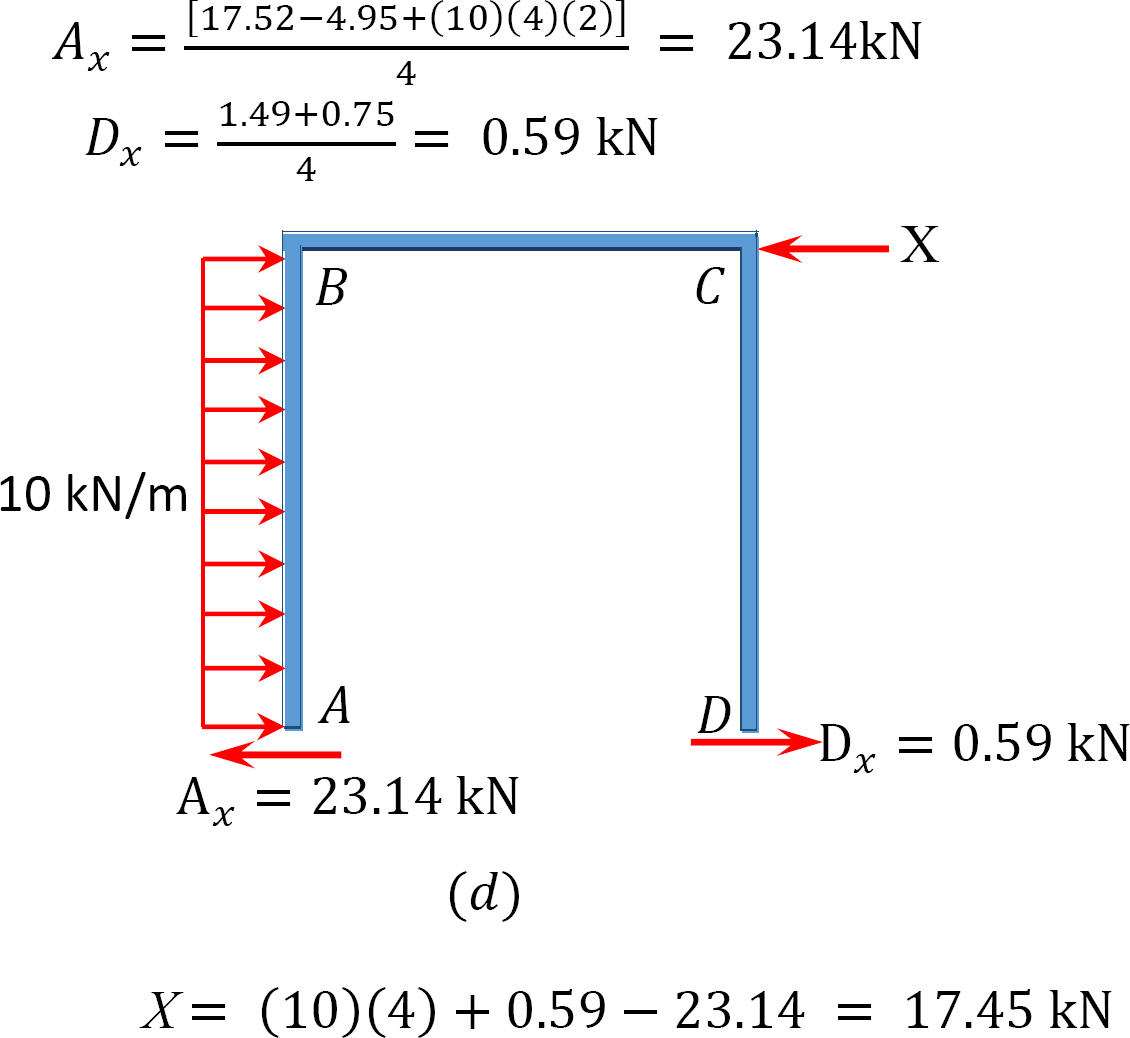
Tabelle 12.9. Verteilungstabelle (Pendelrahmen).
Analyse des Rahmens mit Side-Sway.
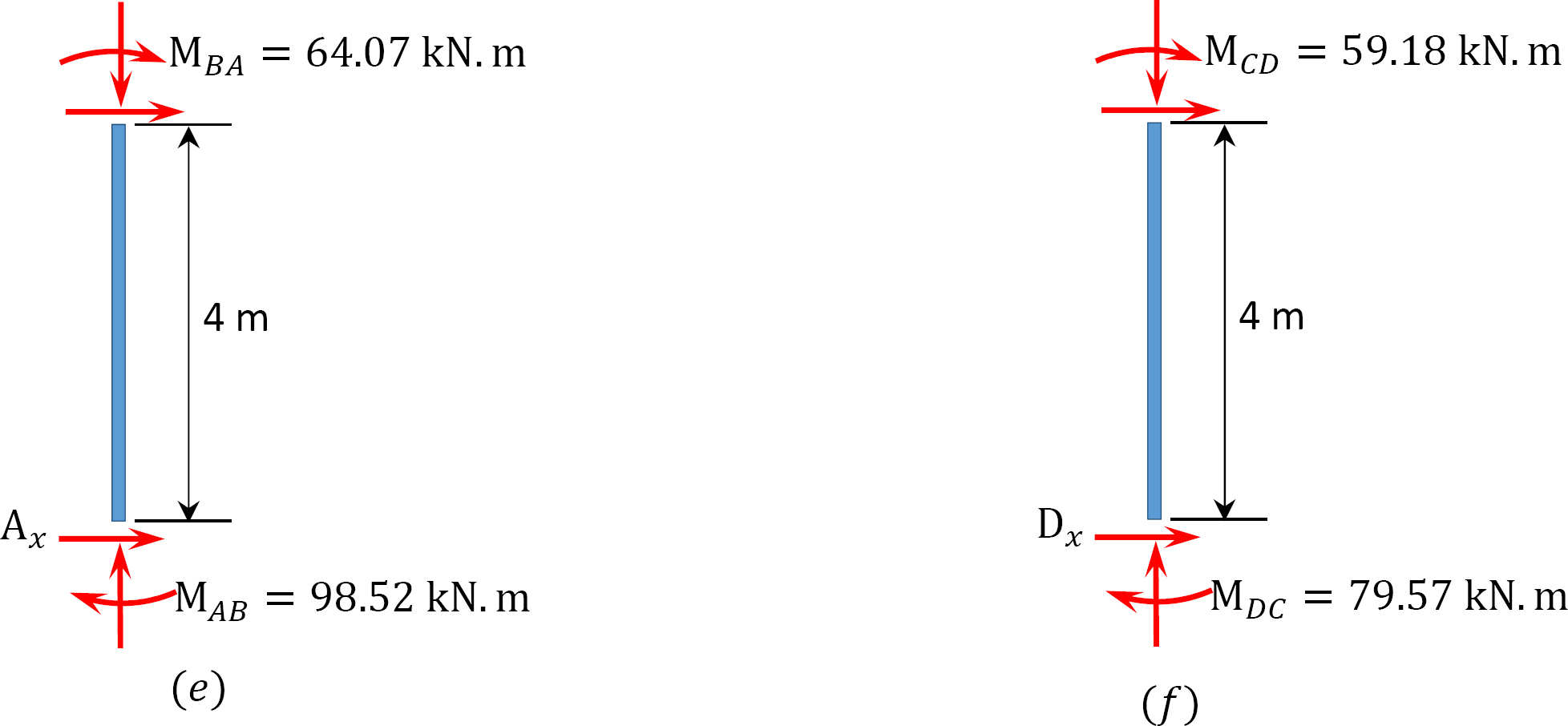

Letzter Endmoment.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Kapitelzusammenfassung
Momentverteilungsmethode zur Analyse unbestimmter Strukturen: Die Momentverteilungsmethode der Analyse ist eine ungefähre Analysemethode. Der Grad der Genauigkeit hängt von der Anzahl der Iterationen ab. Bei diesem Verfahren wird davon ausgegangen, dass alle Gelenke in einer Struktur vorübergehend verriegelt oder geklemmt sind und somit an einer möglichen Drehung gehindert werden. Lasten werden auf die Mitglieder angewendet, und die Momente, die an den Stabenden aufgrund der Fixität entwickelt werden, werden bestimmt. Gelenke in der Struktur werden dann nacheinander entriegelt, und das unausgeglichene Moment an jedem Gelenk wird an Mitglieder verteilt, die sich an diesem Gelenk treffen. Übertragungsmomente an den fernen Enden der Mitglieder werden bestimmt, und der Prozess des Auswuchtens wird fortgesetzt, bis das gewünschte Maß an Genauigkeit erreicht ist. Die Endmomente der Mitglieder werden durch Addieren des Fixed-End-Moments, des verteilten Moments und des Carry-Over-Moments bestimmt. Sobald die Endmomente der Mitglieder bestimmt sind, wird die Struktur bestimmt.
Übungsprobleme
12.1 Verwenden Sie die Momentenverteilungsmethode, um das Endmoment der in Abbildung P12.1 bis Abbildung P12.12 gezeigten Träger zu berechnen und die Biegemoment- und Scherkraftdiagramme zu zeichnen. EI = konstant.
Abb. P12.1. Strahl.
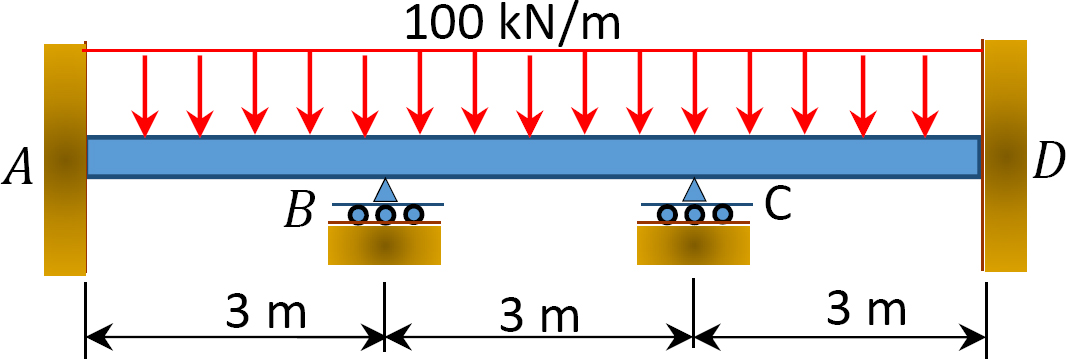
Abb. P12.2. Strahl.
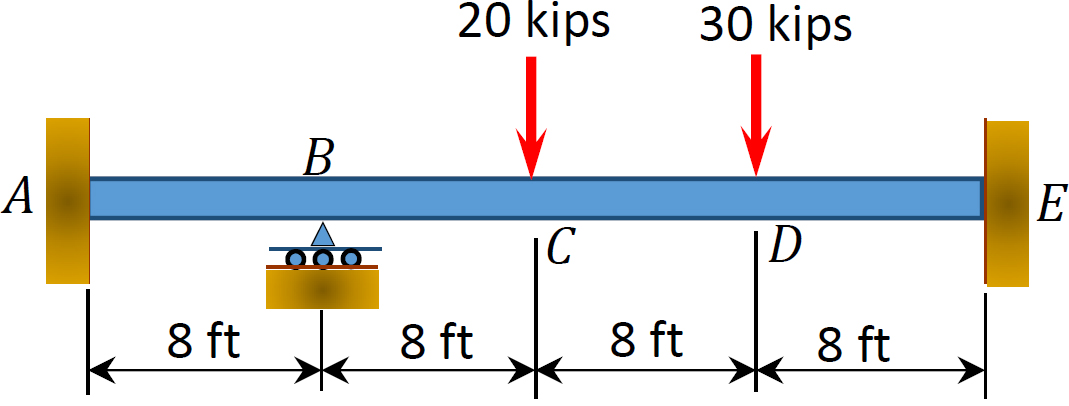
Abb. S12.3. Strahl.
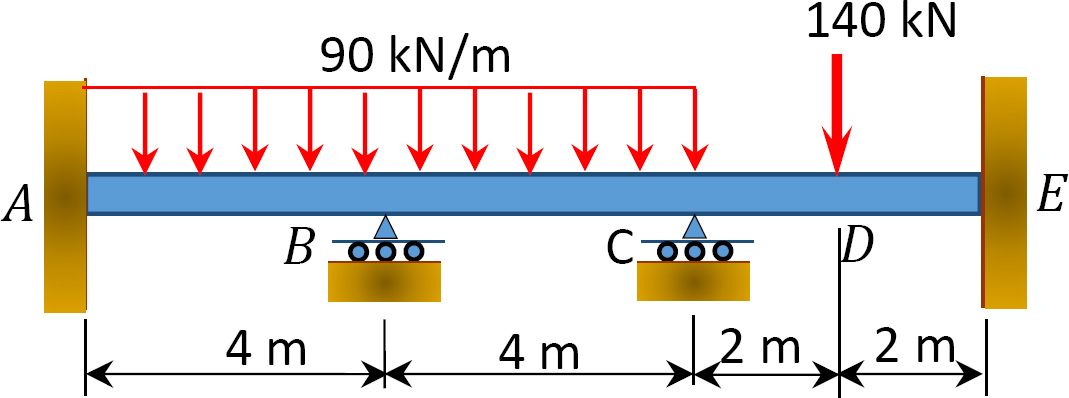
Abb. S12.4. Strahl.
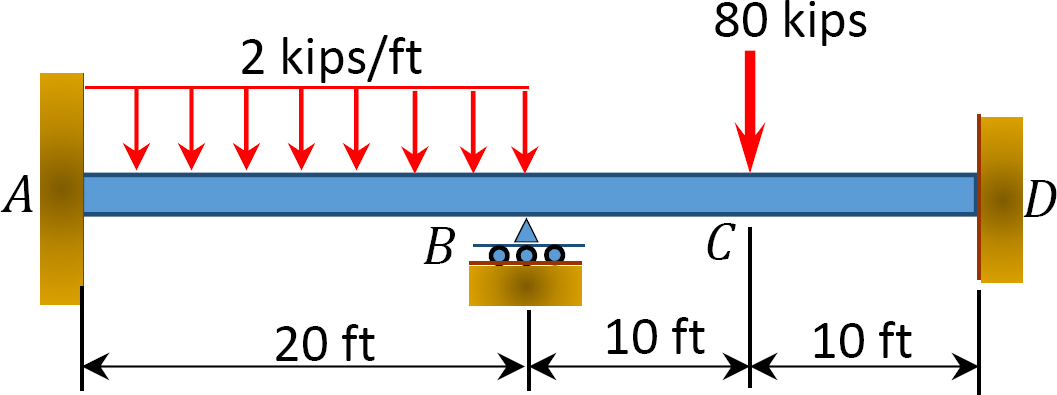
Abb. P12.5. Strahl.
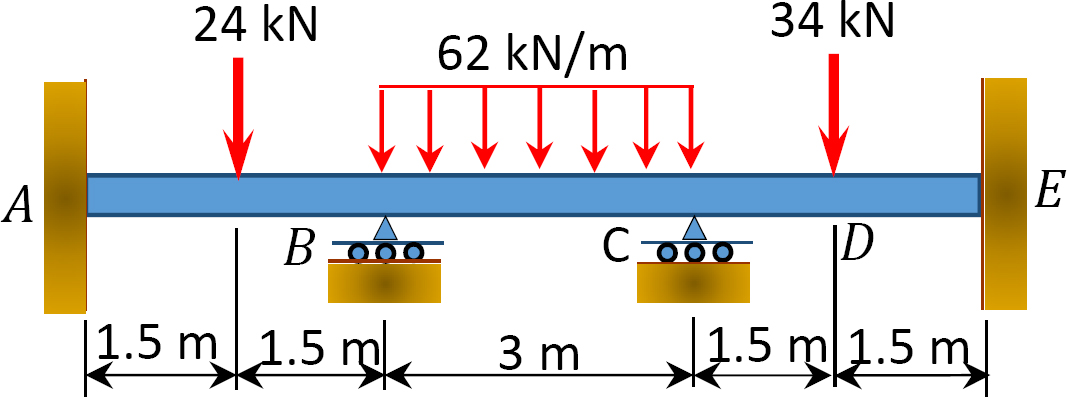
Abb. S12.6. Strahl.
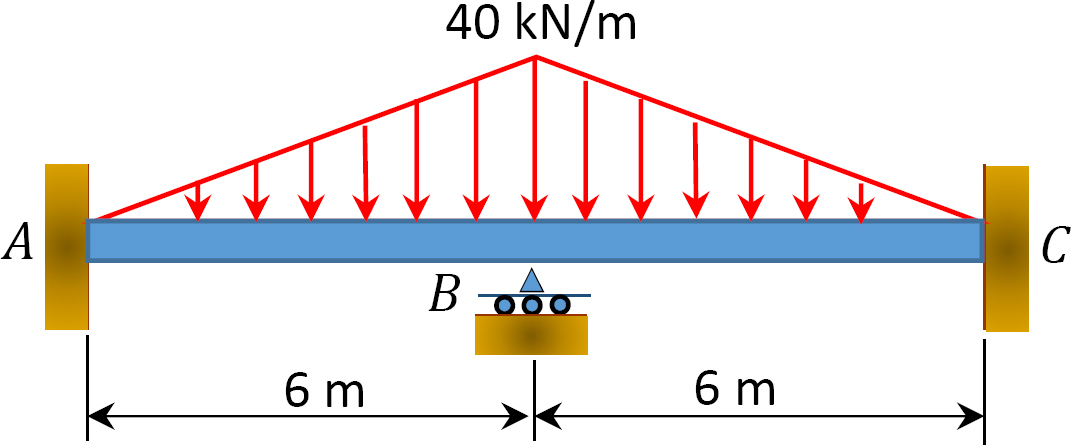
Abb. S12.7. Strahl.
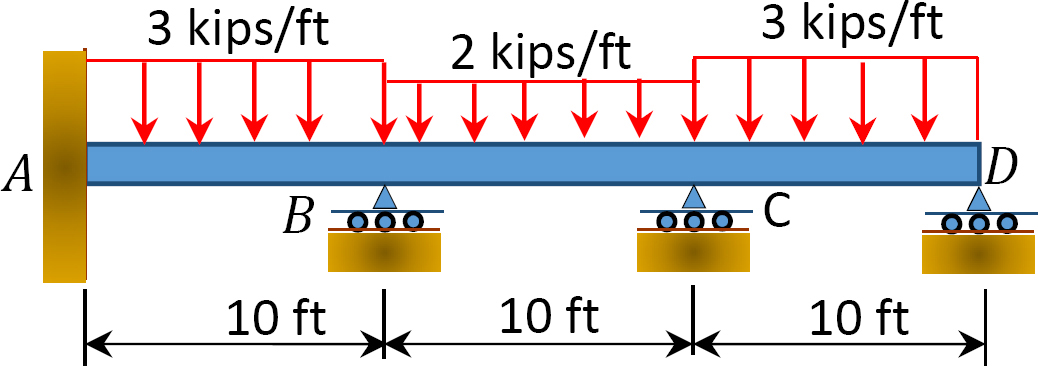
Abb. S12.8. Strahl.
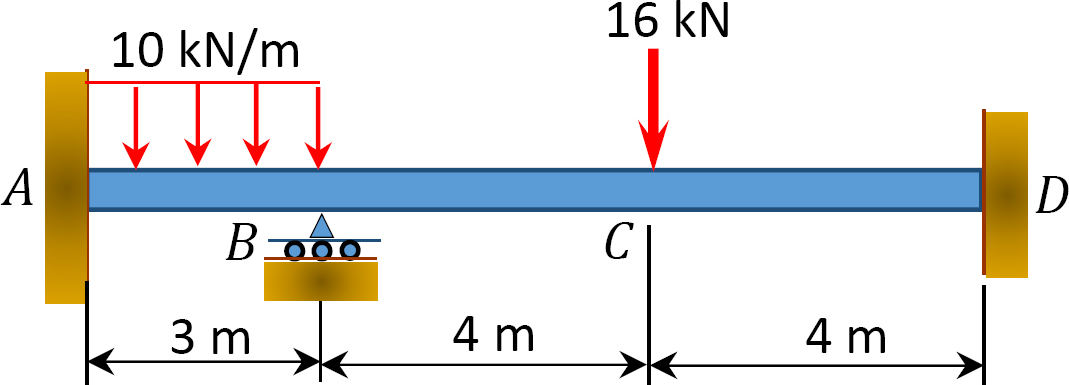
Abb. S12.9. Strahl.
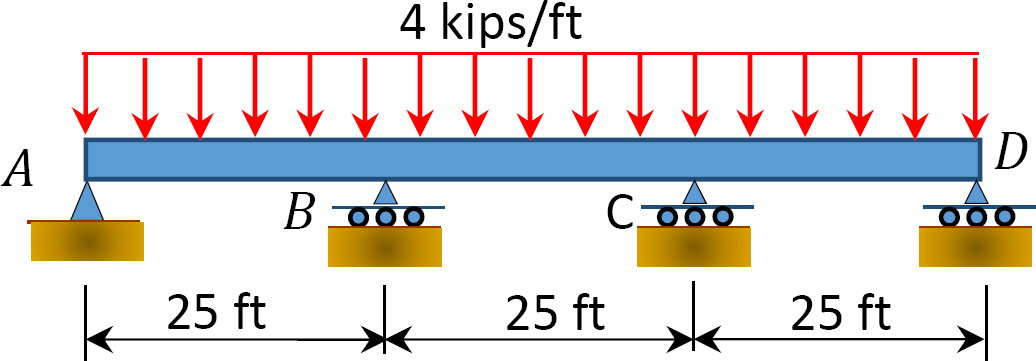
Abb. S12.10. Strahl.
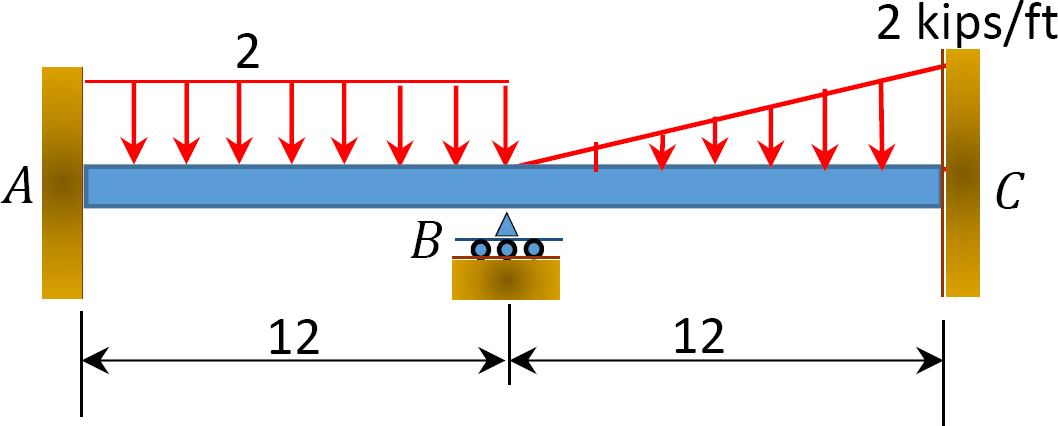
Abb. S12.11. Strahl.
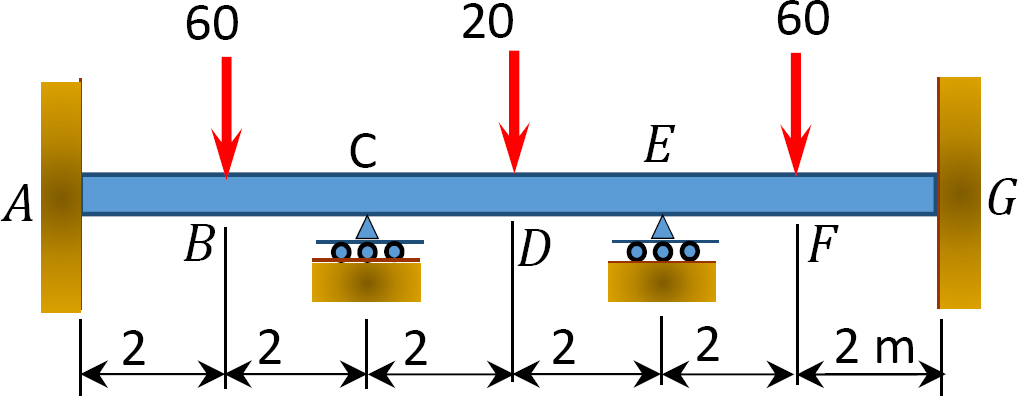
Abb. S12.12. Strahl.
12.2 Verwenden Sie die Momentenverteilungsmethode, um das Endmoment der in Abbildung P12.13 bis Abbildung 12.20 gezeigten Glieder der Rahmen zu berechnen und die Biegemoment- und Scherkraftdiagramme zu zeichnen. EI = konstant.
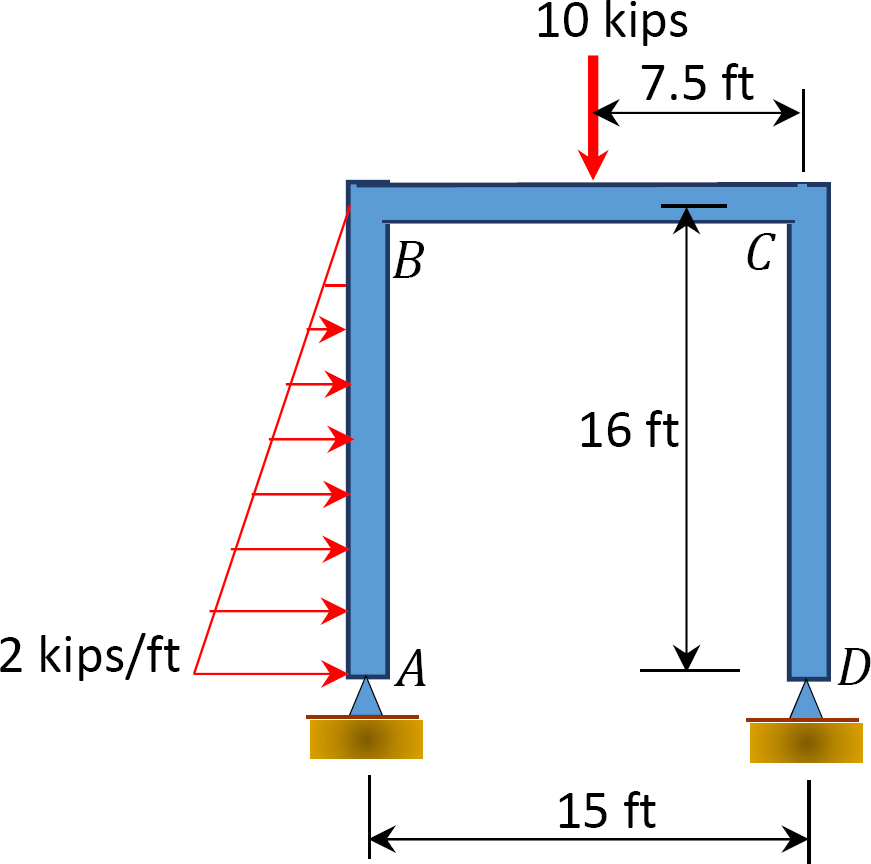
Abb. S12.13. Rahmen.
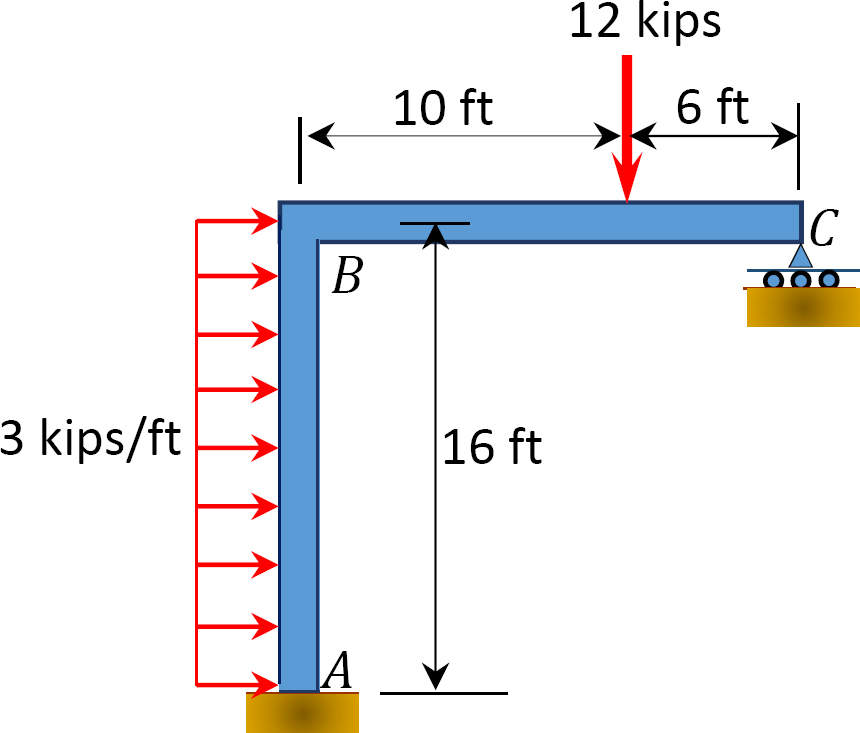
Abb. S12.14. Rahmen.
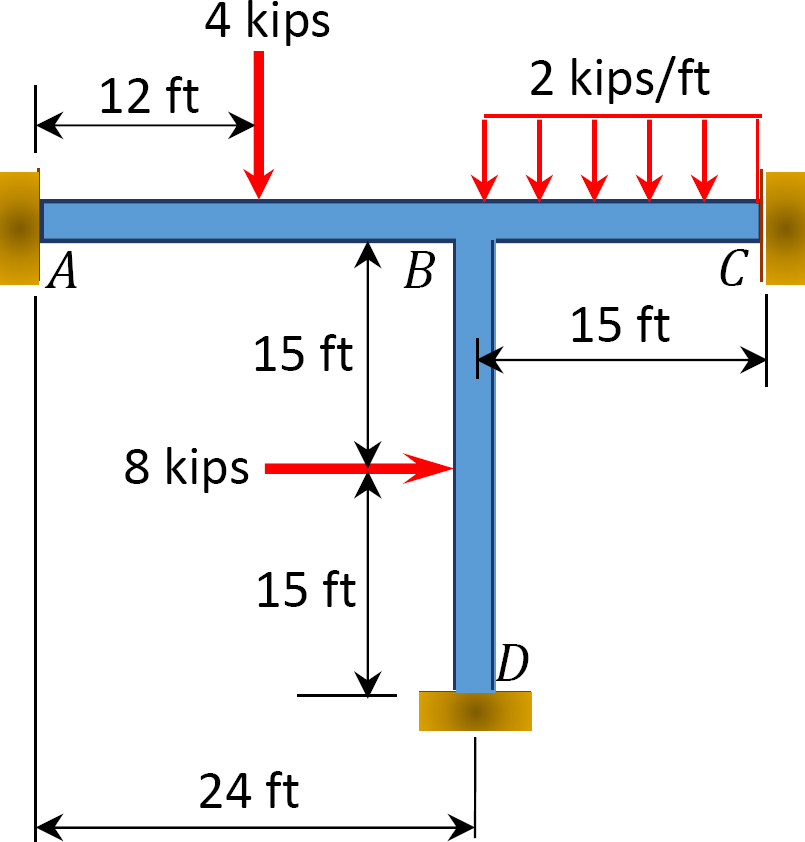
Abb. S12.15. Rahmen.
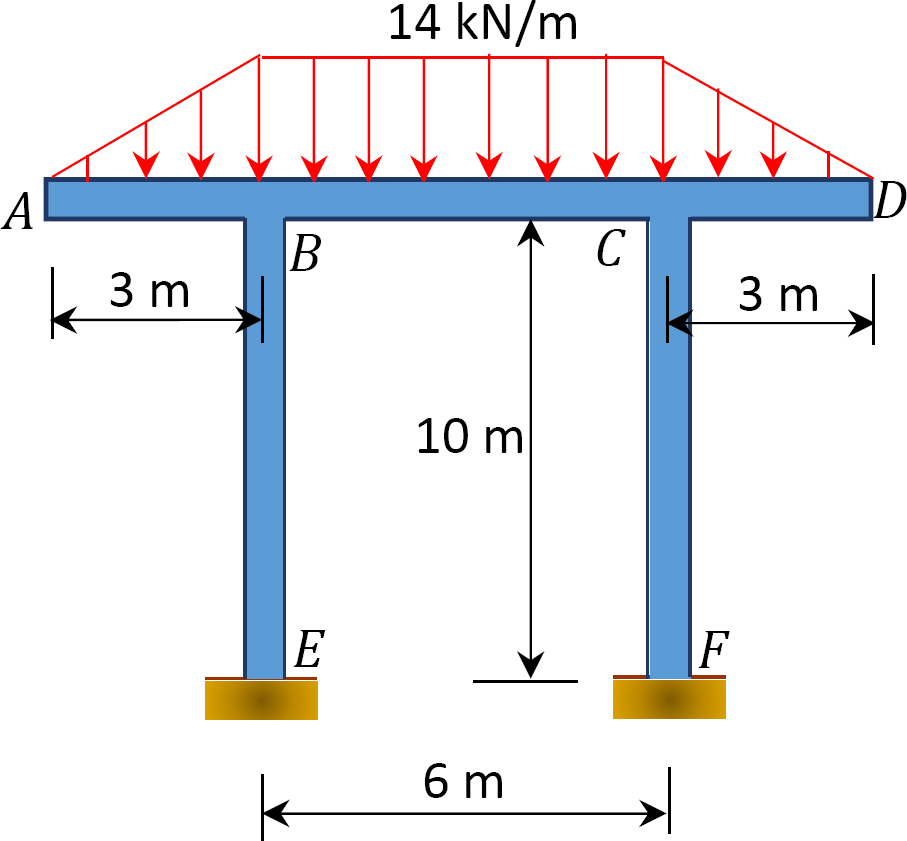
Fig. P12.16. Frame.
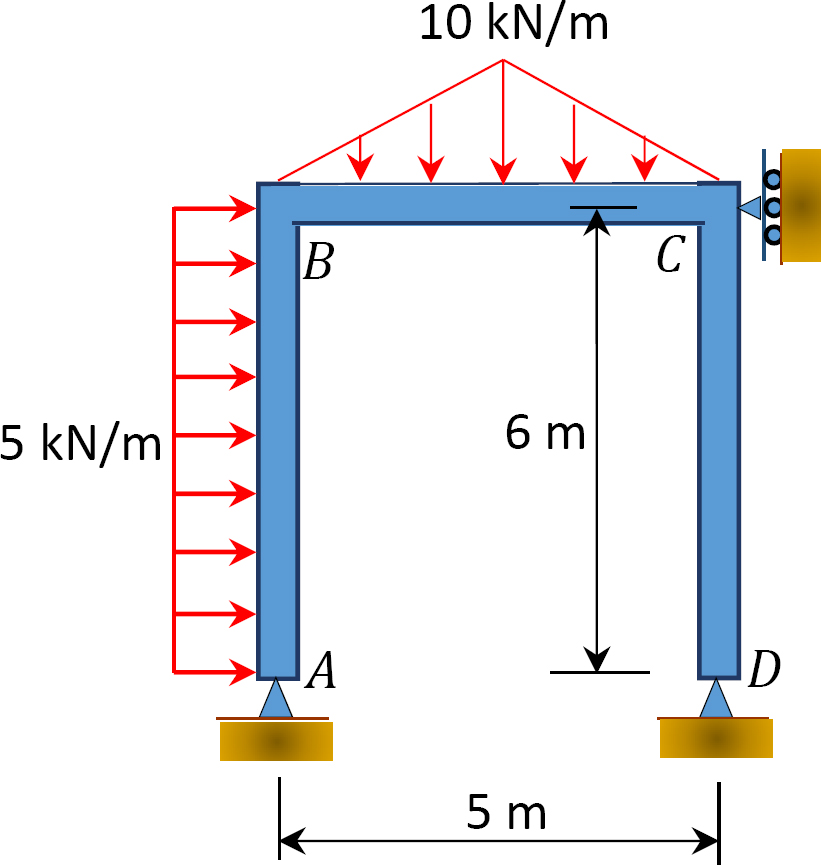
Fig. P12.17. Frame.
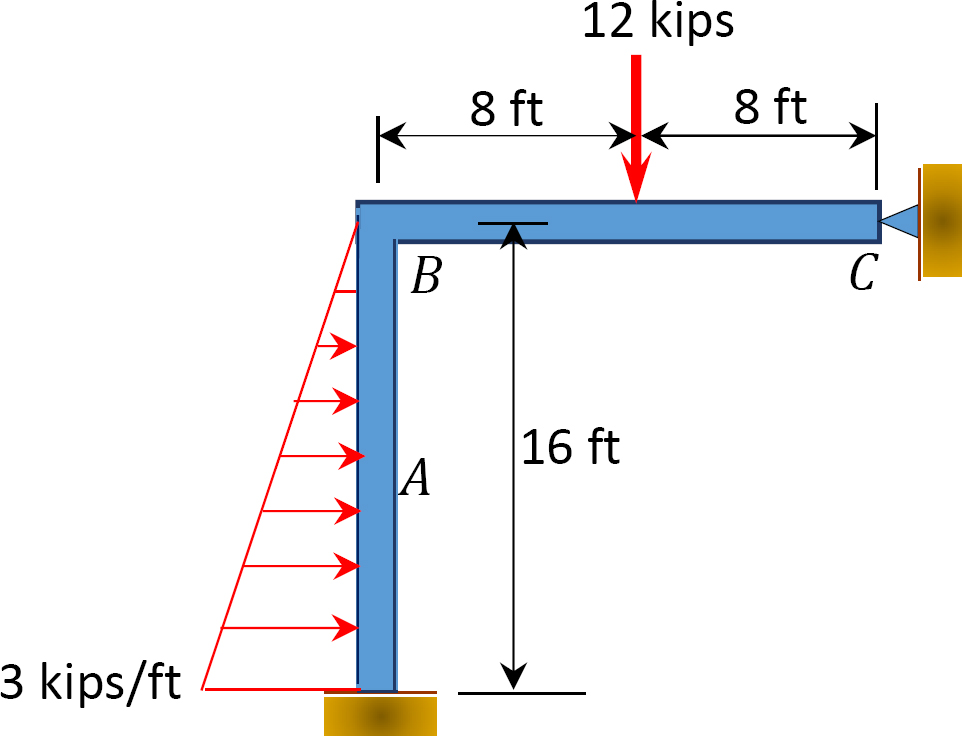
Fig. P12.18. Frame.
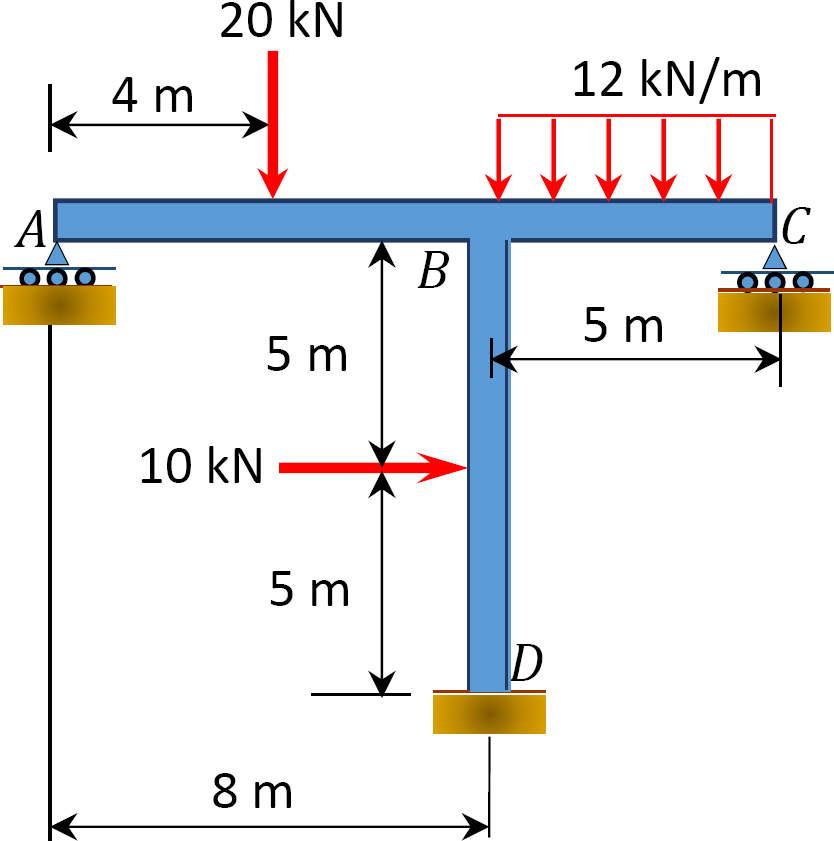
Fig. P12.19. Frame.
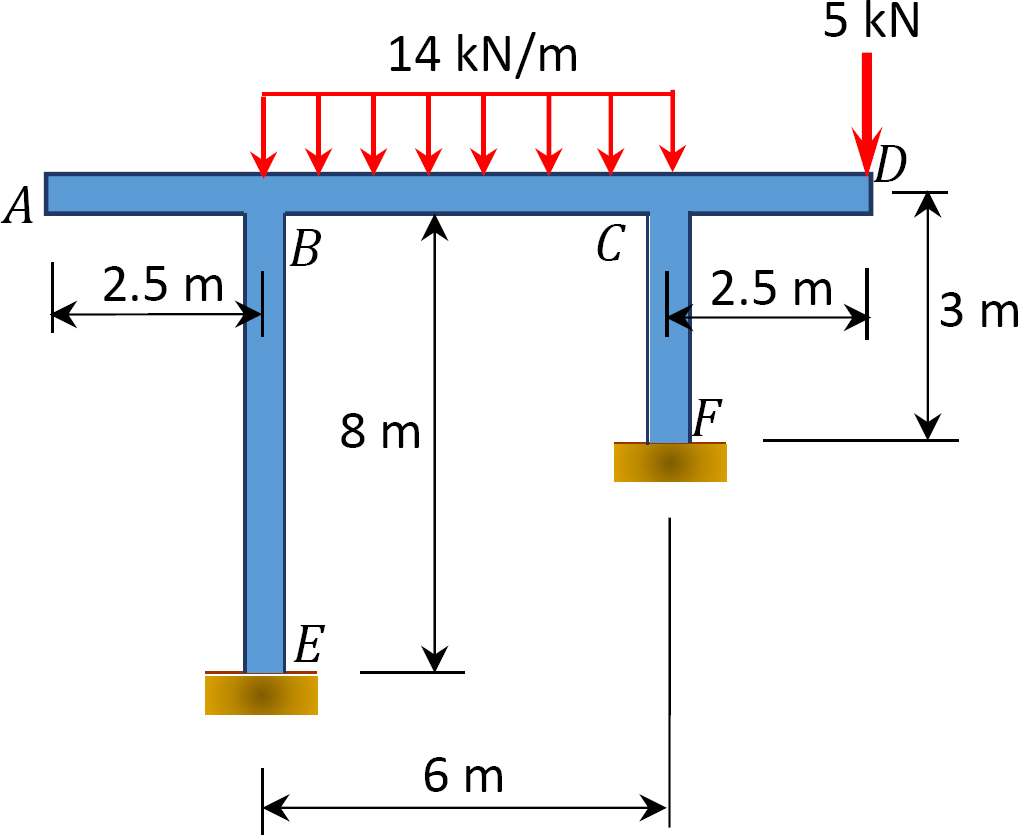
Fig. P12.20. Frame.