Anwendung und Interpretation des Saint-Venant-Prinzips

Alle Statiker verwenden das Saint-Venant-Prinzip, ob aktiv oder unbewusst. Sie können verschiedene Formulierungen dieses Prinzips in den meisten strukturmechanischen Lehrbüchern finden, aber seine genaue Bedeutung ist nicht offensichtlich. Das Saint-Venant-Prinzip sagt uns, dass die genaue Verteilung einer Last nicht weit weg von der belasteten Region wichtig ist, solange die Resultierenden der Last korrekt sind. In diesem Blogbeitrag werden wir das Saint-Venant-Prinzip untersuchen, insbesondere im Zusammenhang mit der Finite-Elemente-Analyse (FE).

Die Geschichte des Saint-Venant-Prinzips

Der französische Wissenschaftler Barré de Saint-Venant formulierte 1855 sein berühmtes Prinzip, aber es war eher eine Beobachtung als eine strenge mathematische Aussage:

“ Ersetzt man die auf einen kleinen Teil der Oberfläche eines elastischen Körpers wirkenden Kräfte durch ein anderes statisch äquivalentes System von auf denselben Teil der Oberfläche wirkenden Kräften, so führt diese Umverteilung der Belastung lokal zu erheblichen Änderungen der Spannungen, wirkt sich jedoch auf die Spannungen in Abständen, die im Vergleich zu den linearen Abmessungen der Oberfläche, auf der die Kräfte verändert werden, groß sind, vernachlässigbar aus.“

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Porträt von Saint-Venant. Bild in der Public Domain, über Wikimedia Commons.

Viele große Köpfe auf dem Gebiet der angewandten Mechanik — Boussinesq, Love, von Mises, Toupin und andere — waren daran beteiligt, Saint-Venants Prinzip in einer genaueren Form zu formulieren und mathematische Beweise dafür zu liefern. Wie sich herausstellt, ist dies für allgemeinere Fälle ziemlich schwierig, und die Forschung zu diesem Thema ist noch nicht abgeschlossen. (Die Argumentation war manchmal ziemlich lebhaft.)

Einfaches Beispiel: Analyse von Spannungen in einer Entfernung

Beginnen wir mit etwas ganz Einfachem: eine dünne rechteckige Platte mit einem kreisförmigen Loch in einiger Entfernung von der belasteten Kante, die axial gezogen wird. Wenn wir an der Spannungskonzentration am Loch interessiert sind, wie wichtig ist dann die tatsächliche Lastverteilung?

Am rechten Rand werden drei verschiedene Lastarten angewendet:

1. Eine konstante axiale Spannung von 100 MPa
2. Eine symmetrische parabolische Spannungsverteilung mit einer Spitzenamplitude von 150 MPa
3. Eine zentrierte Punktlast mit der gleichen Resultierenden wie die beiden vorherigen Lastfälle

Wie in den folgenden Diagrammen zu sehen ist, wird die Spannungsverteilung am Loch nicht durch die Art und Weise beeinflusst, wie die Last angelegt wird. Der Schlüssel hier ist natürlich, dass das Loch weit genug von der Last entfernt ist.

Von Mises Spannungskonturen für die drei Lastfälle.

Eine andere Möglichkeit, dieses Szenario zu visualisieren, ist die Verwendung von Hauptspannungspfeilen. Ein solches Diagramm betont das Spannungsfeld als Fluss und gibt ein gutes Gefühl für die Umverteilung.

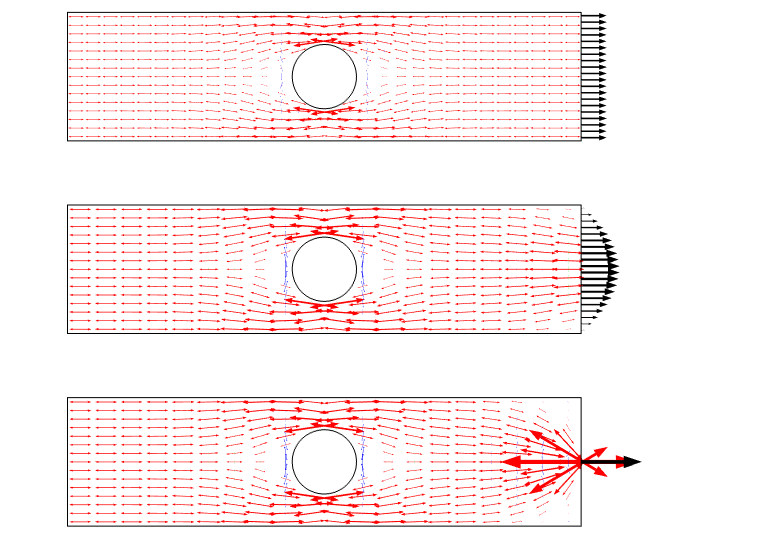
Hauptspannungsdiagramm für die drei Lastfälle. Beachten Sie, dass es eine Singularität gibt, wenn eine Punktlast verwendet wird.

Wenn wir die Spannung entlang einer Linie grafisch darstellen, können wir sehen, dass alle drei Fälle in einem Abstand von der Kante konvergieren, der ungefähr der Breite der Platte entspricht.

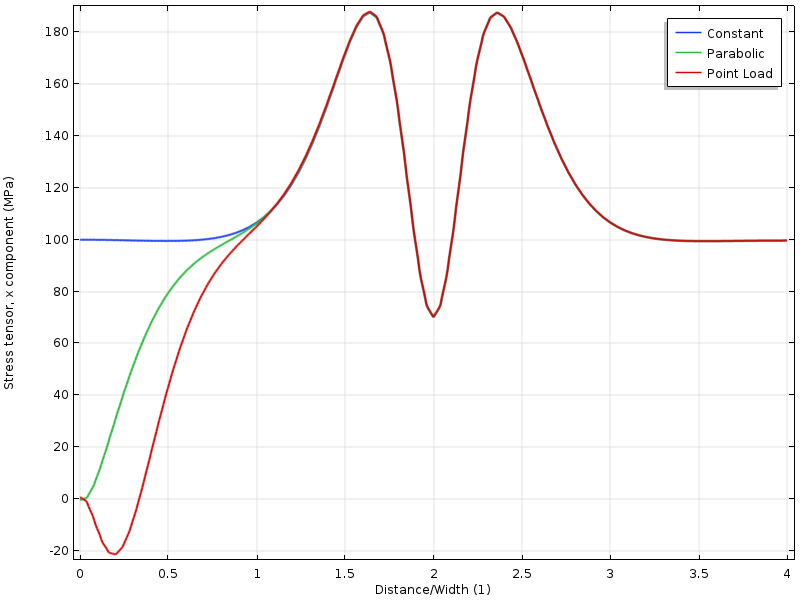
Spannung entlang der oberen Kante als Funktion des Abstands von der belasteten Grenze. Der Abstand wird durch die Breite der Platte normalisiert.

Wenn das Loch näher an die belastete Grenze verschoben wird, erhalten wir eine andere Situation. Der Spannungszustand um das Loch hängt nun von der Lastverteilung ab. Aber noch interessanter ist, dass der Abstand zu dem Punkt, an dem die drei Spannungsfelder übereinstimmen, jetzt doppelt so weit von der belasteten Grenze entfernt ist. Die Anwendung des Saint-Venant-Prinzips erfordert, dass die Spannungen frei umverteilt werden können. In diesem Fall wird diese Umverteilung teilweise durch das Loch blockiert.

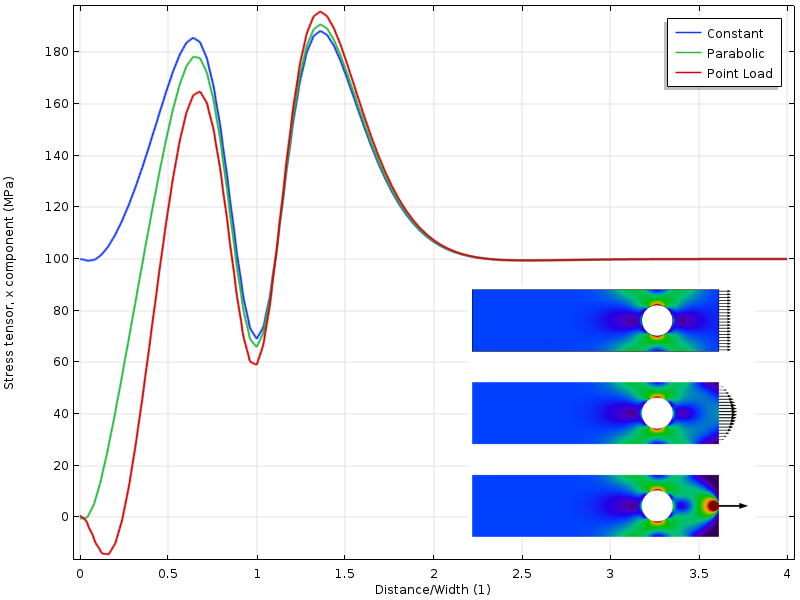
Spannung entlang der oberen Kante mit dem Loch näher an der belasteten Grenze.

Beachten Sie, dass das Saint-Venant-Prinzip besagt, dass es keinen Unterschied im Spannungszustand in einer Entfernung gibt, die in der Größenordnung der linearen Dimension der belasteten Fläche liegt. Die zu berücksichtigende beladene Fläche darf jedoch nicht die tatsächlich beladene Fläche sein! Diese Aussage mag seltsam klingen, aber stellen Sie sich das so vor: Wenn das Loch weit weg ist, können wir den Spannungskonzentrationsfaktor mit einer Formel (meine sagt 4,32) und nicht mit einer FE-Lösung berechnen. Der zweite Ansatz beinhaltet eine implizite Annahme, dass die Last wie im ersten Lastfall gleichmäßig verteilt ist. Selbst wenn also die tatsächliche Last nur auf einen kleinen Teil der Grenze aufgebracht wurde, hängt der kritische Abstand in diesem Fall von der Größe der gesamten Grenze ab.

Wenn das Problem mit der Finite-Elemente-Methode (FEM) gelöst wird, kann sich das Loch beliebig nahe an der Last befinden. Was die Grenze setzt, ist, dass aus physikalischer Sicht die Lastverteilung gut definiert ist. Sobald wir jedoch Annahmen über die Umverteilung treffen, gibt es eine implizite Annahme über die Lastverteilung, die von der tatsächlichen abweichen kann.

Null Resultierende Systeme und Dehnungsenergiedichte

Bisher haben wir gesagt, dass die Spannungen unabhängig von den Lastdetails in einem geeigneten Abstand gleich sind. Da wir es hier mit linearer Elastizität zu tun haben, ist es immer möglich, Lastfälle zu überlagern. Wenn man mit Beweisen des Saint-Venant-Prinzips arbeitet, ist es einfacher, ein Prinzip in dieser Richtung zu formulieren: Die Spannungen, die durch ein Lastsystem ohne resultierende Kraft oder Moment verursacht werden, sind in einem Abstand klein, der in der gleichen Größenordnung liegt wie die Größe der belasteten Grenze.

Wir untersuchen also die Spannung, die durch die Differenz zwischen den beiden Lastsystemen mit gleichen Resultierenden verursacht wird. Die meisten modernen Beweise basieren auf Schätzungen des Zerfalls der Dehnungsenergiedichte für ein solches Null-resultierendes System.

Zurück zum obigen Problem können wir die Differenz zwischen den Lastfällen berechnen. Auf diese Weise können wir den tatsächlichen Zerfall der Spannungs- oder Dehnungsenergiedichte für die Differenz der Spannungsfelder untersuchen.

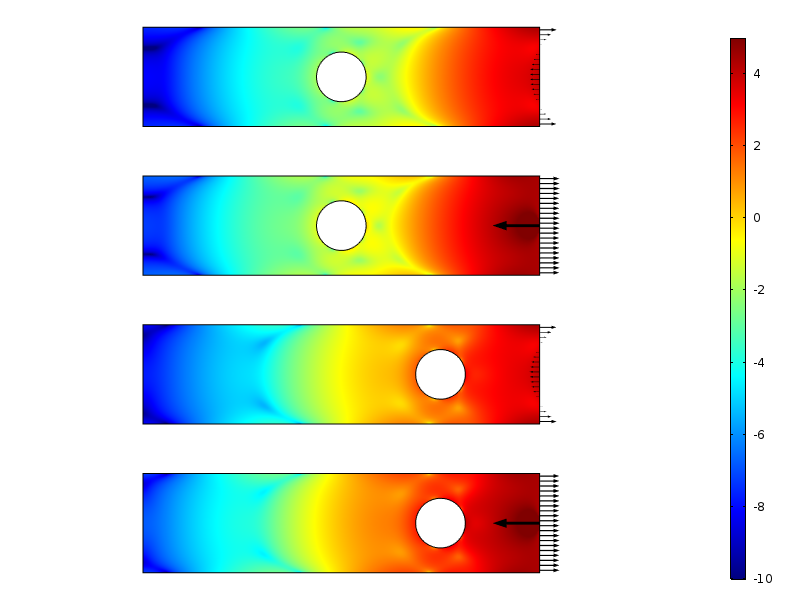
Logarithmus der Dehnungsenergiedichte für die null resultierenden Lastfälle.

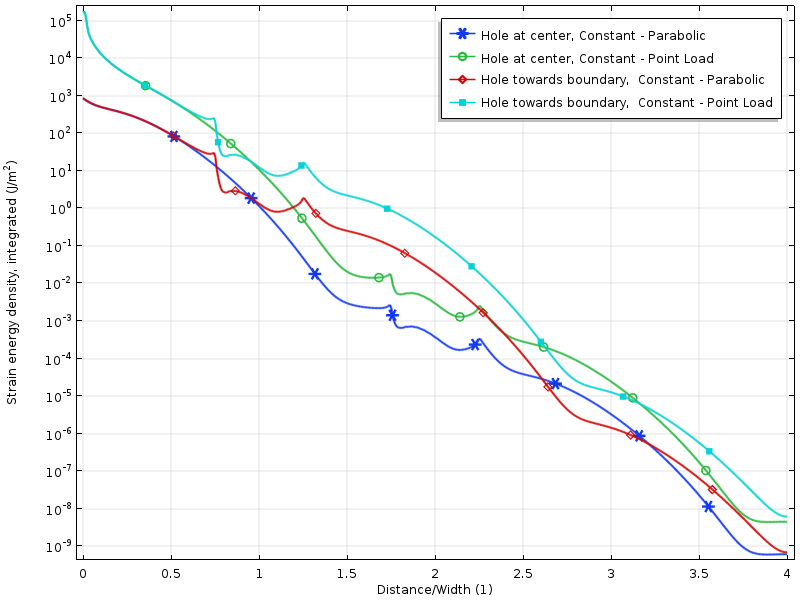
Die Dehnungsenergiedichte entlang der Platte für die resultierenden Nulllastfälle. Die Energie wird entlang der vertikalen Richtung integriert, um eine Größe zu erzeugen, die nur eine Funktion des Abstands von der Last ist.

Der Abfall im Logarithmus der Dehnungsenergiedichte ist mehr oder weniger linear mit dem Abstand von der belasteten Grenze. Dies stimmt tatsächlich mit dem überein, was moderne Beweise vorhersagen: ein exponentieller Zerfall der Dehnungsenergiedichte. Wir können auch deutlich sehen, wie das Loch vorübergehend die Zerfallsrate reduziert.

Anwendung des Saint-Venant-Prinzips auf dünne Strukturen

Für dünnere Strukturen wie Schalen, Balken und Fachwerke ist bekannt, dass das Saint-Venant-Prinzip nicht auf die gleiche Weise angewendet werden kann wie für ein „festeres“ Objekt. Störungen legen längere Strecken zurück als erwartet, da die Lastpfade in einer dünnen Struktur viel begrenzter sind. Dies ist das gleiche Phänomen, das wir mit dem Loch im obigen Beispiel sehen, aber prominenter.

Hier untersuchen wir einen Balken mit einem Standardquerschnitt von IPE100. Das Ende des Balkens ist einer axialen Spannung ausgesetzt, deren Amplitude in beiden Querschnittsrichtungen linear verteilt ist.

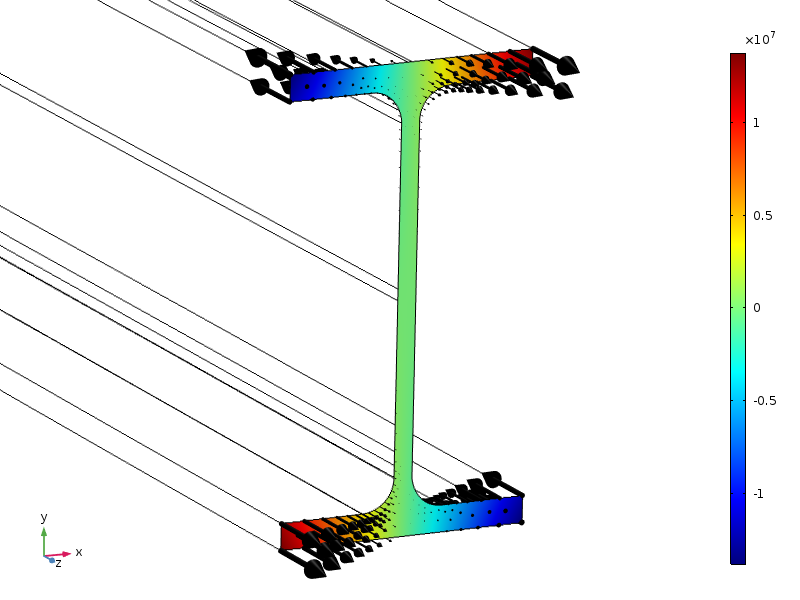
Lastverteilung, dargestellt als Konturen und Pfeile.

Aufgrund der Symmetrien hat diese Last eine resultierende Kraft von Null sowie ein Moment von Null um alle Achsen. Die Höhe des Querschnitts beträgt 100 mm, wenn also die Standardform des Saint-Venant-Prinzips anwendbar ist, sollten die Spannungen in einem Abstand von etwa 100 mm vom Endabschnitt gering sein.

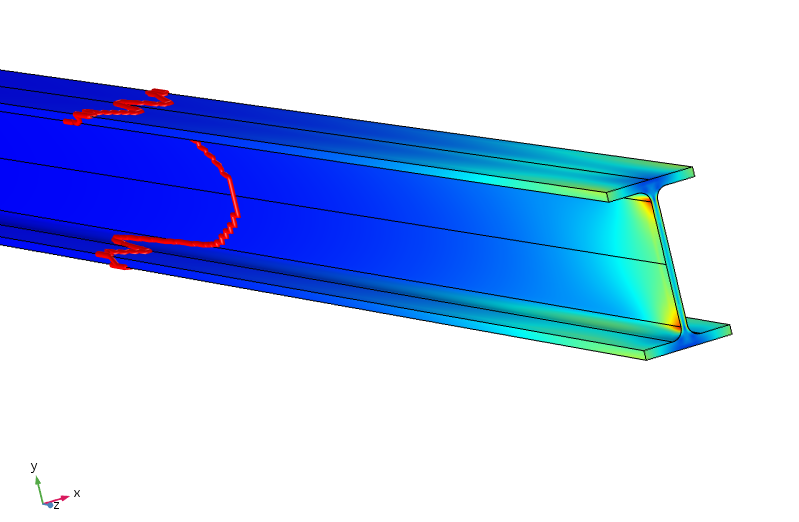
Äquivalente Spannung im Balken. Die rote Kontur zeigt an, wo die Spannung weniger als 5% der angelegten Spitzenspannung beträgt.

Es stellt sich heraus, dass wir fast einen Meter entlang des Balkens fahren müssen, damit die Spannung unter 5% der angelegten Spitzenspannung liegt. Somit ist die Lastumverteilung hier viel weniger effizient, da der Ausgleich zwischen Ober- und Unterflansch eine Momentenübertragung durch den dünnen Steg erfordert.

Wenn Sie mit der Theorie der ungleichmäßigen Torsion von Trägern vertraut sind (d. H. Warping-Theorie oder Wlassow-Theorie), werden Sie erkennen, dass die aufgebrachte Last ein signifikantes Bimoment hat. Das Bimoment ist eine Querschnittsgröße mit der physikalischen Dimension Kraft X Länge2.

Vielleicht (dies ist nur meine persönliche Spekulation) sollte ein effizientes Saint-Venant-Prinzip für diesen Fall nicht nur Kraft und Moment, sondern auch ein Bimoment von Null erfordern. Dies kann durch Hinzufügen von vier Punktlasten erreicht werden, die ein entgegenwirkendes Bimoment bereitstellen. Das Ergebnis einer solchen Analyse ist unten dargestellt.

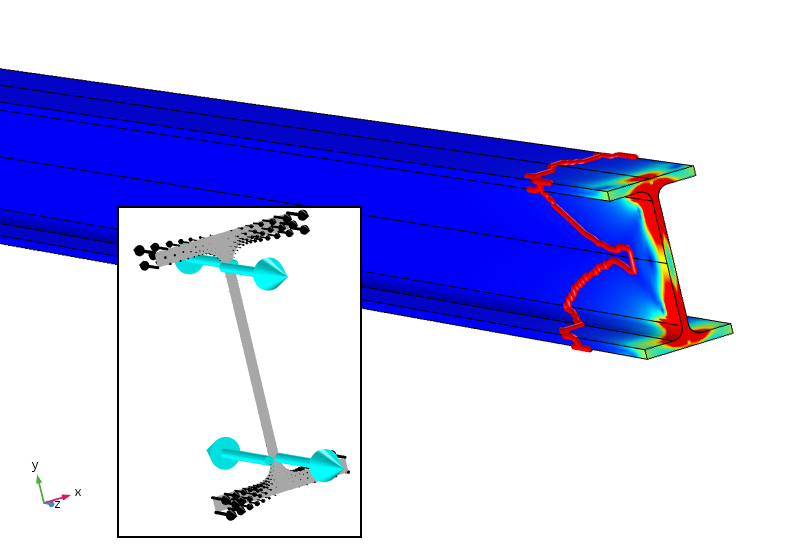
Äquivalente Spannung mit vier Punktlasten, die auch ein Null-Bimoment liefern. Die 5% -Spannungskontur ist jetzt viel näher an der belasteten Grenze.

Die aufgebrachten Punktlasten, die nicht optimal auf den Zweck gelegt werden, ergeben extrem hohe (eigentlich singuläre) lokale Spannungen. Die Spannung fällt jedoch viel schneller ab und liegt nach etwa 100 mm unter 5%. Die 5% -Grenze liegt immer noch in Bezug auf die aufgebrachte verteilte Last, so dass sie nicht an die neuen lokalen Spannungen angepasst wird. Die logarithmische Abklingrate der Dehnungsenergiedichte ist dreimal schneller, nachdem die Punktlasten addiert wurden.

Saint-Venant-Prinzip in der Finite-Elemente-Analyse

In einigen Fällen können Sie das Saint-Venant-Prinzip intuitiv als auf das FE-diskretisierte Problem anwendbar betrachten. Hier betrachten wir verteilte Lasten und fehlerhafte Netze.

Verteilte Lasten

Im FE-Modell werden Lasten immer an den Netzknoten angelegt, obwohl Sie sie als kontinuierliche Grenzlast angeben. Die Last wird intern nach dem Prinzip der virtuellen Arbeit auf die Knoten des Elements verteilt, wie im folgenden Beispiel gezeigt.

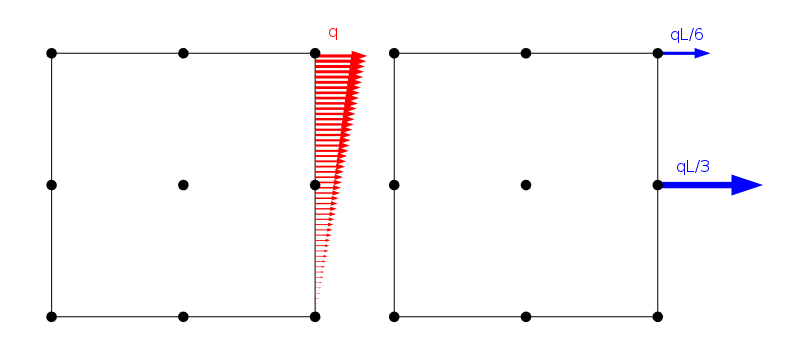
Eine linear verteilte Last und wie sie an den Knoten eines Lagrange-Elements zweiter Ordnung mit Seitenlänge L angewendet wird.

Es gibt jedoch eine unendliche Anzahl von Lastverteilungen, die die gleichen Knotenlasten ergeben, solange sie dieselbe resultierende Kraft und dasselbe resultierende Moment teilen. Offensichtlich ist die Lösung des Finite-Elemente-Problems für alle diese Fälle gleich. Aus Saint-Venants Prinzip können wir jedoch schließen, dass alle diese Lasten im Wesentlichen das gleiche Spannungsfeld ergeben sollten, sobald wir in einiger Entfernung sind.

Da die Größe der Fläche, über die wir Lasten umverteilen, eine Elementfläche ist, ist die lineare Dimension, nach der es keinen Unterschied gibt, im Wesentlichen eine Elementschicht innerhalb der Struktur. Somit entspricht die Lösung in der äußersten Elementschicht möglicherweise nicht der tatsächlichen Belastung, aber weiter innen.

Als Beispiel können wir eine rechteckige Platte mit einer Randlast belasten, die eine exponentielle Spannungsverteilung aufweist. Die mit einem feinen Netz berechnete Spannung ist unten dargestellt.

Konturdiagramm der axialen Spannungsverteilung.

Aufgrund des Saint-Venant-Prinzips wird das Spannungsfeld in einiger Entfernung von der belasteten Kante in einen reinen Biegezustand umverteilt, genau wie wir es erwarten. Dies ist jedoch nicht das Ziel der aktuellen Diskussion. Vielmehr untersuchen wir den Unterschied zwischen der obigen Spannungsverteilung und dem, was wir mit einer Reihe grober Maschen erhalten.

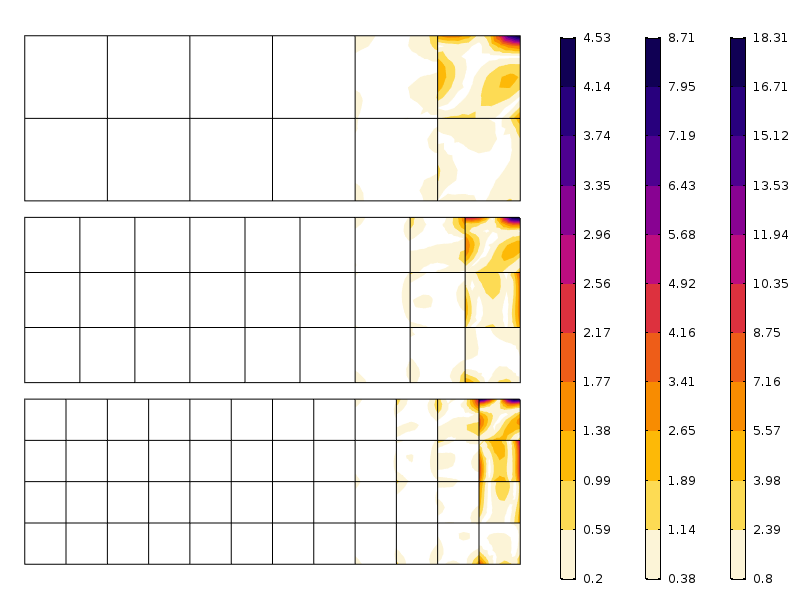
Fehler in der axialen Spannung für drei verschiedene Maschen. Beachten Sie die verschiedenen Skalen. Wie erwartet ist der Fehler kleiner, wenn das Netz feiner ist.

Wie in der Abbildung zu sehen ist, nimmt der Fehler nach der ersten Elementschicht schnell ab. Was wir hier sehen, ist eigentlich eine Kombination aus Netzkonvergenz und der Umverteilung von Spannungen, die durch das Saint-Venant-Prinzip impliziert wird.

Fehlerhaftes Netz

Ein fehlerhaftes Netz tritt auf, wenn die Formfunktionen in zwei verbundenen Elementen nicht übereinstimmen. Der häufigste Fall ist, wenn eine Baugruppe unter Verwendung von Identitätspaaren und Kontinuitätsbedingungen verbunden ist. Um dies zu veranschaulichen, können wir einen geraden Balken mit einem absichtlich nicht übereinstimmenden Netz untersuchen. Mit einem einfachen Lastfall, wie der einachsigen Spannung, ist es möglich, die durch den Übergang verursachten Spannungsstörungen zu untersuchen.

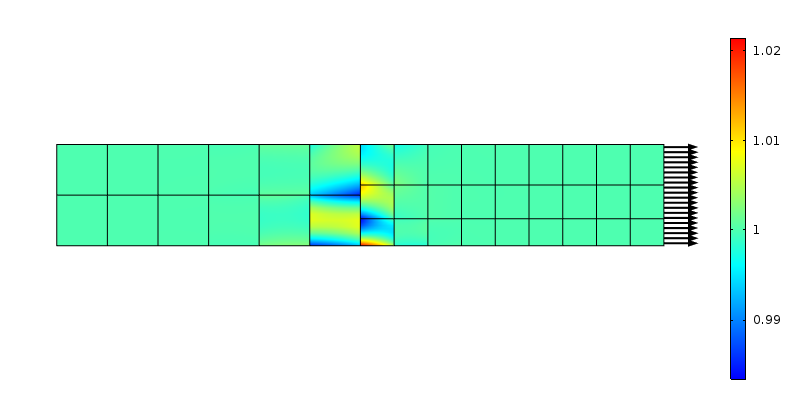
Axiale Spannung an einem nicht konformen Maschenübergang. Elemente zweiter Ordnung werden verwendet.

Die von den Knoten an den beiden Seiten übertragenen Kräfte stimmen nicht mit der Annahme einer konstanten Spannung überein. Dies kann wiederum als lokale Lastumverteilung über einen Bereich angesehen werden, der der Elementgröße entspricht. Mit der Argumentation von Saint-Venant sollte die Störung in einem „elementgroßen“ Abstand vom Übergang verschwinden. Lassen Sie uns untersuchen, was passiert, wenn das Netz in axialer Richtung verfeinert wird.

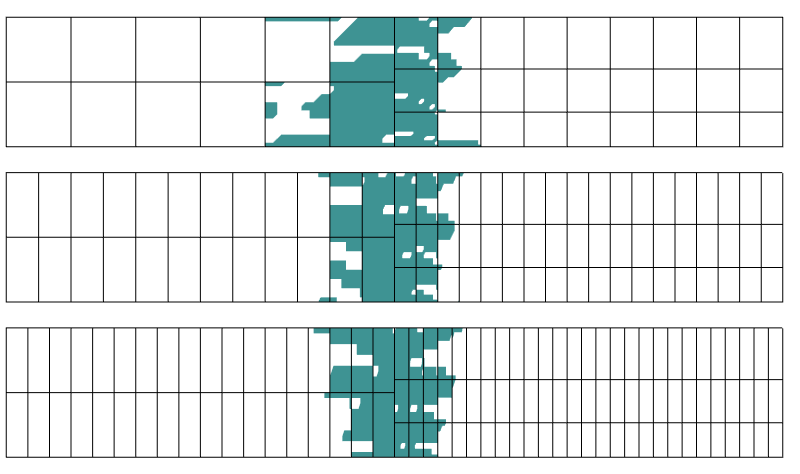
Region mit mehr als 0,1% Fehler in Stress. In axialer Richtung werden drei verschiedene Diskretisierungen verwendet.

Es stellt sich heraus, dass der Bereich der Störung durch die Diskretisierung in der Richtung senkrecht zur Übergangsgrenze nicht wesentlich beeinflusst wird. Genau das sagt uns das Saint-Venant-Prinzip.

Schlußbemerkungen

Ohne Anwendung des Saint-Venant-Prinzips sind viele Strukturanalysen schwierig durchzuführen, weil die genaue Lastverteilung nicht bekannt ist.

Das Prinzip gilt formal nur für linearelastische Materialien. In der Praxis nutzen wir es auch intuitiv täglich für andere Situationen. Wenn beispielsweise das Material im Beispiel „Platte mit Loch“ elastoplastisch wäre, würden wir erwarten, dass die beiden verteilten Lasten gleichwertige Ergebnisse liefern, solange die Streckspannung über der an der Grenze angelegten Spannung liegt, so dass es nur zu einer plastischen Verformung um das Loch herum kommt. Die Punktbelastung ergibt jedoch immer eine andere Lösung, da das Material um den belasteten Punkt nachgibt. Für eine längere Diskussion lesen Sie diesen Blogbeitrag über Singularitäten bei Punktlasten.

Nächste Schritte

Erfahren Sie mehr über die Verwendung der COMSOL Multiphysics® Software für FEA.

Weiterführende Literatur

• Y.C. Fung und P. Tong, Klassische und Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.