![]()
La forma forzada más general de la ecuación de Duffing es
|
(1)
|
Dependiendo de los parámetros elegidos, la ecuación puede tomar un número de formas especiales. Por ejemplo, sin amortiguación ni forzamiento, ![]() y tomando el signo más, la ecuación se convierte en
y tomando el signo más, la ecuación se convierte en
|
(2)
|
(Bender y Orszag, 1978, pág. 547; Zwillinger, 1997, pág. 122). Esta ecuación puede mostrar un comportamiento caótico. Para ![]() , la ecuación representa un «resorte duro», y para
, la ecuación representa un «resorte duro», y para ![]() , representa un «resorte suave».»Si
, representa un «resorte suave».»Si ![]() , las curvas de retrato de fase están cerradas.
, las curvas de retrato de fase están cerradas.
Si en su lugar tomamos ![]() ,
, ![]() , restablecemos el reloj para que
, restablecemos el reloj para que ![]() , y usamos el signo menos, la ecuación es entonces
, y usamos el signo menos, la ecuación es entonces
|
(3)
|
Esto se puede escribir como un sistema de ecuaciones diferenciales ordinarias de primer orden como
|
(4)
|
|||
|
(5)
|
(Wiggins 1990, p. 5) que, en el caso no forzado, se reduce a
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, pág. 6; Ott 1993, pág. 3).
Los puntos fijos de este conjunto de ecuaciones diferenciales acopladas están dadas por
|
(8)
|
so ![]() , y
, y
|
(9)
|
|||
|
(10)
|
dar ![]() . Por lo tanto, los puntos fijos son
. Por lo tanto, los puntos fijos son ![]() ,
, ![]() , y
, y ![]() .
.
El análisis de la estabilidad de los puntos fijos puede ser un punto mediante la linealización de las ecuaciones. La diferenciación da
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
que se puede escribir como la ecuación de matriz
|
(14)
|
Examinar la estabilidad del punto (0,0):
|
(15)
|
|
(16)
|
Pero ![]() , por lo que
, por lo que ![]() es real. Desde
es real. Desde ![]() , siempre habrá una raíz positiva, por lo que este punto fijo es inestable. Ahora mira (
, siempre habrá una raíz positiva, por lo que este punto fijo es inestable. Ahora mira (![]() , 0). La ecuación característica es
, 0). La ecuación característica es
|
(17)
|
que tiene raíces
|
(18)
|
Para ![]() ,
, ![]() , por lo que el punto es asintóticamente estable. Si
, por lo que el punto es asintóticamente estable. Si ![]() ,
, ![]() , por lo que el punto es linealmente estable (Wiggins 1990, p. 10). Sin embargo, si
, por lo que el punto es linealmente estable (Wiggins 1990, p. 10). Sin embargo, si ![]() , el radical da una parte imaginaria y la parte real es
, el radical da una parte imaginaria y la parte real es ![]() , por lo que el punto es inestable. Si
, por lo que el punto es inestable. Si ![]() ,
, ![]() , que tiene una raíz real positiva, entonces, el punto es inestable. Si
, que tiene una raíz real positiva, entonces, el punto es inestable. Si ![]() , entonces
, entonces ![]() , por lo que ambas raíces son positivas y el punto es inestable.
, por lo que ambas raíces son positivas y el punto es inestable.
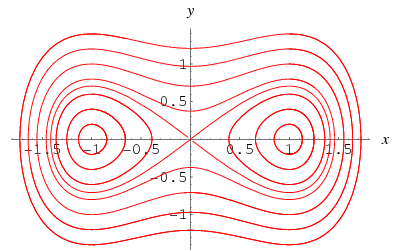
Curiosamente, el caso especial ![]() sin forzamiento,
sin forzamiento,
|
(19)
|
|||
|
(20)
|
puede ser integrado por cuadraturas. Diferenciar (19) y conectar (20) da
|
(21)
|
Multiplicando ambos lados por ![]() da
da
|
(22)
|
Pero esto puede ser escrito
|
(23)
|
así que tenemos un invariante de movimiento ![]() ,
,
|
(24)
|
Resolviendo para ![]() da
da
|
(25)
|
|
(26)
|
so
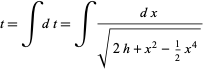 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
así que las ecuaciones del oscilador de Duffing son dadas por el Hamiltoniansystem