yllä olevasta luokittelijoiden diagrammiketjusta. Se melkein muistuttaa ’LinkedList’ tietorakenne. Y1, Y2..Yᴺ ovat kunkin luokittelijan vastemuuttujat (se on 0 tai 1). Vastaus kaikki aikaisemmat luokittelijat(paitsi 1st) kylvetään seuraavaan luokittelija ja nämä tulevat ominaisuuksia yhdessä alkuperäisen syötteen ominaisuuksia (f1..fⁿ).
yleensä luokittaja K rakennetaan täydellisellä syöteominaisuudella : f1, f2,..fⁿ, Y1, Y2,..Yᴷ⁻1
Nyt, tässä yksi kysymys tulee, ”Kuinka jotta luokittimen ketju on päättänyt ?”Tähän on olemassa erilaisia strategioita kuten alla on esitetty :
Ensemble of Classifier chains (ECC): Ensemble model of classification käytetään tässä. Ketjuista valitaan satunnaisotanta, jonka päälle rakennetaan kokonaisuus. Ennustettu tuotos saadaan soveltamalla enemmistöpäätösjärjestelmää Ensemblen tuotoksiin. Se on aivan sama kuin RandomForest luokittelija.
Monte-Carlo Classifier chains (MCC: Se soveltaa Monte-Carlo-menetelmää optimaaliseen luokittelijasekvenssin tuottamiseen.
luokittajille on muitakin menetelmiä, kuten Satunnaishaku-tai riippuvuusmenetelmiä, mutta ne eivät ole kovin yleisiä käytössä.
kunkin luokittajan ulostulo otetaan talteen binäärisen Relevanssijärjestelmän tavoin ja se määrittää luokkamerkinnät lopussa.
Label Power-set Scheme
Binäärirelevanssin peruskäsite & Luokittelijaketju on kutakuinkin sama. Label power-set toimii eri tavalla. Se pitää jokaista koulutustietojen merkkiyhdistelmää erillisenä merkintänä. Esimerkiksi 3-luokan multi-label ongelma, 100, 001, 101, 111, jne pidetään erillisinä etiketteinä.
yleensä luokkaavaruudessa, jonka ulottuvuus on n, voi olla 2ᴺ ei kaikkia mahdollisia merkkiyhdistelmiä.
se ei siis hajoa mihinkään alaongelmiin, vaan ennustaa suoraan luokkamerkkien yhdistelmän kokonaisuutena.
edut & kunkin järjestelmän haitat
Binäärirelevanssi on yksinkertainen järjestelmä, joka on helppo toteuttaa. Se ei kuitenkaan pidä merkintää keskinäisenä riippuvuutena ja voi siksi usein tulkita väärin piilotettujen tietojen suhteita.
luokittajaketju hoitaa luokkamerkkisuhteet täydellisesti. Erityisesti tapauksissa, joissa jotkut luokkamerkinnät ovat toisten osamerkintöjä ja yhden luokkamerkin esiintyminen riippuu voimakkaasti muista merkinnöistä(vanhempien ja lasten suhteet luokkamerkinnöissä. Lapsi etiketti voi tapahtua iff vanhempi etiketti on olemassa). Mutta tämä järjestelmä on monimutkainen luonteeltaan ja kärsii korkea dimensionaliteetti ongelma, jos luokkatilaa on suuri.
Label power-set toimii hyvin tapauksissa, joissa luokkamerkkien eri yhdistelmiä ei ole vähemmän. Se on hyvin suoraviivainen skeema verrattuna binääriseen relevanssiin & Luokittelijaketjuun.
kaikissa tapauksissa edellytetään tietokokonaisuuden ymmärtämistä ennen tiettyä järjestelmää koskevan päätöksen tekemistä.
Tarkkuusmittarit
moniluokkaisessa tai binäärisessä yksimerkintäisessä luokitteluongelmassa absoluuttinen tarkkuus saadaan suhdeluvulla (oikein luokiteltujen tietoilmiöiden lukumäärä / kokonaisilmoitusten määrä).
Katsotaanpa monimerkintätapauksen skenaariota esimerkkiaineistomme avulla. Jos kysymys id 241465 on luokiteltu etiketeillä: ’mallinnus’, ’Keski-raja-lause’,’ asteet-of-freedom ’ niin mitä voimme sanoa? Aineiston varsinaisia luokkamerkintöjä olivat ”tilastollinen merkitsevyys”, ”mallinnus”, ”keskirajauslause”, ”vapausasteet” ja ”spurious-correlation”. Se ei ole täysin väärä ennuste eikä täysin oikea. Jos menemme perinteinen oikea vs total ratio perustuu tarkkuus metriikka, ehdottomasti emme voi arvioida luokittelija. Tarvitsemme jotain, jolla voimme arvioida usean merkin luokittelijan osittaista oikeellisuutta.
Hamming Loss Metric
sen sijaan, että laskettaisiin oikein luokiteltujen tietojen määrää, Hamming Loss laskee ennustuksen aikana luokkamerkkien bittijonoon syntyneen häviön. Se tekee xor-operaation luokkanimikkeiden ja ennustettujen luokkanimikkeiden alkuperäisen binäärijonon välillä data-instanssissa ja laskee keskiarvon koko datajoukossa. Sen ilmaisun antaa
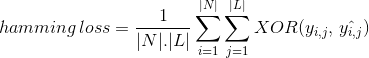
missä
/ n| = tietoilmiöiden lukumäärä
| L / = luokkaavaruuden kardinaalisuus
yᵢ,ⱼ = todellinen luokkamerkinnän bitti dataesiintymässä i
^yᵢ,ⱼ = ennustettu luokkamerkinnän bitti dataesiintymässä i
’hamming lossin arvo vaihtelee 0: sta 1: een. Koska se on häviömittari, sen tulkinta on luonteeltaan Käänteinen toisin kuin normaalitarkkuussuhde. Pienempi arvo hamming tappio osoittaa parempi luokittelija.
osajoukon tarkkuus
on joitakin tilanteita, joissa voidaan mennä absoluuttiseen tarkkuussuhteeseen, jossa merkkiennusteiden tarkan yhdistelmän mittaaminen on tärkeää. Se voi kuulostaa merkitykselliseltä tapauksessa ”tarran tehosarja”. Multi-label-skenaariossa sitä kutsutaan osajoukon tarkkuudeksi.
näiden kahden lisäksi jokaisen yksittäisen binääriluokittajan tarkkuutta voidaan arvioida muilla perinteisillä mittareilla, kuten tarkkuussuhde, F1-pisteet, tarkkuus, takaisinkutsu jne.ja ROC-käyrät.
kyse on teoreettisesta mallinnuksesta monimerkityksistä luokittelua varten. Näemme tapaustutkimuksen käyttäen todellista tietoa seuraavassa artikkelissa. Tiedonetsintäkoodi on saatavilla GitHubissa.
äskettäin kirjoitin kirjan ML (https://twitter.com/bpbonline/status/1256146448346988546)