a fenti diagramból osztályozók lánca látható. Ez majdnem hasonlít a ‘LinkedList’ adatstruktúrára. Y1, Y2..Y az egyes osztályozók válaszváltozói (0 vagy 1 lesz). Az összes korábbi osztályozó válaszai (kivéve az 1.) A következő osztályozóba kerülnek, és ezek az eredeti bemeneti jellemzőkkel(f1) együtt jellemzők lesznek..F).
általában a K osztályozó teljes bemeneti funkciókészlettel épül fel : f1,f2,..F,Y1,Y2,..Yᴷ⁻1
Most itt van egy kérdés, jön -, “Hogy a rend az osztályozó lánc döntött ?”Különböző stratégiák vannak erre az alábbiak szerint:
osztályozó láncok együttese (ECC): itt az osztályozás együttes modelljét használjuk. A láncok véletlenszerű mintavételét választják ki, és erre épül egy együttes. Az előre jelzett kimenet a többségi szavazási rendszer alkalmazásával jön létre az együttes kimeneteken. Ez egészen ugyanaz, mint RandomForest osztályozó.
Monte-Carlo osztályozó láncok (MCC): Monte-Carlo módszert alkalmaz az optimális osztályozó szekvencia generáláshoz.
vannak más módszerek is, például véletlenszerű keresés vagy függőségi módszerek az osztályozók számára, de nem túl gyakoriak a használatban.
az egyes osztályozók kimenetét a bináris relevancia sémához hasonlóan rögzítik, és a végén meghatározzák az osztálycímkéket.
címke teljesítmény-set séma
a bináris relevancia alapvető fogalma & osztályozó lánc többé-kevésbé azonos. Label power-set működik más módon. A képzési adatkészlet minden egyes címkekombinációját külön címkének tekinti. Például egy 3 osztályú többcímkés probléma esetén a 100, 001, 101, 111 stb.
általában egy n dimenziójú osztálytér, az összes lehetséges címkekombinációból 2 db lehet.
tehát nem bomlik semmilyen alproblémára, hanem közvetlenül megjósolja az osztálycímkék egészének kombinációját.
előnyök & az egyes sémák hátrányai
a bináris relevancia egyszerű séma, könnyen megvalósítható. De nem veszi figyelembe a címke közötti függőséget, így gyakran félreértelmezheti a rejtett adatkapcsolatokat.
az osztályozó lánc tökéletesen kezeli az osztálycímke-kapcsolatokat. Különösen azokban az esetekben, amikor egyes osztálycímkék mások alcímkéi, és egy osztálycímke előfordulása nagymértékben függ más címkéktől(szülő-gyermek kapcsolatok az osztálycímkékben. Gyermek címke akkor fordulhat elő, ha a szülő címke ott van). De ez a rendszer összetett természetű, és szenved nagy dimenzió probléma, ha osztály tér nagy.
Label power-set jól működik azokban az esetekben, amikor nem a különböző kombinációi osztály címkék kevesebb. Ez nagyon egyszerű séma a bináris relevancia & osztályozó lánchoz képest.
minden esetben az adatkészlet megértése szükséges, mielőtt döntést hozna egy adott rendszerről.
pontossági mutatók
többosztályú vagy bináris egycímkés osztályozási problémában az abszolút pontosságot az arány adja meg (a helyesen Osztályozott adatpéldányok száma / az adatpéldányok teljes száma).
nézzük meg a többcímkés eset forgatókönyvét a példaadatkészletünk segítségével. Ha a 241465 azonosítójú kérdést címkékkel osztályozzuk: ‘modellezés’,’ Közép-határ-tétel’,’ szabadságfokok’, akkor mit mondhatunk? Az adathalmaz tényleges osztálycímkéi a következők voltak: ‘statisztikai szignifikancia’, ‘modellezés’, ‘Közép-határ-tétel’, ‘szabadságfokok’és’ hamis korreláció’. Sem teljesen téves jóslat, sem teljesen helyes. Ha a hagyományos helyes vs teljes arány alapú pontossági mutatót választjuk, akkor biztosan nem tudjuk megítélni az osztályozót. Szükségünk van valamire, hogy megítéljük a többcímkés osztályozó részleges helyességét.
Hamming Veszteségmutató
a helyesen Osztályozott adatpéldányok számának számlálása helyett a Hamming veszteség kiszámítja az osztálycímkék bitsorában generált veszteséget az előrejelzés során. XOR műveletet hajt végre az osztálycímkék eredeti bináris karakterlánca és az adatpéldány előrejelzett osztálycímkéi között, és kiszámítja az adatkészlet átlagát. Kifejezését az adja
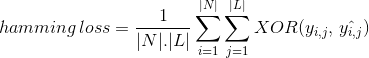
ahol
/ L / = az osztálytér kardinalitása
y xhamsteren,xhamsteren = a j osztálycímke tényleges bitje az I adatpéldányban
^Y. a J osztálycímke várható bitje az i adatpéldányban
‘a hamming veszteség értéke 0-tól 1-ig terjed. Mivel veszteségmutatóról van szó, értelmezése fordított jellegű, ellentétben a normál pontossági aránnyal. A hamming veszteség kisebb értéke jobb osztályozót jelez.
részhalmaz pontossága
vannak olyan helyzetek, amikor abszolút pontossági arányt lehet elérni, ahol fontos a címke-előrejelzések pontos kombinációjának mérése. Ez relevánsnak tűnhet a címkekészlet esetében. A többcímkés forgatókönyvben részhalmaz pontosságaként ismert.
e kettőn kívül minden egyes bináris osztályozó pontosságát más hagyományos mutatók, például pontossági Arány, F1 pontszám, pontosság, visszahívás stb.
ez a többcímkés osztályozás elméleti modellezéséről szól. A következő cikkben valós adatokat használó esettanulmányt fogunk látni. Az adatfeltárási kód elérhető a Github oldalon.
nemrég írtam egy könyvet Az ML-ről (https://twitter.com/bpbonline/status/1256146448346988546)