Capitolo 12
Moment Distribution Method of Analysis of Structures
12.1 Concetti di base
Il moment distribution method of analysis of beams and frames è stato sviluppato da Hardy Cross e presentato formalmente nel 1930. Sebbene questo metodo sia un metodo di deformazione come il metodo slope-deflection, è un metodo approssimativo e, quindi, non richiede la risoluzione di equazioni simultanee, come nel caso di quest’ultimo metodo. Il grado di accuratezza dei risultati ottenuti con il metodo della distribuzione del momento dipende dal numero di approssimazioni successive o dal processo di iterazione.
Per illustrare il concetto del metodo di distribuzione del momento, si consideri il fotogramma mostrato in Figura 12.1. I membri del telaio sono prismatici e si presume che non si deformino assialmente né si traducano l’uno rispetto all’altro. I giunti ACD del telaio sono fissi, mentre il giunto B può ruotare leggermente a causa del carico applicato. Innanzitutto, prima di eseguire la distribuzione del momento tra i membri, si presume che tutti i giunti siano temporaneamente bloccati utilizzando un morsetto.
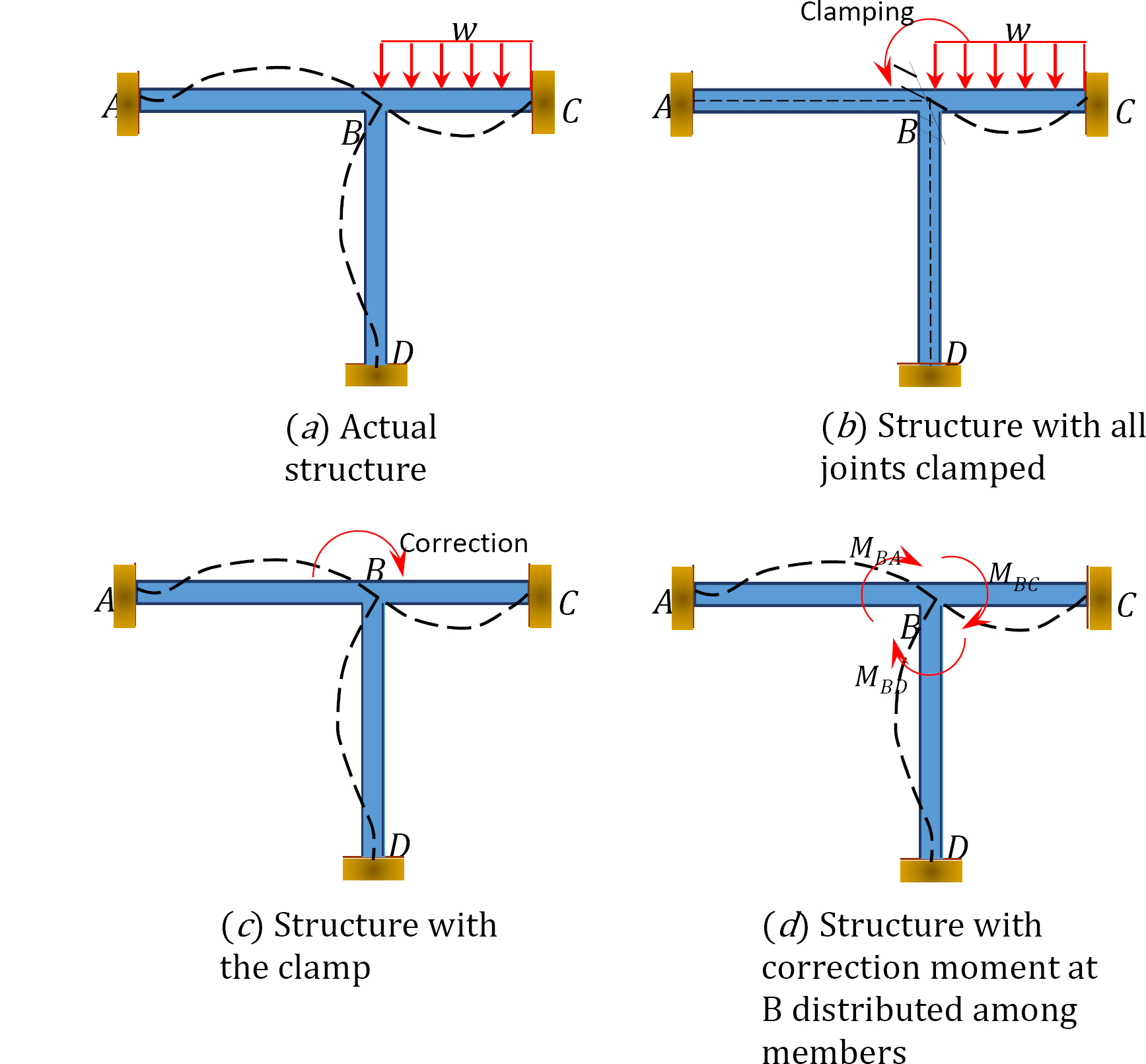
Fig. 12.1. Cornice.
12.2 Convenzione dei segni
La convenzione dei segni per il metodo di distribuzione del momento è simile a quella stabilita per il metodo slope-deflection; cioè, il momento alla fine di un membro è considerato positivo se tende a ruotare la fine del membro in senso orario e negativo se tende a ruotarlo in senso antiorario.
12.3 Definizioni
Momenti sbilanciati: questo metodo di analisi presuppone che i giunti in una struttura siano inizialmente bloccati o bloccati e quindi rilasciati successivamente. Una volta rilasciato un giunto, avviene una rotazione, poiché la somma dei momenti finali fissi dei membri che si riuniscono in quel giunto non è zero. Il valore della somma dei momenti finali ottenuti è il momento sbilanciato in quell’articolazione.
Momenti di riporto: i momenti distribuiti alle estremità dei membri riuniti in una causa congiunta momenti nelle altre estremità, che si presume siano fissi. Questi momenti indotti alle altre estremità sono chiamati momenti di riporto.
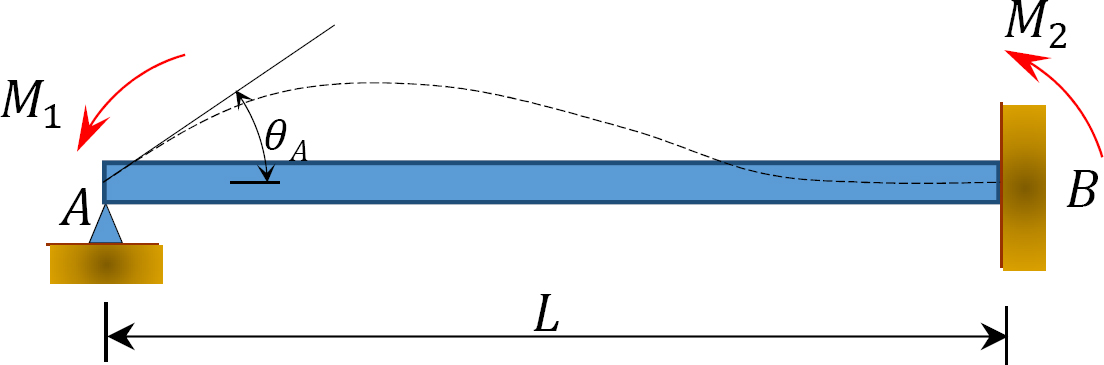
Fig. 12.2. Fascio prismatico scaricato.
Si consideri una trave prismatica scarica fissata all’estremità B, come mostrato nella Figura 12.2. Se un momento M1 viene applicato all’estremità sinistra della trave, le equazioni di pendenza-deflessione per entrambe le estremità della trave possono essere scritte come segue:


Sostituendo 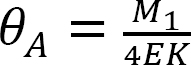 dall’equazione 12.1 nell’equazione 12.2 suggeriscono i seguenti:
dall’equazione 12.1 nell’equazione 12.2 suggeriscono i seguenti:

Equazione 12.3 suggerisce che il momento trasportato nel termine fisso di una trave a causa di un momento applicato all’altra estremità è pari alla metà di un momento applicato.
Fattore di riporto: il rapporto tra il momento indotto e il momento applicato è indicato come fattore di riporto. Per il raggio mostrato nella figura 12.2, il fattore di riporto è il seguente:

Fattore distribuito (DF): Il fattore distribuito è un fattore utilizzato per determinare la proporzione del momento sbilanciato portato da ciascuno dei membri riuniti in un comune. Per i membri riuniti in comune O del quadro mostrato nella figura 12.3, i loro fattori di distribuzione sono calcolati come segue:
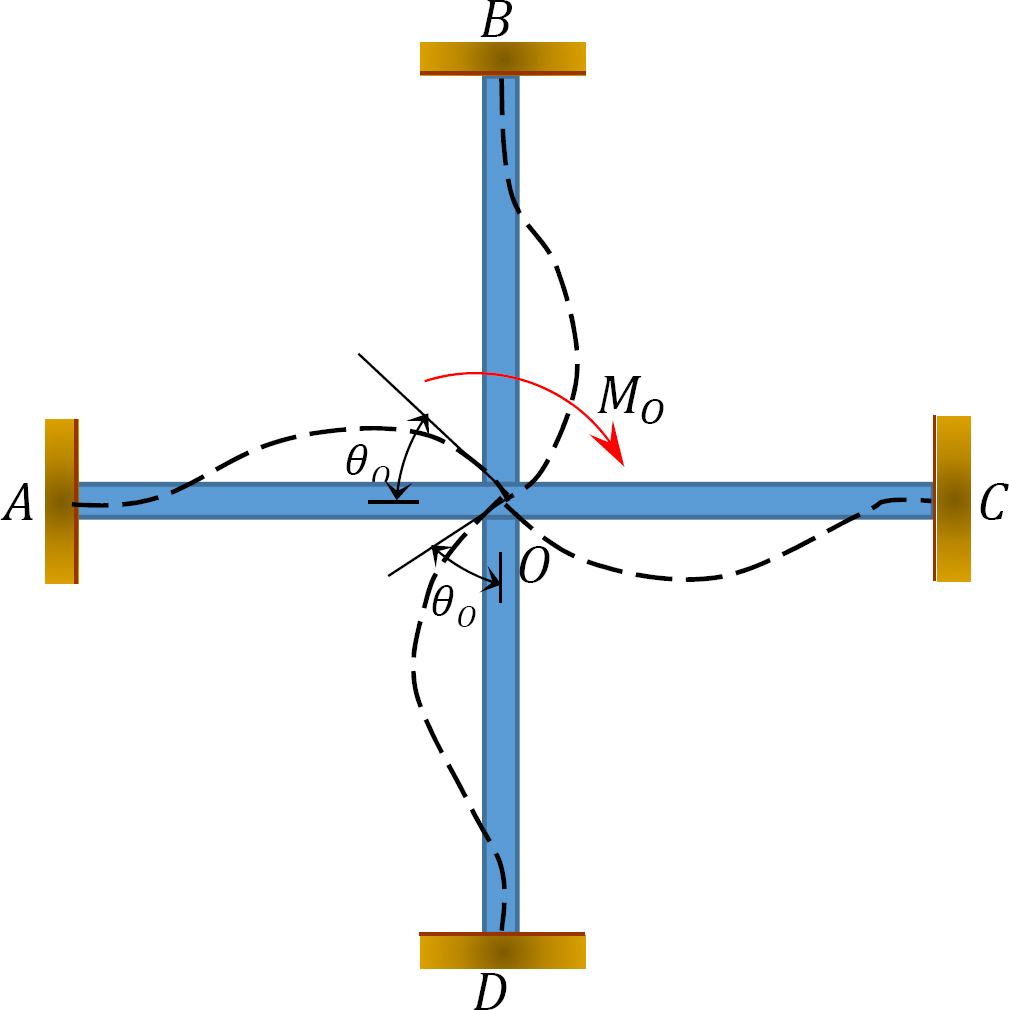
Fig. 12.3. Cornice.

Momenti distribuiti: al momento del rilascio del morsetto immaginario in un giunto, il momento sbilanciato in quel giunto lo fa ruotare. La rotazione torce la fine della riunione dei membri in comune, con conseguente sviluppo di momenti di resistenza. Questi momenti di resistenza sono chiamati momenti distribuiti. I momenti distribuiti per i membri del frame mostrati in Figura 12.3 sono calcolati come segue:
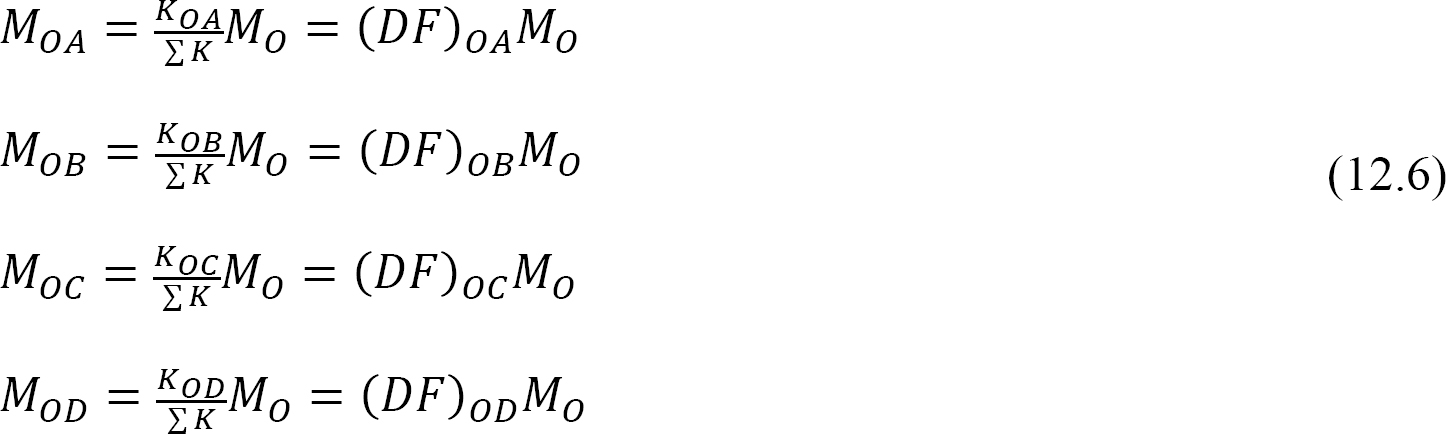
12.4 Modifica della rigidità del membro
A volte il processo di iterazione nel metodo di distribuzione del momento può essere significativamente ridotto regolando la rigidità flessionale di alcuni membri della struttura indeterminata. Questa sezione considera l’influenza di un supporto fisso e pin – end sulla rigidità flessionale di una trave indeterminata.
Caso 1: Una trave incernierata ad un’estremità e fissata all’altra
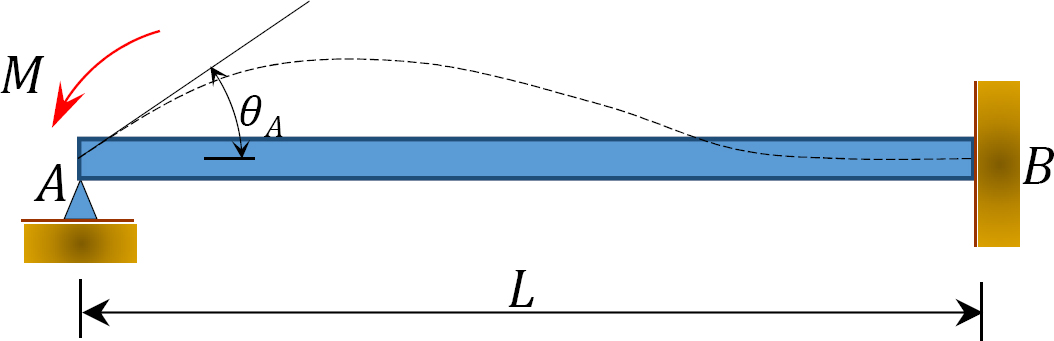
Fig. 12.4. Fascio
Considerare un fascio incernierato all’estremità A e fissato all’estremità B, come mostrato nella Figura 12.4. Applicando un momento M ruota l’estremità della cerniera di una quantità θ. Scrivere l’equazione pendenza-deflessione per la fine A del membro e notare che 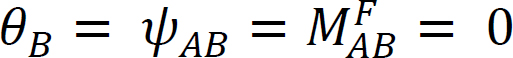 suggerisce quanto segue:
suggerisce quanto segue:
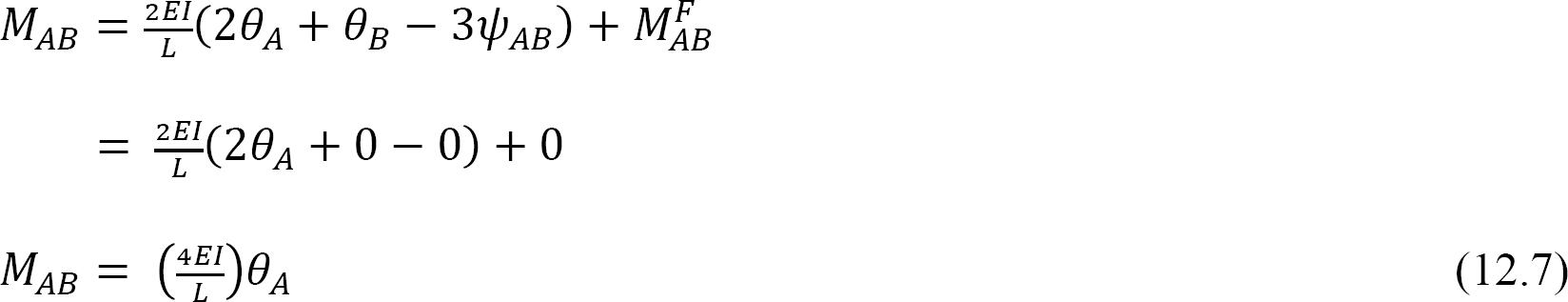
Per definizione, la rigidità flettente di un elemento strutturale è il momento che deve essere applicato a un’estremità dell’elemento per causare una rotazione dell’unità di tale estremità. La seguente espressione per la rigidità alla flessione per il membro fisso con fondo è espresso come segue quando si sostituisce θA = 1 nell’equazione 12.7:

per definizione, la relativa rigidità alla flessione dei membri è determinato dividendo la rigidità alla flessione degli stati di 4E. Dividendo l’equazione 12.8 da 4E suggerisce la seguente espressione per la relativa rigidità per il caso considerato:

Caso 2: Una trave incernierata alle estremità
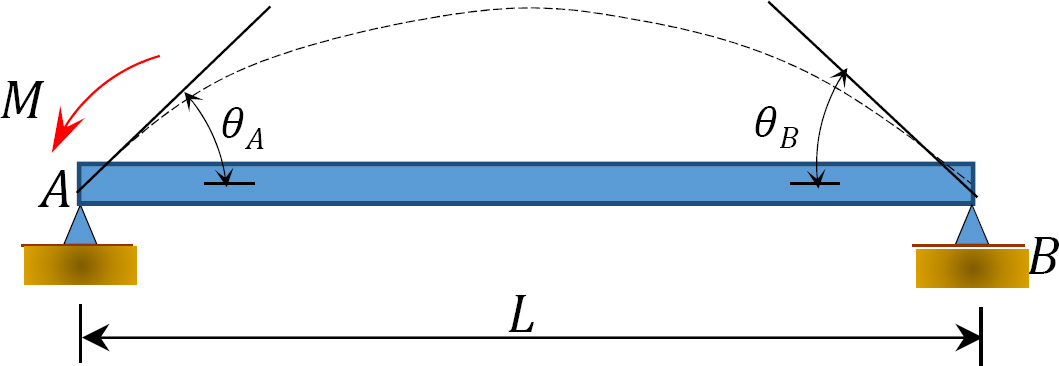
Fig. 12.5. Fascio semplicemente supportato.
Applicando un momento M all’estremità A del raggio semplicemente supportato mostrato in Figura 12.5 ruota il raggio di un angolo θA all’estremità incernierata. Utilizzando l’equazione pendenza-deflessione modificata derivata nella sezione 11.4 del capitolo 11 e notando che 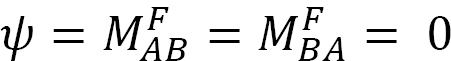 suggerisce la seguente espressione per il momento all’estremità incernierata in cui viene applicato il carico:
suggerisce la seguente espressione per il momento all’estremità incernierata in cui viene applicato il carico:
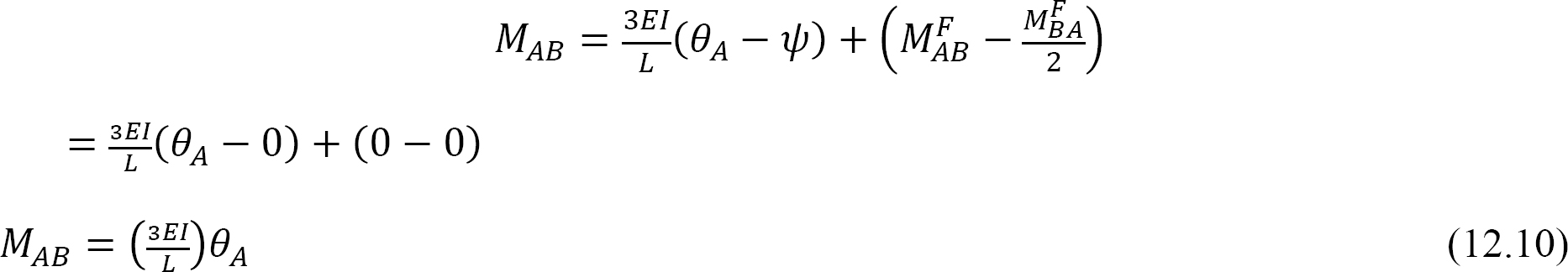
La sostituzione di θA = 1 nell’equazione 12.10 suggerisce la seguente espressione per la rigidità di flessione per un membro con un’estremità lontana incernierata:

La rigidezza relativa per un membro con un battente fine si ottiene dividendo l’equazione 12.11 da 4E, come segue:

Confrontando le equazioni 12.12 e il 12,9 suggerisce che un membro con cerniera fondo è di tre-quarto rigido come un membro con la stessa geometria ma fissata all’estremità. Questo fatto accertato può ridurre sostanzialmente il numero di iterazione quando si analizzano travi o telai con un estremo incernierato utilizzando il metodo della distribuzione del momento. In questi casi, la rigidità relativa del raggio all’estremità vicina viene prima regolata secondo l’equazione 12.12 e il suo fattore di distribuzione viene calcolato con la rigidità regolata. Durante l’operazione di bilanciamento, la fine vicina sarà bilanciata solo una volta senza ulteriori riporti di momenti da o alla sua fine.
12.5 Analisi di travi indeterminate
La procedura per l’analisi di travi indeterminate con il metodo della distribuzione del momento è brevemente riassunta come segue:
Procedura per l’analisi di fasci indeterminati con il metodo di distribuzione del momento
•Calcolare i momenti di estremità fissa per i membri, supponendo che i giunti siano bloccati contro la rotazione.
•Calcolare il fattore di distribuzione per ciascuno dei membri collegati al giunto
•Calcolare il momento sbilanciato a ciascun giunto e distribuire lo stesso alle estremità dei membri collegati a quel giunto.
•Trasferire oltre la metà del momento distribuito alle altre estremità dei membri.
•Aggiungere o sottrarre questi ultimi momenti (momenti ottenuti nei passaggi tre e quattro) ai momenti finali fissi originali.
•Applicare i momenti finali determinati alle articolazioni della struttura data.
•Disegnare il diagramma a corpo libero di ciascuna campata del raggio dato, mostrando i carichi e i momenti alle giunture ottenuti con il metodo di distribuzione del momento.
•Determinare le reazioni di supporto per ogni span.
•Calcolare e costruire la forza di taglio e diagrammi del momento flettente per ogni campata.
•Disegnare un diagramma di momento flettente e una forza di taglio per la trave data combinando i diagrammi al punto 9.
Esempio 12.1
Utilizzando il metodo di distribuzione del momento, determinare i momenti finali e le reazioni ai supporti del raggio mostrati in Figura 12.6 a. Disegnare la forza di taglio e i diagrammi del momento flettente. EI = costante.
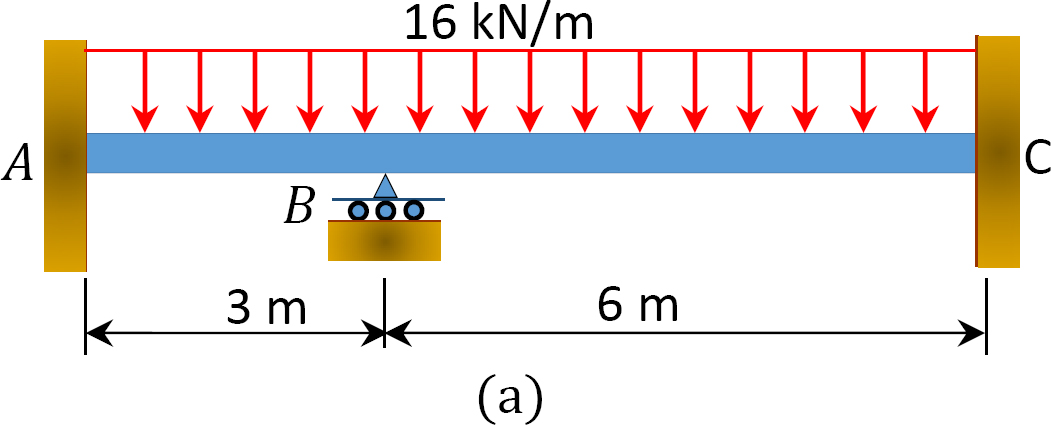
Fig. 12.6. Trave.
Soluzione
Momento finale fisso.
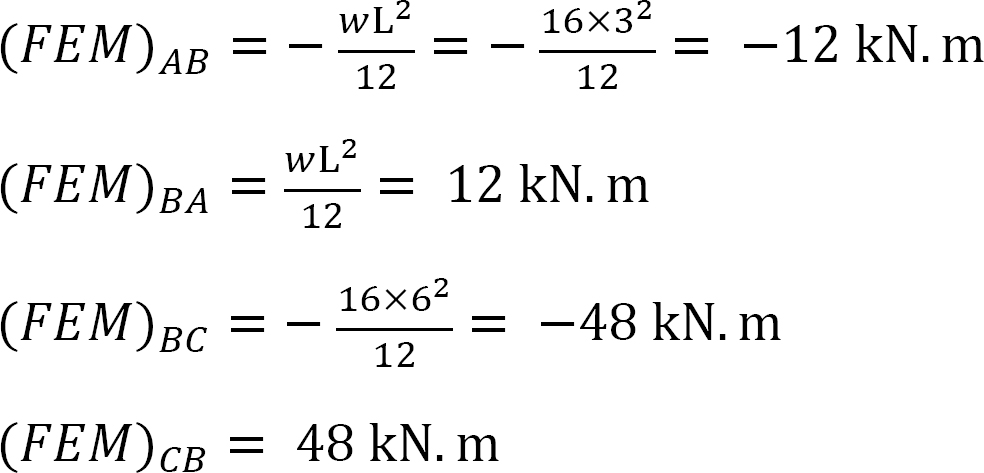
Fattore di rigidezza.
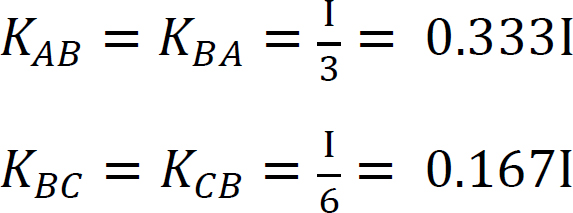
Fattore di distribuzione.
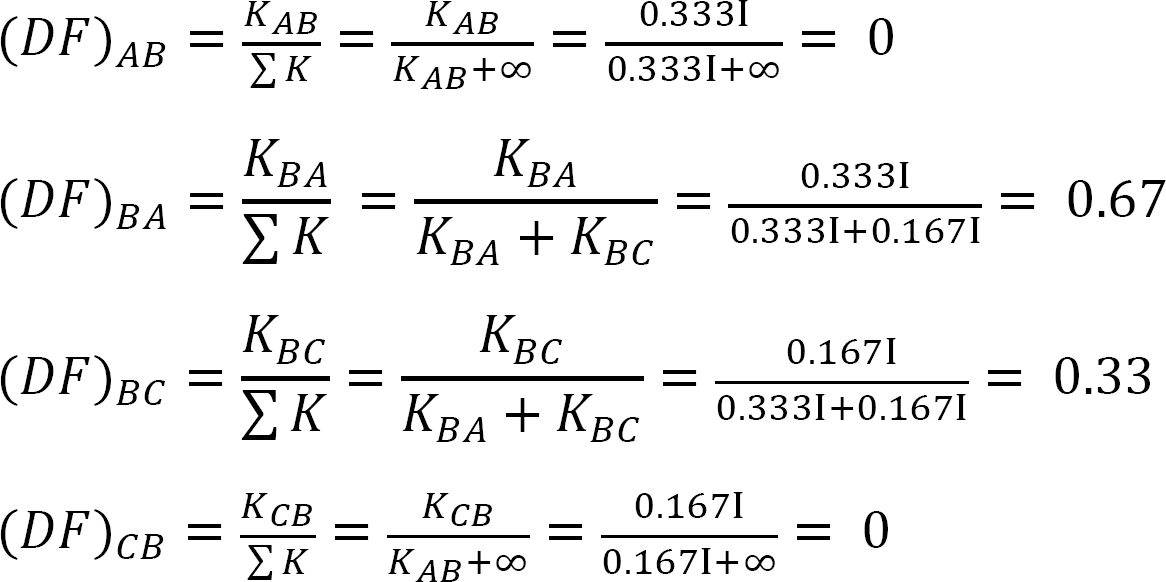
Tabella 12.1. Tabella di distribuzione.
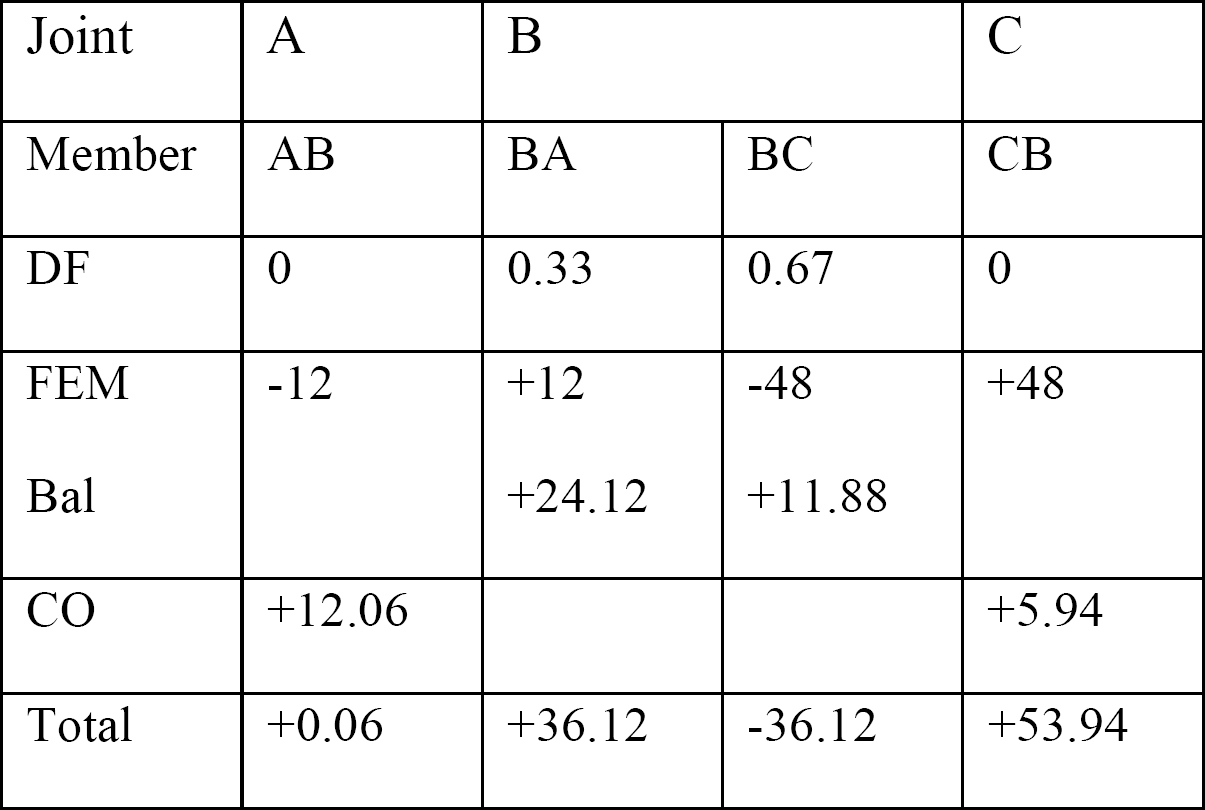
Diagrammi della forza di taglio e del momento flettente.
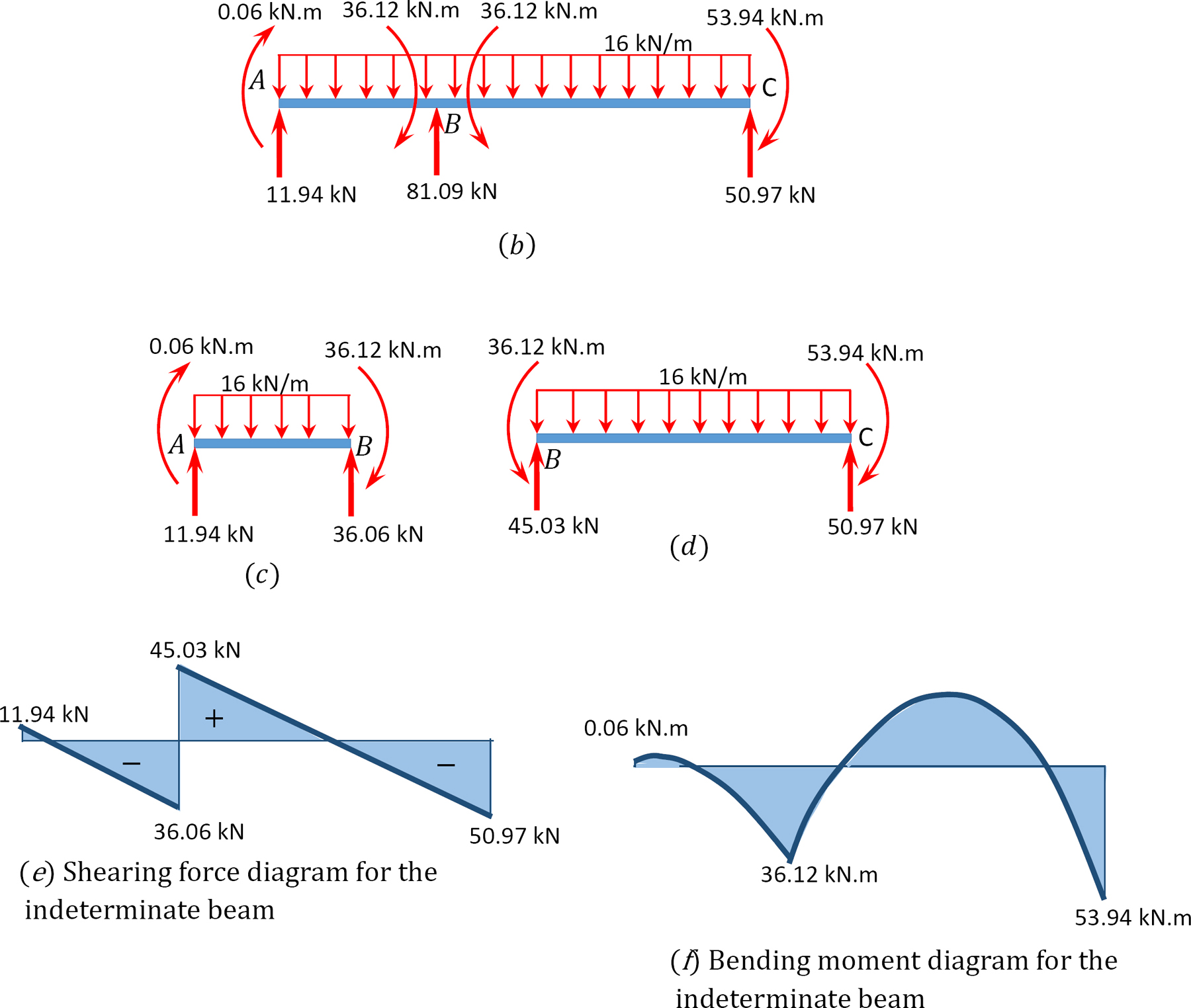
Esempio 12.2
Utilizzando il metodo di distribuzione del momento, determinare i momenti finali e le reazioni ai supporti del raggio mostrati in Figura 12.7 a. Disegnare la forza di taglio e i diagrammi del momento flettente.
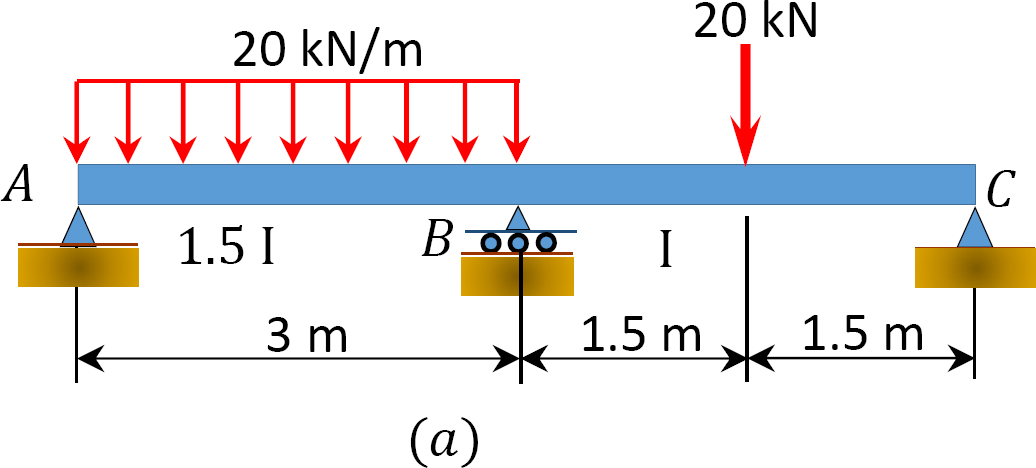
Fig. 12.7. Trave.
Soluzione
Momento finale fisso.
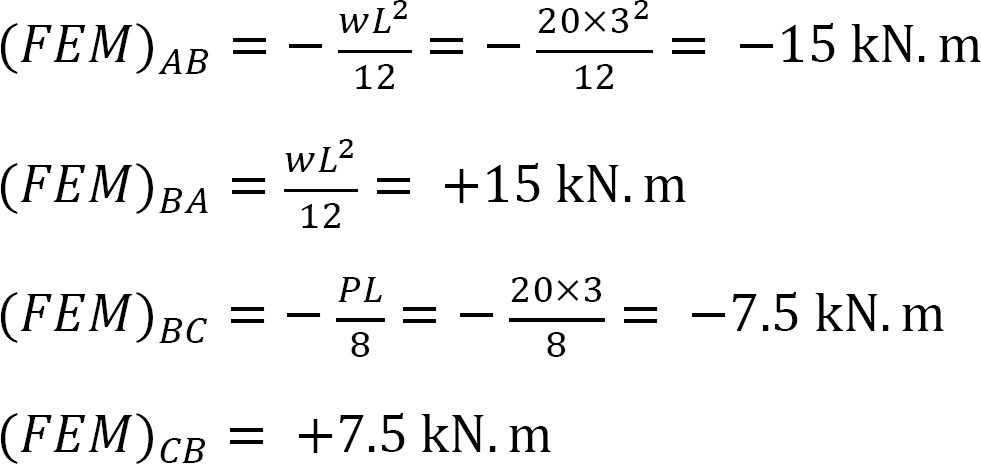
Fattore di rigidezza.
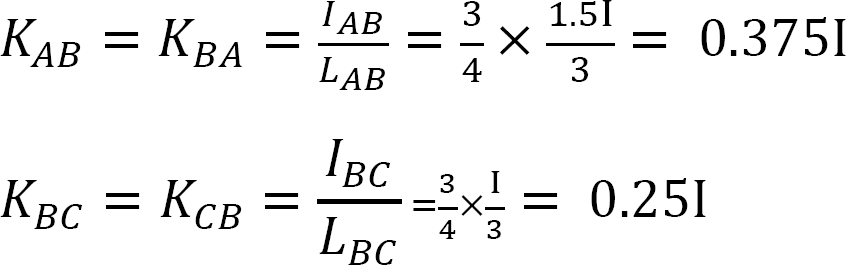
Fattore di distribuzione.
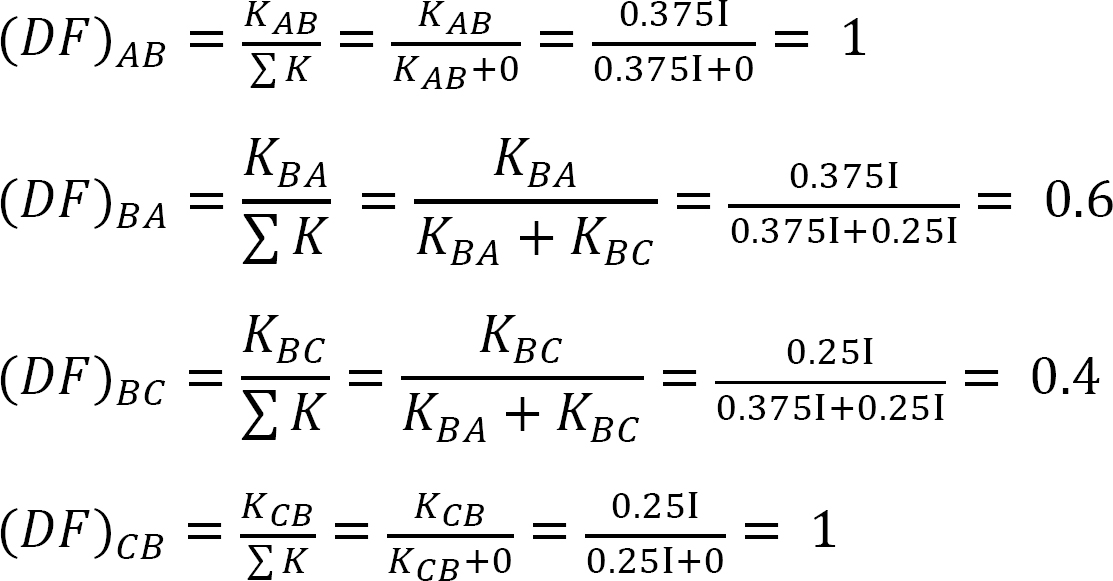
Tabella 12.2. Tabella di distribuzione.
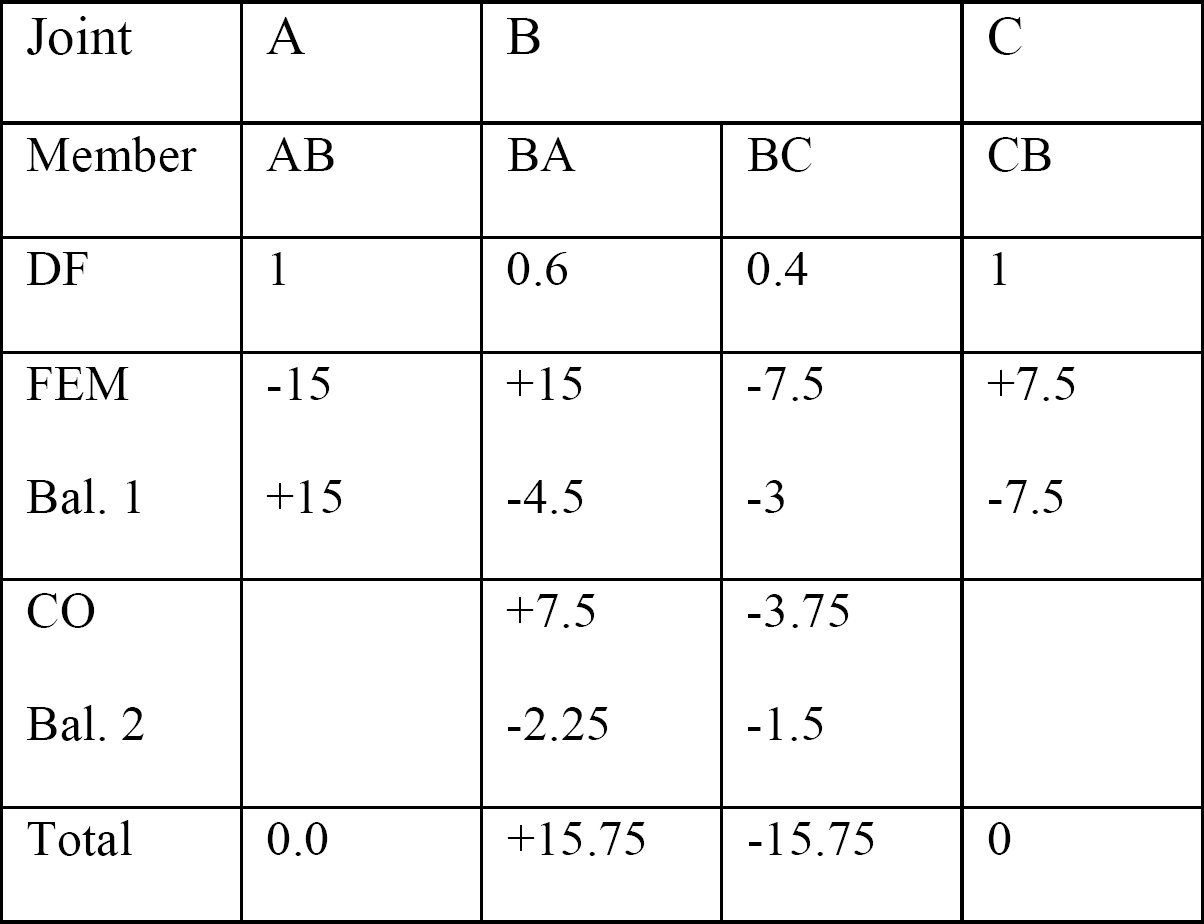
Diagrammi della forza di taglio e del momento flettente.
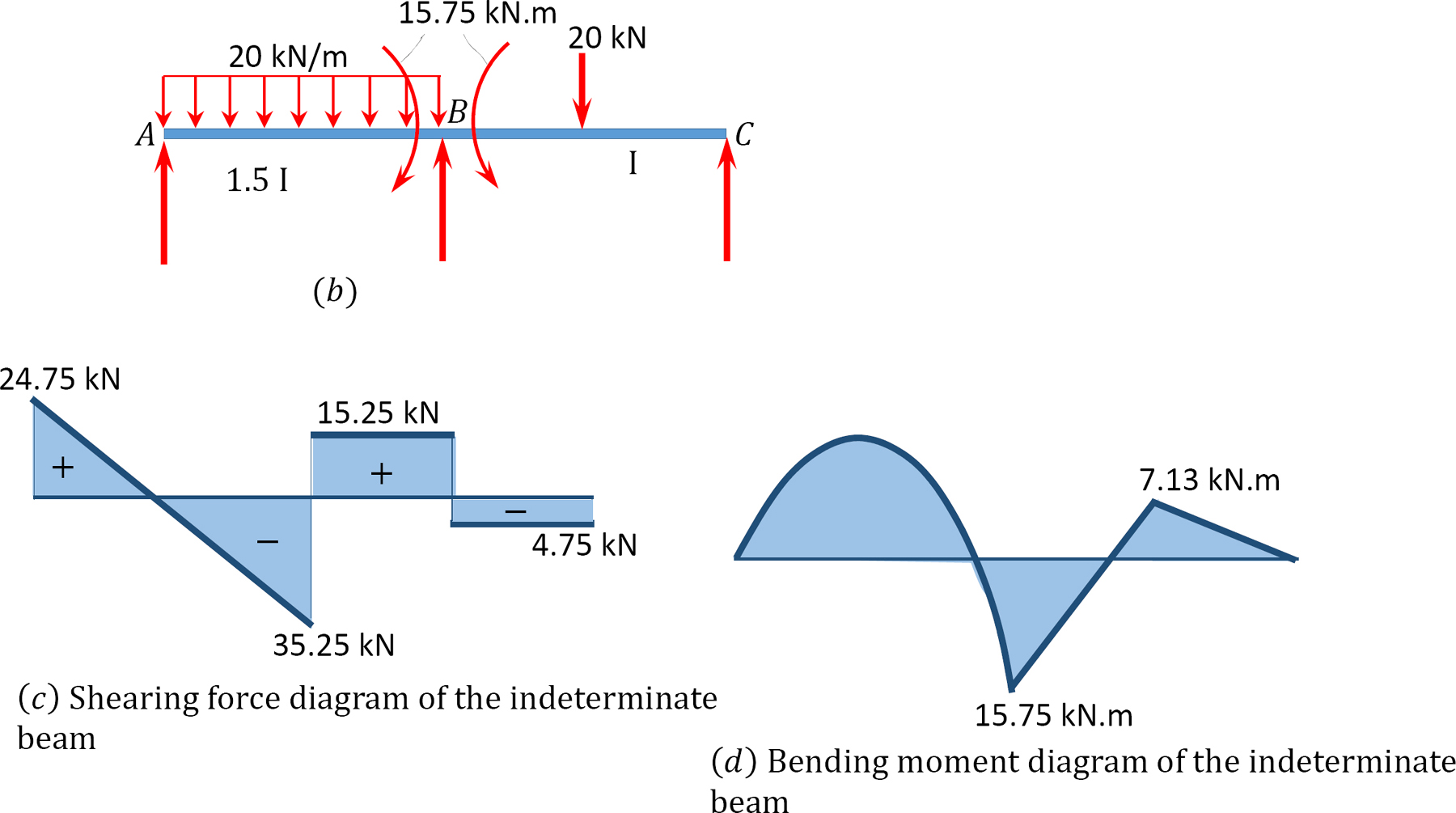
12.6 Analisi di frame indeterminati
La procedura per l’analisi dei frame utilizzando il metodo di distribuzione del momento dipende dal tipo di frame che viene analizzato. I frame sono classificati come frame ondeggianti o non ondeggianti. La procedura per l’analisi dei telai non ondeggianti è simile a quella delle travi indeterminate. Ma per l’analisi dei frame sway, la procedura è diversa. Ci sono due fasi coinvolte nell’analisi dei telai di ondeggiamento, vale a dire le analisi non-sway stage e sway-stage. Queste fasi sono descritte di seguito.
Procedura per l’analisi di frame ondeggianti indeterminati con il metodo di distribuzione del momento
A. Analisi dello stadio non ondeggiante
•Per prima cosa si assume l’esistenza di un puntello immaginario che impedisce al frame di oscillare.
•Calcola le reazioni orizzontali sui supporti del fotogramma e nota la differenza X. Questa è la forza per prevenire l’ondeggiamento.
B. Sway stage analysis
•Assumere momenti arbitrari per agire sulle colonne del frame. La grandezza di questi momenti varierà da colonna a colonna in proporzione a 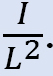
•I valori sono assunti per M2 e M1 è determinato.
•I momenti arbitrari vengono quindi distribuiti come per la condizione di non oscillazione
•Calcolare l’entità delle reazioni orizzontali ai supporti per la condizione di oscillazione. La sommatoria di queste reazioni dà la forza di spostamento arbitraria Y.
•Determina il rapporto 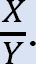 Questo rapporto è chiamato fattore di oscillazione.
Questo rapporto è chiamato fattore di oscillazione.
•Utilizzare il fattore di oscillazione per moltiplicare i momenti distribuiti dell’oscillazione. Questo dà il momento corretto per l’influenza.
Esempio 12.3
Utilizzando il metodo di distribuzione momento, determinare i momenti finali dei membri del fotogramma mostrato in Figura 12.8. EI = costante.
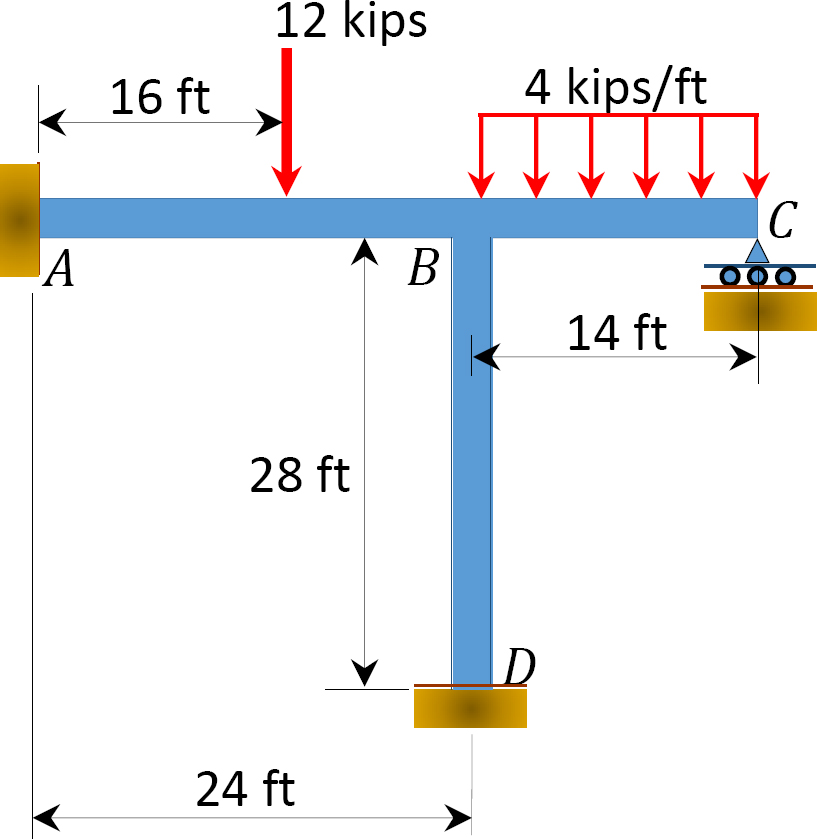
Fig. 12.8. Cornice.
Soluzione
Momento finale fisso.
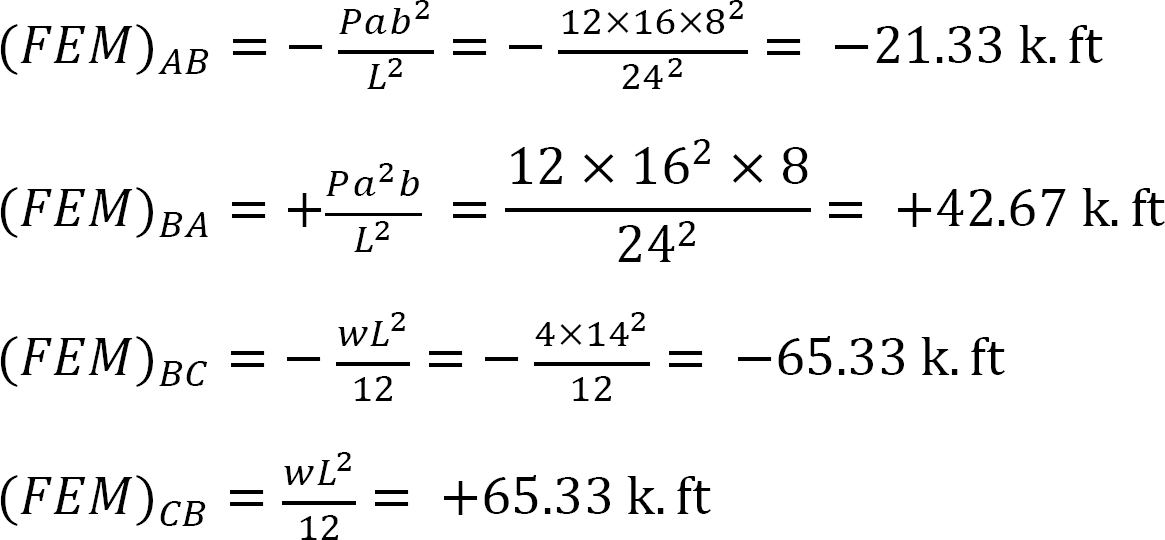
Fattore di rigidezza.
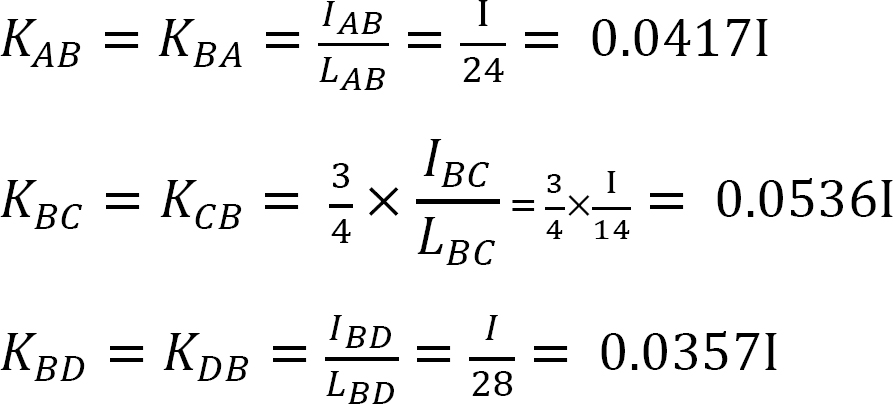
Fattore di distribuzione.
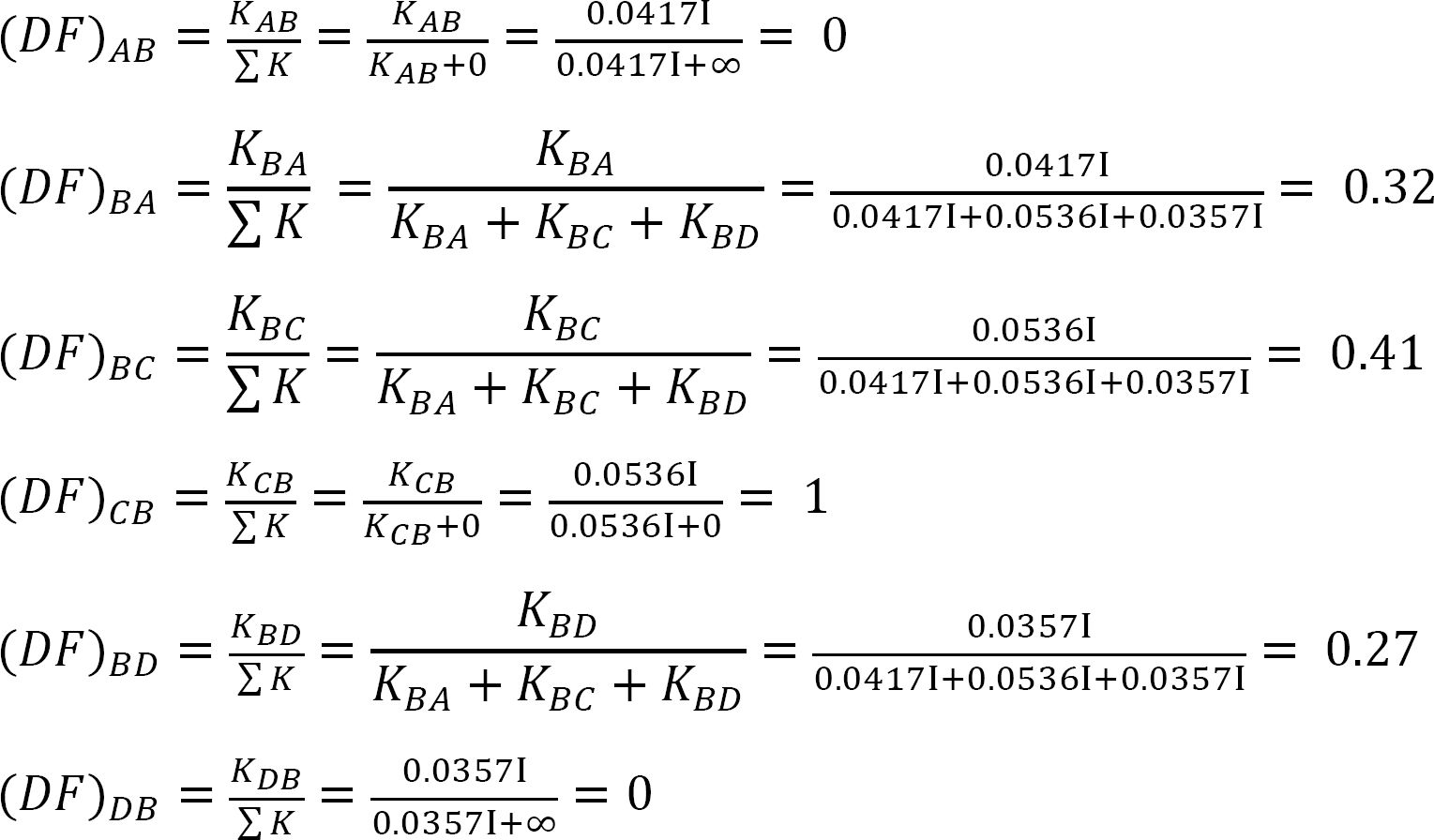
Tabella 12.3. Tabella di distribuzione.
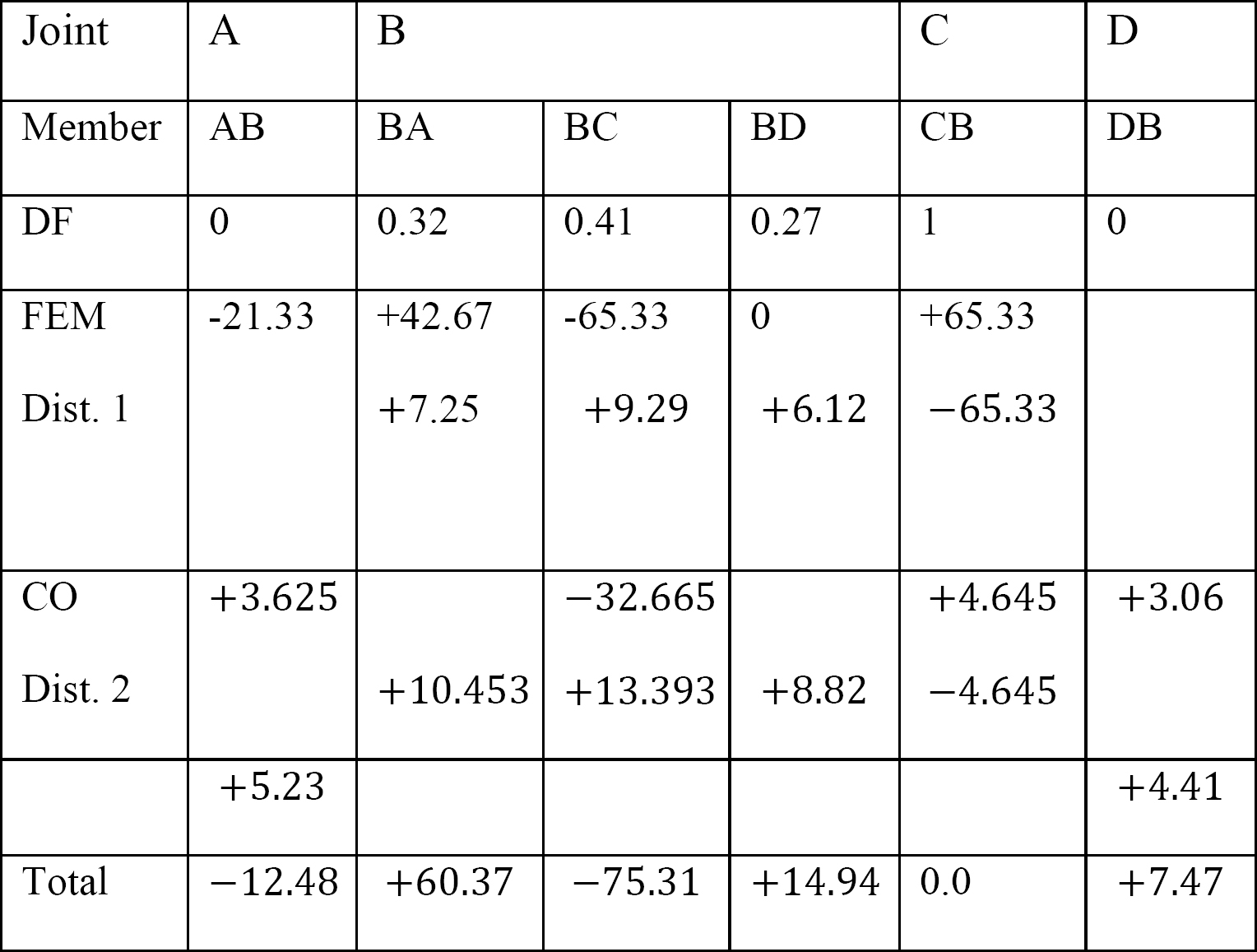
Momenti finali membri finali.
Sostituendo i valori ottenuti di EKθB, EKθC, e EK∆ negli stati fine momento equazioni suggerisce il seguente:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Esempio 12.4
Utilizzando il metodo di distribuzione del momento, determinare i momenti finali sui supporti del fotogramma mostrato in Figura 12.9. EI = costante.
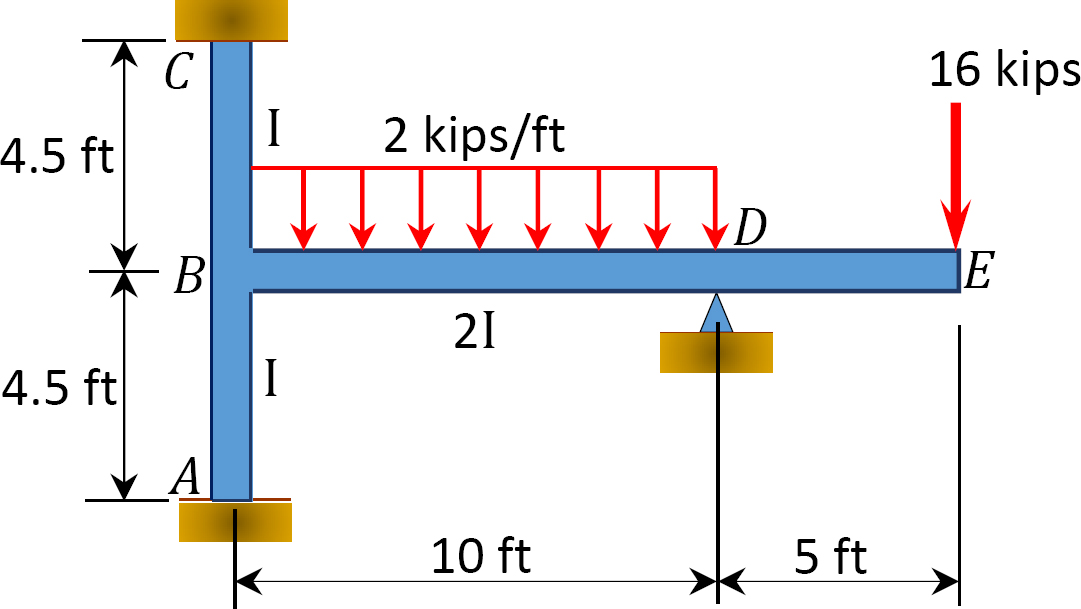
Fig. 12.9. Cornice.
Soluzione
Momento finale fisso.
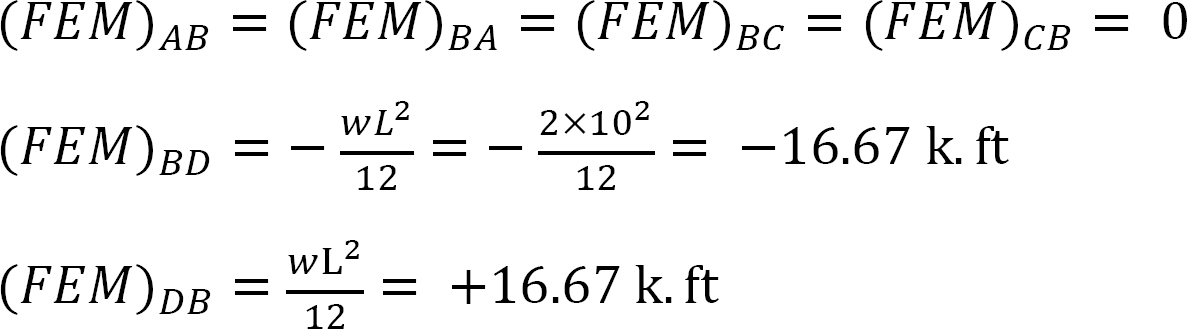
Fattore di rigidezza.
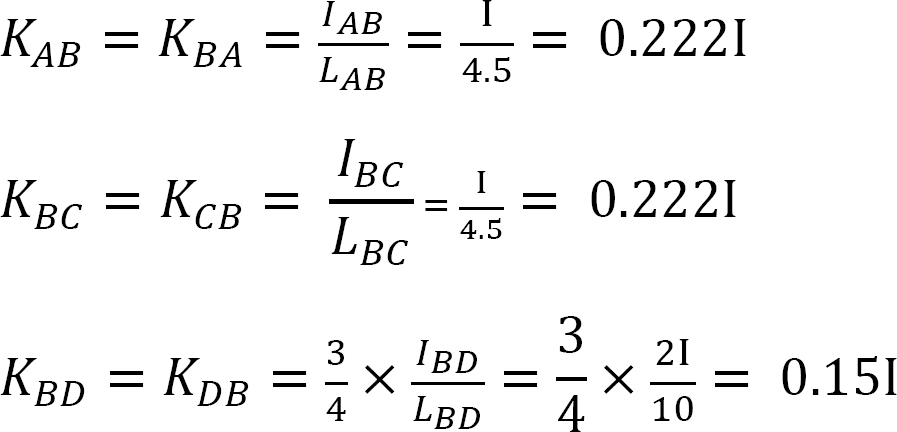
Fattore di distribuzione.

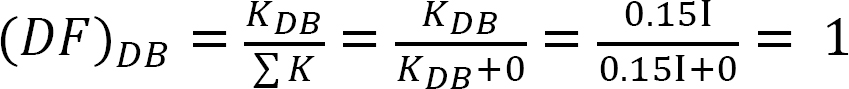
Tabella 12.4. Tabella di distribuzione.
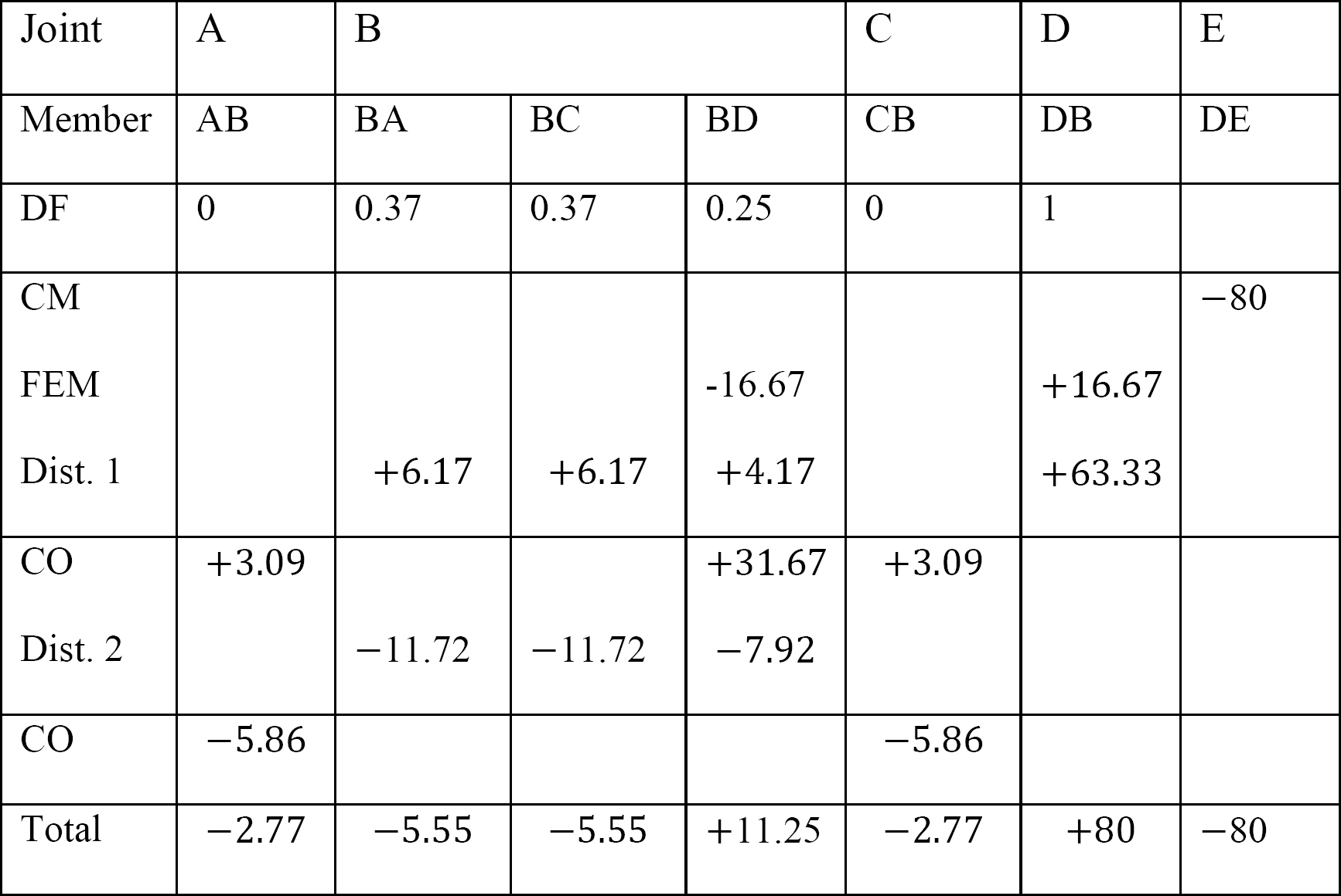
Momenti finali membri finali.
MAB = -2,77 k. ft
MBA = -5,55 k. ft
MBC = -5,55 k. 11.25 k. ft
MCB = -2.77
MDB = +80 k. ft
MDE = -80 k. ft
Esempio 12.5
Utilizzando il metodo di distribuzione del momento, determinare i momenti finali sui supporti del fotogramma mostrato in Figura 12.10. EI = costante.
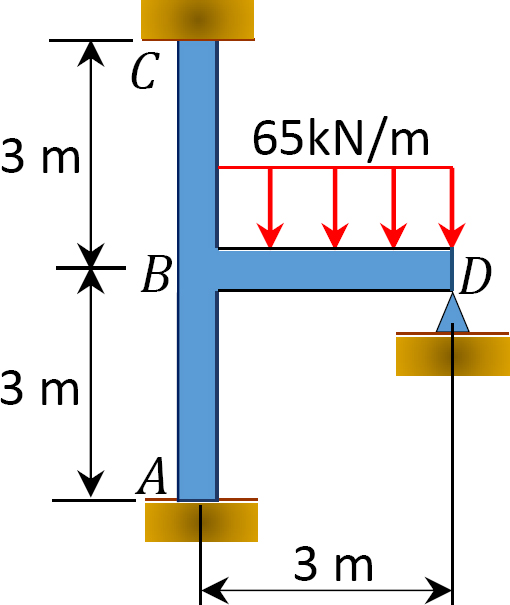
Fig. 12.10. Cornice.
Soluzione
Momento finale fisso.
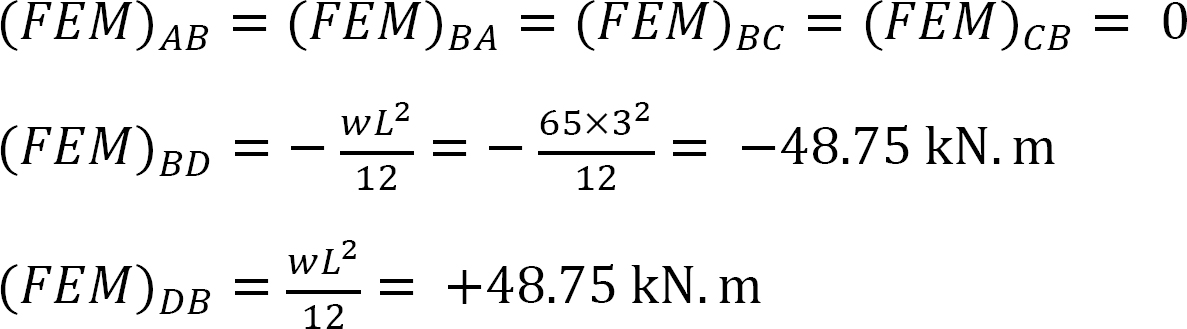
Fattore di rigidezza.
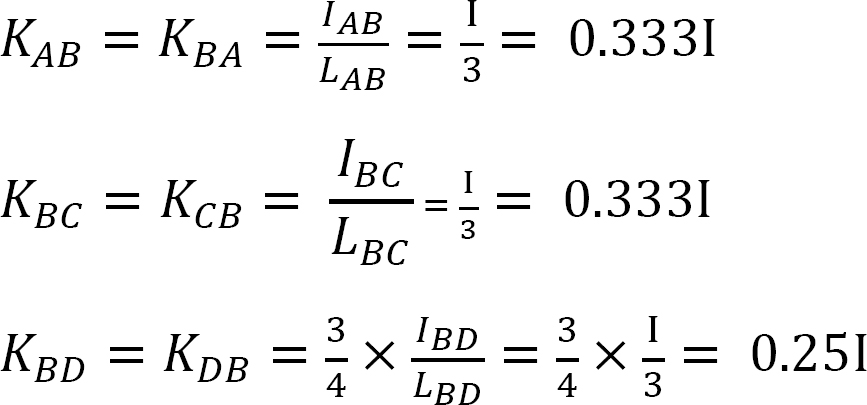
Fattore di distribuzione.
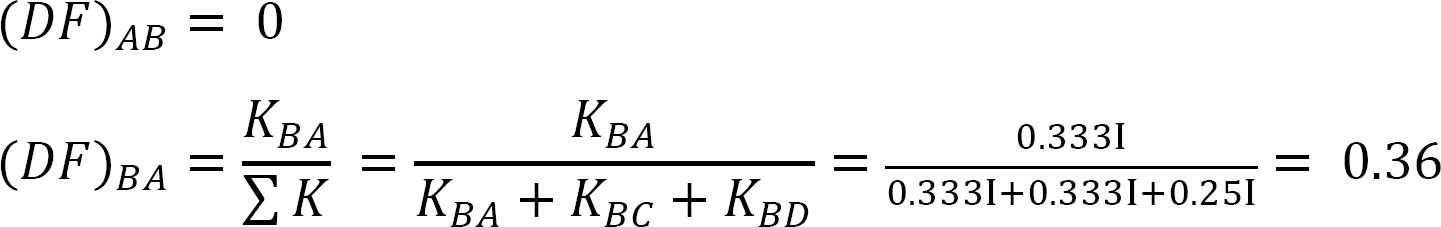

Tabella 12.5. Tabella di distribuzione.
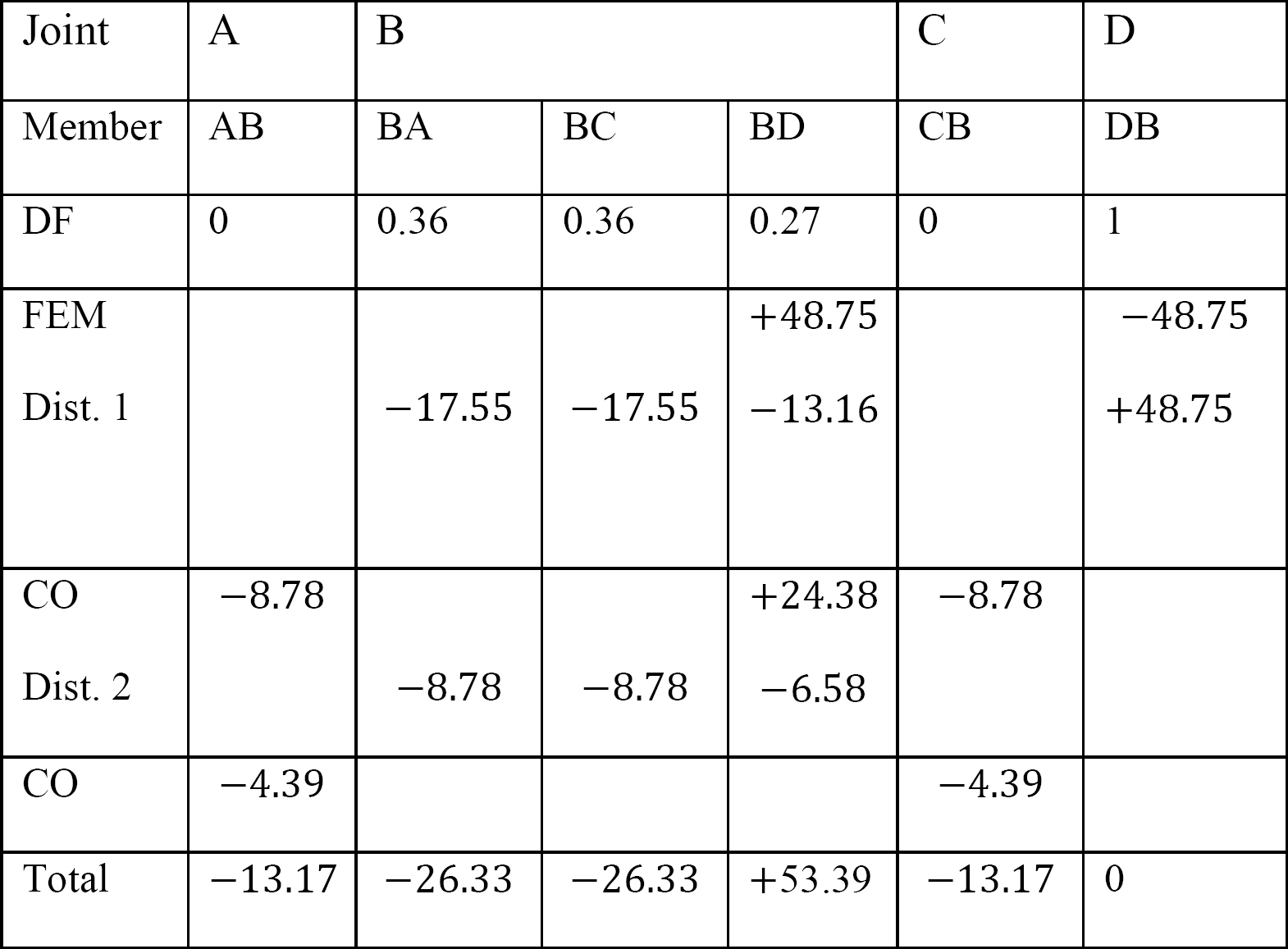
Momenti finali membri finali.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +53.39 k. ft
MCB = -13.17 k. ft
MDB = 0
Esempio 12.6
Utilizzando il momento di metodo di distribuzione, determinare il membro di fine momenti di telaio con il lato ondeggiare mostrato in Figura 12.11 un.
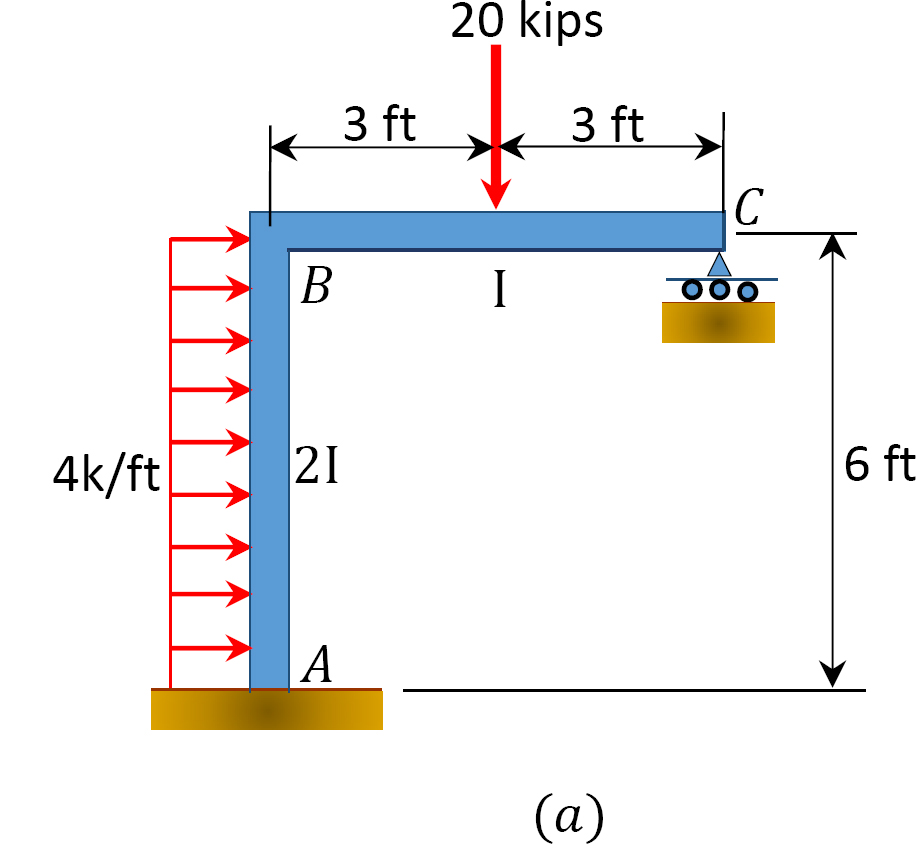
Fig. 12.11. Telaio con oscillazione laterale.
Soluzione
Momento finale fisso.
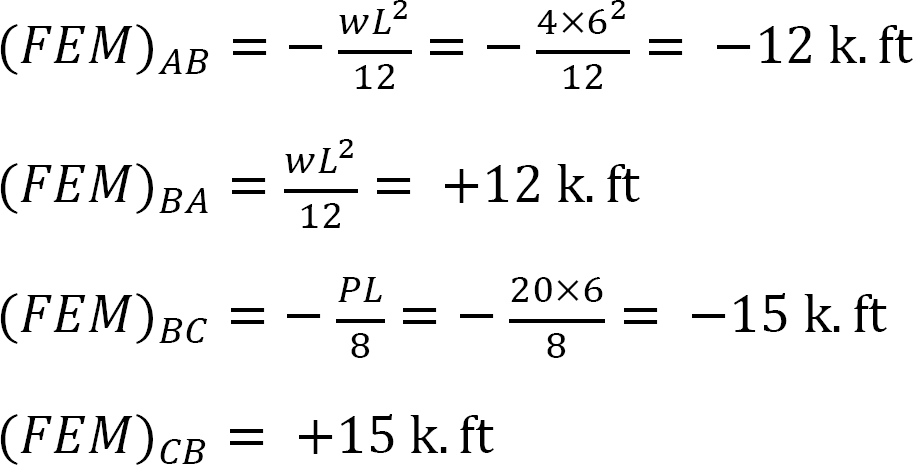
Fattore di rigidezza.
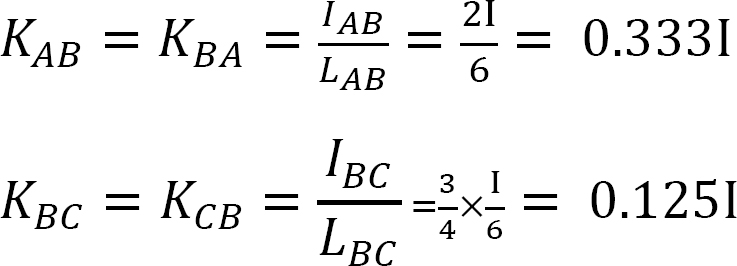
Fattore di distribuzione.
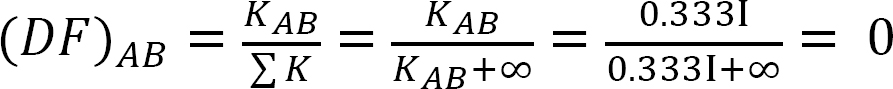

Analisi del telaio senza oscillazione laterale.
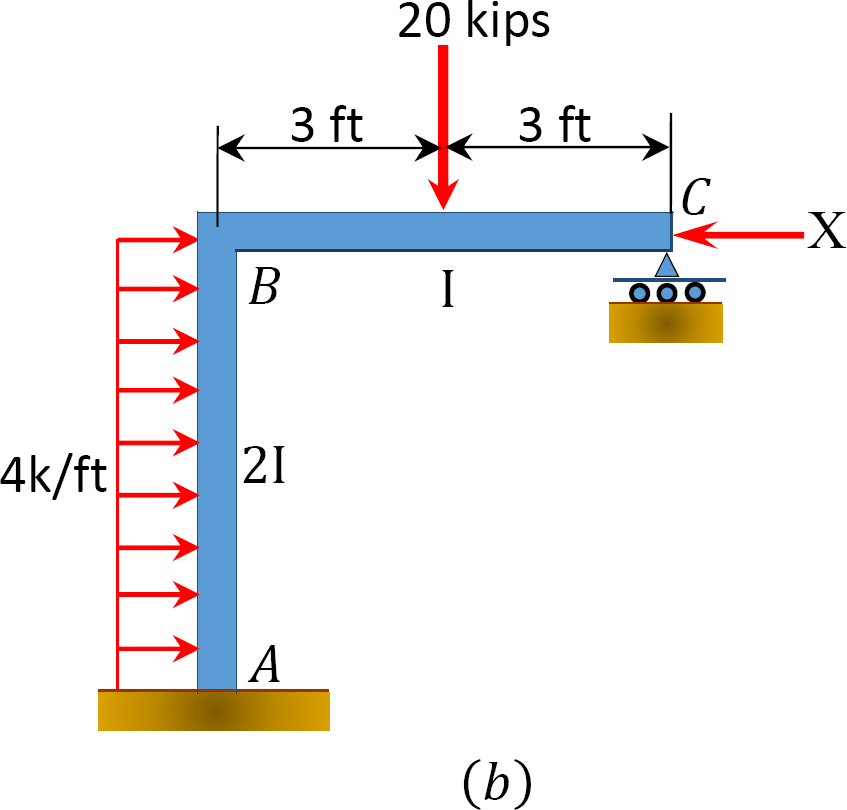
Tabella 12.6. Tavola di distribuzione (nessuna struttura di oscillazione).
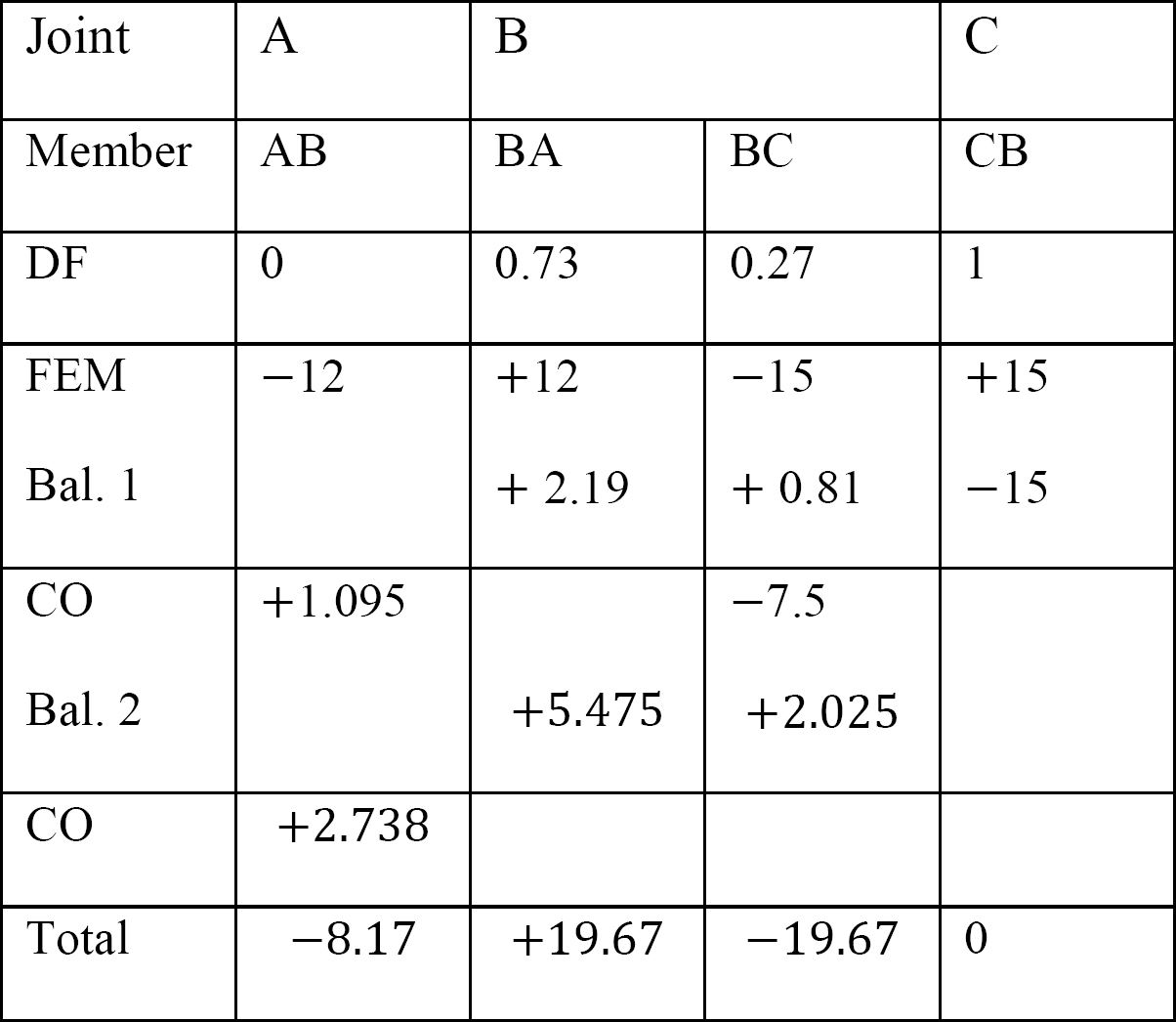
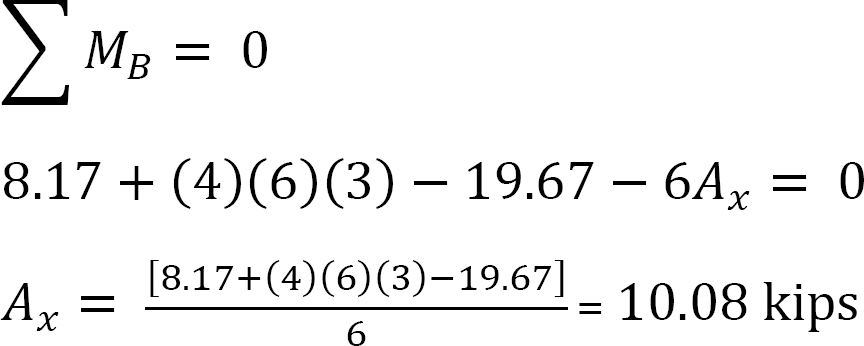
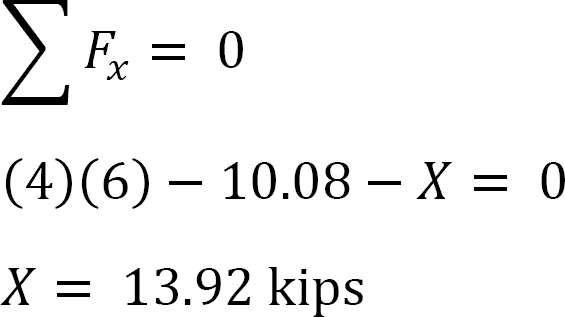
Analisi del telaio con side-sway.
Si supponga che MAB = +20 k. ft
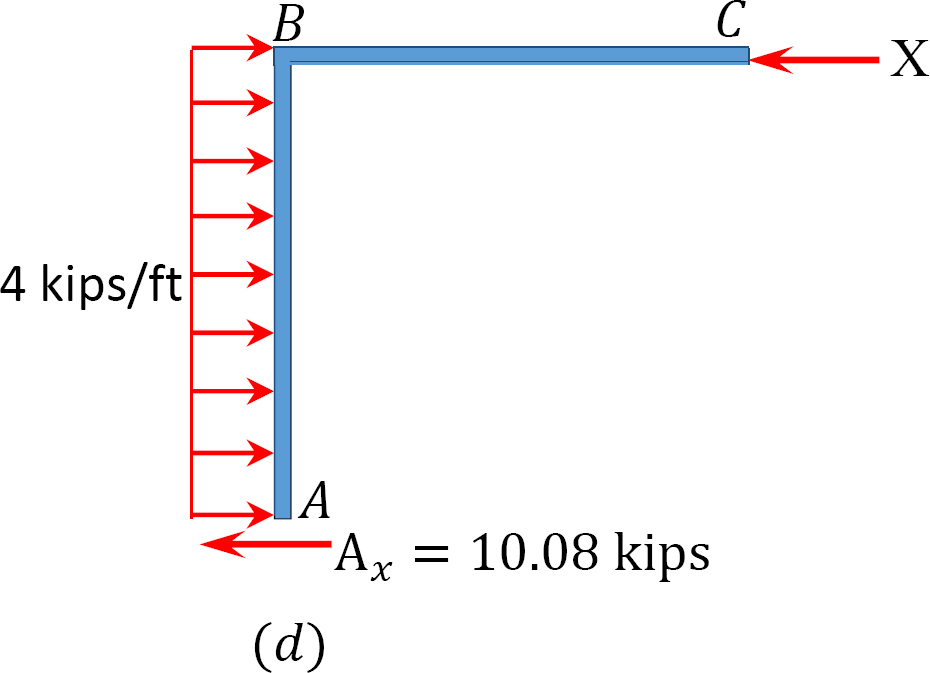
Tabella 12.7. Tabella di distribuzione (cornice ondeggiante).
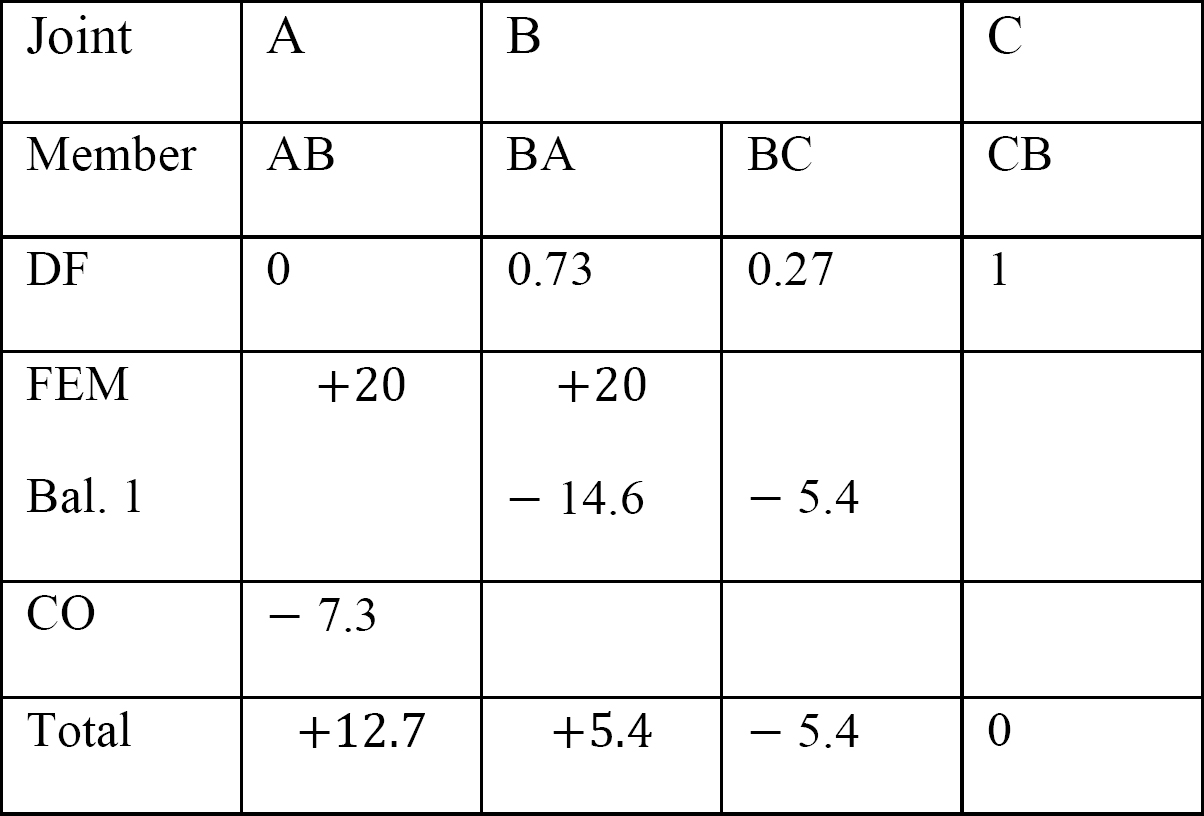
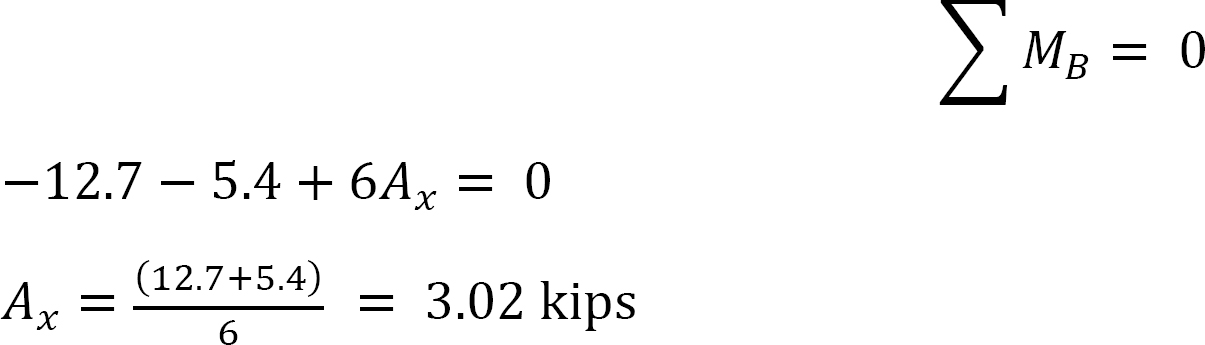
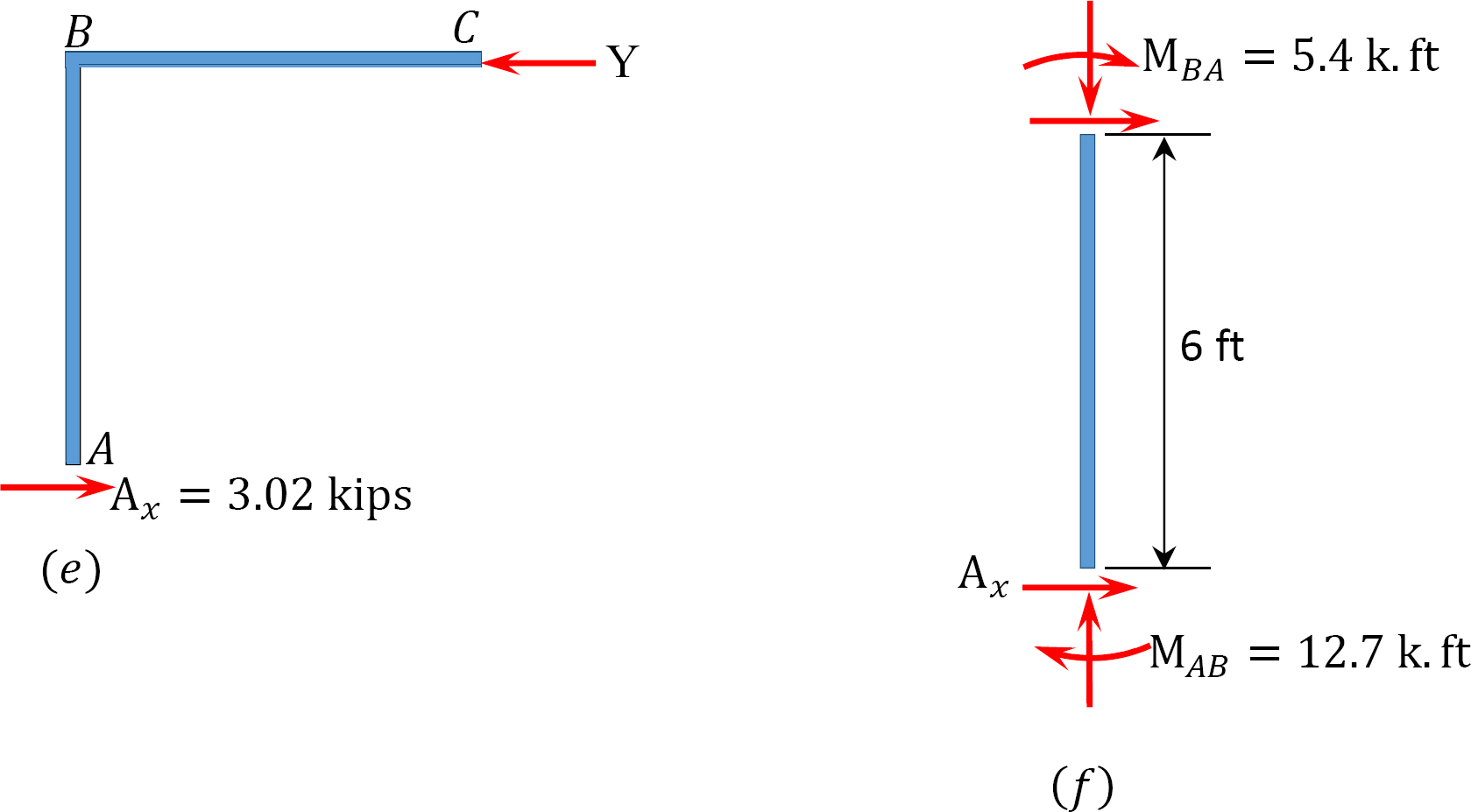
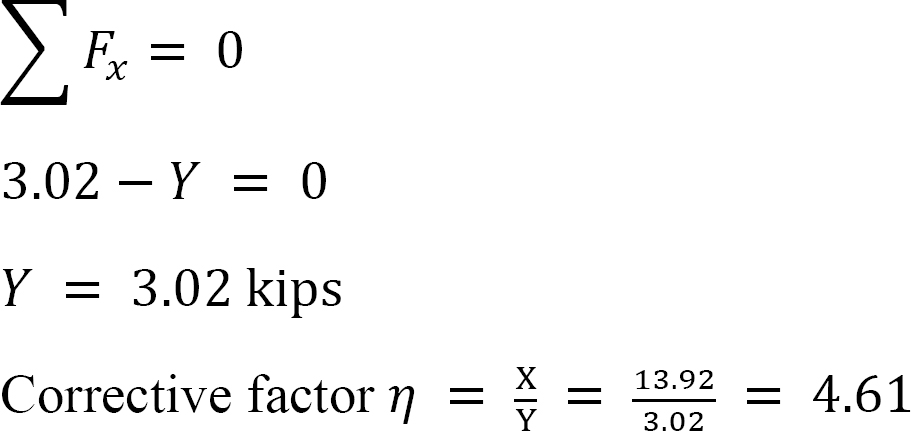
Momenti finali finali.
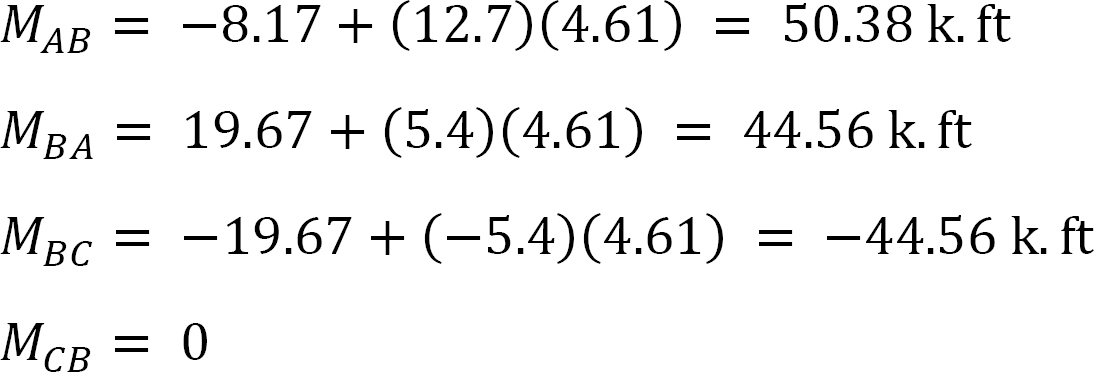
Esempio 12.7
Un frame sway viene caricato come mostrato in Figura 12.12 a. Utilizzando il metodo di distribuzione momento, determinare i momenti finali dei membri del frame.
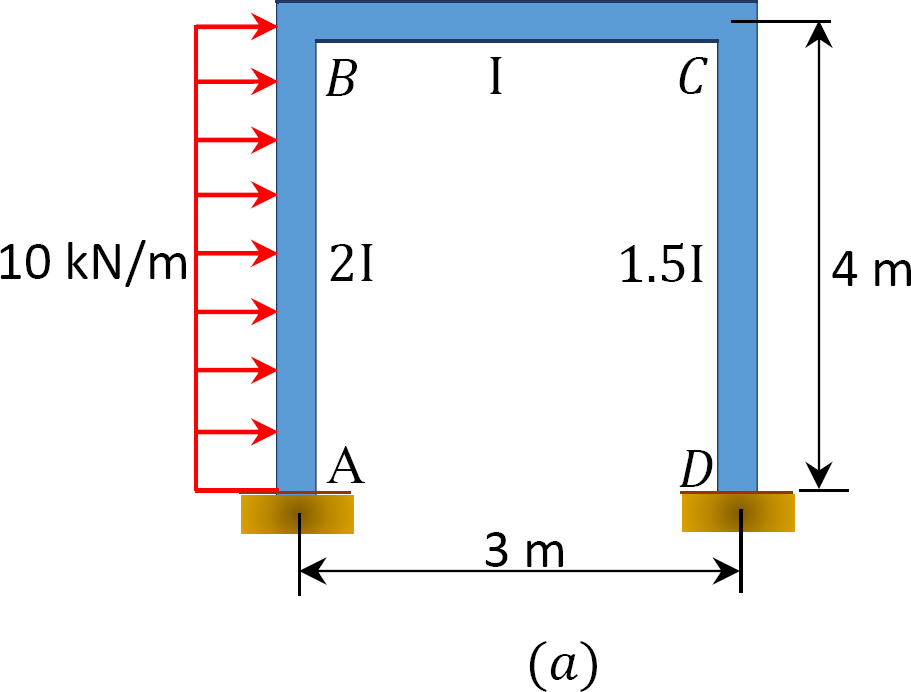
Fig. 12.12. Telaio ondeggiamento caricato.
Soluzione
Momento finale fisso.
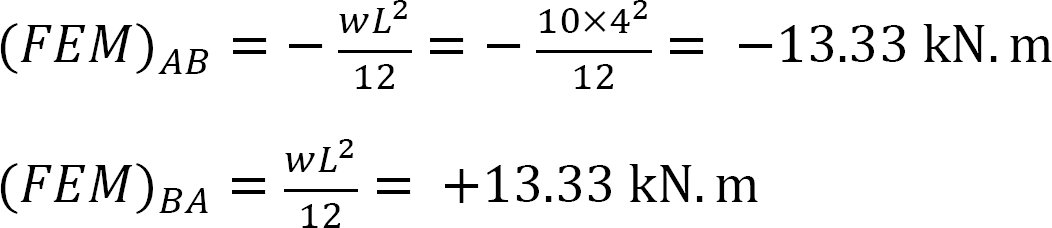
Fattore di rigidezza.
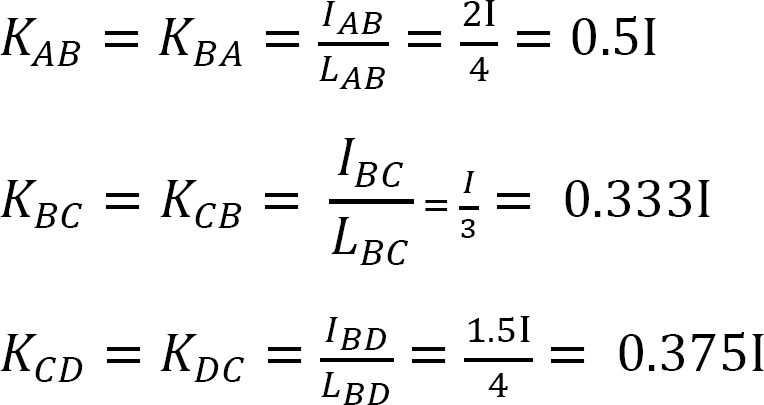
Fattore di distribuzione.

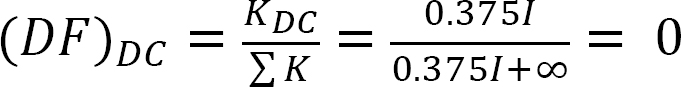
Analisi del telaio senza oscillazione laterale.
Tabella 12.8. Tavola di distribuzione (nessuna struttura di oscillazione).
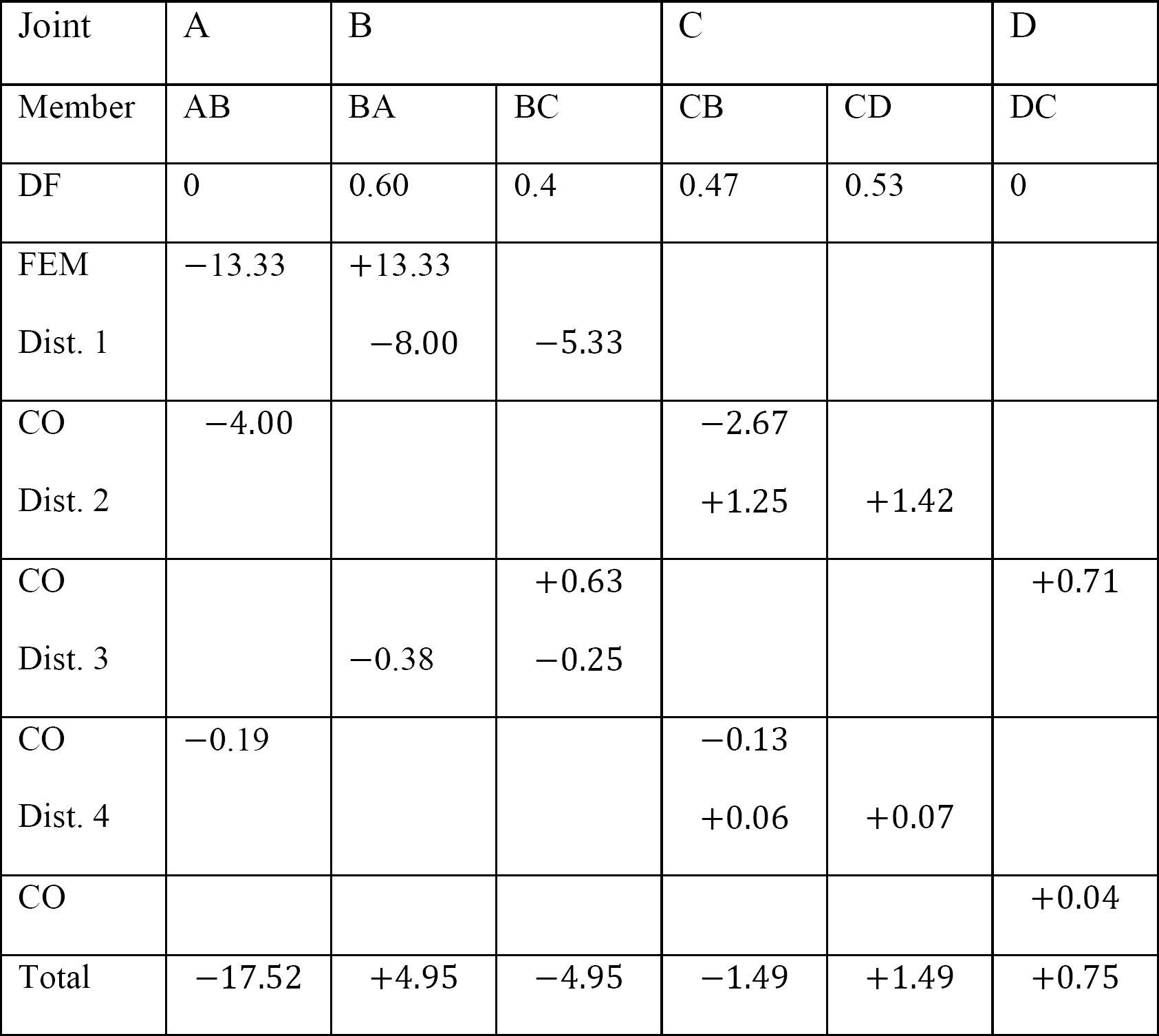
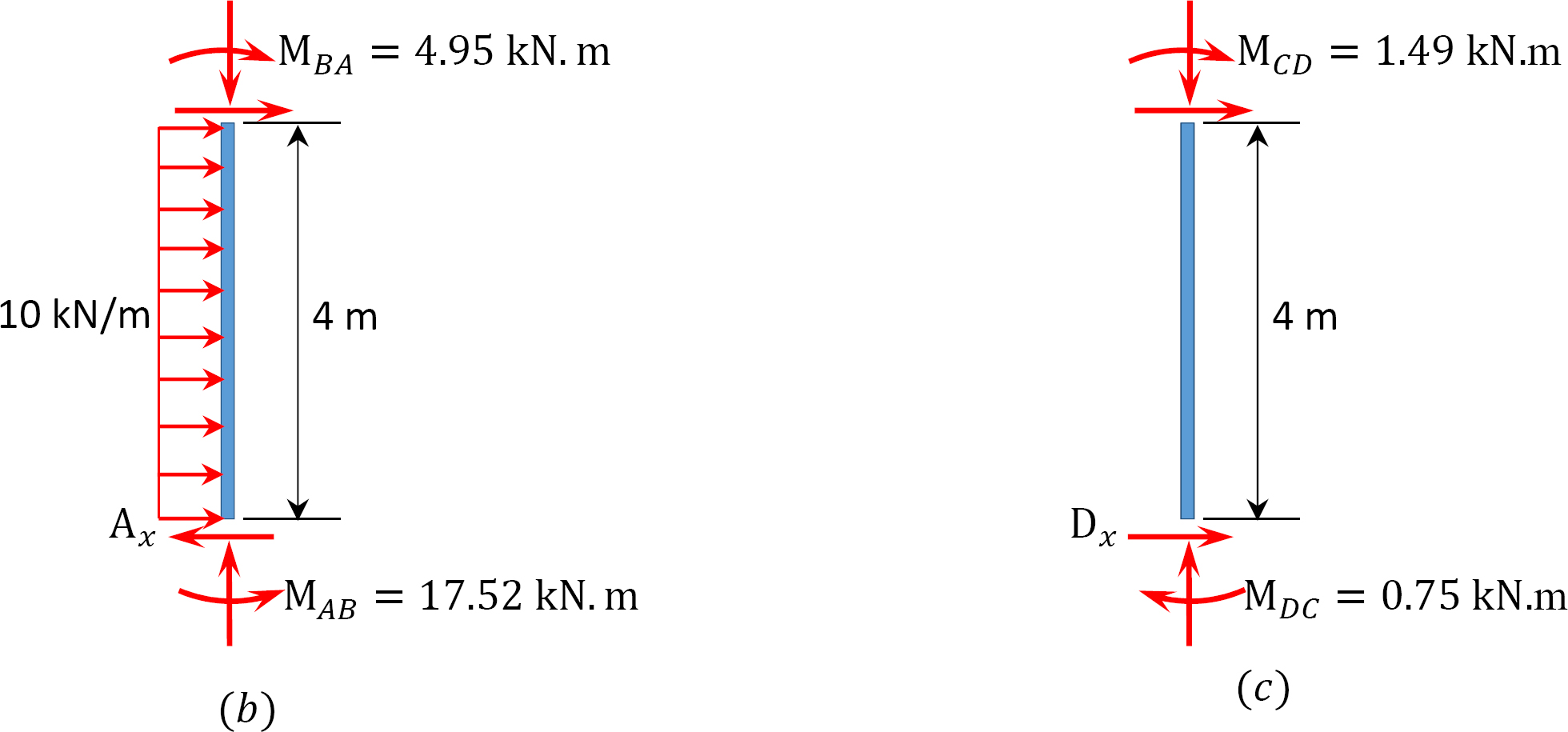
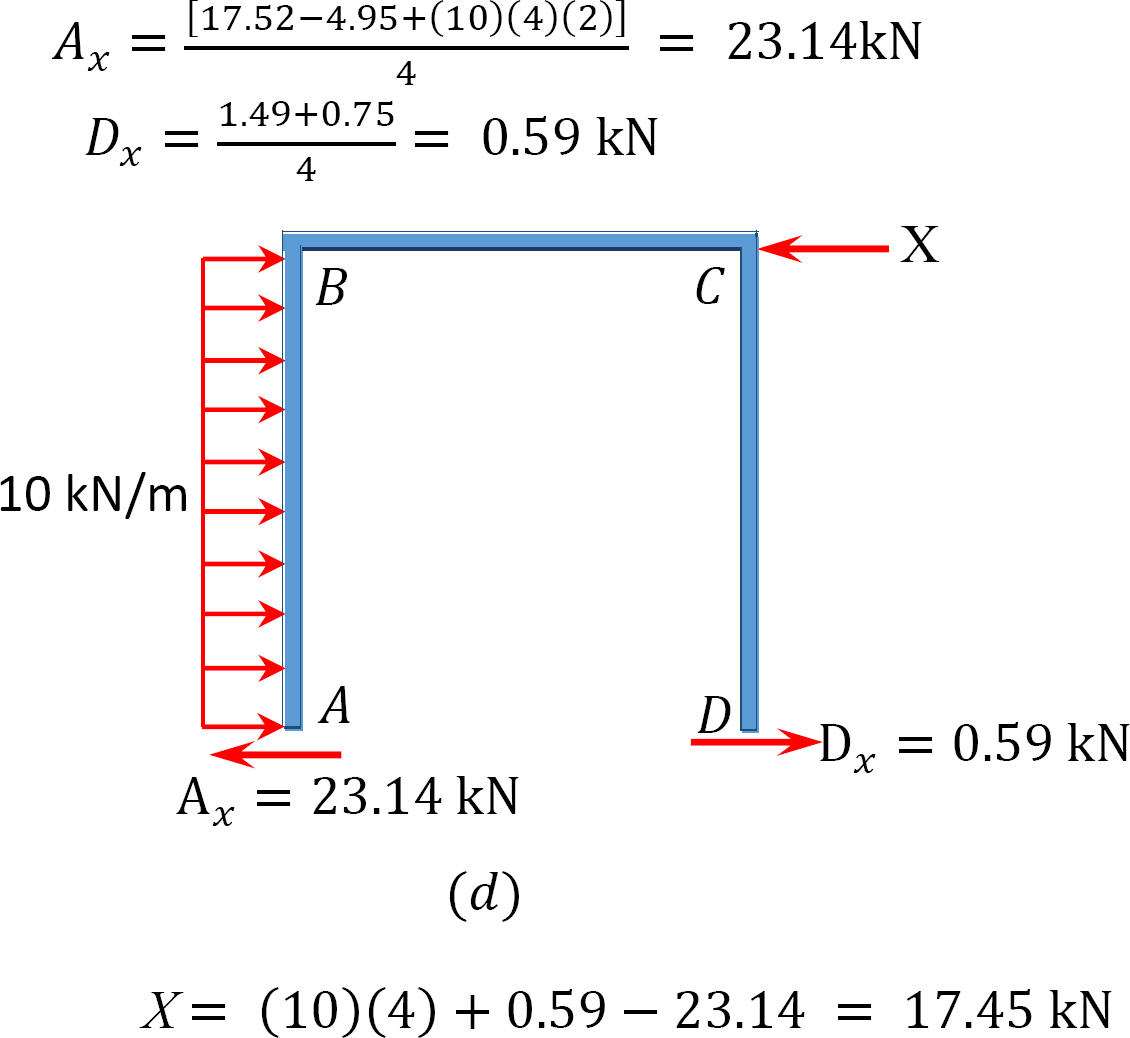
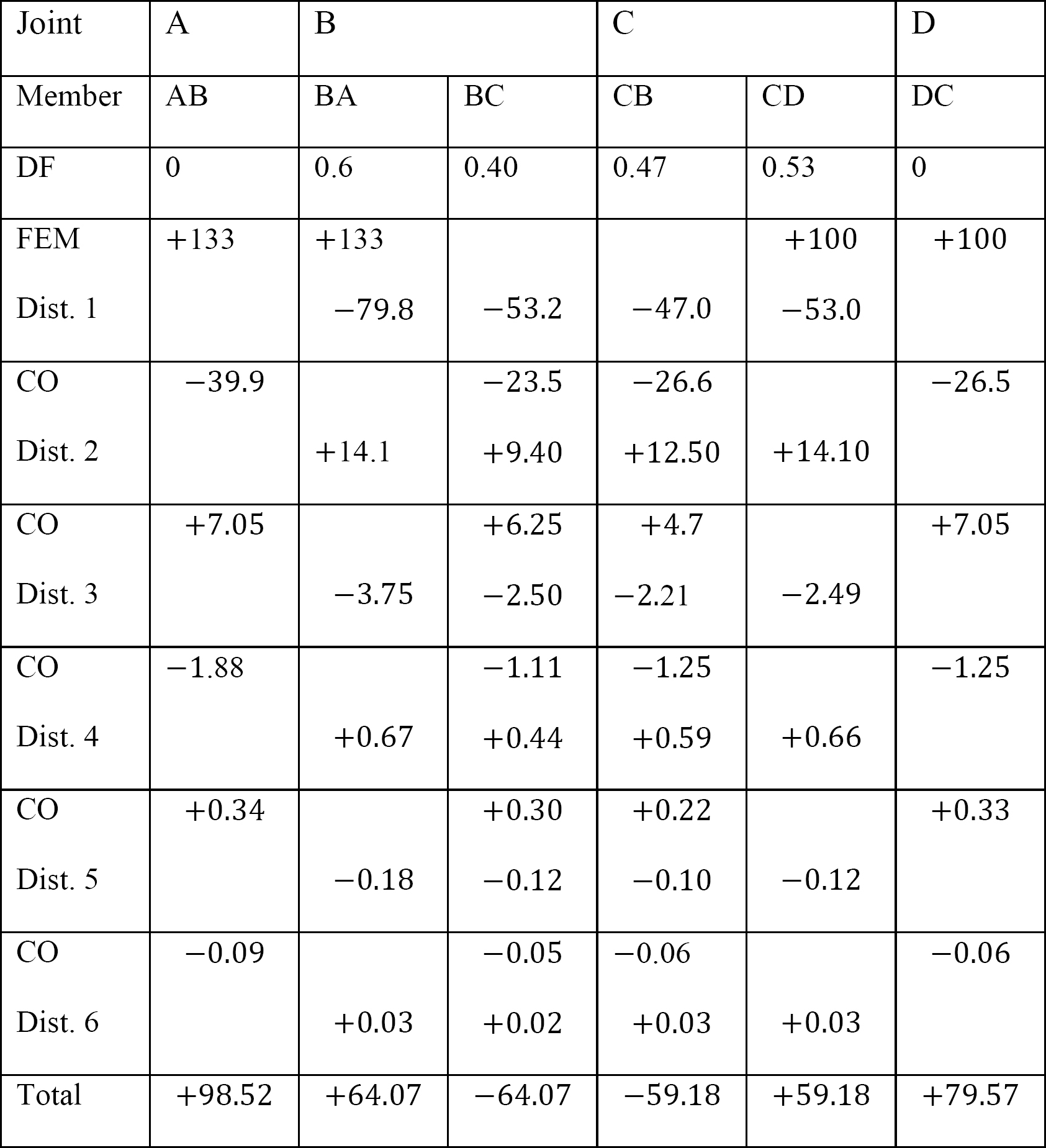
Tabella 12.9. Tabella di distribuzione (cornice ondeggiante).
Analisi del telaio con side-sway.
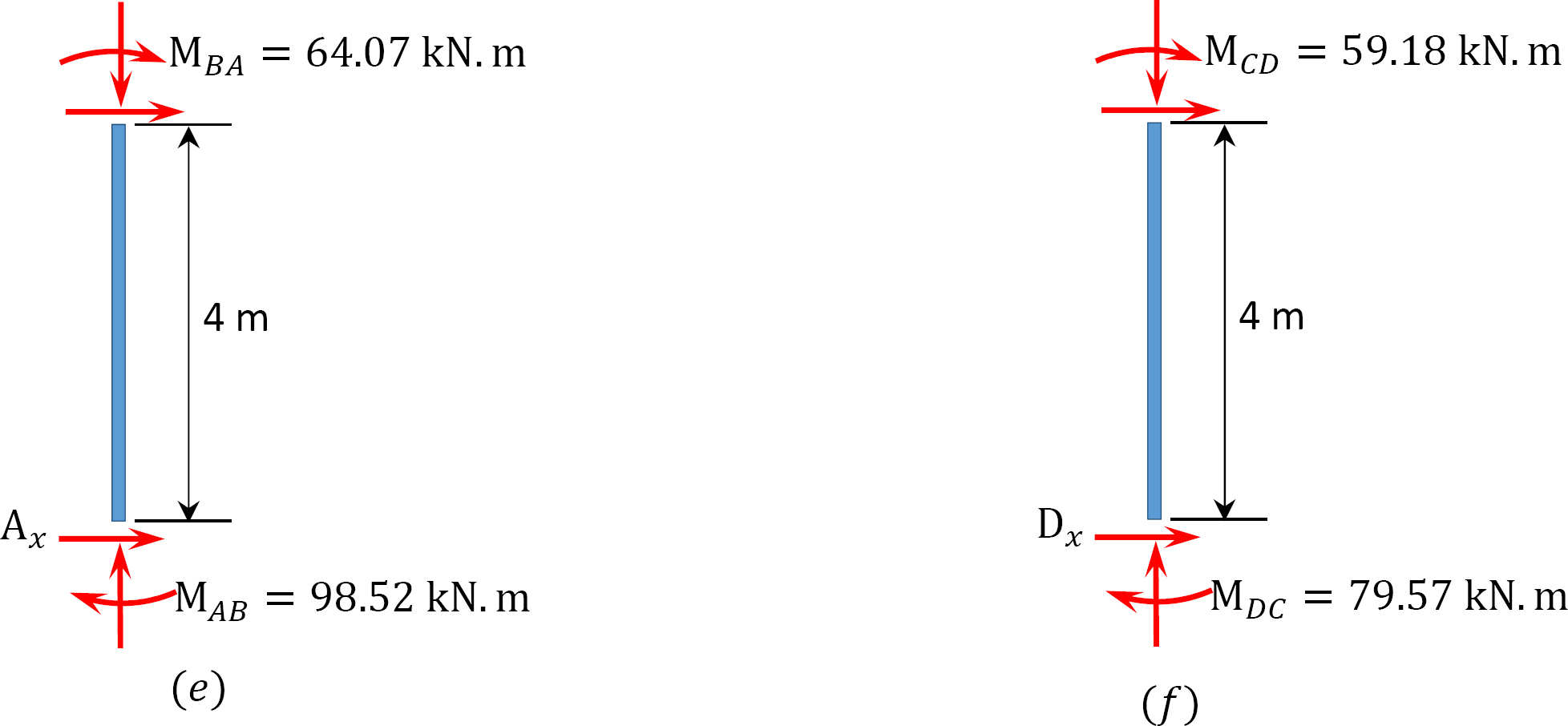

Momento finale finale.
MAB = -17.52 + (98.52)(0.23) = 5.14 nN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 nN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 nN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 nN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 nN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 nN. m
Riassunto del capitolo
Metodo di distribuzione del momento di analisi di strutture indeterminate: Il metodo di distribuzione del momento di analisi è un metodo approssimativo di analisi. Il suo grado di precisione dipende dal numero di iterazioni. In questo metodo, si presume che tutti i giunti in una struttura siano temporaneamente bloccati o bloccati e, quindi, siano impediti da una possibile rotazione. I carichi vengono applicati ai membri e vengono determinati i momenti sviluppati alle estremità dei membri a causa della fissità. I giunti nella struttura vengono quindi sbloccati successivamente e il momento sbilanciato in ogni giunto viene distribuito ai membri che si riuniscono in quel giunto. Vengono determinati i momenti di riporto alle estremità lontane dei membri e il processo di bilanciamento viene continuato fino al livello di precisione desiderato. I momenti finali dei membri sono determinati sommando il momento finale fisso, il momento distribuito e il momento di riporto. Una volta determinati i momenti finali dei membri, la struttura diventa determinata.
Problemi di pratica
12.1 Utilizzare il metodo di distribuzione del momento per calcolare il momento finale dei membri delle travi mostrate nella figura P12. 1 attraverso la figura P12.12 e disegnare i diagrammi del momento flettente e della forza di taglio. EI = costante.
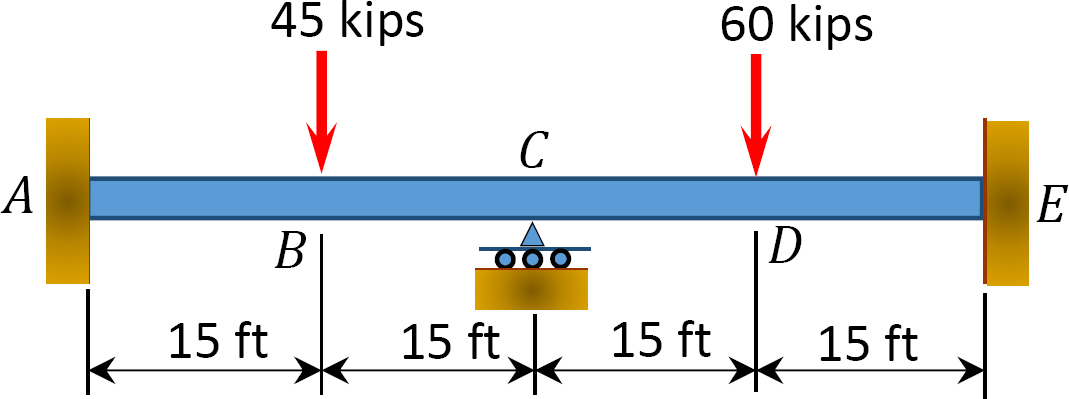
Fig. P12. 1. Trave.
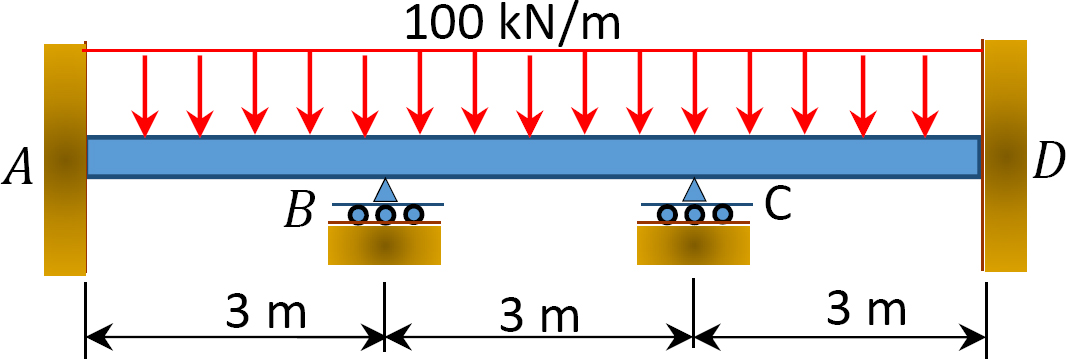
Fig. P12. 2. Trave.
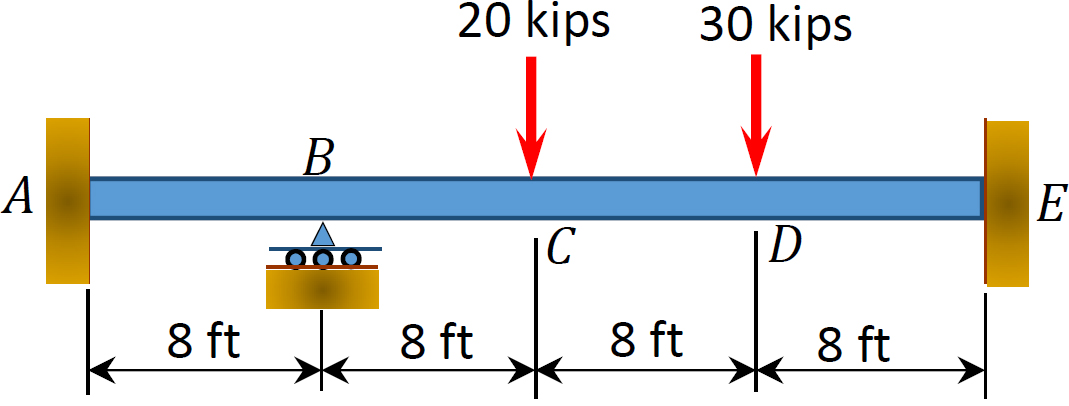
Fig. P12. 3. Trave.
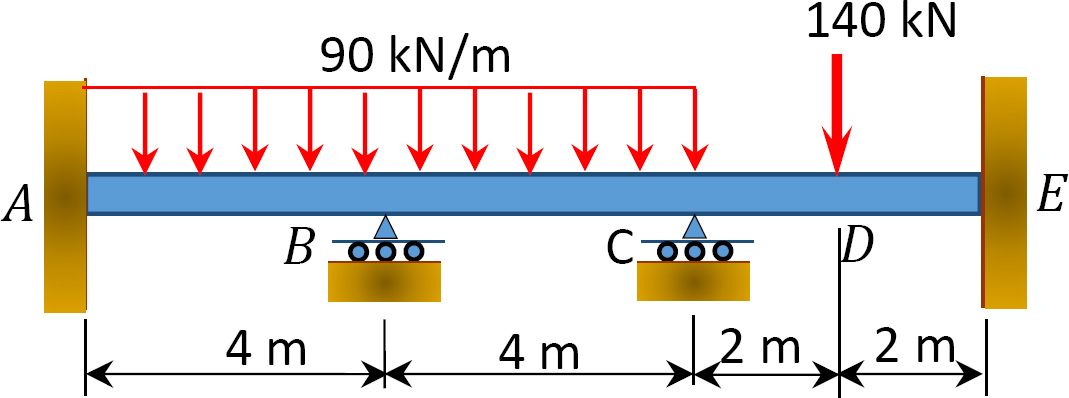
Fig. P12. 4. Trave.
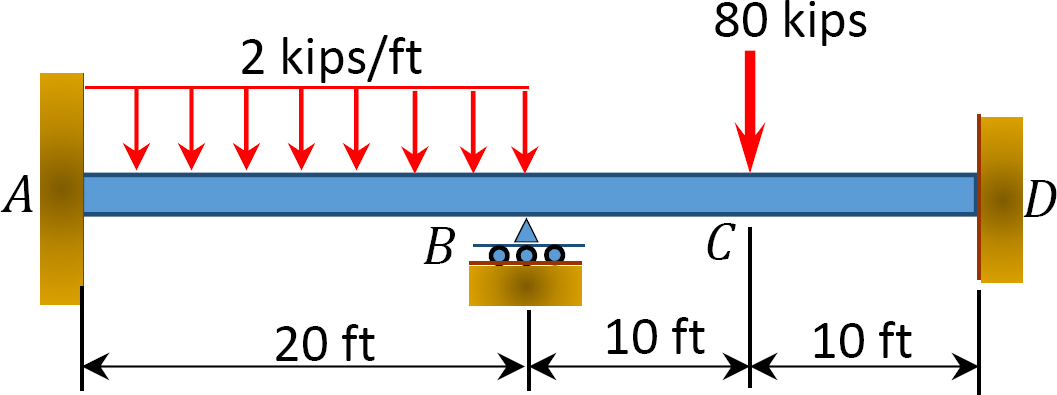
Fig. P12. 5. Trave.
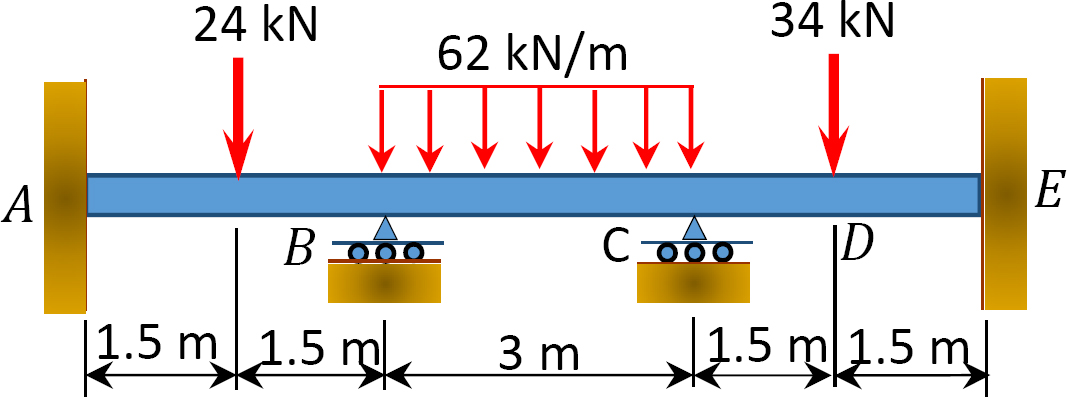
Fig. P12. 6. Trave.
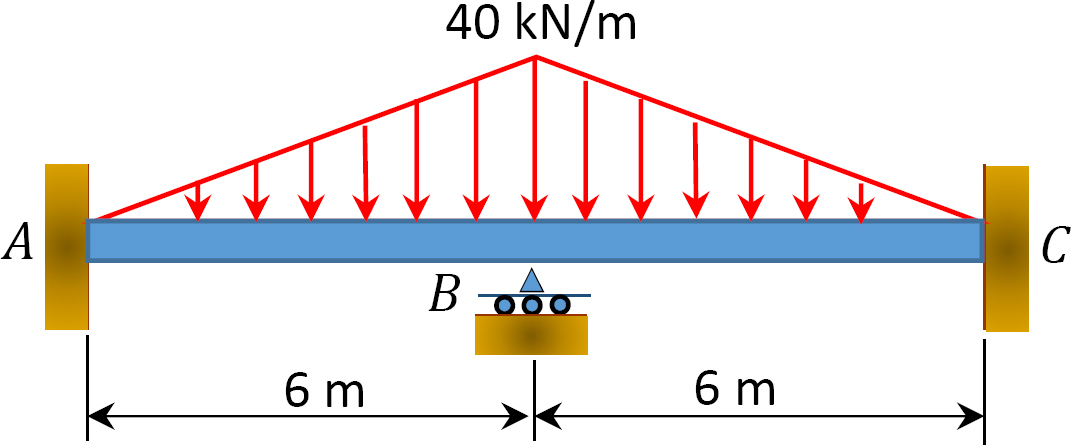
Fig. P12. 7. Trave.
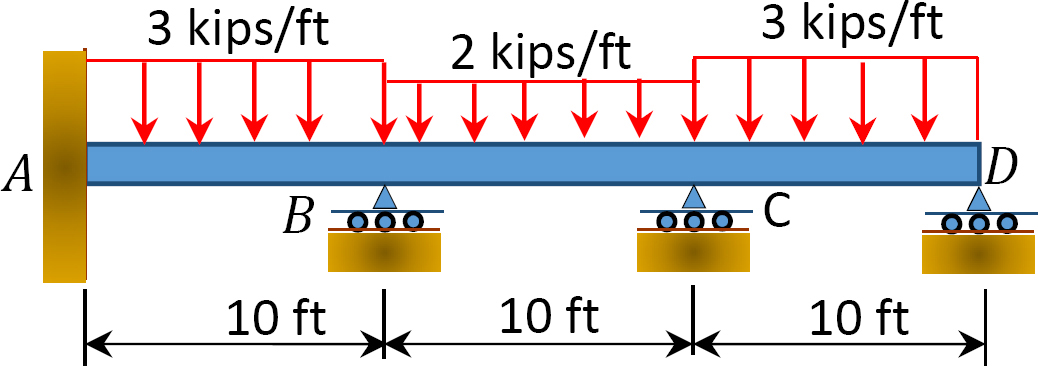
Fig. P12. 8. Trave.
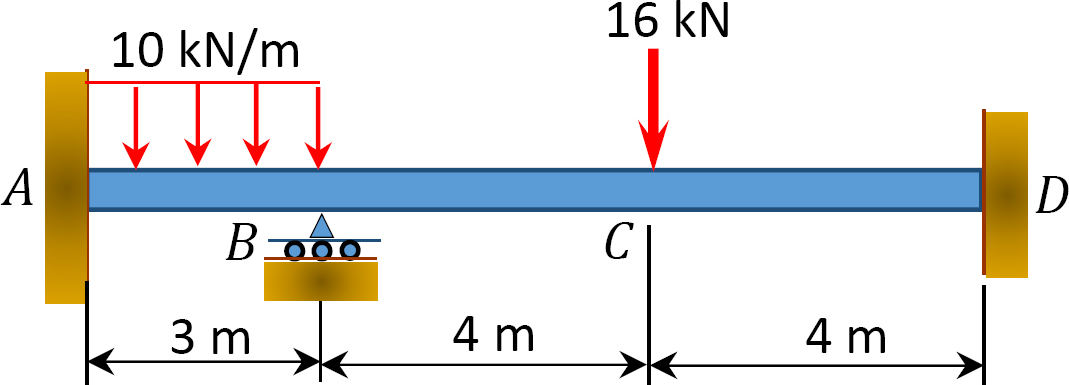
Fig. P12. 9. Trave.
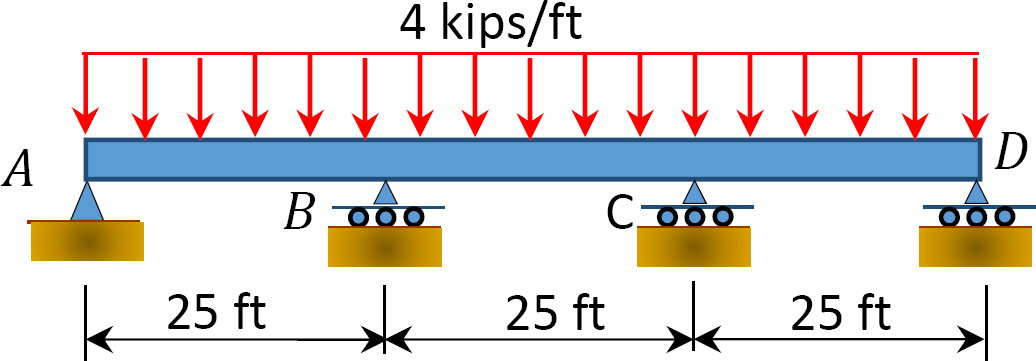
Fig. P12. 10. Trave.
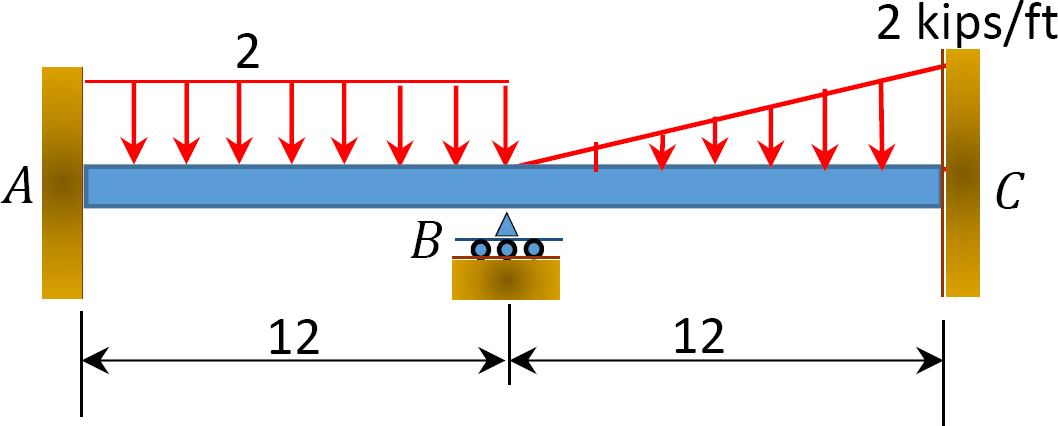
Fig. P12. 11. Trave.
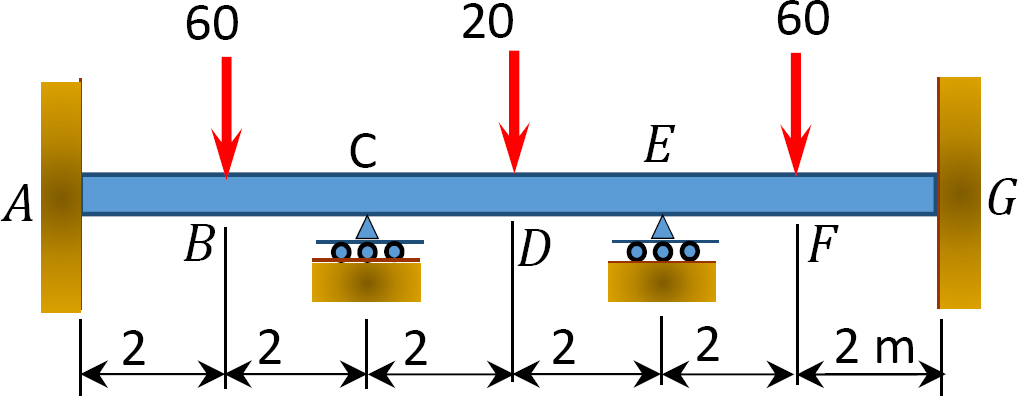
Fig. P12. 12. Trave.
12.2 Utilizzare il metodo di distribuzione del momento per calcolare il momento finale dei membri dei frame mostrati nella Figura P12.13 fino alla Figura 12.20 e disegnare i diagrammi del momento flettente e della forza di taglio. EI = costante.
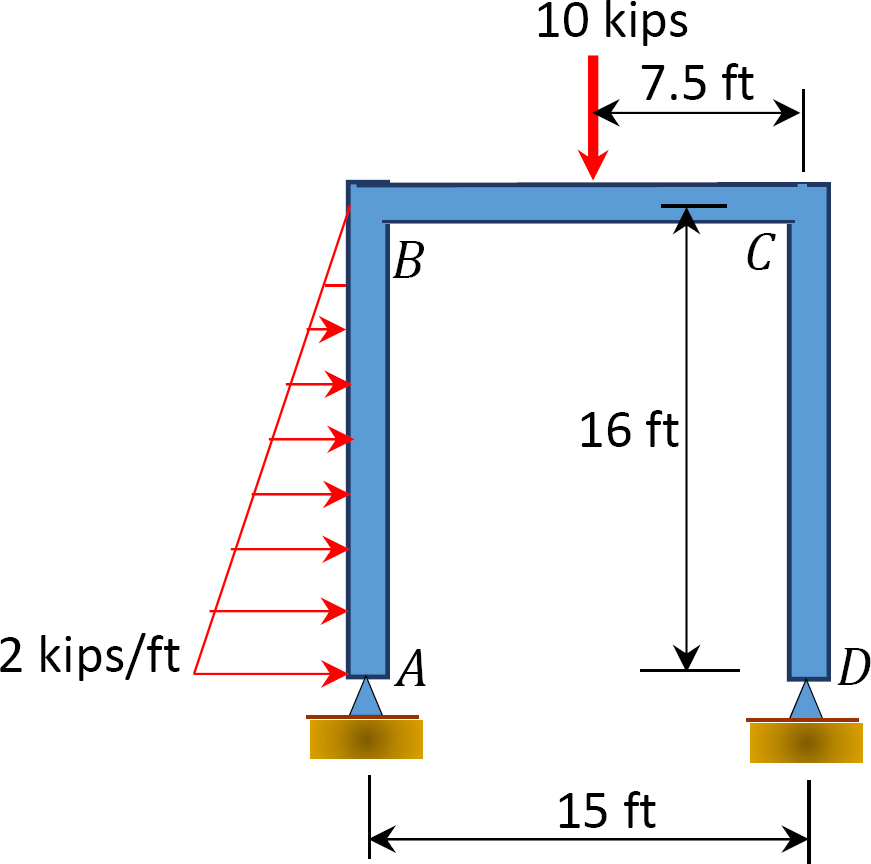
Fig. P12. 13. Cornice.
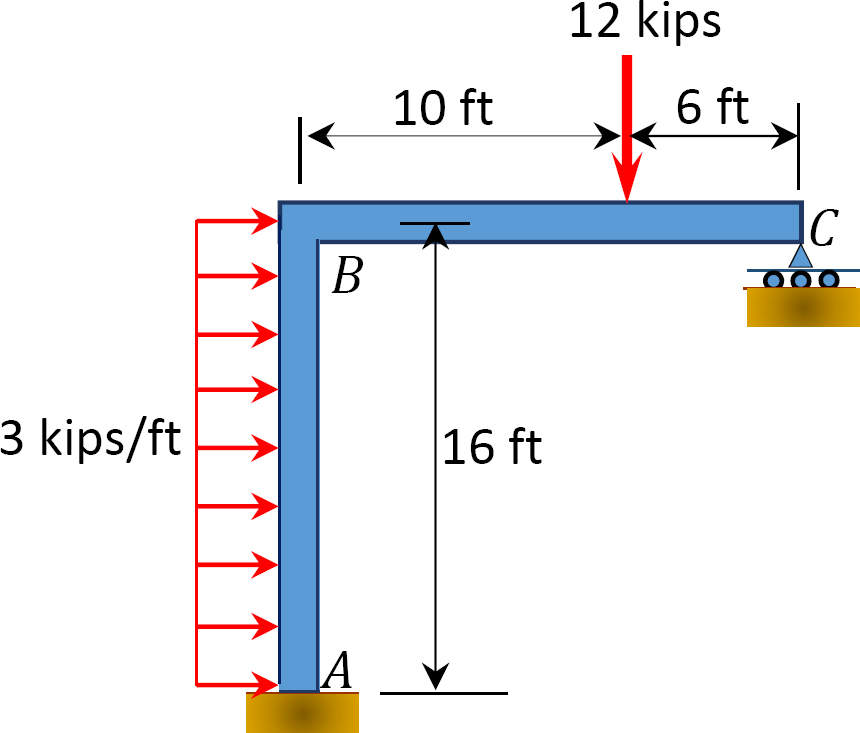
Fig. P12. 14. Cornice.
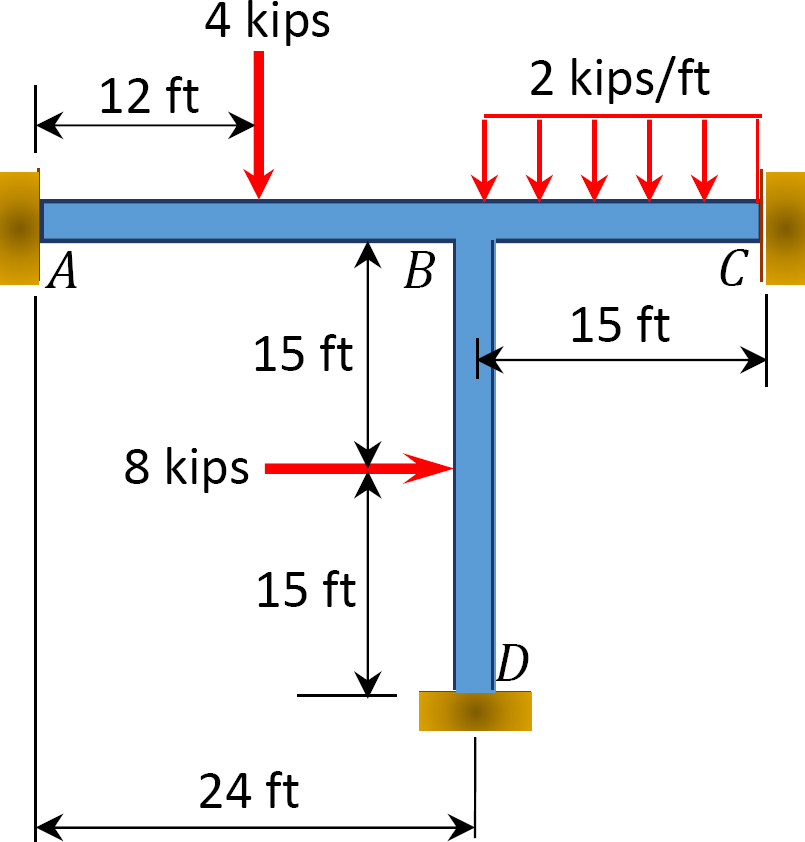
Fig. P12. 15. Cornice.
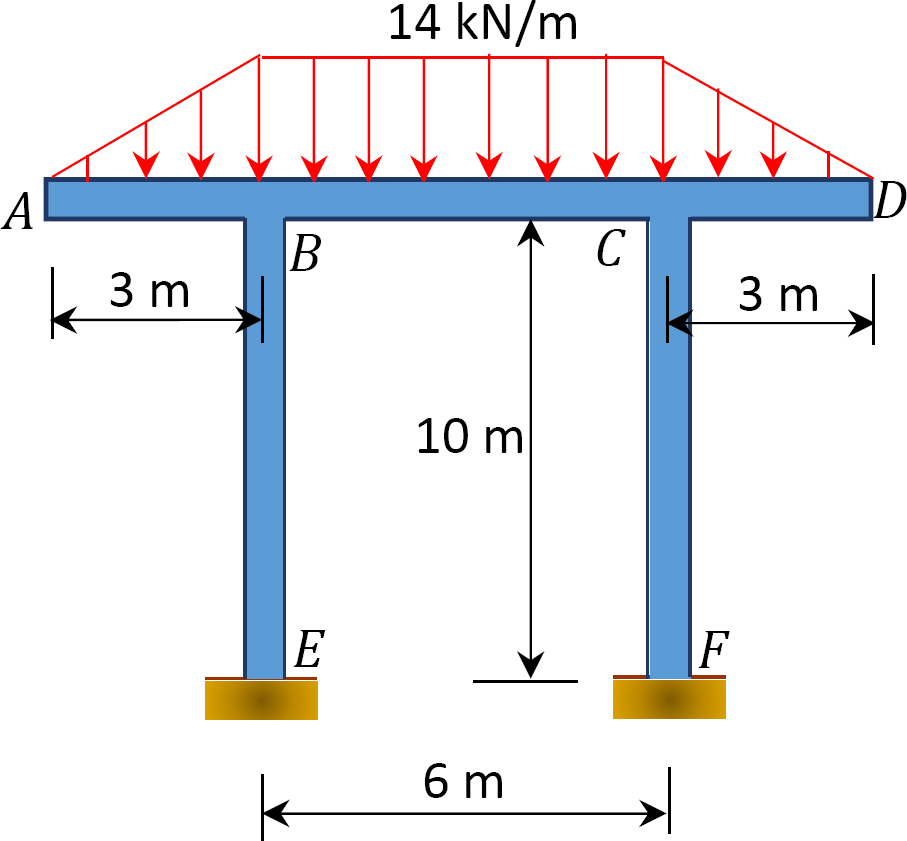
Fig. P12.16. Frame.
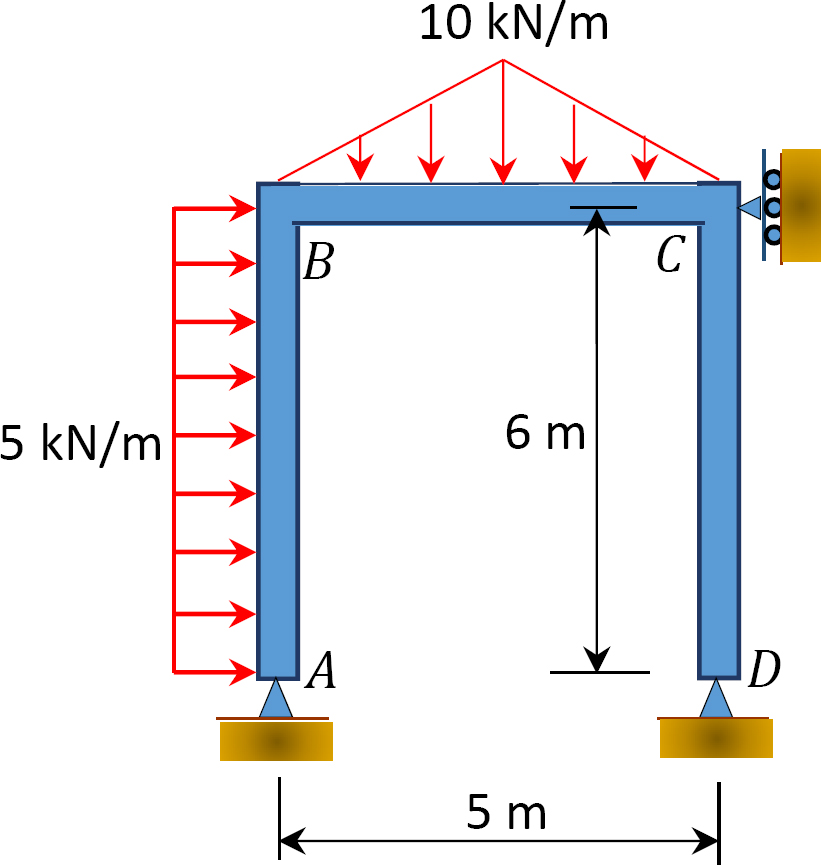
Fig. P12.17. Frame.
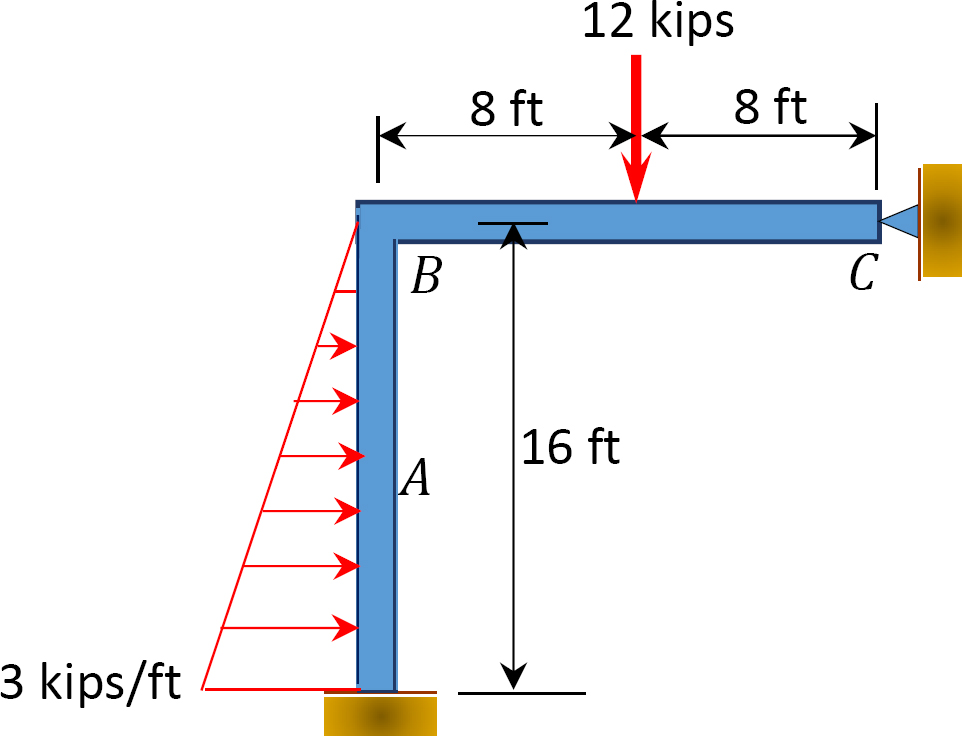
Fig. P12.18. Frame.
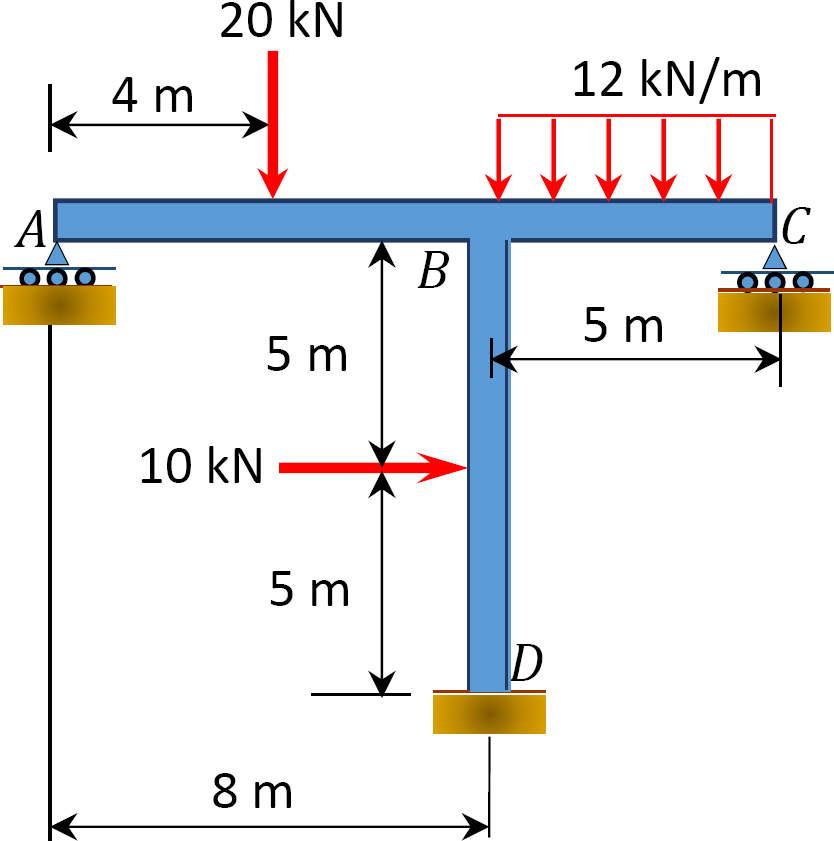
Fig. P12.19. Frame.
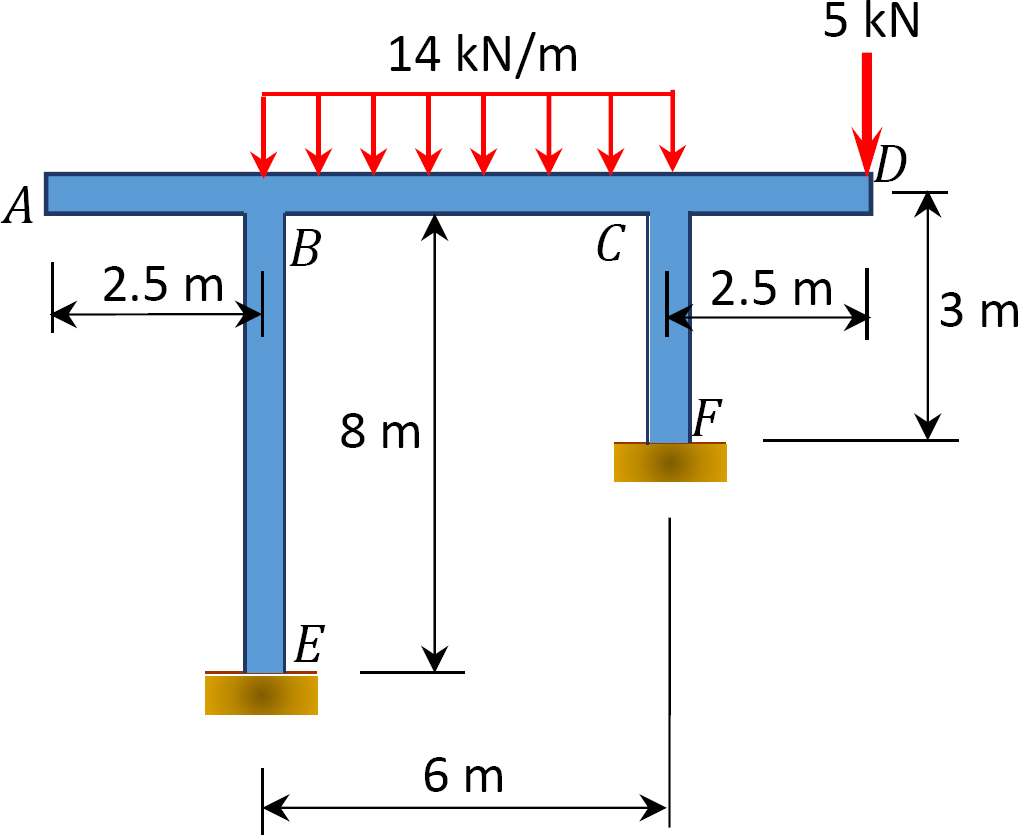
Fig. P12.20. Frame.