Applicare e interpretare il principio di Saint-Venant

Tutti gli ingegneri strutturali utilizzano il principio di Saint-Venant, sia attivamente che inconsciamente. È possibile trovare varie formulazioni di questo principio nella maggior parte dei libri di testo di meccanica strutturale, ma il suo significato esatto non è ovvio. Il principio di Saint-Venant ci dice che la distribuzione esatta di un carico non è importante lontano dalla regione caricata, purché i risultati del carico siano corretti. In questo post del blog, esploreremo il principio di Saint-Venant, in particolare nel contesto dell’analisi degli elementi finiti (FE).

La storia del principio di Saint-Venant

Lo scienziato francese Barré de Saint-Venant formulò il suo famoso principio nel 1855, ma era più un’osservazione che una rigorosa affermazione matematica:

“Se le forze che agiscono su di una piccola porzione di superficie di un corpo elastico sono sostituiti da un altro staticamente equivalente sistema di forze che agiscono sulla stessa porzione di superficie, questa ridistribuzione del carico produce sostanziali modifiche nelle sollecitazioni a livello locale, ma ha un effetto trascurabile sulle sollecitazioni a cui le distanze sono grandi in confronto con le dimensioni lineari della superficie su cui le forze in gioco sono cambiate.”

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Ritratto di Saint-Venant. Immagine di pubblico dominio, tramite Wikimedia Commons.

Molte grandi menti nel campo della meccanica applicata-Boussinesq, Love, von Mises, Toupin e altri – furono coinvolte nell’affermare il principio di Saint-Venant in una forma più esatta e fornire prove matematiche per esso. A quanto pare, questo è abbastanza difficile per i casi più generali e la ricerca sull’argomento è ancora in corso. (L’argomentazione è stata a volte abbastanza vivida.)

Esempio semplice: Analisi delle sollecitazioni a distanza

Iniziamo con qualcosa di abbastanza semplice: una sottile piastra rettangolare con un foro circolare ad una certa distanza dal bordo caricato, che viene tirato assialmente. Se siamo interessati alla concentrazione di stress nel foro, quanto è importante la distribuzione effettiva del carico?

Tre diversi tipi di carico vengono applicati al limite più a destra:

1. Una sollecitazione assiale costante di 100 MPa
2. Una distribuzione simmetrica della sollecitazione parabolica con ampiezza di picco 150 MPa
3. Un carico a punto centrato con lo stesso risultato dei due casi di carico precedenti

Come si vede nei grafici seguenti, la distribuzione della sollecitazione al foro non è influenzata dal modo in cui viene applicato il carico. La chiave qui è, ovviamente, che il foro è abbastanza lontano dal carico.

Contorni di sollecitazione Von Mises per i tre casi di carico.

Un altro modo di visualizzare questo scenario è utilizzando le frecce di stress principali. Tale trama sottolinea il campo di stress come un flusso e dà una buona sensazione per la ridistribuzione.

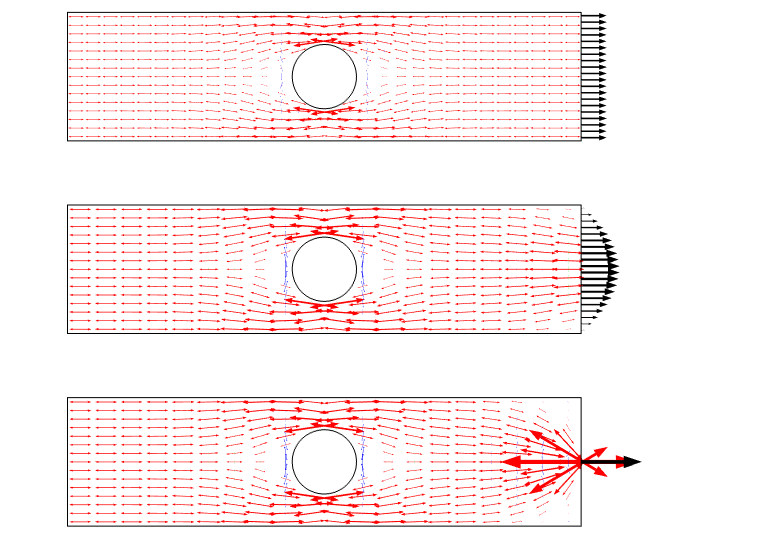
Trama di stress principale per i tre casi di carico. Si noti che esiste una singolarità quando viene utilizzato un carico puntuale.

Graficamente lo stress lungo una linea, possiamo vedere che tutti e tre i casi convergono tra loro ad una distanza dal bordo, che è approssimativamente uguale alla larghezza della piastra.

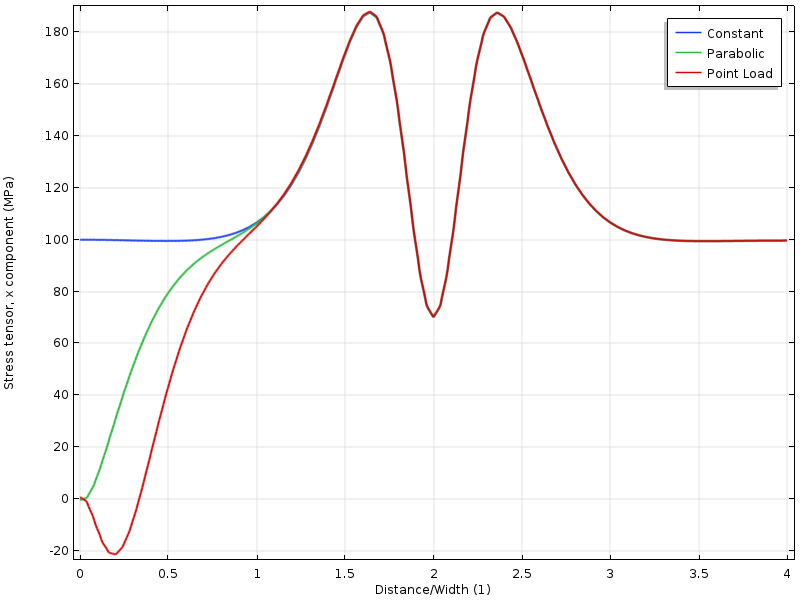
Sollecitazione lungo il bordo superiore in funzione della distanza dal limite caricato. La distanza è normalizzata dalla larghezza della piastra.

Se il foro viene spostato più vicino al limite caricato, otteniamo un’altra situazione. Lo stato di stress attorno al foro ora dipende dalla distribuzione del carico. Ma ancora più interessante è che la distanza da dove i tre campi di stress sono d’accordo ora è il doppio del limite caricato. L’applicazione del principio di Saint-Venant richiede che gli stress siano liberi di ridistribuire. In questo caso, tale ridistribuzione è parzialmente bloccata dal foro.

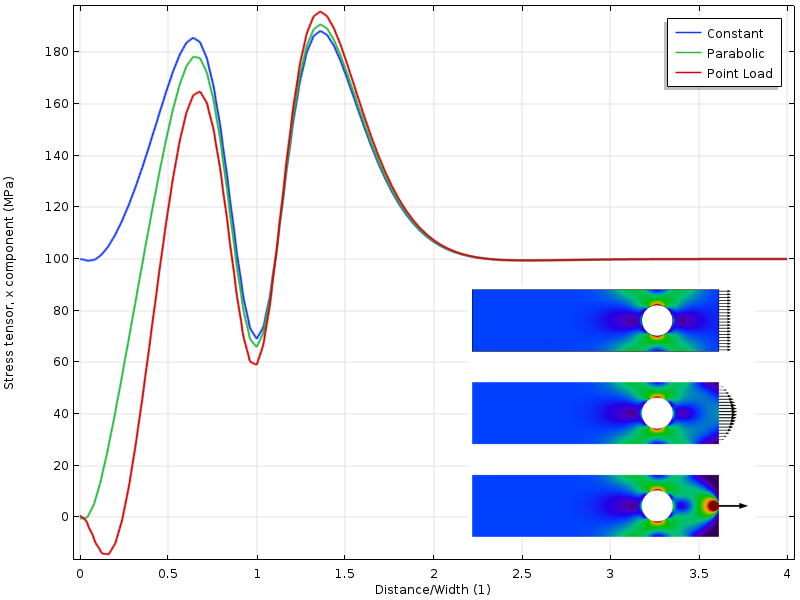
Sollecitare lungo il bordo superiore con il foro più vicino al limite caricato.

Si noti che il principio di Saint-Venant ci dice che non c’è differenza nello stato di stress a una distanza che è dell’ordine della dimensione lineare dell’area caricata. L’area caricata da prendere in considerazione, tuttavia, potrebbe non essere l’area effettivamente caricata! Questa affermazione può sembrare strana, ma pensala in questo modo: quando il buco è lontano, possiamo calcolare il fattore di concentrazione dello stress usando un manuale (il mio dice 4.32) piuttosto che una soluzione FE. L’approccio manuale contiene un’ipotesi implicita che il carico sia distribuito uniformemente come nel primo caso di carico. Quindi, anche se il carico effettivo è stato applicato solo a una piccola parte del confine, la distanza critica in quel caso è correlata alla dimensione dell’intero confine.

Quando si risolve il problema utilizzando il metodo degli elementi finiti (FEM), il foro può essere arbitrariamente vicino al carico. Ciò che imposta il limite è che dal punto di vista fisico, la distribuzione del carico è ben definita. Non appena facciamo ipotesi sulla ridistribuzione, tuttavia, c’è un’ipotesi implicita sulla distribuzione del carico, che può differire da quella effettiva.

Zero sistemi risultanti e densità di energia di deformazione

Finora, abbiamo detto che le sollecitazioni sono le stesse indipendentemente dai dettagli del carico a una certa distanza adeguata. Poiché qui abbiamo a che fare con l’elasticità lineare, è sempre possibile sovrapporre i casi di carico. Quando si lavora con le prove del principio di Saint-Venant, è più facile formulare un principio lungo queste linee: le sollecitazioni causate da un sistema di carico senza forza o momento risultante saranno piccole a una distanza dello stesso ordine di grandezza della dimensione del limite caricato.

Quindi, studiamo lo stress causato dalla differenza tra i due sistemi di carico con risultati uguali. La maggior parte delle prove moderne si basa su stime del decadimento della densità di energia del ceppo per un sistema così nullo.

Tornando al problema sopra, possiamo calcolare la differenza tra i casi di carico. Così facendo ci permette di studiare il decadimento effettivo di stress o densità di energia di deformazione per la differenza dei campi di stress.

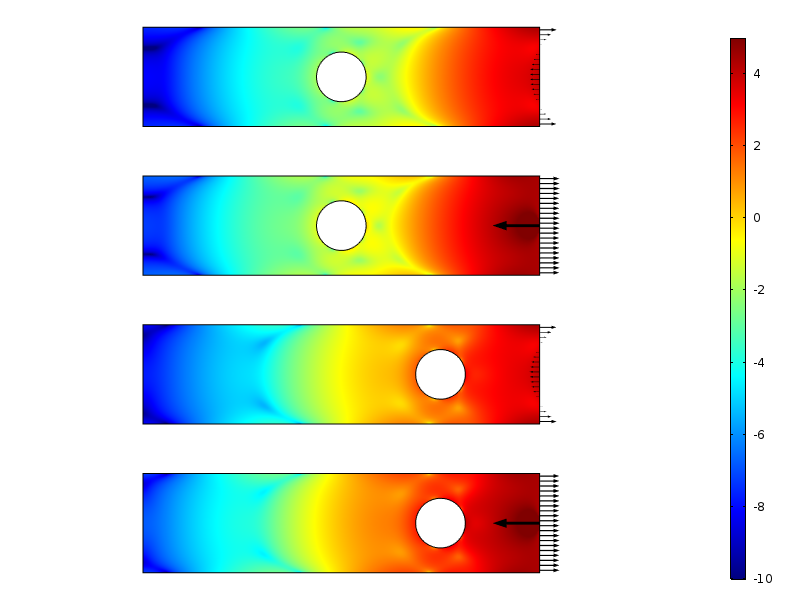
Logaritmo di densità di energia di deformazione per i casi di carico zero.

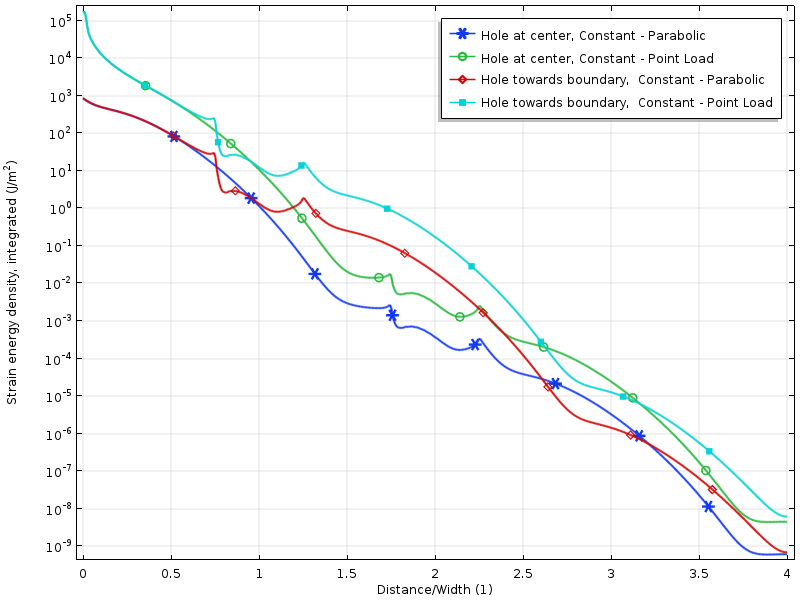
La densità di energia di deformazione lungo la piastra per i casi di carico zero risultante. L’energia è integrata lungo la direzione verticale in modo da produrre una quantità che è solo una funzione della distanza dal carico.

Il decadimento nel logaritmo della densità di energia di deformazione è più o meno lineare con la distanza dal limite caricato. Questo è in realtà in linea con ciò che le prove moderne prevedono: un decadimento esponenziale della densità di energia del ceppo. Possiamo anche vedere chiaramente come il foro riduce temporaneamente il tasso di decadimento.

Applicare il principio di Saint-Venant a Strutture sottili

Per strutture più sottili come gusci, travi e capriate, è noto che il principio di Saint-Venant non può essere applicato allo stesso modo di un oggetto più “solido”. I disturbi percorrono distanze più lunghe di quelle che ci aspettiamo, perché i percorsi di carico in una struttura sottile sono molto più limitati. Questo è lo stesso fenomeno che vediamo con il buco nell’esempio sopra, ma più prominente.

Qui studiamo una trave con una sezione trasversale IPE100 standard. L’estremità del raggio è sottoposta a una sollecitazione assiale, con un’ampiezza che ha una distribuzione lineare in entrambe le direzioni trasversali.

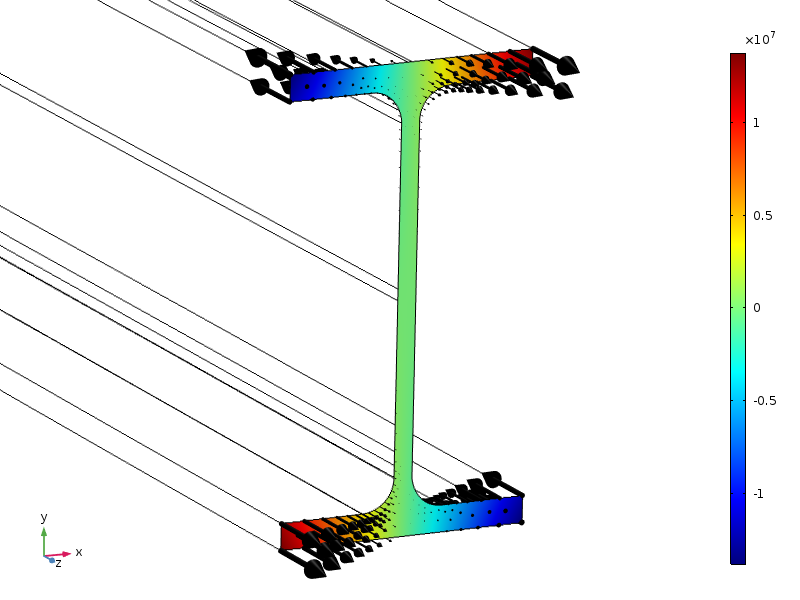
Distribuzione del carico, visualizzata come contorni e frecce.

A causa delle simmetrie, questo carico ha una forza risultante zero, così come un momento zero attorno a tutti gli assi. L’altezza della sezione trasversale è di 100 mm, quindi se è applicabile la forma standard del principio di Saint-Venant, le sollecitazioni dovrebbero essere piccole a una distanza di circa 100 mm dalla sezione terminale.

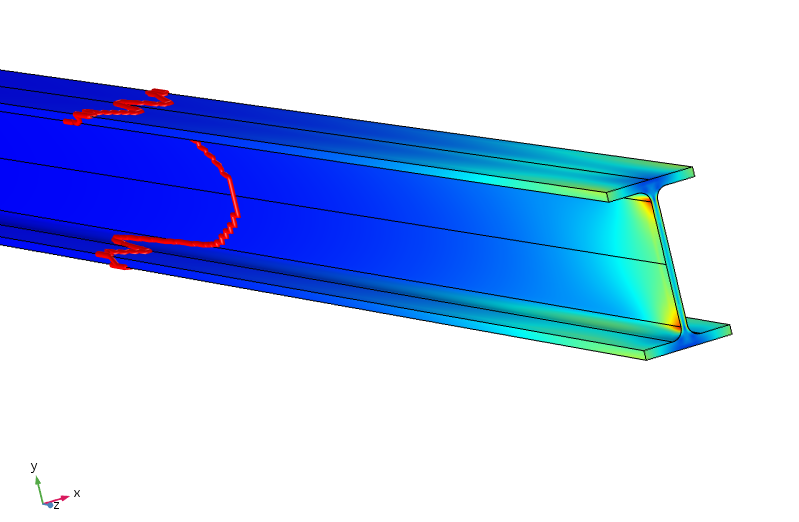
Stress equivalente nel raggio. Il contorno rosso indica dove lo stress è inferiore al 5% dello stress applicato di picco.

Si scopre che affinché lo stress sia inferiore al 5% dello stress applicato al picco, dobbiamo percorrere quasi un metro lungo il raggio. Pertanto, la ridistribuzione del carico è molto meno efficiente qui, poiché l’equilibrio tra le flange superiore e inferiore richiede il trasferimento del momento attraverso il web sottile.

Se si ha familiarità con la teoria della torsione non uniforme delle travi (cioè teoria della deformazione o teoria di Vlasov), si riconoscerà che il carico applicato ha un bimomento significativo. Il bimoment è una quantità trasversale con la forza di dimensione fisica X length2.

Forse (questa è solo la mia speculazione personale), un efficiente principio di Saint-Venant per questo caso dovrebbe richiedere non solo forza e momento ma anche un bimomento di zero. Questo può essere ottenuto aggiungendo quattro carichi puntuali che forniscono un bimomento contrastante. Il risultato di tale analisi è mostrato di seguito.

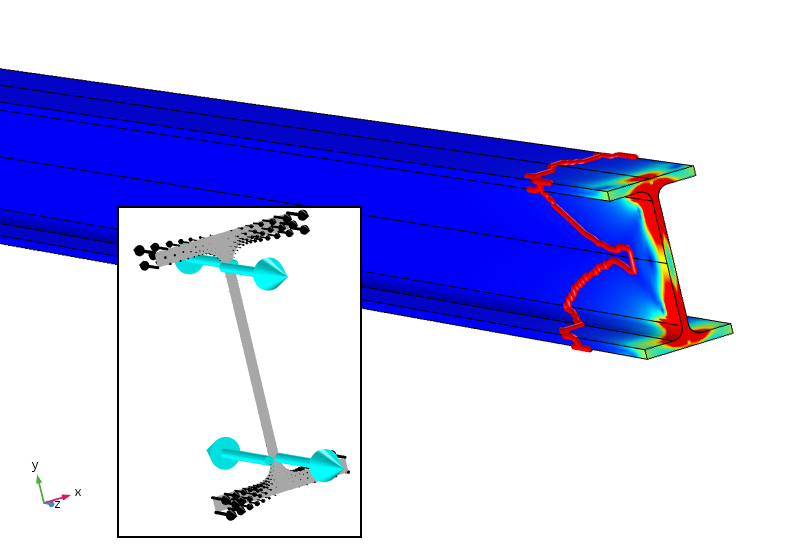
Stress equivalente con carichi a quattro punti che forniscono anche un bimomento zero. Il contorno di stress del 5% è ora molto più vicino al limite caricato.

I carichi puntuali applicati, che non sono posizionati in modo ottimale, danno sollecitazioni locali estremamente elevate (in realtà singolari). Tuttavia, lo stress scende molto più velocemente ed è inferiore al 5% dopo circa 100 mm.Il limite del 5% è ancora in termini di carico distribuito applicato, quindi non viene regolato per le nuove sollecitazioni locali. Il tasso di decadimento logaritmico della densità di energia di deformazione è tre volte più veloce dopo l’aggiunta dei carichi puntuali.

Il principio di Saint-Venant nell’analisi agli elementi finiti

In alcuni casi, è possibile considerare intuitivamente il principio di Saint-Venant come applicabile al problema discretizzato. Qui, guardiamo i carichi distribuiti e le mesh non conformi.

Carichi distribuiti

Nel modello FE, i carichi vengono sempre applicati ai nodi mesh, anche se li si specifica come un carico di confine continuo. Il carico viene distribuito internamente ai nodi dell’elemento utilizzando il principio del lavoro virtuale, come mostrato nell’esempio seguente.

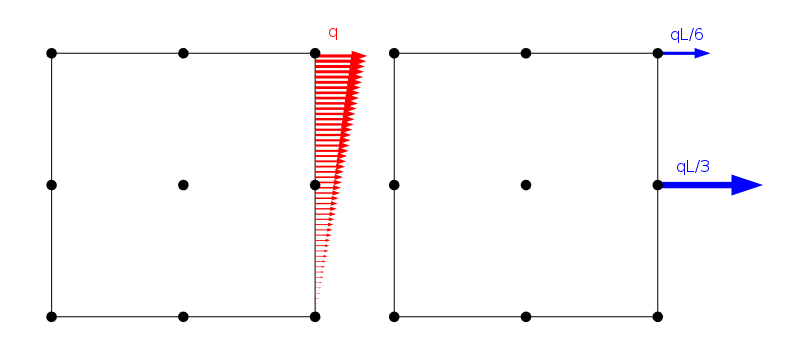
Un carico distribuito linearmente e come viene applicato ai nodi di un elemento Lagrange del secondo ordine con lunghezza laterale L.

Esiste, tuttavia, un numero infinito di distribuzioni di carico che danno gli stessi carichi nodali purché condividano la stessa forza e momento risultante. Ovviamente, la soluzione al problema degli elementi finiti è la stessa per tutti questi casi. Dal principio di Saint-Venant, tuttavia, possiamo concludere che tutti questi carichi dovrebbero dare essenzialmente lo stesso campo di stress non appena ci troviamo a una certa distanza.

Poiché la dimensione dell’area su cui ridistribuiamo i carichi è una faccia di elemento, la dimensione lineare dopo la quale non vi è alcuna differenza è essenzialmente uno strato di elemento all’interno della struttura. Pertanto, la soluzione nello strato più esterno di elementi potrebbe non corrispondere al carico effettivo, ma più in là, lo fa.

Ad esempio, possiamo caricare una piastra rettangolare con un carico limite che ha una distribuzione esponenziale delle sollecitazioni. Lo stress calcolato con una maglia fine è mostrato di seguito.

Trama di contorno della distribuzione delle sollecitazioni assiali.

A causa del principio di Saint-Venant, il campo di sollecitazione viene ridistribuito in uno stato di curvatura puro a una certa distanza dal bordo caricato, proprio come ci aspettiamo. Questo, tuttavia, non è l’obiettivo della discussione in corso. Piuttosto, studiamo la differenza tra la distribuzione dello stress di cui sopra e ciò che otteniamo con un numero di maglie grossolane.

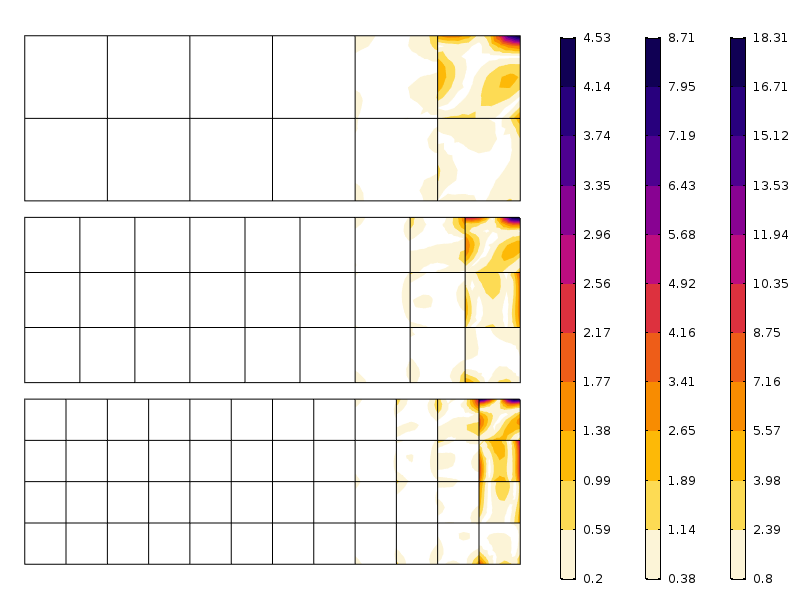
Errore di sollecitazione assiale per tre diverse maglie. Nota le diverse scale. Come previsto, l’errore è più piccolo quando la mesh è più fine.

Come si può vedere nella figura, l’errore diminuisce rapidamente dopo il primo livello di elemento. Quello che vediamo qui è in realtà una combinazione di convergenza delle maglie e la ridistribuzione delle sollecitazioni implicite dal principio di Saint-Venant.

Mesh non conforme

Una mesh non conforme si verifica quando le funzioni di forma in due elementi collegati non corrispondono. Il caso più comune è quando un assembly è collegato utilizzando coppie di identità e condizioni di continuità. Per esemplificare questo, possiamo studiare una barra dritta con una mesh intenzionalmente non compatibile. Con un semplice caso di carico, come la tensione uniassiale, è possibile studiare i disturbi da stress causati dalla transizione.

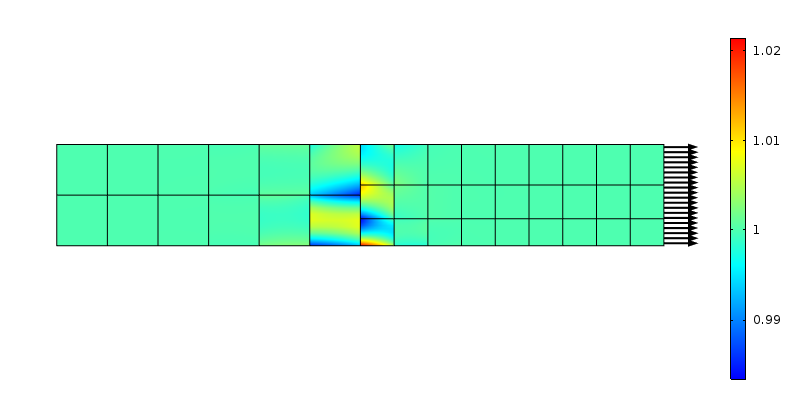
Sollecitazione assiale ad una transizione mesh non conforme. Vengono utilizzati elementi del secondo ordine.

Le forze trasmesse dai nodi ai due lati non corrispondono all’assunzione di stress costante. Ancora una volta, questo può essere visto come una ridistribuzione del carico locale su un’area che è la dimensione dell’elemento. Usando il ragionamento di Saint-Venant, il disturbo dovrebbe svanire a una distanza “di dimensione dell’elemento” dalla transizione. Esaminiamo cosa succede se la mesh viene raffinata nella direzione assiale.

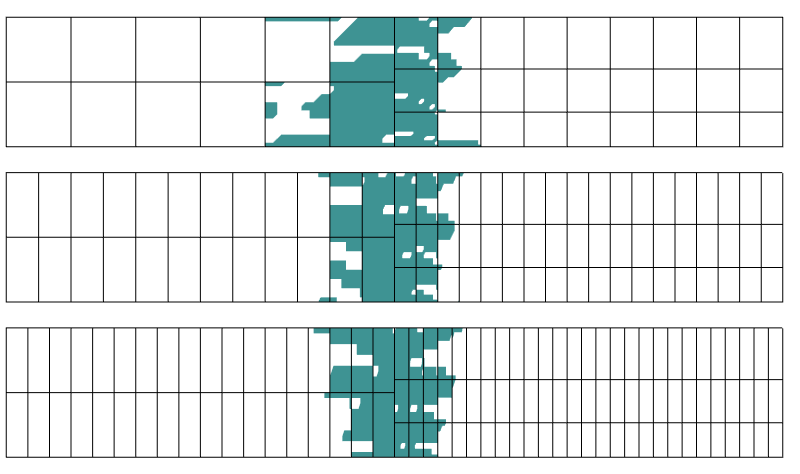
Regione con più dello 0,1% di errore nello stress. Tre diverse discretizzazioni sono utilizzate nella direzione assiale.

Si scopre che la regione di disturbo non è influenzata molto dalla discretizzazione nella direzione perpendicolare al confine di transizione. Questo è esattamente ciò che il principio di Saint-Venant ci dice.

Osservazioni finali

Senza ricorrere al principio di Saint-Venant, molte analisi strutturali sono difficili da eseguire, semplicemente perché la distribuzione dettagliata del carico non è nota.

Il principio è formalmente valido solo per i materiali elastici lineari. In pratica, lo usiamo anche intuitivamente su base giornaliera per altre situazioni. Se, ad esempio, il materiale nell’esempio “piastra con foro” fosse elastoplastico, ci si aspetterebbe che i due carichi distribuiti diano risultati equivalenti, purché la tensione di snervamento sia superiore alla tensione applicata al confine in modo che vi sia solo deformazione plastica attorno al foro. Il carico puntuale, tuttavia, fornisce sempre una soluzione diversa, poiché il materiale cede attorno al punto caricato. Per una discussione più lunga, leggi questo post sul blog sulle singolarità a carichi puntuali.

Passi successivi

Ulteriori informazioni sull’utilizzo del software COMSOL Multiphysics® per FEA.

Ulteriori letture

• Y. C. Fung e P. Tong, Meccanica classica e computazionale dei solidi, World Scientific Publishing Co. Etp. Ltd., 2001.