第12章
構造の解析のモーメント分布法
12.1基本概念
ビームとフレームの解析のモーメント分布法は、ハーディ-クロスによって開発され、1930年に正式に発表された。 この方法は傾き-たわみ法のような変形法であるが,近似法であり,後者の方法のように連立方程式を解く必要はない。 モーメント分布の方法によって得られた結果の精度の程度は、逐次近似の数または反復プロセスに依存する。
モーメント分布の方法の概念を説明するために、図12.1に示すフレームを考えてみましょう。 フレームのメンバーは角柱であり、軸方向に変形したり、互いに相対的に平行に移動したりしないと仮定されます。 フレームの接合箇所ACDは接合箇所Bは応用負荷がわずかに原因で回ることができるが、固定である。 まず、部材間でモーメント分布を行う前に、すべての関節がクランプを使用して一時的にロックされていると仮定します。
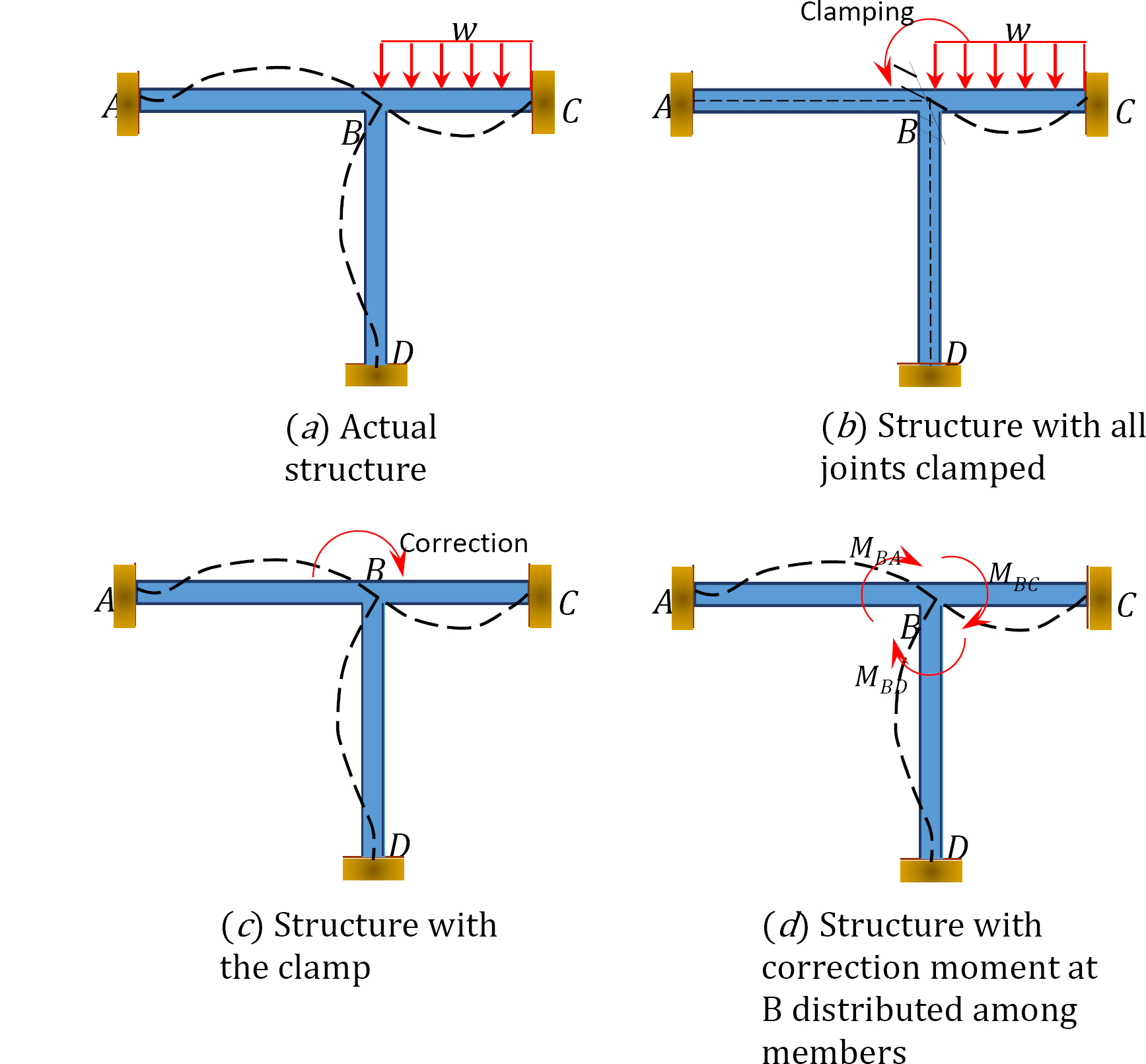
図1.1.1. 12.1. フレーム。
12.2サインコンベンション
モーメント分布法のサインコンベンションは、傾斜偏向法のサインコンベンションと同様です; つまり、メンバーの終わりの瞬間は、メンバーの終わりを時計回りに回す傾向がある場合は正、反時計回りに回す傾向がある場合は負とみなされます。
12.3定義
不均衡なモーメント:この分析方法は、構造内の関節が最初にクランプまたはロックされ、その後連続して解放されることを前提としています。 ジョイントが解放されると、そのジョイントで会合するメンバーの固定終了瞬間の合計がゼロではないため、回転が行われます。 得られた終了モーメントの合計の値は、そのジョイントでのアンバランスモーメントです。
キャリーオーバーモーメント:共同で会合しているメンバーの端に分散された瞬間は、もう一方の端に瞬間を引き起こし、固定されていると仮定されます。 もう一方の端に誘導されたこれらの瞬間は、キャリーオーバー瞬間と呼ばれています。
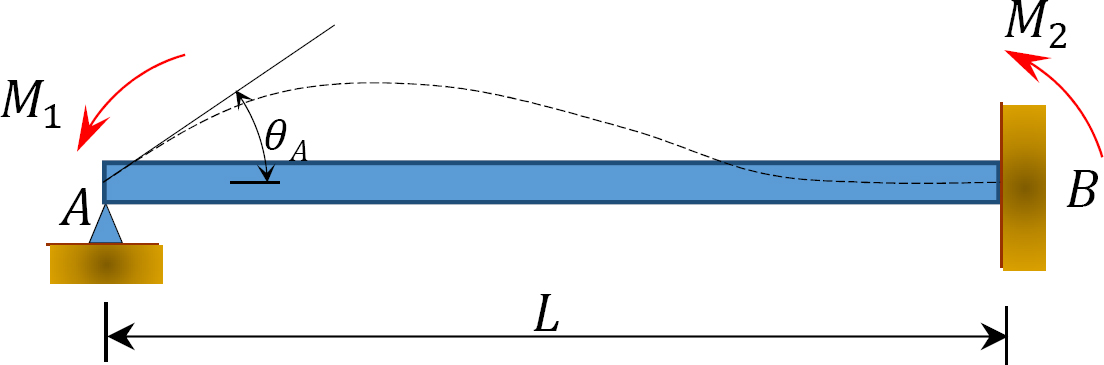
図1.1.1. 12.2. アンロードされたプリズムビーム。
図12.2に示すように、端部Bに固定された無負荷のプリズムビームを考えてみましょう。 モーメントM1がビームの左端に適用される場合、ビームの両端の傾き-たわみ方程式は次のように書くことができます:


式12.1から式12.2に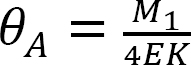 を代入すると、次のようになります:
を代入すると、次のようになります:

式12.3は、もう一方の端に印加されたモーメントによってビームの固定端に運ばれるモーメントが印加されたモーメントの半分に等しいことを示唆しています。
繰越係数:誘起モーメントと印加モーメントの比を繰越係数と呼びます。 図12.2に示すビームの場合、繰越係数は次のようになります:

分散因子(DF): 分散係数は、ジョイントで会合する各メンバーによって運ばれる不均衡な瞬間の割合を決定するために使用される係数である。 図12.3に示すフレームのジョイントOでのメンバー会議の場合、それらの分布係数は次のように計算されます:
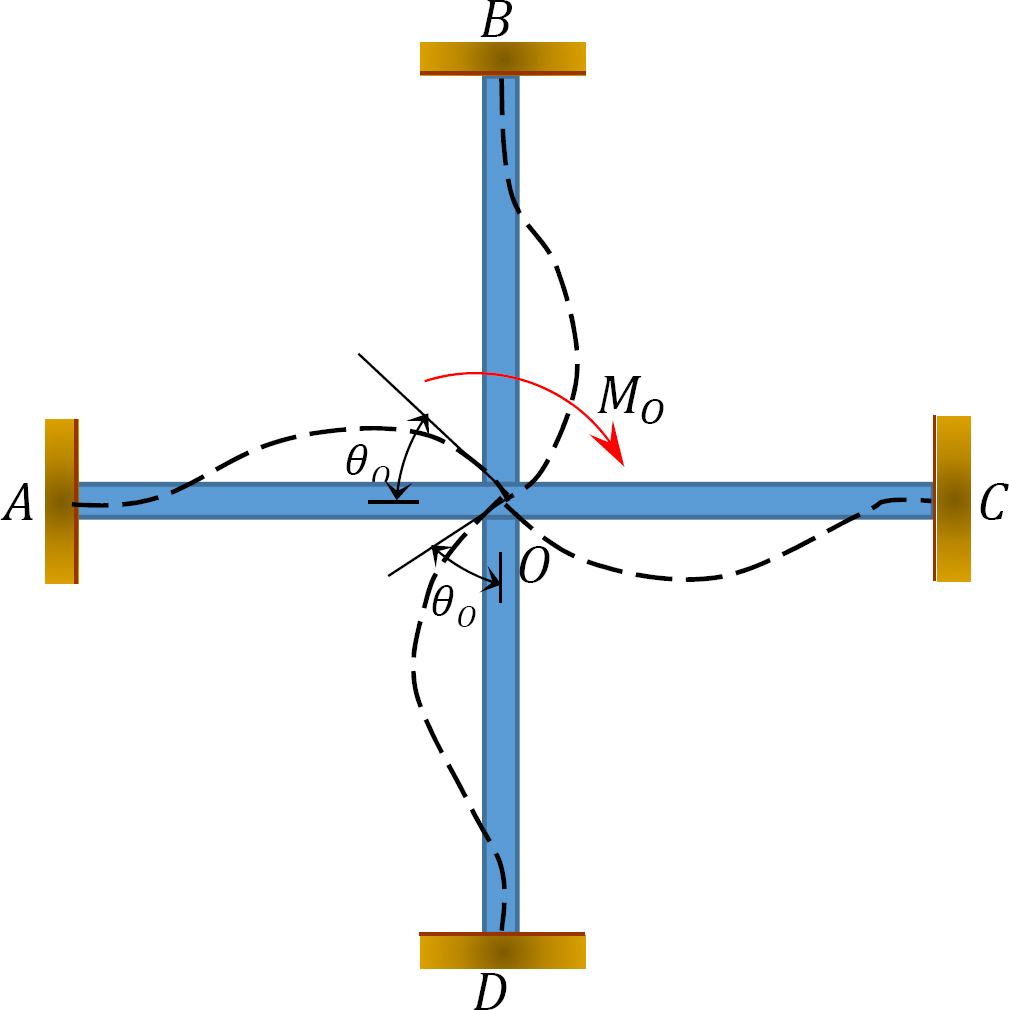
図1.1.1. 12.3. フレーム。

分散モーメント:ジョイントで仮想クランプが解放されると、そのジョイントでの不均衡なモーメントが回転します。 回転は接合箇所で会うメンバーの終わりをねじり、抵抗の時の開発に終って。 これらの抵抗モーメントは分散モーメントと呼ばれます。 図12.3に示すフレームのメンバーの分散モーメントは、次のように計算されます:
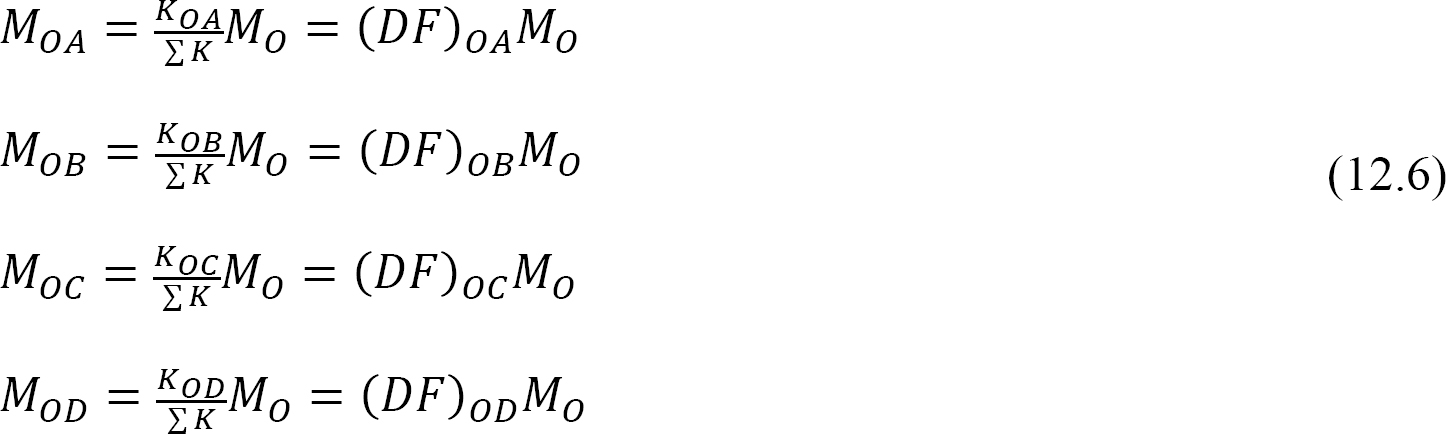
12.4 部材剛性の修正
不確定構造の一部の部材の曲げ剛性を調整することにより、モーメント分布法における反復プロセスを大幅に低減することができ このセクションでは、固定およびピンエンドサポートが不確定ビームの曲げ剛性に及ぼす影響を考慮します。
ケース1: ビームは一方の端にヒンジで固定され、他方の端に固定されています
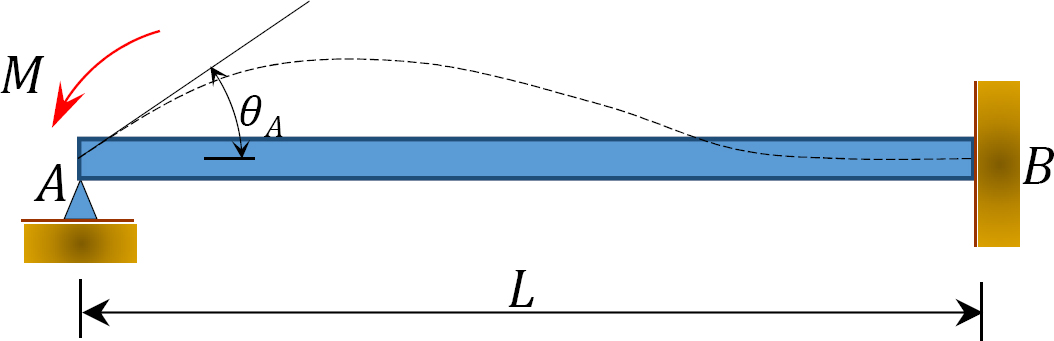
図1.1.1. 12.4. ビーム
図12.4に示すように、端部Aにヒンジ付きで端部Bに固定されたビームを考えてみましょう。 モーメントMを適用すると、ヒンジ端を量θだけ回転させる。 部材の端部Aの傾き-たわみ方程式を書き、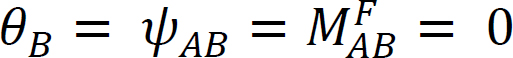 が次のことを示唆していることに注意してください:
が次のことを示唆していることに注意してください:
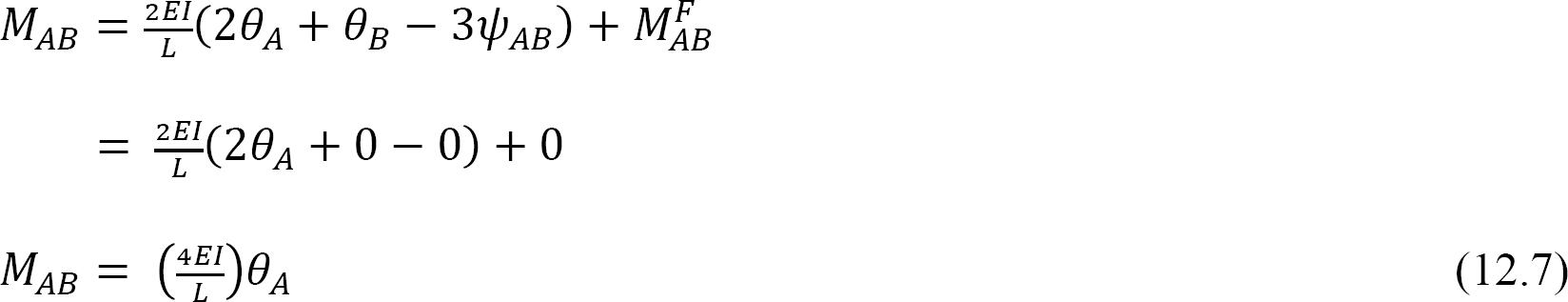
定義により、構造部材の曲げ剛性は、その端部の単位回転を引き起こすために部材の端部に適用されなければならない瞬間である。 遠端が固定された部材の曲げ剛性については、θ a=1を式に代入すると、次のように表されます12.7:

定義により、部材の相対曲げ剛性は、部材の曲げ剛性を4Eで除算することによって決定されます。式12.8を4Eで除算すると、考慮される場合の相対剛性:

ケース2:両端にヒンジ付きのビーム
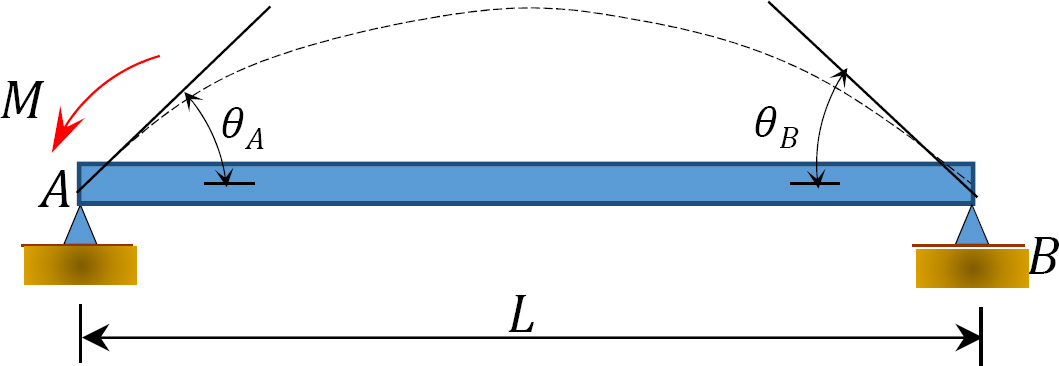
図1.1.1. 12.5. 単に支えられたビーム。
図12.5に示す単純支持ビームの端部AにモーメントMを印加すると、ヒンジ端部で角度θ aだけビームが回転します。 第11章のセクション11.4で導出された修正された傾き-たわみ方程式を使用し、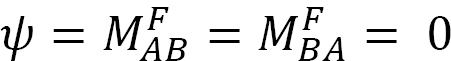 は、荷重が加えられるヒンジ端での瞬間について次の式を示唆していることに注意してください:
は、荷重が加えられるヒンジ端での瞬間について次の式を示唆していることに注意してください:
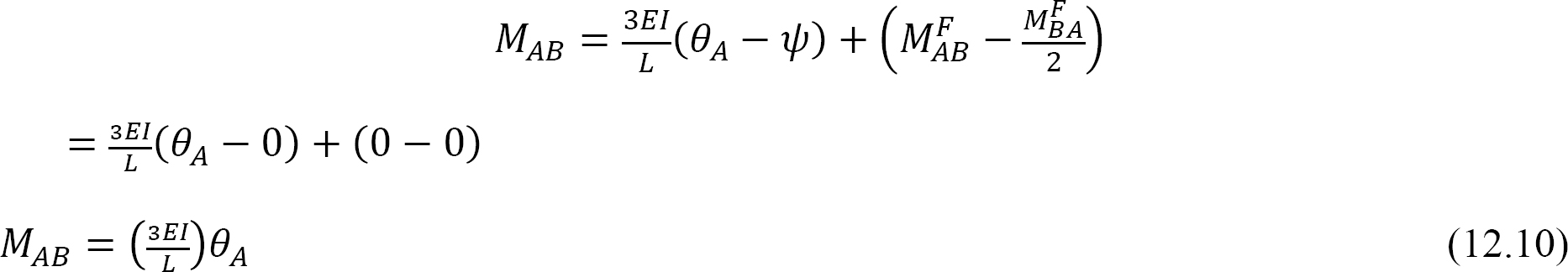
θ a=1を式12.10に代入すると、ヒンジ付き遠端を持つ部材の曲げ剛性について次の式が示唆されます:

ヒンジ付き遠端を持つ部材の相対剛性は、式12.11を4Eで除算することによって、次のように得られます:

式12.12と12.9を比較すると、ヒンジ付き遠端を持つ部材は、同じジオメトリを持つが遠端に固定されている部材と同じくらい硬いことが示唆されます。 この確立された事実は、モーメント分布の方法を用いてヒンジ付き遠端を有するビームまたはフレームを分析する際に、反復回数を実質的に減らすことが このような場合、近端のビームの相対剛性は最初に式12.12に従って調整され、その分配係数は調整された剛性で計算されます。 バランスをとる操作の間に、近い端は端からのまたはへの時のそれ以上の運送無しでちょうど一度バランスをとられます。
12.5不確定ビームの解析
モーメント分布法による不確定ビームの解析手順を以下のように簡単に要約します:
モーメント分布法による不確定ビームの解析手順
•ジョイントが回転に対してクランプされていると仮定して、メンバーの固定端モーメントを計算します。
•ジョイントで接続されている各メンバーの分布係数を計算
•各ジョイントでのアンバランスモーメントを計算し、そのジョイントで接続されているメンバー
•分散された瞬間の半分をメンバーのもう一方の端に持ち越す。
•これらの後者のモーメント(ステップ3と4で得られたモーメント)を元の固定端モーメントに加算または減算します。
•指定された構造の関節に決定された終了モーメントを適用します。
•モーメント分布法によって得られた関節の荷重とモーメントを示す、与えられた梁の各スパンの自由体図を描きます。
•各スパンの支持反応を決定します。
•各スパンのせん断力と曲げモーメント図を計算して構築します。
•ステップ9の図を組み合わせて、指定された梁の曲げモーメントとせん断力図を一つ描きます。
12.1
モーメント分布法を使用して、図12.6aに示すビームの支持体での端モーメントと反応を決定します。 EI=定数です。
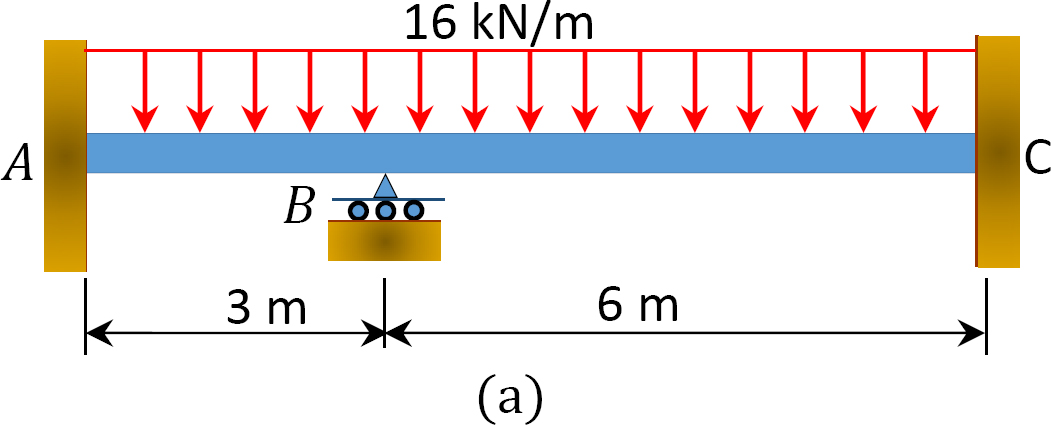
図1.1.1. 12.6. ビーム
ソリューション
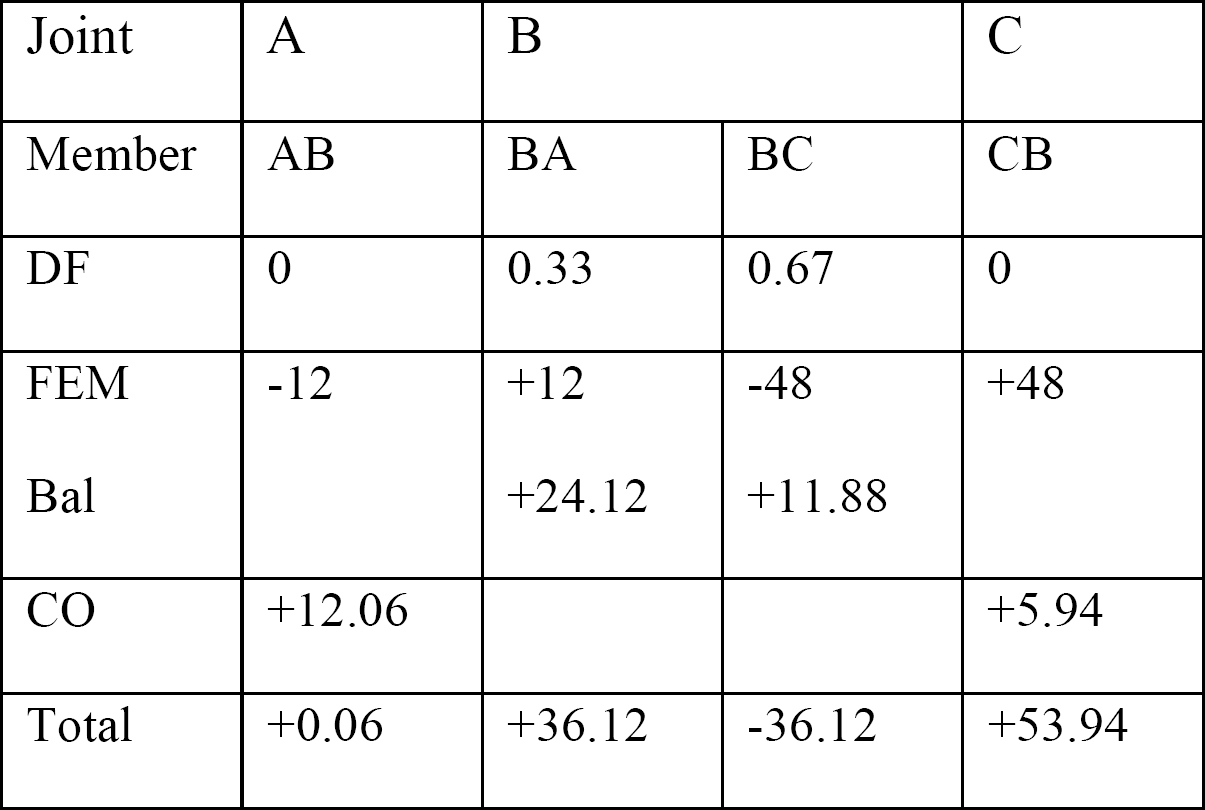
終わりの瞬間を修正しました。
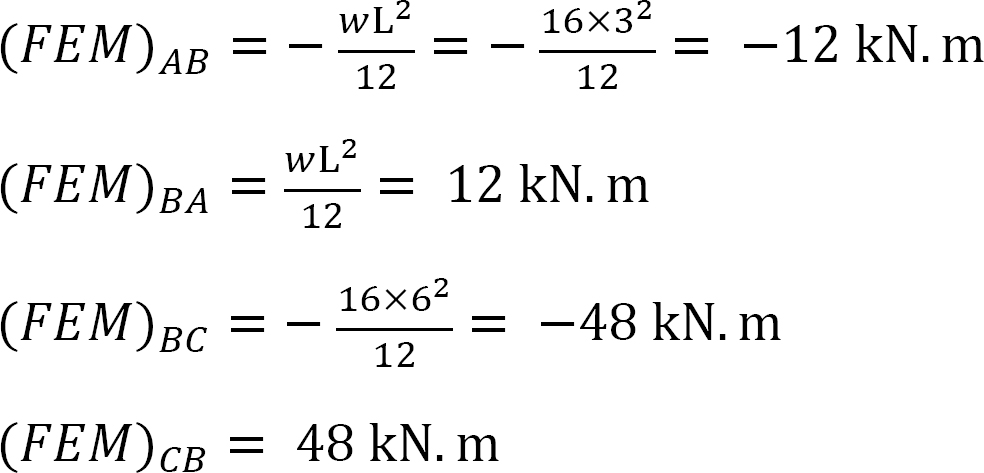
剛さの要因。
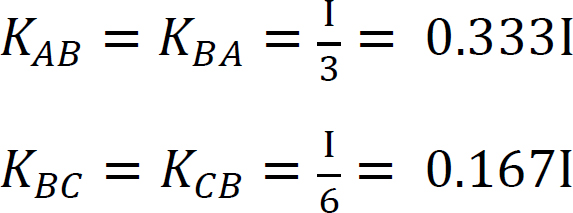
分配係数。
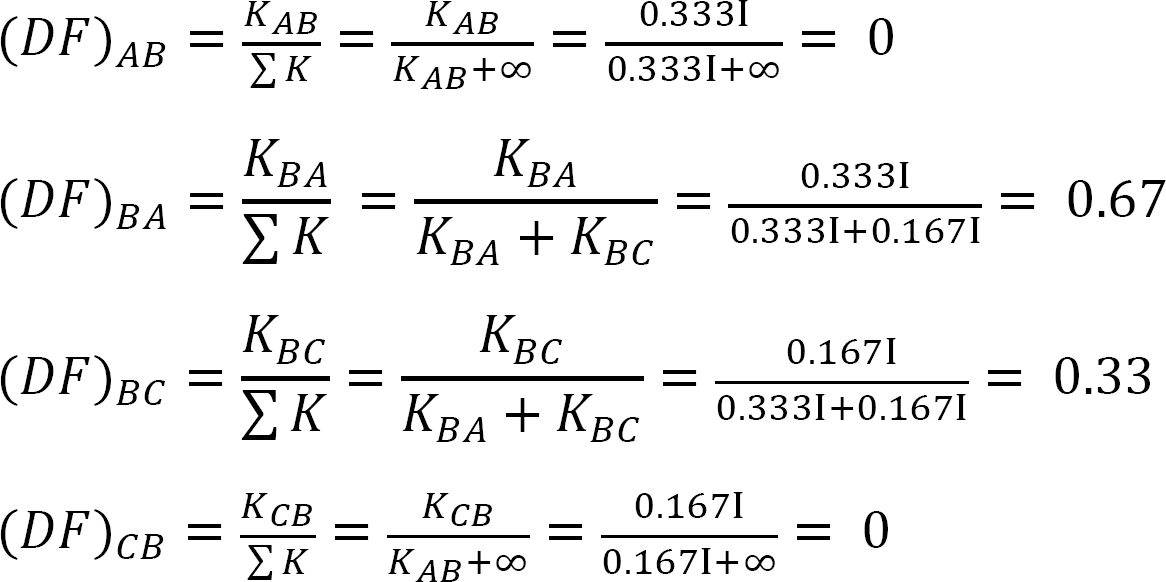
表12.1. 配布テーブル。
せん断力および曲がる時の図表。
例12.2
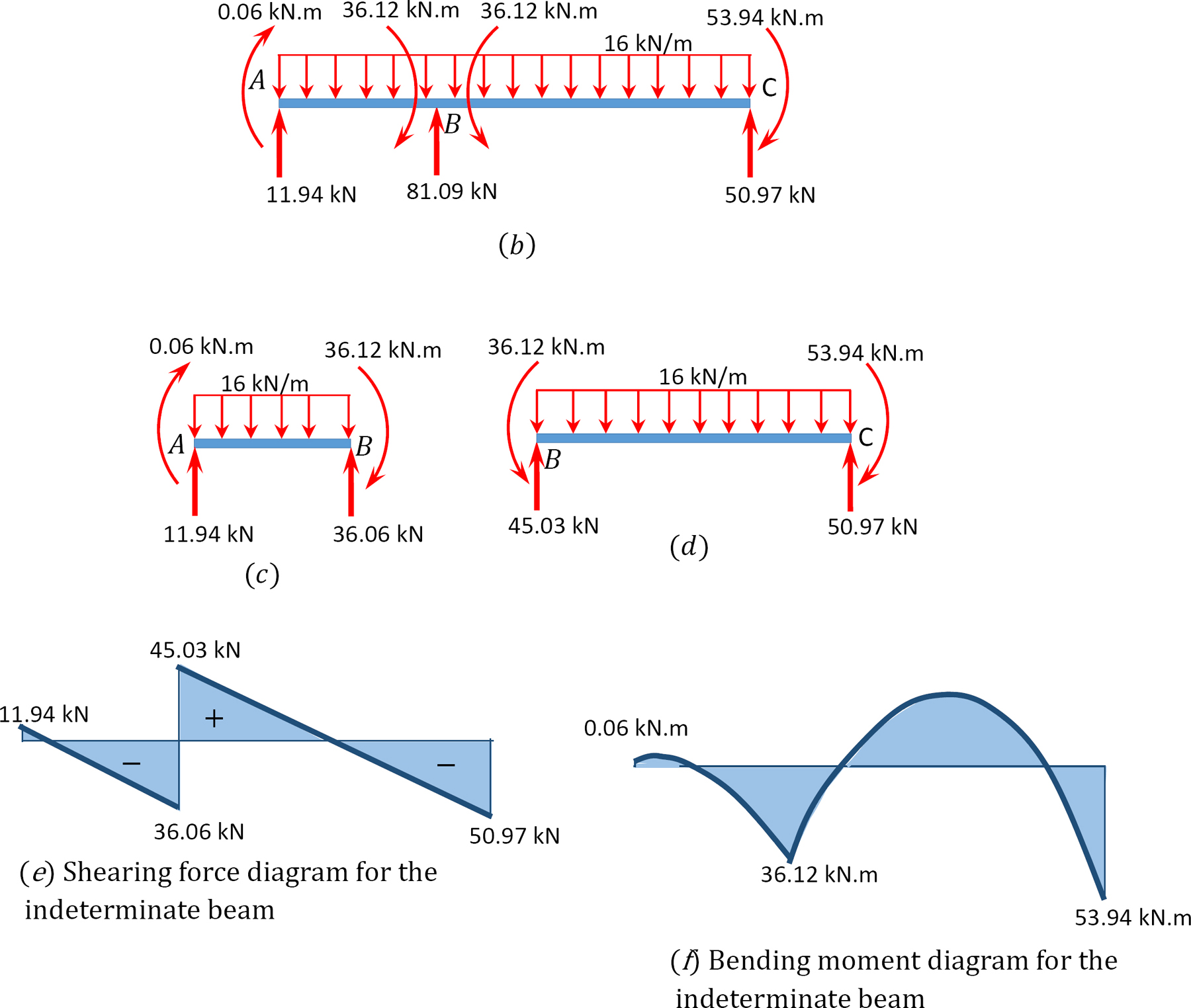
モーメント分布法を使用して、図12.7aに示すビームの支持体での端モーメントと反応を決定します。
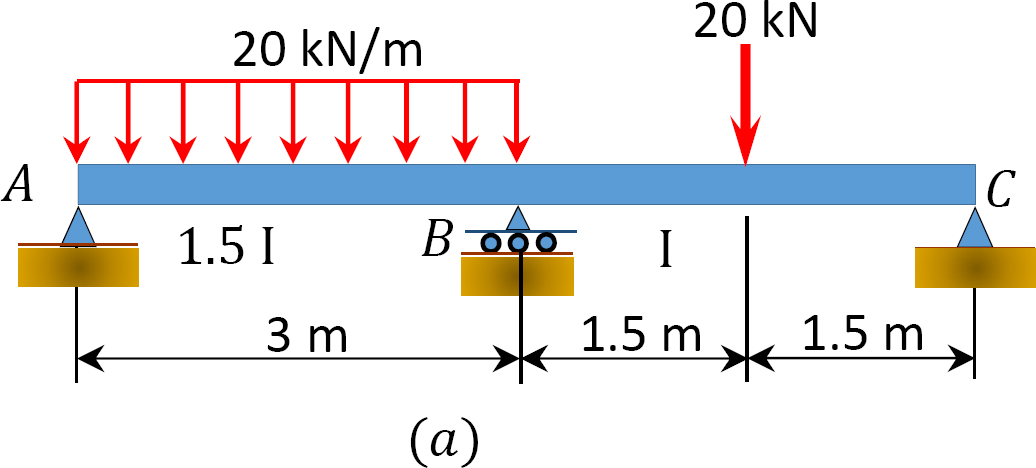
図1.1.1. 12.7. ビーム
ソリューション
終わりの瞬間を修正しました。
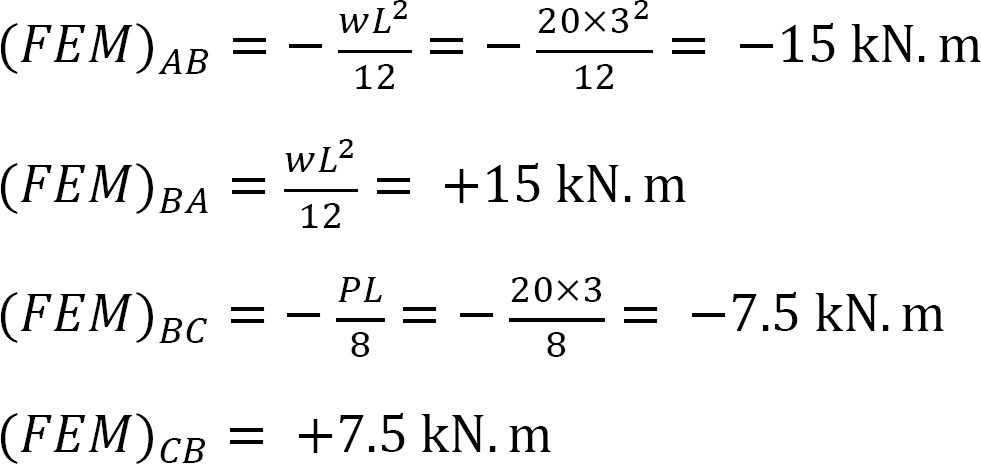
剛さの要因。
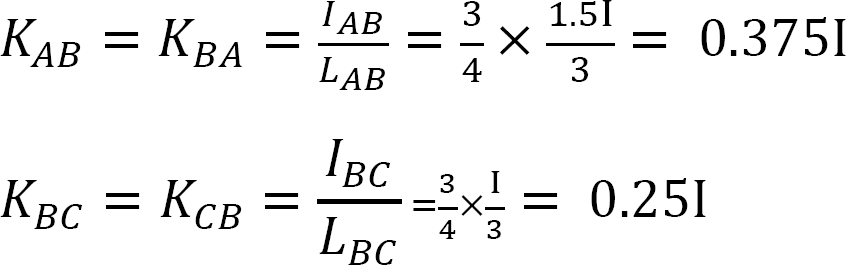
分配係数。
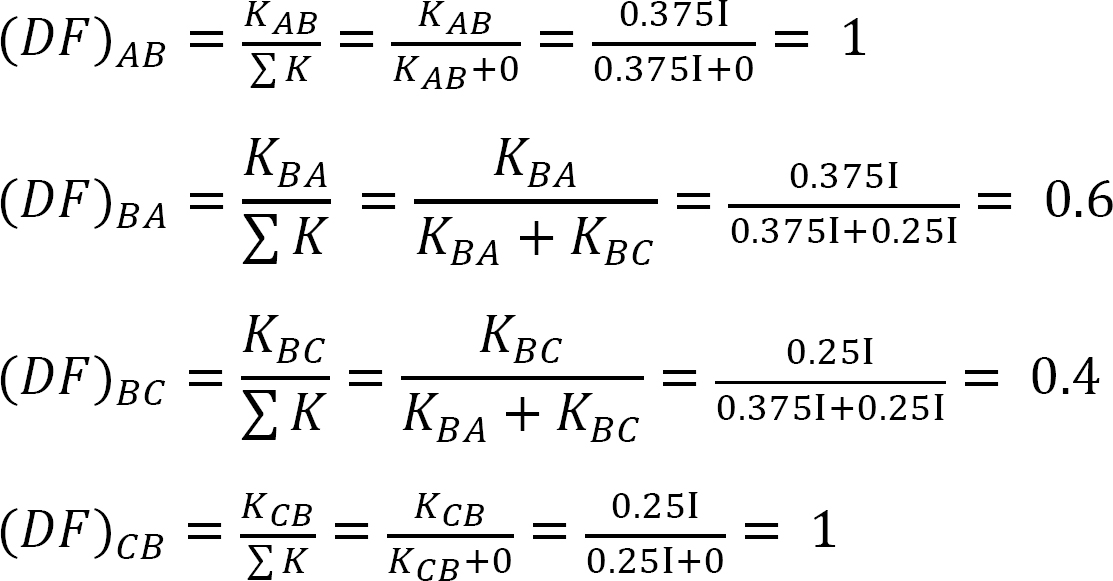
表12.2. 配布テーブル。
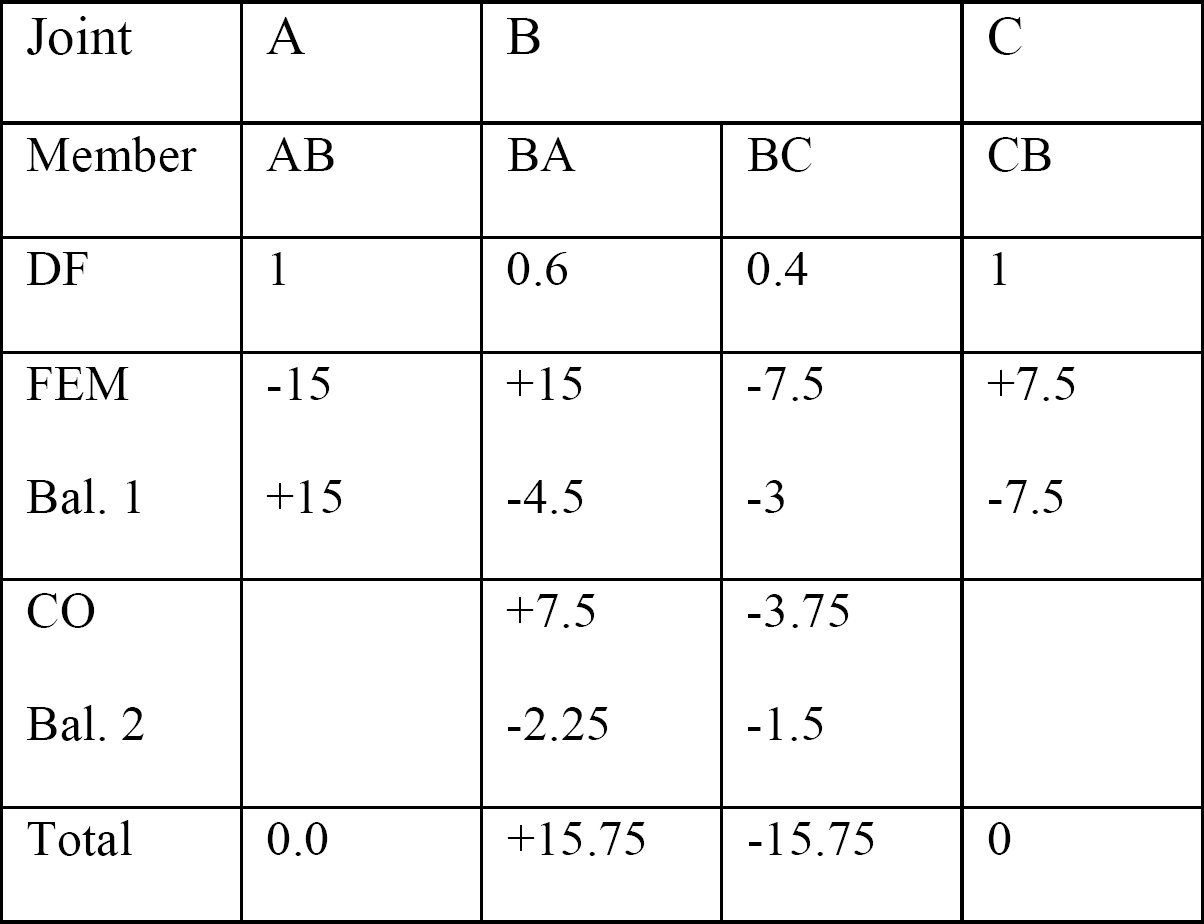
せん断力および曲がる時の図表。
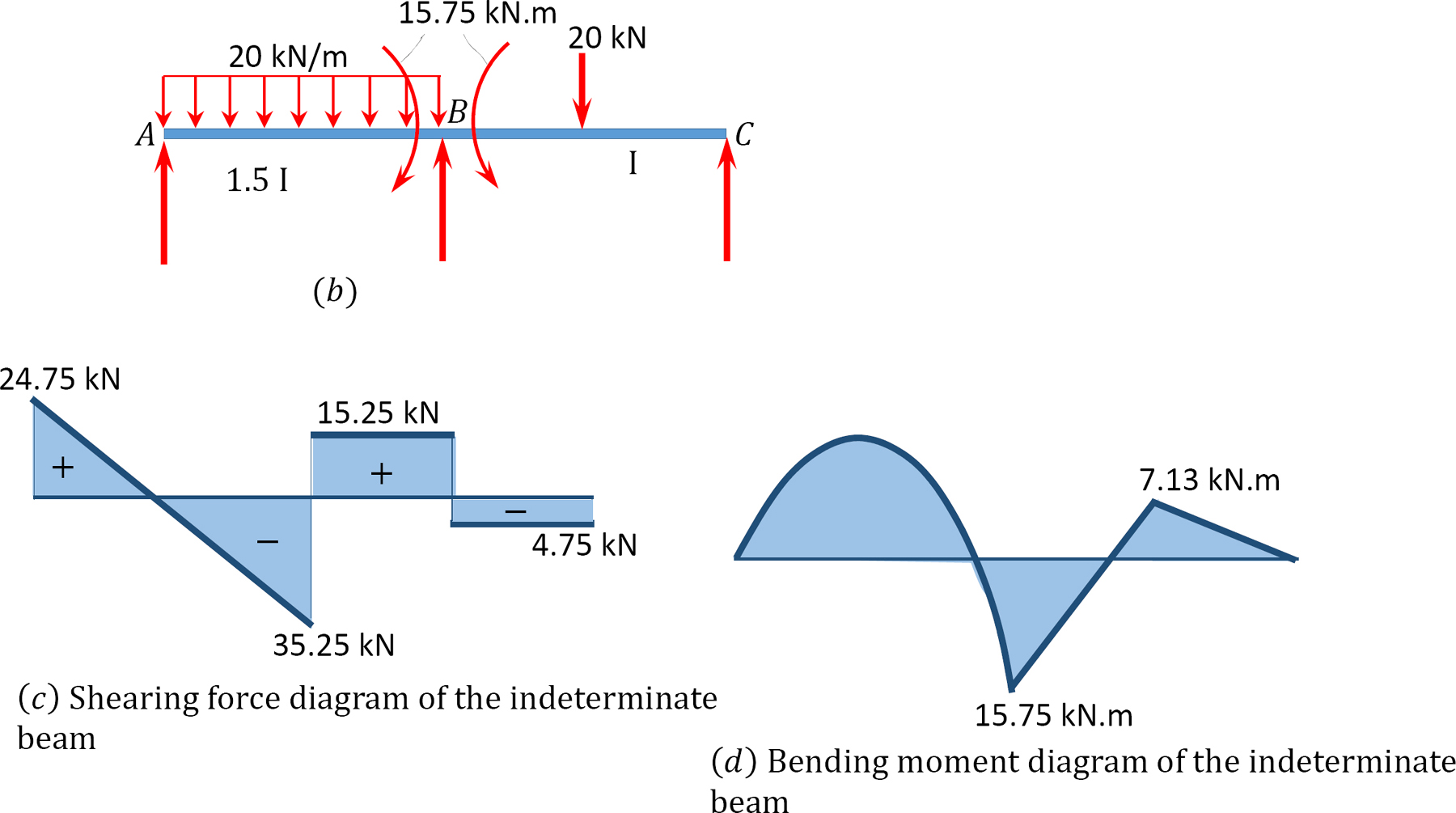
12.6 不確定フレームの解析
モーメント分布法を用いたフレームの解析の手順は、解析されるフレームの種類によって異なります。 フレームは、揺れフレームまたは非揺れフレームに分類されます。 非動揺フレームの解析手順は不確定ビームの解析手順と類似している。 しかし、揺れフレームの分析のために、手順は異なります。 動揺フレームの解析には,非動揺ステージと動揺ステージ解析の二つの段階がある。 これらの段階は以下に記載されています。
モーメント分布法による不確定な揺れフレームの解析手順
A.非揺れステージ解析
•まず、フレームの揺れを防ぐ架空の支柱が存在すると仮定します。
*フレームの支持体での水平反応を計算し、差Xに注意してください。
揺れステージ解析
•フレームの列に作用する任意のモーメントを想定します。 これらのモーメントの大きさは、次のように比例して列ごとに変化します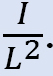
•値はM2に対して仮定され、M1が決定される。
•任意のモーメントは、非動揺条件のために分布しています
•動揺条件のための支持体での水平反応の大きさを計算します。 これらの反応の合計は、任意の変位力Yを与える。
•比を決定する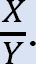 この比は、揺れ係数と呼ばれます。
この比は、揺れ係数と呼ばれます。
•揺れの分布モーメントを乗算するには、揺れ係数を使用します。 これは動揺のための訂正された時を与える。
•フレームの最後のモーメントは、非揺れステージで得られたモーメントと揺れステージの補正されたモーメントの合計です。
12.3
モーメント分布法を使用して、図12.8に示すフレームのメンバーの終了モーメントを決定します。 EI=定数です。
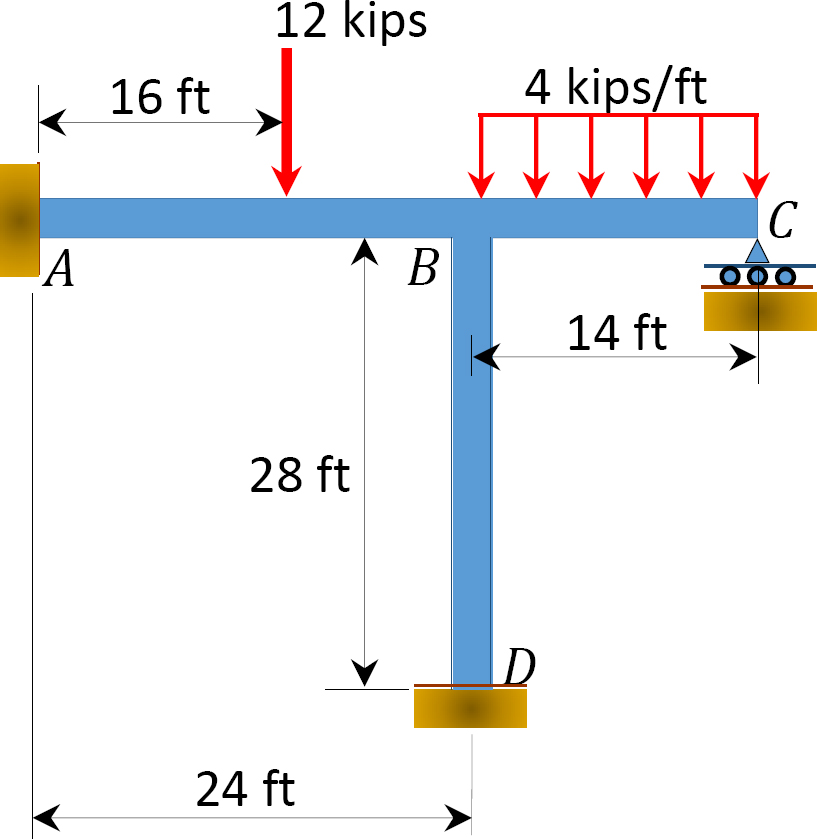
図1.1.1. 12.8. フレーム。
ソリューション
終わりの瞬間を修正しました。
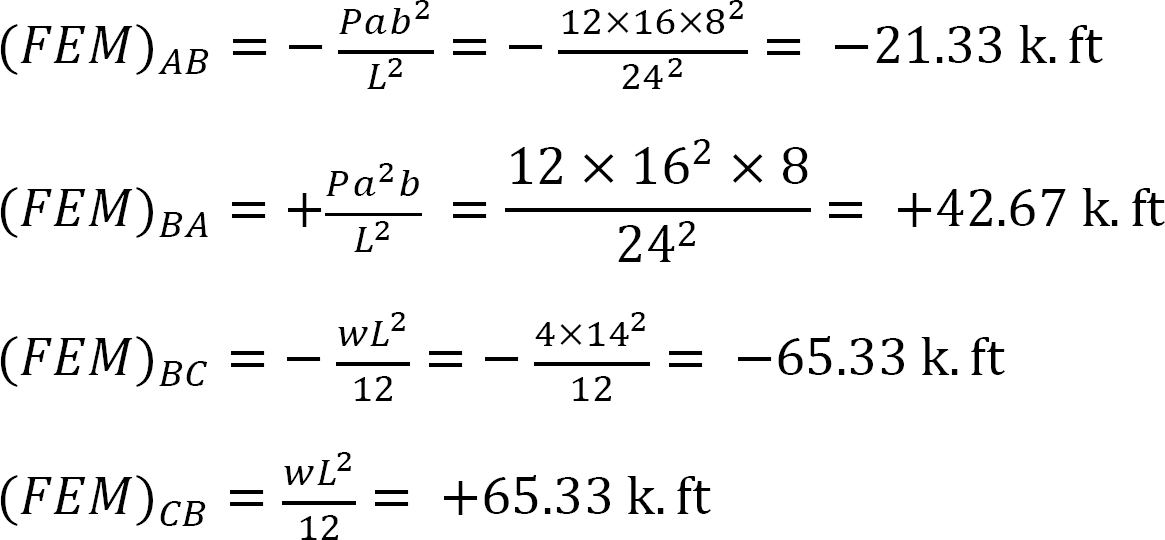
剛さの要因。
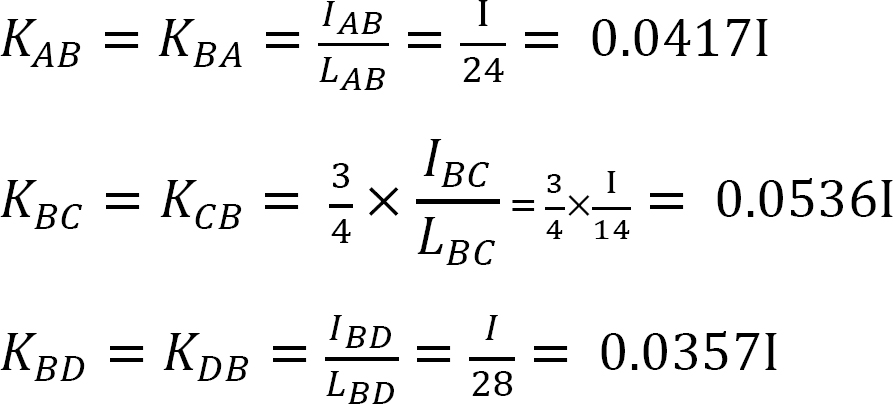
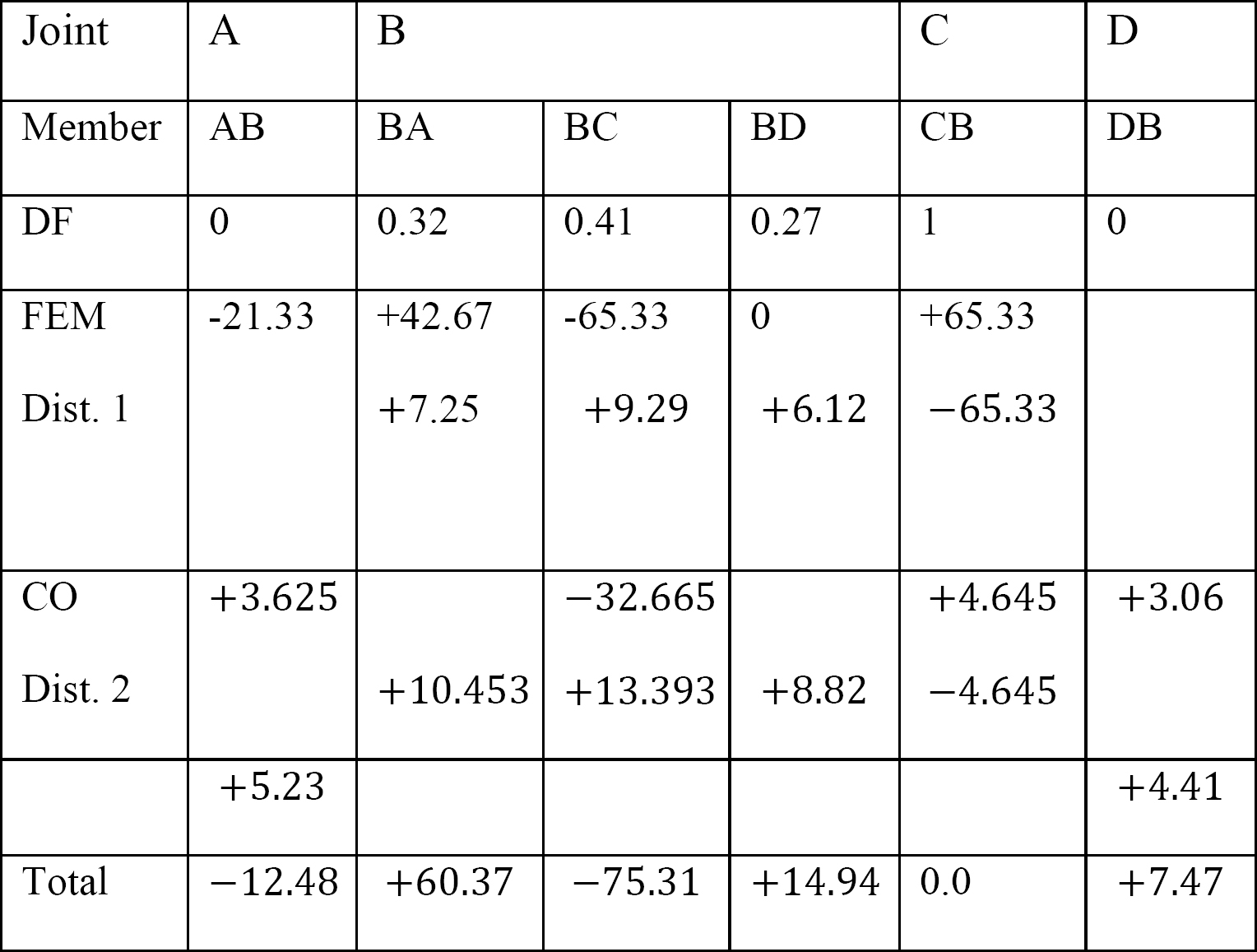
分配係数。
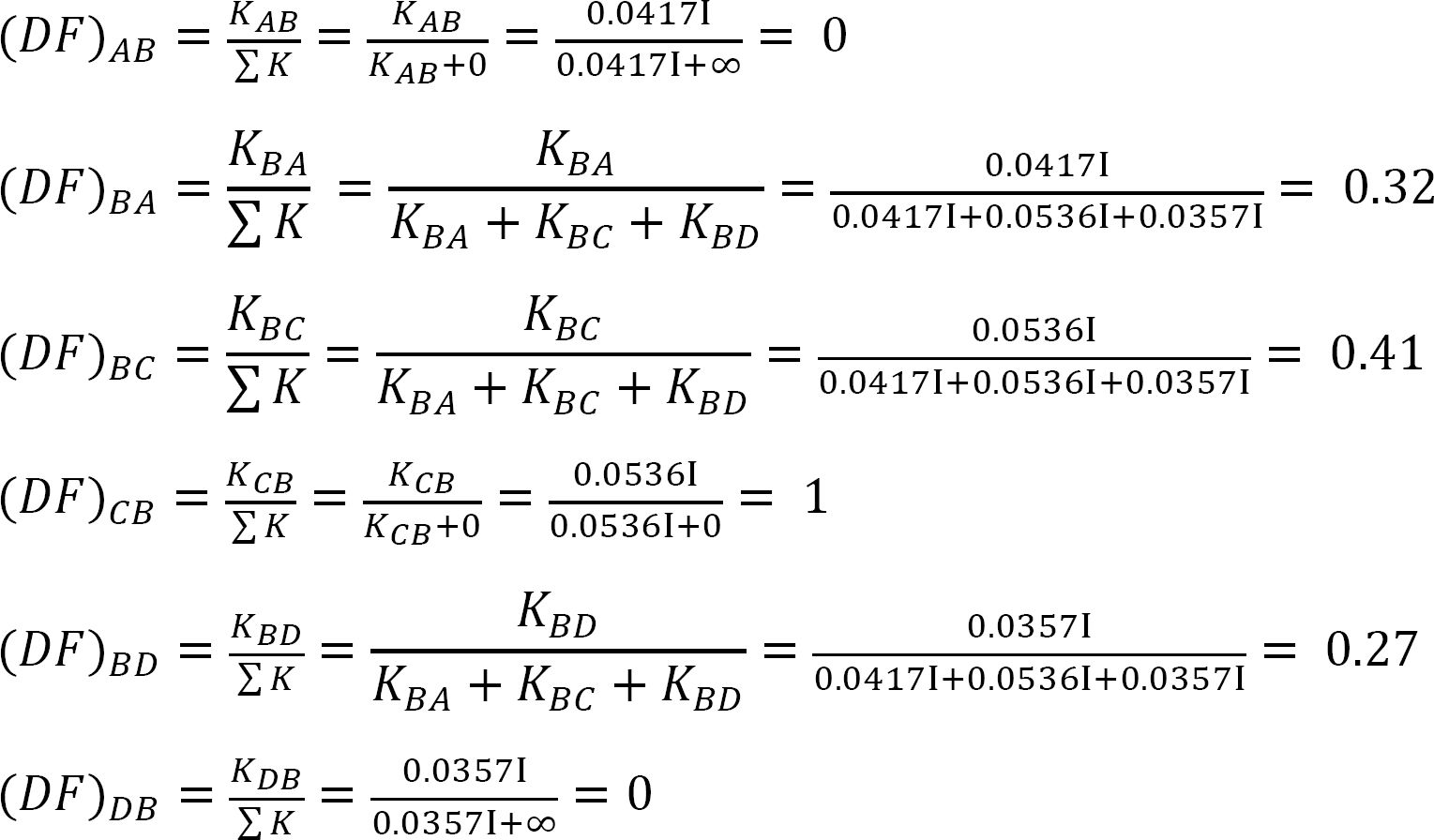
表12.3. 配布テーブル。
最後のメンバーの終わりの瞬間。
得られたEk Β B、Ek Β C、およびEK βの値をメンバー終了モーメント方程式に代入すると、
MAB=-12.48k.ft
MBA=+60.37k.ft
MBC=-75.31k.ft
MBD=-75.31K.ft
MBD=-75.31K.ft
MBD=-75.31K.ft
MBD=-75.31K.ft
MBD=-75.31K.ft
MBD=+14.94k.ft
Mcb=0
mdb=+7.47k.ft
例12.4
モーメント分布法を使用して、図12.9に示すフレームのサポートでの終了モーメントを決定します。 EI=定数です。
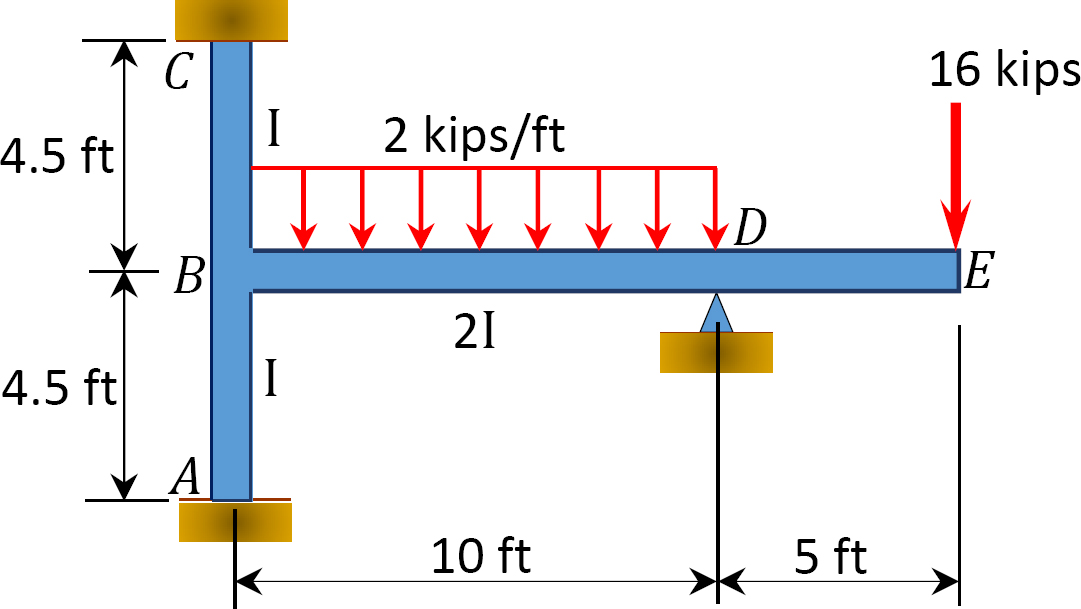
図1.1.1. 12.9. フレーム。
ソリューション
終わりの瞬間を修正しました。
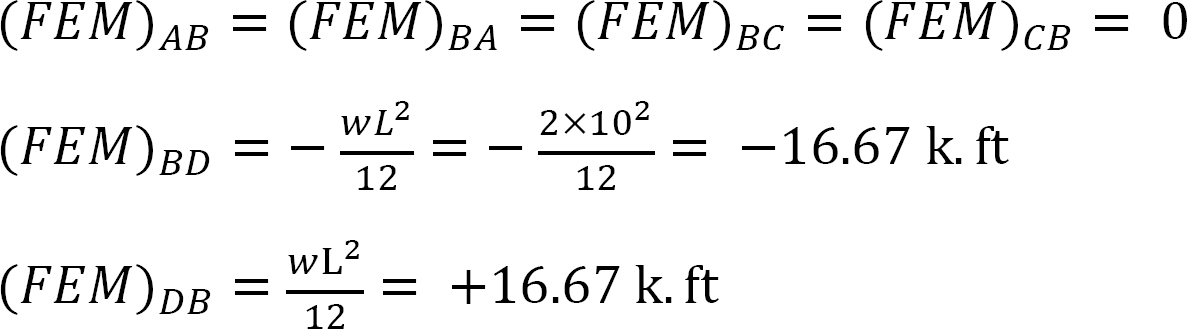
剛さの要因。
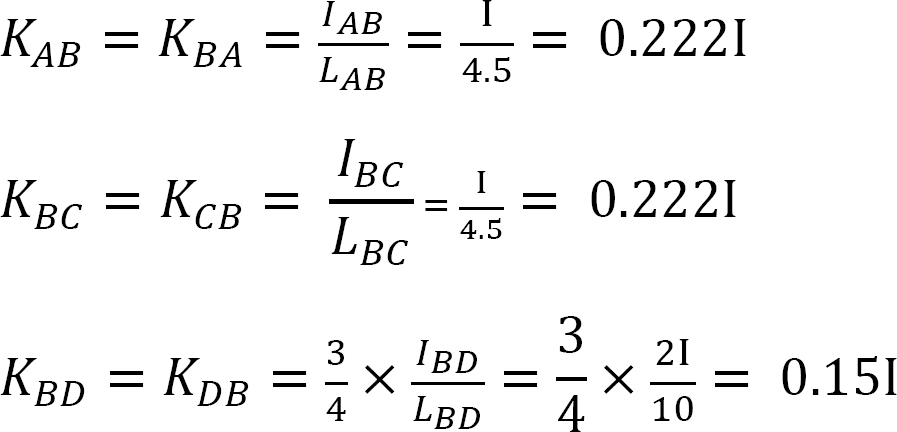
分配係数。

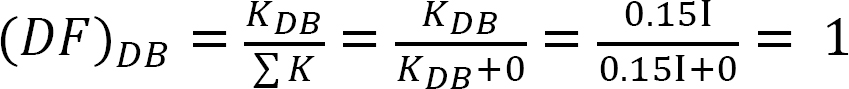
表12.4. 配布テーブル。
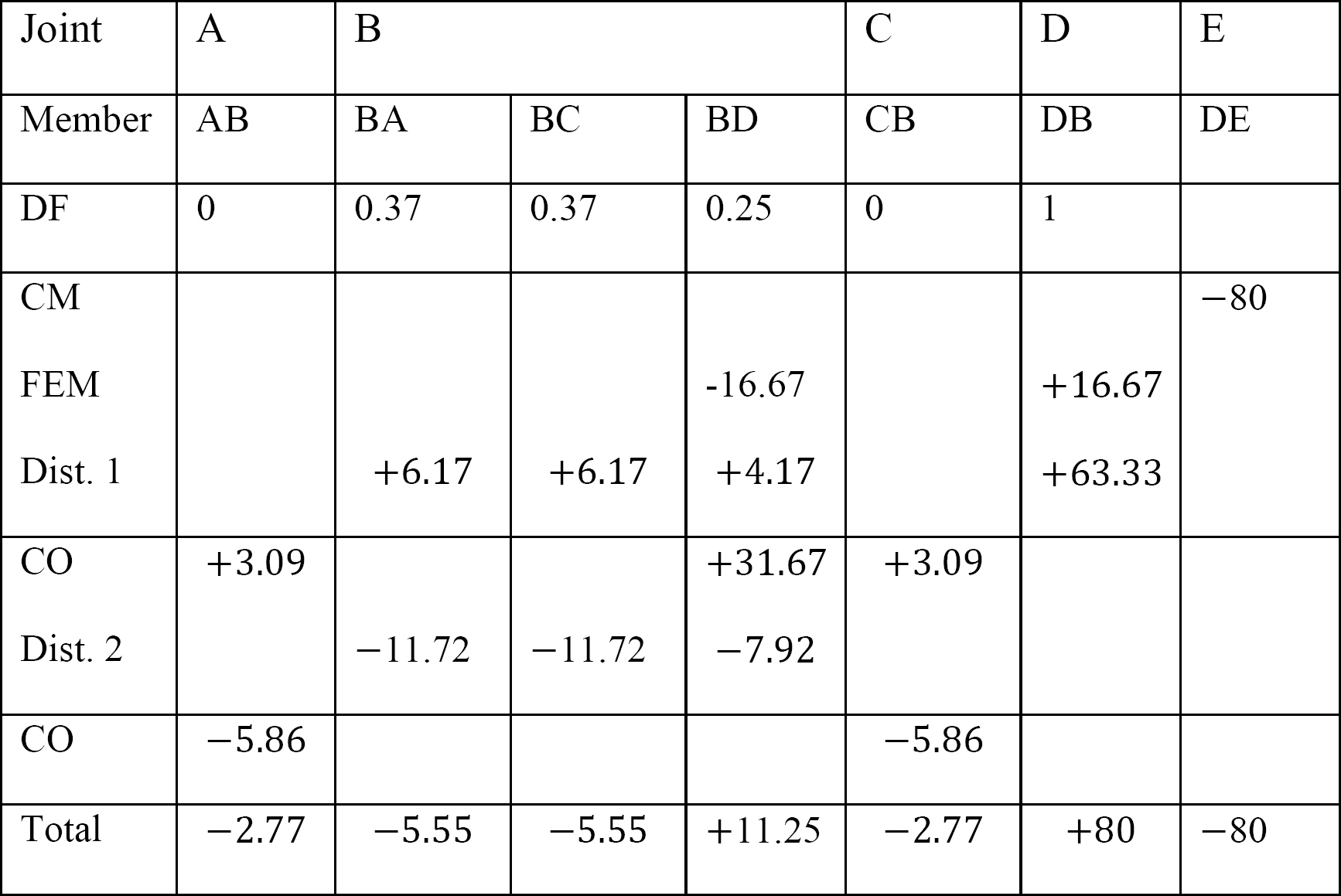
最後のメンバーの終わりの瞬間。
MAB=-2.77k.ft
MBA=-5.55k.ft
MBC=-5.55k.ft
MAB=-2.77k.ft
MBA=-5.55k.ft
MBD=+11.25k.ft
MCB=-2.77
MDB=+80k.ft
MDE=-80k.ft
例12.5
モーメント分布法を使用して、図12.10に示すフレームのサポートでの終了モーメントを決定します。 EI=定数です。
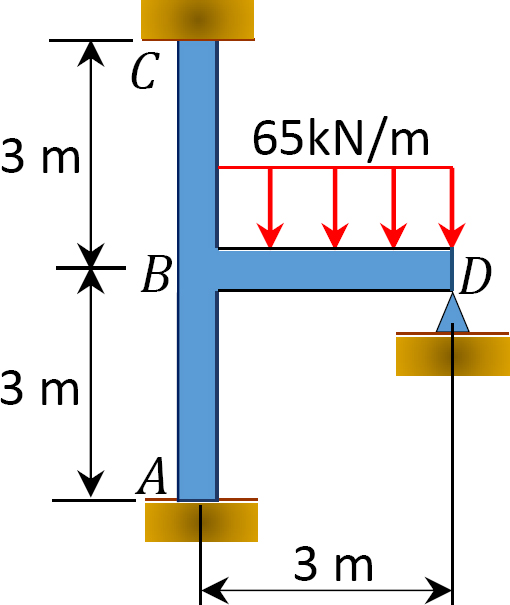
図1.1.1. 12.10. フレーム。
ソリューション
終わりの瞬間を修正しました。
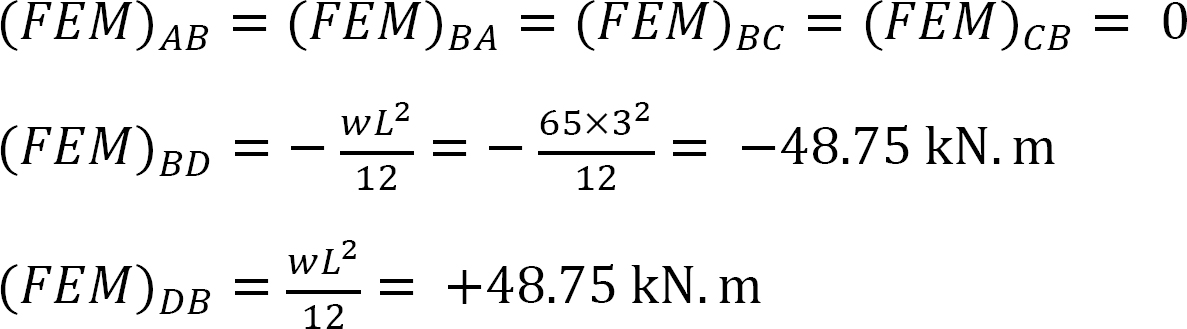
剛さの要因。
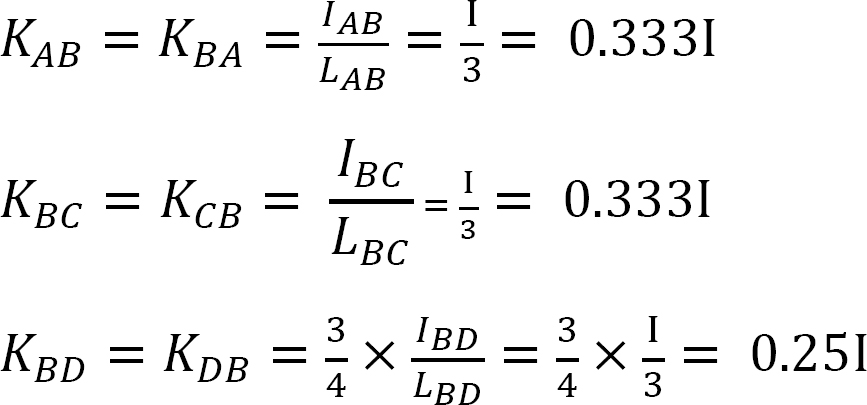
分配係数。
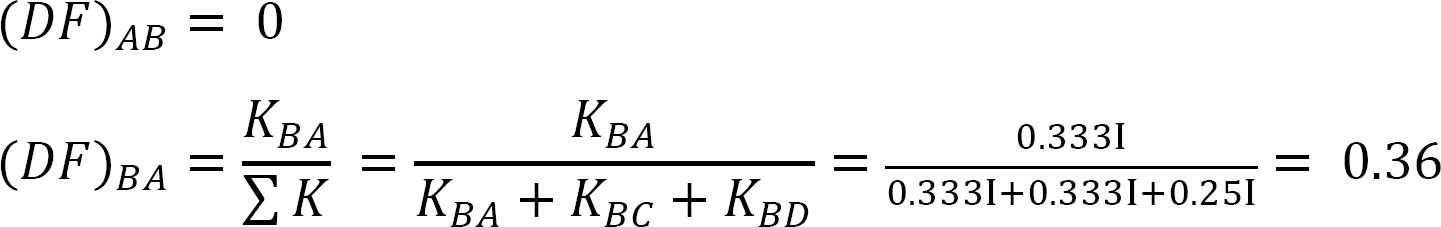

表12.5. 配布テーブル。
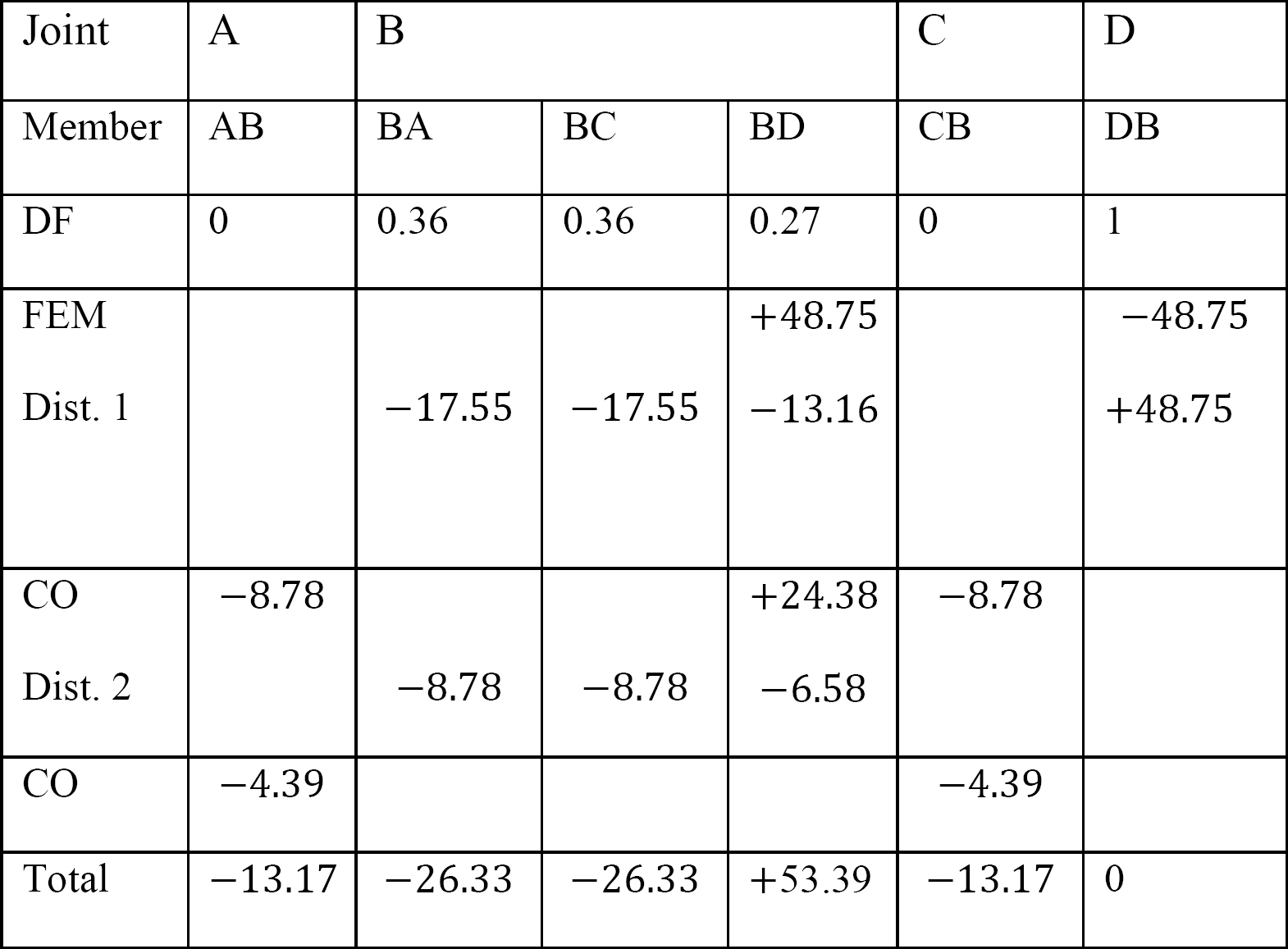
最後のメンバーの終わりの瞬間。
MAB=-13.17k.ft
MBA=-26.33k.ft
MBC=-26.33k.ft
MBD=+53.39K.ft
MCB=-13.17K.ft
= 0
例12.6
モーメント分布法を使用して、図12.11aに示す横揺れを伴うフレームの部材端モーメントを決定します.
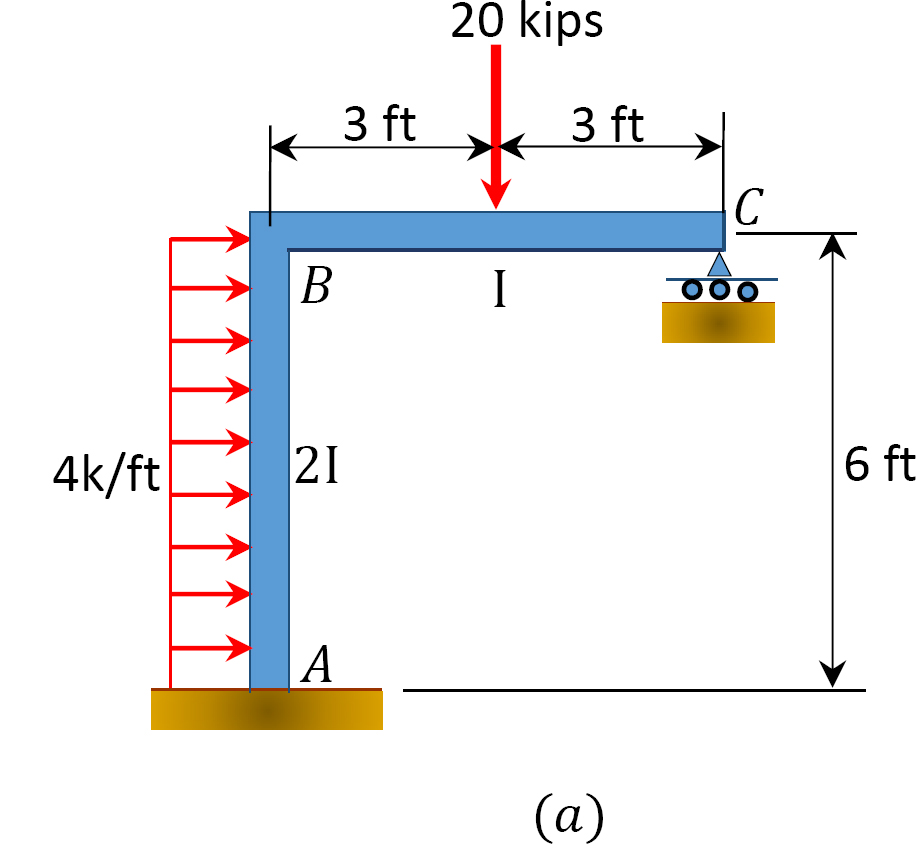
図1.1.1. 12.11. サイド動揺が付いているフレーム。
ソリューション
終わりの瞬間を修正しました。
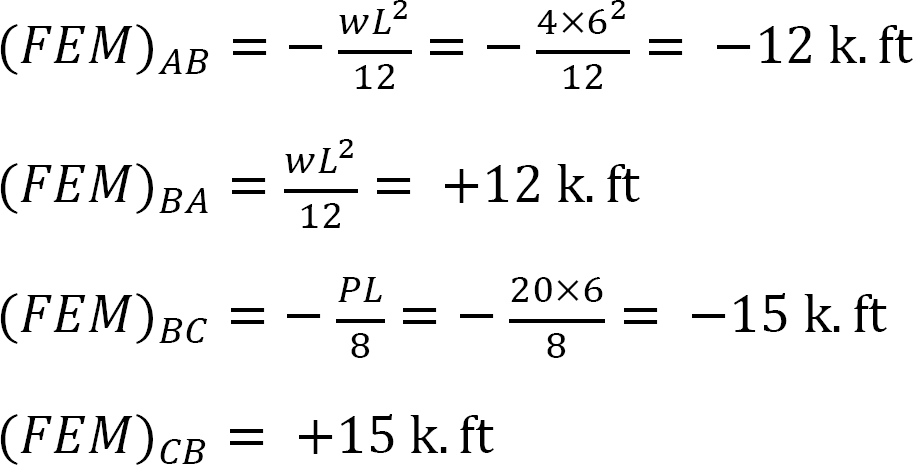
剛さの要因。
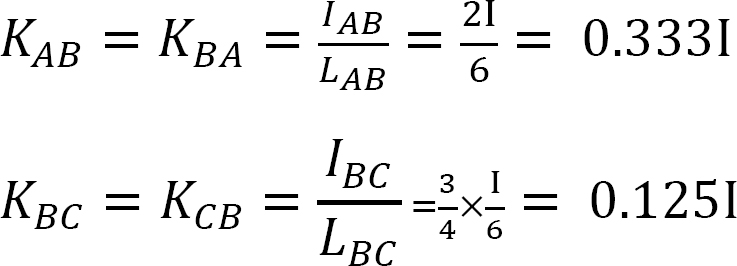
分配係数。
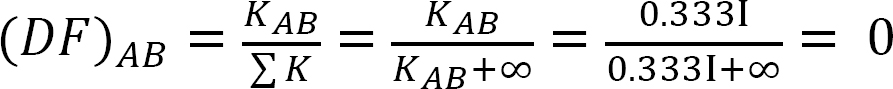

側面動揺のないフレームの分析。
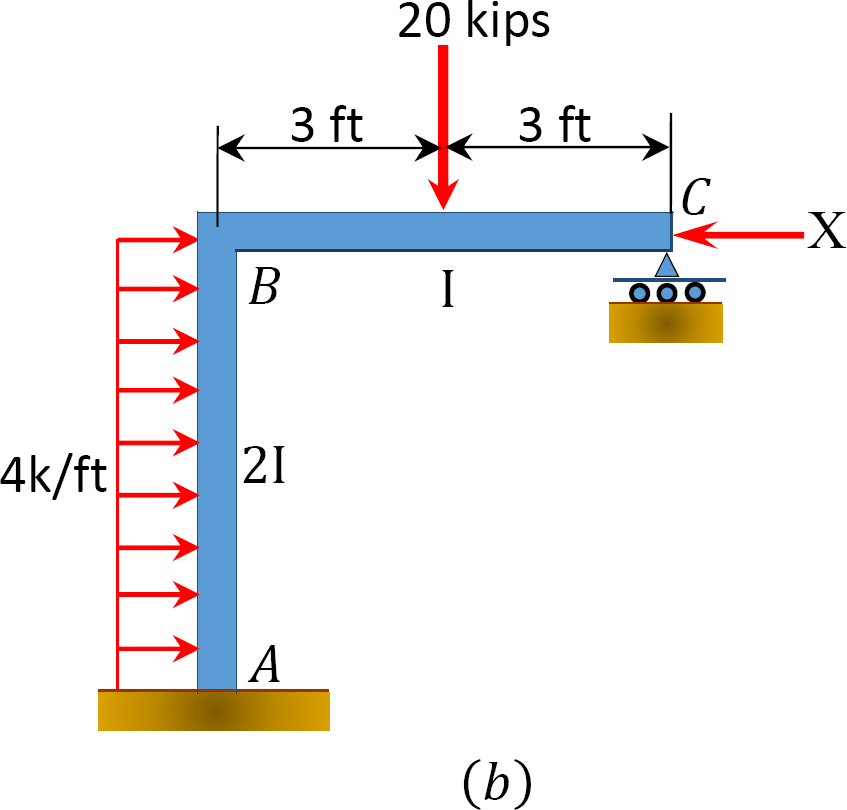
表12.6. 配分のテーブル(動揺フレーム無し)。
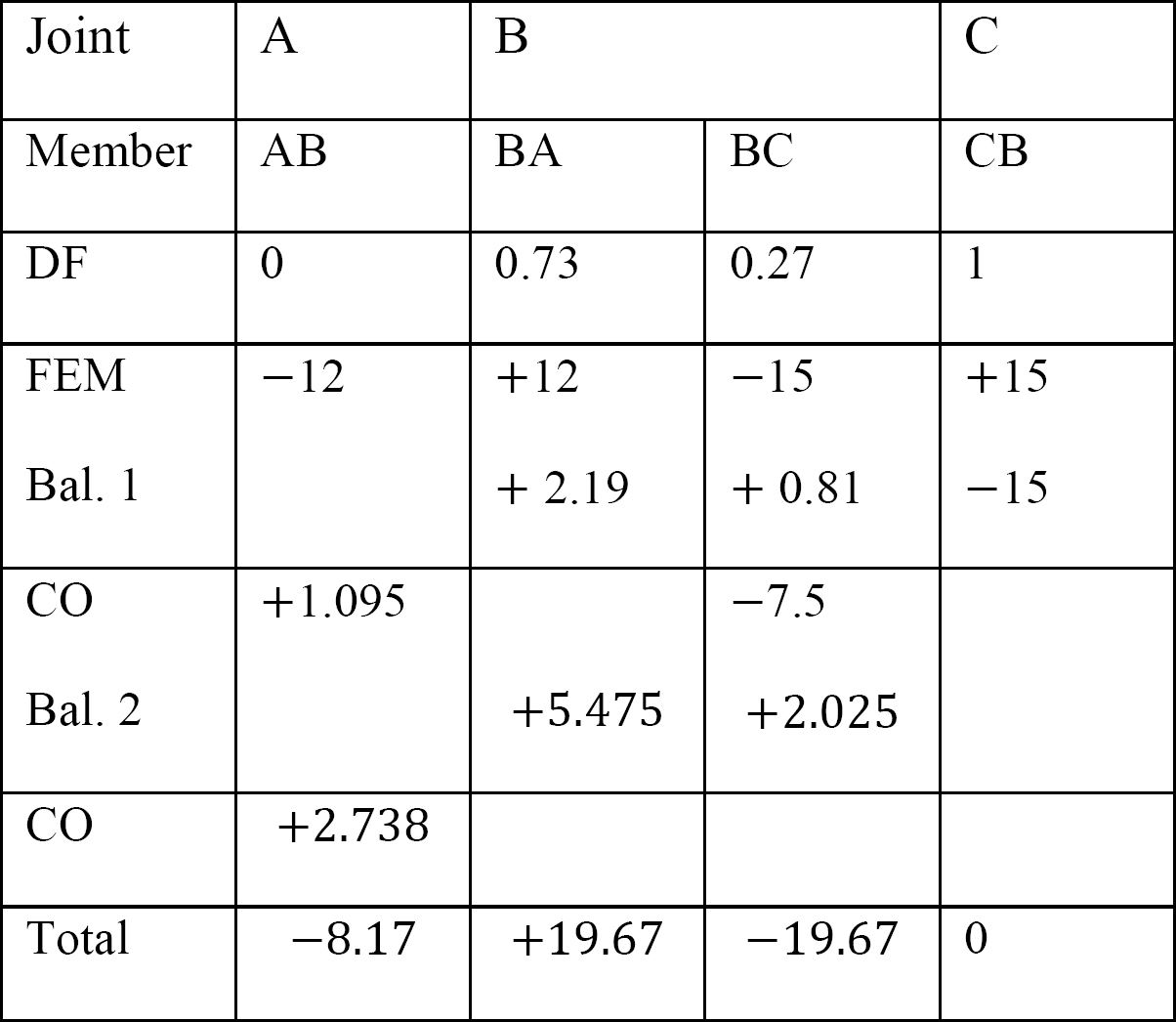
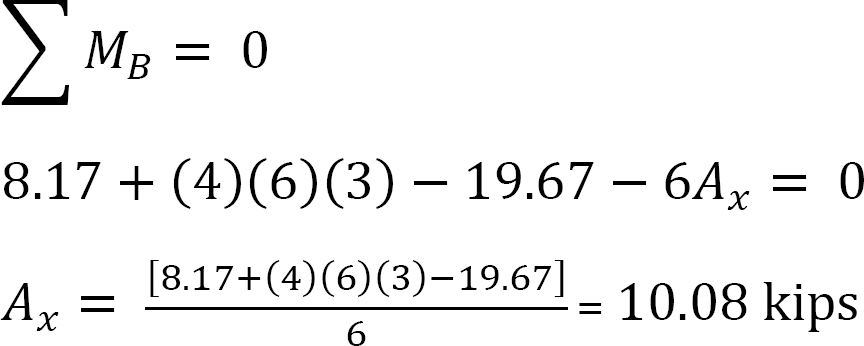
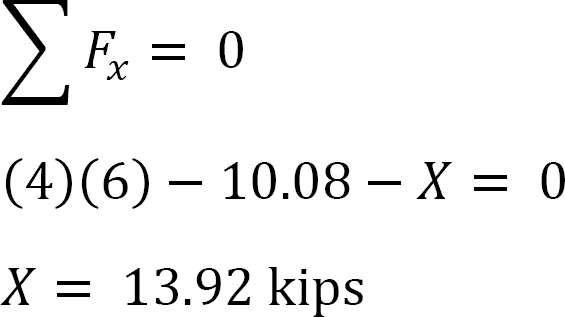
側面動揺のフレームの分析。
MAB=+20k.ftと仮定します。
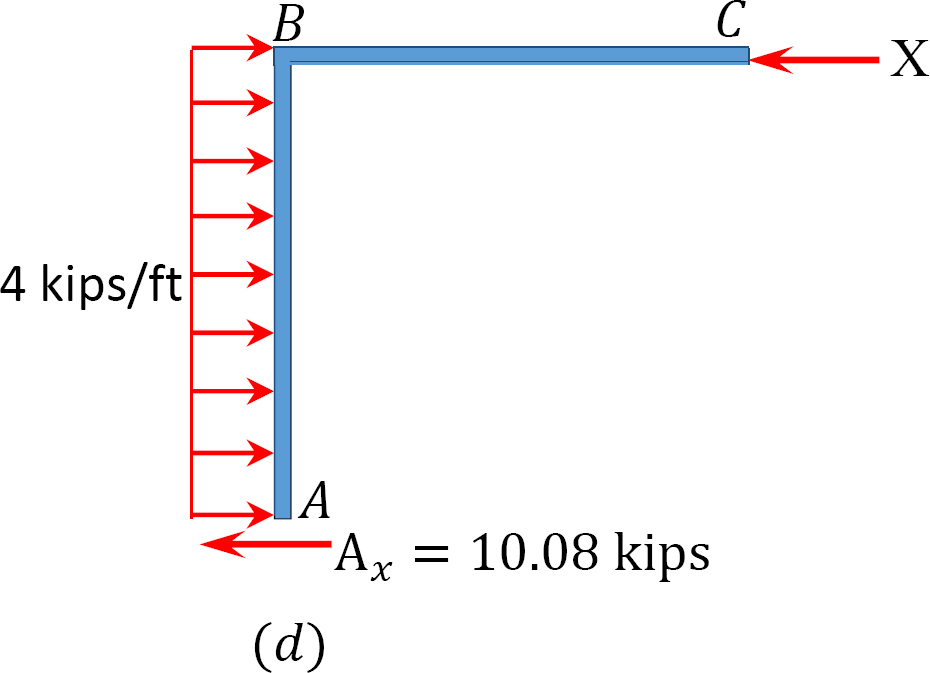
表12.7. 配分のテーブル(動揺フレーム)。
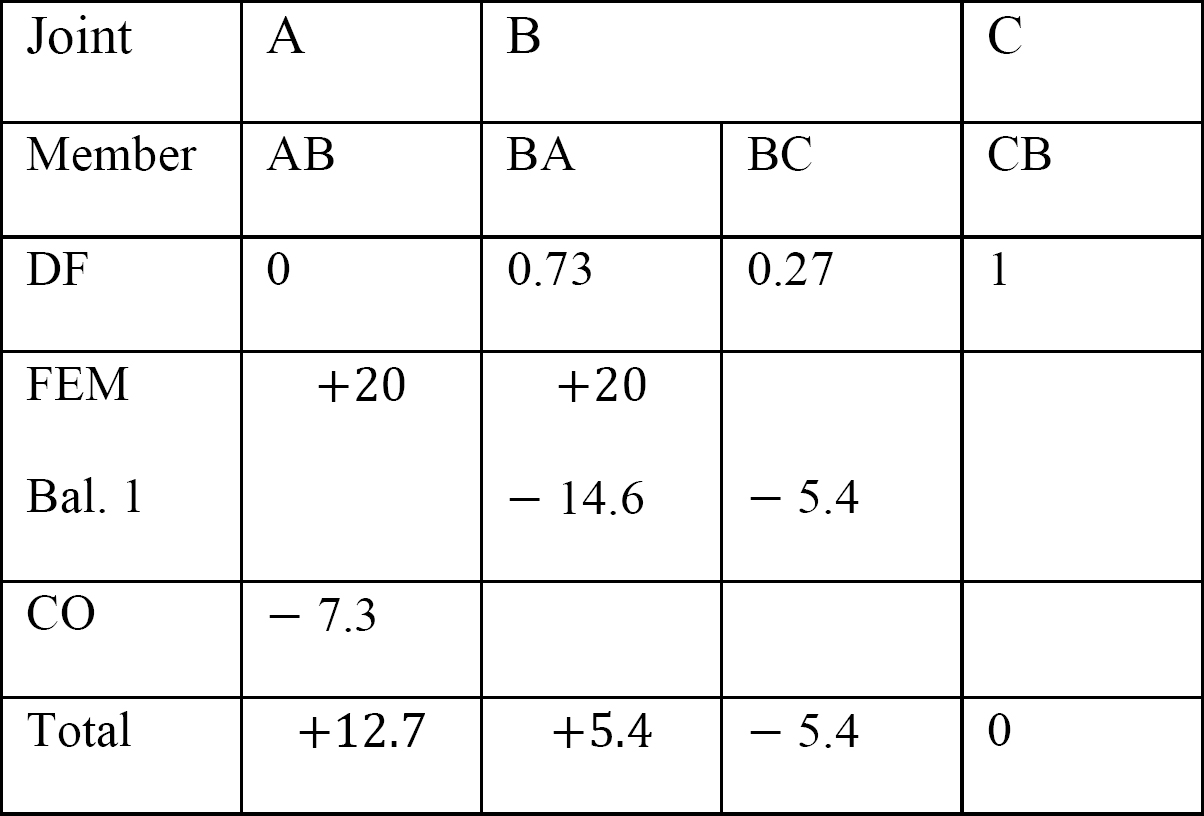
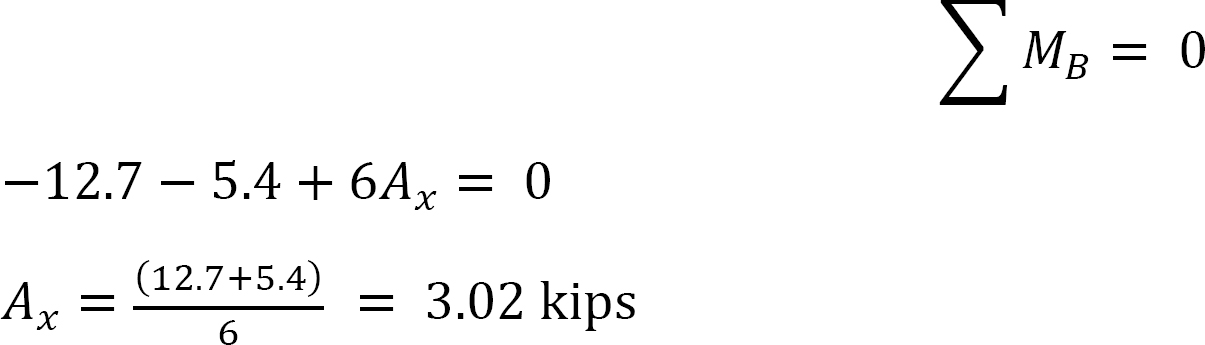
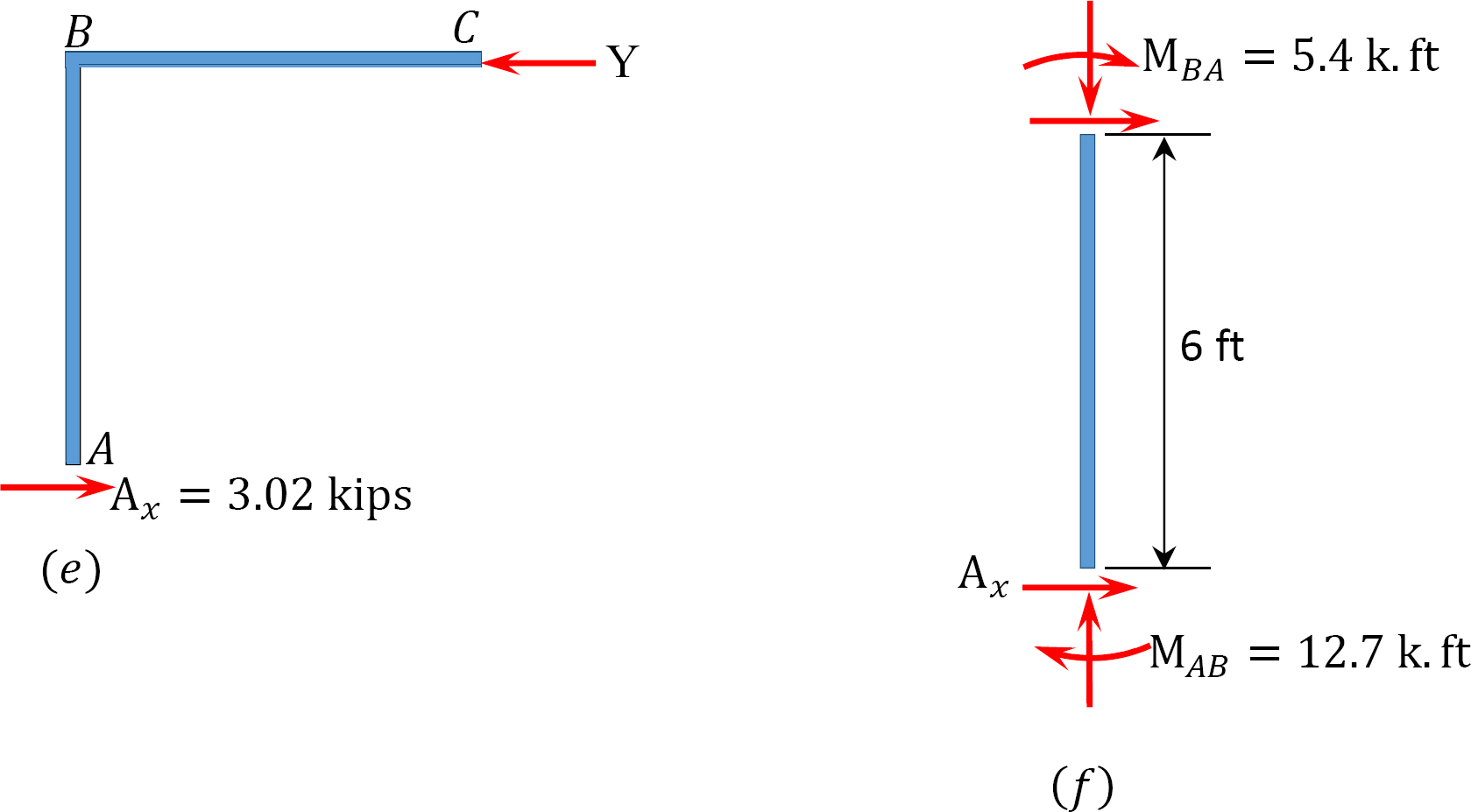
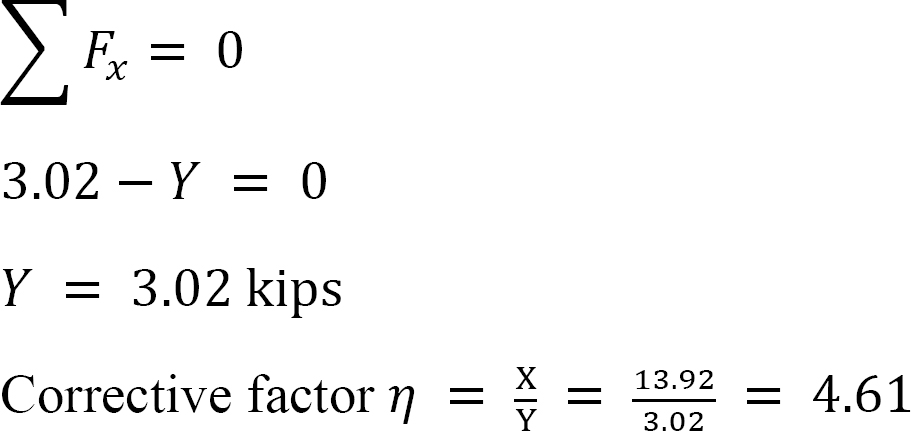
最後の終わりの瞬間。
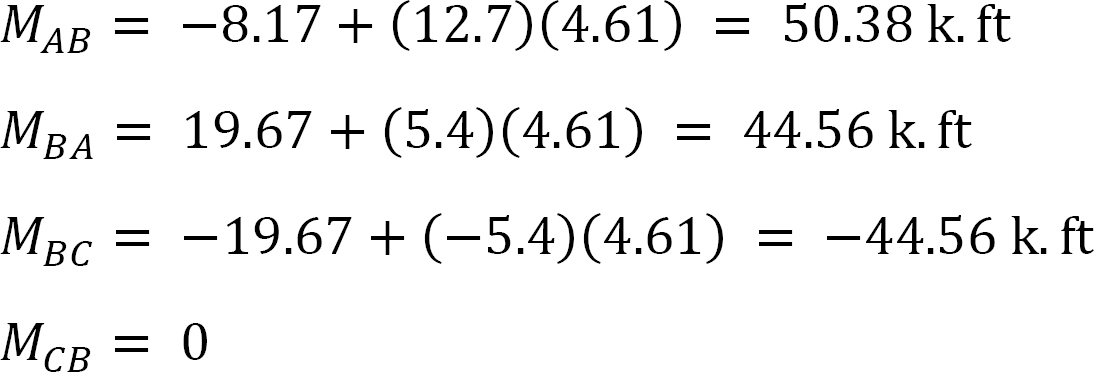
例12.7
図12.12aに示すように、揺れフレームがロードされます。モーメント分布法を使用して、フレームのメンバーの終了モーメントを決定します。
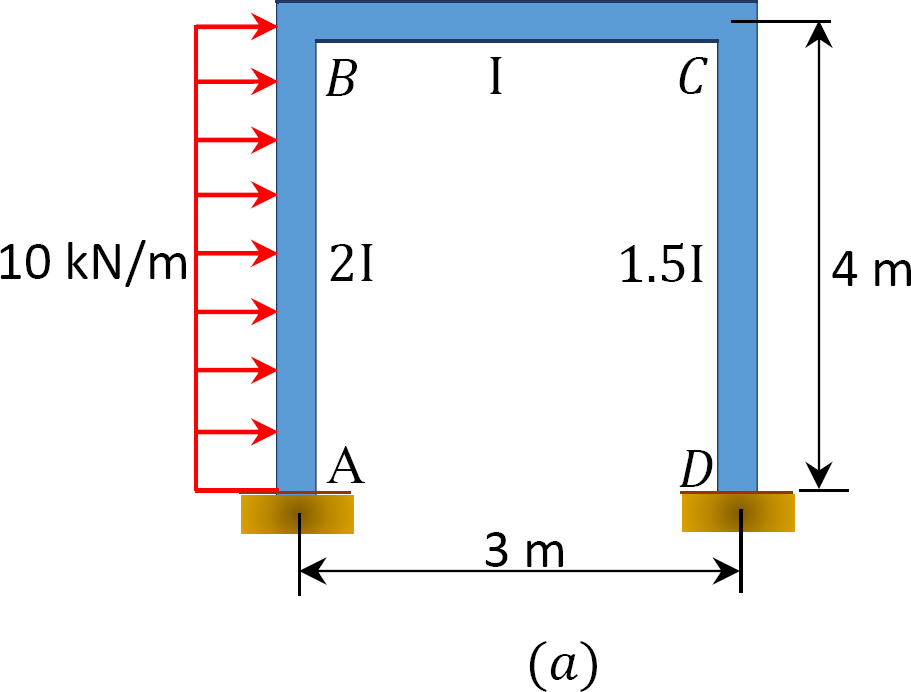
図1.1.1. 12.12. 荷を積まれた動揺フレーム。
ソリューション
終わりの瞬間を修正しました。
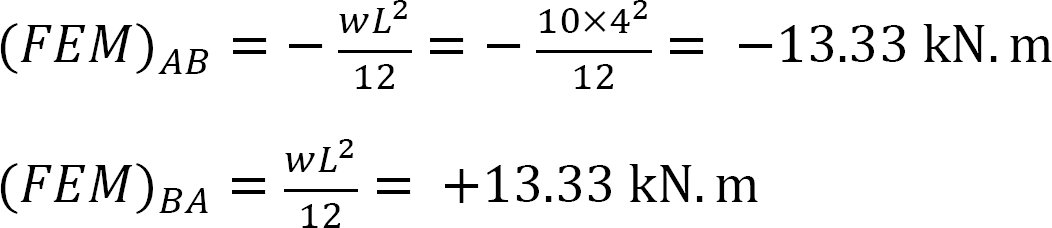
剛さの要因。
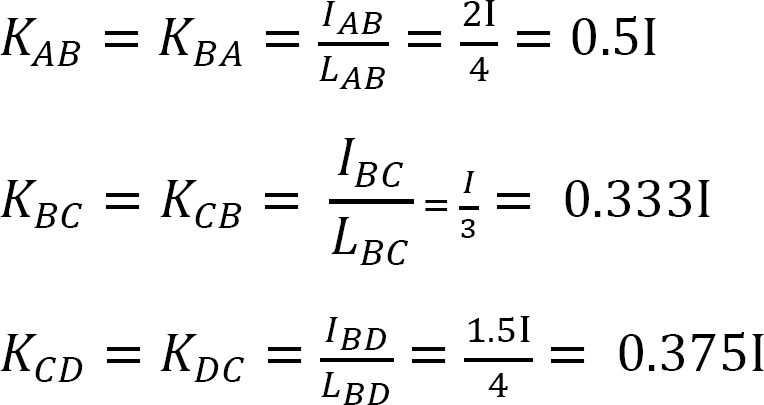
分配係数。

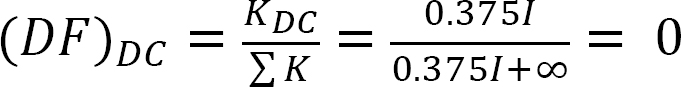
側面動揺のないフレームの分析。
表12.8. 配分のテーブル(動揺フレーム無し)。
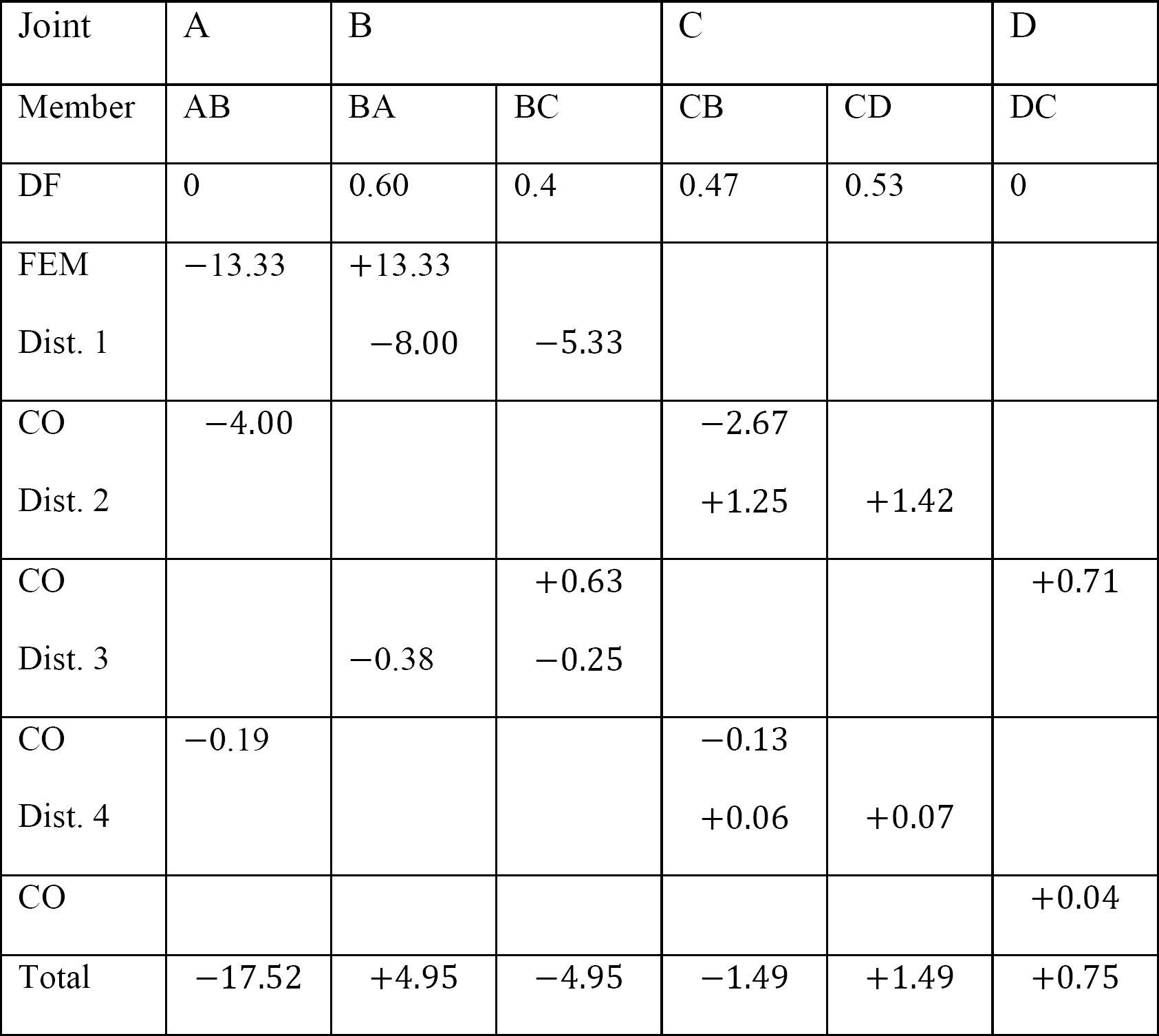
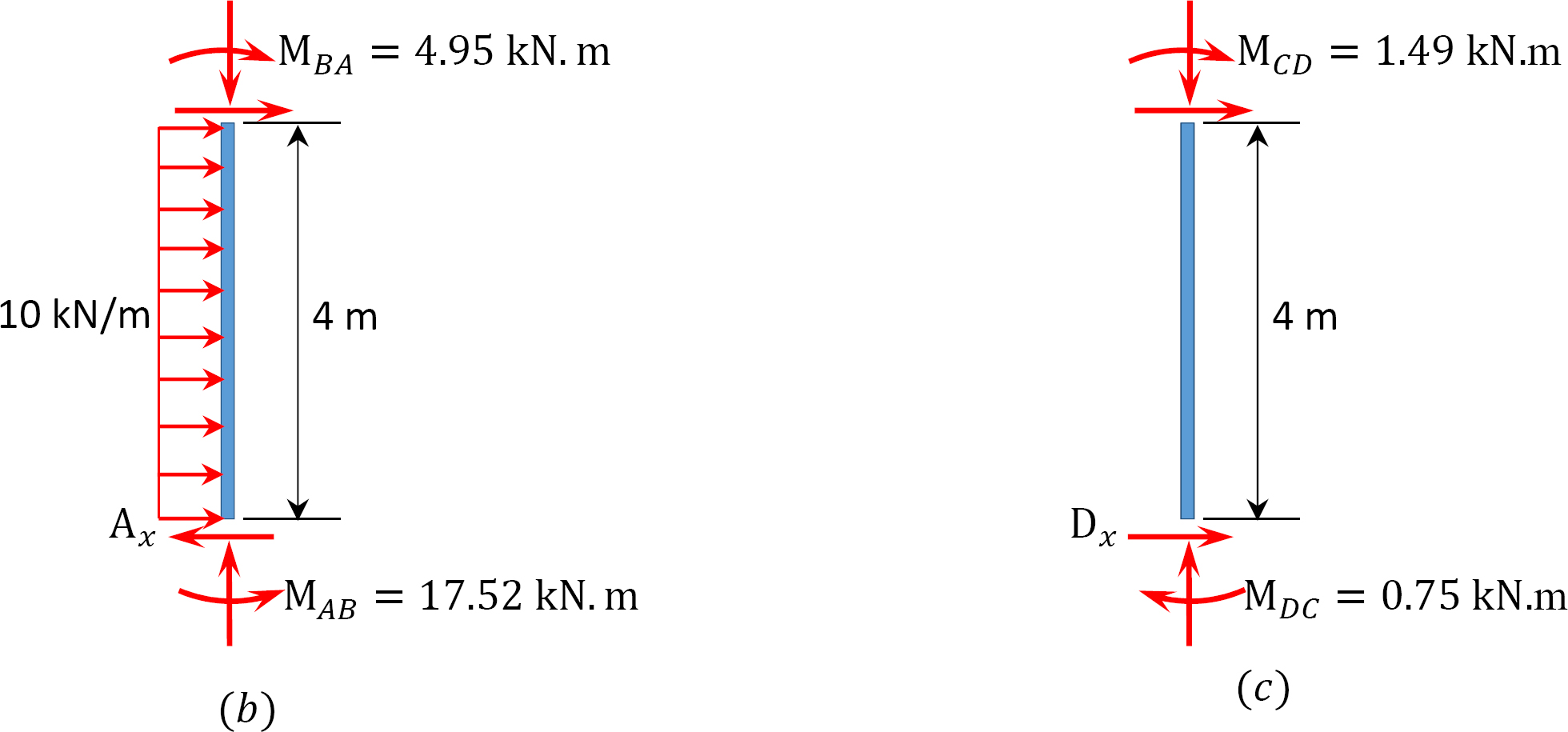
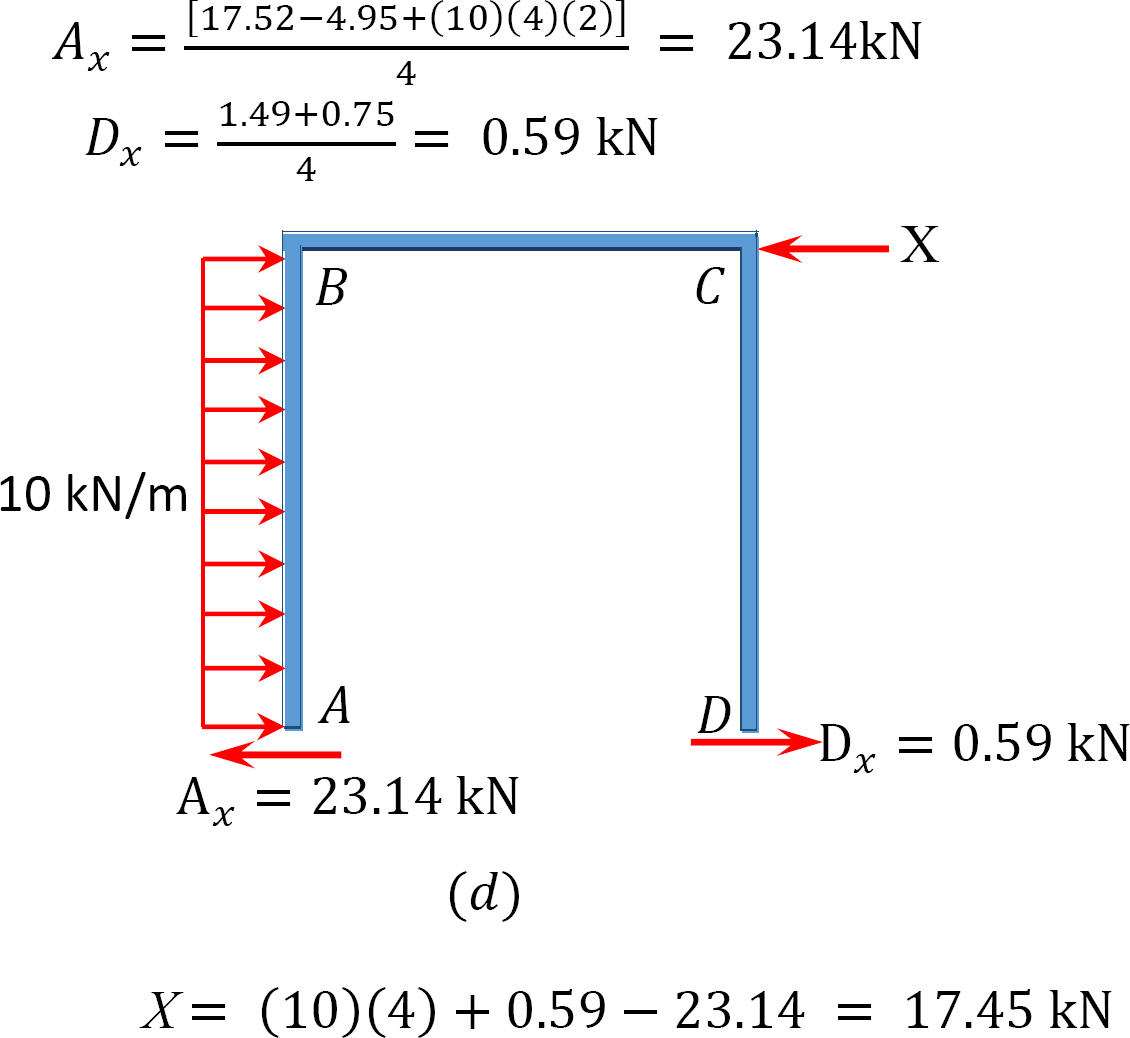
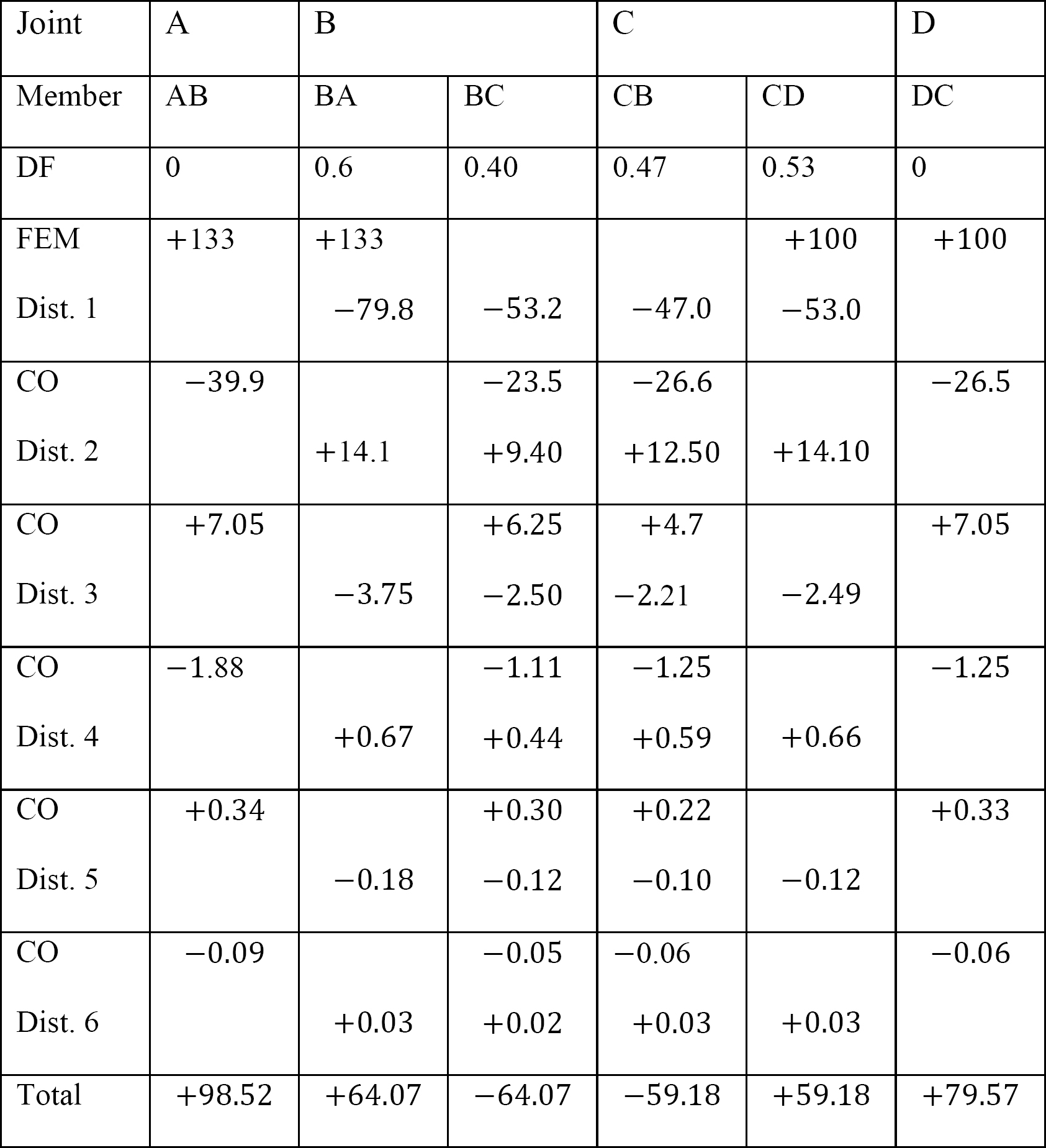
表12.9. 配分のテーブル(動揺フレーム)。
側面動揺のフレームの分析。
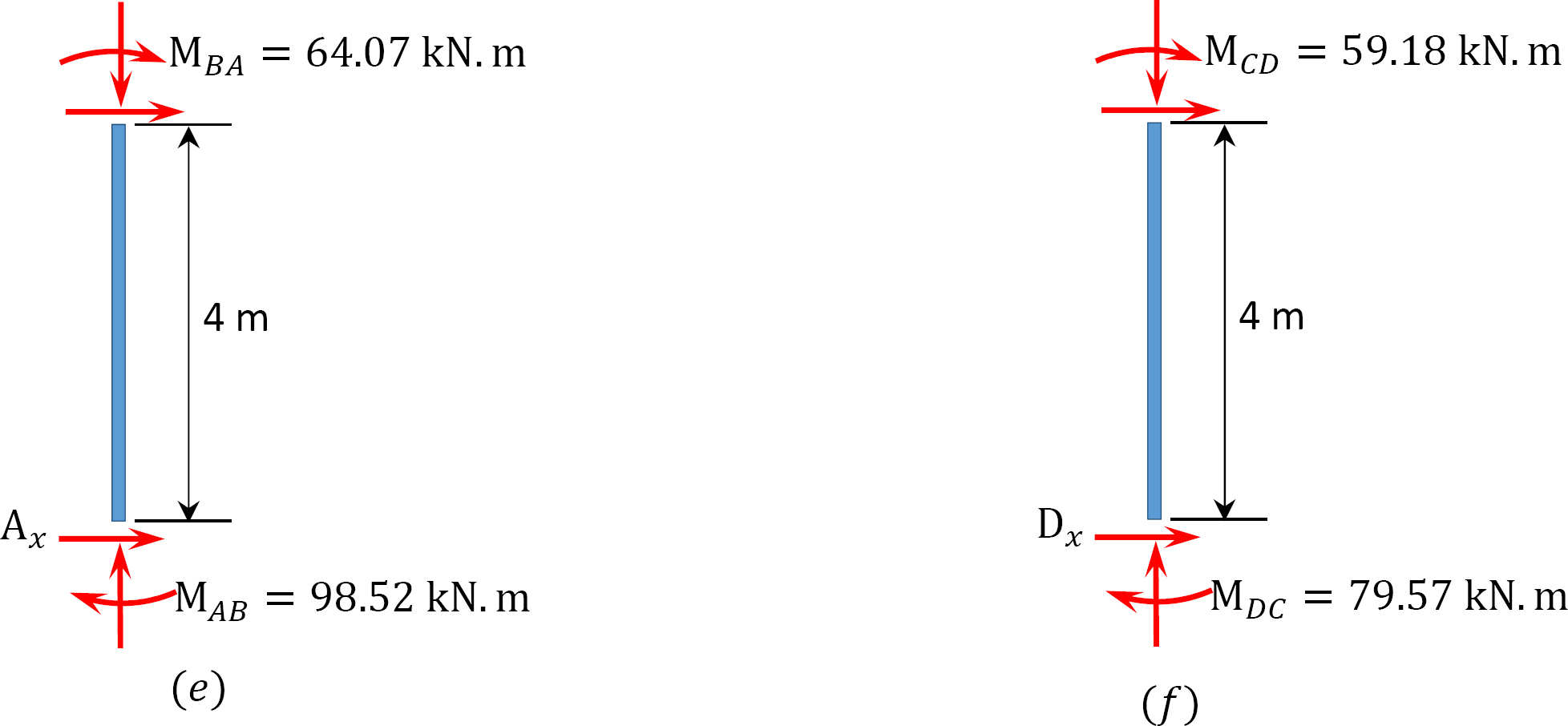

最後の終わりの瞬間。
= -17.52 + (98.52)(0.23) = 5.14 kN. m
= 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC= -4.95 + (-64.07)(0.23) = -19.69 kN. M
MCB= -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD= 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC= 0.75 + (79.57)(0.23) = 19.05 kN. m
章の概要
不確定構造のモーメント分布解析方法:モーメント分布解析方法は、近似解析方法です。 その精度の程度は、反復回数に依存します。 この方法では、構造内のすべての関節が一時的にロックまたはクランプされ、したがって回転の可能性が防止されると仮定される。 部材に荷重を加え,固定性により部材端部に発生するモーメントを決定した。 構造の接合箇所はそれから引き続いて鍵を開けられ、各接合箇所の不均衡な時はその接合箇所で会うメンバーに配られる。 メンバーの遠端でのキャリーオーバーモーメントが決定され、バランスのプロセスは、精度の所望のレベルまで継続されます。 メンバーの終了モーメントは、固定終了モーメント、分散モーメント、および繰越モーメントを合計することによって決定されます。 メンバーの終わりの瞬間が決定されると、構造は確定的になります。
練習問題
12.1モーメント分布法を使用して、図P12.1から図P12.12に示す梁の部材の終了モーメントを計算し、曲げモーメント図とせん断力図を描画します。 EI=定数です。
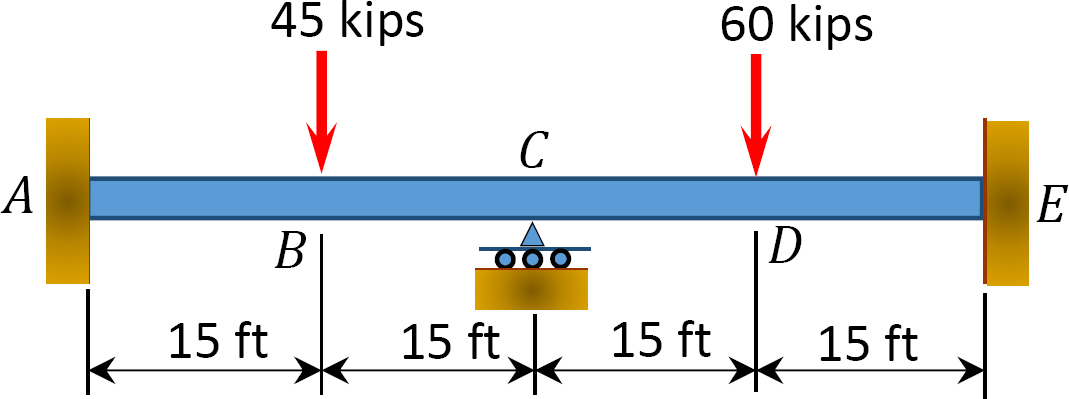
図1.1.1. P12.1. ビーム
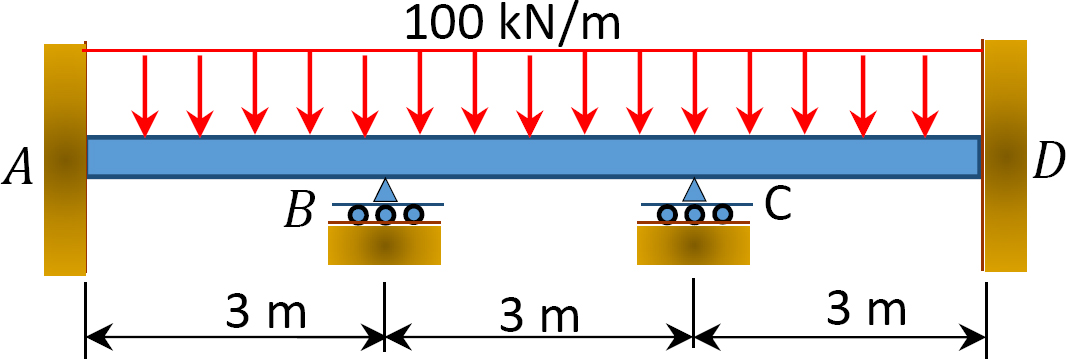
図1.1.1. P12.2. ビーム
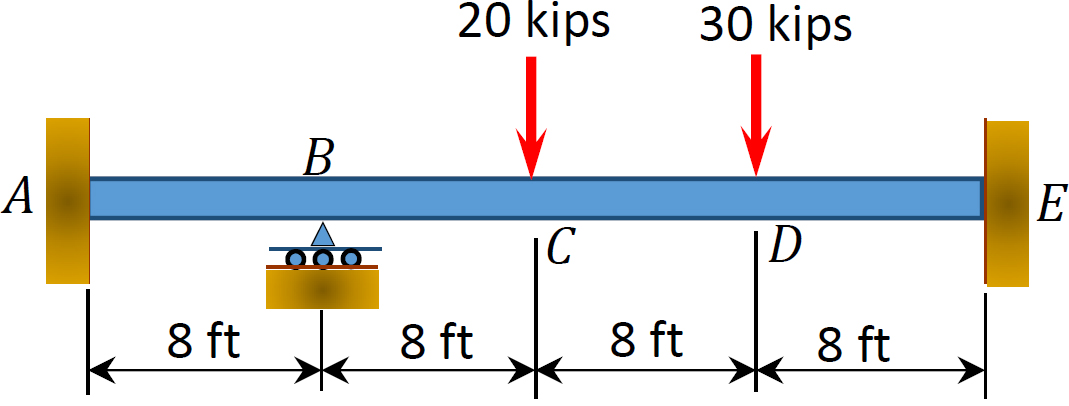
図1.1.1. P12.3. ビーム
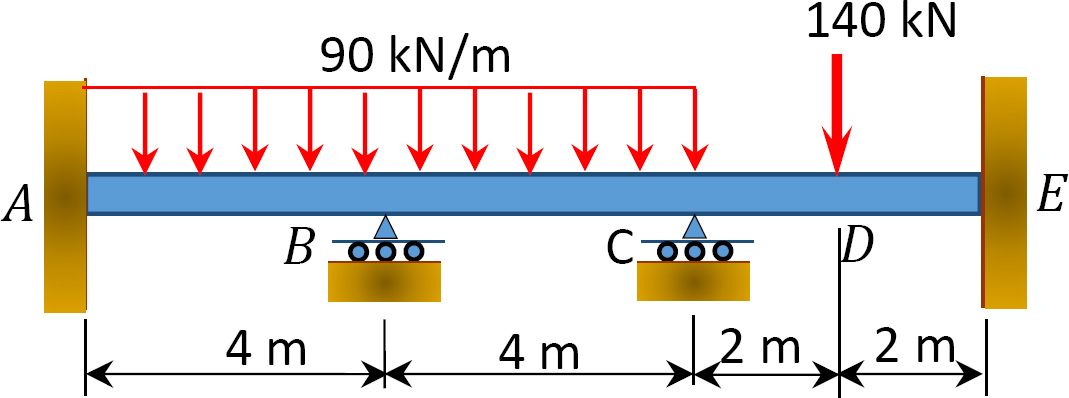
図1.1.1. P12.4. ビーム
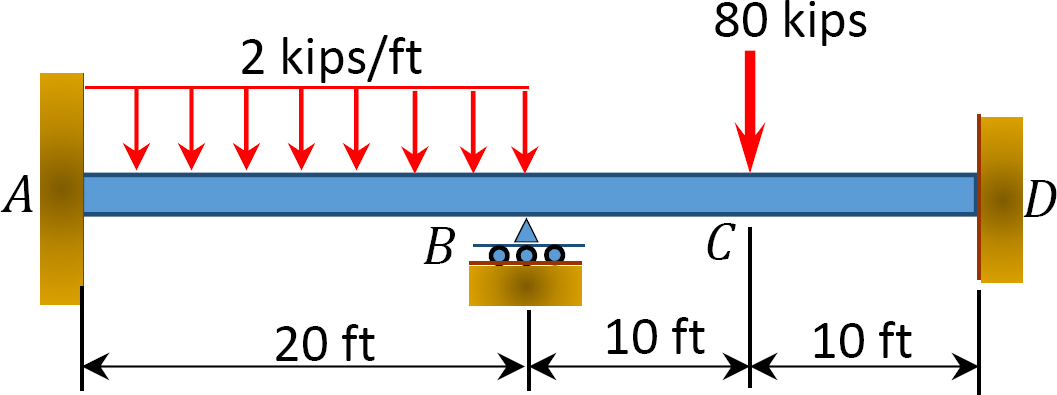
図1.1.1. P12.5 ビーム
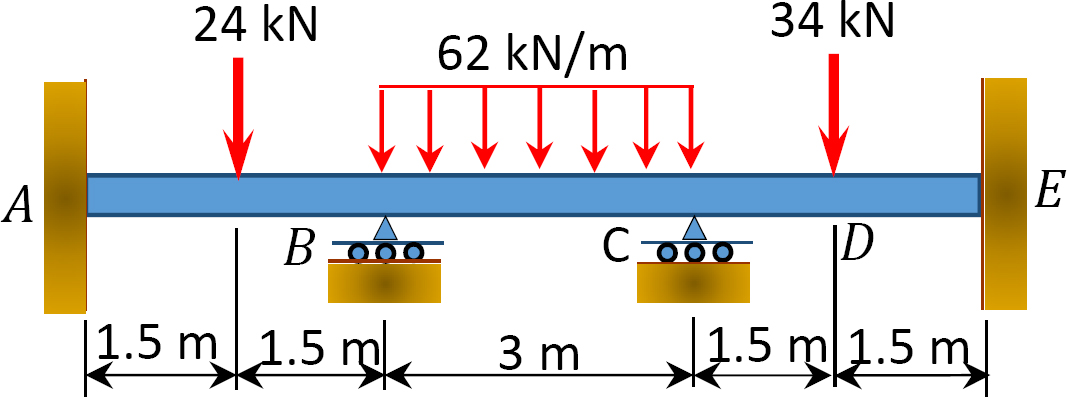
図1.1.1. P12.6. ビーム
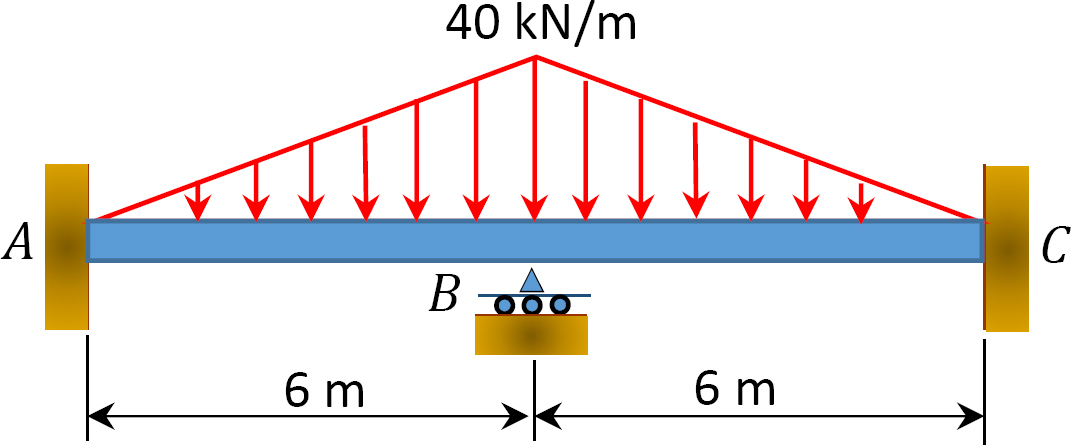
図1.1.1. P12.7 ビーム
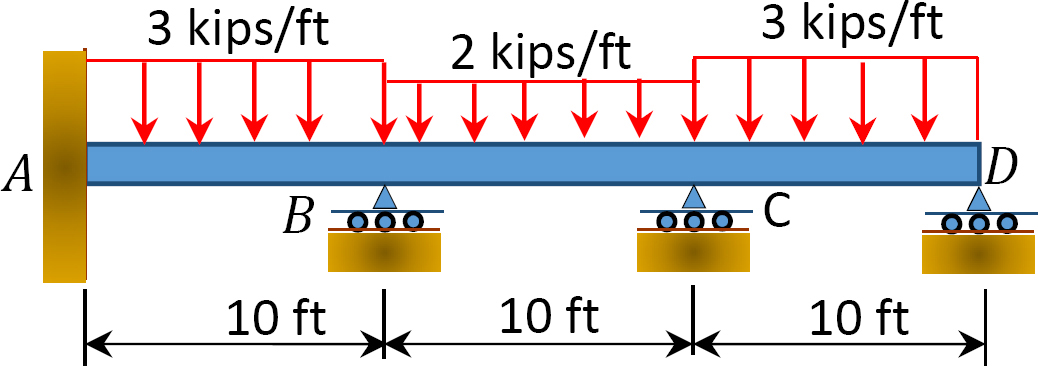
図1.1.1. P12.8 ビーム
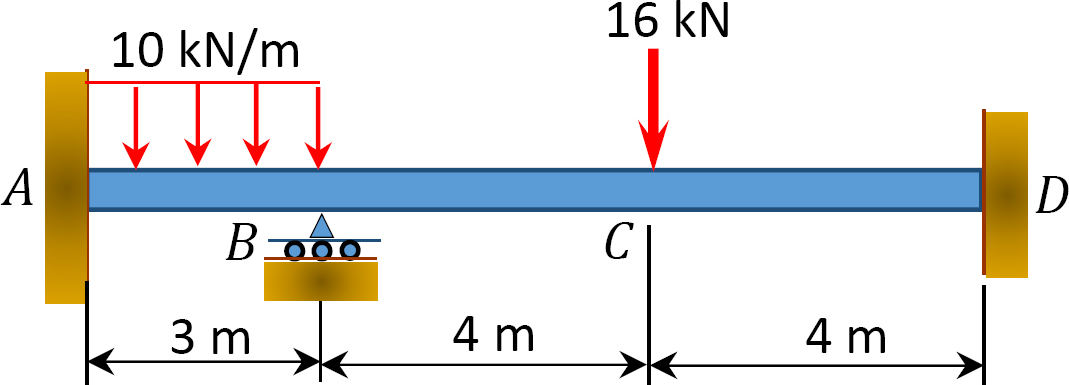
図1.1.1. P12.9 ビーム
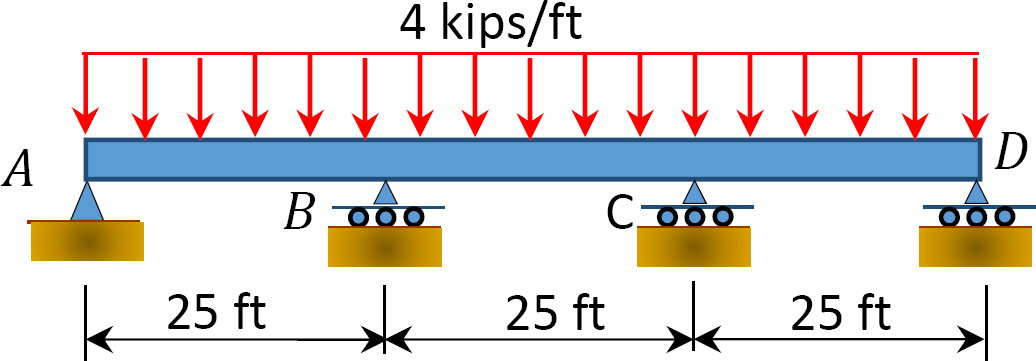
図1.1.1. P12.10 ビーム
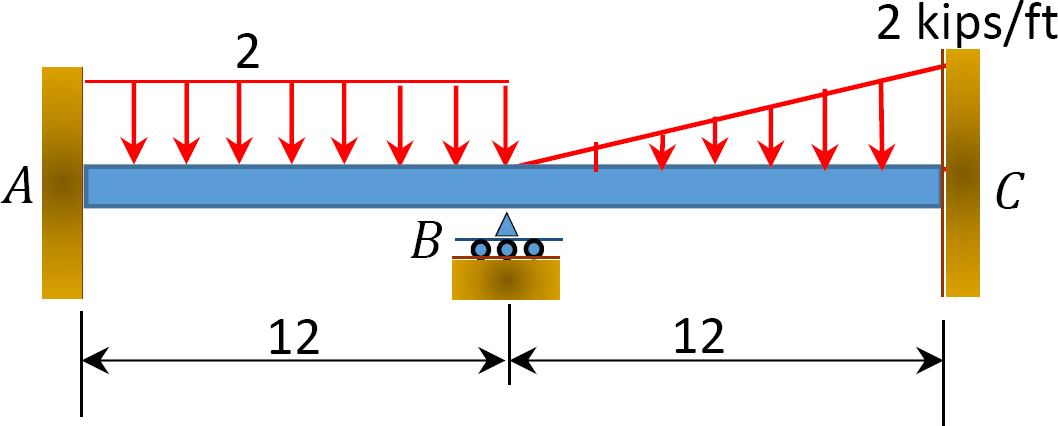
図1.1.1. P12.11. ビーム
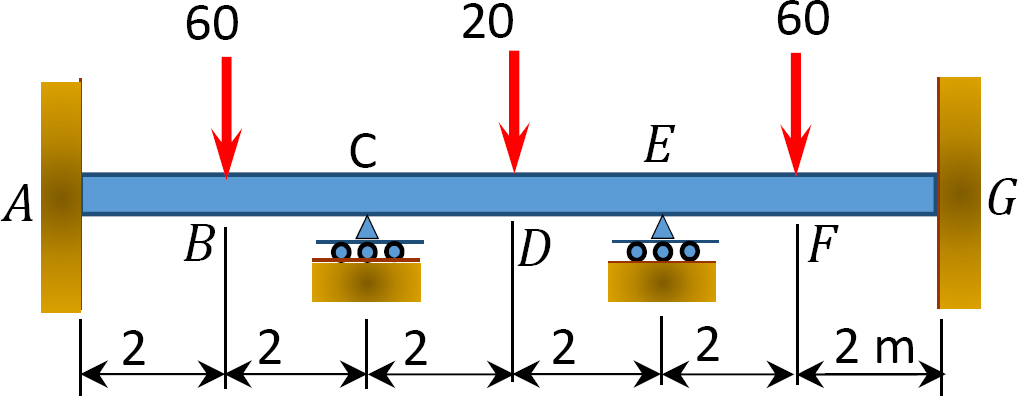
図1.1.1. P12.12 ビーム
12.2モーメント分布法を使用して、図P12.13から図12.20に示すフレームの部材の終了モーメントを計算し、曲げモーメントとせん断力の図を描画します。 EI=定数です。
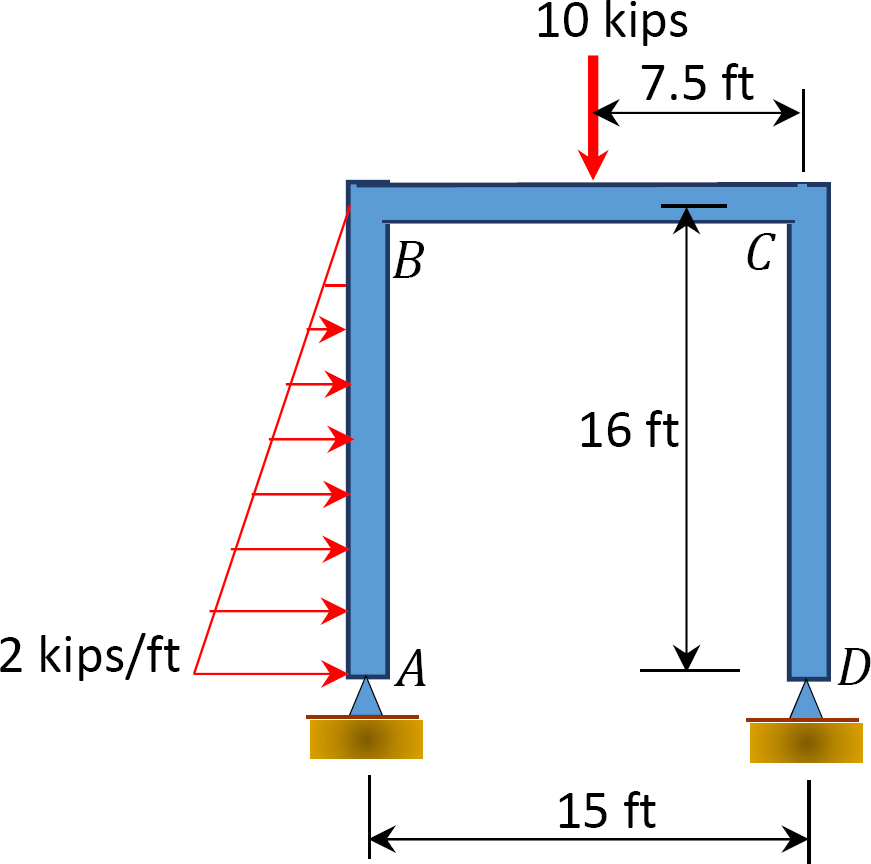
図1.1.1. P12.13. フレーム。
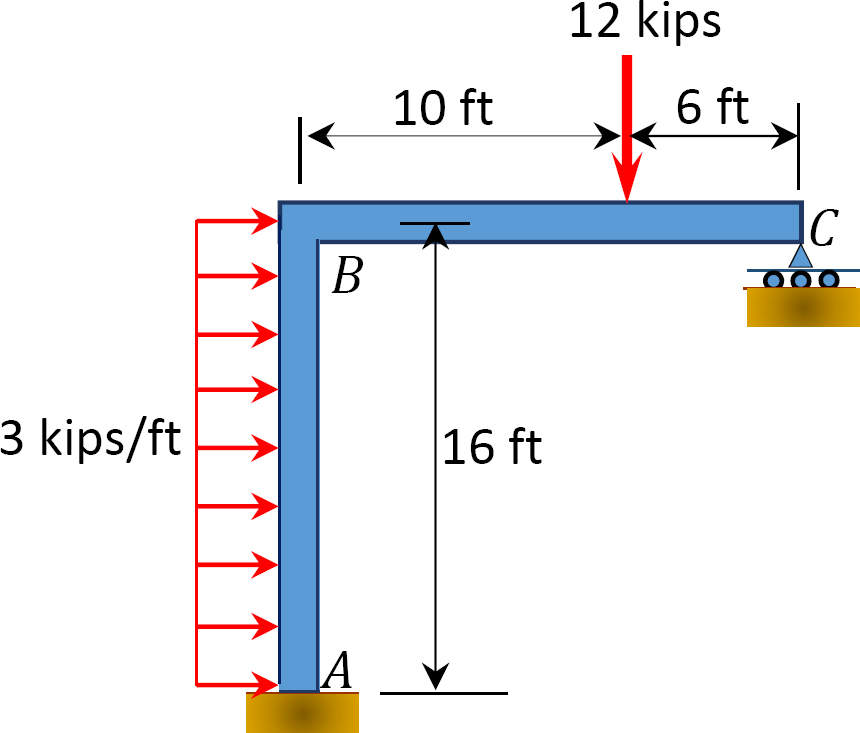
図1.1.1. P12.14 フレーム。
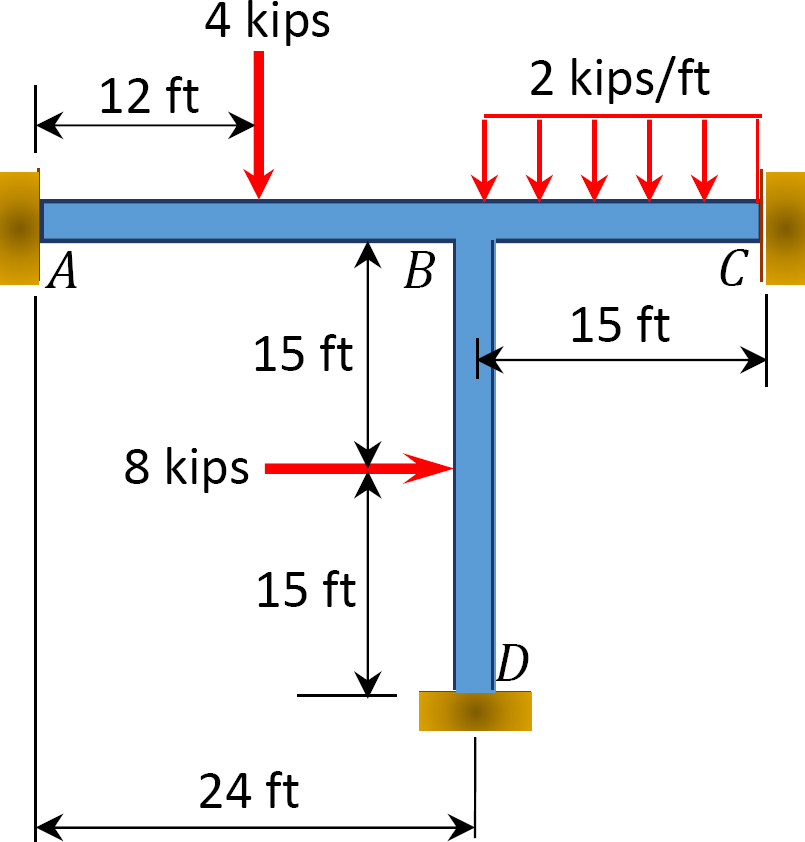
図1.1.1. P12.15 フレーム。
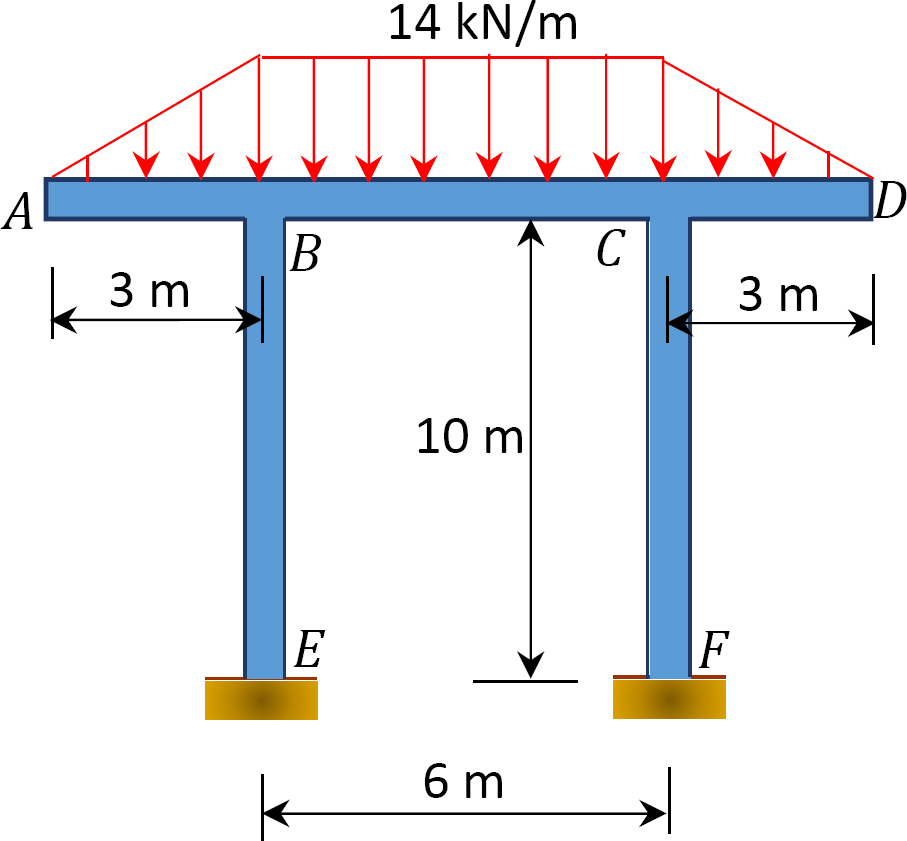
Fig. P12.16. Frame.
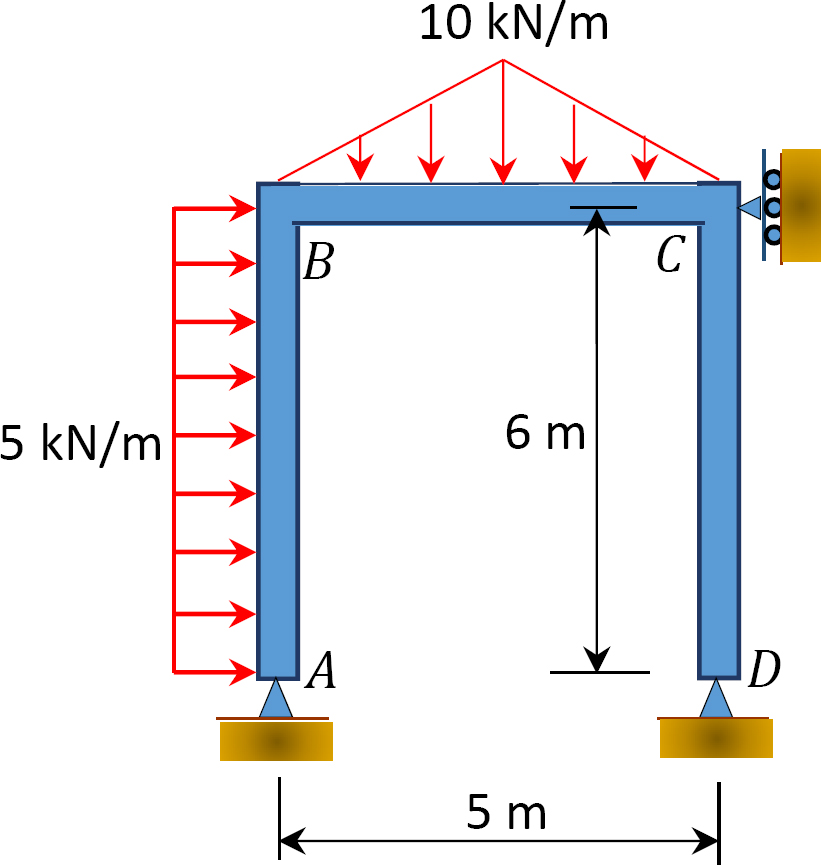
Fig. P12.17. Frame.
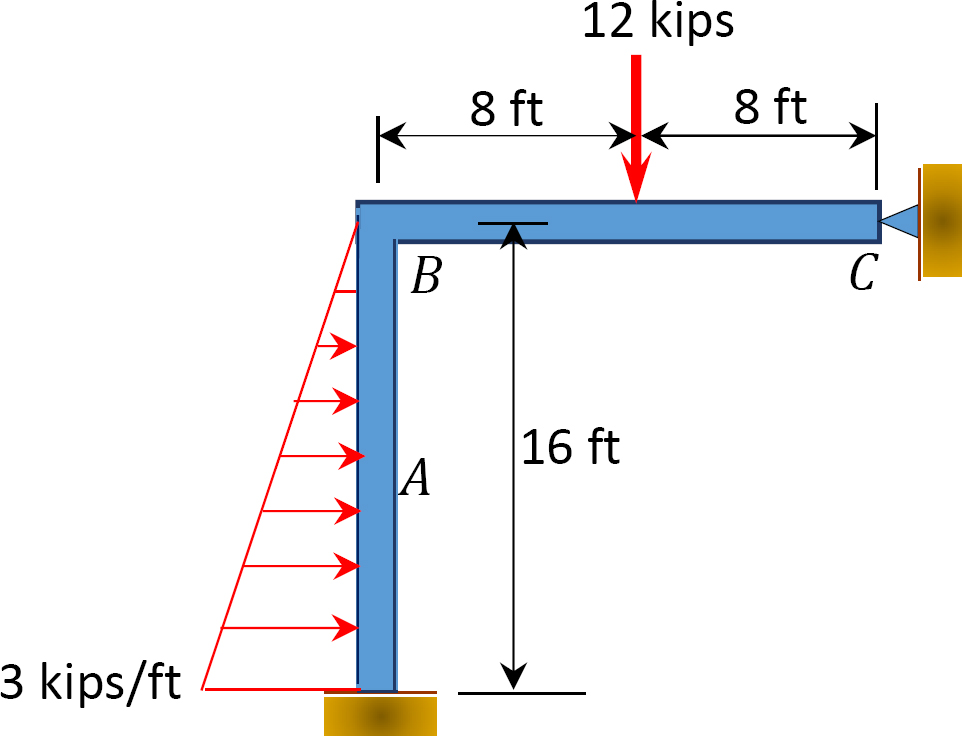
Fig. P12.18. Frame.
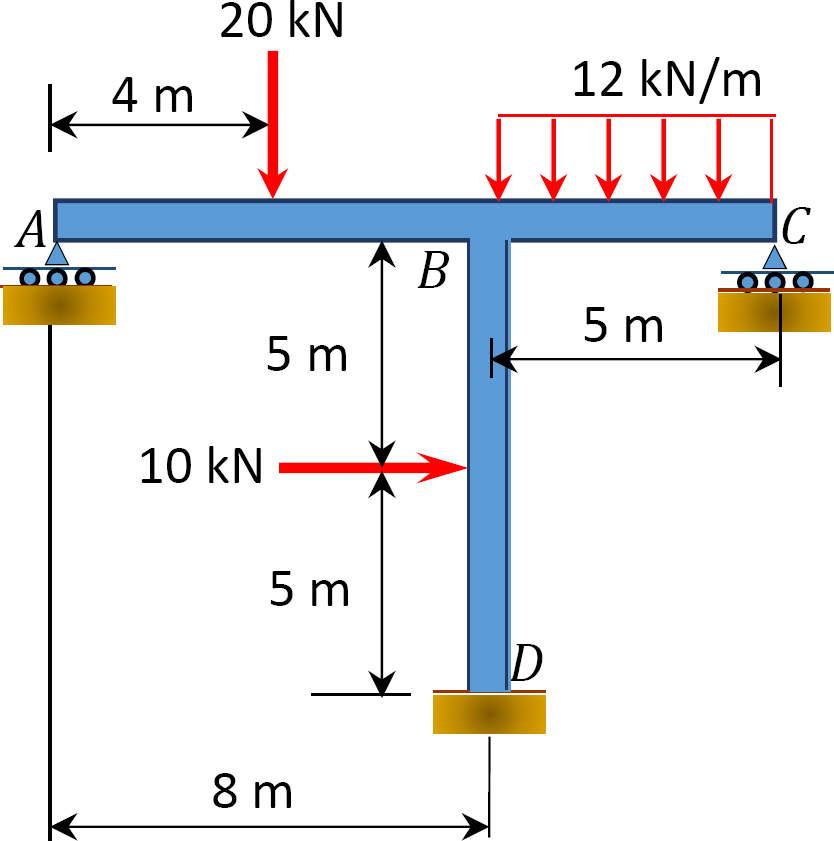
Fig. P12.19. Frame.
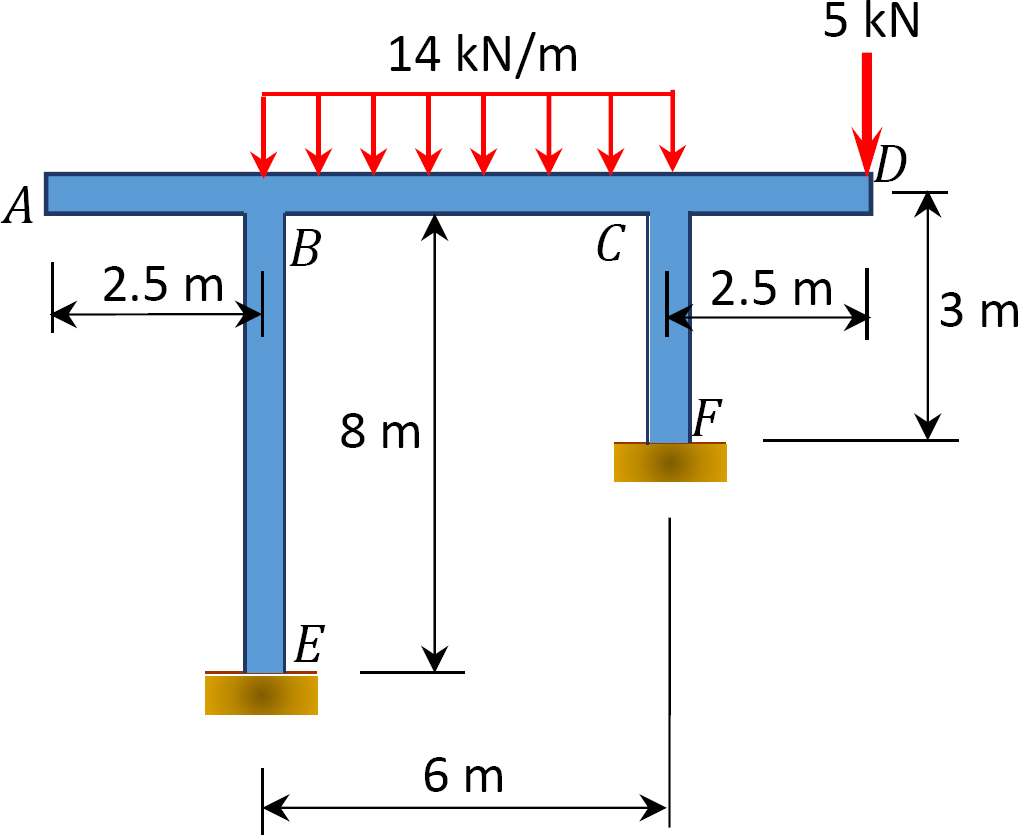
Fig. P12.20. Frame.