분류기의 위 다이어그램 체인에서 표시됩니다. ‘링크 목록’데이터 구조와 거의 유사합니다. 1,2.와이 2020 은 각 분류 자의 반응 변수입니다(0 또는 1 이 될 것입니다). 이전의 모든 분류 자(첫 번째 제외)의 응답은 다음 분류 자에 시드되며 이들은 원래 입력 기능과 함께 기능이됩니다(에프 1..fⁿ).
일반적으로 분류 자 케이 완전한 입력 기능 세트로 빌드됩니다..fⁿ,Y1Y2,..Yᴷ⁻1
이제 여기에 하나의 질문은”어떻게 이해의 분류 체인을까?”아래에 주어진 것과 같이 이것을 위한 다른 전략이 있습니다:
분류기 체인의 앙상블:분류의 앙상블 모델이 여기에 사용됩니다. 체인의 무작위 샘플링이 선택되고 앙상블이 위에 만들어집니다. 예측 출력은 앙상블 출력에 과반수 투표 방식을 적용하여 제공. 그것은 랜덤 포레스트 분류 자처럼 아주 동일합니다.
몬테카를로 분류기 체인(고객 센터): 최적의 분류기 시퀀스 생성을 위해 몬테카를로 방법을 적용합니다.
분류자에 대한 무작위 검색 또는 종속성 방법과 같은 다른 방법이 있지만 사용 중 매우 일반적이지는 않습니다.
각 분류자의 출력은 이진 관련성 체계와 같이 캡처되고 마지막에 클래스 레이블을 결정합니다.
레이블 검정력 설정 방식
이진 관련성&분류자 체인의 기본 개념은 다소 동일합니다. 라벨 파워 세트는 다른 방식으로 작동합니다. 학습 데이터 집합의 각 레이블 조합을 별도의 레이블로 간주합니다. 예를 들어,3 클래스 다중 레이블 문제의 경우 100,001,101,111 등은 별도의 레이블로 간주됩니다.
일반적으로 차원의 클래스 공간 엔,가능한 총 레이블 조합 중 2 개가 될 수 있습니다.
따라서 하위 문제로 분해되지는 않지만 전체 클래스 레이블의 조합을 직접 예측합니다.
장점&각 구성표의 단점
이진 관련성은 구현하기 쉬운 간단한 구성표입니다. 그러나 레이블 상호 의존성을 고려하지 않으므로 종종 숨겨진 데이터 관계를 잘못 해석 할 수 있습니다.
분류자 체인은 클래스 레이블 관계를 완벽하게 처리합니다. 특히 일부 클래스 레이블이 다른 클래스 레이블의 하위 레이블이고 한 클래스 레이블의 발생이 다른 레이블(클래스 레이블의 부모-자식 관계)에 크게 의존하는 경우 특히 그렇습니다. 자식 레이블이 발생할 수 있습니다. 그러나이 계획은 본질적으로 복잡하고 클래스 공간이 큰 경우 높은 차원 문제로 고통 받고 있습니다.
레이블 전원 집합은 클래스 레이블의 다른 조합이 적은 경우에 적합합니다. 이진 관련성&분류 자 체인에 비해 매우 간단한 체계입니다.
모든 경우에 특정 계획에 대한 결정을 내리기 전에 데이터 세트 이해가 필요합니다.
정확도 메트릭
다중 클래스 또는 이진 단일 레이블 분류 문제에서 절대 정확도는 비율에 의해 제공됩니다(올바르게 분류 된 데이터 인스턴스 없음/총 데이터 인스턴스 없음).
예제 데이터 집합을 사용하여 다중 레이블 사례에 대한 시나리오를 살펴보겠습니다. 신분증 241465 의 질문이’모델링’,’중심 한계 정리’,’자유도’라는 레이블로 분류되면 우리는 무엇을 말할 수 있습니까? 데이터 세트의 실제 클래스 레이블은’통계적 유의성’,’모델링’,’중앙 한계 정리’,’자유도’및’가짜 상관 관계’였습니다. 어느 쪽도 아니 그것은 완전히 잘못된 예측도 완전히 옳다. 우리가 전통적인 정확한 대 총 비율 기반 정확도 메트릭을 위해 간다면,확실히 우리는 분류자를 판단 할 수 없을 것입니다. 우리는 다중 레이블 분류 자의 부분적인 정확성을 판단 할 무언가가 필요합니다.
해밍 손실 메트릭
해밍 손실은 올바르게 분류 된 데이터 인스턴스를 계산하지 않고 예측 중에 클래스 레이블의 비트 문자열에서 생성 된 손실을 계산합니다. 데이터 인스턴스에 대한 클래스 레이블의 원래 이진 문자열과 예측 클래스 레이블 간의 연산을 수행하고 데이터 집합 전체의 평균을 계산합니다. 그 표현은 다음과 같습니다
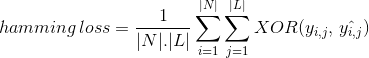
여기서
|엔|=데이터 인스턴스의 수
|엘|=클래스 공간의 카디널리티
와이,클래스 레이블의 실제 비트 제이 데이터 인스턴스에서 나는
^와이,클래스 레이블의 예측 비트 제이 데이터 인스턴스에서 나는
^와이,클래스 레이블의 예측 비트 제이 데이터 인스턴스에서 나는
^
‘해밍 손실’값 범위 0 에 1. 손실 메트릭이기 때문에,그것의 해석은 정상적인 정확도 비율과는 다른 성격에서 반전입니다. 해밍 손실의 낮은 값은 더 나은 분류자를 나타냅니다.
하위 집합 정확도
레이블 예측의 정확한 조합을 측정하는 것이 중요한 절대 정확도 비율로 갈 수있는 경우가 있습니다. ‘라벨 파워 세트’의 경우와 관련이있을 수 있습니다. 다중 레이블 시나리오에서는 하위 집합 정확도라고 합니다.
이 두 가지 외에도 각 이진 분류기의 정확도는 정확도 비율,에프 1 점수,정밀도,리콜 등과 같은 다른 전통적인 메트릭으로 판단 할 수 있습니다.
이것은 다중 라벨 분류에 대한 이론적 모델링에 관한 것입니다. 우리는 다음 기사에서 실제 데이터를 사용하여 사례 연구를 볼 수 있습니다. 데이터 탐색 코드는 깃허브에서 사용할 수 있습니다.
최근 밀리리터에 관한 책을 저술했습니다(https://twitter.com/bpbonline/status/1256146448346988546)