fra diagramkjeden over klassifikatorer er vist. Det ligner nesten ‘LinkedList’ datastruktur. Y1, Y2..Yᴺ er svarvariablene til hver klassifikator (det vil være 0 eller 1). Svar fra alle tidligere klassifikatorer (unntatt 1st) blir sådd inn i neste klassifikator, og disse blir funksjoner sammen med originale inngangsfunksjoner(f1..fⁿ).
generelt vil klassifikator K bli bygget med komplett inngangsfunksjonssett : f1, f2,..fⁿ,Y1,Y2,..Yᴷ⁻1
Nå, her kommer spørsmålet, «Hvordan rekkefølgen på classifier kjeden er besluttet ?»Det er forskjellige strategier for dette som gitt nedenfor :
Ensemble Of Classifier chains (ECC): Ensemble modell for klassifisering brukes over her. Tilfeldig utvalg av kjeder er valgt og et ensemble er bygget på toppen av dette. Forutsatt utgang kommer ved å bruke flertallsvalgordningen på ensembleutgangene. Det er ganske samme Som RandomForest classifier.
Monte-Carlo Klassifiseringskjeder (MCC): Det gjelder Monte-Carlo-metoden for optimal klassifiseringssekvensgenerering.
Det finnes andre metoder som Tilfeldige Søk eller avhengighetsmetoder for klassifiserere, men ikke veldig vanlig i bruk.
utdataene fra hver klassifikator vil bli fanget som Binary Relevance Scheme og vil bestemme klasseetiketter på slutten.
Label Power-set Scheme
Det grunnleggende konseptet For Binær Relevans & Klassifiseringskjeden er mer eller mindre det samme. Label power-set fungerer på en annen måte. Den vurderer hver kombinasjon av etiketter i treningsdatasettet som en egen etikett. For eksempel, for en 3-klasse multi-label problem, 100, 001, 101, 111, etc vil bli betraktet som separate etiketter.
generelt, et klasseromsområde med dimensjon N, kan det være 2ᴺ nei av totalt mulige etikettkombinasjoner.
så det dekomponerer ikke i noen underproblemer, men det forutser direkte kombinasjonen av klassetiketter som helhet.
Fordeler& Ulemper ved hver ordning
Binær Relevans er en enkel ordning, enkel å implementere. Men det anser ikke etiketten inter-avhengighet og dermed kan ofte feiltolke skjulte data relasjoner.
klassifiseringskjeden håndterer klasseetikettrelasjoner perfekt. Spesielt for tilfeller der noen klasseetiketter er underetiketter av andre, og forekomsten av en klasseetikett er sterkt avhengig av andre etiketter (foreldre-barn-relasjoner i klasseetiketter. Barnetikett kan forekomme hvis foreldreetiketten er der). Men denne ordningen er kompleks i naturen og lider av høy dimensjonalitet problem hvis klassen plass er stor.
Label power-set fungerer bra for tilfeller der ingen av ulike kombinasjoner av klasseetiketter er mindre. Det er veldig enkelt i forhold Til Den Binære Relevansen & Klassifiseringskjeden.
i alle tilfellene kreves datasettforståelse før en beslutning tas for en bestemt ordning.
Nøyaktighetsmålinger
i klassifiseringsproblemer med flere klasser eller binære enkeltmerker, er absolutt nøyaktighet gitt av forholdet (ingen dataforekomster riktig klassifisert / totalt antall dataforekomster).
La oss se scenariet for multi-label-saken ved hjelp av vårt eksempeldatasett. Hvis spørsmål med id 241465 er klassifisert med etiketter: ‘modellering’,’ sentralgrenseteorem’,’ frihetsgrader ‘ så hva kan vi si? De faktiske klassemerkene i datasettet var ‘statistisk signifikans’, ‘modellering’, ‘sentralgrenseteorem’, ‘frihetsgrader’og’ falsk korrelasjon’. Verken det er helt feil prediksjon eller det er helt riktig. Hvis vi går for tradisjonell korrekt vs total ratio basert nøyaktighetsmåling, vil vi definitivt ikke kunne dømme klassifikatoren. Vi trenger noe for å bedømme den delvise korrektheten til en multi-label klassifikator.
Hamming Loss Metric
I Stedet for å telle nei av riktig klassifisert dataforekomst, Beregner Hamming Loss tap generert i bitstrengen av klasseetiketter under prediksjon. DET GJØR xor drift mellom den opprinnelige binære streng av klasse etiketter og spådd klasse etiketter for en dataforekomst og beregner gjennomsnittet på tvers av datasettet. Dens uttrykk er gitt av
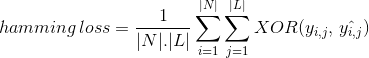
der
| N| = antall dataforekomster
| L / = kardinalitet i klasserommet
yᵢ,ⱼ = faktisk bit av klasseetikett j i dataforekomst i
^yᵢ,ⱼ = spådd bit av klasseetikett j i dataforekomst i
‘hamming loss’ verdi varierer fra 0 til 1. Som det er et tap metrisk, er dens tolkning omvendt i naturen i motsetning til normalt nøyaktighetsforhold. Mindre verdi av hamming tap indikerer en bedre klassifiserer.
Delsettnøyaktighet
det er noen situasjoner der vi kan gå for et absolutt nøyaktighetsforhold der det er viktig å måle den nøyaktige kombinasjonen av etikettforutsigelser. Det kan høres relevant i ‘Label power-set’ saken. I multi-label-scenariet er det kjent som delsettnøyaktighet.
Bortsett fra disse to, kan hver individuelle binære klassifikatorens nøyaktighet bedømmes av andre tradisjonelle beregninger som nøyaktighetsforhold, F1-poengsum, Presisjon, Tilbakekalling, etc og ROC-kurver.
dette handler om teoretisk modellering for multi-label klassifisering. Vi vil se en case studie ved hjelp av reelle data i neste artikkel. Data exploration-koden er tilgjengelig på Github.
nylig forfattet jeg en bok OM ML (https://twitter.com/bpbonline/status/1256146448346988546)