hoofdstuk 12
Moment Distribution Method of Analysis of Structures
12.1 basisconcepten
de moment distribution method of analysis of balken and frames werd ontwikkeld door Hardy Cross en formeel gepresenteerd in 1930. Hoewel deze methode een vervormingsmethode is zoals de helling-afbuigingsmethode, is het een benaderende methode en vereist het dus geen simultane vergelijkingen, zoals het geval was met de laatste methode. De mate van nauwkeurigheid van de resultaten verkregen door de methode van de verdeling van het moment is afhankelijk van het aantal opeenvolgende benaderingen of het iteratieproces.
om het concept van de methode voor de verdeling van het moment te illustreren, wordt het in Figuur 12.1 getoonde kader gebruikt. Leden van het frame zijn prismatisch en worden verondersteld niet axiaal te vervormen of ten opzichte van elkaar te vertalen. Gewrichten ACD van het frame zijn bevestigd, terwijl gezamenlijke B licht kan draaien als gevolg van de toegepaste belasting. Ten eerste, voor het uitvoeren van moment verdeling tussen de leden, worden alle gewrichten verondersteld om tijdelijk worden vergrendeld met behulp van een klem.
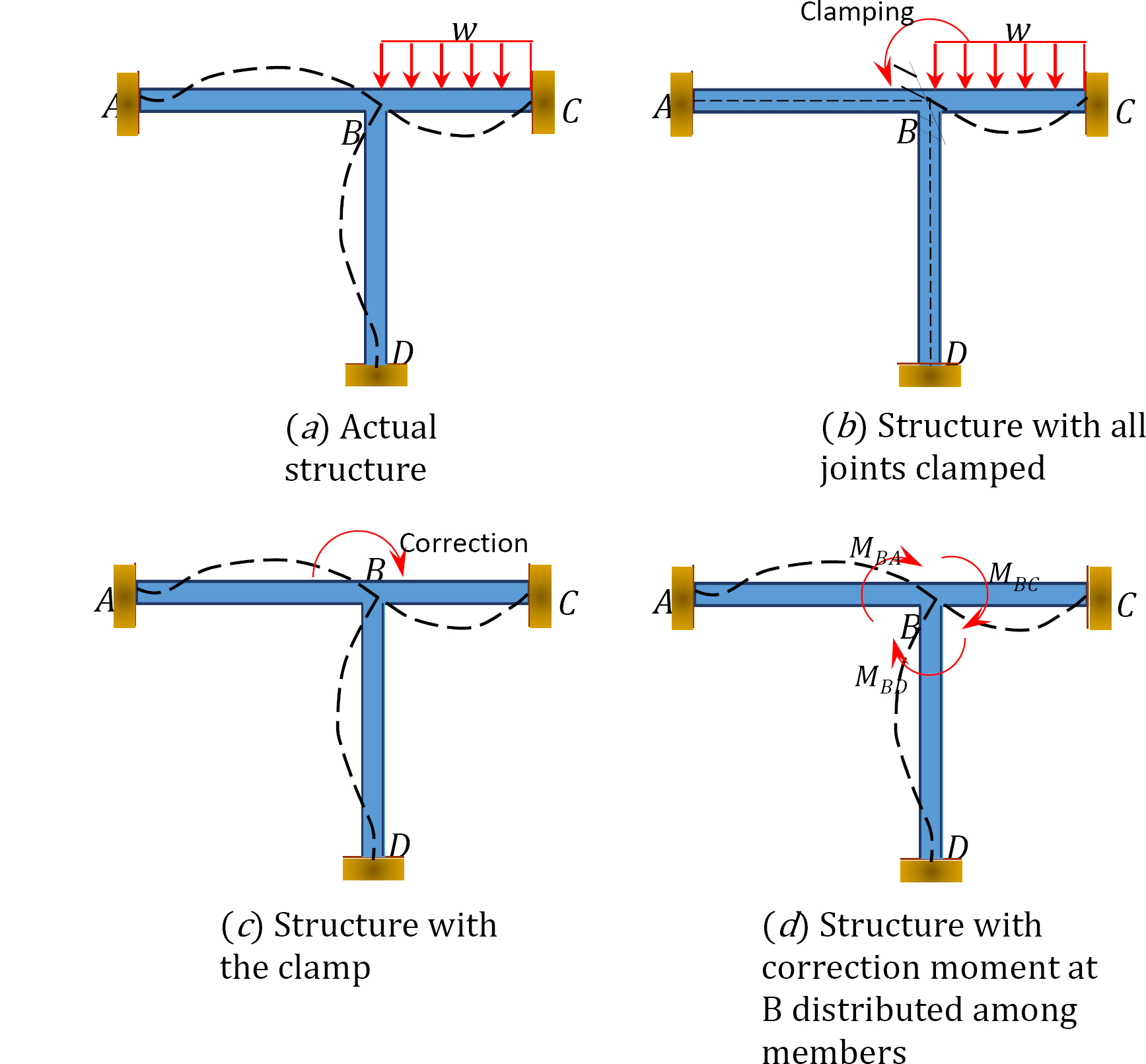
Fig. 12.1. Frame.
12.2 Tekenconventie
de tekenconventie voor het moment verdelingsmethode is vergelijkbaar met die welke is vastgesteld voor de hellings-vervormingsmethode; dat wil zeggen, het moment aan het einde van een lid wordt als positief beschouwd als het de neiging heeft om het einde van het lid met de klok mee te draaien en negatief als het de neiging heeft om het tegen de klok in te draaien.
12.3 definities
ongebalanceerde momenten: bij deze analysemethode wordt ervan uitgegaan dat de voegen in een structuur eerst worden vastgeklemd of vergrendeld en vervolgens achtereenvolgens worden losgelaten. Zodra een joint wordt vrijgegeven, vindt een rotatie plaats, omdat de som van de vaste eindmomenten van de leden die bij die joint samenkomen niet nul is. De waarde van de som van de verkregen eindmomenten is het onevenwichtige moment op dat gewricht.
overdrachtsmomenten: de verdeelde momenten aan de uiteinden van leden die samenkomen op een gezamenlijke oorzaak momenten aan de andere uiteinden, die geacht worden vast te zijn. Deze geïnduceerde momenten aan de andere uiteinden worden carry-over momenten genoemd.
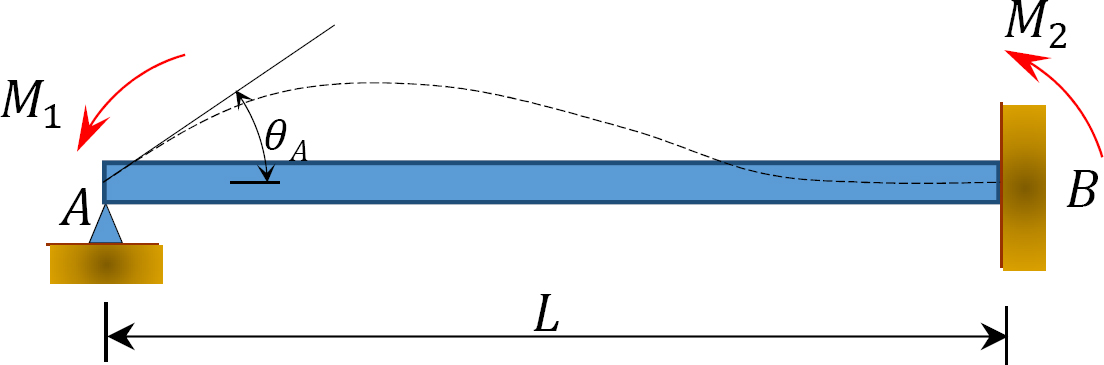
Fig. 12.2. Onbelaste prismatische Balk.
beschouw een onbelaste prismatische balk die aan einde B is bevestigd, zoals weergegeven in Figuur 12.2. Als een moment M1 wordt toegepast op het linker uiteinde van de bundel, kunnen de hellings-afbuigvergelijkingen voor beide uiteinden van de bundel als volgt worden geschreven:


het vervangen van 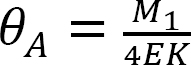 van vergelijking 12.1 in vergelijking 12.2 suggereert het volgende:
van vergelijking 12.1 in vergelijking 12.2 suggereert het volgende:

vergelijking 12.3 suggereert dat het moment dat wordt overgedragen naar het vaste uiteinde van een bundel als gevolg van een moment dat aan het andere uiteinde wordt toegepast, gelijk is aan de helft van het toegepaste moment.
Carry-over factor: de verhouding tussen het geïnduceerde moment en het toegepaste moment wordt de carry-over factor genoemd. Voor de in Figuur 12.2 afgebeelde balk is de carry-over-factor als volgt::

gedistribueerde factor (DF): De verdeelde factor is een factor die wordt gebruikt om het aandeel van het onevenwichtige moment te bepalen dat door elk van de leden in een gezamenlijke vergadering wordt gedragen. Voor de leden die in gezamenlijk O van het in Figuur 12.3 getoonde kader bijeenkomen, worden hun verdelingsfactoren als volgt berekend::
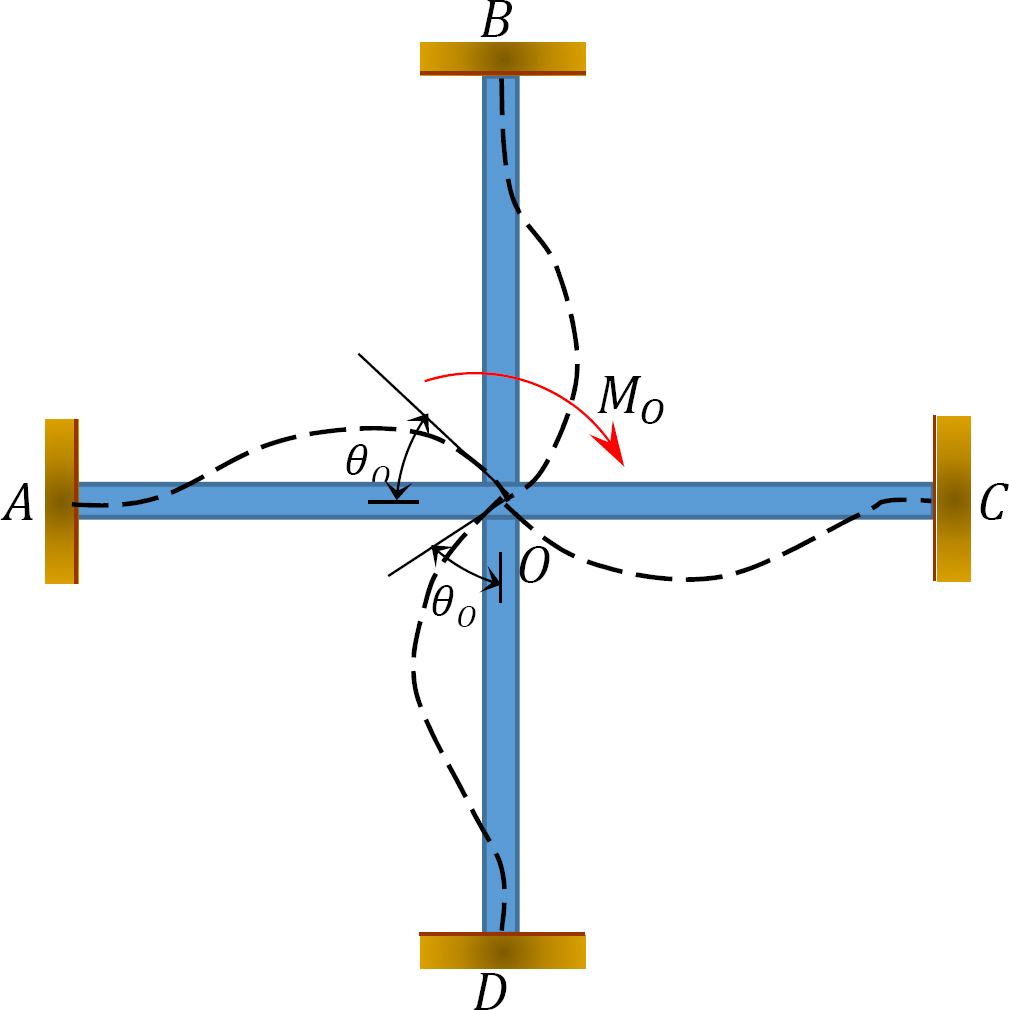
Fig. 12.3. Frame.

gedistribueerde momenten: bij het loslaten van de denkbeeldige klem op een gewricht, veroorzaakt het onevenwichtige moment op dat gewricht het roteren. De rotatie verdraait het einde van de leden die samenkomen in de joint, wat resulteert in de ontwikkeling van weerstandsmomenten. Deze weerstandsmomenten worden gedistribueerde momenten genoemd. De verdeelde momenten voor de leden van het in Figuur 12.3 afgebeelde frame worden als volgt berekend:
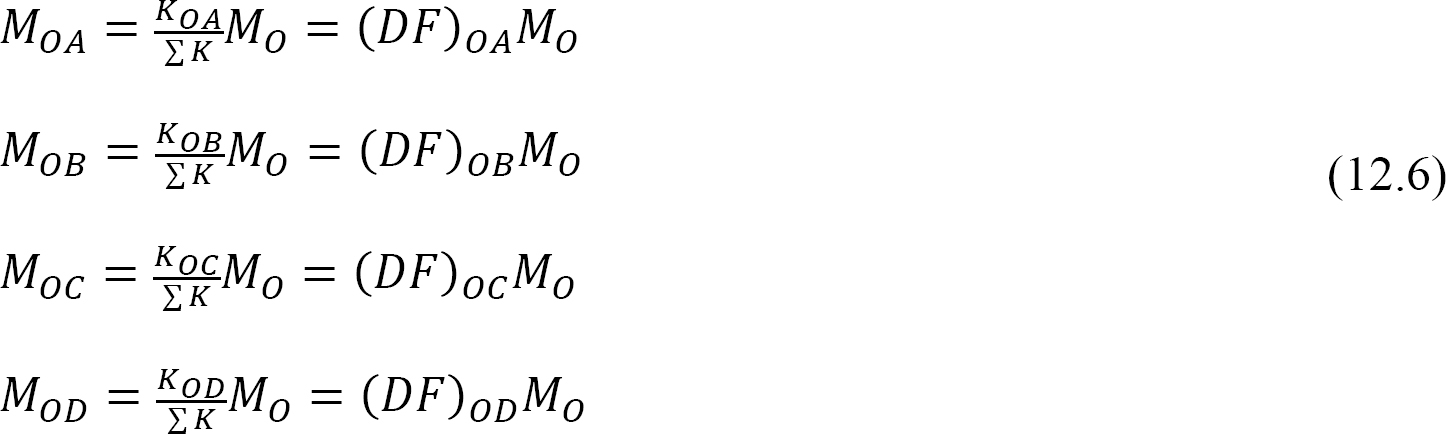
12.4 wijziging van de stijfheid van de leden
soms kan het iteratieproces in de momenteel-verdelingsmethode aanzienlijk worden verminderd door de buigstijfheid van sommige leden van de onbepaalde structuur aan te passen. In dit gedeelte wordt gekeken naar de invloed van een vaste – en een pin-end ondersteuning op de buigstijfheid van een onbepaald Balk.
geval 1: Een balk scharnierend aan de ene kant en bevestigd aan de andere kant
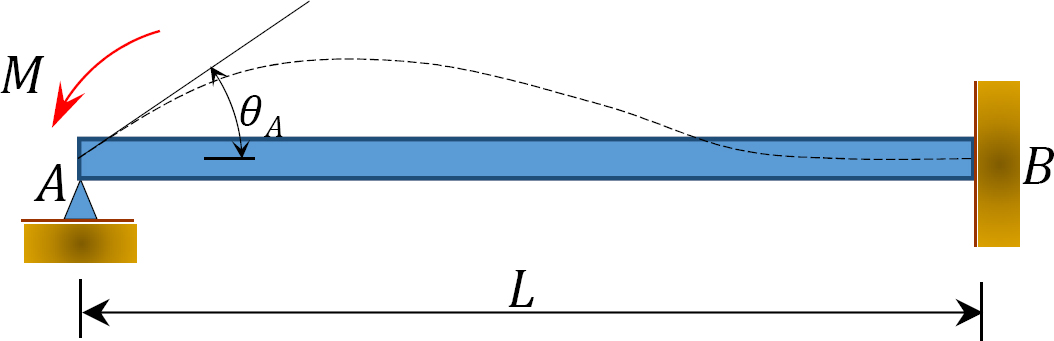
Fig. 12.4. Lichtbundel
beschouw een lichtbundel die scharnierend is aan einde A en vast is aan einde B, Zoals weergegeven in Figuur 12.4. Het aanbrengen van een moment M draait het scharniereinde met een bedrag θ. Het schrijven van de helling-afbuigvergelijking voor het einde A van het lid en opmerkend dat 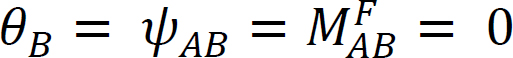 het volgende suggereert:
het volgende suggereert:
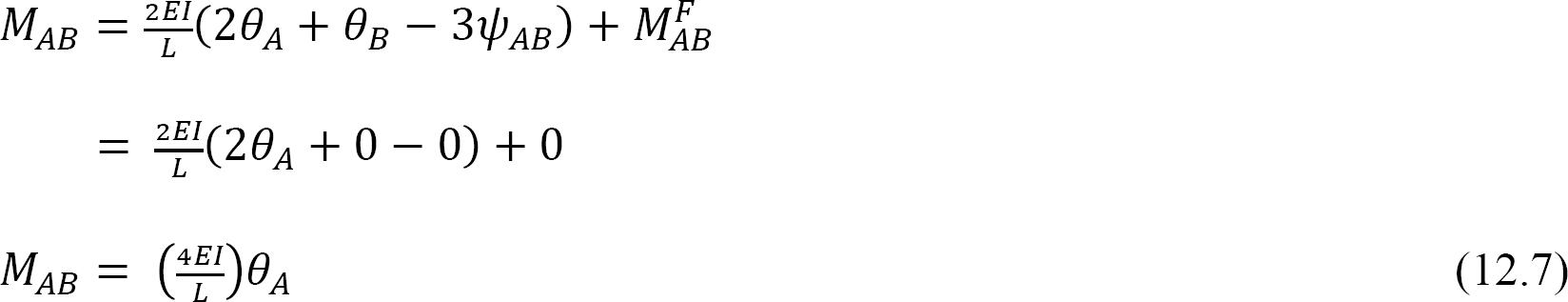
per definitie is de buigstijfheid van een structureel lid het moment dat op een uiteinde van het lid moet worden toegepast om een eenheidsrotatie van dat uiteinde te veroorzaken. De volgende uitdrukking voor de buigstijfheid voor het lid met een vast uiteinde wordt uitgedrukt als volgt te werk bij het vervangen van θA = 1 in vergelijking 12.7:

Per definitie, de relatieve buigstijfheid van een lid is bepaald door de verdeling van de buigstijfheid van de lid-4E. Het verdelen van de vergelijking 12.8 4E suggereert de volgende uitdrukking voor de relatieve stijfheid voor het geval dat wordt beschouwd als:

Geval 2: Een balk scharnieren aan beide uiteinden
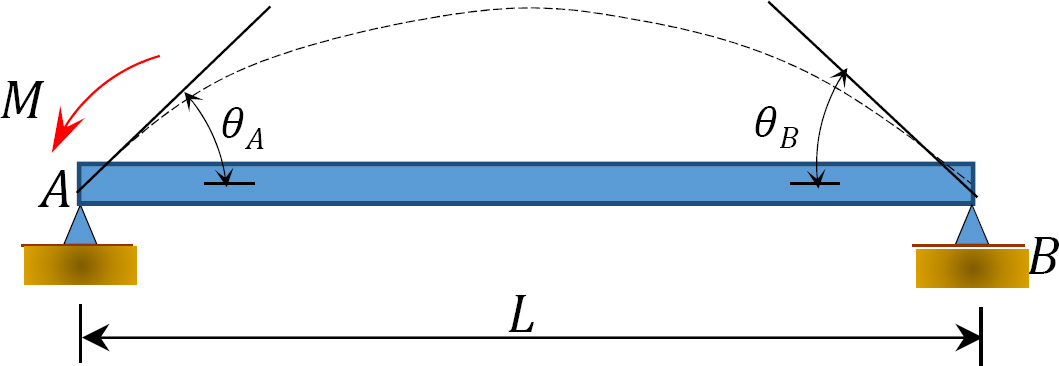
Afb. 12.5. Eenvoudig ondersteunde straal.
door een moment M aan het einde A van de in Figuur 12.5 afgebeelde lichtbundel te gebruiken, draait de lichtbundel onder een hoek θA aan het scharnierende uiteinde. Gebruikmakend van de gewijzigde helling-afbuigvergelijking afgeleid in hoofdstuk 11, punt 11.4, en opmerkend dat 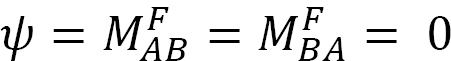 de volgende uitdrukking suggereert voor het moment aan het scharnierende uiteinde waar de belasting wordt uitgeoefend:
de volgende uitdrukking suggereert voor het moment aan het scharnierende uiteinde waar de belasting wordt uitgeoefend:
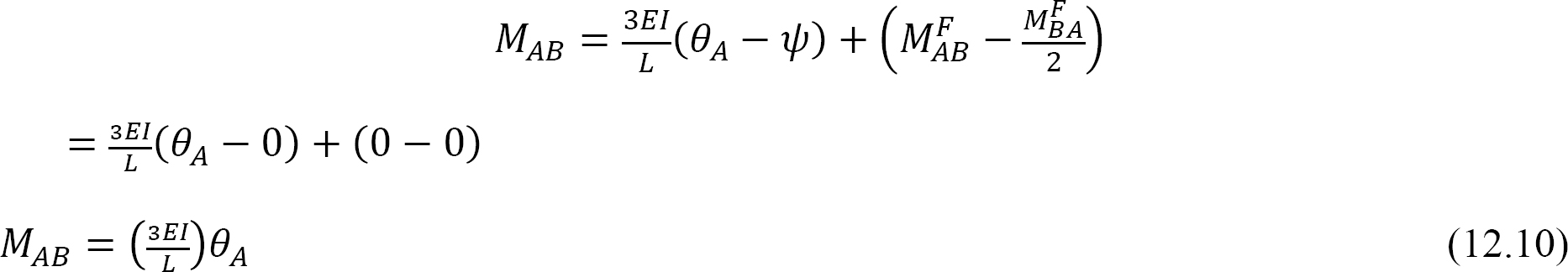
het vervangen van θA = 1 in vergelijking 12.10 suggereert de volgende uitdrukking voor de buigstijfheid voor een lid met een scharnierend uiteinde:

de relatieve stijfheid voor een lid met een scharnierend uiteinde wordt verkregen door vergelijking 12.11 door 4E te delen, als volgt::

het vergelijken van vergelijkingen 12.12 en 12.9 suggereert dat een lid met een scharnierend uiteinde drie vierde zo stijf is als een lid met dezelfde geometrie maar gefixeerd aan het uiteinde. Dit gevestigde feit kan aanzienlijk verminderen het aantal iteratie bij het analyseren van bundels of frames met een scharnierend uiteinde met behulp van de methode van moment distributie. In dergelijke gevallen wordt de relatieve stijfheid van de bundel aan het nabije uiteinde eerst aangepast volgens vergelijking 12.12 en wordt de verdelingsfactor berekend met de aangepaste stijfheid. Tijdens het balanceren zal het nabije einde slechts één keer in evenwicht worden gebracht zonder dat er momenten van of naar het einde worden overgedragen.12.5 analyse van Onbepaalde Bundels
12.5 analyse van Onbepaalde Bundels
de procedure voor de analyse van Onbepaalde bundels met behulp van de methode van momentverdeling wordt kort samengevat als volgt::
procedure voor de analyse van niet-bepaalde bundels volgens de Momentverdelings-methode
•Bereken de vaste-einde momenten voor leden, ervan uitgaande dat de gewrichten worden geklemd tegen rotatie.
* Bereken de verdelingsfactor voor elk van de aangesloten leden op de verbinding
•Bereken het ongebalanceerde moment op elke verbinding en verdeel hetzelfde over de uiteinden van de aangesloten leden op die verbinding.
* draag de helft van het verspreide moment over naar de andere uiteinden van de leden.
* deze laatste momenten (momenten verkregen in stappen drie en vier) optellen of aftrekken naar of van de oorspronkelijke momenten met een vast einde.
* breng de vastgestelde eindmomenten aan op de gewrichten van de gegeven structuur.
•teken het schema van de vrije carrosserie van elke overspanning van de gegeven bundel, waarin de belastingen en momenten bij de verbindingen worden weergegeven die worden verkregen met behulp van de momentverdelings-methode.
* Bepaal de ondersteuningsreacties voor elke span.
* bereken en construeer de schema ‘ s van de afschuifkracht en het buigmoment voor elke overspanning.
* teken één buigmoment en één afschuifkrachtdiagram voor de gegeven bundel door de diagrammen in stap 9 te combineren.
voorbeeld 12.1
Bepaal met behulp van de momentverdelings-methode de eindmomenten en de reacties op de steunen van de in Figuur 12.6 a afgebeelde bundel. teken de afschuifkracht en het buigmomentschema. EI = constant.
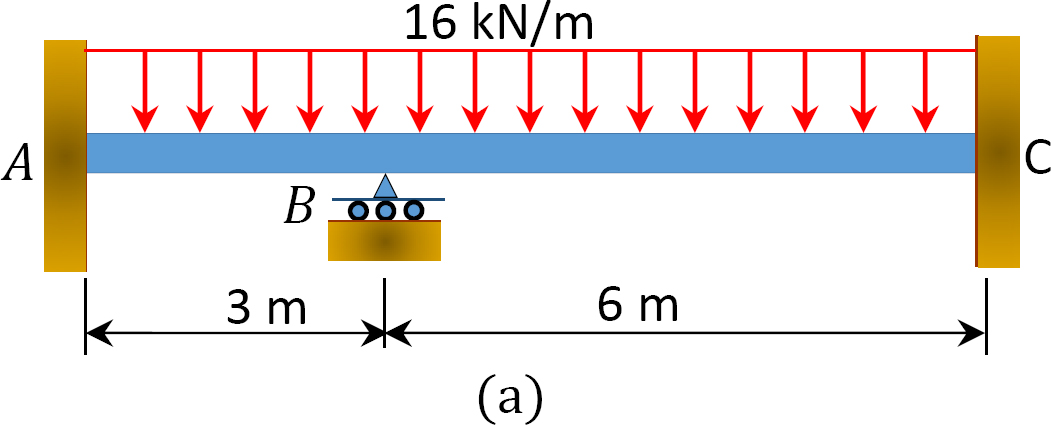
Fig. 12.6. Balk.
oplossing
vast eindmoment.
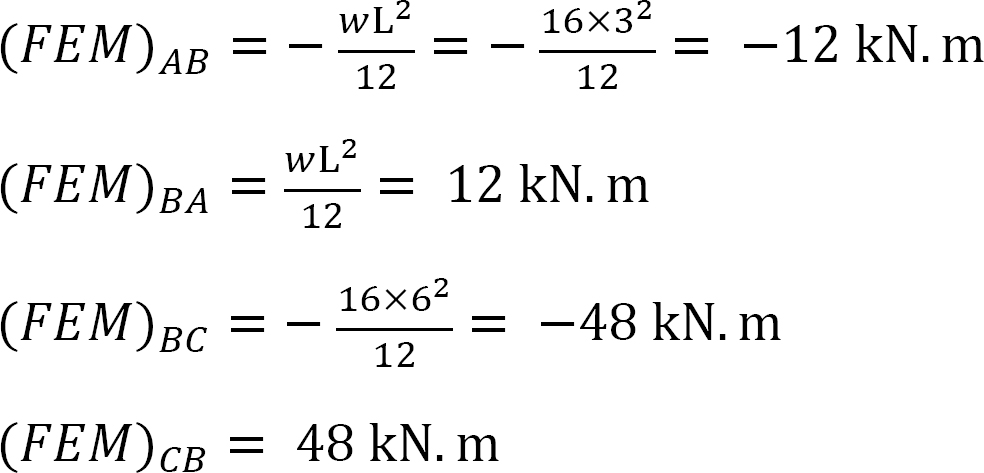
Stijfheidsfactor.
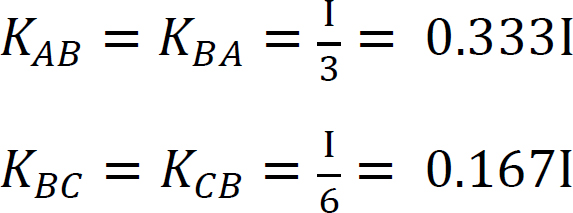
Verdelingsfactor.
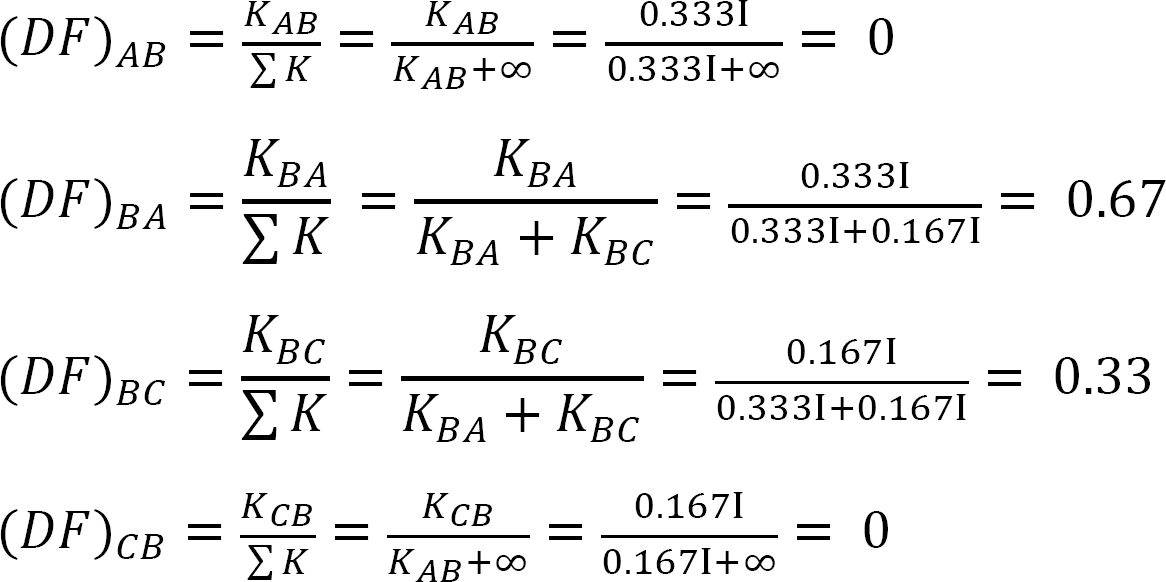
tabel 12.1. Distributie tabel.
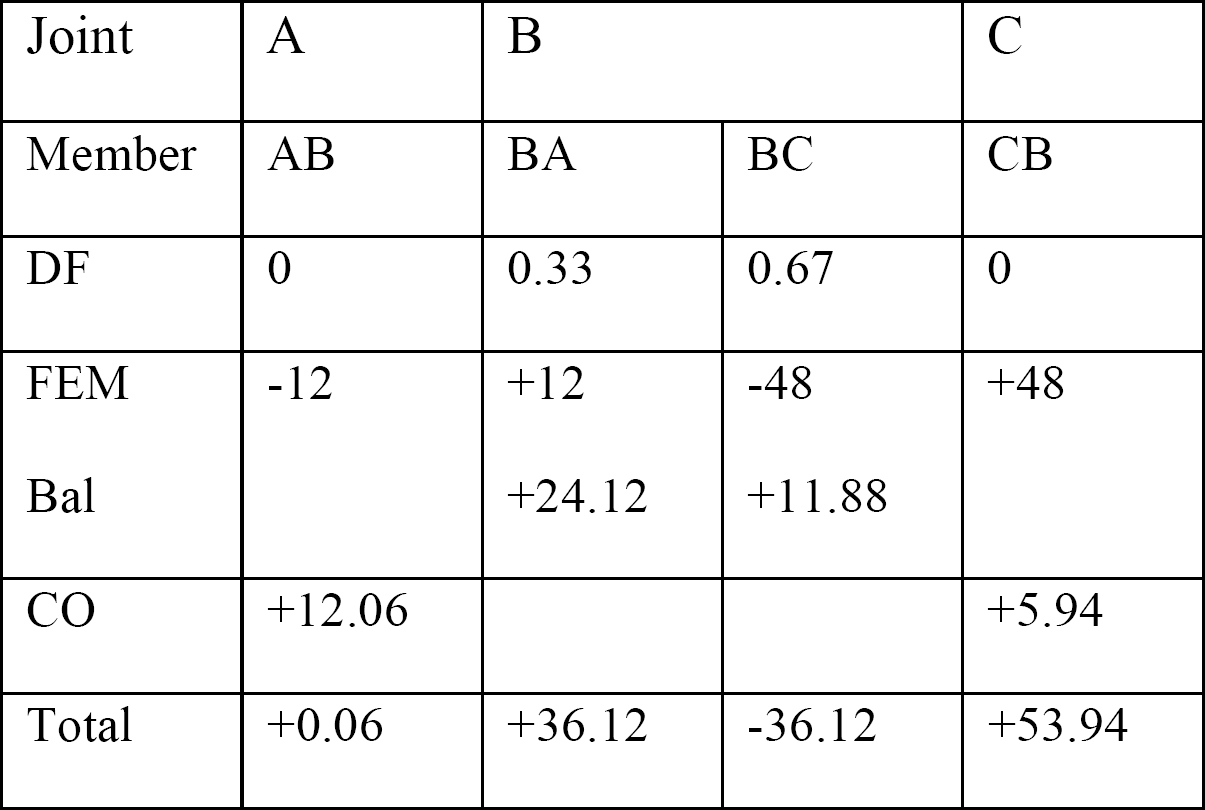
afschuifkracht en buigmoment diagrammen.
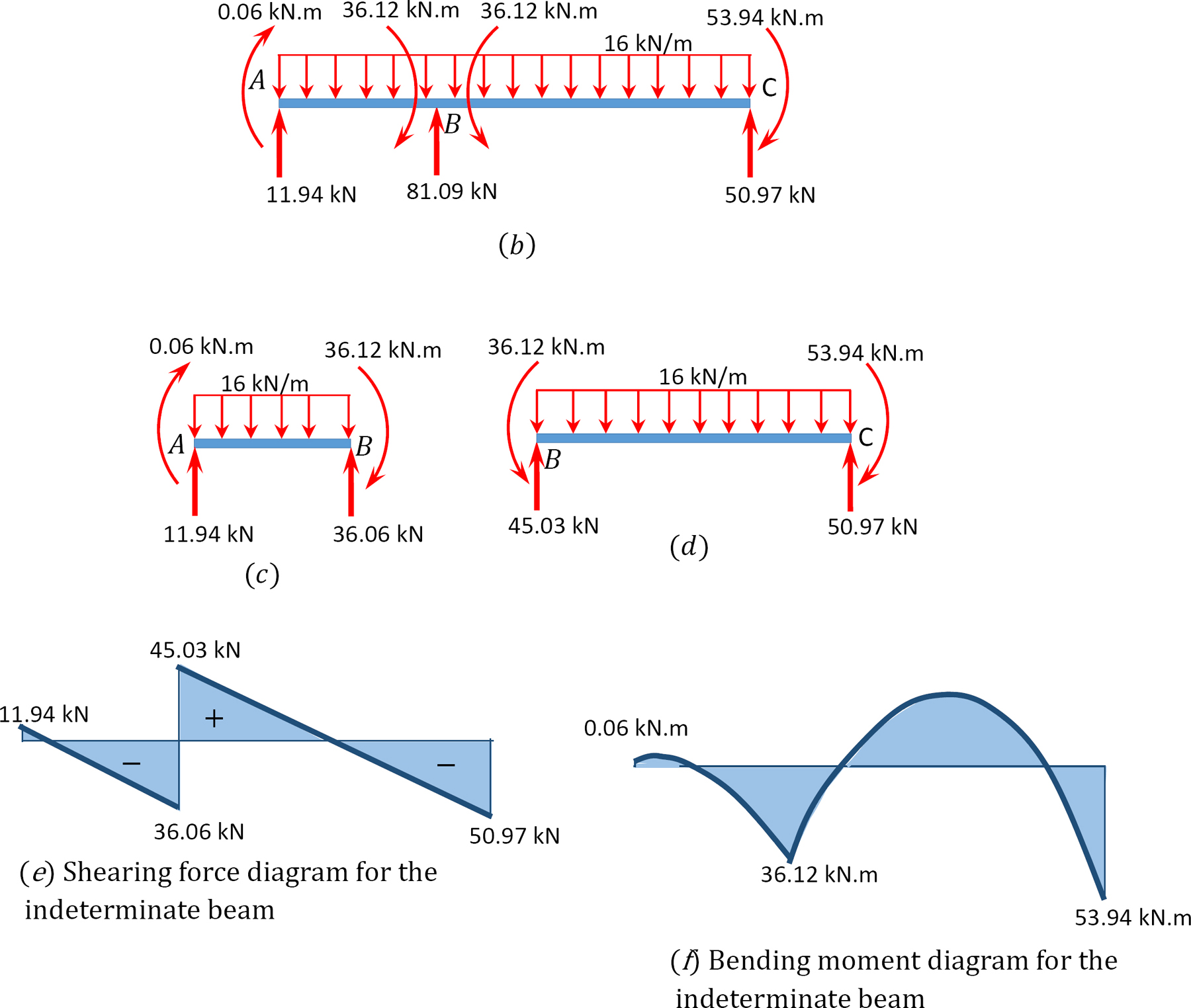
voorbeeld 12.2
Bepaal met behulp van de momentverdelings-methode de eindmomenten en de reacties op de steunen van de in Figuur 12.7 a afgebeelde bundel. teken de afschuifkracht en het buigmomentschema.
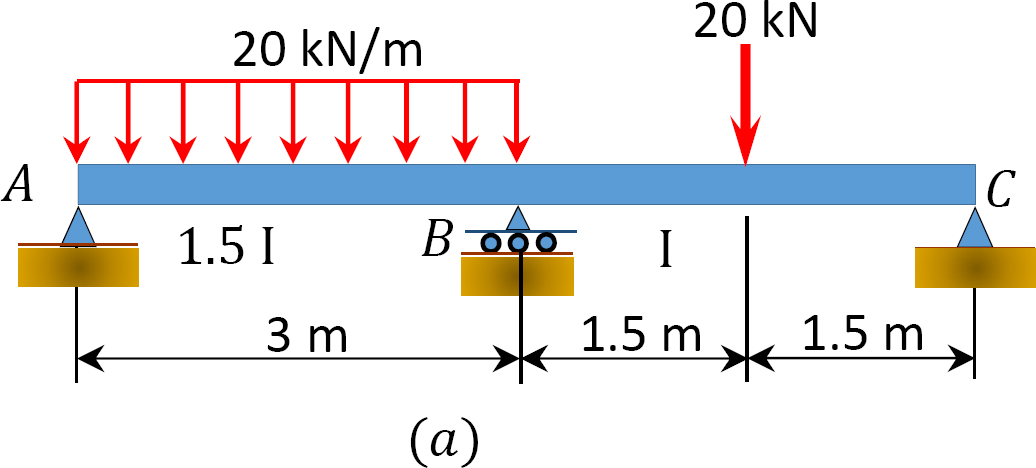
Fig. 12.7. Balk.
oplossing
vast eindmoment.
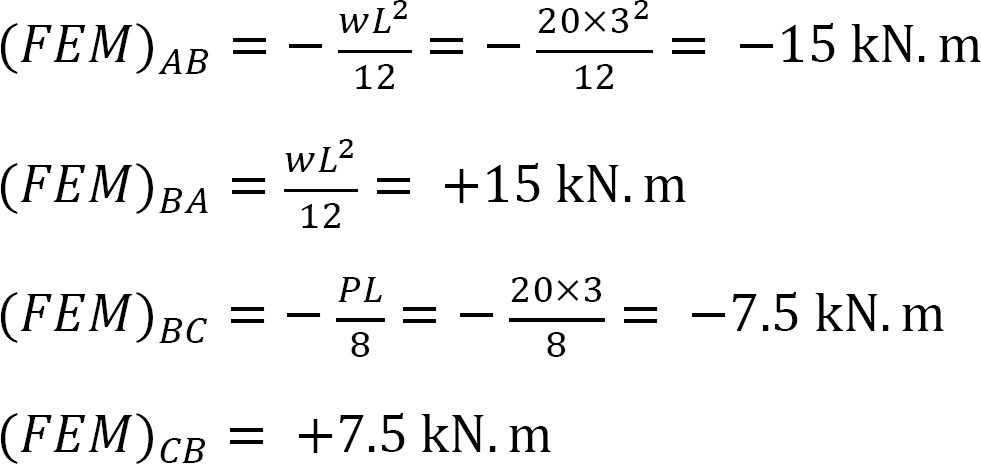
Stijfheidsfactor.
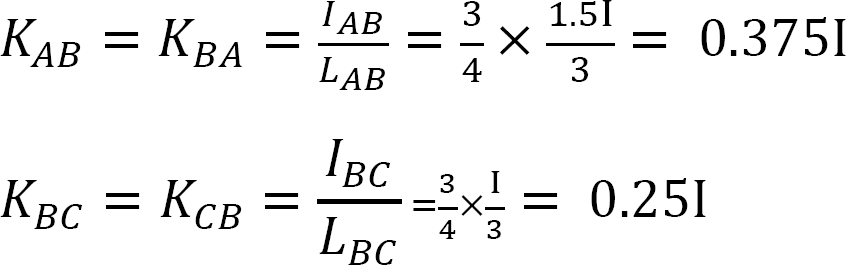
Verdelingsfactor.
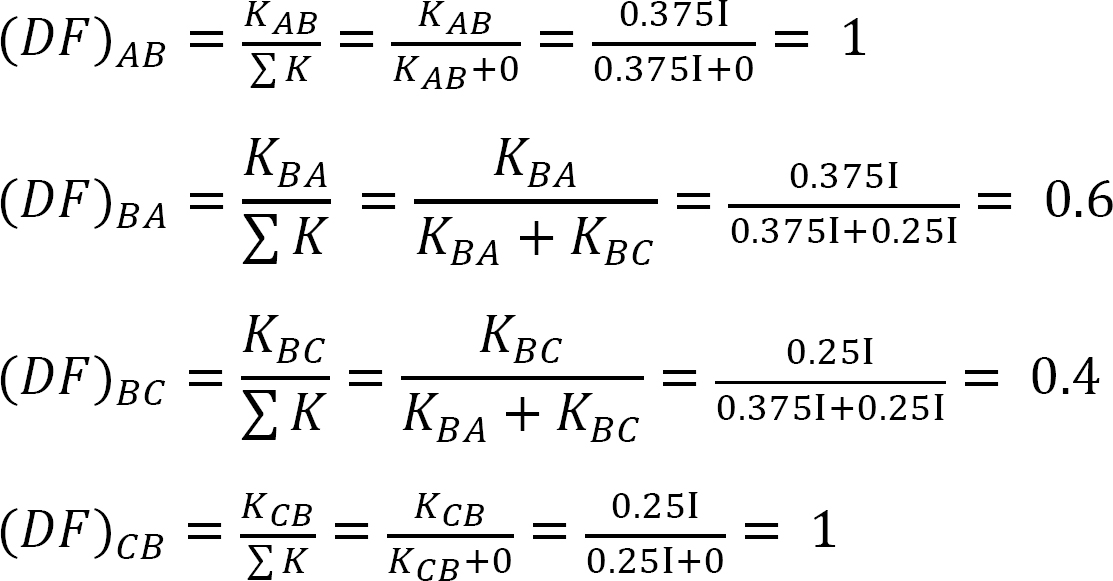
tabel 12.2. Distributie tabel.
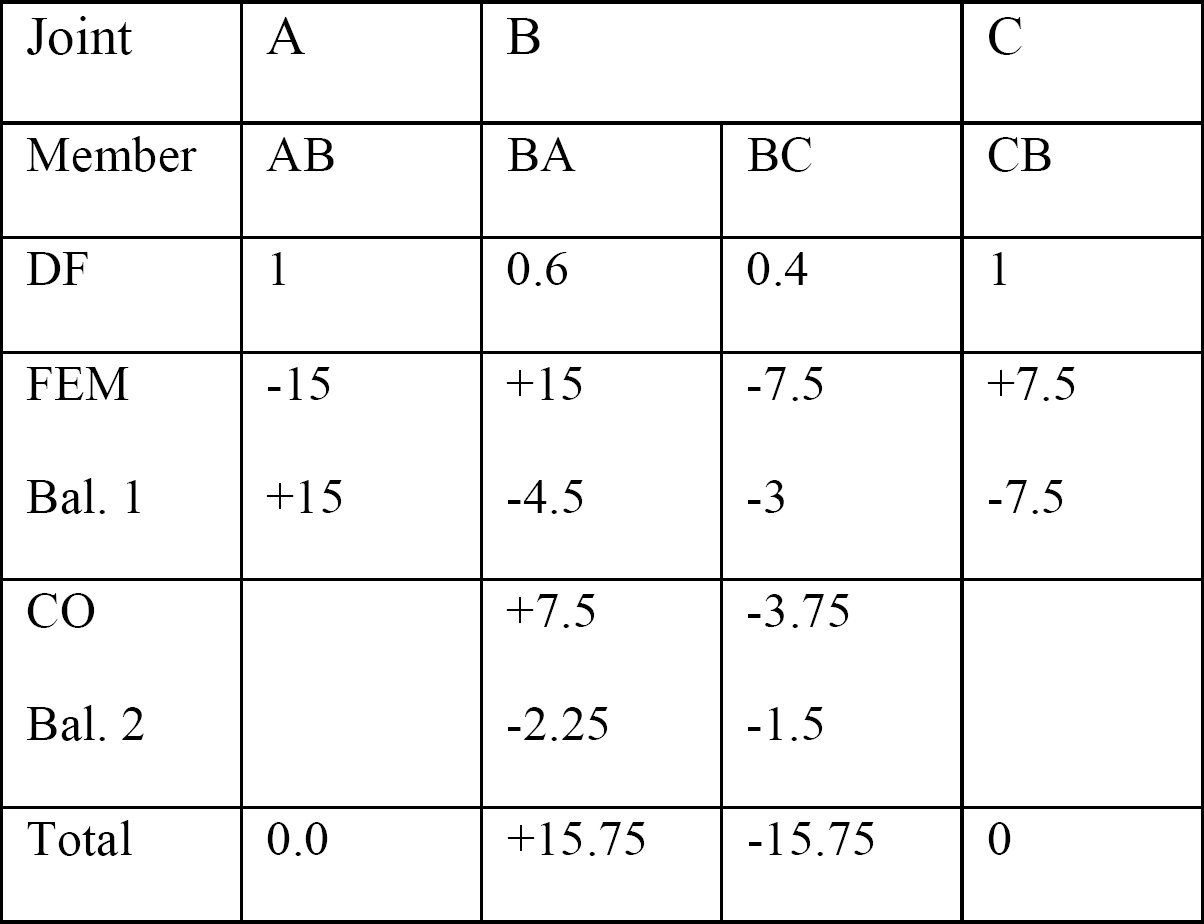
afschuifkracht en buigmoment diagrammen.
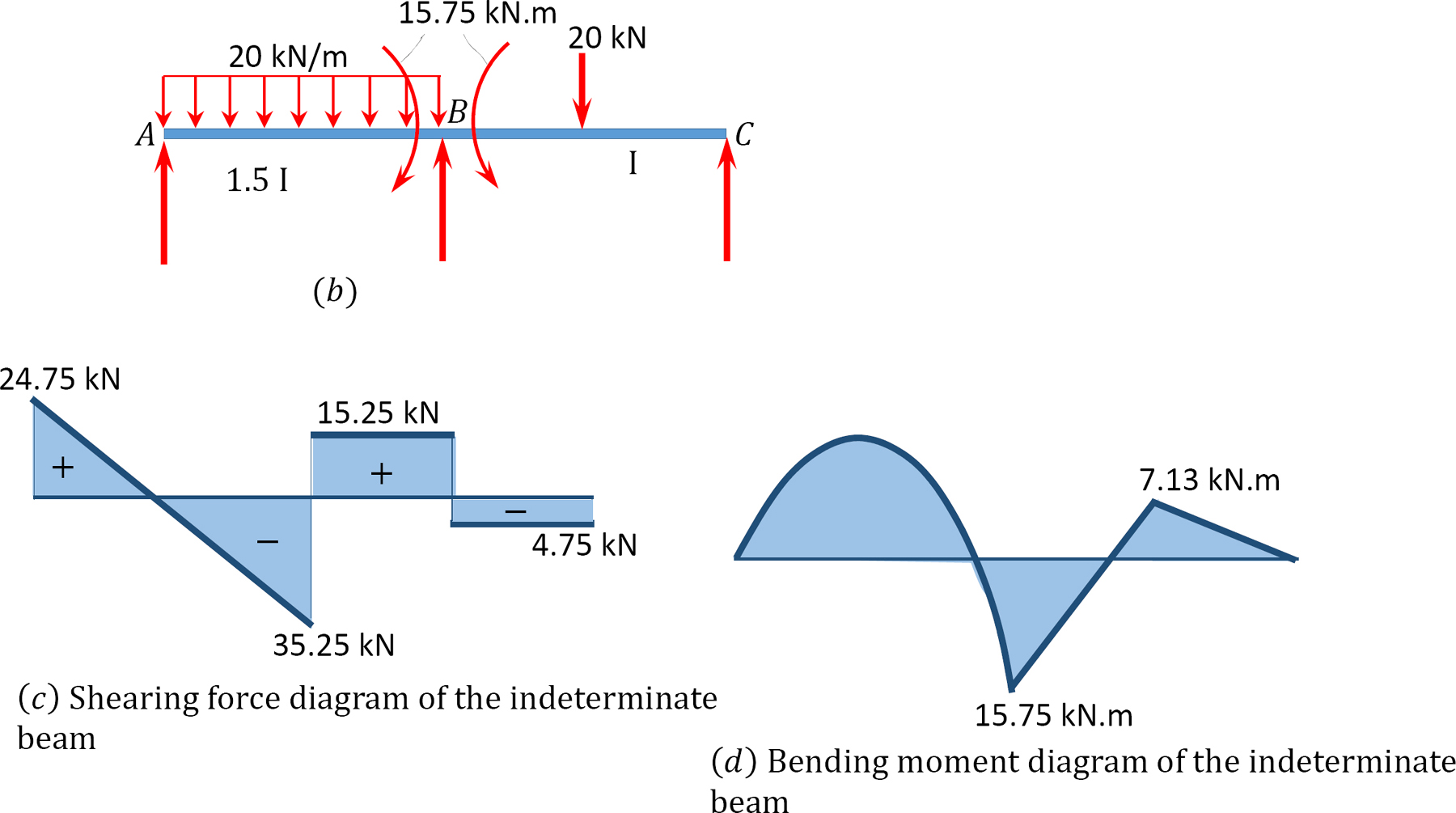
12.6 analyse van Onbepaalde Frames
de procedure voor de analyse van frames met behulp van de momentverdelingsmethode hangt af van het type frame dat wordt geanalyseerd. Frames worden gecategoriseerd als sway-of non-sway frames. De procedure voor de analyse van niet-slingerende frames is vergelijkbaar met die van Onbepaalde balken. Maar voor de analyse van sway frames, de procedure is anders. Er zijn twee fasen betrokken bij de analyse van sway frames, namelijk de non-sway fase en sway-fase analyses. Deze fasen worden hieronder beschreven.
procedure voor de analyse van onbepaald Sway-Frames volgens de Momentverdelingsmethode
A. analyse zonder sway-fase
•neem eerst aan dat er een denkbeeldige steun bestaat die het frame verhindert te slingeren.
•Bereken de horizontale reacties op de steunen van het frame en noteer het verschil X. Dit is de kracht om slingeren te voorkomen.
B. Sway stage analysis
* neem willekeurige momenten aan om op de kolommen van het frame in te spelen. De omvang van deze momenten zal variëren van kolom tot kolom in verhouding tot 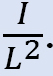
•waarden worden aangenomen voor M2 en M1 wordt bepaald.
* de willekeurige momenten worden dan verdeeld als voor de niet-sway conditie
* Bereken de grootte van de horizontale reacties op de steunen voor de sway conditie. De optelling van deze reacties geeft de willekeurige verplaatsingskracht Y.
* Bepaal de verhouding 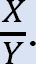 deze verhouding wordt de sway factor genoemd.
deze verhouding wordt de sway factor genoemd.
* gebruik de sway factor om de verdeelde momenten van de sway te vermenigvuldigen. Dit geeft het gecorrigeerde moment voor de sway.
* de laatste momenten voor het frame zijn de som van de momenten verkregen in de niet-sway-fase en het gecorrigeerde moment voor de sway-fase.
voorbeeld 12.3
Bepaal met behulp van de methode voor de verdeling van het moment de eindmomenten van de leden van het in Figuur 12.8 getoonde frame. EI = constant.
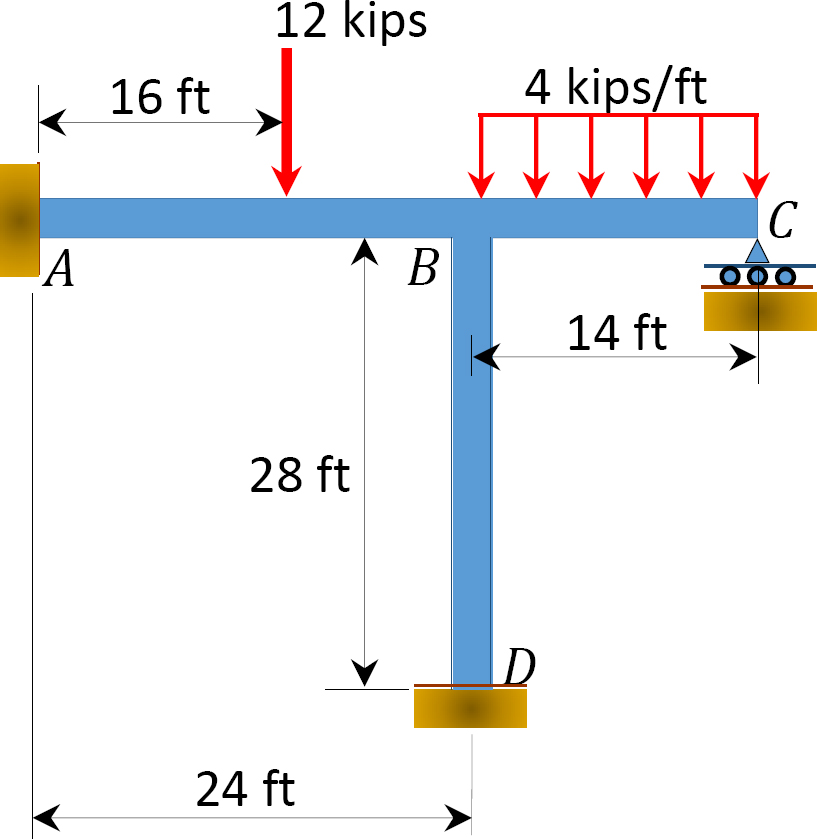
Fig. 12.8. Frame.
oplossing
vast eindmoment.
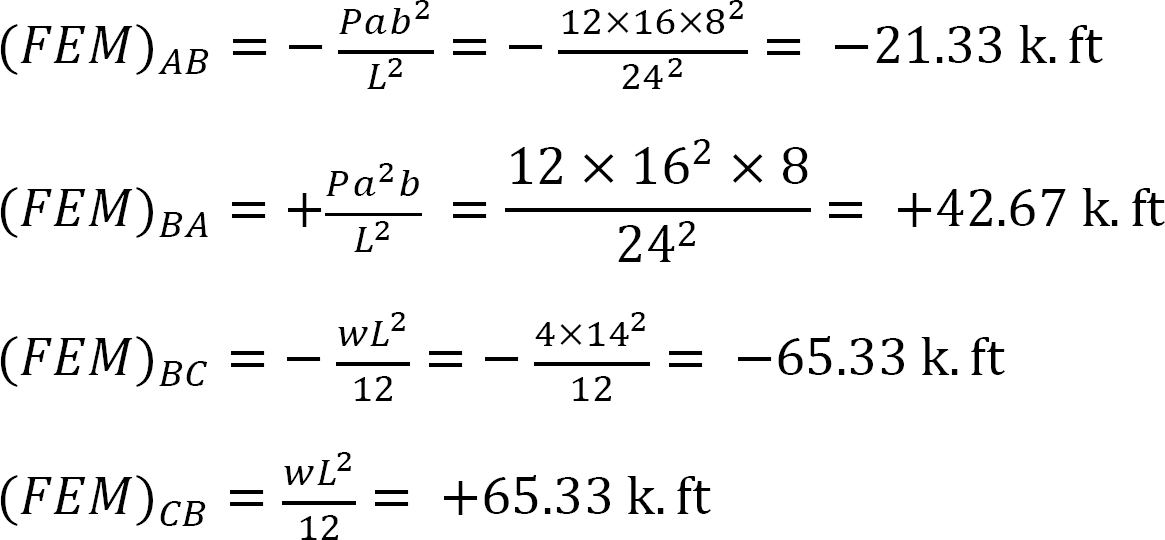
Stijfheidsfactor.
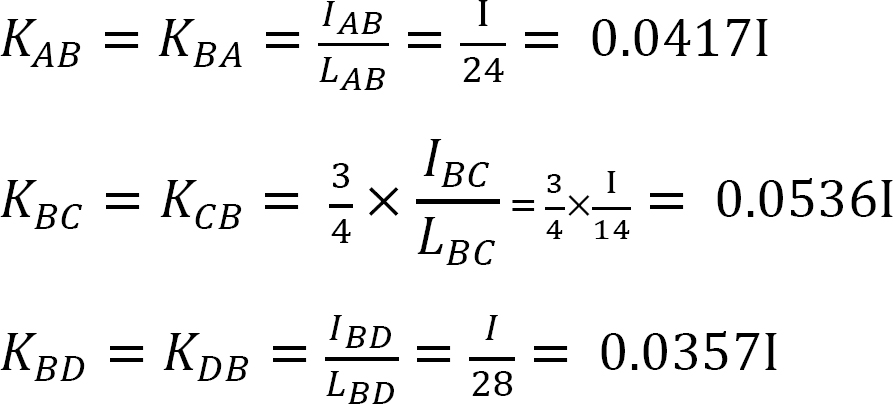
Verdelingsfactor.
tabel 12.3. Distributie tabel.
laatste lid einde momenten.
te Vervangen door de verkregen waarden van EKθB, EKθC, en EK∆ in de lid-end moment vergelijkingen wijst op het volgende:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Voorbeeld 12.4
Bepaal met behulp van de momentverdelings-methode de eindmomenten op de steunen van het in Figuur 12.9 getoonde frame. EI = constant.
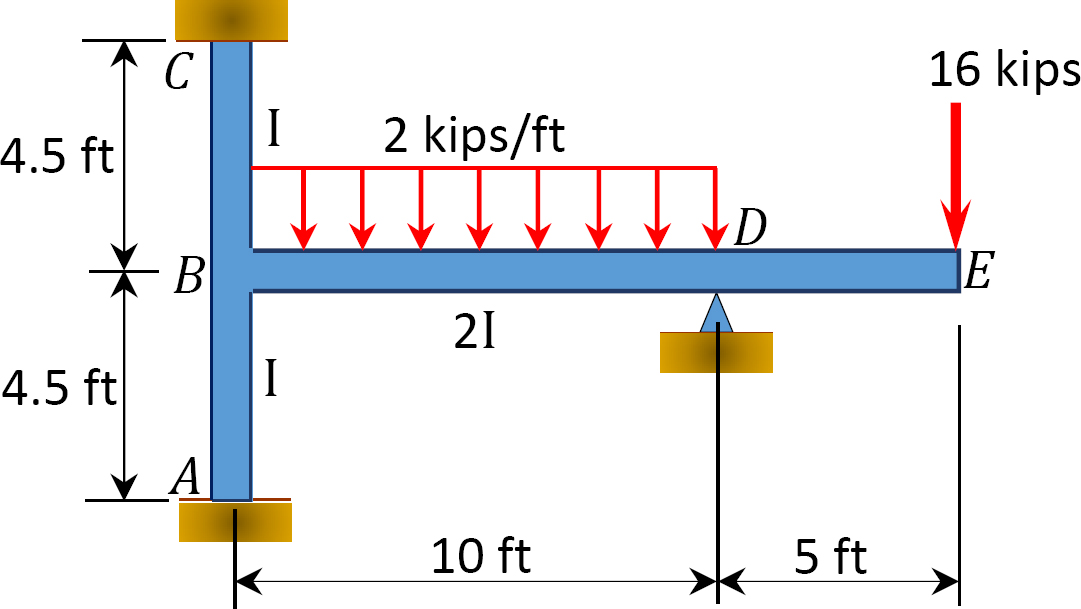
Fig. 12.9. Frame.
oplossing
vast eindmoment.
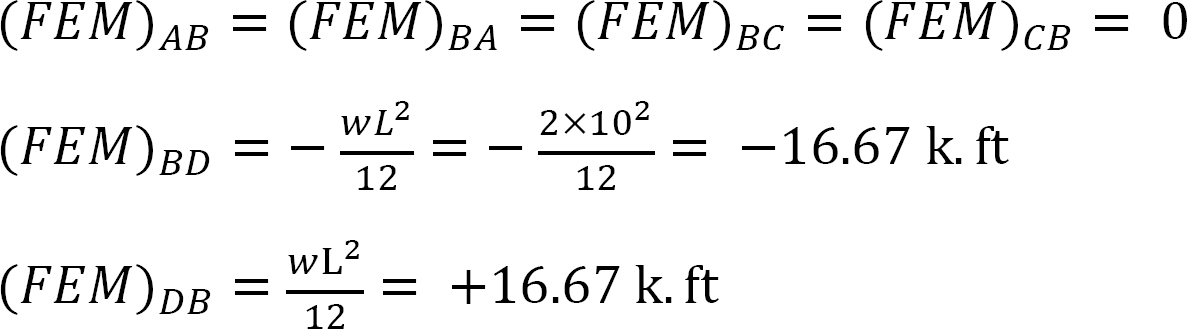
Stijfheidsfactor.
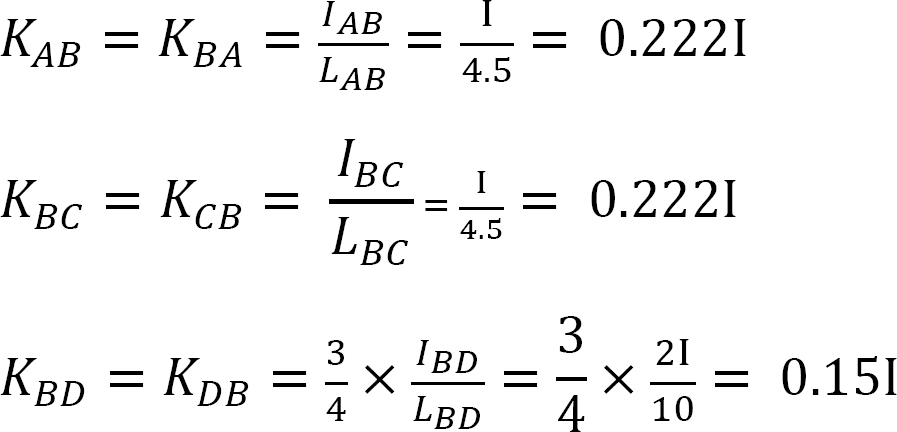
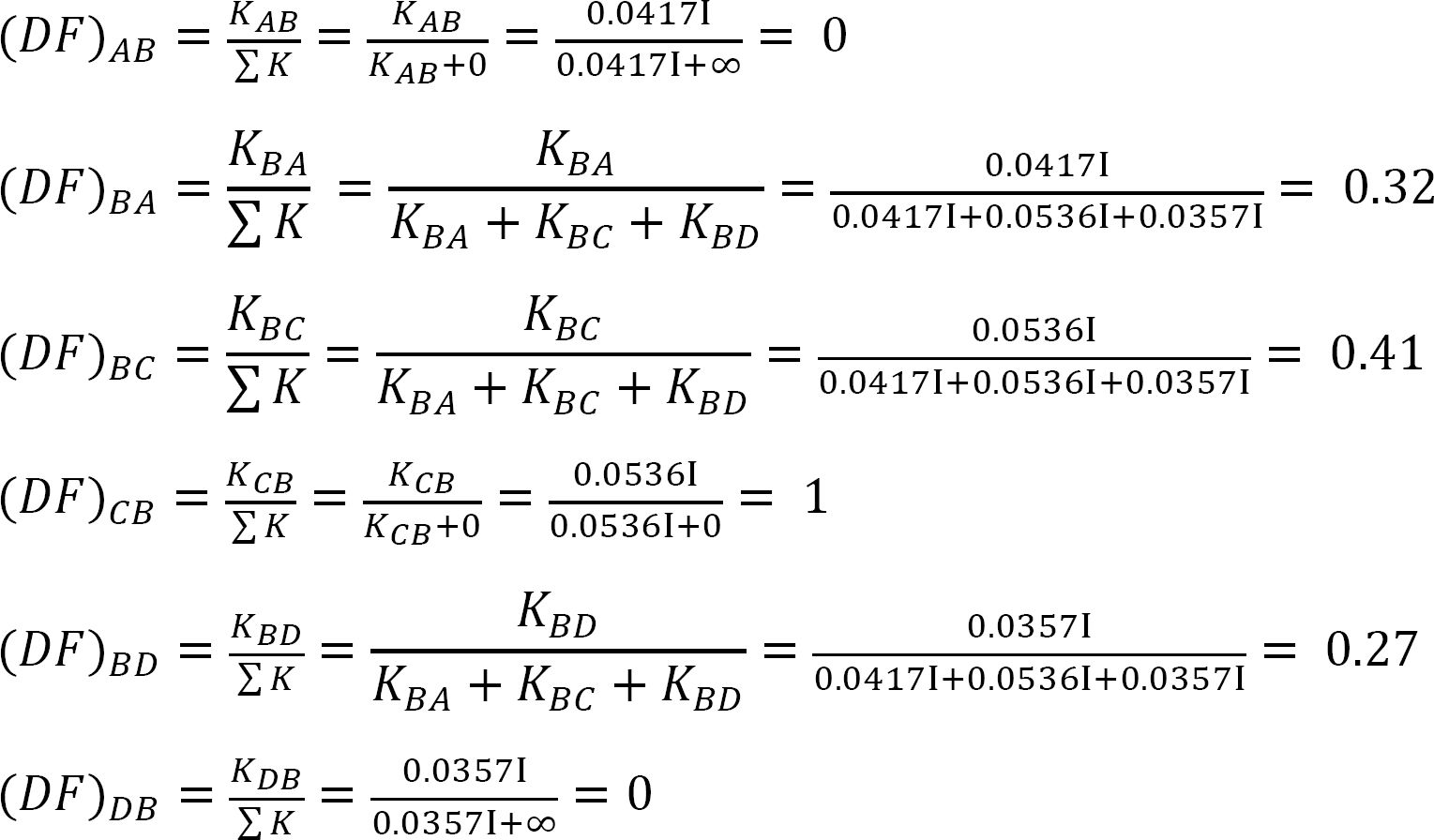
Verdelingsfactor.

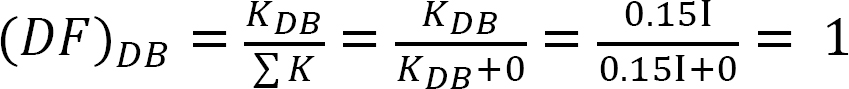
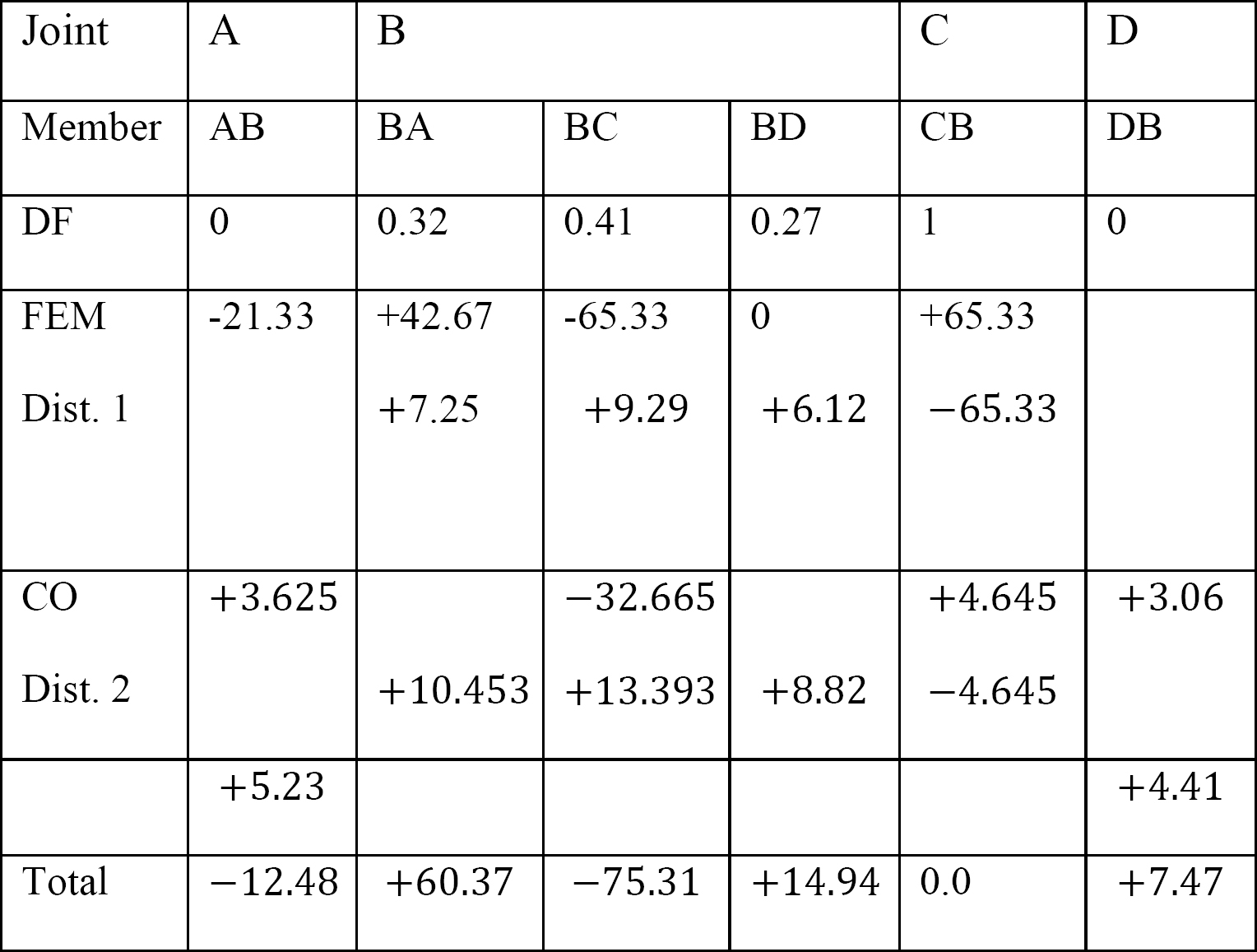
tabel 12.4. Distributie tabel.
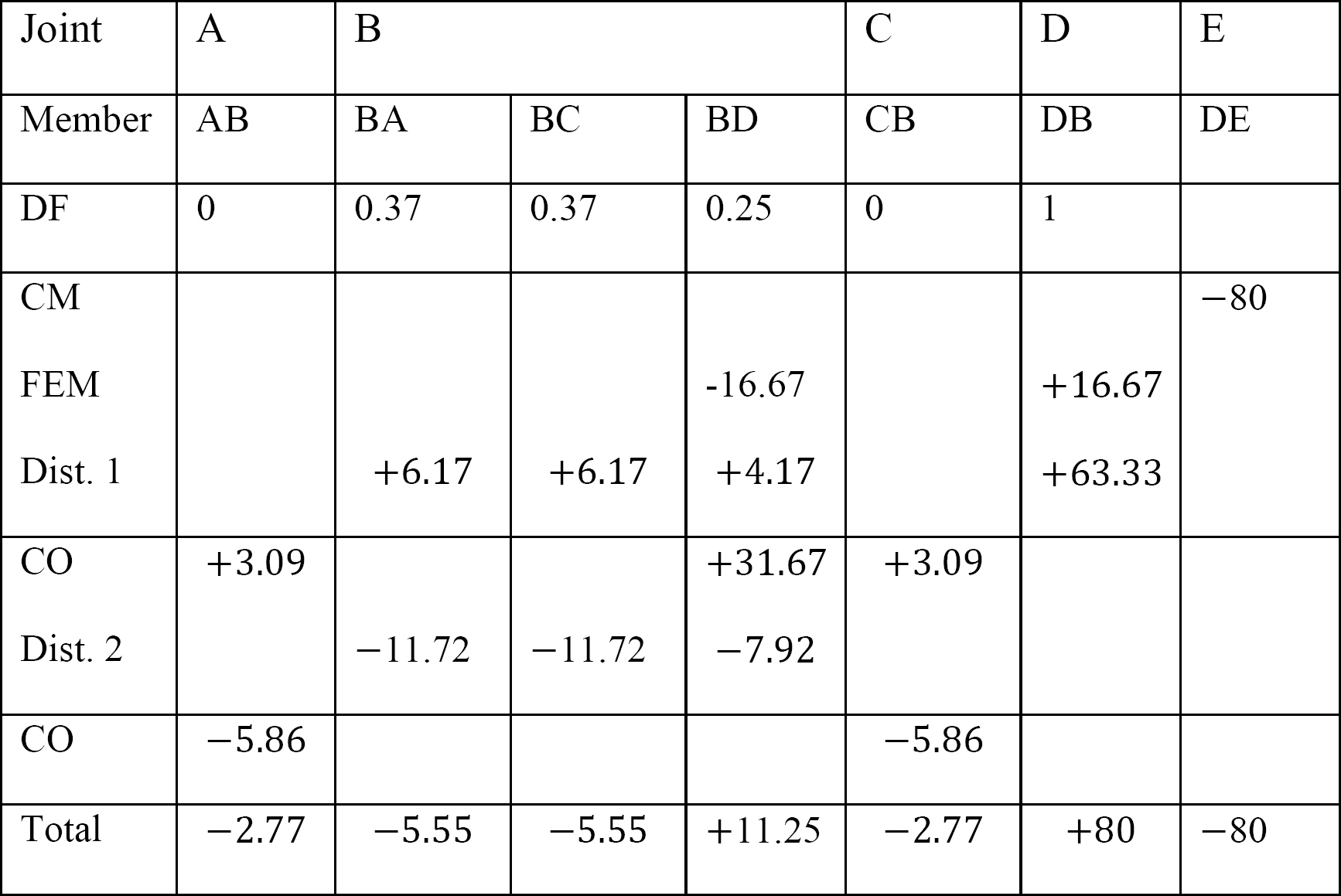
laatste lid einde momenten.
MAB = -2,77 K. ft
MBA = -5,55 k. ft
MBC = -5,55 k. ft
MBD = + 11,25 k. Ft
MCB = -2,77
MDB = +80 K. Ft
MDE = -80 K. Ft
voorbeeld 12.5
Bepaal met behulp van de momentverdelings-methode de eindmomenten op de steunen van het in Figuur 12.10 afgebeelde frame. EI = constant.
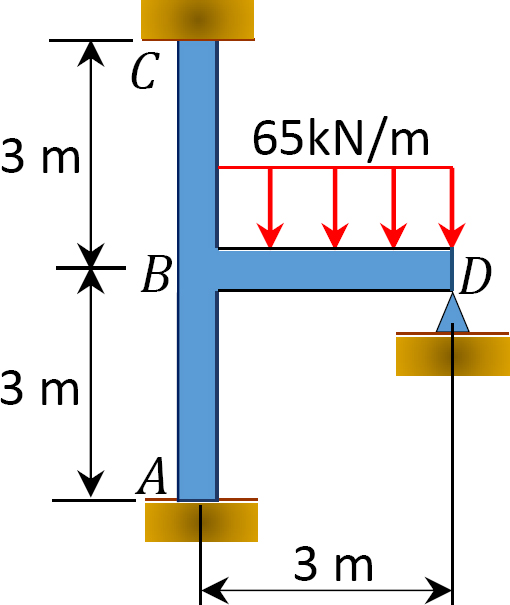
Fig. 12.10. Frame.
oplossing
vast eindmoment.
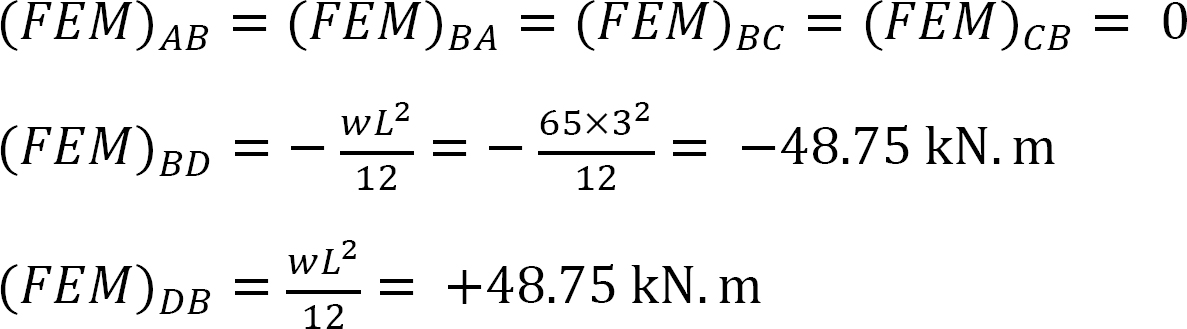
Stijfheidsfactor.
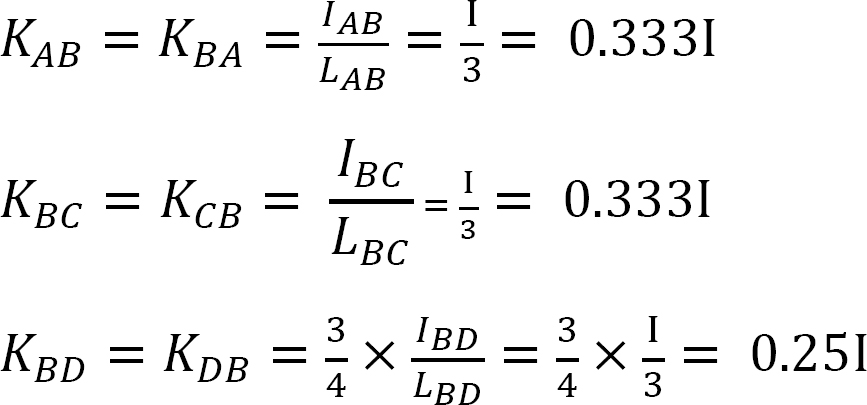
Verdelingsfactor.
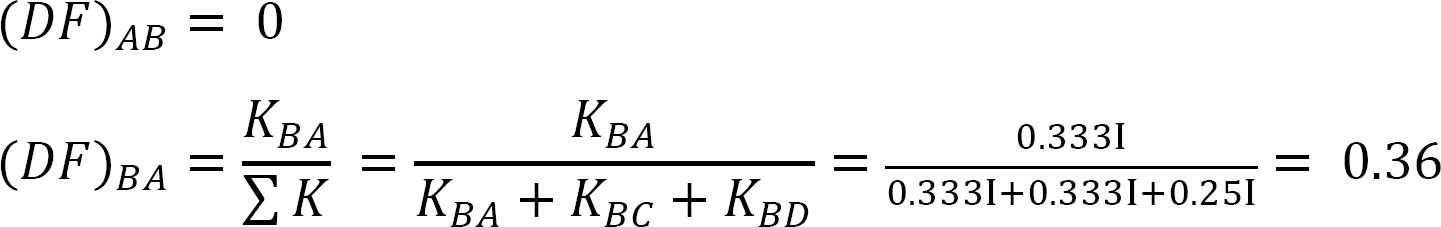

tabel 12.5. Distributie tabel.
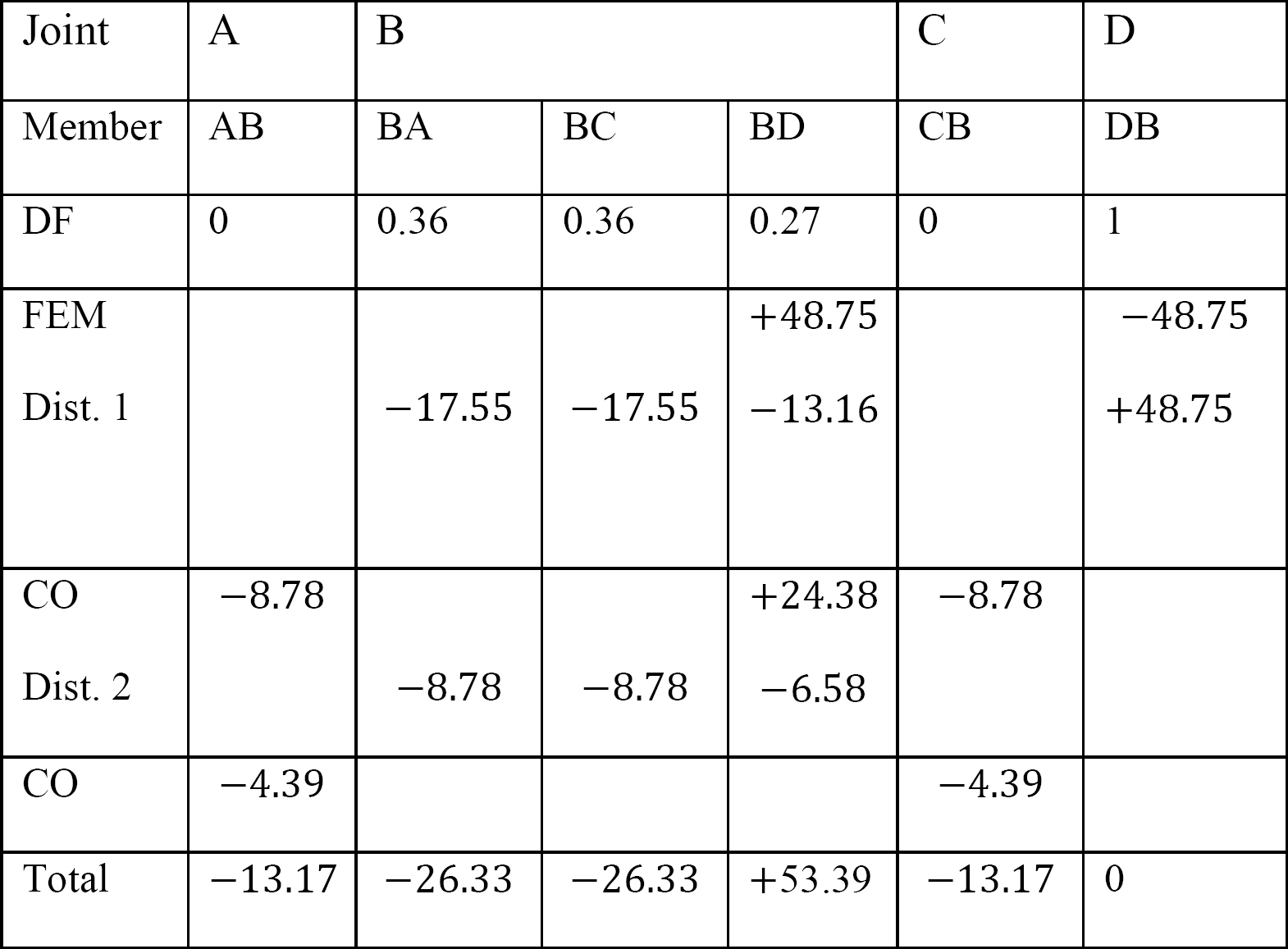
laatste lid einde momenten.
MAB = -13.17 k. ft
MBA = -26.33 k. ft
MBC = -26.33 k. ft
MBD = +53.39 k. ft
MCB = -13.17 k. ft
MDB = 0
Voorbeeld 12.6
met Behulp van het moment distributie methode, bepalen de lid-einde-momenten van het frame met kant-schagen weergegeven in Figuur 12.11 een.
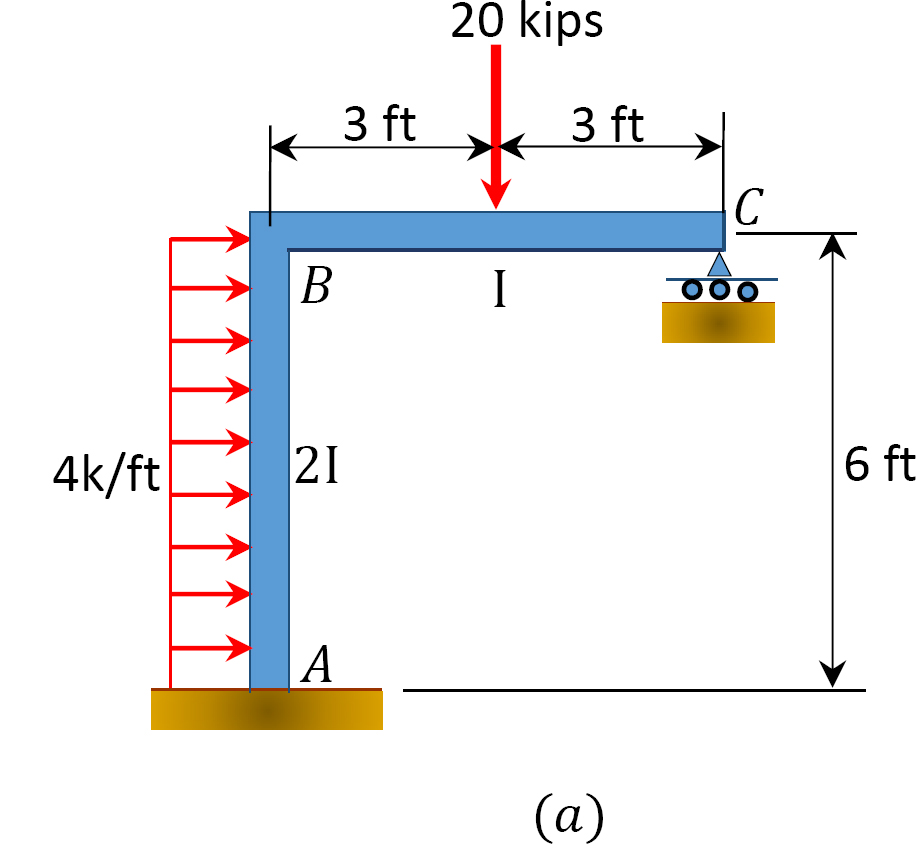
Afb. 12.11. Frame met zijdelingse zwaai.
oplossing
vast eindmoment.
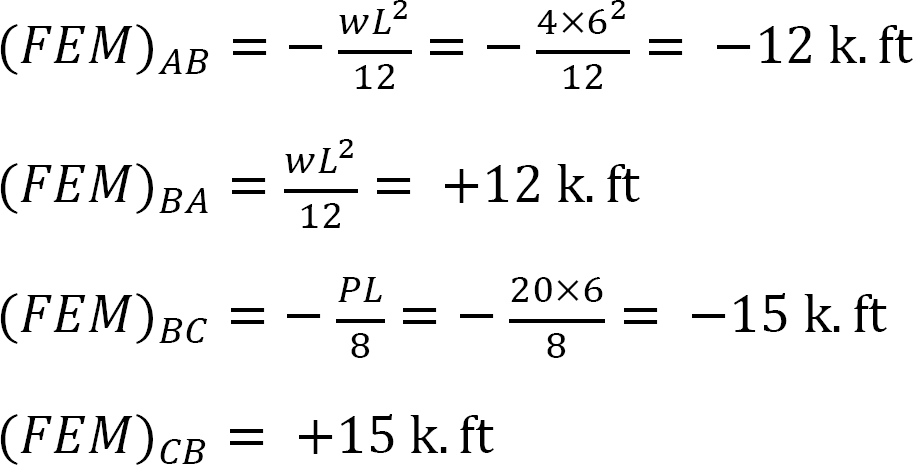
Stijfheidsfactor.
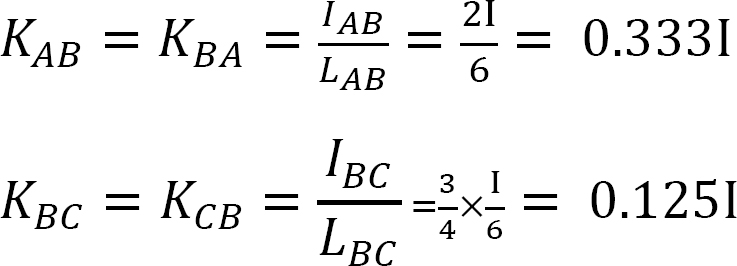
Verdelingsfactor.
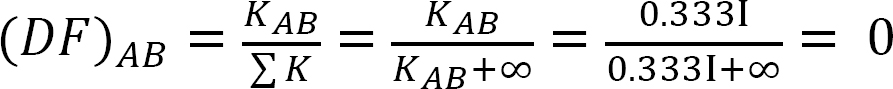

analyse van het frame zonder zijwaartse beweging.
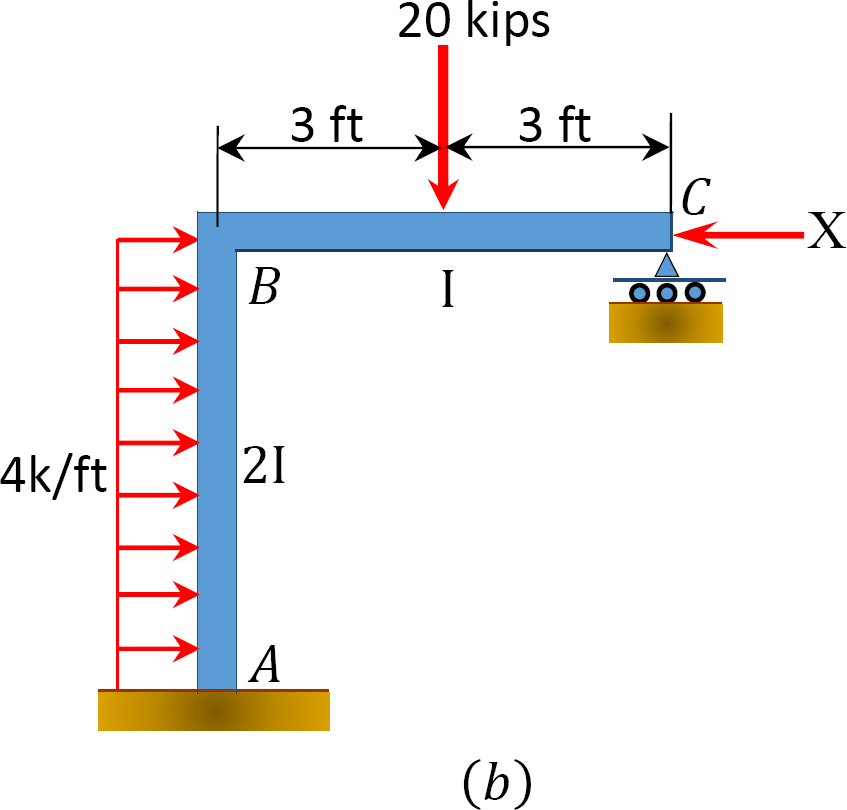
tabel 12.6. Verdeeltafel (geen sway frame).
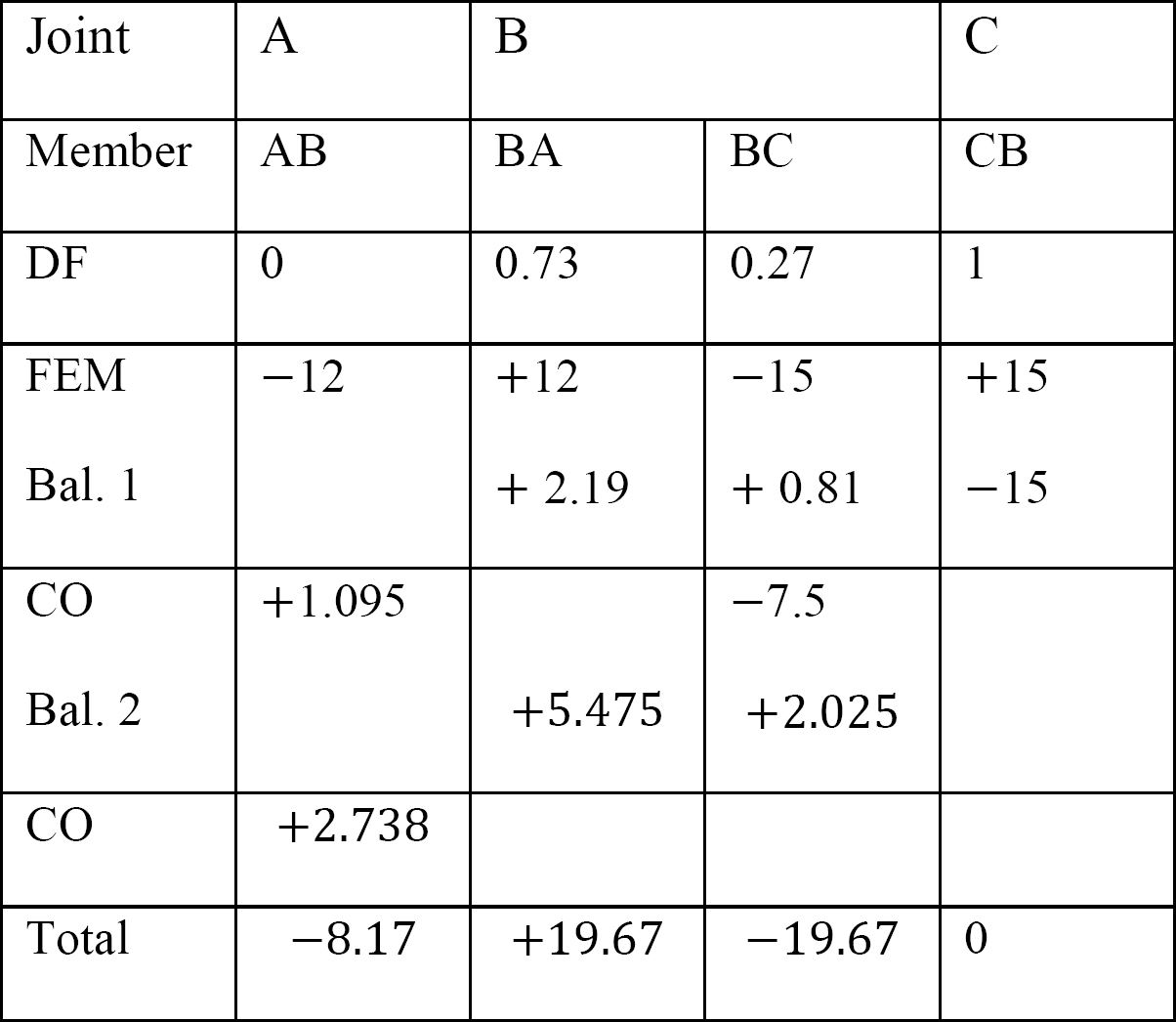
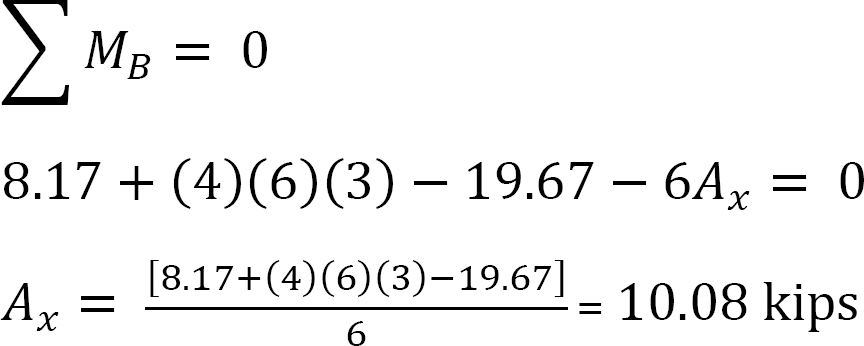
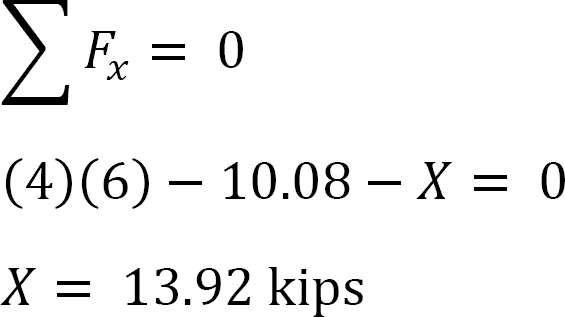
analyse van het frame met zijdelingse slingering.
stel dat MAB = + 20 k. ft
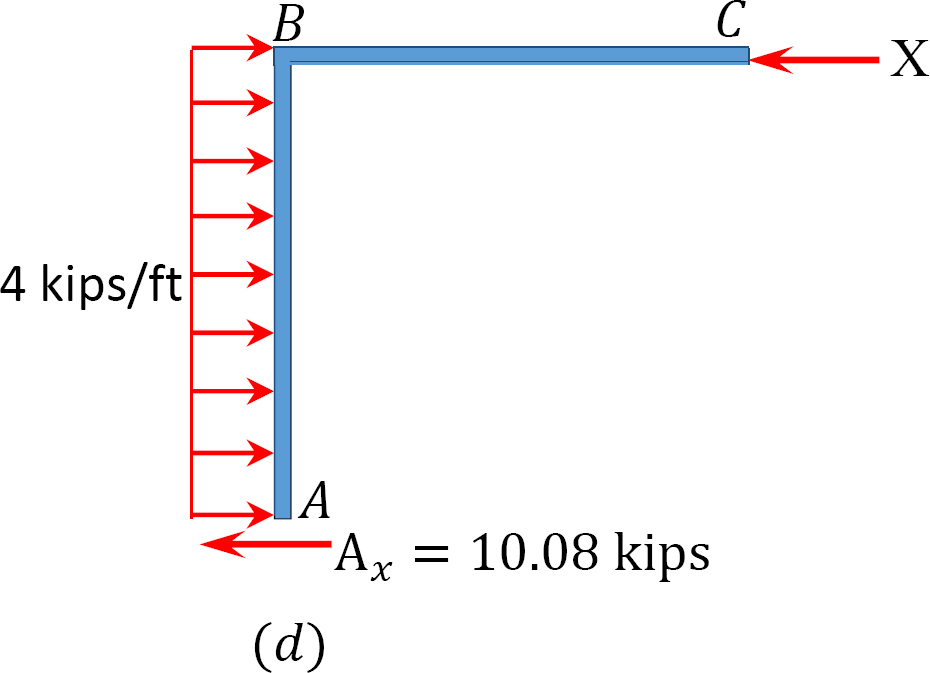
tabel 12.7. Verdeeltafel (sway frame).
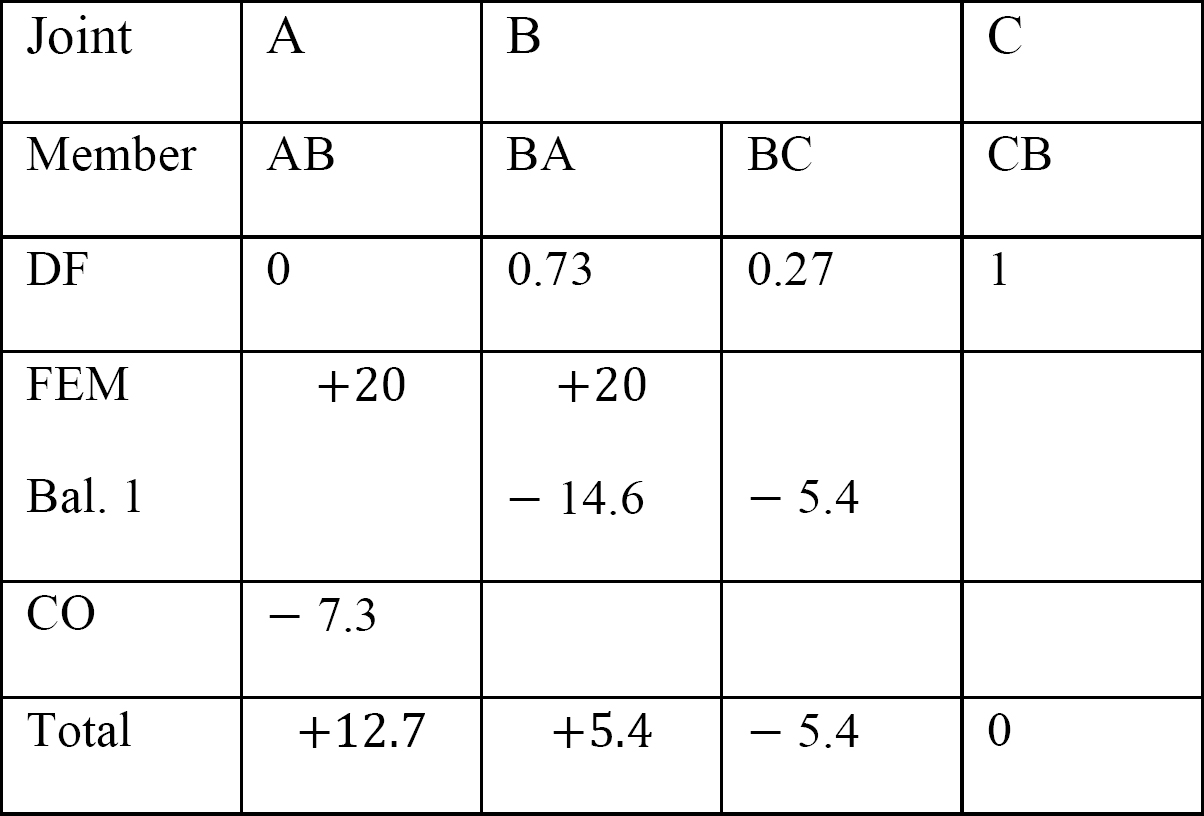
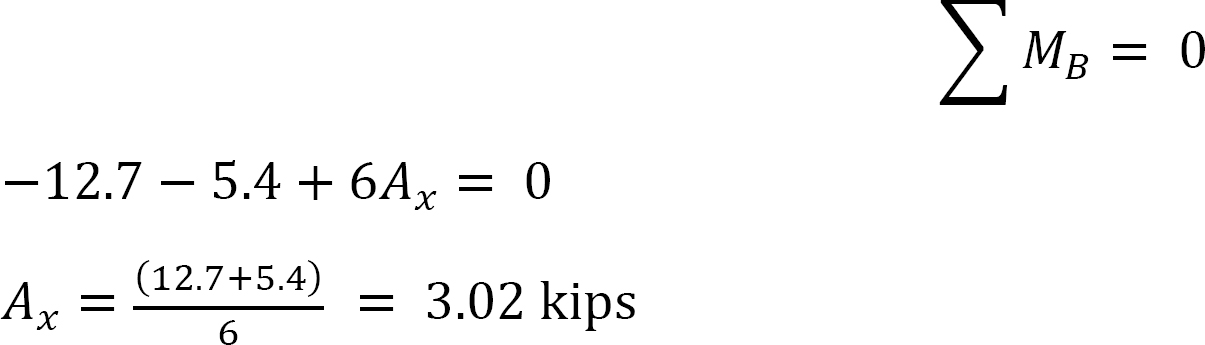
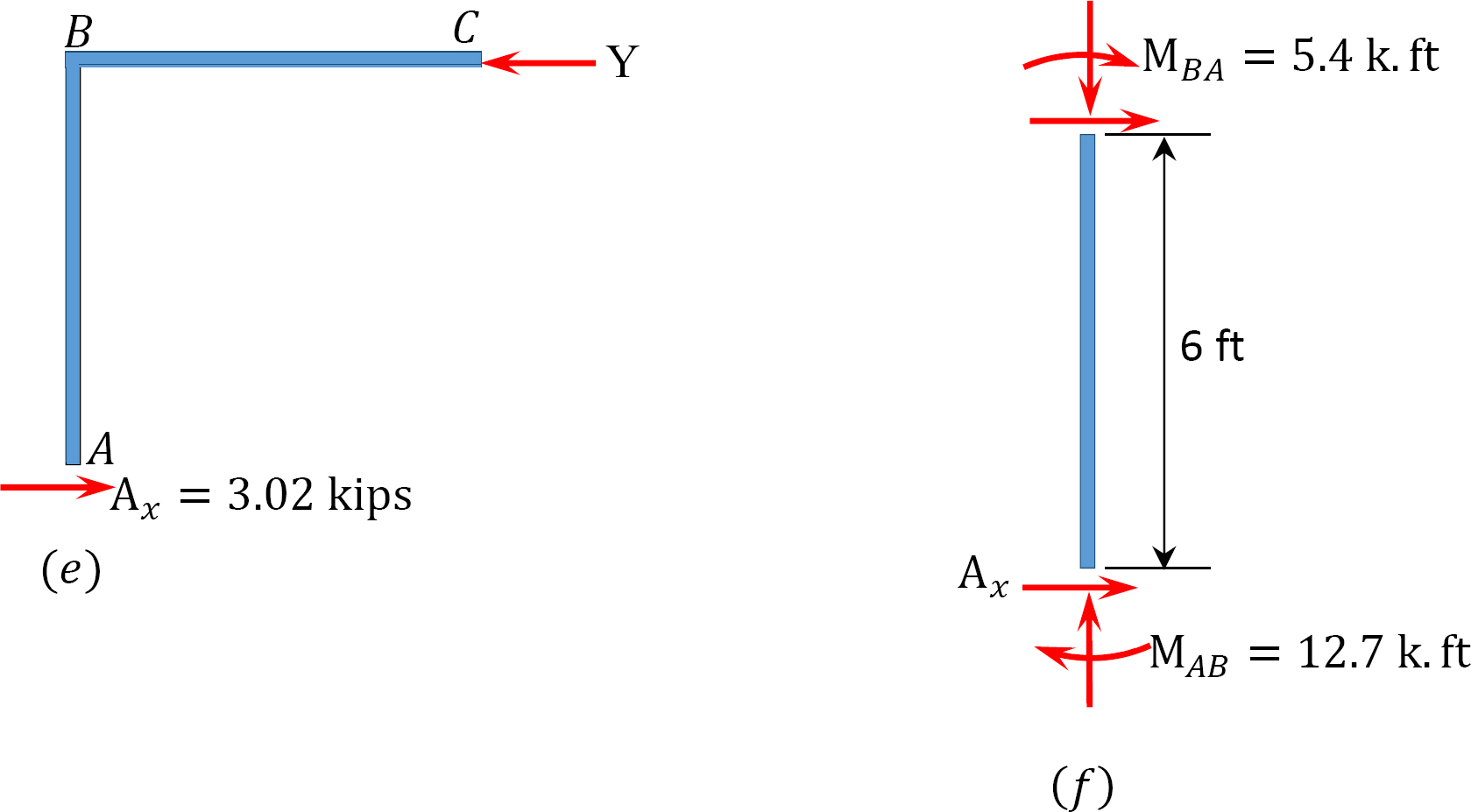
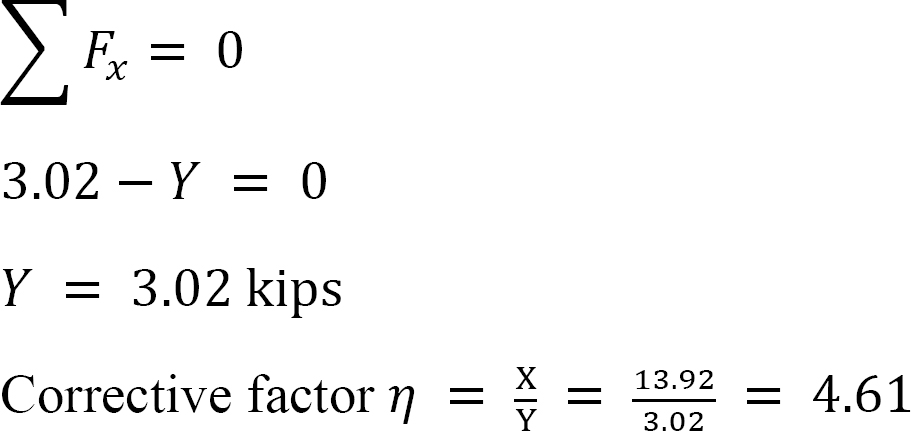
laatste momenten.
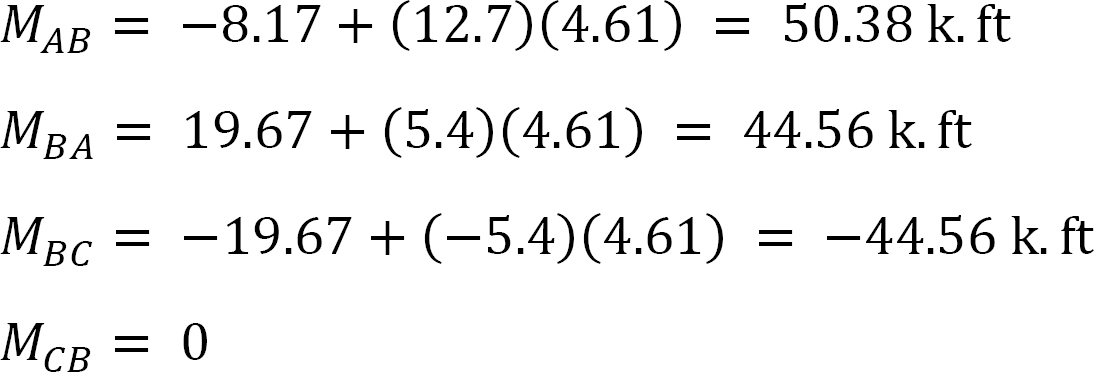
voorbeeld 12.7
een sway frame wordt geladen zoals afgebeeld in Figuur 12.12 a. met behulp van de moment distributie methode, bepalen de eindmomenten van de leden van het frame.
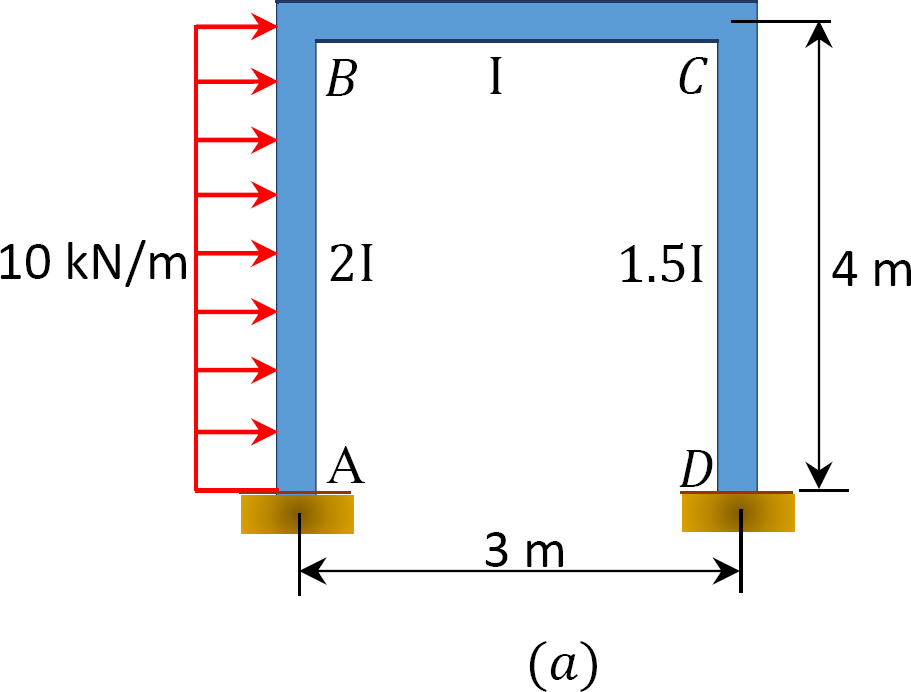
Fig. 12.12. Geladen sway frame.
oplossing
vast eindmoment.
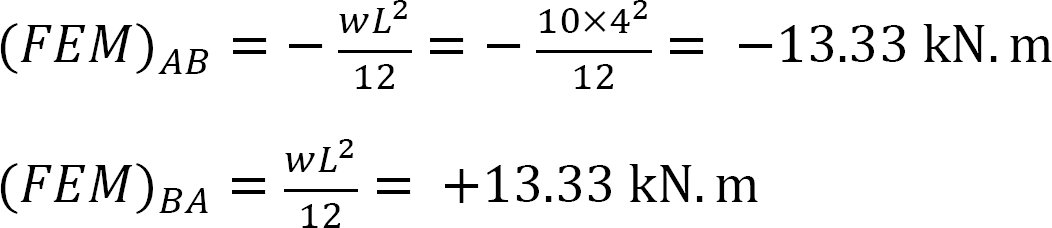
Stijfheidsfactor.
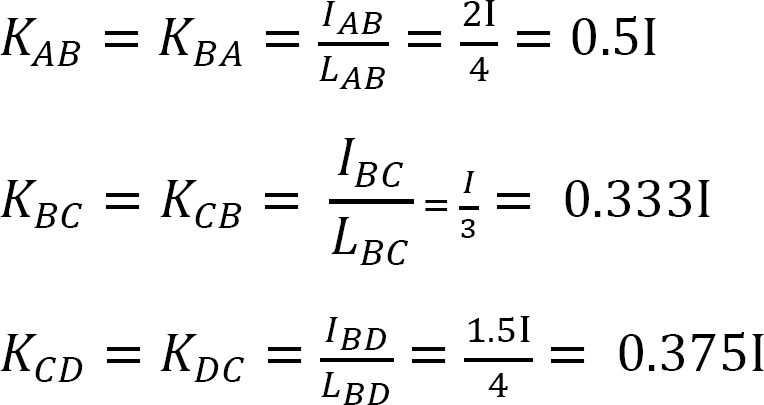
Verdelingsfactor.

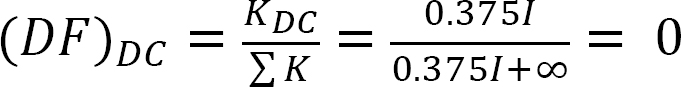
analyse van het frame zonder zijwaartse beweging.
tabel 12.8. Verdeeltafel (geen sway frame).
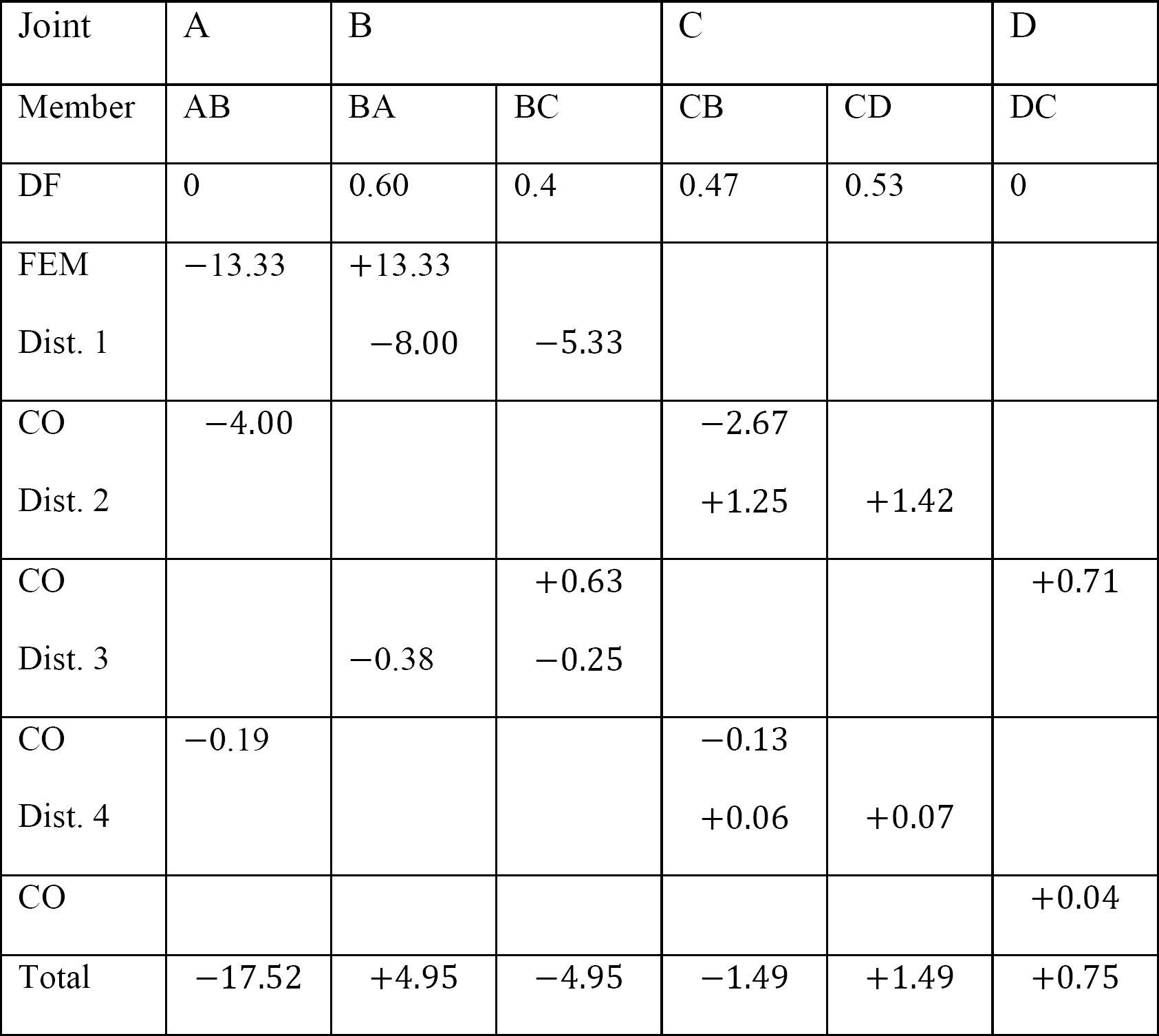
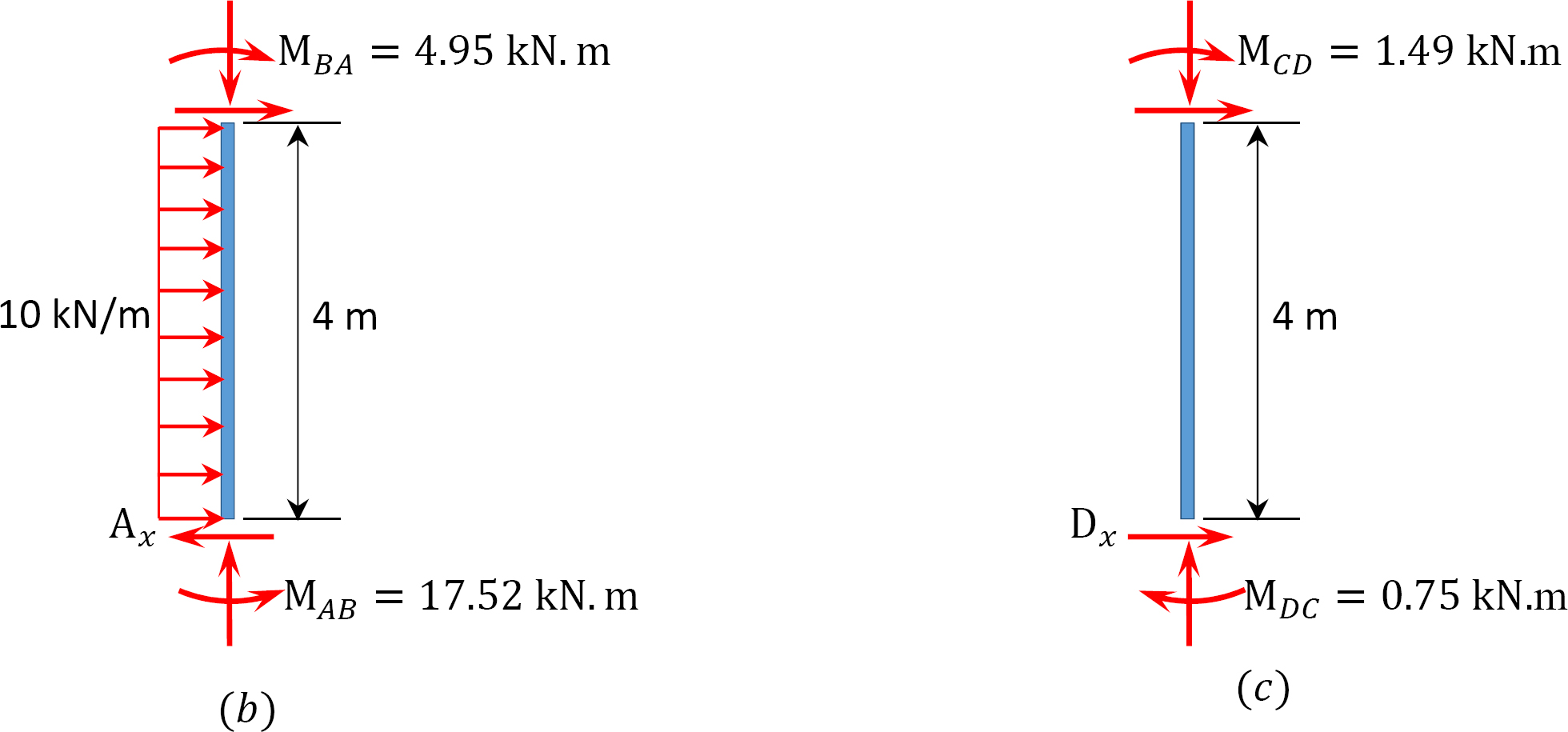
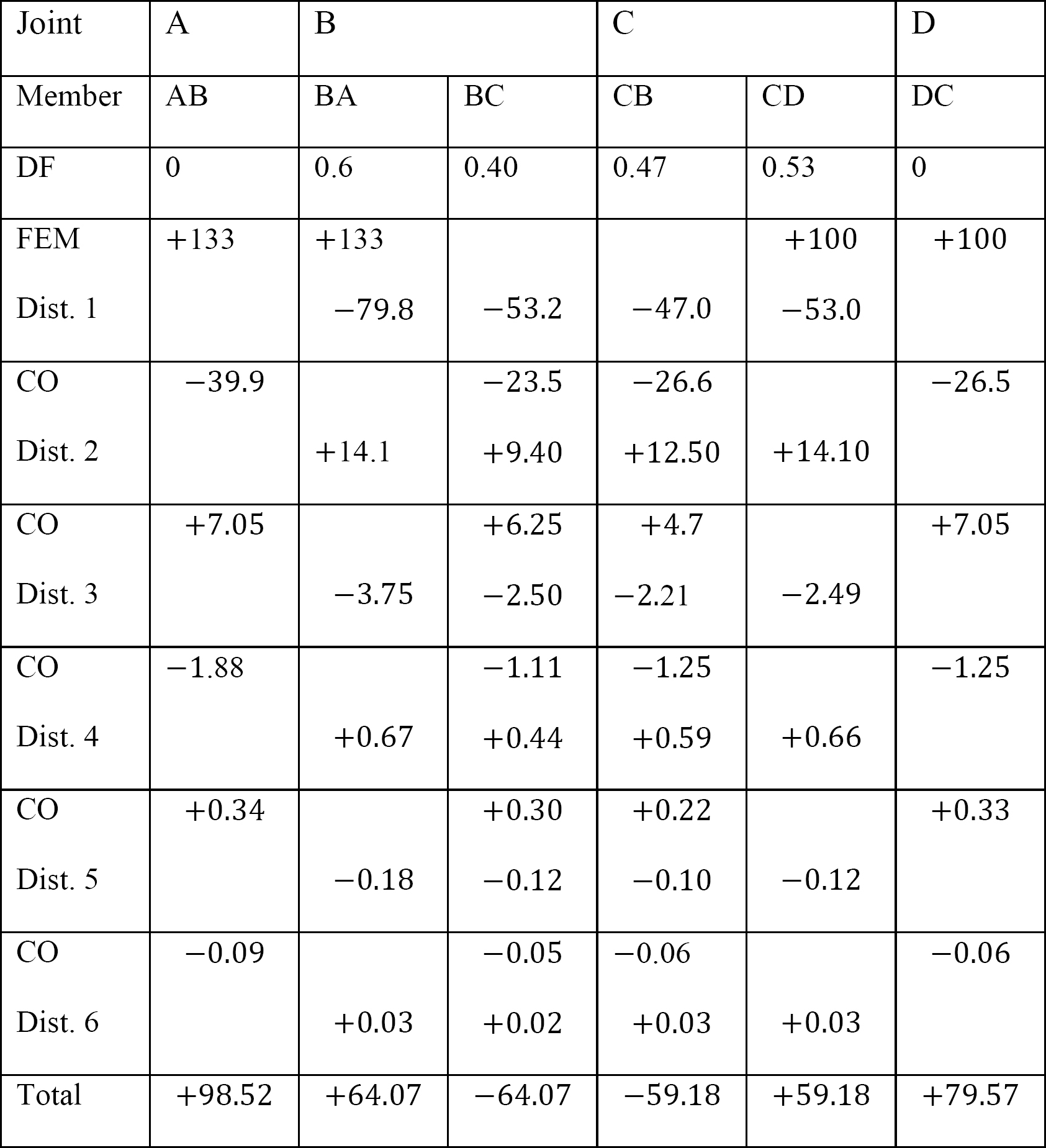
tabel 12.9. Verdeeltafel (sway frame).
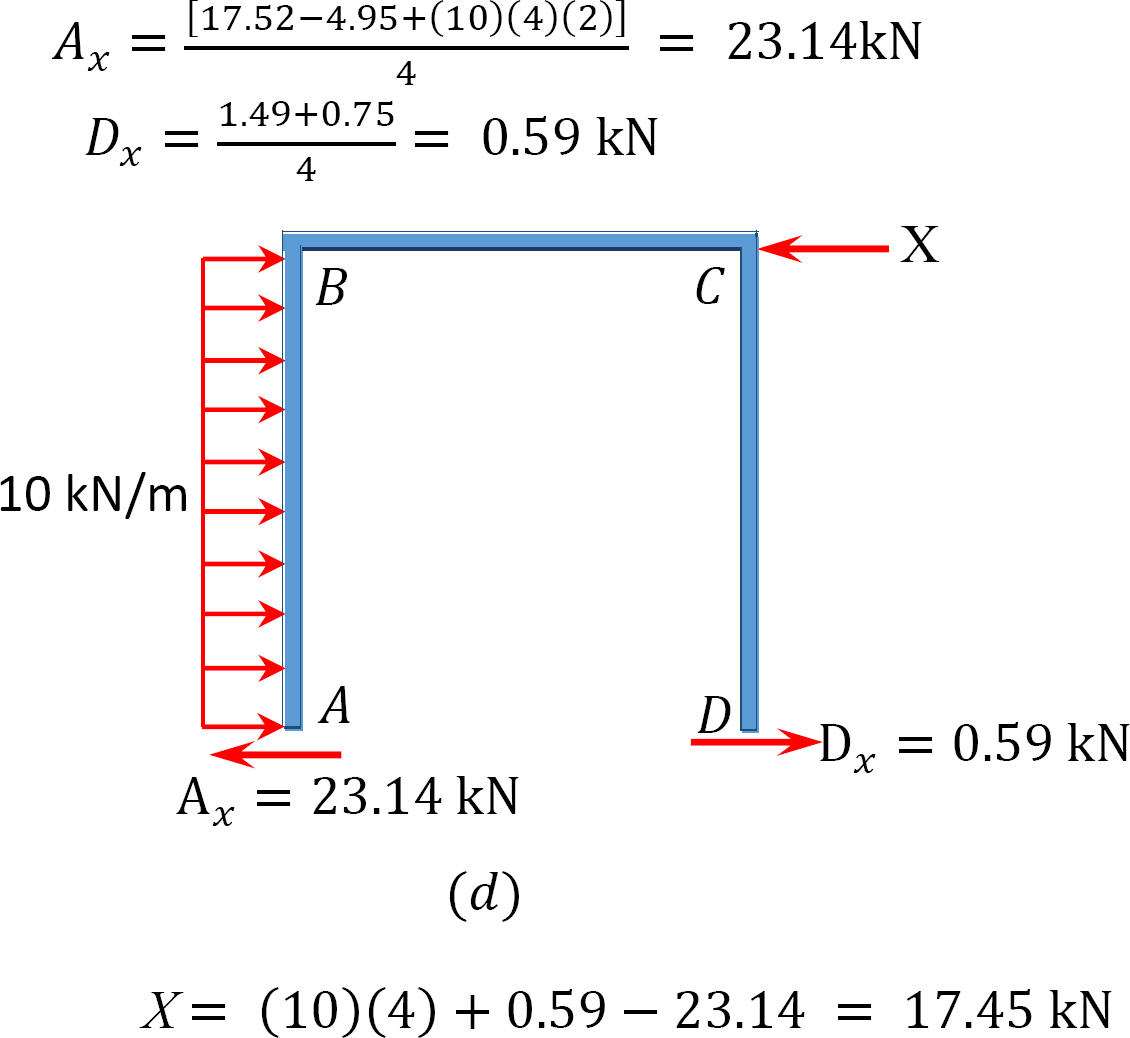
analyse van het frame met zijdelingse slingering.
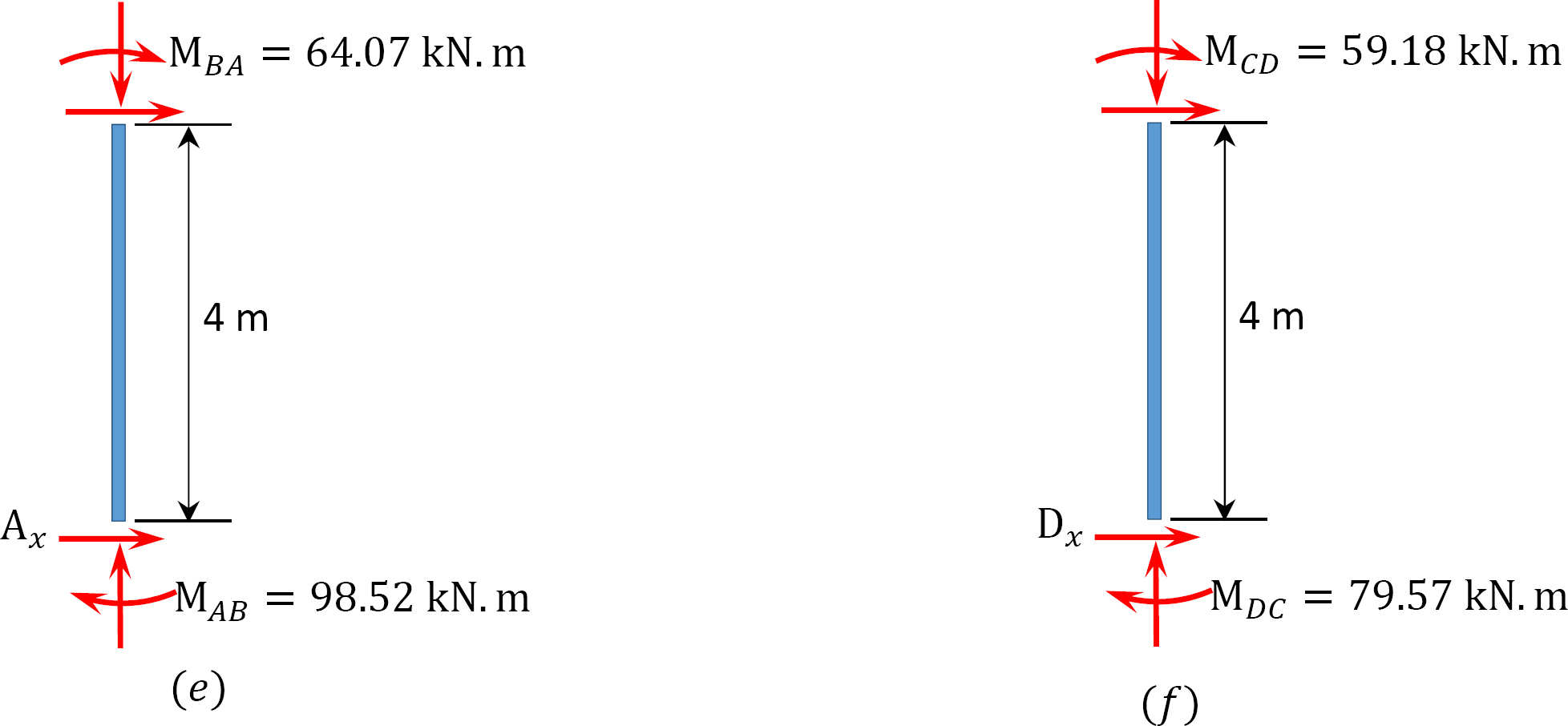

laatste moment.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Hoofdstuksamenvatting
Momentverdeling analysemethode voor onbepaalde structuren: de analysemethode voor momentverdeling is een benaderende analysemethode. De mate van nauwkeurigheid is afhankelijk van het aantal herhalingen. Bij deze methode wordt aangenomen dat alle verbindingen in een structuur tijdelijk worden vergrendeld of geklemd en dus worden voorkomen dat mogelijke rotatie. Belastingen worden toegepast op de leden, en de momenten ontwikkeld aan het lid eindigt als gevolg van fixiteit worden bepaald. Gewrichten in de structuur worden vervolgens achtereenvolgens ontgrendeld en het onevenwichtige moment bij elke joint wordt verdeeld onder de leden die in die joint bijeenkomen. Overdracht momenten aan de verre uiteinden van leden worden bepaald, en het proces van balanceren wordt voortgezet tot het gewenste niveau van nauwkeurigheid. De eindmomenten van leden worden bepaald door het vaste eindmoment, het gedistribueerde moment en het overdrachtmoment op te tellen. Zodra de eindmomenten van de leden zijn bepaald, wordt de structuur bepaald.
Oefenproblemen
12.1 Gebruik de momentverdelingsmethode om het eindmoment van de in Figuur P12.1 tot en met Figuur P12.12 afgebeelde balken te berekenen en teken het buigmoment-en afschuifkrachtdiagrammen. EI = constant.
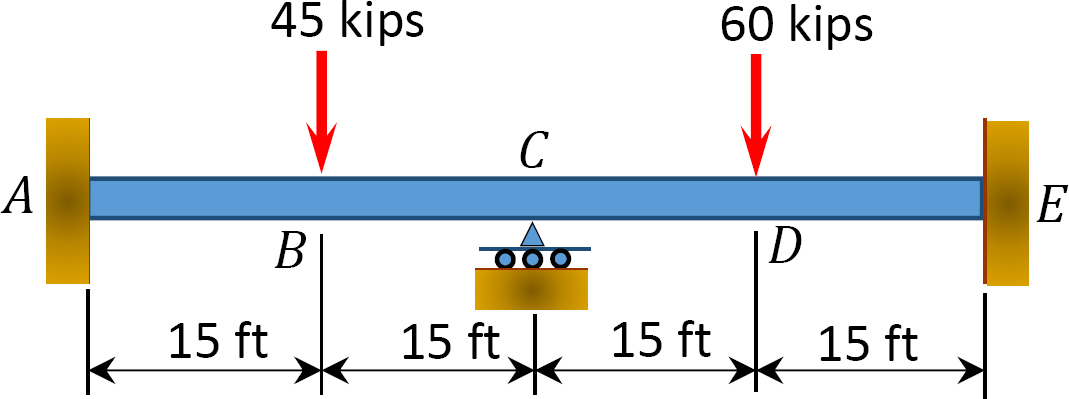
Fig. P12. 1. Balk.
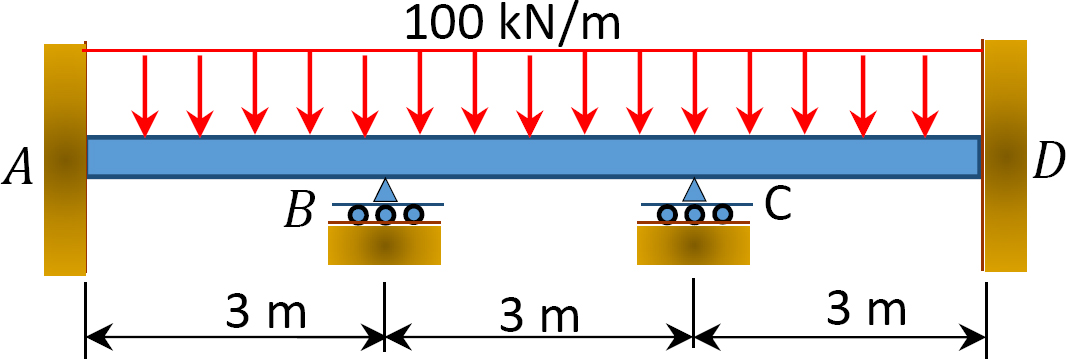
Fig. P12. 2. Balk.
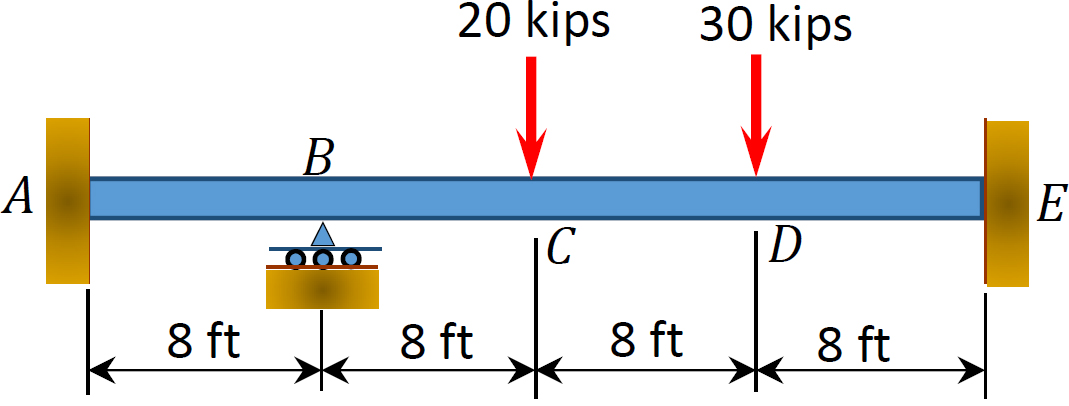
Fig. P12. 3. Balk.
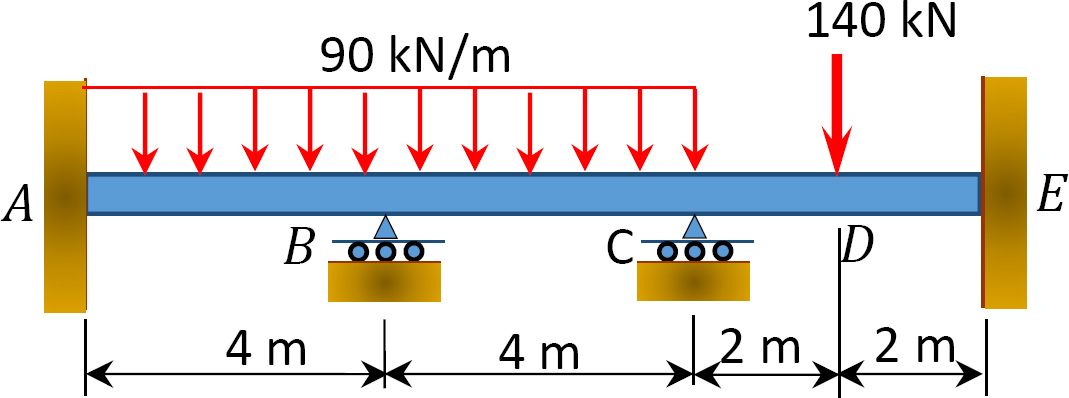
Fig. P12. 4. Balk.
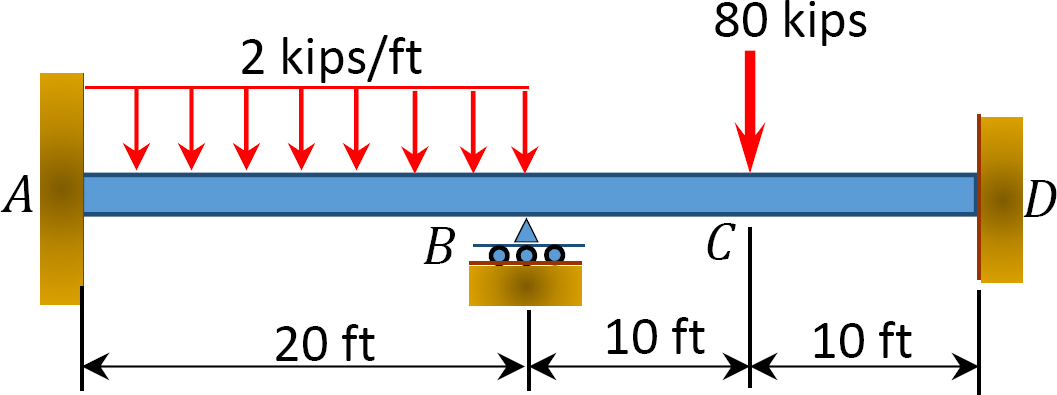
Fig. P12. 5. Balk.
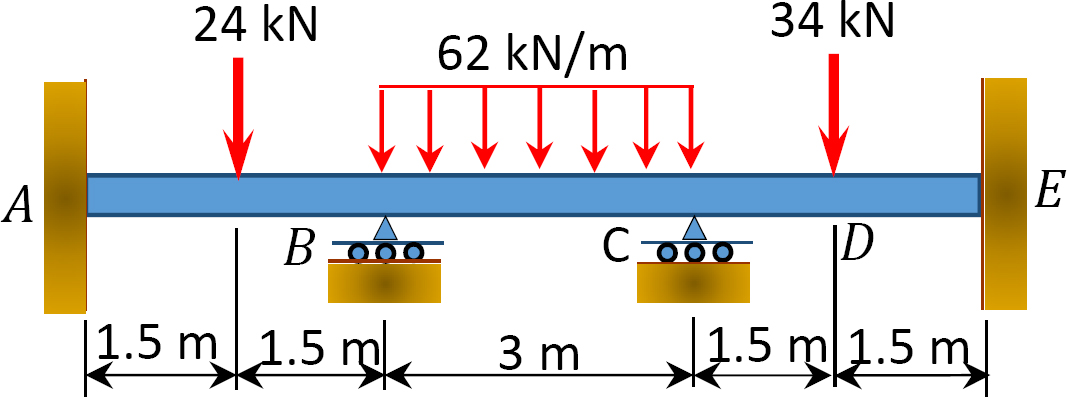
Fig. P12. 6. Balk.
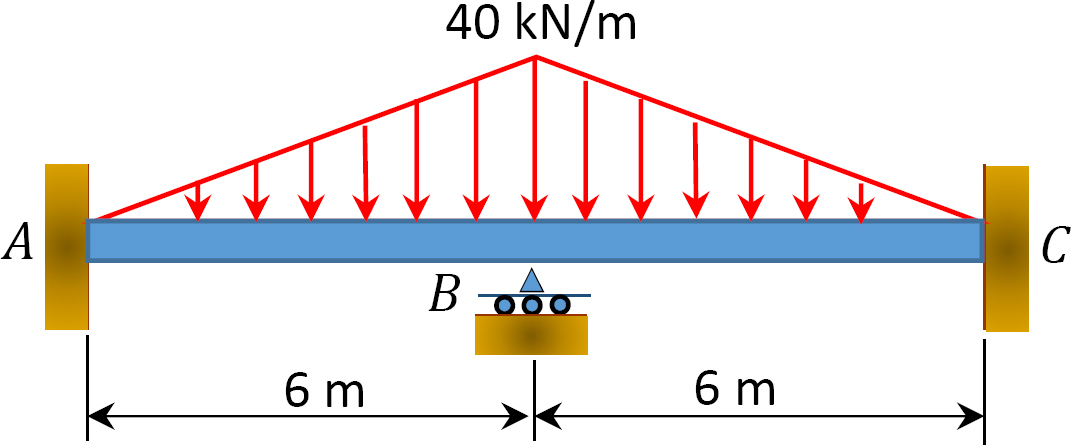
Fig. P12. 7. Balk.
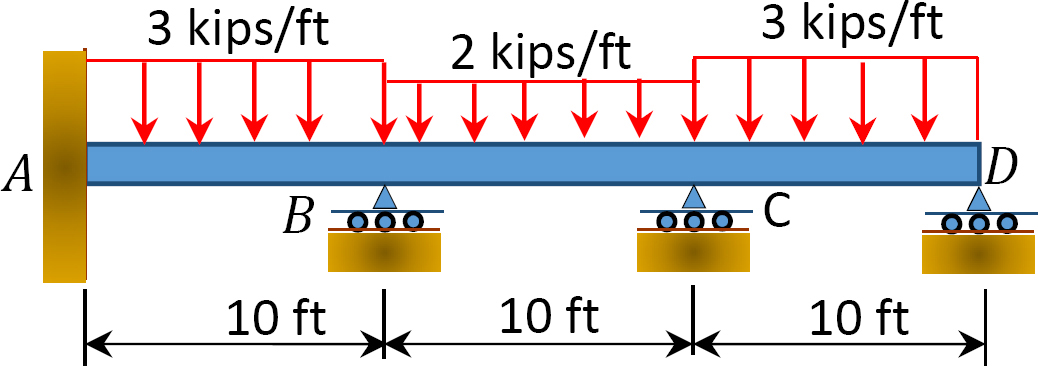
Fig. P12, 8. Balk.
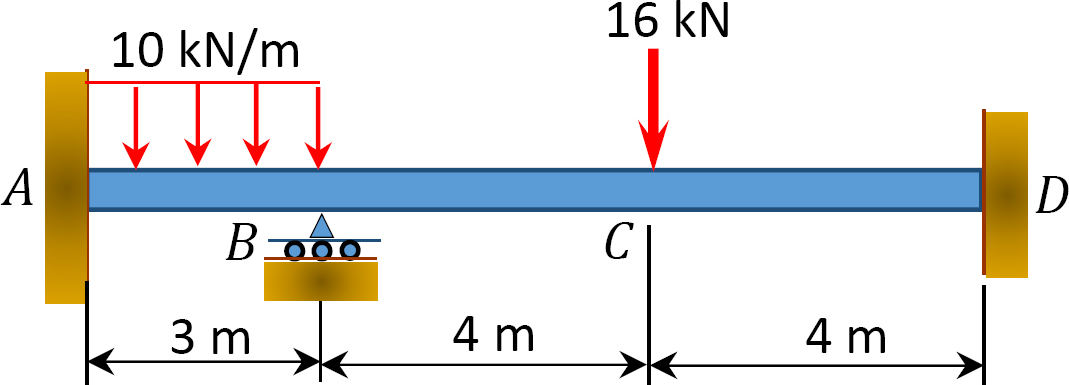
Fig. P12. 9. Balk.
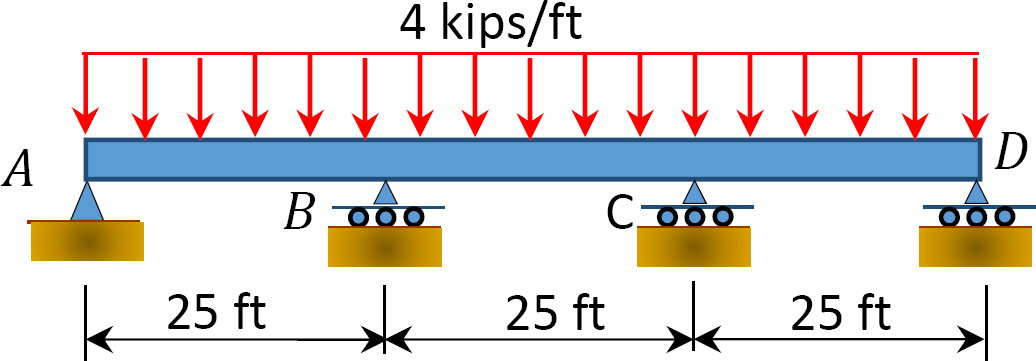
Fig. P12. 10. Balk.
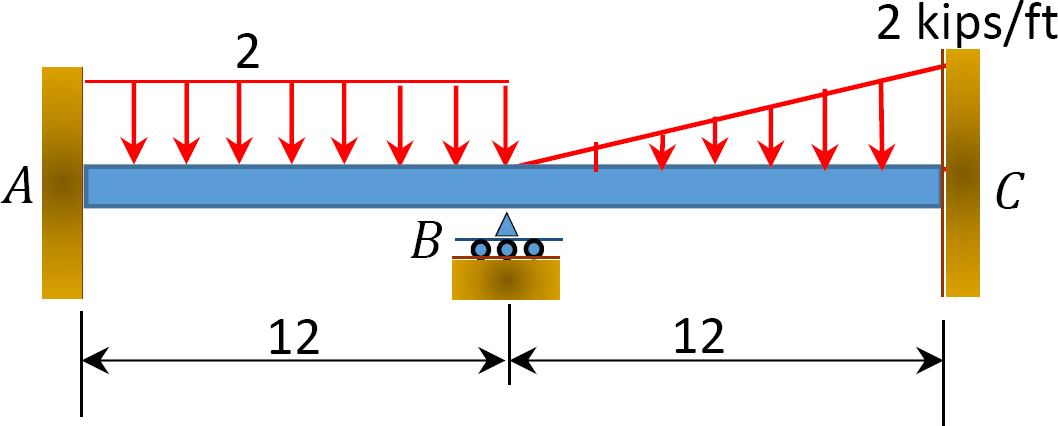
Fig. P12. 11. Balk.
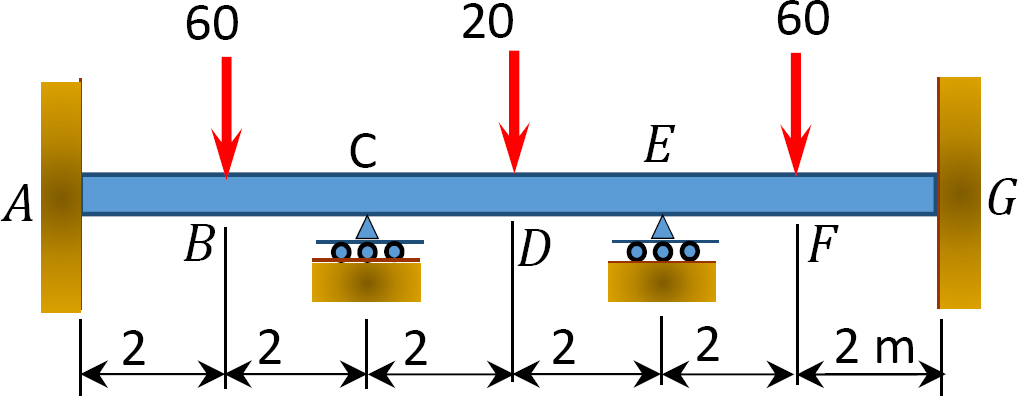
Fig. P12. 12. Balk.
12.2 gebruik de methode voor de verdeling van het moment om het eindmoment van de frames in Figuur P12.13 tot en met Figuur 12.20 te berekenen en teken de schema ‘ s van het buigmoment en de schuifkracht. EI = constant.
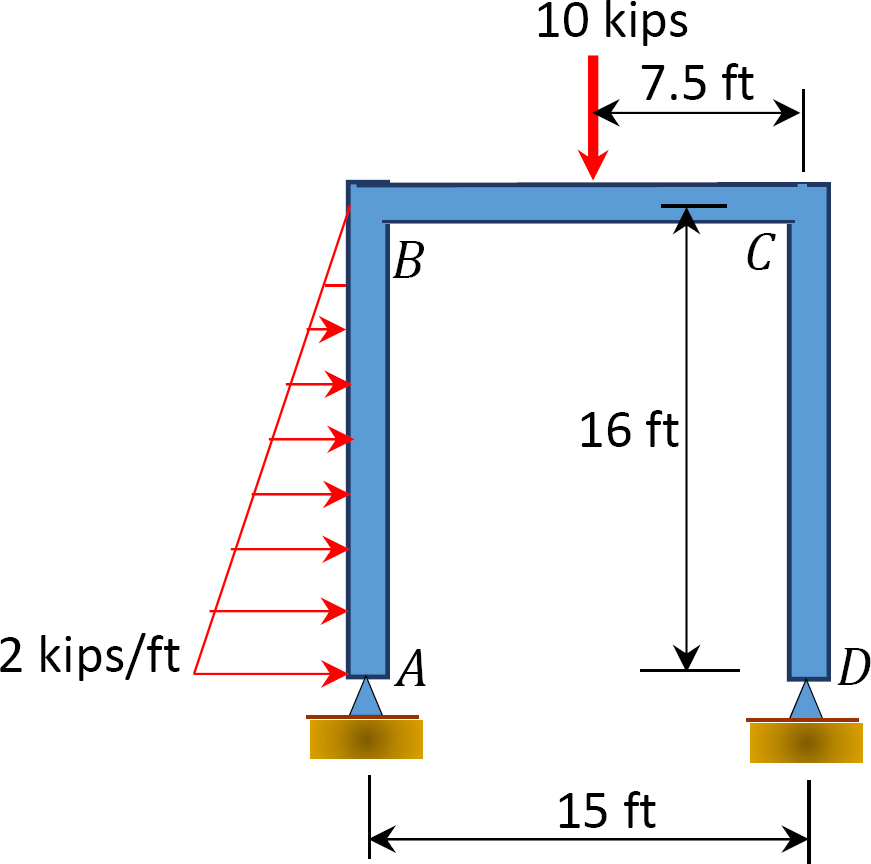
Fig. P12. 13. Frame.
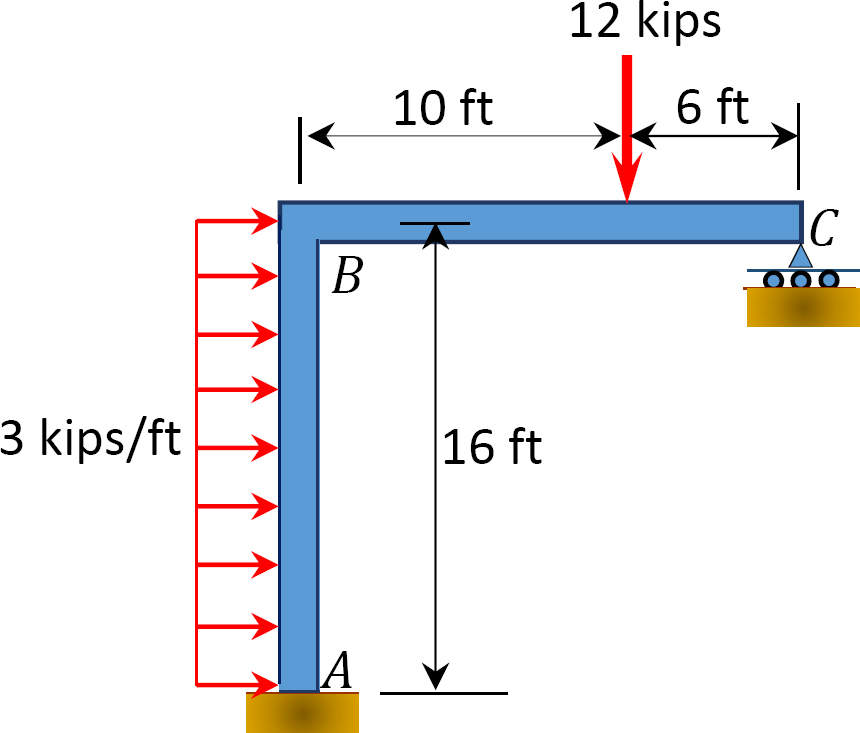
Fig. P12. 14. Frame.
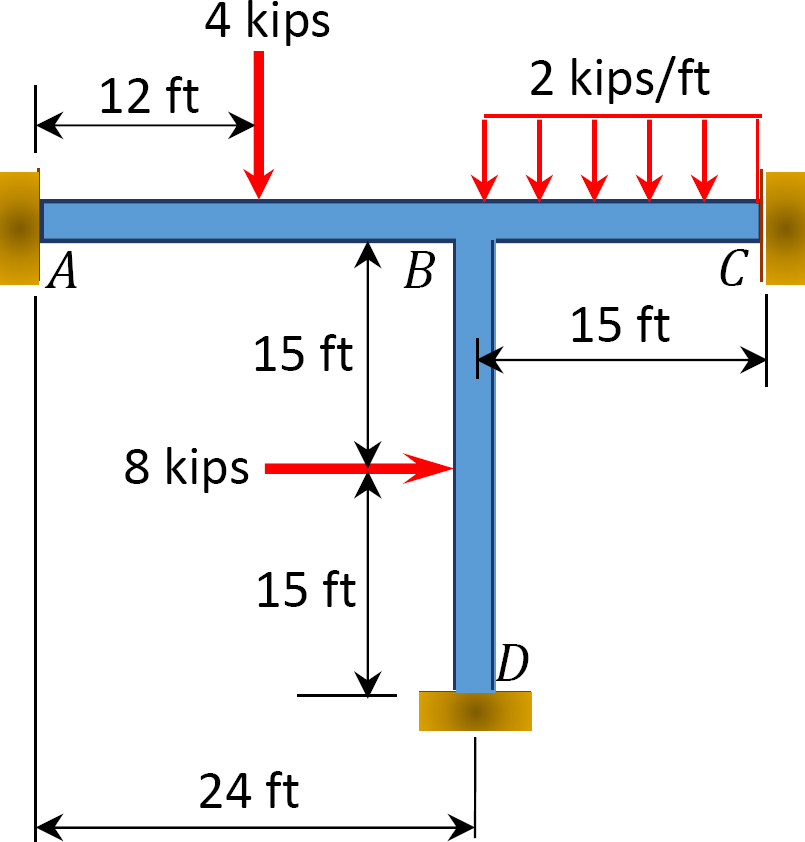
Fig. P12. 15. Frame.
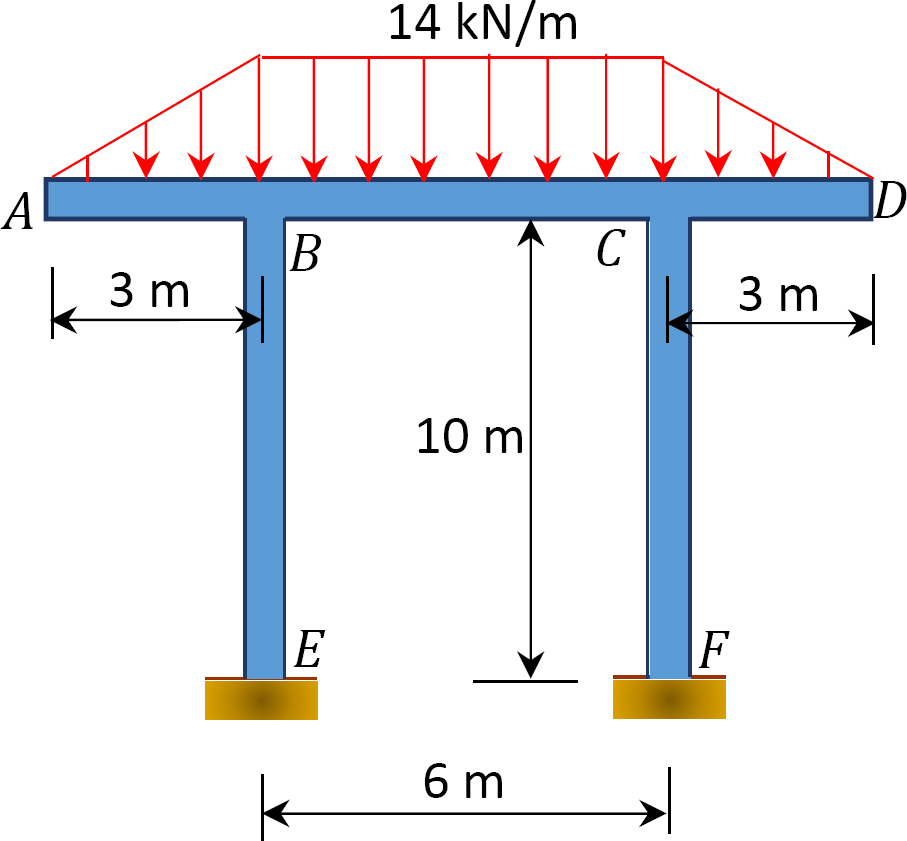
Fig. P12.16. Frame.
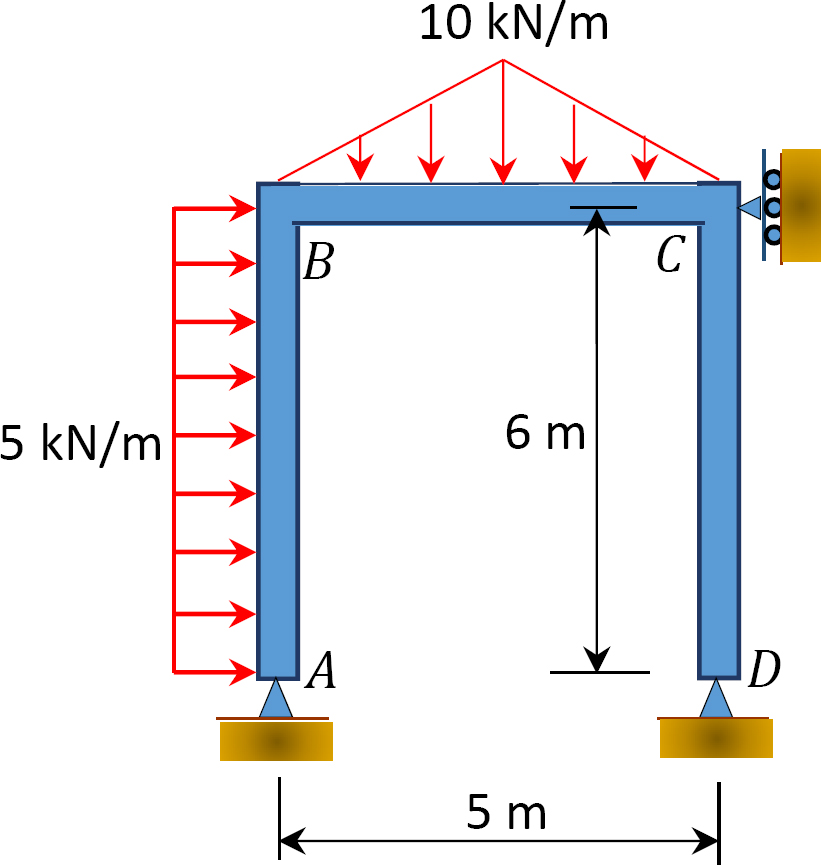
Fig. P12.17. Frame.
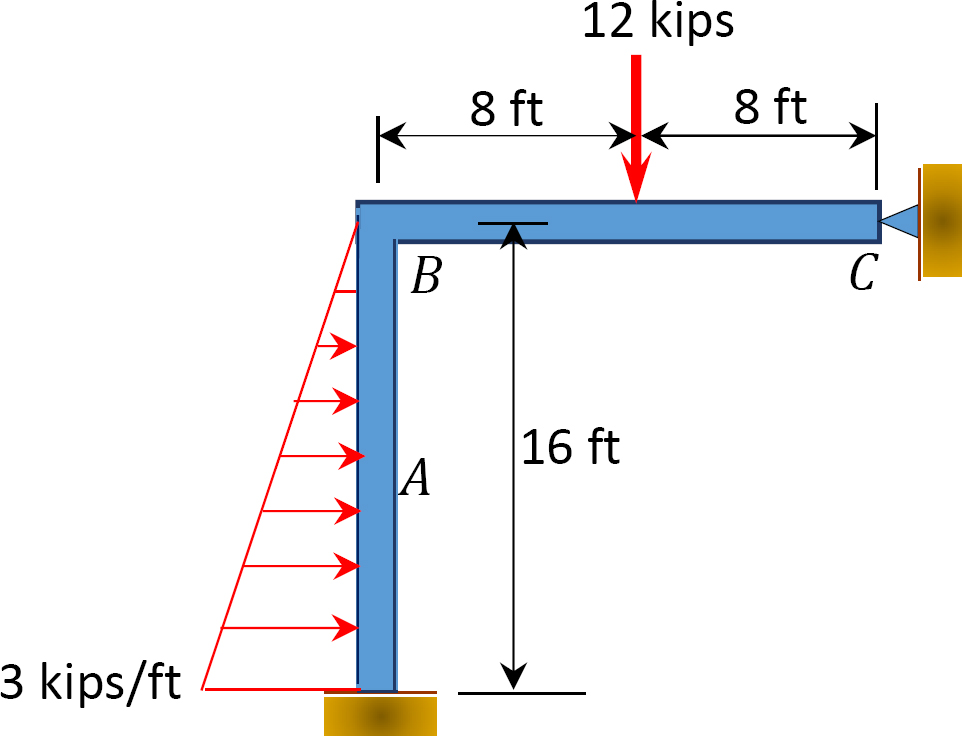
Fig. P12.18. Frame.
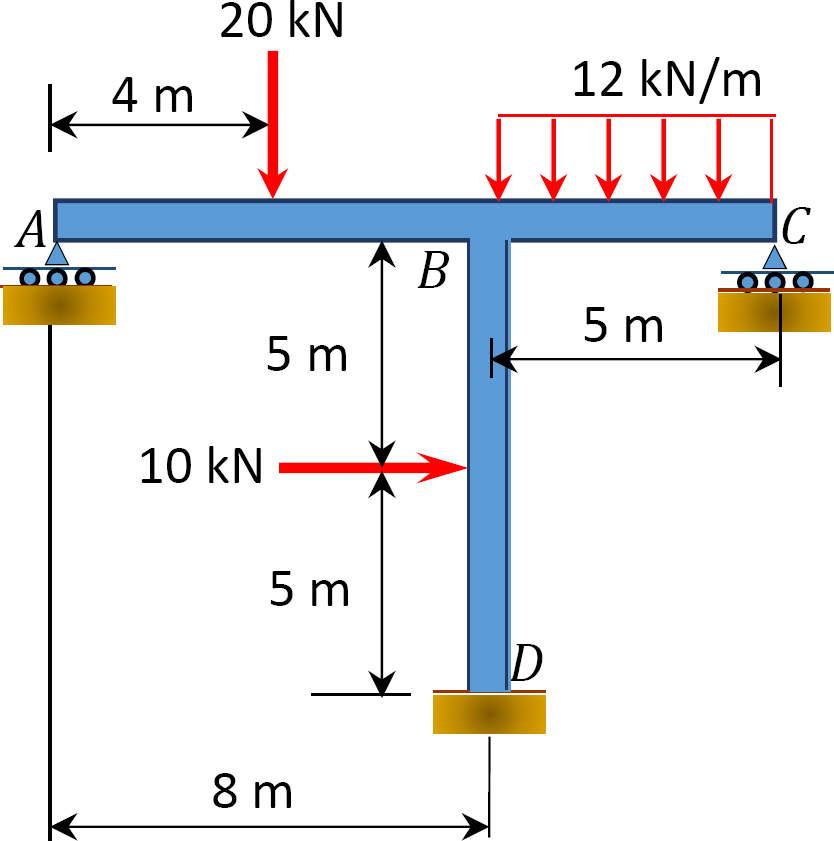
Fig. P12.19. Frame.
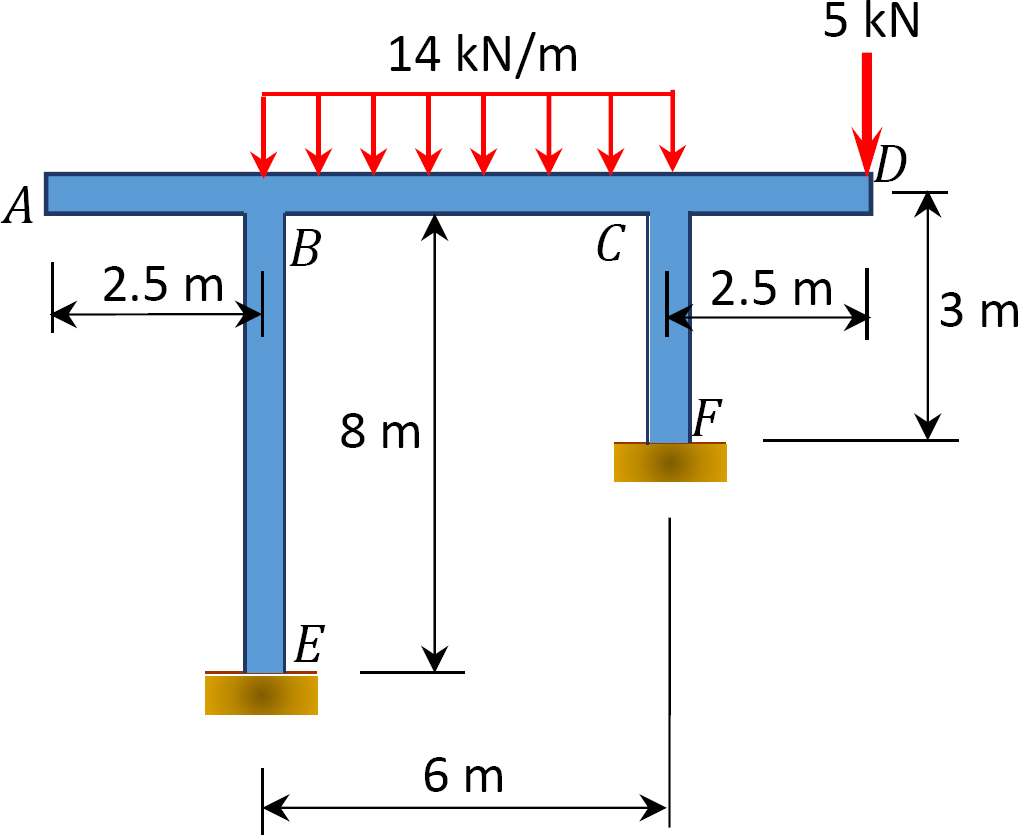
Fig. P12.20. Frame.