Toepassen en interpreteren van het principe van Saint-Venant

alle bouwkundig ingenieurs gebruiken het principe van Saint-Venant, actief of onbewust. U kunt verschillende formuleringen van dit principe in de meeste structurele mechanica leerboeken vinden, maar de exacte betekenis ervan is niet duidelijk. Het principe van Saint-Venant vertelt ons dat de exacte verdeling van een lading niet belangrijk is ver weg van het beladen gebied, zolang de resulterende van de lading correct zijn. In deze blogpost zullen we het principe van Saint-Venant onderzoeken, met name in de context van eindige elementen (FE) analyse.

de geschiedenis van het principe van Saint-Venant

de Franse wetenschapper Barré de Saint-Venant formuleerde zijn beroemde principe in 1855, maar het was meer een observatie dan een strikte wiskundige verklaring:

“Als de krachten op een klein gedeelte van het oppervlak van een elastische lichaam worden vervangen door een ander statisch gelijkwaardig systeem van krachten die op hetzelfde deel van het oppervlak, deze herverdeling van lading produceert een aanzienlijke wijziging in de stress lokaal, maar heeft een verwaarloosbaar effect op de belastingen op afstanden die groot zijn in vergelijking met de afmetingen van het oppervlak waarop de krachten worden gewijzigd.”

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

portret van Saint-Venant. Afbeelding in het publieke domein, via Wikimedia Commons.Veel grote geesten binnen het vakgebied van de toegepaste mechanica-Boussinesq, Love, von Mises, Toupin en anderen-waren betrokken bij het preciezer formuleren van het principe van Saint-Venant en het leveren van wiskundige bewijzen. Zoals blijkt, is dit vrij moeilijk voor meer algemene gevallen, en onderzoek over het onderwerp is nog steeds aan de gang. (De argumentatie is soms heel levendig geweest.)

eenvoudig voorbeeld: het analyseren van spanningen op een afstand

laten we beginnen met iets heel simpels: een dunne rechthoekige plaat met een rond gat op enige afstand van de beladen rand, die axiaal wordt getrokken. Als we geïnteresseerd zijn in de spanningsconcentratie bij het gat, hoe belangrijk is dan de werkelijke belastingverdeling?

drie verschillende belastingtypes worden toegepast op de meest rechtse grens:

1. een constante axiale spanning van 100 MPa
2. een symmetrische parabolische spanningsverdeling met piekamplitude 150 MPa
3. een gecentreerde puntbelasting met dezelfde resultante als de twee vorige belastingsgevallen

zoals te zien is in de onderstaande diagrammen wordt de spanningsverdeling bij het gat niet beïnvloed door de wijze waarop de belasting wordt uitgeoefend. De sleutel hier is natuurlijk dat het gat ver genoeg van de lading is.

Von Mises stresscontouren voor de drie belastinggevallen.

een andere manier om dit scenario te visualiseren is door het gebruik van hoofdspanningspijlen. Zo ‘ n plot benadrukt het stressveld als een flux en geeft een goed gevoel voor de herverdeling.

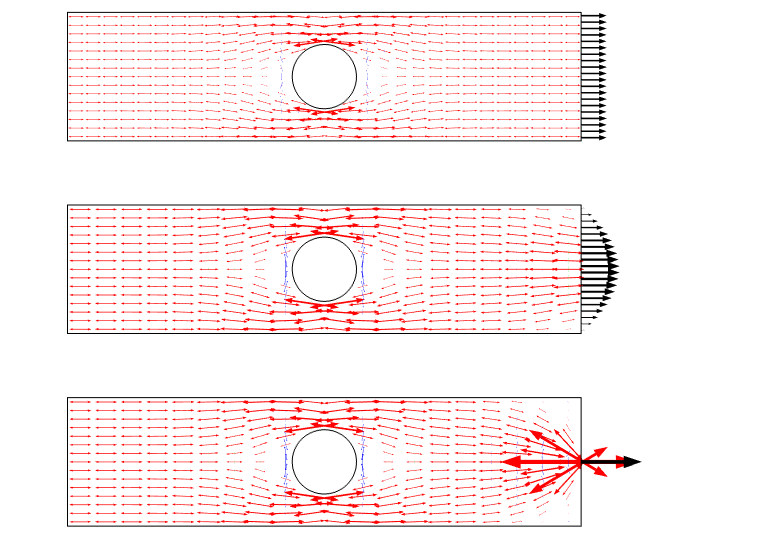
voornaamste spanningsgrafiek voor de drie belastinggevallen. Merk op dat er een singulariteit is wanneer een puntbelasting wordt gebruikt.

door de spanning langs een lijn af te beelden, kunnen we zien dat alle drie de gevallen op een afstand van de rand naar elkaar convergeren, wat ongeveer gelijk is aan de breedte van de plaat.

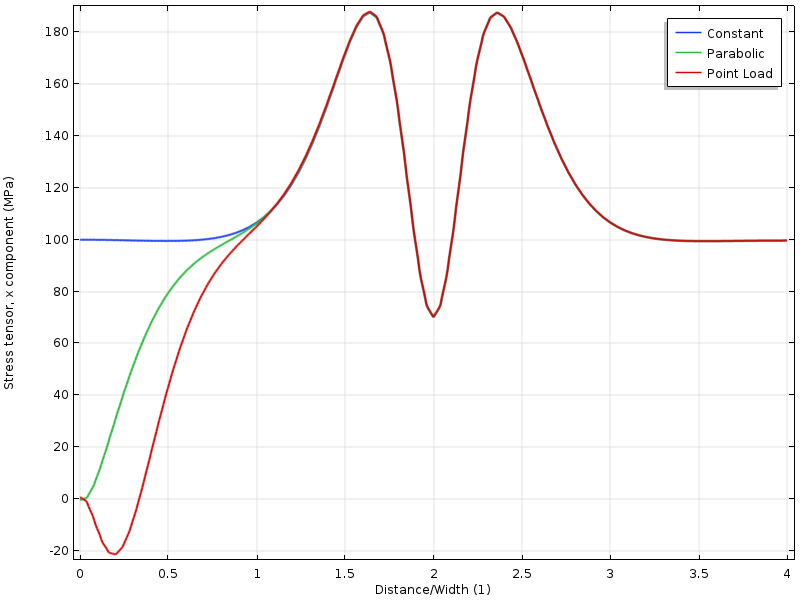
spanning langs de bovenrand als functie van de afstand tot de beladen grens. De afstand wordt genormaliseerd door de breedte van de plaat.

als het gat dichter bij de geladen grens wordt verplaatst, krijgen we een andere situatie. De spanningstoestand rond het gat hangt nu af van de verdeling van de belasting. Maar nog interessanter is dat de afstand tot waar de drie stressvelden het nu eens zijn, twee keer zo ver is van de beladen grens. De toepassing van het beginsel van Saint-Venant vereist dat de spanningen vrij kunnen worden herverdeeld. In dit geval wordt die herverdeling gedeeltelijk geblokkeerd door het gat.

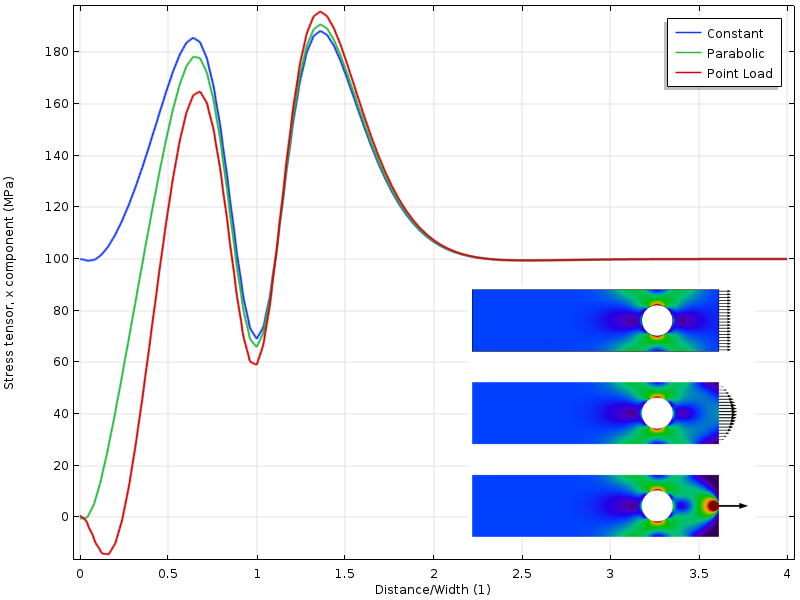
spanning langs de bovenrand met het gat dichter bij de beladen grens.

merk op dat het principe van Saint-Venant ons vertelt dat er geen verschil is in de spanningstoestand op een afstand die gelijk is aan de Orde van de lineaire dimensie van het beladen gebied. Het in aanmerking te nemen beladen gebied mag echter niet het gebied zijn dat daadwerkelijk beladen is! Deze uitspraak klinkt misschien vreemd, maar denk er zo over: als het gat ver weg is, kunnen we de stressconcentratiefactor berekenen met behulp van een handboek (mijn zegt 4.32) in plaats van met een FE-oplossing. De handleidingbenadering bevat een impliciete aanname dat de belasting gelijk is verdeeld zoals in het eerste belastinggeval. Dus zelfs als de werkelijke belasting werd toegepast op slechts een klein deel van de grens, de kritische afstand in dat geval is gerelateerd aan de grootte van de hele grens.

bij het oplossen van het probleem met behulp van de eindige-elementenmethode (FEM), kan het gat willekeurig dicht bij de belasting liggen. Wat de grens bepaalt, is dat de verdeling van de belasting vanuit fysiek oogpunt goed gedefinieerd is. Zodra we echter veronderstellingen maken over de herverdeling, is er een impliciete aanname over de verdeling van de belasting, die kan afwijken van de werkelijke.

nul resulterende systemen en Spanningsenergie-dichtheid

tot nu toe hebben we gezegd dat de spanningen op een geschikte afstand dezelfde zijn, onafhankelijk van de belastingdetails. Omdat we hier te maken hebben met lineaire elasticiteit, is het altijd mogelijk om belastinggevallen over elkaar heen te leggen. Bij het werken met bewijzen van het principe van Saint-Venant is het gemakkelijker om een principe in deze zin te formuleren: de spanningen veroorzaakt door een belastingsysteem zonder resulterende kracht of moment zullen klein zijn op een afstand die van dezelfde orde van grootte is als de grootte van de beladen grens.

zo bestuderen we de stress veroorzaakt door het verschil tussen de twee belastingsystemen met gelijke resultaten. De meeste moderne bewijzen zijn gebaseerd op schattingen van het verval van de spanningsenergie dichtheid voor zo ‘ n nul-resulterend systeem.

terugkomend op het bovenstaande probleem, kunnen we het verschil berekenen tussen de load cases. Door dit te doen kunnen we het werkelijke verval van stress of spanning energiedichtheid bestuderen voor het verschil van de stressvelden.

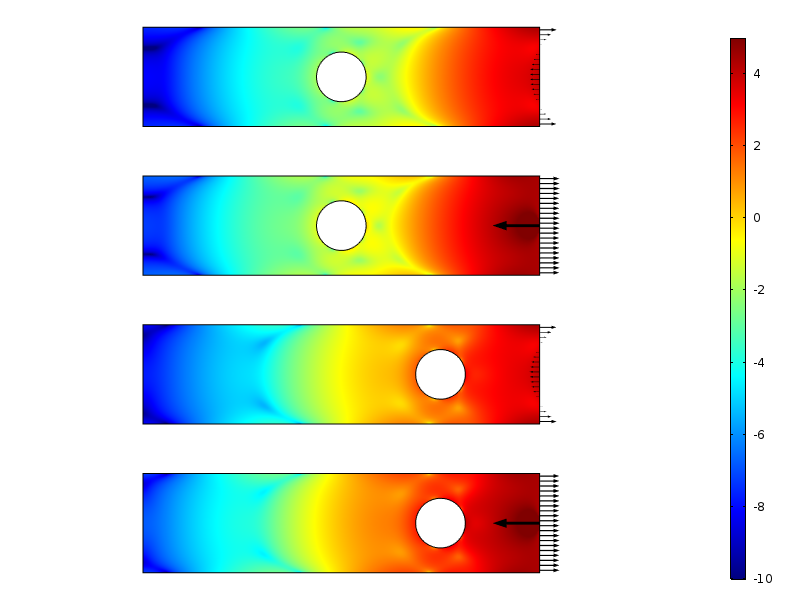
logaritme van de energiedichtheid van de spanning voor de nul-resulterende belastinggevallen.

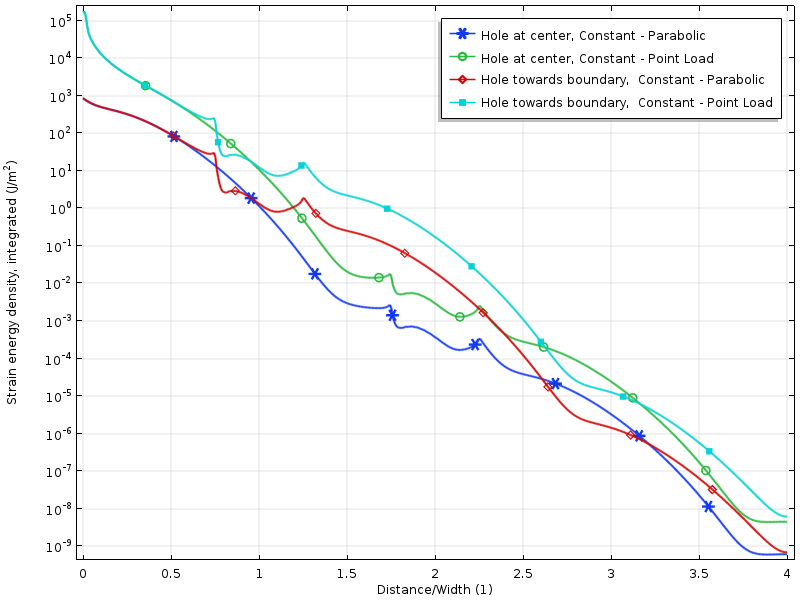
de energiedichtheid van de spanning langs de plaat voor de nulbelastingsgevallen. De energie wordt in de verticale richting geïntegreerd om een hoeveelheid te produceren die slechts een functie is van de afstand tot de belasting.

het verval in de logaritme van de energiedichtheid van de spanning is min of meer lineair met de afstand tot de beladen grens. Dit is eigenlijk in lijn met wat moderne bewijzen voorspellen: een exponentieel verval van de spanning energiedichtheid. We kunnen ook duidelijk zien hoe het gat tijdelijk de vervalsnelheid vermindert.

toepassing van het principe van Saint-Venant op dunne structuren

voor dunnere structuren zoals schelpen, balken en spanten is het bekend dat het principe van Saint-Venant niet op dezelfde manier kan worden toegepast als voor een meer “vast” object. Storingen reizen langere afstanden dan we verwachten, omdat de laadpaden in een dunne structuur veel beperkter zijn. Dit is hetzelfde fenomeen dat we zien met het gat in het voorbeeld hierboven, maar meer prominent.

hier bestuderen we een balk met een standaard ipe100 doorsnede. Het uiteinde van de bundel wordt onderworpen aan een axiale spanning, met een amplitude die een lineaire verdeling in beide dwarsdoorsnede richtingen heeft.

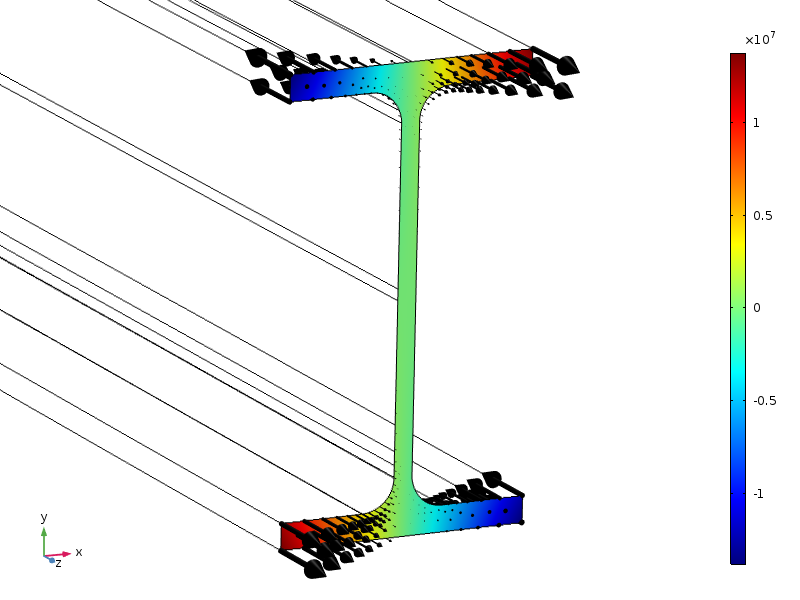
verdeling van de belasting, weergegeven als contouren en pijlen.

vanwege de symmetrieën heeft deze belasting een nul-resulterende kracht, evenals een nulmoment rond alle assen. De hoogte van de doorsnede is 100 mm, dus als de standaardvorm van het principe van Saint-Venant van toepassing is, dan moeten de spanningen klein zijn op een afstand van ongeveer 100 mm van het eindstuk.

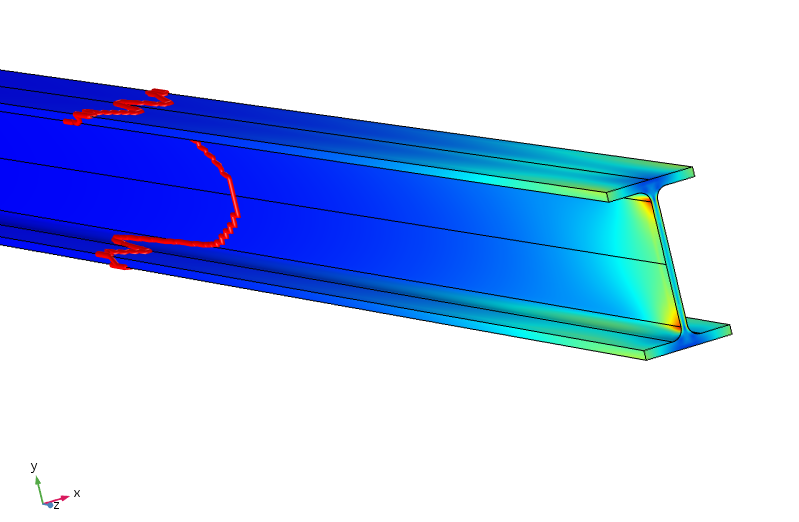
equivalente spanning in de bundel. De rode contour geeft aan waar de spanning minder is dan 5% van de piekbelasting.

om de spanning onder 5% van de piekbelasting te laten liggen, moeten we bijna een meter langs de bundel afleggen. De verdeling van de belasting is hier dus veel minder efficiënt, omdat het evenwicht tussen de boven-en onderkant flenzen momentoverdracht via het dunne web vereist.

als u bekend bent met de theorie voor niet-uniforme torsie van bundels (dwz, kromming theorie of Vlasov theorie), zult u herkennen dat de toegepaste belasting een significante bimoment heeft. De bimoment is een doorsnede-grootheid met de fysieke dimensie kracht X lengte 2.

misschien (Dit is slechts mijn persoonlijke speculatie), zou een efficiënt principe van Saint-Venant in dit geval niet alleen kracht en moment moeten vereisen, maar ook een bimoment van nul. Dit kan worden bereikt door het toevoegen van vier punt belastingen die een tegenwerkende bimoment bieden. Het resultaat van een dergelijke analyse wordt hieronder weergegeven.

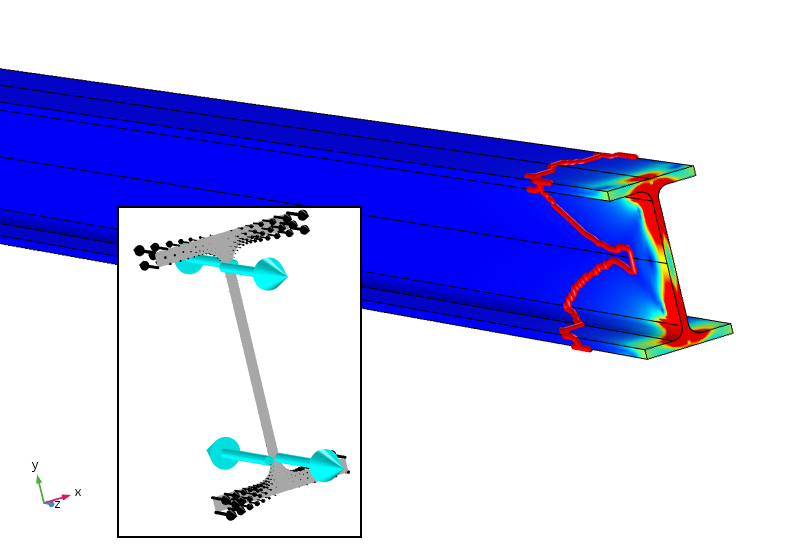
equivalente spanning met vierpuntsbelastingen die ook een bimoment van nul geven. De 5% spanningscontour is nu veel dichter bij de beladen grens.

de uitgeoefende puntbelastingen, die niet optimaal met opzet worden geplaatst, geven extreem hoge (in feite enkelvoudige) lokale belastingen. De spanning daalt echter veel sneller af en ligt na ongeveer 100 mm onder de 5%. de 5% – limiet is nog steeds in termen van de toegepaste verdeelde belasting, dus is deze niet aangepast voor de nieuwe lokale spanningen. De logaritmische vervalsnelheid van de energiedichtheid van de spanning is drie keer sneller nadat de puntbelastingen zijn toegevoegd.

het principe van Saint-Venant in eindige-elementenanalyse

in sommige gevallen kunt u intuïtief het principe van Saint-Venant als toepasbaar beschouwen op het fe-discrete probleem. Hier kijken we naar gedistribueerde ladingen en niet-conforme mazen.

verdeelde belastingen

in het FE-model worden belastingen altijd toegepast op de mesh-knooppunten, ook al specificeert u ze als een continue grensbelasting. De belasting wordt intern verdeeld over de knooppunten van het element met behulp van het principe van virtueel werk, zoals weergegeven in het onderstaande voorbeeld.

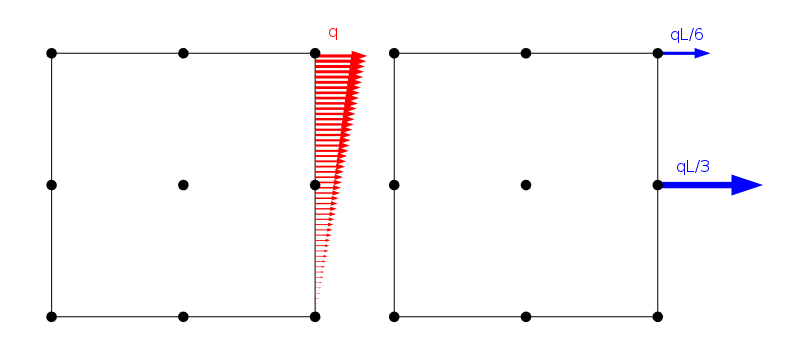
een lineair verdeelde belasting en hoe deze wordt toegepast op de knooppunten van een tweede-orde Lagrange-element met zijlengte L.

er is echter een oneindig aantal belastingsdistributies die dezelfde knoopbelastingen geven zolang ze dezelfde resulterende kracht en moment delen. Uiteraard is de oplossing voor het eindige-elementenprobleem voor al deze gevallen hetzelfde. Uit het principe van Saint-Venant kunnen we echter concluderen dat al deze belastingen in wezen hetzelfde spanningsveld moeten geven zodra we op enige afstand zijn.

aangezien de grootte van het gebied waarover we belastingen herverdelen een elementvlak is, is de lineaire dimensie waarna er geen verschil is in wezen één elementlaag binnen de structuur. Zo kan de oplossing in de buitenste laag van elementen niet overeenkomen met de werkelijke belasting, maar verder in, het doet.

als voorbeeld kunnen we een rechthoekige plaat laden met een grensbelasting die een exponentiële spanningsverdeling heeft. De spanning berekend met een fijn gaas is hieronder weergegeven.

Contourdiagram van de axiale spanningsverdeling.

vanwege het principe van Saint-Venant wordt het spanningsveld herverdeeld in een zuivere buigtoestand op enige afstand van de beladen rand, zoals we verwachten. Dit is echter niet het onderwerp van de huidige discussie. In plaats daarvan onderzoeken we het verschil tussen de stressverdeling hierboven, en wat we krijgen met een aantal grove mazen.

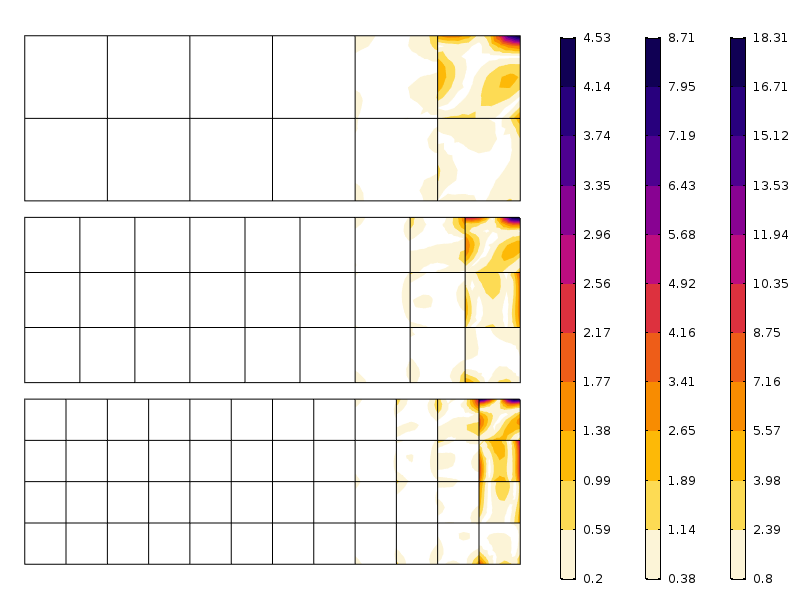
fout in axiale spanning voor drie verschillende mazen. Let op de verschillende schalen. Zoals verwacht is de fout kleiner wanneer het gaas fijner is.

zoals te zien is in de figuur neemt de fout snel af na de eerste elementlaag. Wat we hier zien is eigenlijk een combinatie van gaasconvergentie en de herverdeling van stress die wordt geïmpliceerd door het principe van Saint-Venant.

Nonconforming Mesh

een nonconforming mesh treedt op wanneer de vormfuncties in twee verbonden elementen niet overeenkomen. Het meest voorkomende geval is wanneer een assemblage is verbonden met behulp van identiteitsparen en continuïteit voorwaarden. Om dit te illustreren, kunnen we een rechte staaf bestuderen met een opzettelijk niet-catching gaas. Met een eenvoudige belasting geval, zoals eenassige spanning, is het mogelijk om de stressstoornissen veroorzaakt door de overgang te bestuderen.

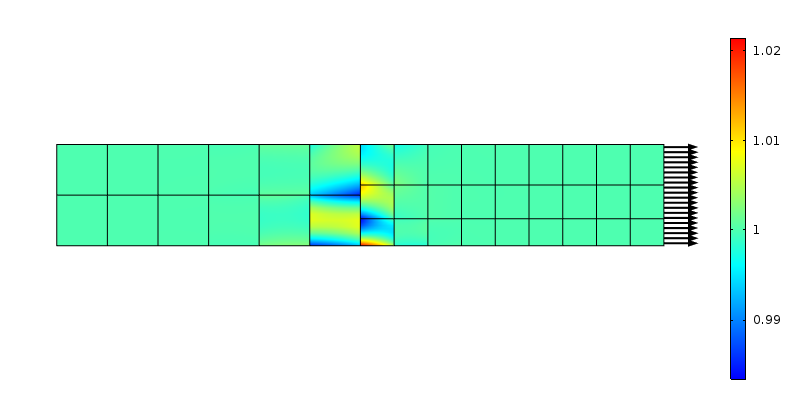
axiale spanning bij een niet-conforme mesh-overgang. Tweede-orde elementen worden gebruikt.

de krachten die door de knooppunten aan beide zijden worden overgedragen, komen niet overeen met de aanname van constante spanning. Nogmaals, dit kan worden gezien als een lokale belasting herverdeling over een gebied dat de grootte van het element. Met behulp van de redenering van Saint-Venant, moet de verstoring verdwijnen op een “element-sized” afstand van de overgang. Laten we onderzoeken wat er gebeurt als het gaas wordt verfijnd in de axiale richting.

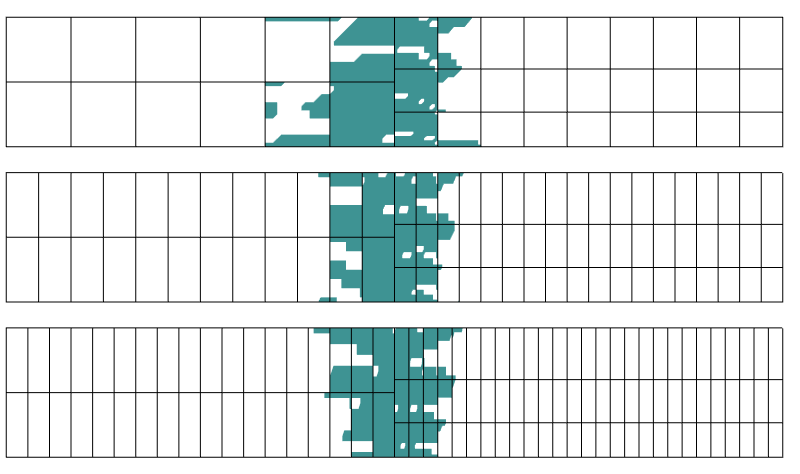
regio met meer dan 0,1% fout in stress. Drie verschillende discretisaties worden gebruikt in de axiale richting.

het blijkt dat het storingsgebied niet veel wordt beïnvloed door de discretisatie in de richting loodrecht op de overgangsgrens. Dat is precies wat het principe van Saint-Venant ons vertelt.

slotopmerkingen

zonder gebruik te maken van het principe van Saint-Venant zijn veel structurele analyses moeilijk uit te voeren, simpelweg omdat de gedetailleerde verdeling van de belasting niet bekend is.

het principe is formeel alleen geldig voor lineair elastische materialen. In de praktijk gebruiken we het ook dagelijks intuïtief voor andere situaties. Als bijvoorbeeld het materiaal in het voorbeeld van de “plaat met gat” elastoplastisch is, zouden we verwachten dat de twee verdeelde belastingen gelijkwaardige resultaten opleveren, zolang de vloeigrens boven de belasting ligt die aan de grens wordt toegepast, zodat er alleen plastische vervorming rond het gat is. De puntbelasting geeft echter altijd een andere oplossing, omdat het materiaal rond het geladen punt levert. Voor een langere discussie, lees deze blog post op singularities at point loads.

volgende stappen

meer informatie over het gebruik van de COMSOL Multiphysics® software voor FEA.

verder lezen

• Y. C. Fung and P. Tong, Classical and Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.