Rozdział 12
metoda rozkładu momentu analizy konstrukcji
12.1 podstawowe pojęcia
metoda rozkładu momentu analizy belek i RAM została opracowana przez Hardy Cross i formalnie przedstawiona w 1930 roku. Chociaż metoda ta jest metodą deformacji, podobnie jak metoda nachylenia-ugięcia, jest to metoda przybliżona, a zatem nie wymaga rozwiązywania równań symultanicznych, jak to miało miejsce w przypadku tej drugiej metody. Stopień dokładności wyników uzyskanych metodą rozkładu momentu zależy od liczby kolejnych przybliżeń lub procesu iteracji.
aby zilustrować koncepcję metody rozkładu momentu, rozważ ramkę pokazaną na rysunku 12.1. Elementy ramy są pryzmatyczne i zakłada się, że nie odkształcają się osiowo ani nie przekładają względem siebie. Złącza ACD ramy są stałe, podczas gdy złącze B może się lekko obracać ze względu na przyłożone obciążenie. Po pierwsze, przed przeprowadzeniem rozkładu momentu między prętami zakłada się, że wszystkie połączenia są tymczasowo zablokowane za pomocą zacisku.
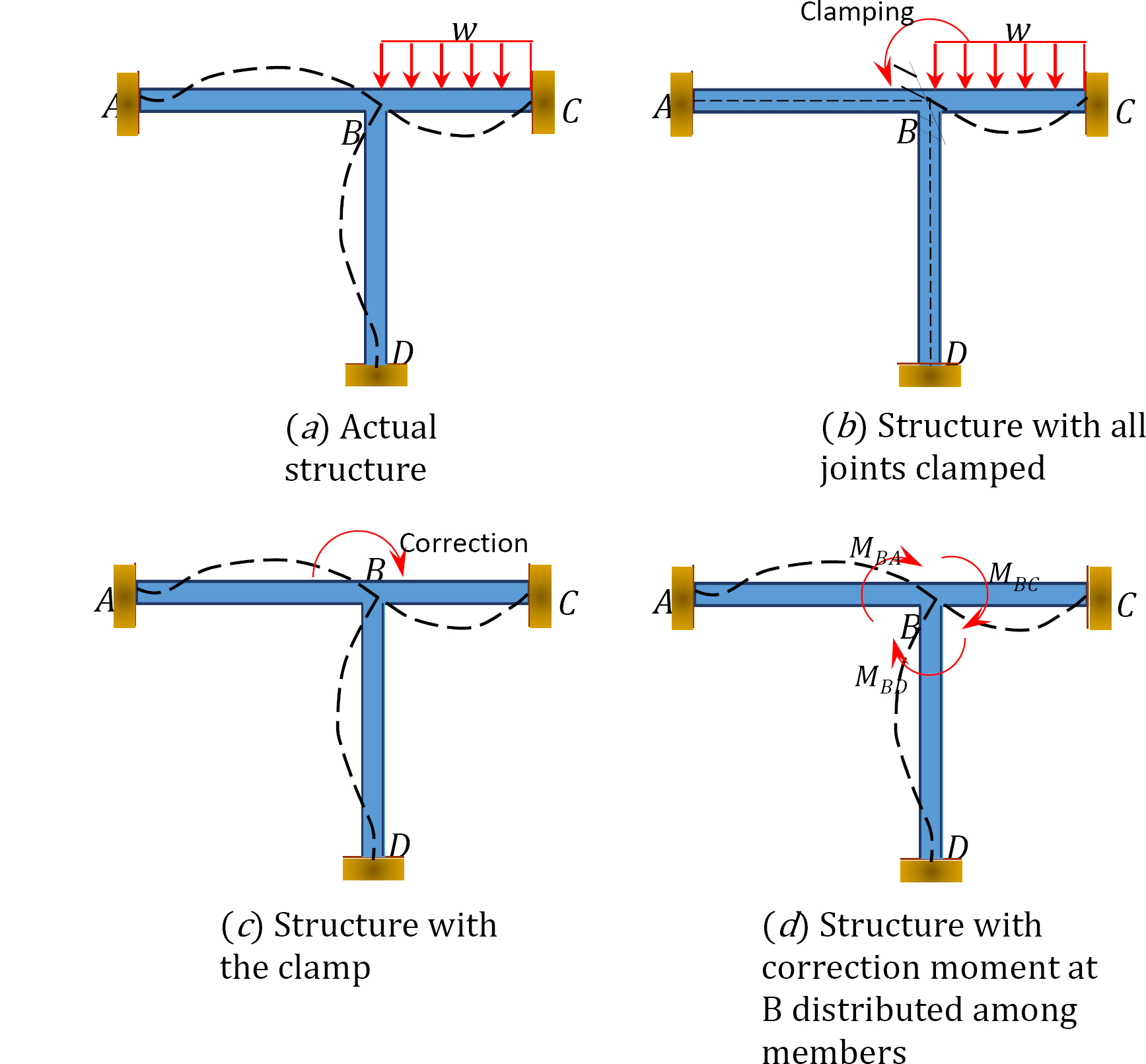
Fig. 12.1. Ramka.
12.2 Konwencja znaku
konwencja znaku dla metody rozkładu momentu jest podobna do tej ustanowionej dla metody nachylenia-ugięcia; oznacza to, że moment na końcu członka jest uważany za pozytywny, jeśli ma tendencję do obracania końca członka zgodnie z ruchem wskazówek zegara i ujemny, jeśli ma tendencję do obracania go w lewo.
12.3 definicje
momenty niezrównoważone: ta metoda analizy zakłada, że połączenia w strukturze są początkowo zaciskane lub blokowane, a następnie uwalniane sukcesywnie. Po zwolnieniu złącza następuje rotacja, ponieważ suma stałych momentów końcowych spotkania członków w tym złączu nie jest równa zeru. Wartością sumy uzyskanych momentów końcowych jest moment niezrównoważony w tym połączeniu.
momenty przeniesienia: rozłożone momenty na końcach spotkania członków na wspólnej powodują momenty na pozostałych końcach, które przyjmuje się za stałe. Te wywołane momenty na innych końcach nazywane są momentami przenoszonymi.
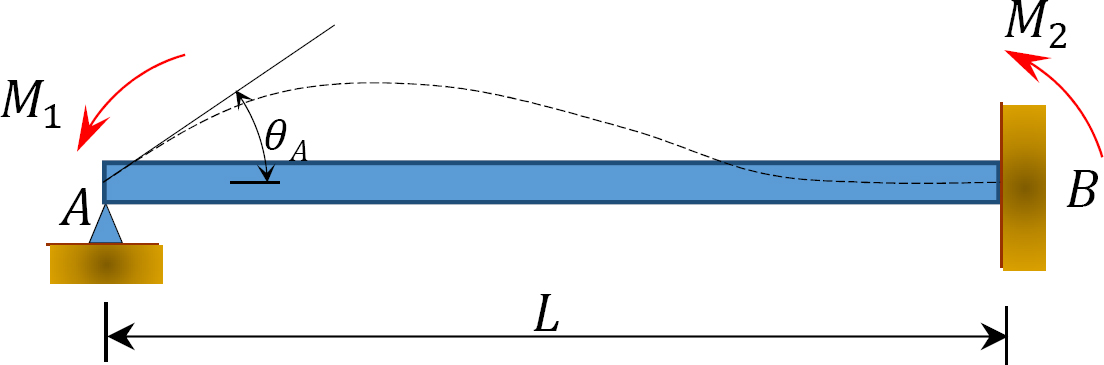
Fig. 12.2. Nieobciążona wiązka pryzmatyczna.
należy rozważyć nieobciążoną wiązkę pryzmatyczną zamocowaną na końcu B, jak pokazano na rysunku 12.2. Jeżeli na lewy koniec wiązki przyłożony jest moment M1, to równania nachylenia i ugięcia dla obu końców wiązki można zapisać następująco:


podstawiając 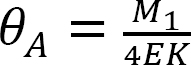 z równania 12.1 do równania 12.2 sugerujemy, co następuje:
z równania 12.1 do równania 12.2 sugerujemy, co następuje:

równanie 12.3 sugeruje, że moment przenoszony na stały koniec wiązki spowodowany momentem przyłożonym na drugim końcu jest równy połowie przyłożonego momentu.
Współczynnik przeniesienia: stosunek momentu wywołanego do momentu przyłożonego jest określany jako współczynnik przeniesienia. Dla wiązki przedstawionej na rysunku 12.2 współczynnik przeniesienia jest następujący:

Współczynnik rozproszony (DF): Współczynnik rozproszony jest czynnikiem stosowanym do określenia proporcji niezrównoważonego momentu niesionego przez każdego z członków na wspólnym posiedzeniu. W przypadku spotkania członków na wspólnym O ramki pokazanej na rysunku 12.3 ich współczynniki rozkładu oblicza się w następujący sposób:
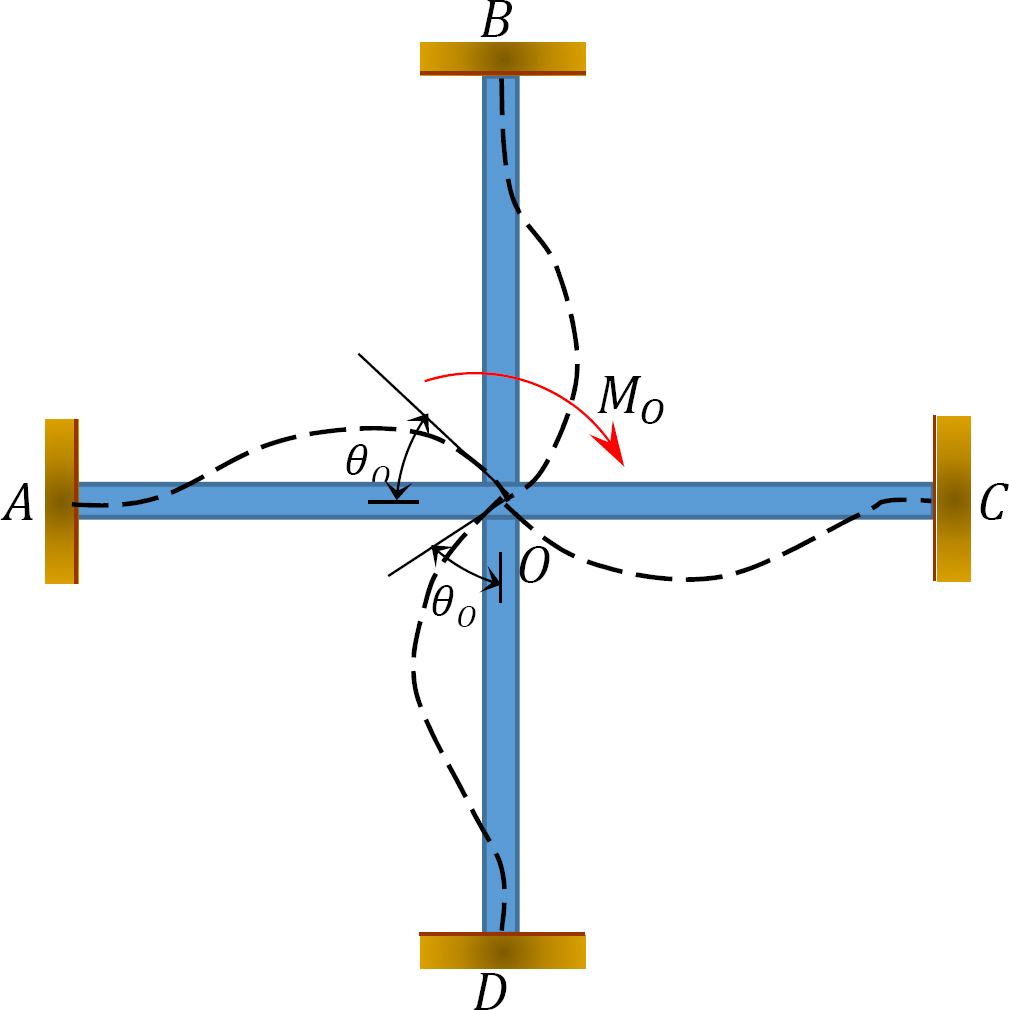
Fig. 12.3. Ramka.

momenty rozłożone: po zwolnieniu wyimaginowanego zacisku w stawie, niezrównoważony moment w tym stawie powoduje jego obrót. Rotacja skręca koniec spotkania członków na wspólnej, co powoduje rozwój momentów oporu. Te momenty oporu nazywane są momentami rozproszonymi. Momenty rozłożone dla elementów ramki pokazanej na rysunku 12.3 oblicza się w następujący sposób:
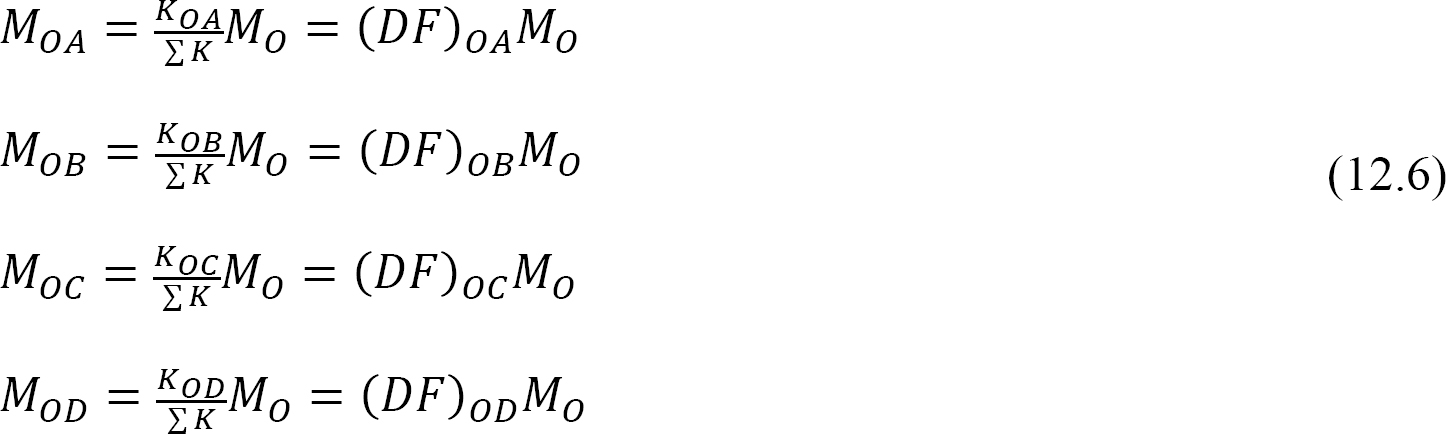
12.4 modyfikacja sztywności prętów
czasami proces iteracji w metodzie rozkładu momentu można znacznie zmniejszyć poprzez regulację sztywności zginania niektórych prętów nieokreślonej struktury. W tej sekcji rozważa się wpływ stałego i sworzniowego wspornika na sztywność zginaną nieokreślonej belki.
Przypadek 1: Belka zawieszona na jednym końcu i zamocowana na drugim
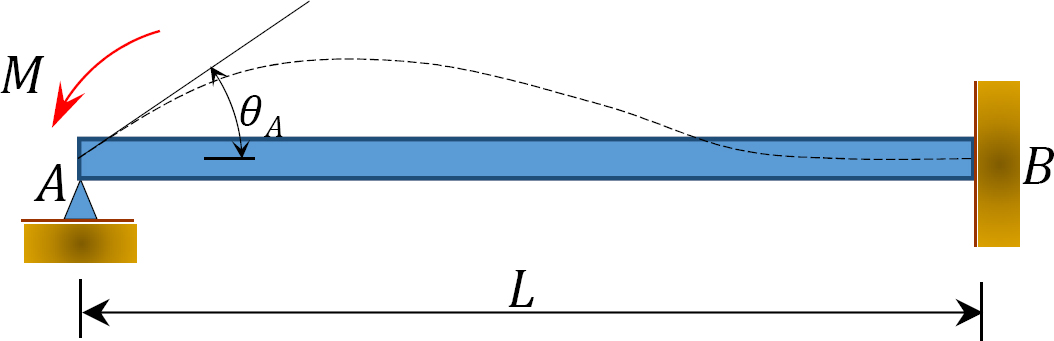
Fig. 12.4. Belka
rozważmy belkę zawiasową na końcu A i zamocowaną na końcu B, jak pokazano na rysunku 12.4. Zastosowanie momentu M obraca koniec zawiasu o kwotę θ. Pisząc równanie nachylenia-ugięcia dla końca a pręta i zauważając, że 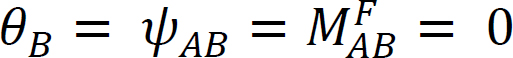 sugeruje co następuje:
sugeruje co następuje:
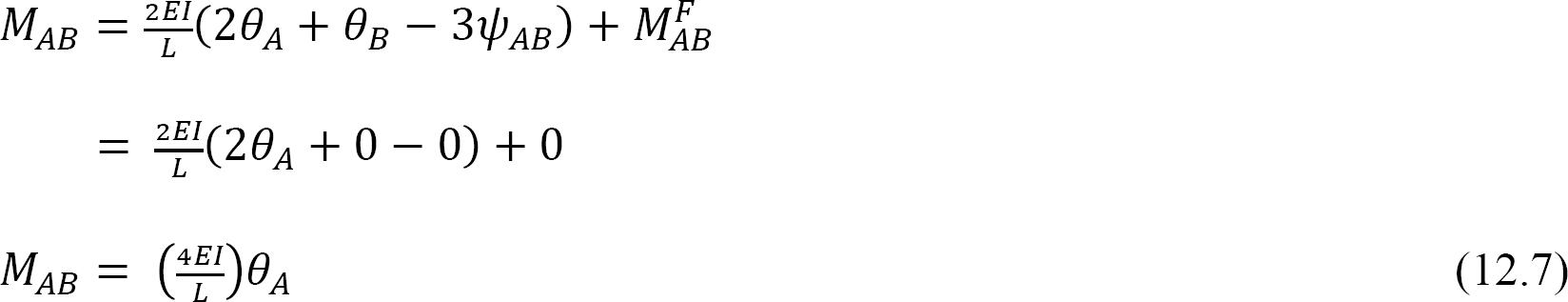
z definicji sztywność zginania elementu konstrukcyjnego jest momentem, który musi być zastosowany do końca elementu, aby spowodować jednostkowy obrót tego końca. Następujące wyrażenie dla sztywności zginania dla pręta o stałym Dalekim końcu wyraża się w następujący sposób, gdy podstawia θA = 1 do równania 12.7:

z definicji względną sztywność zginania pręta określa się przez podzielenie sztywności zginania pręta przez 4E. podzielenie równania 12.8 przez 4E sugeruje następujące wyrażenie dla względnej sztywności dla rozważanego przypadku:

Przypadek 2: belka zawieszona na obu końcach
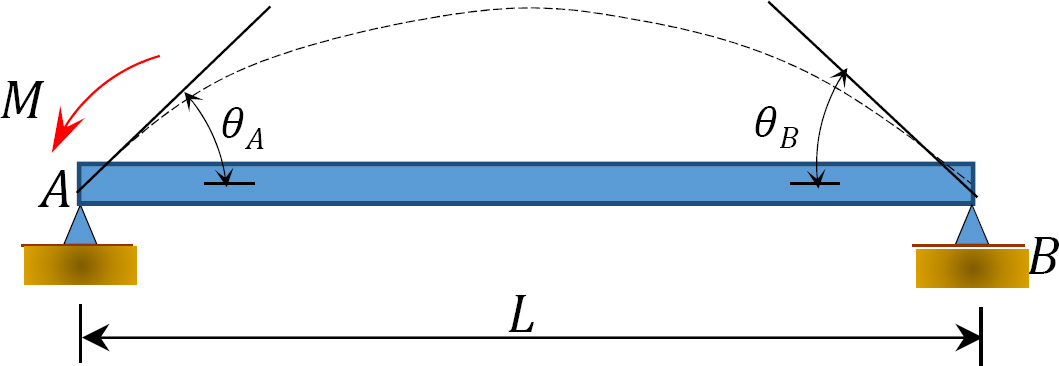
Fig. 12.5. Po prostu podparta belka.
przyłożenie momentu M na końcu a prostej podpartej wiązki pokazanej na rysunku 12.5 obraca wiązkę o kąt θA na zawiasach. Stosując zmodyfikowane równanie nachylenia-ugięcia zawarte w sekcji 11.4 rozdziału 11 i zauważając, że 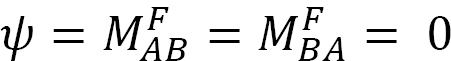 sugeruje następujące wyrażenie dla momentu na zawiasowym końcu, w którym obciążenie jest przykładane:
sugeruje następujące wyrażenie dla momentu na zawiasowym końcu, w którym obciążenie jest przykładane:
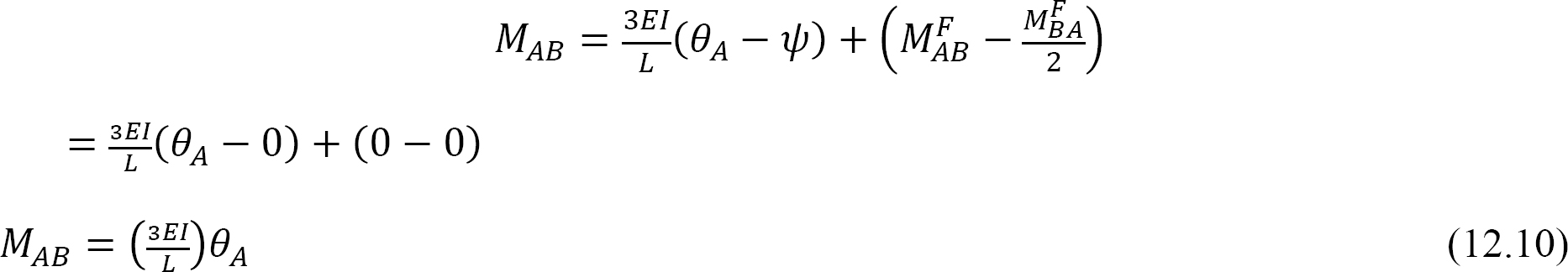
Podstawienie θA = 1 do równania 12.10 sugeruje następujące wyrażenie dla sztywności zginania dla elementu z zawiasowym skrajnym końcem:

względną sztywność dla pręta z zawiasowym skrajnym końcem uzyskuje się przez podzielenie równania 12.11 przez 4E, w następujący sposób:

porównanie równań 12.12 i 12.9 sugeruje, że człon z zawiasowym skrajnym końcem jest o trzy czwarte sztywny jak człon o tej samej geometrii, ale ustalony na skrajnym końcu. Ten ustalony fakt może znacznie zmniejszyć liczbę iteracji podczas analizowania belek lub Ram z zawiasowym skrajnym końcem za pomocą metody rozkładu momentu. W takich przypadkach względną sztywność belki na Bliskim końcu reguluje się najpierw zgodnie ze wzorem 12.12, a jej współczynnik rozkładu oblicza się z dostosowaną sztywnością. Podczas operacji równoważenia Bliski koniec zostanie zrównoważony tylko raz, bez dalszego przenoszenia momentów z lub do końca.
12.5 Analiza wiązek nieokreślonych
procedura analizy wiązek nieokreślonych metodą rozkładu momentu jest krótko podsumowana w następujący sposób:
procedura analizy wiązek nieokreślonych metodą rozkładu momentu
•Oblicz momenty stałe dla prętów, zakładając, że połączenia są zaciśnięte względem obrotu.
•Oblicz współczynnik rozkładu dla każdego z członów połączonych na złączu
•Oblicz moment niezrównoważony na każdym złączu i rozprowadź go na końcach członów połączonych na tym złączu.
•Przenieś ponad połowę rozproszonego momentu na pozostałe końce członków.
•dodawanie lub odejmowanie tych ostatnich momentów (momentów uzyskanych w krokach trzecim i czwartym)do lub od pierwotnych momentów stałych.
•Zastosuj określone momenty końcowe na złączach danej konstrukcji.
•narysuj diagram swobodnego ciała każdego rozpiętości danej wiązki, pokazując obciążenia i momenty na połączeniach uzyskane metodą rozkładu momentu.
•Określ reakcje wsparcia dla każdego zakresu.
•Oblicz i skonstruuj wykresy siły ścinającej i momentu zginającego dla każdego zakresu.
•narysuj jeden moment zginający i jeden schemat siły ścinającej dla danej wiązki, łącząc Schematy w kroku 9.
przykład 12.1
stosując metodę rozkładu momentu, należy określić momenty końcowe i reakcje na podporach wiązki przedstawionej na rysunku 12.6 a. narysować siłę ścinającą i wykresy momentu zginającego. EI = stała.
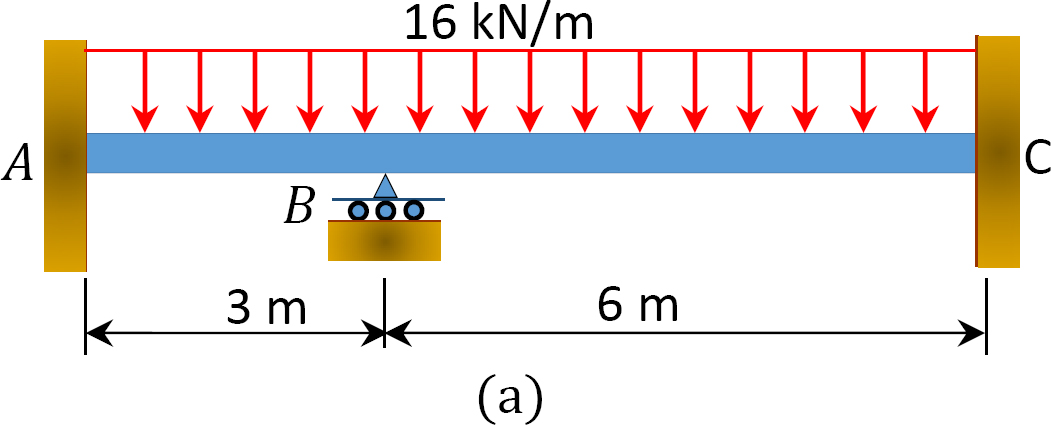
Fig. 12.6. Belka.
rozwiązanie
stały moment końcowy.
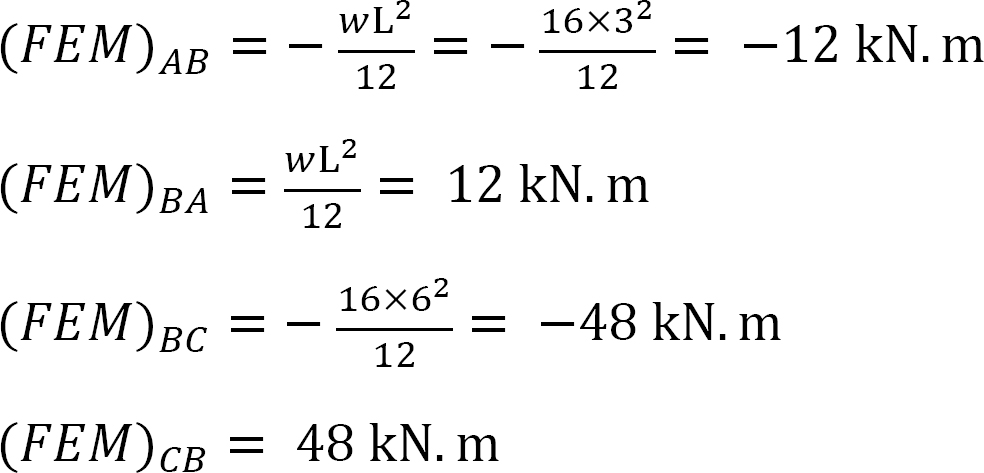
współczynnik sztywności.
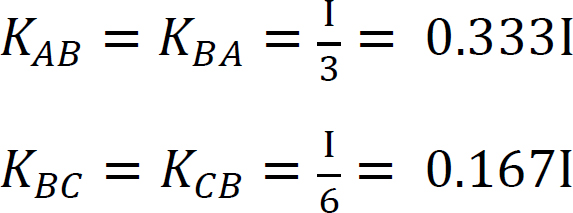
współczynnik dystrybucji.
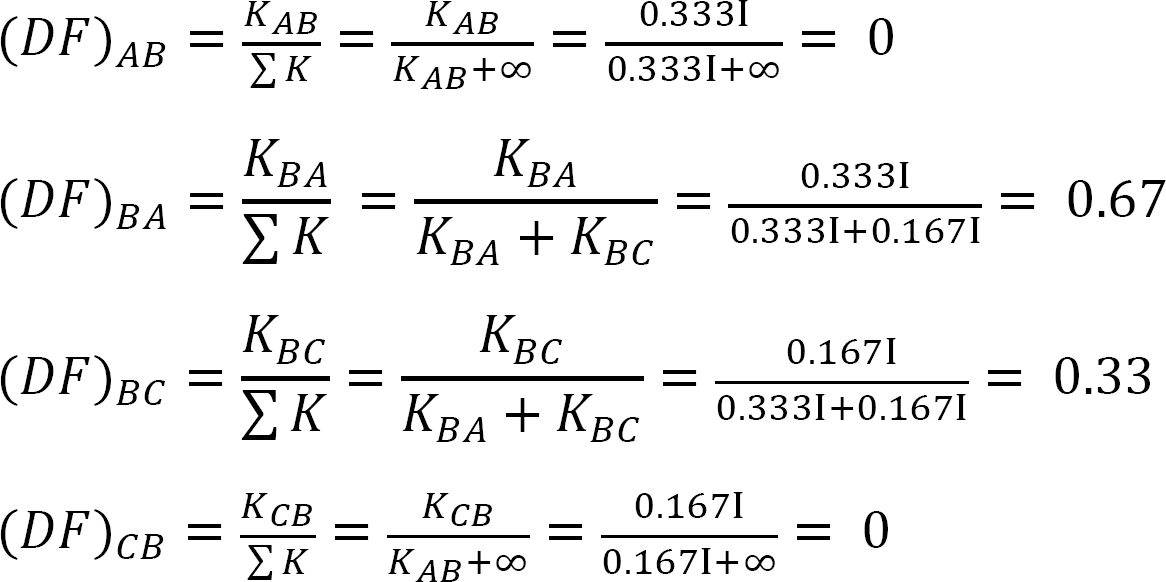
tabela 12.1. Tabela dystrybucji.
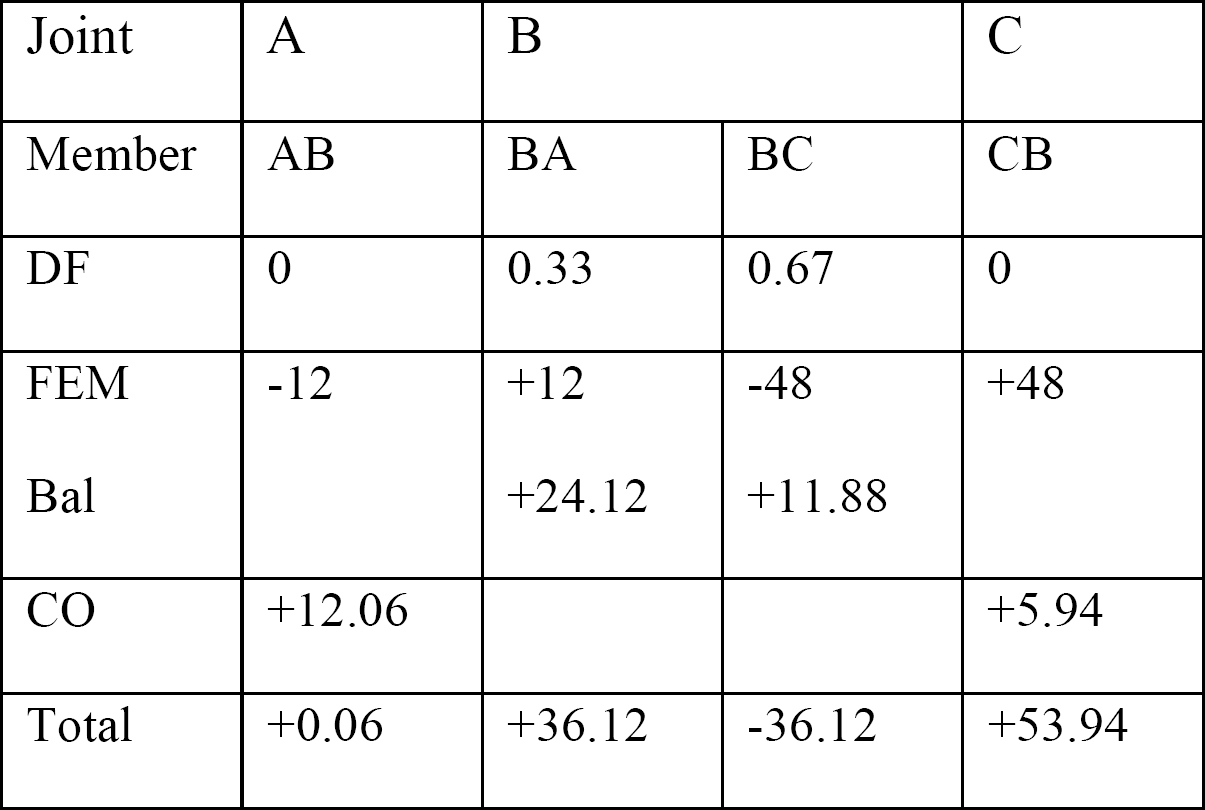
wykresy siły ścinającej i momentu zginającego.
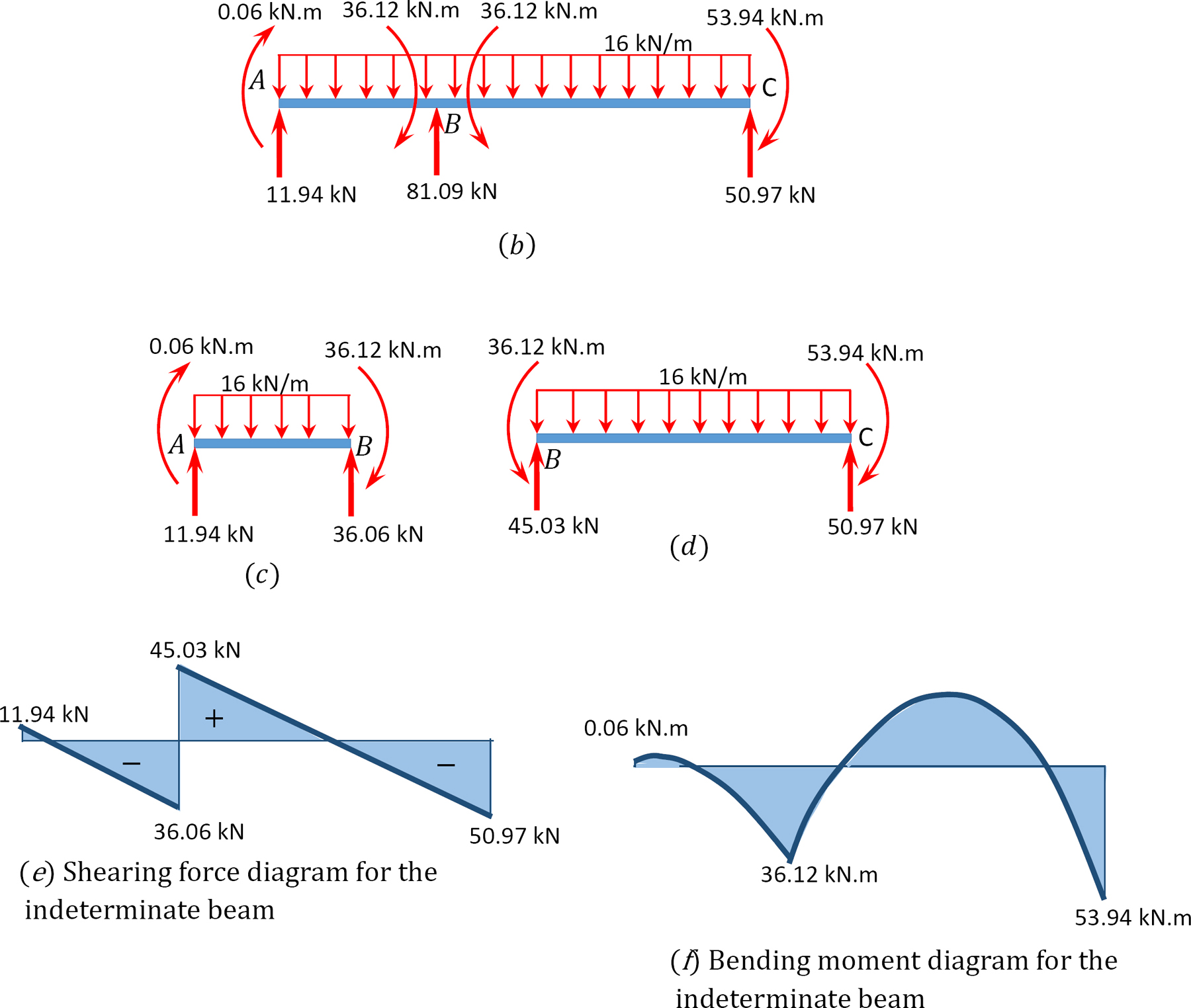
przykład 12.2
stosując metodę rozkładu momentu, należy określić momenty końcowe i reakcje na podporach wiązki przedstawionej na rysunku 12.7 a. narysować siłę ścinającą i wykresy momentu zginającego.
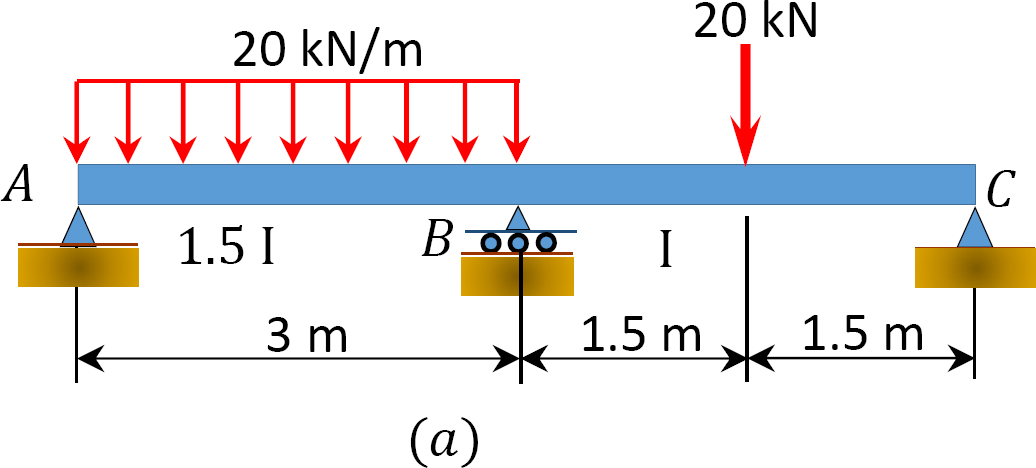
Fig. 12.7. Belka.
rozwiązanie
stały moment końcowy.
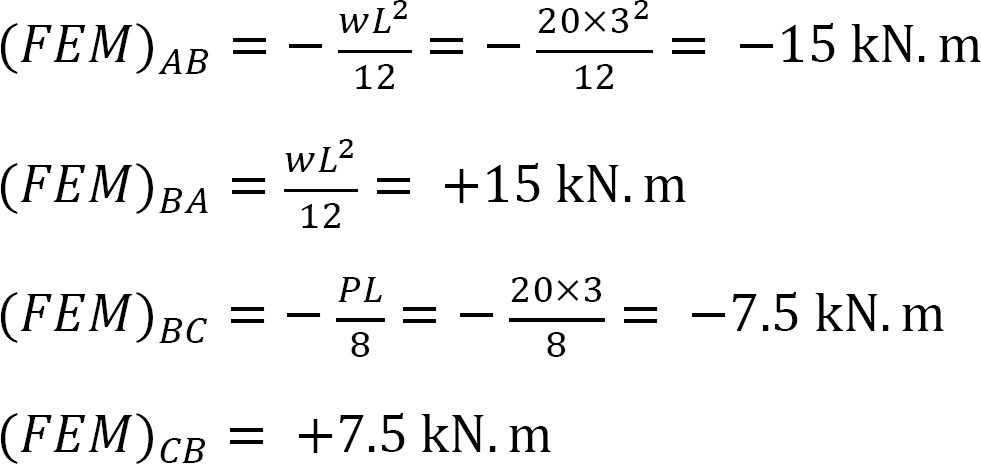
współczynnik sztywności.
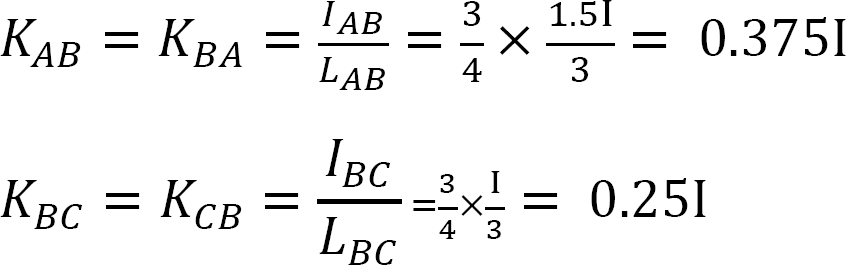
współczynnik dystrybucji.
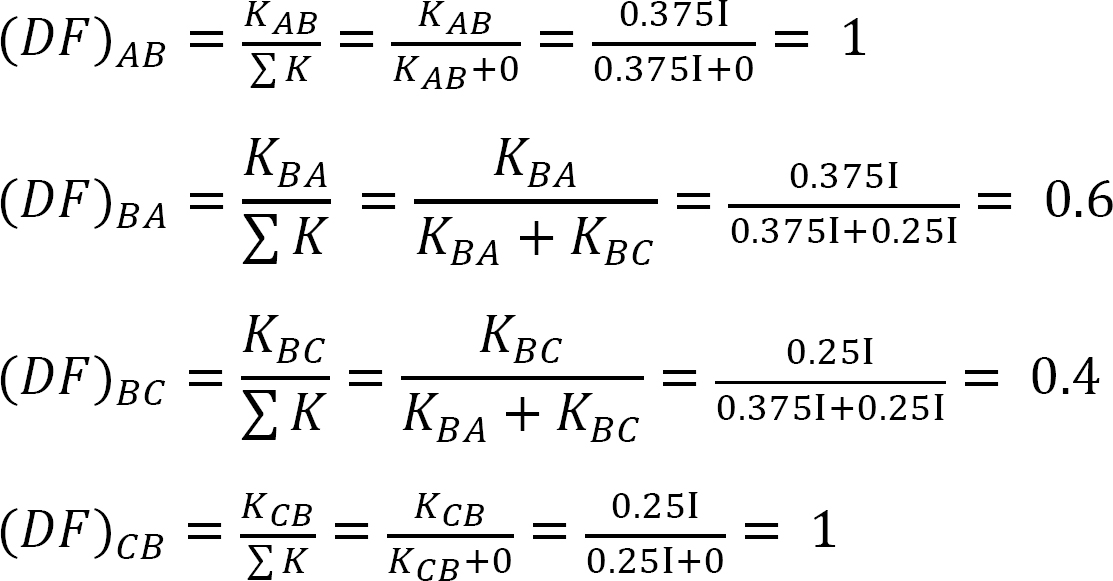
tabela 12.2. Tabela dystrybucji.
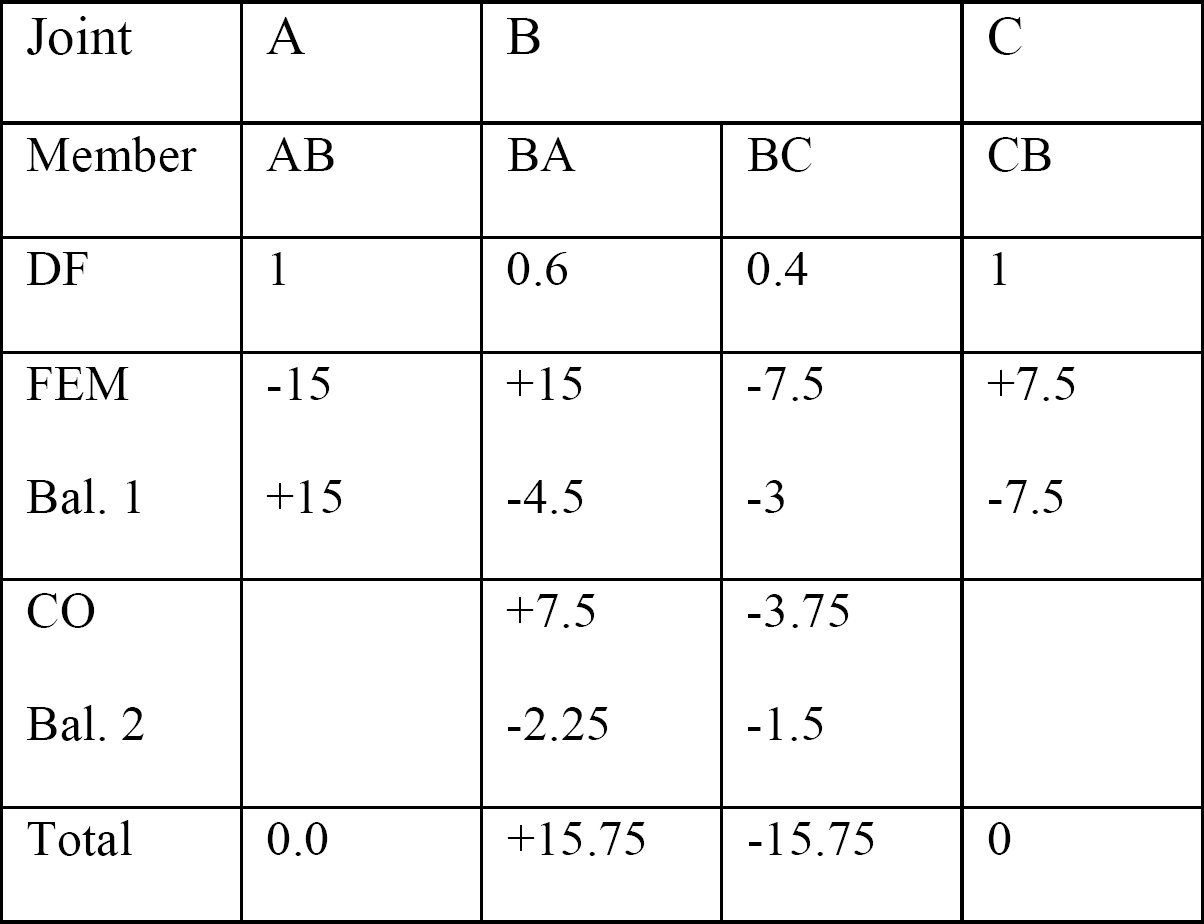
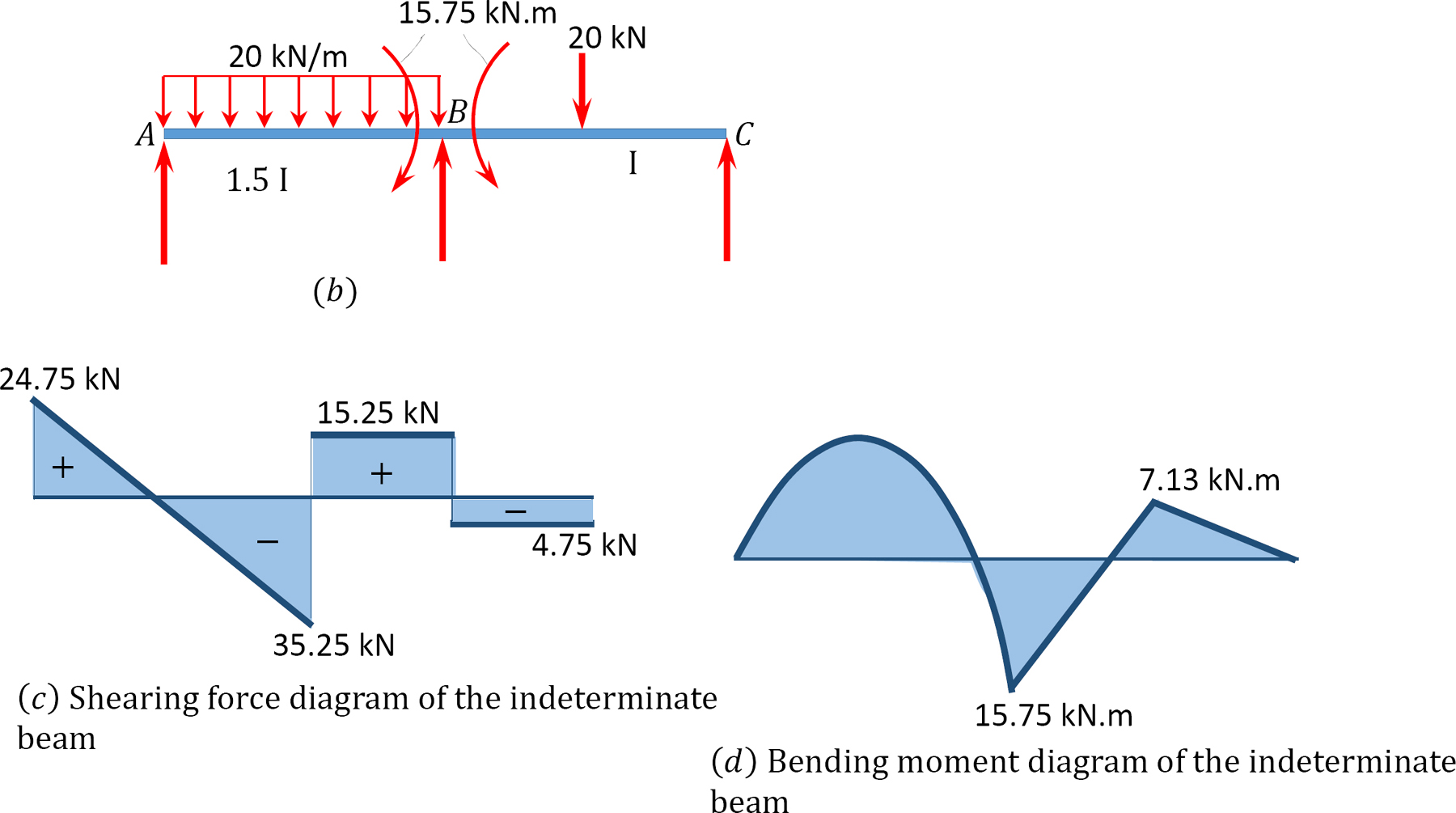
wykresy siły ścinającej i momentu zginającego.
12.6 Analiza nieokreślonych ramek
procedura analizy ramek przy użyciu metody rozkładu momentu zależy od rodzaju analizowanej ramki. Ramki są klasyfikowane jako ramki kołyszące lub bez kołyszące. Procedura analizy RAM bez kołysania jest podobna do tej W przypadku belek nieokreślonych. Ale w przypadku analizy RAM kołysania procedura jest inna. W analizie RAM kołysania biorą udział dwa etapy, a mianowicie etap bez kołysania i analiza kołysania. Etapy te są opisane poniżej.
procedura analizy nieokreślonych ramek kołysania za pomocą metody rozkładu momentu
A. Analiza etapu bez kołysania
•najpierw przyjmij istnienie wymyślonego rekwizytu, który zapobiega kołysaniu się ramki.
•Oblicz reakcje poziome na podporach ramki i zanotuj różnicę X. Jest to siła zapobiegająca kołysaniu.
B. Analiza fazy kołysania
•wartości przyjmuje się dla M2, a M1 określa.
•arbitralne momenty są następnie rozkładane tak, jak dla warunku bez kołysania
•Oblicz wielkość reakcji poziomych na podpórkach dla warunku kołysania. Sumowanie tych reakcji daje arbitralną siłę przemieszczenia Y.
•wyznacz stosunek 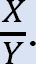 ten stosunek nazywa się współczynnikiem kołysania.
ten stosunek nazywa się współczynnikiem kołysania.
•użyj współczynnika kołysania, aby pomnożyć rozłożone momenty kołysania. Daje to skorygowany moment kołysania.
•Ostatnie momenty kadru są sumacją momentów uzyskanych w fazie bez kołysania i skorygowanym momentem dla fazy kołysania.
przykład 12.3
korzystając z metody rozkładu momentu, określ momenty końcowe prętów ramy pokazanej na rysunku 12.8. EI = stała.
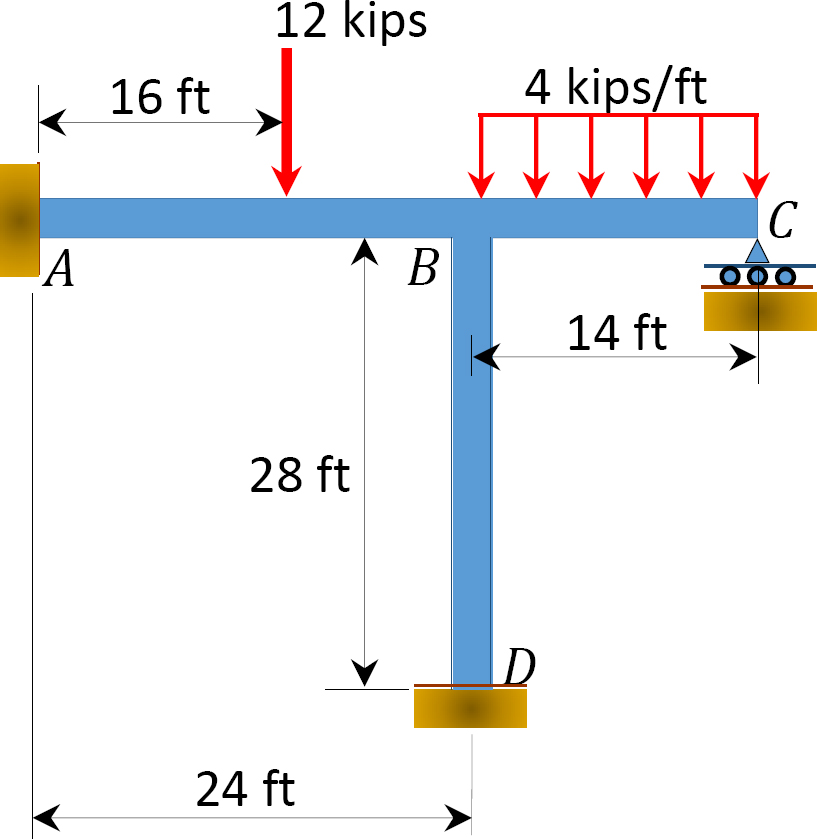
Fig. 12.8. Ramka.
rozwiązanie
stały moment końcowy.
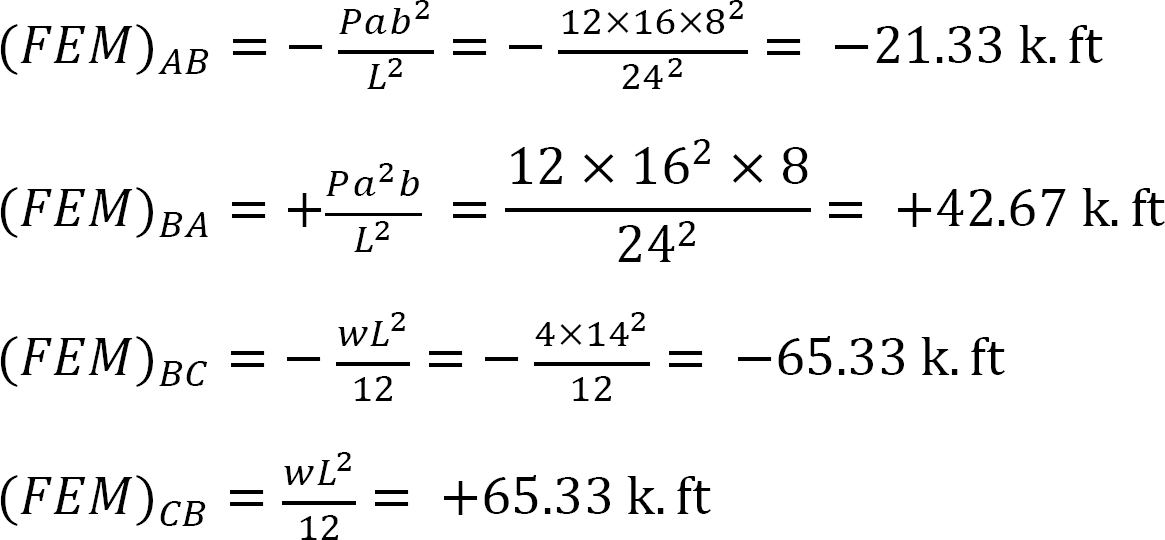
współczynnik sztywności.
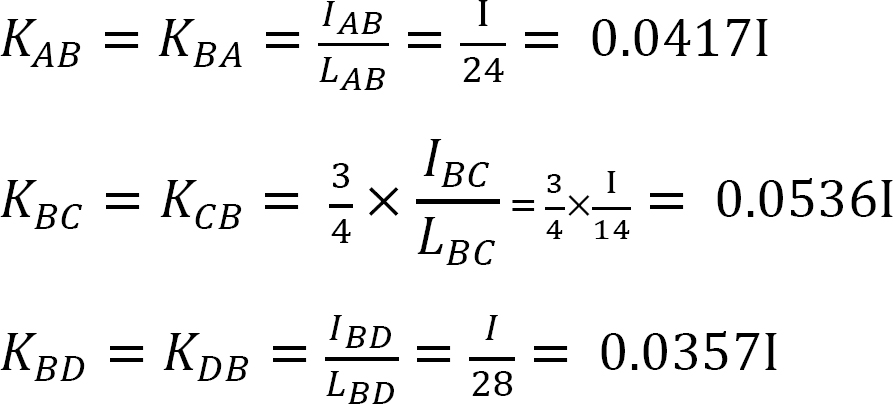
współczynnik dystrybucji.
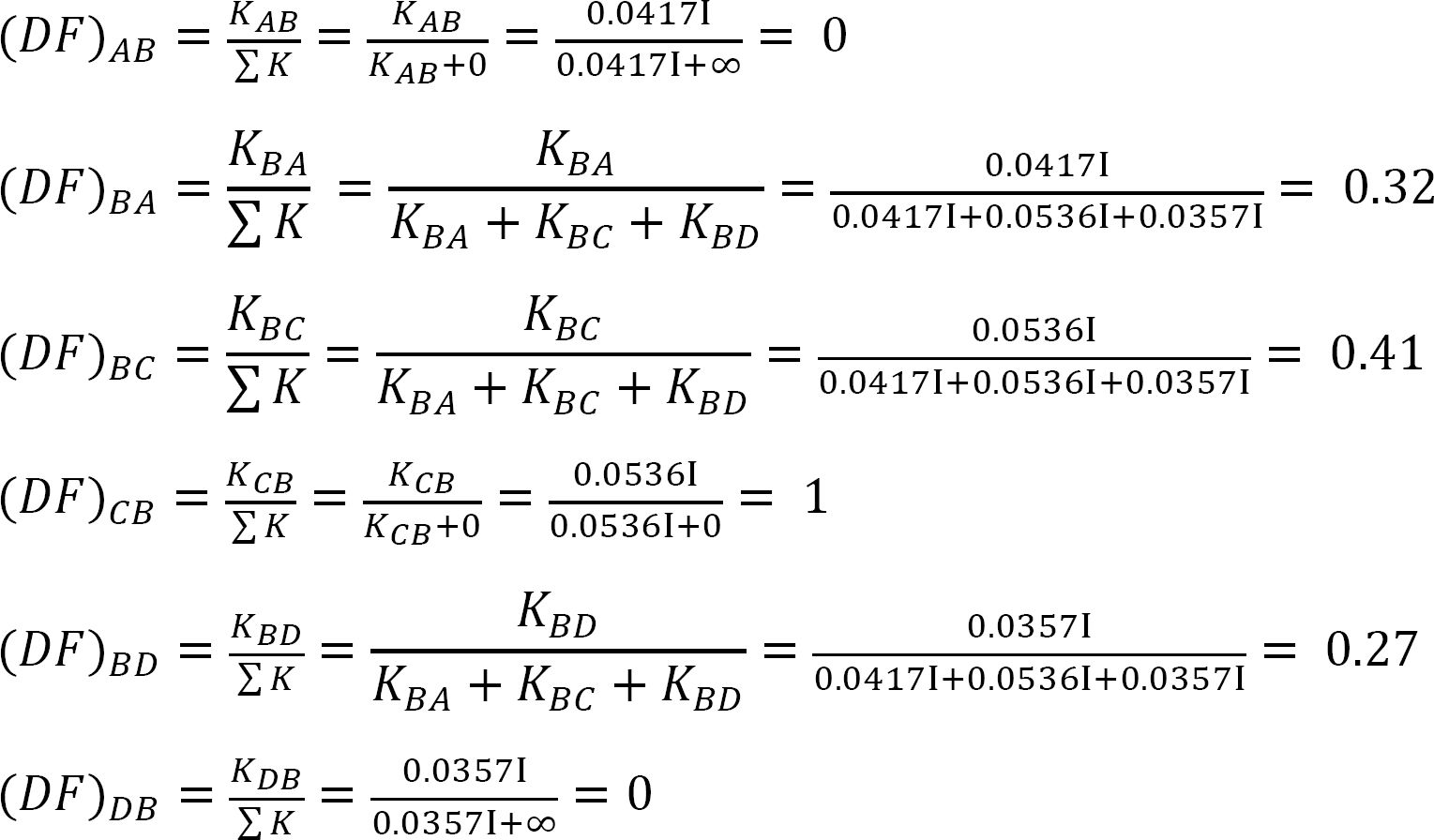
tabela 12.3. Tabela dystrybucji.
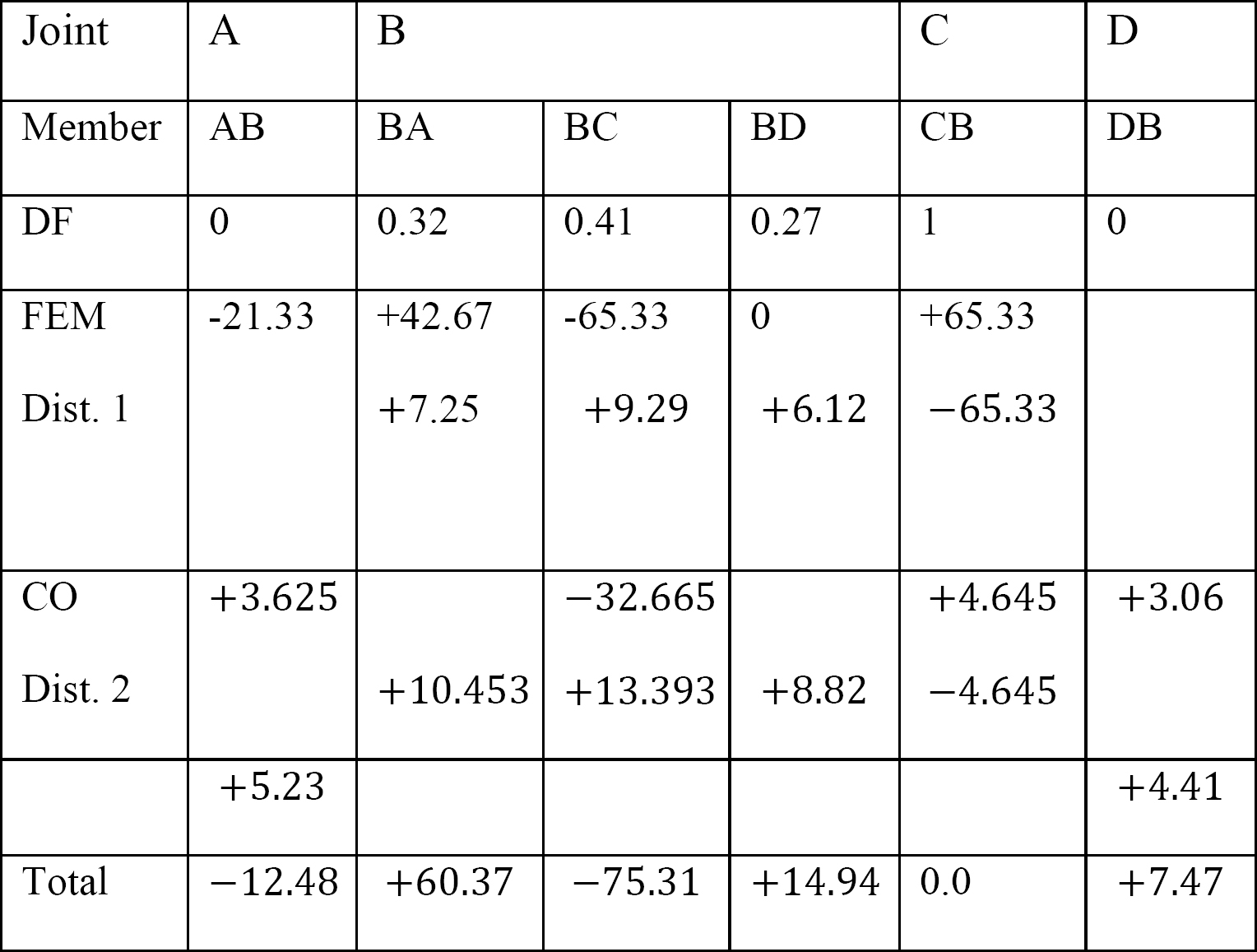
Ostatnie momenty zakończenia członka.
zastąpienie uzyskanych wartości EKθB, EKθC i EK∆ w równaniach momentu końcowego członu sugeruje, co następuje:
MAB = -12,48 K. ft
MBA = +60,37 K. ft
MBC = -75,31 K. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
przykład 12. 4
stosując metodę rozkładu momentu, należy określić momenty końcowe na podporach ramy pokazanej na rysunku 12.9. EI = stała.
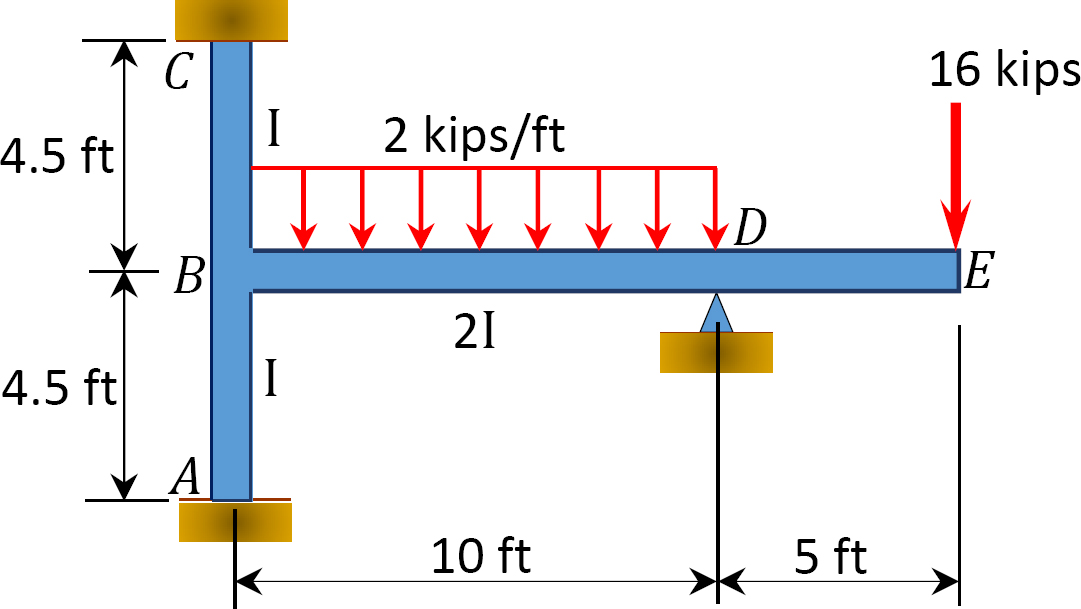
Fig. 12.9. Ramka.
rozwiązanie
stały moment końcowy.
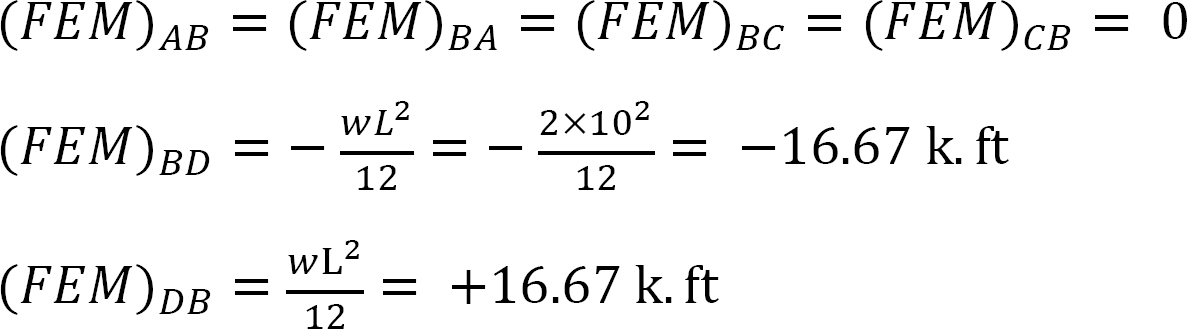
współczynnik sztywności.
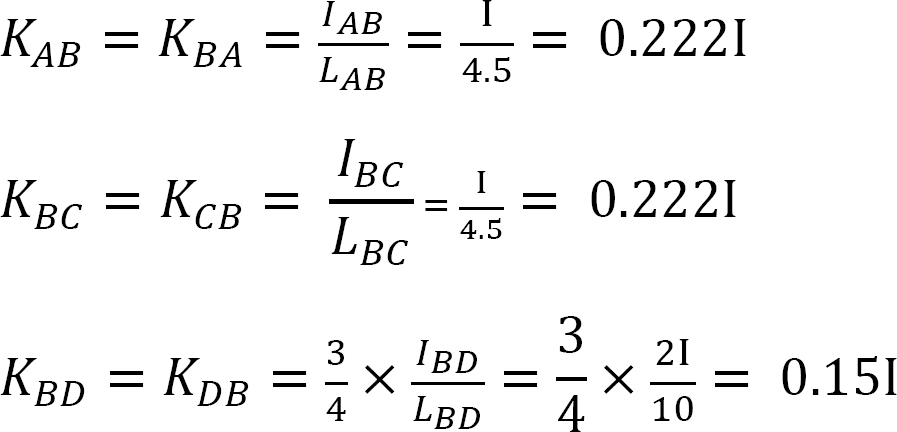
współczynnik dystrybucji.

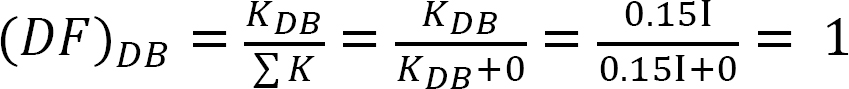
tabela 12.4. Tabela dystrybucji.
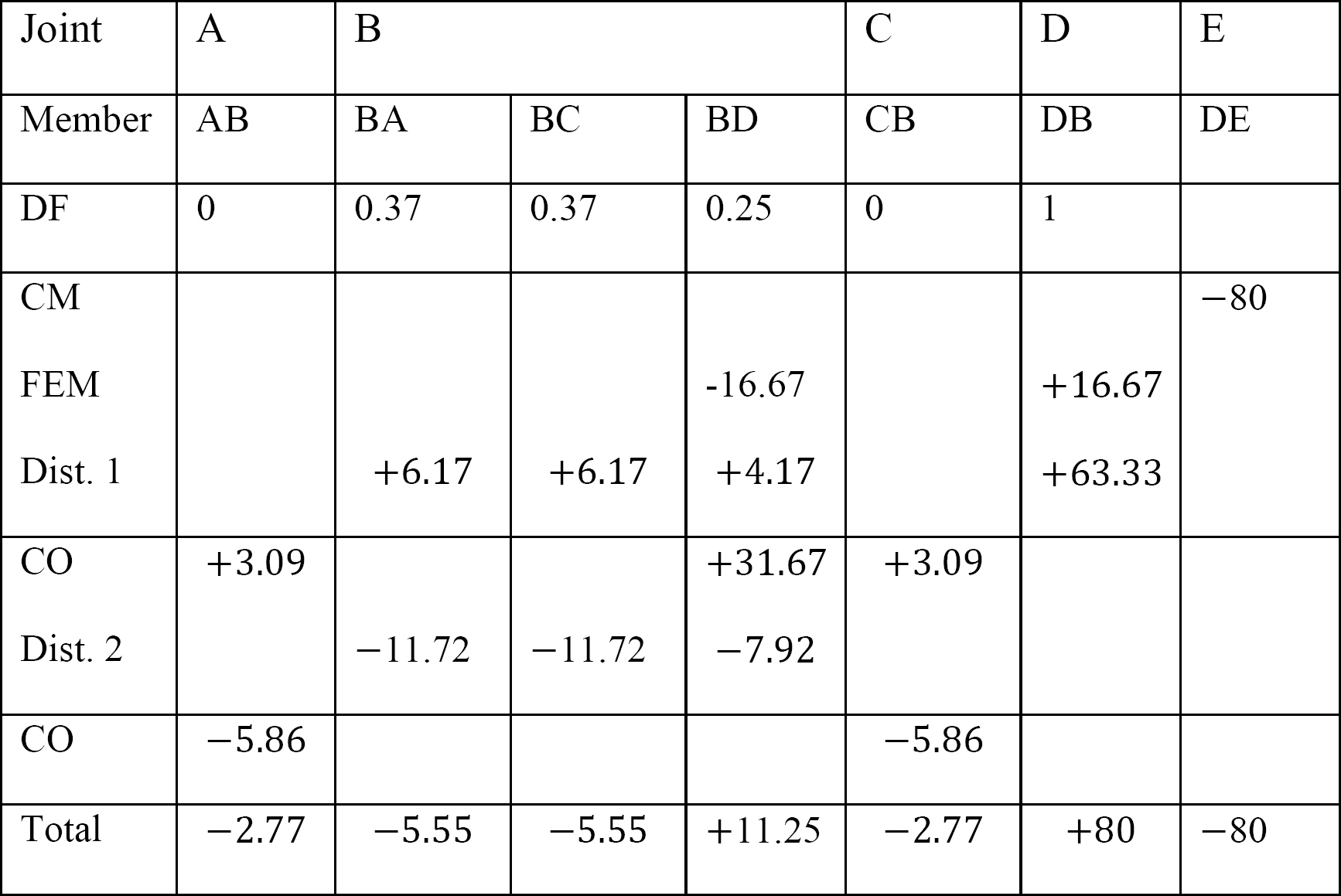
Ostatnie momenty zakończenia członka.
MAB = -2.77 K. ft
MBA = -5.55 K. ft
MBC = -5.55 K. ft
MBD = +11.25 K. ft
MCB = -2.77
MDB = + 80 K. ft
MDE = -80 K. ft
przykład 12.5
stosując metodę rozkładu momentu, należy określić momenty końcowe na podporach ramy pokazanej na rysunku 12.10. EI = stała.
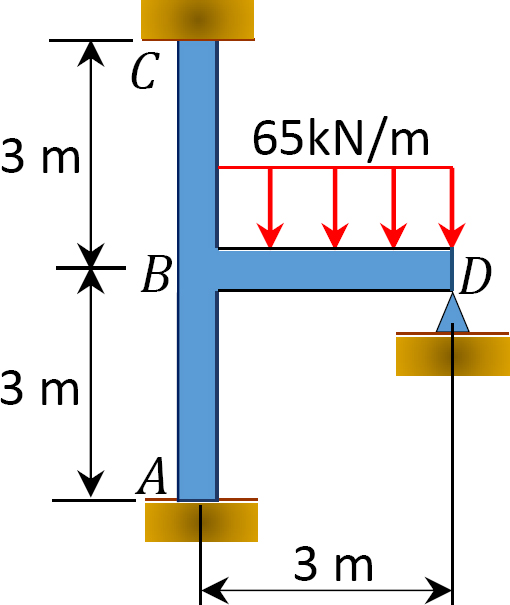
Fig. 12.10. Ramka.
rozwiązanie
stały moment końcowy.
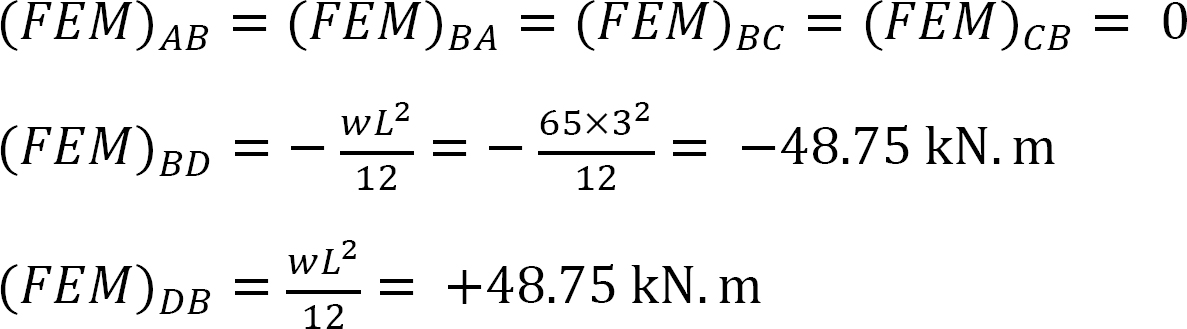
współczynnik sztywności.
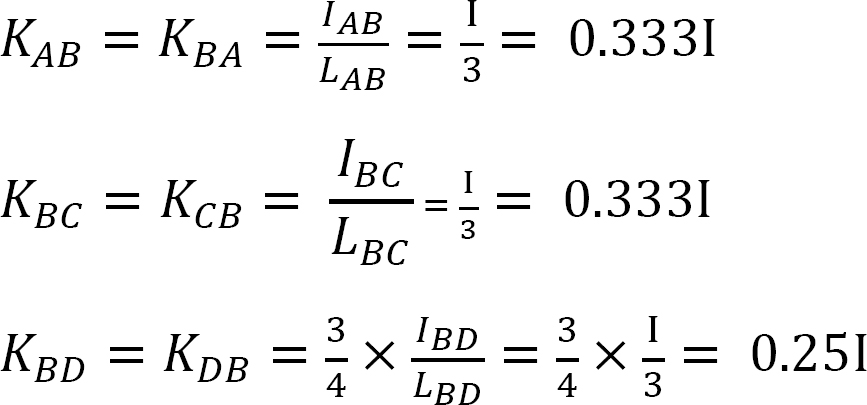
współczynnik dystrybucji.
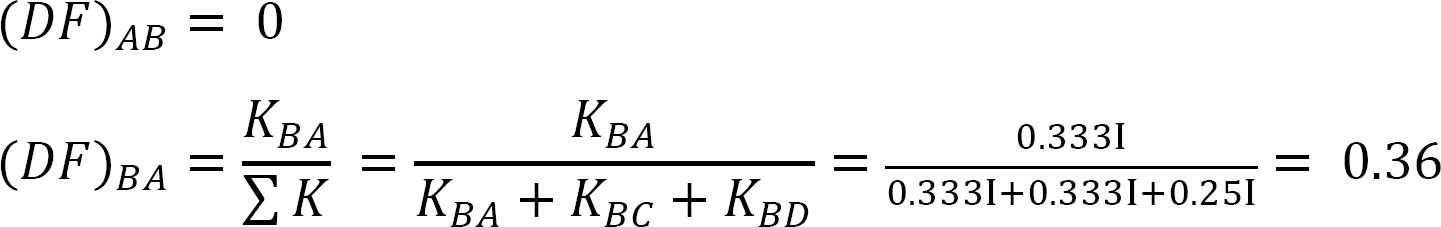

tabela 12.5. Tabela dystrybucji.
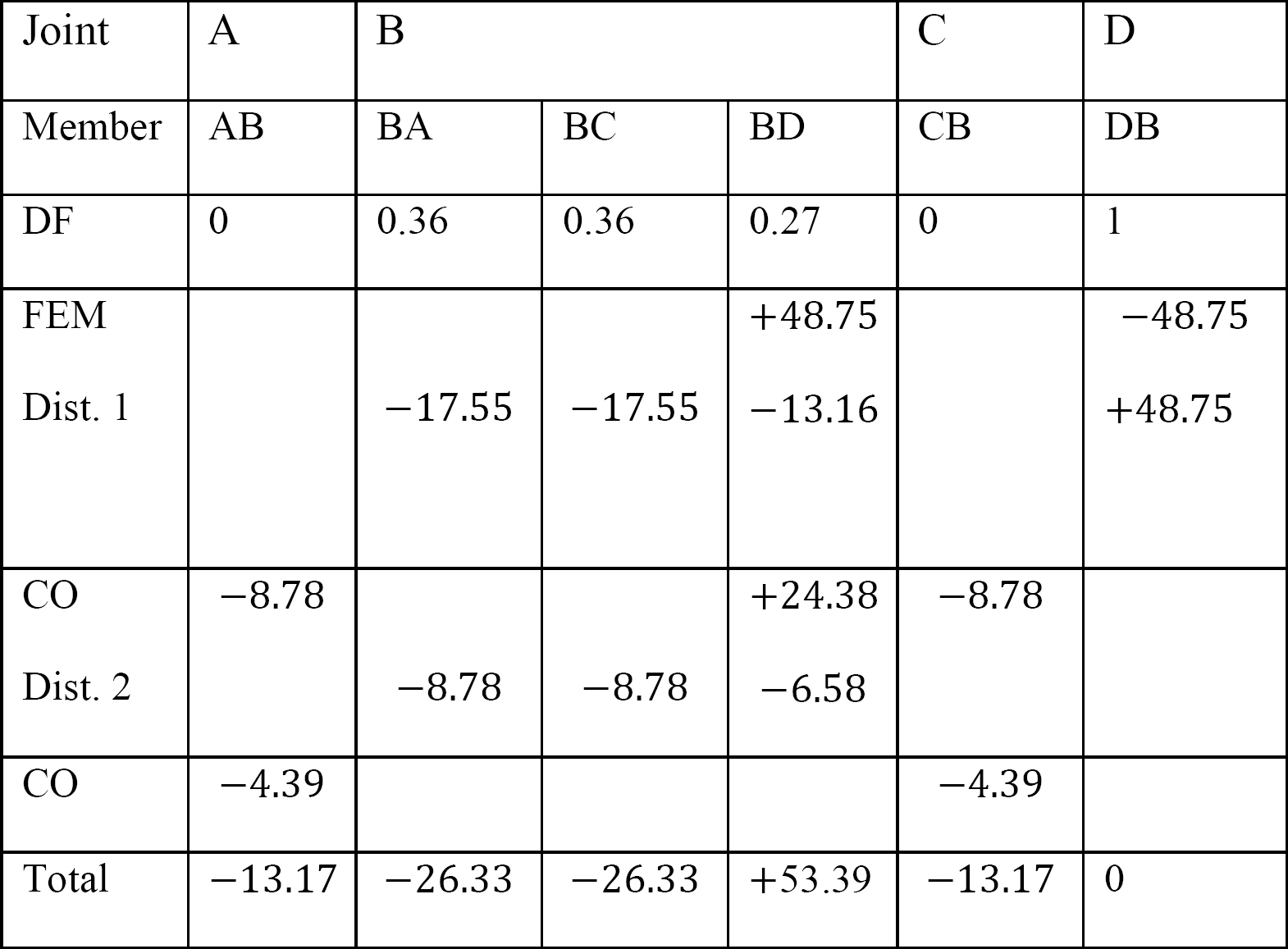
Ostatnie momenty zakończenia członka.
MAB = -13.17 K. ft
MBA = -26.33 K. ft
MBC = -26.33 K. ft
MBD = +53.39 K. ft
MCB = -13.17 K. ft
MDB = 0
przykład 12.6
stosując metodę rozkładu momentu, określ momenty końcowe pręta ramy z kołysaniem bocznym pokazanym na rysunku 12.11 a.
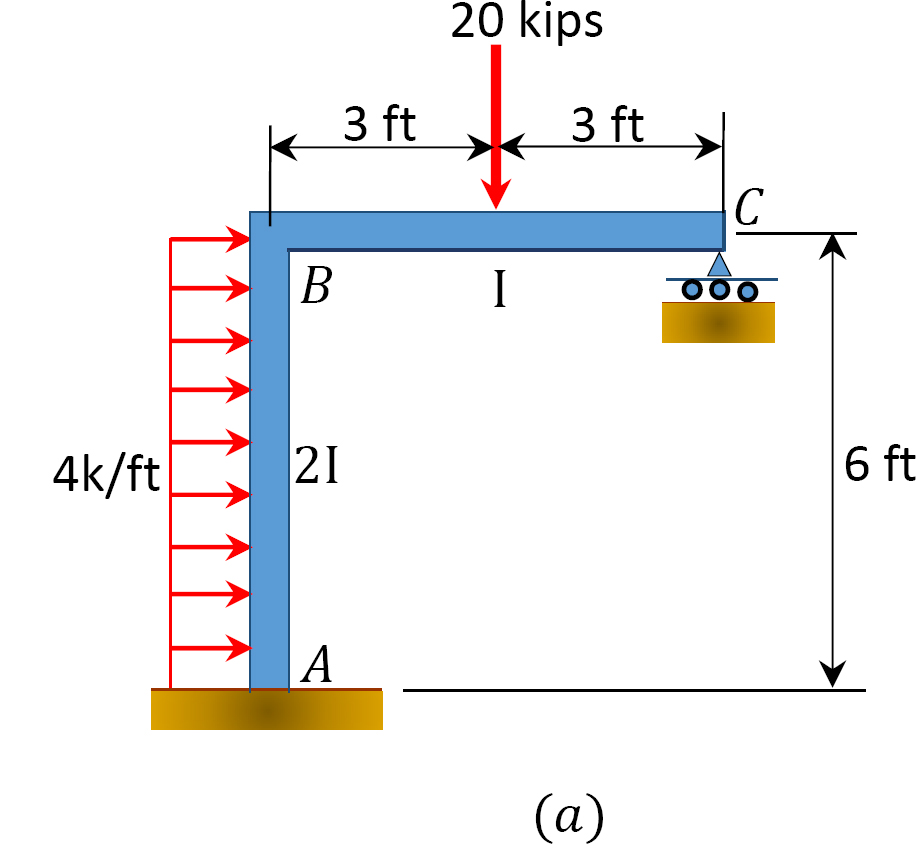
Fig. 12.11. Rama z kołysaniem bocznym.
rozwiązanie
stały moment końcowy.
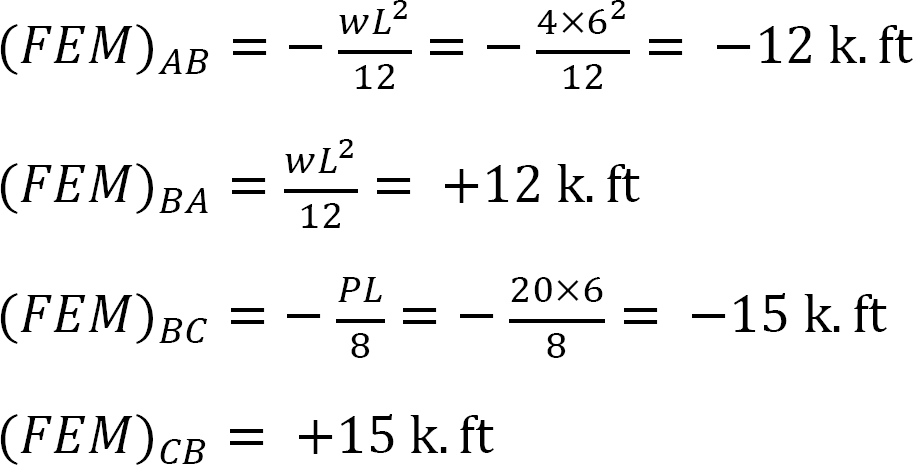
współczynnik sztywności.
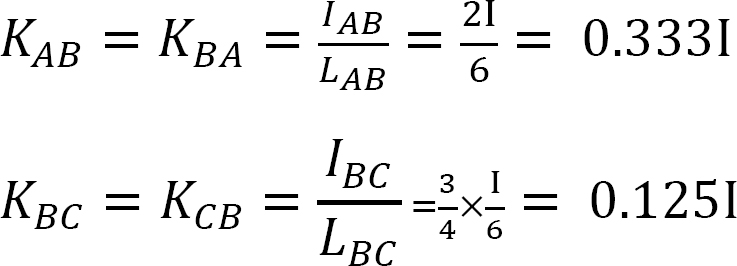
współczynnik dystrybucji.
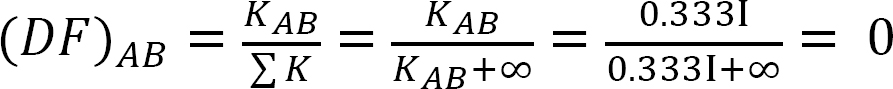

Analiza ramy bez kołysania bocznego.
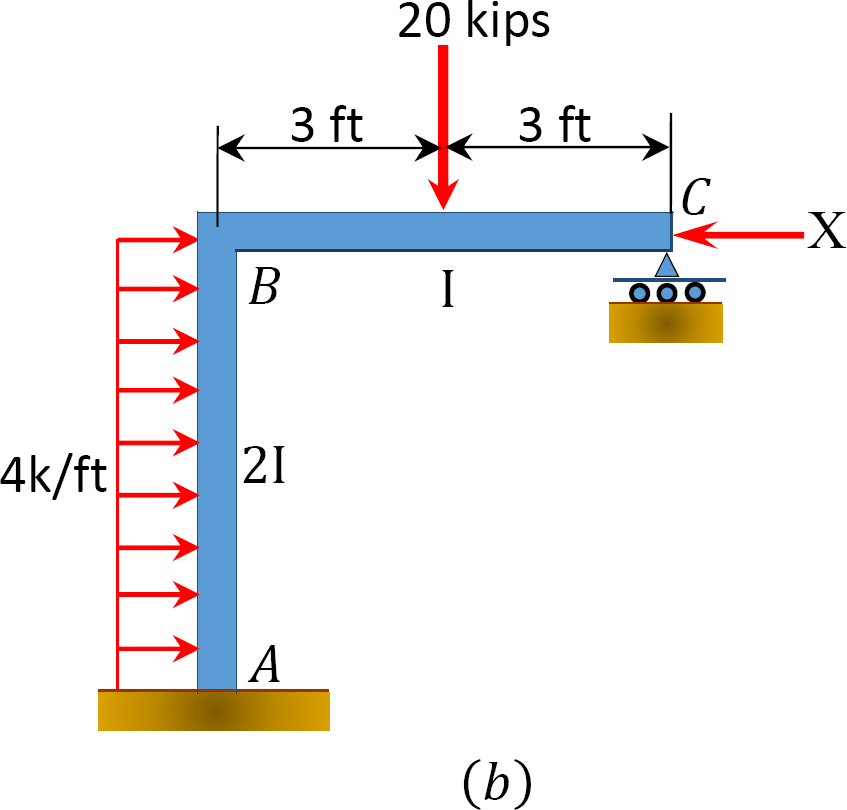
tabela 12.6. Tabela dystrybucji (bez ramki kołysania).
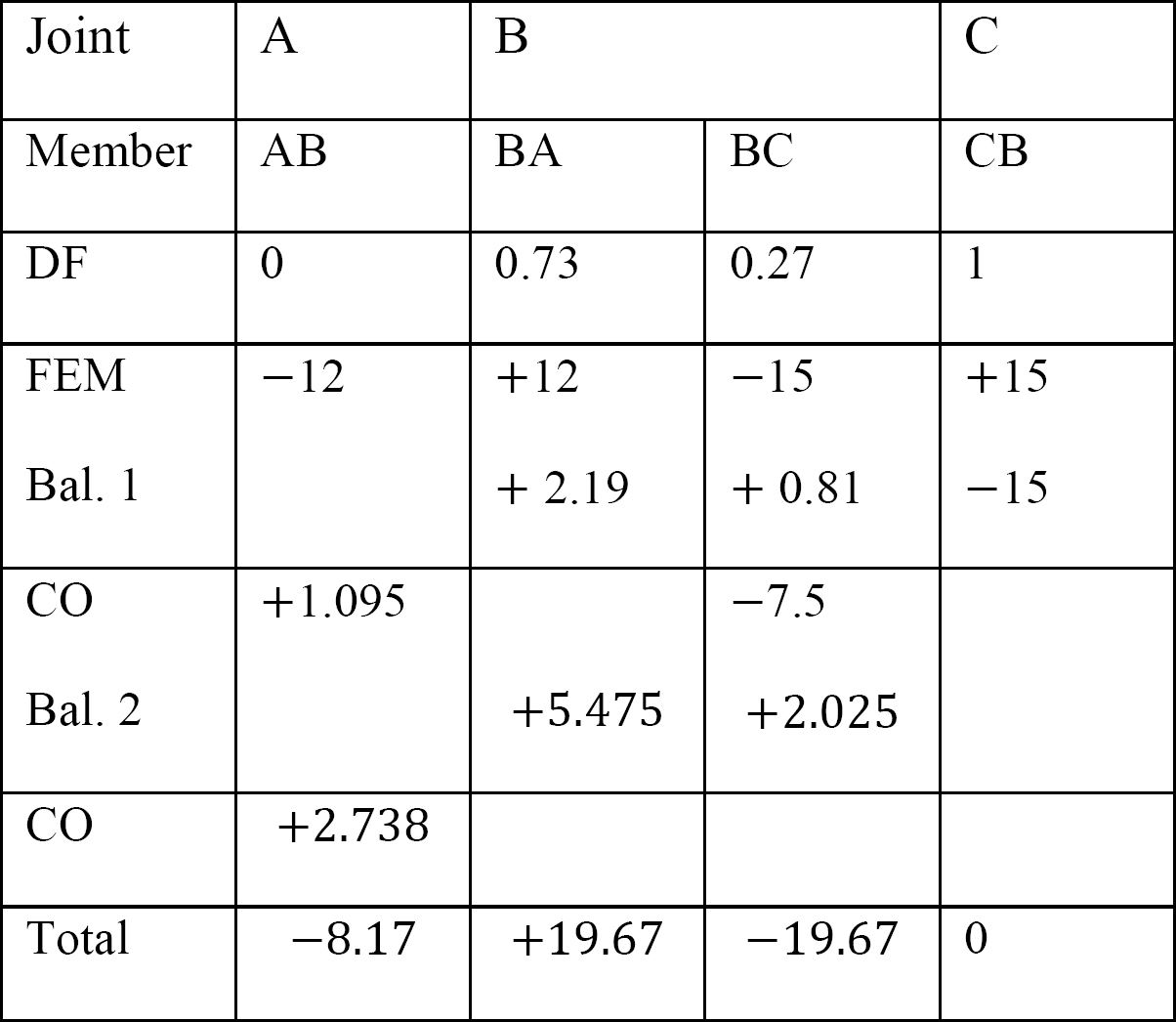
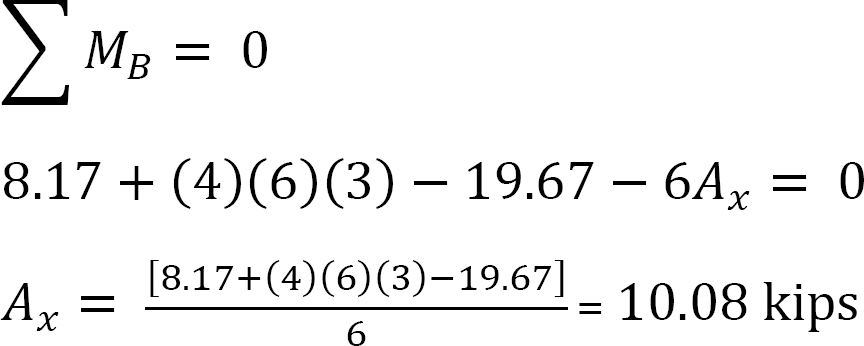
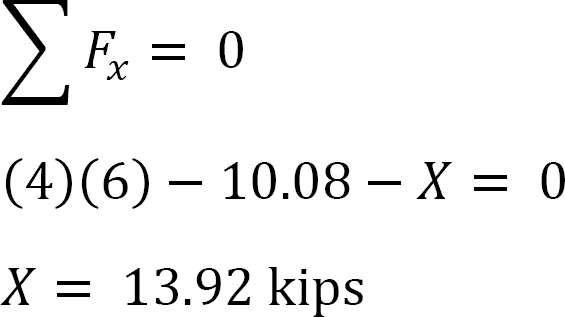
Analiza ramy z kołysaniem bocznym.
Załóżmy, że MAB = +20 K. ft
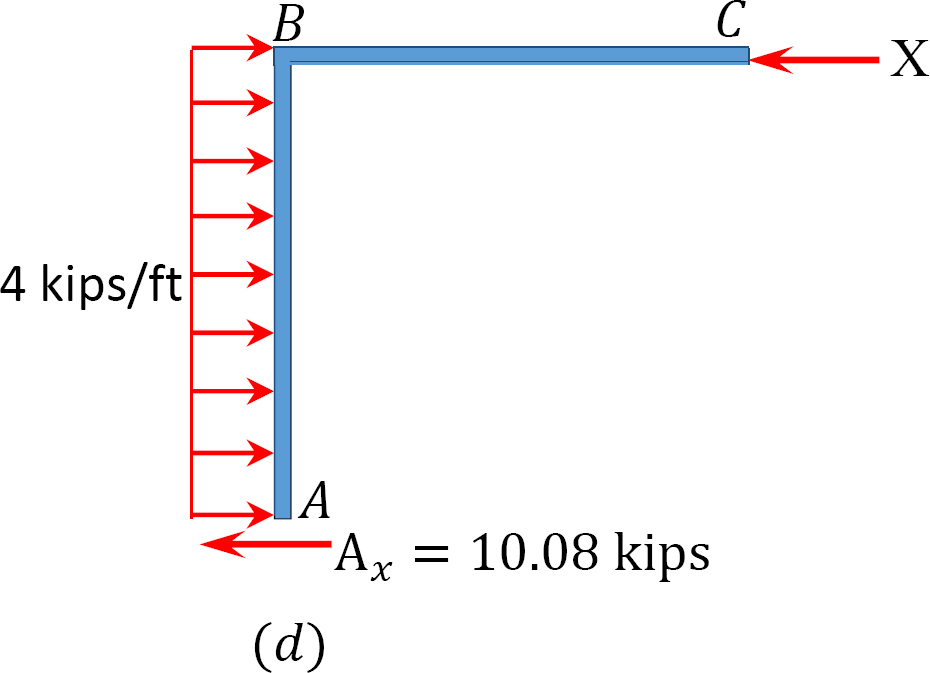
tabela 12.7. Tabela dystrybucji (rama kołysania).
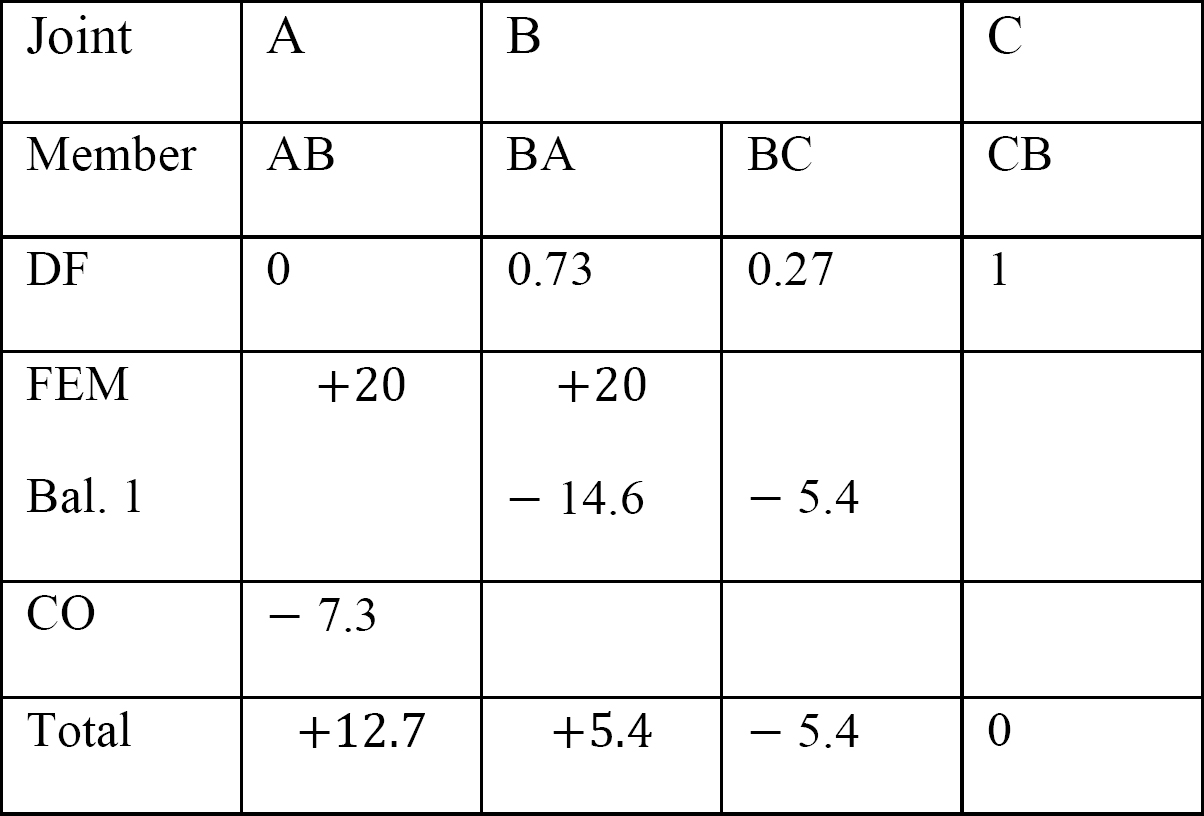
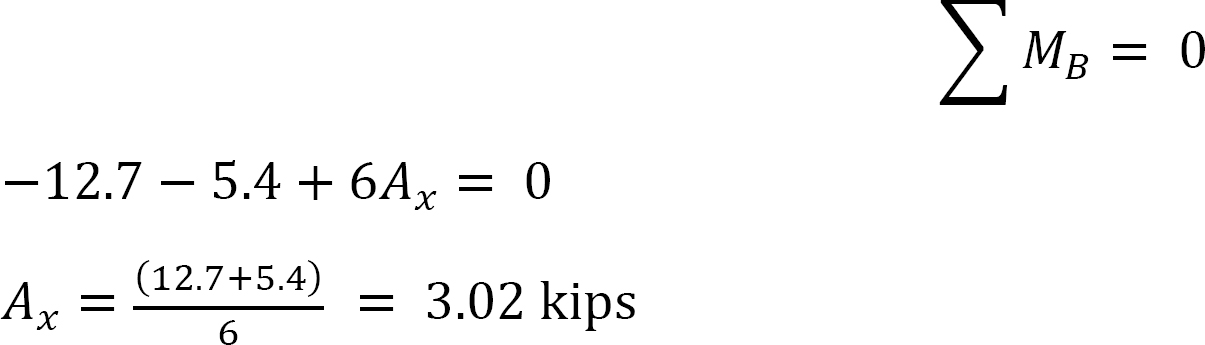
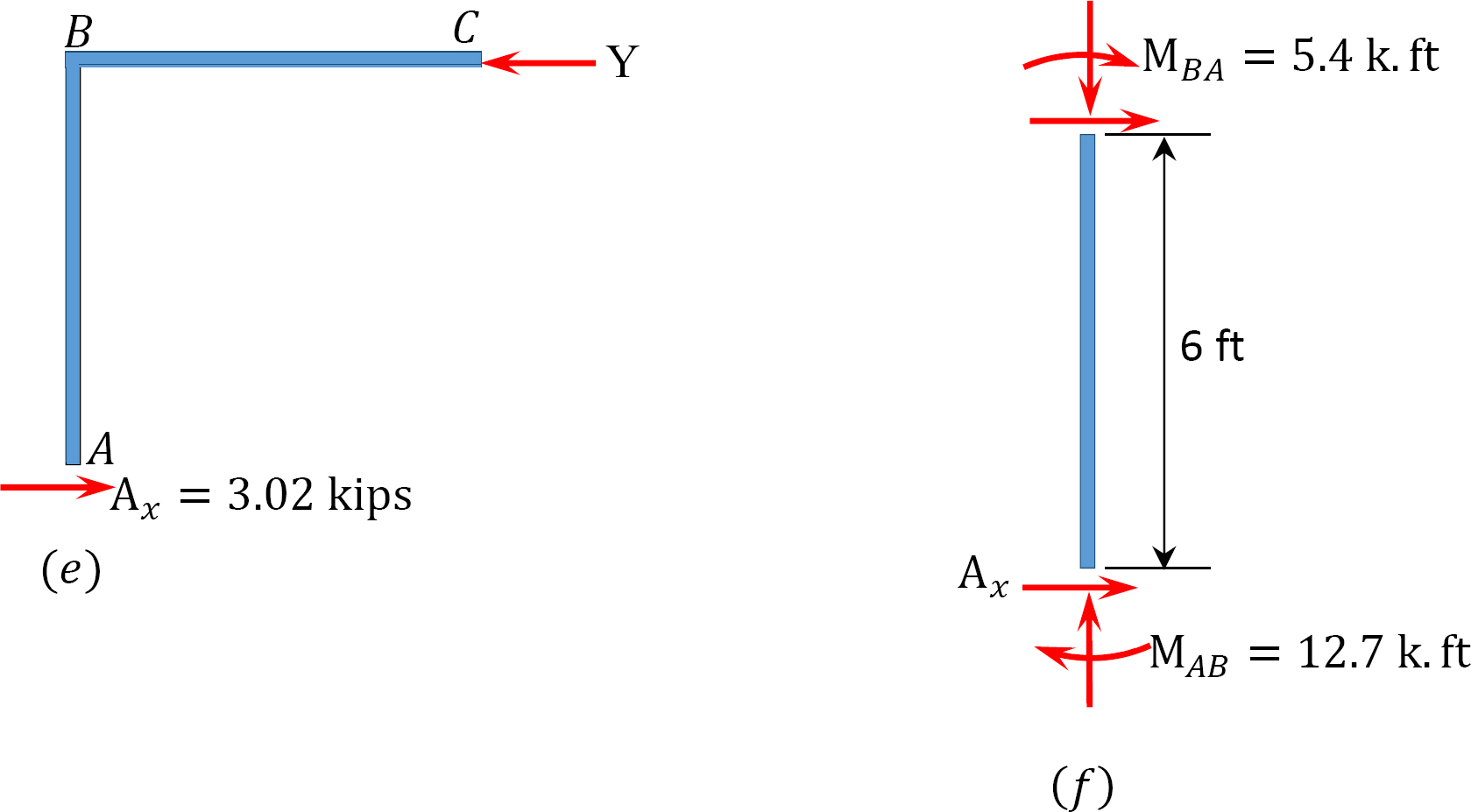
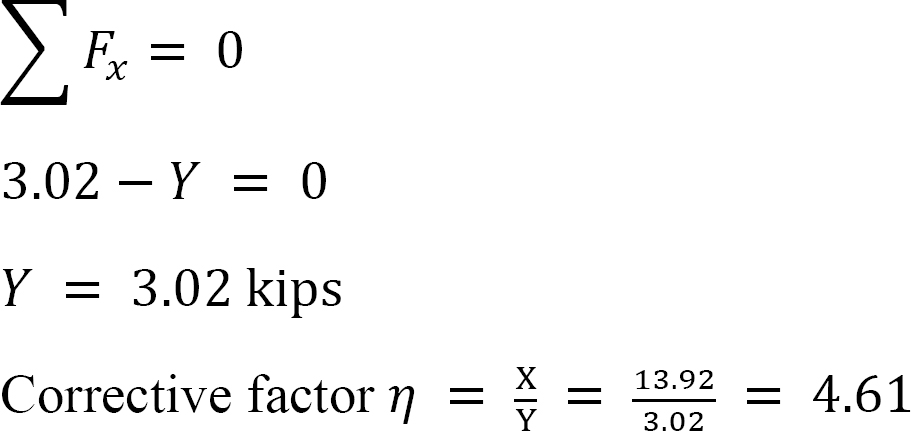
Ostatnie momenty końca.
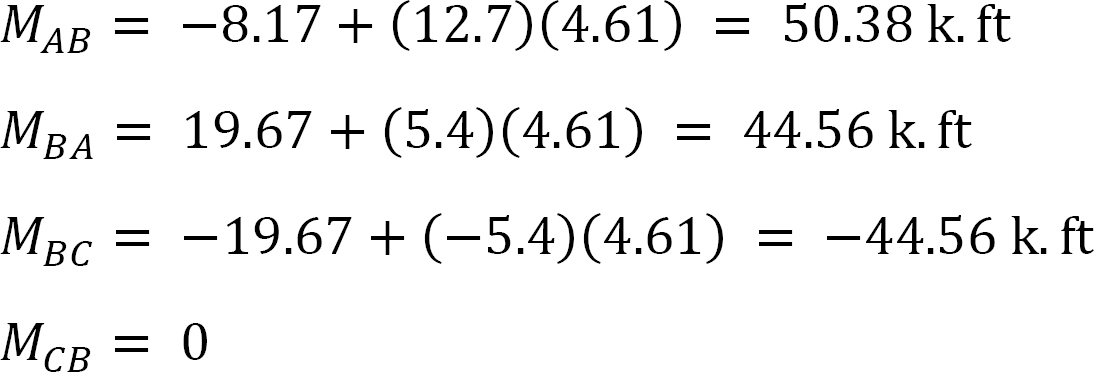
przykład 12.7
ramka kołysania jest ładowana, jak pokazano na rysunku 12.12 a. korzystając z metody rozkładu momentu, określ momenty końcowe elementów ramki.
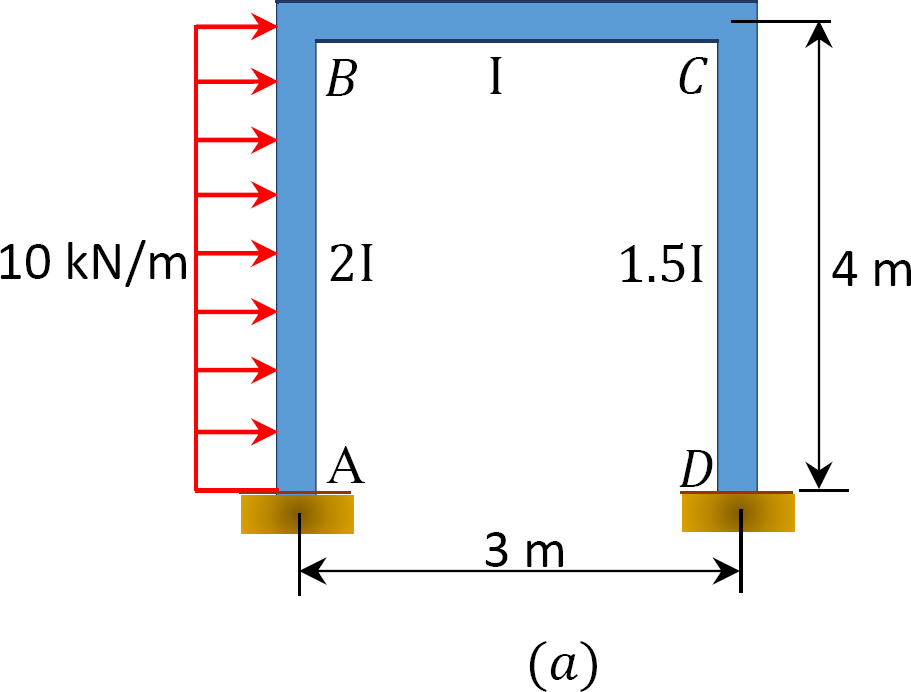
Fig. 12.12. Załadowana rama kołysania.
rozwiązanie
stały moment końcowy.
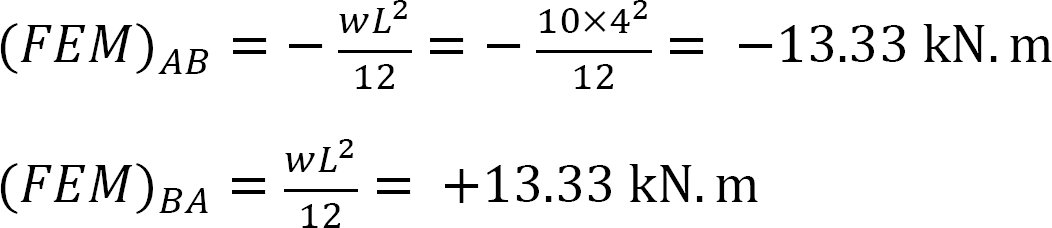
współczynnik sztywności.
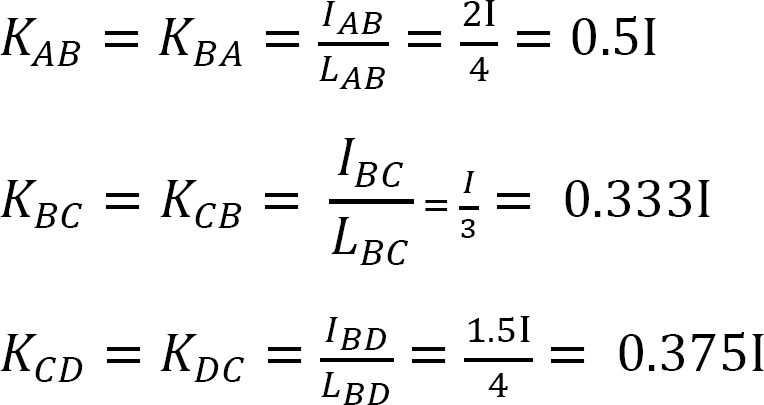
współczynnik dystrybucji.

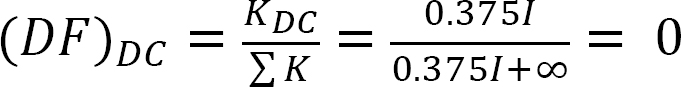
Analiza ramy bez kołysania bocznego.
Tabela dystrybucji (bez ramki kołysania).
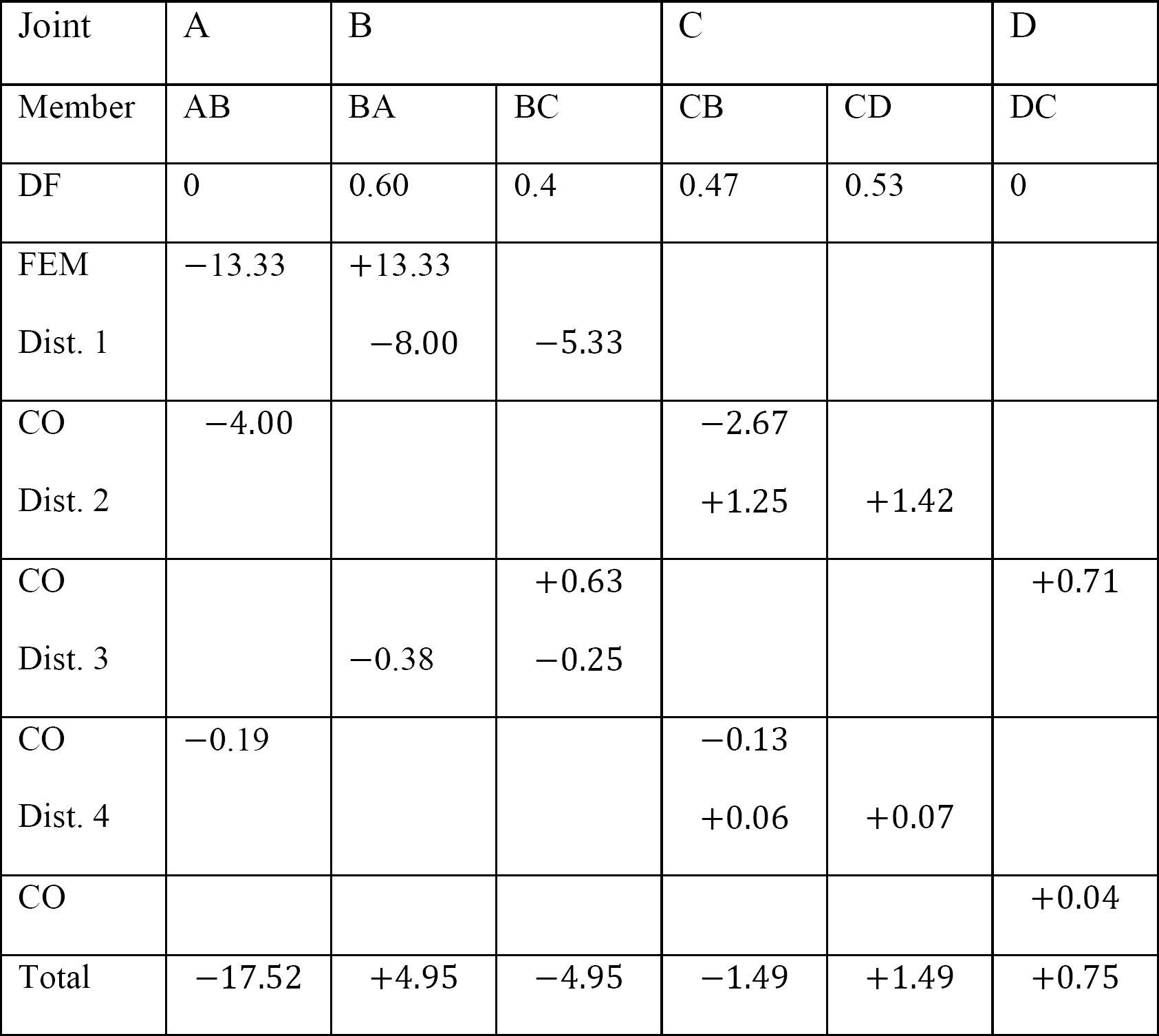
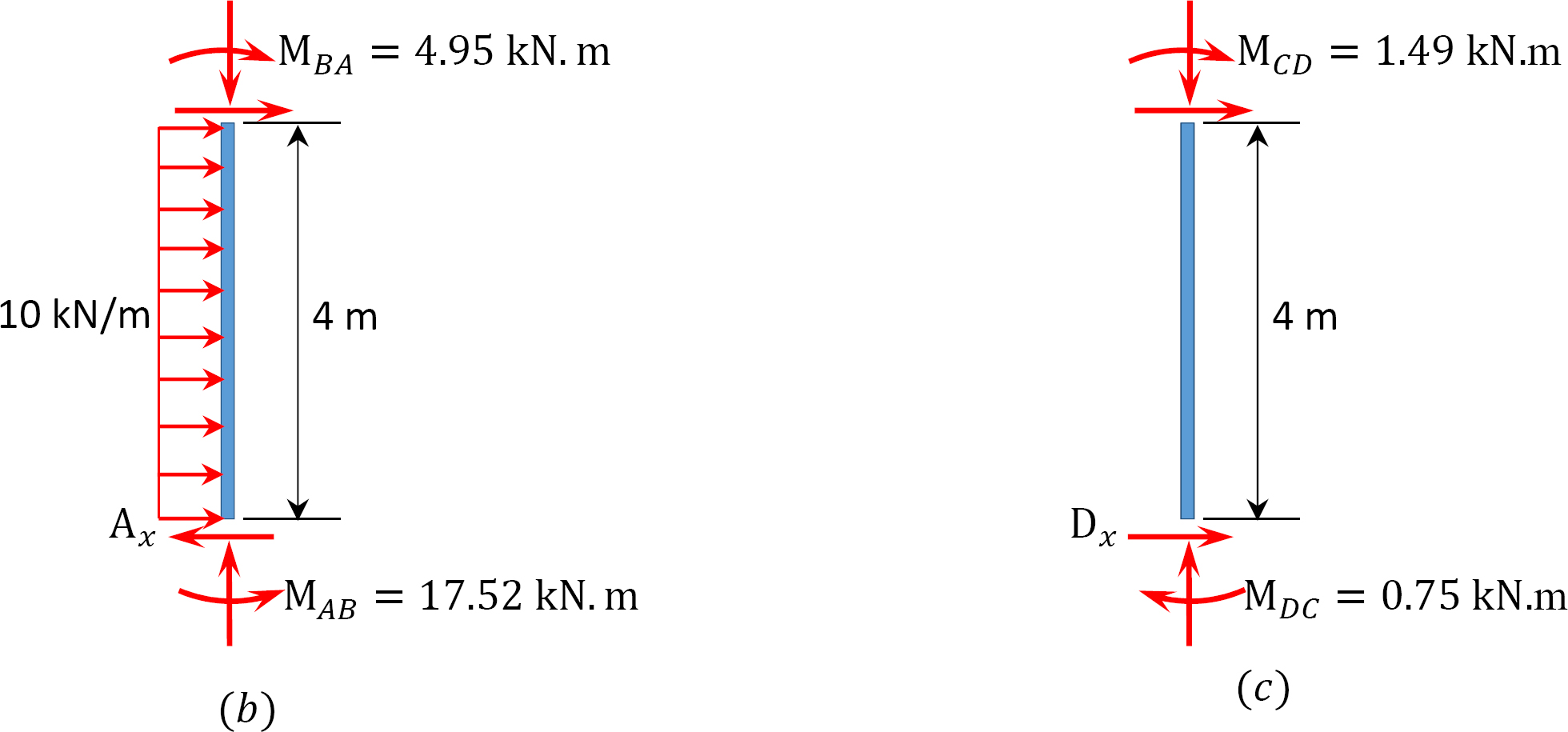
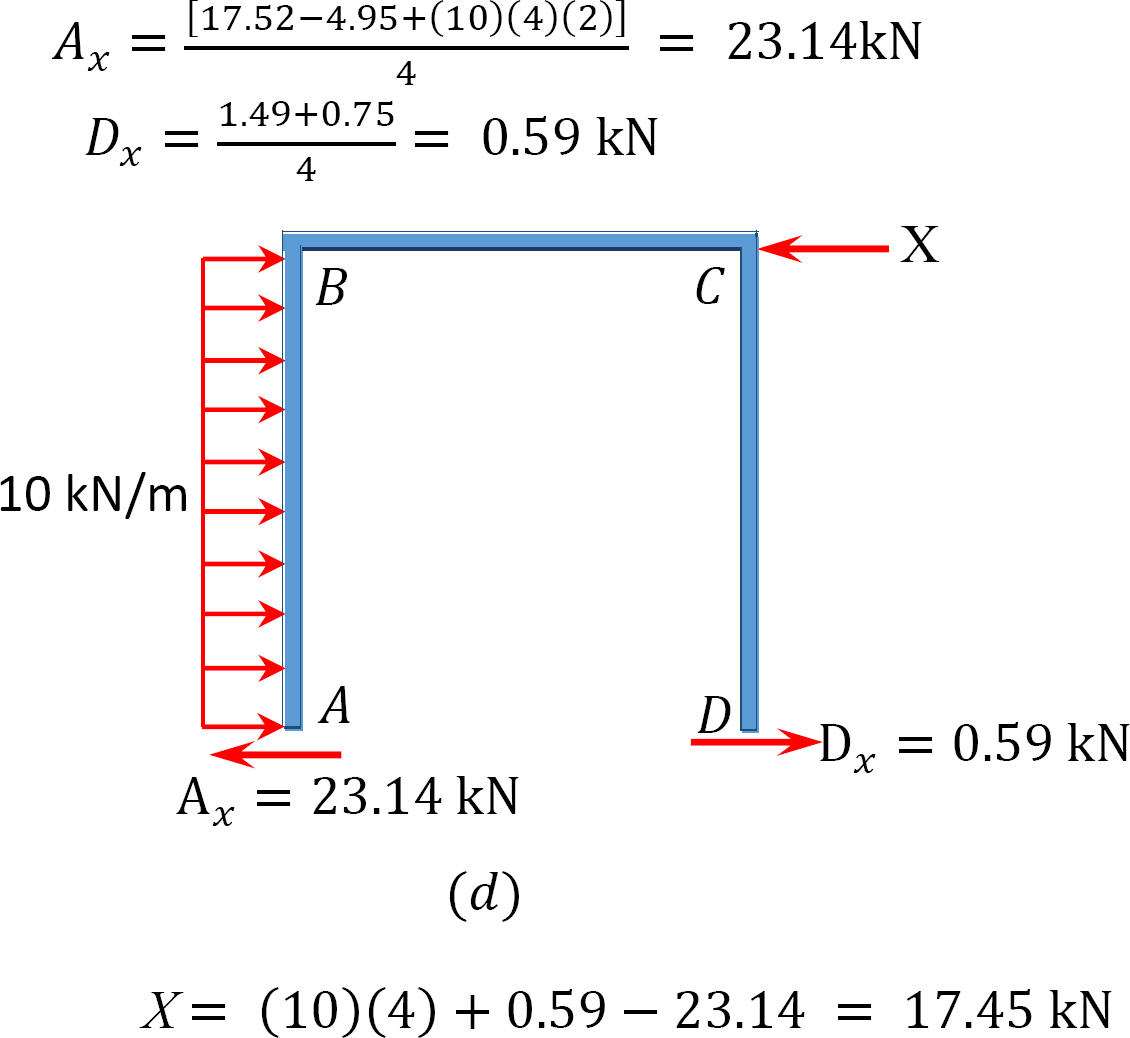
tabela 12.9. Tabela dystrybucji (rama kołysania).
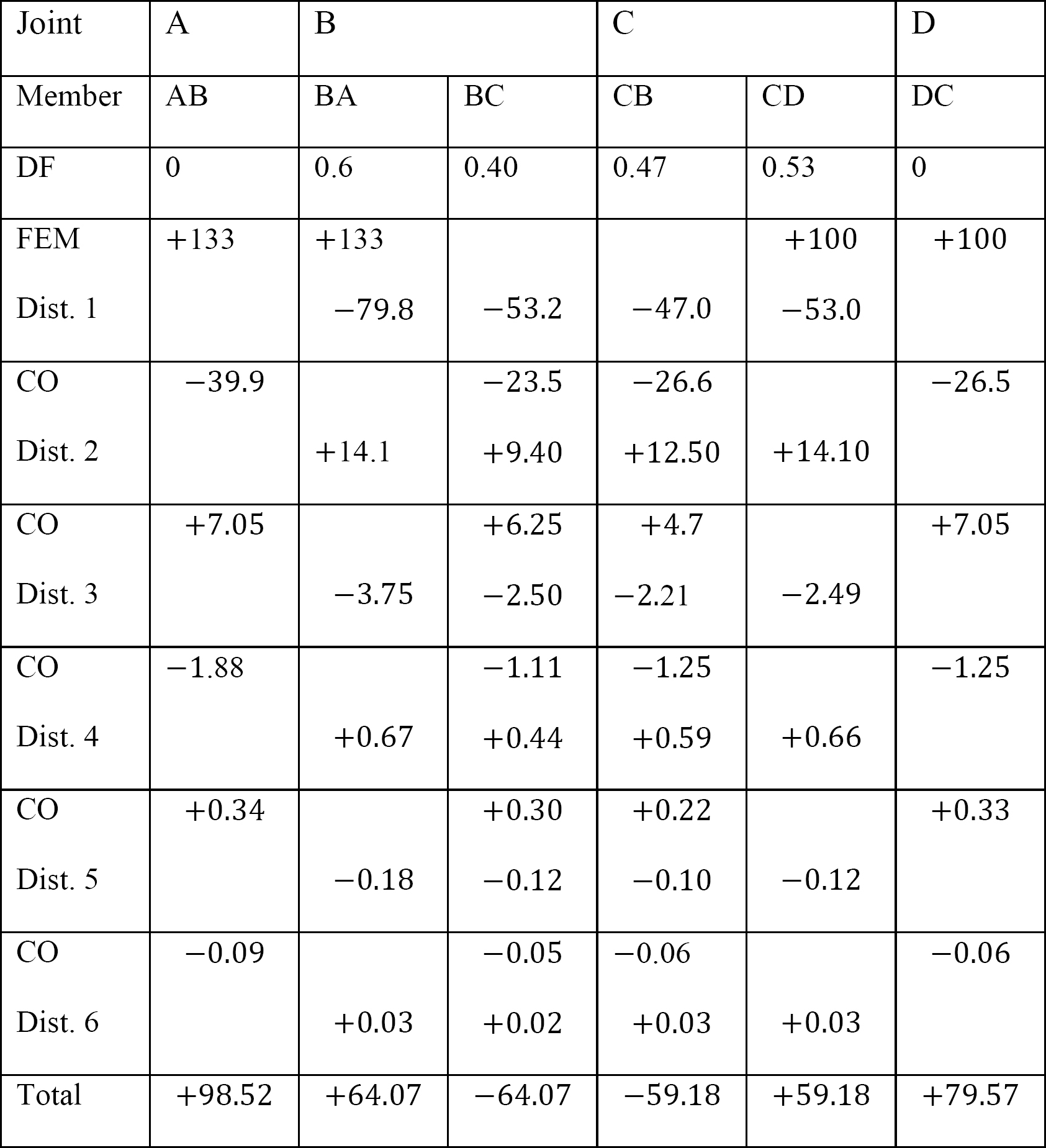
Analiza ramy z kołysaniem bocznym.
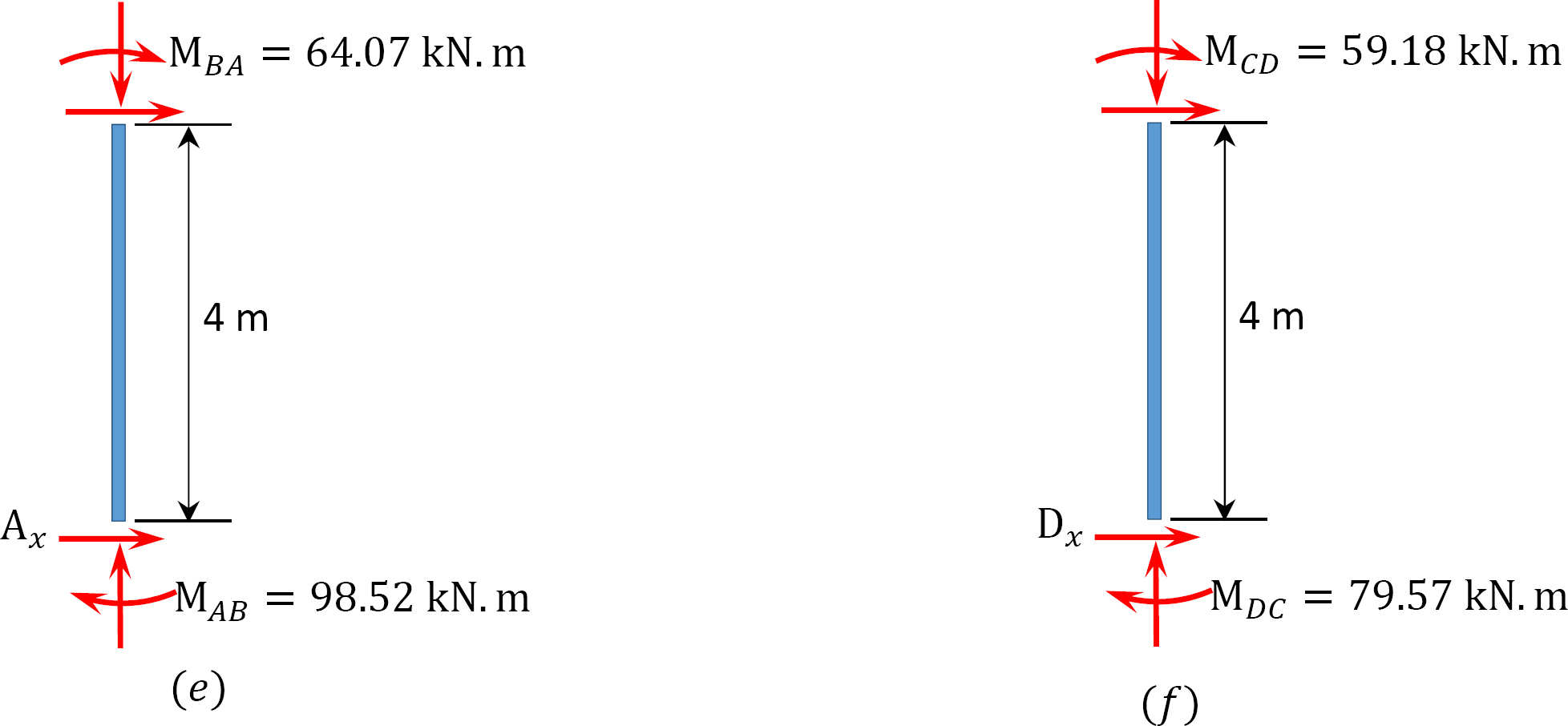

ostatnia chwila.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
podsumowanie rozdziału
rozkład momentu metoda analizy nieokreślonych struktur: rozkład momentu metoda analizy jest przybliżoną metodą analizy. Jego stopień dokładności zależy od liczby iteracji. W tej metodzie zakłada się, że wszystkie połączenia w konstrukcji są tymczasowo zablokowane lub zaciśnięte, a tym samym uniemożliwia się ich obrót. Obciążenia są przykładane do prętów, a momenty rozwinięte na końcach prętów ze względu na mocowanie są określane. Stawy w strukturze są następnie sukcesywnie odblokowane, a niezrównoważony moment przy każdym stawie jest rozdzielany na spotkania członków w tym stawie. Momenty przenoszenia na odległych końcach członków są określane, a proces równoważenia jest kontynuowany aż do pożądanego poziomu dokładności. Momenty końcowe członków są określane przez zsumowanie momentu stałego końca, momentu rozproszonego i momentu przeniesienia. Po określeniu momentów końcowych członków struktura staje się zdeterminowana.
Problemy Z Ćwiczeniami
12.1 użyj metody rozkładu momentu, aby obliczyć moment końcowy prętów belek pokazanych na rysunku P12. 1 do rysunku P12. 12 i narysować wykresy momentu zginającego i siły ścinającej. EI = stała.
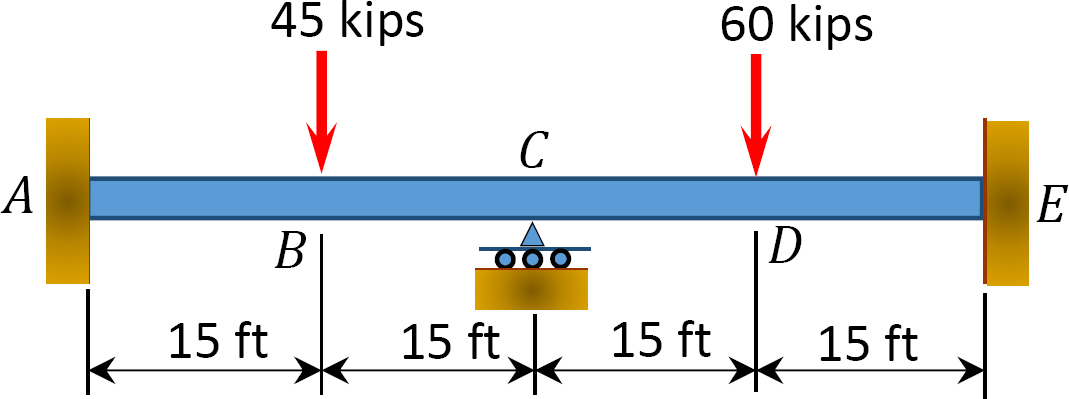
Fig. P12. 1. Belka.
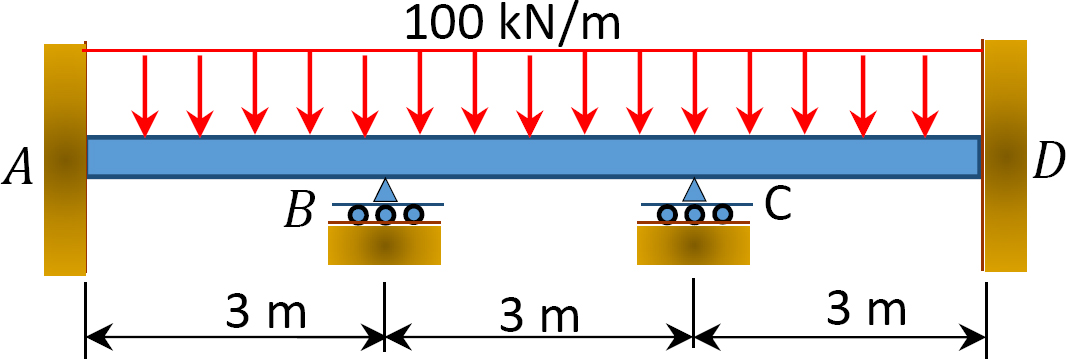
Fig. P12. 2. Belka.
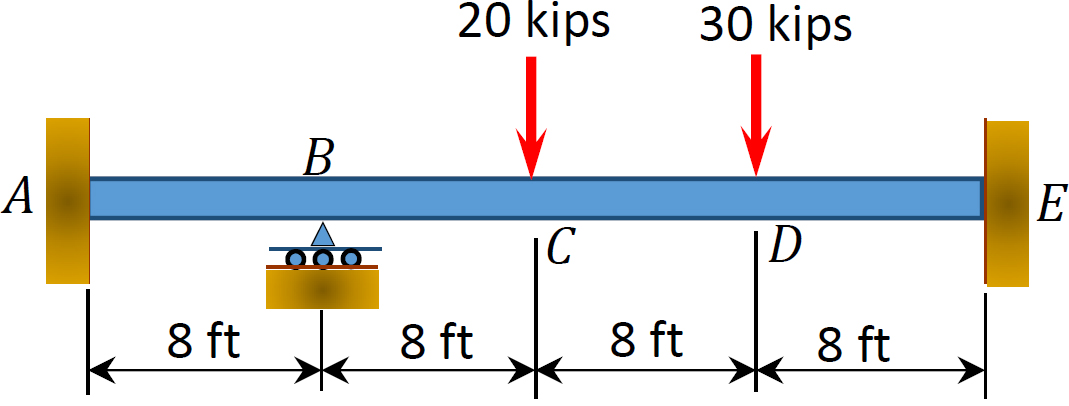
Fig. P12. 3. Belka.
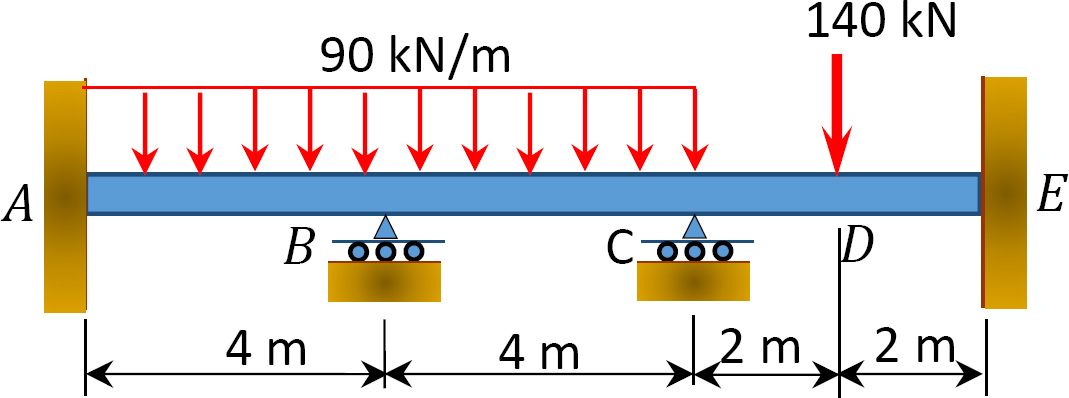
Fig. P12. 4. Belka.
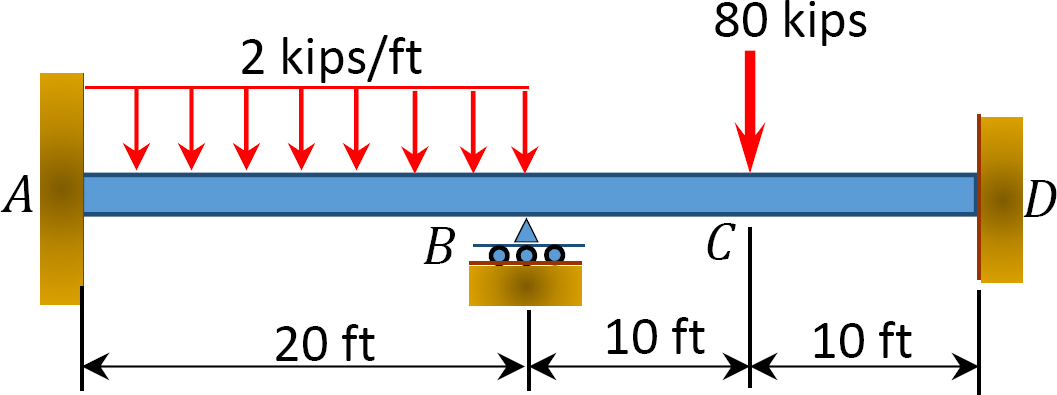
Fig. P12. 5. Belka.
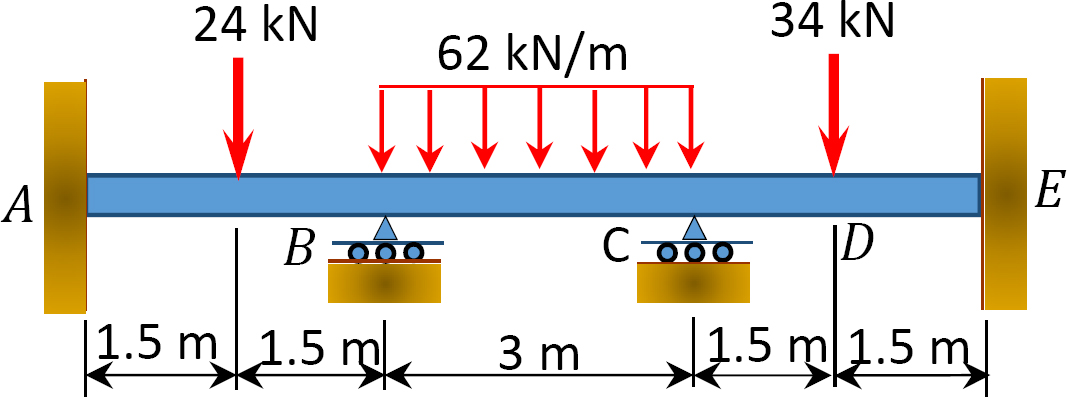
Fig. P12. 6. Belka.
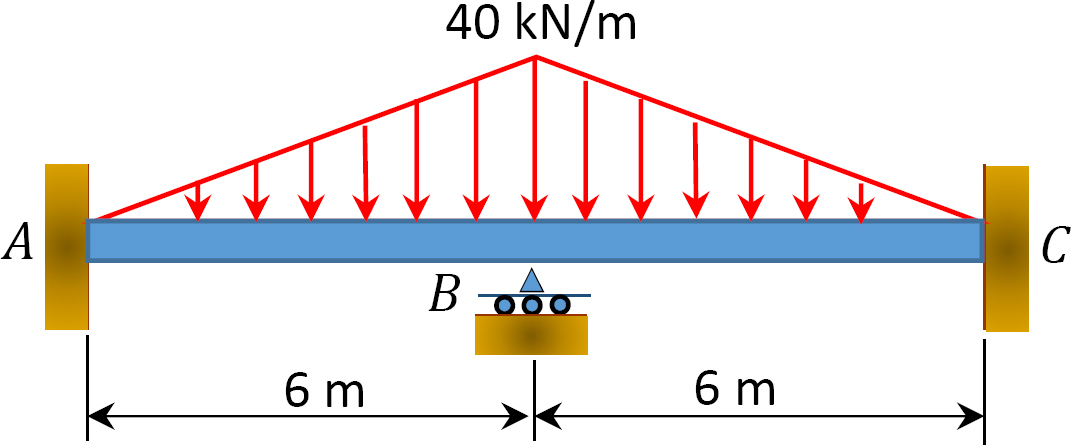
Fig. P12. 7. Belka.
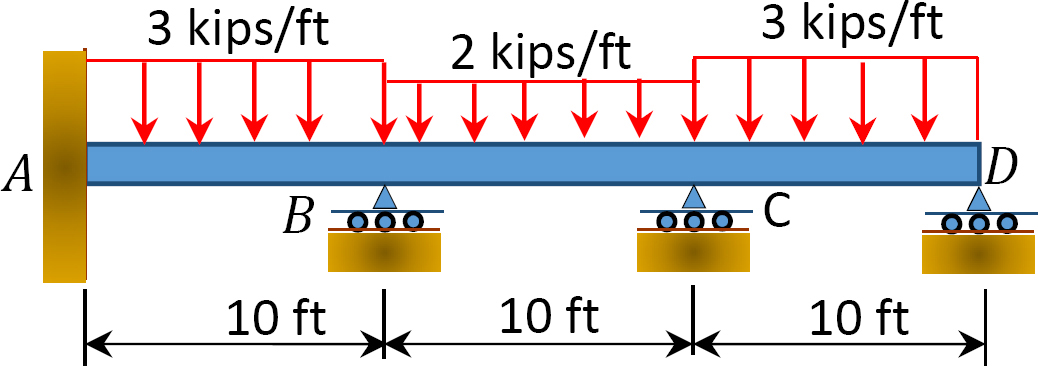
Fig. P12. 8. Belka.
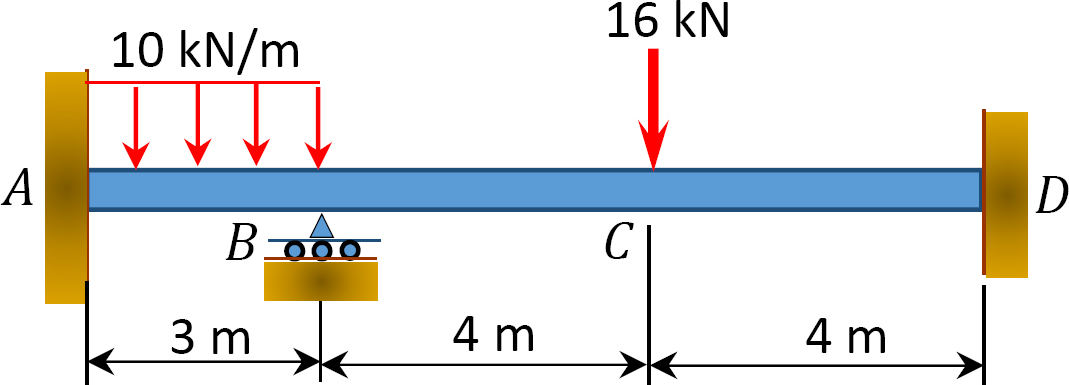
Fig. P12. 9. Belka.
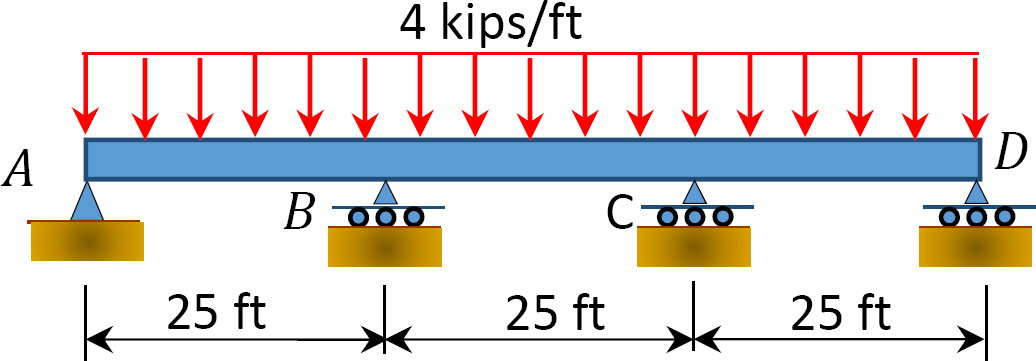
Fig. P12. 10. Belka.
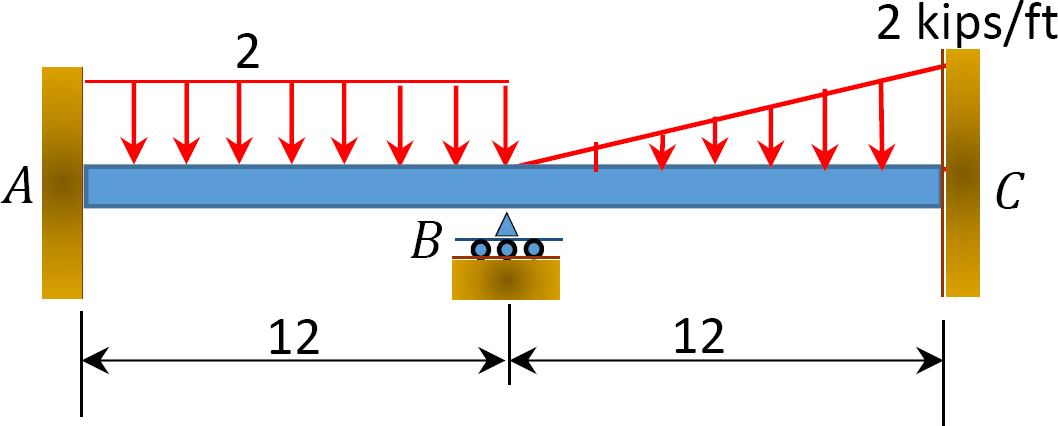
Fig. P12. 11. Belka.
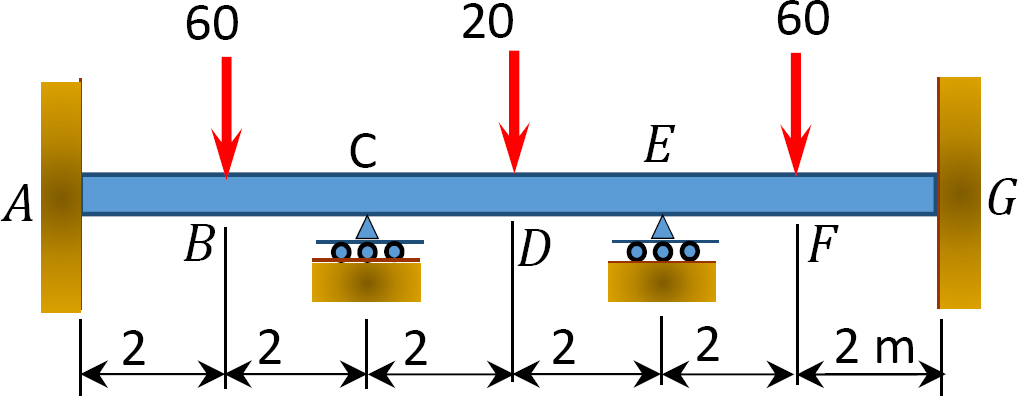
Fig. P12. 12. Belka.
12.2 użyj metody rozkładu momentu do obliczenia momentu końcowego prętów RAM pokazanych na rysunku P12.13 do rysunku 12.20 i narysuj diagramy momentu zginającego i siły ścinającej. EI = stała.
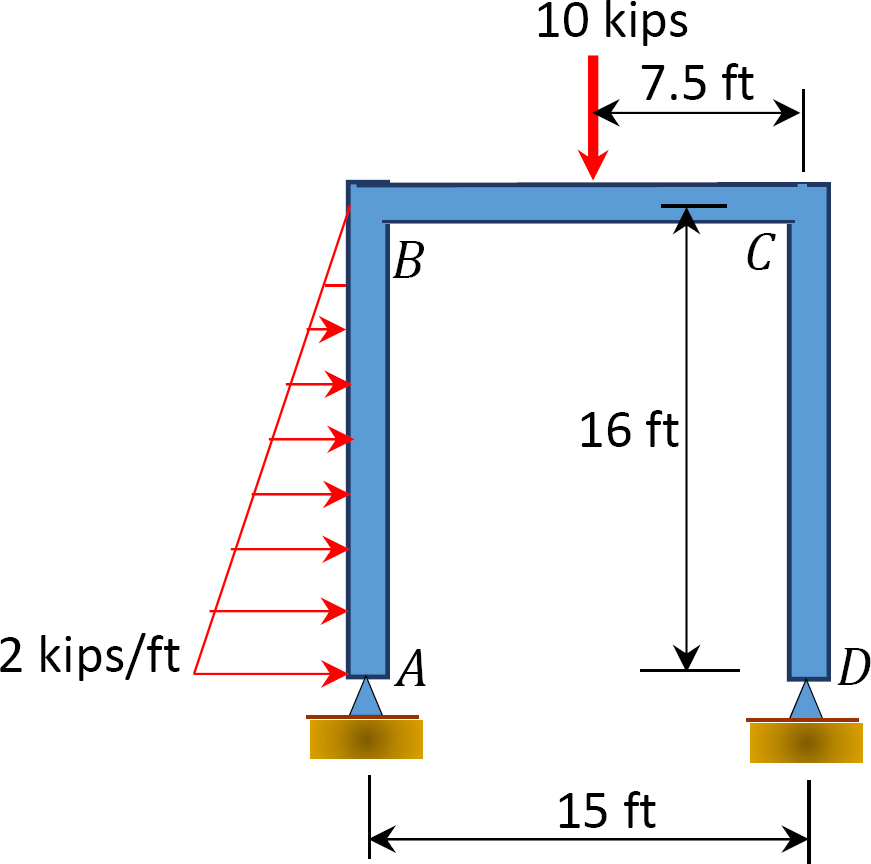
Fig. P12. 13. Ramka.
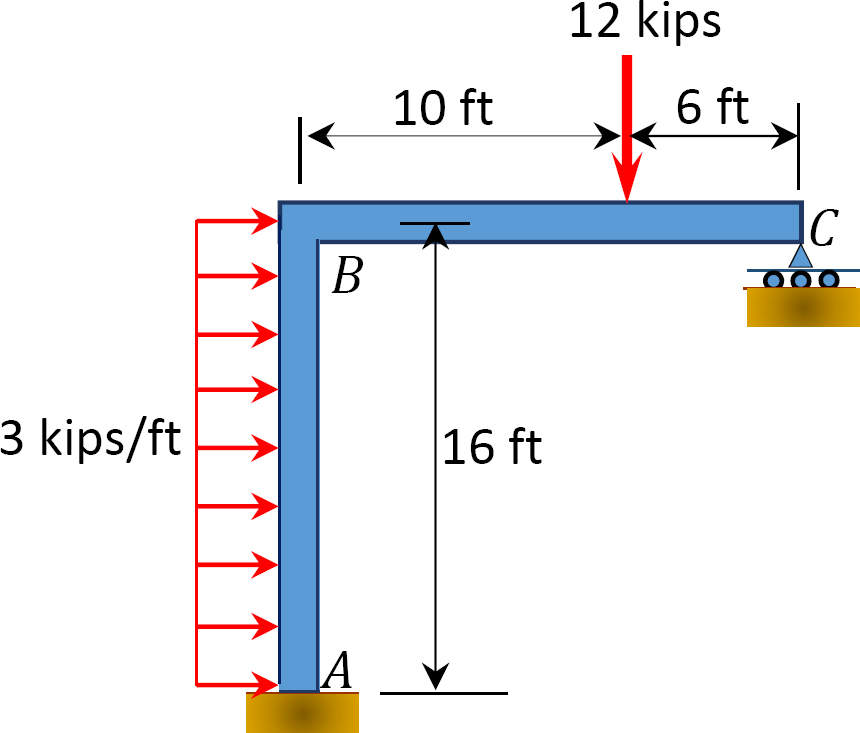
Fig. P12. 14. Ramka.
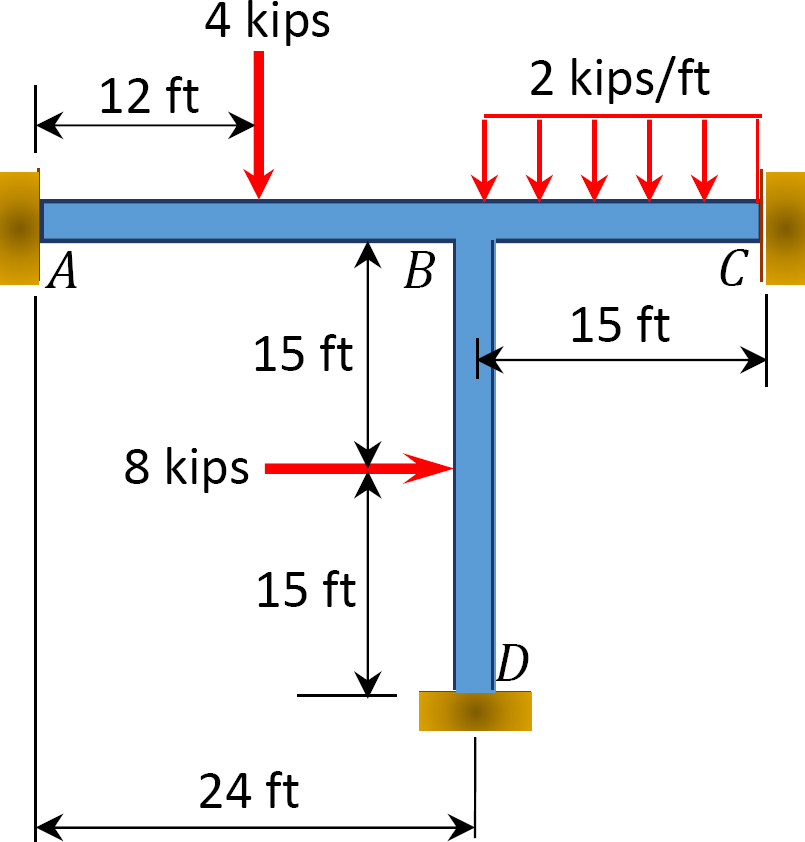
Fig. P12. 15. Ramka.
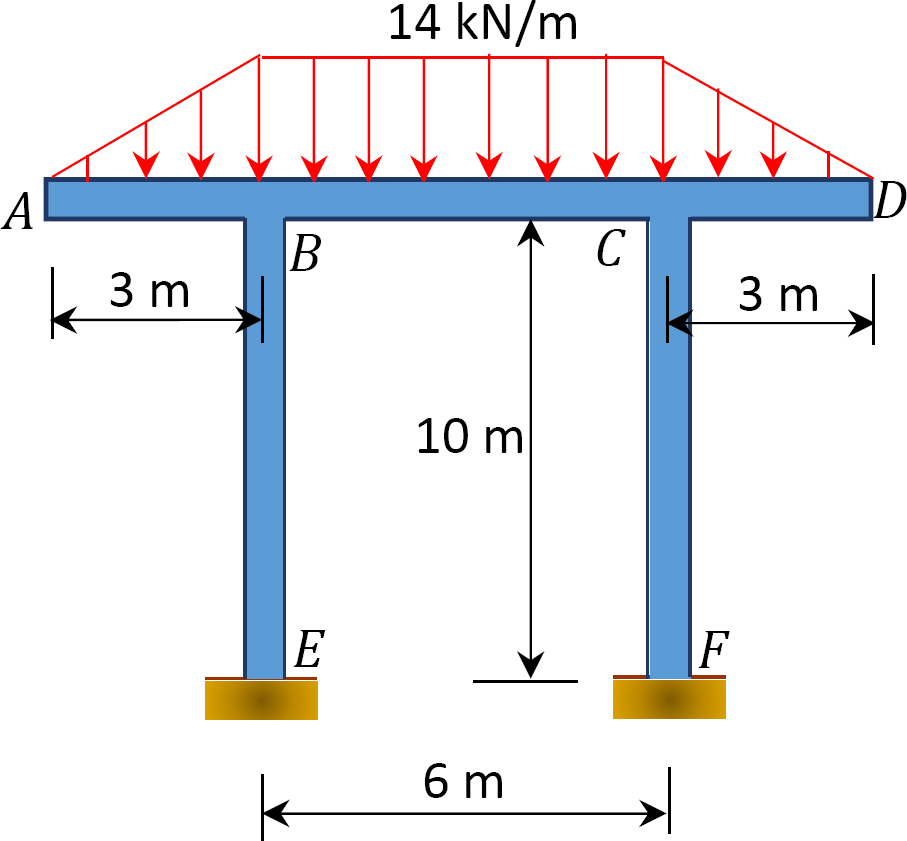
Fig. P12.16. Frame.
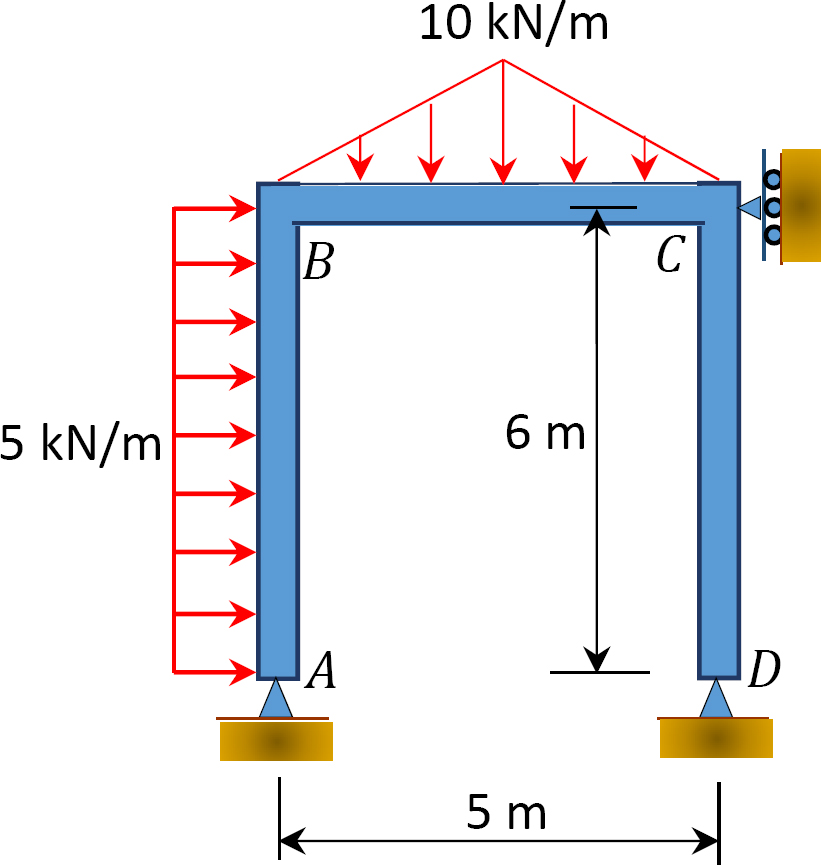
Fig. P12.17. Frame.
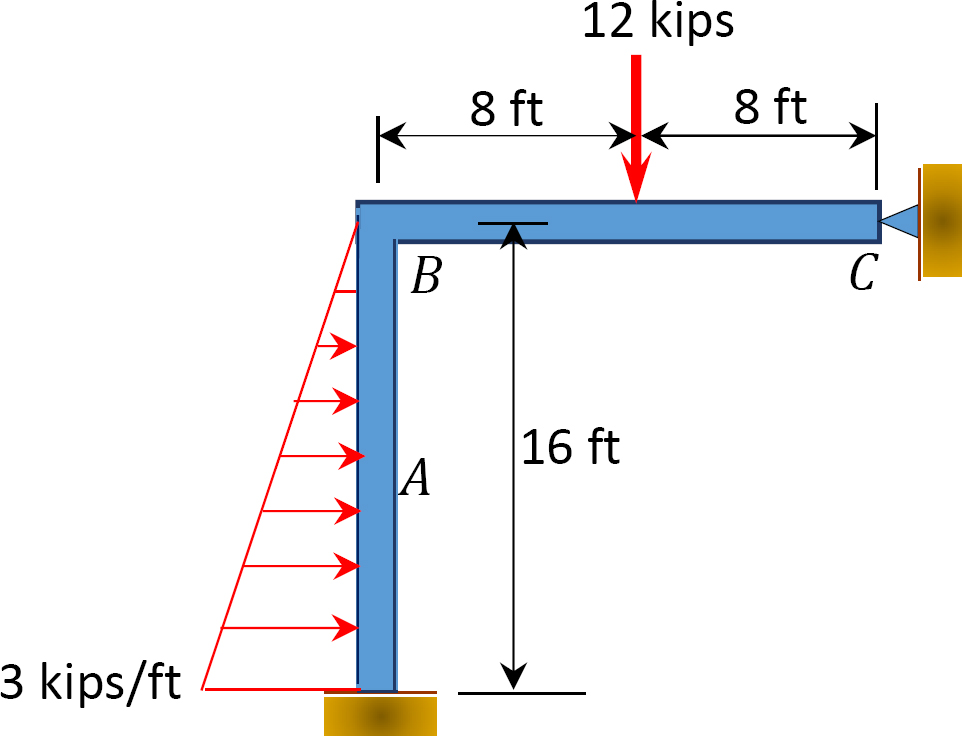
Fig. P12.18. Frame.
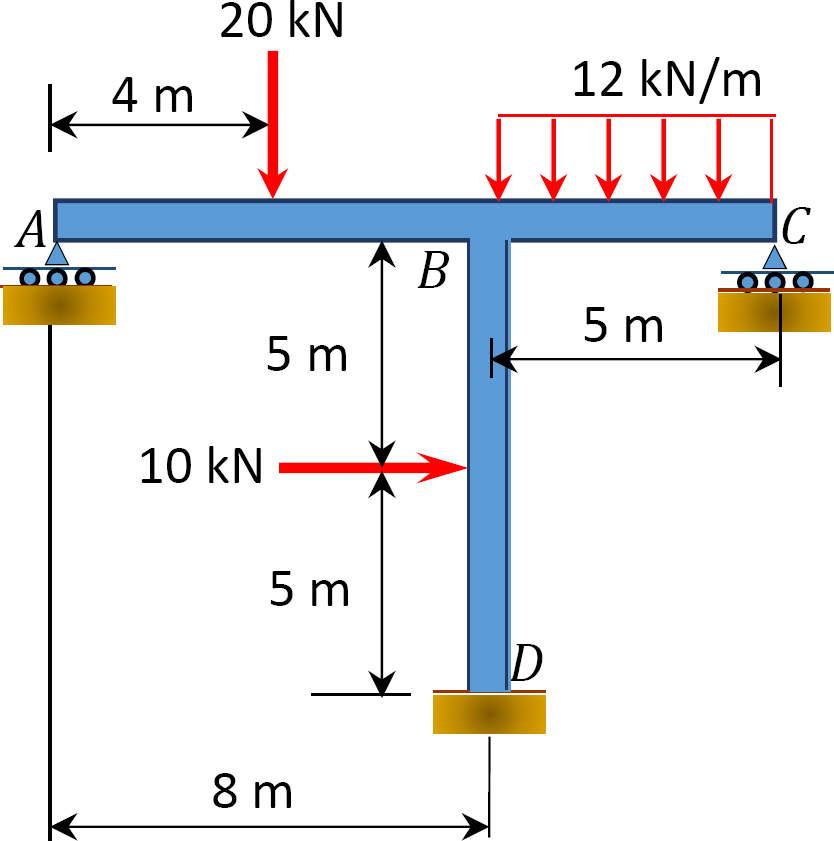
Fig. P12.19. Frame.
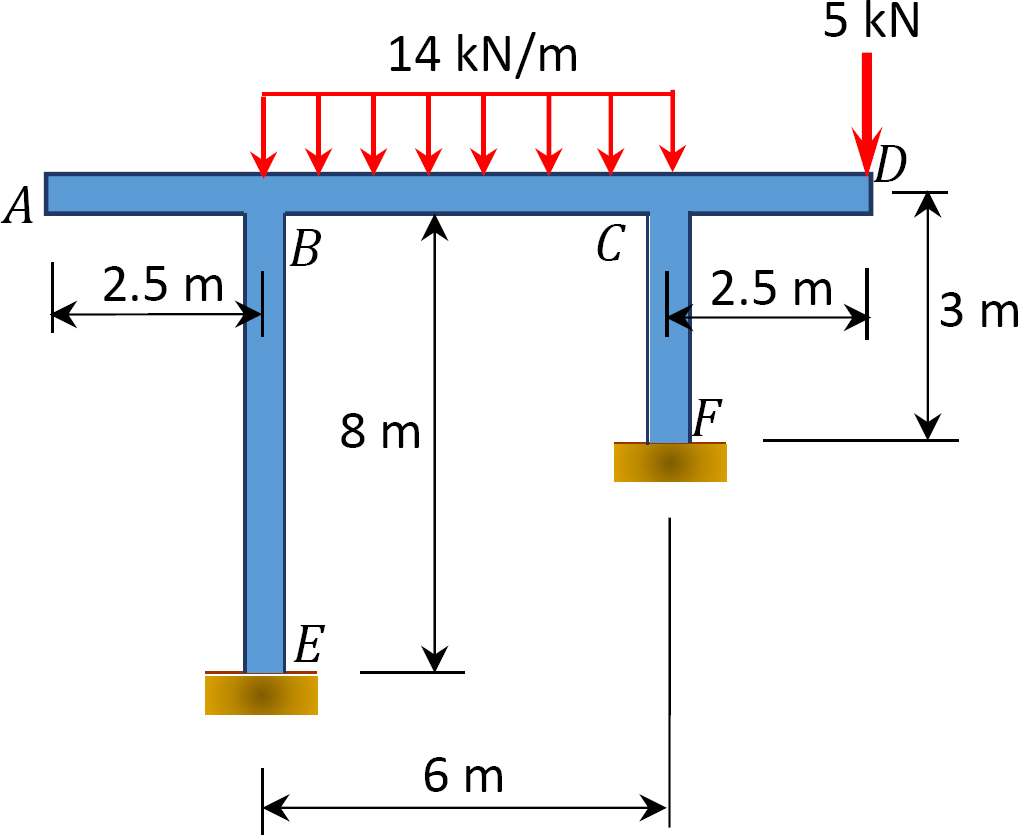
Fig. P12.20. Frame.