![]()
a forma mais geral forçada da equação de Duffing é
|
(1)
|
Dependendo dos parâmetros escolhidos, a equação pode assumir várias formas especiais. Por exemplo, sem amortecimento e sem forçamento, ![]() e tomando o sinal mais, a equação torna-se
e tomando o sinal mais, a equação torna-se
|
(2)
|
(Bender e Orszag 1978, p. 547; Zwillinger 1997, p. 122). Esta equação pode mostrar um comportamento caótico. Para ![]() , a equação representa uma “mola dura”, e para
, a equação representa uma “mola dura”, e para ![]() , representa uma “suave da primavera.”If
, representa uma “suave da primavera.”If![]() , the phase portrait curves are closed.
, the phase portrait curves are closed.
Se, em vez disso, tomamos ![]() ,
, ![]() , redefinir o relógio para que
, redefinir o relógio para que ![]() , e usar o sinal de menos, a equação é então
, e usar o sinal de menos, a equação é então
|
(3)
|
Esta pode ser escrita como um sistema de primeira ordem, equações diferenciais ordinárias, como
|
(4)
|
|||
|
(5)
|
(Wiggins 1990, p. 5) que, a não forçados caso, se reduz a
|
(6)
|
|||
|
(7)
|
(Wiggins 1990, p. 6; Ott, 1993, p. 3).
os pontos fixos deste conjunto de equações diferenciais acopladas são dados por
|
(8)
|
portanto, ![]() , e
, e
|
(9)
|
|||
|
(10)
|
dando ![]() . Por conseguinte, os pontos fixos são
. Por conseguinte, os pontos fixos são![]() ,
, ![]() , e
, e ![]() .
.
a análise da estabilidade dos pontos fixos pode ser ponto linearizando as equações. Diferenciar dá
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
que pode ser escrita como a equação matricial
|
(14)
|
Examinar a estabilidade do ponto de (0,0):
|
(15)
|
|
(16)
|
Mas ![]() , então
, então ![]() é real. Uma vez que
é real. Uma vez que ![]() , haverá sempre uma raiz positiva, de modo que este ponto fixo é instável. Agora olha para (
, haverá sempre uma raiz positiva, de modo que este ponto fixo é instável. Agora olha para (![]() , 0). A equação característica é
, 0). A equação característica é
|
(17)
|
que tem raízes
|
(18)
|
Para ![]() ,
, ![]() , então o ponto é assintoticamente estável. Se
, então o ponto é assintoticamente estável. Se ![]() ,
, ![]() , então o ponto é linearmente estável (Wiggins 1990, p. 10). No entanto, se
, então o ponto é linearmente estável (Wiggins 1990, p. 10). No entanto, se ![]() , o radical dá uma parte imaginária e a parte real é
, o radical dá uma parte imaginária e a parte real é ![]() , então o ponto é instável. Se
, então o ponto é instável. Se ![]() ,
, ![]() , que tem uma raiz real positiva, então o ponto é instável. Se
, que tem uma raiz real positiva, então o ponto é instável. Se ![]() , então
, então ![]() , então ambas as raízes são positivas e o ponto é instável.
, então ambas as raízes são positivas e o ponto é instável.
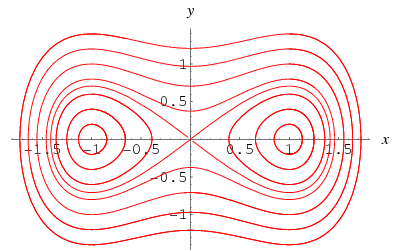
Curiosamente, o caso especial ![]() sem forçar,
sem forçar,
|
(19)
|
|||
|
(20)
|
pode ser integrado por quadratures. A diferenciação (19) e o pluggingin (20) dá
|
(21)
|
Multiplicando ambos os lados por ![]() dá
dá
|
(22)
|
Mas isso pode ser escrito
|
(23)
|
assim, temos uma invariante do movimento ![]() ,
,
|
(24)
|
resolução para ![]() dá
dá
|
(25)
|
|
(26)
|
so
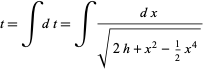 |
(27)
|
(Wiggins 1990, p. 29).
Note that the invariant of motion ![]() satisfies
satisfies
|
(28)
|
|
(29)
|
assim, as equações do oscilador de Duffing são dadas pelo Hamiltoniansystem