Escolha Intertemporal

a função de consumo keynesiano foi baseada em duas hipóteses principais. Em primeiro lugar, a propensão marginal para consumir situa-se entre 0 e 1. Em segundo lugar, a propensão média para consumir diminui à medida que o rendimento aumenta. Estudos empíricos iniciais foram consistentes com estas hipóteses. No entanto, após a Segunda Guerra Mundial, observou-se que a poupança não aumentou à medida que a renda aumentava. O modelo keynesiano, portanto, não conseguiu explicar o fenômeno do consumo, e assim a teoria da escolha intertemporal foi desenvolvida. A análise da escolha intertemporal foi introduzida por John Rae em 1834 na “teoria sociológica do Capital”. Mais tarde, Eugen von Böhm-Bawerk em 1889 e Irving Fisher em 1930 elaboraram o modelo. Alguns outros modelos baseados na escolha intertemporal incluem a hipótese do ciclo de vida proposta por Franco Modigliani e a hipótese da renda permanente proposta por Milton Friedman. O conceito de equilíbrio Walrasiano também pode ser estendido para incorporar a escolha intertemporal. A análise Walrasiana de tal equilíbrio introduz dois conceitos “novos” de preços: preços a prazo e preços à vista.Modelo de consumo intertemporal de Fisher

restrição orçamental Intertemporal com consumo dos períodos 1 e 2 no eixo dos x e eixo dos y, respectivamente.

a figura mostra a escolha intertemporal exercida pelo consumidor, dadas as preferências de utilidade e a restrição orçamental.

Irving Fisher desenvolveu a teoria da escolha intertemporal, em seu livro Teoria do interesse (1930). Ao contrário de Keynes, que relacionava o consumo com a renda atual, o modelo de Fisher mostrou como os consumidores racionais voltados para o futuro escolhem o consumo para o presente e o futuro para maximizar a sua satisfação ao longo da vida.De acordo com Fisher, a impaciência de um indivíduo depende de quatro características de seu fluxo de renda: o tamanho, a forma do tempo, a composição e o risco. Além disso, a Previdência, o autocontrolo, o hábito, a expectativa de vida e o motivo Lego (ou preocupação com a vida dos outros) são os cinco fatores pessoais que determinam a impaciência de uma pessoa que, por sua vez, determina a sua preferência de tempo.

a fim de compreender a escolha exercida por um consumidor em diferentes períodos de tempo tomamos o consumo em um período como uma mercadoria composta. Suponha que existe um consumidor, n {\displaystyle N}

mercadorias e dois períodos. As preferências são dadas por U (x 1 , x 2 ) {\displaystyle U (x_{1}, x_{2})}

em que x t = (x t 1 , … , x t N ) {\displaystyle x_{t}=(x_{t1},\dots ,x_{tN})}

. Rendimento no período}

abaixo de t {\displaystyle Y_{t}}

. Poupança no período de 1 S 1 {\displaystyle S_{1}}

, despesas no período t {\displaystyle t}

é C t {\displaystyle C_{t}}

, e r {\displaystyle r}

é a taxa de juros. Se a pessoa é incapaz de emprestar contra uma renda futura, no primeiro período, então ele está sujeita a restrições de orçamento, em cada período: C 1 + S 1 ≤ Y 1 , {\displaystyle C_{1}+S_{1}\leq Y_{1},}

(1) C 2 ≤ Y 2 + S 1 ( 1 + r ) . {\displaystyle C_{2}\leq Y_{2}+S_{1} (1+r).}

(2)

por outro lado, se tal empréstimo for possível, a pessoa está sujeita a uma única restrição orçamental intertemporal:

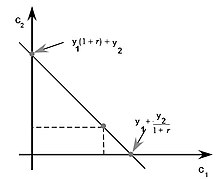
C 1 + C 2 1 + r = Y 1 + Y 2 1 + R. {\displaystyle C_{1}+{\frac {C_{2}}{1+i}}=Y_{1}+{\frac {Y_{2}}{1+r}}.}

(3)

o lado esquerdo mostra o valor actual das despesas e o lado direito mostra o valor actual das receitas. Multiplicando a equação por (1 + r ) {\displaystyle (1+r)}

dar-nos-ia os correspondentes valores futuros.

Agora, o consumidor tem de escolher um C 1 {\displaystyle C_{1}}

e C 2 {\displaystyle C_{2}}

, de modo a Maximizar U ( C 1 , C 2 ) {\displaystyle U(C_{1},C_{2})}

sujeitas a C 1 + C 2 / ( 1 + r ) = Y 1 + Y 2 / ( 1 + r ) . {\displaystyle C_{1}+C_{2}/(1+r)=Y_{1}+Y_{2}/(1+r).}

se o consumidor for um aforrador líquido, um aumento da taxa de juro terá um efeito ambíguo sobre o consumo actual.

se o consumidor for um mutuário líquido, um aumento da taxa de juro reduzirá o seu consumo actual.

um consumidor pode ser um aforrador líquido ou um mutuário líquido. Se ele estiver inicialmente em um nível de consumo onde ele não é um mutuário líquido nem um aforrador líquido, um aumento na renda pode fazer dele um aforrador líquido ou um mutuário líquido dependendo de suas preferências. Um aumento do rendimento corrente ou do rendimento futuro aumentará o consumo actual e futuro (motivos de suavização do consumo).

agora, considere um cenário em que as taxas de juro são aumentadas. Se o consumidor é um poupador, ele vai economizar mais no período atual, devido ao efeito de substituição e consumir mais no período atual, devido ao efeito renda. O efeito líquido torna-se assim Ambíguo. No entanto, se o consumidor for um mutuário líquido, tenderá a consumir menos no período actual devido ao efeito de substituição e ao efeito de rendimento, reduzindo assim o seu consumo corrente global.Artigo principal: hipótese do ciclo de vida

a hipótese do ciclo de vida é baseada no seguinte modelo:

max U t = ∑ t U ( C t ) ( 1 + δ ) − t {\displaystyle \max U_{t}=\sum _{t}U(C_{t})(1+\delta )^{-t}}

sujeito a

∑ t C t ( 1 + r ) − t = ∑ t Y t t t ( 1 + r ) − t + W 0 , {\displaystyle \sum _{t}C_{t}(1+r)^{-t}=\sum _{t}Y_{t}(1+r)^{-t}+W_{0},}

onde

U(Ct) é a satisfação recebido de consumo no período de tempo t, Ct é o nível de consumo no tempo t, Yt é a renda no tempo t, δ é a taxa de tempo preferência (uma medida da preferência individual entre a actividade presente e a actividade futura), W0 é o nível inicial de activos geradores de rendimentos.

Ciclo de Vida de Hipótese

Normalmente, uma pessoa MPC (propensão marginal a consumir) é relativamente alta durante a idade adulta jovem, diminui durante a meia-idade anos, e aumenta quando a pessoa está próxima ou na aposentadoria. O modelo de Hipótese do ciclo de vida (LCH) define o comportamento individual como uma tentativa de suavizar os padrões de consumo ao longo da vida, um pouco independente dos níveis atuais de renda. Este modelo afirma que, no início da vida, a despesa de consumo pode muito bem exceder o rendimento, uma vez que o indivíduo pode estar a fazer grandes compras relacionadas com a compra de uma nova casa, o início de uma família e o início de uma carreira. Nesta fase da vida, o indivíduo irá contrair empréstimos a partir do futuro para apoiar estas necessidades de despesas. No entanto, na metade da vida, estes padrões de despesa começam a nivelar – se e são apoiados ou talvez ultrapassados por aumentos na income.At nesta fase, cada um paga os empréstimos contraídos no passado e começa a poupar para a sua reforma.Após a reforma, a despesa de consumo pode começar a diminuir, no entanto, o rendimento geralmente diminui drasticamente. Nesta fase da vida, o indivíduo salva ou vive de poupanças passadas até à morte.Artigo principal: hipótese da renda permanente após a Segunda Guerra Mundial, notou-se que um modelo no qual o consumo atual era apenas uma função da renda atual era claramente demasiado simplista. Não pôde explicar o fato de que a propensão média a longo prazo para consumir parecia ser aproximadamente constante, apesar da propensão marginal para consumir ser muito menor. Assim, a hipótese de renda permanente de Milton Friedman é um dos modelos que procura explicar esta aparente contradição.

de acordo com a hipótese do rendimento permanente, O consumo permanente, CP, é proporcional ao rendimento permanente, YP. O rendimento permanente é uma noção subjectiva do rendimento futuro médio provável. O consumo permanente é uma noção semelhante de consumo.

consumo real, C, e rendimento real, Y, consistem nestes componentes permanentes mais componentes transitórios não previstos, CT e YT, respectivamente:

CPt =ß2YPt Ct = CPt + CTt YT = YPt + YTt