Aplicar e Interpretar el Principio de Saint-Venant

Todos los ingenieros estructurales utilizan el principio de Saint-Venant, ya sea de forma activa o subconsciente. Puede encontrar varias formulaciones de este principio en la mayoría de los libros de texto de mecánica estructural, pero su significado exacto no es obvio. El principio de Saint-Venant nos dice que la distribución exacta de una carga no es importante lejos de la región cargada, siempre y cuando los resultados de la carga sean correctos. En esta entrada de blog, exploraremos el principio de Saint-Venant, particularmente en el contexto del análisis de elementos finitos (FE).

La Historia del Principio de Saint-Venant

El científico francés Barré de Saint-Venant formuló su famoso principio en 1855, pero fue más una observación que una declaración matemática estricta:

«Si las fuerzas que actúan sobre una pequeña porción de la superficie de un cuerpo elástico se sustituyen por otro sistema estáticamente equivalente de fuerzas que actúan sobre la misma porción de la superficie, esta redistribución de la carga produce cambios sustanciales en las tensiones locales, pero tiene un efecto insignificante en las tensiones a distancias que son grandes en comparación con las dimensiones lineales de la superficie en la que se modifican las fuerzas.»

B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Retrato de Saint-Venant. Imagen en el dominio público, a través de Wikimedia Commons.

Muchas grandes mentes dentro del campo de la mecánica aplicada — Boussinesq, Love, von Mises, Toupin y otros — estuvieron involucradas en afirmar el principio de Saint-Venant en una forma más exacta y proporcionar pruebas matemáticas para ello. Resulta que esto es bastante difícil para casos más generales, y la investigación sobre el tema aún está en curso. (La argumentación a veces ha sido bastante vívida.)

Ejemplo simple: Analizar tensiones a Distancia

Comencemos con algo bastante simple: una placa rectangular delgada con un orificio circular a cierta distancia del borde cargado, que se tira axialmente. Si estamos interesados en la concentración de esfuerzos en el orificio, ¿qué importancia tiene la distribución real de la carga?

Se aplican tres tipos de carga diferentes en el límite más a la derecha:

1. Una tensión axial constante de 100 MPa
2. Una distribución de tensiones parabólicas simétricas con amplitud de pico 150 MPa
3. Una carga puntual centrada con el mismo resultado que los dos casos de carga anteriores

Como se ve en las gráficas a continuación, la distribución de tensiones en el orificio no se ve afectada por la forma en que se aplica la carga. La clave aquí es, por supuesto, que el agujero está lo suficientemente lejos de la carga.

Contornos de tensión de Von Mises para los tres casos de carga.

Otra forma de visualizar este escenario es mediante el uso de flechas de tensión principales. Tal diagrama enfatiza el campo de estrés como un flujo y da una buena sensación para la redistribución.

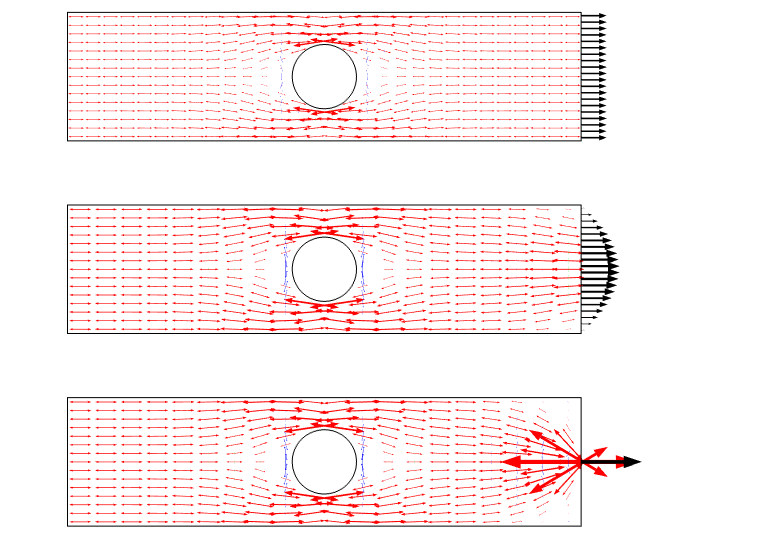
Gráfico de tensión principal para los tres casos de carga. Tenga en cuenta que hay una singularidad cuando se utiliza una carga puntual.

Al graficar la tensión a lo largo de una línea, podemos ver que los tres casos convergen entre sí a una distancia del borde, que es aproximadamente igual al ancho de la placa.

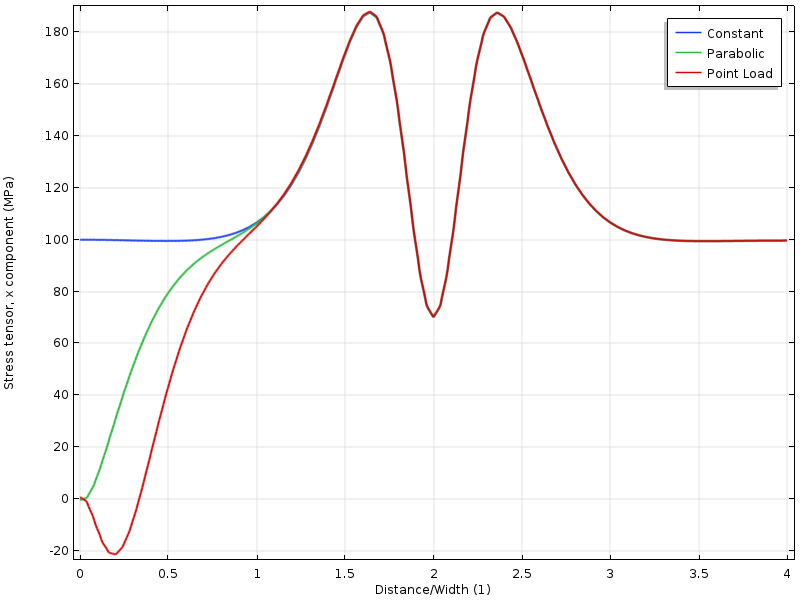
Tensión a lo largo del borde superior en función de la distancia desde el límite cargado. La distancia se normaliza por el ancho de la placa.

Si el agujero se mueve más cerca del límite cargado, obtenemos otra situación. El estado de tensión alrededor del orificio ahora depende de la distribución de la carga. Pero aún más interesante es que la distancia a donde los tres campos de tensión coinciden ahora es el doble de distancia del límite cargado. La aplicación del principio de Saint-Venant requiere que las tensiones sean libres de redistribuir. En este caso, esa redistribución está parcialmente bloqueada por el agujero.

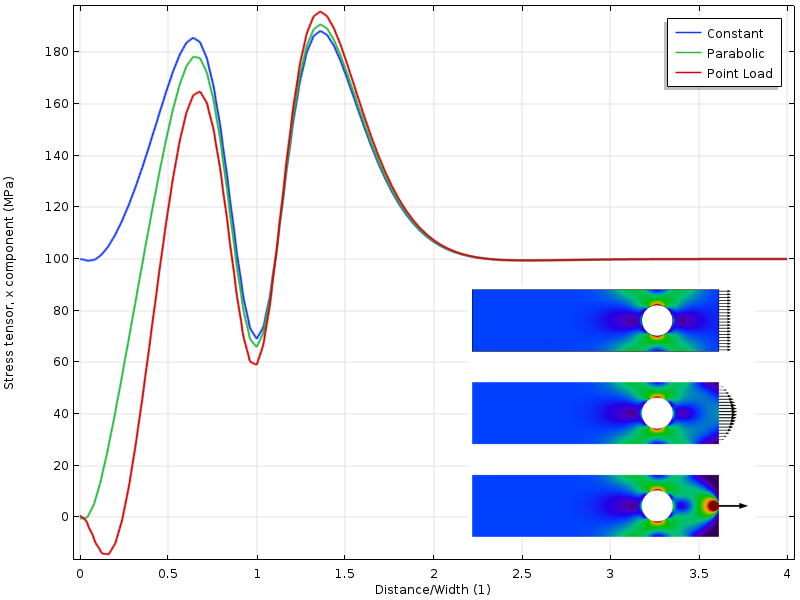
Tensión a lo largo del borde superior con el orificio más cerca del límite cargado.

Nótese que el principio de Saint-Venant nos dice que no hay diferencia en el estado de tensión a una distancia que es del orden de la dimensión lineal del área cargada. Sin embargo, el área cargada a tener en cuenta puede no ser el área que realmente está cargada. Esta afirmación puede sonar extraña, pero piénsalo de esta manera: Cuando el agujero está lejos, podemos calcular el factor de concentración de tensión utilizando un manual (el mío dice 4.32) en lugar de una solución de FE. El enfoque manual contiene una suposición implícita de que la carga se distribuye uniformemente como en el primer caso de carga. Por lo tanto, incluso si la carga real se aplicó solo a una pequeña parte del límite, la distancia crítica en ese caso está relacionada con el tamaño de todo el límite.

Al resolver el problema utilizando el método de elementos finitos (FEM), el orificio puede estar arbitrariamente cerca de la carga. Lo que establece el límite es que desde el punto de vista físico, la distribución de carga está bien definida. Sin embargo, tan pronto como hacemos suposiciones sobre la redistribución, hay una suposición implícita sobre la distribución de la carga, que puede diferir de la real.

Sistemas Cero Resultantes y Densidad de Energía de deformación

Hasta ahora, hemos dicho que las tensiones son las mismas independientemente de los detalles de la carga a una distancia adecuada. Dado que aquí se trata de elasticidad lineal, siempre es posible superponer casos de carga. Cuando se trabaja con pruebas del principio de Saint-Venant, es más fácil formular un principio en estas líneas: Las tensiones causadas por un sistema de carga sin fuerza o momento resultantes serán pequeñas a una distancia que es del mismo orden de magnitud que el tamaño del límite cargado.

Así, estudiamos el estrés causado por la diferencia entre los dos sistemas de carga con resultados iguales. La mayoría de las pruebas modernas se basan en estimaciones de la descomposición de la densidad de energía de deformación para un sistema de resultado cero.

Volviendo al problema anterior, podemos calcular la diferencia entre los casos de carga. Hacerlo nos permite estudiar la desintegración real de la densidad de energía de tensión o tensión para la diferencia de los campos de tensión.

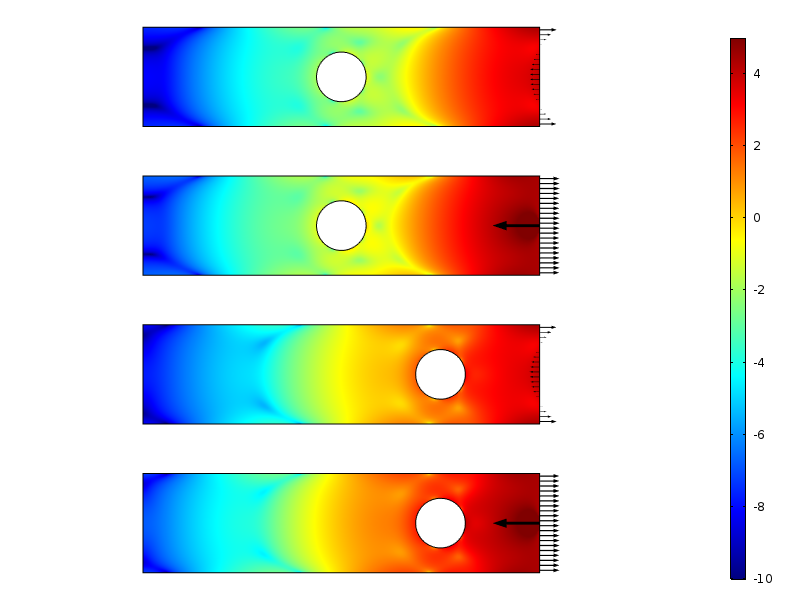
Logaritmo de densidad de energía de deformación para los casos de carga de resultado cero.

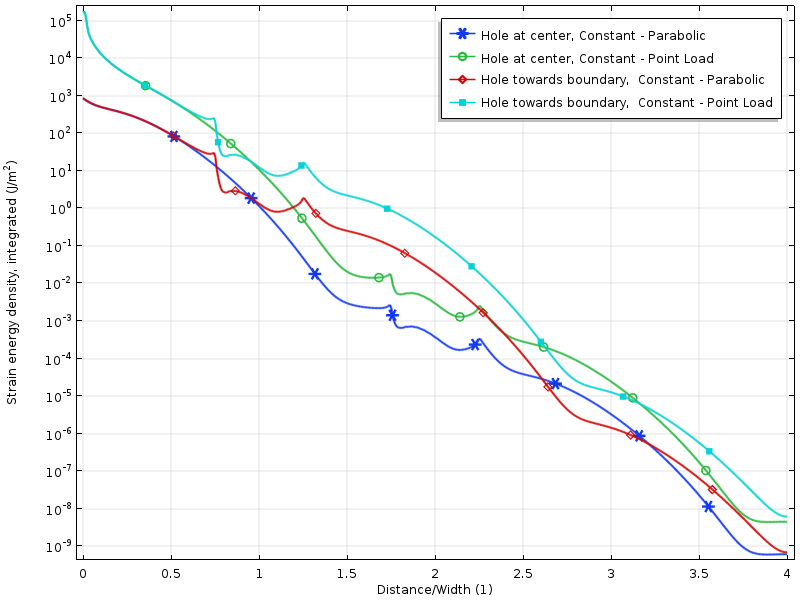
La densidad de energía de deformación a lo largo de la placa para los casos de carga cero resultantes. La energía se integra a lo largo de la dirección vertical para producir una cantidad que es solo una función de la distancia de la carga.

El decaimiento en el logaritmo de la densidad de energía de deformación es más o menos lineal con la distancia desde el límite cargado. Esto está en línea con lo que predicen las pruebas modernas: un decaimiento exponencial de la densidad de energía de deformación. También podemos ver claramente cómo el agujero reduce temporalmente la tasa de decaimiento.

Aplicar el Principio de Saint-Venant a Estructuras Delgadas

Para estructuras más delgadas como conchas, vigas y cerchas, es bien sabido que el principio de Saint-Venant no se puede aplicar de la misma manera que para un objeto más «sólido». Las perturbaciones viajan distancias más largas de lo que esperamos, porque las trayectorias de carga en una estructura delgada son mucho más limitadas. Este es el mismo fenómeno que vemos con el agujero en el ejemplo anterior, pero más prominente.

Aquí, estudiamos una viga con una sección transversal estándar IPE100. El extremo de la viga se somete a una tensión axial, con una amplitud que tiene una distribución lineal en ambas direcciones de sección transversal.

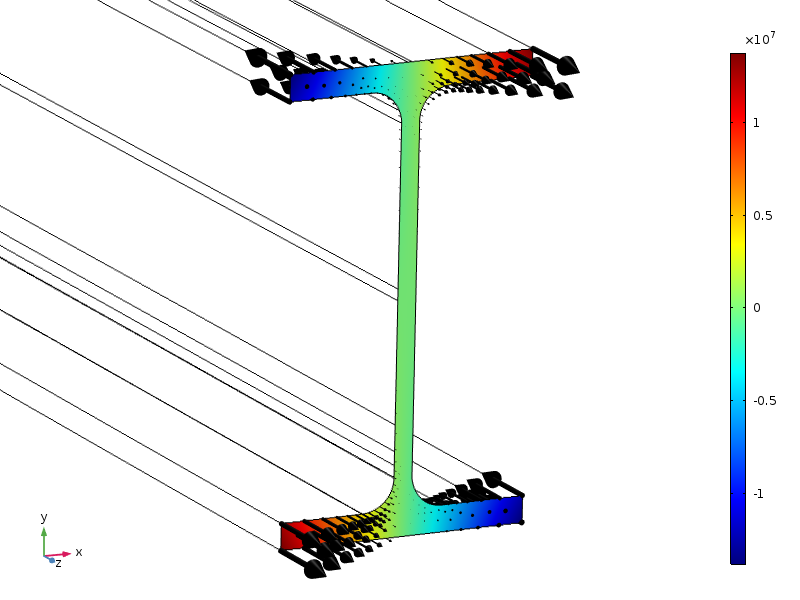
Distribución de carga, mostrada como contornos y flechas.

Debido a las simetrías, esta carga tiene una fuerza resultante cero, así como un momento cero alrededor de todos los ejes. La altura de la sección transversal es de 100 mm, por lo que si se aplica la forma estándar del principio de Saint-Venant, las tensiones deben ser pequeñas a una distancia de aproximadamente 100 mm de la sección final.

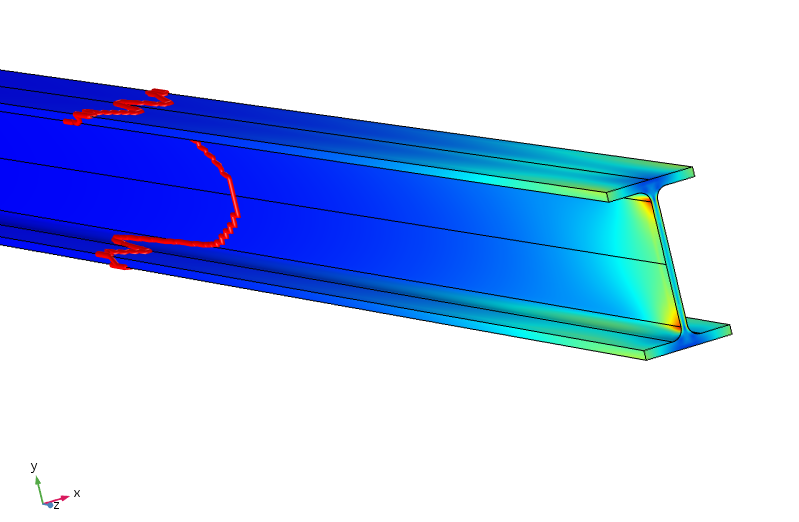
Tensión equivalente en el haz. El contorno rojo indica dónde la tensión es inferior al 5% de la tensión máxima aplicada.

Resulta que para que el esfuerzo esté por debajo del 5% del esfuerzo máximo aplicado, tenemos que viajar casi un metro a lo largo del haz. Por lo tanto, la redistribución de la carga es mucho menos eficiente aquí, ya que el equilibrio entre las bridas superior e inferior requiere la transferencia de momento a través de la banda delgada.

Si está familiarizado con la teoría de torsión no uniforme de vigas (es decir, la teoría de deformación o la teoría de Vlasov), reconocerá que la carga aplicada tiene un bimomente significativo. El bimomente es una cantidad de sección transversal con la fuerza de dimensión física X longitud2.

Tal vez (esto es solo mi especulación personal), un principio eficiente de Saint-Venant para este caso debería requerir no solo fuerza y momento, sino también un bimomento de cero. Esto se puede lograr agregando cuatro cargas puntuales que proporcionan un bimomente contrarrestante. A continuación se muestra el resultado de ese análisis.

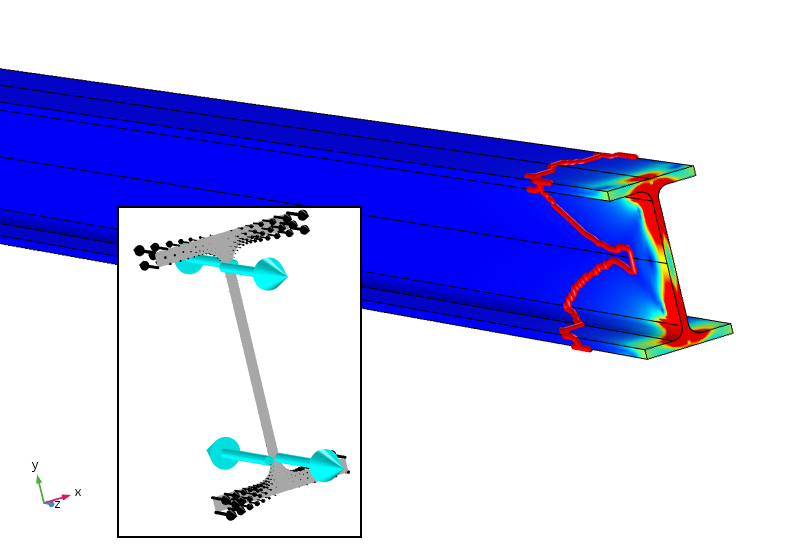
Esfuerzo equivalente con cuatro cargas puntuales que también proporcionan un bimoment cero. El contorno de tensión del 5% ahora está mucho más cerca del límite cargado.

Las cargas puntuales aplicadas, que no se colocan de manera óptima a propósito, dan tensiones locales extremadamente altas (en realidad singulares). Sin embargo, la tensión disminuye mucho más rápido y está por debajo del 5% después de aproximadamente 100 mm. El límite del 5% sigue siendo en términos de la carga distribuida aplicada, por lo que no se ajusta para las nuevas tensiones locales. La tasa de decaimiento logarítmico de la densidad de energía de deformación es tres veces más rápida después de agregar las cargas puntuales.

El Principio de Saint-Venant en el Análisis de Elementos Finitos

En algunos casos, se puede considerar intuitivamente que el principio de Saint-Venant es aplicable al problema discretizado de FE. Aquí, observamos cargas distribuidas y mallas no conformes.

Cargas distribuidas

En el modelo FE, las cargas siempre se aplican en los nodos de malla, aunque se especifiquen como una carga de límite continua. La carga se distribuye internamente a los nodos del elemento utilizando el principio de trabajo virtual, como se muestra en el siguiente ejemplo.

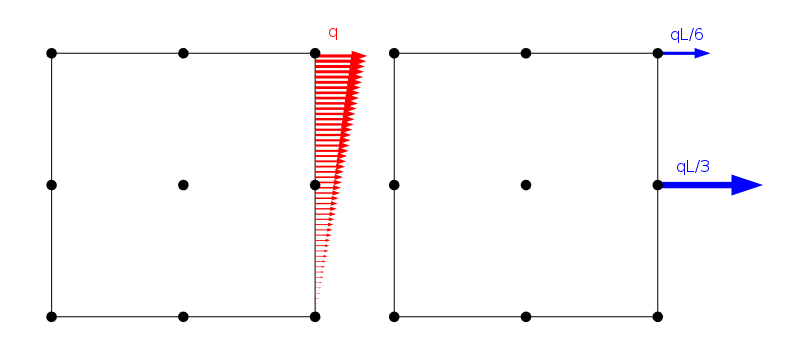
Una carga distribuida linealmente y cómo se aplica en los nodos de un elemento Lagrange de segundo orden con longitud lateral L.

Sin embargo, hay un número infinito de distribuciones de carga que dan las mismas cargas nodales siempre que compartan la misma fuerza y momento resultantes. Obviamente, la solución al problema de los elementos finitos es la misma para todos estos casos. Sin embargo, a partir del principio de Saint-Venant, podemos concluir que todas estas cargas deben dar esencialmente el mismo campo de tensión tan pronto como estemos a cierta distancia.

Dado que el tamaño del área sobre la que redistribuimos cargas es una cara de elemento, la dimensión lineal después de la cual no hay diferencia es esencialmente una capa de elemento dentro de la estructura. Por lo tanto, la solución en la capa más externa de elementos puede no corresponder a la carga real, pero más adentro, sí.

Como ejemplo, podemos cargar una placa rectangular con una carga límite que tiene una distribución exponencial de tensiones. La tensión calculada con una malla fina se muestra a continuación.

Gráfico de contorno de la distribución de tensiones axiales.

Debido al principio de Saint-Venant, el campo de tensión se redistribuye a un estado de flexión pura a cierta distancia del borde cargado, tal como esperamos. Sin embargo, este no es el objetivo del debate actual. Más bien, investigamos la diferencia entre la distribución de tensiones anterior y lo que obtenemos con una serie de mallas gruesas.

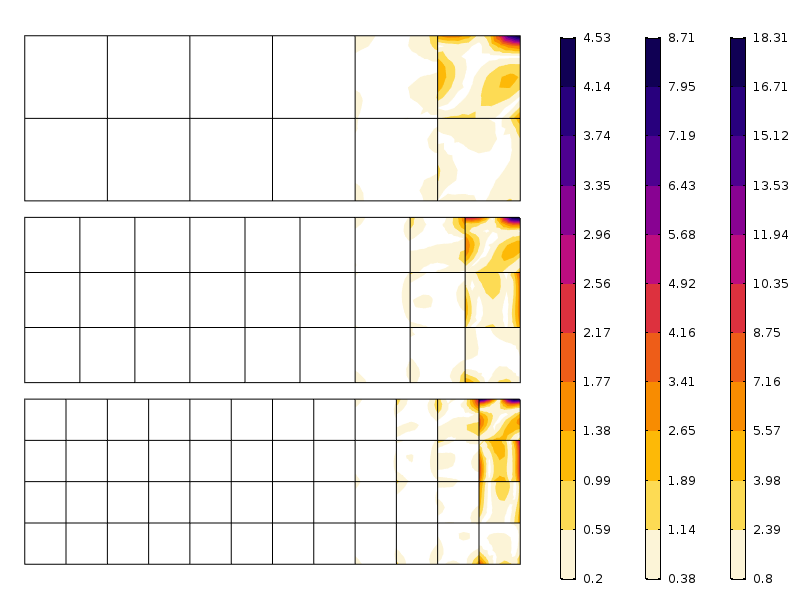
Error en la tensión axial para tres mallas diferentes. Tenga en cuenta las diferentes escalas. Como era de esperar, el error es menor cuando la malla es más fina.

Como se puede ver en la figura, el error disminuye rápidamente después de la primera capa de elementos. Lo que vemos aquí es en realidad una combinación de convergencia de malla y la redistribución de tensiones que implica el principio de Saint-Venant.

Malla no conforme

Una malla no conforme se produce cuando las funciones de forma en dos elementos conectados no coinciden. El caso más común es cuando un ensamblaje se conecta mediante pares de identidad y condiciones de continuidad. Para ejemplificar esto, podemos estudiar una barra recta con una malla intencionalmente no coincidente. Con un caso de carga simple, como la tensión uniaxial, es posible estudiar las perturbaciones de tensión causadas por la transición.

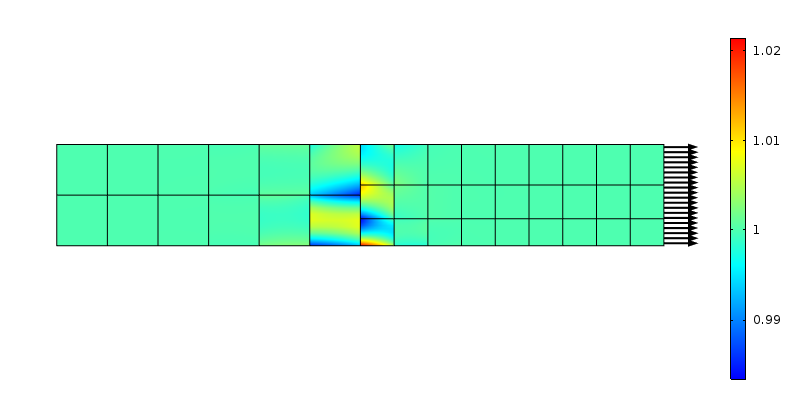
Tensión axial en una transición de malla no conforme. Se utilizan elementos de segundo orden.

Las fuerzas transmitidas por los nodos en los dos lados no coinciden con la suposición de esfuerzo constante. Una vez más, esto puede verse como una redistribución de carga local sobre un área que es el tamaño del elemento. Usando el razonamiento de Saint-Venant, la perturbación debería desaparecer a una distancia «del tamaño de un elemento» de la transición. Investiguemos qué sucede si la malla se refina en la dirección axial.

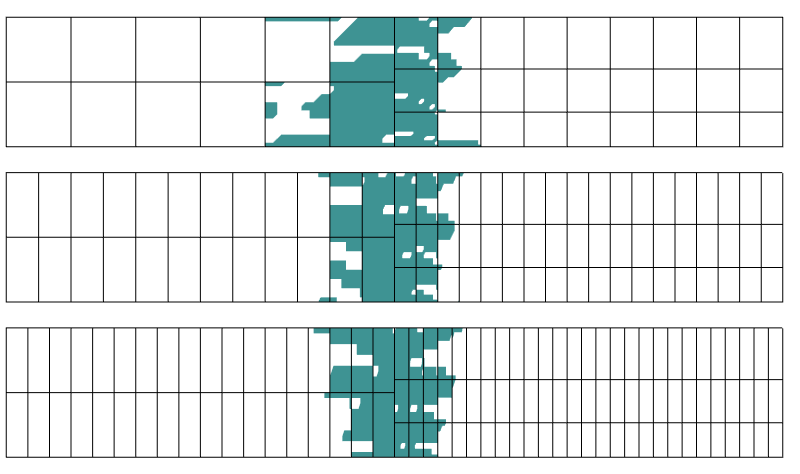
Región con más de 0,1% de error en el estrés. Se utilizan tres discretizaciones diferentes en la dirección axial.

Resulta que la región de perturbación no se ve muy afectada por la discretización en la dirección perpendicular al límite de transición. Esto es exactamente lo que nos dice el principio de Saint-Venant.

Observaciones finales

Sin hacer uso del principio de Saint-Venant, muchos análisis estructurales son difíciles de realizar, simplemente porque no se conoce la distribución detallada de la carga.

El principio es formalmente válido solo para materiales elásticos lineales. En la práctica, también lo usamos intuitivamente a diario para otras situaciones. Si, por ejemplo, el material en el ejemplo de «placa con orificio» fuera elastoplástico, esperaríamos que las dos cargas distribuidas dieran resultados equivalentes, siempre que el esfuerzo de fluencia esté por encima del esfuerzo aplicado en el límite, de modo que solo haya deformación plástica alrededor del orificio. La carga puntual, sin embargo, siempre da una solución diferente, ya que el material rinde alrededor del punto cargado. Para una discusión más larga, lee esta publicación de blog sobre singularidades en cargas puntuales.

Próximos pasos

Obtenga más información sobre el uso del software COMSOL Multiphysics ® para FEA.

Lectura adicional

• Y. C. Fung y P. Tong, Mecánica Sólida Clásica y Computacional, World Scientific Publishing Co. Pte. Ltd., 2001.