Aus dem obigen Diagramm wird eine Kette von Klassifikatoren angezeigt. Es ähnelt fast der Datenstruktur ‚LinkedList‘. Y1, Y2..Yᴺ sind die Antwortvariablen jedes Klassifikators (es wird 0 oder 1 sein). Antworten von allen vorherigen Klassifikatoren (außer 1.) werden in den nächsten Klassifikator eingefügt und diese werden zusammen mit den ursprünglichen Eingabemerkmalen (f1..Fⁿ).
Im Allgemeinen wird der Klassifikator K mit einem vollständigen Eingabe-Feature-Set erstellt: f1, f2,..Fⁿ, Y1,Y2,..Yᴷ⁻1
Nun, hier eine Frage, „Wie sich die Reihenfolge der Klassifikator Kette ist beschlossen ?“ Dafür gibt es verschiedene Strategien, wie unten angegeben :
Ensemble of Classifier Chains (ECC) : Hier wird das Ensemble-Klassifikationsmodell verwendet. Zufällige Stichproben von Ketten werden ausgewählt und darauf wird ein Ensemble aufgebaut. Die vorhergesagte Ausgabe erfolgt durch Anwendung des Mehrheitsabstimmungsschemas auf die Ensemble-Ausgaben. Es ist ganz dasselbe wie randomForest classifier.
Monte-Carlo-Klassifikatorketten (MCC): Es wendet die Monte-Carlo-Methode zur optimalen Erzeugung von Klassifikatorsequenzen an.
Es gibt andere Methoden wie Zufallssuche oder Abhängigkeitsmethoden für Klassifikatoren, die jedoch nicht sehr häufig verwendet werden.
Die Ausgabe jedes Klassifikators wird wie das binäre Relevanzschema erfasst und bestimmt am Ende die Klassenbezeichnungen.
Label Power-Set Scheme
Das grundlegende Konzept der binären Relevanz & Klassifikatorkette ist mehr oder weniger gleich. Label Power-Set funktioniert anders. Es betrachtet jede Kombination von Beschriftungen im Trainingsdatensatz als separate Beschriftung. Für ein 3-Klassen-Multi-Label-Problem werden beispielsweise 100, 001, 101, 111 usw. als separate Labels betrachtet.
Im Allgemeinen kann ein Klassenraum der Dimension N 2ᴺ no der insgesamt möglichen Beschriftungskombinationen sein.
Es zerfällt also nicht in Unterprobleme, sondern sagt direkt die Kombination von Klassenbeschriftungen als Ganzes voraus.
Vorteile & Nachteile jedes Schemas
Binäre Relevanz ist ein einfaches Schema, einfach zu implementieren. Es berücksichtigt jedoch nicht die gegenseitige Abhängigkeit des Labels und kann daher häufig versteckte Datenbeziehungen falsch interpretieren.
Die Klassifikatorkette behandelt Klassenbeschriftungsbeziehungen perfekt. Insbesondere in Fällen, in denen einige Klassenbezeichnungen Unterbezeichnungen anderer sind und das Auftreten einer Klassenbezeichnung stark von anderen Bezeichnungen abhängt (Eltern-Kind-Beziehungen in Klassenbezeichnungen. Untergeordnete Beschriftung kann auftreten, wenn die übergeordnete Beschriftung vorhanden ist). Dieses Schema ist jedoch komplexer Natur und leidet unter einem Problem mit hoher Dimensionalität, wenn der Klassenraum groß ist.
Label Power-Set eignet sich gut für Fälle, in denen die Anzahl der verschiedenen Kombinationen von Klassenbeschriftungen geringer ist. Es ist ein sehr einfaches Schema im Vergleich zur binären Relevance & Klassifikatorkette.
In allen Fällen ist ein grundlegendes Verständnis erforderlich, bevor eine Entscheidung für ein bestimmtes Schema getroffen wird.
Genauigkeitsmetriken
Bei Klassifizierungsproblemen mit mehreren Klassen oder binären Einzelbezeichnungen wird die absolute Genauigkeit durch das Verhältnis (Anzahl der korrekt klassifizierten Dateninstanzen / Gesamtanzahl der Dateninstanzen) angegeben.
Sehen wir uns das Szenario für den Multi-Label-Fall anhand unseres Beispieldatensatzes an. Wenn die Frage mit der ID 241465 mit den Bezeichnungen ‚Modellierung‘, ‚Zentralgrenzsatz‘, ‚Freiheitsgrade‘ klassifiziert ist, was können wir dann sagen? Tatsächliche Klassenbezeichnungen im Datensatz waren ’statistische Signifikanz‘, ‚Modellierung‘, ‚zentraler Grenzwertsatz‘, ‚Freiheitsgrade‘ und ‚falsche Korrelation‘. Weder ist es völlig falsch, noch ist es völlig richtig. Wenn wir uns für die traditionelle Genauigkeitsmetrik correct vs total ratio entscheiden, können wir den Klassifikator definitiv nicht beurteilen. Wir brauchen etwas, um die teilweise Korrektheit eines Multi-Label-Klassifikators zu beurteilen.
Hamming Loss Metric
Anstatt die Anzahl der korrekt klassifizierten Dateninstanzen zu zählen, berechnet Hamming Loss den Verlust, der während der Vorhersage in der Bitfolge der Klassenbeschriftungen generiert wird. Es führt eine XOR-Operation zwischen der ursprünglichen binären Zeichenfolge von Klassenbeschriftungen und vorhergesagten Klassenbeschriftungen für eine Dateninstanz durch und berechnet den Durchschnitt über das Dataset. Sein Ausdruck ist gegeben durch
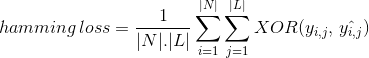
wobei
/ N/ = Anzahl der Dateninstanzen
| L| = Kardinalität des Klassenraums
yᵢ,ⱼ = tatsächliches Bit der Klassenbezeichnung j in der Dateninstanz i
^yᵢ,ⱼ = vorhergesagtes Bit der Klassenbezeichnung j in der Dateninstanz i
‚ hamming loss‘ Wert reicht von 0 bis 1. Da es sich um eine Verlustmetrik handelt, ist ihre Interpretation im Gegensatz zum normalen Genauigkeitsverhältnis umgekehrt. Ein geringerer Wert des Hamming-Verlusts weist auf einen besseren Klassifikator hin.
Teilmengengenauigkeit
Es gibt einige Situationen, in denen wir uns für ein absolutes Genauigkeitsverhältnis entscheiden, in dem die Messung der genauen Kombination von Etikettenvorhersagen wichtig ist. Es kann im Fall ‚Label Power-Set‘ relevant klingen. Im Multi-Label-Szenario wird dies als Teilmengengenauigkeit bezeichnet.
Abgesehen von diesen beiden kann die Genauigkeit jedes einzelnen binären Klassifikators anhand anderer traditioneller Metriken wie Genauigkeitsverhältnis, F1-Score, Präzision, Rückruf usw. und ROC-Kurven beurteilt werden.
Hier geht es um theoretische Modellierung für Multi-Label-Klassifikation. Wir werden im nächsten Artikel eine Fallstudie mit realen Daten sehen. Der Datenexplorationscode ist bei Github verfügbar.
Kürzlich habe ich ein Buch über ML verfasst (https://twitter.com/bpbonline/status/1256146448346988546)