Chapitre 12
Méthode de Distribution des Moments d’Analyse des Structures
12.1 Concepts de base
La méthode de distribution des moments d’analyse des poutres et des cadres a été développée par Hardy Cross et présentée formellement en 1930. Bien que cette méthode soit une méthode de déformation comme la méthode de déviation de pente, elle est une méthode approximative et ne nécessite donc pas de résoudre des équations simultanées, comme ce fut le cas avec cette dernière méthode. Le degré de précision des résultats obtenus par la méthode de distribution des moments dépend du nombre d’approximations successives ou du processus d’itération.
Pour illustrer le concept de la méthode de distribution des moments, considérons le cadre illustré à la figure 12.1. Les éléments du cadre sont prismatiques et sont supposés ne pas se déformer axialement ni se translater les uns par rapport aux autres. Les joints ACD du cadre sont fixes, tandis que le joint B peut tourner légèrement en raison de la charge appliquée. Tout d’abord, avant de procéder à la répartition des moments entre les organes, on suppose que tous les joints sont temporairement verrouillés à l’aide d’une pince.
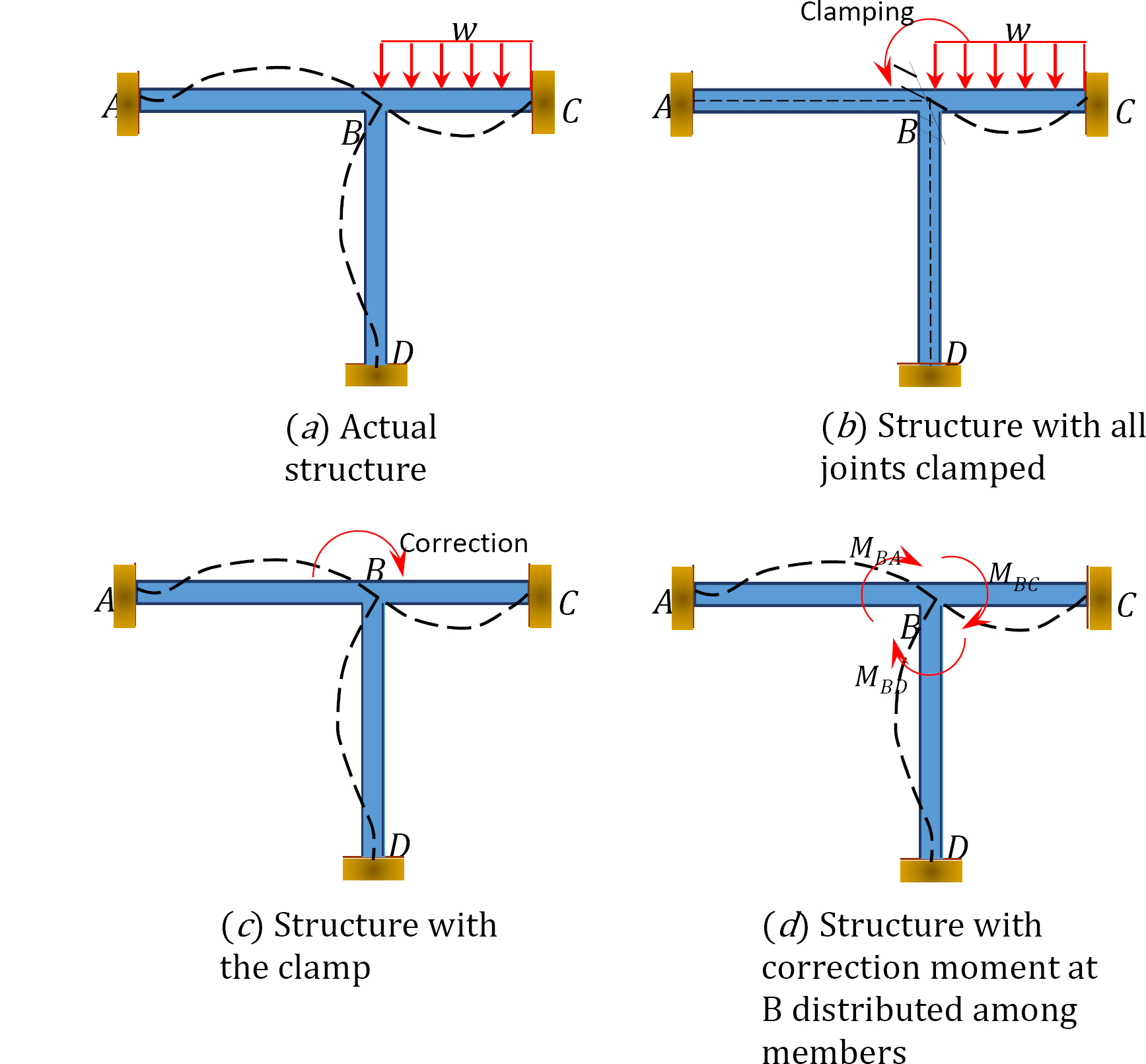
Fig. 12.1. Cadre.
12.2 Convention de signe
La convention de signe pour la méthode de distribution de moment est similaire à celle établie pour la méthode de déviation de pente; c’est-à-dire que le moment à la fin d’un élément est considéré comme positif s’il tend à tourner l’extrémité de l’élément dans le sens des aiguilles d’une montre et négatif s’il tend à le tourner dans le sens antihoraire.
12.3 Définitions
Moments déséquilibrés: Cette méthode d’analyse suppose que les joints d’une structure sont initialement serrés ou verrouillés puis relâchés successivement. Une fois qu’un joint est libéré, une rotation a lieu, car la somme des moments de fin fixes des membres se réunissant à ce joint n’est pas nulle. La valeur de la somme des moments de fin obtenus est le moment déséquilibré à cette articulation.
Moments de report: Les moments distribués aux extrémités des membres se réunissant à une cause commune provoquent des moments aux autres extrémités, qui sont supposés fixes. Ces moments induits aux autres extrémités sont appelés moments de report.
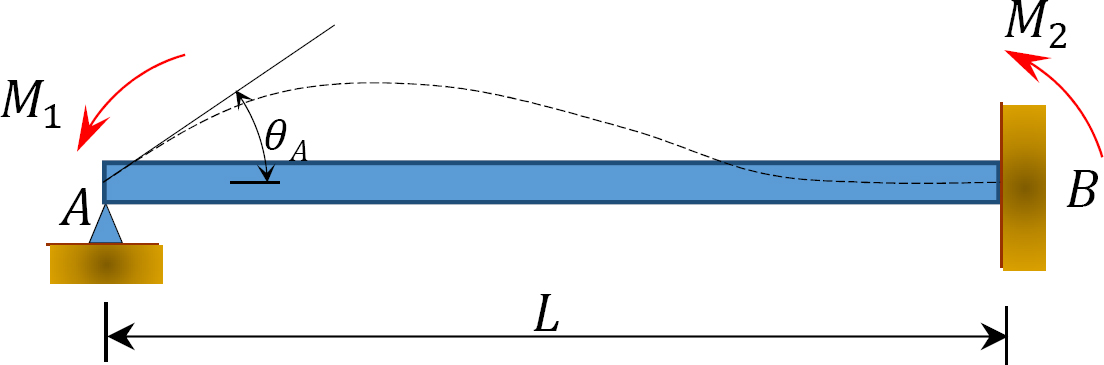
Fig. 12.2. Poutre prismatique non chargée.
Considérons une poutre prismatique non chargée fixée à l’extrémité B, comme le montre la figure 12.2. Si un moment M1 est appliqué à l’extrémité gauche du faisceau, les équations pente-déviation pour les deux extrémités du faisceau peuvent s’écrire comme suit:


La substitution de 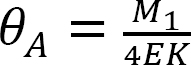 de l’équation 12.1 à l’équation 12.2 suggère ce qui suit:
de l’équation 12.1 à l’équation 12.2 suggère ce qui suit:

L’équation 12.3 suggère que le moment reporté à l’extrémité fixe d’une poutre dû à un moment appliqué à l’autre extrémité est égal à la moitié du moment appliqué.
Facteur de report: Le rapport du moment induit au moment appliqué est appelé facteur de report. Pour le faisceau illustré à la figure 12.2, le facteur de report est le suivant:

Facteur distribué (DF): Le facteur distribué est un facteur utilisé pour déterminer la proportion du moment déséquilibré porté par chacun des membres réunis à un joint. Pour les membres réunis au joint O de la trame illustrée à la figure 12.3, leurs facteurs de répartition sont calculés comme suit:
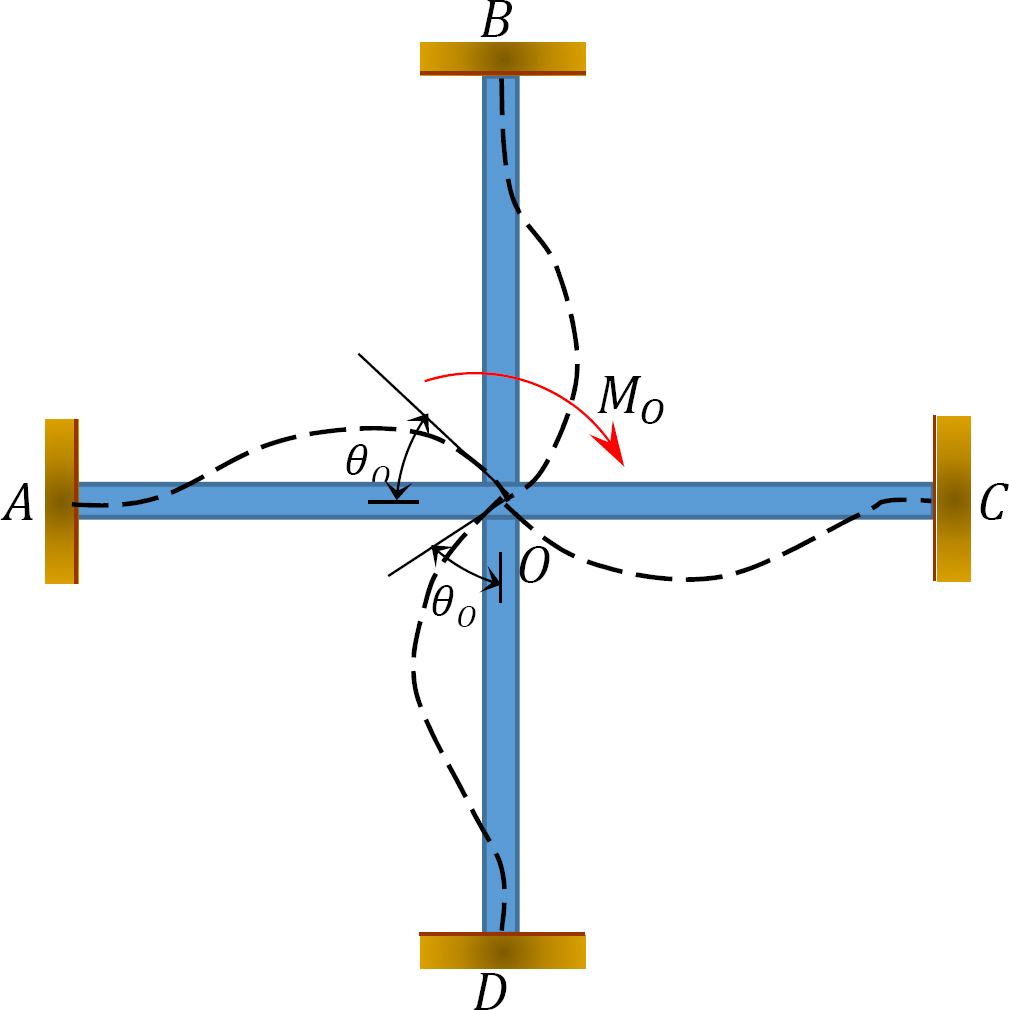
Fig. 12.3. Cadre.

Moments distribués: Lors de la libération de la pince imaginaire au niveau d’un joint, le moment déséquilibré au niveau de ce joint le fait tourner. La rotation tord la fin de la réunion des membres à l’articulation, ce qui entraîne le développement de moments de résistance. Ces moments de résistance sont appelés moments distribués. Les moments distribués pour les membres de la trame représentés à la figure 12.3 sont calculés comme suit:
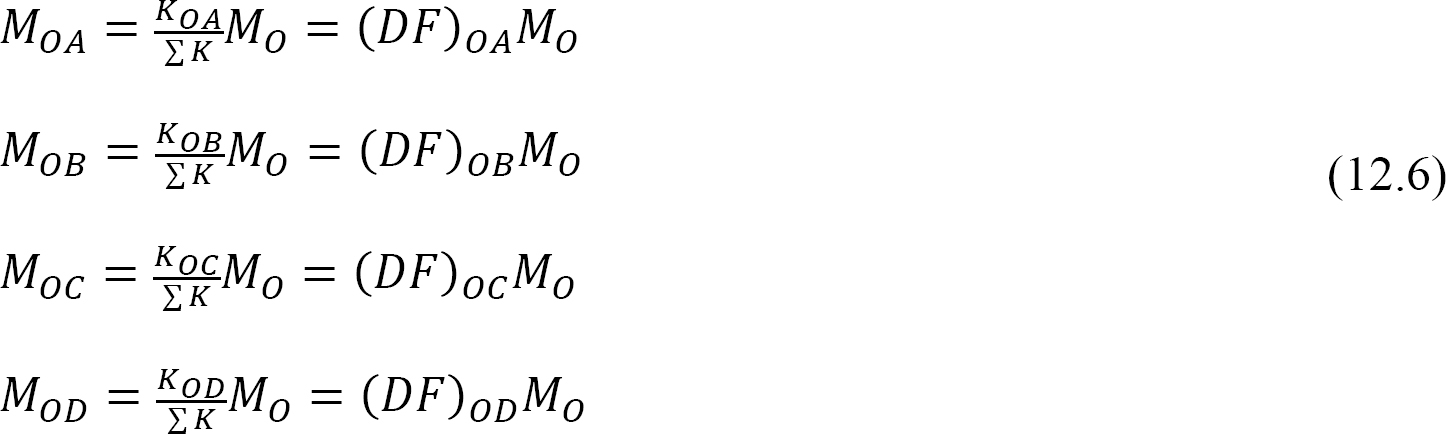
12.4 Modification de la rigidité des éléments
Parfois, le processus d’itération dans la méthode de distribution des moments peut être considérablement réduit en ajustant la rigidité en flexion de certains éléments de la structure indéterminée. Cette section examine l’influence d’un support fixe et d’un support d’extrémité de goupille sur la rigidité en flexion d’une poutre indéterminée.
Cas 1: Une poutre articulée à une extrémité et fixée à l’autre
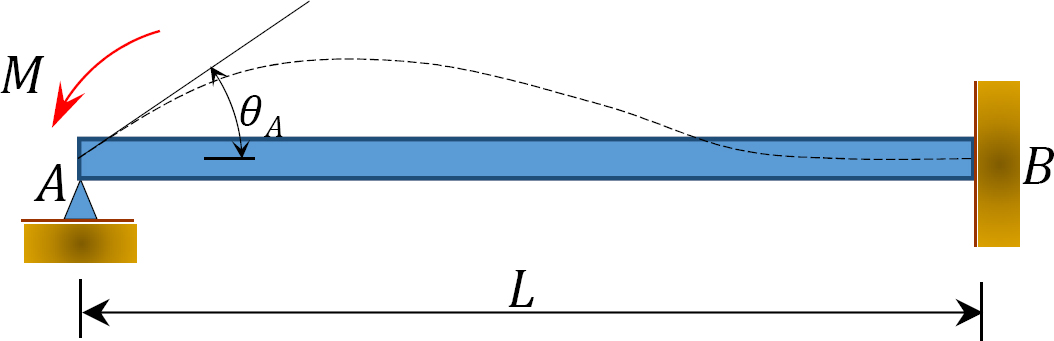
Fig. 12.4. Poutre
Considérons une poutre articulée à l’extrémité A et fixée à l’extrémité B, comme le montre la figure 12.4. L’application d’un moment M fait tourner l’extrémité d’articulation d’une quantité θ. Écrire l’équation pente-déviation pour l’extrémité A du membre et noter que 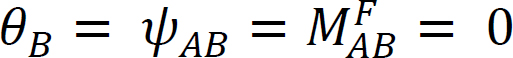 suggère ce qui suit:
suggère ce qui suit:
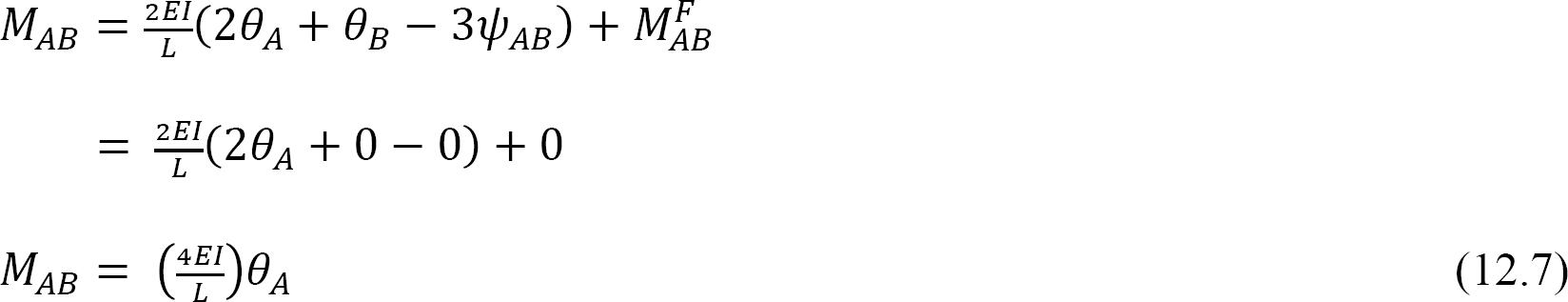
Par définition, la rigidité en flexion d’un élément de structure est le moment qui doit être appliqué à une extrémité de l’élément pour provoquer une rotation unitaire de cette extrémité. L’expression suivante pour la rigidité en flexion de l’élément à extrémité fixe est exprimée comme suit lors de la substitution de θA = 1 dans l’équation 12.7:

Par définition, la rigidité en flexion relative d’un élément est déterminée en divisant la rigidité en flexion de l’élément par 4E. La division de l’équation 12.8 par 4E suggère l’expression suivante de la rigidité relative pour le cas considéré:

Cas 2 : Une poutre articulée aux deux extrémités
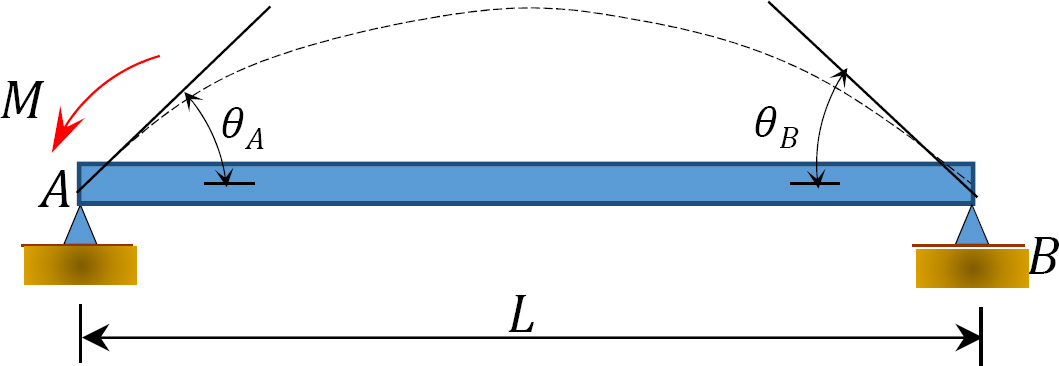
Fig. 12.5. Poutre simplement supportée.
L’application d’un moment M à l’extrémité A de la poutre simplement supportée représentée à la figure 12.5 fait tourner la poutre d’un angle θA à l’extrémité articulée. En utilisant l’équation pente-déviation modifiée dérivée de la section 11.4 du chapitre 11 et en notant que 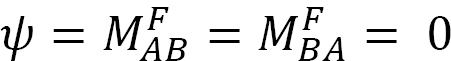 suggère l’expression suivante pour le moment à l’extrémité articulée où la charge est appliquée:
suggère l’expression suivante pour le moment à l’extrémité articulée où la charge est appliquée:
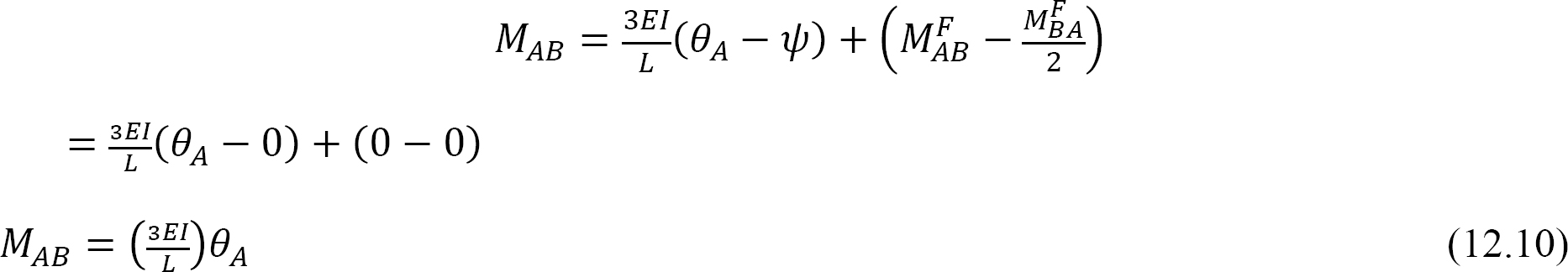
La substitution de θA = 1 dans l’équation 12.10 suggère l’expression suivante pour la rigidité en flexion d’un élément à extrémité articulée:

La rigidité relative d’un élément à extrémité articulée est obtenue en divisant l’équation 12.11 par 4E, comme suit:

La comparaison des équations 12.12 et 12.9 suggère qu’un élément à extrémité articulée est aux trois quarts aussi rigide qu’un élément de même géométrie mais fixé à l’extrémité. Ce fait établi peut réduire considérablement le nombre d’itérations lors de l’analyse de poutres ou de cadres à extrémité articulée en utilisant la méthode de distribution des moments. Dans de tels cas, la raideur relative de la poutre à l’extrémité proche est d’abord ajustée selon l’équation 12.12, et son facteur de distribution est calculé avec la raideur ajustée. Pendant l’opération d’équilibrage, l’extrémité proche ne sera équilibrée qu’une seule fois sans report supplémentaire de moments depuis ou vers sa fin.
12.5 Analyse des faisceaux indéterminés
La procédure d’analyse des faisceaux indéterminés par la méthode de distribution des moments est brièvement résumée comme suit:
Procédure d’Analyse de Faisceaux Indéterminés par la Méthode de Distribution des Moments
• Calculez les moments d’extrémité fixe pour les membres, en supposant que les articulations sont serrées contre la rotation.
• Calculer le facteur de distribution pour chacun des éléments connectés au niveau de l’articulation
• Calculer le moment déséquilibré au niveau de chaque articulation et le répartir aux extrémités des éléments connectés au niveau de cette articulation.
• Reportez plus de la moitié du moment distribué aux autres extrémités des membres.
• Additionnez ou soustrayez ces derniers moments (moments obtenus aux étapes trois et quatre) aux moments fixes d’origine ou à partir de ceux-ci.
• Appliquer les moments de fin déterminés aux articulations de la structure donnée.
• Dessinez le diagramme de corps libre de chaque travée de la poutre donnée, montrant les charges et les moments au niveau des joints obtenus par la méthode de répartition des moments.
• Déterminer les réactions de support pour chaque travée.
• Calculez et construisez les diagrammes de force de cisaillement et de moment de flexion pour chaque travée.
• Dessinez un diagramme de moment de flexion et un diagramme de force de cisaillement pour la poutre donnée en combinant les diagrammes de l’étape 9.
Exemple 12.1
En utilisant la méthode de répartition des moments, déterminez les moments de fin et les réactions aux supports de la poutre illustrée à la figure 12.6a. Dessinez les diagrammes de la force de cisaillement et des moments de flexion. EI = constante.
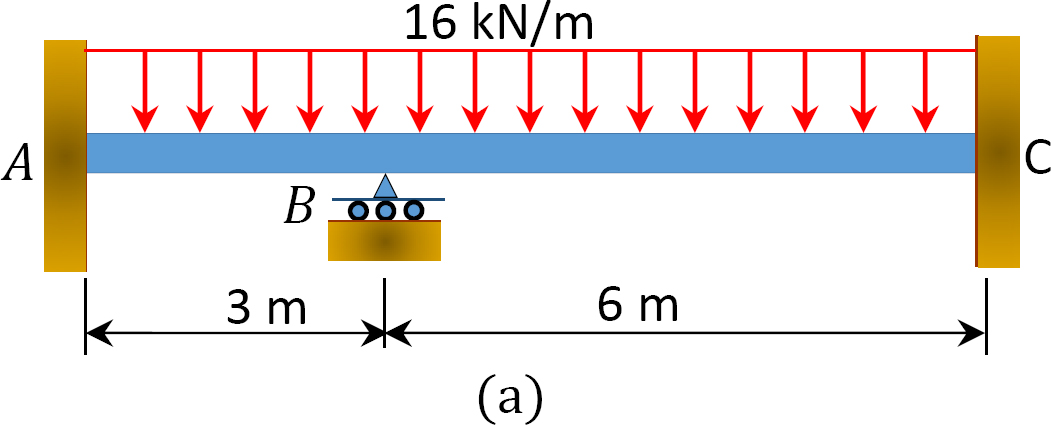
Fig. 12.6. Poutre.
Solution
Moment de fin fixe.
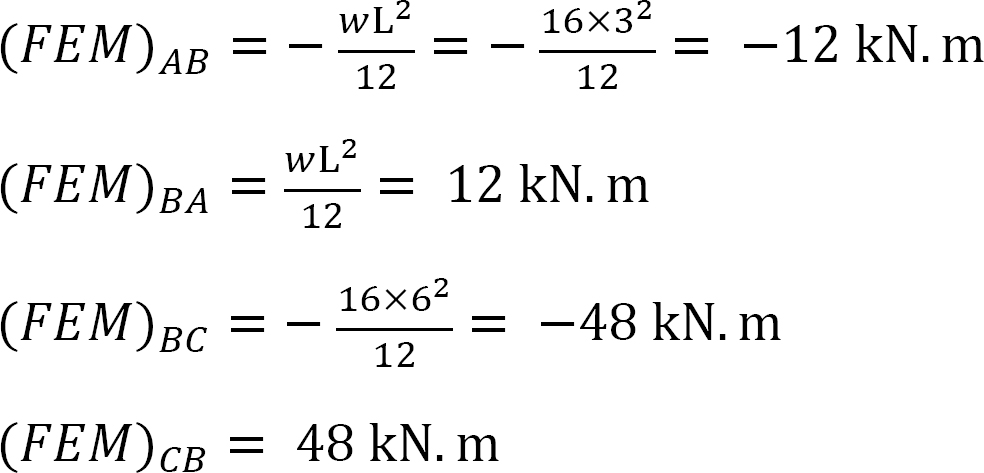
Facteur de rigidité.
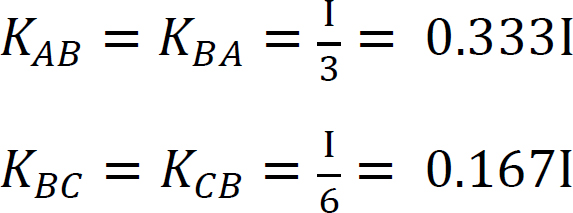
Facteur de distribution.
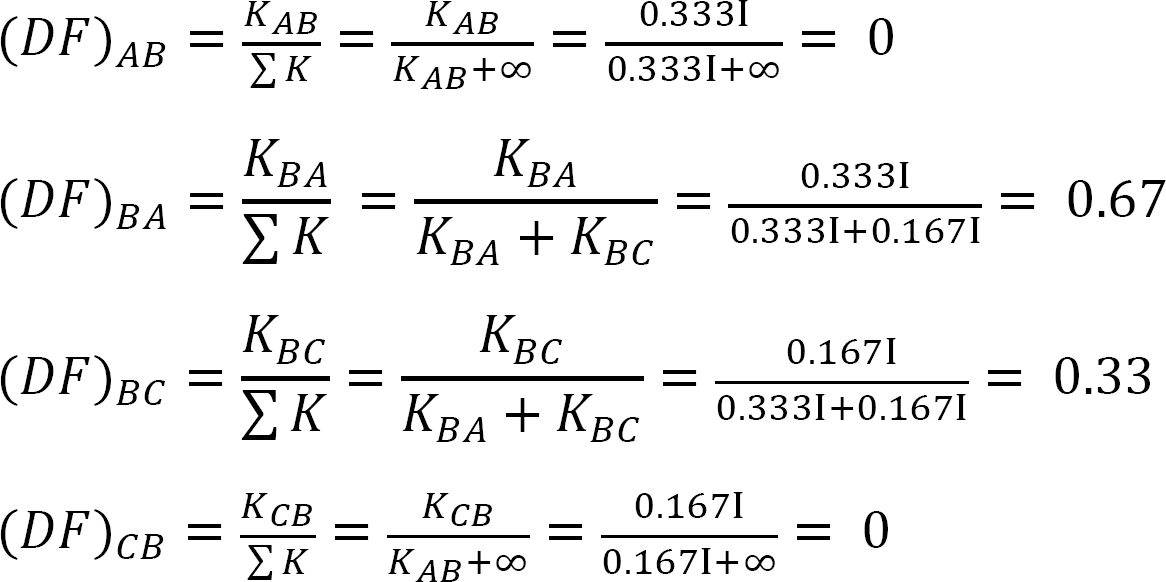
Tableau 12.1. Tableau de distribution.
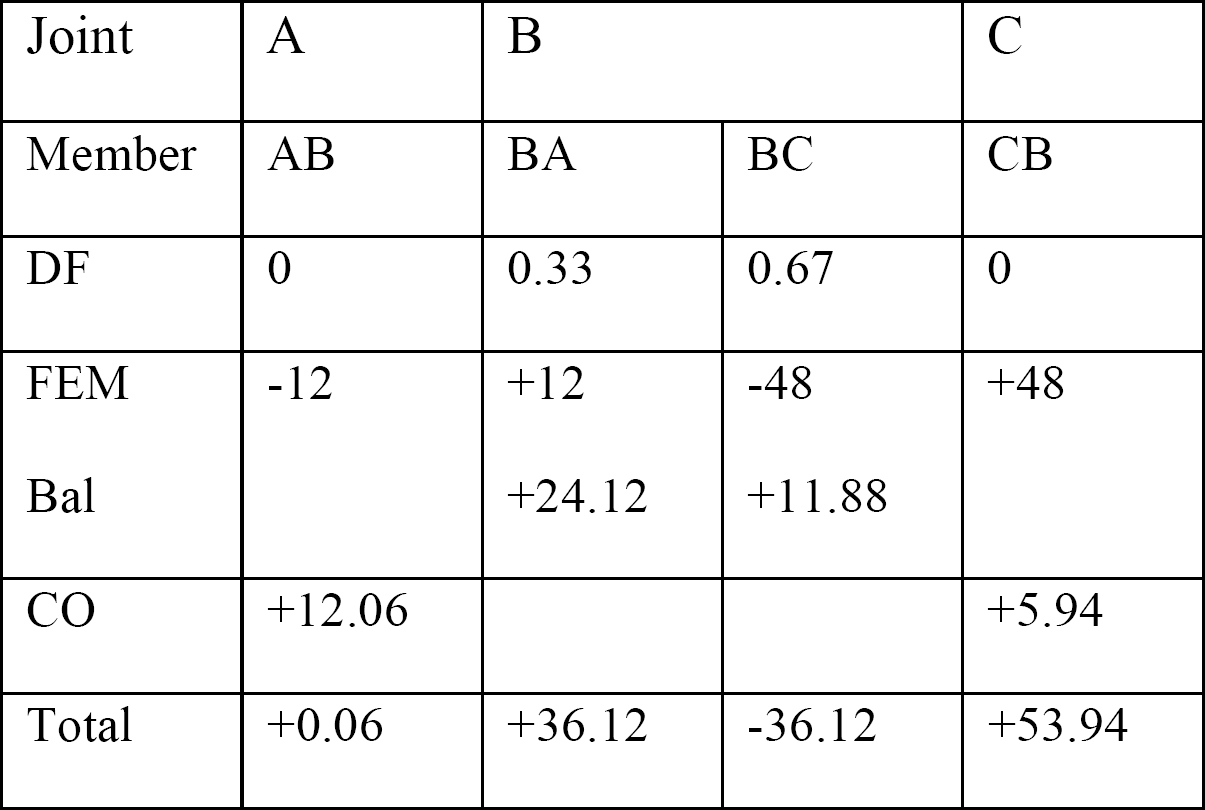
Diagrammes de force de cisaillement et de moment de flexion.
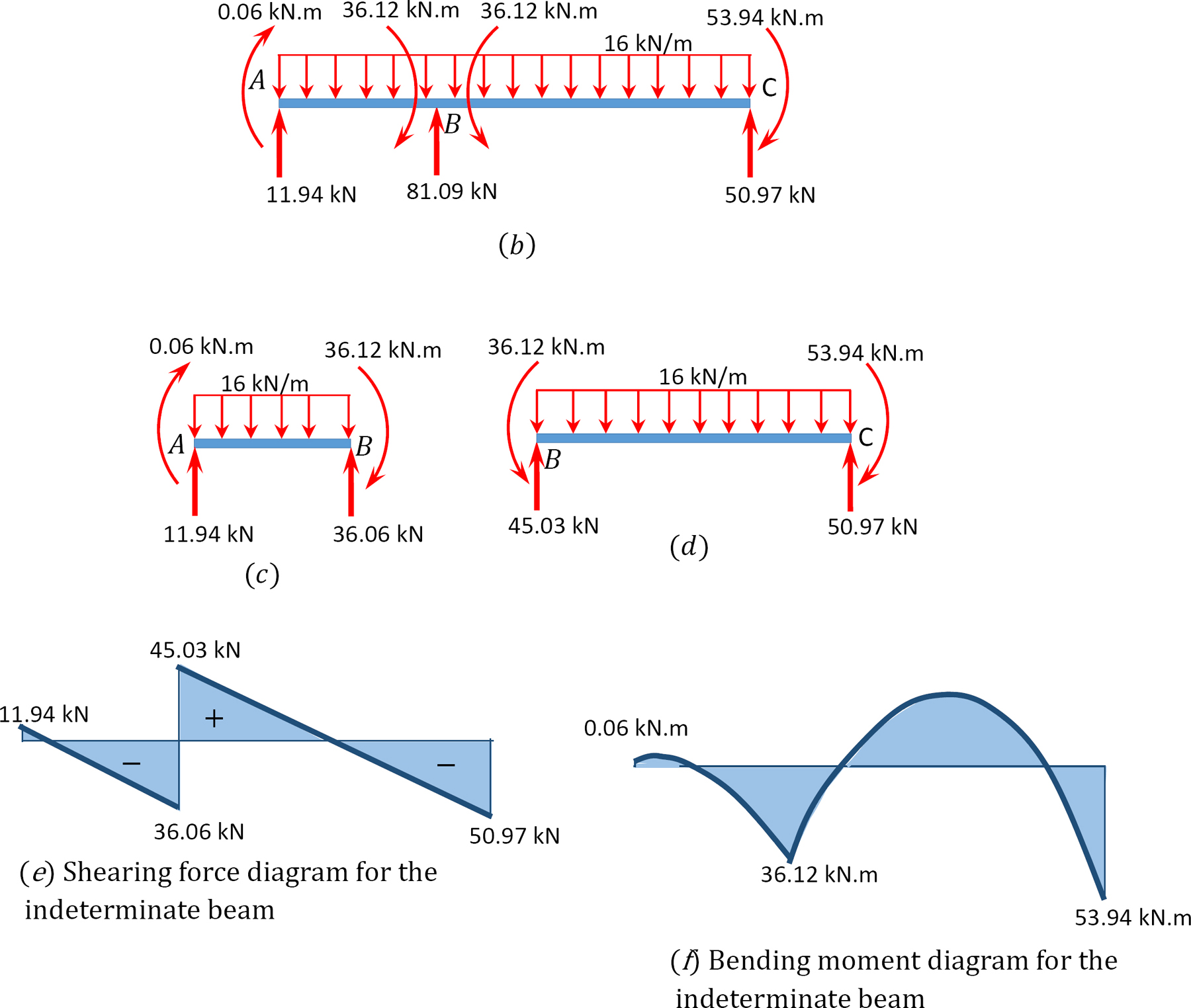
Exemple 12.2
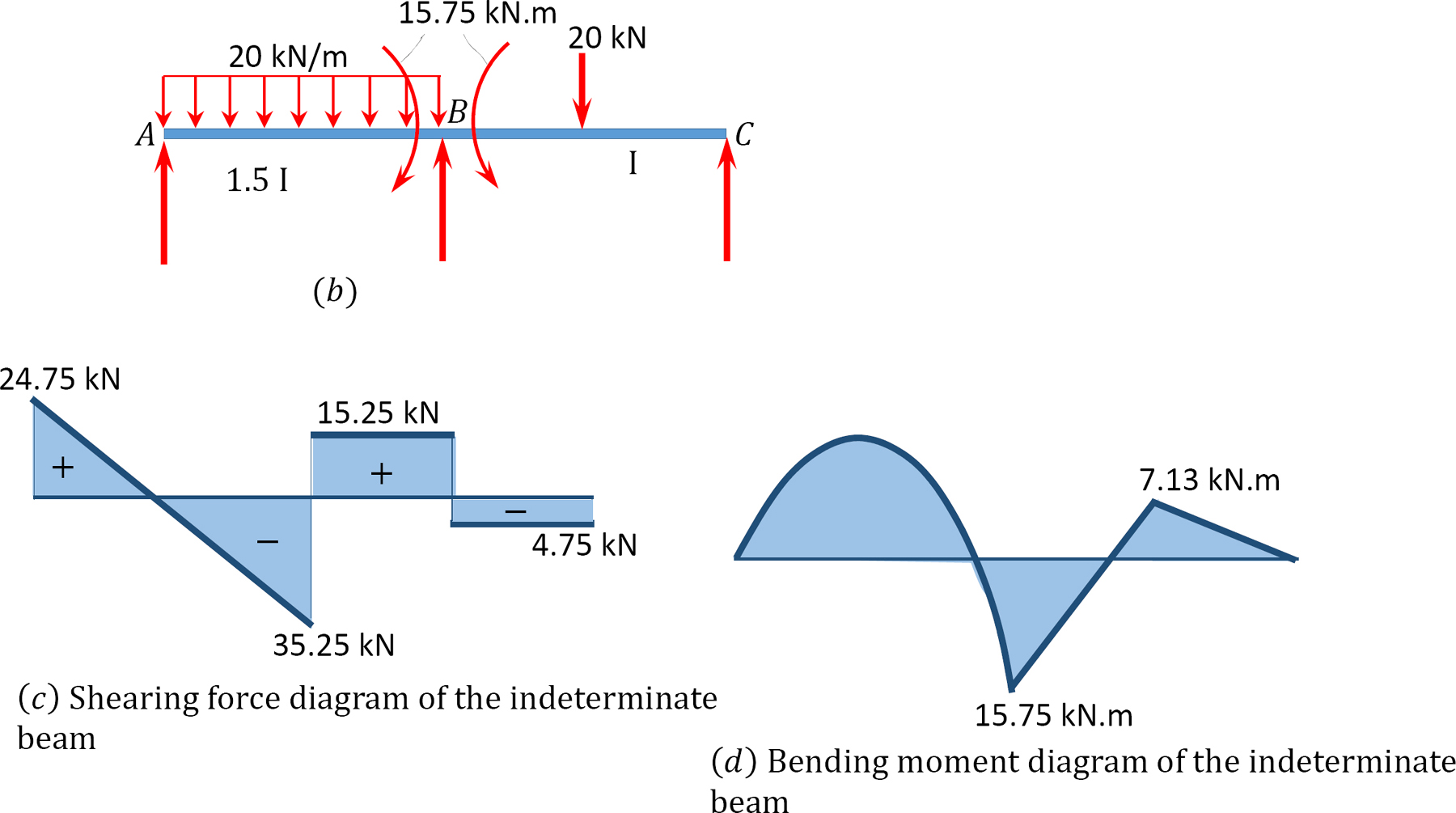
En utilisant la méthode de répartition des moments, déterminez les moments de fin et les réactions aux supports de la poutre illustrée à la figure 12.7a. Dessinez les diagrammes de la force de cisaillement et des moments de flexion.
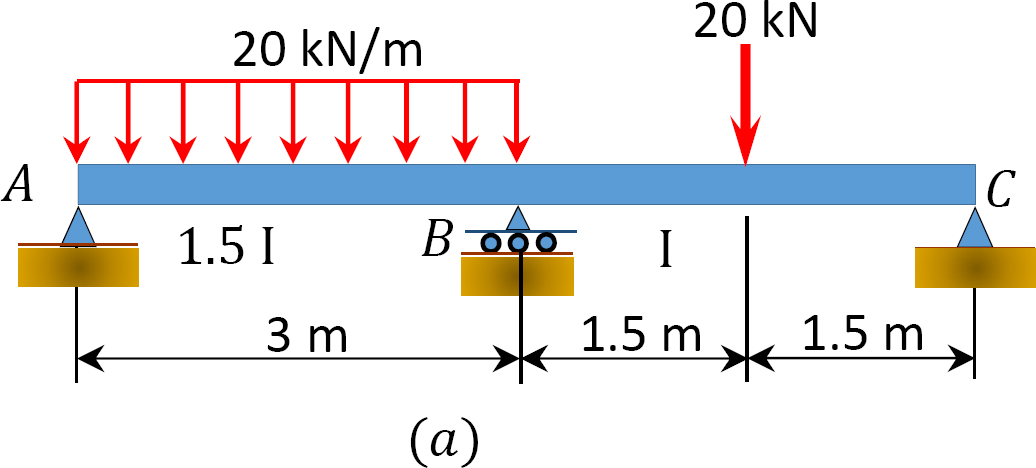
Fig. 12.7. Poutre.
Solution
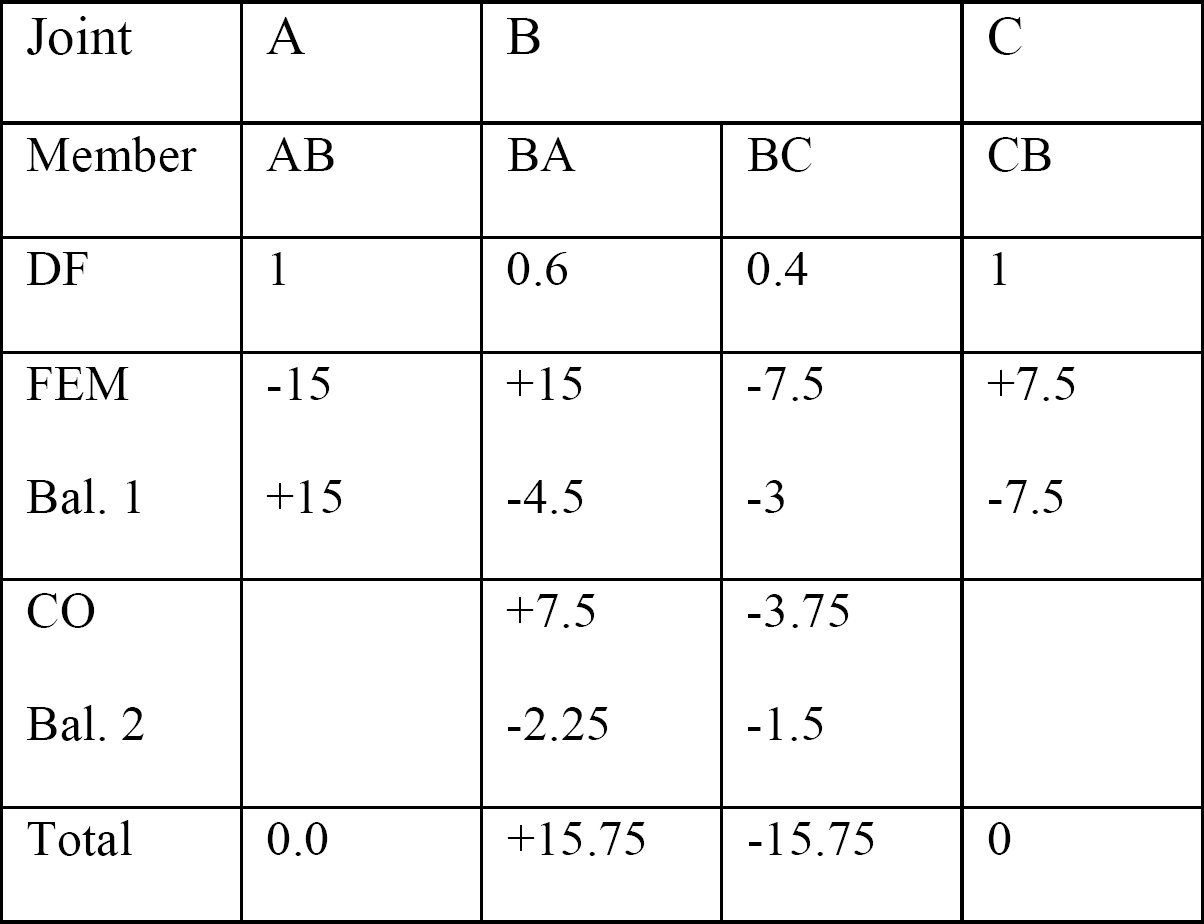
Moment de fin fixe.
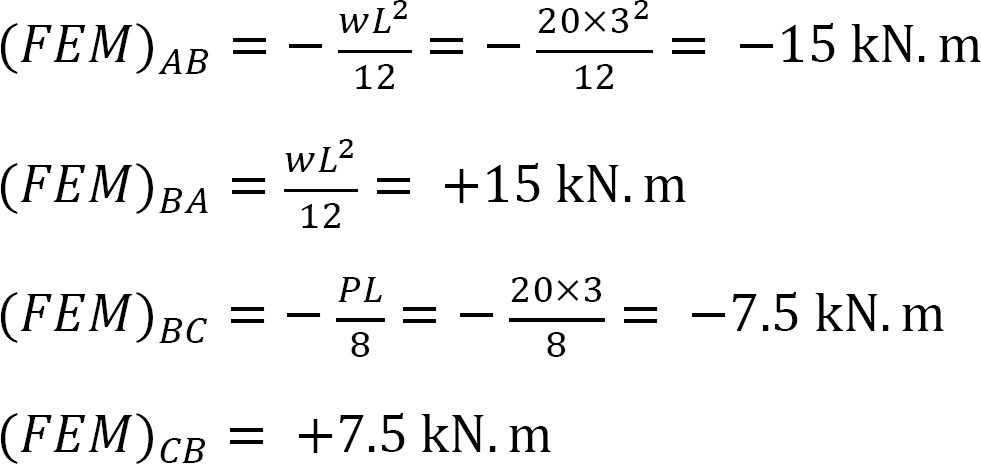
Facteur de rigidité.
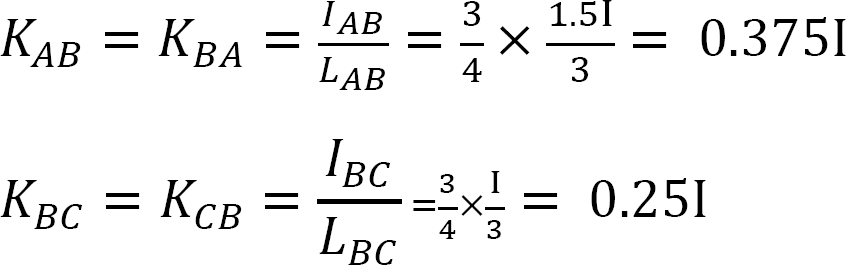
Facteur de distribution.
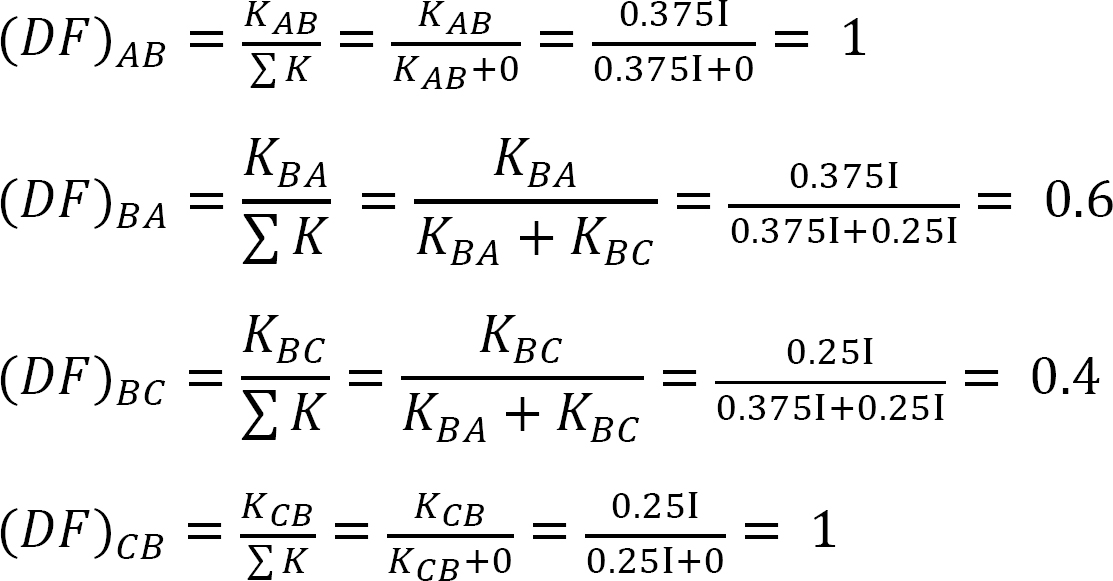
Tableau 12.2. Tableau de distribution.
Diagrammes de force de cisaillement et de moment de flexion.
12.6 Analyse des trames indéterminées
La procédure d’analyse des trames à l’aide de la méthode de distribution des moments dépend du type de trame en cours d’analyse. Les cadres sont classés en tant que cadres oscillants ou non oscillants. La procédure d’analyse des trames non oscillantes est similaire à celle des poutres indéterminées. Mais pour l’analyse des trames de balancement, la procédure est différente. Il y a deux étapes impliquées dans l’analyse des trames de balancement, à savoir l’étape de non-balancement et les analyses de balancement. Ces étapes sont décrites ci-après.
Procédure d’Analyse des Trames de balancement indéterminées par la Méthode de Distribution des Moments
A.Analyse d’étape de non-balancement
• Calculez les réactions horizontales aux supports du cadre et notez la différence X. C’est la force pour empêcher le balancement.
D. Analyse d’étape de balancement
• Les valeurs sont supposées pour M2 et M1 est déterminé.
• Les moments arbitraires sont ensuite répartis comme pour la condition de non-balancement
• Calculez l’amplitude des réactions horizontales au niveau des supports pour la condition de balancement. La somme de ces réactions donne la force de déplacement arbitraire Y.
• Déterminer le rapport 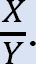 Ce rapport est appelé facteur de balancement.
Ce rapport est appelé facteur de balancement.
• Utilisez le facteur de balancement pour multiplier les moments distribués du balancement. Cela donne le moment corrigé pour le balancement.
• Les derniers moments de la trame sont la somme des moments obtenus dans l’étape de non-balancement et le moment corrigé pour l’étape de balancement.
Exemple 12.3
En utilisant la méthode de distribution des moments, déterminez les moments de fin des membres de la trame illustrée à la figure 12.8. EI = constante.
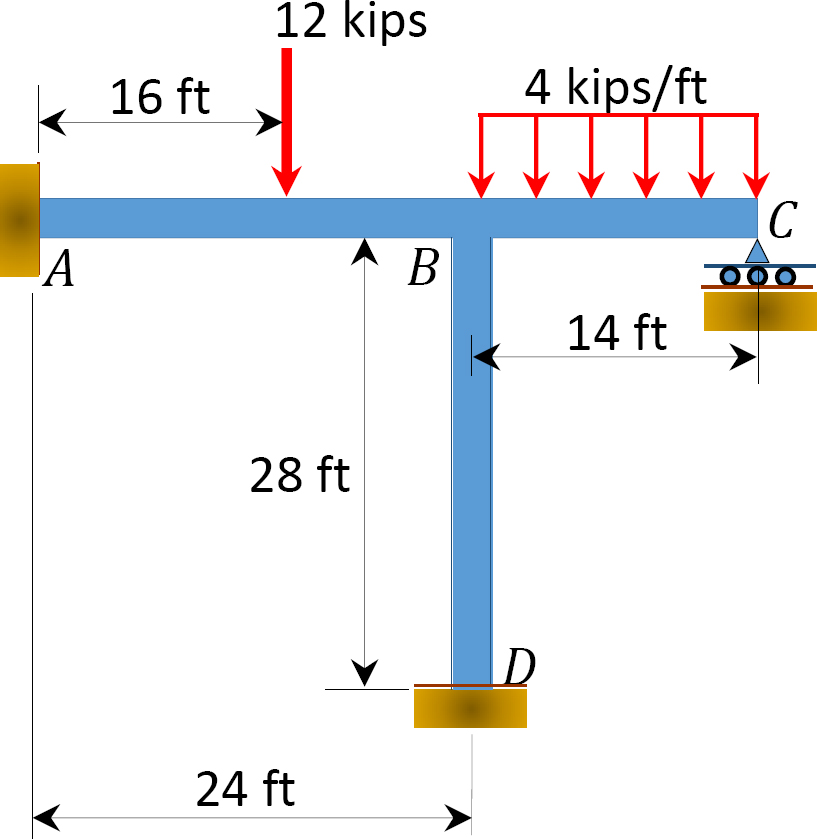
Fig. 12.8. Cadre.
Solution
Moment de fin fixe.
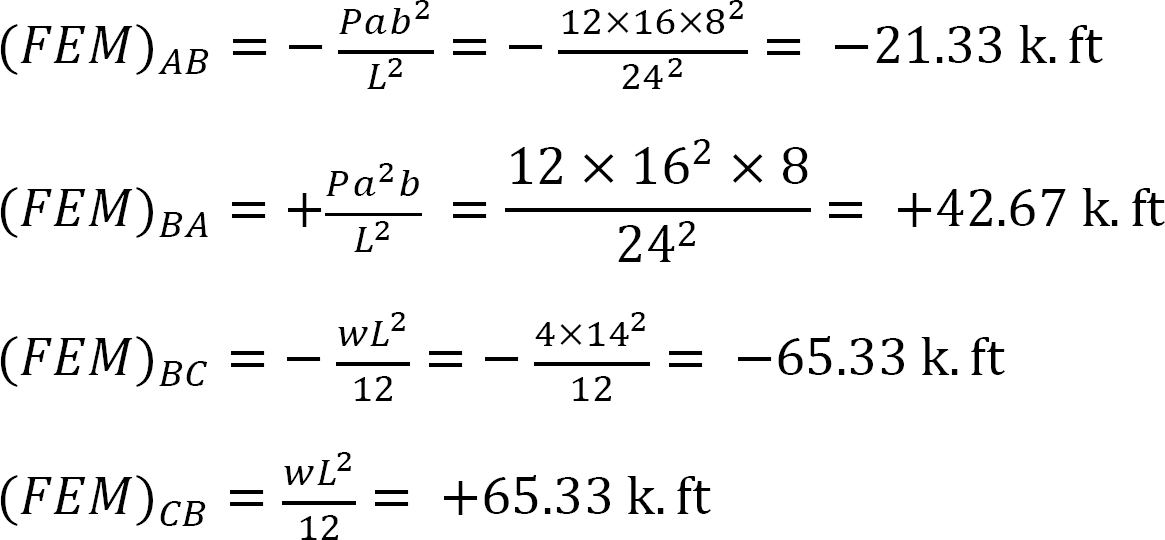
Facteur de rigidité.
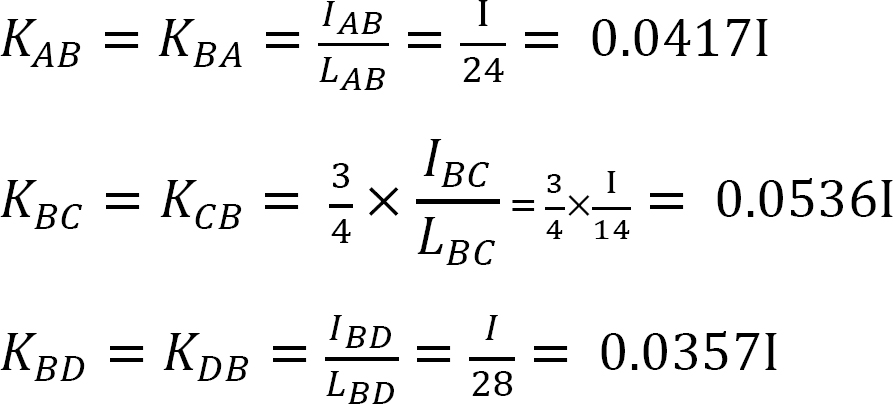
Facteur de distribution.
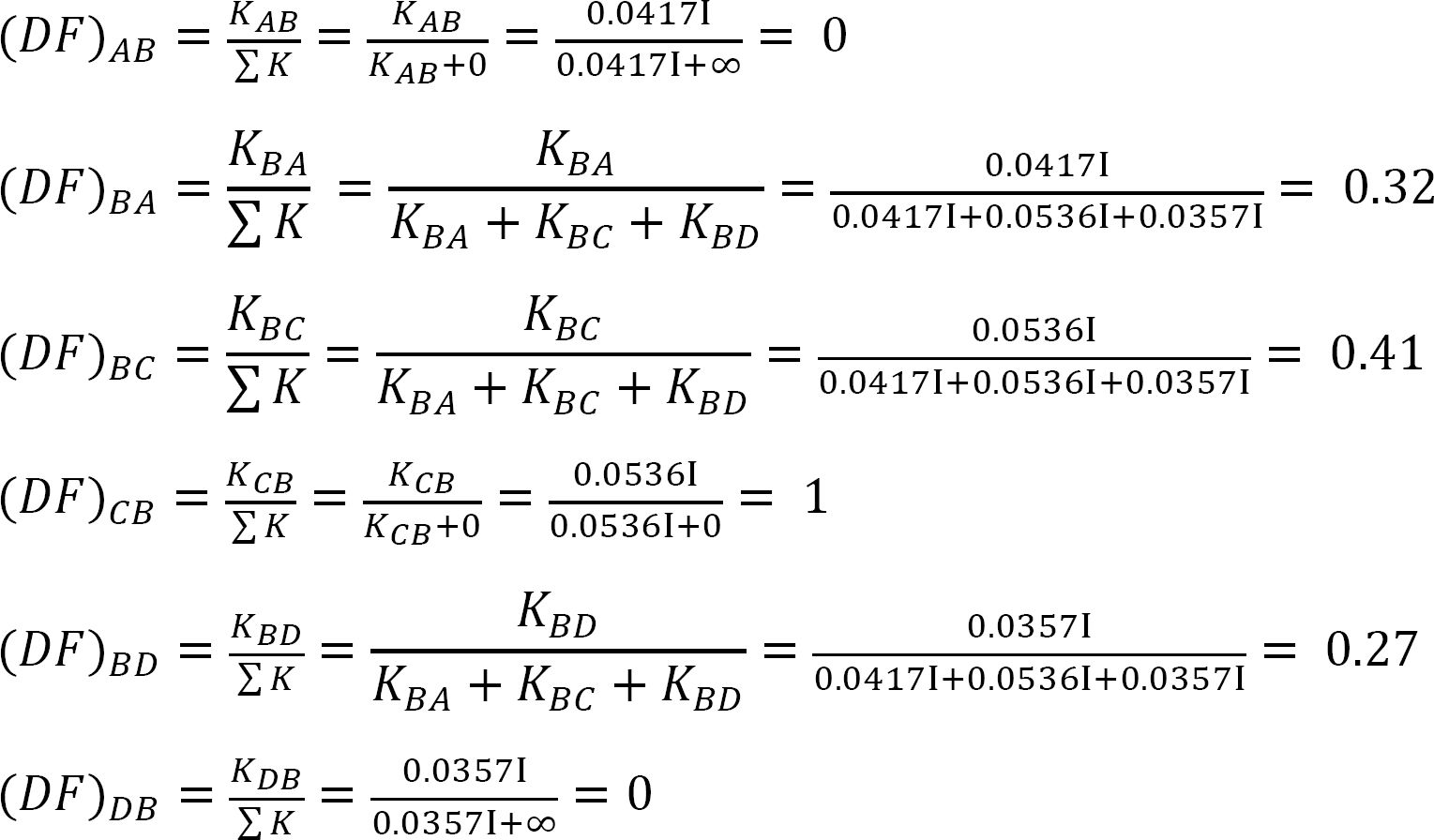
Tableau 12.3. Tableau de distribution.
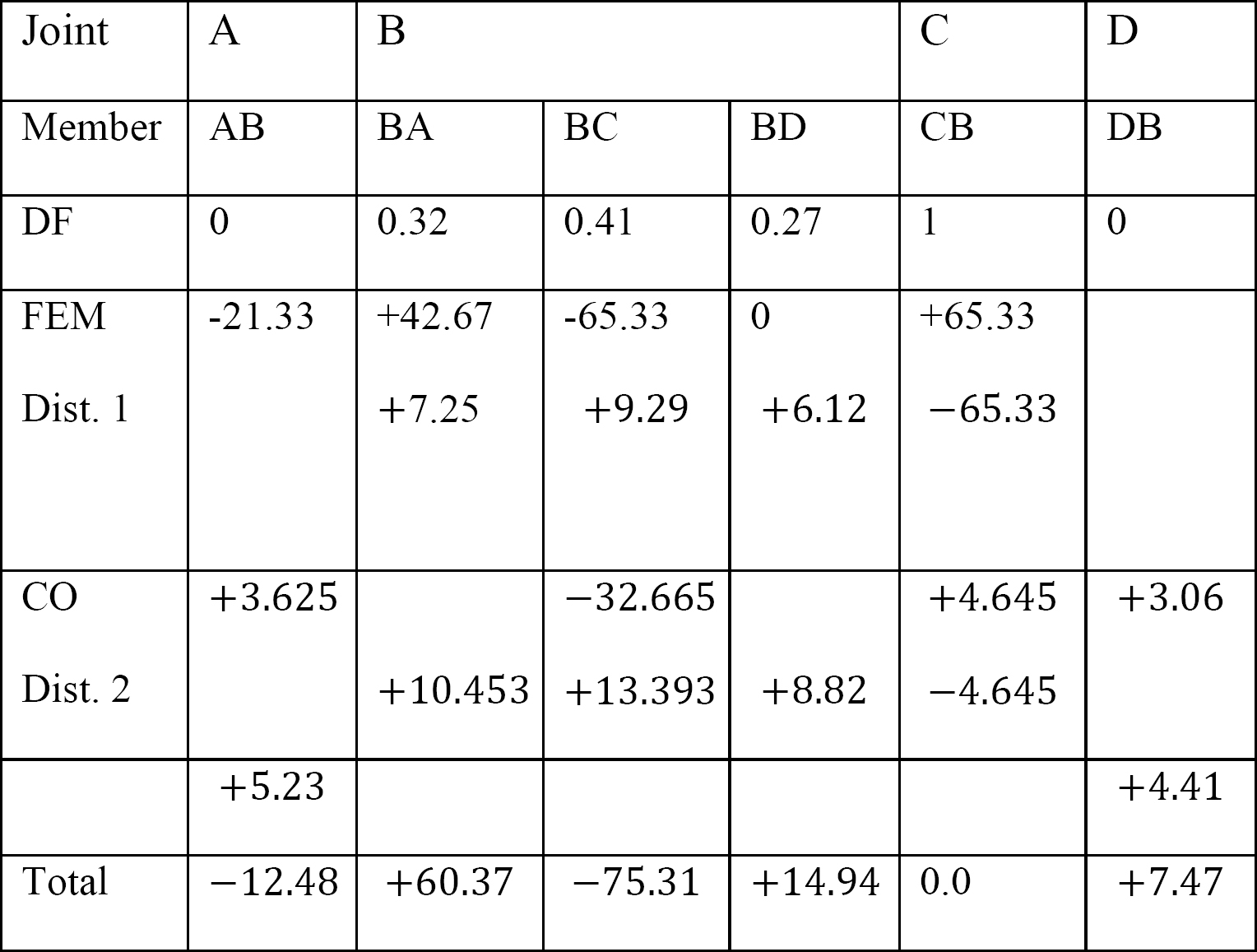
Derniers moments de fin de membre.
La substitution des valeurs obtenues de EKθB, EKθC et EK∆ dans les équations de moment de fin de membre suggère ce qui suit :
MAB = -12,48 k.ft
MBA = +60,37 k. ft
MBC = -75,31 k. ft
MBD= +14,94 k. ft
MCB = 0
MDB = +7,47 k. ft
Exemple 12.4
En utilisant la méthode de distribution des moments, déterminez les moments de fin sur les supports du cadre illustré à la figure 12.9. EI = constante.
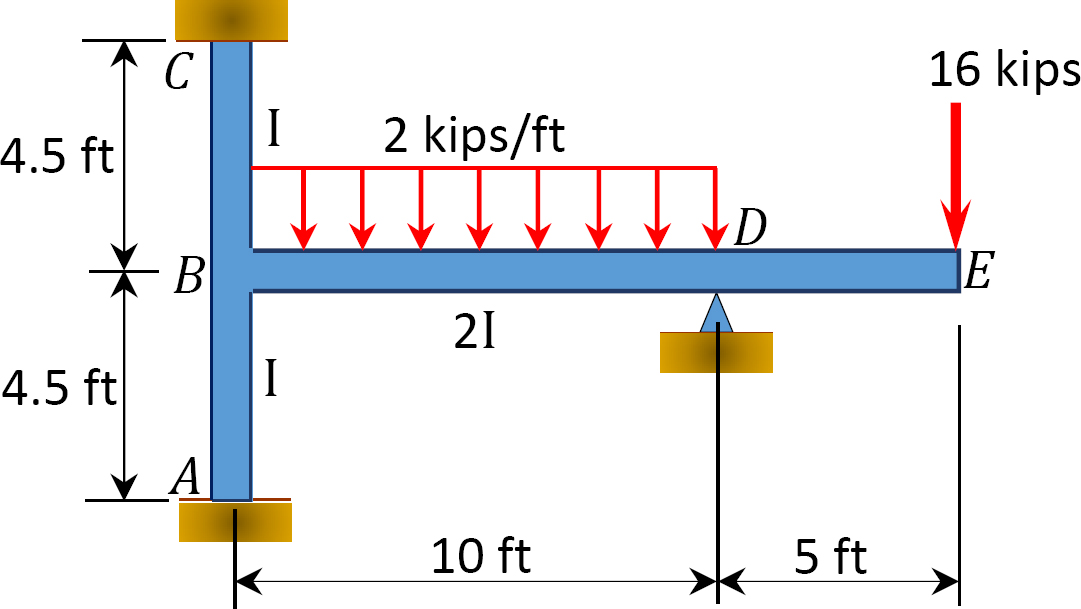
Fig. 12.9. Cadre.
Solution
Moment de fin fixe.
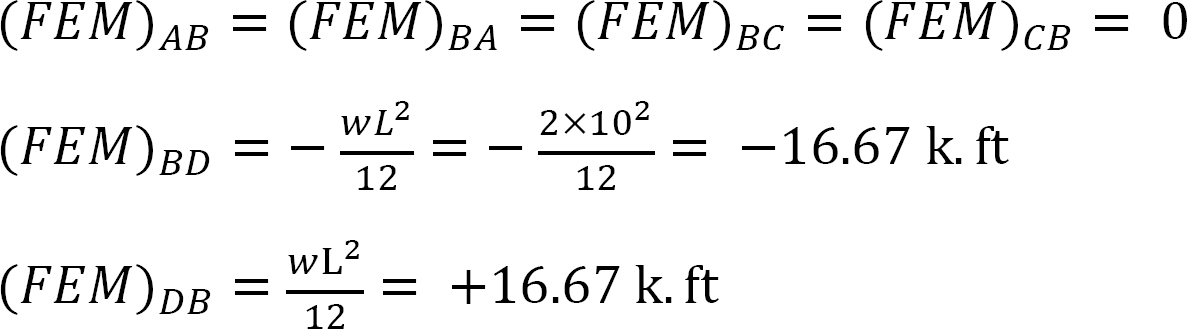
Facteur de rigidité.
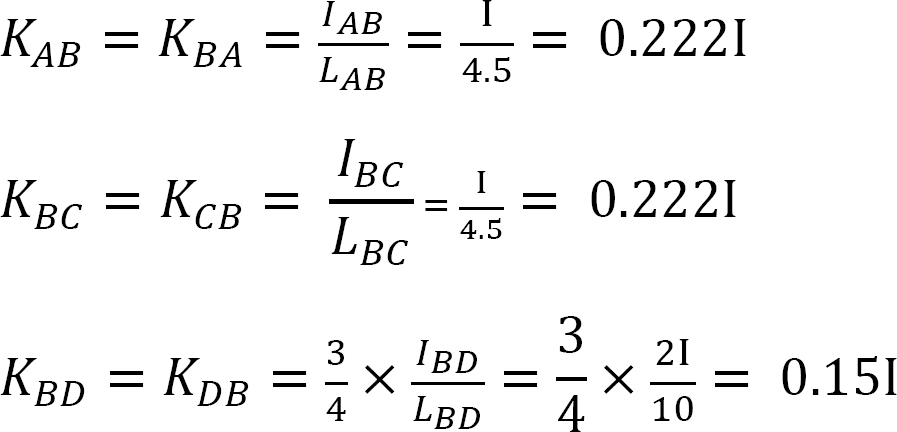
Facteur de distribution.

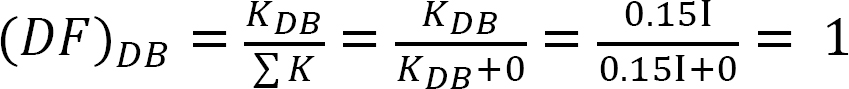
Tableau 12.4. Tableau de distribution.
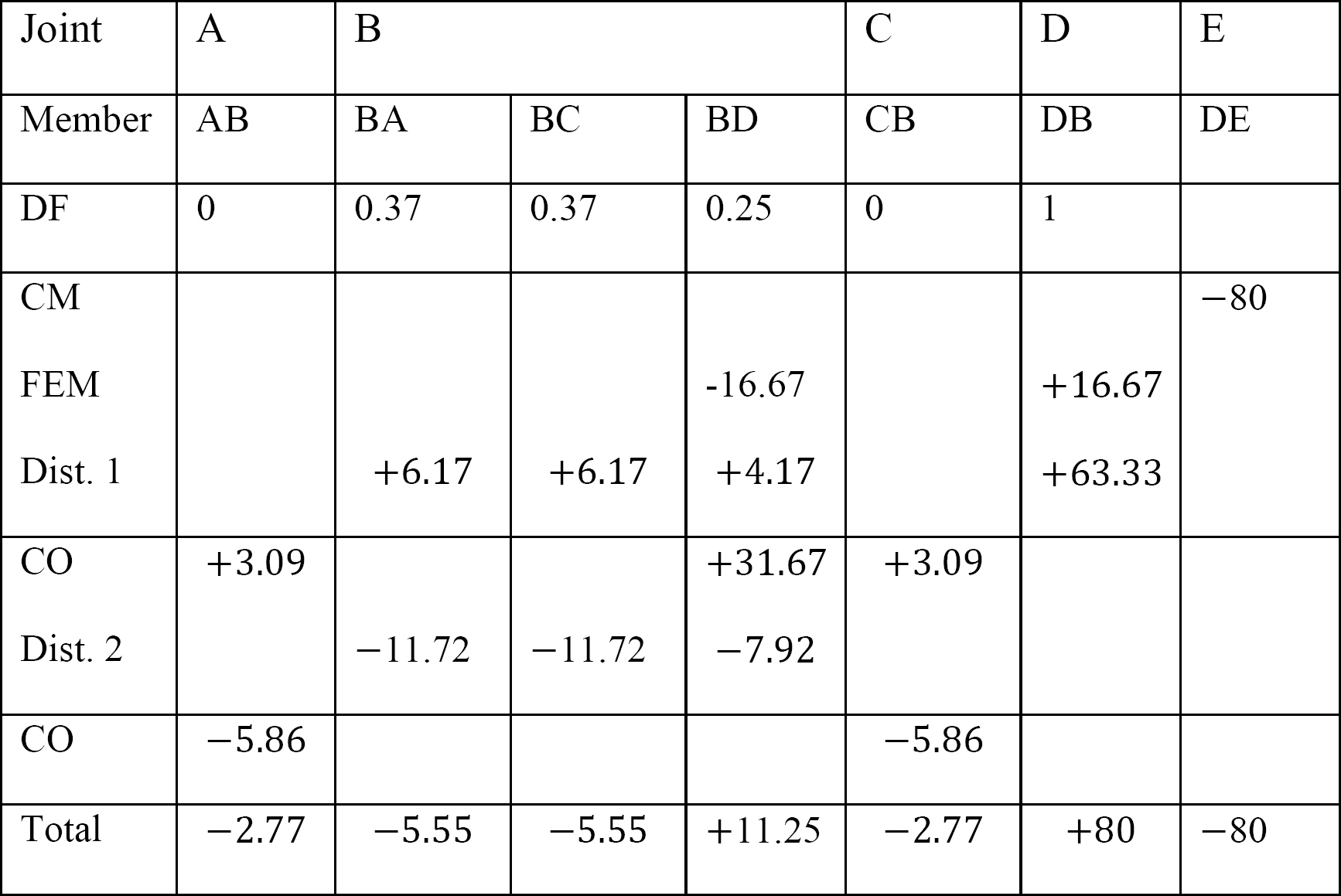
Derniers moments de fin de membre.
MAB = -2,77 k. ft
MBA = -5,55 k. ft
MBC = -5,55 k. ft
MBD = +11,25 k. ft
MCB = -2,77
MDB = +80 k. ft
MDE = -80 k. ft
Exemple 12.5
En utilisant la méthode de distribution des moments, déterminez les moments de fin sur les supports du cadre illustré à la figure 12.10. EI = constante.
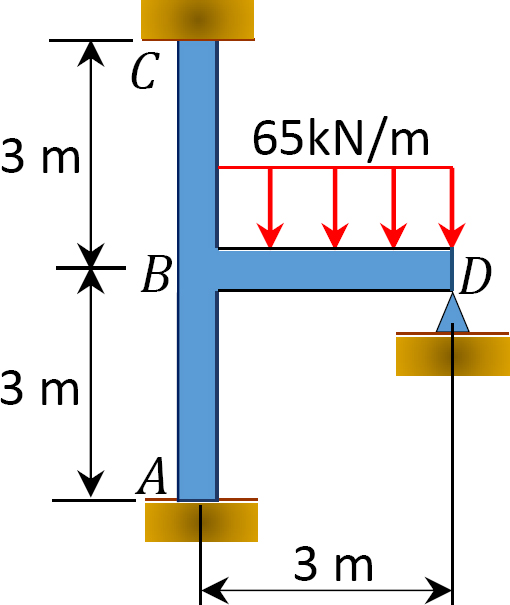
Fig. 12.10. Cadre.
Solution
Moment de fin fixe.
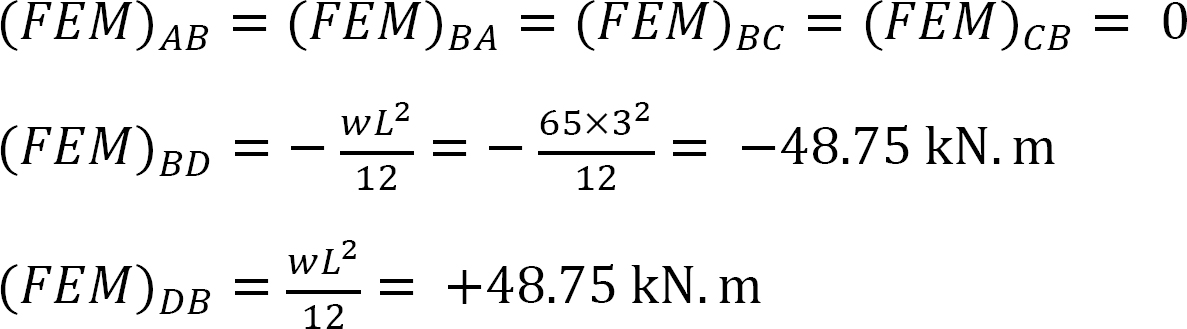
Facteur de rigidité.
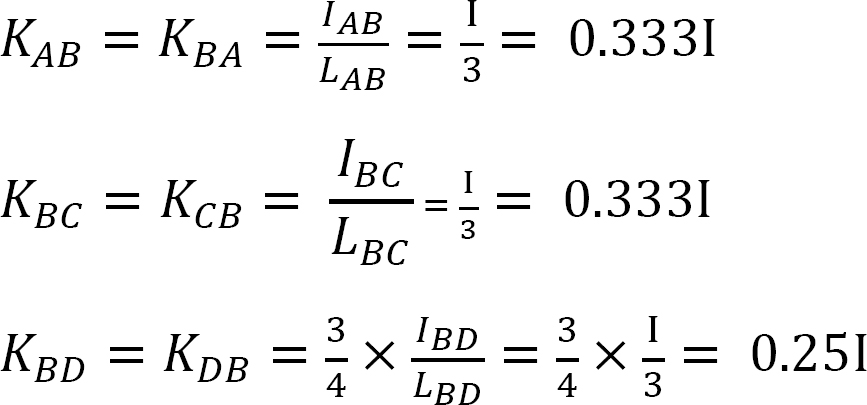
Facteur de distribution.
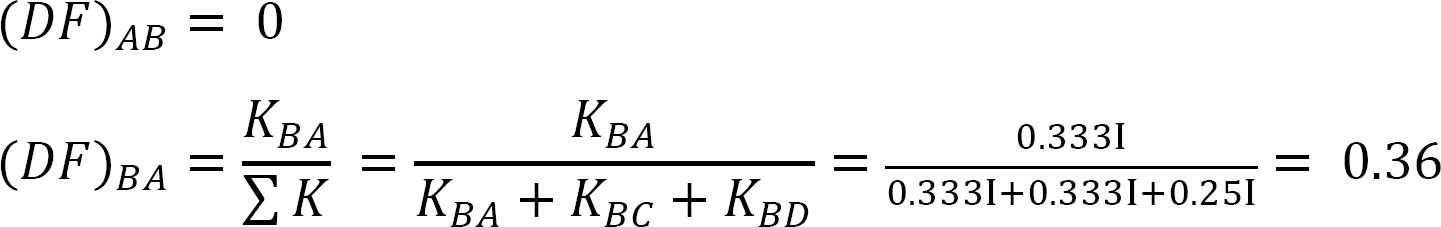

Tableau 12.5. Tableau de distribution.
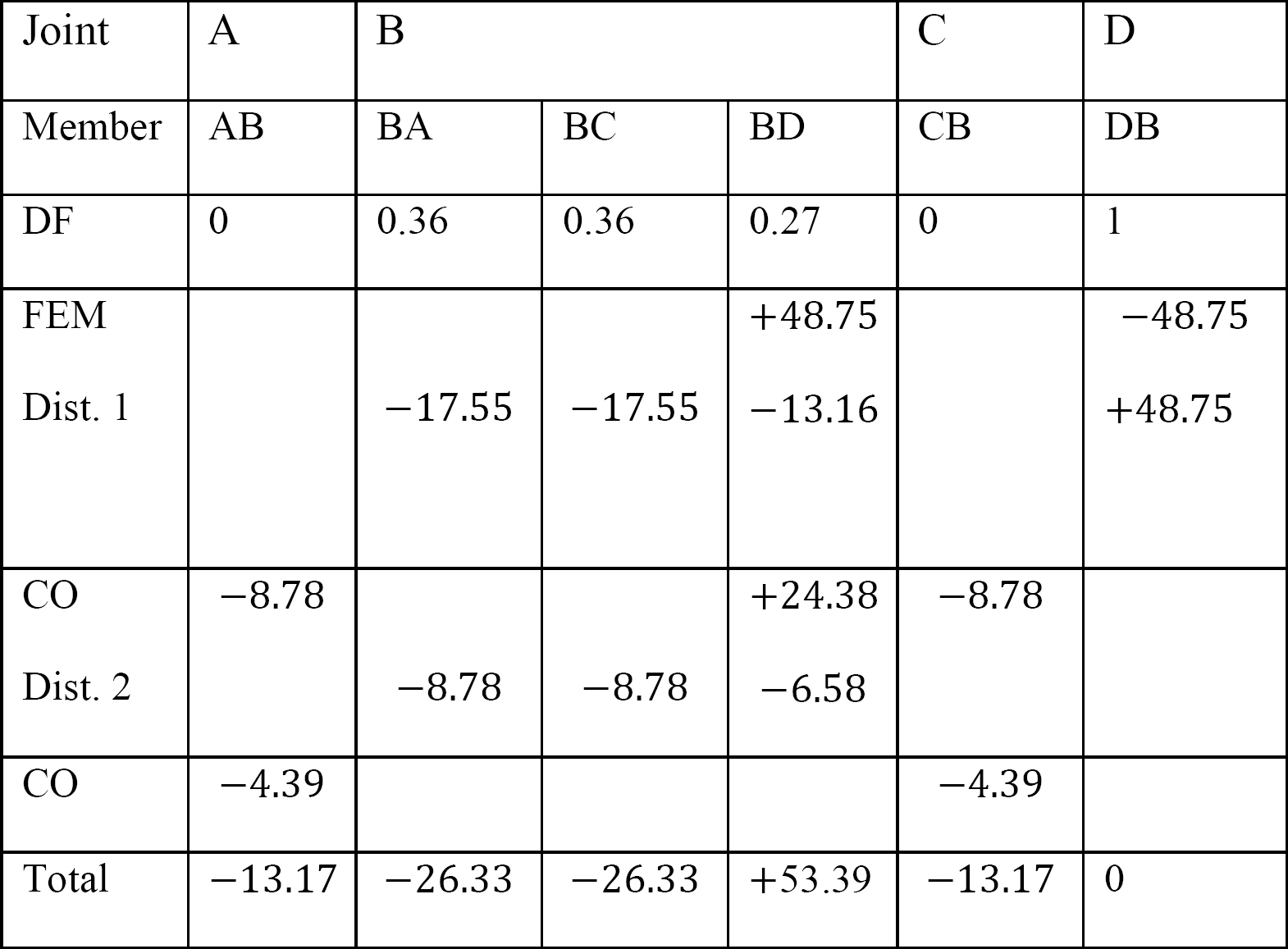
Derniers moments de fin de membre.
MAB = -13,17 k. ft
MBA = -26,33 k. ft
MBC = -26,33 k. ft
MBD = +53,39 k. ft
MCB = -13,17 k. ft
MDB = 0
Exemple 12.6
À l’aide de la méthode de distribution des moments, déterminer les moments de fin de membre du cadre avec balancement latéral illustré à la figure 12.11a.
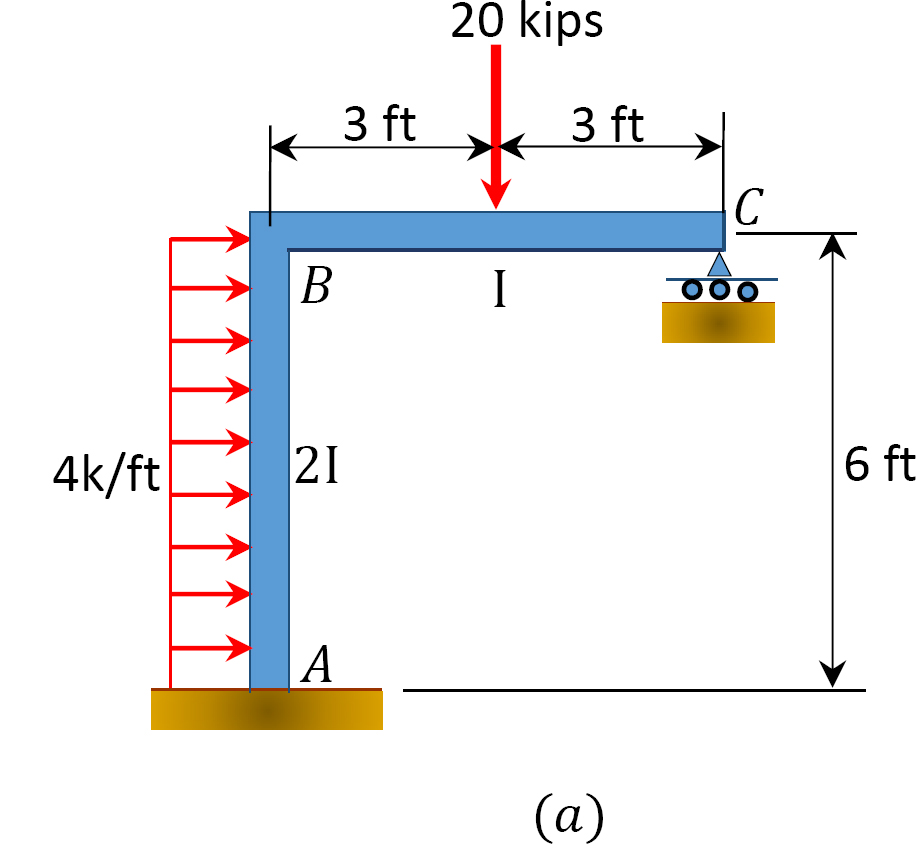
Fig. 12.11. Cadre avec balancement latéral.
Solution
Moment de fin fixe.
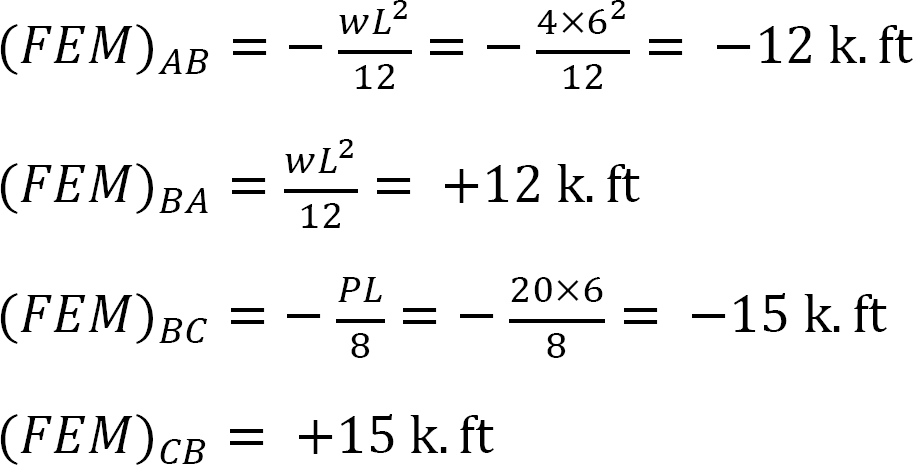
Facteur de rigidité.
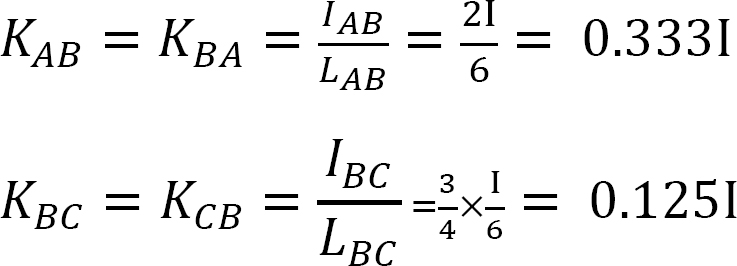
Facteur de distribution.
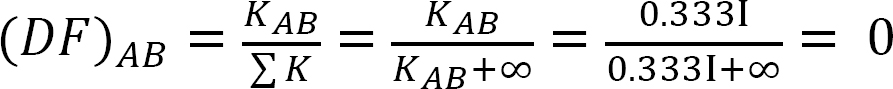

Analyse du cadre sans balancement latéral.
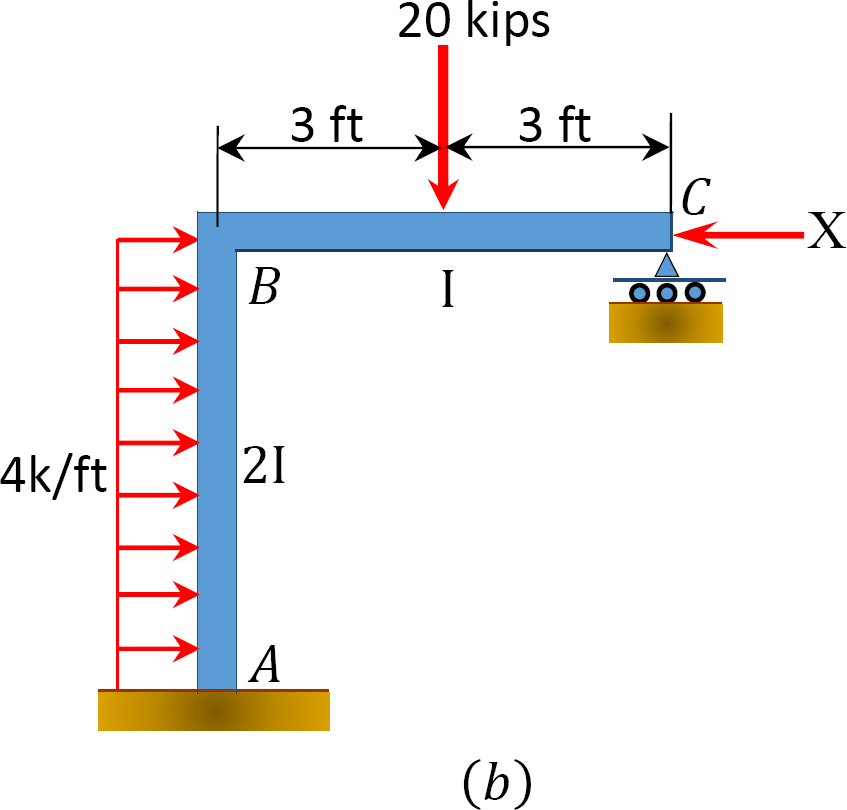
Tableau 12.6. Tableau de distribution (pas de cadre de balancement).
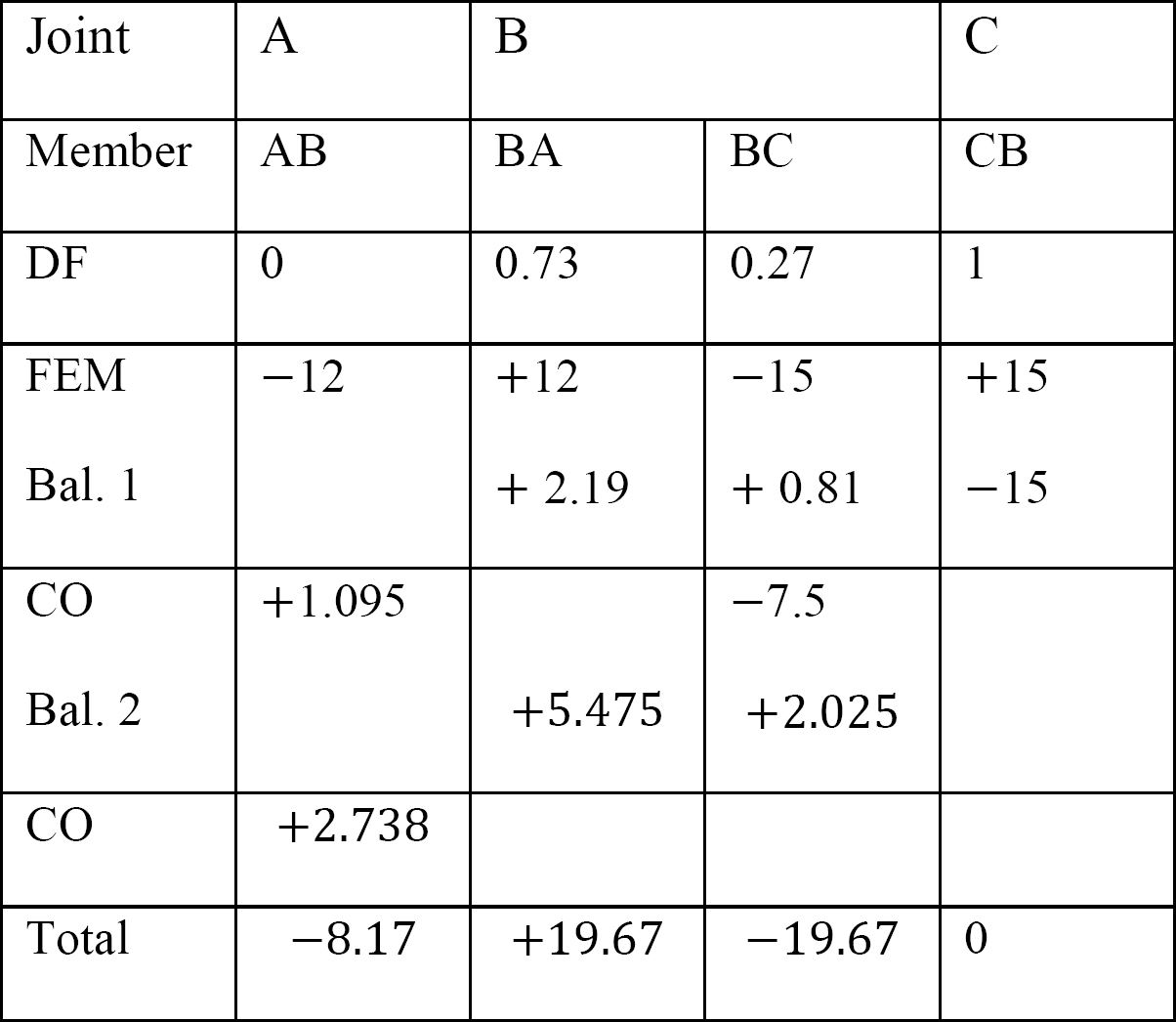
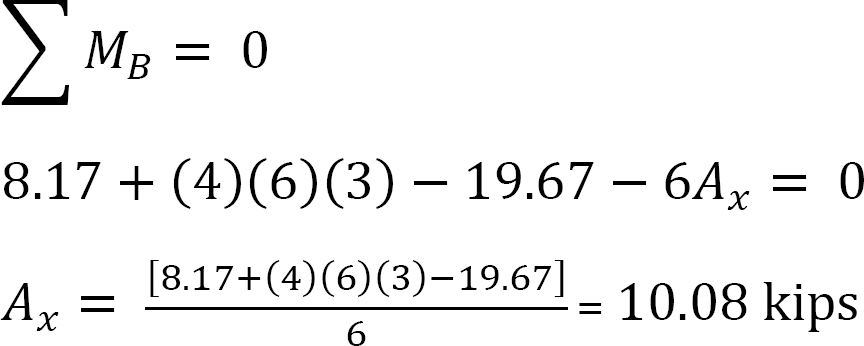
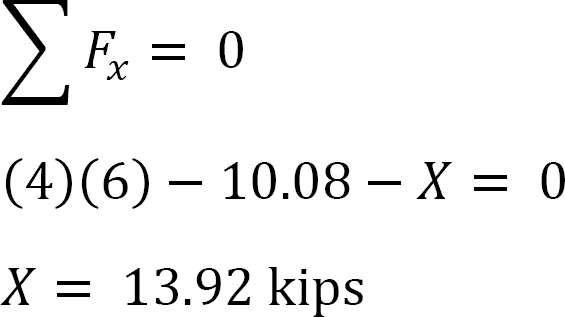
Analyse du cadre avec balancement latéral.
Supposons que MAB = + 20 k. ft
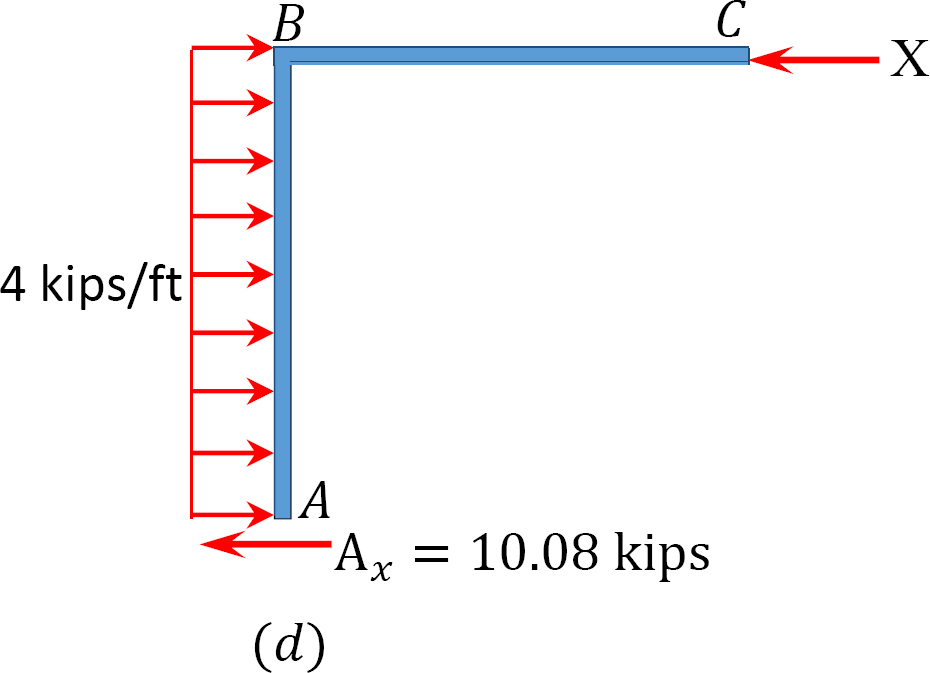
Tableau 12.7. Table de distribution (cadre de balancement).
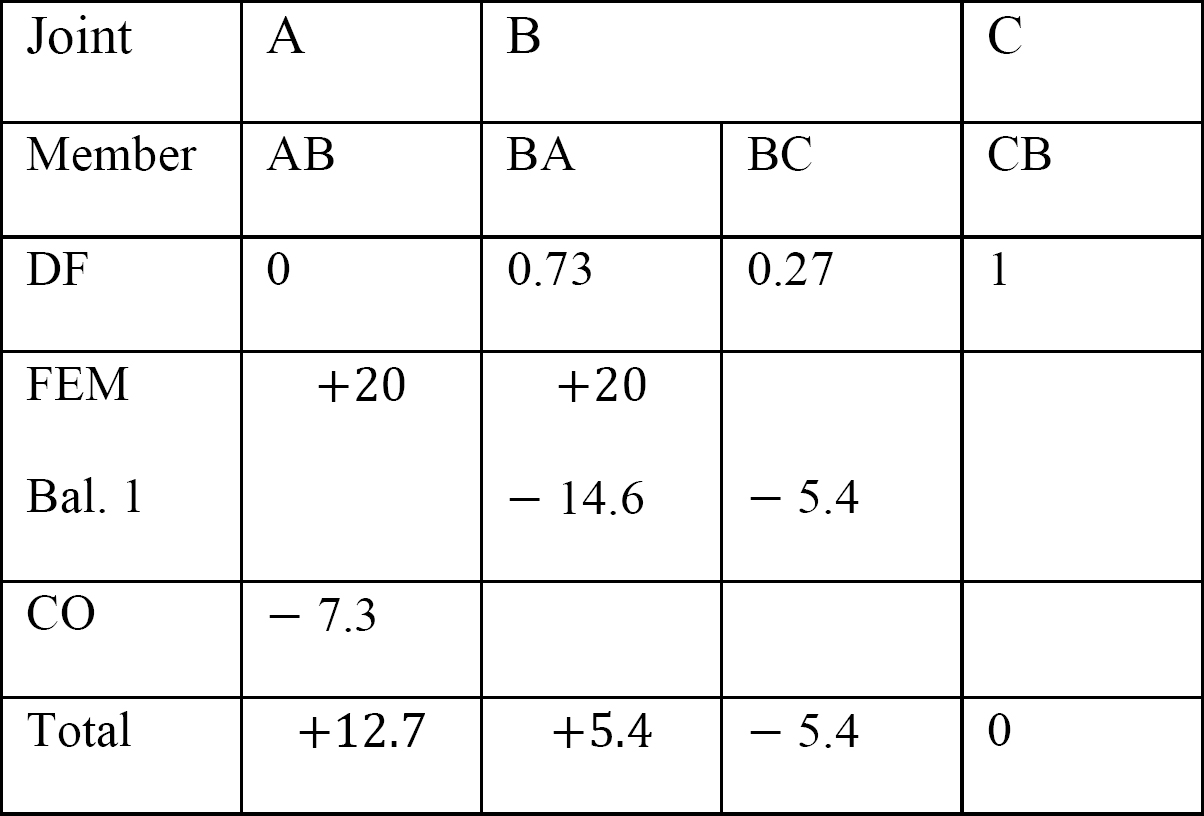
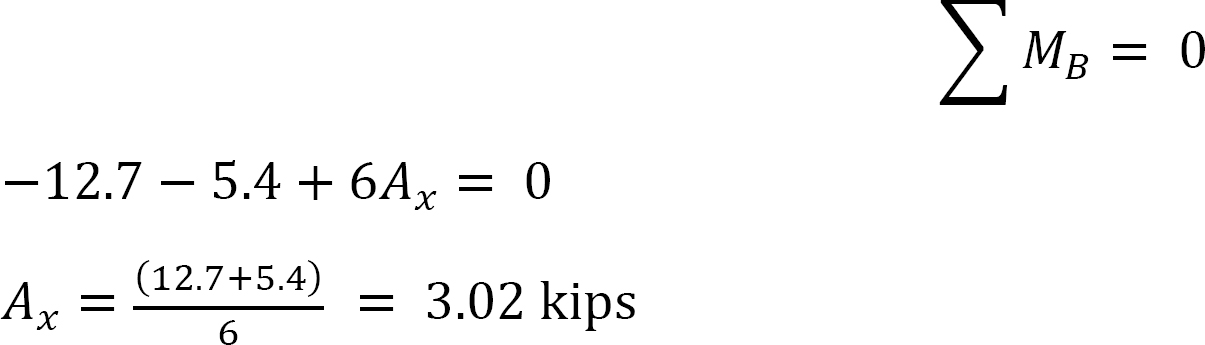
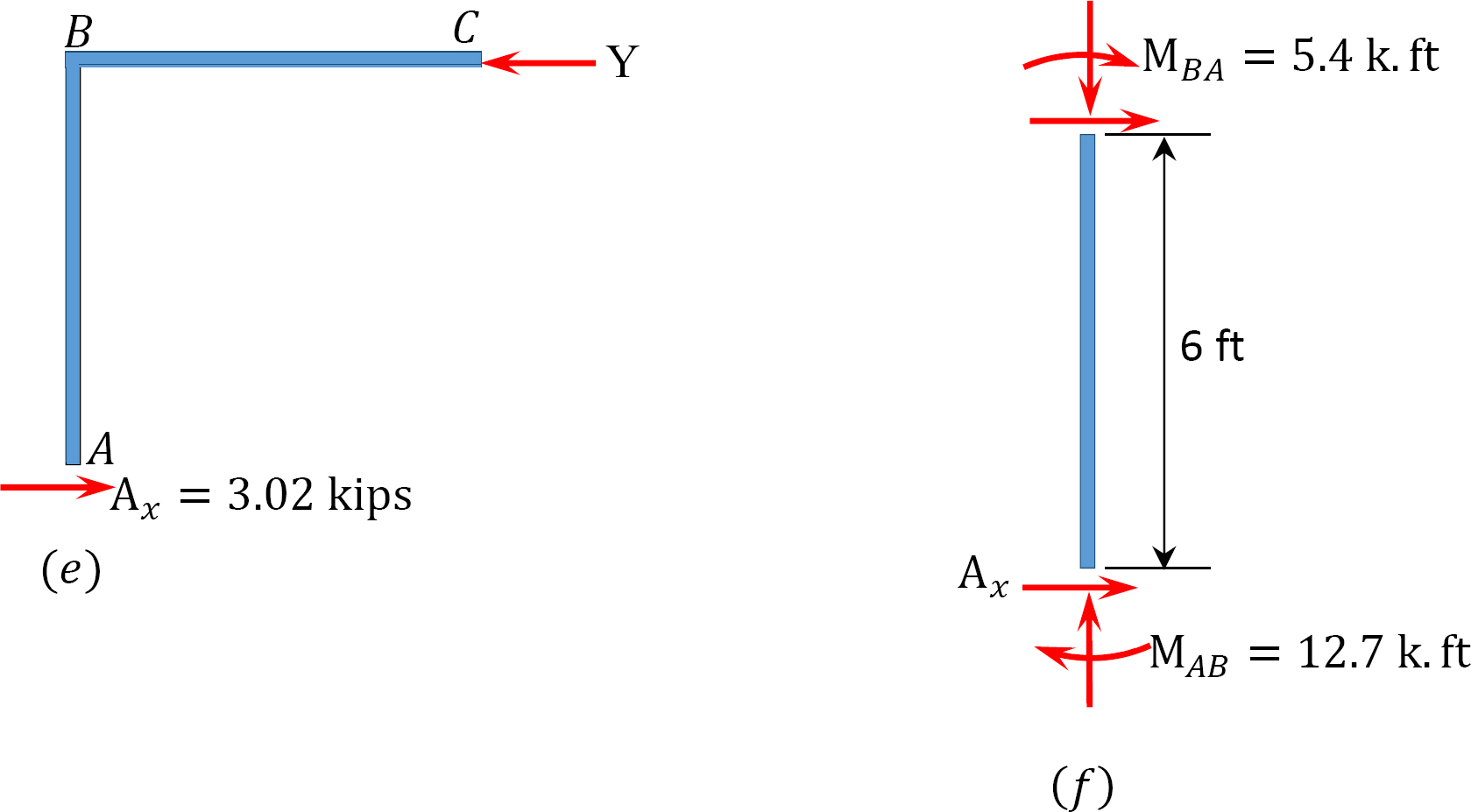
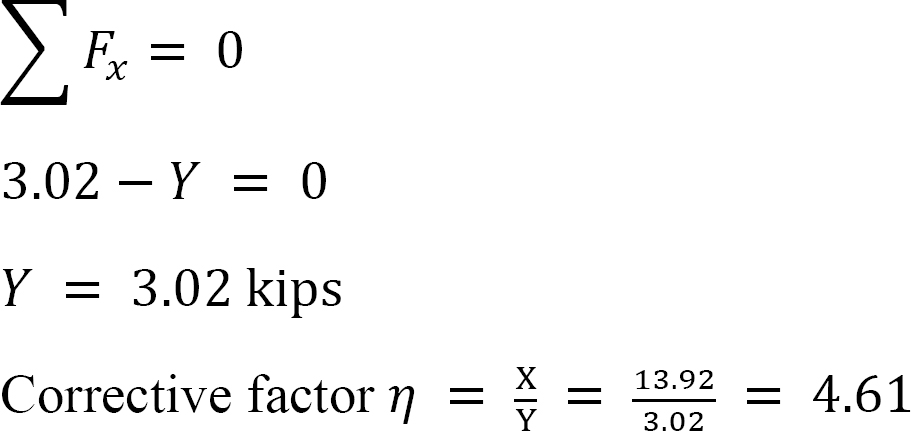
Derniers moments de fin.
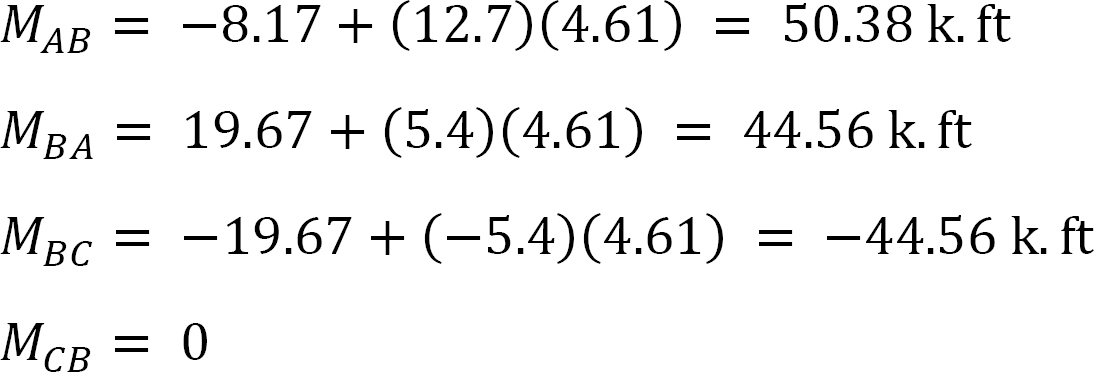
Exemple 12.7
Une trame de balancement est chargée comme le montre la figure 12.12a. À l’aide de la méthode de distribution des moments, déterminez les moments de fin des membres de la trame.
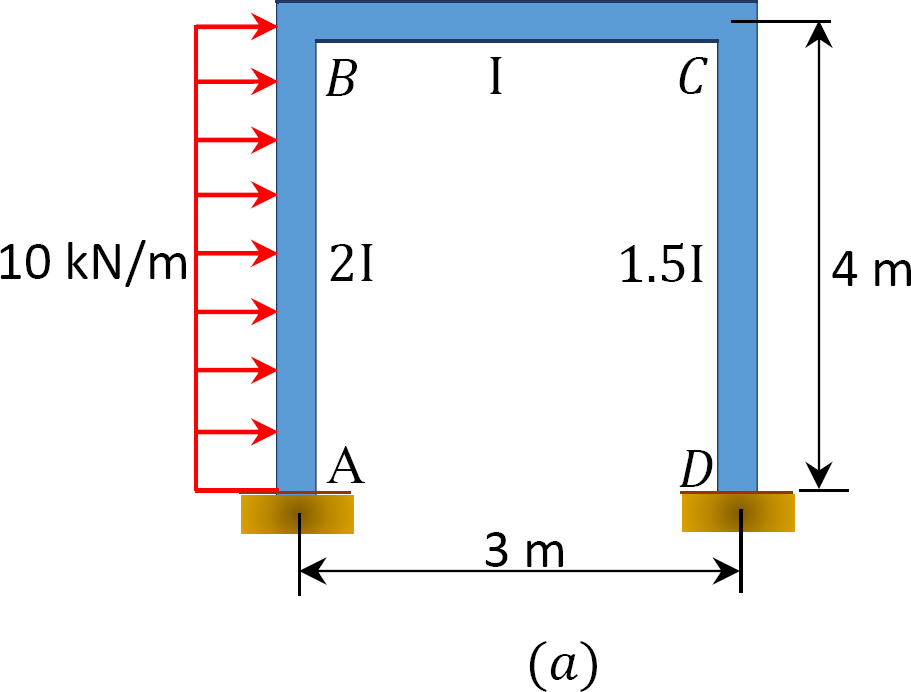
Fig. 12.12. Cadre de balancement chargé.
Solution
Moment de fin fixe.
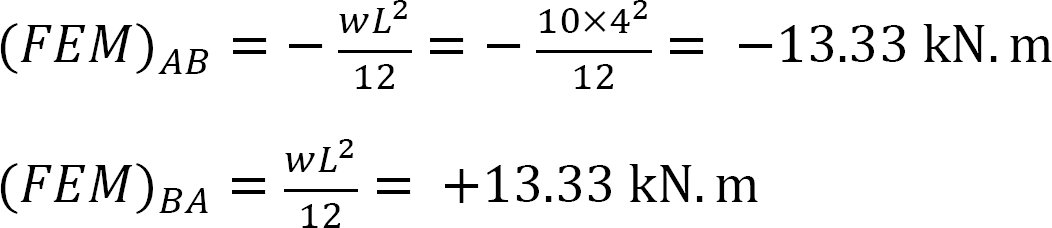
Facteur de rigidité.
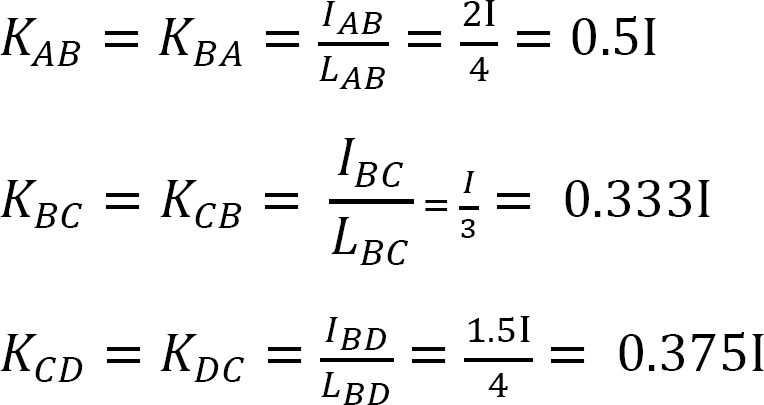
Facteur de distribution.

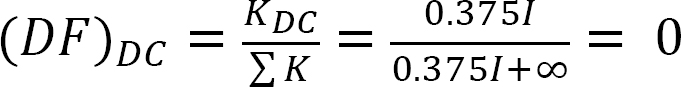
Analyse du cadre sans balancement latéral.
Tableau 12.8. Tableau de distribution (pas de cadre de balancement).
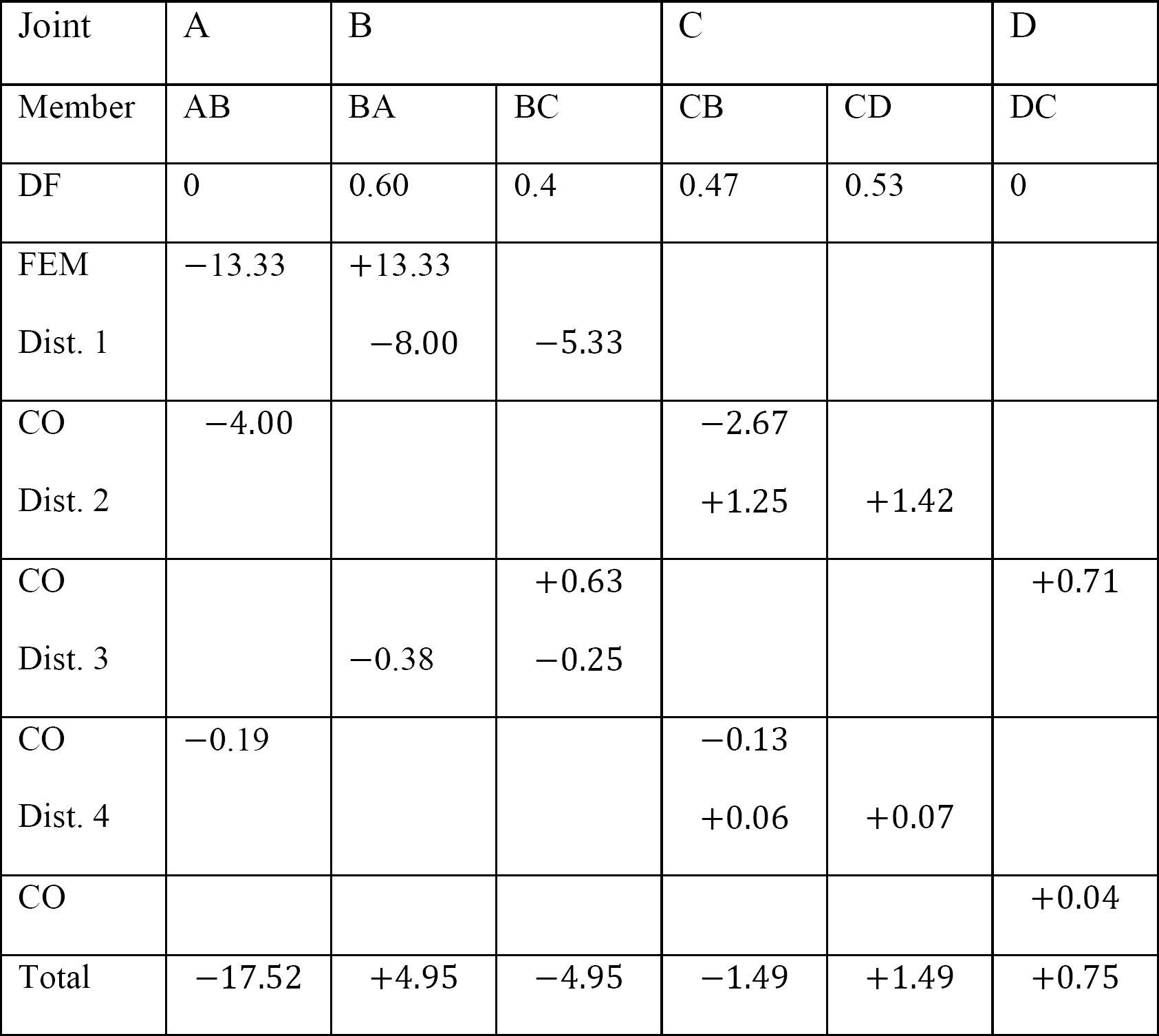
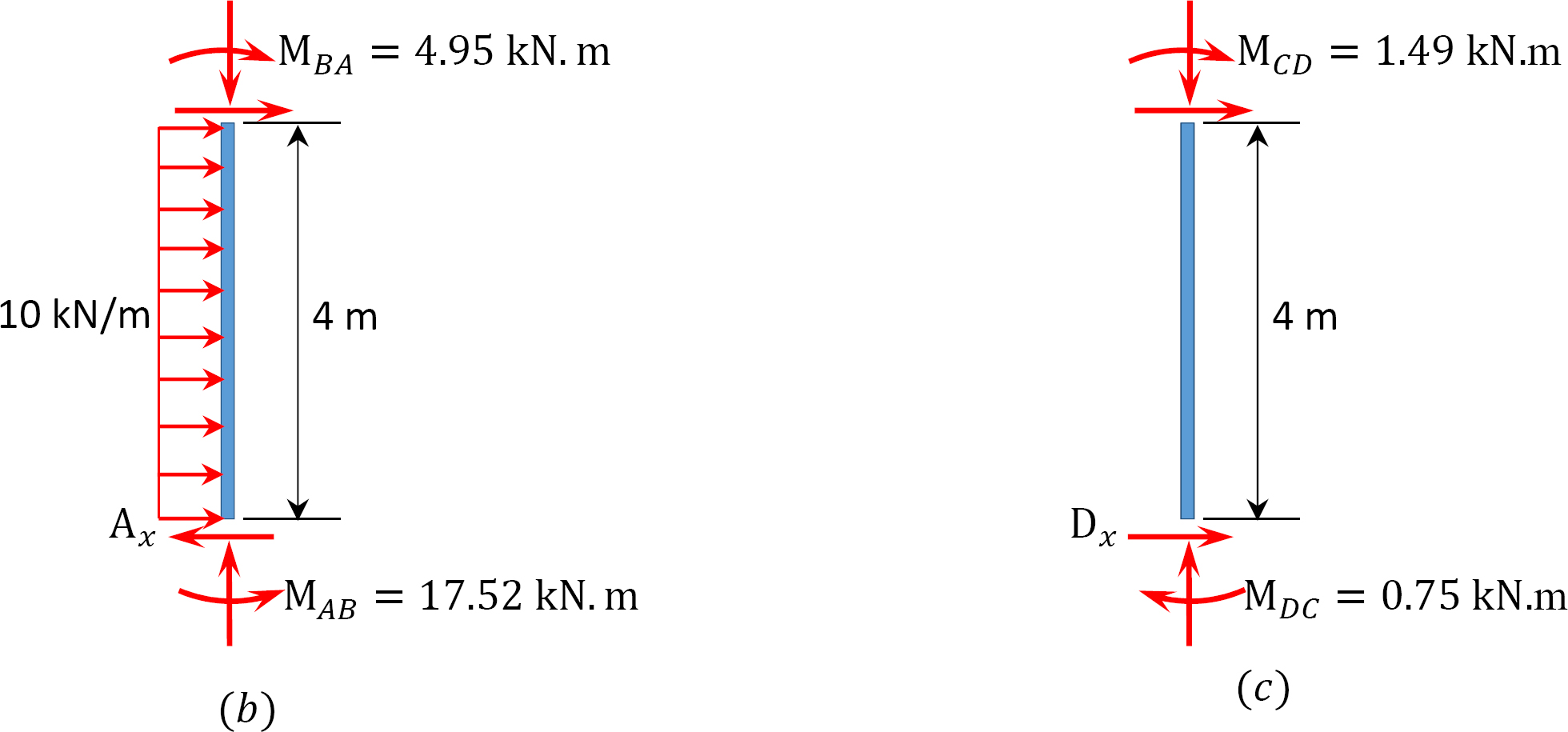
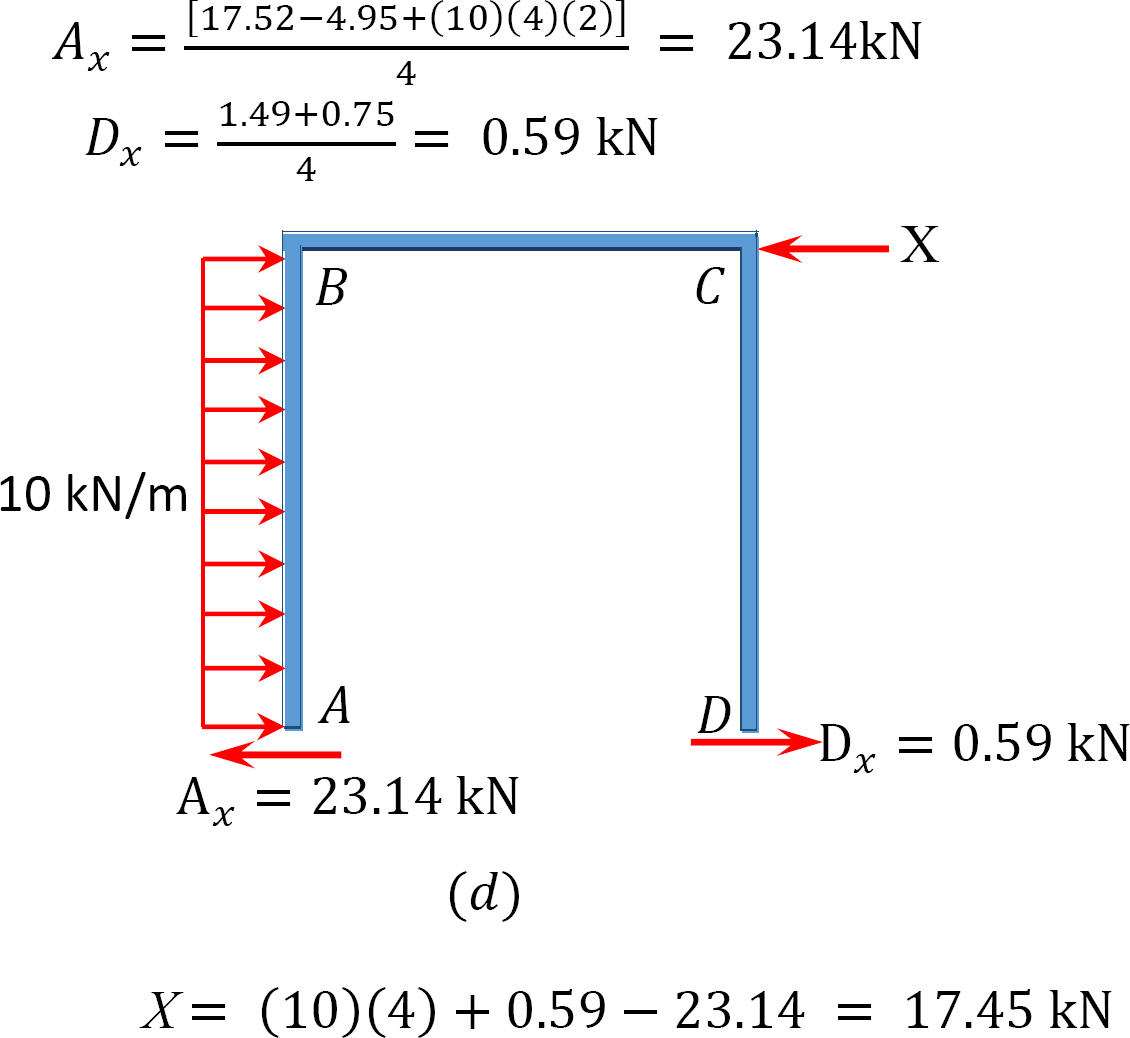
Tableau 12.9. Table de distribution (cadre de balancement).
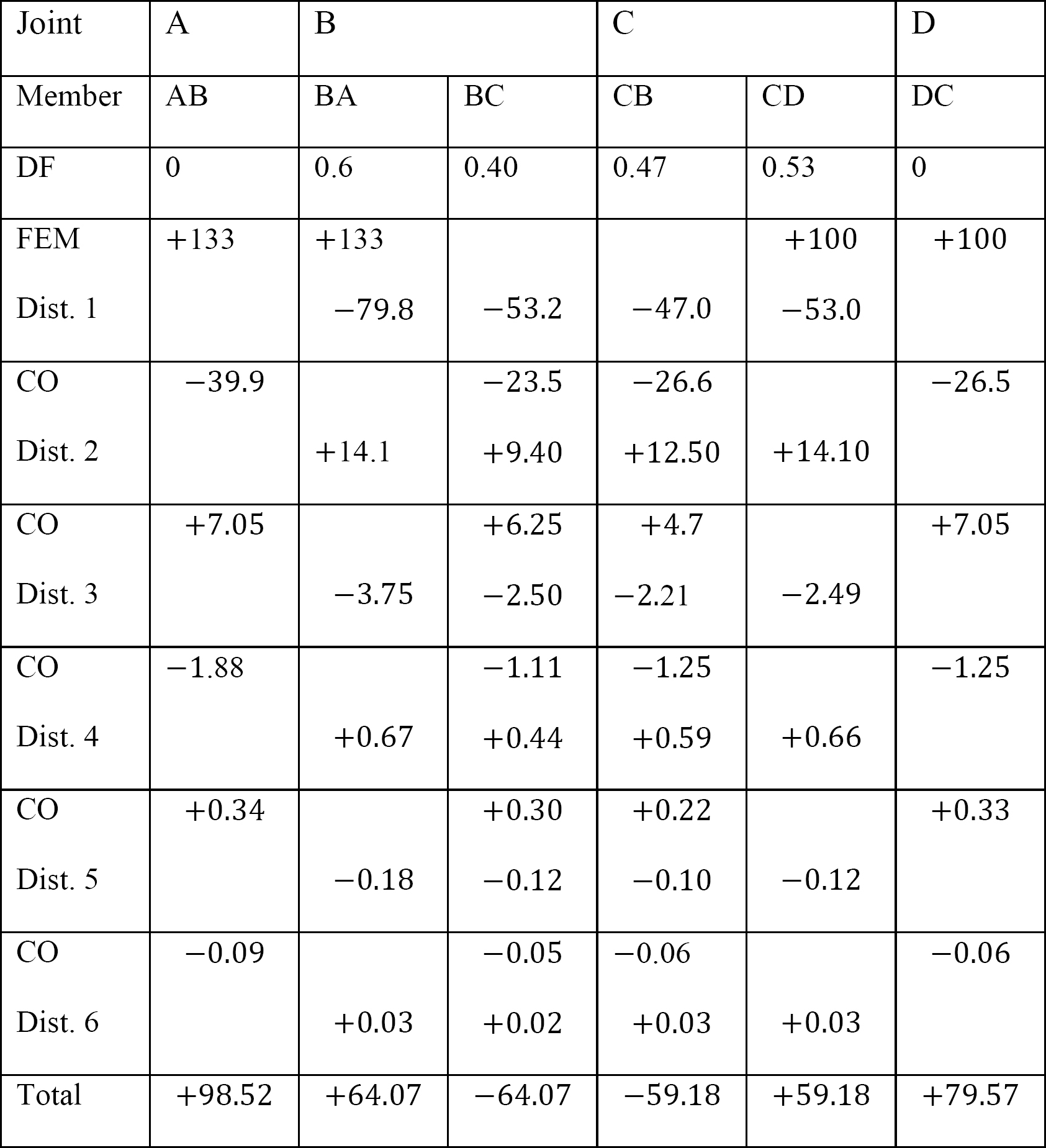
Analyse du cadre avec balancement latéral.
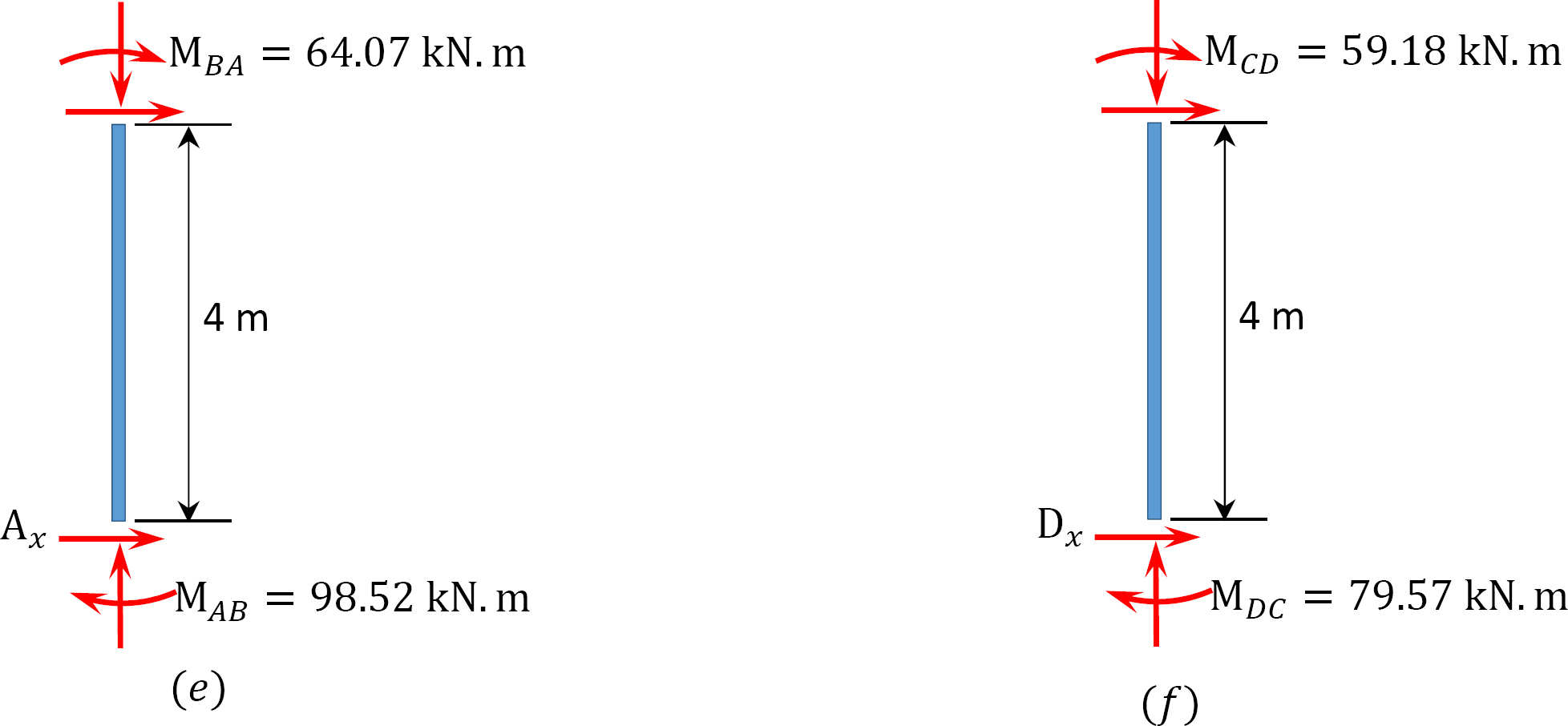

Moment de fin final.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Résumé du chapitre
Méthode de distribution des moments d’analyse des structures indéterminées: La méthode d’analyse de la distribution des moments est une méthode d’analyse approximative. Son degré de précision dépend du nombre d’itérations. Dans cette méthode, on suppose que tous les joints d’une structure sont temporairement verrouillés ou serrés et, par conséquent, sont empêchés d’une rotation possible. Des charges sont appliquées aux éléments et les moments développés aux extrémités des éléments en raison de la fixité sont déterminés. Les articulations de la structure sont ensuite déverrouillées successivement, et le moment de déséquilibre au niveau de chaque articulation est distribué aux organes se réunissant au niveau de cette articulation. Les moments de report aux extrémités des membres sont déterminés et le processus d’équilibrage se poursuit jusqu’au niveau de précision souhaité. Les moments de fin des membres sont déterminés en additionnant le moment de fin fixe, le moment distribué et le moment de report. Une fois que les moments de fin des membres sont déterminés, la structure devient déterminée.
Problèmes de pratique
12.1 Utilisez la méthode de distribution des moments pour calculer le moment de fin des éléments des poutres représentées sur la figure P12.1 à la figure P12.12 et tracez les diagrammes du moment de flexion et de la force de cisaillement. EI = constante.
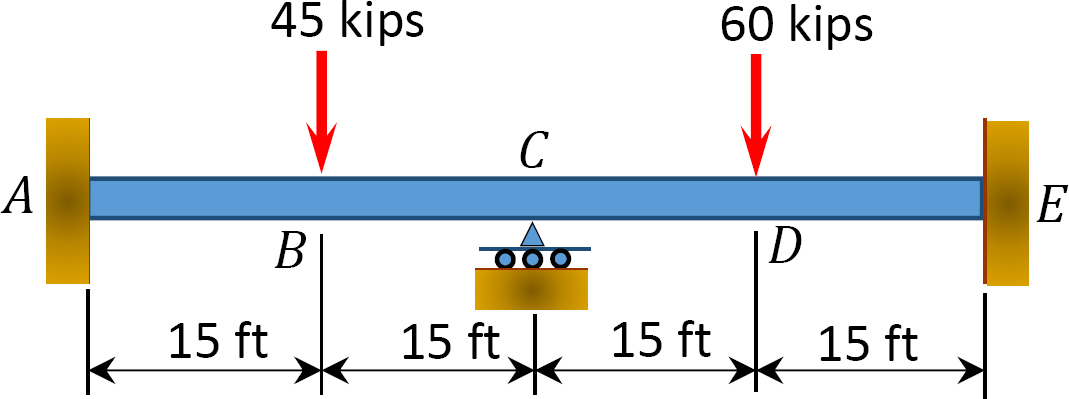
Fig. P12.1. Poutre.
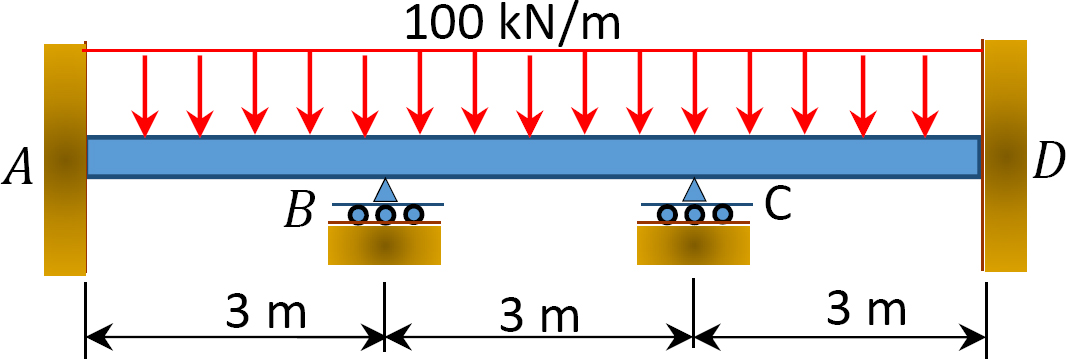
Fig. P12.2. Poutre.
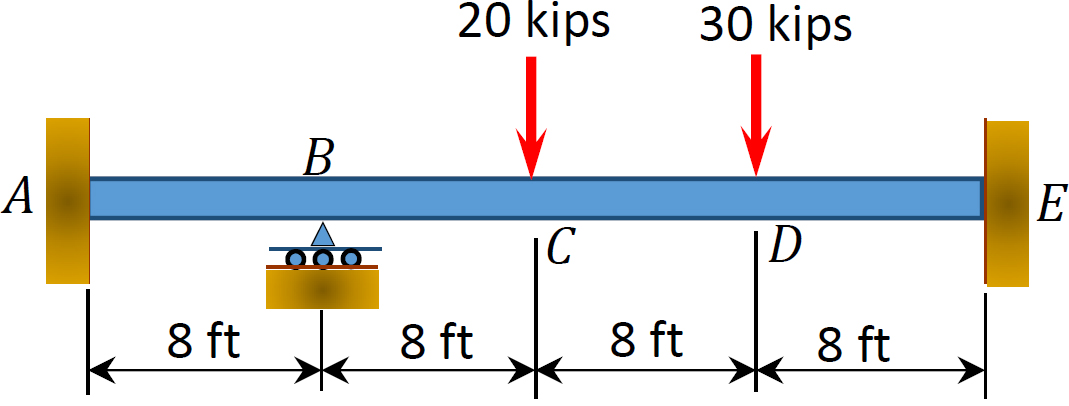
Fig. P12.3. Poutre.
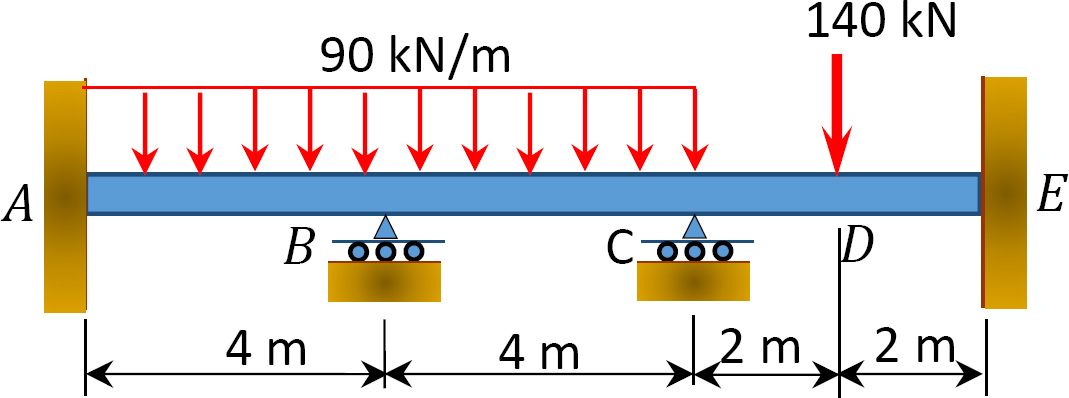
Fig. P12.4. Poutre.
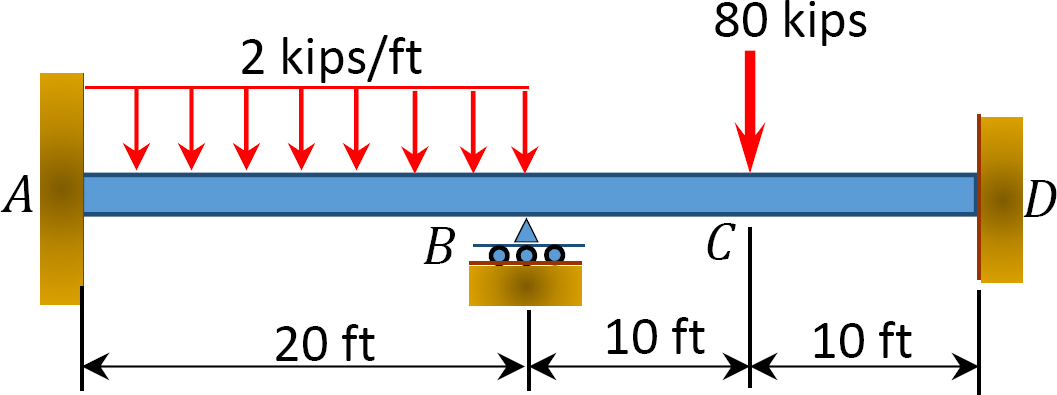
Fig. P12.5. Poutre.
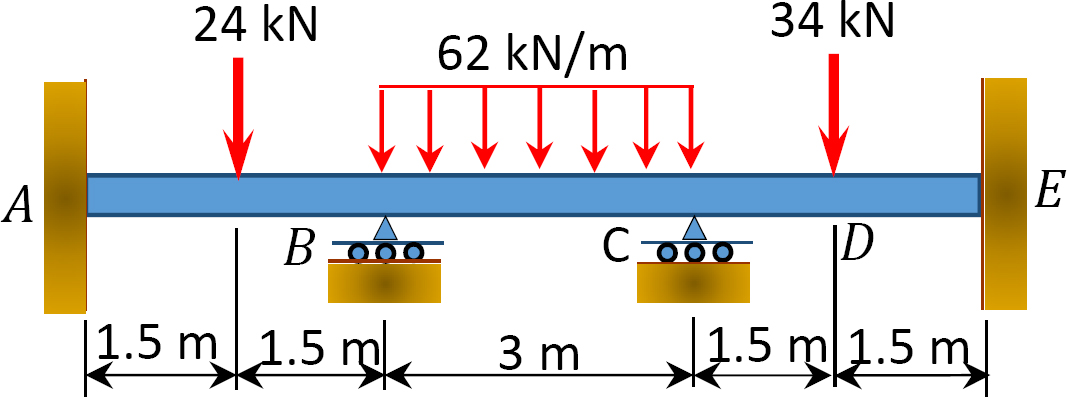
Fig. P12.6. Poutre.
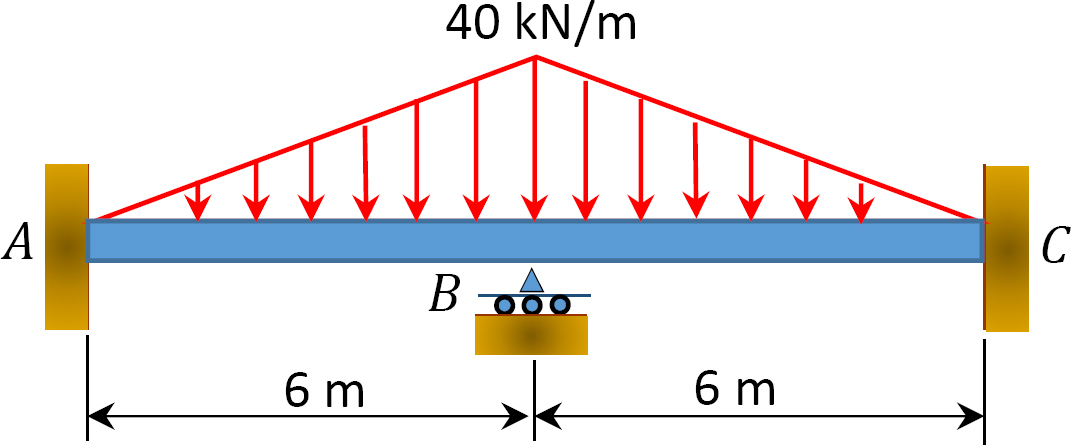
Fig. P12.7. Poutre.
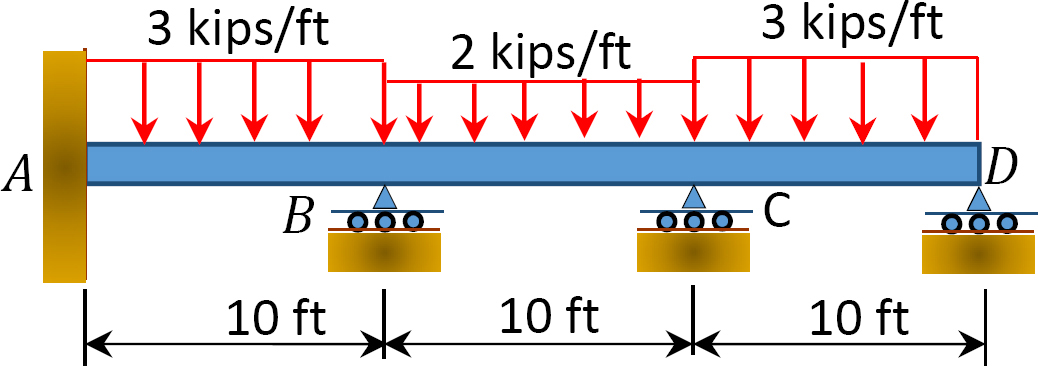
Fig. P12.8. Poutre.
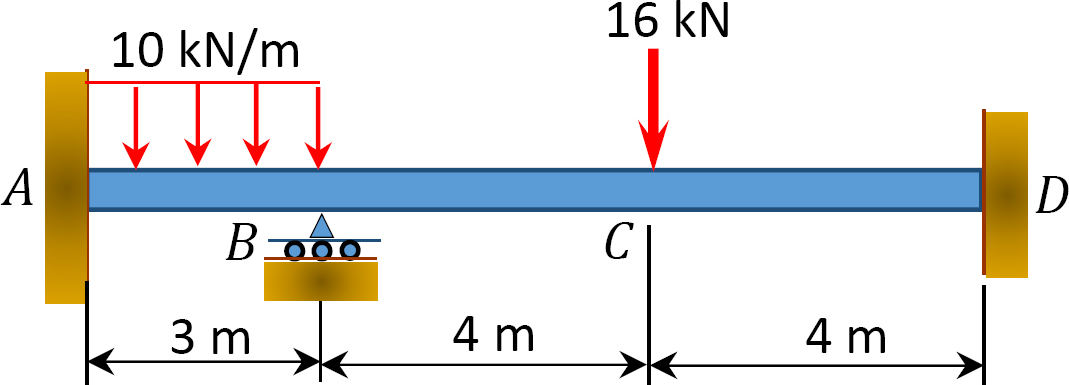
Fig. P12.9. Poutre.
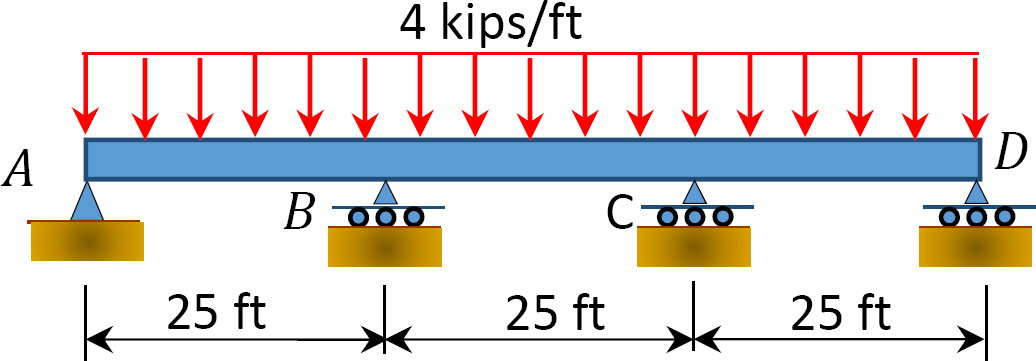
Fig. P12.10. Poutre.
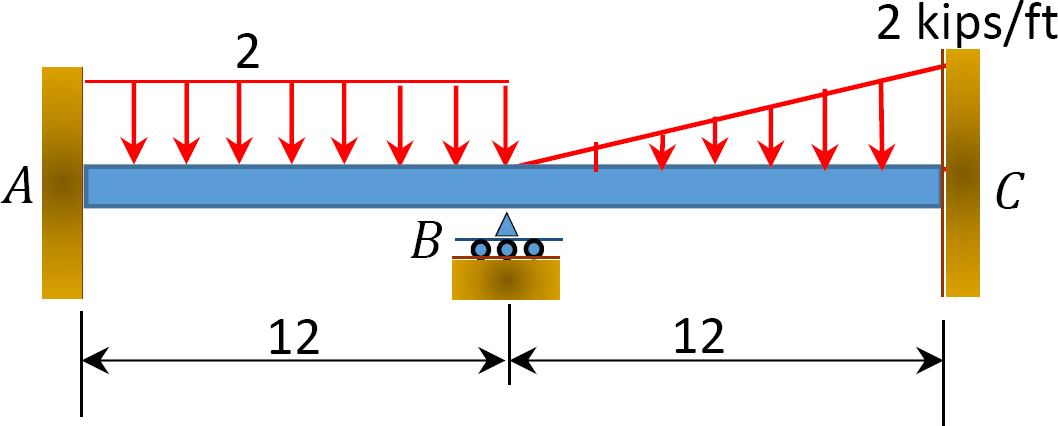
Fig. P12.11. Poutre.
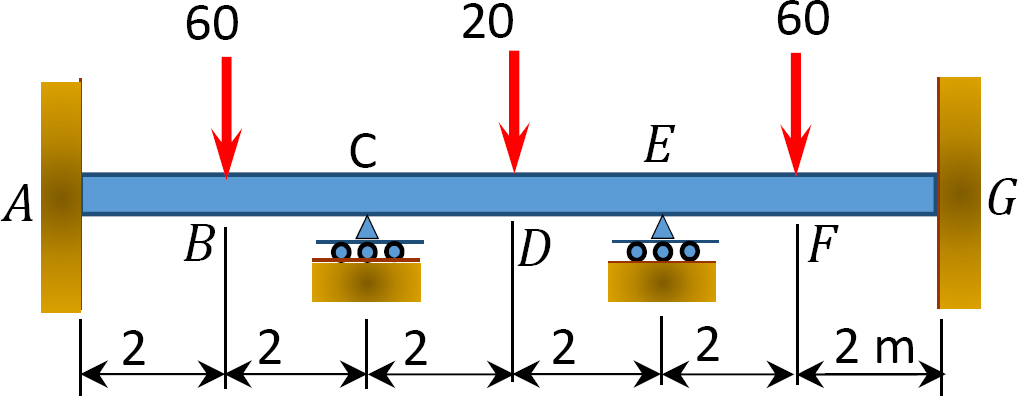
Fig. P12.12. Poutre.
12.2 Utilisez la méthode de distribution de moment pour calculer le moment de fin des éléments des trames représentées sur la figure P12.13 à la figure 12.20 et tracez les diagrammes de moment de flexion et de force de cisaillement. EI = constante.
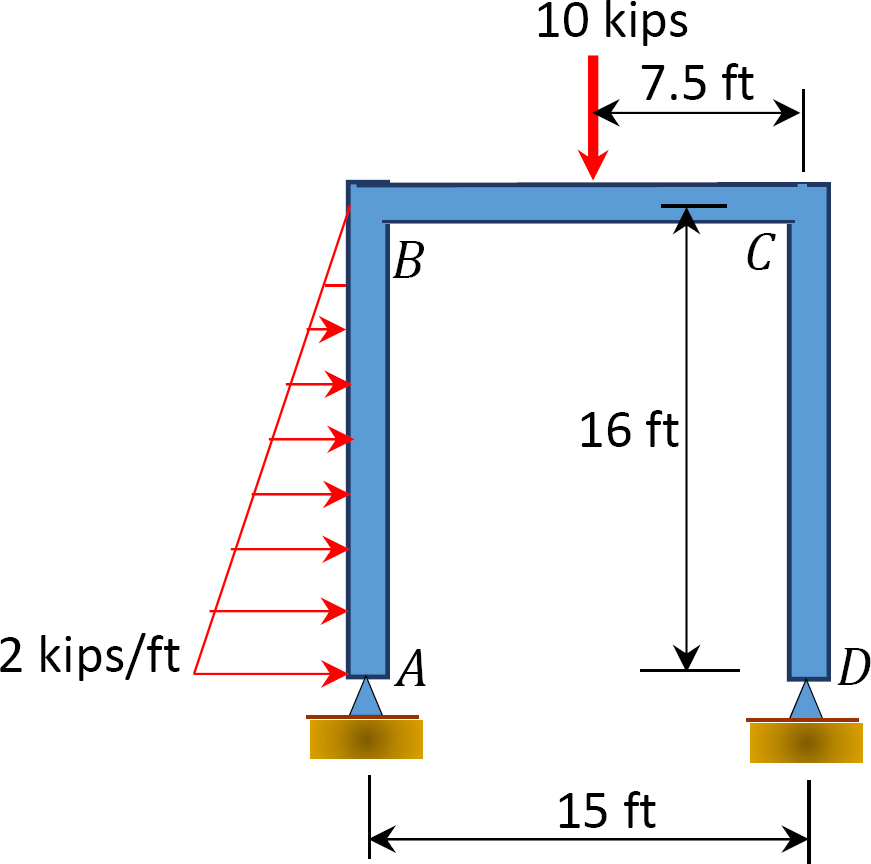
Fig. P12.13. Cadre.
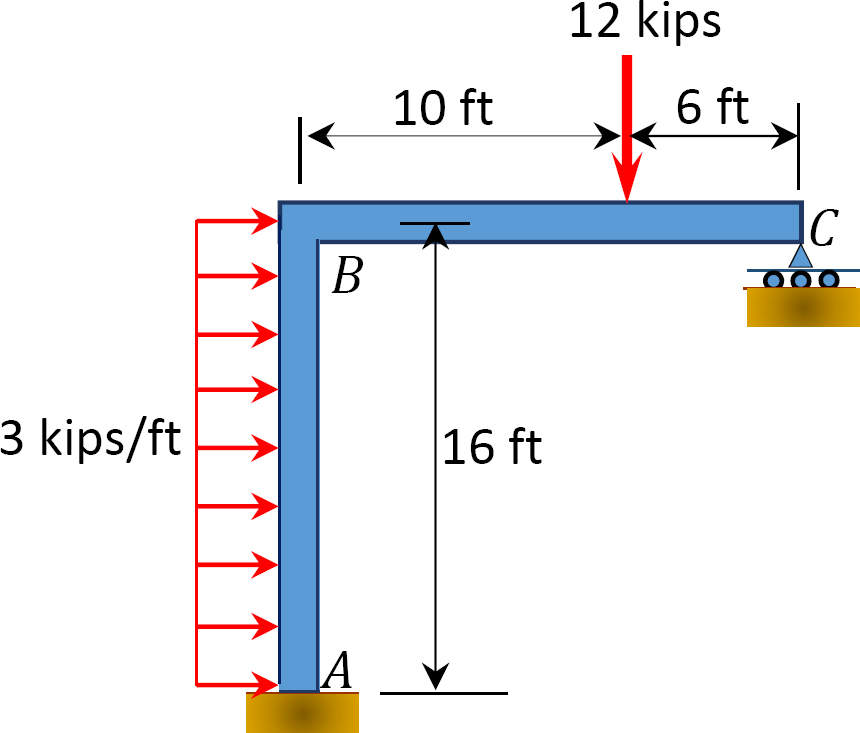
Fig. P12.14. Cadre.
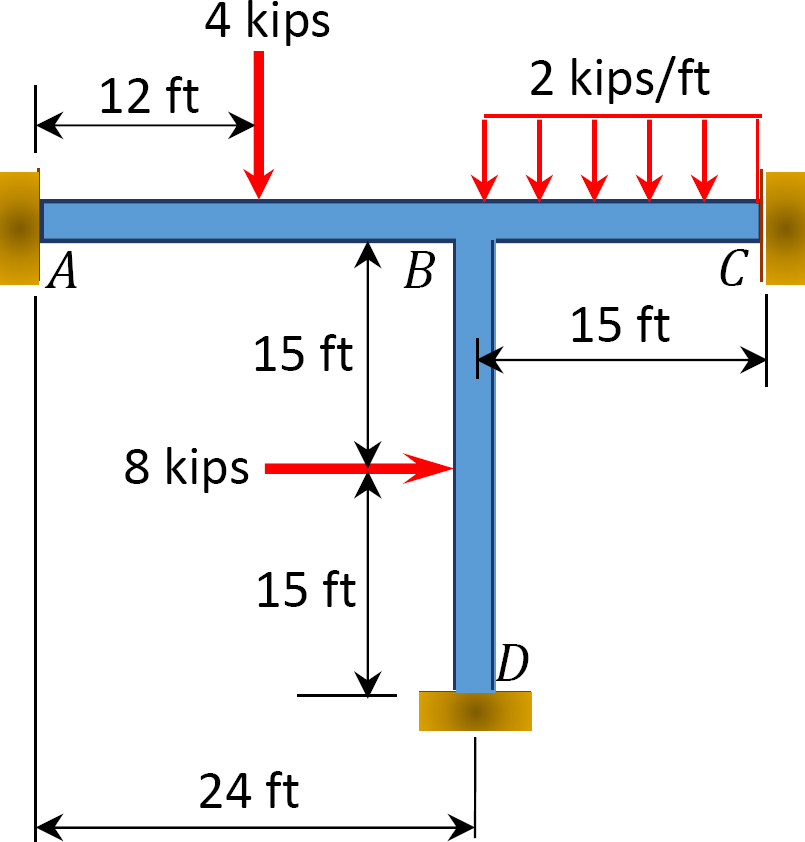
Fig. P12.15. Cadre.
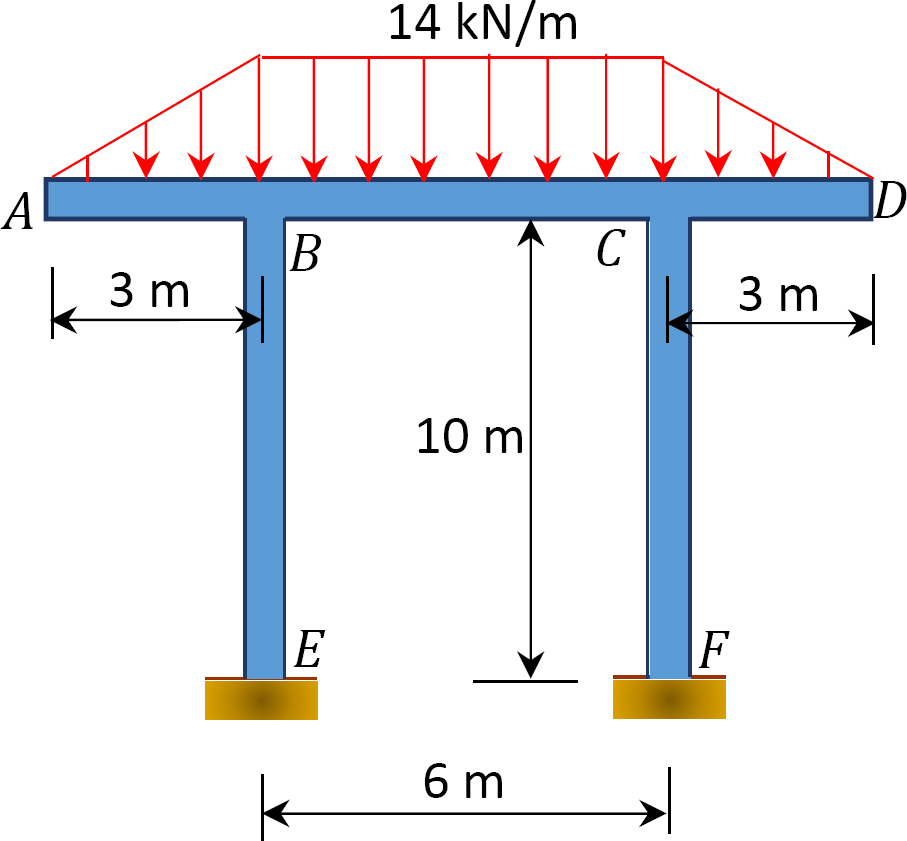
Fig. P12.16. Frame.
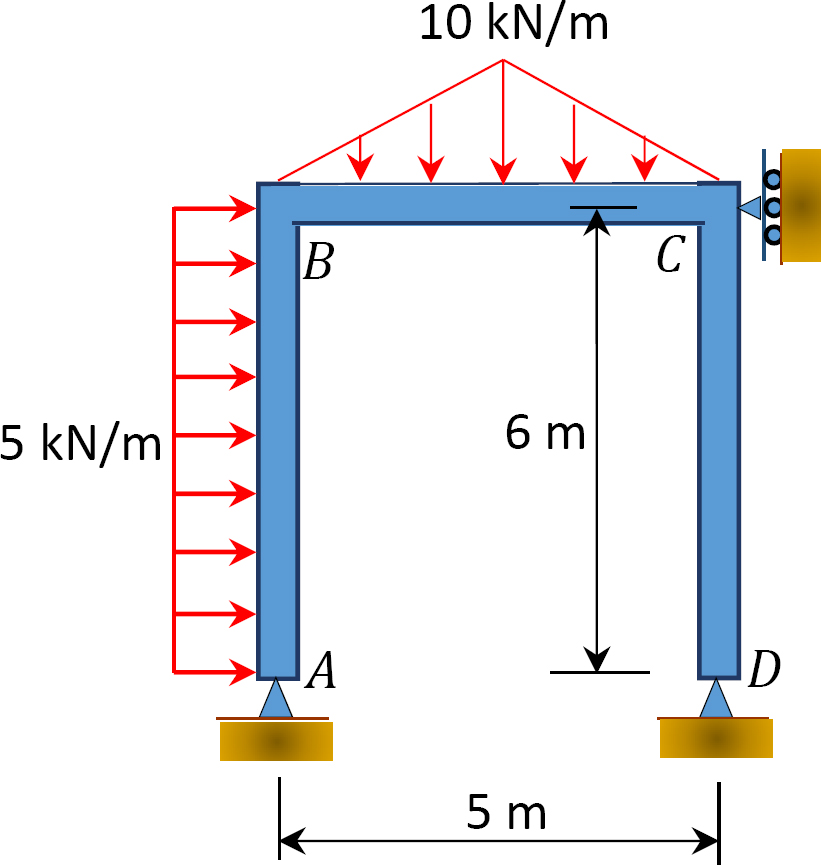
Fig. P12.17. Frame.
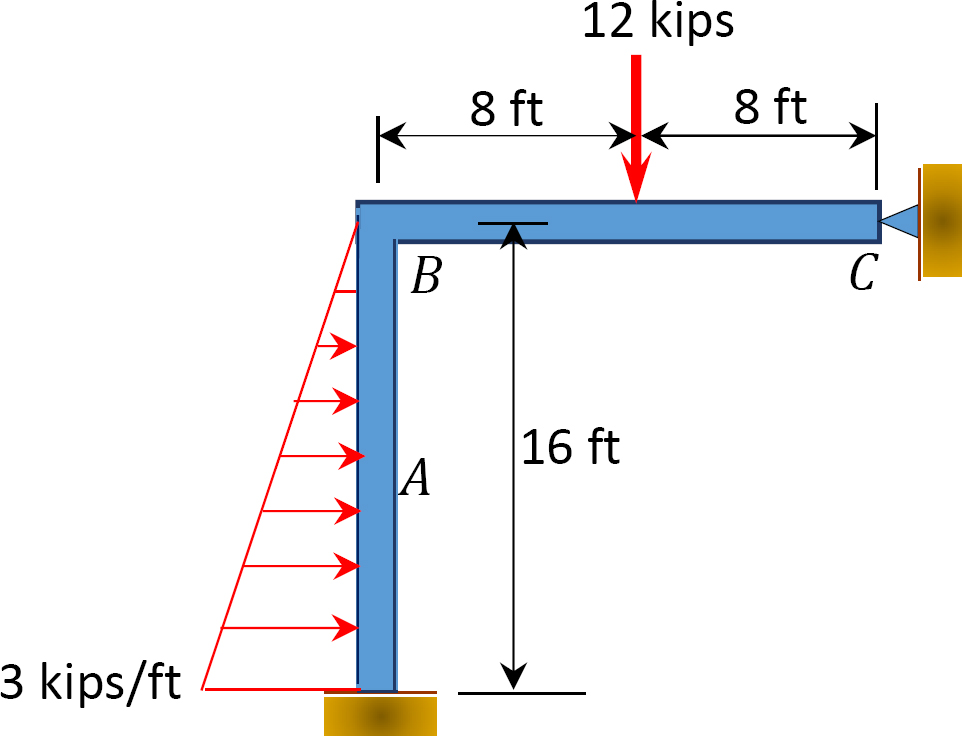
Fig. P12.18. Frame.
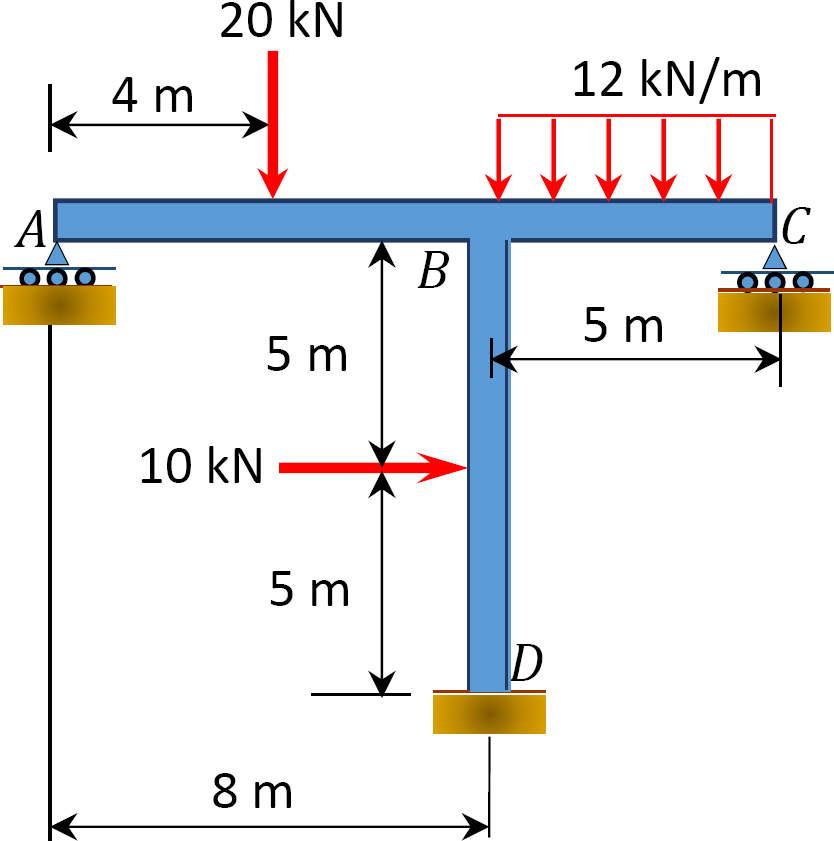
Fig. P12.19. Frame.
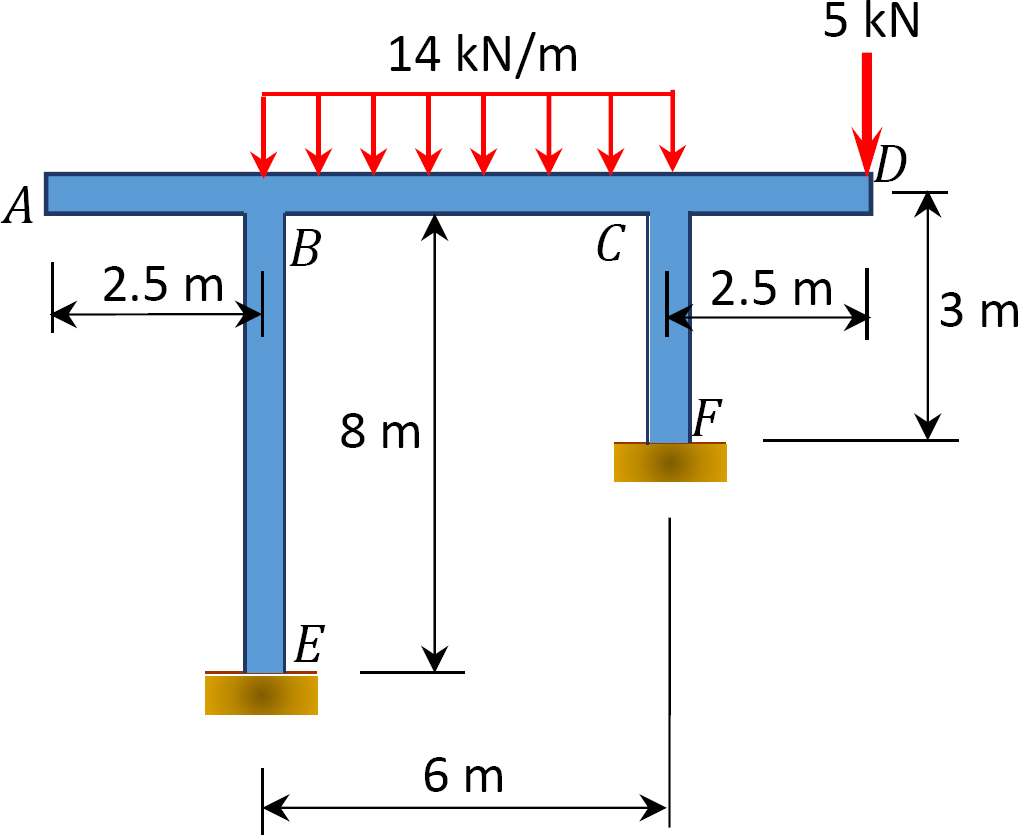
Fig. P12.20. Frame.