Kapitel 12
Momentfördelningsmetod för analys av strukturer
12.1 grundläggande begrepp
momentfördelningsmetoden för analys av balkar och ramar utvecklades av Hardy Cross och presenterades formellt 1930. Även om denna metod är en deformationsmetod som lutningsavböjningsmetoden, är den en ungefärlig metod och kräver således inte att lösa samtidiga ekvationer, vilket var fallet med den senare metoden. Graden av noggrannhet för de resultat som erhållits med metoden för momentfördelning beror på antalet successiva approximationer eller iterationsprocessen.
för att illustrera begreppet metoden för momentfördelning, överväga ramen som visas i Figur 12.1. Ramens medlemmar är prismatiska och antas inte deformeras axiellt eller översättas i förhållande till varandra. Fogar ACD av ramen är fixerade, medan Fog B kan rotera något på grund av den applicerade belastningen. Först, innan man utför momentfördelning mellan medlemmar, antas alla fogar vara tillfälligt låsta med en klämma.
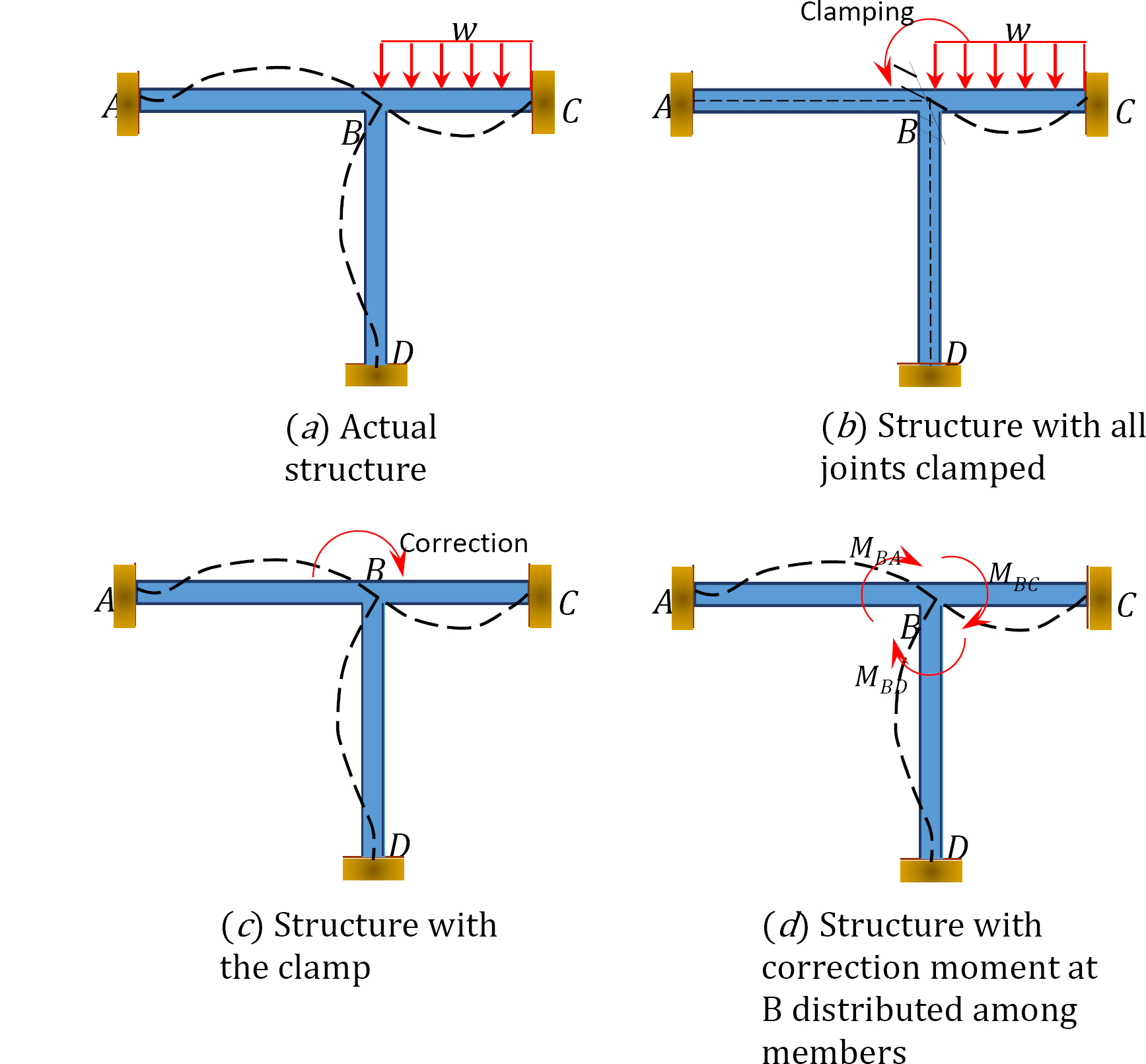
Fig. 12.1. Ram.
12.2 Teckenkonventionen
teckenkonventionen för momentfördelningsmetoden liknar den som fastställts för lutningsavböjningsmetoden; det vill säga ögonblicket i slutet av en medlem anses vara positivt om det tenderar att vrida medlemmens ände medurs och negativt om det tenderar att vrida det moturs.
12.3 definitioner
obalanserade stunder: denna analysmetod förutsätter att lederna i en struktur initialt kläms fast eller låses och sedan släpps successivt. När en fog har släppts sker en rotation, eftersom summan av de fasta slutmomenten för medlemmarna som möts vid den leden inte är noll. Värdet av summan av de erhållna slutmomenten är det obalanserade ögonblicket vid den leden.
Överföringsmoment: de distribuerade ögonblicken i medlemmarnas ändar som möts vid en gemensam orsak stunder i de andra ändarna, som antas vara fixade. Dessa inducerade ögonblick i andra ändar kallas överföringsmoment.
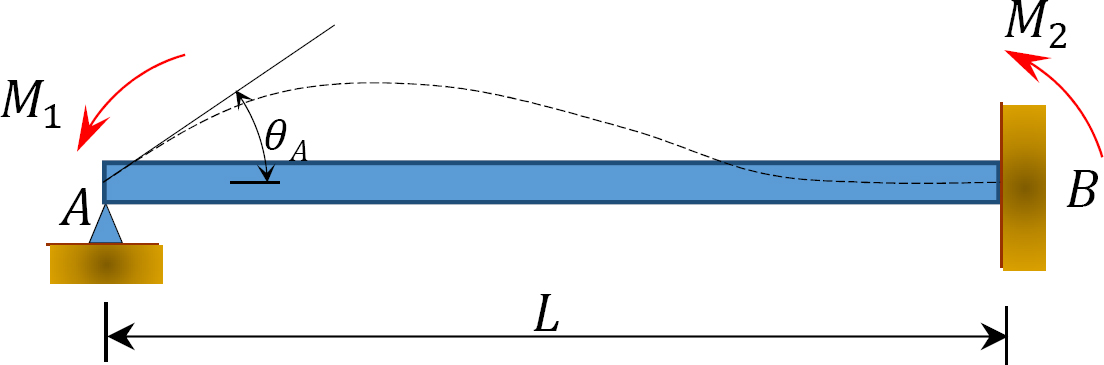
Fig. 12.2. Lossad prismatisk stråle.
Tänk på en lossad prismatisk stråle fixerad vid slutet B, som visas i Figur 12.2. Om ett ögonblick M1 appliceras på strålens vänstra ände kan lutningsavböjningsekvationerna för båda ändarna av strålen skrivas enligt följande:


att ersätta 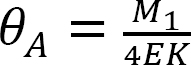 från ekvation 12.1 till ekvation 12.2 föreslår följande:
från ekvation 12.1 till ekvation 12.2 föreslår följande:

ekvation 12.3 antyder att det ögonblick som överförs till den fasta änden av en stråle på grund av ett ögonblick som appliceras i den andra änden är lika med hälften av det applicerade ögonblicket.
överföringsfaktor: förhållandet mellan det inducerade ögonblicket och det applicerade ögonblicket kallas överföringsfaktorn. För strålen som visas i Figur 12.2 är överföringsfaktorn följande:

distribuerad faktor (DF): Den distribuerade faktorn är en faktor som används för att bestämma andelen av det obalanserade ögonblicket som bärs av var och en av medlemmarna som möts vid en gemensam. För medlemmarnas möte vid gemensam O i ramen som visas i Figur 12.3 beräknas deras fördelningsfaktorer enligt följande:
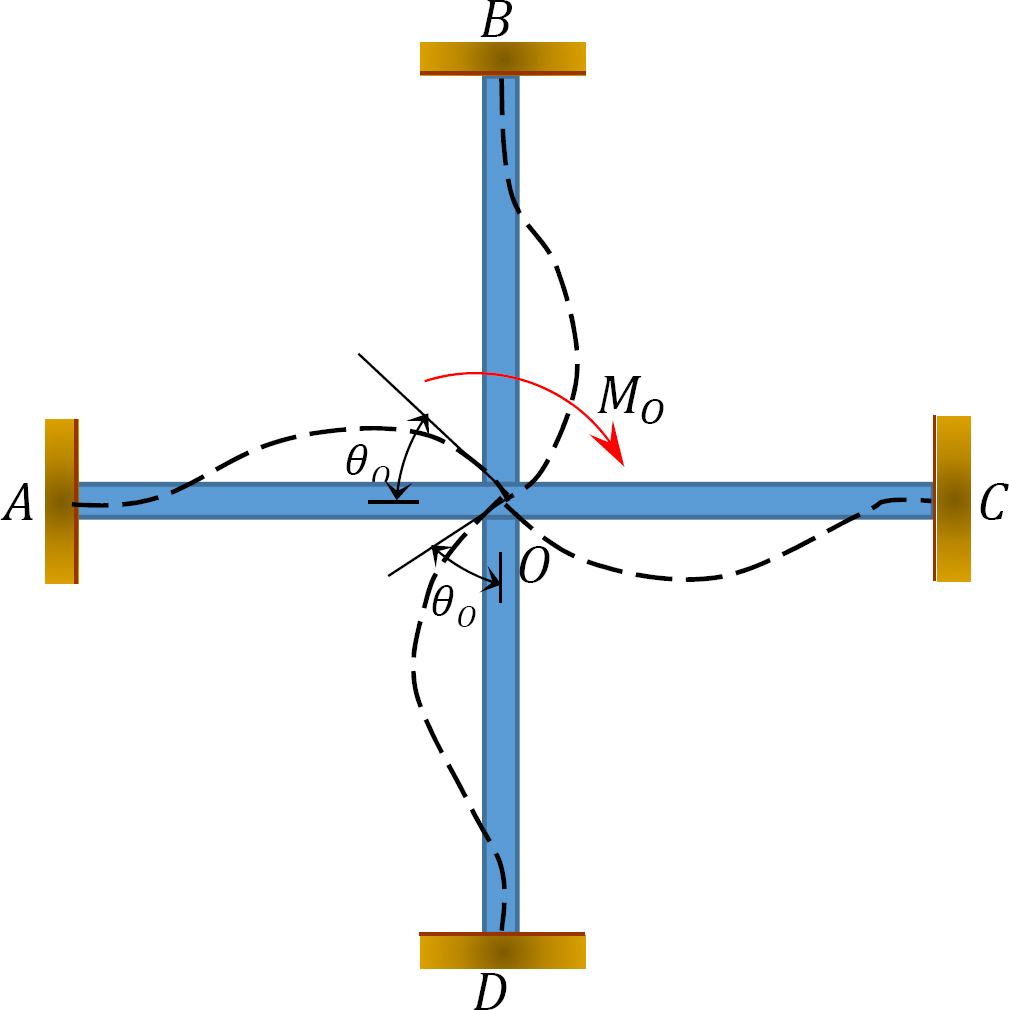
Fig. 12.3. Ram.

distribuerade ögonblick: vid frisläppandet av den imaginära klämman vid en fog får det obalanserade ögonblicket vid den fogen att rotera. Rotationen vrider slutet av medlemmarnas möte vid fogen, vilket resulterar i utvecklingen av motståndsmoment. Dessa motståndsmoment kallas distribuerade ögonblick. De distribuerade ögonblicken för ramens medlemmar som visas i Figur 12.3 beräknas enligt följande:
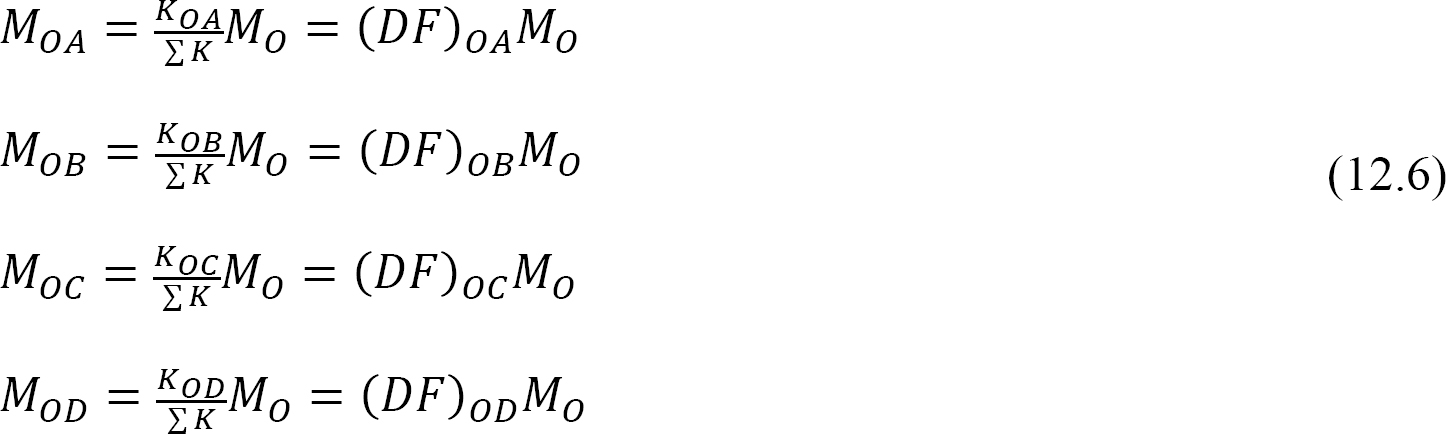
12.4 modifiering av Medlemsstyvhet
ibland kan iterationsprocessen i momentfördelningsmetoden minskas avsevärt genom att justera böjstyvheten hos vissa medlemmar i den obestämda strukturen. Detta avsnitt betraktar påverkan av ett fast – och ett stiftstöd på böjstyvheten hos en obestämd stråle.
fall 1: En Balk gångjärn i ena änden och fixerad vid den andra
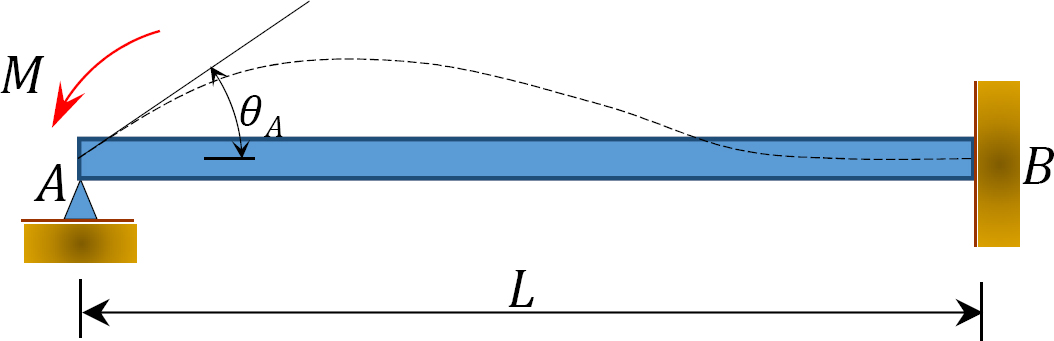
Fig. 12.4. Balk
Tänk på en balk som är ledad i slutet A och fixerad i slutet B, som visas i Figur 12.4. Applicering av ett ögonblick m roterar gångjärnsänden med en mängd XVIII. Skriva lutningsavböjningsekvationen för medlemmens slut A och notera att 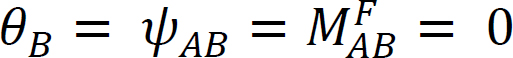 föreslår följande:
föreslår följande:
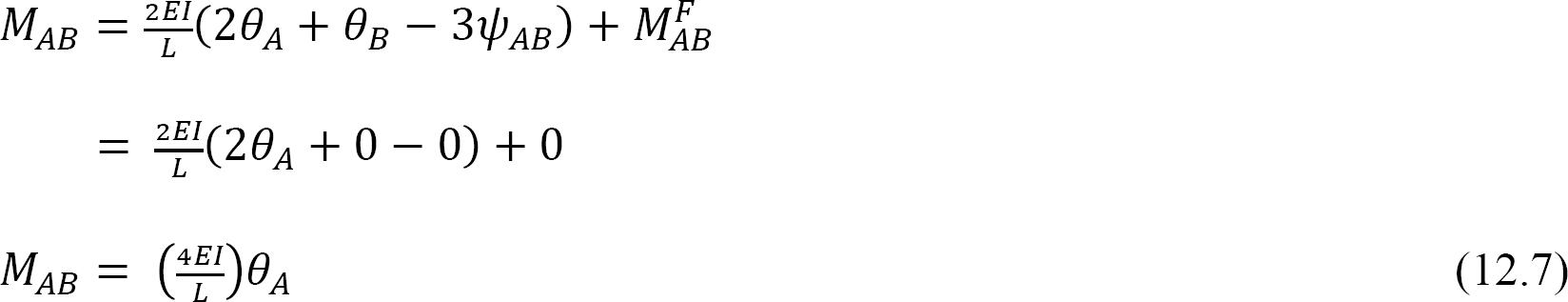
per definition är böjstyvheten hos ett strukturellt element det ögonblick som måste tillämpas på en ände av elementet för att orsaka en enhetsrotation av den änden. Följande uttryck för böjstyvheten för elementet med en fast bortre ände uttrycks på följande sätt när man ersätter bisexa = 1 i ekvation 12.7:

per definition bestäms den relativa böjstyvheten hos en medlem genom att dividera böjstyvheten hos medlemmen med 4E. dividera ekvationen 12,8 med 4E föreslår följande uttryck för relativ styvhet för det fall som behandlas:

Fall 2: en Balk gångjärn i båda ändarna
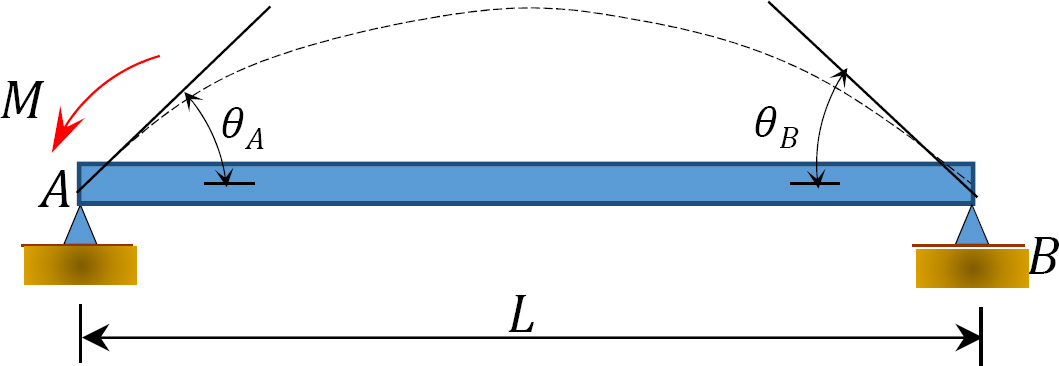
Fig. 12.5. Helt enkelt stöds beam.
applicera ett ögonblick M i slutet A av den helt enkelt stödda strålen som visas i Figur 12.5 roterar strålen med en vinkel bisexa vid den gångjärnsänden. Använda den modifierade lutnings-avböjningsekvationen härledd i avsnitt 11.4 i kapitel 11 och notera att 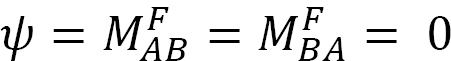 föreslår följande uttryck för det ögonblick vid den gångjärnsände där lasten appliceras:
föreslår följande uttryck för det ögonblick vid den gångjärnsände där lasten appliceras:
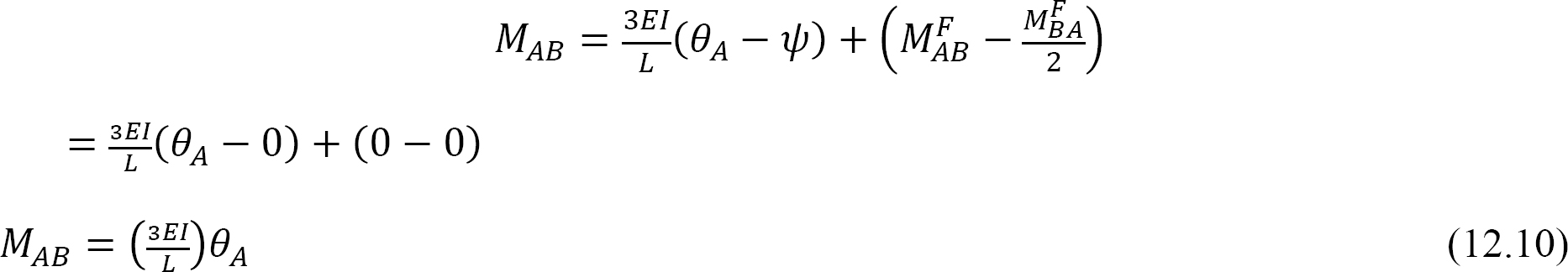
genom att ersätta 1 i ekvationen 12.10 föreslår man följande uttryck för böjstyvheten för en medlem med en gångjärns bortre ände:

den relativa styvheten för en medlem med en gångjärns bortre ände erhålles genom att dividera ekvation 12.11 med 4E, enligt följande:

jämförelse av ekvationerna 12.12 och 12.9 antyder att en medlem med en gångjärns bortre ände är tre fjärdedelar så styv som en medlem med samma geometri men fixerad vid den bortre änden. Detta etablerade faktum kan väsentligt minska antalet iterationer vid analys av balkar eller ramar med en gångjärns ände med hjälp av metoden för momentfördelning. I sådana fall justeras strålens relativa styvhet vid den närmaste änden först Enligt ekvation 12.12, och dess fördelningsfaktor beräknas med den justerade styvheten. Under balanseringsoperationen kommer den närmaste änden att balanseras bara en gång utan ytterligare överföring av ögonblick från eller till dess slut.
12.5 analys av obestämda strålar
förfarandet för analys av obestämda strålar med metoden för momentfördelning sammanfattas kortfattat enligt följande:
förfarande för analys av obestämda strålar med Momentfördelningsmetoden
•beräkna de fasta momenten för medlemmar, förutsatt att lederna är fastklämda mot rotation.
•beräkna fördelningsfaktorn för var och en av de medlemmar som är anslutna vid leden
•beräkna det obalanserade ögonblicket vid varje led och fördela detsamma till ändarna av medlemmar som är anslutna vid den leden.
•Rita frikroppsdiagrammet för varje spännvidd i den givna strålen, som visar belastningarna och ögonblicken vid lederna som erhållits med momentfördelningsmetoden.
•Bestäm stödreaktionerna för varje spännvidd.
•beräkna och konstruera skjuvkraften och böjmomentsdiagrammen för varje spännvidd.
exempel 12.1
med hjälp av momentfördelningsmetoden bestämmer du slutmomenten och reaktionerna vid balkens stöd som visas i Figur 12.6 a. Rita skjuvkraften och böjmomentdiagrammen. EI = konstant.
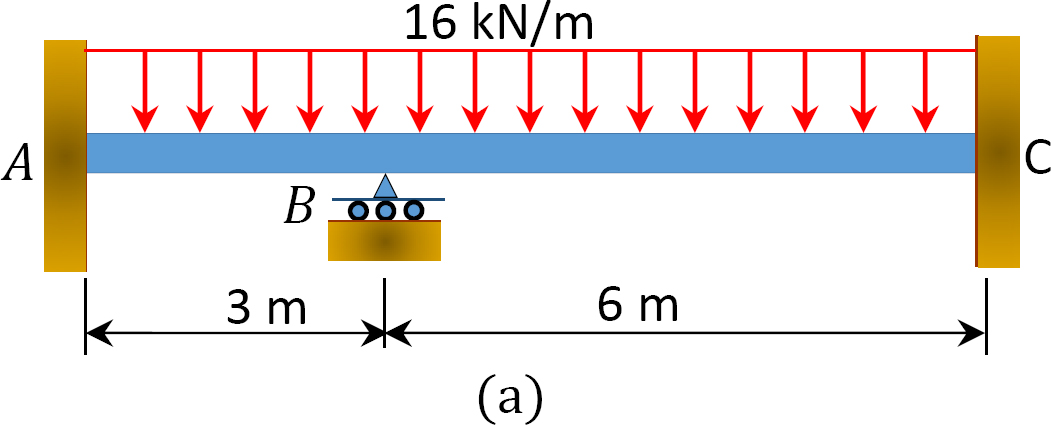
Fig. 12.6. Balk.
lösning
fast slutmoment.
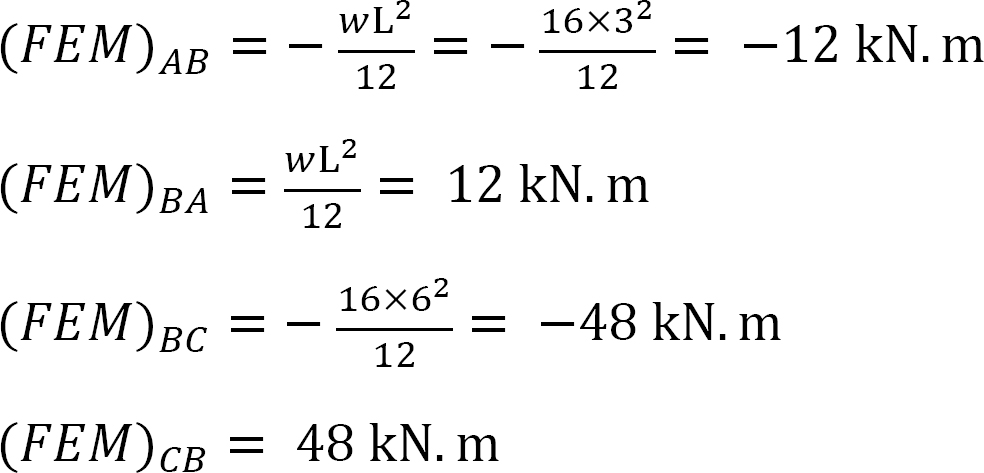
Styvhetsfaktor.
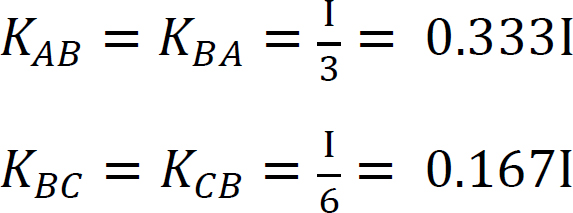
Fördelningsfaktor.
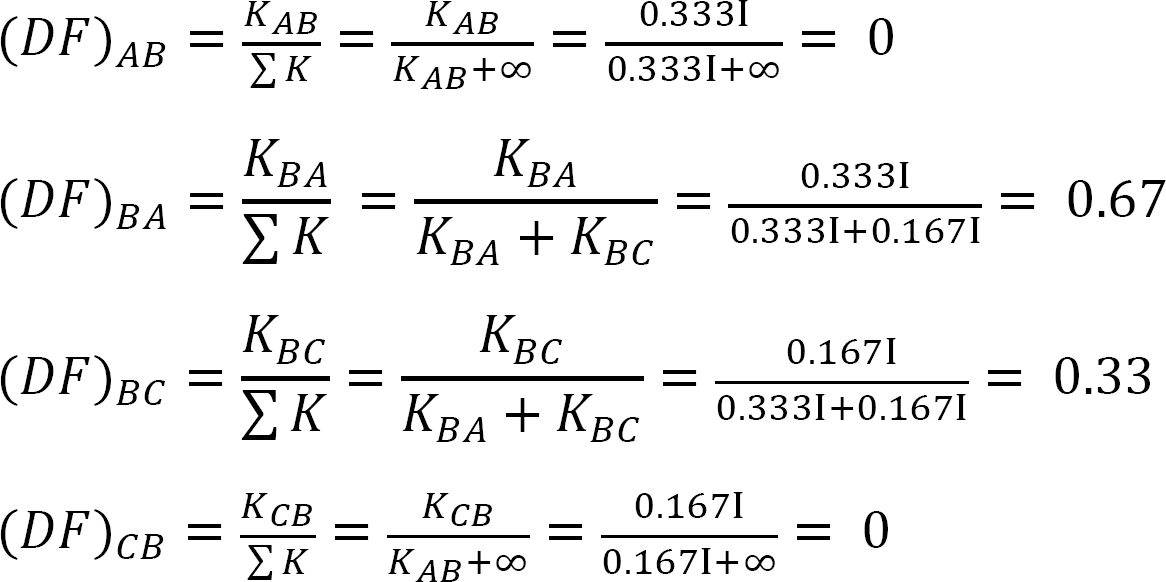
tabell 12.1. Distributionstabell.
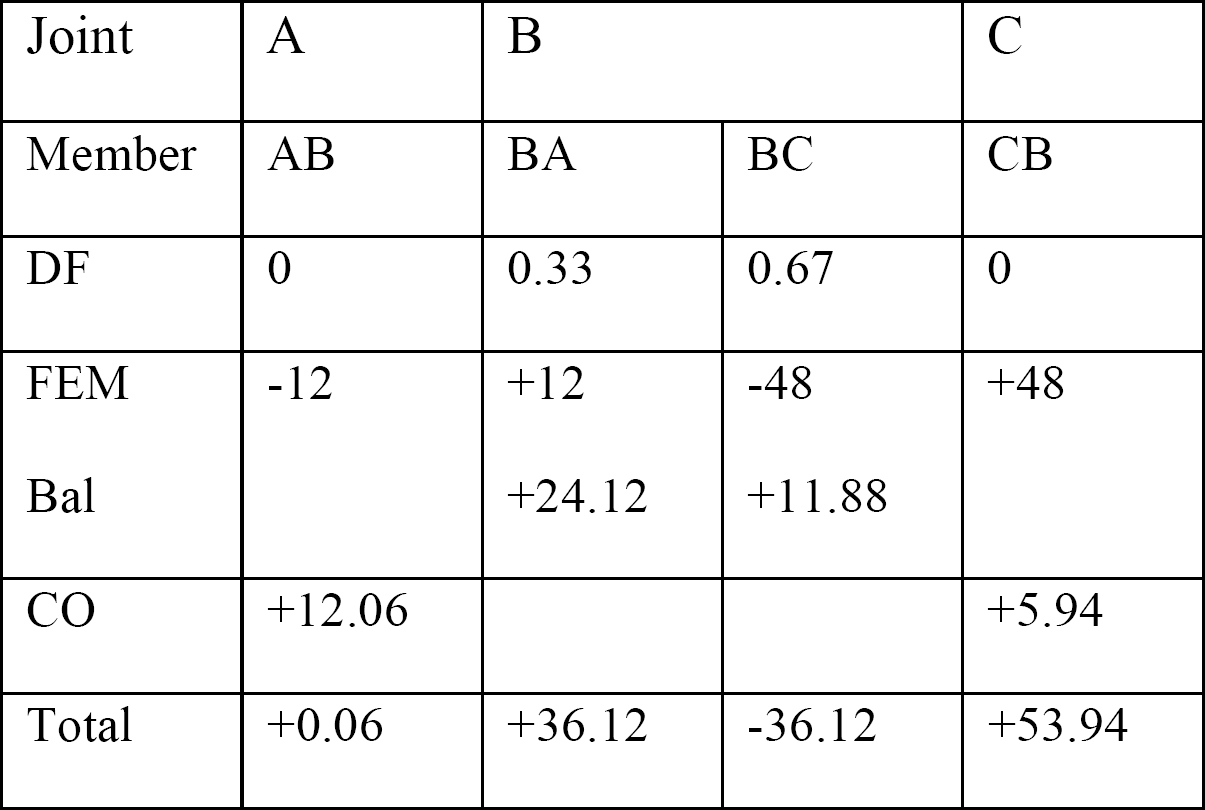
skjuvkraft och böjmoment diagram.
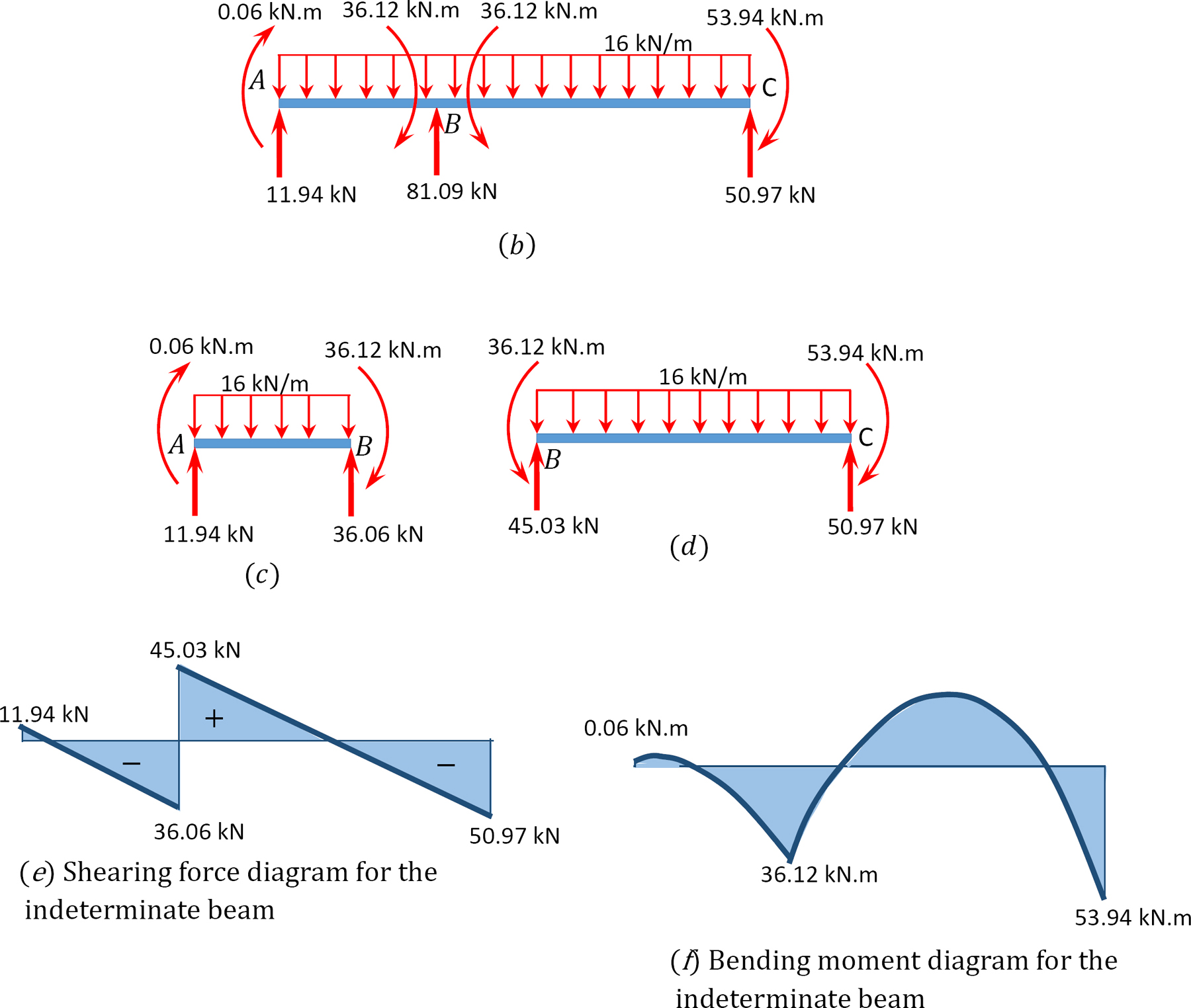
exempel 12.2
med hjälp av momentfördelningsmetoden bestämmer du slutmomenten och reaktionerna vid balkens stöd som visas i Figur 12.7 A. Rita skjuvkraften och böjmomentdiagrammen.
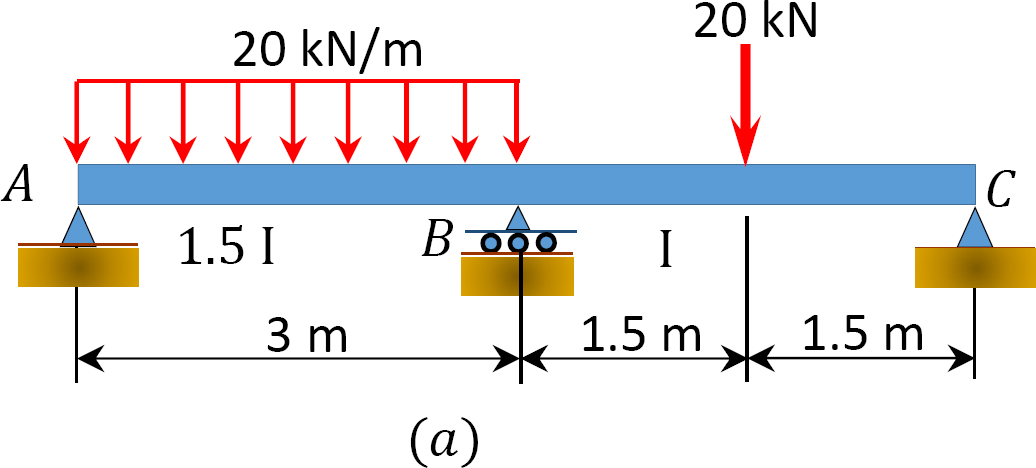
Fig. 12.7. Balk.
lösning
fast slutmoment.
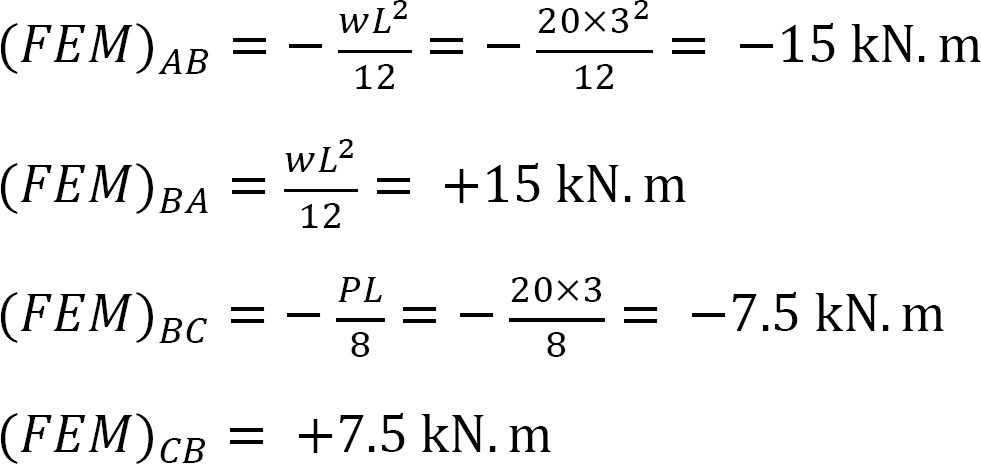
Styvhetsfaktor.
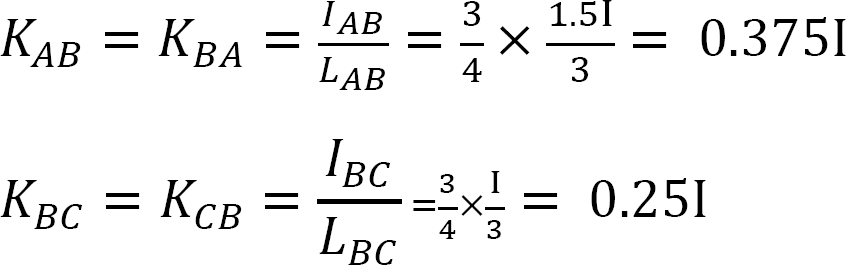
Fördelningsfaktor.
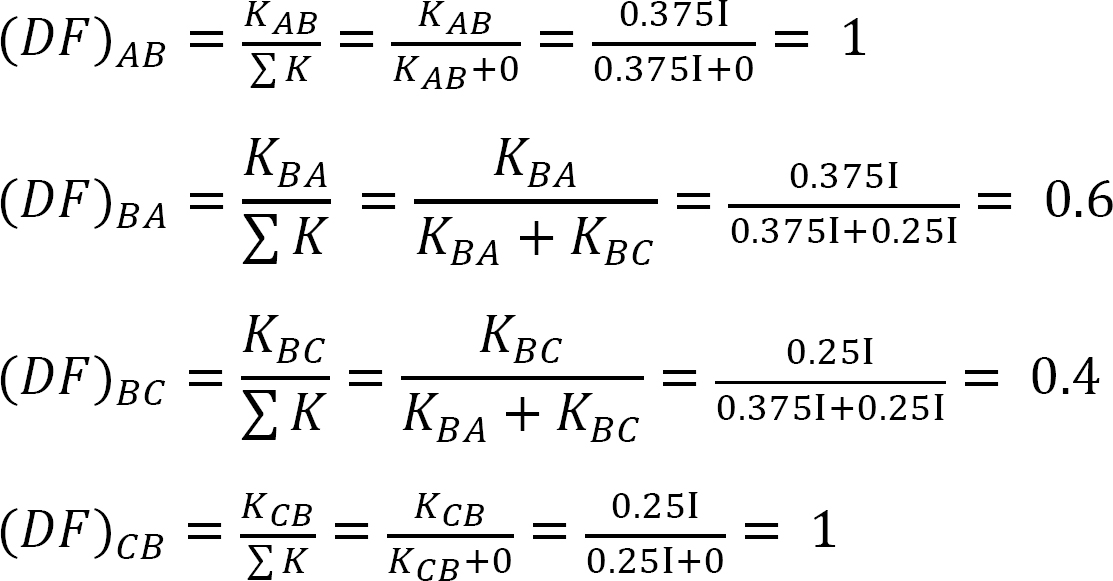
tabell 12.2. Distributionstabell.
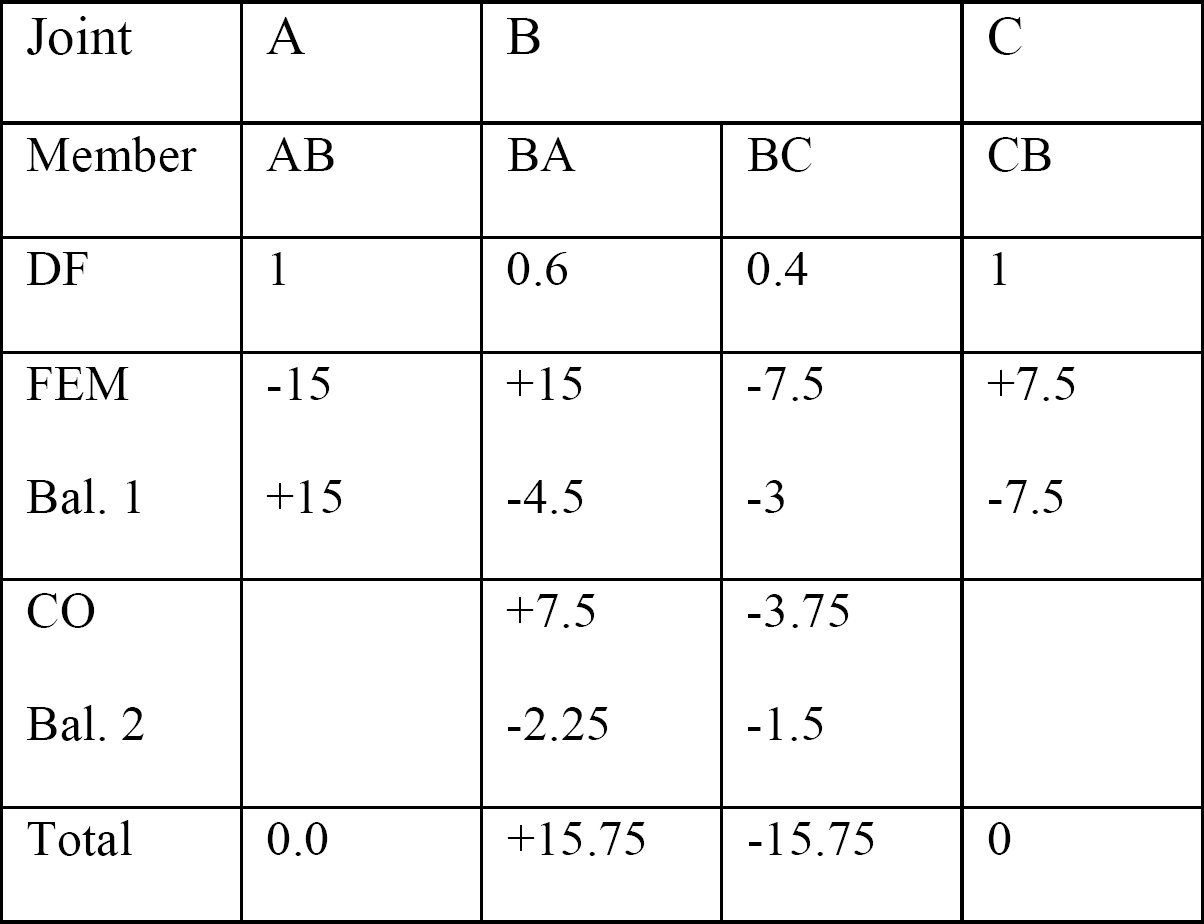
skjuvkraft och böjmoment diagram.
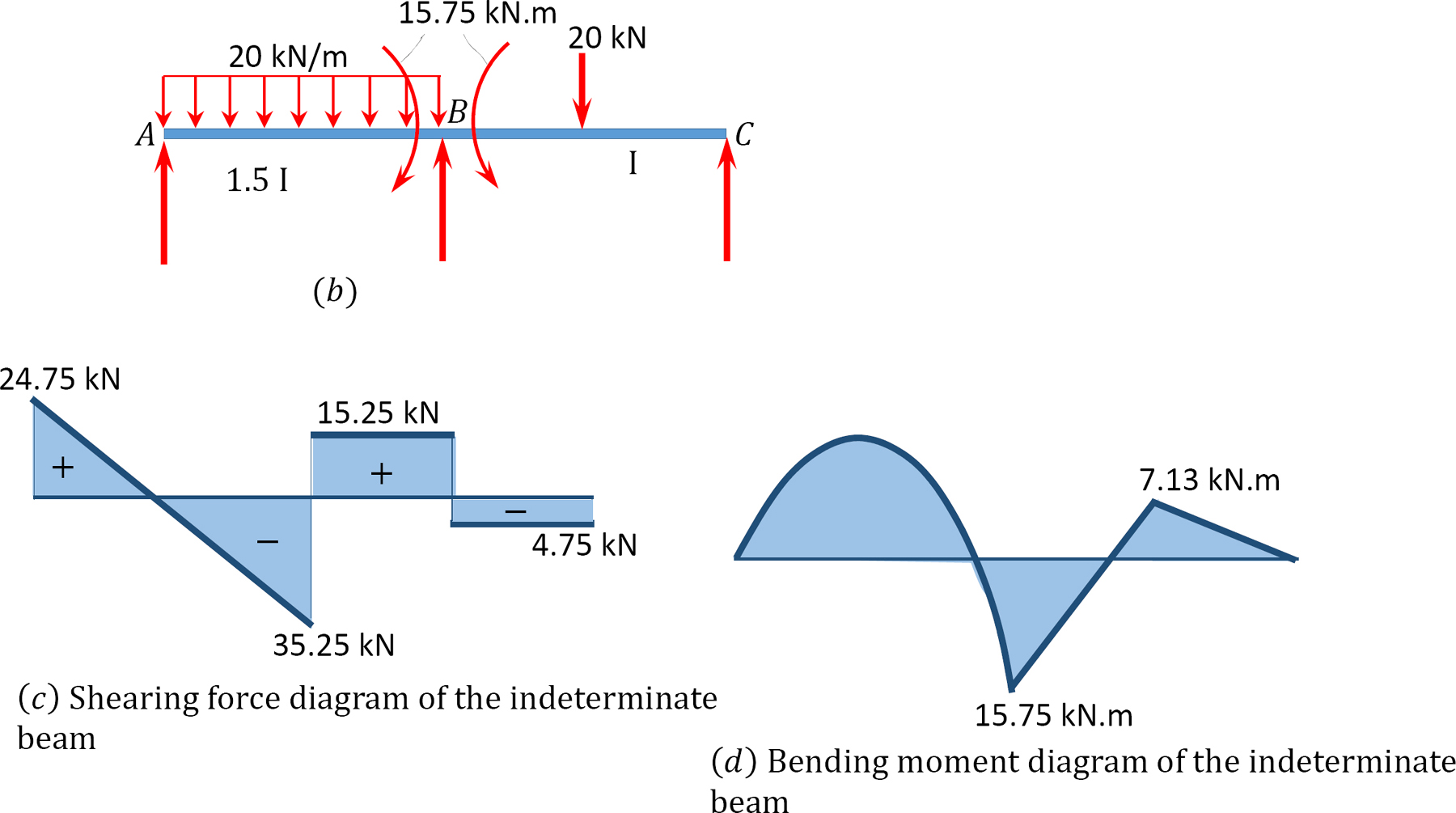
12.6 analys av obestämda ramar
proceduren för analys av ramar med momentfördelningsmetoden beror på vilken typ av ram som analyseras. Ramar kategoriseras som sway-eller icke-sway-ramar. Förfarandet för analys av icke-svängningsramar liknar det för obestämda balkar. Men för analys av svängramar är proceduren annorlunda. Det finns två steg involverade i analysen av sway-ramar, nämligen icke-sway-scenen och sway-scenen analyser. Dessa steg beskrivs nedan.
förfarande för analys av obestämda Svängramar med Momentfördelningsmetoden
A. icke-svängstegsanalys
•Antag först förekomsten av en imaginär prop som förhindrar att ramen svänger.
•beräkna de horisontella reaktionerna vid ramens stöd och notera skillnaden X. Detta är kraften för att förhindra svängning.
B. Sway stage analysis
•värden antas för M2 och M1 bestäms.
* beräkna storleken på de horisontella reaktionerna vid stöden för sway-tillståndet. Summeringen av dessa reaktioner ger den godtyckliga förskjutningskraften Y.
detta förhållande kallas svängfaktorn.
exempel 12.3
med hjälp av momentfördelningsmetoden bestämmer du medlemmarnas slutmoment för ramen som visas i Figur 12.8. EI = konstant.
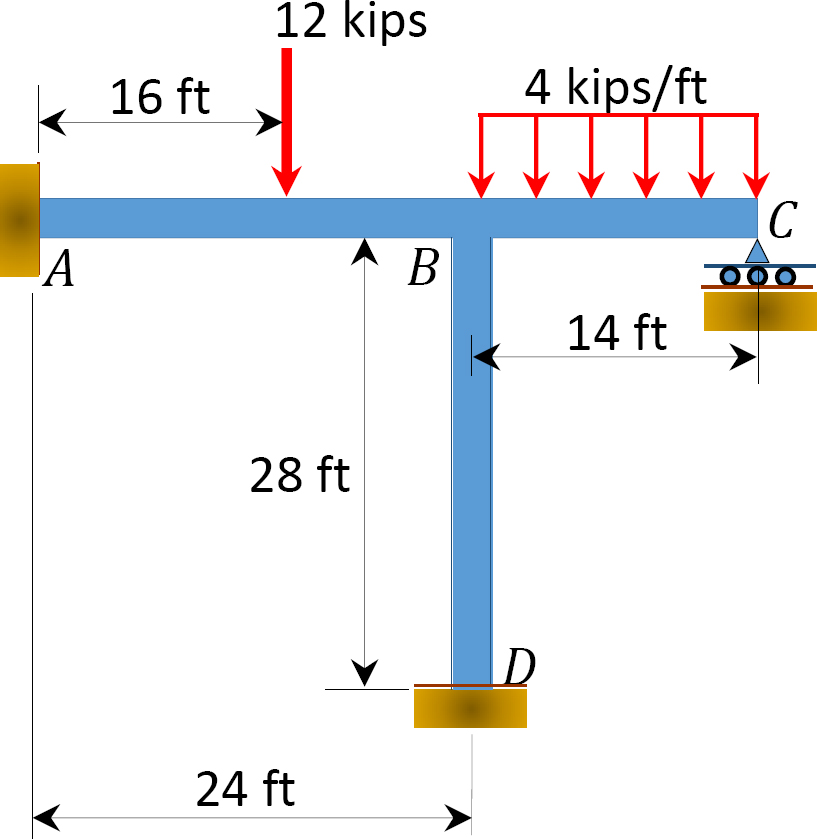
Fig. 12.8. Ram.
lösning
fast slutmoment.
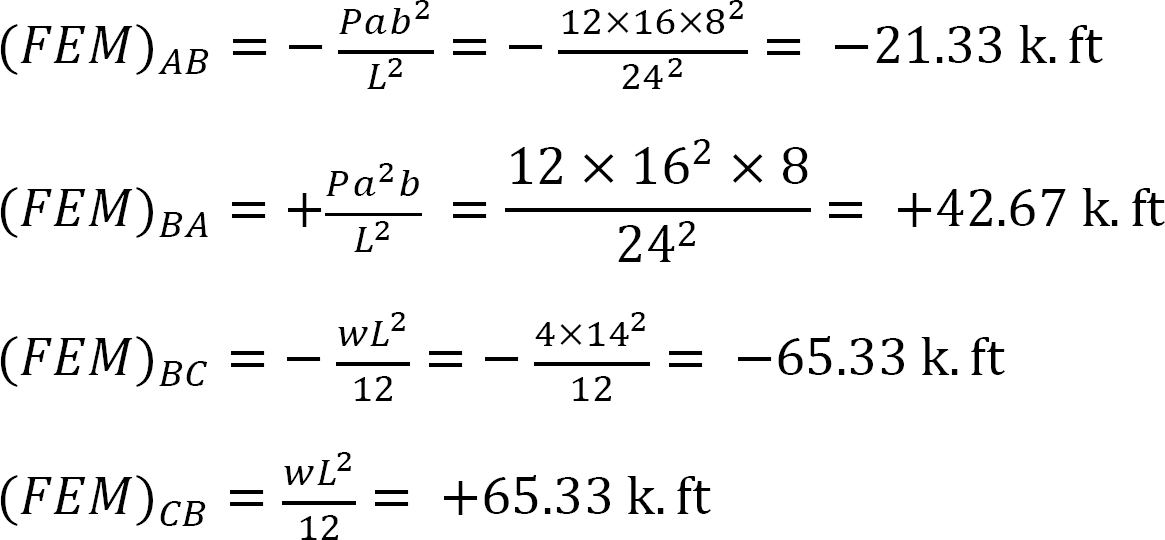
Styvhetsfaktor.
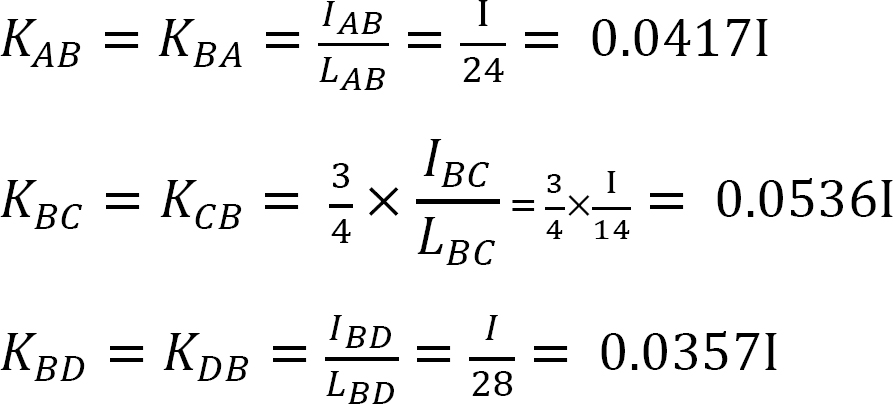
Fördelningsfaktor.
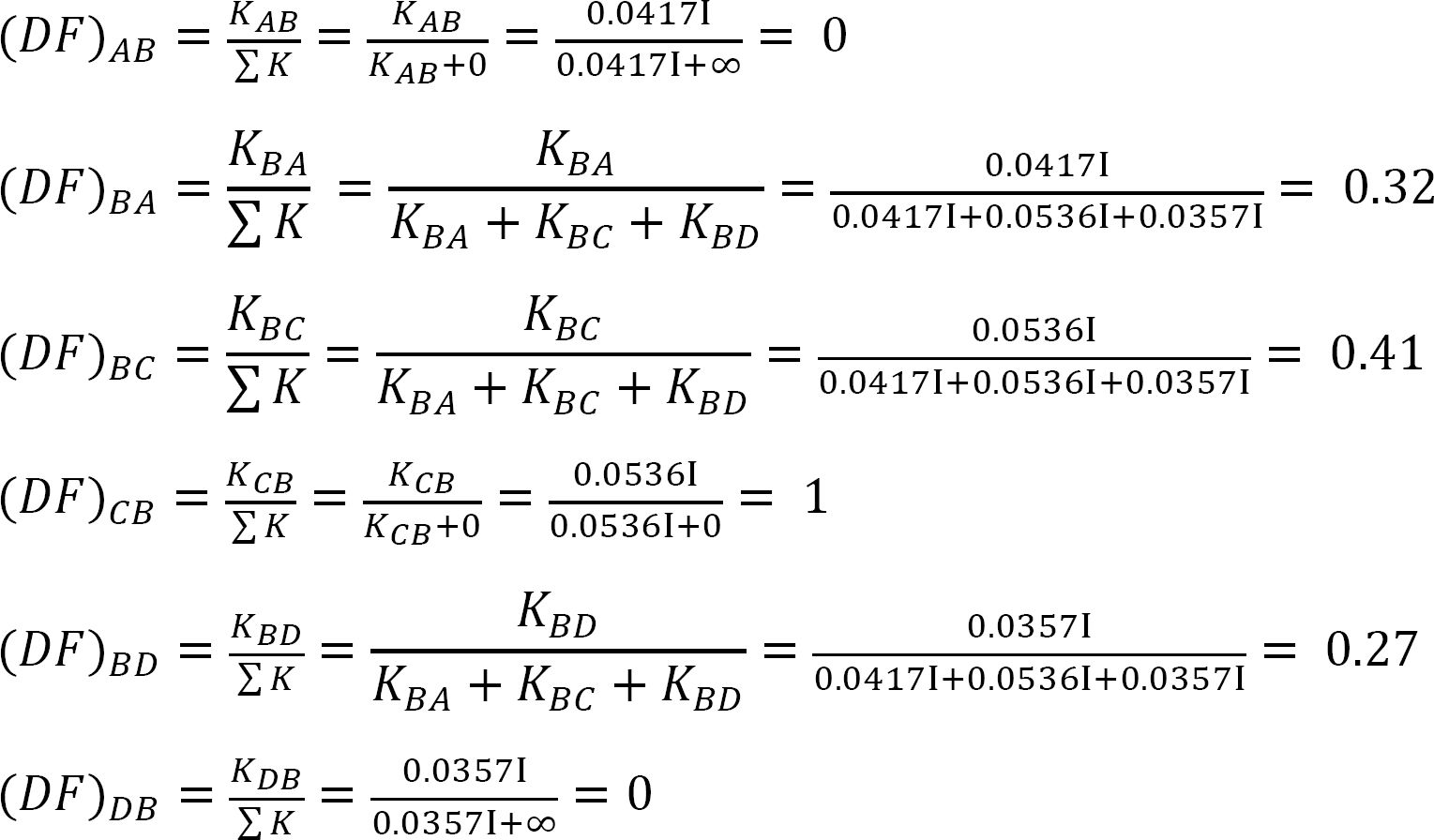
tabell 12.3. Distributionstabell.
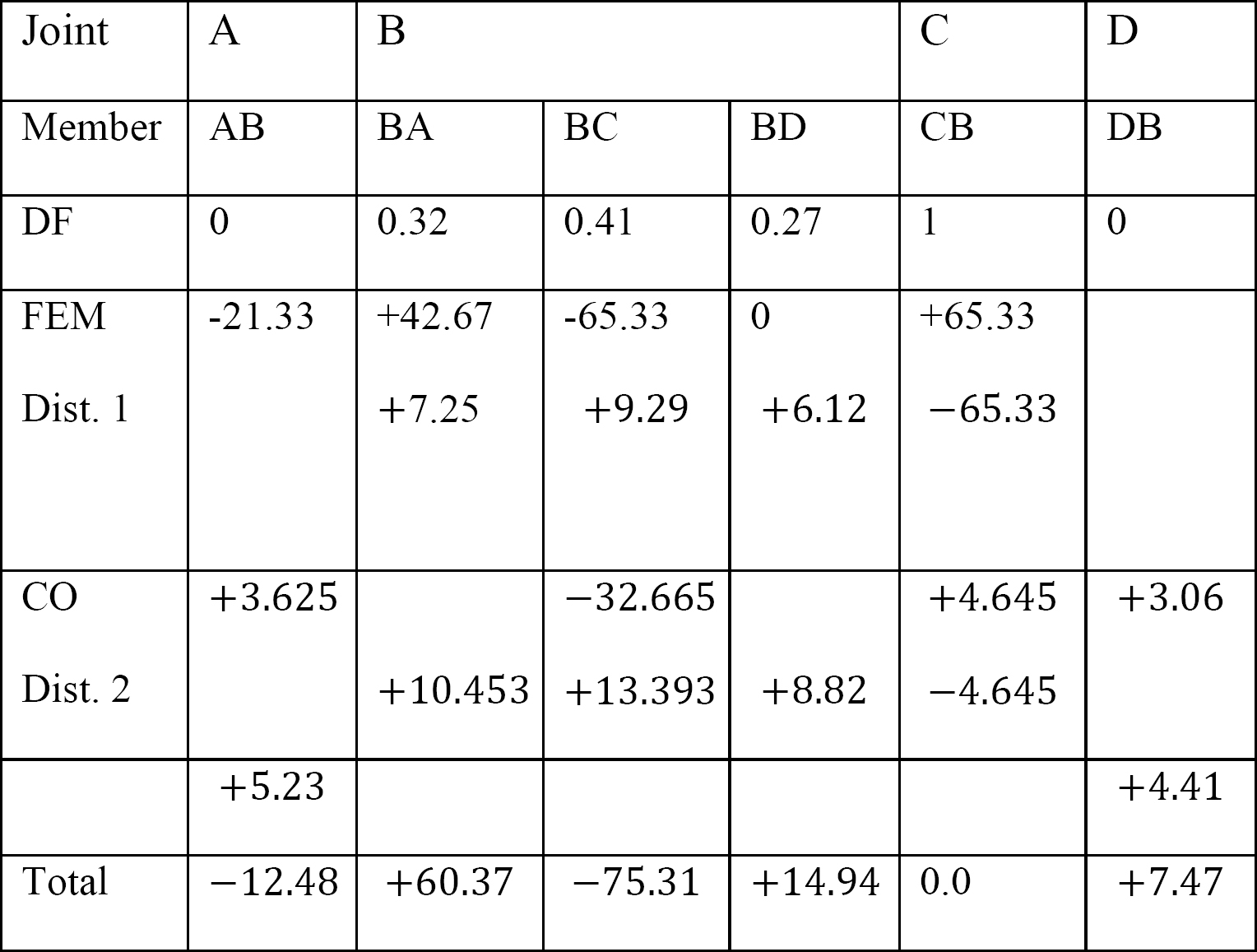
sista medlem slut stunder.
genom att ersätta de erhållna värdena för EK Acubbib, ek Acubbicc och EK acubbib i Medlemmens slutmomentekvationer föreslår följande:
MAB = -12.48 k. ft
MBA = +60.37 k. ft
MBC = -75.31 k. ft
MBD = +14,94 k. ft
MCB = 0
MDB = +7,47 k. ft
exempel 12.4
med hjälp av momentfördelningsmetoden bestämmer du slutmomenten vid ramens stöd som visas i Figur 12.9. EI = konstant.
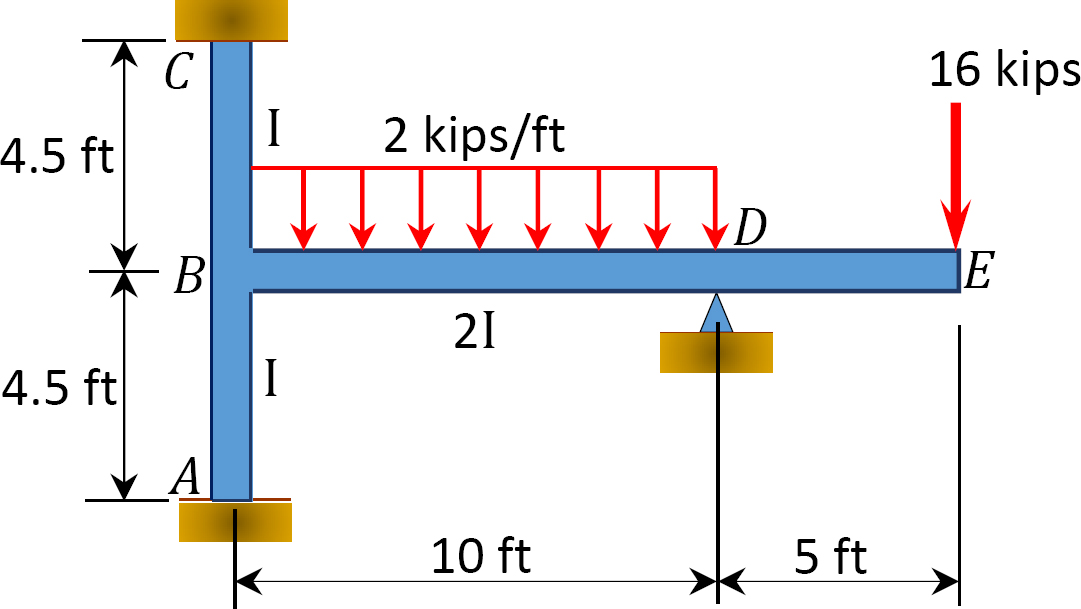
Fig. 12.9. Ram.
lösning
fast slutmoment.
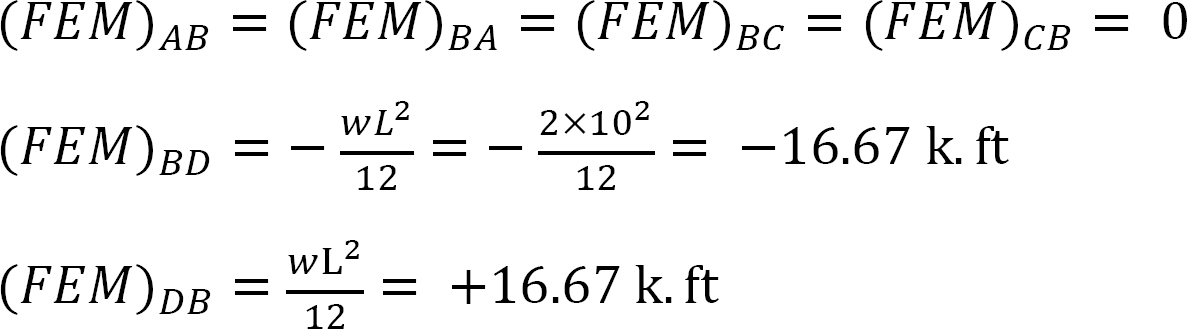
Styvhetsfaktor.
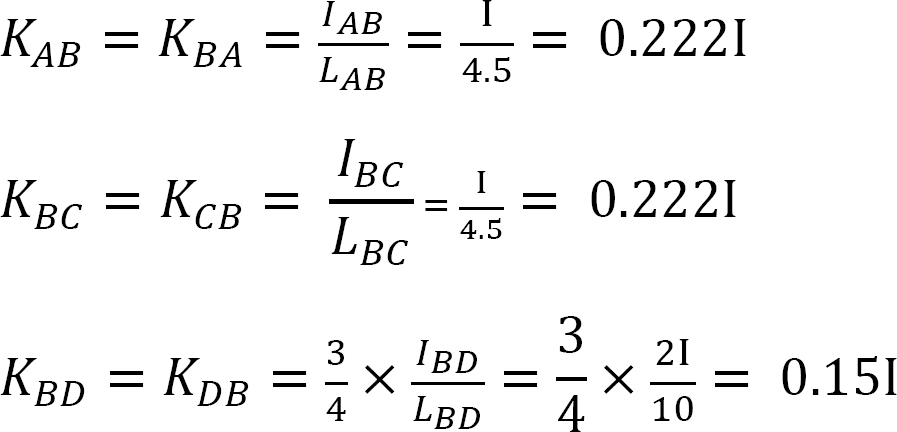
Fördelningsfaktor.

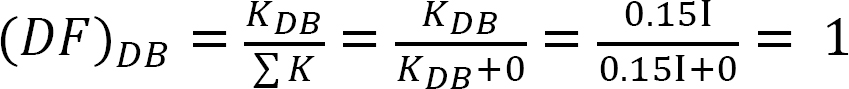
tabell 12.4. Distributionstabell.
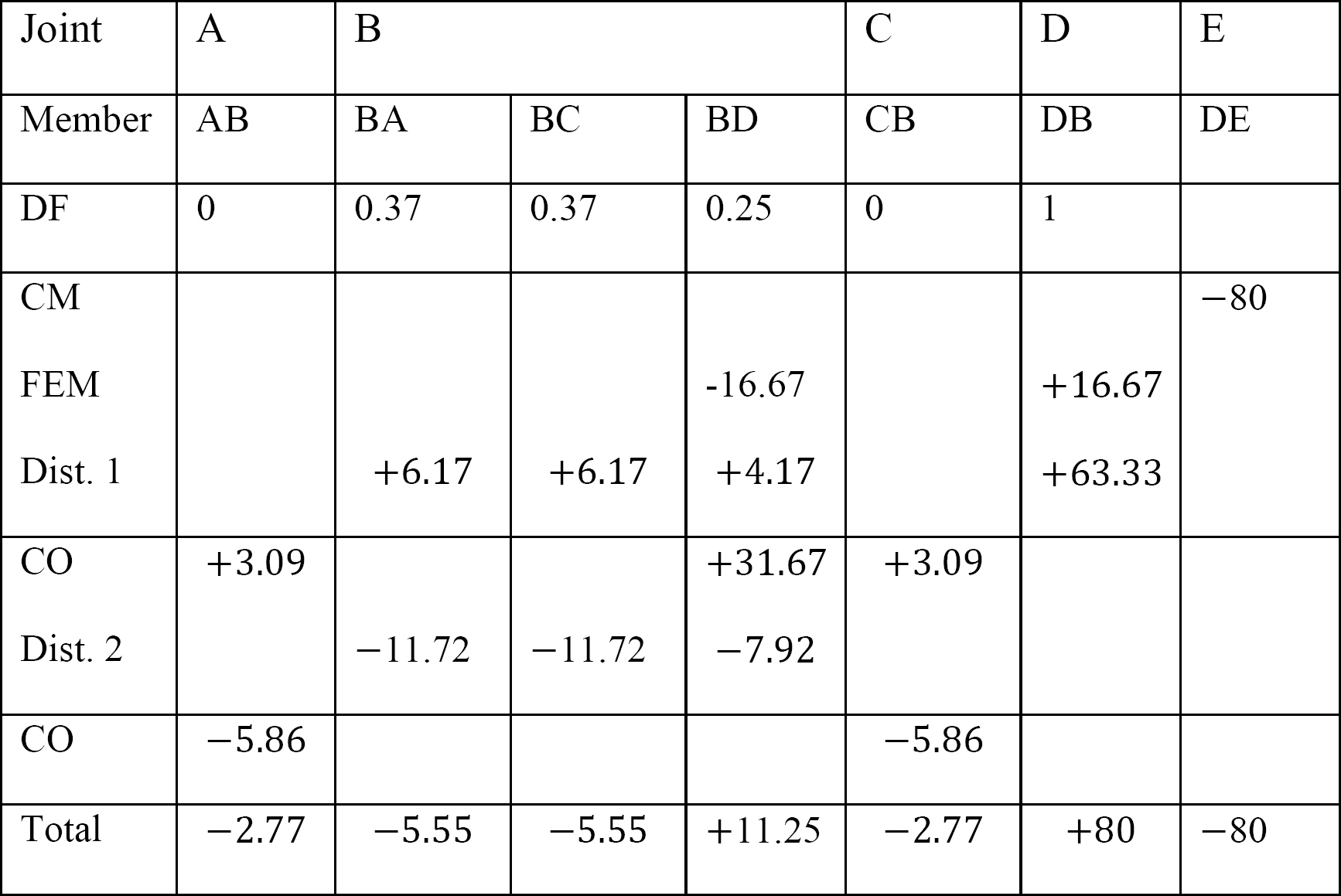
sista medlem slut stunder.
MAB = -2,77 k. ft
MBA = -5,55 k. ft
MBC = -5,55 k. ft
MBD = + 11,25 k. ft
MCB = -2,77
MDB = + 80 K. ft
mde = -80 k. ft
exempel 12.5
med hjälp av momentfördelningsmetoden bestämmer du slutmomenten vid ramens stöd som visas i Figur 12.10. EI = konstant.
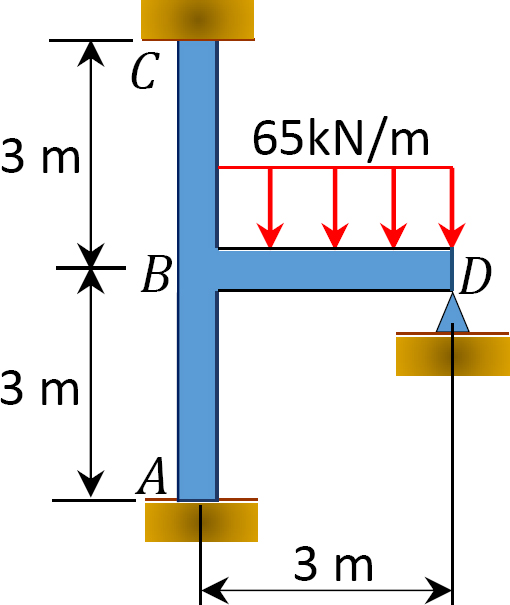
Fig. 12.10. Ram.
lösning
fast slutmoment.
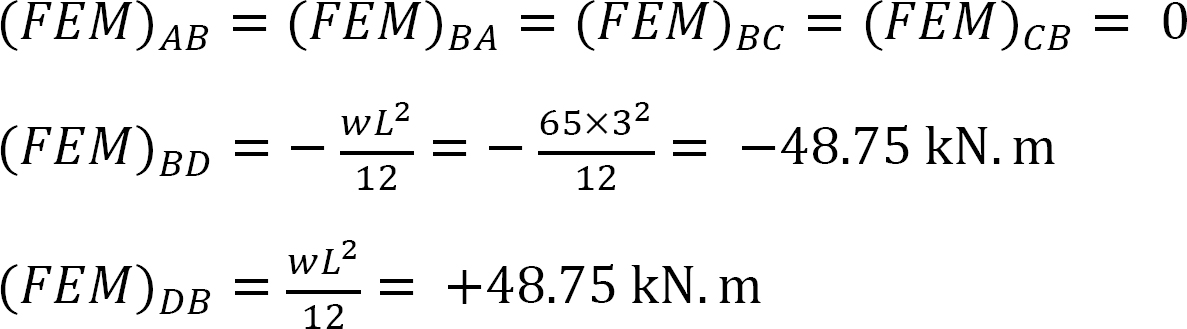
Styvhetsfaktor.
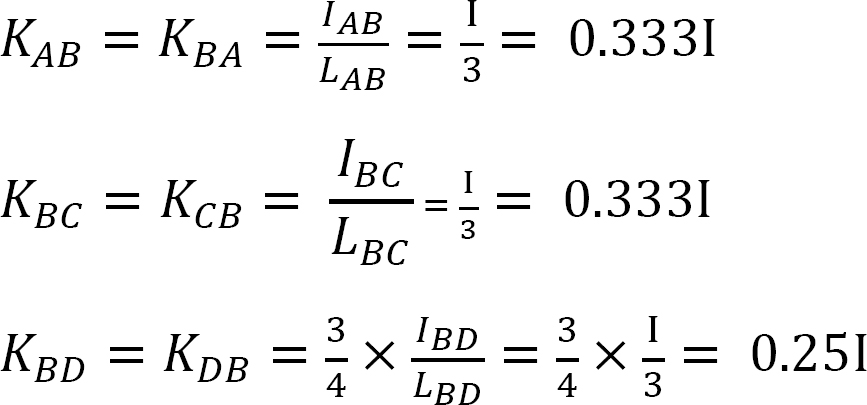
Fördelningsfaktor.
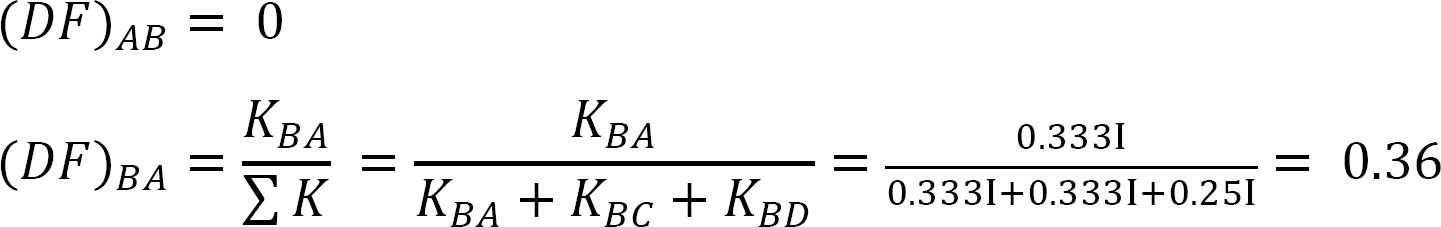

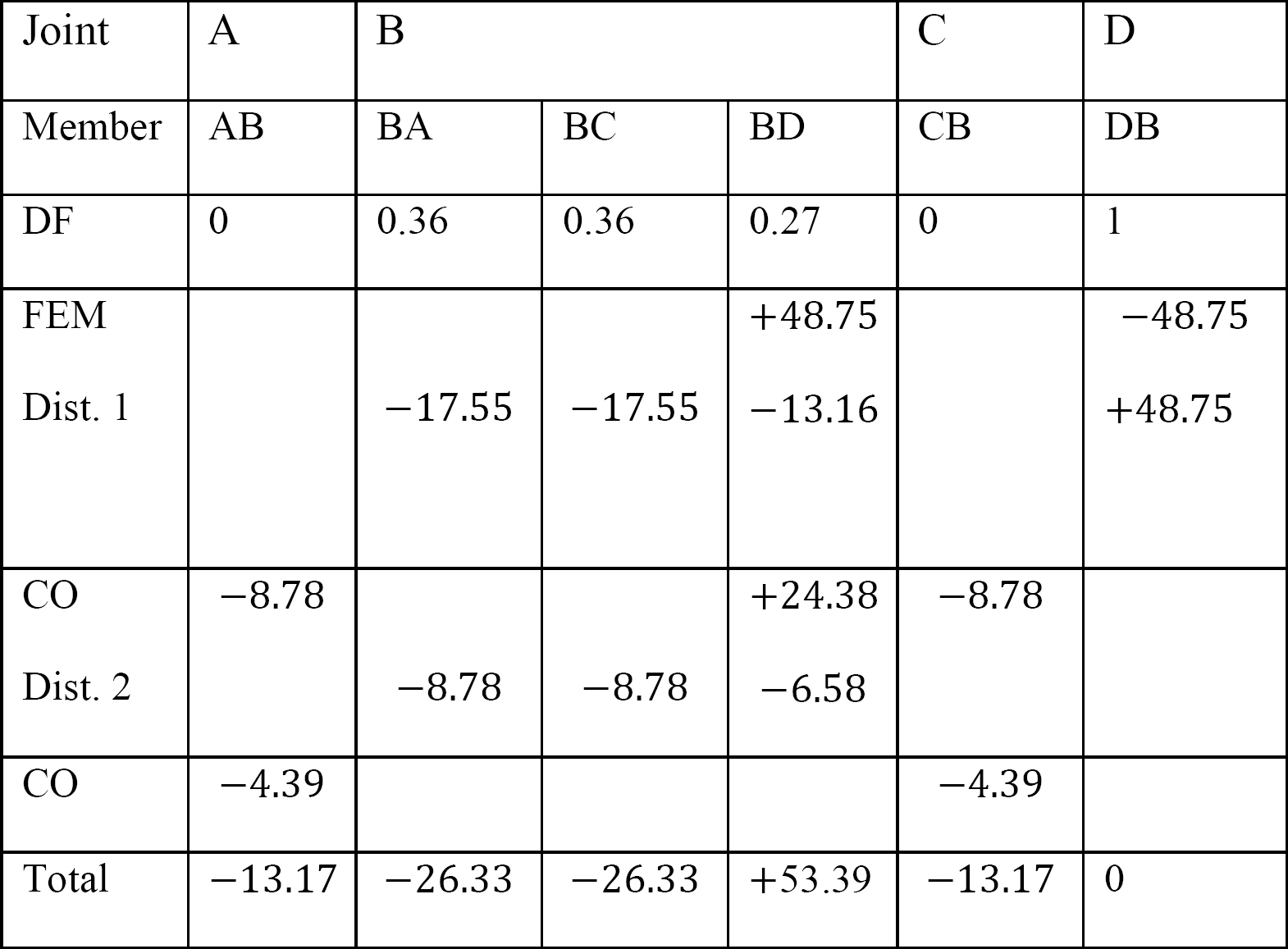
tabell 12.5. Distributionstabell.
sista medlem slut stunder.
MAB = -13,17 k. ft
MBA = -26,33 k. ft
MBC = -26,33 k. ft
MBD = +53,39 k. ft
MCB = -13,17 k. ft
MDB = 0
exempel 12.6
med hjälp av momentfördelningsmetoden bestämmer du ramens ändmoment med sidosvängning som visas i Figur 12.11 a.
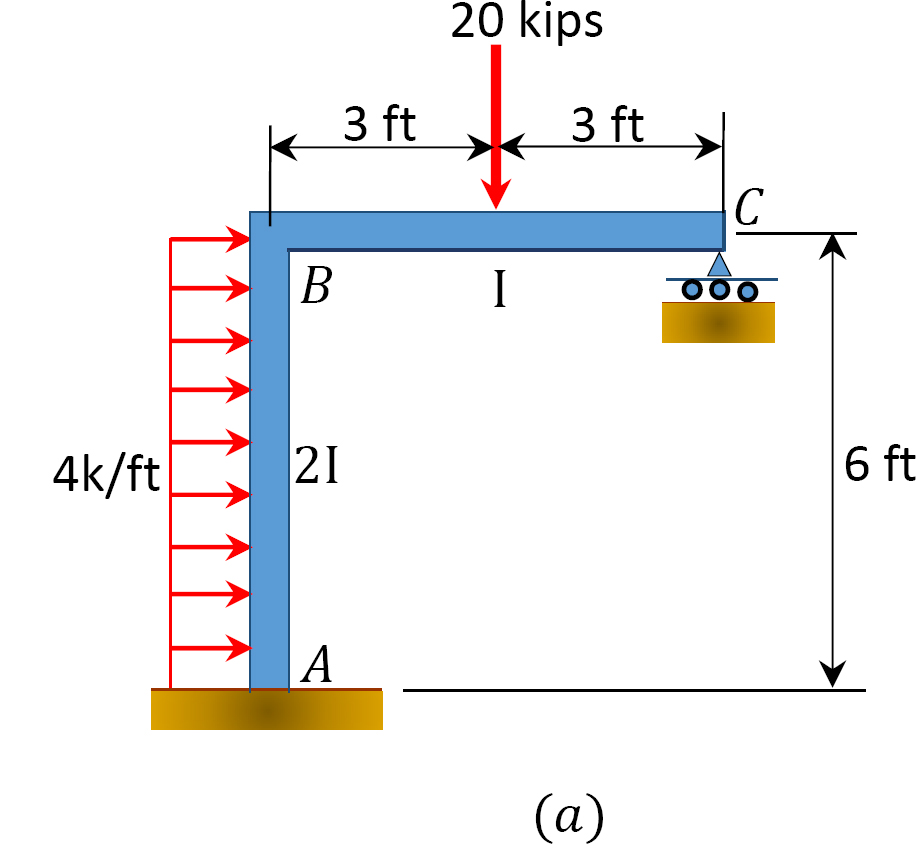
Fig. 12.11. Ram med sida-sway.
lösning
fast slutmoment.
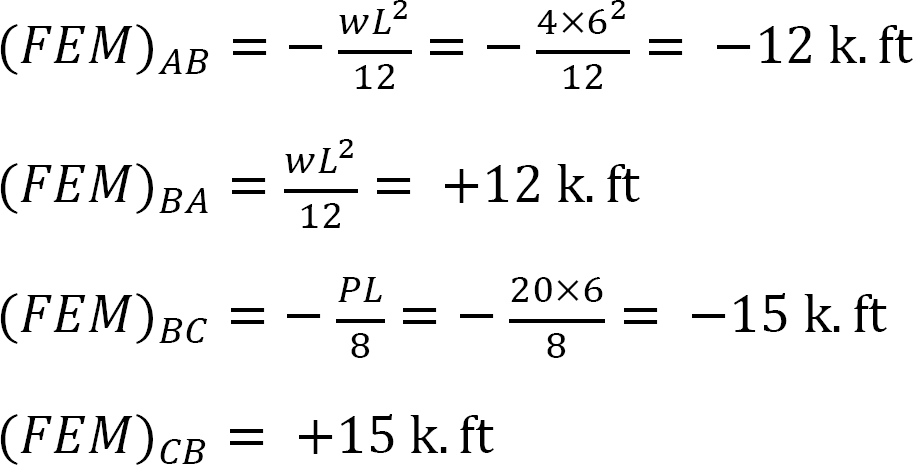
Styvhetsfaktor.
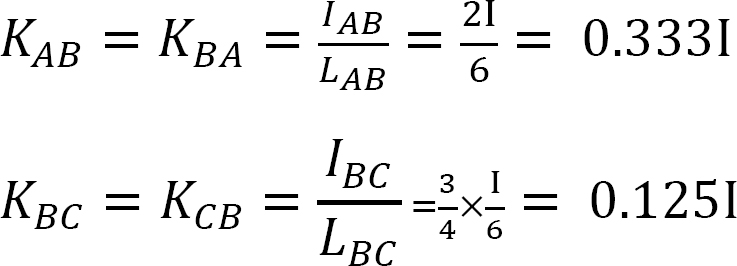
Fördelningsfaktor.
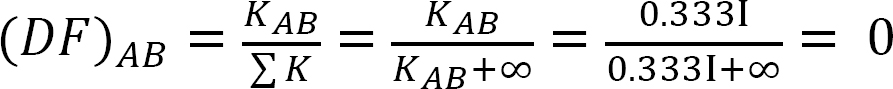

analys av RAM utan sidosving.
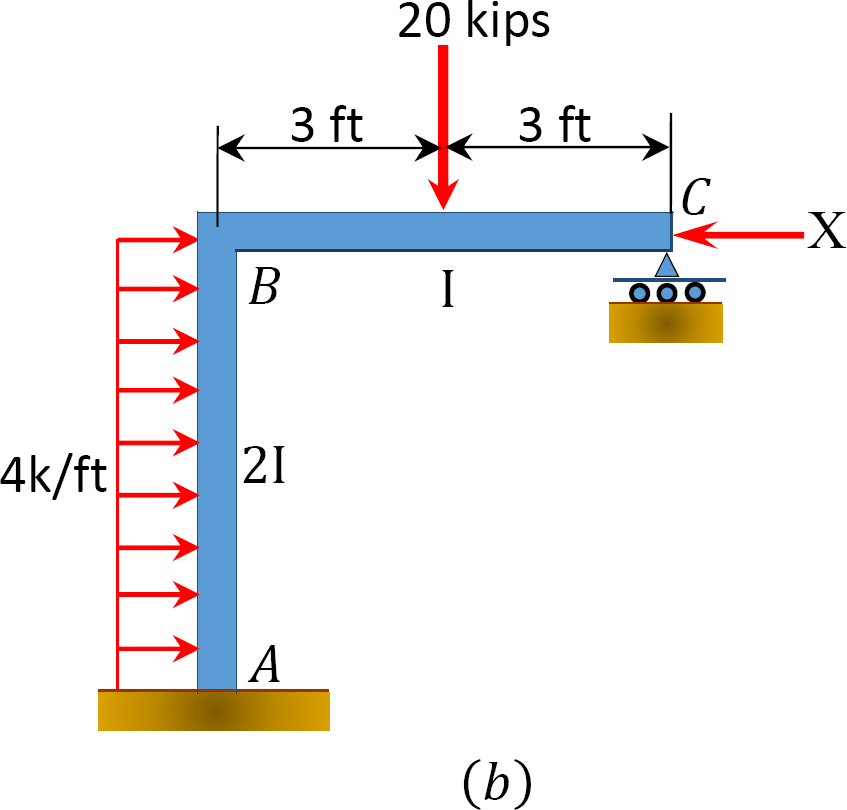
tabell 12.6. Distributionstabell (ingen svängningsram).
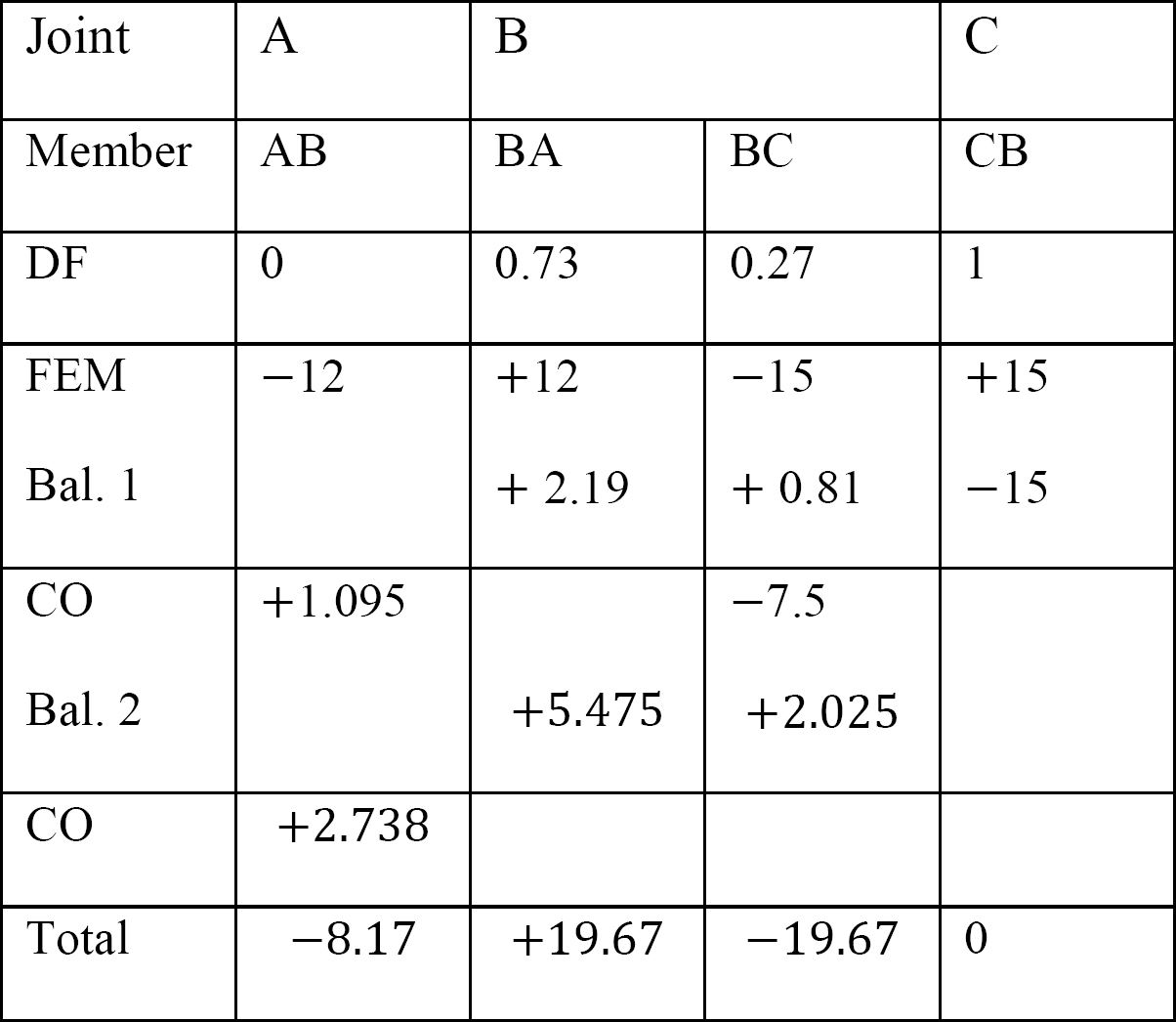
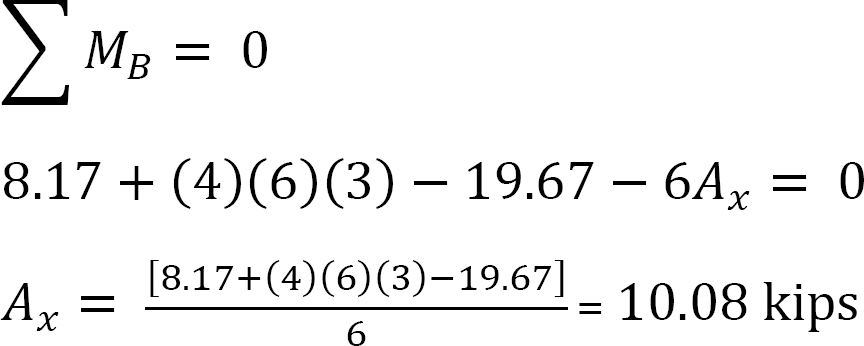
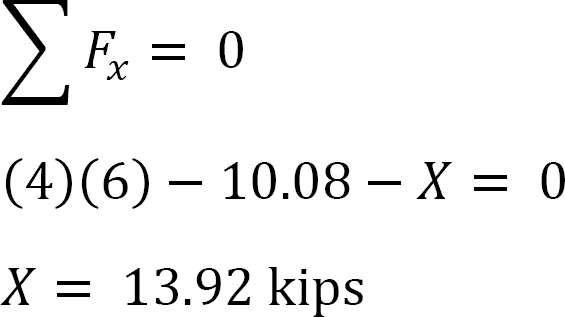
analys av ram med sido-sway.
Antag att MAB = + 20 K. ft
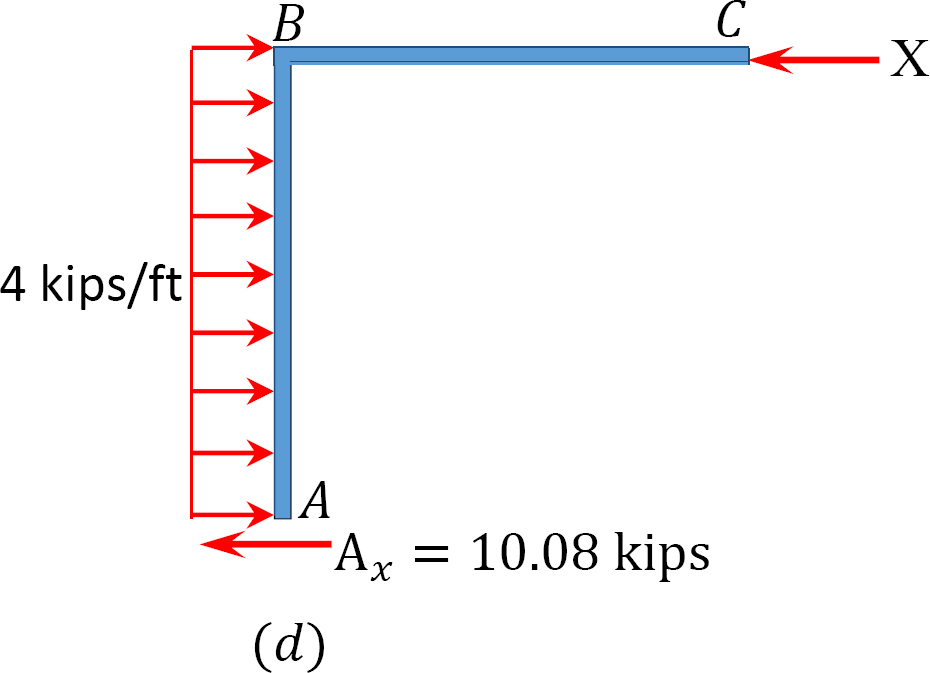
tabell 12.7. Distributionstabell (sväng ram).
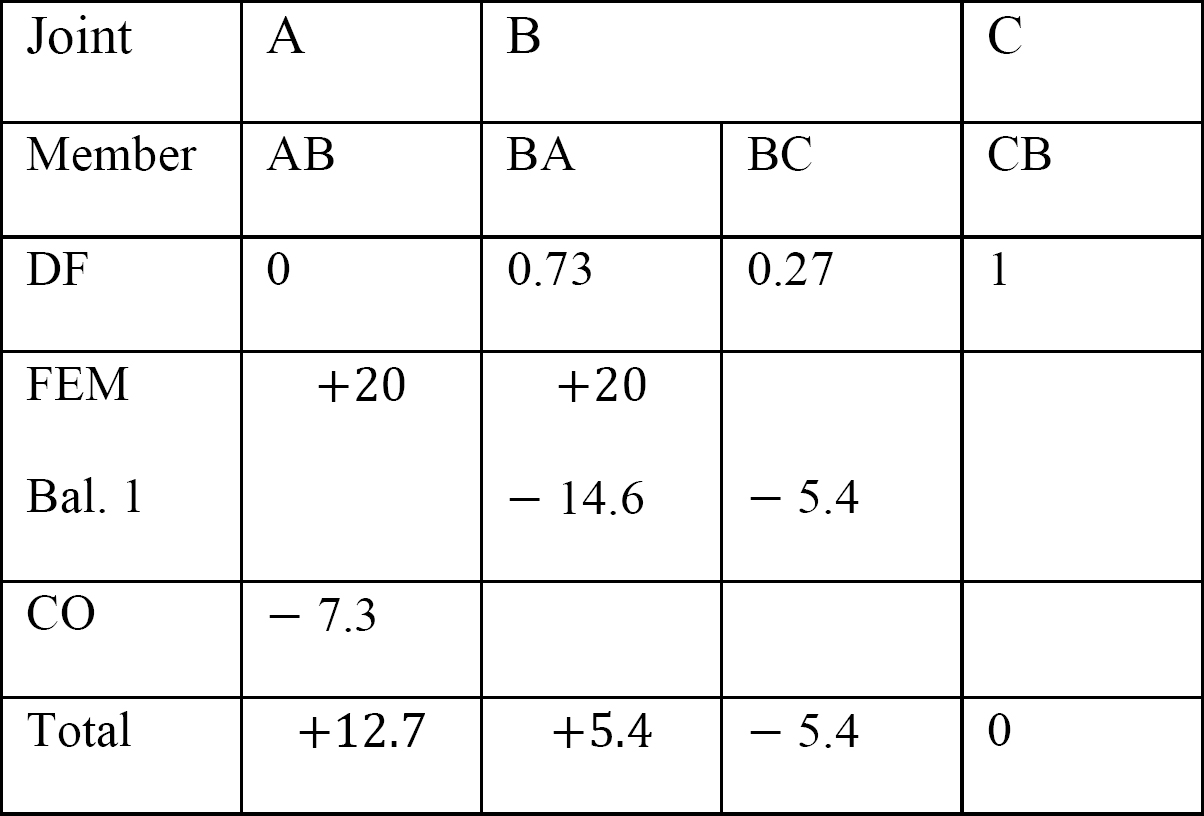
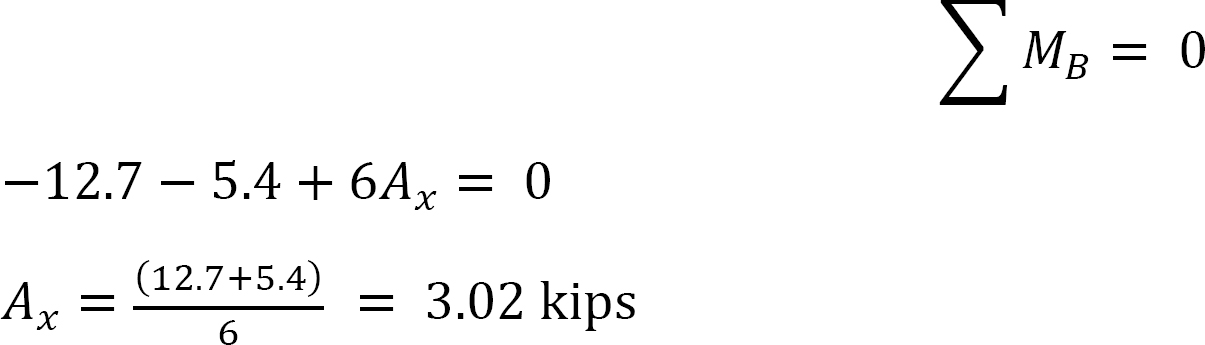
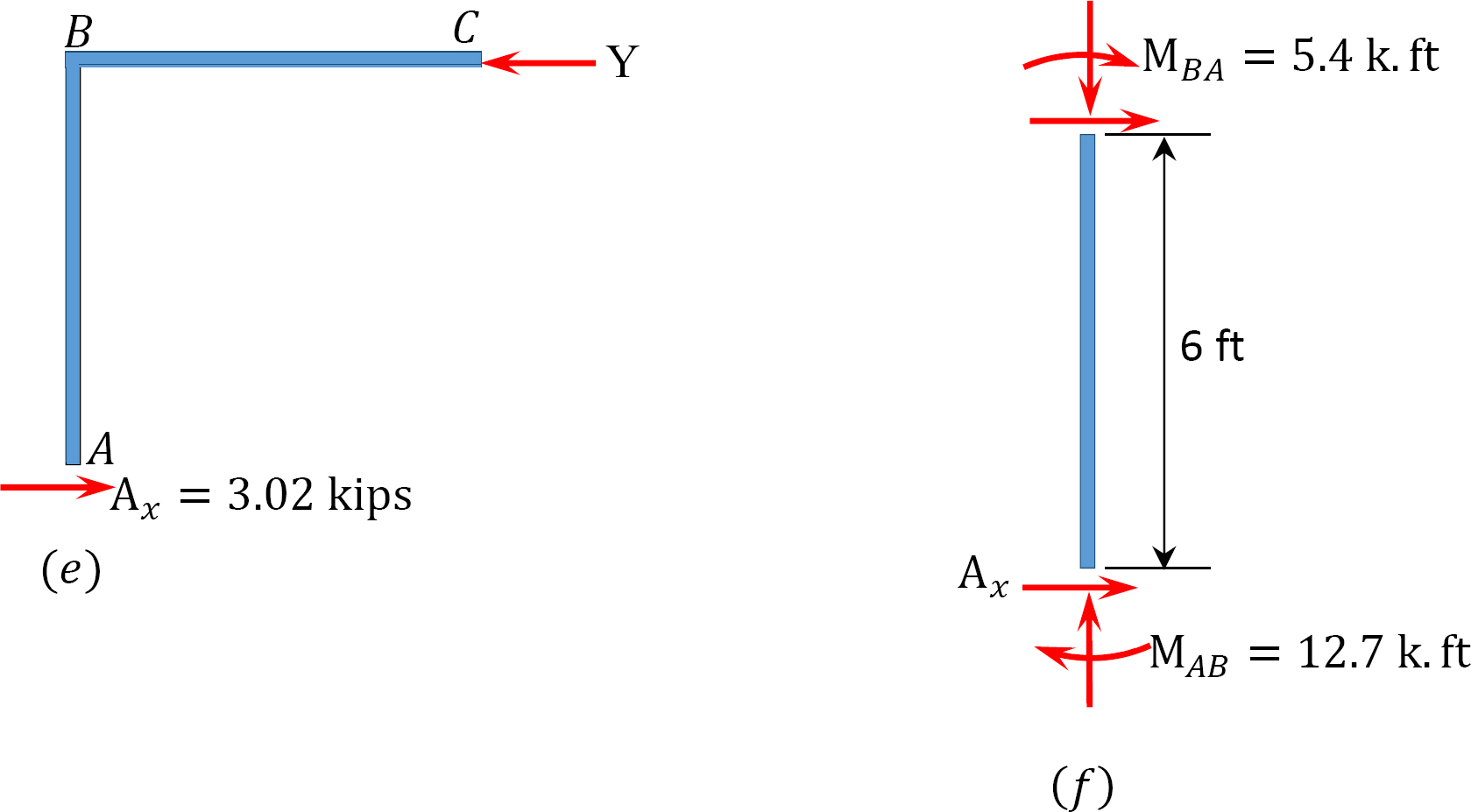
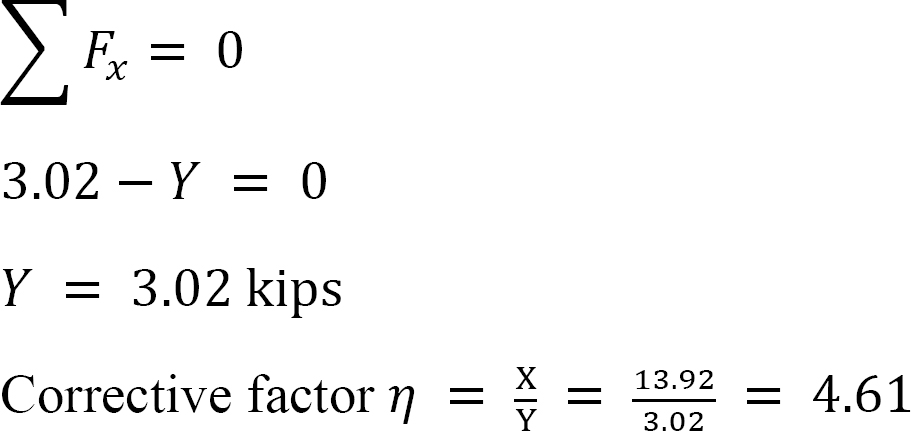
sista slutmoment.
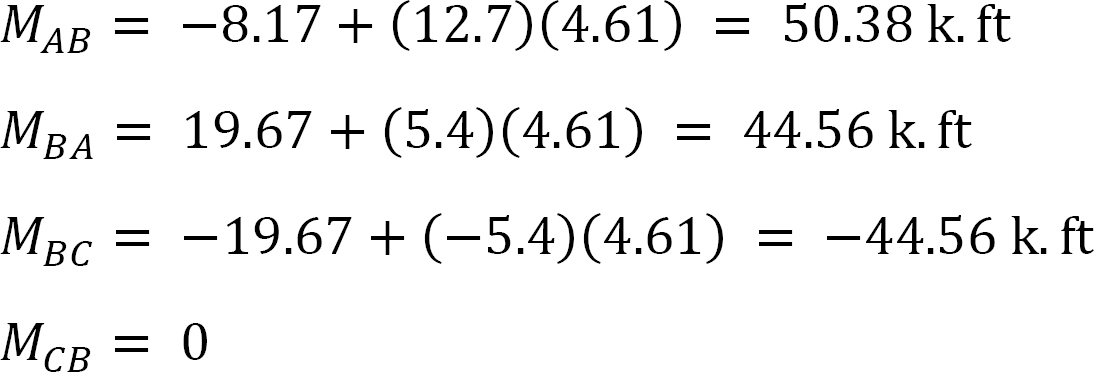
exempel 12.7
en svängningsram laddas som visas i Figur 12.12 a. med hjälp av momentfördelningsmetoden bestämmer du slutmomenten för ramens medlemmar.
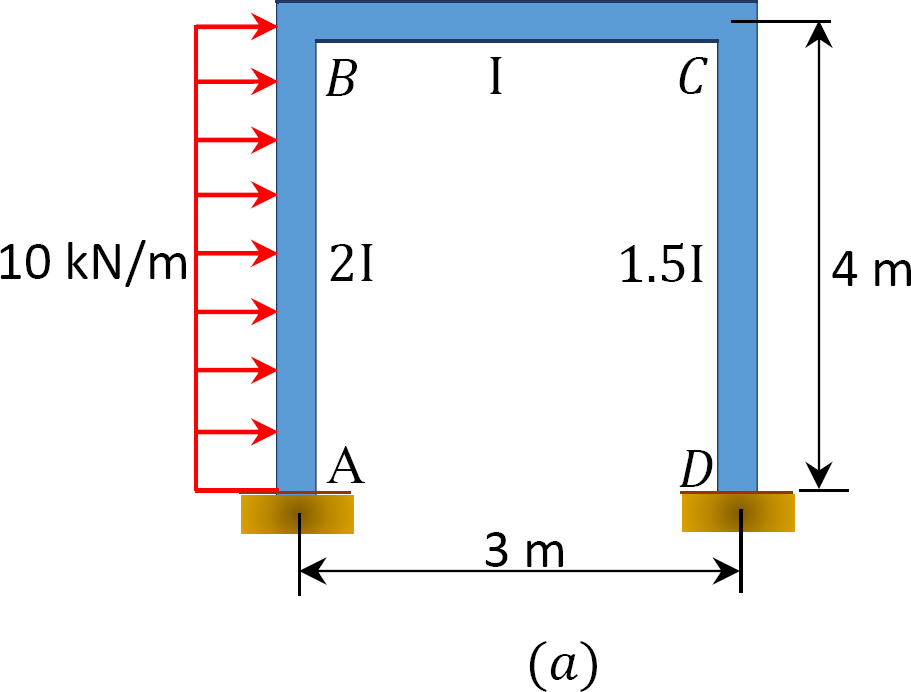
Fig. 12.12. Laddad sway ram.
lösning
fast slutmoment.
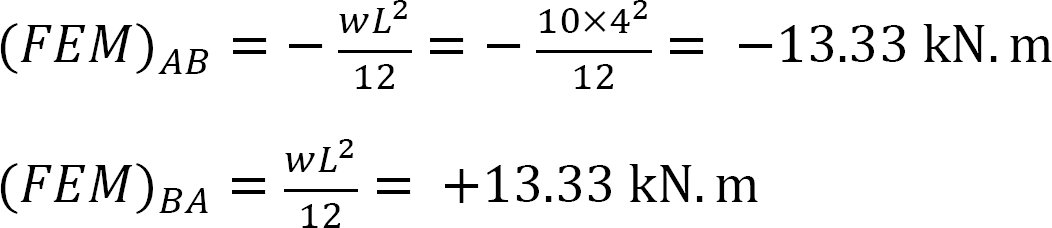
Styvhetsfaktor.
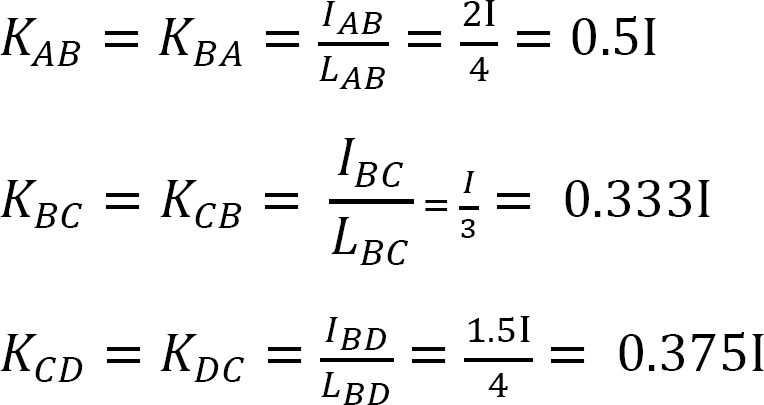
Fördelningsfaktor.

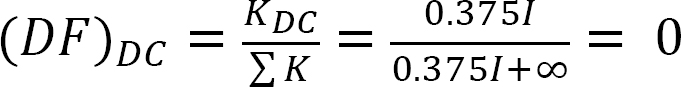
analys av RAM utan sidosving.
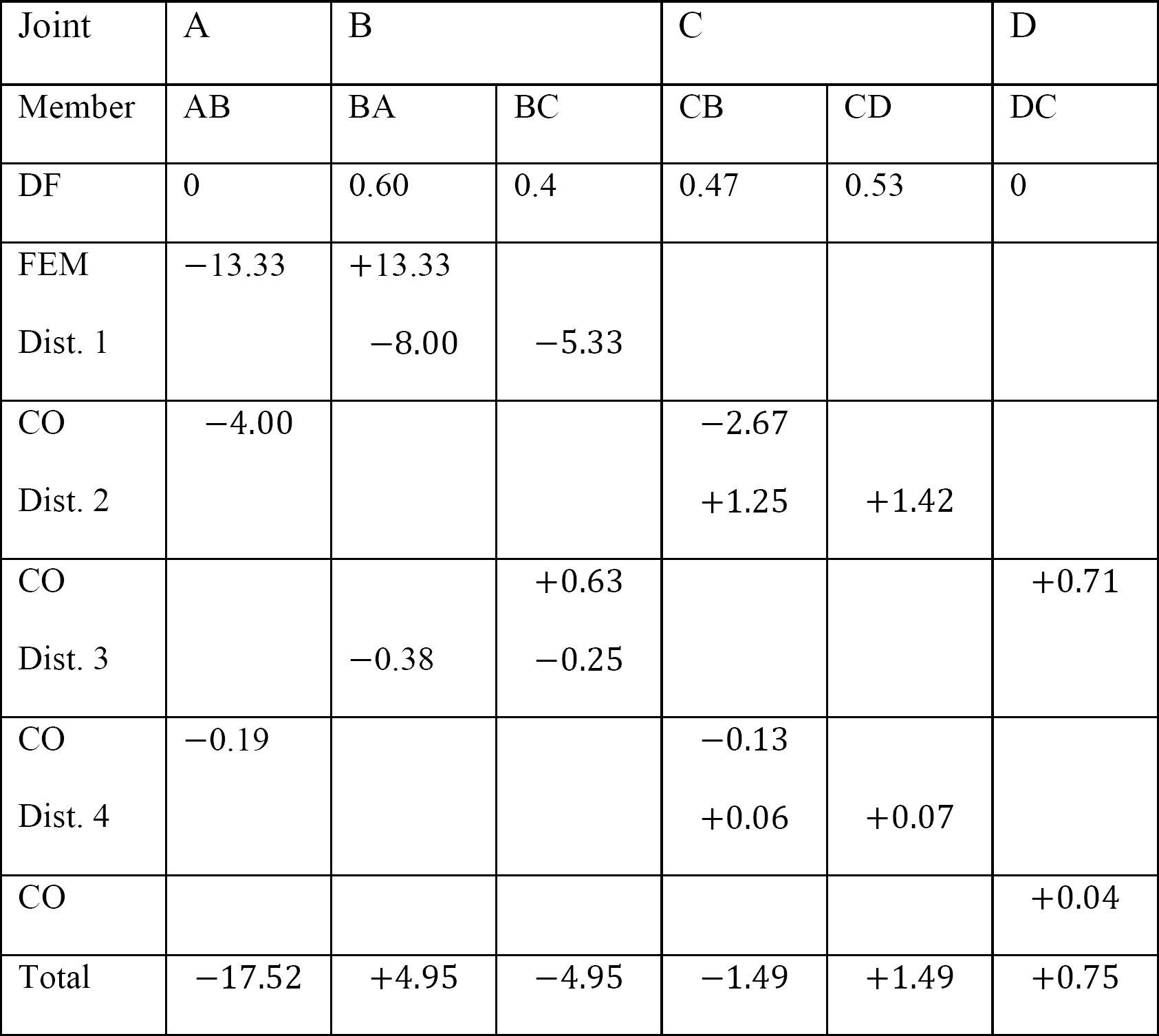
tabell 12.8. Distributionstabell (ingen svängningsram).
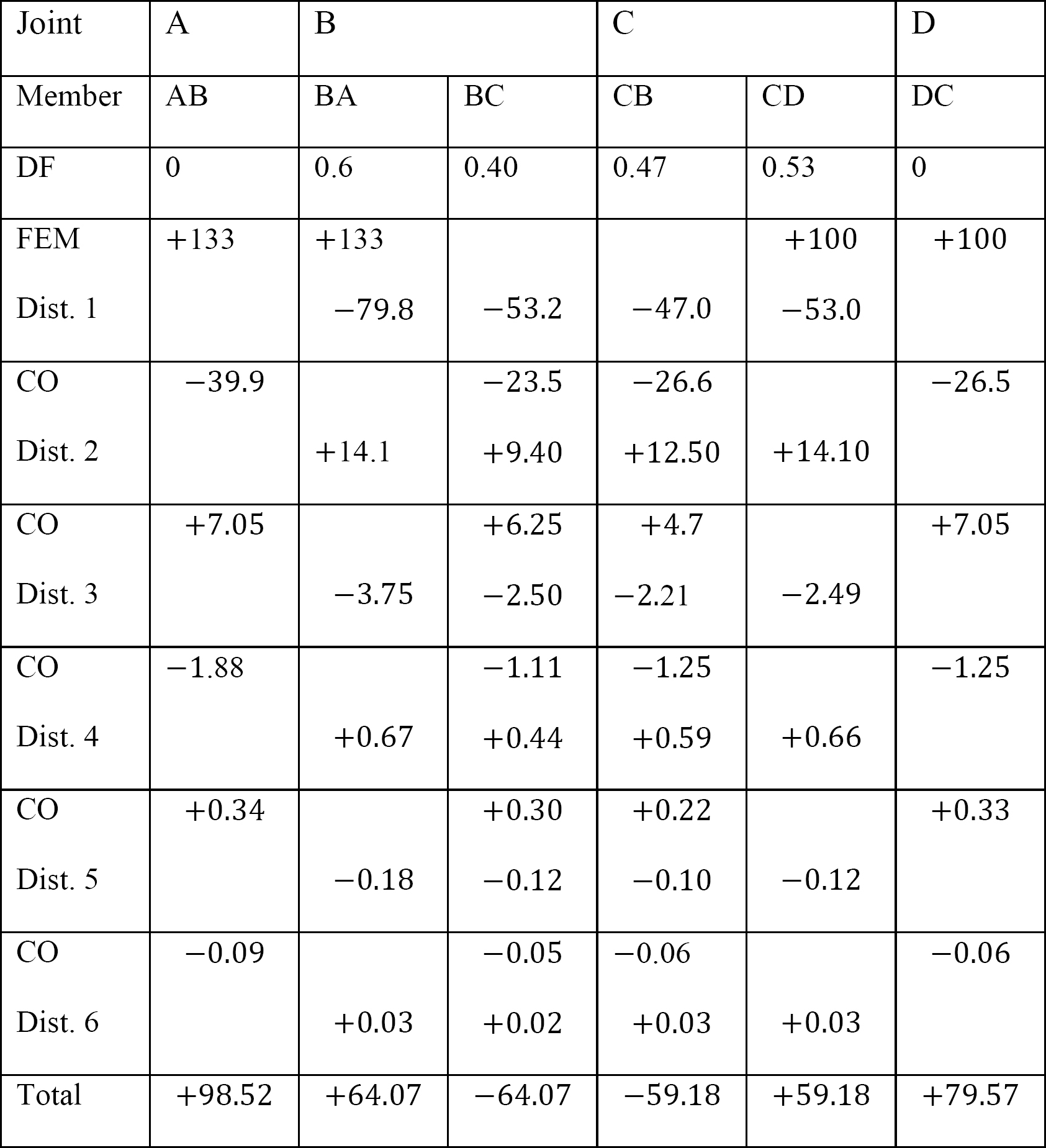
tabell 12.9. Distributionstabell (sväng ram).
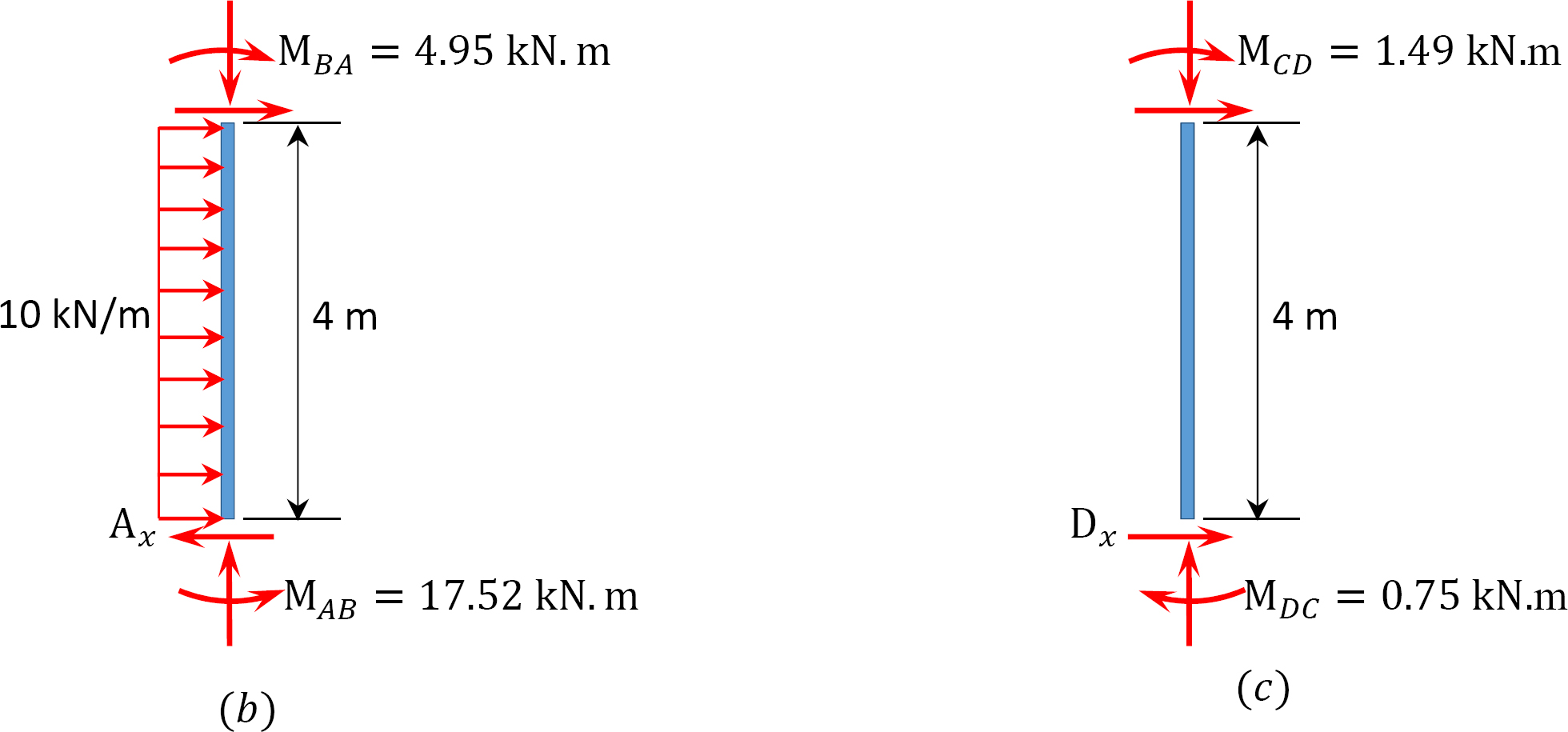
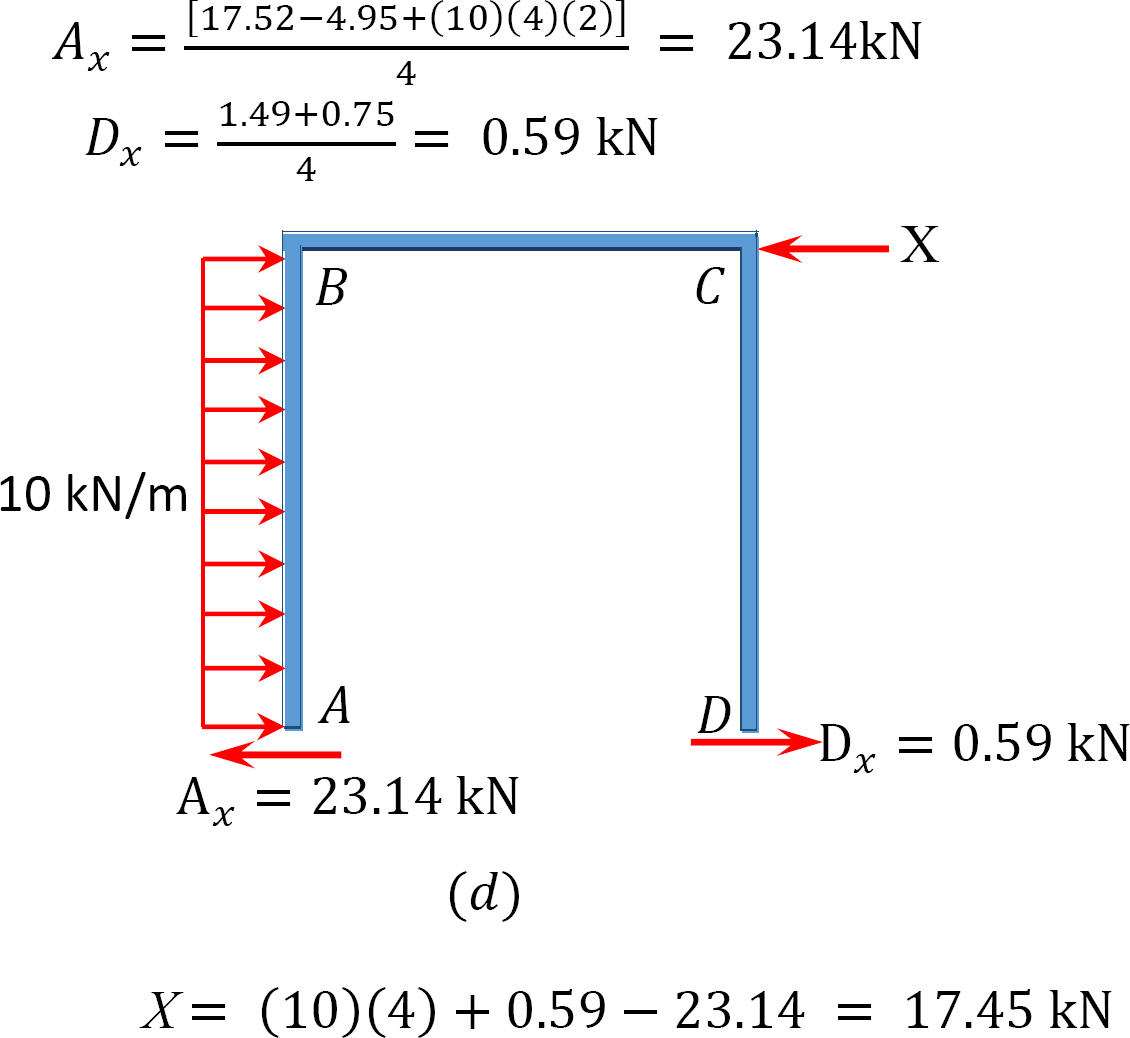
analys av ram med sido-sway.
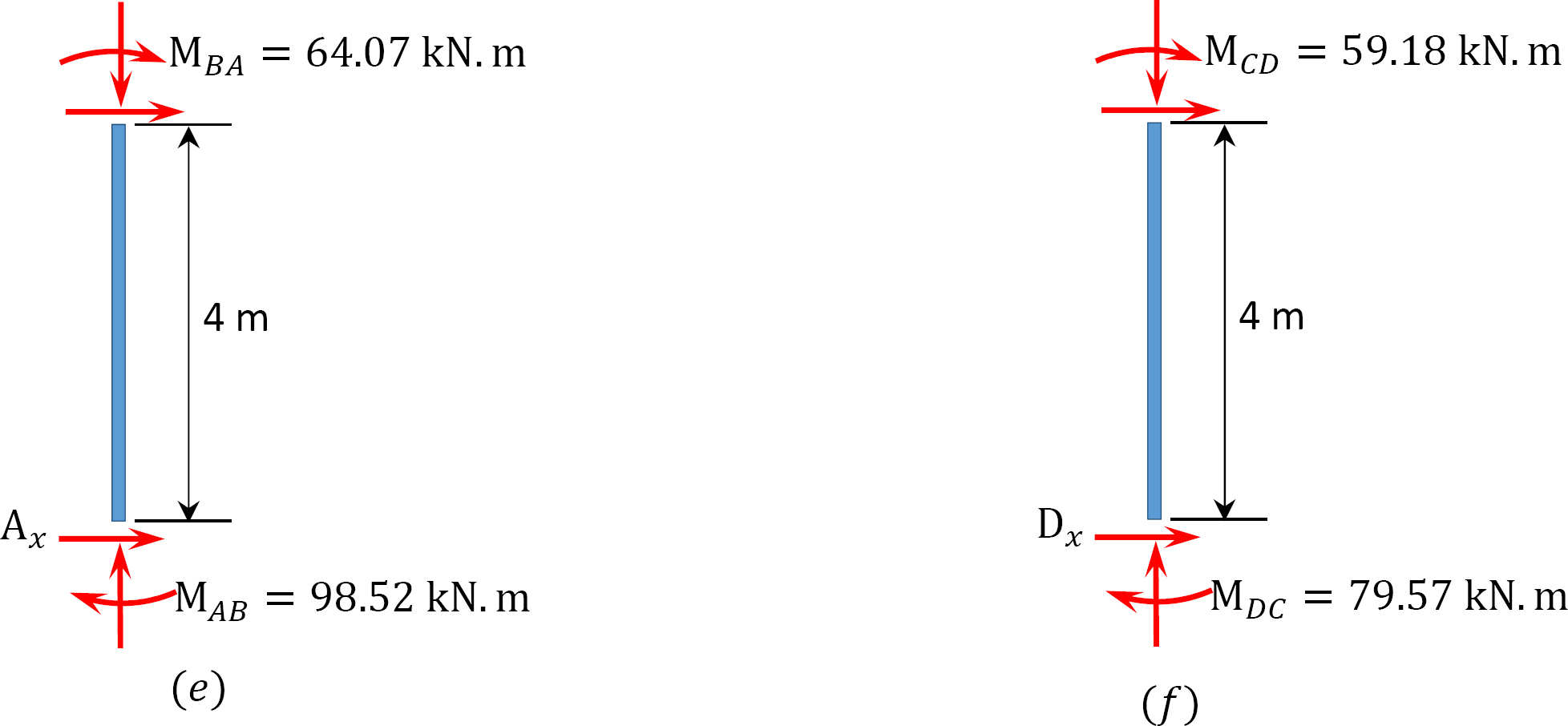

sista slutmomentet.
MAB = -17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = -4.95 + (-64.07)(0.23) = -19.69 kN. m
MCB = -1.49 + (-59.18)(0.23) = -15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
kapitelöversikt
Momentfördelningsmetod för analys av obestämda strukturer: momentfördelningsmetoden för analys är en ungefärlig analysmetod. Graden av noggrannhet är beroende av antalet iterationer. I denna metod antas att alla fogar i en struktur är tillfälligt låsta eller klämda och därmed förhindras från eventuell rotation. Belastningar appliceras på medlemmarna, och de stunder som utvecklats vid medlemmens ändar på grund av fixitet bestäms. Fogar i strukturen låses sedan upp successivt, och det obalanserade ögonblicket vid varje led distribueras till medlemmar som möts vid den leden. Överför ögonblick vid medlemmarnas yttersta ändar bestäms, och balanseringsprocessen fortsätter tills önskad nivå av noggrannhet. Medlemmarnas slutmoment bestäms genom att lägga till det fasta slutmomentet, det distribuerade ögonblicket och överföringsmomentet. När medlemmarnas slutmoment är bestämda blir strukturen bestämd.
Övningsproblem
12.1 Använd momentfördelningsmetoden för att beräkna slutmomentet för medlemmar av strålarna som visas i Figur P12.1 till figur P12.12 och rita böjmomentet och skjuvkraftsdiagrammen. EI = konstant.
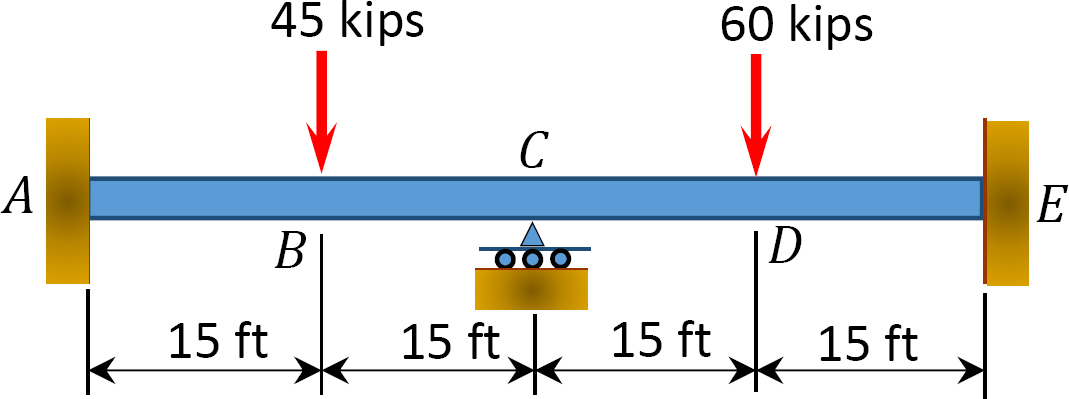
Fig. P12. 1. Balk.
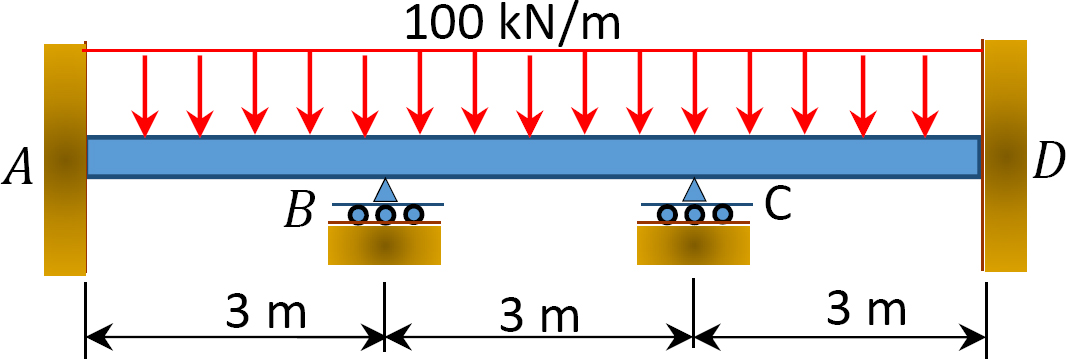
Fig. P12. 2. Balk.
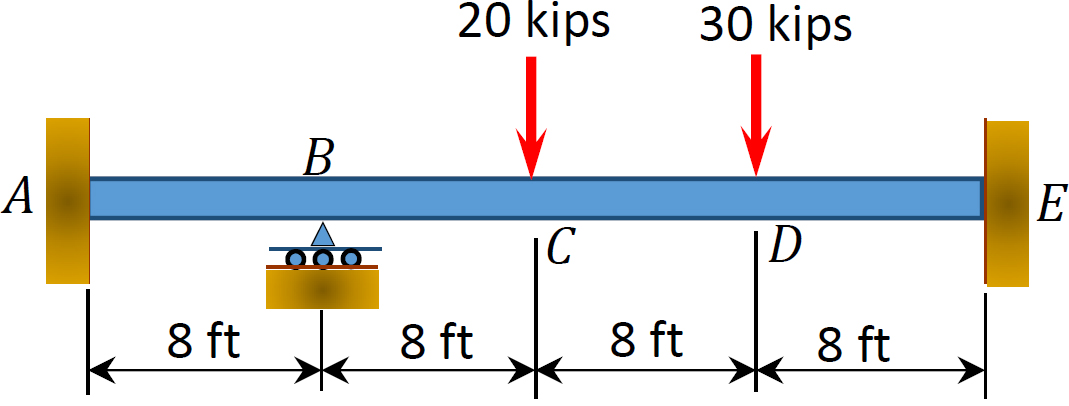
Fig. P12. 3. Balk.
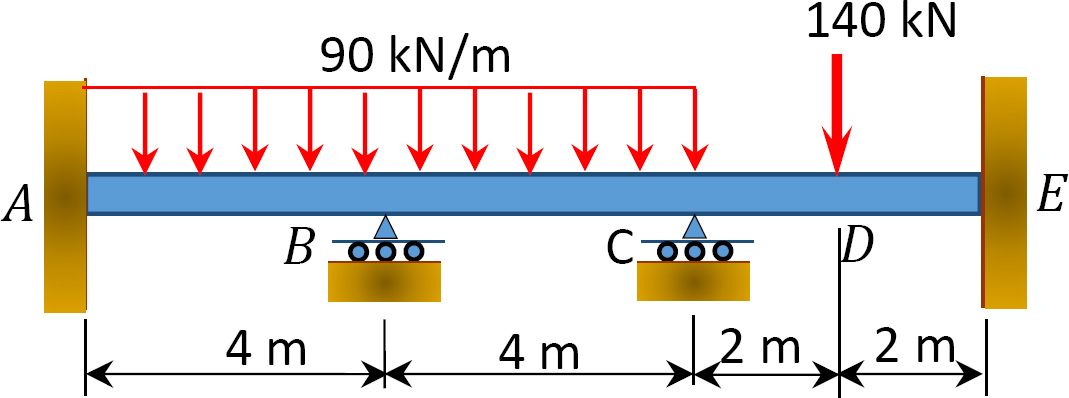
Fig. P12. 4. Balk.
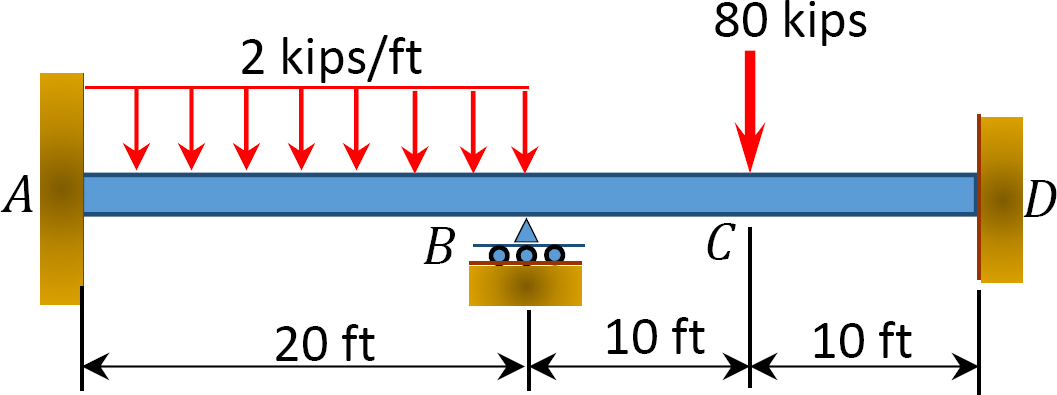
Fig. P12. 5. Balk.
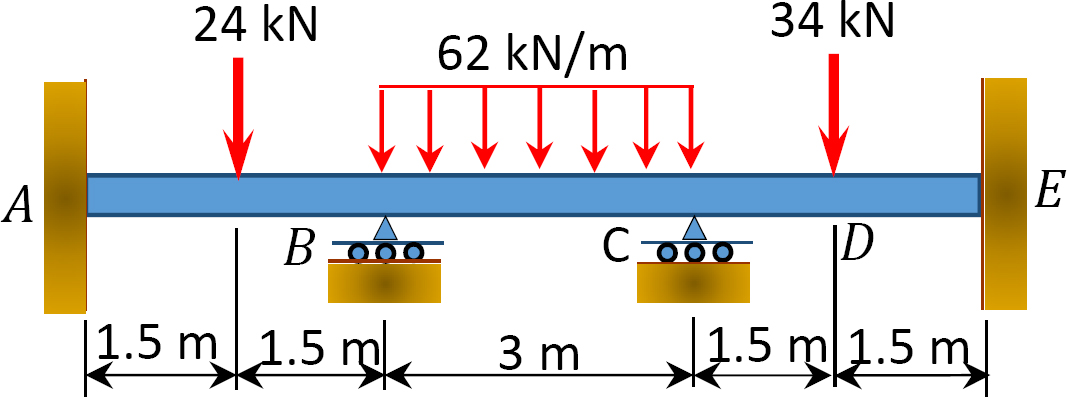
Fig. P12. 6. Balk.
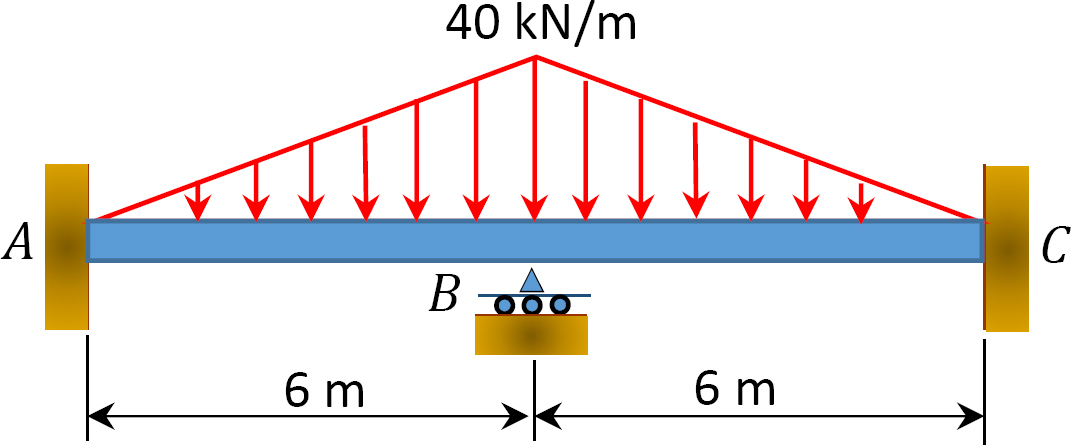
Fig. P12. 7. Balk.
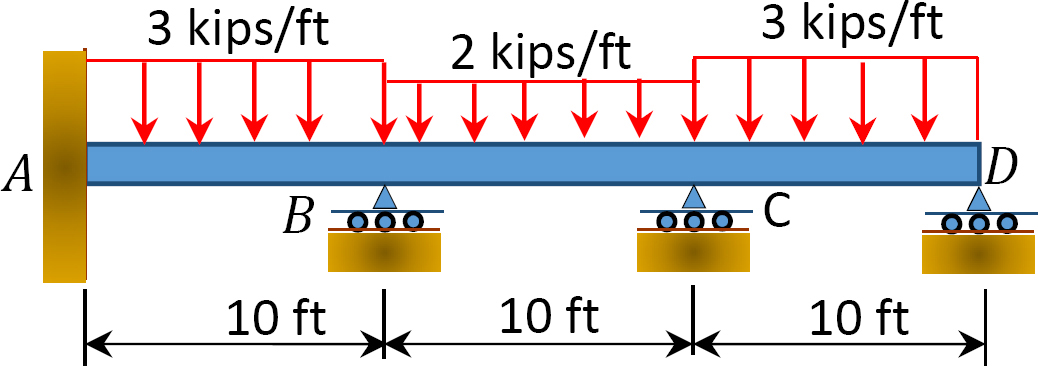
Fig. P12. 8. Balk.
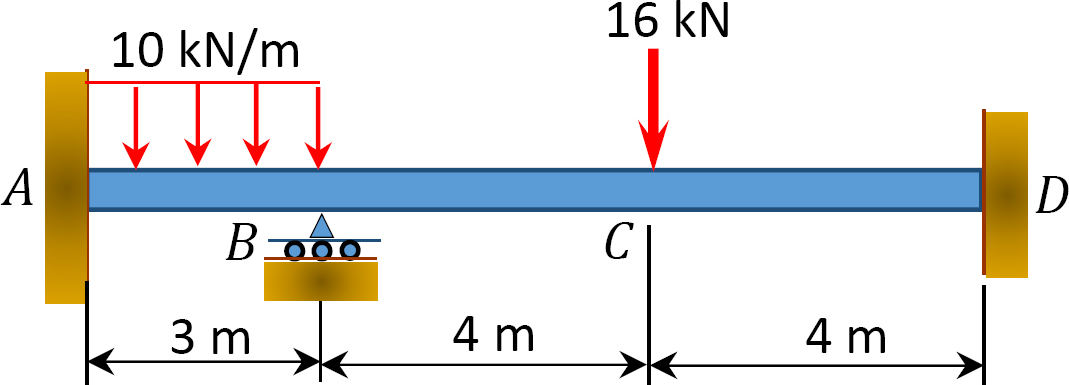
Fig. P12. 9. Balk.
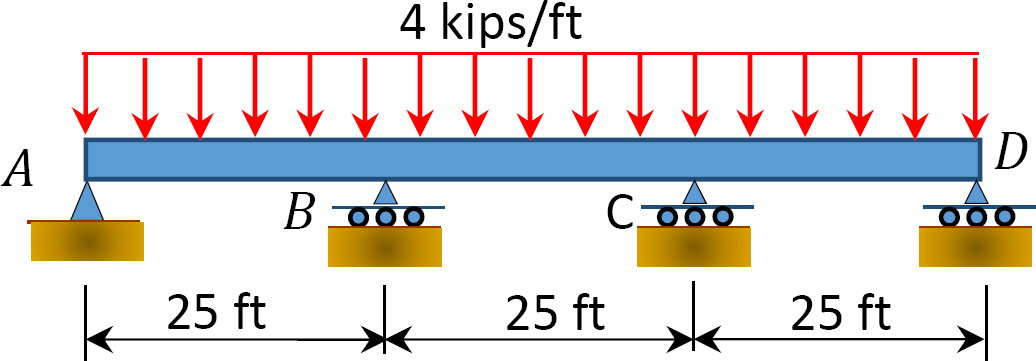
Fig. P12. 10. Balk.
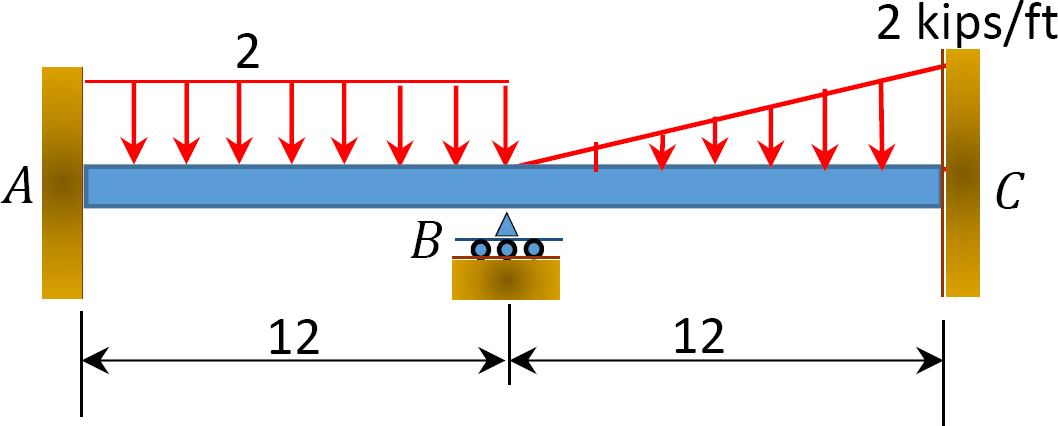
Fig. P12. 11. Balk.
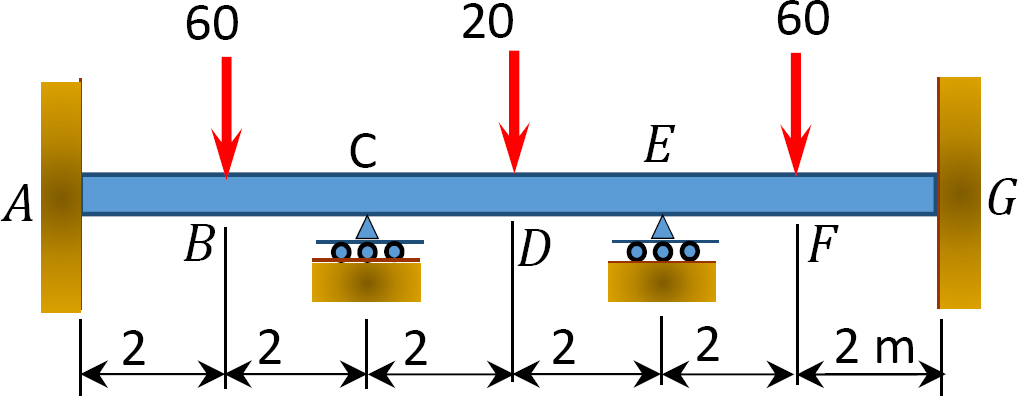
Fig. P12. 12. Balk.
12.2 använd momentfördelningsmetoden för att beräkna slutmomentet för medlemmarna i ramarna som visas i Figur P12.13 till figur 12.20 och rita böjmomentet och skjuvkraftsdiagrammen. EI = konstant.
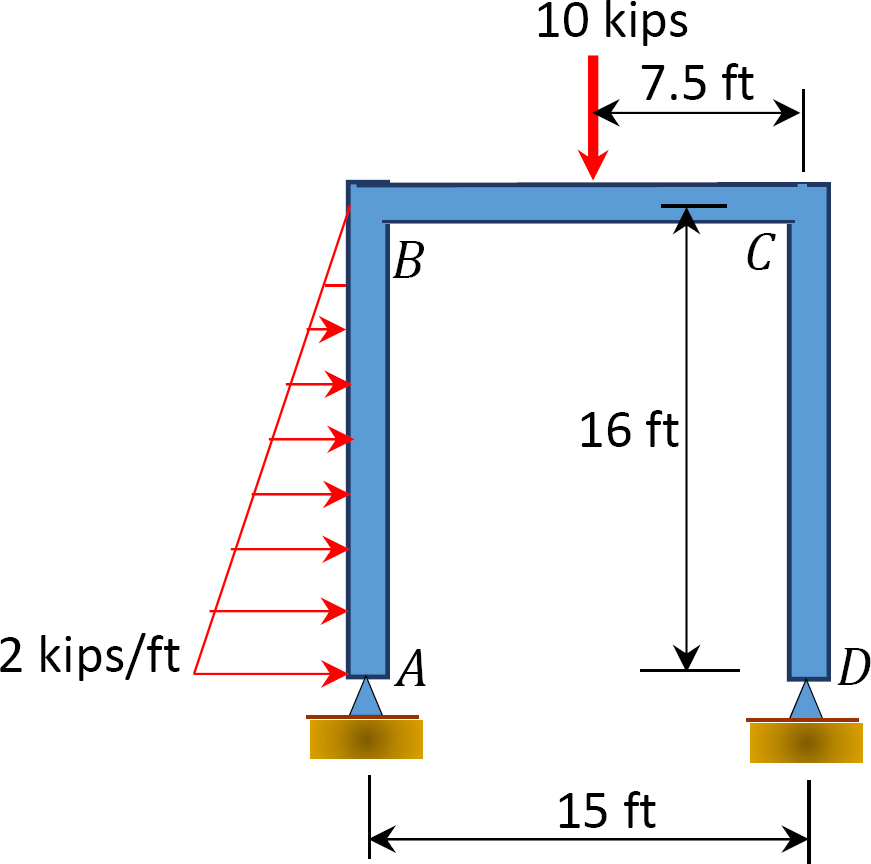
Fig. P12. 13. Ram.
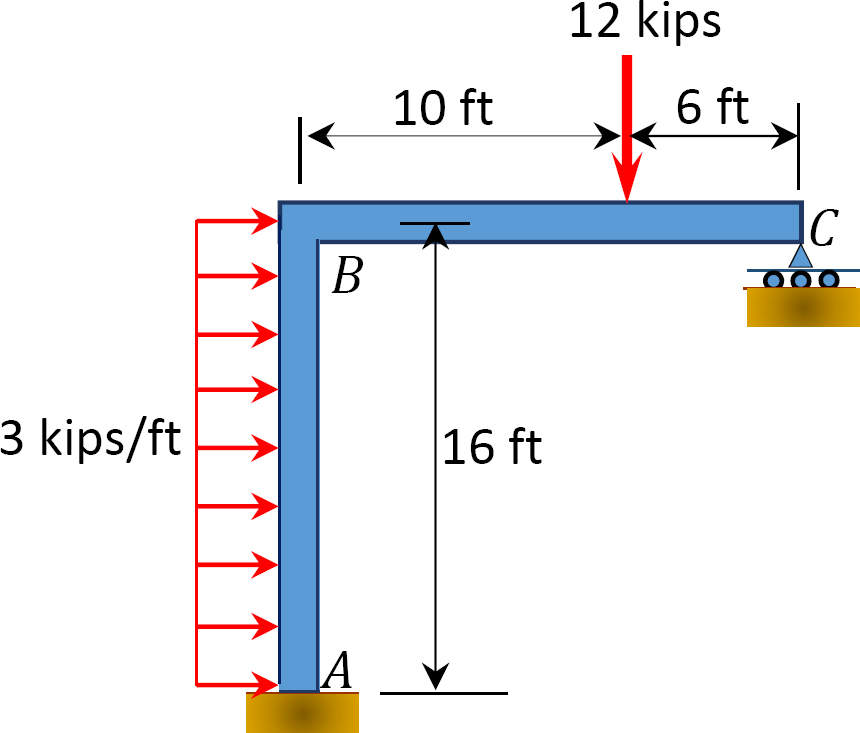
Fig. P12. 14. Ram.
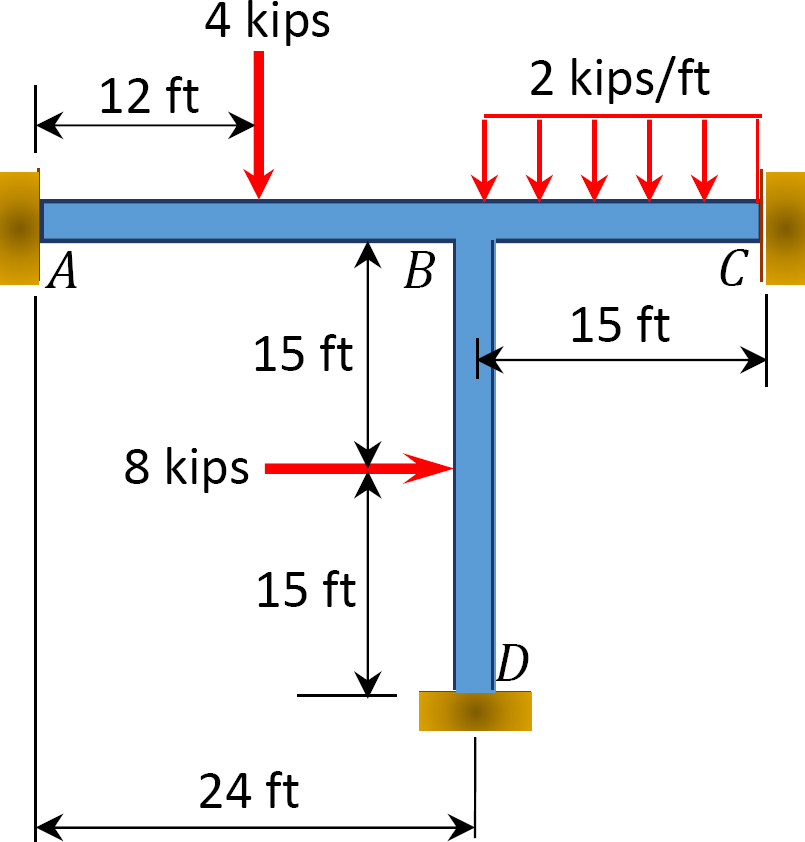
Fig. P12. 15. Ram.
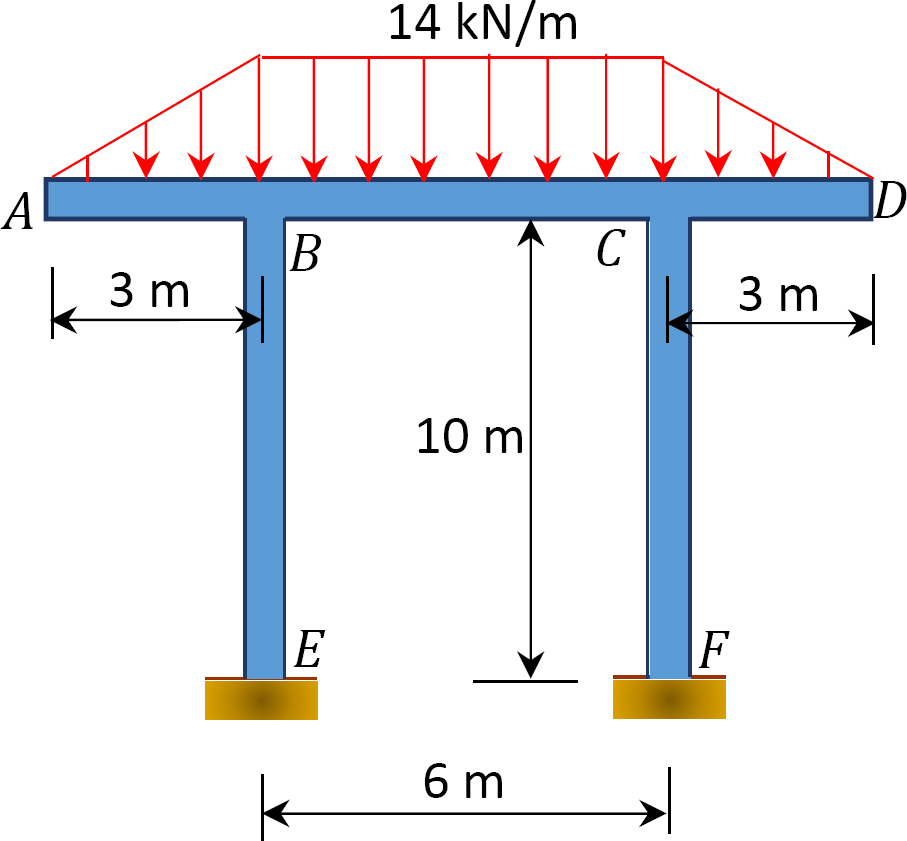
Fig. P12.16. Frame.
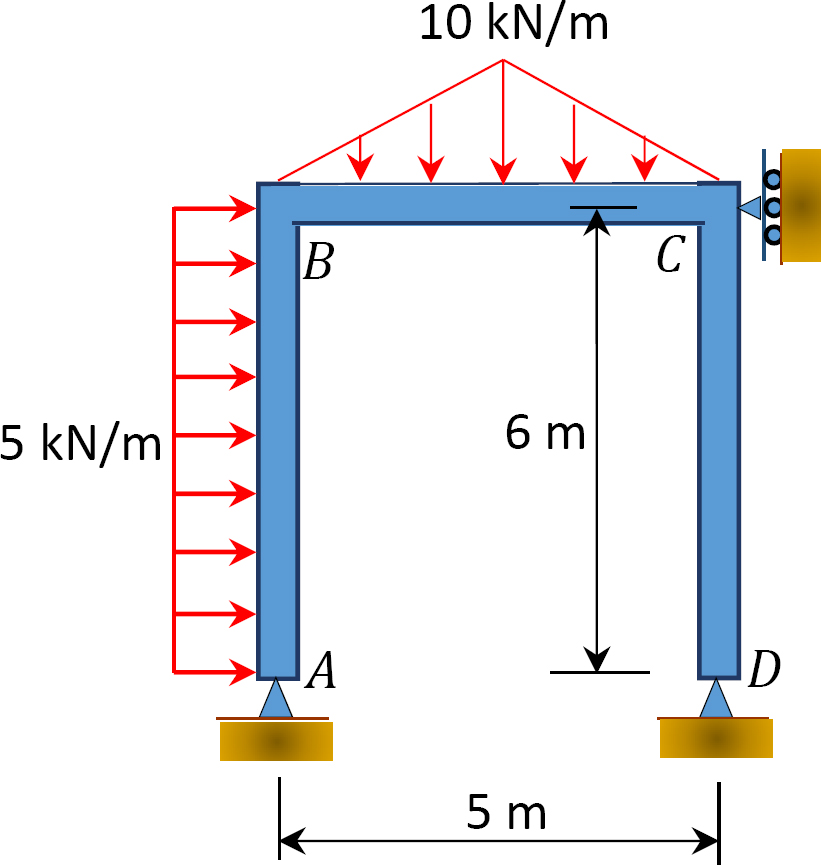
Fig. P12.17. Frame.
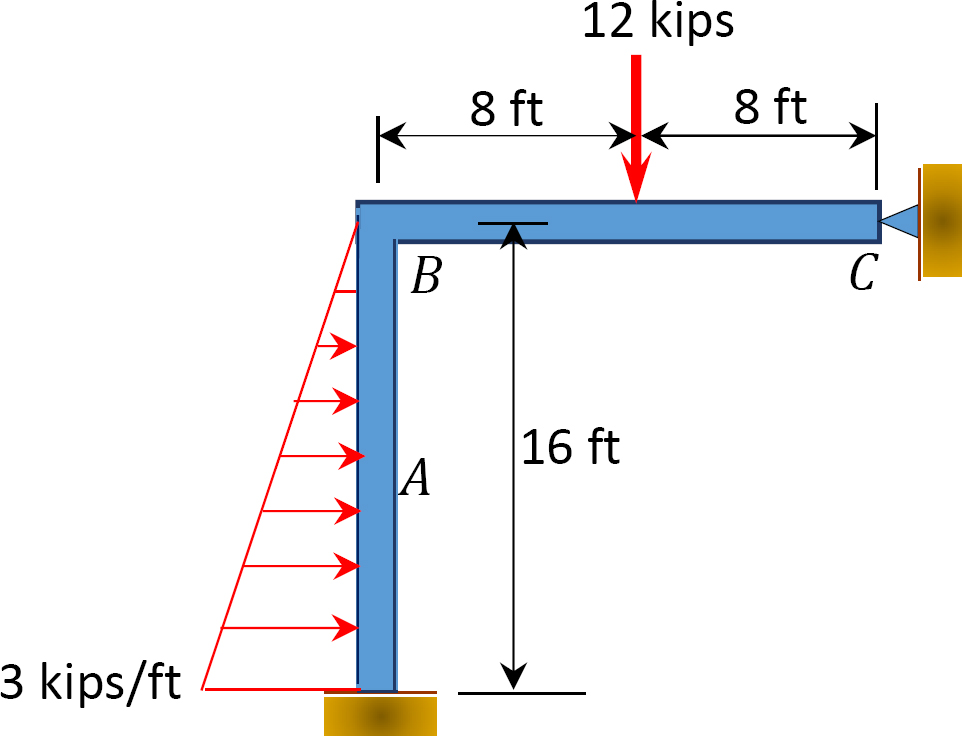
Fig. P12.18. Frame.
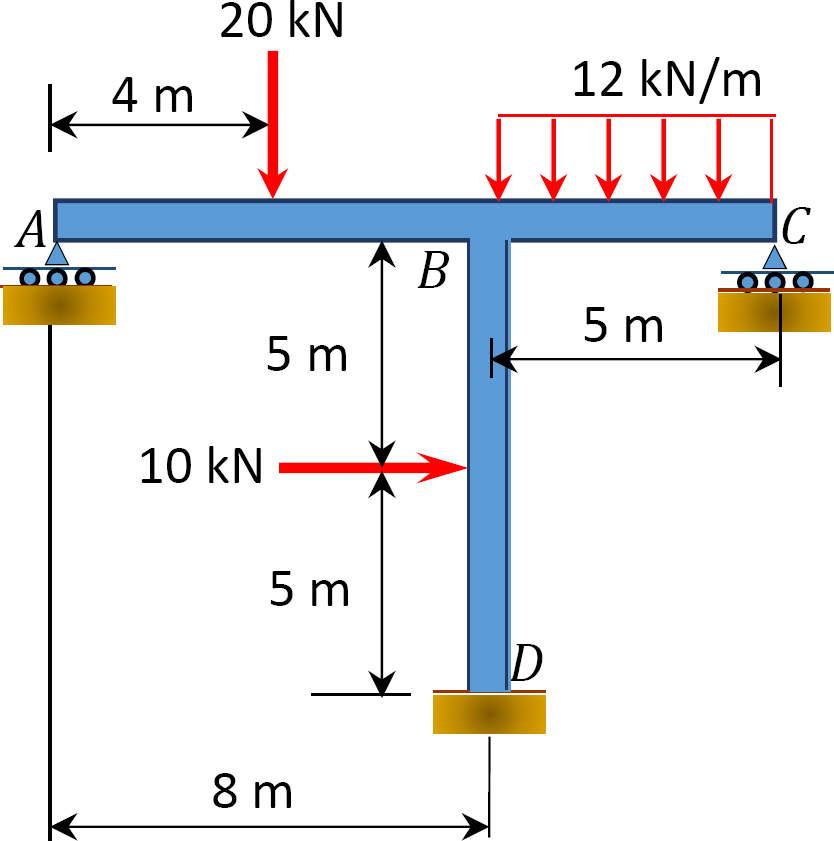
Fig. P12.19. Frame.
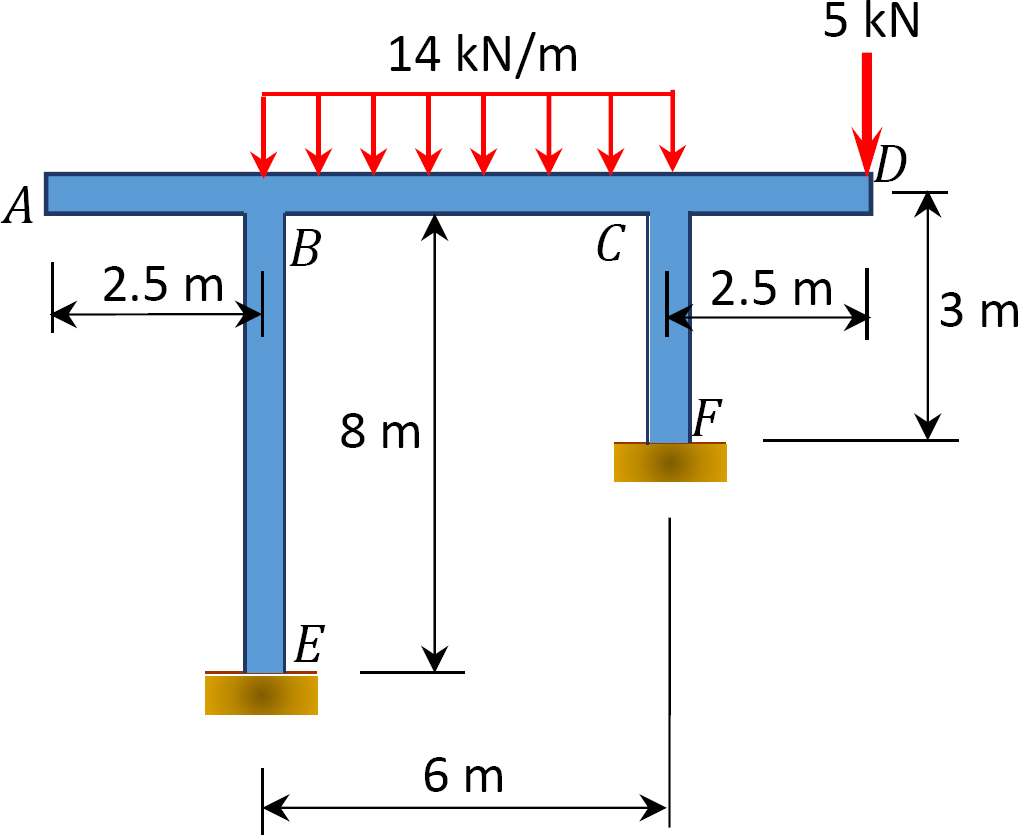
Fig. P12.20. Frame.