Todos os engenheiros estruturais uso de Saint-Venant princípio, seja ativamente ou inconscientemente. Você pode encontrar várias formulações deste princípio na maioria dos livros de mecânica estrutural, mas seu significado exato não é óbvio. O princípio de Saint-Venant nos diz que a distribuição exata de uma carga não é importante longe da região carregada, desde que os resultados da carga sejam corretos. Neste post, vamos explorar o princípio de Saint-Venant, particularmente no contexto da análise de elementos finitos (FE).
the History of Saint-Venant’s Principle
the French scientist Barré de Saint-Venant formulated his famous principle in 1855, but it was more of an observation than a strict mathematical statement:
“Se as forças que atuam sobre uma pequena parte da superfície de um corpo elástico são substituídos por outro estaticamente equivalente do sistema de forças que atuam sobre a mesma porção da superfície, esta redistribuição de carga produz alterações substanciais no salienta localmente, mas tem um efeito insignificante sobre as tensões nas distâncias que são grandes em comparação com as dimensões lineares, de superfície na qual as forças são alterados.”
B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Retrato de Saint-Venant. Imagem de domínio público, via Wikimedia Commons.Muitas grandes mentes dentro do campo da mecânica aplicada — Boussinesq, Love, von Mises, Toupin e outros — estavam envolvidas em afirmar o princípio de Saint-Venant de uma forma mais exata e fornecendo provas matemáticas para ele. Ao que parece, isto é bastante difícil para casos mais gerais, e a investigação sobre o tema ainda está em curso. (A argumentação tem sido, por vezes, bastante vívida.)
exemplo simples: analisar tensões a uma distância
vamos começar com algo bastante simples: uma placa rectangular fina com um orifício circular a alguma distância da aresta carregada, que está a ser puxada axialmente. Se estamos interessados na concentração de tensão no buraco, então quão importante é a distribuição de carga real?
três tipos de carga diferentes são aplicados no limite mais à direita:
- Um axial constante estresse de 100 MPa
- Uma parabólica simétrica distribuição de tensão com amplitude de pico de 150 MPa
- Um centrado no ponto de carga com a mesma resultante como os dois anteriores, casos de carga
Como visto nos grácos abaixo, a distribuição de tensão no buraco não é afetado pela forma como a carga é aplicada. A chave aqui é, claro, que o buraco está suficientemente longe da carga.

von Mises stress contours for the three load cases.Outra forma de visualizar este cenário é usando setas de estresse principais. Tal enredo enfatiza o campo de estresse como um fluxo e dá um bom sentimento para a redistribuição.
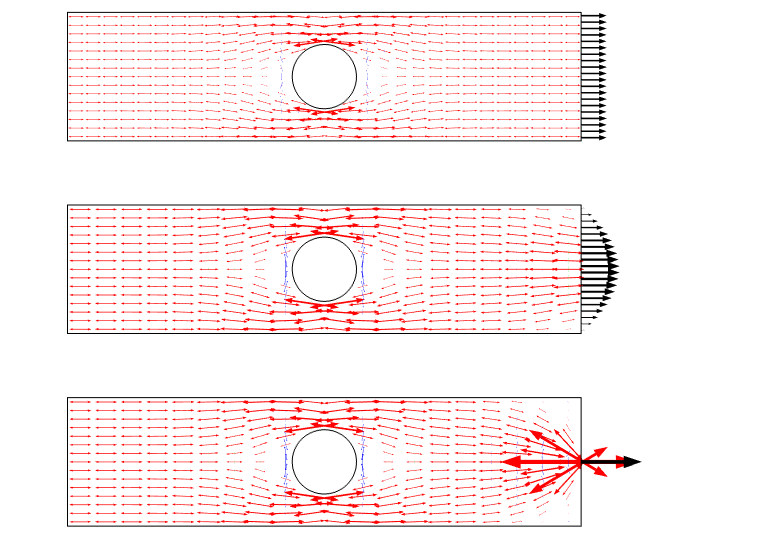
principal parcela de esforço para os três casos de carga. Note que há uma singularidade quando uma carga pontual é usada.
graficando a tensão ao longo de uma linha, podemos ver que todos os três casos convergem uns para os outros a uma distância da aresta, que é aproximadamente igual à largura da placa.
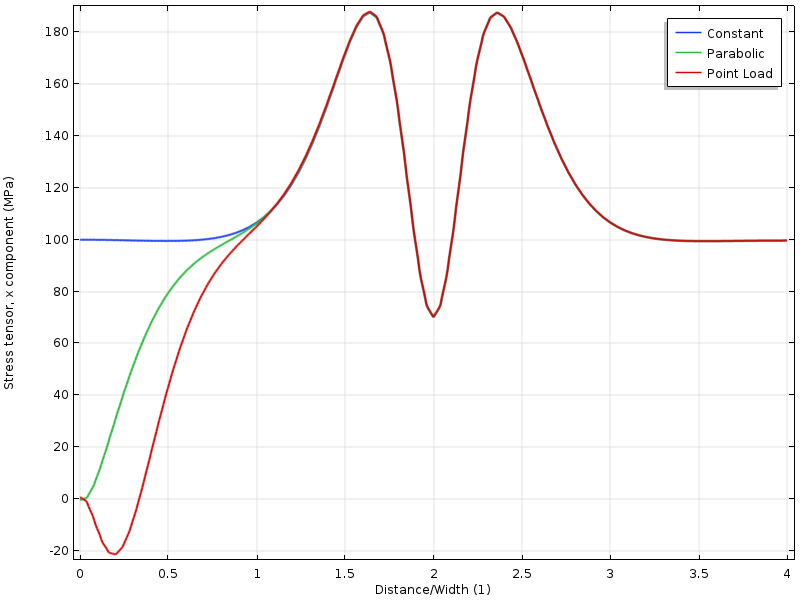
tensão ao longo do bordo superior em função da distância do limite carregado. A distância é normalizada pela largura da placa.Se o buraco for movido para mais perto do limite carregado, teremos outra situação. O estado de tensão em torno do buraco agora depende da distribuição de carga. Mas ainda mais interessante é que a distância para onde os três campos de tensão concordam agora é duas vezes mais longe do limite carregado. A aplicação do princípio de Saint-Venant requer que as tensões sejam livres de redistribuir. Neste caso, essa redistribuição é parcialmente bloqueada pelo buraco.
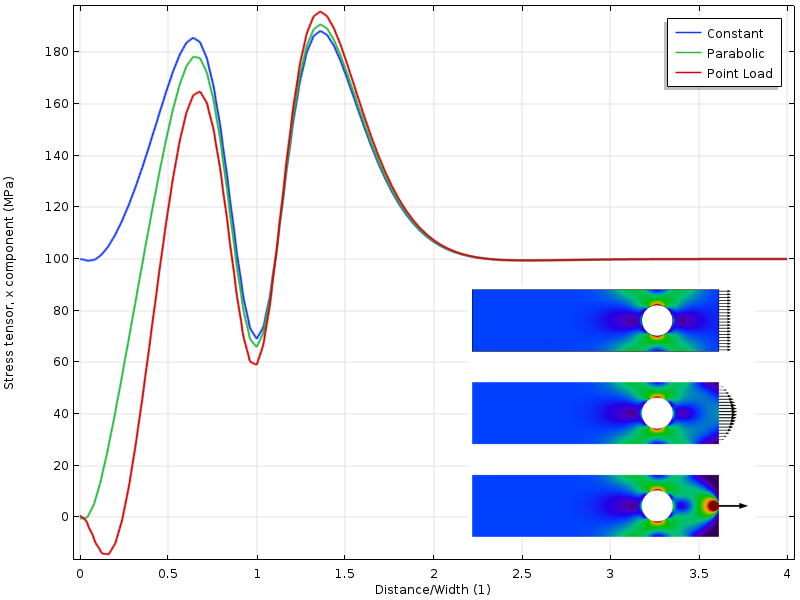
tensão ao longo da borda superior com o buraco mais próximo do limite carregado.
Note que o princípio de Saint-Venant nos diz que não há diferença no estado de estresse a uma distância que é da ordem da dimensão linear da área carregada. A área carregada a tomar em consideração, no entanto, pode não ser a área efectivamente carregada! Esta afirmação pode parecer estranha, mas pense desta forma: quando o buraco está longe, Podemos calcular o Fator de concentração de estresse usando um manual (o meu diz 4.32) ao invés de uma solução FE. A abordagem do manual contém uma suposição implícita de que a carga está uniformemente distribuída como no primeiro caso de carga. Assim, mesmo se a carga real foi aplicada a apenas uma pequena parte do limite, a distância crítica nesse caso está relacionada com o tamanho do limite inteiro.
ao resolver o problema usando o método do elemento finito (FEM), então o buraco pode ser arbitrariamente próximo à carga. O que define o limite é que do ponto de vista físico, a distribuição de carga está bem definida. Assim que fazemos suposições sobre redistribuição, no entanto, há uma suposição implícita sobre a distribuição de carga, que pode diferir da atual.Até agora, dissemos que as tensões são as mesmas independentes dos detalhes da carga em alguma distância adequada. Uma vez que estamos lidando com elasticidade linear aqui, é sempre possível sobrepor casos de carga. Ao trabalhar com provas do princípio de Saint-Venant, é mais fácil formular um princípio ao longo destas linhas: as tensões causadas por um sistema de carga sem força resultante ou momento será pequeno a uma distância que é da mesma ordem de magnitude que o tamanho do limite carregado.Assim, estudamos o stress causado pela diferença entre os dois sistemas de carga com resultados iguais. A maioria das provas modernas são baseadas em estimativas do decaimento da densidade de energia da estirpe para um sistema de tal resultado nulo.Voltando ao problema acima, podemos calcular a diferença entre os casos de carga. Isso nos permite estudar o decaimento real da densidade de energia de tensão ou tensão para a diferença dos campos de tensão.
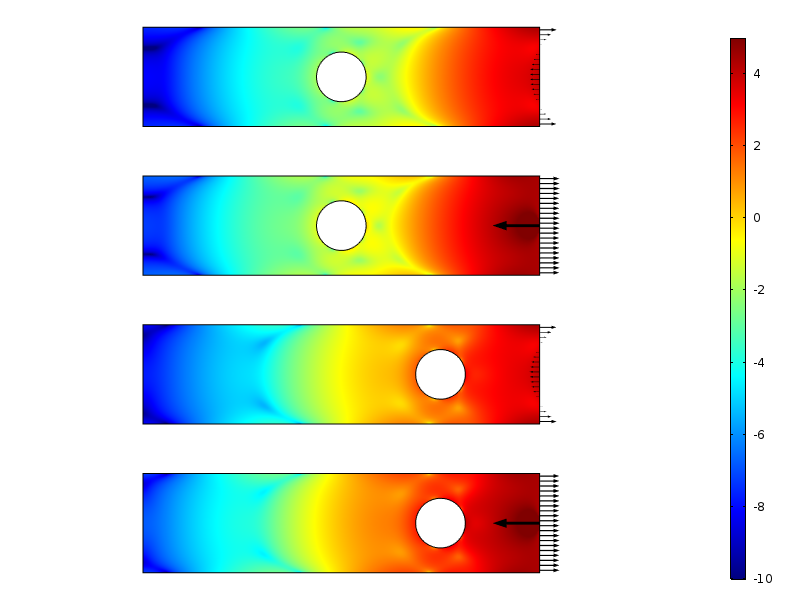
logaritmo da densidade de energia da estirpe para os casos de carga de resultado nulo.
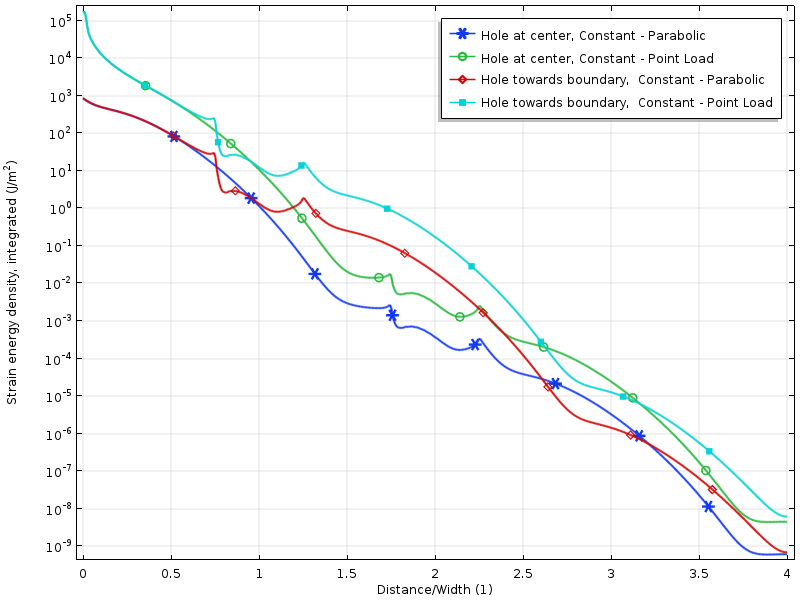
a densidade de energia da estirpe ao longo da placa para os casos de carga resultante zero. A energia é integrada ao longo da direção vertical, a fim de produzir uma quantidade que é apenas uma função da distância da carga.
o decaimento no logaritmo da densidade de energia da estirpe é mais ou menos linear com a distância do limite carregado. Isto está na verdade em linha com o que as provas modernas prevêem: um decaimento exponencial da densidade de energia da estirpe. Também podemos ver claramente como o buraco reduz temporariamente a taxa de decaimento.
aplicando o princípio de Saint-Venant a estruturas finas
para estruturas mais finas como conchas, vigas e tresses, é bem conhecido que o princípio de Saint-Venant não pode ser aplicado da mesma forma que para um objeto mais “sólido”. Os distúrbios percorrem distâncias mais longas do que esperamos, porque os caminhos de carga numa estrutura fina são muito mais limitados. Este é o mesmo fenômeno que vemos com o buraco no exemplo acima, mas mais proeminente.
aqui, nós estudamos um feixe com uma seção transversal padrão IPE100. A extremidade do feixe é submetida a uma tensão axial, com uma amplitude que tem uma distribuição linear em ambas as direções transversais.Um exemplo de aplicação do princípio de Saint-Venant a estruturas finas como as vigas.
distribuição de carga, exibida como contornos e setas.
devido às simetrias, esta carga tem uma força resultante zero, bem como um momento zero em todos os eixos. A altura da secção transversal é de 100 mm, pelo que, se for aplicável a forma-padrão do princípio de Saint-Venant, as tensões devem ser pequenas a uma distância de aproximadamente 100 mm da secção final.
um modelo para analisar a tensão equivalente em um feixe.Tensão equivalente no feixe . O contorno vermelho indica onde a tensão é inferior a 5% do Pico aplicado.
acontece que para que a tensão seja inferior a 5% do Pico aplicado, temos que viajar quase um metro ao longo do feixe. Assim, a redistribuição da carga é muito menos eficiente aqui, uma vez que o equilíbrio entre as flanges superior e inferior requer transferência de momento através da teia fina.Se você está familiarizado com a teoria da torção não-uniforme de vigas (isto é, teoria de deformação ou teoria de Vlasov), você reconhecerá que a carga aplicada tem um bimomente significativo. O bimomente é uma quantidade transversal com a dimensão física da força X length2.
Talvez (isso é só a minha especulação), um eficiente Saint-Venant princípio, para este caso deve exigir não apenas força e momento, mas também um bimoment de zero. Isto pode ser conseguido adicionando cargas de quatro pontos que fornecem um bimomente de contra-ação. O resultado dessa análise é mostrado abaixo.
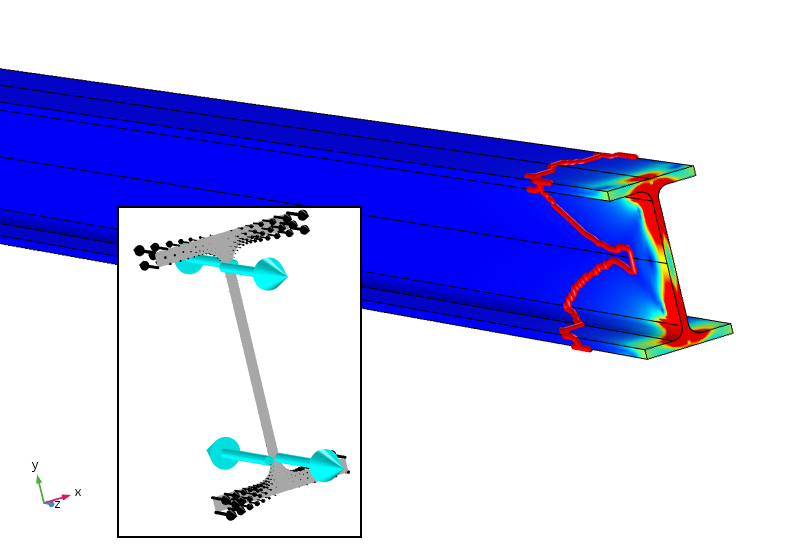
tensão equivalente com cargas de quatro pontos que também fornecem uma bimomente zero. O contorno de tensão de 5% está agora muito mais próximo do limite carregado.
as cargas do ponto aplicadas, que não são colocadas de forma otimizada de propósito, dão tensões locais extremamente elevadas (na verdade singular). No entanto, a tensão cai muito mais rapidamente e é inferior a 5% após cerca de 100 mm. o limite de 5% ainda está em termos da carga distribuída aplicada, por isso não é ajustado para as novas tensões locais. A taxa de decaimento logarítmico da densidade de energia da estirpe é três vezes mais rápida após as cargas pontuais serem adicionadas.
princípio de Saint-Venant em Análise de Elementos Finitos
em alguns casos, você pode intuitivamente considerar o princípio de Saint-Venant para ser aplicável ao problema descretizado FE. Aqui, olhamos para cargas distribuídas e malhas não-conformantes.
cargas distribuídas
no modelo FE, as cargas são sempre aplicadas nos nós de malha, embora você as especifique como uma carga de contorno contínuo. A carga é distribuída internamente para os nós do elemento usando o princípio do trabalho virtual, como mostrado no exemplo abaixo.
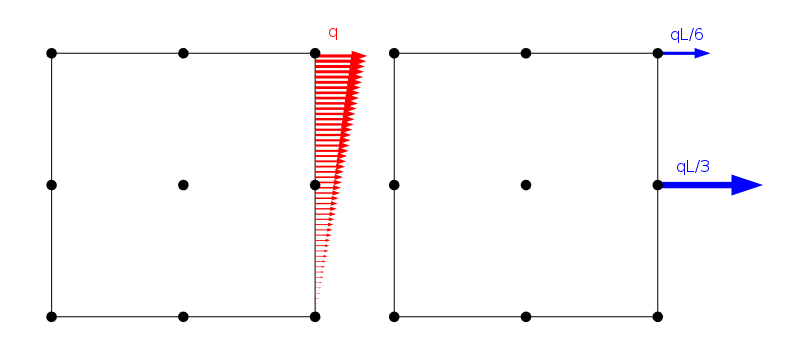
uma carga linearmente distribuída e como ela é aplicada nos nós de um elemento Lagrange de segunda ordem com comprimento lateral L.
existe, no entanto, um número infinito de distribuições de carga que dão as mesmas cargas nodal, desde que eles compartilham a mesma força resultante e momento. Obviamente, a solução para o problema do elemento finito é a mesma para todos esses casos. De acordo com o princípio de Saint-Venant, no entanto, podemos concluir que todas essas cargas devem dar essencialmente o mesmo campo de tensão assim que estivermos a alguma distância.
uma vez que o tamanho da área sobre a qual redistribuímos cargas é um elemento face, a dimensão linear após a qual não há diferença é essencialmente uma camada de elemento dentro da estrutura. Assim, a solução na camada externa de elementos pode não corresponder à carga real, mas mais adiante, corresponde.Como exemplo, podemos carregar uma placa retangular com uma carga limite que tem uma distribuição exponencial de stress. A tensão calculada com uma malha fina é mostrada abaixo.

contour plot of the axial stress distribution.Por causa do princípio de Saint-Venant, o campo de tensão é redistribuído para um estado de flexão puro a alguma distância da borda carregada, assim como esperamos. No entanto, este não é o objectivo da actual discussão. Em vez disso, investigamos a diferença entre a distribuição de stress acima, e o que obtemos com uma série de malhas grosseiras.
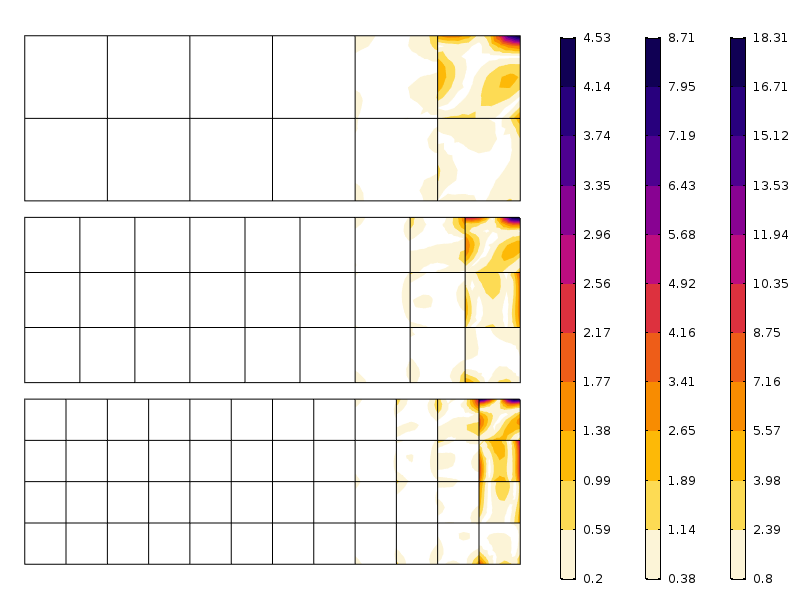
erro na tensão axial para três malhas diferentes. Repara nas diferentes escalas. Como esperado, o erro é menor quando a malha é mais fina.
como pode ser visto na figura, o erro diminui rapidamente após a primeira camada do elemento. O que vemos aqui é, na verdade, uma combinação de convergência de malha e a redistribuição de tensões implícitas pelo princípio de Saint-Venant.
Malha de não conformação
uma malha de não conformação ocorre quando as funções de forma em dois elementos conectados não coincidem. O caso mais comum é quando um conjunto é conectado usando pares de identidade e condições de continuidade. Para exemplificar isso, podemos estudar uma barra reta com uma malha intencionalmente não amatching. Com um simples caso de carga, como tensão uniaxial, é possível estudar os distúrbios de estresse causados pela transição.
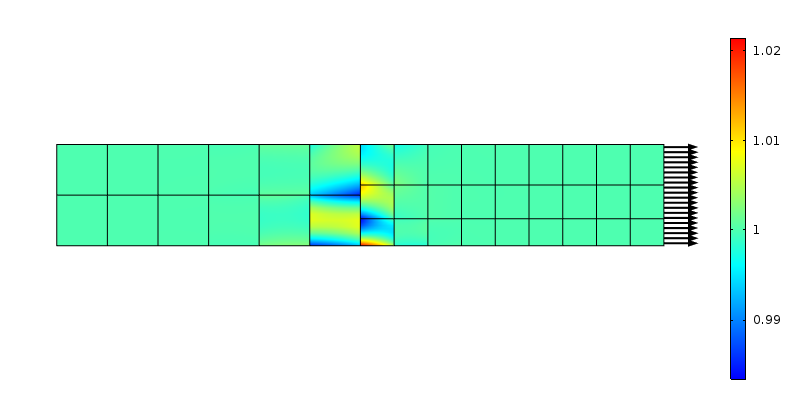
stress Axial at a nonconforming mesh transition. São utilizados elementos de segunda ordem.
as forças transmitidas pelos Nós nos dois lados não coincidem com a suposição de tensão constante. Mais uma vez, isso pode ser visto como uma redistribuição de carga local sobre uma área que é o tamanho do elemento. Usando o raciocínio de Saint-Venant, a perturbação deve desaparecer a uma distância “do tamanho de um elemento” da transição. Vamos investigar o que acontece se a malha for refinada na direcção axial.
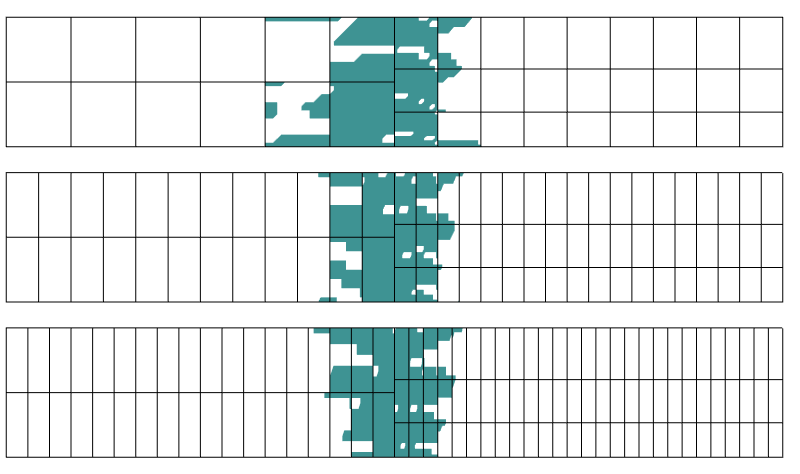
região com mais de 0, 1% de erro no stress. Três discretizações diferentes são usadas na direção axial.
acontece que a região de perturbação não é muito afetada pela discretização na direção perpendicular ao limite de transição. Isto é exatamente o que o princípio de Saint-Venant nos diz.Sem fazer uso do princípio de Saint-Venant, muitas análises estruturais são difíceis de realizar, simplesmente porque a distribuição detalhada da carga não é conhecida.
o princípio é formalmente válido apenas para materiais elásticos lineares. Na prática, também a usamos intuitivamente diariamente para outras situações. Se, por exemplo, o material na “placa com um buraco” exemplo fosse elastoplástico, esperaríamos que as duas cargas distribuídas dessem resultados equivalentes, desde que a tensão de rendimento esteja acima da tensão aplicada na fronteira para que haja apenas deformação plástica em torno do buraco. A carga do ponto, no entanto, sempre dá uma solução diferente, uma vez que o material rende em torno do ponto carregado. Para uma discussão mais longa, leia este post sobre singularidades no point loads.
próximas etapas
Saiba mais sobre o uso do software Multiphysics ® COMSOL para a FEA.
Further Reading
- Y. C. Fung and P. Tong, Classical and Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.