från ovanstående diagram kedja av klassificerare visas. Det liknar nästan’ LinkedList ’ datastruktur. Y1, Y2..Y DB är svarsvariablerna för varje klassificerare (det kommer att vara 0 eller 1). Svar från alla tidigare klassificerare(utom 1: a) såddas in i nästa klassificerare och dessa blir funktioner tillsammans med originalinmatningsfunktioner (f1..f.
i allmänhet kommer klassificerare K att byggas med komplett inmatningsfunktionsuppsättning: f1, f2,..f ci,Y1,Y2,..Yᴷ⁻1
Nu, här frågan kommer: ”Hur är det för klassificerare kedjan är beslutat ?”Det finns olika strategier för detta enligt nedan:
Ensemble of Classifier chains (ECC): Ensemblemodell för klassificering används här. Slumpmässigt urval av kedjor väljs och en ensemble byggs ovanpå detta. Förutspådd produktion kommer genom att tillämpa majoritetsröstningssystemet på ensembleutgångarna. Det är ganska samma som RandomForest classifier.
Monte-Carlo Klassificeringskedjor (MCC): Det gäller Monte-Carlo metod för optimal klassificerare sekvensgenerering.
det finns andra metoder som slumpmässig sökning eller beroende metoder för klassificerare, men inte särskilt vanligt i bruk.
utmatningen från varje klassificerare kommer att fångas som det binära Relevansschemat och bestämmer klassetiketter i slutet.
Label Power-set Scheme
det grundläggande begreppet binär relevans & Klassificeringskedjan är mer eller mindre densamma. Label power-set fungerar på ett annat sätt. Den betraktar varje kombination av etiketter i träningsdatasetet som en separat etikett. Till exempel, för en 3-Klass multi-label problem, 100, 001, 101, 111, etc kommer att betraktas som separata etiketter.
i allmänhet kan ett klassutrymme med dimension N, det kan finnas 2 kg antal totala möjliga etikettkombinationer.
så det sönderdelas inte i några delproblem, men det förutsäger direkt kombinationen av klassetiketter som helhet.
fördelar & nackdelar med varje schema
binär relevans är ett enkelt schema, lätt att implementera. Men det anser inte att etiketten är beroende av varandra och kan därför ofta misstolka dolda dataförhållanden.
klassificeringskedjan hanterar perfekt klassetikettrelationer. Speciellt för fall där vissa klassetiketter är undenetiketter till andra och förekomsten av en klassetikett är starkt beroende av andra etiketter(föräldra-barn-relationer i klassetiketter. Barn etikett kan uppstå iff förälder etikett finns). Men det här systemet är komplext och lider av högdimensionalitetsproblem om klassutrymmet är stort.
Label power-set fungerar bra för fall där ingen av olika kombinationer av klassetiketter är mindre. Det är mycket ett enkelt system jämfört med den binära relevansen & Klassificeringskedjan.
i alla fall krävs datauppsättningsförståelse innan man fattar ett beslut för ett visst system.
Noggrannhetsmått
i klassificeringsproblem med flera klasser eller binär enkel etikett ges absolut noggrannhet av förhållandet (antal datainstanser korrekt klassificerade / totalt antal datainstanser).
Låt oss se scenariot för multi-label-fallet med vårt exempeldataset. Om fråga med id 241465 klassificeras med etiketter: ’modellering’, ’central-limit-theorem’,’ frihetsgrader’, vad kan vi säga? Faktiska klassetiketter i datauppsättningen var ’statistisk betydelse’, ’modellering’, ’central-limit-teorem’, ’frihetsgrader’och’ falsk korrelation’. Varken det är helt fel förutsägelse eller det är helt rätt. Om vi går för traditionell korrekt vs total ratio baserad noggrannhet metrisk, definitivt kommer vi inte att kunna bedöma klassificerare. Vi behöver något för att bedöma den partiella korrektheten hos en multi-label klassificerare.
Hamming Loss Metric
istället för att räkna nej av korrekt klassificerad datainstans beräknar Hamming Loss förlust genererad i bitsträngen av klassetiketter under förutsägelse. Det gör XOR-operation mellan den ursprungliga binära strängen av klassetiketter och förutsagda klassetiketter för en datainstans och beräknar genomsnittet över datauppsättningen. Dess uttryck ges av
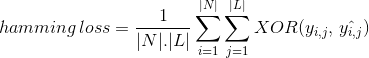
där
/ N / = antal datainstanser
/ L / = kardinalitet av klassutrymme
y: oc, oc = faktisk bit av klassetikett j i datainstansen i
^y: oc, oc = förutsagd bit av klassetikett j i datainstansen i
’hamming förlust’ värde varierar från 0 till 1. Eftersom det är en förlustmått är dess tolkning omvänd i naturen till skillnad från normalt noggrannhetsförhållande. Mindre värde av hamming förlust indikerar en bättre klassificerare.
delmängd noggrannhet
det finns vissa situationer där vi kan gå för ett absolut noggrannhetsförhållande där det är viktigt att mäta den exakta kombinationen av etikettförutsägelser. Det kan låta relevant i fallet ’Label power-set’. I scenariot med flera etiketter är det känt som delmängd noggrannhet.
bortsett från dessa två kan varje enskild binär klassificeringsnoggrannhet bedömas av andra traditionella mätvärden som noggrannhetsförhållande, F1-poäng, Precision, återkallelse, etc och ROC-kurvor.
det här handlar om teoretisk modellering för klassificering med flera etiketter. Vi kommer att se en fallstudie med verkliga data i nästa artikel. Datautforskningskoden finns på Github.
nyligen jag skrivit en bok om ML (https://twitter.com/bpbonline/status/1256146448346988546)